Class 5

Balbharti Maharashtra State Board Class 5 Environmental Studies Solutions Chapter 4 Evolution Notes, Textbook Exercise Important Questions and Answers.

5th Standard EVS 2 Lesson Number 4 Question Answer Evolution Maharashtra Board

Std 5 EVS 2 Chapter 4 Question Answer

1. Fill in the blank.

Question a.
The first systematic explanation of the concept of evolution was given by ………………… .
Charles Darwin
Willard Libby
Louis Leakey
Answer:
The first systematic explanation of the concept of evolution was given by Charles Darwin.

Question b.
……………… are the most evolved animals among vertebrates
Aquatic animals
Amphibians
Mammals
Answer:
Mammals are the most evolved animals among vertebrates

2. Answer the question in one sentence.

What do we call animals which live in water and also on land?
Answer:
Amphibians live in water and also on land.

Where did the first humans appear?
Answer:
The first human appeared on the African continent.

3. Give reasons for the following:

Question a.
The species of dinosaurs, which were enormous in size, suddenly became extinct.
Answer:
The species of dinosaurs, which were enormous in size, suddenly became extinct, because –

1. According to Darwin, the species that cannot adapt to environmental changes become extinct in the process of evolution.
2. Some sudden natural disaster or environmental change is believed to be responsible for the extinction of enormous dinosaurs.

Question b.
In the course of time, a new species with characteristics different from the original species is created.
Answer:
In the process of survival by adapting to environmental changes, certain internal physical changes occur in some species of animals.
Over a period of time, these changes become inherited characteristics seen in all subsequent generations. Thus, in the course of time, a new species with characteristics different from the original species is created.

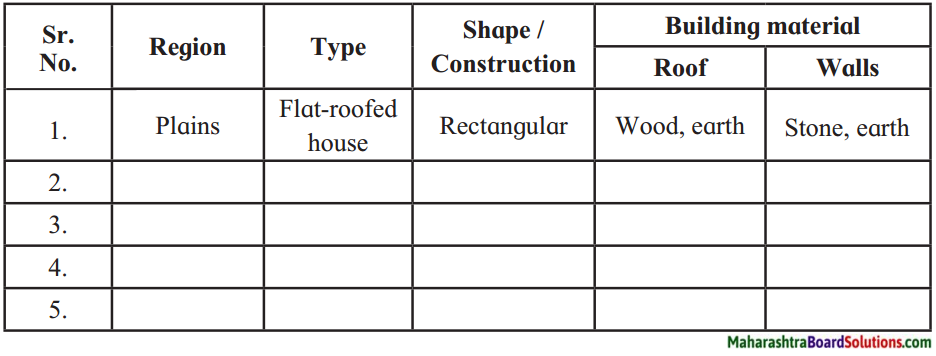
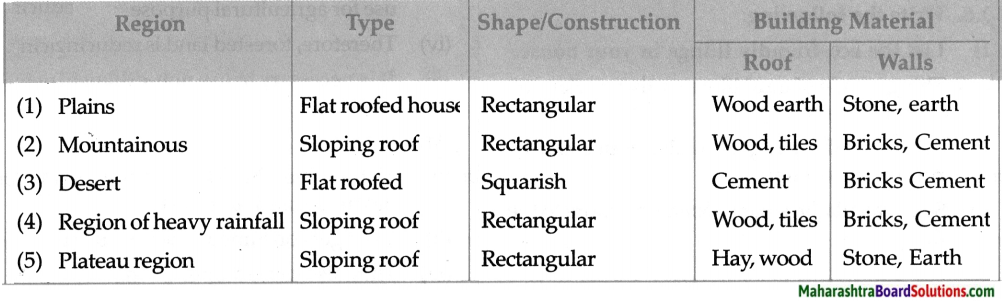
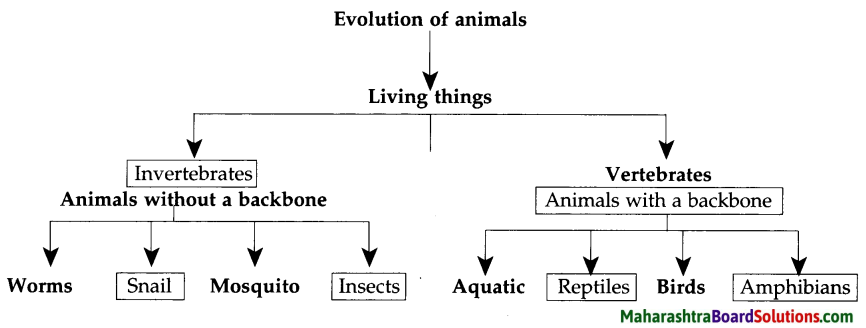
4. Fill in the blanks in the concept chart given below.

Question 1.
Fill in the blanks in the concept chart given below.

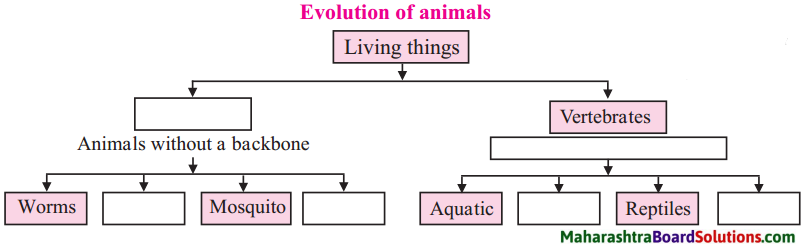
Answer:

Activity :

Question 1.
Make a model of a dinosaur.

Project :

Queston 1.
Collect pictures of invertebrates and vertebrates. Stick them in a notebook and write down their characteristics.

Environmental Studies Part 2 Standard 5th Solutions Chapter 4 Evolution Additional Important Questions and Answers

Fill in the blanks :

1. The word ……… generally means a gradual and continuous change.
2. In the process of survival by adapting to environmental changes, certain internal ……………. changes occur in some animals of a species.
3. Sometimes during evolution, the original species becomes ………..
4. During evolution, sometimes more than one species evolve from the ………….. species.
5. The first systematic explanation of the concept of evolution was given by …………
6. Species which are capable of adapting to environmental changes are able to …………
7. Species that cannot adapt to environmental changes become ………….
8. …………………… means a ‘terrible lizard’.
9. Some sudden natural………………….. is believed to be responsible for the extinction of Dinosaurs.
10. Fossils of dinosaurs with ………………… have been discovered
11. It is supposed that some species of two legged and winged dinosaurs evolved into …………..
12. The ……………………… organisms evolved gradually and various classes of plants and animals came into being.
13. Animals without a backbone are called ……………
14. Animals which have a backbone are called ……….
15. …………………….. are animals which live in water and also on land.
16. Animals which crawl are called ………………..
17. A mammals baby is …………………. on the mother’s milk for some time after birth.
18. The platypus and anteater are also considered as ……………
19. ………………… are somewhat like humans in appearance.
20. Apes mostly lived on ………….
21. Some ape species that evolved give rise to ………….. species.
22. The first human species is called the …………… man.
23. Primitive means ………………..

Answer:

1. evolution
2. physical
3. extinct
4. original
5. Charles Darwin
6. survive
7. extinct
8. Dinosaurs
9. disaster
10. wings
11. birds
12. multicellular
13. invertebrates
14. Vertebrates
15. Amphibians
16. Reptiles
17. fed
18. mammals
19. Apes
20. trees
21. human
22. primitive
23. the first

Match the columns :

Question 1.

Column ‘A’	Column ‘B’
1. Charles Darwin	a. a gradual and continuous change
2. Evolution	b. means ‘terrible lizard’
3. Dinosaur	c. gradually evolved into plants and animals
4. Multicellular	d. explained the concept of evolution
5. Invertebrates	e. frogs
6. Aquatic	f. snake
7. Amphibians	g. cow
8. Reptiles	h. snails
9. Mammals	i. fish

Answer:

Column ‘A’	Column ‘B’
1. Charles Darwin	d. explained the concept of evolution
2. Evolution	a. a gradual and continuous change
3. Dinosaur	b. means ‘terrible lizard’
4. Multicellular	c. gradually evolved into plants and animals
5. Invertebrates	e. frogs
6. Aquatic	i. fish
7. Amphibians	e. frogs
8. Reptiles	f. snake
9. Mammals	g. cow

Answer each question in one sentence:

Question 1.
What does evolution mean?
Answer:
Evolution means a gradual and continuous change

Question 2.
What changes occur in some species, during the process of survival?
Answer:
In the process of survival, by adapting to environmental changes, certain internal physical changes occur in some animals of a species.

Question 3.
What happens to the internal changes over a period of time?
Answer:
Over a period of time, these internal changes become inherited characteristics seen in all generations.

Question 4.
When does an original species become extinct?
Answer:
During evolution, a new species with characteristics different from the original may be created. Sometimes the original species becomes extinct.

Question 5.
Name the scientist who explained the concept of evolution.
Answer:
The first scientist to give us a systematic explanation of the concept of evolution was Charles Darwin

Question 6.
Which species are able to survive?
Answer:
Species which are capable of adapting to environmental changes are able to survive.

Question 7.
Which species become extinct in the process of evolution?
Answer:
The species that cannot adapt to environmental changes become extinct in the process of evolution

Question 8.
What does dinosaur mean?
Answer:
Dinosaur means a ‘terrible lizard’.

Question 9.
How did the dinosaurs suddenly become extinct?
Answer:
Some sudden natural disaster or environmental change is believed to be responsible for the extinction of dinosaurs.

Question 10.
Why do we suppose that some species of dinosaurs have evolved into birds?
Answer:
Fossils of dinosaurs with wings have been discovered. Hence, it is supposed that some species of two-legged and winged dinosaurs evolved into birds.

Question 11.
How did plants and animals come into being?
Answer:
Unicellular organisms gave rise to multicellular organisms which in turn gradually evolved into various classes of plants and animals.

Question 12.
What are invertebrates?
Answer:
Animals without a backbone are called ‘invertebrates’. For example: a snail.

Question 13.
What are vertebrates?
Answer:
Animals which have a backbone are called vertebrates. For example: A cow

Question 14.
What do we call animals which live in water and also on land?
Answer:
Animals which live in water and also on land are called ‘Amphibians’. For example: Frog

Question 15.
What are Aquatic animals?
Answer:
Living organisms that live only in water are called ‘Aquatic animals’. For example Fish

Question 16.
What are Reptiles?
Answer:
Animals which crawl are called Reptiles. For example: Snake

Question 17.
Which species are the most evolved animals among vertebrates?
Answer:
Mammals are the most evolved animals among vertebrates.

Question 18.
Where do apes mostly live?
Answer:
Apes mostly lived on trees.

Question 19.
How did the Human species evolve?
Answer:
Some ape species found in grasslands were forced to move around on ground. These species evolved gradually and in time gave rise to human species.

Question 20.
What is the first human species called?
Answer:
The first human species is called the ‘primitive man’.

Question 21.
What does primitive mean?
Answer:
‘Primitive’ means ‘the first’.

Question 22.
Who are Apes?
Answer:
Apes are somewhat like humans in appearance.

Give reasons for the following :

Question 1.
In the course of time, a new species with characteristics different from the original species is created. Answer:

1. In the process of survival by adapting to environmental changes, certain physical changes occur in some animals of a species.
2. These internal changes become inherited characteristics in the following generations.
3. Thus a new species with characteristics different from the original is created.

Question 2.
A frog is an amphibian.
Answer:

1. Animals which are able to live in water and also on land are called amphibiAnswer:
2. Therefore a frog is considered an amphibian.

Question 3.
The platypus and some species of anteaters are considered mammals.
Answer:

1. Platypus and some species of anteaters are exceptions to the characteristics of mammals.
2. Though they lay eggs, they suckle their young ones.
3. Therefore, they are considered mammals.

Answer the following questions in brief :

Question 1.
Explain the concept Evolution as stated by Charles Darwin.
Answer:

1. Charles Darwin explained ‘evolution’ in the following manner. In the process of survival by adapting to environmental changes, certain internal physical changes occur in some animals of a species.
2. Over a period of time, these internal changes become inherited characteristics of the following generation.
3. Thus a new evolved species with characteristics different from the original is created
4. Sometimes the original species become extinct.
5. Sometimes more than one species evolve from the original one.

Question 2.
Give the characteristics of mammals.
Answer:
The characteristics of most of the mammals are as follows:

1. Growth of the baby in the mother’s womb, sometime before birth.
2. The baby is fed on the mother’s milk for sometime after birth.

Question 3.
How and where did the human species evolve?
Answer:

1. Apes are somewhat like humans in appearance
2. They mostly lived on trees. Those species of apes which continued to live on trees retained their original ape like form.
3. Some ape species found in grasslands were forced to move on the ground.
4. These species evolved gradually, giving rise to the human species.
5. This happened first on the ‘African continent’.

Question 4.
How did various classes of plants and animals come into being?
Answer:

1. Life on earth began with unicellular organisms known as protozoa.
2. These unicellular organisms gave rise to multicellular living things.
3. Multicellular organisms evolved gradually and thus various classes of plants and animals came into being

Question 5.
How did birds form from dinosaurs?
Answer:

1. Dinosaurs became extinct because of some sudden natural disaster or environmental change
2. Fossils of dinosaurs with wings have been discovered
3. It is thus believed that some species of two legged and winged dinosaurs evolved into birds.

Question 6.
How many and which are the stages of evolution of animals?
Answer:
There are two stages of evolution of animals. They are:

1. Invertebrates: These are animals without a backbone.
2. Vertebrates: Animals which have a backbone are vertebrates. Aquatic animals, amphibians, birds, reptiles and mammals are all vertebrates.

Glossary :

1. gradual : taking place in stages over an extended period.
2. adapt : become adjusted to new conditions.
3. extinction : the process on state of becoming extinct.
4. species : group of living organisms
5. survival : the state or fact of surviving
6. inherited : receive or be left with something from predecessor

Class 5 Environmental Studies Questions and Answers:

• Chapter 1 What is History? Class 5 Questions And Answers
• Chapter 2 History and the Concept of ‘Time’ Class 5 Questions And Answers
• Chapter 3 Life on Earth Class 5 Questions And Answers
• Chapter 4 Evolution Class 5 Questions And Answers
• Chapter 5 Evolution of Mankind Class 5 Questions And Answers
• Chapter 6 Stone Age: Stone Tools Class 5 Questions And Answers
• Chapter 7 From Shelters to Village-settlements Class 5 Questions And Answers
• Chapter 8 Beginning of Settled Life Class 5 Questions And Answers
• Chapter 9 Settled Life and Urban Civilization Class 5 Questions And Answers
• Chapter 10 Historic Period Class 5 Questions And Answers

Balbharti Maharashtra State Board Class 5 Environmental Studies Solutions Chapter 11 Our Home and Environment Notes, Textbook Exercise Important Questions and Answers.

5th Standard EVS 1 Lesson Number 11 Question Answer Our Home and Environment Maharashtra Board

Std 5 EVS 1 Chapter 11 Question Answer

Use your brain power?

Question 1.
For what purpose do birds use their nest.
Answer:
Birds use their nest to lay their eggs and bring up their young ones.

what’s the solution?

Question 1.
What can we do to build houses without harming the environment?
Answer:
To build houses without harming the environment we can build permanent eco-friendly houses where we have good ventilation and use non exhaustible sources of energy.

1. Which of the following houses would be suitable in a mountainous region.

Question 1(a).
Which of the following houses would be suitable in a mountainous region. Put a ✓ in the appropriate box. Give reasons for selecting that house.
Answer:

This house is made of natural material available in the mountainous region, that is stone, it is strong to withstand mountainous winds.

Question 1(b).
What materials will you mainly use for building a multi-storeyed house?
(a) Mortar / Coal / Cement / Bricks
(b) Cement / Bricks / Cotton / Iron
(c) Iron / Cement / Mortar / Bricks
Answer:
Iron / Cement / Mortar / Bricks

2. Arrange the following considerations from the most to least important factor in house building:

Question 1.
Arrange the following considerations from the most to least important factor in house building:
(a) Luxury
(b) Structure
(c) Climate
Answer:
(a) Climate
(b) Structure
(c) Luxury

3. Write the following:

Question (a)
List the eco-friendly things in your house.
Answer:
Things made of mud like a earthen water pot. (Personal response)

Question (b)
Which of the gadgets in the house can be run on solar energy?
Answer:
Solar calculator, solar cooker. Add more to the list.

4. What are the types of pollution that can be observed at a construction site?

Question 1.
What are the types of pollution that can be observed at a construction site?
Answer:
The types of pollution that are seen at a construction site are air, water, soil and noise.

Make friends with maps!

Question 1.
Observe the map and the pictures and complete the following chart.

Answer:

Try this.

Question 1.
Complete the table given below regarding the original source.

Answer:

Environmental Studies Part 1 Standard 5th Solutions Chapter 11 Our Home and Environment Additional Important Questions and Answers

1. Fill in the blanks with the correct answers from the options given below:

Question 1.
A section of our society becomes homeless this is a ………………. problem.
(a) political
(b) social
(c) economic
Answer:
(b) social

Question 2.
Houses are built in large numbers due to increasing …………………. .
(a) population
(b) natural resources
(c) land
Answer:
(a) population

Question 3.
Glass is made from ……………… .
(a) soil
(b) limestone
(c) sand
Answer:
(c) sand

Question 4.
The city of Mumbai comprises of ………………….. islands.
(a) 6
(b) 7
(c) 8
Answer:
(b) 7

Question 5.
Land obtained by filling water bodies is called ………………….. .
(a) coastal lands
(b) reclaimed land
(c) marshy lands
Answer:
(b) reclaimed land

Question 6.
People build houses to suit the ………………… of their region.
(a) climate
(b) population
(c) situation
Answer:
(a) climate

Question 7.
Water, food, clothing and shelter are the basic …………………. of every human being.
(a) height
(b) weight
(c) needs
Answer:
(c) needs

Question 8.
The ……………….. of the world is increasing all the time.
(a) time
(b) population
(c) water
Answer:
(b) population

Question 9.
Shortage of …………………. land, leads to forest land being used for agriculture.
(a) agricultural
(b) geographical
(c) water
Answer:
(a) agricultural

Question 10.
Trees are …………………. in great numbers and forests are reduced.
(a) watered
(b) fellect
(c) grown
Answer:
(b) fellect

Question 11.
……………… is needed to produce construction material.
(a) Energy
(b) Humans
(c) Forest
Answer:
(a) Energy

Question 12.
Energy is produced using natural …………………. like coal, natural gas or mineral oil.
(a) trees
(b) fuels
(c) minerals
Answer:
(b) fuels

Question 13.
Burning of natural fuels leads to ……………… pollution.
(a) air
(b) water
(c) land
Answer:
(a) air

Question 14.
……………….. or ……………… energy are non-exhaustible sources of energy.
(a) air
(b) wind
(c) solar
Answer:
(b) wind & (c) solar

Name the following:

Question 1.
Government provides shelter for homeless in cities.
Answer:
Night shelters

Question 2.
Source from which cement is made.
Answer:
Limestone

Question 3.
Natural fuels
Answer:
Coal, natural gas, mineral oil.

Question 4.
Pollution caused by burning fuel.
Answer:
Air

Question 5.
Non exhaustible sources of energy.
Answer:
Solar energy, Wind energy and Biogas.

Question 6.
Two continents having water tourism
Answer:
Europe and North America.

Question 3.
Complete the co-relation:
Answer:
1. Mountainous region: Sloping roof:: Plain: Flat roof.
2. Cement: Limestone :: Bricks : Soil.
3. Coal: Exhaustible energy:: Solar energy: Non exhaustible energy.

Answer in one sentence:

Question 1.
What are the different things from which a house gives us protection?
Answer:
A house protects us from sun, wind, cold, rain and wild animals.

Question 2.
Where do homeless people live?
Answer:
Homeless people seek shelter at the roadside, on footpaths, under bridges, in tumble down buildings, in railway or bus stations and open grounds.

Question 3.
What is water tourism?
Answer:
In the coastal region, where under water shelters are built for tourist to view the sea bed and marine life is called water tourism.

Question 4.
Why are many people forced to be ‘homeless’?
Answer:
Many people are forced to be ‘homeless’ because they have insufficient or no means of livelihood.

Question 5.
What are the basic needs of every human being?
Answer:
Water, food, clothing and shelter are the basic needs of every human being.

Question 6.
Why are houses being built in large numbers?
Answer:
The population of the world is increasing all the time. That is why, houses are being built in large numbers.

Question 7.
What are the ill-effects of urbanization on land?
Answer:
Due to growing urbanization, land which was used for agriculture is now being used to build roads or to raise settlements. This leads to shortage of agricultural land.

Question 8.
Why are trees felled?
Answer:
Shortage of agricultural land leads man to cut down forests and use the land for agriculture.

Question 9.
From where do we get energy?
Answer:
We get energy by using natural fuels like coal, natural gas or mineral oil.

Question 10.
What ill-effects do we face when we use natural fuels?
Answer:
Using natural fuels not only leads to its exhaustion but also to air pollution.

Question 11.
Which are non-exhaustible sources of energy?
Answer:
Solar energy and wind energy are non- exhaustible sources of energy.

Give reasons:

Question 1.
Differences occur in the construction of houses according to the regions.
Answer:
There are differences in the construction of houses according to the region because :
1. People build houses to suit the climate of the region.
2. Using the natural resources that are available.

Question 2.
Many people are forced to be ‘homeless’.
Answer:
Many people are forced to be homeless because they have insufficient or no means of livelihood.

Question 3.
Houses are being built in large numbers.
Answer:
Houses are being built in large numbers because the population of the world is increasing all the time.

Question 4.
Forested land is reducing.
Answer:

1. Growing urbanization uses agricultural land to build roads and to raise settlements.
2. This leads to shortage of agricultural land.
3. So trees are felled in a great number to make use for agricultural purpose.
4. Therefore, forested land is reducing.

Question 5.
It is necessary to use non-exhaustible sources of energy.
Answer:

1. Natural fuels like coal, natural gas or mineral oil can be used only once.
2. They get consumed when we use them.
3. They also cause air pollution.
4. It takes lakhs of years for these resources to be formed in nature.
5. Therefore it is necessary to use non exhaustible sources of energy.

Answer briefly:

Question 1.
How are natural resources obtained to build a house?
Answer:
Natural resources are obtained to build a house are as follows:

1. Digging up hills for quarryingf.
2. Extracting sand from seashores and riverbeds.
3. Extracting stone and earth from the ground.
4. Drawing out excessive amount of ground water.
5. Felling trees to clear land.
6. Filling up ponds, lakes, streams, rivers, creeks and low lying areas to reclaimed land.

Question 2.
Why do people become homeless?
Answer:
People become homeless because

1. Lack of affordable housing.
2. Poverty and unemployment.
3. Inadequate’ income.
4. Natural disasters.
5. Physical and mental disorders.

Question 3.
What are the main uses of a house?
Answer:
The main uses of a house are as follows:

1. A shelter.
2. A resting place.
3. Protection against the sun, wind, cold and rains.
4. Protection from wild animals and from anti-social elements.

Question 4.
What is the government doing towards the ‘homeless’?
Answer:
1. A section of society being ‘homeless’ is a social problem.
2. That is why the government implements many schemes to provide homes to the homeless.
In some of the cities, the government makes ‘night shelters’ available to the homeless.

Write short notes on:

Question 1.
Characteristics of eco-friendly houses
Answer:
The characteristics of eco-friendly houses are as follows:

1. Minimum consumption of natural resources.
2. Use of non exhaustible sources of energy such as biogas, wind energy and solar energy.
3. Recycling of water.
4. Recycling of garbage.
5. Avoiding artificial materials and artificial colours.
6. Provision for natural light and ventilation in the house.

Question 2.
Uses of a house
Answer:
Uses of a house are as follows:
1. A shelter.
2. A resting place.
3. Protection against the sun, the wind, the cold and the rains.
4. Protection from wild animals.
5. Keeping ourselves safe from anti-sodal elements.

What’s the solution?

Question 1.
Construction work is going on opposite Ajit’s house. That means constant loud noise and a lot of dust in the air. Ajit and his family have to suffer this all the time. What can Ajit do to find a way out of this problem?
Answer:
Ajit and his family will have to keep their windows closed to avoid the dust and noise. They should use ear plugs when the noise is intense.

Glossary:

1. forested – covered with forests
2. urbanization – population shift from rural to urban areas
3. reclaimed – recovered.
4. shortage – a state in which something cannot be obtained in sufficient amount
5. felled – cut down.
6. luxury – state of great comfort.
7. quarrying – cut into and obtain stone
8. inadequate – lacking the quantity required
9. consumption – action of using up a resource
10. artificial – made by human beings, not natural.
11. DABUR Pivot Point Calculator

Class 5 Environmental Studies Questions and Answers:

• Our Earth and Our Solar System Class 5 Questions And Answers
• Motions of the Earth Class 5 Questions And Answers
• The Earth and its Living World Class 5 Questions And Answers
• Environmental Balance Class 5 Questions And Answers
• Family Values Class 5 Questions And Answers
• Rules Are for Everyone Class 5 Questions And Answers
• Let us Solve Our own Problems Class 5 Questions And Answers
• Public Facilities and My School Class 5 Questions And Answers
• Maps – Our Companions Class 5 Questions And Answers
• Getting to Know India Class 5 Questions And Answers
• Our Home and Environment Class 5 Questions And Answers
• Food for All Class 5 Questions And Answers

Balbharti Maharashtra State Board Class 5 Environmental Studies Solutions Chapter 14 Transport Notes, Textbook Exercise Important Questions and Answers.

5th Standard EVS 1 Lesson Number 14 Question Answer Transport Maharashtra Board

Std 5 EVS 1 Chapter 14 Question Answer

1. Write five sentences on how you have benefited from transport facilities.

Question 1.
Write five sentences on how you have benefited from transport facilities.
Answer:
Due to transport facilities:

1. Work gets done soon.
2. Time and effort are saved.
3. Trade is facilitated easily.
4. Connection to different parts of the world easily.
5. It has improved lifestyle by education and health services.

2. List four other facilities that have become available in the local area due to transport facilities.

Question 1.
List four other facilities that have become available in the local area due to transport facilities.
Answer:
Due to transport, we are able to get vegetables and fruits. Milk is supplied on time. We are able to go to the market and malls. We are able to visit relatives and friends.

3. Suggest four solutions to reduce the burden on the local transport.

Question 1.
Suggest four solutions to reduce the burden on the local transport.
Answer:
To reduce the burden on local transport build flyovers, walk short distance, avoid unnecessary travel and go to school and work place close to our house.

4. Find the area in your locality with the least pollution. why is this the least polluted area?

5. What is the full form of CNG and LPG.

Question 1.
What is the full form of:
Answer:
1. CNG: Compressed National Gas
2. LPG: Liquidified Petroleum Gas

6.

Question (a)
In the above picture, which vehicle is causing pollution?
Answer:
The Bus

Question (b)
What remedy will you suggest to reduce the pollution caused by this vehicle?
Answer:
The bus should do PUC to control the smoke given out.

Can you tell?

Question 1.
(a) Walking
(b) Riding a bicycle
(c) Using a private vehicle
(d) Using a public vehicle
Which of the above options will you choose on the following occasions?
Answer:

1. Going to study at a friend’s house who lives near by [a]
2. Going to your school which is about one kilometre away. [b]
3. Taking materials to a science exhibition in another town. [c]
4. Going to a wedding in the next town. [d]

Environmental Studies Part 1 Standard 5th Solutions Chapter 14 Transport Additional Important Questions and Answers

Fill in the blanks with the correct answers from the options given below:

Question 1.
Using a vehicle saves ……………….. and ……………… .
(a) time
(b) money
(c) effort
(d) energy
Answer:
(a) time , (c) effort

Question 2.
The burning of fuel in vehicles emits ……………… and ………………… .
(a) water
(b) ash
(c) gases
(d) smoke
Answer:
(c) gas , (d) smoke

Question 3.
If there are traffic jams, ……………….. and …………………. pollution in that area increases.
(a) air
(b) water
(c) noise
(d) land
Answer:
(a) air , (c) noise

Question 4.
Indigenous trees adopt easily to the local environment and help in enhancing ……………….. .
(a) nature
(b) climate
(c) biodiversity
Answer:
(c) biodiversity

Question 5.
We use ………………… in automobiles.
(a) fuels
(b) water
(c) turbines
(d) air
Answer:
(a) fuels

Question 6.
Automobiles cause ………………… and ………………. pollution.
(a) air
(b) land
(c) noise
(d) water
Answer:
(a) air , (c) noise

Question 7.
Different parts of the world are now ………………… due to transport facilities.
(a) known
(b) connected
(c) enemies
(d) friends
Answer:
(b) connected

Question 8.
The transport of goods even on a ………………… level has become simple and easy.
(a) national
(b) state
(c) global
(d) equal
Answer:
(c) global

Question 9.
There is constant ………………. on a busy road.
(a) smoke
(b) water
(c) breeze
(d) traffic
Answer:
(d) traffic

Question 10.
When fuel is burnt in vehicles, minute particles of carbon and lead are released into the ……………………. .
(a) water
(b) air
(c) land
(d) fire
Answer:
(b) air

Question 11.
Growth and development of plants is affected adversely, due to …………………. pollution.
(a) water
(b) air
(c) land
(d) fire
Answer:
(b) air

Question 12.
Constant traffic through forest areas can ……………….. the habitat of plants and animals living there.
(a) harm
(b) protect
(c) befriend
(d) develop
Answer:
(a) harm

Question 13.
The constant sounds of vehicles create …………………… on a large scale.
(a) headache
(b) noise
(c) accidents
(d) music
Answer:
(b) noise

Question 14.
Traffic ………………. causes injuries, deaths and damage to the vehicles.
(a) accidents
(b) jam
(c) noise
(d) smoke
Answer:
(a) accidents

Question 15.
We should cultivate habits such as ………………… short distances.
(a) jogging
(b) riding
(c) flying
(d) walking
Answer:
(d) walking

Question 16.
Our environment is sensitive, that is why, ………………. has destructive effects on it.
(a) pollution
(b) solution
(c) resolution
(d) transportation
Answer:
(a) pollution

2. Match the following:

Question 1.
Match the following:

‘A’	‘B’
1. Karanj	(a) Traffic accidents
2. LPG	(b) Noise
3. Headaches	(c) Local variety
4. Deaths	(d) Fuel

Answer:

‘A’	‘B’
1. Karanj	(c) Local variety
2. LPG	(d) Fuel
3. Headaches	(b) Noise
4. Deaths	(a) Traffic accidents

Name the following:

Question 1.
Pollution caused by automobiles.
Answer:
Air and noise.

Question 2.
Gases emitted through burning of fuels.
Answer:
Carbon monoxide, nitrogen dioxide, suphur dioxide.

Question 3.
Indigenous variety of trees.
Answer:
Banyan, Peepul, Neem, Karanj.

Question 4.
Fuels that do not cause pollution.
Answer:
LPG and CNG.

Answer in one sentence:

Question 1.
What facilities grow due to speedier modem means of transport?
Answer:
Modem means of transport speeds up facilities of tourism, health and education.

Question 2.
What is air pollution?
Answer:
An excess of carbon and lead substances lowers the quality of air in the environment which is called air pollution.

Question 3.
What harm do traffic accidents cause?
Answer:
Traffic accidents cause injuries, deaths and damage to the vehicles.

Question 4.
What habit should we cultivate if we have to travel a short distance?
Answer:
If we have to travel a short distance, we should cultivate the habit of working.

Question 5.
What mode of transport saves time and effort?
Answer:
Using a vehicle saves time and effort.

Question 6.
What causes air and noise pollution?
Answer:
Automobiles causes air and noise pollution.

Question 7.
What do vehicles constantly emit?
Answer:
Due to burning of fuel in vehicles, they constantly emit smoke and some poisonous gases.

Question 8.
Name some poisonous gases emitted by burning of fuels.
Answer:
Some of the poisonous gases emitted by burning of fuels include carbon monoxide, nitrogen dioxide and sulphur dioxide.

Question 9.
What happens when there is constant traffic through forest areas?
Answer:
Constant traffic through forest areas can harm the habitat of plants and animals living there so, the wild animals in these forests migrate elsewhere.

Question 10.
What are the ill-effects of noise pollution to man?
Answer:
Noise pollution causes restlessness, irritability, headaches, lack of concentration, psychological disorders etc.

What are the effects of following on humans, plants and animals?

Question 1.
Air pollution on humans
Answer:
It increases trachea, lung and eye disorders, e.g. burning of the eyes

Question 2.
Air pollution on plants.
Answer:
The leaves of plants shrivel up and fall, sprouts, get scorched. The growth and development of plants is affected.

Question 3.
Air pollution on animals.
Answer:
The habitat of the animals is harmed and wild animals migrate elsewhere.

Question 4.
Sound pollution on humans.
Answer:
Sound pollution causes restlessness, irritability, headaches, lack of concentration, and psychological disorders.

Answer in brief:

Question 1.
What are sailing ships?
Answer:
In olden times, ships did not use fuel engines. They had sails which helped to use the force of wind. They were called sailing ships.

Question 2.
What options should we consider to help reduce pollution?
Answer:
We can help reduce pollution in the following ways:
1. By cultivating a habit to walk short distances.
2. By riding a bicycle for slightly longer distances.
3. By using public transport as far as possible.

Write short notes:

Question 1.
Remedies for reducing pollution.
Answer:
The following are the remedies for reducing pollution:

1. Use fuels that cause less pollution.
2. Maintain and repair vehicles from time to time.
3. Use public transport mostly.
4. Use private vehicles only when necessary.
5. Plant indigenous trees to enhance biodiversity.
6. Use LPG and CNG fuels which do not cause pollution.

Question 2.
Advantages of using a bicycle.
Answer:
The advantages of using a bicycle are as follows:

1. Physical exercise
2. Small loads can be carried
3. Pollution free
4. Self-reliance
5. Saves time
6. Can be stored in a small space
7. Saves money
8. Less crowding of vehicles on the streets

What’s the solution?

Question 1.
Rohan and Sania walk to school. Their school is thirty minutes away from their house. There is a cultural function at their school today. Their grandmother will accompany them to the function. But she gets tired easily because of her age. Which of the options listed below would you suggest for taking her to school?
(a) Walking
(b) Autorickshaw
(c) Bus
(d) Scooter
(e) Car
Answer:
Bus

Can you tell?

1. Observe the pictures and answer the following questions:

Picture: 1

Question 1.
Where have the children stopped?
Answer:
The children have stopped on the road divide.

Question 2.
Why have they stopped there?
Answer:
They have stopped there to cross the road due to heavy traffic.

Question 3.
What are the children doing?
Answer:
The children are rubbing their eyes, coughing and closing their ears.

Question 4.
What is troubling them?
Answer:
The noise and air pollution due to transport routes is troubling them.

Picture – 2:

1. State the difference between the plants close to the road and those for away from the road based on the following points:

Question (a)
Freshness of leaves.
Answer:
The leaves close to the road appear dull compared to the one’s that are far away from the road.

Question (b)
Colour of the leaves.
Answer:
The leaves near the road are brown as they are covered with a thick layer of dust and mud whereas those far away are green in colour.

Question (c)
Appearance of plants.
Answer:
The growth of plants is affected due to the pollution. The plants near the road have few leaves.

Glossary:

1. restlessness – lacking quiet and rest
2. irritability -the state of being irritable
3. pyschological – problem related to the mind
4. indigenous – occuring naturally in a particular place.
5. shrivel – wrinkle and contract
6. scorched – burnt
7. migrate – move from one region to another
8. facilitated – made easier
9. remedies – medicine or treatment.

Class 5 Environmental Studies Questions and Answers:

• Methods of Preserving Food Class 5 Questions And Answers
• Transport Class 5 Questions And Answers
• Communication and Mass Media Class 5 Questions And Answers
• Water Class 5 Questions And Answers
• Clothes – Our Necessity Class 5 Questions And Answers
• The Environment and Us Class 5 Questions And Answers
• Constituents of Food Class 5 Questions And Answers
• Our Emotional World Class 5 Questions And Answers
• Busy at Work – Our Internal Organs Class 5 Questions And Answers
• Growth and Personality Development Class 5 Questions And Answers
• Infectious Diseases and how to Prevent them Class 5 Questions And Answers
• Substances, Objects and Energy Class 5 Questions And Answers
• Community Health and Hygiene Class 5 Questions And Answers

Maharashtra State Board 5th Std Textbook Solutions Answers Guide

• Maharashtra State Board Class 5 Maths Solutions
• Maharashtra State Board Class 5 EVS Solutions
• Maharashtra State Board Class 5 English Solutions
• Maharashtra State Board Class 5 Hindi Solutions
• Maharashtra State Board Class 5 Marathi Solutions

Maharashtra State Board Textbook Solutions

Expert Teachers have created Maharashtra State Board Class 5 Maths Solutions. You can also Download the Maharashtra Board 5th Std Maths Digest Pdf Free Download to help you to revise the complete Syllabus and score more marks in your examinations.

Maharashtra State Board 5th Std Maths Textbook Solutions

Class 5 Maths Solution Maharashtra Board Part 1

Maharashtra Board Class 5 Maths Chapter 1 Roman Numerals

• Chapter 1 Roman Numerals Problem Set 1

Maharashtra Board Class 5 Maths Chapter 2 Number Work

• Chapter 2 Number Work Problem Set 2
• Chapter 2 Number Work Problem Set 3
• Chapter 2 Number Work Problem Set 4
• Chapter 2 Number Work Problem Set 5
• Chapter 2 Number Work Problem Set 6

Maharashtra Board Class 5 Maths Chapter 3 Addition and Subtraction

• Chapter 3 Addition and Subtraction Problem Set 7
• Chapter 3 Addition and Subtraction Problem Set 8
• Chapter 3 Addition and Subtraction Problem Set 9
• Chapter 3 Addition and Subtraction Problem Set 10
• Chapter 3 Addition and Subtraction Problem Set 11
• Chapter 3 Addition and Subtraction Problem Set 12
• Chapter 3 Addition and Subtraction Problem Set 13

Maharashtra Board Class 5 Maths Chapter 4 Multiplication and Division

• Chapter 4 Multiplication and Division Problem Set 14
• Chapter 4 Multiplication and Division Problem Set 15
• Chapter 4 Multiplication and Division Problem Set 16

Maharashtra Board Class 5 Maths Chapter 5 Fractions

• Chapter 5 Fractions Problem Set 17
• Chapter 5 Fractions Problem Set 18
• Chapter 5 Fractions Problem Set 19
• Chapter 5 Fractions Problem Set 20
• Chapter 5 Fractions Problem Set 21
• Chapter 5 Fractions Problem Set 22
• Chapter 5 Fractions Problem Set 23

Maharashtra Board Class 5 Maths Chapter 6 Angles

• Chapter 6 Angles Problem Set 24
• Chapter 6 Angles Problem Set 25
• Chapter 6 Angles Problem Set 26
• Chapter 6 Angles Problem Set 27

Maharashtra Board Class 5 Maths Chapter 7 Circles

• Chapter 7 Circles Problem Set 28
• Chapter 7 Circles Problem Set 29
• Chapter 7 Circles Problem Set 30
• Chapter 7 Circles Problem Set 31

5th Std Maths Digest Pdf Maharashtra Board Part 2

Maharashtra Board Class 5 Maths Chapter 8 Multiples and Factors

• Chapter 8 Multiples and Factors Problem Set 32
• Chapter 8 Multiples and Factors Problem Set 33
• Chapter 8 Multiples and Factors Problem Set 34
• Chapter 8 Multiples and Factors Problem Set 35

Maharashtra Board Class 5 Maths Chapter 9 Decimal Fractions

• Chapter 9 Decimal Fractions Problem Set 36
• Chapter 9 Decimal Fractions Problem Set 37
• Chapter 9 Decimal Fractions Problem Set 38
• Chapter 9 Decimal Fractions Problem Set 39
• Chapter 9 Decimal Fractions Problem Set 40
• Chapter 9 Decimal Fractions Problem Set 41
• Chapter 9 Decimal Fractions Problem Set 42

Maharashtra Board Class 5 Maths Chapter 10 Measuring Time

• Chapter 10 Measuring Time Problem Set 43
• Chapter 10 Measuring Time Problem Set 44
• Chapter 10 Measuring Time Problem Set 45

Maharashtra Board Class 5 Maths Chapter 11 Problems on Measurement

• Chapter 11 Problems on Measurement Problem Set 46
• Chapter 11 Problems on Measurement Problem Set 47

Maharashtra Board Class 5 Maths Chapter 12 Perimeter and Area

• Chapter 12 Perimeter and Area Problem Set 48
• Chapter 12 Perimeter and Area Problem Set 49
• Chapter 12 Perimeter and Area Problem Set 50

Maharashtra Board Class 5 Maths Chapter 13 Three Dimensional Objects and Nets

• Chapter 13 Three Dimensional Objects and Nets Problem Set 51

Maharashtra Board Class 5 Maths Chapter 14 Pictographs

• Chapter 14 Pictographs Problem Set 52

Maharashtra Board Class 5 Maths Chapter 15 Patterns

• Chapter 15 Patterns Problem Set 53

Maharashtra Board Class 5 Maths Chapter 16 Preparation for Algebra

• Chapter 16 Preparation for Algebra Problem Set 54
• Chapter 16 Preparation for Algebra Problem Set 55
• Chapter 16 Preparation for Algebra Problem Set 56

Maharashtra State Board Class 5 Textbook Solutions

Maharashtra State Board Environmental Studies EVS Part 1 & Part 2 Standard 5th Solutions Digest Answers Pdf Download, 5th Std EVS 1, 2 Digest Pdf, Environmental Studies Part 1, 2 Standard 5th Question Answer.

Maharashtra State Board 5th Std EVS Textbook Solutions

Environmental Studies Part 1 Standard 5th Digest

Maharashtra State Board Environmental Studies EVS Part 1 Standard 5th Digest Solutions Question Answer Pdf.

• Chapter 1 Our Earth and Our Solar System
• Chapter 2 Motions of the Earth
• Chapter 3 The Earth and its Living World
• Chapter 4 Environmental Balance
• Chapter 5 Family Values
• Chapter 6 Rules Are for Everyone
• Chapter 7 Let us Solve Our own Problems
• Chapter 8 Public Facilities and My School
• Chapter 9 Maps – Our Companions
• Chapter 10 Getting to Know India
• Chapter 11 Our Home and Environment
• Chapter 12 Food for All
• Chapter 13 Methods of Preserving Food
• Chapter 14 Transport
• Chapter 15 Communication and Mass Media
• Chapter 16 Water
• Chapter 17 Clothes – Our Necessity
• Chapter 18 The Environment and Us
• Chapter 19 Constituents of Food
• Chapter 20 Our Emotional World
• Chapter 21 Busy at Work – Our Internal Organs
• Chapter 22 Growth and Personality Development
• Chapter 23 Infectious Diseases and how to Prevent them
• Chapter 24 Substances, Objects and Energy
• Chapter 25 Community Health and Hygiene

Environmental Studies Part 2 Standard 5th Digest

Maharashtra State Board Environmental Studies EVS Part 2 Standard 5th Digest Solutions Question Answer Pdf.

• Chapter 1 What is History?
• Chapter 2 History and the Concept of ‘Time’
• Chapter 3 Life on Earth
• Chapter 4 Evolution
• Chapter 5 Evolution of Mankind
• Chapter 6 Stone Age: Stone Tools
• Chapter 7 From Shelters to Village-settlements
• Chapter 8 Beginning of Settled Life
• Chapter 9 Settled Life and Urban Civilization
• Chapter 10 Historic Period

Maharashtra State Board Class 5 Textbook Solutions

Maharashtra State Board 5th Std English Textbook Digest Answers Pdf Download, English Balbharati Workbook Std 5 Answers, 5th Standard English Question Answer.

Maharashtra State Board 5th Std English Balbharati Textbook Solutions

Balbharti English Textbook Std 5 Pdf Free Download Unit 1

• Chapter 1 What a Bird Thought
• Chapter 2 Daydreams
• Chapter 3 Be a Good Listener
• Chapter 4 Strawberries
• Chapter 5 The Twelve Months
• Chapter 6 Announcements
• Chapter 7 Major Dhyan Chand
• Chapter 8 Peer Profile

English Balbharati Workbook Std 5 Answers Unit 2

• Chapter 9 The Triantiwontigongolope
• Chapter 10 Three Sacks of Rice
• Chapter 11 Be a Good Speaker
• Chapter 12 Count your Garden
• Chapter 13 The Adventures of Gulliver
• Chapter 14 A Lesson for All
• Chapter 15 Bird Bath
• Chapter 16 Write your own Story

English Balbharati Std 5 Textbook Digest Unit 3

• Chapter 17 On the Water
• Chapter 18 Weeds in the Garden
• Chapter 19 Be a Good Host and Guest
• Chapter 20 Only One Mother
• Chapter 21 The Journey to the Great Oz
• Chapter 22 A Book Review
• Chapter 23 Write your own Poem
• Chapter 24 Senses Alert

English Balbharati Std 5 Answers Unit 4

• Chapter 25 The Man in the Moon
• Chapter 26 Water in the Well
• Chapter 27 The Legend of Marathon
• Chapter 28 All about Money
• Chapter 29 A Lark
• Chapter 30 Be a Netizen
• Chapter 31 Give your Mind a Workout!
• Chapter 32 Helen Keller
• Chapter 33 Rangoli

Maharashtra State Board Class 5 Textbook Solutions

Maharashtra State Board 5th Standard Hindi Sulabhbharati Digest Pdf Download, 5th Standard Hindi Textbook Questions and Answers.

Maharashtra State Board 5th Std Hindi Sulabhbharati Textbook Solutions

5th Std Hindi Digest Pdf Download पहली इकाई

• Chapter 1 नंदनवन
• Chapter 2 बूँदें
• Chapter 3 योग्‍य चुनाव
• Chapter 4 कश्मीरा
• Chapter 5 पहचान हमारी – भाग (१)
• Chapter 6 पेटूराम
• Chapter 7 बधाई कार्ड
• Chapter 8 करो और जानो
• Chapter 9 नीम
• Chapter 10 गड़ा धन
• Chapter 11 मित्रता
• Chapter 12 बचत
• Chapter 13 पहचान हमारी – भाग (२)
• Chapter 14 मैं सड़क हूँ
• Chapter 15 व्यायाम
• Chapter 16 बोलो और जानो
• स्वयं सध्ययन
• पुनरावर्तन १
• पुनरावर्तन २

Hindi Sulabhbharati 5th Standard Pdf दूसरी इकाई

• Chapter 1 गाँव और शहर
• Chapter 2 जीवन
• Chapter 3 भाई-भाई का प्रेम
• Chapter 4 बालिका दिवस
• Chapter 5 रोबोट
• Chapter 6 जुड़े हम
• Chapter 7 (अ) बोध, (ब) समान – विरुद्ध
• Chapter 8 बीज
• Chapter 9 मुझे पहचानो
• Chapter 10 मुझे जानो
• Chapter 11 वीरों को प्रणाम
• Chapter 12 सपूत
• Chapter 13 राष्ट्रीय त्योहार
• Chapter 14 (अ) हम अलग – रूप एक, (ब) धुक-धुक गाड़ी
• Chapter 15 ज्ञानी
• Chapter 16 बचाव
• Chapter 17 निरिक्षण
• Chapter 18 चलों-चलें
• स्वयं सध्ययन
• पुनरावर्तन ३
• पुनरावर्तन ४

Maharashtra State Board Class 5 Textbook Solutions

Maharashtra State Board 5th Standard Marathi Sulabhbharati Digest Pdf Download, 5th Standard Marathi Textbook Question Answer, Textbook Workbook Answers.

Maharashtra State Board 5th Std Marathi Sulabhbharati Textbook Solutions

5th Standard Marathi Digest Pdf Download

• Chapter 1 नाच रे मोरा
• Chapter 2 हत्तीचे चातुर्य
• Chapter 3 खेळूया शब्दांशी
• Chapter 4 हि पिसे कोणाची ?
• Chapter 5 डराव डराव
• Chapter 6 ऐकुया खेळूया
• Chapter 7 खेळत खेळत वाचुया!
• Chapter 8 कोणापासून काय घ्यावे?
• Chapter 9 सिंह आणि बेडूक
• Chapter 10 बैलपोळा
• Chapter 11 इंधनबचत
• Chapter 12 बोलावे कसे?
• Chapter 13 अनुभव-१
• Chapter 14 चित्रसंदेश
• Chapter 15 नदीचे गाणे
• Chapter 16 मी नदी बोलते
• Chapter 17 आमची सहल
• Chapter 18 पैशांचे व्यवहार
• Chapter 19 अनुभव-२
• Chapter 20 गमतीदार पत्र
• Chapter 21 छोटेसे बहीणभाऊ
• Chapter 22 वाचूया लिहूया
• Chapter 23 प्रामाणिक इस्त्रीवाला
• Chapter 24 ऐका पहा करा
• Chapter 25 मालतीची चतुराई
• Chapter 26 पतंग
• Chapter 27 महर्षी विठ्ठल रामजी शिंदे
• Chapter 28 फुलपाखरू आणि मधमाशी

Maharashtra State Board Class 5 Textbook Solutions

Balbharti Maharashtra State Board Class 5 Hindi Solutions Sulabhbharati पुनरावर्तन ४ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 5 Hindi Sulabhbharati Solutions पुनरावर्तन ४

5th Standard Hindi Digest पुनरावर्तन ४ Textbook Questions and Answers

1. सुनो, और दोहराओ:

प्रश्न 1.
सुनो, और दोहराओ:

उत्तर:
(अ) 1. मैं जा रह्य / रही हूँ।
2. हम जा रहे हैं / रही हैं।
3. तू जा रहा है / रही है।
4. तुम जा रहे हो / रही हो।
5. आप जा रहे हैं। रही हैं।

(ब) 1. यह जा रहा है। रही है।
2. ये जा रहे हैं / रही हैं।
3. वह जा रहा है / रही है।
4. वे जा रहे हैं / रही हैं।

2. तुम्हारे मित्र के पास कॉपी खरीदने के लिए पैसे नहीं हैं । तुम्हारी माँ ने मेला देखने के लिए तुम्हें तीस रुपये दिए हैं। इस स्थिति में तुम्हारे मन में कौन से भाव जागते हैं ? बताओ।

प्रश्न 1.
तुम्हारे मित्र के पास कॉपी खरीदने के लिए पैसे नहीं हैं । तुम्हारी माँ ने मेला देखने के लिए तुम्हें तीस रुपये दिए हैं। इस स्थिति में तुम्हारे मन में कौन से भाव जागते हैं ? बताओ।
उत्तर:
उन तीस रुपयों में से अपने मित्र को कॉपी खरीदकर दूंगा तथा बचे हुए पैसों से मेला घूम लूँगा।

3. पढ़ो, और समझो:

प्रश्न 1.
पढ़ो, और समझो:
उत्तर:

1. जहाँ विद्यार्थी पढ़ते हैं – विद्यालय
2. जादू दिखाने वाला – जादूगर
3. खेल खेलने वाला – खिलाड़ी
4. सच बोलनेवाला – सत्यवादी
5. चित्र बनाने वाला – चित्रकार
6. मूर्तियाँ बनाने वाला – मूर्तिकार
7. सोने के गहने बनाने वाला – सुनार
8. जो कभी न हारा हो – अजेय
9. जो साग-सब्ज़ी खाता हो – शाकाहारी
10. जहाँ अनाथ रहते हैं – अनाथालय
11. जो रोगियों का इलाज करता है – डॉक्टर
12. जो लकड़ी का काम करता है – बढ़ई
13. जो मिट्टी के बरतन बनाता है – कुम्हार
14. जो जूते सिलता है – मोची
15. जो कपड़े सिलता है – दर्जी

4. सड़क पार करते समय तुम क्या सावधानी बरतते हो? लिखो।

प्रश्न 1.
सड़क पार करते समय तुम क्या सावधानी बरतते हो? लिखो।

उत्तर:
सड़क पार करते समय जेब्रा क्रॉसिंग पर से जाना चाहिए।

5. पढ़ाई करने के बाद भी तुम्हें परीक्षा से डर लग रहा है, तो तुम क्या करोगे? बताओ।

प्रश्न 1.
पढ़ाई करने के बाद भी तुम्हें परीक्षा से डर लग रहा है, तो तुम क्या करोगे? बताओ।
(क) बड़ों से बातचीत करोगे ।
(ख) खेलने जाओगे।
(ग) गाना सुनोगे अथवा गाओगे ।
(घ) आराम करोगे ।
उत्तर:
(क) बड़ों से बातचीत करेंगे।

Hindi Sulabhbharati Class 5 Solutions पुनरावर्तन ४ Additional Important Questions and Answers

प्रश्न 1.
चित्रों को देखकर नीचे दी गई शब्द – पहेली बूझो; (एक अक्षर का एक से अधिक बार उपयोग कर सकते हैं।)
उत्तर:
फूल: कमल, हरसिंगार, गुलाब, गुड़हल, डहलिया, रजनीगंधा, बेला, सूरजमुखी, सदाबहार।
फल: केला, अमरूद, अनार, चीकू, अंगूर, सेब, पपीता, आम, अंजीर, संतरा, सीताफल, अनन्नास।
अन्य शब्द: नीम, पीला, ताला, अंदर, चीता, कान, पतला, खीर, गेंद, जल, दानी