Perimeter and Area Class 5 Problem Set 49 Question Answer Maharashtra Board
Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 12 Perimeter and Area Problem Set 49 Textbook Exercise Important Questions and Answers.
Std 5 Maths Chapter 12 Perimeter and Area
Question 1.
How much wire will be needed to make a rectangle 7 cm long and 4 cm wide?
Solution:
Perimeter of a rectangle
= 2 x length + 2 x breadth
= 2 x 7 + 2 x 4
= 14 + 8
= 22 cm
∴ 22 cm wire will be needed to make a rectangle
![]()
Question 2.
If the length of a rectangle is 20 m and its width is 12m, what is its perimeter?
Solution:
Perimeter of a rectangle
= 2 x length + 2 x breadth
= 2×20 + 2×12
= 40 + 24
= 64 m
∴ Perimeter is 64 m
Question 3.
Each side of a square is 9 m long. Find its perimeter.
Solution:
Perimeter of a square
= 4 x length of one side
= 4 x 9
= 36 m
∴ Perimeter is 36 m
Question 4.
If we take 4 rounds around a field that is 160 m long and 90 m wide, what is the distance we walk in kilometres?
Solution:
Perimeter of a rectangular field
= 2 x length + 2 x breadth
= 2 x 160 + 2 x 90
= 320 + 180
= 500 m
In one round distance walked is 500 m, hence, distance walked in 4 rounds
= 500 x 4
= 2000 m
= 2km
∴ The distance walked in 4 rounds is 2 km
![]()
Question 5.
Sanju completes 12 rounds around a square park every day. If one side of the park is 120 m, find out in kilometres and metres the distance that Sanju covers daily.
Solution:
Perimeter of a square
= 4 x length of one side
= 4 x 120
= 480 m
So, in one round the distance can be covered is 480 m, hence in 12 rounds the distance can be covered is
= 480 x 12
= 5760 m
= 5000 m + 760 m
∴ Sanju covers 5 km 760 m daily
Question 6.
The length of a rectangular plot of land is 50 m and its width is 30 m. A triple fence has to be put along its edges. If the wire costs 60 rupees permetre, what will be the total cost of the wire needed for the fence?
Solution:
Perimeter of a rectangular plot
= 2 x length + 2 x breadth
= 2 x 50 + 2 x 30
= 100 + 60 – 160 m
For a triple fence, wire needed
= 3 x 160 = 480 m
Cost of the wire needed
= wire needed x rate
= 480 x 60
= 28800 rupees
∴ The total cost of the wire needed for the fence is ₹ 28,800
![]()
Question 7.
A game requires its players to run around a square playground. Each side of the playground is 20 m long. One player took 5 rounds around the playground. How many metres did he run altogether?
Solution:
Perimeter of a square
= 4 x length of one side
= 4 x 20
= 80 m
In one round 80 m.
So in 5 round
= 80 x 5
= 400
= 400 m
∴ He runs altogether = 400 m
Question 8.
Four rounds of wire fence have to be put around a field. If the field is 60 m long and 40 m wide, how much wire will be needed?
Solution:
Perimeter of rectangular field
= 2 x length + 2 x breadth
= 2 x 60 + 2 x 40
= 120 + 80
= 200 m
Hence, wire required for 4 rounds
= 200 x 4
= 800 m
∴ Wire required for 4 rounds
= 800 m
![]()
Question 9.
The sides of a triangle are 24.7cm, 20.4 cm and 10.5 cm respectively. What is the perimeter of the triangle?
Solution:
Perimeter of triangle
= 24.7 + 20.4 + 10.5
= 55.6
∴ The perimeter of a triangle
= 55.6 cm
Question 10.
Look at the figures on the sheet of graph paper. Measure their sides with the help of the lines on the graph paper. Write the perimeter of each in the right box.
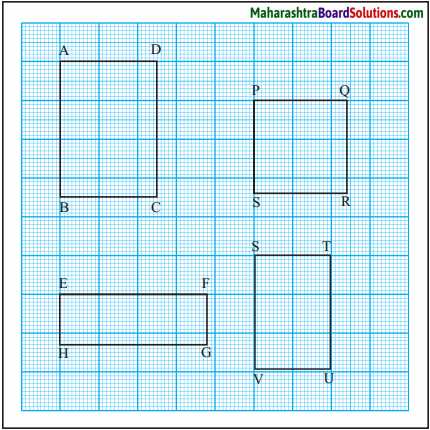
(1) Perimeter of
rectangle ABCD
= [ ] cm
(2) Perimeter of
rectangle EFGH
= [ ] cm
(3) Perimeter of
square PQRS
= [ ] cm
(4) Perimeter of
rectangle STUV
= [ ] cm
Solution:
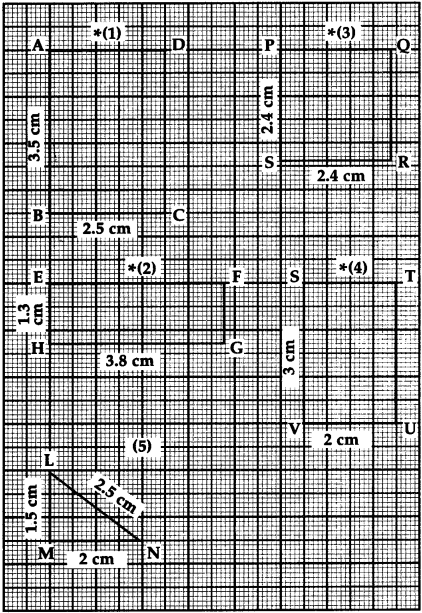
![]()
(1) Perimeter of a rectangle ABCD
= 2 x length + 2 x breadth
= 2 x 3.5 + 2 x 2.5
= 7 + 5
= 12 cm
∴ 12 cm
(2) Perimeter of a rectangle EFGH
= 2 x length + 2 x breadth
= 2 x 3.8 + 2 x 1.3
= 7.6 + 2.6
= 10.2 cm
∴ 10.2 cm
(3) Perimeter of a rectangle PQRS
= 2 x length + 2 x breadth
= 2 x 2.4 + 2 x 2.4
= 4.8+ 4.8
= 9.6 cm
∴ 9.6 cm
![]()
(4) Perimeter of a rectangle STUV
= 2 x length + 2 x breadth
= 2 x 3 + 2 x 2
= 6 + 4
= 10 cm
∴ 10 cm
(5) Perimeter of a triangle LMN
= 1.5 + 2.5 + 2
= 6 cm
∴ 6 cm
Area : Revision
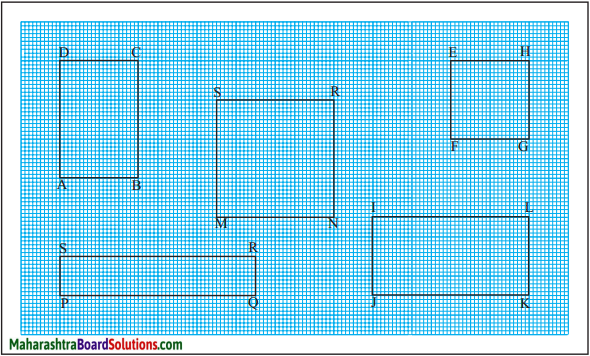
Of the figures given above, figure ABCD has six squares of 1 cm each inside it. It means that its area is 6 sq cm.
In the same way, count the squares in each figure and write its area.
(1) Area of MNRS = [ ] sq cm
(2) Area of EFGH = [ ] sq cm
(3) Area of PQRS = [ ] sq cm
(4) Area of IJKL = [ ] sq cm
Atul : Sir, why is the unit for area written as sq cm? We measure the sides in centimetres.
Teacher : Centimetre is a standard unit of length. In order to measure area, we need a standard unit of area. For this, a square with a side 1 cm is taken as the standard unit. The area of this square is 1 square centimetre. That is why this unit is written as sq cm, in short.
To measure large areas like fields, parks and playgrounds, a square with side 1 m, that is, an area of 1 sq m, is taken as the standard unit.
![]()
To measure the areas oftalukas or districts, a square with side 1km, or 1sq km is the standard unit used.
Formula for the area of a rectangle
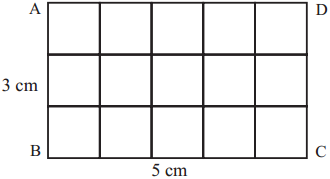
(1) In the rectangle ABCD given alongside, 1 cm divisions were marked off on each side. The points on opposite sides were joined as shown in the figure. The length of the sides of each square thus created is 1cm. Therefore, the area of each square is 1 sq cm.
In ABCD, 3 rows with 5 squares each have been created.
The number of squares in rectangle ABCD is 3 × 5 = 15.
Therefore, the area of rectangle ABCD is 15 sq cm.
Here, the length of the figure is 5 cm and its breadth is 3 cm.
Note that the product of 3 and 5 is 15.
(2) In the rectangle with sides 4 cm and 2 cm, make squares of 1 sq cm each as shown above. Count the number of squares.

Note that here too, the number of squares formed are the same as the product of the length and width of the rectangle.
Therefore, The area of a rectangle = length × breadth
Formula for the area of a square
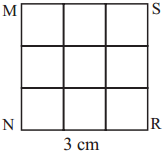
(1) Look at the square given alongside. The side of the square is 3 cm long. 9 squares of 1 cm each are formed within this square.
![]()
Therefore, the area of this square is 9 sq cm.
Here, there are 3 rows with 3 squares each, i.e., there are 3 × 3 = 9 squares.
The length of each side of the square is 3 cm.
The product of two sides of the square is 3 × 3 = 9.
(2) Measure the area of a square with side 5 cm, in the same way.
The answer will be 25 sq cm.
Note that 5 × 5 = 25
Therefore, The area of a square = length of a side × length of a side
It is not necessary to divide a square or rectangle into small squares every time you calculate their area. The advantage of a formula is that you can calculate the area simply by substituting the appropriate values.
Word problems
Example (1) What is the area of a rectangle of length 20 cm and width 15 cm?
Area of a rectangle = length × breadth
= 20 × 15 = 300.
Therefore, the area of the rectangle is 300 sq cm.
Example (2) A wall that is 4 m long and 3 m wide has to be painted. If the labour charges are ₹ 25 per sq m, what is the cost of labour for painting this wall?
First let us calculate the area of the wall to be painted.
Area of the wall = length of the wall × breadth of the wall = 4 × 3 = 12
Thus, the area of the wall is 12 sq m.
Labour cost of 1 sq m is 25 rupees.
So the labour cost for 12 sq m will be = 12 × 25 = 300
The cost of labour for painting the wall will be 300 rupees.
Example (3) What will be the area of a square with sides 15 cm?
Area of a square = length of side × length of side
= 15 × 15 = 225
The area of the square is 225 sq cm.
![]()
Example (4) One side of a square room is 4 m. If the cost of labour for laying 1 sq m of the floor is 35 rupees, what will be the total cost of labour?
First we must find the area of the square room.
Area of the square room = length of side × length of side = 4 × 4 = 16
Therefore, the area of the square room is 16 sq m.
The labour cost of laying 1 sq m of flooring is 35 rupees.
Therefore, the cost of laying 16 sq m of flooring is 16 × 35 = 560 rupees.
Perimeter and Area Problem Set 49 Additional Important Questions and Answers
Question 1.
Devendra walks five rounds of a square garden everyday. If the side of the garden is 150 m, how many kilometres does Devendra walk every morning?
Solution:
Perimeter of a square garden
= 4 x one side of the garden
= 4 x 150
= 600 m
In 5 rounds walking
= 5 x 600
= 3000 m
= 3 km
3 km
Question 2.
The length of a rectangular play ground is 75 m and its breadth is 50 m. Rupali walks four rounds. How many kilometres did she walk?
Solution:
Perimeter of rectangle
= 2 x length + 2 x breadth
= 2 x 75 + 2 x 50
= 150 + 100
= 250 m
In 4 rounds walking
= 4 x 250
= 1000 m
= 1 km
∴ 1 km
![]()
Question 3.
Length of the rectangle is 10 cm and its breadth is 8 cm and one square is side 9 cm. Whose perimetre is more? By how much?
Solution:
Perimeter of a rectangle
= 2 x length + 2 x breadth
= 2 x 10 + 2 x 8
= 20 + 16
= 36 cm ……………….. (i)
Perimeter of a square
= 4 x length of side
= 4 x 9
36 cm ……………….. (ii)
From (i) and (ii) perimeter of both is equal.
∴ perimeter of both is equal
Class 5 Maths Solution Maharashtra Board