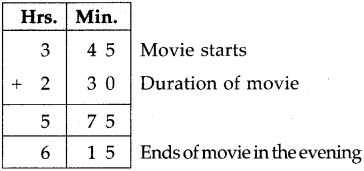
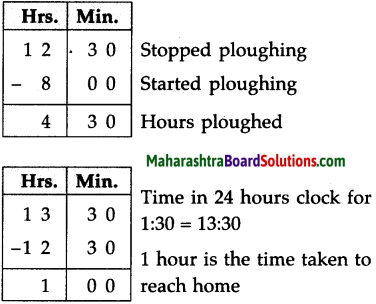
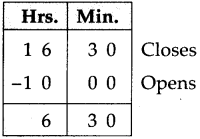
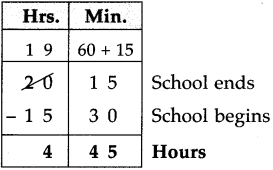
Class 10th Sanskrit Aamod Chapter 12 आदिशङ्कराचार्यः Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Amod Chapter 12 आदिशङ्कराचार्यः Notes, Textbook Exercise Important Questions and Answers.
Std 10 Sanskrit Chapter 12 Question Answer
Sanskrit Amod Std 10 Digest Chapter 12 आदिशङ्कराचार्यः Textbook Questions and Answers
भाषाभ्यास:
1. पूर्णवाक्येन उत्तरं लिखत ।
प्रश्न अ.
गुरुमुपगम्य शङ्करः किम् अधीतवान् ?
उत्तरम् :
गुरुमुपगम्य शङ्करः वेद-वेदाङ्गानि, विविधशास्त्राणि च अधीतवान्।
प्रश्न आ.
शङ्करः किमर्थम् आक्रोशत् ?
उत्तरम् :
यदा शकर स्नाने मग्नः आसीत् तदा एक: ननतस्य पादम् अगृह्णात् अत: भीत्या शङ्करः उच्चैः आक्रोशत्।
प्रश्न इ.
शङ्करः मात्रे किं प्रतिश्रुत्य गृहाद् निरगच्छत् ?
उत्तरम् :
‘मात: यदा त्वं स्मरिष्यसि तदा एवं त्वत्समीपमागमिष्यामि’ इति मात्रे प्रतिश्रुत्य शङ्करः गृहद् निरगच्छत्।

प्रश्न ई.
शङ्करः कस्य शिष्यः अभवत् ?
उत्तरम् :
शङ्कर: गोविन्दभगवत्पादानां शिष्यः अभवत्।
प्रश्न उ.
शङ्करः संन्यासदीक्षां गृहीत्वा किम् अकरोत्?
उत्तरम् :
शङ्कर: संन्यासदीक्षां गृहीत्वा वैदिकधर्मस्य प्रचारार्थ प्रस्थानम् अकरोत्।
प्रश्न ऊ.
शिष्यगणेन सह आचार्यः स्नानार्थं कुत्र अगच्छत्?
उत्तरम् :
शिष्यगणेन सह आचार्यः स्नानार्थ गङ्गानदीम् अगच्छत्।
प्रश्न ए.
शङ्कराचार्यः आसेतुहिमाचलं पर्यटन् किम् अकरोत् ?
उत्तरम् :
शङ्कराचार्यः आसेतुहिमाचलं पर्यटन् अद्वैतसिद्धान्तस्य प्रचारम् अकरोत्।

2. माध्यमभाषया उत्तरत।
प्रश्न अ.
शङ्करेण संन्यासार्थ कथम् अनुमतिः लब्धा ?
उत्तरम् :
‘आदिशङ्कराचार्य:’ या पाठामध्ये शंकराचार्यांच्या जीवनातील दोन प्रसंग उद्धृत करण्यात आले आहेत. पहिल्या प्रसंगात, एका अटळ परिस्थितीत सापडले असताना, संन्यासी बनू इच्छिणाऱ्या शंकराचार्यांना त्यांची माता कशी अनुमती देते, याचे वर्णन आले आहे.
एकदा शंकर स्नानासाठी पूर्णा नदीवर गेले होते. स्नान करत असताना अनपेक्षितपणे एका मगरीने त्यांचा पाय पकडला. वेदना असहा झाल्याने शंकर जोरात ओरडू लागले. तेव्हा त्यांची आई आर्याबा तिथे पोहोचली. अशा दयनीय अवस्थेत शंकराला रडताना पाहून त्याची आई सुद्धा गांगरून गेली.
हा अनावस्था प्रसंग म्हणजे आयुष्याचा शेवट अशी शंकराची समजूत झाली व त्याने संन्यासी होण्याची अतृप्त इच्छा आईकडे बोलून दाखविली. हतबल झालेल्या आबिने मनात नसतानाही ही शंकराची शेवटची इच्छा मानून, संन्यास घेण्यासाठी अनुमती दिली.
In the lesson, आदिशङ्कराचार्यः, two incidents of शंकराचार्य’s life are given. The first incident explains how आदिशङ्कराचार्य, who was keen to become a monk was granted permission by his mother for practising monkship due to an inescapable situation.
Once, it went to पूर्ण river for bathing, a crocodile caught his leg. शंकर screamed loudly with pain. His mother अर्याम्बा came there. Seeing शंकर crying in miserable condition, even his mother got perturbed.
शंकर finding / thinking this situation as the end of his life, expressed his unfulfilled wish to become a monk to his mother and requested her to permit for the same. Unwillingly, helpless अर्याम्बा granted शंकर for monkship, considering this as his last wish.

प्रश्न आ.
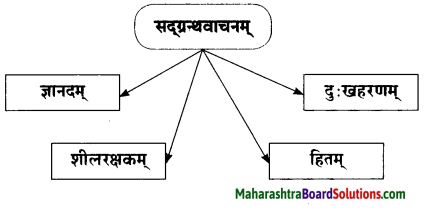
ज्ञानग्रहणविषये शङ्कराचार्याणां किं मतम्?
उत्तरम् :
‘आदिशङ्कराचार्य:’ या पाठामध्ये शंकराचार्यांच्या जीवनातील दोन प्रसंग उद्धृत करण्यात आले आहेत. दुसऱ्या प्रसंगातून शंकराचार्यांच्या शिकवणीचा उलगडा होतो. ती शिकवण अशी – जो (कोणी) ज्ञान देतो, तो गुरु मानावा.
एकदा आचार्य त्यांच्या शिष्यांसमवेत स्नान करण्याकरिता गेले होते. रस्त्यात फाटके कपडे घातलेला, मलिन शरीर असलेला एक माणूस त्यांच्या समोर आला. त्याच्या विचित्र अवताराला पाहून शिष्यांनी त्याला हाकलले. पण त्या मनुष्याने आचार्यांना प्रभावित केले.
त्या माणसाने शिष्यांना विचारले? “तुम्ही आत्मा व शरीर यापैकी कोणाला दूर करत आहात? कारण, आत्मा हा परमेश्वराचा अंश आहे, म्हणून तो सर्वांमध्ये सारखाच आहे. प्रत्येक शरीर हे पंचतत्त्वांनी युक्त आहे.”
वेदांताचे खरे सार ऐकल्यावर शंकराचार्यांनी त्या मनुष्यास नमस्कार करून त्यांची नम्रता दर्शवली. आचार्यांनी गुरु असूनही त्या माणसाला गुरुत्व बहाल केले व पुनश्च त्यांच्या ज्ञानविषयक सिद्धांतांचा प्रत्यय शिष्यांना करून दिला. तो सिद्धान्त असा – जो कोणी ज्ञान देतो, तो गुरु मानावा.
In the lesson, आदिशङ्कराचार्यः, two incidents of शंकराचार्य’s life are given. The second event unfolds आदिशङ्कराचार्य’s preaching – whosoever imparts knowledge is the preceptor.
Once, आचार्य went to river गङ्गा for bathing along with his desciples. On the way, they came across a man with torn clothes and unclean body. Seeing his strange attire, a desciple warded him off. But the man impressed आचार्य with his wise speech.
The man asked desciples, whom do you ward off, a soul or body? Because, the soul is a part of the lord. Hence, is same among all. It consists of five eternal elements; so your and mine body are not different .
शंकराचार्य bowed down to that man after listening to the real knowledge of वेदान्त from him. being a preceptor too, considered him as गुरु; following this principle, whosoever imparts knowledge is the preceptor.
3. प्रश्ननिर्माणं कुरुत।
प्रश्न अ.
माता आर्याम्बा पुत्रस्य विवाहविषये सदैव चिन्तयति स्म ।
उत्तरम् :
माता आर्याम्बा पुत्रस्य विवाहविषये अचिन्तयत् ।

प्रश्न आ.
नक्राद् मुक्तः शङ्करः मातुः चरणी प्राणमत् ।
उत्तरम् :
‘कस्मात् मुक्तः शङ्कर: मातुः चरणौ प्राणमत्?
प्रश्न इ.
आचार्यः स्तोत्रं रचितवान् ।
उत्तरम् :
आचार्यः किं रचितवान् ?
4. सन्धिविग्रहं कुरुत।
प्रश्न अ.
चास्ताम्
उत्तरम् :
चास्ताम् – च + आस्ताम्।

प्रश्न आ.
त्वत्समीपमागमिष्यामि
उत्तरम् :
त्वत्समीपमागमिष्यामि – त्वत् + समीपम् + आगमिष्यामि।
प्रश्न इ.
गुरुमुपागच्छत्
उत्तरम् :
गुरुमुपागच्छत् – गुरुम् + उपागच्छत्।
प्रश्न ई
मुनिरभ्यगात्
उत्तरम् :
मुनिरभ्यगात् – मुनिः + अभ्यगात्।
प्रश्न उ.
मातैव
उत्तरम् :
मातैव – तस्मात् + माता + एव।

5. मेलनं कुरुत ।
प्रश्न 1.
विशेष्यम् – शिवगुरुः, आर्याम्बा, शङ्करः, जगत्, मनुष्यः ।
विशेषणम् – मलिनकायः, प्रसन्नः, विशालम्, दिवङ्गतः, विरक्तः, चिन्तामना ।
उत्तरम् :
| विशेषणम् |
विशेष्यम् |
| 1. मलिनकायः |
मनुष्यः |
| 2. विशालम् |
जगत् |
| 3. दिवङ्गतः |
शिवगुरुः |
| 4. विरक्तः |
शङ्करः |
| 5. चिन्तामग्ना |
आर्याम्बा |
6. सूचनानुसारं कृती: कुरुत ।
प्रश्न अ.
सः पठनार्थं गुरुमुपागच्छत् । (बहुवचनं कुरुत ।)
उत्तरम् :
ते पठनार्थं गुरुम् उपागच्छन्।

प्रश्न आ.
आचार्यः शिष्यगणेन सह गङ्गास्नानार्थं गच्छति स्म । (‘स्म’ निष्कासयत ।)
उत्तरम् :
आचार्यः शिष्यगणेन सह गङ्गास्नानार्थम् अगच्छत् ।
प्रश्न इ.
मात्रे प्रतिश्रुत्य सः गृहाद् निरगच्छत् । (पूर्वकालकवाचकं निष्कासयत ।)
उत्तरम् :
माने प्रत्यक्षुणोत् स: गृहाद् निरगच्छत् च।
प्रश्न ई.
यदा त्वं स्मरिष्यसि तदा एव त्वत्समीपमागमिष्यामि । (लकारं लिखत ।)
उत्तरम् :
शङ्कर: मातरं वदति।

प्रश्न उ.
आचार्यः तं प्रणनाम । (लङ्-लकारे परिवर्तयत ।)
उत्तरम् :
आचार्य : तं प्राणमत्।
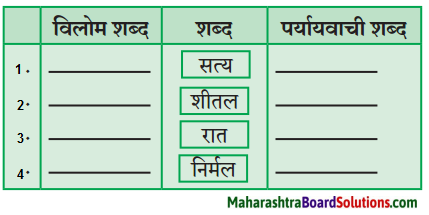
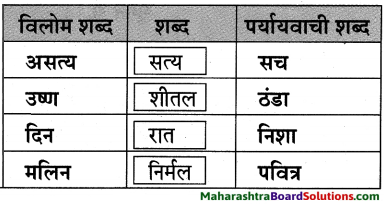
8. समानार्थकशब्दं लिखत ।
प्रश्न 1.
समानार्थकशब्दं लिखत
दिवङ्गतः, शीघ्रम्, चिन्तामना, मग्नः, नक्र:, पादः, पुत्रः, शिष्यः, ईश्वरः, पण्डितः, गृहम् ।
उत्तरम् :
- दिवङ्गतः – परिंगतः, परलोकगतः, मृतः।
- शीघ्रम् – झटिति, सत्वरम्, तूर्णम्, त्वरितम्।
- चिन्तामग्ना – चिन्ताकुला।
- मग्नः – लीनः, रत: व्यग्रः।
- नक्रः – मकरः, गुम्भीरः, कुटिचर:, मायादः ।
- पादः – चरण:, पदम्।
- पुत्रः . – तनयः, आत्मजः, सुतः, सूनुः ।
- शिष्यः – विद्यार्थी, छात्रः, अन्तेवासी।
- ईश्वरः – भगवान्, देवः, परमेश्वरः, सुरः।
- पण्डितः – विद्वान, विचक्षणः, बुधः।
- गृहम् – गेहम, सदनम्, निकेतनम्।

9. स्थानाधारण शब्दपेटिकां पूरयत ।
प्रश्न 1.
स्थानाधारण शब्दपेटिकां पूरयत
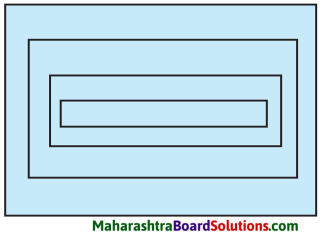
(कालडीग्रामः, केरलप्रदेशः, भारतदेशः, आलुवानगरम्,)
उत्तरम् :
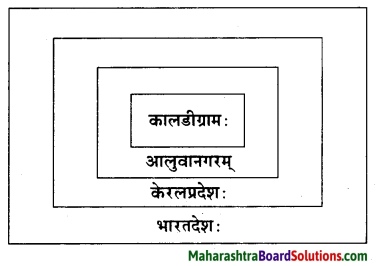
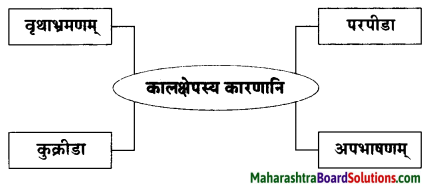
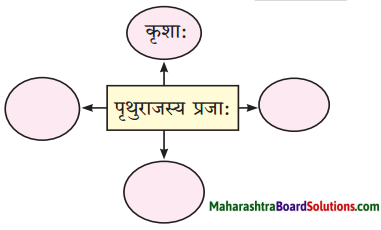
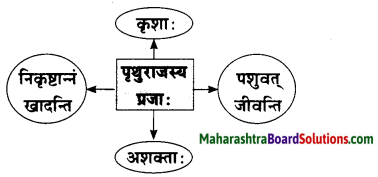
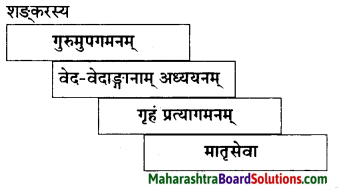
10. प्रवाहि जालचित्रं पूरयत ।
प्रश्न 1.
प्रवाहि जालचित्रं पूरयत ।
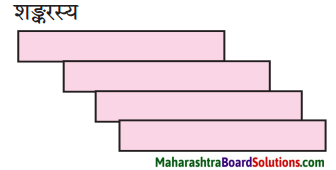
(गृहं प्रत्यागमनम्, गुरुमुपगमनम्, मातृसेवा, वेद-वेदाङ्गानाम् अध्ययनम्)
उत्तरम् :
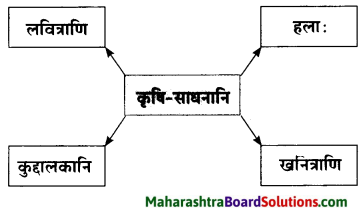
11. जालरेखाचित्रं पूरयत ।
प्रश्न अ.
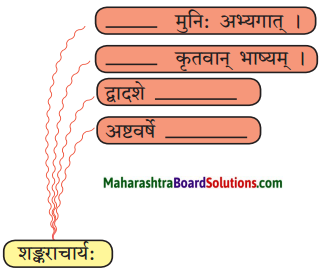
उत्तरम् :
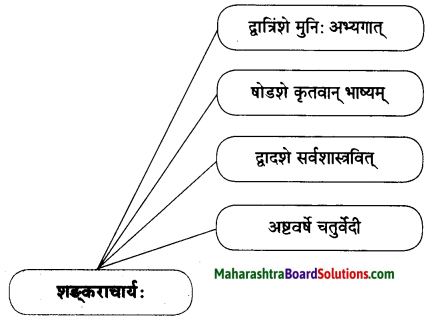
प्रश्न आ.
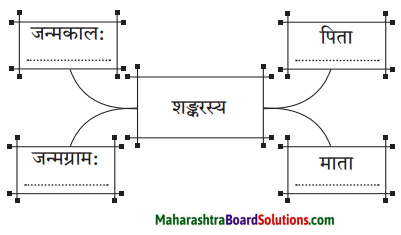
उत्तरम् :
Sanskrit Amod Class 10 Textbook Solutions Chapter 12 आदिशङ्कराचार्यः Additional Important Questions and Answers
अवबोधनम् :
(क) उचितं कारणं चित्वा वाक्यं पुनर्लिखत।
प्रश्न 1.
शङ्करस्य मातैव पुत्रस्य पालनम् अकरोत् यतः …………………
(अ) शङ्कराय केवलं माता अरोचत।
(ब) बाल्ये एव तस्य पिता शिवगुरुः दिवङ्गतः।
उत्तरम् :
(ब) बाल्ये एव तस्य पिता शिवगुरुः दिवङ्गतः।
प्रश्न 2.
आर्याम्बा चिन्तामग्ना जाता यतः ……………….
(अ) शङ्कर: ऐहिकविषयेषु अरुचिं प्रादर्शयत्।
(ब) शङ्करः ऐहिकविषयेषु रुचिं प्रादर्शयत्।
उत्तरम् :
(अ) शङ्करः ऐहिकविषयेषु अरुचिं प्रदर्शयत् ।

प्रश्न 3.
शङ्कर: उच्चैः आक्रोशत् यतः ………………
(अ) सः नदीजले अमज्जत्।
(ब) नक्र: तस्य पादम् अगृह्णात्।
उत्तरम् :
(ब) नक्र: तस्य पादम् अगृणात्।
प्रश्न 4.
आर्याम्बा रोदनम् आरभत यतः ………………………
(अ) शङ्करं नक्रेण गृहीतं दृष्ट्वा सा भीता जाता।
(ब) नक्र: तस्याः पादम् अगृह्णात्।
उत्तरम् :
(अ) शकरं नक्रेण गृहीतं दृष्ट्वा सा भीता जाता।
प्रश्न 5.
शङ्कर: मलिनकायं मनुष्य प्रणनाम यतः ………………………
(अ) मलिनकाय: मनुष्यः शङ्करं सङ्कटात् अरक्षत्।
(ब) स: मलिनकाय; मनुष्य: वेदान्तस्य सारं जानाति स्म।
उत्तरम् :
(ब) स: मलिनकाय; मनुष्य : वेदान्तस्य सारं जानाति स्म।

(ख) उचितं पर्यायं चित्वा वाक्यं पुनर्लिखत।
प्रश्न 1.
- शङ्करस्य ……………… शिवगुरुः आसीत्। (पिता/माता)
- ……………. एव शङ्करस्य पालनम् अकरोत्। (पिता / माता)
- पठनादिकं समाप्य शङ्करः …………. प्रत्यागतवान्। (गृह/नदी)
- ……. वयसि उपनीतः सः पठनार्थ गुरुम् उपागच्छत्। (पञ्चमे/दशमे)
उत्तरम् :
- पिता
- माता
- गृहं
- पञ्चमे
प्रश्न 2.
- आर्याम्बा पुत्रं ……. गृहीतम् अपश्यत्। (नक्रेण, मत्स्येन)
- शङ्करः …………… आर्ततया प्रार्थयत। (गुरुम्, मातरम्)
- शङ्कर: मातरं …………. महत्त्वम् अवाबोधयत्। (संन्यासस्य, संसारस्य)
- शङ्कराचार्य: …………… शिष्यः अभवत्। (गोविन्दहरदासानां गोविन्दभगवात्पादानां)
उत्तरम् :
- चक्रेण
- मातरम्
- संन्यासस्य
- गोविन्दभगवात्पादाना

प्रश्न 3.
- आचार्य: शिष्यगणेन सह …………. अगच्छत्। (गङ्गास्नानार्थम्/समुद्रस्नानार्थम्)
- यस्मात् ज्ञानं लभते सः ………….. (ज्येष्ठः / गुरु:)
- शिष्या: मलिनकायं मनुष्यं …………. इति अवदन्। (अपसर/आगच्छ)
- सर्वेषां …………….. पञ्चमहाभूतात्मकानि। (स्तोत्राणि / शरीराणि)
- स: ……… सिद्धान्तस्य प्रचारम् अकरोत्। (अद्वैत / परमाणु)
उत्तरम् :
- गङ्गास्नानार्थम्
- गुरु:
- अपसर
- शरीराणि
- अद्वैत
(ग) पूर्णवाक्येन उत्तरत।
प्रश्न 1.
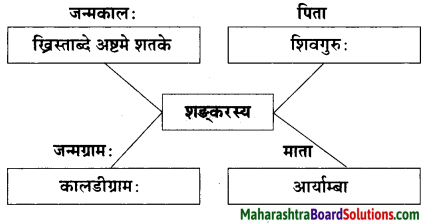
शङ्कराचार्यस्य जन्म कदा अभवत्?
उत्तरम् :
शङ्कराचार्यस्य जन्म ख्रिस्ताब्दे अष्टमे शतके अभवत्।
प्रश्न 2.
शङ्कर: गृहं प्राप्य किम् अकरोत् ?
उत्तरम् :
शङ्करः गृहं प्राप्य मातृसेवाम् आरभत।

प्रश्न 3.
किमर्थम् आर्याम्बा चिन्तामग्ना जाता?
उत्तरम् :
शङ्करस्य ऐहिकविषयेषु अरुचि दृष्ट्वा आर्याम्बा चिन्तामग्ना जाता।
प्रश्न 4.
शङ्कर: मातरं किं प्रार्थयत?
उत्तरम् :
शङ्कर: मातरम् प्रार्थयत यत् सः जीवितुं न शक्नोति। अत: मरणात् पूर्वं स: संन्यासी भवितुम् इच्छति।
प्रश्न 5.
शङ्कराचार्यानुसारेण कः गुरुः?
उत्तरम् :
शङ्कराचार्यानुसारेण यस्माद् ज्ञानं लभते स: गुरुः ।
(च) वाक्यं पुनलिखित्वा सत्यम् असत्यम् इति लिखत।
प्रश्न 1.
1. शङ्कराचार्यस्य जन्म एकोनविंशतितमे शतके अभवत्।
2. शङ्कर: अतीव प्रज्ञावान् बालकः ।
उत्तरम् :
1. असत्यम्।
2. सत्यम्।

शब्दज्ञानम्
(क) सन्धिविग्रहः।
- बालकोऽयम् – बालकः + अयम्।
- सदैव – सदा + एव।
- गृहीतमपश्यत् – गृहीतम् + अपश्यत्।
- तथैव – तथा + एव।
- इदानीमेव – इदानीम् + एव।
- नक्राद् मुक्तः – नक्रात् + मुक्तः ।
- जगद् एव – जगत् + एव।
- शिष्यो भूत्वा – शिष्यः + भूत्वा।
- यस्माद् ज्ञानम् – यस्मात् + ज्ञानम्।
- स गुरुः – सः + गुरुः।
- कोऽपि – कः + अपि।
- शरीराद् भिन्नम् – शरीरात् + भिन्नम्।
- त्वद् भिन्नः – त्वत् + भिन्नः ।
- कस्मादपि – कस्मात् + अपि।
- गुरुरेव – गुरु: + एव।
- तत्रैव – तत्र + एव।

(ख) त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि ।
| त्वान्त अव्यय धातु + त्वा / ध्या / ट्वा / वा / इत्वा/अयित्वा |
ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य |
तुमन्त अव्यय धातु + तुम् / धुम् / ट्म् / ट्म् / इतुम् अयित्वा |
| दृष्ट्वा, श्रुत्वा, भूत्वा |
समाप्य, प्राप्य, आगत्य |
भवितुम् |
(ग) प्रश्ननिर्माणं कुरुत।
प्रश्न 1.
माता आर्याम्बा पुत्रस्य विवाहविषये सदैव चिन्तयति स्म।
उत्तरम् :
माता आर्याम्बा कस्य विवाहविषये सदैव चिन्तयति स्म?
प्रश्न 2.
कालडी ग्राम : पूर्णानदीतीरे वर्तते।
उत्तरम् :
कालडी ग्रामः कुत्र वर्तते?

प्रश्न 3.
माता शङ्करस्य पालनम् अकरोत्।
उत्तरम् :
का पुत्रशङ्करस्य पालनम् अकरोत्?
प्रश्न 4.
शङ्करः गृहं प्राप्य मातृसेवाम् आरभत।
उत्तरम् :
शङ्करः गृहं प्राप्य किम् आरभत?
प्रश्न 5.
आर्याम्बा पुत्रं नक्रेण गृहीतम् अपश्यत्।
उत्तरम् :
आर्याम्बा कं नक्रेण गृहीतम् अपश्यत्?
प्रश्न 6.
शङ्कर: मातरं आर्ततया प्रार्थयत।
उत्तरम् :
शङ्कर: मातरं पूर्व कथं प्रार्थयत?

प्रश्न 7.
शङ्कर: मरणात् पूर्व संन्यासी भवितुम् इच्छति।
उत्तरम् :
शङ्कर: मरणात् पूर्व कः भवितुम् इच्छति?
प्रश्न 8.
विवशा माता शङ्कराय संन्यासार्थम् अनुमतिम् अयच्छत्।
उत्तरम् :
कीदृशी माता शङ्कराय संन्यासार्थम् अनुमतिम् अयच्छत्।
प्रश्न 9.
शङ्कर: मातरं संन्यासस्य महत्वम् अवाबोधयत्।
उत्तरम् :
शङ्कर: का संन्यासस्य महत्त्वम् अवाबोधयत्?
प्रश्न 10.
विशालं जगद् संन्यासिनः गृहम्।
उत्तरम् :
विशालं जगद् कस्य गृहम्?
प्रश्न 11.
वैदिकधर्मस्य स्थापनार्थ शङ्कर: प्रस्थानम् अकरोत्।
उत्तरम् :
किमर्थं शङ्करः प्रस्थानम् अकरोत् ?
प्रश्न 12.
दरिद्रः मनुष्य: मार्गे आचार्यस्य पुरतः आगच्छत्।
उत्तरम् :
कीदृशः मनुष्यः मार्गे आचार्यस्य पुरतः आगच्छत्?

प्रश्न 13.
आत्मा परमेश्वरस्य अंशः।
उत्तरम् :
कः परमेश्वरस्य अंश:?
प्रश्न 14.
आचार्यः षोडशे भाष्यं कृतवान्।
उत्तरम् :
आचार्यः कदा भाष्यं कृतवान् ?
(घ) विभक्त्यन्तरूपाणि।
- प्रथमा – सः, नक्र:, सा, अहम्, संन्यासी, त्वम्, सः, गुरुः, कः, जीर्णवस्त्रधारी, शिष्याः, आत्मा, अहम्, सः, सः, जन्म, पिता, माता, अयम्।
- द्वितीया – पादम्, मातरम्, अनुमतिम्, संन्यासम्, चरणौ, जगत, दीक्षाम्, सर्वाणि, दर्शनानि, ज्ञानम्, तम्, कम्, शरीरम, आत्मानम्, शरीराणि, गुरुम्, शास्त्राणि, सेवाम्।
- तृतीया – नक्रेण, आर्ततया, चेतसा। चतुर्थी – तुभ्यम्, मात्रे, गणेन, मनसा, वचसा, कर्मणा।
- पञमी – नक्रात्, वशात, तेभ्यः, गृहात्, शरीरात्, त्वत्, मुखात, कस्मात, यस्मात्।
- षष्ठी – मातुः, एकस्याः, धर्मस्य, तस्यतस्य, परमेश्वरस्य, सर्वेषाम्, तत्त्वस्य, नगरस्य, गुरोः, तस्य, पुत्रस्य, आचार्यस्य, शङ्करस्य।
- सप्तमी – एकस्मिन्, दिने, स्नाने, एकस्मिन्, दिने, मार्गे, द्वादशे, षोडशे, दिशि, प्रदेशे, तीरे, शतके, बाल्ये, पञ्चमे, वयसि।
- सम्बोधन – अम्ब, वत्स, मातः।

(च) विशेषण – विशेष्य – सम्बन्धः।
| विशेषणम् |
विशेष्यम् |
| 1. जगद्गुरोः |
शङ्कराचार्यस्य |
| 2. अष्टमे |
शतके |
| 3. दिवङ्गतः |
शिवगुरुः |
| 4. पञमे |
वयसि |
| 5. विरक्तः |
शङ्करः |
| 6. चिन्तामग्ना |
आर्याम्बा |
| 7. एकस्मिन् |
दिने |
| 8. एक: |
नक्र: |
| 9. भयाकुला |
सा |
| 10. विवशा |
माता |
| 11. विशालम् |
जगत् |
| 12. सर्वाणि |
दर्शनानि |
| 13. दरिद्र |
मनुष्यः |
| 14. मलिनकायः |
मनुष्यः |
| 15. जीर्णवस्त्रधारी |
मनुष्यः |
| 16. पञ्चमहाभूतात्मकानि |
शरीराणि |

(छ) लकारं लिखत।
प्रश्न 1.
शङ्करस्य पिता शिवगुरु: माता आर्याम्बा च आस्ताम्।
उत्तरम् :
लङ्लकारः
प्रश्न 2.
- यदा त्वं स्मरिष्यसि तदा एव त्वसमीपमागमिष्यामि।
- शङ्कर; उच्चैः आक्रोशत्।
- नक्रात् त्रायस्व।
- देहि अनुमतिम्।
- यथा तुभ्यं रोचते तथैव भवतु।
- इदानीमेव संन्यासं स्वीकुरु।
- शङ्कर: मातरं संन्यासस्य महत्वम् अवाबोधयत्।
उत्तरम् :
- लृट्लकारः
- लङ्लकारः
- लोट्लकारः
- लोट्लकारः
- लट्लकारः
- लोट्लकार:
- लङ्लकार:
प्रश्न 3.
- आचार्य: तं प्रणनाम।
- शिष्या: अपसर इति अवदन्।
- शिष्या: अपसर इति अवदन्।
उत्तरम् :
- लिट्लकार :
- लोट्लकार:
- लल्लकार:

पृथक्करणम्
1. क्रमेण योजयत।
- शङ्करस्य पठनार्थं गुरुं प्रति गमनम्।
- शिवगुरु: दिवङ्गतः।
- शङ्कराचार्यस्य जन्म।
- मात्रा शङ्करस्य पालनम्।
- गोविन्दभगवत्पादानां शिष्यत्वम्।
- मात्रै प्रतिश्रुत्य गृहात् निर्गमनम्।
- वैदिकधर्मस्य स्थापनार्थ प्रस्थानम्।
- मातरं संन्यासस्य महत्वबोधनम्।
- संन्यासार्थम् अनुमतियाचना।
- नक्रेण पादग्रहणम्।
- मात्रा अनुमतिप्रदानम्।
- शङ्करस्य आक्रोशः।
उत्तरम् :
- शङ्कराचार्यस्य जन्म।
- शिवगुरु: दिवङ्गतः।
- मात्रा शङ्करस्य पालनम्।
- शङ्करस्य पठनार्थं गुरुं प्रति गमनम्।
- मातरं संन्यासस्य महत्त्वबोधनम्।।
- मात्रे प्रतिश्रुत्य गृहात् निर्गमनम्।
- गोविन्दभगवत्पादानां शिष्यत्वम्।
- वैदिकधर्मस्य स्थापनार्थं प्रस्थानम्।
- नक्रेण पादग्रहणम्।
- शङ्करस्य आक्रोशः।
- संन्यासार्थम् अनुमतियाचना।
- मात्रा अनुमतिप्रदानम्।
(ग) कः कं वदति।
प्रश्न 1.
नक्रात् त्रायस्व!
उत्तरम् :
शङ्कर: मातरं वदति।

प्रश्न 2.
इतः परम् अहं न जीवामि।
उत्तरम् :
शङ्कर : मातरं वदति।
प्रश्न 3.
यथा तुभ्यं रोचते तथैव भवतु।
उत्तरम् :
माता शङ्करं वदति।
प्रश्न 4.
मम अनुमतिः अस्ति।
उत्तरम् :
माता शङ्करं वदति।
प्रश्न 5.
‘अपसर, अपसर!’
उत्तरम् :
शिष्या: मलि कायं / दरिद्रं / जीर्णवस्त्रधारिणं मनुष्यं वदन्ति।
प्रश्न 6.
आत्मा तु परमेश्वरस्य अंशः एव।
उत्तरम् :
दरिद्रः/मलिनकाय:/जीर्णवस्वधारी मनुष्य : शिष्यान् वदति।

प्रश्न 7.
कथं तव शरीरं मम शरीराद् भिन्नम्?
उत्तरम् :
दरिद्रः/मलिनकाय:/जीर्णवस्त्रधारी मनुष्य : शिष्यान् वदति।
(च) वाक्यं पुनलिखित्वा सत्यम् असत्यम् इति लिखत।
प्रश्न 1.
- सर्वेषां शरीराणि सप्तमहाभूतात्मकानि ।
- आचार्यः तत्रैव कनकधारास्तोत्रं रचितवान्।
- आत्मा तु ईश्वरस्य / भगवतः अंशः।
- आचार्य: दरिद्राय अकुप्यत्।
उत्तरम् :
- असत्यम्।
- असत्यम्।
- सत्यम्।
- असत्यम्।
(छ)
प्रश्न 1.
एष: गद्यांश: कस्मात् पाठात् उद्धृतः?
उत्तरम् :
एषः गद्यांश: ‘आदिशङ्कराचार्यः’ इति पाठात् उद्धृतः ।

पृथक्करणम्
(क) क्रमेण योजयत।
प्रश्न 1.
1. मार्गे मलिनकायपुरुषस्य आगमनम्।
2. शिष्यगणेन सह गङ्गास्नानार्थ गमनम्।
3. ‘मनीषापञ्चकम्’ इति स्तोत्रस्य रचना।
4. मलिनकायपुरुषस्य मुखात् वेदान्ततत्त्वसारस्य श्रवणम्।
उत्तरम् :
2. शिष्यगणेन सह गङ्गास्नानार्थं गमनम्।
1. मार्गे मलिनकायपुरुषस्य आगमनम्।
4. मलिनकायपुरुषस्य मुखात् वेदान्ततत्त्वसारस्य श्रवणम्।
3. ‘मनीषापञ्चकम्’ इति स्तोत्रस्य रचना।
भाषाभ्यासः
(क) समानार्थकशब्दाः
- अनुमतिः – अनुज्ञा।
- पिता – तातः, जनकः ।
- माता – अम्बा, जननी, जनयित्री।
- बाल्ये – शैशवे।
- श्रुत्वा – निशम्य, आकर्ण्य।
- दृष्ट्वा – अवलोक्य, विलोक्य, वीक्ष्य।
- चेतसा – मनसा ।
- दरिद्रः – निर्धनः, दीनः।
- शरीरम् – वपुः, देहम् ।
- गुरुः – उपाध्यायः, अध्यापकः, निषेकादिकृत्।

विरुद्धार्थकशब्दाः
- अनुमतिः × नकारः, अपतापः ।
- असाधारण: × साधारणः।
- समाप्य × आरभ्य ।
- झटिति × शनैः शनैः, मृदुः मुदुः ।
- रोदनम् × हास्यम्।
- अधुना × अनन्तरम्।
- मुक्तः × बद्धः।
- समीपम् × दूरम्।
- दरिद्रः × धनवान्।
- भिन्नः × समानः ।

(ग) पूर्वकालवाचकं निष्कासयत।
प्रश्न 1.
शङ्कर: गृहं प्राप्य मातृसेवाम् आरभत।
उत्तरम् :
शङ्कर: गृहं प्राप्नोत् मातृसेवाम् आरभत च।
प्रश्न 2.
प्रश्नं श्रुत्वा सर्वे आश्चर्यचकिताः अभवन्।
उत्तरम् :
प्रश्नं अश्रुण्वन् सर्वे आश्चर्यचकिता: अभवन् च।
(च) वचनं परिवर्तयत।
प्रश्न 1.
सः गृहात् निरगच्छत्। (बहुवचनं कुरुत।)
उत्तरम् :
ते गृहात् निरगच्छन्।

प्रश्न 2.
सः मनुष्यः अपृच्छत्। (बहुवचनं कुरुत।)
उत्तरम् :
ते मनुष्या: अपृच्छन्।
(छ) लकारं परिवर्तयत।
प्रश्न 1.
मम अनुमतिः अस्ति । (लङ्लकारे परिवर्तयत।)
उत्तरम् :
मम अनुमतिः आसीत्।

समासा:
| समस्तपदम् |
अर्थ |
समासविग्रहः |
समासनाम |
| भयाकुला |
perplexed with fear |
भयेन आकुला। |
तृतीया तत्पुरुष समास |
| अरुचिः |
no interest |
न रुचिः । |
नञ्तत्पुरुष समास |
| अनिच्छन्ती |
not desiring |
न इच्छन्ती। |
नञ्तत्पुरुष समास |
| मलिनकायः |
one who has unclean body |
मलिनः कायः यस्य सः। |
बहुव्रीहि समास |
| जीर्णवस्त्रधारी |
wearing torn clothes |
जीर्णवस्वं धारयति इति। |
उपपद तत्पुरुष समास |
| सर्वशास्वस्ववित् |
knows all scriptures |
सर्वशास्त्राणि वेत्ति इति। |
उपपद तत्पुरुष समास |
| पूर्णानदी |
river named पूर्णा |
पूर्णा नाम नदी। |
कर्मधारय समास |
| चिन्तामग्ना |
engrossed in worry |
चिन्तायां मग्ना। |
सप्तमी तत्पुरुष समास |
| मातृसेवा |
service to mother |
मातुः सेवा। |
षष्ठी तत्पुरुष समास |
आदिशङ्कराचार्यः Summary in Marathi and English
प्रस्तावना :
शंकराचार्य हे आठव्या शतकातील अद्वैत वेदांताचे उद्गाते व भारतीय तत्त्वज्ञ मानले जातात. शंकराचार्यांनी द्वारका, जगन्नाथपुरी, शृंगेरी व ज्योतिर्मठ येथे चार पीठे स्थापून त्यांच्या चार मुख्य शिष्यांना पीठासीन आचार्य नेमून आचार्य परंपरा घालून दिली व लोकांना मार्गदर्शन करणे सुरू ठेवले. त्यांनी प्रस्थानत्रयींवर (वेद, उपनिषदे, गीता) विपुल भाष्य लिहिले. तसेच त्यांनी आज प्रचलित असणाऱ्या अनेक काव्यात्मक स्तोत्रांची रचना केली.
‘आदिशङ्कराचार्यः’ या पाठामध्ये त्यांच्या जीवनातील दोन प्रसंग उद्धृत करण्यात आले आहेत. पहिल्या प्रसंगात, एका अटळ परिस्थितीत सापडले असताना, संन्यासी बनू इच्छिणाऱ्या शंकराचार्यांना त्यांची माता कशी अनुमती देते, याचे वर्णन आले आहे. दुसऱ्या प्रसंगातून शंकराचार्यांच्या शिकवणीचा उलगडा होतो. ती शिकवण अशी – जो (कोणी) ज्ञान देतो, तो गुरु मानावा.
शङ्कराचार्य runs an early eigth century Indian philosopher and theologian who consolidated the doctrine of अद्वैत वेदान्त. शङ्कराचार्य is reputed to have founded four mathas (monasteries) at द्वारका, जगन्नाथपुरी, शृंगेरी and ज्योतिर्मठ. He placed his primary four disciples to head it and guide people.
He wrote copious commentaries on the vedic canon (ब्रह्मसूत्र). principal उपनिषद् and भगवद्गीता. Also, he composed poetic words in the form of 45, which are prevalant even today. In the lesson, आदिशङ्कराचार्य:, two incidents of his life are given.
The first incident explains how आदिशङ्कराचार्य, who was keen to become a monk was granted by his mother for practising monkship, due to an inescapable situation. The second event unfolds आदिशङ्कराचार्य’s preaching – whosoever imparts knowledge is the preceptor.

परिच्छेदः 1
भारतस्य दक्षिणदिशि ……………… चिन्तामग्ना जाता।
अनुवादः

पहिला प्रसंग :
संन्यासाकरिता अनुमती मिळाली.
भारताच्या दक्षिणदिशेस, केरळ प्रदेशात आलुवा नगराच्या जवळ कालडी नावाचे गाव आहे. ते गाव पूर्णा नदीजवळ आहे. तेथे आठव्या शतकात जगद्गुरु शंकराचार्यांचा जन्म झाला.
शिवगुरु हे त्यांचे वडील आणि आर्यांबा त्यांची आई होती. लहानपणीच त्यांचे वडील शिवगुरु यांचे निधन झाले. त्यामुळे केवळ आईनेच मुलाचे पालनपोषण केले. जेव्हा ते पाच वर्षांचे झाले, तेव्हा मुंज झाल्यावर शिकण्यासाठी ते गुरुंजवळ गेले. तिथे या बालकाने वेद-वेदांगे व विविधशास्त्रे असामान्य वेगाने आत्मसात केली.
अभ्यास संपल्यावर शंकर घरी परतला. घरी परतल्यावर त्यांनी मातृसेवा सुरू केली. आर्यांबा सतत त्याच्या विवाहाचा विचार करत असे. पण मनाने, वाणीने व कर्माने (सांसारिक सुखापासून) विरक्त असलेल्या शंकरने आईकडे संन्यास घेण्याकरिता परवानगी मागितली. शंकराची ऐहिक विषयांतील नावड (अलिप्तता) पाहून आर्यांबा चिंतातुर झाल्या.
First incident :
Received permission for renunciation
In the southern direction of India, there is a village named कालडी near आलुवा city in केरळ region. That village is near पृर्णा river. There, the world’s preceptor 1844 was born in eight century CE. His father was शिवगुरु and mother was आर्यांम्बा.
In his childhood itself, his father शिवगुरु passed away. Therefore, the mother alone reared her son. He who was initiated at the age of five approached the preceptor for studying. There, this child acquired knowledge of वेद-वेदाङ्ग and many scriptures with exceptional speed. After completing studies, शङ्कर returned home.
After coming home, he started serving his mother. Mother आर्यांबा always used to think about his marriage. But, शङ्कर who was detached (from worldly objects) by mind (mentally), speech and by his deeds, asked for permission (from his mother) for renunciation. आर्यांबा was distressed seeing the disinterest of शङ्कर in worldly pleasures.

परिच्छेद: 2
एकस्मिन् दिने …….. प्रस्थानम् अकरोत्।
अनुवादः
एके दिवशी शंकर पूर्णानदीवर स्नानासाठी गेला. जेव्हा तो स्नान करण्यात मग्न होता, तेव्हा एक मगर तेथे आली.
मगरीने पटकन त्याचा पाय पकडला. तेव्हा शंकर जोरात ओरडला. “आई! मला वाचव! मगरीपासून मला वाचव!”
तो आक्रोश ऐकून, नदीवर पोहोचल्या आर्याबेने मुलाला मगरीने धरलेले पाहिले. भीतीने गांगरलेल्या तिनेही रडणे सुरू केले. शंकराने, आईला आर्ततेने विनवणी केली. “हे आई, यापुढे मी जगू शकणार नाही. मरण्यापूर्वी मला संन्यासी होण्याची इच्छा आहे. तेव्हा आता तरी मला अनुमती दे.”
मनात नसताना सुद्धा हतबल आई (त्याला) म्हणाली – “बाळा, जशी तुझी इच्छा आहे. तसेच होऊ दे. आताच संन्यास स्वीकार, माझी अनुमती आहे.” त्याच क्षणी आश्चर्य घडले. देवकृपेने मगरीने शंकराला मुक्त केले. नदीकाठी येऊन त्याने आईच्या चरणांना नमस्कार केला.
नंतर शंकरने आईला संन्यासाचे महत्व समजावून दिले. संन्यासी फक्त एकीचा पुत्र नाही. हे विशाल जगच, त्याचे घर आहे. ‘हे माते, तू जेव्हा माझी आठवण काढशील, तेव्हा मी तुझ्याकडे येईन’ असे आईला वचन देऊन तो घरातून निघून गेला.
त्यानंतर, गोविन्दभगवत्पादांचे शिष्य होऊन सर्व दर्शनांचे अध्ययन केले. त्यांच्याकडून संन्यासदीक्षा घेऊन वैदिक धर्म स्थापनेसाठी प्रस्थान केले.
One day शंकर went to the river पृर्णा for bathing, When he was busy in taking a bath, a crocodile came there. A crocodile caught his leg swiftly. At that time, शंकर screamed loudly. “O mother! Please save me. Save me from (this) a crocodile.”
Listening to the loud cry who had reached the riverbank आर्यांम्बा saw her son seized by the crocodile. Perplexed with fear, even she started crying. शंकर requested mother intensely. “O mother! Henceforth, I shall not live. I wish to become a monk, before I die. Now please give me permission.”
Unwillingly helpless mother said- “O child, whatever you wish, let it happen. Now itself you accept renunciation. I grant you permission.” At that very moment, a wonder happened. By god’s grace, शंकर was released by the crocodile. Coming to the river-bank, he bowed down to mother’s feet.
Later शड्कर made mother realised importance of renunciation. A monk is not a son of a lady alone. This big world itself is his home. He went from his house after assuring the mother ‘O mother, whenever you will remember me, I will come to you.” Then, he learnt all दर्शनs by becoming a desciple of गोविन्दभगवत्पाद.
He proceeded further to establish वैदिक धर्म, after receiving an initiation from them (गोविन्दभगवत्पाद) to (become a monk.

परिच्छेदः 3
एकस्मिन् दिने ……………….. मुनिरभ्यगात्।
अनुवादः
दुसरा प्रसंग

जो (कोणी) ज्ञान देतो, तो गुरु मानावा.
एके दिवशी, आचार्य शिष्यगणासोबत गंगानदीवर स्नान करण्याकरिता गेले. तेव्हा, रस्त्यात कोणीतरी गरीब, मलिन (मळकट) शरीर असलेला, फाटक कपड घातलला माणूस त्याच्या समार आला. त्याला पाहून ‘बाजूला हो, बाजूला हो’ असे शिष्य म्हणाले.
तेव्हा त्या माणसाने विचारले – “बाजूला हो, बाजूला हो” असे कोणास म्हणत आहात? शरीरास का आत्म्यास? खरेतर, आत्मा हा परमेश्वराचाच अंश आहे. म्हणून तो सर्वांमध्ये सारखाच आहे. तसेच, सर्वांची शरीरे पंचमहाभूतांनी युक्त आहेत. तर मग, तुमचे शरीर माझ्या शरीराहून भिन्न कसे व तुम्ही देखील माझ्याहून निराळे कसे?’ वेदांताचे सार (खरा अर्थ) त्याच्या मुखातून ऐकल्यावर आचार्यांनी त्याला नमस्कार केला. ज्ञान कोणाकडूनही ग्रहण केले पाहिजे.
‘जो कोणी ज्ञान देतो तो गुरु’ या विचाराने आचार्यांनी तेथेच ‘मनीषापञ्चकम्’ स्तोत्र रचले. अशा प्रकारे, आसेतुहिमाचल हिंडणाऱ्या त्यांनी अद्वैत तत्त्वज्ञानाचा प्रचार केला. मुनींनी (शंकराचायांनी) वयाच्या आठव्या वर्षी चार वेद जाणले. बाराव्या वर्षी सर्वशास्त्रांचे जाणकार झाले. सोळाव्या वर्षी भाष्यांची रचना केली. (आणि) बत्तीसाव्या वर्षी ते स्वगृही (पंचत्वात विलीन) निघून गेले.
Second incident :
Whosoever imparts knowledge is the preceptor.
One day, आचार्य went to the river गंगा for bathing along with his disciples. Then, on the way, a certain poor man having grubby body, wearing torn clothes came in front of him. Seeing him, desciples said to him loudly, “Get aside, go away.”
That man asked – “Whom do you ask to get aside? To the body or to the soul? Indeed, the soul is a part of god. Hence, it is similar among all. Likewise, all bodies consist of five eternal elements.
Then, how your body is different than my body? and how am I different than you? Having heard the essence (real meaning) of वेदान्त from his mouth, आचार्य (preceptor) saluted him. Knowledge should be acquired from anyone.
Whosoever imparts knowledge is the preceptor, with such thought आचार्य composed ‘मनीषापञ्चकम्’ स्तोत्र there itself. In this way, he propogated and philosophy wandering all over India.
He (शङ्कराचार्य) grasped the four वेदs at the age of eight, he mastered all the scriptures at the age of twelve. He composed (magnificent) भाष्य (commentary) at the age of sixteen. He reached the heavenly abode at the age of thirty-two.

शब्दार्थाः
- दिवङ्गतः – passed away – वारले
- विरक्तः – detached – विरक्त
- अधीतवान् – studied – अभ्यास केला
- अनुमतिः – permission – परवानगी
- चिन्तामग्ना जाता – was distressed – चिंतातुर झाली
- वचसा – by speech – वाणीने
- जगद्गुरोः – of the world’s preceptor – जगद्गुरुंचा
- ऐहिकविषयेषु – in worldly pleasures – सांसारिक सुखामध्ये
- संन्यासार्थम् – for renunciation – संन्यास घेण्यासाठी
- मग्न: – engaged – मग्न होते
- नक्र: – crocodile – मगर
- संन्यास – renunciation – ऐहिक जगाचा त्याग
- भयाकुला – perplexed with fear – भीतीने गांगरलेली
- विवशा – helpless – हतबल
- अनिच्छन्ती – not desiring – इच्छा नसताना
- आर्ततया – intensely – आर्ततेने
- अगृह्णात् – caught – पकडले
- आक्रोशत् – screamed – ओरडला
- अवाबोधयत् – made realise – समजावून दिले
- त्रायस्व – please save – वाचव
- प्रतिश्रुत्य – having promised – वचन देऊन
- झटिति – quickly /swiftly – झटकन/पटकन
- इत:परम् – henceforth – यापुढे
- प्रस्थानम् अकरोत् – set off – प्रस्थान केले
- जीर्णवस्वधारी – one who was wearing tom clothes – फाटके-तुटके कपडे घातलेला
- आत्मा – soul – आत्मा
- सर्वशास्त्रवित् – knower of all scriptures – सर्व शास्त्रे जाणणारा
- पर्यटन् – wandering – हिंडून
- सारम् – essence (real meaning) – सार (मूलतत्त्व)
- ग्रहाम् – should be comprehended – ग्रहण करण्यायोग्य
- पञ्चमहाभूता – consisting of five – पंचमहाभूतांनी युक्त
- त्मकानि – eternal elments
- आसेतुहिमाचलम् – from Himalyas to सेतू (whole India) – हिमालयापासून सेतू (संपूर्ण भारत)
- अपसर – get aside/go back – बाजूला हो/मागे हो
- प्रणनाम – saluted – नमस्कार केला
- प्रचारम् अकरोत् – propogated – प्रचार केला
Aamod Sanskrit Book 10th Class Solutions
![]()
![]()
![]()
![]()