Prasanna

Problems on Measurement Class 5 Problem Set 46 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 11 Problems on Measurement Problem Set 46 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 11 Problems on Measurement

Question 1.
Add :

(1) ₹ 9, 50 paise + ₹ 14, 60 paise
Solution:

₹	Paise
1
9 + 14	5 0 6 0
2 4	1 0

50 paise + 60 paise
= 110 paise
= 1 ₹ 10 paise
∴ ₹ 24, 10 paise

(2) 6 cm 5 mm + 7 cm 9 mm
Solution:

cm	mm
1
6 + 7	5 9
1 4	4

5 mm + 9 mm
= 14 mm 14 mm
= 1 cm 4 mm
∴ 14 cm 4 mm

(3) 22 m 50 cm + 25 m 75 cm
Solution:

m	cm
1
2 2 + 2 5	5 0 7 5
4 8	2 5

50 cm + 75 cm
= 125 cm
= 1 m 25 cm
∴ 48 m 25 cm

(4) 15 km 740 m + 13 km 950 m
Solution:

km	m
1
1 5 + 13	7 4 0 9 5 0
2 9	6 9 0

740 m + 950 m
= 1690 m 1690 m
= 1km 690 m
∴ 29 km 690 m

(5) 25 kg 650 g + 29 kg 770 g
Solution:

kg	gm
1
2 5 + 29	6 5 0 7 7 0
5 5	4 2 0

650 gm + 770 gm
= 1420 gm
= 1 kg 420 gm
∴ 55 kg 420 gm

(6) 19l 840ml + 25l 250ml
Solution:

l	ml
1 1
1 9 + 2 5	8 4 0 2 5 0
4 5	0 9 0

840 ml + 250 ml
= 1090 ml
= 11 + 90 ml
∴ 45 l 90 ml

Question 2.
Subtract :

(1) ₹ 19, 50 paise – ₹ 12, 60 paise
Solution:

₹	Paise
1 8	1 5 0
1 9 – 1 2	5 0 6 0
6	9 0

We cannot subtract 60 paise from 50 paise. So convert 1 ₹ into 100 paise.
₹ 6, 90 paise

∴ ₹ 6, 90 paise

(2) 24 cm 2 mm – 3 cm 8 mm
Solution:

cm	mm
2 3	1 2
2 4 – 3	2 8
2 0	4

We cannot subtract 8 mm from 2 mm. So, convert 1 cm = 10 mm

∴ 20 cm 4 mm

(3) 20 m 30 cm – 17 m 60 cm
Solution:

m	cm
1 9	1 3 0
2 0 – 1 7	3 0 6 0
2	. 7 0

We cannot subtract 60 cm from 30 cm. So, convert 1 m = 100 cm

∴ 2 m 70 cm

(4) 40 km 255 m – 17 km 960 m
Solution:

km	m
3 9	12 2 5
4 0 -1 7	2 2 5 9 6 0
2 2	2 6 5

We cannot subtract 960 m from 225 m. So, convert 1 km = 1000 m

∴ 22 km 265 m

(5) 35 kg 150 g – 26 kg 470 g
Solution:

kg	gm
3 4	1 1 5 0
3 5 – 2 6	1 5 0 4 7 0
8	6 8 0

We cannot subtract 470 gm from 150 gm. So, convert I kg= 1000gm

∴ 8 kg 680 gm

(6) 46 l 200 ml – 38 l 750 ml
Solution:

l	ml
4 5	1 2 0 0
4 6 – 3 8	2 0 0 7 5 0
7	4 5 0

We cannot subtract 750 ml from 200 ml. So, convert 1 l = 1000 ml

∴ 7 l 450 ml

Word problems

Study the following examples.

Example (1) If a shopkeeper has 150 kg 500 g of rice and sells 75 kg 750 g, how much rice will be left?

74 kg 750 g of rice is left.

Example (2) A can of milk has 20 l 450 ml of milk. Another can has 18 l 800 ml. How much milk is there in the two cans altogether?

The total quantity of milk is 39l 250ml.

Example (3) At a speed of 90 km per hour, what distance will a train cover in two and a half hours?

The speed of the train is 90 kmph. That is, it travels 90 km in one hour. It travels 90 more km in the second hour.
In the next half an hour, 90 ÷ 2 = 45 km
The total distance travelled is 90 + 90 + 45 = 225 km.

Example (4) If one dress requires 3 m 25 cm of cloth, how much do 4 dresses need?

Manju’s method :
3 m 25 cm for the 1st dress
+ 3 m 25 cm for the 2nd dress
+ 3 m 25 cm for the 3rd dress
3 m 25 cm for the 4th dress
_________
12 m 100 cm
1 m is 100 cm, therefore 12 + 1 = 13 m

Example (5)
If a wire that is 9 m 50 cm long is cut into pieces of 5 cm each, how many pieces will be made?
9 m 50 cm = (900 + 50) cm
To find out how many pieces of 5 cm can be made from a wire 950 cm long, let us use division.
190 pieces will be made.

Example (6) A play started at 30 minutes past 6 in the evening and finished two and three quarter hours later. What time did the play get over?

The play got over at 15 minutes past 9 at night.

Note : The units for length, mass and capacity are written in decimal form. This makes it easy to carry out addition and subtraction of length, mass and capacity.

Units of measuring time are not in decimal form. It is a little more difficult to carry out additions and subtractions of those quantities.

Problems on Measurement Problem Set 46 Additional Important Questions and Answers

Add the following:

(1) 12 km 880 m + 7 km 620 m
Solution:

km	m
1
1 2 + 7	8 8 O 6 2 0
2 0	5 0 0

880m + 620 m = 1500 m
= 1km 500 m
∴ 20 km 500 m

(2) ₹ 62, 45 paise + ₹ 37, 55 paise
Solution:

₹	Paise
1
6 2 + 3 7	4 5 5 5
1 0 0	0 0

45 paise + 55 paise
100 paise = 1 ₹
∴ 100 rupees

Subtract the following:

(1) 15 m 15 cm – 4 m 65 cm
Solution:

kg	gm
1 4	1 1 5
1 5 – 4	1 5 6 5
1 0	5 0

We cannot subtract 65 cm from 15 cm. So, convert l m = 100 cm
∴ 10 m 50 cm

(2) 29 kg 880 gm – 8 kg 900 gm
Solution:

kg	gm
2 8	1 8 8 0
2 9 – 8	8 8 0 9 0 0
2 0	9 8 0

We cannot subtract 900 gin from 880 gm. So, convert 1 kg = 1000 gm
∴ 20 kg 980 gm

Class 5 Maths Solution Maharashtra Board

• Problems on Measurement Problem Set 46 Class 5 Maths Solutions
• Problems on Measurement Problem Set 47 Class 5 Maths Solutions
• Perimeter and Area Problem Set 48 Class 5 Maths Solutions
• Perimeter and Area Problem Set 49 Class 5 Maths Solutions
• Perimeter and Area Problem Set 50 Class 5 Maths Solutions

Multiplication and Division Class 5 Problem Set 15 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 4 Multiplication and Division Problem Set 15 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 4 Multiplication and Division

Question 1.
Solve the following and write the quotient and remainder.
(1) 1284 ÷ 32
Solution :

Quotient = 40
Remainder = 4

(2) 5586 ÷ 87
Solution :

Quotient = 64
Remainder =18

(3) 1207 ÷ 27
Solution:

Quotient = 44
Remainder =19

(4) 8543 ÷ 41
Solution :

Quotient = 208
Remainder =15

(5) 2304 ÷ 43
Solution:

Quotient = 53
Remainder = 25

(6) 56,741 ÷ 26
Solution:

Quotient =2182
Remainder = 9

Question 2.
How many hours will it take to travel 336 km at a speed of 48 km per hour?
Solution:
Time = Distance ÷ Speed

Answer:
It will take 7 hours.

Question 3.
Girija needed 35 cartons to pack 1400 books. There are an equal number of books in every carton. How many books did she pack into each carton?
Solution:
No. of cartons x No. of books in each carton = Total no. of books 35 x No. of books in each carton = 1400 No. of books in each carton = 1400 35

Answer:
She packs 40 books in each carton.

Question 4.
The contribution for a picnic was 65 rupees each. Altogether, 2925 rupees were collected. How many had paid for the picnic?
Solution:

Answer:
45 persons paid for the picnic.

Question 5.
Which number, on being multiplied by 56, gives a product of 9688?
Solution:

Answer:
173

Question 6.
If 48 sheets are required for making one notebook, how many notebooks at the most will 5880 sheets make and how many sheets will be left over?
Solution:

Answer:
122 notebooks can be made and 24 sheets left over.

Question 7.
What will the quotient be when the smallest five-digit number is divided by the smallest four-digit number?
Solution:
Smallest five-digit number is 10,000 and smallest four-digit number is 1,000.
So, 10000 ÷ 1000 = 10

Answer:
Quotient = 10

Mixed examples

A farmer brought 140 trays of chilli seedlings. Each tray had 24 seedlings. He planted all the seedlings in his field, putting 32 in a row. How many rows of chillies did he plant?

Let us find out the total number of seedlings when there were 24 seedlings in each of the 140 trays. We shall multiply 140 and 24.

Total number of seedlings 3,360.
To find out how many rows were planted with 32 seedlings in each row, we shall divide 3,360 by 32.
The quotient is 105.
Therefore, the number of rows is 105.
Carry out the multiplication of 105 × 32 and verify your answer.

Multiplication and Division Problem Set 15 Additional Important Questions and Answers

Solve the following and write the quotient and remainder.

(1) 9148 ÷ 37
Solution

Quotient = 247
Remainder = 9

(2) 1175 ÷ 15
Solution :

Quotient =78
Remainder = 5

Solve the following word problems:

(1) If 45 kg of sugar cost 1305 rupees, what is the rate of sugar per kg?
Solution:

Answer:
The rate per kg of sugar is 29 rupees.

(2) 17 people spent ₹ 83,475. How much did each person spend and what is the amount left?
Solution:

Answer:
Each person spent ₹ 4,910 and the amount left is ₹ 5

Class 5 Maths Solution Maharashtra Board

• Multiplication and Division Problem Set 14 Class 5 Maths Solutions
• Multiplication and Division Problem Set 15 Class 5 Maths Solutions
• Multiplication and Division Problem Set 16 Class 5 Maths Solutions

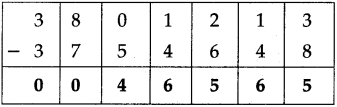
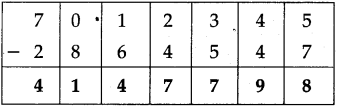
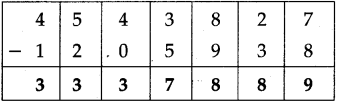
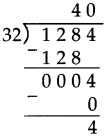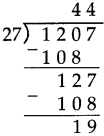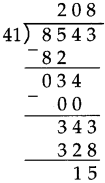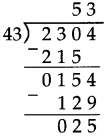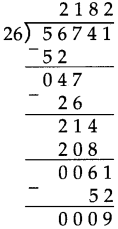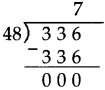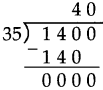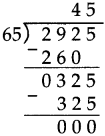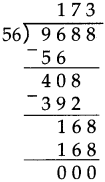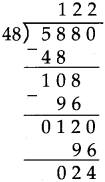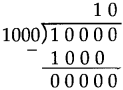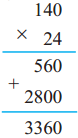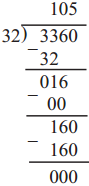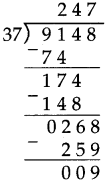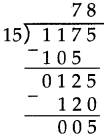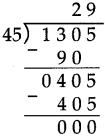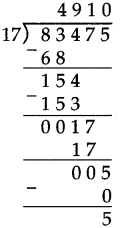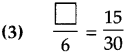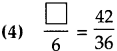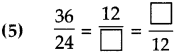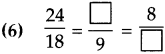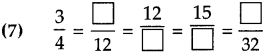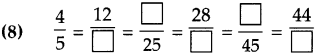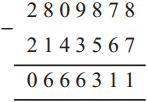Number Work Class 5 Problem Set 6 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 2 Number Work Problem Set 6 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 2 Number Work

Question 1.
Write the proper symbol, ‘<’ or ‘>’ in the box.
(1) 5,705 [ < ] 15,705
(2) 22,74,705 [  ] 12,74,705
(3) 35,33,302 [  ] 35,32,302
(4) 99,999 [  ] 9,99,999
(5) 4,80,009 [  ] 4,90,008
(6) 35,80,177 [  ] 35,88,172
Answer:
(1) <
(2) >
(3) >
(4) <
(5) <
(6) <

Question 2.
Solve the problems given below.

(1) The Swayamsiddha Savings Group made 3,45,000 papads while the Swabhimani Group made 2,95,000. Which group made more papads?
Answer:
Here, 3,45,000 > 2,95,000
Hence, the Swayamsiddha saving group made more papads.

(2) Children of the Primary School in Ahmadnagar District collected 2,00,000 seeds while those in Pune District collected 3,25,000. Which children collected more seeds?
Answer:
Here, 3,25,000 > 2,00,000
Hence, Pune District children collected more seeds.

(3) The number of people who took part in the Republic Day flag hoisting ceremony was 2,01,306 in Pandharpur taluka and 1,97,208 in Malshiras taluka. In which taluka did a larger number of people participate?
Answer:
Here, 2,01,306 > 1,97,208
Hence, people of Pandharpur taluka participated in larger number

(4) At an exhibition, the Annapoorna Savings Group sold goods worth 5,12,345. The Nirman Group sold goods worth 4,12,900. This figure was 4,33,000 for the Srujan Group and 5,11,937 for the Savitribai Phule group.

Which group had the largest sales?

Which group had the smallest?

Write the sales figures in ascending order.
Answer:
Among the numbers 5,12,345; 4,12,900; 4,33,000; 5,11,937

5,12,345 is largest and 4,12,900 is smallest. Hence, Annapoorna group had the largest sale and Nirman Group had the smallest sales.

Sales in ascending order

4,12,900 < 4,33,000 < 5,11,937 < 5,12,345

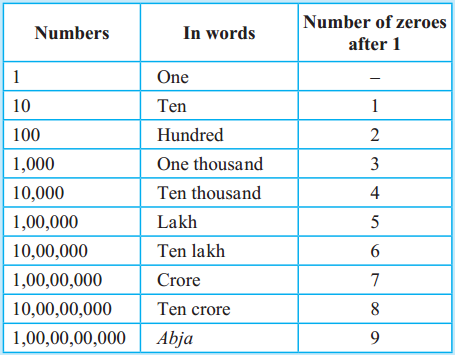
Introducing crores

99,99,999 is the biggest seven-digit number. On adding the number 1 to it, we get the smallest eight-digit number, 1,00,00,000. We read this number as ‘one crore’. The new place created to write this number is called the ‘crores’ place.

From the following examples, you can learn to read eight-digit numbers.

Number – Reading

8,45,12,706 – Eight crore forty-five lakh twelve thousand seven hundred and six
5,61,63,589 – Five crore sixty-one lakh sixty-three thousand five hundred and eighty-nine
6,09,04,034 – Six crore nine lakh four thousand and thirty-four

Something more

On the left of the crores place are the places for ten crores, abja, and ten abja in that order. The place value of each of these is ten times the value of the one on its right. According to the Census of the year 2011, the population of our country is 1,21,01,93,422. We read this as ‘one Abuja twenty-one crore one lakh ninety-three thousand four hundred and twenty-two.

Roman Numerals Problem Set 4 Additional Important Questions and Answers

Question 1.
Write the proper symbol, ‘<‘ or ‘>’ in the box.
(1) 68,34,170 [     ] 8,43,170
(2) 5,04,132 [     ] 5,04,123
(3) 1,01,001 [     ] 1,00,101
(4) 14,55,432 [     ] 4,54,532
Answer:
(1) >
(2) >
(3) >
(4) >

Question 2.
Write the numbers in words.

(1) 15,97,21,409
Answer:
Fifteen crore, ninety-seven lakh, twenty-one thousand, four hundred and nine

(2) 99,99,99,999
Answer:
Ninety-nine crore, ninety-nine lakh, ninety- nine thousand, nine hundred and ninety nine.

(3) 7,54,21,607
Answer:
Seven crore, fifty-four lakh, twenty-one thousand, six hundred and seven.

(4) 5,16,36,854
Answer:
Five crore, sixteen lakh, thirty-six thousand, eight hundred and fifty four.

Question 3.
Write in figures.

(1) One crore, fifteen lakh, fifty-nine thousand, seven hundred and four
Answer:
1,15,59,704

(2) Sixty-five crore, seventy lakh, fifty thousand and thirty nine
Answer:
65,70,50,039

(3) Four crore, fifty-nine lakh, fourty-three thousand, five hundred and thirty four
Answer:
4,59,43,534

(4) Eighteen crore, seventy-six lakh, fifty-four thousand and one
Answer:
18,76,54,001

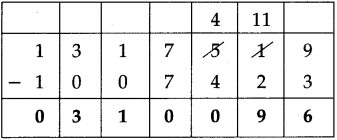
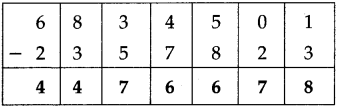
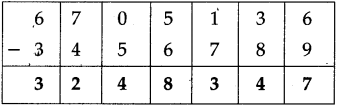
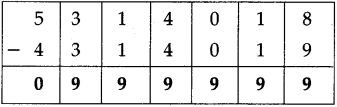
Question 4.
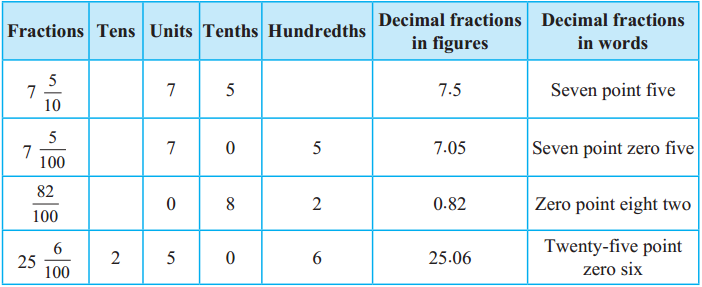
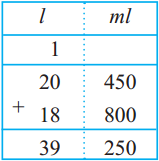
Fill in the blanks in the table below:

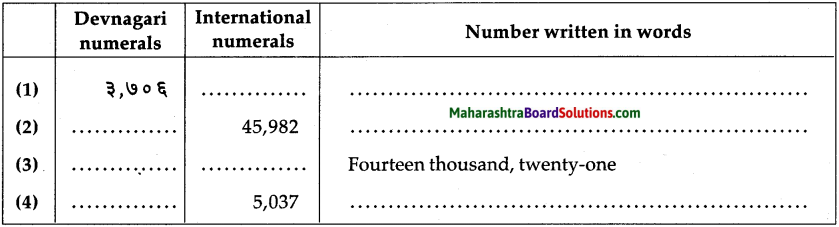
Answer:

Question 5.
Write the following numbers in words.
(1) 17,301
(2) 45,019
(3) 40,018
(4) 28,740
Answer:
(1) Seventeen thousand, three hundred and one.
(2) Forty-five thousand and nineteen.
(3) Forty thousand and eighteen
(4) Twenty-eight thousand seven hundred and forty

Question 6.
How many rupees do they make?
(1) 8 notes of rupees 2,000, 3 notes of rupees 100,11 notes of rupees 10.
Answer:
16,410

(2) 9 notes of rupees 2,000, 18 notes of rupees 100,18 notes of rupees 50,18 notes of rupees 10.
Answer:
20,880

(3) Write the smallest and the biggest five-digit numbers that can be made using the digits only once.
(a) 6, 8, 0,1, 9
(b) 3, 5,1,2, 8
Answer:
Smallest number : (i) 10,689 (ii) 12358
Biggest number : (i) 98,610 (ii) 85321

(4) Write the smallest and the biggest number from the following numbers.
(a) 35,798
(b) 39,785
(c) 39,587
(d) 35,789
Answer:
Smallest number : 35,789
Biggest number : 39,785

(5) Write the number from the given number which is neither biggest nor smallest.
(a) 45, 798
(b) 45, 789
(c) 45, 897
Answer:
45,798.

(6) Write the biggest and the smallest three-digit numbers that can be made using the digits 0,1, 2, 3, 4, 5, 6, 7, 8, 9 only once.
Answer:
Biggest three-digit number : 987
Smallest three-digit number : 102

Question 7.
Read the numbers and write them in words.
(1) 2,65,048
(2) 1,80,794
(3) 1,06,709
(4) 8,80,006
Answer:
(1) Two lakh sixty-five thousand and forty- eight,
(2) One lakh eighty thousand seven hundred and ninety-four.
(3) One lakh six thousand seven hundred and nine.
(4) Eight lakh eighty thousand and six.

Question 8.
Read the numbers and write them in figures.
(1) Two lakh five thousand three hundred and six.
(2) Six lakh and six
(3) Nine lakh forty thousand and thirty seven.
(4) Five lakh ninety-nine thousand and fifteen.
Answer:
(1) 2,05,306
(2) 6,00,006
(3) 9,40,037
(4) 5,99,015

Question 9.
Write six, six-digit numbers using the digits 0,.3,5,7,9,1 only once with 9 lakh fifty-seven thousand in all numbers.
Answer:
(1) 9,57,301
(2) 9,57,310
(3) 9,57,103
(4) 9,57,130
(5) 9,57,013
(6) 9,57,031

Question 9.
(A) Match the columns:

(A)	(B)
(1) Nine lakh nine thousand nine	(a) 9,09,090
(2) Nine lakh june thousand nine hundred nine	(b) 9,90,090
(3) Nine lakh nine thousand ninety	(c) 9,09,009
(4) Nine lakh ninety thousand ninety	(d) 9,09,909

Answer:
(1 – c),
(2 – d),
(3 – a),
(4 – b)

(B) Match the columns:

(A)	(B)
(1) Thirty-three lakh, three thousand and three	(a) 33,30,300
(2) Thirty-three lakh, thirty thousand, three hundred	(b) 33,03,003
(3) Thirty lakh, three thousand and thirty.	(c) 30,30,003
(4) Thirty lakh, thirty thousand and three	(d) 30,03,030

Answer:
(1 – b),
(2 – a),
(3 – d),
(4 – c)

Question 10.
Read the numbers and write them in words.
(1) 34,87,569
(2) 70,85,039
(3) 48,07,102
(4) 67,40,960
(5) 88,00,080
(6) 40,40,004
Answer:
(1) Thirty-four lakh, eighty-seven thousand, five hundred and sixty-nine.
(2) Seventy lakh, eight-five thousand and thirty-nine.
(3) Forty-eight lakh, seven thousand, one hundred and two.
(4) Sixty-seven lakh, forty thousand, nine hundred and sixty.
(5) Eighty-eight lakh and eighty.
(6) Forty lakh, forty thousand and four.

Question 11.
Read the numbers and write them in figures.
(1) Fifty-nine lakh, seven thousand, seventeen.
(2) Twenty-two lakh, ten thousand, five hundred.
(3) Fifty-two lakh, twenty-five thousand, four hundred and fifteen.
(4) Thirty lakh, thirty thousand and thirty.
Answer:
(1) 59,07,017
(2) 22,10,500
(3) 52,25,415
(4) 30,30,030

Question 12.
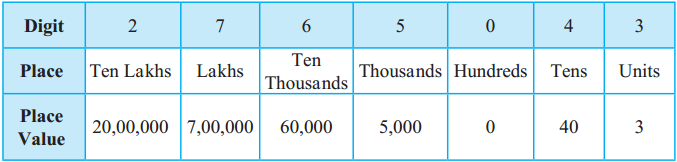
Write the place value of the underlined digit.
(1) 68,03,512
(2) 3,42,157
(3) 84,52,170
(4) 79,345
(5) 38,14,093
(6) 8,10,618
(7) 35,10,387
Answer:
(1) 8,00,000
(2) 40,000
(3) 2,000
(4) 5
(5) 90
(6) 600
(7) 30,00,000

Question 13.
Write the numbers in their expanded form.
(1) 78,15,692
(2)50,95,182
(3)6,40,078
(4) 9,58,802
Answer:
(1) 70,00,000 + 8,00,000 + 10,000 + 5,000 + 600 + 90 + 2
(2) 50,00,000 + 90,000 + 5,000 + 100 + 80 + 2
(3) 6,00,000 + 40,000 + 70 + 8
(4) 9,00,000 + 50,000 + 8,000 + 800 + 2

Question 14.
Write the place name and place value of each digit in the following numbers.
(1) 27,306
(2) 1,70,425
(3) 75,68,041
(4) 55,555
Answer:
(1) 27,306
(2) 1,70,425
(3) 75,68,041
(4) 55,555

Question 15.
The expanded form of the number is given. Write the number.
(1) 70,000 + 6,000 + 500 + 40 + 8
(2) 8,00,000 +-30,000 + 5,000 + 400 + 3
(3) 60,00,000 + 2,00,000 + 70 + 4
(4) 20,00,000 + 5,00,000 + 900 + 5
Answer:
(1) 76,548
(2) 8,35,403
(3) 62,00,074
(4) 25,00,905

Question 16.
Considering the number 50,43,176.
Fill in the blanks.
(1) The digit in the ten thousand place is ……………………………………….. .
(2) Place value of 1 is ……………………………………….. .
(3) The digit in the lakhs place is ……………………………………….. .
(4) Place value of 5 is ……………………………………….. .
(5) The digit 7 is in ……………………………………….. place.
Answer:
(1) 4
(2) 100
(3) 0
(4) 50,00,000
(5) tens

Question 17.
Write the proper symbols ‘<‘ or ‘>’ in the box.
(1) 12,625 [     ] 21,526
(2) 23,564 [     ] 23,546
(3) 36,60,660 [     ] 36,60,606
(4) 89,14,507 [     ] 89,15,407
Answer:
(1) <
(2) >
(3) >
(d) <

Question 18.
Solve the problems given below.
(1) Population of city A is 8,57,238 and that of city B is 8,75,461. Population of which city is more?
Answer:
city B

(2) Yearly income of Rajnikant is? 3,48,600 and that of Shashikant is? 3,46,500. Whose income is less?
Answer:
Shashikant

Question 19.
Profit of the four companies A, B, C, D is as follows.

Now, answer the following questions.
(1) Which company made maximum profit?
(2) Which company made minimum profit?
(3) Write the profit of the companies in the descending order.
Answer:
(1) B
(2) C
(3) profit of company B > D > A > C

Question 20.
In a certain election, candidates : Tavade, Patel, Chauhan, and Shinde got the votes as follows.

Now, answer the following questions.
(1) Who got the highest number of votes?
(2) Who got the least number of votes?
(3) Write the number of votes obtained in the ascending order.
Answer:
(1) Patel
(2) Shinde
(3) 34,67,008 < 37,51,386 < 43,51,239 < 48,00,173

Question 21.
Compare the following using >, < or = signs.
(1) 3,97,48,632 [     ] 3,97,58,632
(2) 1,50,15,178 [     ] 1,50,15,780
(3) 3,74,98,561 [     ] 96,42,748
(4) 30,49,75,831 [     ] 30,49,00,831
Answer:
(1) <
(2) <
(3) >
(4) >

Question 22.
Circle the correct answer:
(1) Mark periods 617231801 according to the Indian Number system.
(a) 61,72,31,801
(b) 16,172,31
(c) 617,231,801
Answer:
(a) 61,72,31,801

(2) Mark periods 90289164 according to the international Number system.
(a) 9,0289,164
(b) 902891,64
(c) 90,289,164
Answer:
(c) 90,289,164

(3) 1,00,00,000 is read as ……………………………….. .
(a) ten crore
(b) one crore
(c) hundred thousand
Answer:
(b) one crore

Class 5 Maths Solution Maharashtra Board

• Roman Numerals Problem Set 1 Class 5 Maths Solutions
• Number Work Problem Set 2 Class 5 Maths Solutions
• Number Work Problem Set 3 Class 5 Maths Solutions
• Number Work Problem Set 4 Class 5 Maths Solutions
• Number Work Problem Set 5 Class 5 Maths Solutions 
• Number Work Problem Set 6 Class 5 Maths Solutions

Fractions Class 5 Problem Set 23 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 23 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 5 Fractions

Question 1.
What is \(\frac{1}{3}\) of each of the collections given below?

(1) 15 pencils
(2) 21 balloons
(3) 9 children
(4) 18 books
Answer:
(1) 15 pencils → \(\frac{1}{3}\) of 15 = 5, 15 ÷ 3 = 5 pencils.
(2) 21 baloons → \(\frac{1}{3}\) of 21 = 7,21 ÷ 3 = 7 baloons.
(3) 9 children → \(\frac{1}{3}\) of 9 = 3, 9 ÷ 3 = 3 chi1dren.
(4) 18 books → \(\frac{1}{3}\) of 18 = 6, 18 ÷ 3 = 6 books.

Question 2.
What is \(\frac{1}{5}\) of each of the following?
(1) 20 rupees
(2) 30 km
(3) 15 litres
(4) 25 cm
Answer:
(1) 20 rupees → \(\frac{1}{5}\) of 20 = 4, 20 ÷ 5 = 4 rupees.
(2) 30 km → \(\frac{1}{5}\) of 30 = 6, 30 ÷ 5 = 6km.
(3) 15 litres → \(\frac{1}{5}\) of 15 = 3, 15 ÷ 5 = 3 litres.
(4) 25 cm → \(\frac{1}{5}\) of 25 = 5, 25 ÷ 5 = 5cm.

Question 3.
Find the part of each of the following numbers equal to the given fraction.

(1) \(\frac{2}{3}\) of 30
Solution:
\(\frac{2}{3}\) x 30 So, we take \(\frac{1}{3}\) of 30, twice
\(\frac{1}{3}\) x 30 = 10, twice of 10 is 2 x 10 = 20
It means that \(\frac{2}{3}\) x 30 = 20

(2) \(\frac{7}{11}\) of 22
Solution:
\(\frac{7}{11}\) x 22 So, we take of 22, 7 times
\(\frac{1}{11}\) x 22 = 2, seven times of 2 is 2 x 7 = 14

(3) \(\frac{3}{8}\) of 64
Solution:
\(\frac{3}{8}\) x 64 So, we take \(\frac{1}{8}\) of 64, thrice
\(\frac{1}{8}\) x 64 = 8, 3 times 8 is 3 x 8 = 24

(4) \(\frac{5}{13}\) of 65
Solution:
\(\frac{5}{13}\) x 65 So, we take \(\frac{1}{13}\) of 65, 5 times
\(\frac{1}{13}\) x 65 = 55 times of 5 is 5 x 5 = 25

Mixed fractions

Half of each of the three circles is coloured. That is, 3 parts, each equal to \(\frac{1}{2}\) of the circle, are coloured.

The coloured part is \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\), that is, \(\frac{3}{2}\) or 1 + \(\frac{1}{2}\).

1 + \(\frac{1}{2}\) is written as 1 \(\frac{1}{2}\). 1 \(\frac{1}{2}\) is read as ‘one and one upon two’.

In the fraction 1 \(\frac{1}{2}\), 1 is the integer part and \(\frac{1}{2}\) is the fraction part. Hence, such fractions are called mixed fractions or mixed numbers. 2 \(\frac{1}{4}\), 3 \(\frac{2}{5}\), 7 \(\frac{4}{9}\) are all mixed fractions.

Fractions in which the numerator is greater than the denominator are called improper fractions.

\(\frac{3}{2}\), \(\frac{5}{3}\) are improper fractions. We can convert improper fractions into mixed fractions.

For example,

Activities
1. Colour the Hats.

In the picture alongside :
Colour \(\frac{1}{3}\) of the hats red.
Colour \(\frac{3}{5}\) of the hats blue.
How many hats have you coloured red?
How many hats have you coloured blue?
How many are still not coloured?

2. Make a Magic Spinner.

Take a white cardboard disc. As shown in the figure, divide it into six equal parts.

Colour the parts red, orange, yellow, green, blue and violet.

Make a small hole at the centre of the disc and fix a pointed stick in the hole.

Your magic spinner is ready.

What fraction of the disc is each of the coloured parts?
Give the disc a strong tug to make it turn fast. What colour does it appear to be now?

The Clever Poet

There was a king who had a great love for literature. A certain poet knew that if the king read a good poem it made him very happy. Then the king would give the poet an award. Once, the poet composed a good poem. He thought if he showed it to the king, he would win a prize. So, he went to the king’s palace. But, it was not easy to meet the king. You had to pass a number of gates and guards. The first guard asked the poet why he wanted to meet the king. So, the poet told him the reason. Seeing the chance of getting a share of the award, the guard demanded, ‘You must

give me \(\frac{1}{10}\) of your prize. Only then will I let you go in.’ The poet could do nothing but agree. The second guard stopped him and said, ‘I will let you go in only if you promise me \(\frac{2}{5}\) of your prize.’ The third guard, too, was a greedy man. He said, ‘I will not let you go, unless you promise me \(\frac{1}{4}\) of your prize.’ The king’s palace was just a little distance away. Now, the poet told the guard, ‘Why only \(\frac{1}{4}\), I shall give you half the prize!’ The guard was pleased and let him in.

The king liked the poem. He asked the poet, ‘What is the prize you want?’ ‘I shall be happy if Your Majesty awards me 100 lashes of the whip.’ The king was surprised. ‘Are you out of your mind!’ he exclaimed. ‘I have never met anyone so crazy as to ask for a whipping !’

‘Your Majesty, if you wish to know the reason, the three palace guards must be called here.’ When the guards came, the poet explained, ‘Your Majesty, all of them have a share in the 100 lashes that you have awarded to me. Each of them has fixed his own share of the prize I get. The first guard

must get \(\frac{1}{10}\) of the award, that is, [ ] lashes. The second must get \(\frac{2}{5}\), which is [ ], and the third must get half the award, that is, [ ] lashes !’ The king could now see how greedy the guards were and how clever the poet was. He saw to it that each guard got the punishment he deserved. He gave the poet a prize for his poem. He also gave him an extra 100 gold coins for exposing the greed of the guards.

What was the clever idea of the poet which the king appreciated so much?

Fractions Problem Set 23 Additional Important Questions and Answers

Question 1.
What is \(\frac{1}{3}\) of each of the collections given below?

(1) 24 marbles →
(2) 6 erasers →
Answer:
(1) 24 marbles → \(\frac{1}{3}\) of 24 = 8, 24 ÷ 3 = 8 marbles.
(1) 6 erasers → \(\frac{1}{3}\) of 6 = 2, 6 ÷ 3 = 2 erasers.

Question 2.
What is \(\frac{1}{5}\) of each of the following?

(1) 35 gm →
(2) 40m →
Answer:
(1) 35 gm → \(\frac{1}{5}\) of 35 = 7, 35 ÷ 5 = 7 gm.
(2) 40m → \(\frac{1}{5}\) of 40 = 8, 40 ÷ 5 = 8m.

Question 3.
Find the part of each of the following numbers equal to the given fraction:

(1) \(\frac{7}{9}\) of 45
Solution:
\(\frac{7}{9}\) x 45 So, we take \(\frac{1}{9}\) of 45, 7 times
\(\frac{1}{9}\) x 45 = 5, 7 times of 5 is 7 x 5 = 35

(2) \(\frac{3}{7}\) of 28
Solution:
\(\frac{3}{7}\) x 28 So, we take \(\frac{1}{7}\) of 28, thrice
\(\frac{1}{7}\) x 28 = 4, 3 times of 4 is 4 x 3 = 12

Question 4.
Find the proper number in the box:








Answer:
(1) 3
(2) 36
(3) 3
(4) 7
(5) 8, 18
(6) 12, 6
(7) 9, 16, 20, 24
(8) 15, 20, 35, 36, 55

Question 5.
Find an equivalent fraction with denominator 3, for each of the following fractions.

Answer:

Question 6.
Find an equivalent fraction with numerator 30 for each of the following fractions.

Answer:

Question 7.
Find two equivalent fractions for each of the following fraction.
\(\text { (1) } \frac{5}{7}\)
\(\text { (2) } \frac{8}{9}\)
\(\text { (3) } \frac{7}{13}\)
Answer:
(1)
(2)
(3)

Question 8.
Match the columns (A) and (B) for having equivalent fractions:

	(A)	(B)
(1)	\(\frac{3}{4}\)	(a) \(\frac{15}{27}\)
(2)	\(\frac{5}{9}\)	(b) \(\frac{2}{3}\)
(3)	\(\frac{7}{11}\)	(c) \(\frac{27}{36}\)
(4)	\(\frac{8}{12}\)	(d) \(\frac{28}{44}\)

Answer:
(1) ↔ (c)
(2) ↔ (a)
(3) ↔ (d)
(4) ↔ (b)

Question 9.
Convert the given fractions into like fractions:
\(\text { (1) } \frac{1}{10}, \frac{2}{3}\)
\(\text { (2) } \frac{3}{7}, \frac{4}{5}\)
\(\text { (3) } \frac{1}{3}, \frac{3}{5}\)
\(\text { (3) } \frac{1}{4}, \frac{2}{5}\)
Answer:
\(\text { (1) } \frac{3}{30}, \frac{20}{30}\)
\(\text { (2) } \frac{15}{35}, \frac{28}{35}\)
\(\text { (3) } \frac{5}{15}, \frac{9}{15}\)
\(\text { (3) } \frac{5}{20}, \frac{8}{20}\)

Question 10.
Write the proper symbol from <, > or = in the box:





Answer:
(1) >
(2) >
(3) >
(4) >
(5) >

Question 11.
Add the following:
\(\text { (1) } \frac{1}{6}+\frac{2}{6}\)
\(\text { (2) } \frac{1}{4}+\frac{3}{4}\)
\(\text { (3) } \frac{5}{13}+\frac{2}{13}+\frac{3}{13}\)
\(\text { (4) } \frac{2}{9}+\frac{3}{7}\)
\(\text { (5) } \frac{3}{11}+\frac{2}{3}\)
\(\text { (6) } \frac{1}{10}+\frac{4}{5}\)
Answer:
\(\text { (1) } \frac{3}{6}\)
\(\text { (2) } \frac{4}{4}\)
\(\text { (3) } \frac{10}{13}\)
\(\text { (4) } \frac{41}{63}\)
\(\text { (5) } \frac{31}{33}\)
\(\text { (6) } \frac{9}{10}\)

Question 12.
Subtract the following:
\(\text { (1) } \frac{5}{6}-\frac{1}{6}\)
\(\text { (2) } \frac{3}{5}-\frac{2}{5}\)
\(\text { (3) } \frac{7}{16}-\frac{3}{16}-\frac{1}{16}\)
\(\text { (4) } \frac{5}{6}-\frac{7}{12}\)
\(\text { (5) } \frac{13}{16}-\frac{5}{8}\)
\(\text { (6) } \frac{4}{9}-\frac{3}{10}\)
Answer:
\(\text { (1) } \frac{4}{6}\)
\(\text { (2) } \frac{1}{5}\)
\(\text { (3) } \frac{3}{16}\)
\(\text { (4) } \frac{3}{12}\)
\(\text { (5) } \frac{3}{13}\)
\(\text { (6) } \frac{13}{90}\)

Question 13.
What is \(\frac{1}{4}\) of each of the collections given below:
(1) 20 marbles
(2) 12 pens
(3) 24 notebooks
(4) 8 ladoos
Answer:
(1) 5 marbles
(2) 3 pens
(3) 6 notebooks
(4) 2 ladoos

Question 14.
What is \(\frac{1}{6}\) of each of the following:
(1) 18 bananas
(2) 12 gms
(3) 30 metres
(4) 24 ₹
Answer:
(1) 3 bananas
(2) 2 gms
(3) 5 metres
(4) 4 ₹

Question 15.
Find the part of each of the following numbers equal to the given fraction.
(1) \(\frac{2}{5}\) of 25
(2) \(\frac{3}{7}\) of 21
(3) \(\frac{4}{9}\) of 36
(4) \(\frac{4}{17}\) of 34
Answer:
(1) 10
(2) 9
(3) 16
(4) 8

Question 16.
Printed price of. the book was 80. Vikram purchased the book by paying of the printed price of the book. How much he paid for the book?
Answer:
64 ₹

Class 5 Maths Solution Maharashtra Board

• Fractions Problem Set 17 Class 5 Maths Solutions
• Fractions Problem Set 18 Class 5 Maths Solutions
• Fractions Problem Set 19 Class 5 Maths Solutions
• Fractions Problem Set 20 Class 5 Maths Solutions
• Fractions Problem Set 21 Class 5 Maths Solutions
• Fractions Problem Set 22 Class 5 Maths Solutions
• Fractions Problem Set 23 Class 5 Maths Solutions

Decimal Fractions Class 5 Problem Set 36 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 36 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 9 Decimal Fractions

Write the following mixed fractions in decimal form and read them aloud.

\(\text { (1) } 3 \frac{9}{10}\)
Answer:
3.9, Three-point nine.

\(\text { (2) } 1 \frac{4}{10}\)
Answer:
1.4, One point four.

\(\text { (3) } 5 \frac{3}{10}\)
Answer:
5.3, Five-point three.

\(\text { (4) } \frac{8}{10}\)
Answer:
0.8, Zero points eight.

\(\text { (5) } \frac{7}{10}\)
Answer:
0.5, Zero points five.

Hundredths

If \(\frac{1}{10}\) is divided into 10 equal parts, each part becomes \(\frac{1}{100}\) or one hundredth. Therefore, note that 1 tenth =10 hundredths, or 0.1=0.10. By multiplying \(\frac{1}{100}\) by 10 we get \(\frac{10}{100}\) = \(\frac{1}{10}\). Therefore, it is possible to create a hundredths place next to the tenths place. After creating a hundredths place we can write \(\frac{14}{100}\) as 0.14.

\(\frac{14}{100}=\frac{10+4}{100}=\frac{10}{100}+\frac{4}{100}=\frac{1}{10}+\frac{4}{100}\) meaning that when writing \(\frac{14}{100}\) in decimal form, 1 is written in the tenths place and 4 is written in the hundredths place. This fraction is written as 0.14 and is read as ‘zero point one four’. Similarly, 6 \(\frac{57}{100}\) is written as 6.57 and 50 \(\frac{71}{100}\) is written as 50.71.

While writing \(\frac{3}{100}\) in decimal form, we must remember that there is no number in the tenths place and so, we put 0 in that place, which means that \(\frac{3}{100}\) is written as 0.03.

Study how the decimal fractions in the table below are written and read.

Decimal Fractions Problem Set 36 Additional Important Questions and Answers

\(\text { (1) } 4 \frac{6}{10}\)
Answer:
4.6, Four point six. 7

\(\text { (2) } 4 \frac{6}{10}\)
Answer:
2.7, Two point seven.

\(\text { (3) } 4 \frac{6}{10}\)
Answer:
6.2, Six points two.

\(\text { (4) } 4 \frac{6}{10}\)
Answer:
21.1, Twenty-one point one.

\(\text { (5) } 4 \frac{6}{10}\)
Answer:
17.5, Seventeen points five.

Class 5 Maths Solution Maharashtra Board

• Decimal Fractions Problem Set 36 Class 5 Maths Solutions
• Decimal Fractions Problem Set 37 Class 5 Maths Solutions
• Decimal Fractions Problem Set 38 Class 5 Maths Solutions
• Decimal Fractions Problem Set 39 Class 5 Maths Solutions
• Decimal Fractions Problem Set 40 Class 5 Maths Solutions
• Decimal Fractions Problem Set 41 Class 5 Maths Solutions
• Decimal Fractions Problem Set 42 Class 5 Maths Solutions

Addition and Subtraction Class 5 Problem Set 11 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 3 Addition and Subtraction Problem Set 11 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 3 Addition and Subtraction

Question 1.
Subtract the following:

(1) 8,57,513 – 4,82,256
Solution:

Answer:
3,75,257

(2) 13,17,519 – 10,07,423
Solution:

Answer:
3,10,096

(3) 68,34,501 – 23,57,823
Solution:

Answer:
44,76,678

(4) 45,43,827 – 12,05,938
Solution:

Answer:
33,37,889

(5) 70,12,345 – 28,64,547
Solution:

Answer:
41,47,798

(6) 38,01,213 – 37,54,648
Solution:

Answer:
46,565

Study the following word problem.

In 2001, the population of a city was 21,43,567. In 2011, it was 28,09,878. By how much did the population grow?

The population grew by 6,66,311.

Addition and Subtraction Problem Set 11 Additional Important Questions and Answers

Subtract the following:

(1) 53,14,018 – 43,14,019
Solution:

Answer:
9,99,999

(2) 67,05,136 – 34,56,789
Solution:

Answer:
32,48,347

Class 5 Maths Solution Maharashtra Board

• Addition and Subtraction Problem Set 7 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 8 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 9 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 10 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 11 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 12 Class 5 Maths Solutions
• Addition and Subtraction Problem Set 13 Class 5 Maths Solutions

Multiples and Factors Class 5 Problem Set 35 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 8 Multiples and Factors Problem Set 35 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 8 Multiples and Factors

Determine whether the pairs of numbers given below are co-prime numbers.
(1) 22, 24
Answer:
Common factors of 22 and 24 are 1 and 2. (Not only 1 common factor) So, 22, 24 are not co-prime numbers.

(2) 14, 21
Answer:
Common factors of 14 and 21 are 1 and 7. So, this pair is not co-prime numbers.

(3) 10, 33
Answer:
Common factors of 10 and 33 is only 1. So, 10 and 33 are co-prime numbers.

(4) 11, 30
Answer:
Common factors of 11 and 30 is only 1. So, 11 and 30 are co-prime numbers.

(5) 5, 7
Answer:
Common factor of 5 and 7 is only 1. So, 5 and 7 are co-prime numbers.

(6) 15, 16
Answer:
Common factors of 15 and 16 is only 1. So, 15 and 16 are co-prime numbers.

(7) 50, 52
Answer:
Common factors of 50 and 52 are 1 and 2. So, 50 and 52 are not co-prime numbers.

(8) 17, 18
Answer:
Common factors of 17 and 18 is only 1. So, 17 and 18 are co-prime numbers.

Activity 1 :

• Write numbers from 1 to 60.
• Draw a blue circle around multiples of 2.
• Draw a red circle around multiples of 4.
• Do all numbers with a blue circle also have a red circle around them?
• Do all the numbers with a red circle have a blue circle around them?
• Are all multiples of 2 also multiples of 4?
• Are all multiples of 4 also multiples of 2?

Activity 2 :

• Write numbers from 1 to 60.
• Draw a triangle around multiples of 2.
• Draw a circle around multiples of 3.
• Now find numbers divisible by 6. Can you find a property that they share?

Eratosthenes’ method of finding prime numbers
Eratosthenes was a mathematician who lived in Greece about 250 BC. He discovered a method to find prime numbers. It is called Eratosthenes’ Sieve. Let us see how to find prime numbers between 1 and 100 with this method.

• 1 is neither a prime nor a composite number. Put a square [ ] around it
• 2 is a prime number, so put a circle around it.
• Next, strike out all the multiples of 2. This tells us that of these 100 numbers more than half of numbers are not prime numbers.
• The first number after 2 not yet struck off is 3. So, 3 is a prime number.
• Draw a circle around 3. Strike out all the multiples of 3.
• The next number after 3 not struck off yet is 5. So, 5 is a prime number.
• Draw a circle around 5. Put a line through all the multiples of 5.
• The next number after 5 without a line through it is 7. So, 7 is a prime number.
• Draw a circle around 7. Put a line through all the multiples of 7.

In this way, every number between 1 and 100 will have either a circle or a line through it. The circled numbers are prime numbers. The numbers with a line through them are composite numbers.

One more method to find prime numbers

See how numbers from 1 to 36 have been arranged in six columns in the table alongside.

Continue in the same way and write numbers up to 102 in these six columns.

You will see that, in the columns for 2, 3, 4, and 6, all the numbers are composite numbers except for the prime numbers 2 and 3. This means that all the remaining prime numbers will be in the columns for 1 and 5. Now isn’t it easier to find them? So, go ahead, find the prime numbers!

Something more

• Prime numbers with a difference of two are called twin prime numbers. Some twin prime number pairs are 3 and 5, 5 and 7, 29 and 31 and 71 and 73. 5347421 and 5347423 are also a pair of twin prime numbers.
• There are eight pairs of twin prime numbers between 1 and 100. Find them.
• Euclid the mathematician lived in Greece about 300 BC. He proved that if prime numbers, 2, 3, 5, 7, ……., are written in serial order, the list will never end, meaning that the number of prime numbers is infinite.

Multiples and Factors Problem Set 35 Additional Important Questions and Answers

Determine whether the pairs of numbers given below are co-prime numbers.

(1) (12,18)
Answer:
Common factors of 12 and 18 are 1, 2, 3, 6. Hence 12 and 18 are not co-prime numbers.

(2) (26, 39)
Answer:
Common factors of 26 and 39 are 1 and 13. Hence, 26 and 39 are not co-prime numbers.

(3) (23, 29)
Answer:
Common factor of 23 and 29 is only 1. Hence, 23 and 29 are co-prime numbers.

(4) (28, 32)
Answer:
Common factors of 28 and 32 are 1, 2, 4 (not only 1). Hence, 28, 32 are not co-prime numbers.

Class 5 Maths Solution Maharashtra Board

• Multiples and Factors Problem Set 32 Class 5 Maths Solutions
• Multiples and Factors Problem Set 33 Class 5 Maths Solutions
• Multiples and Factors Problem Set 34 Class 5 Maths Solutions
• Multiples and Factors Problem Set 35 Class 5 Maths Solutions

Multiples and Factors Class 5 Problem Set 34 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 8 Multiples and Factors Problem Set 34 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 8 Multiples and Factors

Question 1.
Write all the prime numbers between 1 and 20.
Answer:
2, 3, 5, 7, 11, 13, 17, 19.

Question 2.
Write all the composite numbers between 21 and 50.
Answer:
Composite numbers between 21 and 50 are 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49.

Question 3.
Circle the prime numbers in the list given below. 22, 37, 43, 48, 53, 60, 91, 57, 59, 77, 79, 97, 100
Answer:

Question 4.
Which of the prime numbers are even numbers?
Answer:
Only even prime number is 2. (the Rest of the even numbers are composites.)

Co-prime numbers

Dada : Tell me all the factors of 12 and 18.

Anju : I’ll tell the factors of 12: 1, 2, 3, 4, 6, 12.

Manju : I’ll give the factors of 18: 1, 2, 3, 6, 9, 18.

Dada : Now find the common factors of 12 and 18.

Anju : Common factors ?

Dada : 1, 2, 3 and 6 are in both groups, which means that they are common factors. Now tell me the factors of 10 and 21.

Sanju : Factors of 10 : 1, 2, 5, 10.

Manju : Factors of 21: 1, 3, 7, 21.

Dada : Which of the factors in these two groups are common?

Sanju : 1 is the only common factor.

Dada : Numbers which have only 1 as a common factor are called co-prime numbers, so 10 and 21 are co-prime numbers. The common factors of 12 and 18 are 1, 2, 3 and 6; which means that the common factors are more than one. Therefore, 12 and 18 are not co-prime numbers. Now tell me whether 8 and 10 are co-prime numbers.

Manju : The factors of 8 are 1, 2, 4 and 8 and the factors of 10 are 1, 2, 5 and 10. These numbers have two factors, 1 and 2, in common, so 8 and 10 are not co-prime numbers.

Multiples and Factors Problem Set 32 Additional Important Questions and Answers

Question 1.
21 to 50
Answer:
23, 29, 31, 37, 41, 43, 47

Question 2.
Which of the number is neither prime nor composite?
Answer:
1

Question 13.
Between nearest which two prime numbers the prime number 43 lies?
Answer:
43 lies between prime numbers 41 and 47.

Question 14.
Which of the prime numbers are odd numbers?
Answer:
All prime numbers are odd except 2.

Class 5 Maths Solution Maharashtra Board

• Multiples and Factors Problem Set 32 Class 5 Maths Solutions
• Multiples and Factors Problem Set 33 Class 5 Maths Solutions
• Multiples and Factors Problem Set 34 Class 5 Maths Solutions
• Multiples and Factors Problem Set 35 Class 5 Maths Solutions