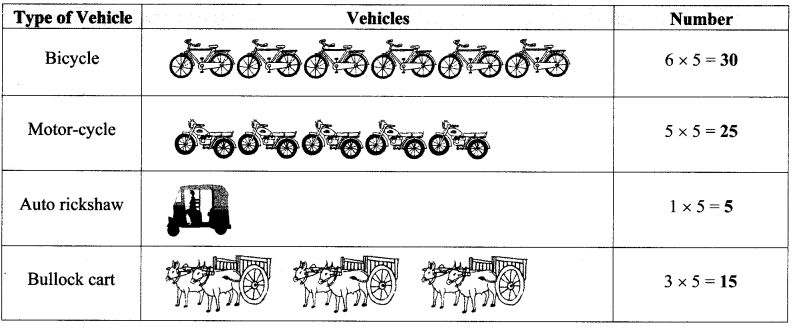
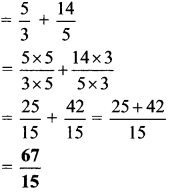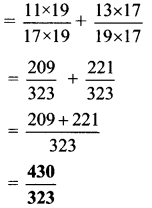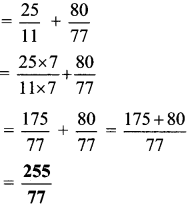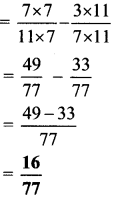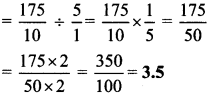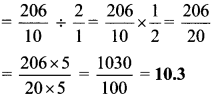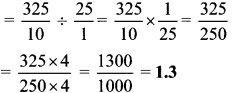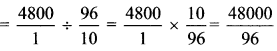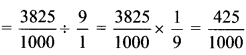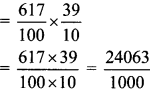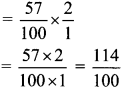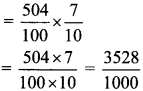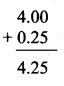Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 3 Integers Class 6 Practice Set 5 Answers Solutions.
6th Standard Maths Practice Set 5 Answers Chapter 3 Integers
Question 1.
Add:
- 8 + 6
- 9 + (-3)
- 5 + (-6)
- – 7 + 2
- – 8 + 0
- – 5 + (-2)
Solution:
| 1. 8 + 6 = (+8) + (+6) = +14 | 2. 9 + (-3) = (+9) + (- 3) = +6 | 3. 5 + (-6) = (+5) + (-6) = -1 |
| 4. -7 + 2 = (-7) + (+2) = -5 | 5. -8 + 0 = (-8) + 0 = -8 | 6. -5 + (-2) = (-5) + (-2) = -7 |
Question 2.
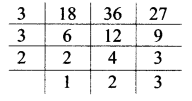
Complete the table given below:
| + | 8 | 4 | -3 | -5 |
| -2 | -2 + 8 = +6 | |||
| 6 | ||||
| 0 | ||||
| -4 |
Solution:
| + | 8 | 4 | -3 | -5 |
| -2 | (-2) + (+8) = +6 | (-2) +(+4) = 2 | (-2) +(-3) =-5 | (-2) +(-5) =-7 |
| 6 | (+6) + (+8) = 14 | (+6) + (+4) = 10 | (+6) + (-3) = 3 | (+6) + (-5) = 1 |
| 0 | 0 + (+8) = 8 | 0 + (+4) = 4 | 0 + (-3) = -3 | 0 + (-5) = -5 |
| -4 | (-4) + (+8) = 4 | (-4) +(+4) = 0 | (-4) + (-3) = -7 | (-4) + (-5) = -9 |
Maharashtra Board Class 6 Maths Chapter 3 Integers Practice Set 5 Intext Questions and Activities
Question 1.
On the playground, mark a timeline showing the years from 2000 to 2024. With one child standing at the position of the 2017, ask the following questions: (Textbook pg. no. 15)
- While playing this game, what is his/her age?
- Five years ago, which year was it? And what was his / her age then?
- In which year will he / she go to Std X? How old will he / she be then?
The child should find answers to such questions by walking the right number of units and in the right direction on the timeline.
[Assume child born year is 2009]
Solutions:
- Age of child is 8 years.
- Five years ago, year was 2012. His/her age is 3 years.
- In 2024, he/she will go the Std X. His/her age is 15 years.
Question 2.
On a playground mark a timeline of 100 years. This will make it possible to count the years from 0 to 2100 on it. Important historical events can then be shown in proper centuries. (Textbook pg. no. 16)
Solution:
(Students should attempt this activity on their own)
Question 3.
Observe the figures and write appropriate number in the boxes given below. (Textbook pg. no. 16 and 17)
i.
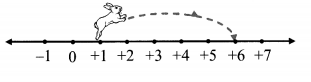
a. At first the rabbit was at the number ____
b. It hopped ___ units to the right.
c. It is now at the number ___
Solution:
i.
a. +1
b. 5
c. +6
ii.
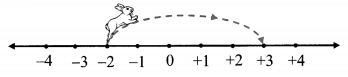
a. At first the rabbit was at the number ___
b. It hopped ____ units to the right.
c. It is now at the number ____
Solution:
ii.
a. -2
b. 5
c. +3
iii.
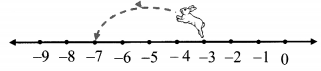
a. At first the rabbit was at the number ___
b. It hopped ____ units to the left.
c. It is now at the number ___
Solution:
iii.
a. -3
b. 4
c. -7
iv.
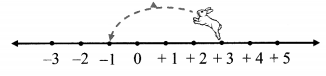
a. At first the rabbit was at the number ___
b. It hopped___units to the left.
c. It is now at the number ____
Solution:
iv.
a. +3
b. 4
c. -1