Uncategorized

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.5 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

Practice Set 4.5 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion

Question 1.
Which number should be subtracted from 12, 16 and 21 so that resultant numbers are in continued proportion?
Solution:
Let the number to be subtracted be x.
∴ (12 – x), (16 – x) and (21 – x) are in continued proportion.

∴ 84 – 4x = 80 – 5x
∴ 5x – 4x = 80 – 84
∴ x = -4
∴ -4 should be subtracted from 12,16 and 21 so that the resultant numbers in continued proportion.

Question 2.
If (28 – x) is the mean proportional of (23 – x) and (19 – x), then find the value ofx.
Solution:
(28 – x) is the mean proportional of (23 – x) and (19-x). …[Given]

∴ -5(19 – x) = 9(28 – x)
∴ -95 + 5x = 252 – 9x
∴ 5x + 9x = 252 + 95
∴ 14x = 347
∴ x = \(\frac { 347 }{ 14 }\)

Question 3.
Three numbers are in continued proportion, whose mean proportional is 12 and the sum of the remaining two numbers is 26, then find these numbers.
Solution:
Let the first number be x.
∴ Third number = 26 – x
12 is the mean proportional of x and (26 – x).
∴ \(\frac { x }{ 12 }\) = \(\frac { 12 }{ 26 – x }\)
∴ x(26 – x) = 12 x 12
∴ 26x – x² = 144
∴ x² – 26x + 144 = 0
∴ x² – 18x – 8x + 144 = 0
∴ x(x – 18) – 8(x – 18) = 0
∴ (x – 18) (x – 8) = 0
∴ x = 18 or x = 8
∴ Third number = 26 – x = 26 – 18 = 8 or 26 – x = 26 – 8 = 18
∴ The numbers are 18, 12, 8 or 8, 12, 18.

Question 4.
If (a + b + c)(a – b + c) = a² + b² + c², show that a, b, c are in continued proportion.
Solution:
(a + b + c)(a – b + c) = a² + b² + c² …[Given]
∴ a(a – b + c) + b(a – b + c) + c(a – b + c) = a2 + b2 + c2
∴ a² – ab + ac + ab – b² + be + ac – be + c² = a² + b² + c²
∴ a² + 2ac – b² + c² = a² + b² + c²
∴ 2ac – b² = b²
∴ 2ac = 2b²
∴ ac = b²
∴ b² = ac
∴ a, b, c are in continued proportion.

Question 5.
If \(\frac { a }{ b }\) = \(\frac { b }{ c }\) and a, b, c > 0, then show that,
i. (a + b + c)(b – c) = ab – c²
ii. (a² + b²)(b² + c²) = (ab + be)²
iii. \(\frac{a^{2}+b^{2}}{a b}=\frac{a+c}{b}\)
Solution:
Let \(\frac { a }{ b }\) = \(\frac { b }{ c }\) = k
∴ b = ck
∴ a = bk =(ck)k
∴ a = ck² …(ii)

i. (a + b + c)(b – c) = ab – c²
L.H.S = (a + b + c) (b – c)
= [ck² + ck + c] [ck – c] … [From (i) and (ii)]
= c(k² + k + 1) c (k – 1)
= c² (k² + k + 1) (k – 1)
R.H.S = ab – c²
= (ck²) (ck) – c² … [From (i) and (ii)]
= c²k³ – c²
= c²(k³ – 1)
= c² (k – 1) (k² + k + 1) … [a³ – b³ = (a – b) (a² + ab + b²]
∴ L.H.S = R.H.S
∴ (a + b + c) (b – c) = ab – c²

ii. (a² + b²)(b² + c²) = (ab + bc)²
b = ck; a = ck²
L.H.S = (a² + b²) (b² + c²)
= [(ck²) + (ck)²] [(ck)² + c²] … [From (i) and (ii)]
= [c²k⁴ + c²k²] [c²k² + c²]
= c²k² (k² + 1) c² (k² + 1)
= c4k² (k² + 1)²
R.H.S = (ab + bc)²
= [(ck²) (ck) + (ck)c]² …[From (i) and (ii)]
= [c²k³ + c²k]²
= [c²k (k² + 1)]2 = c⁴(k² + 1)²
∴ L.H.S = R.H.S
∴ (a² + b²) (b² + c²) = (ab + bc)²

iii. \(\frac{a^{2}+b^{2}}{a b}=\frac{a+c}{b}\)

9th Standard Algebra Practice Set 4.5 Question 6. Find mean proportional of \(\frac{x+y}{x-y}, \frac{x^{2}-y^{2}}{x^{2} y^{2}}\).
Solution:
Let a be the mean proportional of \(\frac{x+y}{x-y}\) and \(\frac{x^{2}-y^{2}}{x^{2} y^{2}}\)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 5.4 8th Std Maths Answers Solutions Chapter 5 Expansion Formulae.

Practice Set 5.4 8th Std Maths Answers Chapter 5 Expansion Formulae

Question 1.
Expand:
i. (2p + q + 5)²
ii. (m + 2n + 3r)²
iii. (3x + 4y – 5p)²
iv. (7m – 3n – 4k)²
Solution:
i. (2p + q + 5)² = (2p)² + (q)² + (5)² + 2(2p) (q) + 2(q) (5) + 2(2p) (5)
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= 4p² + q² + 25 + 4pq + 10q + 20p

ii. (m + 2n + 3r)² = (m)² + (2n)² + (3r)² + 2(m) (2n) + 2(2n) (3r) + 2(m) (3r)
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= m² + 4n² + 9r² + 4mn + 12nr + 6mr

iii. (3x + 4y – 5p)² = (3x)² + (4y)² + (- 5p)² + 2(3x) (4y) + 2(4y) (- 5p) + 2(3x) (- 5p)
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= 9x + 16y² + 25p² + 24xy – 40py – 30px

iv. (7m – 3n – 4k)² = (7m)² + (- 3n)² + (- 4k)² + 2(7m) (- 3n) + 2 (- 3n) (- 4k) + 2 (7m) (- 4k)
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= 49m² + 9n² + 16k² – 42mn + 24nk – 56km

Question 2.
Simplify:
i. (x – 2y + 3)² + (x + 2y – 3)²
ii. (3k – 4r – 2m)² – (3k + 4r – 2m)²
iii. (7a – 6b + 5c)² + (7a + 6b – 5c)²
Solution:
i. (x – 2y + 3)² + (x + 2y – 3)²
= [(x)² + (- 2y)² + (3)² + 2 (x) (- 2y) + 2 (- 2y) (3) + 2 (x) (3)] + [(x)² + (2y)² + (- 3)² + 2 (x) (2y) + 2 (2y) (- 3) + 2 (x) (- 3)]
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= x² + 4y² + 9 – 4xy – 12y + 6x + x² + 4y² + 9 + 4xy – 12y – 6x
= x + x² + 4y² + 4y² + 9 + 9 – 4xy + 4xy – 12y – 12y + 6x – 6x
= 2x² + 8y² + 18 – 24y

ii. (3k – 4r – 2m)² – (3k + 4r – 2m)²
= [(3k)² + (- 4r)² + (- 2m)² + 2 (3k) (- 4r) + 2 (- 4r) (- 2m) + 2 (3k) (- 2m)] – [(3k)² + (4r)² + (- 2m)² + 2 (3k) (4r) + 2 (4r) (- 2m) + 2 (3k) (- 2m)]
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= (9k² + 16r² + 4m² – 24kr + 16rm – 12km) – (9k² + 16r² + 4m² + 24kr – 16rm – 12km)
= 9k² + 16r² + 4m² – 24kr + 16rm – 12km – 9k² – 16r² – 4m² – 24kr + 16rm + 12km
= 9k² – 9k² + 16r² – 16r² + 4m² – 4m² – 24kr – 24kr + 16rm + 16rm – 12km + 12km
= 32rm – 48kr

iii. (7a – 6b + 5c)² + (7a + 6b – 5c)²
= [(7a)² + (- 6b)² + (5c)² + 2(7a) (-6b) + 2(-6b) (5c) + 2(7a) (5c)] + [(7a)² + (6b)² + (- 5c)² + 2 (7a) (6b) + 2 (6b) (- 5c) + 2 (7a) (- 5c)]
… [(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac]
= 49a² + 36b² + 25c² – 84ab – 60bc + 70ac + 49a² + 36b² + 25c² + 84ab – 60bc – 70ac
= 49a² + 49a² + 36b² + 36b² + 25c² + 25c² – 84ab + 84ab – 60bc – 60bc + 70ac – 70ac
= 98a² + 72b² + 50c² – 120bc

Maharashtra Board Class 8 Maths Chapter 5 Expansion Formulae Practice Set 5.4 Intext Questions and Activities

Question 1.
Fill in the boxes with appropriate terms in the steps of expansion. (Textbook pg. no. 27)
(2p + 3m + 4n)²
= (2p)² + (3m)² + __ + 2 × 2p × 3m + 2 × __ × 4n + 2 × 2p × __
= __ + 9m² + __ + 12pm + __ + __
Solution:
(2p + 3m + 4n)²
= (2p)² + (3m)² + (4n)² + 2 x 2p x 3m + 2 x 3m x 4n + 2 x 2p x 4n
= 4p² + 9m² + 16n² + 12pm + 24mn + 16pn

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 16 Quadrilaterals Class 6 Practice Set 37 Answers Solutions.

6th Standard Maths Practice Set 37 Answers Chapter 16 Quadrilaterals

Question 1.
Observe the figures below and find out their names:

Solution:
i. Pentagon (5 sides)
ii. Hexagon (6 sides)
iii. Heptagon (7 sides)
iv. Octagon (8 sides)

Maharashtra Board Class 6 Maths Chapter 16 Quadrilaterals Practice Set 37 Intext Questions and Activities

Question 1.
Observe the figures given below and say which of them are quadrilaterals. (Textbook pg. no. 81)

Solution:
Is a quadrilateral: (i)

Question 2.
Draw a quadrilateral. Draw one diagonal of this quadrilateral and divided it into two triangles. Measures all the angles in the figure. Is the sum of the measures of the four angles of the quadrilateral equal to the sum of the measures of the six angles of the two triangles? Verity that this is so with other quadrilaterals. (Textbook pg. no. 84)
Solution:

m∠PQR = 104°
m∠QRP = 26°
m∠RPQ = 50°
m∠PRS = 34°
m∠RSP = 106°
m∠SPR = 40°
∴ Sum of the measures of the angles of quadrilateral = m∠PQR + m∠QRP + m∠RPQ + m∠PRS + m∠RSP + m∠SPR
= 104° + 26° + 50° + 34° + 106° + 40°
= 360°
Also, we observe that
Sum of the measures of the angles of quadrilateral = Sum of the measures of angles of the two triangles (PQR and PRS)
= (104°+ 26°+ 50°)+ (34° + 106° + 40°)
= 180° + 180°
= 360°
[Note: Students should drew different quadrilaterals and verify the property.]

Question 3.
For the pentagon shown in the figure below, answer the following: (Textbook pg. no. 84)

1. Write the names of the five vertices of the pentagon.
2. Name the sides of the pentagon.
3. Name the angles of the pentagon.
4. See if you can sometimes find players on a field forming a pentagon.

Solution:

1. The vertices of the pentagon are points A, B, C, D and E.
2. The sides of the pentagon are segments AB, BC, CD, DE and EA.
3. The angles of the pentagon are ∠ABC, ∠BCD, ∠CDE, ∠DEA and ∠EAB.
4. The players shown in the above figure form a pentagon. The players are standing on the vertices of

Question 4.
Cut out a paper in the shape of a quadrilateral. Make folds in it that join the vertices of opposite angles. What can these folds be called? (Textbook pg. no. 83)

Solution:
The folds are called diagonals of the quadrilateral.

Question 5.
Take two triangular pieces of paper such that . one side of one triangle is equal to one side of the other. Let us suppose that in ∆ABC and ∆PQR, sides AC and PQ are the equal sides. Join the triangles so that their equal sides lie B side by side. What figure do we get? (Textbook pg. no. 83)

Solution:
If we place the triangles together such that the equal sides overlap, the two triangles form a quadrilateral.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 2 Angles Class 6 Practice Set 3 Answers Solutions.

6th Standard Maths Practice Set 3 Answers Chapter 2 Angles

Question 1.
Use the proper geometrical instruments to construct the following angles. Use the compass and the ruler to bisect them:

1. 50°
2. 115°
3. 80°
4. 90°

Solution:

Maharashtra Board Class 6 Maths Chapter 2 Angles Practice Set 3 Intext Questions and Activities

Question 1.
Construct an angle bisector to obtain an angle of 30°. (Textbook pg. no. 11)
Solution: .
In order to get a bisected angle of a given measure, the student has to draw the angle having twice the measurement of required bisected angle.

For getting measurement of 30° (for the bisected angle), one has to make an angle of 60° (i.e. 30° × 2).

Step 1:
Draw ∠ABC of 60°.

Step 2:
Cut arcs on the rays BA and BC. Name these points as D and E respectively.

Step 3:
Place the compass point on point D and draw an arc inside the angle.
Without changing the distance of the compass, place the compass point on point E and cut the previous arc. Name the point of intersection as O

Step 4:
Draw ray BO.
Ray BO is the angle bisector of ∠ABC.
i.e. m∠ABO = m∠CBO = 30°

Question 2.
Construct an angle bisector to draw an angle of 45°. (Textbook pg. no. 11)
Solution:
For getting measurement of 45° (for the bisected angle), one has to make an angle of 90° (i.e. 45° × 2).
Step 1:
Draw ∠PQR of 90°.

Step 2:
Cut arcs on the rays QP and QR.
Name these points as M and N respectively.

Step 3:
Place the compass point on point M and draw an arc inside the angle.
Without changing the distance of the compass, place the compass point on point N and cut the

Step 4:
Draw ray QO.
Ray QO is the angle bisector of ∠PQR.
i.e. m∠PQO = m∠RQO = 45°

Question 3.
Ask three or more children to stand in a straight line. Take two long ropes. Let the child in the middle hold one end of each rope. With the help of the ropes, make the children on either side stand along a straight line. Tell them to move so as to form an acute angle, a right angle, an obtuse angle, a straight angle, a reflex angle and a full or complete angle in turn. Keeping the rope stretched will help to ensure that the children form straight lines. (Textbook pg. no. 6)
Solution:

Question 4.
Look at the pictures below and identify the different types of angles. (Textbook pg. no. 8)

Solution:
i. Complete angle
ii. Reflex and Acute angle
iii. Acute and Obtuse angle

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 5 Decimal Fractions Class 6 Practice Set 15 Answers Solutions.

6th Standard Maths Practice Set 15 Answers Chapter 5 Decimal Fractions

Question 1.
Write the proper number in the empty boxes.

Solution:

Question 2.
Convert the common fractions into decimal fractions:
i. \(\frac { 3 }{ 4 }\)
ii. \(\frac { 4 }{ 5 }\)
iii. \(\frac { 9 }{ 8 }\)
iv. \(\frac { 17 }{ 20 }\)
v. \(\frac { 36 }{ 40 }\)
vi. \(\frac { 7 }{ 25 }\)
vii. \(\frac { 19 }{ 200 }\)
Solution:
i. \(\frac { 3 }{ 4 }\)

ii. \(\frac { 4 }{ 5 }\)

iii. \(\frac { 9 }{ 8 }\)

iv. \(\frac { 17 }{ 20 }\)

v. \(\frac { 36 }{ 40 }\)

vi. \(\frac { 7 }{ 25 }\)

vii. \(\frac { 19 }{ 200 }\)

Question 3.
Convert the decimal fractions into common fractions:
i. 27.5
ii. 0.007
iii. 90.8
iv. 39.15
v. 3.12
vi. 70.400
Solution:
i. 27.5
= \(\frac { 275 }{ 10 }\)

ii. 0.007
= \(\frac { 7 }{ 1000 }\)

iii. 90.8
= \(\frac { 908 }{ 10 }\)

iv. 39.15
= \(\frac { 3915 }{ 100 }\)

v. 3.12
= \(\frac { 312 }{ 100 }\)

vi. 70.400
= 70.4
= \(\frac { 704 }{ 10 }\)

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 10 Equations Class 6 Practice Set 27 Answers Solutions.

6th Standard Maths Practice Set 27 Answers Chapter 10 Equations

Question 1.
Rewrite the following using a letter:
i. The sum of a certain number and 3.
ii. The difference is obtained by subtracting 11 from another number.
iii. The product of 15 and another number.
iv. Four times a number is 24.
Solution:
i. Let the number be x.
∴ x + 3 represents the sum of a certain number x and 3.

ii. Let the number be x.
∴ x – 11 represents the number obtained by subtracting 11 from another number x.

iii. Let the number be x.
∴ 15x represents the product of 15 and another number x.

iv. Let the number be x.
∴ 4x = 24 represents four the product of a number x four times.

Question 2.
Find out which operation must be done on both sides of these equations in order to solve them:

1. x + 9 = 11
2. x – 4 = 9
3. 8x = 24
4. \(\frac { x }{ 6 }\) = 3

Solution:

1. Subtract 9 from both sides.
2. Add 4 to both sides.
3. Divide both sides by 8.
4. Multiply both sides by 6.

Question 3.
Given below are some equations and the values of the variables. Are these values the solutions to those equations?

No.	Equation	Value of the Variable	Solution (Yes/No)
i.	y – 3 = 11	y = 3	No
ii.	17 = n + 7	n = 10
iii.	30 = 5x	x = 6
iv.	\(\frac { m }{ 2 }\) = 14	m = 7

Solution:

No.	Equation	Value of the Variable	Solution (Yes/No)
i.	y – 3 = 11	y = 3	No
ii.	17 = n + 7	n = 10	Yes
iii.	30 = 5x	x = 6	Yes
iv.	\(\frac { m }{ 2 }\) = 14	m = 7	No

i. y – 3 = 11
∴ y – 3 + 3 = 11 + 3
…. (Adding 3 to both sides)
∴ y + 0 = 14
∴ y = 14

ii. 17 = n + 7
∴ 17 – 7 = n + 7 – 7
…. (Subtracting 7 from both sides)
∴ 17 + (-7) = n + 7 – 7
∴ 10 = n
∴  n = 10

iii. 30 = 5x
∴ \(\frac{30}{5}=\frac{5x}{5}\)
…. (Dividing both sides by 5)
∴  6 = 1x
∴ 6 = x
∴  x = 6

iv. \(\frac { m }{ 2 }\) = 14
∴ \(\frac { m }{ 2 }\) × 2 = 14 × 2
…. (Multiplying both sides by 2)
\(\frac { m\times2 }{ 2\times1 }\) = 28
∴ m = 28

Question 4.
Solve the following equations:
i. y – 5 = 1
ii. 8 = t + 5
iii. 4x = 52
iv. 19 = m – 4
v. \(\frac { p }{ 4 }=9\)
vi. x + 10 = 5
vi. m – 5 = -12
vii. p + 4 = -1
Solution:
i. y – 5 = 1
∴y – 5 + 5 = 1 + 5
…. (Adding 5 to both sides)
∴y + 0 = 6
∴y = 6

ii. 8 = t + 5
∴8 – 5 = t + 5 – 5
……(Subtracting 5 from both sides)
∴8 + (-5) = t + 0
∴ 3 = t
∴t = 3

iii. 4x = 52
∴\(\frac{4x}{4}=\frac{52}{4}\)
…. (Dividing both sides by 4)
∴ 1x = 13
∴ x = 13

iv. 19 = m -4
∴ 19 + 4 = m – 4 + 4
…. (Adding 4 to both sides)
∴ 23 = m + 0
∴ m = 23

v. \(\frac { p }{ 4 }\) = 9
∴ \(\frac { p }{ 4 }\) × 4 = 9 × 4 …. (Multiplying both sides by 4)
∴ \(\frac { p\times4 }{ 4\times1 }=36\)
∴ 1p = 36
∴ p = 36

vi. x + 10 = 5
∴ x + 10 – 10 = 5 – 10
…. (Subtracting 10 from both sides)
∴ x + 0 = 5 + (-10)
∴ x = -5

vii. m – 5 = -12
∴m – 5 + 5 = – 12 + 5
…. (Adding 5 to both sides)
∴m + 0 = -7
∴m = -7

viii. p + 4 = – 1
∴p + 4 – 4 = -1 – 4
…. (Subtracting 4 from both sides)
∴p + 0 = (-1) + (-4)
∴P = -5

Question 5.
Write the given information as an equation and find its solution:
i. Haraba owns some sheep. After selling 34 of them in the market, he still has 176 sheep. How many sheep did Haraba have at first?

ii. Sakshi prepared some jam at home and filled it in bottles. After giving away 7 of the bottles to her friends she still has 12 for herself. How many bottles had she made in all? If she filled 250g of jam in each bottle, what was the total weight of the jam she made?

iii. Archana bought some kilograms of wheat. She requires 12 kg per month and she got enough wheat milled for 3 months. After that, she had 14 kg left. How much wheat had Archana bought altogether?
Solution:
i. Let the number of sheep before selling be x.
∴ x – 34 = 176
∴ x – 34 + 34 = 176 + 34 ….(Adding 34 to both sides)
∴ x + 0 = 210
∴ x = 210
The number of sheep with Haraba before selling is 210.

ii. Let the total number of bottles be x.
∴ x – 7 = 12
∴ x – 7 + 7 = 12 + 7 ….(Adding 7 to both sides)
∴ x + 0 = 19
∴ x = 19
Weight of jam in each bottle = 250g
∴ Total weight of jam = 19 × 250g = 4750 g = \(\frac { 4750 }{ 1000 }\)kg = 4.75 kg
∴ The total number of bottles of jam made by Sakshi is 19, and the total weight of jam made is 4.75 kg.

iii. Let the total wheat bought by Archana be x kg.
Wheat used in 1 month = 12 kg
∴ Wheat used in 3 months = 3 × 12 = 36 kg
∴ x – 36 = 14
∴ x – 36 + 36 = 14 + 36 ….(Adding 36 to both sides)
∴ x + 0 = 50
∴ x = 50
∴ The total amount of wheat bought by Archana was 50 kg.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 15 Triangles and their Properties Class 6 Practice Set 36 Answers Solutions.

6th Standard Maths Practice Set 36 Answers Chapter 15 Triangles and their Properties

Question 1.
Observe the figures below and write the type of the triangle based on its angles:

Solution:
i. right angled
ii. Obtuse angled
iii. acute angled

Question 2.
Observe the figures below and write the type of the triangle based on its sides:

Solution:
i. equilateral
ii. scalene
iii. isosceles

Question 3.
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.

Solution:
The two roads which Avinash can choose to go to school are

1. Road AB + Road BC
2. Road AC

The three roads together form ∆ABC.
Road AC is shorter because the sum of the lengths of any two sides (side AB + side BC) of a triangle is always greater than the third side (side AC).

Question 4.
The lengths of the sides of some triangles are given. Say what types of triangles they are.

1. 3 cm, 4 cm, 5 cm
2. 3.4 cm, 3.4 cm, 5 cm
3. 4.3 cm, 4.3 cm, 4.3 cm
4. 3.7 cm, 3.4 cm, 4 cm

Solution:

1. Since, no two sides have equal lengths, the given triangle is a scalene triangle.
2. Since, two sides have equal length, the given triangle is an isosceles triangle.
3. Since, all the three sides have equal lengths, the given triangle is an equilateral triangle.
4. Since, no two sides have equal lengths, the given triangle is a scalene triangle.

Question 5.
The lengths of the three segments are given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
i. 17 cm, 7 cm, 8 cm
ii. 7 cm, 24 cm, 25 cm
iii. 9 cm, 6 cm, 16 cm
iv. 8.4 cm, 16.4 cm, 4.9 cm
v. 15 cm, 20 cm, 25 cm
vi. 12 cm, 12 cm, 16 cm
Solution:
i. The lengths of the three sides are 17 cm, 7 cm, 8 cm.
a. 7 cm + 17 cm = 24 cm, greater than 8 cm
b. 8 cm +17 cm = 25 cm, greater than 7 cm
c. 7 cm + 8 cm =15 cm, not greater than 17 cm
The sum of lengths of two sides in (c) is not greater than the length of the third side.
∴ Triangle cannot be drawn with sides 17 cm, 7 cm, 8 cm.

ii. The lengths of the three sides are 7 cm, 24 cm, 25 cm.
a. 7 cm + 24 cm = 31 cm, greater than 25 cm
b. 25 cm + 7 cm = 32 cm, greater than 24 cm
c. 24 cm + 25 cm = 49 cm, greater than 7 cm
The sum of lengths of two sides is greater than the length of the third side.
∴ Triangle can be drawn with sides 7 cm, 24 cm, 25 cm.

iii. The lengths of the three sides are 9 cm, 6 cm, 16 cm.
a. 9 cm + 16 cm = 25 cm, greater than 6 cm
b. 6 cm + 16 cm = 22 cm, greater than 9 cm
c. 9 cm+ 6 cm =15 cm, not greater than 16 cm
The sum of lengths of two sides in (c) is not greater than the length of the third side.
∴ Triangle cannot be drawn with sides 9 cm, 6 cm, 16 cm.

iv. The lengths of the three sides are 8.4 cm, 16.4 cm, 4.9 cm.
a. 8.4 cm + 16.4 cm = 24.8 cm, greater than 4.9 cm
b. 4.9 cm + 16.4 cm = 21.3 cm, greater than 8.4 cm
c. 8.4 cm + 4.9 cm = 13.3 cm, not greater than 16.4 cm
The sum of lengths of two sides in (c) is not greater than the length of the third side.
∴ Triangle cannot be drawn with sides 8.4 cm, 16.4 cm, 4.9 cm.

v. The lengths of the three sides are 15 cm, 20 cm, 25 cm.
a. 15 cm + 20 cm = 35 cm, greater than 25 cm
b. 25 cm + 20 cm = 45 cm, greater than 15 cm
c. 15 cm + 25 cm = 40 cm, greater than 20 cm
The sum of lengths of two sides is greater than the length of the third side.
∴ Triangle can be drawn with sides 15 cm, 20 cm, 25 cm.

vi. The lengths of the three sides are 12 cm, 12 cm, 16 cm.
a. 12 cm + 12 cm = 24 cm, greater than 16 cm
b. 12 cm + 16 cm = 28 cm, greater than 12 cm
c. 12 cm + 16 cm = 28 cm, greater than 12 cm
The sum of lengths of two sides is greater than the length of the third side.
∴ Triangle can be drawn with sides 12 cm, 12 cm, 16 cm.

Maharashtra Board Class 6 Maths Chapter 15 Triangles and their Properties Practice Set 36 Intext Questions and Activities

Question 1.
In the given figure, some points and some line segments joining them have been drawn. Which of these figures is a triangle? Which figure is not a triangle? Why not? (Textbook pg. no. 77)

Solution:
ABC it is a closed figure with three sides. Hence, ABC is a triangle.
PQRS has three sides but it is not a closed figure. Hence, PQRS is not a triangle.

Question 2.
As seen above, ∆ABC has three sides. Line segment AB is one side. Write the names of the other two sides. ∆ABC has three angles. ∠ABC is one among them. Write the names of the other angles. (Textbook pg. no. 77)
Solution:
The names of other two sides are: seg BC and seg AC
The names of other angles are: ∠BCA and ∠CAB

Question 3.
Measure the sides of the following triangles in centimeters, using a divider and ruler. Enter the lengths in the table below. What do you observe? (Textbook pg. no. 77)

In ∆ABC	In ∆PQR	In ∆XYZ
l (AB) =       cm	l (QR) =       cm	l (XY) =       cm
l (BC) =       cm	l (PQ) =       cm	l (YZ) =       cm
l (AC) =       cm	l (PR) =        cm	l (XZ) =       cm

Solution:

In ∆ABC	In ∆PQR	In ∆XYZ
l (AB) = 2.6 cm	l (QR) = 2.8 cm	l (XY) = 2.8 cm
l (BC) = 2.6 cm	l (PQ) = 3.8 cm	l (YZ) = 2.6 cm
l (AC) = 2.6 cm	l (PR) = 3.8 cm	l (XZ) = 4.3 cm

We observe that,

1. ∆ABC is an equilateral triangle,
2. ∆PQR is an isosceles triangle, and
3. ∆XYZ is a scalene triangle.

Question 4.
Measure all the angles of the triangles given below. Enter them in the following table. (Textbook pg. no. 78)

In ∆DEF	In ∆PQR	In ∆LMN
Measure of ∠D = m ∠D =___	Measure of ∠P = m ∠P =___	Measure of ∠L =__
Measure of ∠E = m ∠E =___	Measure of ∠Q =___=___	Measure of ∠M =___
Measure of ∠F = ___=___	Measure of ∠R =___=___	Measure of ∠N =___
Observation: All three angles are acute angles.	Observation: One angle is right angle and two are acute angles.	Observation: One angle is an obtuse angle and two are acute.

Solution:

In ∆DEF	In ∆PQR	In ∆LMN
Measure of ∠D = m ∠D = 60º	Measure of ∠P = m ∠P = 45º	Measure of ∠L = 30º
Measure of ∠E = m ∠E = 68º	Measure of ∠Q = m = 90º	Measure of ∠M = 116º
Measure of ∠F = m = 52º	Measure of ∠R = m ∠R = 45º	Measure of ∠N = 34º

1. ADEF is an acute angled triangle,
2. APQR is a right angled triangle,
3. ALMN is an obtuse angled triangle.

Question 5.
Observe the set squares in your compass box. What kind of triangles are they? (Textbook pg. no. 78)

Solution:
The first set square is a scalene triangle and also a right angled triangle.
The second set square is an isosceles triangle and also a right angled triangle.

Question 6.
Properties of a triangle. (Textbook pg. no. 79)
Take a triangular piece of paper. Choose three different colors or signs to mark the three comers of the triangle on both sides of the paper. Fold the paper at the midpoints of two sides as observe?

Solution:
The three angles of the triangle form a straight angle.
∴ m∠A + m∠B + m∠C = 180°
Hence, the sum of the measures of the angles of a triangle is 180°.

Question 7.
Properties of a triangle (Textbook pg. no. 79)
Take a triangular piece of paper and make three different types of marks near the three angles. Take a point approximately at the center of the triangle. From this point, draw three lines that meet the three sides. Cut the paper along those lines. Place the three angles side by side as shown. See how the three angles of a triangle together form a straight angle, or, an angle that measures 180°.

Solution:
The three angles of the triangle form a straight angle.
Hence, the sum of the measures of the angles of a triangle is 180°.

Question 8.
Draw any triangle on a paper. Name its vertices A, B, C. Measure the lengths of its three sides using a divider and scale and enter them in the table. (Textbook pg. no. 79)

Length of side	Sum of the lengths of two sides	Length of the third side
l (AB) =         cm	l (AB) + l (BC) =         cm	l (AC) =         cm
l (BC) =         cm	l (BC) + l (AC) =         cm	l (AB) =         cm
l (AC) =         cm	l (AC) + l (AB) =        cm	l (BC) =         cm

Solution:

Length of side	Sum of the lengths of two sides	Length of the third side
l (AB) = 2.7 cm	l (AB) + l (BC) = 6.6 cm	l (AC) = 5.6 cm
l (BC) = 2.9 cm	l (BC) + l (AC) = 9.5 cm	l (AB) = 2.7 cm
l (AC) = 5.6 cm	l (AC) + l (AB) = 8.3 cm	l (BC) = 3.9 cm

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 5 Decimal Fractions Class 6 Practice Set 14 Answers Solutions.

6th Standard Maths Practice Set 14 Answers Chapter 5 Decimal Fractions

Question 1.
In the table below, write the place value of each of the digits in the number 378.025.

Place	Hundreds	Tens	Units	Tenths	Hundredths	Thousandths
	100	10	1	\(\frac { 1 }{ 10 }\)	\(\frac { 1 }{ 100 }\)	\(\frac { 1 }{ 1000 }\)
Digit	3	7	8	0	2	5
Place value	300			\(\frac { 0 }{ 10 }=0\)		\(\frac { 5 }{ 1000 }\) = 0.005

Solution:

Place	Hundreds	Tens	Units	Tenths	Hundredths	Thousandths
	100	10	1	\(\frac { 1 }{ 10 }\)	\(\frac { 1 }{ 100 }\)	\(\frac { 1 }{ 1000 }\)
Digit	3	7	8	0	2	5
Place value	300	7 × 10 = 70	8 × 1 = 8	\(\frac { 0 }{ 10 }=0\)	\(\frac { 2 }{ 100 }\) = 0.02	\(\frac { 5 }{ 1000 }\) = 0.005

Question 2.
Solve :
i. 905.5 + 27.197
ii. 39 + 700.65
iii. 40 + 27.7 + 2.451
Solution:
i. 905.5 + 27.197

ii. 39 + 700.65

iii. 40 + 27.7 + 2.451

Question 3.
Subtract:
i. 85.96 – 2.345
ii. 632.24 – 97.45
iii. 200.005 – 17.186
Solution:
i. 85.96 – 2.345

ii. 632.24 – 97.45

iii. 200.005 – 17.186

Question 4.
Avinash traveled 42 km 365 m by bus, 12 km 460 in by car and walked 640 m. How many kilometers did he travel altogether? (Write your answer in decimal fractions)
Solution:
Distance traveled in bus = 42 km 365 m
= 42 km + \(\frac { 365 }{ 1000 }\) km
= 42 km + 0.365 km

= 42.365 km
Distance travelled in car = 12 km 460 m
= 12 km + \(\frac { 460 }{ 1000 }\) km
= 12 km + 0.460 km

= 12.460 km
Distance walked = 640 m
= \(\frac { 640 }{ 1000 }\) = 0.640 km
∴ Total distance travelled = Distance travelled in bus + Distance travelled in car + Distance walked
= 42.365 + 12.460 + 0.640

= 55.465 km
∴ Distance travelled altogether by Avinash is 55.465 km.

Question 5.
Ayesha bought 1.80 m of cloth for her salwaar and 2.25 for her kurta. If the cloth costs Rs 120 per metre, how much must she pay the shopkeeper?
Solution:
Total length of cloth bought = 1.80 m + 2.25 m
= 4.05 m

Cost of 1 m of cloth = Rs 120
∴ Cost of 4.05 m of cloth = 4.05 x 120

∴ Amount to be paid to the shopkeeper is Rs 486.

Question 6.
Sujata bought a watermelon weighing 4.25 kg and gave 1 kg 750 g to the children in her neighbourhood. How much of it does she have left?
Solution:
Total weight of watermelon = 4.25 kg
Weight of watermelon given to children = 1 kg 750 g
= 1 kg + \(\frac { 750 }{ 1000 }\) kg
= 1 kg + 0.75 kg

= 1.75 kg
∴ Weight of watermelon left = Total weight of watermelon – Weight of watermelon given to children
= 4.25 kg – 1.75 kg

= 2.5 kg
∴ Weight of watermelon left with Sujata is 2.5 kg.

Question 7.
Anita was driving at a speed of 85.6 km per hour. The road had a speed limit of 55 km per hour. By how much should she reduce her speed to be within the speed limit?
Solution:
Speed at which Anita is driving = 85.6 km per hr.
Speed limit = 55 km per hr.
∴ Anita should reduce her speed by 85.6 km per hr – 55 km per hr.

= 30.6 km per hr.
∴ Anita should reduce her speed by 30.6 km per hour to be within the speed limit.

Maharashtra Board Class 6 Maths Chapter 4 Operations on Fractions Practice Set 14 Intext Questions and Activities

Question 1.
Nandu went to a shop to buy a pen, notebook, eraser and a paint box. The shopkeeper told him the prices. A pen costs four and a half rupees, an eraser one and a half, a notebook six and a half and a paintbox twenty-five rupees and fifty paise. Nandu bought one of each article. Prepare his bill.
If Nandu gave a 100 rupee note, how much money does he get back? (Textbook pg. no. 29)

Nandu will get __ rupees back.
Solution:
100 – 38 = 62.00
Nandu will get Rs 62 rupees back.

Question 2.
Take a pen and notebook with you when you go to the market with your parent. Note the weight of every vegetable your mother buys. Find out the total weight of those vegetables. (Textbook pg. no. 30)
Solution:
(Students should attempt this activity on their own.)

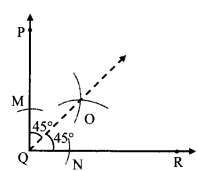
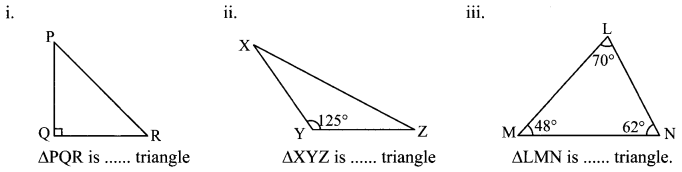
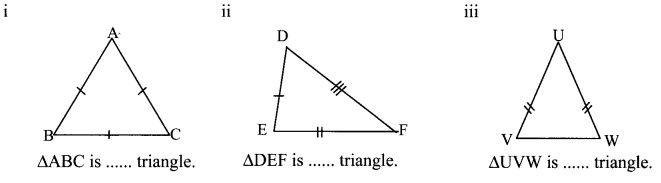
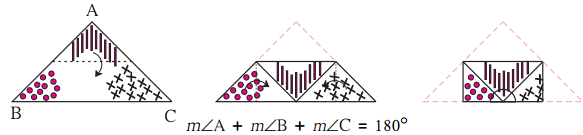
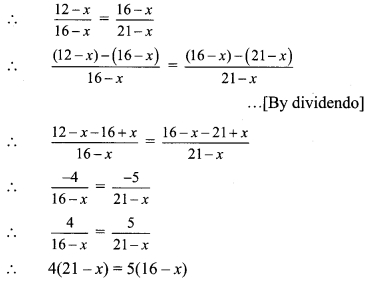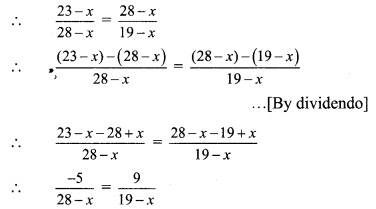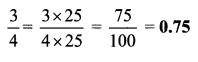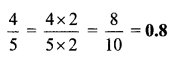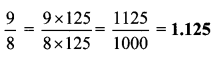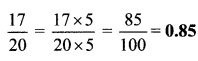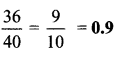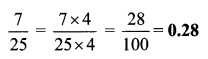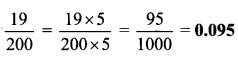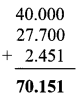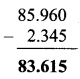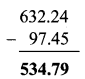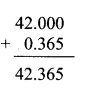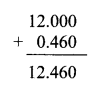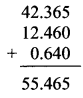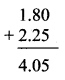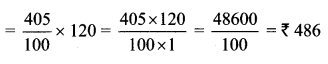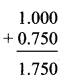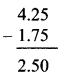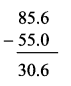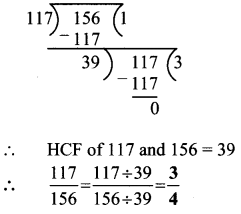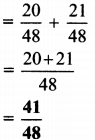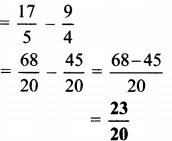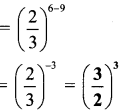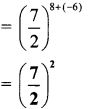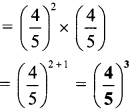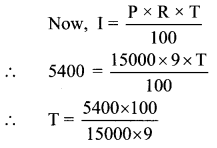Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Miscellaneous Problems Set 1 Answers Solutions.

Maharashtra Board Miscellaneous Problems Set 1 Class 7 Maths Solutions

Question 1.
Solve the following:
i. (-16) × (-5)
ii. (72) ÷ (-12)
iii. (-24) × (2)
iv. 125 ÷ 5
v. (-104) ÷ (-13)
vi. 25 × (-4)
Solution:
i. (-16) × (-5) = 80

ii. 72 ÷ (-12) = \(\frac { 72 }{ -12 }\)
= \(\frac{1}{(-1)} \times \frac{72}{12}\)
(-1) × 12
= -6

iii. (-24) × 2 = -48

iv. 125 ÷ 5 = \(\frac { 125 }{ 5 }\)
= 25

v. (-104) ÷ (-13) = \(\frac { -104 }{ -13 }\)
= \(\frac { 104 }{ 13 }\)
= 8

vi. 25 × (-4) = -100

Question 2.
Find the prime factors of the following numbers and find their LCM and HCF:
i. 75,135
ii. 114,76
iii. 153,187
iv. 32,24,48
Solution:
i. 75 = 3 × 25
= 3 × 5 × 5
135 = 3 × 45
= 3 × 3 × 15
= 3 × 3 × 3 × 5
∴ HCF of 75 and 135 = 3 × 5
= 15
LCM of 75 and 135 = 3 × 5 × 5 × 3 × 3
= 675

ii. 114 = 2 × 57
= 2 × 3 × 19
76 = 2 × 38
= 2 × 2 × 19
∴ HCF of 114 and 76 = 2 × 19
= 38
LCM of 114 and 76 = 2 × 19 × 3 × 2
= 228

iii. 153 = 3 × 51
= 3 × 3 × 17
187 = 11 × 17
∴ HCF of 153 and 187 = 17
LCM of 153 and 187 = 17 × 3 × 3 × 11
= 1683

iv. 32 = 2 × 16
= 2 × 2 × 8
= 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2
24 = 2 × 12
= 2 × 2 × 6
= 2 × 2 × 2 × 3
48 = 2 × 24
= 2 × 2 × 12
= 2 × 2 × 2 × 6
= 2 × 2 × 2 × 2 × 3
∴ HCF of 32, 24 and 48 = 2 × 2 × 2
= 8
LCM of 32,24 and 48 = 2 × 2 × 2 × 2 × 2 × 3
= 96

Question 3.
Simplify:
i. \(\frac { 322 }{ 391 }\)
ii. \(\frac { 247 }{ 209 }\)
iii. \(\frac { 117 }{ 156 }\)
Solution:
i. \(\frac { 322 }{ 391 }\)

ii. \(\frac { 247 }{ 209 }\)

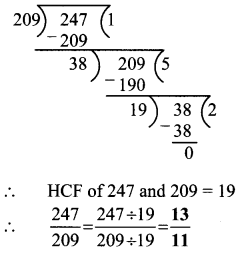
iii. \(\frac { 117 }{ 156 }\)

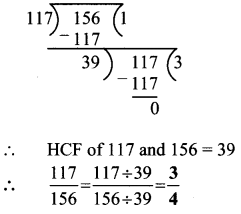
Question 4.
i. 784
ii. 225
iii. 1296
iv. 2025
v. 256
Solution:
i. 784

∴ 784 = 2 × 2 × 2 × 2 × 7 × 7
∴ √784 = 2 × 2 × 7
= 28

ii. 225

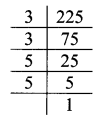
∴ 225 = 3 × 3 × 5 × 5
∴ √225 = 3 × 5
= 15

iii. 1296

∴ 1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
∴ √1296 = 2 × 2 × 3 × 3
= 36

iv. 2025

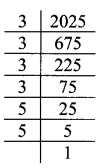
∴ 2025 = 3 × 3 × 3 × 3 × 5 × 5
∴ √2025 = 3 × 3 × 5
= 45

v. 256

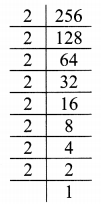
∴ 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ √256 = 2 × 2 × 2 × 2
= 16

Question 5.
There are four polling booths for a certain election. The numbers of men and women who cast their vote at each booth is given in the table below. Draw a joint bar graph for this data.

Polling Booths	Navodaya Vidyalaya	Vidyaniketan School	City High School	Eklavya School
Women	500	520	680	800
Men	440	640	760	600

Solution:

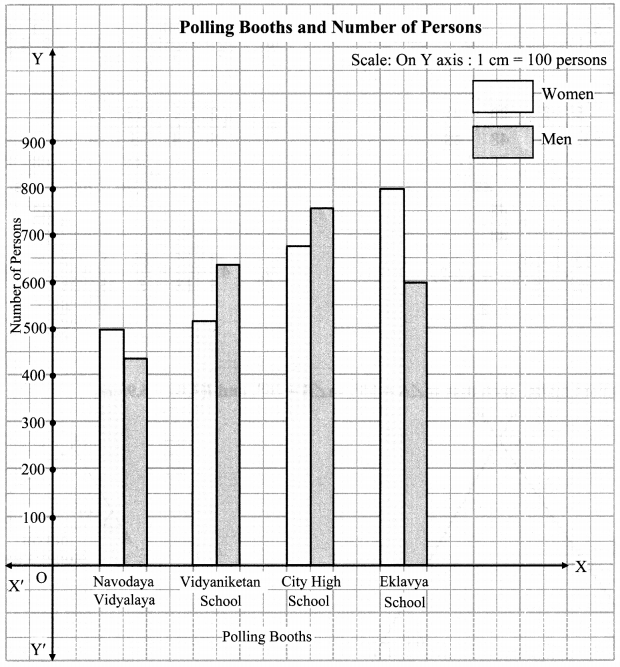
Question 6.
Simplify the expressions:
i. 45 ÷ 5 + 120 × 4 – 12
ii. (38 – 8) × 2 ÷ 5 + 13
iii. \(\frac{5}{3}+\frac{4}{7} \div \frac{32}{21}\)
iv. 3 × {4 [85 + 5 – (15 – 3)] + 2}
Solution:
i. 45 ÷ 5 + 120 × 4 – 12
= 9 + 80 – 12
= 89 – 12
= 77

ii. (38 – 8) × 2 ÷ 5 + 13
= 30 × 2 ÷ 5 + 13
= 60 ÷ 5 + 13
= 12 + 13
= 25

iii. \(\frac{5}{3}+\frac{4}{7} \div \frac{32}{21}\)
\(\frac{5}{3}+\frac{4}{7} \times \frac{21}{32}\)
\(\frac{5}{3}+\frac{3}{8}=\frac{40}{24}+\frac{9}{24}\)
\(\frac{49}{24}\)

iv. 3 × {4 [85 + 5 – (15 – 3)] + 2}
= 3 × {4[90 – 5] + 2}
= 3 × {4 × 85 + 2}
= 3 × (340 + 2)
= 3 × 342
= 1026

Question 7.
Solve:
i. \(\frac{5}{12}+\frac{7}{16}\)
ii. \(3 \frac{2}{5}-2 \frac{1}{4}\)
iii. \(\frac{12}{5} \times \frac{(-10)}{3}\)
iv. \(4 \frac{3}{8} \div \frac{25}{18}\)
Solution:
i. \(\frac{5}{12}+\frac{7}{16}\)

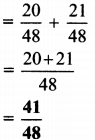
ii. \(3 \frac{2}{5}-2 \frac{1}{4}\)

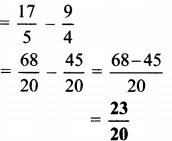
iii. \(\frac{12}{5} \times \frac{(-10)}{3}\)
= 4 × (-2)
= -8

iv. \(4 \frac{3}{8} \div \frac{25}{18}\)
= \(\frac{7}{4} \times \frac{9}{5}\)
= \(\frac { 63 }{ 20 }\)

Question 8.
Construct ∆ABC such that m∠A = 55°, m∠B = and l(AB) = 5.9 cm.
Solution:

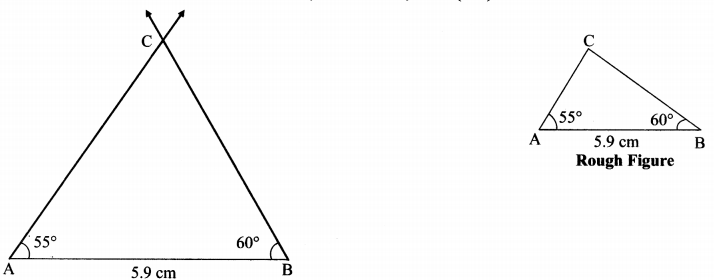
Question 9.
Construct ∆XYZ such that, l(XY) = 3.7 cm, l(YZ) = 7.7 cm, l(XZ) = 6.3 cm.
Solution:

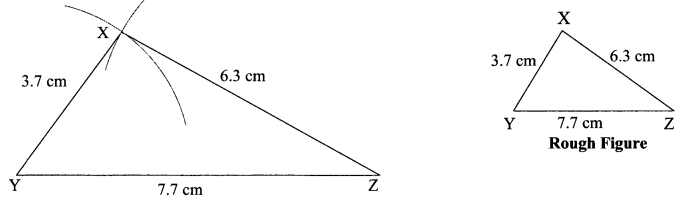
Question 10.
Construct ∆PQR such that, m∠P = 80°, m∠Q = 70°, l(QR) = 5.7 cm.
Ans:
In ∆PQR,
m∠P + m∠Q + m∠R = 180° …. (Sum of the measures of the angles of a triangle is 180°)
∴ 80 + 70 + m∠R = 180
∴ 150 + m∠R = 180
∴ m∠R = 180 – 150
∴ m∠R = 30°

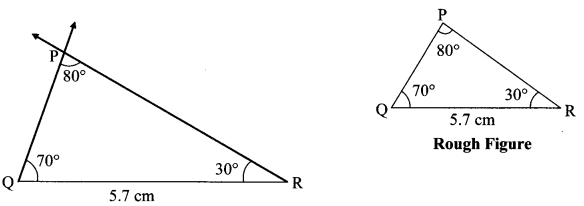
Question 11.
Construct ∆EFG from the given measures. l(FG) = 5 cm, m∠EFG = 90°, l(EG) = 7 cm.
Solution:

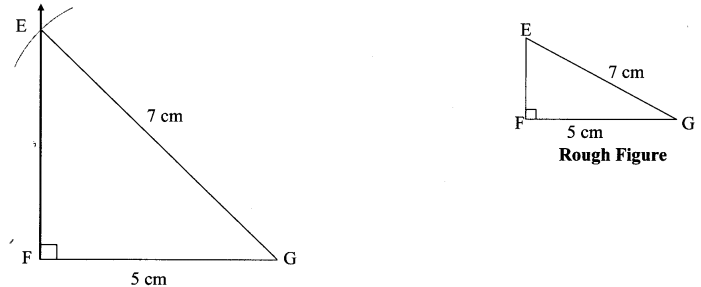
Question 12.
In ∆LMN, l(LM) = 6.2 cm, m∠LMN = 60°, l(MN) 4 cm. Construct ∆LMN.
Solution:

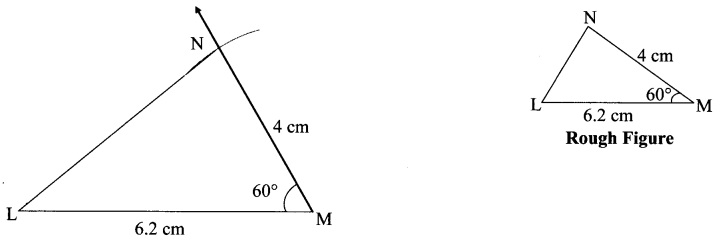
Question 13.
Find the measures of the complementary angles of the following angles:
i. 35°
ii. a°
iii. 22°
iv. (40 – x)°
Solution:
i. Let the measure of the complementary
angle be x°.
35 + x = 90
∴35 + x-35 = 90 – 35
….(Subtracting 35 from both sides)
∴x = 55
∴The complementary angle of 35° is 55°.

ii. Let the measure of the complementary angle be x°.
a + x = 90
∴a + x – a = 90 – a
….(Subtracting a from both sides)
∴x = (90 – a)
∴The complementary angle of a° is (90 – a)°.

iii. Let the measure of the complementary angle be x°.
22 + x = 90
∴22 + x – 22 = 90 – 22
….(Subtracting 22 from both sides)
∴x = 68
∴The complementary angle of 22° is 68°.

iv. Let the measure of the complementary angle be a°.
40 – x + a = 90
∴40 – x + a – 40 + x = 90 – 40 + x
….(Subtracting 40 and adding x on both sides)
∴a = (50 + x)
∴The complementary angle of (40 – x)° is (50 + x)°.

Question 14.
Find the measures of the supplements of the following angles:
i. 111°
ii. 47°
iii. 180°
iv. (90 – x)°
Solution:
i. Let the measure of the supplementary
angle be x°.
111 + x = 180
∴ 111 + x – 111 = 180 – 111
…..(Subtracting 111 from both sides)
∴ x = 69
∴ The supplementary angle of 111° is 69°.

ii. Let the measure of the supplementary angle be x°.
47 + x = 180
∴47 + x – 47 = 180 – 47
….(Subtracting 47 from both sides)
∴x = 133
∴The supplementary angle of 47° is 133°.

iii. Let the measure of the supplementary angle be x°.
180 + x = 180
∴180 + x – 180 = 180 – 180
….(Subtracting 180 from both sides)
∴x = 0
∴The supplementary angle of 180° is 0°.

iv. Let the measure of the supplementary angle be a°.
90 – x + a = 180
∴90 – x + a – 90 + x = 180 – 90+ x
….(Subtracting 90 and adding x on both sides)
∴a = 180 – 90 + x
∴a = (90 + x)
∴The supplementary angle of (90 – x)° is (90 + x)°.

Question 15.
Construct the following figures:
i. A pair of adjacent angles
ii. Two supplementary angles which are not adjacent angles.
iii. A pair of adjacent complementary angles.
Solution:
i.

ii.

iii.

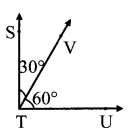
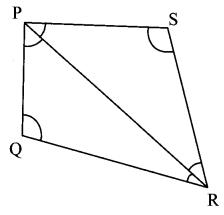
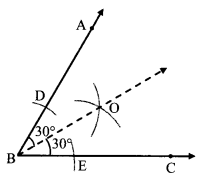
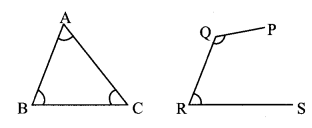
Question 16.
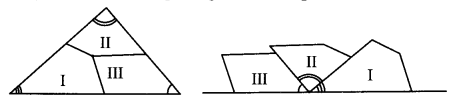
In ∆PQR the measures of ∠P and ∠Q are equal and m∠PRQ = 70°, Find the measures of the following angles.

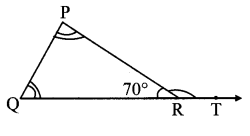
1. m∠PRT
2. m∠P
3. m∠Q

Solution:
Here, ∠PRQ and ∠PRT are angles in a linear pair.
m∠PRQ + m∠PRT = 180°
∴70 + m∠PRT = 180
∴m∠PRT = 180 – 70
∴m∠PRT = 110°
Now, ∠PRT is the exterior angle of ∆PQR.
∴m∠P + m∠Q = m∠PRT
∴m∠P + m∠P = m∠PRT ….(The measures of ∠P and ∠Q is same)
∴2m∠P = 110
∴m∠P = \(\frac { 110 }{ 2 }\)
∴m∠P = 55°
∴m∠Q =

Question 17.
Simplify
i. 5⁴ × 5³
ii. \(\left(\frac{2}{3}\right)^{6} \div\left(\frac{2}{3}\right)^{9}\)
iii. \(\left(\frac{7}{2}\right)^{8} \times\left(\frac{7}{2}\right)^{-6}\)
iv. \(\left(\frac{4}{5}\right)^{2} \div\left(\frac{5}{4}\right)\)
Solution:
Simplify
i. 5⁴ × 5³
= 5⁴⁺³
= 5⁷

ii. \(\left(\frac{2}{3}\right)^{6} \div\left(\frac{2}{3}\right)^{9}\)

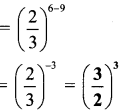
iii. \(\left(\frac{7}{2}\right)^{8} \times\left(\frac{7}{2}\right)^{-6}\)

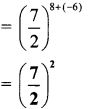
iv. \(\left(\frac{4}{5}\right)^{2} \div\left(\frac{5}{4}\right)\)

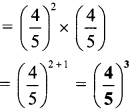
Question 18.
Find the value:
i. 17¹⁶  ÷ 17¹⁶
ii. 10^-3
iii. (2³)²
iv. 4⁶ × 4^-4
Solution:
i. 17¹⁶  ÷ 17¹⁶
= 17⁰
= 1

ii. 10^-3
= \(\frac{1}{10^{3}}\)
= \(\frac{1}{1000}\)

iii. (2³)²
= 2^3×2
= 2⁶
= 2 × 2 × 2 × 2 × 2 × 2
= 64

iv. 4⁶ × 4^-4
= 4^6+(-4)
= 4²
= 4 × 4
= 16

Question 19.
Solve:
i. (6a – 5b – 8c) + (15b + 2a – 5c)
ii. (3x + 2y) (7x – 8y)
iii. (7m – 5n) – (-4n – 11m)
iv. (11m – 12n + 3p) – (9m + 7n – 8p)
Solution:
i. (6a – 5b – 8c) + (15b + 2a – 5c)
= (6a + 2a) + (-5b + 15b) + (-8c – 5c)
= 8a + 10b – 13c

ii. (3x + 2y) (7x – 8y)
= 3x × (7x – 8y) + 2yx (7x – 8y)
= 21x² – 24xy + 14xy – 16y²
= 21x² – 10xy – 16y²

iii. (7m – 5n) – (-4n – 11m)
= 7m – 5n + 4n + 11m
= (7m + 11m) + (-5n + 4n)
= 18m – n

iv. (11m – 12n + 3p) – (9m + 7n – 8p)
= 11m – 12n + 3p – 9m – 7n + 8p
= (11m – 9m) + (-12n – 7n) + (3p + 8p)
= 2m – 19n + 11p

Question 20.
Solve the following equations:
i 4(x + 12) = 8
ii. 3y + 4 = 5y – 6
Solution:
i. 4(x + 12) = 8
∴4x + 48 = 8
∴4x + 48 – 48 = 8 – 48
….(Subtracting 48 from both sides)
∴ 4x = -40
∴ x = \(\frac { -40 }{ 4 }\)
∴ x = -10

ii. 3y + 4 = 5y – 6
∴ 3y + 4 + 6 = 5y – 6 + 6
….(Adding 6 on both sides)
∴ 3y + 10 = 5y
∴ 3y + 10 – 3y = 5y – 3y
….(Subtracting 3y from both sides)
∴ 10 = 2y
∴ 2y = 10
∴ y = \(\frac { 10 }{ 2 }\)
∴ y = 5

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Miscellaneous Problems Set 2 Answers Solutions.

Maharashtra Board Miscellaneous Problems Set 2 Class 7 Maths Solutions

Question 1.
Angela deposited Rs 15000 in a bank at a rate of 9 p.c.p.a. She got simple interest amounting to Rs 5400. For how many years had she deposited the amount?
Solution:
Here, P = Rs 15000, R = 9 p.c.p.a., I = Rs 5400

∴ T = 4
∴ Angela had deposited the amount for 4 years.

Question 2.
Ten men take 4 days to complete the task of tarring a road. How many days would 8 men take?
Solution:
Let us suppose that 8 men require x days to tar the road.
Number of days required by 10 men to tar the road = 4
The number of men and the number of days required to tar the road are in inverse proportion.
∴ 8 × x = 10 x 4
∴ \(x=\frac{10 \times 4}{8}\)
∴ x = 5
∴ 8 men will require 5 days to tar the road.

Question 3.
Nasruddin and Mahesh invested Rs 40,000 and Rs 60,000 respectively to start a business. They made a profit of 30%. How much profit did each of them make?
Solution:
Total amount invested = Rs 40,000 + Rs 60,000
= Rs 1,00,000
Profit earned = 30%
∴ Total profit = 30% of 1,00,000
= \(\frac { 30 }{ 100 }\) × 100000
= Rs 30000
Proportion of investment = 40000 : 60000
= 2:3 …. (Dividing by 20000)
Let Nasruddin’s profit be Rs 2x and Mahesh’s profit be Rs 3x.
∴ 2x + 3x = 30000
∴ 5x = 30000
∴ x = \(\frac { 30000 }{ 5 }\).
∴ x = 6000
∴ Nasruddin’s profit = 2x = 2 × 6000 = Rs 12000
Mahesh’s profit = 3x = 3 × 6000 = Rs 18000
∴ The profits of Nasruddin and Mahesh are Rs 12000 and Rs 18000 respectively.

Question 4.
The diameter of a circle is 5.6 cm. Find its circumference.
Solution:
Diameter of the circle (d) = 5.6 cm
Circumference = πd
= \(\frac{22}{7} \times 5.6\)
= \(\frac{22}{7} \times \frac{56}{10}\)
= 17.6 cm
∴ The circumference of the circle is 17.6 cm.

Question 5.
Expand:
i. (2a – 3b)²
ii. (10 + y)²
iii. \(\left(\frac{p}{3}+\frac{q}{4}\right)^{2}\)
iv. \(\left(y-\frac{3}{y}\right)^{2}\)
Solution:
i. Here, A = 2a and B = 3b
∴ (2a – 3b)² = (2a)² – 2 × 2a × 3b + (3b)²
…. [(A – B)² = A² – 2AB + B²]
= 4a² – 12ab + 9b²

ii. Here, a = 10 and b = y
(10 + y)² = 102 + 2 × 10xy + y²
…. [(a + b)² = a² + 2ab + b²]
= 100 + 20y + y²

iii. Here, a = \(\frac { p }{ 3 }\) and b = \(\frac { q }{ 4 }\)
\(\left(\frac{p}{3}+\frac{q}{4}\right)^{2}=\left(\frac{p}{3}\right)^{2}+2 \times \frac{p}{3} \times \frac{q}{4}+\left(\frac{q}{4}\right)^{2}\)
…. [(a + b)² = a² + 2ab + b²]
\(\frac{p^{2}}{9}+\frac{p q}{6}+\frac{q^{2}}{16}\)

iv. Here, a = y and b = \(\frac { 3 }{ y }\)
\(\left(y-\frac{3}{y}\right)^{2}=y^{2}-2 \times y \times \frac{3}{y}+\left(\frac{3}{y}\right)^{2}\)
…. [(a – b)² = a² – 2ab + b²
= \(y^{2}-6+\frac{9}{y^{2}}\)

Question 6.
Use a formula to multiply:
i. (x – 5)(x + 5)
ii. (2a – 13)(2a + 13)
iii. (4z – 5y)(4z + 5y)
iv. (2t – 5)(2t + 5)
Solution:
i. Here, a = x and b = 5
(x – 5)(x + 5) = (x)² – (5)²
…. [(a + b)(a – b) = a² – b²]
= x² – 25

ii. Here, A = 2a and B = 13
(2a – 13)(2a + 13) = (2a)² – (13)²
…. [(A + B)(A – B) = A² – B²]
= 4a² – 169

iii. Here, a = 4z and b = 5y
(4z – 5y)(4z + 5y) = (4z)² – (5y)²
…. [(a + b)(a – b) = a² – b²]
= 16z² – 25y²

iv. Here, a = 2t and b = 5
(2t – 5)(2t + 5) = (2t)² – (5)²
…. [(a + b)(a – b) = a² – b²]
= 4t² – 25

Question 7.
The diameter of the wheel of a cart is 1.05 m. How much distance will the cart cover in 1000 rotations of the wheel?
Solution:
Diameter of the wheel (d) = 1.05 m
∴ Distance covered in 1 rotation of wheel = Circumference of the wheel
= πd
= \(\frac{22}{7} \times 1.05\)
= 3.3 m
∴ Distance covered in 1000 rotations = 1000 x 3.3 m
= 3300 m
= \(\frac { 3300 }{ 1000 }\) km …[1m = \(\frac { 1 }{ 1000 }\)km]
= 3.3 km
∴ The distance covered by the cart in 1000 rotations of the wheel is 3.3 km.

Question 8.
The area of a rectangular garden of length 40 m, is 1000 sq m. Find the breadth of the garden and its perimeter. The garden is to be enclosed by 3 rounds of fencing, leaving an entrance of 4 m. Find the cost of fencing the garden at a rate of Rs 250 per metre.
Solution:
Length of the rectangular garden = 40 m
Area of the rectangular garden = 1000 sq. m.
∴ length × breadth = 1000
∴ 40 × breadth = 1000
∴ breadth = \(\frac { 1000 }{ 40 }\)
= 25 m
Now, perimeter of the rectangular garden = 2 × (length + breadth)
= 2 (40 + 25)
= 2 × 65
= 130 m
Length of one round of fence = circumference of garden – width of the entrance
= 130 – 4
= 126 m
∴ Total length of fencing = length of one round of wire × number of rounds = 126 × 3
= 378 m
∴ Total cost of fencing = Total length of fencing × cost per metre of fencing
= 378 × 250
= 94500
∴ The cost of fencing the garden is Rs 94500.

Question 9.
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
Solution:

In ∆ABC, ∠B = 90°, and l(BC) = 21, and l(AB) = 20
∴ According to Pythagoras’ theorem,
∴ l(AC)² = l(BC)² + l(AB)²
∴ l(AC)² = 21² + 20²
∴ l(AC)² = 441 + 400
∴ l(AC)² = 841
∴ l(AC)² = 29²
∴ l(AC) = 29
Perimeter of ∆ABC = l(AB) + l(BC) + l(AC)
= 20 + 21 + 29
= 70
∴ The length of hypotenuse AC is 29 units, and the perimeter of ∆ABC is 70 units.

Question 10.
If the edge of a cube is 8 cm long, find its total surface area.
Solution: ,
Total surface area of the cube = 6 × (side)²
= 6 × (8)²
= 6 × 64
= 384 sq. cm
The total surface area of the cube is 384 sq.cm.

Question 11.
Factorize: 365y⁴z³ – 146y²z⁴
Solution:
= 365y⁴z³ – 146y²z⁴
= 73 (5y⁴z³ – 2y²z⁴)
= 73y² (5y²z³ – 2z⁴)
= 73y²z³(5y² – 2z)