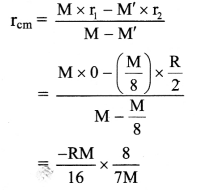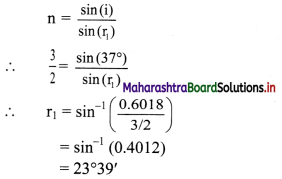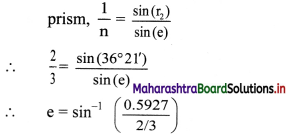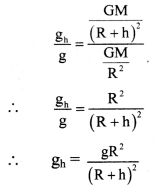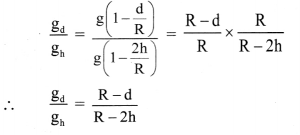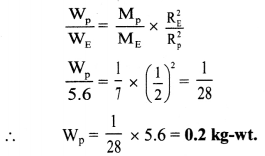Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 9 Optics Textbook Exercise Questions and Answers.
Optics Class 11 Exercise Question Answers Solutions Maharashtra Board
Class 11 Physics Chapter 9 Exercise Solutions Maharashtra Board
Physics Class 11 Chapter 9 Exercise Solutions
1. Multiple Choise Questions
Question 1.
As per recent understanding light consists of
(A) rays
(B) waves
(C) corpuscles
(D) photons obeying the rules of waves
Answer:
(D) photons obeying the rules of waves
Question 2.
Consider the optically denser lenses P, Q, R and S drawn below. According to Cartesian sign convention which of these have positive focal length?

(A) OnlyP
(B) Only P and Q
(C) Only P and R
(D) Only Q and S
Answer:
(B) Only P and Q

Question 3.
Two plane mirrors are inclined at angle 40° between them. Number of images seen of a tiny object kept between them is
(A) Only 8
(B) Only 9
(C) 8 or 9
(D) 9 or 10
Answer:
(C) 8 or 9
Question 4.
A concave mirror of curvature 40 cm, used for shaving purpose produces image of double size as that of the object. Object distance must be
(A) 10 cm only
(B) 20 cm only
(C) 30 cm only
(D) 10 cm or 30 cm
Answer:
(D) 10 cm or 30 cm
Question 5.
Which of the following aberrations will NOT occur for spherical mirrors?
(A) Chromatic aberration
(B) Coma
(C) Distortion
(D) Spherical aberration
Answer:
(A) Chromatic aberration
Question 6.
There are different fish, monkeys and water of the habitable planet of the star Proxima b. A fish swimming underwater feels that there is a monkey at 2.5 m on the top of a tree. The same monkey feels that the fish is 1.6 m below the water surface. Interestingly, height of the tree and the depth at which the fish is swimming are exactly same. Refractive index of that water must be
(A) 6/5
(B) 5/4
(C) 4/3
(D) 7/5
Answer:
(B) 5/4
Question 7.
Consider following phenomena/applications: P) Mirage, Q) rainbow, R) Optical fibre and S) glittering of a diamond. Total internal reflection is involved in
(A) Only R and S
(B) Only R
(C) Only P, R and S
(D) all the four
Answer:
(A) Only R and S
Question 8.
A student uses spectacles of number -2 for seeing distant objects. Commonly used lenses for her/his spectacles are
(A) bi-concave
(B) piano concave
(C) concavo-convex
(D) convexo-concave
Answer:
(A) bi-concave
Question 9.
A spherical marble, of refractive index 1.5 and curvature 1.5 cm, contains a tiny air bubble at its centre. Where will it appear when seen from outside?
(A) 1 cm inside
(B) at the centre
(C) 5/3 cm inside
(D) 2 cm inside
Answer:
(B) at the centre
Question 10.
Select the WRONG statement.
(A) Smaller angle of prism is recommended for greater angular dispersion.
(B) Right angled isosceles glass prism is commonly used for total internal reflection.
(C) Angle of deviation is practically constant for thin prisms.
(D) For emergent ray to be possible from the second refracting surface, certain minimum angle of incidence is necessary from the first surface.
Answer:
(A) Smaller angle of prism is recommended for greater angular dispersion.
Question 11.
Angles of deviation for extreme colours are given for different prisms. Select the one having maximum dispersive power of its material.
(A) 7°, 10°
(B) 8°, 11°
(C) 12°, 16°
(D) 10°, 14°
Answer:
(A) 7°, 10°
Question 12.
Which of the following is not involved in formation of a rainbow?
(A) refraction
(B) angular dispersion
(C) angular deviation
(D) total internal reflection
Answer:
(D) total internal reflection
Question 13.
Consider following statements regarding a simple microscope:
(P) It allows us to keep the object within the least distance of distinct vision.
(Q) Image appears to be biggest if the object is at the focus.
(R) It is simply a convex lens.
(A) Only (P) is correct
(B) Only (P) and (Q) are correct
(C) Only (Q) and (R) are correct
(D) Only (P) and (R) are correct
Answer:
(D) Only (P) and (R) are correct
2. Answer the following questions.
Question 1.
As per recent development, what is the nature of light? Wave optics and particle nature of light are used to explain which phenomena of light respectively?
Answer:
- As per recent development, it is now an established fact that light possesses dual nature. Light consists of energy carrier photons. These photons follow the rules of electromagnetic waves.
- Wave optics explains the phenomena of light such as, interference, diffraction, polarisation, Doppler effect etc.
- Particle nature of light can be used to explain phenomena like photoelectric effect, emission of spectral lines, Compton effect etc.
Question 2.
Which phenomena can be satisfactorily explained using ray optics?
Answer:
Ray optics or geometrical optics: Ray optics can be used for understanding phenomena like reflection, refraction, double refraction, total internal reflection, etc.
Question 3.
What is focal power of a spherical mirror or a lens? What may be the reason for using P = \(\frac {1}{f}\) its expression?
Answer:
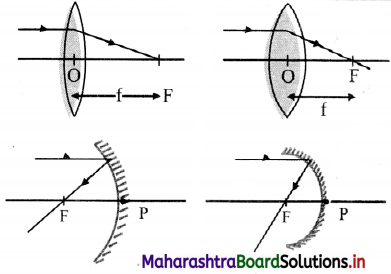
- Converging or diverging ability of a lens or of a mirror is defined as its focal power.
- This implies, more the power of any spherical mirror or a lens, the more is its ability to converge or diverge the light that passes through it.
- In case of convex lens or concave mirror, more the convergence, shorter is the focal length as shown in the figure.
- Similarly, in case of concave lens or convex mirror, more the divergence, shorter is the focal length.
- This explains that the focal power of any spherical lens or mirror is inversely proportional to the focal length.
- Hence, the expression of focal power is given by the formula, P = \(\frac {1}{f}\).
Question 4.
At which positions of the objects do spherical mirrors produce (i) diminished image (ii) magnified image?
Answer:
i. Amongst the two types of spherical mirrors, convex mirror always produces a diminished image at all positions of the object.
ii. Concave mirror produces diminished image when object is placed:
- Beyond radius of curvature (i.e., u > 2f)
- At infinity (i.e., u = ∞)
iii. Concave mirror produces magnified image when object is placed:
- between centre of curvature and focus (i.e., 2f > u > f)
- between focus and pole of the mirror (i.e., u < f)

Question 5.
State the restrictions for having images produced by spherical mirrors to be appreciably clear.
Answer:
i. In order to obtain clear images, the formulae for image formation by mirrors or lens follow the given assumptions:
- Objects and images are situated close to the principal axis.
- Rays diverging from the objects are confined to a cone of very small angle.
- If there is a parallel beam of rays, it is paraxial, i.e., parallel and close to the principal axis.
ii. In case of spherical mirrors (excluding small aperture spherical mirrors), rays farther from the principle axis do not remain parallel to the principle axis. Thus, the third assumption is not followed and the focus gradually shifts towards the pole.
iii. The relation (f = \(\frac {R}{2}\)) giving a single point focus is not followed and the image does not get converged at a single point resulting into a distorted or defective image.
iv. This defect arises due to the spherical shape of the reflecting surface.
Question 6.
Explain spherical aberration for spherical mirrors. How can it be minimized? Can it be eliminated by some curved mirrors?
Answer:
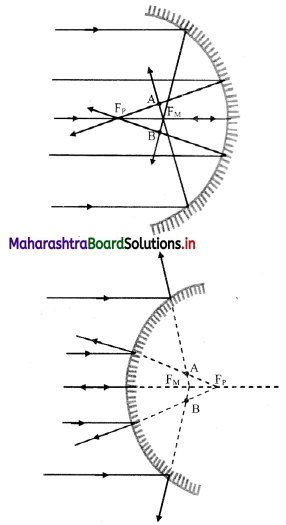
- In case of spherical mirrors (excluding small aperture spherical mirror), The rays coming from a distant object farther from principal axis do not remain parallel to the axis. Thus, the focus gradually shifts towards the pole.
- The assumption for clear image formation namely, ‘If there is a parallel beam of rays, it is paraxial, i.e., parallel and close to the principal axis’, is not followed in this case.
- The relation f (f = \(\frac {R}{2}\)) giving a single point focus is not followed and the image does not get converged at a single point resulting into a distorted or defective image.
- This phenomenon is known as spherical aberration.
- It occurs due to spherical shape of the reflecting surface, hence known as spherical aberration.
- The rays near the edge of the mirror converge at focal point FM Whereas, the rays near the principal axis converge at point FP. The distance between FM and FP is measured as the longitudinal spherical aberration.
- In spherical aberration, single point image is not possible at any point on the screen and the image formed is always a circle.
- At a particular location of the screen (across AB in figure), the diameter of this circle is minimum. This is called the circle of least confusion. Radius of this circle is transverse spherical aberration.
Remedies for Spherical Aberration:
- Spherical aberration can be minimized by reducing the aperture of the mirror.
- Spherical aberration in curved mirrors can be completely eliminated by using a parabolic mirror.
Question 7.
Define absolute refractive index and relative refractive index. Explain in brief with an illustration for each.
Answer:
i. Absolute refractive index of a medium is defined as the ratio of speed of light in vacuum to that in the given medium.
ii. A stick or pencil kept obliquely in a glass containing water appears broken as its part in water appears to be raised.
iii. As the speed of light is different in two media, the rays of light coming from water undergo refraction at the boundary separating two media.
iv. Consider speed of light to be v in water and c in air. (Speed of light in air ~ speed of light in vacuum)
∴ refractive index of water = \(\frac {n_w}{n_s}\) = \(\frac {n_w}{n_{vacuum}}\) = \(\frac {c}{v}\)
v. Relative refractive index of a medium 2 is the refractive index of medium 2 with respect to medium 1 and it is defined as the ratio of speed of light v1 in medium 1 to its speed v1 in medium 2.
∴ Relative refractive index of medium 2,
1n2 = \(\frac {v_1}{v_2}\)
vi. Consider a beaker filled with water of absolute refractive index n1 kept on a transparent glass slab of absolute refractive index n2.
vii. Thus, the refractive index of water with respect to that of glass will be,
nw2 = \(\frac {n_2}{n_1}\) = \(\frac {c/v_2}{c/v_1}\) = \(\frac {v_1}{v_2}\)
Question 8.
Explain ‘mirage’ as an illustration of refraction.
Answer:
i. On a hot clear Sunny day, along a level road, there appears a pond of water ahead of the road. Flowever, if we physically reach the spot, there is nothing but the dry road and water pond again appears some distance ahead. This illusion is called mirage.
ii. Mirage results from the refraction of light through a non-uniform medium.
iii. On a hot day the air in contact with the road is hottest and as we go up, it gets gradually cooler. The refractive index of air thus decreases with height. Hot air tends to be less optically dense than cooler air which results into a non-uniform medium.
iv. Light travels in a straight line through a uniform medium but refracts when traveling through a non-uniform medium.
v. Thus, the ray of light coming from the top of an object get refracted while travelling downwards into less optically dense air and become more and more horizontal as shown in Figure.
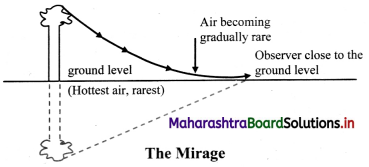
vi. As it almost touches the road, it bends (refracts) upward. Then onwards, upward bending continues due to denser air.
vii. As a result, for an observer, it appears to be coming from below thereby giving an illusion of reflection from an (imaginary) water surface.
Question 9.
Under what conditions is total internal reflection possible? Explain it with a suitable example. Define critical angle of incidence and obtain an expression for it.
Answer:
Conditions for total internal reflection:
i. The light ray must travel from denser medium to rarer medium.
ii. The angle of incidence in the denser medium must be greater than critical angle for the given pair of media.
Total internal reflection in optical fibre:
iii. Consider an optical fibre made up of core of refractive index n1 and cladding of refractive index n2 such that, n1 > n2.
iv. When a ray of light is incident from a core (denser medium), the refracted ray is bent away from the normal.
v. At a particular angle of incidence ic in the denser medium, the corresponding angle of refraction in the rarer medium is 90°.
vi. For angles of incidence greater than ic, the angle of refraction become larger than 90° and the ray does not enter into rarer medium at all but is reflected totally into the denser medium as shown in figure.
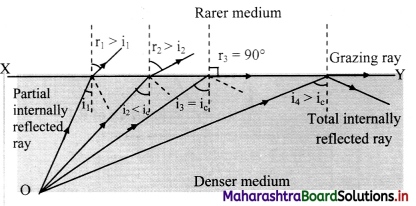
critical angle of incidence and obtain an expression:
i. Critical angle for a pair of refracting media can be defined as that angle of incidence in the denser medium for which the angle of refraction in the rarer medium is 90°.
ii. Let n be the relative refractive index of denser medium with respect to the rarer.
iii. Then, according to Snell’s law,
n = \(\frac {n_{denser}}{n_{rarer}}\) = \(\frac {sin r}{sin i_c}\) = \(\frac {sin 90°}{sin i_c}\)
∴ sin (ic) = \(\frac {1}{n}\)

Question 10.
Describe construction and working of an optical fibre. What are the advantages of optical fibre communication over electronic communication?
Answer:
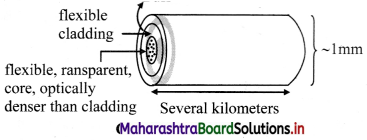
Construction:
- An optical fibre consists of an extremely thin, transparent and flexible core surrounded by an optically rarer flexible cover called cladding.
- For protection, the whole system is coated by a buffer and a jacket.
- Entire thickness of the fibre is less than half a mm.
- Many such fibres can be packed together in an outer cover.
Working:

- Working of optical fibre is based on the principle of total internal reflection.
- An optical signal (a ray of light) entering the core suffers multiple total internal reflections before emerging out after a several kilometres.
- The optical signal travels with the highest possible speed in the material.
- The emerged optical signal has extremely low loss in signal strength.
Advantages of optical fibre communication over electronic communication:
- Broad bandwidth (frequency range): For TV signals, a single optical fibre can carry over 90000 independent signals (channels).
- Immune to EM interference: Optical fibre being electrically non-conductive, does not pick up nearby EM signals.
- Low attenuation loss: loss being lower than 0.2 dB/km, a single long cable can be used for several kilometres.
- Electrical insulator: Optical fibres being electrical insulators, ground loops of metal wires or lightning do not cause any harm.
- Theft prevention: Optical fibres do not use copper or other expensive material which are prone to be robbed.
- Security of information: Internal damage is most unlikely to occur, keeping the information secure.
Question 11.
Why are prism binoculars preferred over traditional binoculars? Describe its working in brief.
Answer:
- Traditional binoculars use only two cylinders. Distance between the two cylinders can’t be greater than that between the two eyes. This creates a limitation of field of view.
- A prism binocular has two right angled glass prisms which apply the principle of total internal reflection.
- The incident light rays are reflected internally twice giving the viewer a wider field of view. For this reason, prism binoculars are preferred over traditional binoculars.
Working:
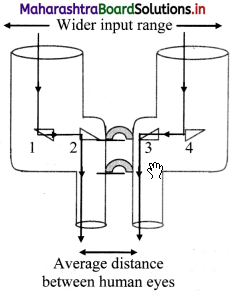
- The prism binoculars consist of 4 isosceles, right angled prisms of material having critical angle less than 45°.
- The prism binoculars have a wider input range compared to traditional binoculars.
- The light rays incident on the prism binoculars, first get total internally reflected by the isosceles, right angled prisms 1 and 4.
- These reflected rays undergo another total internal reflection by prisms 2 and 3 to form the final image.
Question 12.
A spherical surface separates two transparent media. Derive an expression that relates object and image distances with the radius of curvature for a point object. Clearly state the assumptions, if any.
Answer:
i. Consider a spherical surface YPY’ of radius curvature R, separating two transparent media of refractive indices n1 and n2 respectively with ni1 < n2.
ii. P is the pole and X’PX is the principal axis. A point object O is at a distance u from the pole, in the medium of refractive index n1.
iii. In order to minimize spherical aberration, we consider two paraxial rays.
iv. The ray OP along the principal axis travels undeviated along PX. Another ray OA strikes the surface at A.
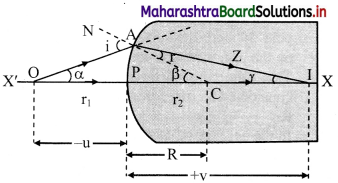
v. As n1 < n2, the ray deviates towards the normal (CAN), travels along AZ and real image of point object O is formed at I.
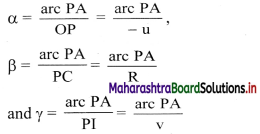
vi. Let α, β and γ be the angles subtended by incident ray, normal and refracted ray with the principal axis.
∴ i = (α + β) and r = (β – γ)
vii. As, the rays are paraxial, all the angles can be considered to be very small.
i.e., sin i ≈ i and sin r ≈ r
Angles α, β and γ can also be expressed as,
viii. According to Snell’s law,
n1 sin (i) = n2 sin (r)
For small angles, Snell’s law can be written
as, n1i = n2r
∴ n1 (α + β) = n2 (β – γ)
∴ (n2 – n1)β = n1α + n2γ
Substituting values of α, β and γ, we get,
(n2 – n1) \(\frac {arc PA}{R}\) = n1(\(\frac {arc PA}{-u}\)) + n2(\(\frac {arc PA}{v}\))
∴ \(\frac {(n_2-n_1)}{R}\) = \(\frac {n_2}{v}\) – \(\frac {n_1}{u}\)
Assumptions: To derive an expression that relates object and image distances with the radius of curvature for a point object, the two rays considered are assumed to be paraxial thus making the angles subtended by incident ray, normal and refracted ray with the principal axis very small.
Question 13.
Derive lens makers’ equation. Why is it called so? Under which conditions focal length f and radii of curvature R are numerically equal for a lens?
Answer:
i. Consider a lens of radii of curvature Ri and R2 kept in a medium such that refractive index of material of the lens with respect to the medium is denoted as n.
ii. Assuming the lens to be thin, P is the common pole for both the surfaces. O is a point object on the principal axis at a distance u from P.
iii. The refracting surface facing the object is considered as first refracting surface with radii R1.
iv. In the absence of second refracting surface, the paraxial ray OA deviates towards normal and would intersect axis at I1. PI1 = V1 is the image distance for intermediate image I1.
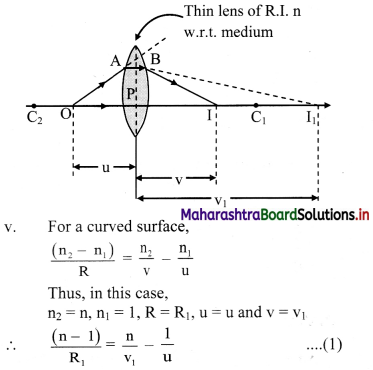
Before reaching I1, the incident rays (AB and OP) strike the second refracting surface. In this case, image I1 acts as a virtual object for second surface.
vii. For second refracting surface,
n2 = 1, n1 = n, R = R2, u = v1 and PI = v
∴ \(\frac{(1-\mathrm{n})}{\mathrm{R}_{2}}=\frac{1}{\mathrm{v}}-\frac{\mathrm{n}}{\mathrm{v}_{1}}-\frac{(\mathrm{n}-1)}{\mathrm{R}_{2}}=\frac{1}{\mathrm{v}}-\frac{\mathrm{n}}{\mathrm{v}_{1}}\) ………… (2)
viii. Adding equations (1) and (2),
(n – 1) \(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)=\frac{1}{v}-\frac{1}{u}\)
For object at infinity, image is formed at focus, i.e., for u = ∞, v = f. Substituting this in above equation,
\(\frac{1}{\mathrm{f}}=(\mathrm{n}-1)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) …………. (3)
This equation in known as the lens makers’ formula.
ix. Since the equation can be used to calculate the radii of curvature for the lens, it is called the lens makers’ equation.
x. The numeric value of focal length f and radius of curvature R is same under following two conditions:
Case I:
For a thin, symmetric and double convex lens made of glass (n = 1.5), R1 is positive and R2 is negative but, |R1| = |R2|.
In this case,
\(\frac{1}{\mathrm{f}}=(1.5-1)\left(\frac{1}{\mathrm{R}}-\frac{1}{-\mathrm{R}}\right)=0.5\left(\frac{2}{\mathrm{R}}\right)=\frac{1}{\mathrm{R}}\)
∴ f = R
Case II:
Similarly, for a thin, symmetric and double concave lens made of glass (n = 1.5), R1 is negative and R2 is positive but, |R1| = |R2|.
In this case,
\(\frac{1}{\mathrm{f}}=(1.5-1)\left(\frac{1}{-\mathrm{R}}-\frac{1}{\mathrm{R}}\right)=0.5\left(-\frac{2}{\mathrm{R}}\right)=-\frac{1}{\mathrm{R}}\)
∴ f = -R or |f| = |R|

3. Answer the following questions in detail.
Question 1.
What are different types of dispersions of light? Why do they occur?
Answer:
i. There are two types of dispersions:
a. Angular dispersion
b. Lateral dispersion
ii. The refractive index of material depends on the frequency of incident light. Hence, for different colours, refractive index of material is different.
iii. For an obliquely incident ray, the angles of refraction are different for each colour and they separate as they travel along different directions resulting into angular dispersion.
iv. When a polychromatic beam of light is obliquely incident upon a plane parallel transparent slab, emergent beam consists of all component colours separated out.
v. In this case, these colours are parallel to each other and are also parallel to their initial direction resulting into lateral dispersion
Question 2
Define angular dispersion for a prism. Obtain its expression for a thin prism. Relate it with the refractive indices of the material of the prism for corresponding colours.
Answer:
i. If a polychromatic beam is incident upon a prism, the emergent beam consists of all the individual colours angularly separated. This phenomenon is known as angular dispersion for a prism.
ii. For any two component colours, angular dispersion is given by,
δ21 = δ2 – δ1
iii. For white light, we consider two extreme colours viz., red and violet.
∴ δVR = δV – δR
iv. For thin prism,
δ = A(n – 1)
δ21 = δ2 – δ1
= A(n2 – 1) – A(n1 – 1) = A(n2 – n1)
where n1 and n2 are refractive indices for the two colours.
v. For white light,
δVR = δV – δR
= A(nV – 1) – A(nR – 1) = A(nV – nR).
Question 3.
Explain and define dispersive power of a transparent material. Obtain its expressions in terms of angles of deviation and refractive indices.
Answer:
Ability of an optical material to disperse constituent colours is its dispersive power.
It is measured for any two colours as the ratio of angular dispersion to the mean deviation for those two colours. Thus, for the extreme colours of white light, dispersive power is given by,
\(\omega=\frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\left(\frac{\delta_{\mathrm{V}}+\delta_{\mathrm{R}}}{2}\right)} \approx \frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\delta_{\mathrm{Y}}}=\frac{\mathrm{A}\left(\mathrm{n}_{\mathrm{V}}-\mathrm{n}_{\mathrm{R}}\right)}{\mathrm{A}\left(\mathrm{n}_{\mathrm{Y}}-1\right)}=\frac{\mathrm{n}_{\mathrm{V}}-\mathrm{n}_{\mathrm{R}}}{\mathrm{n}_{\mathrm{Y}}-1}\)
Question 4.
(i) State the conditions under which a rainbow can be seen.
Answer:
A rainbow can be observed when there is a light shower with relatively large raindrop occurring during morning or evening time with enough sunlight around.
(ii) Explain the formation of a primary rainbow. For which angular range with the horizontal is it visible?
Answer:
i. A ray AB incident from Sun (white light) strikes the upper portion of a water drop at an incident angle i.
ii. On entering into water, it deviates and disperses into constituent colours. The figure shows the extreme colours (violet and red).
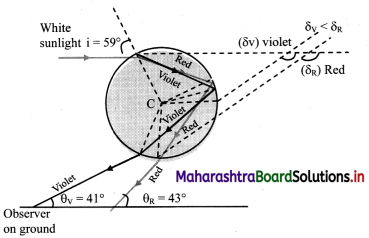
iii. Refracted rays BV and BR strike the opposite inner surface of water drop and suffer internal reflection.
iv. These reflected rays finally emerge from V’ and R’ and can be seen by an observer on the ground.
v. For the observer they appear to be coming from opposite side of the Sun.
vi. Minimum deviation rays of red and violet colour are inclined to the ground level at θR = 42.8° ≈ 43° and θV = 40.8 ≈ 41° respectively. As a result, in the rainbow, the red is above and violet is below.
(iii) Explain the formation of a secondary rainbow. For which angular range with the horizontal is it visible?
Answer:
i. A ray AB incident from Sun (white light) strikes the lower portion of a water drop at an incident angle i.
ii. On entering into water, it deviates and disperses into constituent colours. The figure shows the extreme colours (violet and red).
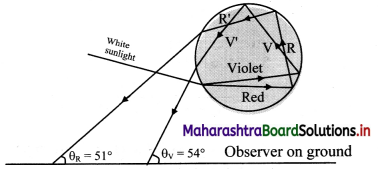
iii. Refracted rays BV and BR finally emerge the drop from V’ and R’ after suffering two internal reflections and can be seen by an observer on the ground.
iv. Minimum deviation rays of red and violet colour are inclined to the ground level at θR ≈ 51° and θV ≈ 53° respectively. As a result, in the rainbow, the violet is above and red is below.
(iv) Is it possible to see primary and secondary rainbow simultaneously? Under what conditions?
Answer:
Yes, it is possible to see primary and secondary rainbows simultaneously. This can occur when the centres of both the rainbows coincide.

Question 5.
(i) Explain chromatic aberration for spherical lenses. State a method to minimize or eliminate it.
Answer:
Lenses are prepared by using a transparent material medium having different refractive index for different colours. Hence angular dispersion is present.
If the lens is thick, this will result into notably different foci corresponding to each colour for a polychromatic beam, like a white light. This defect is called chromatic aberration.
As violet light has maximum deviation, it is focussed closest to the pole.
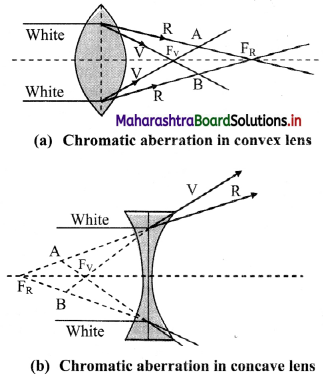
Reducing/eliminating chromatic aberration:
- Eliminating chromatic aberrations for all colours is impossible. Hence, it is minimised by eliminating aberrations for extreme colours.
- This is achieved by using either a convex and a concave lens in contact or two thin convex lenses with proper separation. Such a combination is called achromatic combination.
(ii) What is achromatism? Derive a condition to achieve achromatism for a lens combination. State the conditions for it to be converging.
Answer:
i. To eliminate chromatic aberrations for extreme colours from a lens, either a convex and a concave lens in contact or two thin convex lenses with proper separation are used.
ii. This combination is called achromatic combination. The process of using this combination is termed as achromatism of a lens.
iii. Let ω1 and ω2 be the dispersive powers of materials of the two component lenses used in contact for an achromatic combination.
iv. Let V, R and Y denote the focal lengths for violet, red and yellow colours respectively.
v. For lens 1, let
K1 = (\(\frac {1}{R_1}\)–\(\frac {1}{R_2}\))1 and K2 = (\(\frac {1}{R_1}\)–\(\frac {1}{R_2}\))2
vi. For the combination to be achromatic, the resultant focal length of the combination must be the same for both the colours,

This is the condition for achromatism of a combination of lenses.
Condition for converging:
For this combination to be converging, fY must be positive.
Using equation (3), for fY to be positive, (fY)1 < (fY)2 ⇒ ω1 < ω2
Question 6.
Describe spherical aberration for spherical lenses. What are different ways to minimize or eliminate it?
Answer:
i. All the formulae used for image formation by lenses are based on some assumption. However, in reality these assumptions are not always true.
ii. A single point focus in case of lenses is possible only for small aperture spherical lenses and for paraxial rays.
iii. The rays coming from a distant object farther from principal axis no longer remain parallel to the axis. Thus, the focus gradually shifts towards pole.
iv. This defect arises due to spherical shape of the refracting surface, hence known as spherical aberration. It results into a blurred image with unclear boundaries.
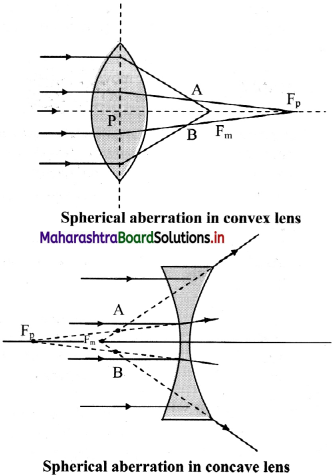
v. As shown in figure, the rays near the edge of the lens converge at focal point FM. Whereas, the rays near the principal axis converge at point FP. The distance between FM and FP is measured as the longitudinal spherical aberration.
vi. In absence of this aberration, a single point image can be obtained on a screen. In the presence of spherical aberration, the image is always a circle.
vii. At a particular location of the screen (across AB in figure), the diameter of this circle is minimum. This is called the circle of least confusion. Radius of this circle is transverse spherical aberration.
Methods to eliminate/reduce spherical aberration in lenses:
i. Cheapest method to reduce the spherical aberration is to use a planoconvex or planoconcave lens with curved side facing the incident rays.
ii. Certain ratio of radii of curvature for a given refractive index almost eliminates the spherical aberration. For n = 1.5, the ratio is
\(\frac {R_1}{R_2}\) = \(\frac {1}{6}\) and for n = 2, \(\frac {R_1}{R_2}\) = \(\frac {1}{5}\)
iii. Use of two thin converging lenses separated by distance equal to difference between their focal lengths with lens of larger focal length facing the incident rays considerably reduces spherical aberration.
iv. Spherical aberration of a convex lens is positive (for real image), while that of a concave lens is negative. Thus, a suitable combination of them can completely eliminate spherical aberration.
Question 7.
Define and describe magnifying power of an optical instrument. How does it differ from linear or lateral magnification?
Answer:
i. Angular magnification or magnifying power of an optical instrument is defined as the ratio of the visual angle made by the image formed by that optical instrument (β) to the visual angle subtended by the object when kept at the least distance of distinct vision (α).
ii. The linear magnification is the ratio of the size of the image to the size of the object.
iii. When the distances of the object and image formed are very large as compared to the focal lengths of the instruments used, the magnification becomes infinite. Whereas, the magnifying power being the ratio of angle subtended by the object and image, gives the finite value.
iv. For example, in case of a compound microscope,
Mmin = \(\frac {D}{f}\) = \(\frac {25}{5}\) = 5 and Mmax = 1 + \(\frac {D}{f}\) = 6
Hence image appears to be only 5 to 6 times bigger for a lens of focal length 5 cm.
For Mmin = \(\frac {D}{f}\) = 5, V = ∞
∴ Lateral magnification (m) = \(\frac {v}{u}\) = ∞
Thus, the image size is infinite times that of the object, but appears only 5 times bigger.
Question 8.
Derive an expression for magnifying power of a simple microscope. Obtain its minimum and maximum values in terms of its focal length.
Answer:
i. Figure (a) shows visual angle a made by an object, when kept at the least distance of distinct vision (D = 25 cm). Without an optical instrument this is the greatest possible visual angle as we cannot get the object closer than this.
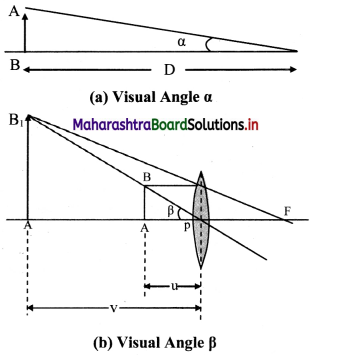
ii. Figure (b) shows a convex lens forming erect, virtual and magnified image of the same object, when placed within the focus.
iii. The visual angle p of the object and the image in this case are the same. However, this time the viewer is looking at the image which is not closer than D. Hence the same object is now at a distance smaller than D.
iv. Angular magnification or magnifying power, in this case, is given by
M = \(\frac {Visual angle of theimage}{Visual angle of the object at D}\) = \(\frac {β}{α}\)
For small angles,
M = \(\frac {β}{α}\) ≈ \(\frac {tan(β)}{tan(α)}\) = \(\frac {BA/PA}{BA/D}\) = \(\frac {D}{u}\)
v. For maximum magnifying power, the image should be at D. For thin lens, considering thin lens formula.

Question 9.
Derive the expressions for the magnifying power and the length of a compound microscope using two convex lenses.
Answer:
i. The final image formed in compound microscope (A” B”) as shown in figure, makes a visual angle β at the eye.
Visual angle made by the object from distance D is α.
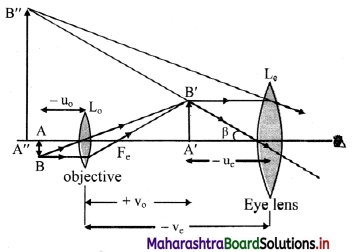
From figure,
tan β = \(\frac {A”B”}{v_c}\) = \(\frac {A’B’}{u_c}\)
and tan α = \(\frac {AB}{D}\)

Question 10.
What is a terrestrial telescope and an astronomical telescope?
Answer:
- Telescopes used to see the objects on the Earth, like mountains, trees, players playing a match in a stadium, etc. are called terrestrial telescopes.
- In such case, the final image must be erect. Eye lens used for this purpose must be concave and such a telescope is popularly called a binocular.
- Most of the binoculars use three convex lenses with proper separation. The image formed by second lens is inverted with respect to object. The third lens again inverts this image and makes final image erect with respect to the object.
- An astronomical telescope is the telescope used to see the objects like planets, stars, galaxies, etc. In this case there is no necessity of erect image. Such telescopes use convex lens as eye lens.
Question 11.
Obtain the expressions for magnifying power and the length of an astronomical telescope under normal adjustments.
Answer:
i. For telescopes, a is the visual angle of the object from its own position, which is practically at infinity.
ii. Visual angle of the final image is p and its position can be adjusted to be at D. However, under normal adjustments, the final image is also at infinity making a greater visual angle than that of the object.
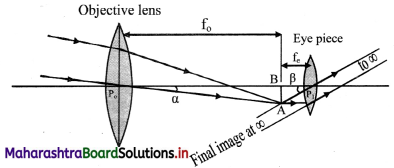
iii. The parallax at the cross wires can be avoided by using the telescopes in normal adjustments.
iv. Objective of focal length f0 focusses the parallel incident beam at a distance f0 from the objective giving an inverted image AB.
v. For normal adjustment, the intermediate image AB forms at the focus of the eye lens. Rays refracted beyond the eye lens form a parallel beam inclined at an angle β with the principal axis.
vi. Angular magnification or magnifying power for telescope is given by,
M = \(\frac {β}{α}\) ≈ \(\frac {tan(β)}{tan(α)}\) = \(\frac {BA/P_cB}{BA/P_0B}\) = \(\frac {f_0}{f_e}\)
vii. Length of the telescope for normal adjustment is, L = f0 + fe.
Question 12.
What are the limitations in increasing the magnifying powers of (i) simple microscope (ii) compound microscope (iii) astronomical telescope?
Answer:
i. In case of simple microscope
\(\mathrm{M}_{\max }=\frac{\mathrm{D}}{\mathrm{u}}=1+\frac{\mathrm{D}}{\mathrm{f}}\)
Thus, the limitation in increasing the magnifying power is determined by the value of focal length and the closeness with which the lens can be held near the eye.
ii. In case of compound microscope,
M = \(\mathrm{m}_{0} \times \mathrm{M}_{\mathrm{e}}=\frac{\mathrm{v}_{0}}{\mathrm{u}_{\mathrm{o}}} \times \frac{\mathrm{D}}{\mathrm{u}_{\mathrm{e}}}\)
Thus, in order to increase m0, we need to decrease u0. Thereby, the object comes closer and closer to the focus of the objective. This increases v0 and hence length of the microscope. Therefore, mQ can be increased only within the limitation of length of the microscope.
iii. In case of telescopes,
M = \(\frac {f_0}{f_e}\)
Where f0 = focal length of the objective
fe = focal length of the eye-piece
Length of the telescope for normal adjustment is, L = f0 + fe.
Thus, magnifying power of telescope can be increased only within the limitations of length of the telescope.
4. Solve the following numerical examples
Question 1.
A monochromatic ray of light strikes the water (n = 4/3) surface in a cylindrical vessel at angle of incidence 53°. Depth of water is 36 cm. After striking the water surface, how long will the light take to reach the bottom of the vessel? [Angles of the most popular Pythagorean triangle of sides in the ratio 3 : 4 : 5 are nearly 37°, 53° and 90°]
Answer:
From figure, ray PO = incident ray
ray OA = refracted ray
QOB = Normal to the water surface.
Given that,
∠POQ = angle of incidence (θ1) = 53°
Seg OB = 36 cm and nwater = \(\frac {4}{3}\)
From Snell’s law,
n1 sin θ1 = n2 sin θ2
∴ nwater = \(\frac {sinθ_1}{sinθ_2}\)
Or sin θ2 = \(\frac {sinθ_1}{n_{water}}\) = \(\frac {sin(53°)×3}{4}\)
∴ θ2 ~ 37°
ΔOBA forms a Pythagorean triangle with angles 53°, 37° and 90°.
Thus, sides of ΔOBA will be in ratio 3 : 4 : 5 Such that OA forms the hypotenuse. From figure, we can infer that,
Seg OB = 4x = 36 cm
∴ x = 9
∴ seg OA = 5x = 45 cm and
seg AB = 3x = 27 cm.
This means the light has to travel 45 cm to reach the bottom of the vessel.
The speed of the light in water is given by,
v = \(\frac {c}{n}\)
∴ v = \(\frac {3×10^8}{4/3}\) = \(\frac {9}{4}\) × 108 m/s
∴ Time taken by light to reach the bottom of vessel is,
t = \(\frac {s}{v}\) = \(\frac {45×10^{-2}}{\frac {9}{4} × 10^8}\) = 20 × 10-10 = 2 ns or 0.002 µs
Question 2.
Estimate the number of images produced if a tiny object is kept in between two plane mirrors inclined at 35°, 36°, 40° and 45°.
Answer:
i. For θ1 =35°
n1 = \(\frac {360}{θ_1}\) = \(\frac {360}{35}\) = 10.28
As ni is non-integer, N1 = integral part of n1 = 10
ii. For θ2 = 36°
n2 = \(\frac {360}{36}\) = 10
As n2 is even integer, N2 = (n2 – 1) = 9
iii. For θ3 = 40°
n3 = \(\frac {360}{36}\) = 9
As n3 is odd integer.
Number of images seen (N3) = n3 – 1 = 8
(if the object is placed at the angle bisector) or Number of images seen (N3) = n3 = 9
(if the object is placed off the angle bisector)
iv. For θ4 = 45°
n4 = \(\frac {360}{45}\) = 8
As n4 is even integer,
N4 = n4 – 1 = 7

Question 3.
A rectangular sheet of length 30 cm and breadth 3 cm is kept on the principal axis of a concave mirror of focal length 30 cm. Draw the image formed by the mirror on the same diagram, as far as possible on scale.
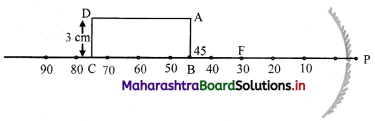
Answer:
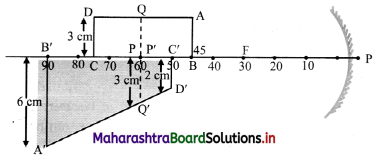
[Note: The question has been modified and the ray digram is inserted in question in order to find the correct position of the image.]
Question 4.
A car uses a convex mirror of curvature 1.2 m as its rear-view mirror. A minibus of cross section 2.2 m × 2.2 m is 6.6 m away from the mirror. Estimate the image size.
Answer:
For a convex mirror,
f = +\(\frac {R}{2}\) = \(\frac {1.2}{2}\) = +0.6m
Given that, a minibus, approximately of a shape of square is at distance 6.6 m from mirror.
i.e., u = -6.6 m

∴ h2 = 0.183 m
i.e., h2 0.2 m
Question 5.
A glass slab of thickness 2.5 cm having refractive index 5/3 is kept on an ink spot. A transparent beaker of very thin bottom, containing water of refractive index 4/3 up to 8 cm, is kept on the glass block. Calculate apparent depth of the ink spot when seen from the outside air.
Answer:
When observed from the outside air, the light coming from ink spot gets refracted twice; once through glass and once through water.
∴ When observed from water,
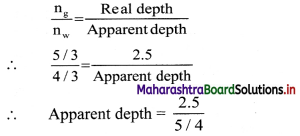
∴ Apparent depth = 2 cm
Now when observed from outside air, the total real depth of ink spot can be taken as (8 + 2) cm = 10 cm.
∴ \(\frac {n_w}{n_{air}}\) = \(\frac {Real depth}{Apparent depth}\)
∴ Apparent depth = \(\frac {10}{4/3}\)
= \(\frac {10×3}{4}\) = 7.5 cm
Question 64.
A convex lens held some distance above a 6 cm long pencil produces its image of SOME size. On shifting the lens by a distance equal to its focal length, it again produces the image of the SAME size as earlier. Determine the image size.
Answer:
For a convex lens, it is given that the image size remains unchanged after shifting the lens through distance equal to its focal length. From given conditions, it can be inferred that the object distance should be u = –\(\frac {f}{2}\)
Also, h1 = 6 cm, v1 = v2
From formula for thin lenses,

Question 7.
Figure below shows the section ABCD of a transparent slab. There is a tiny green LED light source at the bottom left corner B. A certain ray of light from B suffers total internal reflection at nearest point P on the surface AD and strikes the surface CD at point Question Determine refractive index of the material of the slab and distance DQ. At Q, the ray PQ will suffer partial or total internal reflection?
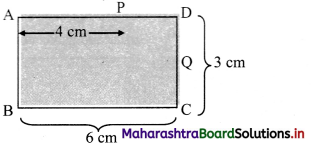
Answer:
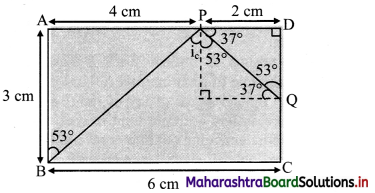
As, the light ray undergo total internal reflection at P, the ray BP may be incident at critical angle.
For a Pythagorean triangle with sides in ratio 3 : 4 : 5 the angle opposite to side 3 units is 37° and that opposite to 4 units is 53°.
Thus, from figure, we can say, in ΔBAP
∠ABP = 53°
∠BPN = ic = 53°
∴ nglass = \(\frac {1}{sin_c}\) = \(\frac {1}{sin(53°)}\) ≈ \(\frac {1}{0.8}\) = \(\frac {5}{4}\)
∴ Refractive index (n) of the slab is \(\frac {5}{4}\)
From symmetry, ∆PDQ is also a Pythagorean triangle with sides in ratio QD : PD : PQ = 3 : 4 : 5.
PD = 2 cm ⇒ QD = 1.5 cm.
As critical angle is ic = 53° and angle of incidence at Q, ∠PQN = 37° is less than critical angle, there will be partial internal reflection at Question
Question 8.
A point object is kept 10 cm away from a double convex lens of refractive index 1.5 and radii of curvature 10 cm and 8 cm. Determine location of the final image considering paraxial rays only.
Answer:
Given that, R1 = 10 cm, R2 = -8 cm,
u = -10 cm and n = 1.5
From lens maker’s equation,


Question 9.
A monochromatic ray of light is incident at 37° on an equilateral prism of refractive index 3/2. Determine angle of emergence and angle of deviation. If angle of prism is adjustable, what should its value be for emergent ray to be just possible for the same angle of incidence.
Answer:
By Snell’s law, in case of prism,
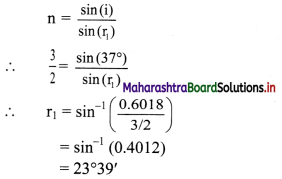
For equilateral prism, A = 60°
Also, A= r1 + r2
∴ r2 = A – r1 = 60° – 23°39′ = 36°21′
Applying snell’s law on the second surface of
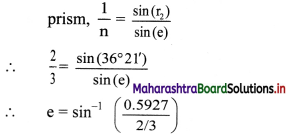
= sin-1 (0.889)
= 62°44′
≈ 63°
For any prism,
i + e = A + δ
∴ δ = (i + e) – A
= (37 + 63) – 60
= 40°
For an emergent ray to just emerge, the angle r’2 acts as a critical angle.
∴ r’2 = sin-1 (\(\frac {1}{n}\))
= sin-1 (\(\frac {2}{3}\))
= 41°48′
As, A = r’1 + r’2 and i to be kept the same.
⇒ A’ = r’1 + r’2‘
= 23°39′ + 41°48′
= 65°27’
Question 10.
From the given data set, determine angular dispersion by the prism and dispersive power of its material for extreme colours. nR = 1.62 nv = 1.66, δR = 3.1°
Answer:
Given: nR = 1.62, nV = 1.66, δR = 3.1°
To find:
i. Angular dispersion (δvr)
ii. Dispersive power (ωVR)
Formula:
i. δ = A (n – 1)
ii. δVR = δV – δR
(iii) ω = \(\frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\left(\frac{\delta_{\mathrm{V}}+\delta_{\mathrm{R}}}{2}\right)}\)
Calculation: From formula (i),
δR = A(nR – 1)
∴ A = \(\frac{\delta_{R}}{\left(n_{R}-1\right)}=\frac{3.1}{(1.62-1)}=\frac{3.1}{0.62}\)
= 5
δV = A(nv – 1) = 5 × (1.66 – 1) = 3.3C
From formula (ii),
δVR = 3.3 – 3.1 = 0.2°
From formula (iii),
ωVR = \(\frac{3.3-3.1}{\left(\frac{3.3+3.1}{2}\right)}=\frac{0.2}{6.4} \times 2=\frac{0.2}{3.2}=\frac{1}{16}\)
= 0.0625
Question 11.
Refractive index of a flint glass varies from 1.60 to 1.66 for visible range. Radii of curvature of a thin convex lens are 10 cm and 15 cm. Calculate the chromatic aberration between extreme colours.
Answer:
Given the refractive indices for extreme colours. As, nR < nV
nR = 1.60 and nV = 1.66
For convex lens,
R1 = 10 cm and R10 = -15 cm

= 0.11
∴ fV = 11 cm
∴ Longitudinal chromatic aberration
= fV – fR = 11 – 10 = 1 cm
Question 12.
A person uses spectacles of ‘number’ 2.00 for reading. Determine the range of magnifying power (angular magnification) possible. It is a concave convex lens (n = 1.5) having curvature of one of its surfaces to be 10 cm. Estimate that of the other.
Answer:
For a single concavo-convex lens, the magnifying power will be same as that for simple microscope As, the number represents the power of the lens,
P = \(\frac {1}{f}\) = 2 ⇒ f = 0.5 m.
∴ Range of magnifying power of a lens will be,
Mmin = \(\frac {D}{f}\) = \(\frac {0.25}{0.5}\) = 0.5
and Mmin = 1 + \(\frac {D}{f}\) = 1 + 0.5 = 1.5
Given that, n = 1.5, |R1| = 10 cm
f = 0.5 m = 50 cm
From lens maker’s equation,

Question 13.
Focal power of the eye lens of a compound microscope is 6 dioptre. The microscope is to be used for maximum magnifying power (angular magnification) of at least 12.5. The packing instructions demand that length of the microscope should be 25 cm. Determine minimum focal power of the objective. How much will its radius of curvature be if it is a biconvex lens of n = 1.5.
Answer:
Focal power of the eye lens,
Pe = \(\frac {1}{f_e}\) = 6D
∴ fe = \(\frac {1}{6}\) = 0.1667 m = 16.67 cm
Now, as the magnifying power is maximum,
ve = 25 cm,
Also (Me)max = 1 + \(\frac {D}{f_e}\) = 1 + \(\frac {25}{16.67}\) ≈ 2.5
Given that,
M = m0 × Me = 12.5
∴ m0 × 2.5 = 12.5
∴ m0 = \(\frac {v_0}{u_0}\) = 5 ……….. (1)
From thin lens formula,
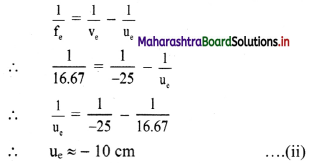
Length of a compound microscope,
L = |v0| +|u0|
∴ 25 = |v0| + 10
∴ |v0|= 15 cm
∴ |u0| = \(\frac {v_0}{5}\) = 3 cm …………… (from 1)
From lens formula for objective,
\(\frac {1}{f_0}\) = \(\frac {1}{v_0}\) – \(\frac {1}{u_0}\)
= \(\frac {1}{15}\) – \(\frac {1}{-3}\)
= \(\frac {2}{5}\)
∴ f0 = 2.5 cm = 0.025 m
Thus, focal power of objective,
P = \(\frac {1}{f_0(m)}\)
= \(\frac {1}{0.025}\) = 40 D
Using lens maker’s equation for a biconvex lens,
\(\frac{1}{f_{o}}=(n-1)\left(\frac{1}{R}-\frac{1}{-R}\right)\)
∴ \(\frac{1}{2.5}=(1.5-1)\left(\frac{2}{R}\right)=\frac{1}{R}\)
∴ R = 2.5 cm
11th Physics Digest Chapter 9 Optics Intext Questions and Answers
Can you recall? (Textbook rage no 159)
What are laws of reflection and refraction?
Answer:
Laws of reflection:
a. Reflected ray lies in the plane formed by incident ray and the normal drawn at the point of incidence and the two rays are on either side of the normal.
b. Angles of incidence and reflection are equal (i = r).
Laws of refraction:
a. Refracted ray lies in the plane formed by incident ray and the normal drawn at the point of incidence; and the two rays are on either side of the normal.
b. Angle of incidence (θ1) and angle of refraction (θ2) are related by Snell’s law, given by, n1 sin θ1 = n2 sin θ2 where, n1, n2 = refractive indices of medium 1 and medium 2 respectively.

Can you recall? (Textbook page no. 159)
Question 1.
What is refractive index?
Answer:
The ratio of velocity of light in vacuum to the velocity’ of light in a medium is called the refractive index of the medium.
Question 2.
What is total internal reflection?
Answer:
For angles of incidence larger than the critical angle, the angle of refraction is larger than 90°. Thus, all the incident light gets reflected back into the denser medium. This is called total internal reflection.
Question 3.
How does a rainbow form?
Answer:
- The rainbow appears in the sky after a rainfall.
- Water droplets present in the atmosphere act as small prism.
- When sunlight enters these water droplets it gets refracted and dispersed.
- This dispersed light gets totally reflected inside the droplet and again is refracted while coming out of the droplet.
- As a combined effect of all these phenomena, the seven coloured rainbow is observed.
Question 4.
What is dispersion of light?
Answer:
Splitting of a white light into its constituent colours is known as dispersion of light.
11th Std Physics Questions And Answers:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()