Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 12 Magnetism Textbook Exercise Questions and Answers.
Magnetism Class 12 Exercise Question Answers Solutions Maharashtra Board
Class 11 Physics Chapter 12 Exercise Solutions Maharashtra Board
Physics Class 11 Chapter 12 Exercise Solutions
1. Choose the correct option.
Question 1.
Let r be the distance of a point on the axis of a bar magnet from its center. The magnetic field at r is always proportional to
(A) \(\frac {1}{r^2}\)
(B) \(\frac {1}{r^3}\)
(C) \(\frac {1}{r}\)
(D) Not necessarily \(\frac {1}{r^3}\) at all points
Answer:
(B) \(\frac {1}{r^3}\)
Question 2.
Magnetic meridian is the plane
(A) perpendicular to the magnetic axis of Earth
(B) perpendicular to geographic axis of Earth
(C) passing through the magnetic axis of Earth
(D) passing through the geographic axis
Answer:
(C) passing through the magnetic axis of Earth
![]()
Question 3.
The horizontal and vertical component of magnetic field of Earth are same at some place on the surface of Earth. The magnetic dip angle at this place will be
(A) 30°
(B) 45°
(C) 0°
(D) 90°
Answer:
(B) 45°
Question 4.
Inside a bar magnet, the magnetic field lines
(A) are not present
(B) are parallel to the cross sectional area of the magnet
(C) are in the direction from N pole to S pole
(D) are in the direction from S pole to N pole
Answer:
(D) are in the direction from S pole to N pole
Question 5.
A place where the vertical components of Earth’s magnetic field is zero has the angle of dip equal to
(A) 0°
(B) 45°
(C) 60°
(D) 90°
Answer:
(A) 0°
Question 6.
A place where the horizontal component of Earth’s magnetic field is zero lies at
(A) geographic equator
(B) geomagnetic equator
(C) one of the geographic poles
(D) one of the geomagnetic poles
Answer:
(D) one of the geomagnetic poles
Question 7.
A magnetic needle kept nonparallel to the magnetic field in a nonuniform magnetic field experiences
(A) a force but not a torque
(B) a torque but not a force
(C) both a force and a torque
(D) neither force nor a torque
Answer:
(C) both a force and a torque
2. Answer the following questions in brief.
Question 1.
What happens if a bar magnet is cut into two pieces transverse to its length/ along its length?
Answer:
i. When a magnet is cut into two pieces, then each piece behaves like an independent magnet.
ii. When a bar magnet is cut transverse to its length, the two pieces generated will behave as independent magnets of reduced magnetic length. However, the pole strength of all the four poles formed will be same as that of the original bar magnet. Thus, the new dipole moment of the smaller magnets will be,
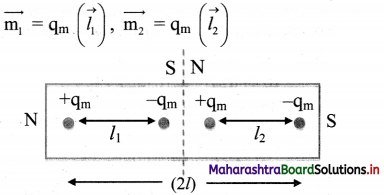
iii. When the bar magnet is cut along its length, the two pieces generated will behave like an independent magnet with reduced pole strength. However, the magnetic length of both the new magnets will be same as that of the original bar magnet. Thus, the new dipole moment of the smaller magnets will be,

Question 2.
What could be the equation for Gauss’ law of magnetism, if a monopole of pole strength p is enclosed by a surface?
Answer:
i. According to Gauss’ law of electrostatics, the net electric flux through any Gaussian surface is proportional to net charge enclosed in it. The equation is given as,
øE = ∫\(\vec{E}\) . \(\vec{dS}\) = \(\frac {q}{ε_0}\)
ii. Similarly, if a monopole of a magnet of pole strength p exists, the Gauss’ law of magnetism in S.I. units will be given as,
øE = ∫\(\vec{B}\) . \(\vec{dS}\) = µ0P
![]()
3. Answer the following questions in detail.
Question 1.
Explain the Gauss’ law for magnetic fields.
Answer:
i. Analogous to the Gauss’ law for electric field, the Gauss’ law for magnetism states that, the net magnetic flux (øB) through a closed Gaussian surface is zero. øB = ∫\(\vec{B}\) . \(\vec{dS}\) = 0
ii. Consider a bar magnet, a current carrying solenoid and an electric dipole. The magnetic field lines of these three are as shown in figures.
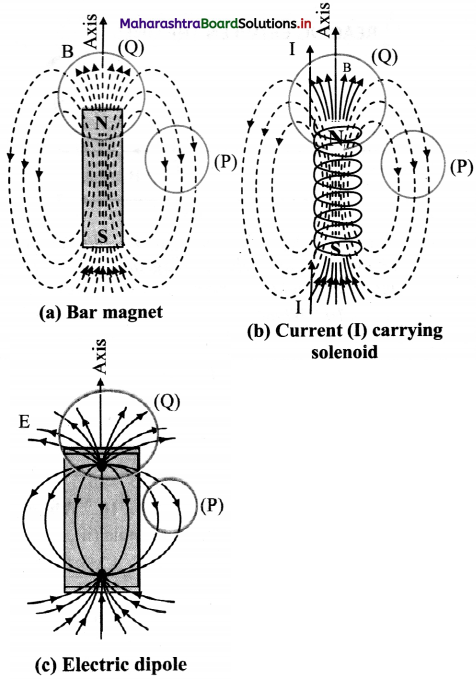
iii. The areas (P) and (Q) are the cross – sections of three dimensional closed Gaussian surfaces. The Gaussian surface (P) does not include poles while the Gaussian surface (Q) includes N-pole of bar magnet, solenoid and the positive charge in case of electric dipole.
iv. The number of lines of force entering the surface (P) is equal to the number of lines of force leaving the surface. This can be observed in all the three cases.
v. However, Gaussian surface (Q) of bar magnet, enclose north pole. As, even thin slice of a bar magnet will have both north and south poles associated with it, the number of lines of Force entering surface (Q) are equal to the number of lines of force leaving the surface.
vi. For an electric dipole, the field lines begin from positive charge and end on negative charge. For a closed surface (Q), there is a net outward flux since it does include a net (positive) charge.
vii. Thus, according to the Gauss’ law of electrostatics øE = ∫\(\vec{E}\) . \(\vec{dS}\) = \(\frac {q}{ε_0}\), where q is the positive charge enclosed.
viii. The situation is entirely different from magnetic lines of force. Gauss’ law of magnetism can be written as øB = ∫\(\vec{B}\) . \(\vec{dS}\) = 0
From this, one can conclude that for electrostatics, an isolated electric charge exists but an isolated magnetic pole does not exist.
Question 2.
What is a geographic meridian? How does the declination vary with latitude? Where is it minimum?
Answer:
A plane perpendicular to the surface of the Earth (vertical plane) and passing through geographic axis is geographic meridian.
i. Angle between the geographic and the magnetic meridian at a place is called magnetic declination (a).
ii. Magnetic declination varies with location and over time. As one moves away from the true north the declination changes depending on the latitude as well as longitude of the place. By convention, declination is positive when magnetic north is east of true north, and negative when it is to the west. The declination is small in India. It is 0° 58′ west at Mumbai and 0° 41′ east at Delhi.
![]()
Question 3.
Define the angle of dip. What happens to angle of dip as we move towards magnetic pole from magnetic equator?
Answer:
Angle made by the direction of resultant magnetic field with the horizontal at a place is inclination or angle of dip (ø) at the place.
At the magnetic pole value of ø = 90° and it goes on decreasing when we move towards equator such that at equator value of (ø) = 0°.
4. Solve the following problems.
Question 1.
A magnetic pole of bar magnet with pole strength of 100 Am is 20 cm away from the centre of a bar magnet. Bar magnet has pole strength of 200 Am and has a length 5 cm. If the magnetic pole is on the axis of the bar magnet, find the force on the magnetic pole.
Answer:
Given that, (qm)1 = 200 Am
and (2l) = 5 cm = 5 × 10-2 m
∴ m = 200 × 5 × 10-2 = 10 Am²
For a bar magnet, magnetic dipole moment is,
m = qm (21)
For a point on the axis of a bar magnet at distance, r = 20 cm = 0.2 m,
Ba = \(\frac{\mu_{0}}{4 \pi} \times \frac{2 m}{r^{3}}\)
= 10-7 × \(\frac{2 \times 10}{(0.2)^{3}}\)
= 0.25 × 10-3
= 2.5 × 10-4 Wb/m²
The force acting on the pole will be given by,
F = qm Ba = 100 × 2.5 × 10-4
= 2.5 × 10-2 N
Question 2.
A magnet makes an angle of 45° with the horizontal in a plane making an angle of 30° with the magnetic meridian. Find the true value of the dip angle at the place.
Answer:
Let true value of dip be ø. When the magnet is kept 45° aligned with declination 30°, the horizontal component of Earth’s magnetic field.
B’H = BH cos 30° Whereas, vertical component remains unchanged.
∴ For apparent dip of 45°,
tan 45° = \(\frac{\mathrm{B}_{\mathrm{V}}^{\prime}}{\mathrm{B}_{\mathrm{H}}^{\prime}}=\frac{\mathrm{B}_{\mathrm{V}}}{\mathrm{B}_{\mathrm{H}} \cos 30^{\circ}}=\frac{\mathrm{B}_{\mathrm{v}}}{\mathrm{B}_{\mathrm{H}}} \times \frac{1}{\cos 30^{\circ}}\)
But, real value of dip is,
tan ø = \(\frac {B_V}{B_H}\)
∴ tan 45° = \(\frac {tan ø}{cos 30°}\)
∴ tan ø = tan 45° × cos 30°
= 1 × \(\frac {√3}{2}\)
∴ ø = tan-1 (0.866)
![]()
Question 3.
Two small and similar bar magnets have magnetic dipole moment of 1.0 Am² each. They are kept in a plane in such a way that their axes are perpendicular to each other. A line drawn through the axis of one magnet passes through the centre of other magnet. If the distance between their centres is 2 m, find the magnitude of magnetic field at the midpoint of the line joining their centres.
Answer:
Let P be the midpoint of the line joining the centres of two bar magnets. As shown in figure, P is at the axis of one bar magnet and at the equator of another bar magnet. Thus, the magnetic field on the axis of the first bar magnet at distance of 1 m from the centre will be,
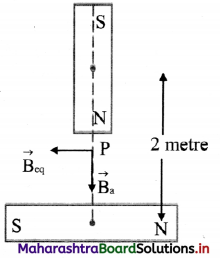
Ba = \(\frac{\mu_{0}}{4 \pi} \frac{2 m}{r^{3}}\)
= 10-7 × \(\frac {2×1.0}{(1)^3}\)
= 2 × 10-7 Wb/m²
Magnetic field on the equator of second bar magnet will be,
Beq = \(\frac{\mu_{0}}{4 \pi} \frac{m}{r^{3}}\)
= 10-7 × \(\frac {1.0}{(1)^3}\)
= 1 × 10-7 Wb/m²
The net magnetic field at P,
Bnet = \(\sqrt {B_a^2+B_{eq}^2}\)
= \(\sqrt {(2×10^{-7})^2+(1×10^{-7})^2}\)
= \(\sqrt {(10^{-7})^2×(4+1)}\)
= √5 × 10-7 Wb/m²
Question 4.
A circular magnet is made with its north pole at the centre, separated from the surrounding circular south pole by an air gap. Draw the magnetic field lines in the gap. Draw a diagram to illustrate the magnetic lines of force between the south poles of two such magnets.
Answer:
i. For a circular magnet:
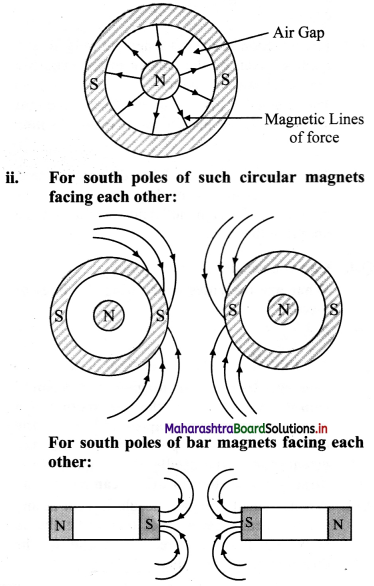
Question 5.
Two bar magnets are placed on a horizontal surface. Draw magnetic lines around them. Mark the position of any neutral points (points where there is no resultant magnetic field) on your diagram.
Answer:
The magnetic lines of force between two magnets will depend on their relative positions. Considering the magnets to be placed one besides the other as shown in figure, the magnetic lines of force will be as shown.
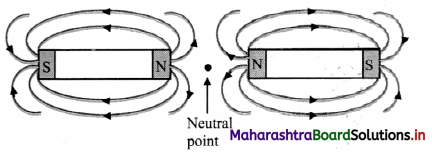
11th Physics Digest Chapter 12 Magnetism Intext Questions and Answers
Can you recall? (Textbook page no. 221)
Question 1.
What are the magnetic lines of force?
Answer:
The magnetic field around a magnet is shown by lines going from one end of the magnet to the other. These lines are named as magnetic lines of force.
![]()
Question 2.
What are the rules concerning the lines of force?
Answer:
i. Magnetic lines of force originate from the north pole and end at the south pole.
ii. The magnetic lines of force of a magnet or a solenoid form closed loops. This is in contrast to the case of an electric dipole, where the electric lines of force originate from the positive charge and end on the negative charge.
iii. The direction of the net magnetic field \(\vec {B}\) at a point is given by the tangent to the magnetic line of force at that point.
iv. The number of lines of force crossing per unit area decides the magnitude of magnetic field \(\vec {B}\)
v. The magnetic lines of force do not intersect. This is because had they intersected, the direction of magnetic field would not be unique at that point.
Question 3.
What is a bar magnet?
Answer:
Bar magnet is a magnet in the shape of bar having two poles of equal and opposite pole strengths separated by certain distance (2l).
Question 4.
If you freely hang a bar magnet horizontally, in which direction will it become stable?
Answer:
A bar magnet suspended freely in air always aligns itself along geographic N-S direction.
Try this (Textbook page no. 221)
You can take a bar magnet and a small compass needle. Place the bar magnet at a fixed position on a paper and place the needle at various positions. Noting the orientation of the needle, the magnetic field direction at various locations can be traced.
Answer:
When a small compass needle is kept at any position near a bar magnet, the needle always aligns itself in the direction parallel to the direction of magnetic lines of force.
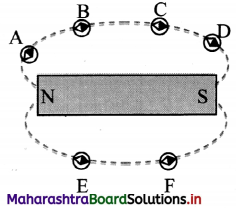
Hence, by placing it at different positions, A, B, C, D,… as shown in the figure, the direction of magnetic lines of force can be traced. The direction of magnetic field will be a tangent at that point.
![]()
Internet my friend: (Text book page no. 227)
https://www.ngdc.noaa.gov
[Students are expected to visit above mentioned link and collect more information about Geomagnetism.]
11th Std Physics Questions And Answers:
- Units and Measurements Class 11 Physics Questions And Answers
- Mathematical Methods Class 11 Physics Questions And Answers
- Motion in a Plane Class 11 Physics Questions And Answers
- Laws of Motion Class 11 Physics Questions And Answers
- Gravitation Class 11 Physics Questions And Answers
- Mechanical Properties of Solids Class 11 Physics Questions And Answers
- Thermal Properties of Matter Class 11 Physics Questions And Answers
- Sound Class 11 Physics Questions And Answers
- Optics Class 11 Physics Questions And Answers
- Electrostatics Class 11 Physics Questions And Answers
- Electric Current Through Conductors Class 11 Physics Questions And Answers
- Magnetism Class 11 Physics Questions And Answers
- Electromagnetic Waves and Communication System Class 11 Physics Questions And Answers
- Semiconductors Class 11 Physics Questions And Answers
