Prasanna

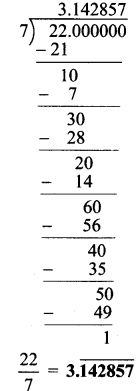
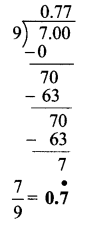
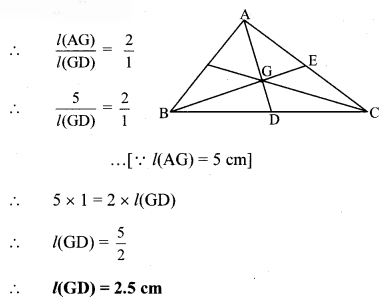
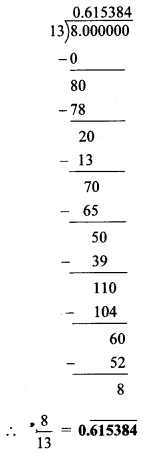
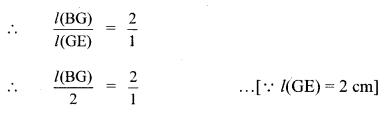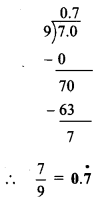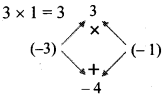Balbharti Maharashtra State Board Class 12 Political Science Important Questions Chapter 3 Key Concepts and Issues Since 1991: Humanitarian Issues Important Questions and Answers.

Maharashtra State Board 12th Political Science Important Questions Chapter 3 Key Concepts and Issues Since 1991: Humanitarian Issues

Complete the following statements by selecting the appropriate option.

Question 1.
The Rio de Janeiro Earth Summit (1992) focused on
(a) Environment and development
(b) Nuclear non-proliferation
(c) International trade
(d) Gender issues
Answer:
(a) Environment and development

Question 2.
The 2002 Earth Summit recognised as the most important goal at all level.
(a) poverty
(b) socio-economic develop
(c) sustainable development
(d) gender issues
Answer:
(c) sustainable development

Question 3.
The 2030 Agenda for sustainable Development was adopted in the year
(a) 2015
(b) 2002
(c) 1992
(d) 2019
Answer:
(a) 2015

Question 4.
The Second UN Decade for poverty eradication was in
(a) 1997-2006
(b) 1971-1980
(c) 2008-2017
(d) 1992-2003
Answer:
(c) 2008-2017

Question 5.
The Revolution aimed to make India self-sufficient in food grains.
(a) Import substitution
(b) Green
(c) White
(d) Infrastructural
Answer:
(b) Green

Question 6.
The is a scheme introduced in 1978-79 to create opportunities for self-employment in
the rural sector.
(a) MGNREGA
(b) JRY
(c) IRDP
(d) KVY
Answer:
(c) IRDP

Complete the following sentences by selecting the appropriate reason.

Question 1.
Green Revolution was introduced in India in the 1960’s to ………………
(a) make India self sufficient in food grains.
(b) generate employment and tackle poverty.
(c) to combine economic growth with social justice.
Answer:
(a) make India self sufficient in food grain

Question 2.
The Department of Women and Child Development was set up as a separate Ministry in 2006 to …………..
(a) facilitate health and education programmes for women.
(b) provided political representation to women
(c) empower women to live with dignity and contribute as equal partners in development.
Answer:
(c) make India self sufficient in food grains.

State the appropriate concept for the given statements.

Question 1.
Introduction of high yielding variety of seeds and irrigation methods.
Answer:
Green Revolution

Question 2.
Think tank of the Government of India, providing both directional and policy inputs.
Answer:
NITI Aayog

Question 3.
The responsible interaction with the environment to avoid depletion or degradation of natural resources.
Answer:
Sustainable development

Question 4.
Deprivation of common necessities that determine the quality of life.
Answer:
Poverty

Question 5.
A view that free market economy promotes development.
Answer:
Capitalism

Question 6.
Blueprint for prosperity for people and planet adopted by the UN in 2015.
Answer:
2030 Agenda for Sustainable Development

Question 7.
Agency set up in 1950 to formulate a plan for effective and balanced utilisation of India’s resources.
Answer:
Planning Commission

Question 8.
India’s policy towards poverty and development.
Answer:
Growth with Social Justice and Equity

Question 9.
The process by which oppressed persons gain control over their own lives.
Answer:
Empowerment

Question 10.
Socially constructed characteristics of women and men such as behaviour, norms, roles and relationships.
Answer:
Gender

Find the odd word.

Question 2.
Pollution, Deforestation, Poverty, Water Scarcity.
Answer:
Poverty (not a direct environment concern)

Question 2.
Brundtland Commission, Rio+20 Summit, Johannesburg Earth Summit, United Nations Development Programme (UNDP).
Answer:
UNDP (not a commission/ summit associated with sustainable development)

Expand the following abbreviations.

(1) UNCED
(2) ECOSOC
(3) UNDP
(4) IRDP
(5) JGSY
(6) MPI
Answer:
(1) UNCED – United Nations Conference on Environment and Development
(2) ECOSOC – Economic and Social Council of the UN.
(3) UNDP – United Nations Development Programme
(4) IRDP – Integrated Rural Development Programme
(5) JGSY – Jawahar Gram Samridhi Yojana
(6) MPI – Multidimensional Poverty Index

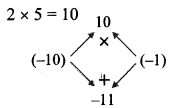
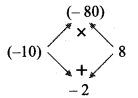
Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

State whether the following statements are true or false with reason.

Question 1.
Rio Earth Summit (1992) was a landmark in environment issues.
Answer:
This statement is True.

1. Rio de Janeiro Earth Summit (1992) sought to raise public awareness on the need to integrate environment and development.
2. It’s objective was to create a partnership between developing and more industrialized nations to ensure a healthy future for the planet.

Question 2.
The perception of poverty has undergone a change in recent times.
Answer:
This statement is True.

1. The traditional perception of poverty focused on the deprivation of the basic necessities of life such as food, shelter, etc.
2. The new perception of poverty as expressed by the ECOSOC, considers poverty as lack of basic capacity to participate effectively in society.
3. It is perceived as a denial of choices, opportunities and human dignity.

Question 3.
The 2030 Agenda for Sustainable Development (2015) is a significant document.
Answer:
This statement is True.

1. The 2030 Agenda for Sustainable Development (2015) adopted by the UN, provides a blueprint for prosperity of the people and planet for now and in the future
2. It mentions seventeen Sustainable Development Goals for action by all countries in a global partnership for e.g., No Poverty, Climate action, Gender equality, etc.

Question 4.
The economic reforms initiated in India after 1991 had far-reaching implications.
Answer:
This statement is True.

1. After 1991, India introduced the policies of economic liberalisation and privatisation of the public sector and brought an increase in economic and industrial growth rate.
2. These reforms changed the role of the State to focus more on social development such as in heath care, sanitation, education, etc.

Explain the correlation between the following.

Question 1.
Department of Women and Child Development – Women’s empowerment.
Answer:
The Department of Women and Child Development, Government of India came into existence as separate ministry in 2006. Before this, it was a department under HRD ministry: The Department of Women and Child Development was constituted with the intention of addressing gaps in State action for women and children and to create gender equitable and child-centered legislations, policies and programmes.

It aims to achieve the empowerment of women i.e., to live in dignity and to contribute as equal partners in development in an environment free from discrimination, injustice and violence. The Ministry has prepared the National Policy for the Empowerment of Women (2001). The Draft of the National Policy for women (2016) aims at women’s empowerment by following a socially inclusive rights-based approach.

Express your opinion of the following.

Question 1.
There is a need to protect the environment.
Answer:
I agree with this statement.
The environment refers to all living and non-living things that make up our surroundings. Many environmental problems result due to unplanned management, human activities and technological development that interfere with the environment. Protection of environment refers to conservation and preservation of environment by reducing pollution, soil erosion, global warming, deforestation etc.

Main environmental concerns hence are climate change, water scarcity, pollution, loss of biodiversity, etc. Environmental degradation and depletion of resources will result in spread of pests and vector diseases, extinction of species, natural disasters like floods; acid rain, melting of glaciers, etc. Life on this earth cannot exist unless we restore environmental balance.

Question 2.
Poor political representation of women is a major concern.
Answer:
I agree with this statement.
Poor political representation of women is a significant gender concern in India. The first Lok Sabha had only 24 women of total 489 members i.e., 5%, and the 17th Lok Sabha (2019) has 78 women (14%). This is the highest representation of women in Lok Sabha till date. The Women’s Reservation Bill which proposes to reserve 33% of all seats in Lok Sabha and in State Assemblies for women is pending in the Lok Sabha. This bill was first introduced in Parliament in 1996, by the United Front government of Prime Minister H.D. Deve Gowda.

As per the bill, seats will be reserved for women on a rotational basis. The UPA-I government (2004-2009) again introduced the bill in May 2008 and it was passed in May 2010 by the Rajya Sabha. Currently, the bill is still pending in Lok Sabha. However, there exists 33% reservation for women in rural and urban local bodies (as per 73rd and 74th Amendment Acts).

Answer the following question in 80 to 100 words.

Question 1.
What is the Green Revolution?
Answer:
Green Revolution refers to a large increase in crop production that is achieved by the use of high yielding crop varieties, pesticides, artificial fertilizers, machines and better management of agricultural resources. Norman Borlaug, an agricultural scientist of USA is considered as ‘Father of the Green Revolution’ for which he was awarded the Nobel Peace Prize (1970). In India, M.S. Swaminathan is credited with introducing the Green Revolution in 1965 especially in Punjab, Haryana and Uttar Pradesh.

This was necessitated due to famine and acute food shortages due to low productivity in food production. Green Revolution was mainly in wheat, maize and gram production. During it’s early years, the Green Revolution yielded great economic prosperity leading to significant increases in agricultural output and farmers incomes. However, this did not benefit marginal farmers who could not afford expensive inputs.

Question 2.
What is empowerment? Suggest measures for empowerment of women.
Answer:
Empowerment refers to the process by which oppressed or marginalized sections of the population become stronger, especially in controlling their own life and claiming their own rights. This may happen socially, economically, politically or nationally. The approach to women’s issues has progressed from ‘welfare’ to ‘development’ to ‘empowerment’.

Some of the measures for empowerment of women include-

1. Political empowerment – giving women better representation in legislative bodies and in the decision making process.
2. Economic empowerment – such as strengthening women’s access to property inheritance and land rights, skill training, work opportunities, micro-credit, increased right to economic resources and power.
3. Social empowerment – through literacy/education, training and raising awareness, freedom from domestic violence, access to information, health services and sanitation.

In India, schemes to empower women include Beti Bachao Beti Padhao Yojana (2015), Support to Training and Employment Programme for Women (STEP), Mahila Shakti Kendras (2017) etc.

Question 3.
Describe international efforts to deal with environmental concerns.
Answer:
There have been many international efforts to deal with environmental concerns as well as about the relationship between economic development and environmental degradation.
1. UN Conference on Human Environment (Stockholm, 1972) The purpose was to encourage and provide guidelines for protection of the environment.

2. World Commission on Environment and Development (1983) also called Brundtland commission put forward the concept of sustainable growth.

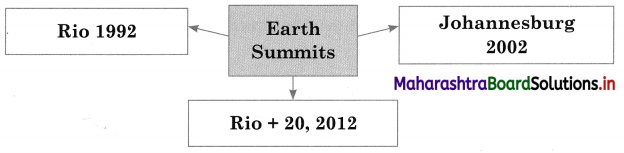
3. Rio de Janeiro Earth Summit (1992) sought to raise public awareness on the need to integrate environment and development and to create a partnership between developing and more industrialized nations to ensure a healthy future for the planet.

4. Earth Summit at Johannesburg (2002) recognized sustainable development as the most important goal for institutions at the national, regional and international levels

5. UN Conference on sustainable development (Rio-2012) is also called Rio Earth Summit or Rio+20. Environmental sustainability is defined as responsible interaction with the environment to avoid depletion or degradation of natural resources and allow for long¬term environmental quality. It’s goal is to conserve natural resources, to reduce pollution, to develop alternate sources of power, etc.

Question 4.
Elaborate on the aspects of development in India.
Answer:
The purpose of development is to ensure welfare of the people and is associated with economic growth. The traditional approaches to development focus on the predominant role of the State in promoting economic growth (Socialist) or role of free market economy (Capitalist). Since the 1990s, the alternative view of development that focuses on both material and non-material aspects has become acceptable. The focus today is development based on equity, participation, empowerment and sustainability.

1. Modernisation of the economy – During the Nehruvian period, the focus was on land reforms, irrigation and large-scale industrialisation to provide employment and increase productivity.
2. Self – reliance – This included ‘import substitution’ strategy to develop indigenous industry.
3. Socialist pattern of society – It was based on promotion of the Welfare State, employment generation and importance ,to the public sector. The Planning Commission (March 1950 to 31st December 2014) was created to chalk out Five Year Plans for development.

“Growth with Social Justice and Equity’ has been India’s policy towards poverty and development. Its development strategy has evolved over the years. In the early stages, government played a dominant role through the public sector.

Question 5.
Describe the 2030 Agenda for Sustainable Development adopted in 2015 by the UN.
Answer:
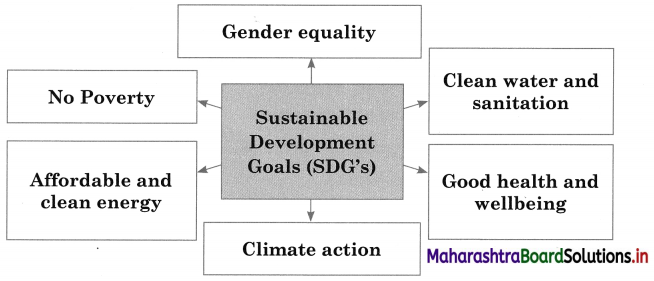
In 2015, the United Nations adopted the ‘2030 Agenda for Sustainable Development. It provides a blueprint for peace and prosperity for people and the planet for now and into the future. The Agenda mentions 17 Sustainable Development Goals (SDGs) for action by all developed and developing countries in a global partnership.

The Sustainable Development Goals are:

1. No Poverty
2. Zero hunger
3. Good health and well being
4. Quality
5. Gender equality
6. Clean water and sanitation
7. Affordable and clean energy
8. Decent work and economic growth
9. Industry, innovation and infrastructure
10. Reduced inequalities
11. Sustainable cities and communities
12. Responsible consumption and production
13. Climate action
14. Life below water
15. Life on land
16. Peace, justice and strong institutions
17. Partnership goals

Answer the following question with reference to the given points.

Question 1.
Explain condition of women in India.
(a) Economic inequality
(b) Trafficking and exploitation
(c) Literacy rate
(d) Political representation
Answer:
All over the world, women have to face serious problems such as discrimination and violence, under representation in economic and political decision-making, inequalities in education, health care, landholdings and workplaces and even in human rights.

Some of the important gender issues:
(a) Economic inequality – Participation of women in the labour market is about 28% only. There is also income inequality due to wide gender wage gaps as well as inequality of opportunities to women e.g., unequal access to education and finance. In many countries, women are either not encouraged to work or employed in the informal sector. Women continue to be underrepresented in high-level, highly paid positions and experience gender discrimination and sexual harassment in the workplace. Women experience high levels of poverty, unemployment and other economic hardships.

(b) Trafficking and exploitation – Women are often exploited and denied basic rights. They are trafficked for purpose of sexual and economic exploitation particularly prostitution, ‘sold’ as brides, subjected to sexual crimes, forced labour, street begging, etc. Trafficking in women means that they are deceived or forced/sold, physically confined, abused with no access to protection or health care.

(c) Literacy rate – low literacy among women is acute in India. As per 2011 census report, female literacy rate is only 65.46% while for males it is 82.14%. The reasons for the low female literacy are-

1. traditional patriarchal notions that do not consider female education as economically advantageous
2. Schools in rural areas are not easily accessible and travel may not safe or easy.
3. Benefits of schemes like R.T.E have not reached many rural females.
4. Social evils like child marriage, female foeticide, dowry, etc.

(d) Political Representation – Poor political representation of women is a significant gender concern in India. The First Lok Sabha had only 24 women of total 489 members i.e., 5% and the 17th Lok Sabha (2019) has 78 women (14%). This is the highest representation of women in Lok Sabha till date. The Women’s Reservation Bill which proposes to reserve 33% of all seats in Lok Sabha and in State Assemblies for women is pending in the Lok Sabha. However, there exists 33% reservation for women in rural and urban local bodies.

Question 2.
Describe the following poverty alleviation programmes in India.
(a) Integrated Rural Development Programme (IRDP)
(b) Jawahar Gram Samridhi Yojana (JGSY)
(c) Pradhan Mantri Gramin Awaas Yojana (PMGAY)
(d) Mahatma Gandhi National Rural Employment Guarantee Act. (MGNREGA)
(e) Saansad Adarsh Gram Yojana.
Answer:
The poverty alleviation programmes in India have been designed for both rural areas and urban areas. Most of the programmes are designed to target the rural poverty as prevalence of poverty is high in rural areas.
(a) Integrated Rural Development Programme (IRDP) – It was first introduced in 1978¬79. The main objective of IRDP is to create sustainable opportunities for self-employment in the rural sector.

(b) Jawahar Gram Samridhi Yojana (JGSY) – It is the revised version of the Jawahar Rozgar Yojana (JRY). It was started in 1999. The main aim of this programme was development infrastructure like roads to connect the villages to different areas and other social, education (schools) and infrastructure like hospitals in the rural areas.

(c) Pradhan Mantri Gramin Awaas Yojana – It was started in 1985. This scheme aimed at creating housing for everyone.

(d) Mahatma Gandhi National Rural Employment Guarantee Act. (MGNREGA) – It was launched in 2005. It provides 100 days assured employment every year to every rural household.

(e) Saansad Adarsh Gram Yojana – It was started in 2014. According to this yojana, each Member of Parliament will take the responsibility of developing three villages by 2019. The idea is to make India’s villages to be fully developed with physical and institutional infrastructure.

Question 3.
Discuss the following humanitarian issues.
(a) Environmental degradation
(b) Poverty
(c) Gender issues
Answer:
Humanitarian issues refer to concerns about issues affecting human welfare with the aim of alleviation of sufferings. Examples of humanitarian issues include natural disasters, famine, epidemics, armed conflicts, poverty, inequalities and injustice, environmental problems, etc.

(a) Environmental degradation – Indiscriminate exploitation of natural resources had resulted in environmental depletion and degradation. This results in significant environmental concerns such as deforestation, soil erosion,loss of biodiversity, climate change, endangerment of species, water scarcity, acid rain, pollution, spread of diseases etc. The relationship between economic development and environmental degradation has been considered at various international conferences like Rio Earth Summit, etc.

Environmental degradation has serious consequences for humans, animals, plants as well as the ecological balance. The causes of degradation include resource depletion due to overuse, landfills and illegal dumping, waste production, overpopulation and consumption behaviour, etc.

(b) Poverty – The traditional perception of poverty is where people are unable to provide for their basic necessities of life. It is the deprivation of common necessities that determine the quality of life including food, clothing, shelter and safe drinking water. The alternative view of poverty focuses on both material and non-material aspects i.e., focus on community ties, values and availability of common resources, participatory decision making and political and economic decentralisation.

The purpose of development is to ensure welfare of the people and is associated with economic growth. The traditional approaches to development focus on the predominant role of the State in promoting economic growth (socialist) or role of free market economy (capitalist). Since the 1990s, the alternate view of development that focuses on both material and non material aspects has become acceptable. The focus today is development based on equity, participation, empowerment and sustainability.

(c) Gender issues – There is a distinct link between poverty and unsatisfactory conditions of women. In most parts of the world women are poor due to cultural norms, unequal power equations between men and women. In the 1970s, women empowerment came to be accepted as an important philosophy to bring about gender justice. The UN ‘Decade for Women’ began in 1976 to-

1. link women’s issues with developmental issues
2. promote equal rights and opportunities for women across the globe.

Question 4.
Discuss the vision of the development process in India.
(a) Modernisation of the economy
(b) Self-reliance
(c) Socialist pattern of society
Answer:
The purpose of development is to ensure welfare of the people and is associated with economic growth. The traditional approaches to development focus on the predominant role of the State in promoting economic growth (Socialist) or role of free market economy (Capitalist). Since the 1990s, the alternative view of development that focuses on both material and non material aspects has become acceptable. The focus today is development based on equity, participation, empowerment and sustainability. India’s vision of development had three aspects:

(a) Modernisation of the economy – This implied industrialization to provide employment to a growing labour force and to increase productivity During the Nehruvian period, the focus was on large scale industrialization and factory production. Land reforms and irrigation were looked at as the means to achieve agricultural growth and productivity.

(b) Self-reliance – This included ‘import substitution’ strategy to develop indigenous industry. Aid taken from Soviet Union, France, etc. was utilised mainly in the public sector and for infrastructure.

(c) Socialist pattern of society – The approach of planning for development was based on promotion of the welfare State, employment generation and importance to the public sector. The Planning Commission (March 1950 31st December 2014) was created to chalk out Five Year Plans for development.

“Growth with Social Justice and Equity” has been India’s policy towards poverty and development. Its development strategy has evolved over the years. In the early stages, government played a dominant role through the public sector.

Balbharti Maharashtra State Board Class 12 Psychology Important Questions Chapter 5 Emotions Important Questions and Answers.

Maharashtra State Board 12th Psychology Important Questions Chapter 5 Emotions

Choose the correct option and complete the following statements.

Question 1.
According to the theory, we experience physiological arousal and feelings simultaneously and independently.
(a) James-Lange
(b) Cannon-Bard
(c) Schachter-Singer
Answer:
(b) Cannon-Bard

Question 2.
According to Ekman, there are basic emotions.
(a) 2
(b) 5
(c) 6
Answer:
(c) 6

Question 3.
is an emotion that is in response to some threat.
(a) Sadness
(b) Fear
(c) Disgust
Answer:
(b) Fear

Question 4.
Plutchik’s model explains that there are primary emotions.
(a) 8
(b) 6
(c) 12
Answer:
(b) 6

Question 5.
is not a primary/ basic emotion according to Plutchik.
(a) Trust
(b) Anticipation
(c) Jealousy
Answer:
(c) Jealousy

Question 6.
Emotions are controlled by the ……………….. in the brain.
(a) cerebral cortex
(b) limbic system
(c) RAS
Answer:
(b) limbic system

Question 7.
Aniket shows creativity and has meaningful relationships. He has …………. emotional well-being.
(a) high
(b) low
(c) moderate
Answer:
(a) high

State whether the following statements are true or false.

Question 1.
“I feel sad because I cry”, This is the premise of the Schachter – Singer theory.
Answer:
False

Question 2.
Pride and guilt are considered as higher cognitive emotions.
Answer:
True

Question 3.
The fight or flight reaction is a reaction to sadness.
Answer:
False

Question 4.
Low serotonin levels are associated with clinical depression.
Answer:
True

Answer the following in one sentence each.

Question 1.
What is the premise of the facial feedback hypothesis?
Answer:
According to the facial feedback hypothesis, our facial expressions provide feedback to our brain about our emotions.

Question 2.
What are complex emotions?
Answer:
Complex emotions are emotions which result form the combination of basic emotions for e.g., surprise and sadness lead to disappointment.

Question 3.
According to Ekman, which are the basic emotions?
Answer:
According to Ekman, there are six basic (universal) types of emotions, i.e., happiness, sadness, anger, fear, surprise, disgust.

Question 4.
When does a person experience disgust?
Answer:
A person usually experiences disgust as a response to some unwanted stimulus.

Question 5.
According to Plutchik, how do emotions result?
Answer:
According to Plutchik, emotions result due to evolving over a period of time for increasing our chances of survival.

Question 6.
Why is Plutchik’s model important?
Answer:
Plutchik’s model is important from the perspective of emotional literacy, i.e., understanding emotional levels, complexity and change as well as appropriate emotional labelling.

Question 7.
What does emotional well-being mean?
Answer:
Emotional well-being means managing both positive and negative emotions, so that we can lead a healthy and productive life.

Question 8.
What does anger management mean?
Answer:
Anger management is an intervention programme to prevent anger from turning into a habit or obstacle by creating awareness of and responsibility for our emotions.

Explain the concepts in 25 – 30 words each.

Question 1.
Emotions
Answer:
The word emotion is derived from the latin word ‘emovere’, which means to stir up or to move. An emotion refers to an involuntary, aroused state of an organism involving physical, cognitive and behavioural components. It is described as a combination of bodily arousal, e.g., increased heartrate, thoughts and feelings, i.e. emotional tone and expressive behaviour i.e. facial expression.

Question 2.
Emotional well-being.
Answer:
Emotional well-being means managing our emotions, both positive and negative ones, so that we can lead a healthy and productive life. Persons who have high emotional well-being experience benefits such as-

1. better able to deal with stress
2. better self-regulation
3. increased productivity in tasks undertaken
4. increased creativity and openness to new experiences
5. life satisfaction due to meaningful activities and relationship.

Question 3.
Emotional Abuse.
Answer:
Emotional abuse is any kind of abuse that is emotional rather than physical in nature. It occurs when one person subjects or exposes another person to intentionally harmful behaviour that may result in anxiety, depression and psychological trauma in the victim.
The types of emotional abuse may be-

1. verbal abuse such as blaming, insulting, labeling, threatening, swearing, etc.
2. nonverbal abuse such as ignoring, rejection, bullying, spying, etc.

Question 4.
Anger Management.
Answer:
Anger management is an intervention programme to prevent anger from turning into a habit or obstacle. It enables the person to create awareness of and responsibility for his/her emotions. Anger management involves two aspects (i) managing one’s own anger (ii) learning to respond effectively to anger in others. The three R’s in anger management are Relax, Reassess and Respond.

Answer the following questions in 35 – 40 words each.

Question 1.
What are the techniques to deal with emotional abuse?
Answer:
Emotional abuse is any kind of abuse that is emotional rather than physical in nature. It occurs when one person subjects or exposes another person to intentionally harmful behaviour that may result in anxiety, depression and psychological trauma for the victim.
The techniques to deal with emotional abuse-

1. Accept that emotional abuse is not because of you, i.e., don’t justify the actions of the abuser.
2. Respond assertively to the abuser but seek distance from him/her.
3. Give yourself time to heal.
4. Prioritize your self-care, eating right, exercise, etc.
5. Mobilise support from family and friends. If needed, seek professional help.

Question 2.
What are the benefits of emotional well-being?
Answer:
Emotional well-being means managing our emotions, both positive and negative ones, so that we can lead a healthy and productive life. Persons who have high emotional well-being experience benefits such as-

1. better able to deal with stress
2. better self-regulation
3. increased productivity in tasks undertaken
4. increased creativity and openness to new experiences
5. life satisfaction due to meaningful activities and relationship.

Write short notes on the following in 50 – 60 words each.

Question 1
Characteristics of emotions
Answer:
The word emotion is derived from the latin word ‘emovere’, which means to stir up or to move. An emotion refers to an involuntary, aroused state of an organism involving physical, cognitive and behavioural components. It is described as a combination of bodily arousal, e.g., increased heartrate, thoughts and feelings, i.e. emotional tone and expressive behaviour i.e. facial expression.
Some characteristics of emotions are-

1. Emotions may be positive, e.g., joy or negative, e.g., anger.
2. Emotions may occur for a brief period or may be long lasting.
3. Emotions may be important for our survival, e.g., fear or for our psychological well-being, e.g., love.
4. Emotions differ in intensity in expression for e.g., annoyance-anger-rage.
5. Complex emotions (higher cognitive level emotions) result from the combination of basic emotions, for e.g., surprise and sadness lead to disappointment.
6. According to Ekman, there are six basic (universal) types of emotions, i.e., happiness, sadness, anger, fear, surprise, disgust.

Question 2.
Physiological changes during emotions.
Answer:
Physiological changes refer to automatic reactions that take place in our body in response to some stimulus, for e.g., if you saw a snake, the brain at the cognitive level perceived the stimulus as dangerous. This leads to physiological arousal such as dilated pupils, increased heart rate, increased pulse rate, sweating. At the emotional level you experience fear. The Autonomic Nervous System and Glandular system signal the pituitary gland which activates the adrenal glands to secrete the cortisol hormone. This triggers “the fight or flight” response. At the behavioural level there is an action plan such as running away or calling for help, etc.

Answer the following questions 80 – 100 words each.

Question 1.
Theories of emotions.
Points:
(i) James-Lange theory
(ii) Cannon-Bard theory
(iii) Schachter-Singer theory
Answer:
The word emotion is derived from the latin word ‘emovere’, which means to stir up or to move. An emotion refers to an involuntary, aroused state of an organism involving physical, cognitive and behavioural components. It is described as a combination of bodily arousal, e.g., increased heartrate, thoughts and feelings, i.e. emotional tone and expressive behaviour, i.e., facial expression.
The main theories of emotions are-
(i) James-Lange theory – It was one of the earliest theories to explain emotion. According to William James and Carl Lange, physiological arousal instigates the experience of emotion. It proposes that each specific emotion is attached to a different pattern of physiological arousal. For e.g., we feel sad because we cry. The sequence of events in emotional experience is Emotion Stimulus – Physiological Response Pattern → Affective Experience.

(ii) Cannon-Bard theory – According to Walter Cannon and Philip Bard, we may experience the same physiological arousal but emotions can be different, for e.g., we don’t cry only when we are sad but we also cry when we are angry or extremely happy. We experience physiological arousal and feelings at the same time and independently. For e.g., seeing a man with a gun prompts the feeling of fear as well as a racing heartbeat.

(iii) Schachter and Singer’s Two Factor theory – According to Stanley Schachter and Jerome Singer, emotion is based on two factors, i.e., physiological arousal and cognitive label, for e.g., an environmental stimuli (growling dog) elicits a physiological response (increased heart rate). We cognitively label this response (fear).

Question 2.
Emotional well-being.
Points:
(i) Meaning
(ii) Aspects
(iii) Benefits
Answer:
The word emotion is derived from the latin word ‘emovere’, which means to stir up or to move. An emotion refers to an involuntary, aroused state of an organism involving physical, cognitive and behavioural components. It is described as a combination of bodily arousal, e.g., increased heart rate, thoughts and feelings, i.e. emotional tone and expressive behaviour i.e. facial expression.

(i) Meaning – Emotional well-being means managing our emotions, both positive and negative ones, so that we can lead a healthy and productive life. Emotional well-being is not easily observable. It can be guaged on the basis of how a person rationally handles a situation involving some stressors or leading to negative emotions. Emotional well-being refers to understanding and managing one’s emotions without getting overwhelmed by negative emotions but instead encouraging positive emotions.

(ii) Aspects – The aspects of emotional well-being are at three levels viz. physical, emotional and social.

1. Physical level, i.e., well balanced diet, exercise.
2. Emotional level, i.e., practise mindfulness, raising levels of motivation and optimism.
3. Social level, i.e., engaging in prosocial behaviour, meaningful relationships.

(iii) Benefits – Persons who have high emotional well-being experience benefits such as-

1. Coping with stress – It helps to deal with stress using healthy methods such as exercise, social support, etc.
2. Better self-regulation – It enables the person to label how they feel and accept negative emotions life fear, anger, etc.
3. Increases productivity in tasks undertaken – The ability to focus is enhanced, the person feels positive and energized.
4. Increases creativity – The person indulges in divergent thinking, shows curiosity is open to new experiences.
5. Life satisfaction – The individual is able to have meaningful interactions and relationships, show empathy, altruism and engage in activities like volunteer work.