Class 9 English Chapter 1.5 Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 9 English Solutions My English Coursebook Chapter 1.5 The Necklace Notes, Textbook Exercise Important Questions and Answers.
The Necklace Poem 9th Std Question Answer
My English Coursebook Std 9 Digest Chapter 1.5 The Necklace Textbook Questions and Answers
Warming up!
Chit-chat:
- Do you like jewellery and ornaments?
- Do you like to dress up for special occasions?
- How do you do that?
- What makes a person happy and confident’?
- during special functions and parties?

Talking about Myself:
Write a few lines about yourself – your name, appearance. family, the place where you live, your school, your friends. neighbours. relatives, your likes, dislikes, hobbies, what you are good at, etc.
Now create an imaginary ‘persona’ for yourself. It should be quite different from your real self. Or, you may choose a fictional character – a character from a novel, story, etc. Write a few lines about this imaginary persona and introduce yourself in that role.
Imaginary Persona
- Hi, I am Vishalbahu.
- I like to obstruct and punish criminals.
- I simply love stunts and fights.
- I enjoy flying secretly all over the world.
- I don’t like people who trouble common people.
- I hate crimes and injustice caused to innocent people.
- I find exercises, combats very interesting.
- I can do any impossible things in the world.
- I am good at every difficult or hard work.
- I am not so good at office work and housework.

A Turn by Turn Story:
Form groups of 6-8. One person chooses any familiar object and announces its name in the group. All the others talk about it one by one, adding one (new) complete sentence at a time. The person who has chosen the object takes down all the sentences. After 2-3 rounds, read the sentences together and try to build a story around them.
Part I
English Workshop:
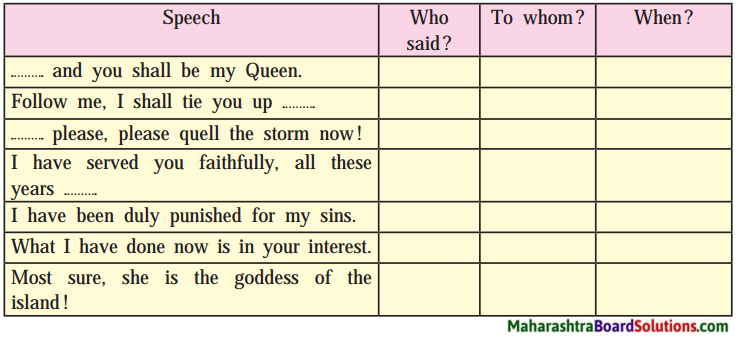
1. Read each of the following sentences aloud. Write who said it and to whom.
Question 1.
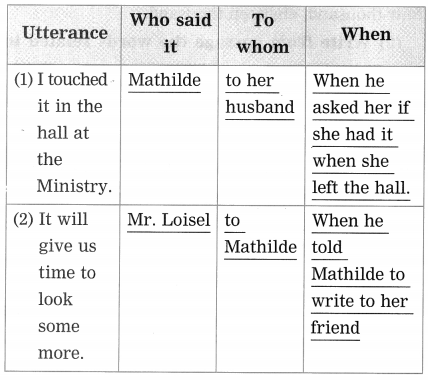
(a) Look. here’s something for you.”
(b) “Why. the dress you go to the theater in!”
(c) ‘I would rather not go to the party.”
(d) ‘Choose, my dear.”
(e) You have nothing else?”
(f) “Would you lend me this, just this?”
(g) “What ! … How ! … That’s impossible!
Answer:
(b) Mathilde’s husband said to Mathilde.
(c) Mathilde said to her husband.
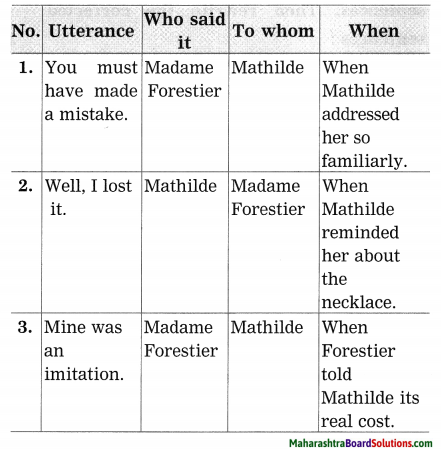
(d) Madame Forestier said this to Mathilde.
(e) Mathilde said this to Madame Forestier.
(f) Mathilde said this to Madame Forestier.
(g) Mathilde’s husband said this to Mathilde.

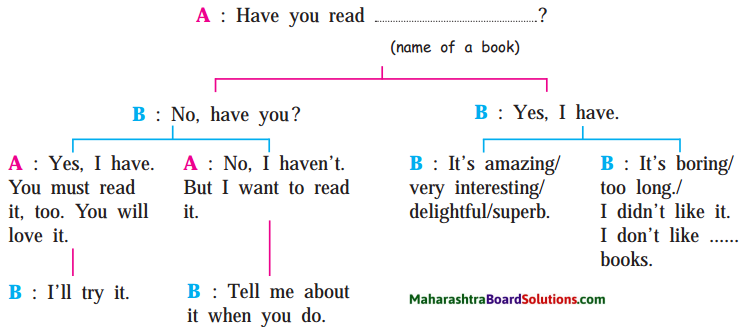
2. Read the conversations in the story aloud using proper intonation.
Question 1.
Read the conversations in the story aloud using proper intonation.
3. Write a few lines about what Mathilde had and what she dreamt about.
Question 1.
Write a few lines about what Mathilde had and what she dreamt about.
4. Write what you think about the following thoughts and actions of Mathilde.
Question a.
Mathilde was beautiful, and so she wanted to marry an aristocrat.
Answer:
She was not wrong to think so, because I think every woman, beautiful or not, wants to marry a person, who has a good position and wealth.
Question b.
Mathilde was sad because she did not get any luxuries.
Answer:
Her thinking was not correct. Not every one gets a luxurious life. She should have managed in whatever they were earning and lived a simple but happy life.

Question c.
Mathilde felt that her house was shabby and poorly furnished.
Answer:
Her feelings are wrong because it depends on the people who live in the house to keep the house clean, tidy and beautiful with whatever furniture, things they have got.
Question d.
Mathilde wanted other people to envy her.
Answer:
Mathilde’s thought was wrong because happiness does not depend on making the people envy you. She wished that people would have admired her if she had rich dresses and jewels.
Question e.
Mathilde was not happy to see the invitation.
Answer:
Mathilde did not care about the importance of the invitation, her husband had received. She was thinking only about the dress she would wear there.
Question f.
Mathilde wanted a new dress for herself.
Answer:
Mathilde wanted a new dress for herself only to selfishly corner her husband for extorting money from him to buy a new dress. Her thought was silly and unreasonable.

Question g.
Mathilde borrowed a diamond necklace from her friend and wore it to the party.
Answer:
Borrowing a diamond necklace was not a dire need of Mathilde. She could have used flowers instead; but she wanted another woman’s necklace to make a show of her beauty. She did not understand that borrowing is begging.
Question h.
Mathilde lost her necklace.
Answer:
Mathilde was so overwhelmed and captivated by her success that she was not aware of her responsibility of safe-keeping the borrowed necklace carefully. She lost it only because of her carelessness.

5. Prepare a formal invitation using the following format:

Language Study:
6. Read the phrases: The necklace, an error, all these things, another woman, one evening, her husband. In all these phrases we see some words used before the nouns. They specify or make it clear what noun we are talking about. These words that are used at the beginning of a noun phrase are known as determiners.
Determiners include articles (a, an, the), possessive pronouns (my, our, your, her, etc.), words like this, that, much, many, all, and numbers.
Part II
Chit-chat:
- Have you ever lost anything valuable?
- Name a book/movie that made you think.
- What was it about?
- What was the best part about the book/movie?

English Workshop:
1. Spot and circle the error m the following sentences. Then rewrite the sentences after correcting them.
Question 1.
Spot and circle the error m the following sentences. Then rewrite the sentences after correcting them.
(a) But they could not found it.
(b) You must right to your friend.
(c) At the end of one week, they have lose all hope.
(d) He would borrowed the rest.
(e) You should have return it sooner.
(f) And this life lasted for ten year.
(g) “No, I am Mathilde bisel.”
(h) Madame Forestier were stunned.
Answer:
(a) But they could not find it.
(b) You must write to your friend.
(c) At the end of one week, they have lost all hope.
(d) They stared at each other
(e) He would borrow the rest.
(f) You should have returned it sooner.
(g) And this life lasted ten years.
(h) “No, I am Mathilde Loisel.”
(i) Madame Forestier was stunned.

2. Complete the following table.
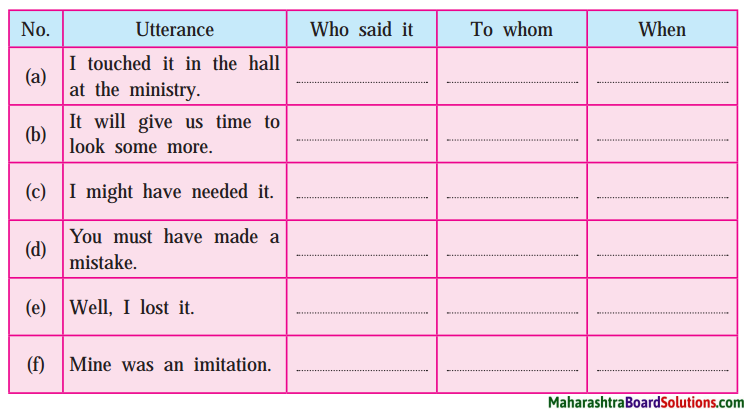
Question 1.
Complete the following table.
3. Write what you think about the following thoughts and actions of Mathilde
Question a.
Mathilde was shocked despaired over the loss of her necklace
Answer:
I think her reaction to the loss of her necklace was natural. But she herself was responsible for the tragedy. Her stubborn behaviour is to be blamed for the loss.
Question b.
Mathilde wrote a note to her friend as dictated by her husband.
Answer:
The couple couldn’t find the lost necklace even after a long search. They expected to find it some day. For that they needed some more time and Mathilde was compelled to write the false letter to I her friend. Her action of telling lies and betraying her friend was immoral and ridiculous.
Question c.
Mathilde and her husband decided to replace the necklace.
Answer:
I think that their decision of replacing the necklace was immature and insincere. Instead, they should have clearly and openly told Madame Forestier about the incident. It could have saved them from the horrible life they had to face and the dreadful debt they had to pay.

Question d.
Mathilde returned the diamond necklace to her friend
Answer:
I think, it was her moral responsibility to return the borrowed diamond necklace immediately after the party day but she delayed. She did so to hide the fact that she had lost the diamond necklace. Her negligence made her to make one more wrong.
Question e.
Mathilde did not tell her friend about the loss and replacement.
Answer:
It was another big mistake she committed. It was her thoughtless action. Had she told her friend about the loss of the necklace, further ruinous incidents wouldn’t have occurred and the remedy for the problem would have been very simple and easy.
Question f.
Mathilde worked very very hard to pay the debt.
Answer:
Mathilde’s action shows that she was a completely transformed woman. She had changed her attitude towards her lifestyle. She forgot her dreams of living a luxurious life. She worked hard and saved money for repaying the debt. She felt duty-bound for coming out of the devastating situation, she was responsible for.

Question g.
Mathilde and her husband paid off the debt in ten years.
Answer:
The income of Mathilde’s husband was meagre. So both of them worked very hard for ten long years to save money for repaying the debt. They curtailed their needs severely, her husband worked extra to ease the burden of debt. Somehow they faced the woes together bravely and sincerely.
4. Form pairs. Discuss how ‘Part II’ of the story could have been different. Write your storyline in the form of bullets showing the main events.
Question 1.
Form pairs. Discuss how ‘Part II’ of the story could have been different. Write your storyline in the form of bullets showing the main events.
Answer:
The cabman, who dropped them at their door found the necklace after two days while cleaning his cab → behind the space of the seats → fallen from the gaps of the seats → remembered the lady wearing the necklace → was an honest and God-fearing man → went to their house →handed over the necklace to them → it could have changed the whole story.

5. Imagine what must have happened after Mathilde’s friend discovered that the diamonds were real. Do you think she would return it to Mathilde? Would that make Mathilde happy?
Question 1.
Imagine what must have happened after Mathilde’s friend discovered that the diamonds were real. Do you think she would return it to Mathilde? Would that make Mathilde happy?
Answer:
Mathilde’s friend was rich but a kind-hearted and generous woman. She knew that Mathilde had to face many miseries for ten years. I think she would return the necklace to Mathilde. Mathilde would be happy to find some relief after ruinous sufferings.
6. Discuss the following and write about it in your own words in 5-6 lines.
Question 1.
Discuss the following and write about it in your own words in 5-6 lines.
(a) What would you do, if something like this happens to you?
(b) What opinion do you form about Mathilde’s husband from lier story?
(c) Which events in the story (Part I and Part II) changed Mathilde’s life?
Answer:
(Use the following points to write your answers.)
(a) Points:
- would go to friend and explain-
- would ask for time to return the money for the necklace –
- since friend rich, she may have accepted the idea.)
(b) Points:
- Husband
- good – kind – supportive
- considerate – a very nice human being.
(c) Points :
- Invitation to party – borrowing the necklace
- losing the necklace – returning the necklace by borrowing money

Language study:
7. Read the table of verb forms given below.
Question 1.
Read the table of verb forms given below.
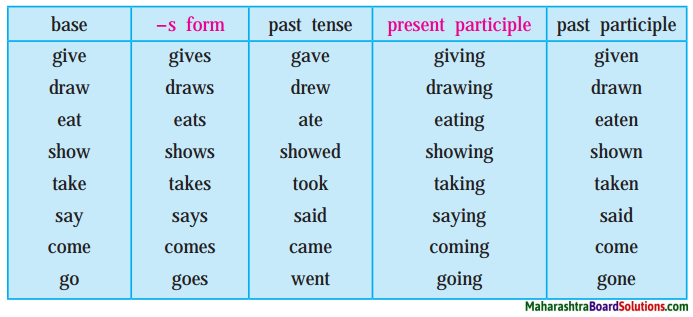
The base form is used as an infInitive: You may go. She will go.
in orders: Go home. and in the simple present tense: I go to school. We go
home. Do you go there every day? The children/They go up, etc.
Note that we use the ‘-s form’ with ‘he’, ‘she’, ‘it’, third-person singular subjects to show the simple present.
The past tense form has ‘-ed’ at the end. But many commonly used verbs have different past tense forms. Examples: Came, went, spoke.
. The ‘-ing’ form is known as the present participle. It is used with forms of ‘be’ to show continuous action – Examples: I am eating. You were eating. She was eating.
It is also used in certain constructions like He sat copying a manuscript.
The past participle used with forms of ‘have’ shows completed action – Examples: I have eaten. They have come, etc.
It is also used in certain constructions like ‘They looked at each other, stunned!’
It is also used in passive constructions. We will learn about ‘passive voice’ later.
Make a table of verb forms for your own reference. Try to arrange the verbs in alphabetical order. Keep adding new verbs to your table from time to time. When you write, check your work to see whether you have used the correct verb form.
Question 1.
Read the different following information about different forms of verbs:
Answer:
1. The base form is used as an infinitive: You may go. She will go.
In orders: Go home. And in simple present tense: I go to school. We go home. Do you go there every day? The children/They go up, etc.
2. Note that we use the e-s form’ with ‘he’, ‘she’, ‘it’, third person singular subjects to show
the simple present.
3. The past tense form has ‘-ed’ at the end. But many commonly used verbs have different past tense forms. Examples: came, went, spoke.
4. The ‘-ing’ form is known as the present participle. It is used with forms of ‘be’ to show continuous action – Examples: I am eating. You were eating. She was eating. It is also used in certain constructions like : He sat copying a manuscript.
5. The past participle used with forms of ‘have’ shows completed action.
Examples: I have eaten. They have come, etc.
It is also used in certain constructions like ‘They looked at each other, stunned!’

My English Coursebook 9th Class Solutions Chapter 1.5 The Necklace Additional Important Questions and Answers
Read the following passage and do the activities :
Simple Factual Activities :
Question 1.
Say whether the following statements are True or False :
Answer:
- Mathilde was married to a big officer at the Ministry of Education. – False
- Mathilde’s former schoolmate was very rich. – True
- Mathilde had rich dresses, jewels and everything that she loved. – False
- Mathilde was happy with the invitation brought by her husband – False
Question 2.
Who said to whom? Complete the table :
(Answers are directly given.)
Answer:
| Dialogue |
Who said |
To whom |
| 1. “Here’s something for you.” |
Mathilde’s husband |
Mathilde |
| 2. “What do you want me to do with that?” |
Mathilde |
Mathilde’s husband |
Question 3.
What did the envelope hold?
Answer:
The envelope held an invitation from the Minister of Education and Mme. Georges Rampouneau to Mr and Mrs. Loisel.

Question 4.
State whether the following statements ) are True or False :
Answer:
- Mathilde’s husband suggested her to wear the dress she wore when she went to the theatre. – True
- Mathilde was upset for three days because she had no good dress to wear. – False
- Mathilde was ready to wear flowers. – False
- She demanded four hundred francs for her dress. – True
Question 5.
Write who said it and to whom :
“But I don’t know what you like.”
Answer:
Madame Forestier said this to Mathilde.
Question 6.
Choose the correct option from the brackets and complete the sentences :
(Answers are directly given.)
Answer:
- Mathilde went to Madame Forestier. (The jeweller/Madame Forestier)
- Madame Forestier took out a large box from her mirrored wardrobe. (large box/necklace)
- Mathilde tried on the jewellery in the mirror. (dress/jewellery)
- Mathilde discovered a diamond necklace in Madame Forestier’s large box. (a black satin box/a diamond necklace)
Question 7.
What did Madame Forestier’s large box contain?
Answer:
Madame Forestier’s large box contained bracelets, necklaces and other jewellery.

Question 8.
Complete the following sentences using the information given in the passage:
(Answers are directly given.)
Answer:
- Mathilde was floating in a cloud of happiness.
- Both, husband and wife left at about four o’clock in the morning.
- In front of the mirror Mathilde took a final look at herself in all her glory.
- She no longer had the necklace round her neck.
Question 9.
Who said it and to whom :
Question a.
“I no longer have Madame Forestier’s necklace.”
Answer:
Mathilde said this to her husband.
Question 10.
Complete the following sentences with the information given in the passage :
(Answers are directly given.)
Answer:
- She remained in her ball dress all night, her mind blank.
- At the end of one week they had lost all hope.
- The husband and wife were sick with grief and anguish.
- Mr. Loisel said, “We must consider how to replace the jewel.”
Question 11.
Who said this to whom :
1. “I might have needed it.”
2. “Don’t sell it for three days.”
Answer:
1. Madame Forestier said this to Mathilde.
2. Mr. Loisel and Mathilde said to the jeweler.

Question 12.
Say if the following statements are True or False:
(Answers are directly given.)
Answer:
- Madame Forestier was rather angry with Mathilde for returning the necklace late. – True
- A string of diamonds they found at Palais Royal was worth thirty-six thousand francs. – False
- The new necklace cost them thirty- four thousand francs. – False
- Mr Loisel borrowed money from every type of money-lender. – True
Question 13.
Complete the sentences using the information from the passage :
(Answers are directly given.)
Answer:
- At the end of ten years, they had paid off everything.
- How little is needed for one to be ruined or saved!
- Mathilde played her part heroically.
- She came to know the drudgery of housework.
Question 14.
Answer the following questions :
Question a.
Who is Madame Loisel?
Answer:
Madame Loisel is Mathilde.
Question b.
What work did Mathilde’s husband do for a tradesman?
Answer:
Mathilde’s husband did accounts for a tradesman.

Question 15.
Say whether the following statements are True or False:
(Answers are directly given.)
Answer:
- Madame Forestier recognised her dear friend immediately. _ False
- Madame Forestier still looked young, beautiful and charming. – True
- It had taken them ten years to pay for the imitation diamond neclace. – True
- The imitation was not worth five hundred francs at most! – False
Complex Factual Activities :
Question 1.
Complete the following :
(Answers are directly given.)
Answer:

Question 2.
Why was Mathilde married to a minor official’?
Answer:
Mathilde was a pretty, charming girl but was born in a family of clerks. This had decided her future. Because of her ill-fate she had to marry a ‘minor official’.
Question 3.
Why did Mathilde weep with misery after visiting her schoolmate?
Answer:
Mathilde wept with misery after visiting her schoolmate because she couldn’t get the riches and the luxurious life in which the schoolmate was relishing. She dreamt of all those things her friend was enjoying. She herself could not have them because of her destiny.
Question 4.
Mathilde was sad, restless and anxious though her dress was ready because ….
Answer:
Mathilde was sad, restless and anxious though her dress was ready because she had no jewels, she had not a single precious stone to wear. She almost had decided not to go to the party.

Question 5.
Mathilde’s husband turned pale because….
Answer:
Mathilde’s husband turned pale because he had been saving the exact amount demanded by Mathilde to buy a gun for a hunting summer, in the country near Nanterre. He would lose his opportunity for buying dress for Mathilde.
Question 6.
Write the following sentences in order of their occurrence :
1. Her friend put a large box of jewellery before Mathilde.
2. She fled home with her treasure.
3. Mathilde went to Madame Forestier.
4. She discovered a diamond necklace.
Answer:
3. Mathilde went to Madame Forestier.
1. Her friend put a large box of jewellery before Mathilde.
4. She discovered a diamond necklace.
2. She fled home with her treasure.
Question 7.
Which sentences tell us that Mathilde greatly desired the necklace?
Answer:
The Sentences: Her heart began to beat with uncontrolled desire. Her hands trembled as she took it. She stood lost in ecstasy as she looked at herself in the mirror. She asked her friend anxiously, “Would you lend me this, just this?”

Question 8.
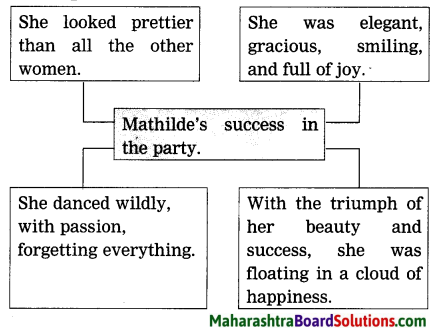
Complete the web :
Answer:
Question 9.
Describe the efforts made by the couple to find the lost necklace:
Answer:
They looked in the folds of Mathilde’s dress, in the folds of her cloak, in her pockets, everywhere. Mr. Loisel walked over the whole route they had walked to find the necklace. He went to the police station, to the newspapers to offer a reward, to the cab companies and everywhere they expected to find the necklace but found nothing.
Question 10.
Complete the web
(Answers are directly given.)
Answer:

Question 11.
How did life of Mathilde change after the horrible incident?
Answer:
Mathilde’s life was completely changed. She dismissed her maid and did extremely unpleasant labours in the kitchen. She washed the dishes, the dirty linen, she carried the garbage down to the street every morning, carried up the water and dressed like a common woman. She had to bargain at markets, quarrel and face insults over every miserable sou. She lived the horrible life of the very poor.

Question 12.
Arrange the following sentences in order of their occurence:
1. Mathilde tells Madame Forestier about her hard time and miseries.
2. Madame Forestier tells that the necklace was an imitation.
3. Madame Forestier did not recognise Mathilde because she was completely changed.
4. Mathilde met Madame Forestier in the Champs Elysees on Sunday.
Answer:
4. Mathilde met Madame Forestier in the Champs Elysees on Sunday.
3. Madame Forestier did not recognise Mathilde because she was completely changed.
1. Mathilde tells Madame Forestier about her hard time and miseries.
2. Madame Forestier tells that the necklace was an imitation.
Activities based on vocabulary:
Question 1.
Match the words in Column ‘A’ with their meaning in Column ‘B’ :
| ‘A’ |
‘B’ |
| 1. aristocrat |
(a) destiny |
| 2. fate |
(b) great success |
| 3. shabby |
(c) nobleman |
| 4. triumph |
(d) nearly worn out |
Answer:
| ‘A’ |
‘B’ |
| 1. aristocrat |
(c) nobleman |
| 2. fate |
(a) destiny |
| 3. shabby |
(d) nearly worn out |
| 4. triumph |
(b) great success |

Question 2.
Write any four words from the passage that show the feeling of great pain:
Answer:
regret, despair, misery and tormented.
Question 3.
Write English terms that stand for the French terms Monsieur and Mme:
Answer:
Mr and Mrs.
Question 4.
Write the long forms of the following contracted forms:
- Let’s
- don’t
- hadn’t
- what’s.
Answer:
- Let us
- do not
- had not
- what is.
Question 5.
Write four words from the passage that reflect (show) that the person is in difficult situation.
Answer:
stammered, stunned, distressed, stuttered.

Question 6.
Fill in the blanks with proper letters so as to find the words: (Answers are directly given.)
Answer:
1. the objects such as rings, necklaces, etc. that

2. a large cupboard for hanging clothes.
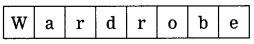
3. a piece of ornament consisting of chain of beads, diamonds, etc. worn around the neck =

4. a strong wish to have something =

Question 7.
Write any four adjectives from the passage.
Answer:
elegant, gracious, smiling, panic-stricken.
Question 8.
Write any four adverbs with ‘-ly’ from the passage.
Answer:
wildly, fmally, sadly, suddenly.
Question 9.
Which words from the passage are related with ‘success’?
Answer:
full of joy, triumph, cloud of happiness, glory.

Question 10.
Write the meanings of:
(Answers are directly given.)
Answer:
- glimmer of hope: a small sign of hope/success.
- a hollow, pale figure: a person having empty mind and almost white face because of frustration and exhaustion.
- sick with grief and anguish: mentally ill because of great sadness and pain.
- cloak: ladies’ garment without sleeves, worn over their other clothes.
Question 11.
Find and write all the numbers mentioned in the passage :
Answer:
Forty thousand, thirty-six thousand, thirty- four thousand, eighteen thousand.
Question 12.
Write from passage the words related to money matters.
Answer:
worth, sell, borrow, notes, agreements, dealt, money-lender.

Question 13.
Write from the passage the phrases related to ‘housework’.
Answer:
Drudgery of housework, odious labours of the kitchen, washing dishes, washing dirty linen, carry the garbage, carry up the water, bargain at markets.
Question 14.
Match from the passage the adjectives in Column ‘A’ with the nouns in Column ‘B’ :
| ‘A’ |
‘B’ |
| 1. dreadful |
(a) sou |
| 2. miserable |
(b) labours |
| 3. horrible |
(c) debt |
| 4. odious |
(d) life |
Answer:
| ‘A’ |
‘B’ |
| 1. dreadful |
(c) debt |
| 2. miserable |
(a) sou |
| 3. horrible |
(d) life |
| 4. odious |
(b) labours |

Question 15.
Match the words in Column ‘A’ with their meaning in Column ‘B’ :
| ‘A’ |
‘B’ |
| 1. familiarly |
(a) artificial/not real |
| 2. astonished |
(b) in a friendly manner |
| 3. imitation |
(c) very surprised |
| 4. innocent |
(d) having not done anything wrong |
Answer:
| ‘A’ |
‘B’ |
| 1. familiarly |
(b) in a friendly manner |
| 2. astonished |
(c) very surprised |
| 3. imitation |
(a) artificial/not real |
| 4. innocent |
(d) having not done anything wrong. |

Question 16.
Write from the passage the verbs that end : with ‘-ed’.
Answer:
astonished, addressed, stammered, uttered, changed, stunned, smiled, moved.
Activities based on contextual grammar :
Question 1.
Find and write the adjectives from the passage for the following nouns :
- house
- girl
- official
- mansion.
Answer:
- shabby and poorly furnished
- pretty and charming
- minor
- grand and palatial.
Question 2.
He turned a little pale.
(Change the sentence into simple present Tense.)
Answer:
He turns a little pale.

Question 3.
Choose the correct option of the question tag:
I can give you four hundred francs.
(i) , can I?
(ii) , don’t I?
(iii) , can’t I?
(iv) , couldn’t I?
Answer:
I can give you four hundred francs, can’t I?
Question 4.
She replied,” I am upset that I have no jewels.” (Choose the correct option to transform it into Reported speech.)
a. She replied that I was upset that I had no jewels.
b. She replied that she is upset that she has no jewels.
c. She replied she was upset that she has no jewels.
d. She replied that she was upset that she had no jewels.
Answer:
c. She replied she was upset that she has no jewels.
Question 5.
Choose the correct wh-question from the alternatives to get the underlined part as an answer:
She discovered, in a black satin box, a diamond necklace.
(a) What did she discover in a black satin box?
(b) When did she discover a diamond necklace in a black satin box?
(c) Where did she discover a diamond necklace?
(d) Why did she discover a diamond necklace?
Answer:
(c) Where did she discover a diamond necklace?
Question 6.
Write the following sentence in simple present tense:
She threw her arms around her friend’s neck.
Answer:
She throws her arms around her friend’s neck.

Question 7.
Find the determiners from the following sentences and underline them :
(Answers are directly underlined.)
Answer:
1. They were dropped off at their door in the Rue des Martyrs.
2. Forgetting everything in the triumph of her beauty.
Question 8.
Do as directed :
- She took a final look at herself. (Write simple present tense form for the underlined word.)
- The day of the party arrived. (Rewrite the sentence using simple future tense.)
- She danced wildly (Use past progressive tense and rewrite the sentence.)
Answer:
- She takes a final look at herself.
- The day of the party will arrive.
- She was dancing wildly.
Question 9.
It was worth forty thousand francs.
(Use ‘They’ in place of ‘It’ and rewrite the correct sentence.)
Answer:
They were worth forty thousand francs.

Question 10.
He went to get the new necklace. (Rewrite the sentence using simple present tense for the underlined verb.)
Answer:
He goes to get the new necklace.
Question 11.
Change the following sentences in passive voice :
1. They dismissed their maid.
2. They rented a garret under the roof.
Answer:
1. Their maid was dismissed by them.
2. A garret under the roof was rented by them.
Question 12.
How strange life is!
(Make it an assertive sentence,)
Answer:
Life is very strange.

Question 13.
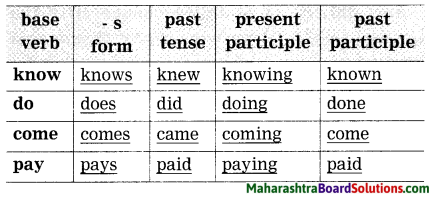
Complete the table with the correct forms of the given verbs.
Answer:
Do as directed :
Question 1.
1. She had no rich dresses : (Make the sentence affirmative without changing the meaning.)
2. These were the only things she loved. (Make the sentence negative without changing the meaning.)
Answer:
1. She had poor dresses.
2. She loved nothing but (except) these things.
Question 2.
They could not find it.
(Begin with It could not… and change the voice.)
Answer:
It could not be found by them.

Question 3.
He said to Mathilde, “Tell her you have broken the clasp of the necklace.”
(Change into Indirect speech.)
Answer:
He told Mathilde to tell her she had broken the clasp of the necklace.
Question 4.
Use simple present tense form and rewrite the following sentences :
Question a.
He went to the police station.
Answer:
He goes to the police station.
Question b.
They lost all hope.
Answer:
They lose all hope.

Question 5.
How you’ve changed!
(Make an assertive sentence.)
Answer:
You’ve completely changed,
Question 6.
They were similar.
(Make it negative without changing meaning.)
Answer:
They were not different.
Question 7.
I am Mathilde Loisel.
(Choose correct Question Tag,)
(i) , am I?
(ii) , amn’t I?
(iii) , aren’t I?
(iv) , don’t I?
Answer:
(iii) , aren’t I?

Question 8.
Fill in the table with correct verb forms.
(Answers are directly given.)
Answer:
| base form |
Past tense |
Past participle |
| bring |
brought |
brought |
| see |
saw |
seen |
| feel |
felt |
felt |
| sing |
sang |
sung |
Personal Response:
Question 1.
What do you feel when you receive an invitation for a party? Why?
Answer:
When I receive an invitation for a party, I feel very happy because we get to meet our friends and relatives at the party and we can spend some time rejoicing. We also get to eat tasty food in the party.

Question 2.
Was Mathilde’s husband a considerate person? How do you know that?
Answer:
Mathilde’s husband was really a very considerate person. Though his wife was obstinate and stubborn, he tried to fulfill all her unreasonable wishes. He sacrificed his own hunting joy and gave his savings to please Mathilde. This shows that he was a very considerate person.
Question 3.
Mathilde asked her friend, “Would you lend me this, just this?”
Why, do you think, did Mathilde say ‘just this’?
Answer:
I think, Mathilde was fully satisfied with the diamond necklace she got. It looked beautiful in her neck as she had desired. So she did not want anything else except that diamond necklace and so she insisted to lend her that and only that necklace.
Question 4.
Why, do you think, did Mathilde not notice the loss of her necklace?
Answer:
I think, she was thinking only about the triumph of her beauty and success in the party. She had lost her attention towards her necklace. Secondly, they left the party early in the morning, could not find a cab and had to walk for a long distance. This also must be the cause of the distraction.

Question 5.
Do you think, the arrangement made by Mr Loisel with the jeweller, was fair? Give your reason:
Answer:
Yes I think the arrangement was fair. According to the arrangement the jeweller would take the necklace back for thirty-four thousand if the other (the lost) necklace was found before the end of February. It would help them to get some more time to find the necklace and again they would ; be losing only two thousand francs instead of thirty- 5 six thousand.
Question 6.
Why does Madame Forestier speak coldly to Mathilde?
Answer:
Mathilde returned the necklace after so many days. Madame Forestier did not like it and was angry with Mathilde. It is the usual tradition to return the borrowed things immediately after the work is done, but Mathilde did not do it. By speaking coldly Madame Forestier expresssed her anger and displeasure.
Question 7.
What is meant by the horrible life of the very poor?
Answer:
The horrible life of the poor means a very tiring, bad, unpleasant and painful life. The poor are the people who live a miserable life with very little or no money at all. They have no money to satisfy their day-to-day basic needs. They have to work hard all the day to make both ends meet. Mathilde experienced this horrible life of the poor for saving money to clear the debt.

Question 8.
Write what you think about the following thought and action of Mathilde :
Mathilde told her friend about the lost necklace.
Answer:
Mathilde was now a relieved person. Though it was her fault, she must have thought that she should tell the truth to her friend and tell her how she struggled for ten long years that made her look old.
Question 9.
Who do you think was responsible for Mathilde’s misery? Was it her friend, she herself, her husband or the circumstances?
Answer:
It was Mathilde who was mainly responsible for her misery. Her wilfulness and obstinate behaviour were the root cause of the disastrous incident. She borrowed the necklace and lost it and that led to her misery. Her friend and her husband were, in no way, responsible for it. Of course the circumstances, to some extent too are responsible for it.
Oral Work:
Question 1.
Read the conversations in the story aloud using proper intonation.

Writing Skill:
Question 1.
Prepare a formal invitation using the format given on the textbook page no. 27.
Answer:

Activities Based on Language study
Do as directed!
Question 1.
Complete the words by using correct letters :
- o _ h e r
- y o _ n g
- p _ o u d
- s p e _ k
Answer:
- o t h e r
- y o u n g
- p r o u d
- s p e a k
Question 2.
Copy the following sentences correctly in your notebook :
Answer:
1. He said,” Here’s something for you!”
2. “What’s the matter? Let’s see, Mathilde.”

Question 3.
Put the following words in alphabetical order:
1. glory, street, amount, pleasure.
2. mansion, mirror, mutter, matter.
Answer:
1. amount, glory, pleasure, street.
2. mansion, matter, mirror, mutter.
Question 4.
Punctuate the following sentences :
1. you could wear flowers he said they are very fashionable at this time of year
2. what is the matter asked her husband
Answer:
1. “You could wear flowers,” he said,
“They are very fashionable at this time of year.”
2. “What is the matter?” asked her husband.

Question 5.
Write four small words (minimum letters each) using the letters in the given word:
‘schoolmate’ :
Answer:
- school
- come
- late
- home.
Question 7.
Write related words as shown in the example :
(Answers are directly given.)
Answer:
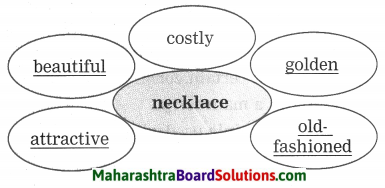
Question 8.
Complete the following word-chain withing for.m. Add four words, each beginning with the last letter of the previous word:
going → ………………. →……………. →…………… → ………….. .
Answer:
going → growing → gaining → guarding → grumbling.
Question 9.
Make your own meaningful sentence by using the phrase ‘to be aware of’.
Answer:
We should be aware of the consequences of bad habits.

Question 10.
Add a prefix or suffix to make new words. and use any one of the root words in your own sentence:
1. annoy
2. exhaust
Answer:
1. annoyance
2. exhaustion
Sentence: There is no need to exhaust yourself for such a petty job.
Question 11.
Add a clause to expand the sentence meaningfully:
I don’t remember ………………………………… .
Answer:
I don’t remember when I met him last.
My English Coursebook Std 9 Digest Pdf Unit 1
![]()
![]()

![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()