Class 7

Class 7 Hindi Abhyas-2 Textbook Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati अभ्‍यास – २ Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Abhyas-2 Textbook Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions अभ्‍यास – २ Textbook Questions and Answers

Question 1.
‘यातायात सप्ताह’ तथा ‘क्रीडा सप्ताह’ पर पोस्टर बनाइए और कक्षा में प्रदर्शनी लगाइए।
(सामग्री – चित्र, चार्ट पेपर, समाचार पत्र, पत्रिका की कतरने, उद्घोष आदि।)
Answer:
छात्र अपेक्षित कृति स्वयं करेंगे।

Question 2.
दिए गए शब्द कार्ड देखिए, पढ़िए और उनकी सहायता से सरल, मिश्र तथा संयुक्त वाक्य बनाकर कक्षा में सुनाइए।
(एक शब्द कार्ड का प्रयोग अनेक बार कर सकते हैं।)

Answer:
सरल वाक्य:
(१) भारत उत्तम देश है।
(२) यह उत्तम घर है।
(३) यह वही घर है।
(४) यह जी रहा है।

संयुक्त वाक्य:
सड़क की बाईं ओर घर है और दाई ओर कुऔं है।
भारत उत्तम देश है और यह राष्ट्रीय एकात्मता का उदाहरण हैं। कुएँ का पानी उत्तम है और वह सड़क के दाई ओर है।

मिश्र वाक्य:
जहाँ सड़क है, वहीं बाई ओर कुआँ है।
जहाँ पानी है, वही दाई ओर घर है।
भारत में राष्ट्रीय एकात्मता है क्योंकि यह उत्तम देश है।

Question 3.
‘रमेश पुस्तक पढ़ता है।’ इस वाक्य को सभी काल में परिवर्तित करके उसका भेद लिखिए।

Answer:
वर्तमानकाल:
(१) सामान्य वर्तमानकाल – रमेश पुस्तक पढ़ता है।
(२) अपूर्ण वर्तमानकाल – रमेश पुस्तक पढ़ रहा है।
(३) संदिग्ध वर्तमानकाल – रमेश पुस्तक पढ़ता होगा।

भूतकाल:
(१) सामान्य भूतकाल . रमेश ने पुस्तक पड़ा।
(२) पूर्ण भूतकाल – रमेश ने पुस्तक पढ़ा था।
(३) अपूर्ण भूतकाल – रमेश पुस्तक पढ़ रहा था।
(४) संदिग्ध भूतकाल – रमेश ने पुस्तक पढ़ा होगा।
(५) हेतुहेतुमद् भूतकाल – यदि रमेश पुस्तक पढ़ता तो पास हो जाता।

भविष्य काल:
(१) सामान्य भविष्यकाल – रमेश पुस्तक पढ़ेगा।
(२) संभाव्य भविष्यकाल – शायद रमेश पुस्तक पढ़ेगा।

Question 4.
अपने आसपास दिखाई देने वाले सांकेतिक चिह्नों के चित्र बनाओ और उन्हें नामांकित करो।
Answer:
छात्र स्वयं करेंगे।

Hindi Sulabhbharati 7th Standard Digest Guide दूसरी इकाई

• अस्‍पताल Question Answer
• बेटी युग Question Answer
• दाे लघुकथाएँ Question Answer
• शब्द संपदा Question Answer
• बसंत गीत Question Answer
• चंदा मामा की जय Question Answer
• रहस्‍य Question Answer
• हम चलते सीना तान के Question Answer

Class 7 Hindi Chapter 8 Ham Chalte Sina Tan Ke Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 8 हम चलते सीना तान के Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 8 Ham Chalte Sina Tan Ke Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 8 हम चलते सीना तान के Textbook Questions and Answers

विचार मंथन

‘हम सब एक हैं।’ इस विषय पर एक अनुच्छेद लिखिए।
Answer:
भारत एक लोकतांत्रिक देश है। जहाँ विभिन्न धर्मों को मानने वाले लोग एक साथ रहते हैं। उनकी भाषाएँ अलग हैं। उनका रंग भी अलग-अलग हैं। वे अलग-अलग प्रदेश में रहते भी हैं। फिर भी हम एक हैं। हमारी संस्कृति एक है। अनेकता में एकता ही इस हिंदुस्तान की विशेषता है। हमारे पर्व-त्योहार हमें मिलकर रहना सिखाते हैं। यहाँ की प्रकृति भी हमें एकता का संदेश देती है। एकता में शक्ति होती है। जिस प्रकार एक फूल कितना भी सुंदर हो, वह एक गुलदस्ते का मुकाबला नहीं कर सकता है।

विविध रंगों के फूल जब एक साथ मिल जाते हैं, तो वे गुलदस्ते बन जाते हैं। ठीक हमारा देश भी अनेक धर्मों, जातियों, वर्गों, भाषाओं एवं प्रदेशों से मिलकर एक खूबसूरत देश बनता है। जिसका एक राष्ट्रगान है। एक राष्ट्रगीत है जिसमें हमारी एकता की महिमा का गान है। अत: अनेक होते हुए भी हम सब भारतमाता के बेटे हैं और हम सब एक हैं।

अध्ययन कौशल

अब तक पड़े हुए मुहावरों-कहावतों का वर्ण क्रमानुसार संग्रह बनाइए और चर्चा कीजिए।
Answer:
(छात्र चर्चा स्वयं करेंगे।)

• अनाप-शनाप बोलना।
• आँखें खुली की खुली रहना।
• कमर कसना।
• करवटें बदलना।
• खाट पकड़ना।
• खून पसीना एक करना।
• गला फाड़कर रोना।
• ठान लेना।
• दरार पड़ना।
• तारीफ के पुल बाँधना।
• दूध का दूध
• मात देना।
• पानी का पानी करना।
• मुँह लटकाना।
• सिर आँखों पर रखना।
• सीना तान कर चलना।
• हथियार डालना।

जरा सोचो….. लिखो

‘यदि तुम सैनिक होते तो… ‘ विषय पर एक अनुच्छेद लिखिए। (अनुच्छेद-लेखन)
Answer:
यदि मैं सैनिक होता तो मैं अपने देश के गौरव और स्वाभिमान की रक्षा के लिए सदैव तत्पर रहता। मैं अपने देश के अस्तित्व को कभी मिटने नहीं देता। आज कल पड़ोसी देश से आतंकवाद की घटनाएँ दिन-प्रतिदिन बढ़ती जा रही हैं। अनायास ही सैनिक मौत के घाट पर उतारे जा रहे हैं। ऐसे में यदि मैं सैनिक होता तो वही करता जो हमारे वीर सैनिक कर रहे हैं। अपना सिर कटा देते हैं, किंतु देश की आन-बान-शान को बनाए रखते हैं। आतंकवादियों के मंसुबे को कभी कामयाब नहीं होने देते हैं। मैं भी इसी प्रकार देश की सेवा करता। देश के सैनिकों का मनोबल बनाए रखने के लिए सर्जिकल स्ट्राइक करके आतंकवाद का समूल नाश करने का प्रयास करता।

पसंदीदा विषय पर चार पंक्तियों की कविता लिखिए। (कविता-लेखन)
Answer:

सुनो तो जरा:

किसी शहीद और उसके परिवार के बारे में सुनो : मुद्दे – जन्म, तिथी, गाँव, शिक्षा, घटना

मेरी कलम से:

शालेय प्रतिज्ञा का श्रुतलेखन करो और प्रतिज्ञा के मूल्यों का अपने व्यवहारों से सत्यापन करो।

निम्न पंक्तियों का अर्थ लिखिए।

Question 1.
हिंदुस्तान ………… तान के।
Answer:
प्रस्तुत पंक्ति का अर्थ यह है कि हम सब भारतमाता के बेटे हैं। हम गर्व से चलते हैं। हम भारत की मिट्टी में खेलकर-खाकर बड़े हुए हैं। भारतमाता ने हमें ममता और समता से पाला है उनके इस एहसान का हमें कर्ज चुकाना है।

Question 2.
जो वीरत्व …………………….” तान के।
Answer:
प्रस्तुत पंक्ति का अर्थ यह है कि हम भारत के सैनिक युद्धभूमि में अपनी वीरता और विवेक दुश्मनों को दिखा देंगे। उसकी गाथा का देश के गाँव, नगर और घर-घर में गुणगान करेंगे। देशवासियों के अनगिनत कंठों से हमारे पराक्रम की गाथा सुनाई देगी। हम भारतमाता के बेटे गर्व से प्रगति पथ पर चलते हैं।

Question 3.
इस कविता का केंद्रीय भाव अपने शब्दों में स्पष्ट कीजिए।
Answer:
प्रस्तुत कविता का मुख्य भाव यह है कि हम सब भारतमाता के बेटे हैं। भले ही हमारा धर्म, जाति, वर्ण, भाषा और प्रदेश अलग-अलग है। किंतु हम सभी भारत के सैनिक पहले हिंदुस्तानी हैं। हम अपने देश को और उसके निशान को मिटने नहीं देंगे। युद्ध में दुश्मनों को अपनी वीरता दिखाएँगे।

Question 4.
अपने देश के राष्ट्रीय प्रतीकों के नाम बताइए।
Answer:
हमारे देश के राष्ट्रीय प्रतीक निम्नलिखित हैं –

(१) राष्ट्रीय ध्वज – तिरंगा
(२) राष्ट्रीय पशु – बाघ
(३) राष्ट्रीय पक्षी – मोर
(४) राष्ट्रीय फल – आम
(५) राष्ट्रीय फूल – कमल
(६) राष्ट्रीय खेल – हॉकी
(७) राष्ट्रीय पर्व – गणतंत्र दिवस (२६ जनवरी)
– स्वतंत्रता दिवस (१५ अगस्त)
– गाँधी जयंती (२ अक्टूबर)
(८) राष्ट्रीय गीत – वंदे मातरम्
(९) राष्ट्रगान – जन-गण-मन
(१०) राष्ट्रीय ध्येय वाक्य – सत्यमेव जयते।

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए।

1. पर्वत
2. मरुस्थल
3. शीश
4. श्रम
5. कर्ज
6. नगर
7. सैनिक
8. वीरत्व

Answer:

1. गिरि
2. रेगिस्तान
3. सिर
4. परिश्रम
5. ऋण
6. शहर
7. सिपाही
8. वीरता

खोजबीन

Answer:

सदैव ध्यान में रखो

मानव सेवा ही सच्ची सेवा है।

भाषा की ओर

अर्थ के आधार पर वाक्य पढ़ो, समझो और उचित स्थान पर लिखो:

Answer:
पहले वाक्य में क्रिया के करने या होने की सामान्य सूचना मिलती है ।
अतः यह वाक्य विधानार्थक वाक्य है ।

दूसरे वाक्य में आने का अभाव सूचित होता है क्योंकि इसमें नहीं का प्रयोग हुआ है ।
अतः यह निषेधार्थक वाक्य है ।

तीसरे वाक्य में प्रश्न पूछने का बोध होता है । इसके लिए क्यों का प्रयोग हुआ है ।
अतः यह प्रश्नार्थक वाक्य है ।

चौथे वाक्य में आदेश दिया है । इसके लिए चलो शब्द का प्रयोग हुआ है ।
अतः यह आज्ञार्थक वाक्य है ।

पाँचवें वाक्य में विस्मय-आश्चर्य का भाव प्रकट हुआ है । इसके लिए वाह शब्द का प्रयोग हुआ है ।
अतः यह विस्मयार्थक वाक्य है ।

छठे वाक्य में संदेह या संभावना व्यक्त की गई है । इसके लिए होगा शब्द का प्रयोग हुआ है ।
अतः यह संभावनार्थक वाक्य है।

सातवें वाक्य में इच्छा या आशीर्वाद व्यक्त किया गया है । इसके लिए खूब पढ़ो, खूब बढ़ो का प्रयोग हुआ है ।
अतः यह इच्छार्थक वाक्य है ।

आठवें वाक्य में एक क्रिया का दूसरी क्रिया पर निर्भर होने का बोध होता है । इसके लिए यदि, तो शब्दों का प्रयोग हुआ है ।
अतः यह संकेतार्थक वाक्य है।

Hindi Sulabhbharti Class 7 Solutions Chapter 8 हम चलते सीना तान के Additional Important Questions and Answers

निम्नलिखित प्रश्नों के एक शब्द में उत्तर लिखिए।

Question 1.
हम सब किसके बेटे हैं?
Answer:
भारतमाता

Question 2.
हम किसकी मिट्टी में खेले-खाए हैं?
Answer:
हिंदुस्तान

Question 3.
भारतमाता की पूजा में हमने किसके फूल चढ़ाए हैं?
Answer:
श्रम

Question 4.
हम किसके निशान को गिरने नहीं देंगे?
Answer:
देश

Question 5.
हम सैनिक वीरत्व और विवेक किसमें दिखलाएँगे?
Answer:
समर

निम्नलिखित शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।

(रजकण, भारतमाता, हिंदुस्तान, अगणित, सदियों)

Question 1.
फौजी वर्दी में हम सबसे पहले ……………..” के।
Answer:
हिंदुस्तान

Question 2.
…………….’ के बेटे हम चलते सीना तान के। कर्ज चुकाने हैं
Answer:
भारतमाता

Question 3.
हमको उन …………….. के एहसान के।
Answer:
रजकण

Question 4.
जिसकी पूजा में ………….. से श्रम के फूल चढ़ाए हैं।
Answer:
सदियों

Question 5.
जिसकी रक्षा में पुरुखों ने ………………… शीश कटाए हैं।
Answer:
अगणित

निम्नलिखित वाक्य सही है या गलत लिखिए।

Question 1.
हिंदुस्तान में अलग-अलग धर्मों के लोग रहते हैं।
Answer:
सही

Question 2.
भारत में एक भाषा बोली जाती है।
Answer:
गलत

Question 3.
भारतमाता हमें ममता और समता से पालती है।
Answer:
सही

Question 4.
भारतमाता की रक्षा में अनेक शीश कट गए।
Answer:
सही

Question 5.
हम भारतमाता के गौरव के रखवाले हैं।
Answer:
सही

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।

Question 1.
हमें किसका कर्ज चुकाना है और क्यों?
Answer:
हमें भारतमाता के एहसान का कर्ज चुकाना है; क्योंकि हम इस पवित्र मिट्टी में खेलकर बड़े हुए हैं।

Question 2.
भारतमाता की पूजा में हमने किसके फूल चढ़ाए हैं?
Answer:
भारतमाता की पूजा में हमने श्रम के फूल चढ़ाए हैं।

Question 3.
युद्ध में सैनिक क्या करेंगे?
Answer:
युद्ध में सैनिक अपनी विवेक और वीरता दिखलाएंगे। व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. धर्म
2. विवेक

Answer:

1. अधर्म
2. अविवेक

निम्नलिखित शब्दों के तीन-तीन पर्यायवाची शब्द लिखिए।

1. बन
2. सागर
3. घर

Answer:

1. अरण्य, कानन, जंगल
2. सिंधु, समुद्र, जलधि
3. आवास, सदन, गृह

निम्नलिखित वाक्यों के अर्थ के आधार पर उनके भेद का नाम लिखिए। :

1. बच्चे हँसते-हँसते खेल रहे थे। ।
2. माला घर नहीं जाएगी।
3. इसे हिमालय क्यों कहते हैं?
4. सदैव सत्य के पथ पर चलो।
5. वाह! क्या बनावट है ताजमहल की!
6. कश्मीर का सौंदर्य देखकर तुम्हें आश्चर्य होगा।
7. खूब पढ़ो, खूब बढ़ो।
8. यदि बिजली आएगी, तो रोशनी होगी।

Answer:

1. विधानार्थक वाक्य
2. निषेधार्थक वाक्य
3. प्रश्नार्थक वाक्य
4. आज्ञार्थक वाक्य
5. विस्मयार्थक वाक्य
6. संभावनार्थक वाक्य
7. इच्छार्थक वाक्य
8. संकेतार्थक वाक्य

Hindi Sulabhbharati 7th Standard Digest Guide दूसरी इकाई

• अस्‍पताल Question Answer
• बेटी युग Question Answer
• दाे लघुकथाएँ Question Answer
• शब्द संपदा Question Answer
• बसंत गीत Question Answer
• चंदा मामा की जय Question Answer
• रहस्‍य Question Answer
• हम चलते सीना तान के Question Answer

Class 7 Hindi Chapter 3 Do Laghu Kathayen Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 3 दाे लघुकथाएँ Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 3 Do Laghu Kathayen Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 3 दाे लघुकथाएँ Textbook Questions and Answers

विचार मंथन

‘सत्यमेव जयते।’ की संकल्पना स्पष्ट कीजिए।
Answer:
‘सत्यमेव जयते।’ सूक्ति का अर्थ है – सत्य की सदैव जीत होती है। संस्कृत भाषा की यह सूक्ति महाभारत से ली गई है। प्राचीन काल से यह बात प्रचलित है। झूठ कितना भी छुपाया जाए; वह एक दिन सामने आ ही जाता है। महाभारत काल में ऐसी अनेक कहानियाँ हैं; जिससे यह साबित होता है कि अंत में जीत सत्य की ही होती है। आज कल सिनेमा और धारावाहिकों में भी यही दिखाया जाता है कि जीत सत्य की ही होती है। इसी से प्रभावित होकर आजादी के बाद हमारे देश के ध्येय वाक्य के रूप में “सत्यमेव जयते” को ही स्वीकार किया गया। अत: यह शाश्वत सत्य है कि जीत सदैव सत्य की ही होती है।

अध्ययन कौशल

Answer:
आदरणीय अध्यक्ष महोदय, कुशल निर्णायक मंडल एवं प्रिय श्रोतागण! आज मैं आपके सामने ‘त्योहारों के महत्त्व’ विषय पर अपने विचार प्रकट करने जा रहा हूँ। त्योहारों का नाम सुनते ही मन खुशी से झूम उठता है। आँखों के सामने मनमोहक, आकर्षक और रंग-बिरंगे नज़ारे तैरने लगते हैं। कभी गणेशोत्सव, कभी नवरात्रि, कभी दीपावली के पटाखें, कभी होली के रंग में सराबोर गाँव-नगर तो कहीं नए-नए परिधानों में सजे लोग।

अध्यक्ष महोदय, इन सब झाकियों में नज़ारे भले ही अलगअलग दिखते हैं, किंतु सभी का उद्देश्य एक है आपसी भाईचारा। भारत ‘त्योहारों का देश’ कहा जाता है। कहा भी गया है”अगर चाहते हैं उमंग तो, आपस का व्यवहार न भूलें। कैसी भी हो मायूसी पर, हम अपने त्योहार न भूलें।” अंत में मैं इतना ही कहना चाहता हूँ कि यदि ये त्योहार न आएँ तो हम अपने घर-परिवार और रिश्तेदारों से पूर्ण रूप से मिल न पाएँगे। इसलिए हमें अपने त्योहारों को धूमधाम से मनाना चाहिए।

बताओ तो सही

अकबर के नौ रत्नों के बारे में बताइए।
Answer:
अकबर के दरबार में नौ गुणवान दरबारी थे; जिन्हें कालांतर में ‘अकबर के नवरत्न’ के नाम से जाना जाता है।

• अबुल फजल
• मुल्ला दो प्याजा
• तानसेन
• बीरबल
• राजा टोडरमल
• फैजी
• राजा मानसिंह
• फकीर अजीओद्दीन
• रहीम

सुनो तो जरा:

चतुराई संबंधी कोई सुनी हुई कहानी सुनाओ।

खोजबीन:

योग्य विकल्प चुनकर वाक्य फिर से लिखिए।

Question 1.
जब बादशाह ने बीरबल की दूसरी शर्त सुनी तो वे बीरबल …………..”
(क) से खुश हो गए।
(ख) का मुँह देखने लगे।
(ग) की होशियारी जान चुके।
Answer:
जब बादशाह ने बीरबल की दूसरी शर्त सुनी तो वे बीरबल का मुँह देखने लगे।

Question 2.
क्रोधित होकर उस चित्रकार ने सेठ से …………..।
(क) पैसे माँगे।
(ख) पूरे पैसे माँगे।
(ग) सभी चित्रों के पैसे माँगे।
Answer:
क्रोधित होकर उस चित्रकार ने सेठ से सभी चित्रों के पैसे माँगे।

Question 3.
कला और कलाकार का सम्मान करने से ………..।
(क) कला, संस्कृति की रक्षा एवं संवर्धन होता है।
(ख) चित्रकार नाराज हो जाते हैं।
(ग) बादशाह मुश्किल में पड़ जाते हैं।
Answer:
कला और कलाकार का सम्मान करने से कला, संस्कृति की रक्षा एवं संवर्धन होता है।

निम्नलिखित प्रश्नों के उत्तर विस्तार से लिखिए।

Question 1.
‘हरे घोड़े के संदर्भ में बीरबल की चतुराई का वर्णन कीजिए।
Answer:
बादशाह और बीरबल दोनों यह बात अच्छी तरह जानते थे कि संसार में हरा घोड़ा नहीं होता। फिर भी बीरबल ने घोड़े के मालिक की दो शर्ते बताकर बादशाह को निरुत्तर कर दिया। न तो बादशाह दूसरी शर्त पूरी कर सकेंगे और न ही उन्हें हरा घोड़ा देखने को मिलेगा। इस प्रकार बीरबल ने अपनी चतुराई का परिचय दिया।

Question 2.
घोड़े के मालिक की शर्ते लिखिए।
Answer:
घोड़े के मालिक की दो शर्ते थीं। पहली शर्त यह थी कि बादशाह को घोड़ा लेने स्वयं ही जाना पड़ेगा। दूसरी शर्त यह थी कि जब घोड़े का रंग दूसरे घोड़ों से अलग है, तो उसे देखने का दिन भी अलग ही होना चाहिए। यानि सप्ताह के सात दिनों के अलावा किसी भी दिन बादशाह घोड़ा देख सकते थे।

Question 3.
चित्रकार की परेशानी का कारण बताइए।
Answer:
चित्रकार ने कई बार चित्र बनाए, लेकिन वह कंजूस सेठ हर बार कह देता कि चित्र ठीक नहीं है। वह उसे पैसे नहीं दे रहा था। इसलिए चित्रकार बेहद परेशान था।

वाचन जगत से

पसंदीदा चित्रकथा पढ़ो और इसी प्रकार अन्य चित्रकथा बनाकर सुनाओ।

सदैव ध्यान में रखो

निर्णय से पहले पक्ष-विपक्ष दोनों का विचार करना चाहिए।

भाषा की ओर

निम्नलिखित वाक्य पढ़ो तथा मोटे और में छपे शब्दों पर ध्यान दो

1. नागपुर से रायगढ़ की ओर गए।
2. ताकत के लिए संतुलित आहार आवश्यक है।
3. जन्म के बाद एक मामी जी ने मुझे गोद ले लिया।
4. जलाशय चाँदी की भाँति चमचमा रहा था।
5. शौनक बड़ी बहन के साथ विद्यालय जाने की तैयारी में लग गया।
6. मुकेश की ओर कोई देख रहा था।
7. अपनी माँ के लिए मैंने साड़ी खरीदी।
8. चित्रकार ने सेठ के सामने दर्पण रखा।
9. सेठ काम कराने के बाद भी पैसे नहीं देता था।
10. अकबर बीरबल के साथ सैर करने गए।

Answer:

1. की ओर
2. के लिए
3. के बाद
4. की भाँति
5. के साथ
6. की ओर
7. के लिए
8. के सामने
9. के बाद
10. के साथ

Hindi Sulabhbharti Class 7 Solutions Chapter 3 दाे लघुकथाएँ Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए।

Question 1.
अकबर के दरबार में कितने रत्ल थे?
Answer:
नौ रत्न

Question 2.
एक बार अकबर किसके साथ सैर कर रहे थे?
Answer:
बीरबल

Question 3.
अकबर ने बीरबल को कितने दिन में घोड़ा लाने के लिए कहा?
Answer:
एक सप्ताह

Question 4.
घोड़े के मालिक की कितनी शर्ते थीं?
Answer:
दो

Question 5.
सप्ताह में कितने दिन होते हैं?
Answer:
सात

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।

Question 1.
बादशाह का मन क्या देखकर प्रसन्न हो गया?
Answer:
बादशाह का मन चारों तरफ हरियाली देखकर प्रसन्न हो गया।

Question 2.
बादशाह और बीरबल दोनों कौन-सी बात अच्छी तरह जानते थे?
Answer:
बादशाह और बीरबल दोनों यह बात अच्छी तरह से जानते थे कि संसार में कहीं भी हरे रंग का घोड़ा नहीं होता।

Question 3.
एक सप्ताह तक बीरबल क्या करते रहे?
Answer:
एक सप्ताह तक बीरबल इधर-उधर घूमते रहे।

Question 4.
बादशाह मन-ही-मन क्यों प्रसन्न थे?
Answer:
बादशाह मन-ही-मन प्रसन्न थे क्योंकि बीरबल ने अपनी चतुराई से उन्हें फिर मात दे दी।

Question 5.
दूसरी शर्त क्या थी?
Answer:
दूसरी शर्त यह थी कि सप्ताह के सात दिनों के अलावा अकबर किसी दूसरे दिन घोड़ा देख सकते थे।

कोष्ठक में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।

(दयालु, दरबार, चित्रकार, बुद्धिमान, न्याय)

Question 1.
बेचारा …………. अपने घर लौट आया।
Answer:
चित्रकार

Question 2.
चित्रकार की पत्नी बहुत ……….. थी।
Answer:
बुद्धिमान

Question 3.
बादशाह अकबर बहुत ………. हैं।
Answer:
दयालु

Question 4.
तीन दिन बाद चित्रकार ………. में आया।
Answer:
दरबार

Question 5.
बीरबल के …………. से बादशाह अकबर बहुत खुश हुए।
Answer:
न्याय

निलिखित बाक्य सही है या गलत लिखिए।

Question 1.
सेठ बहुत गरीब था।
Answer:
गलत

Question 2.
सेठ बहुत ही कंजूस था।
Answer:
सही

Question 3.
सेठ ने चित्रकार से अपना चित्र बनवाया।
Answer:
सही

Question 4.
चित्रकार पैसे लेकर दरबार पहुंचा।
Answer:
गलत

Question 5.
बीरबल के न्याय से बादशाह बहुत खुश हुए।
Answer:
सही

निम्नलिखित प्रश्नों के दो-तीन वाक्यों में उत्तर लिखिए।

Question 1.
जब चित्रकार ने पैसे माँगे तो सेठ ने क्या कहा?
Answer:
जब चित्रकार ने पैसे माँगे तो सेठ ने कह दिया, “चित्र ठीक नहीं है, दोबारा बनाकर लाओ।”

Question 2.
कौन-सा देश विश्व में विख्यात होता है ?
Answer:
कला में निपुण कलाकारों की इज्जत जहाँ होती है, वह देश विश्व में विख्यात होता है।

Question 3.
बीरबल ने चित्रकार से क्या कहा?
Answer:
बीरबल ने चित्रकार से कहा कि तुम्हारे चित्रों में सचमुच बहुत कमियाँ हैं। तीन दिन बाद इस सेठ का हू-ब-हू चित्र बनाकर दरबार में ले आना। तुम्हें पैसे मिल जाएंगे।

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. प्रसिद्ध
2. विश्वास
3. प्रसन्न
4. बुद्धिमानी
5. दयालु
6. उपस्थित
7. इज्जत

Answer:

1. अप्रसिद्ध
2. अविश्वास
3. अप्रसन्न
4. मूर्खता
5. निर्दयी
6. अनुपस्थित
7. बेइज्जत

निम्नलिखित शब्दों के तीन-तीन पर्यायवाची शब्द लिखिए।

1. प्रसिद्ध
2. घोड़ा
3. चतुराई
4. पत्नी
5. प्रसन्न

Answer:

1. विख्यात, प्रख्यात, मशहूर
2. अश्व, हय, तुरग
3. कुशलता, योग्यता, होशियारी
4. भार्या, अर्धांगिनी, दारा
5. आनंद, उल्लास, मोद

कोष्ठक में से उचित क्रियाविशेषण शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।

(तुरंत, धीरे-धीरे, तेज़, अचानक, तत्काल)

Question 1.
बाहर हवा बहुत …………. चल रही है।
Answer:
तेज़

Question 2.
बादशाह घूमने के लिए ……………… तैयार हो गए।
Answer:
तत्काल

Question 3.
ताजे फल …………….. बिक गए।
Answer:
तुरंत

Question 4.
नल से पानी ………………. बह रहा है।
Answer:
धीरे-धीरे

Question 5.
सभी बैठे थे कि बिजली ……… चली गई।
Answer:
अचानक

पाठ से स्त्रीलिंग एकवचन और बहुवचन तथा पुल्लिंग एकवचन और बहुवचन शब्दों की सूची बनाकर वाक्य प्रयोग कीजिए।
Answer:

Hindi Sulabhbharati 7th Standard Digest Guide दूसरी इकाई

• अस्‍पताल Question Answer
• बेटी युग Question Answer
• दाे लघुकथाएँ Question Answer
• शब्द संपदा Question Answer
• बसंत गीत Question Answer
• चंदा मामा की जय Question Answer
• रहस्‍य Question Answer
• हम चलते सीना तान के Question Answer

Class 7 Hindi Chapter 2 Phool Aur Kaante Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 2 फूल और काँटे Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 2 Phool Aur Kaante Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 2 फूल और काँटे Textbook Questions and Answers

स्वयं अध्ययन:

दिए गए चित्रों से संबंधित सुनी हुई कोई कविता सुनाओ।

बताओ तो सही:

Answer:
फूल का नाम
गुलाब – गुलाब एक बहुवर्षीय, झाड़ीदार, कंटीला, पुष्पीय पौधा है। जिसमें कई रंग के सुंदर सुगंधित फूल लगते हैं। इसकी १०० से भी अधिक प्रजातियाँ अस्तित्व में हैं। गुलाब की अधिकतर जातियाँ एशियाई मूल की हैं। भारत सरकार ने १२ फरवरी को ‘गुलाब-दिवस’ के रूप में घोषित किया है। गुलाब का फूल अपनी कोमलता, सुंदरता व सुगंध के लिए विशेष प्रसिद्ध है।
गुलाब के उपयोग –

• गुलाब के फूल का उपयोग भगवान के चरणों में चढ़ाने के लिए करते हैं।
• गर्मियों में गुलाब के फूलों का रस चेहरे पर मलने से चेहरे पर ताजगी बनी रहती है।
• आँखों की जलन व खुजली दूर करने के लिए गुलाब के जल का उपयोग किया जाता है।
• गुलाब के घर में महकते रहने से घर का वातावरण पवित्र व शांत बना रहता है।
• गुलाब के फूल से शरबत व गुलकंद बनाई जाती है, जो सेहत के लिए अत्यंत फायदेमंद होती है।
• कान में दर्द होने पर गुलाब की पत्तियों का रस डालने से कान के दर्द से राहत मिलती है।
• गुलाब के फूलों से खुशबूदार इत्र बनाए जाते हैं।
• गुलाब की गंध – गुलाब का फूल खुशबू के लिए भी विशेष प्रसिद्ध है।
• इसकी हलकी, मधुर, भीनी व मोहक गंध सबके मन को आकर्षित करती है।
• भारतवर्ष में ऋतु के अनुसार गुलाब दो प्रकार के माने जाते हैं।

(१) सदागुलाब और (२) चैती गुलाब

सदागुलाब पूरे साल भर फूलता रहता है। चैती गुलाब केवल बसंत ऋतु में ही फूलता है। चैती गुलाब अपनी सुगंध के लिए विशेष प्रसिद्ध होता है। यही फूल अधिकतर इत्र और दवा बनाने के काम में लाया जाता है। ऐसा कहा जाता है कि गुलाब के इस का नूरजहाँ ने १६१२ इ.स. में अपने विवाह के अवसर पर उपयोग किया था। गुलाब का फूल अपनी गंध और औषधीय गुणों के कारण संसार में विशेष रूप से प्रसिद्ध है।

खोजबीन:

अपने आसपास के पेड़-पौधों के नामों का वर्गीकरण कीजिए।
Answer:

वाचन जगत से:

सदैव ध्यान में रखो:

प्रत्येक परिस्थिति का सामना हँसते हुए करना चाहिए।

कविता के आधार पर रिक्त स्थानों की पूर्ति कीजिए।

Question 1.
रात में उनपर …………..”चाँद भी.
एक ही-सी …………… है डालता।
Answer:
चमकता, चाँदनी

Question 2.
प्यार डूबी तितलियों के …………..” कतर,
भौर का वेध देता ………….” तन।
Answer:
पर, श्याम

Question 3.
……… काँटा किसी की उँगलियाँ,
फाड़ देता है किसी का वर ……….।
Answer:
छेदकर, वसन

Question 4.
निज सुगंध औ’ ……….. रंग से,
है सदा देता ……. जी की खिला।
Answer:
निराले, कली

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।

Question 1.
फूल किनको गोद में लेता है?
Answer:
फूल तितलियों को गोद में लेता है।

Question 2.
बड़प्पन की कसर रह जाने पर क्या काम नहीं देती?
Answer:
बड़प्पन की कसर रह जाने पर कुल की बड़ाई काम नहीं देती।

Question 3.
कौन एक-सा बरसता है?
Answer:
मेह (मेघ) एक-सा बरसता है।

Question 4.
फूल किसको रस पिलाता है?
Answer:
फूल भंवरो को रस पिलाता है।

Question 5.
काँटा किसका तन बेध देता है?
Answer:
काँटा भँवरे का तन बेध देता है।

Question 6.
भौरे का तन किस रंग का है?
Answer:
भँवरे का तन साँवले रंग का है।

भाषा की ओर

निम्नलिखित वर्षों से समानार्थी और विरुद्धार्थी शब्दों की जोड़ियाँ हूँढ़िए और अपने वाक्यों में प्रयोग कीजिए।

समानार्थी शब्दों का बाक्य में प्रयोग:

• पुष्प – बगीचे में पुष्प खिले हैं।
• फूल – भगवान के चरणों में पड़ा फूल पवित्र होता है।
• तन – सैनिक तन-मन से देश की रक्षा करता है।
• बदन – सैनिक का सारा बदन लहु-लूहान था।
• जल – जल ही जीवन है।
• पानी – पानी के बिना मनुष्य का जीवन सूना है।
• हवा – शाम के समय ठंडी हवा चलती है।
• पवन – चक्रवाती पवन बहुत तीव्र गति की होती है।

विरुद्धार्थी शब्दों का वाक्य में प्रयोग:

• रात x दिन – मोहन अपने भविष्य के लिए रात-दिन पढ़ाई करता है।
• छोटा x बड़ा- हमारे मन में छोटे-बड़े का भेदभाव नहीं होना चाहिए।
• मान x अपमान – राम मोहन को मान देता है किंतु मोहन ने उसका सबके सामने अपमान कर दिया।
• पावन x अपावन – आज के आधुनिक युग में भी कुछ लोग पावन विचारों के हैं, तो कुछ लोगों के आचरण बिलकुल अपावन हो चुके हैं।

विचार मंथन:

निम्नलिखित विषय पर अपने विचार लिखिए।

Answer:
भूल – उपर्युक्त पंक्ति के माध्यम से ‘भूल’ का अर्थ यह है कि मनुष्य को यह नहीं भूलना चाहिए कि उसका जन्म अच्छे कमों के लिए हुआ है, न कि बुरे कर्म करने के लिए। हमें हमेशा दूसरों के बारे में अच्छा सोचना चाहिए व उनकी मदद करनी चाहिए और यह नहीं भूलना चाहिए कि हमारा एक-दूसरे के साथ भाईचारे व मानवता का संबंध है। फूल – उपर्युक्त पंक्ति में ‘फूल’ का अर्थ यह है कि हमें अपने जीवन में अपने व्यवहार से फूल के समान लोगों के जीवन को महकाना चाहिए। दूसरों की मदद करके अपने व समाज के लोगों की जीवनरूपी बगिया को सुंदर बनाने का सतत प्रयास करना चाहिए। शूल – उपर्युक्त पंक्ति में ‘शूल’ का अर्थ यह है कि अपने कार्यों से दूसरों की राह में काँटों के समान रूकावट पैदा नहीं करनी चाहिए। ‘शूल’ यह शब्द शत्रुता व बुरे व्यक्ति के प्रतीक के रूप में इस पंक्ति में प्रयोग किया गया है।
हमें अपने जीवन में ‘फूल’ के समान एक अच्छा मनुष्य बनने का प्रयास करना चाहिए न कि ‘शूल’ के समान बुरा व्यक्ति। सम्मान हमेशा फूल’ को ही मिलता है ‘शूल’ को नहीं।

Hindi Sulabhbharti Class 7 Solutions Chapter 2 फूल और काँटे Additional Important Questions and Answers

निम्नलिखित शब्दों में से उचित शब्द चनकर रिक्त स्थानों की पूर्ति कीजिए।

(जगह, मेह, ढंग, पर, फूल, आँख)

Question 1.
फूल और काँटे दोनों का ………… भिन्न-भिन्न होता है।
Answer:
ढंग

Question 2.
काँटा तितलियों के . कतर देता है।
Answer:
पर

Question 3.
फूल और काँटे एक ही ……..’ जन्म लेते हैं।
Answer:
जगह

Question 4.
काँटा सबकी . .. में खटकता है।
Answer:
आँख

Question 5.
…………” उन पर एक समान बरसते हैं।
Answer:
मेह

Question 6.
………… अपनी सुगंध से सबको आकर्षित करता है।
Answer:
फूल

निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए।

Question 1.
रात में पौधों पर क्या चमकता है?
Answer: चाँद

Question 2.
काँटा किसमें छेद कर डालता है?
Answer:
उँगलियों में

Question 3.
निराले रंग किसके हैं?
Answer:
फूल के

Question 4.
भगवान के सिर पर कौन सजता है?
Answer:
पुष्प, फूल

कविता में आए लयात्मक शब्दों को ढूँडकर लिखिए।
उदाहरण: पिला – खिला
Answer:

• पालता – डालता
• बही – नहीं
• बसन – तन
• पर – कसर

निम्नलिखित बाक्य सही है या गलत लिखिए।

Question 1.
फूल वस्त्र को फाड़ देता है।
Answer:
गलत

Question 2.
फूल और काँटों का स्वभाव एक समान होता है।
Answer:
गलत

Question 3.
फूल की सुगंध से सबका मन प्रसन्न होता है।
Answer:
सही

Question 4.
फूल काँटों को अनूठा रस पिलाते हैं।
Answer:
गलत

Question 5.
कुल की बड़ाई से मनुष्य महान बनता है।
Answer:
गलत

Question 6.
मनुष्य स्वयं के गलत कार्यों से लोगों की आँखों में खटकता है।
Answer:
सही

निम्नलिखित प्रश्नों के उत्तर दो-तीन वाक्यों में लिखिए।

Question 1.
चाँद रात के समय प्रकृति का कौन-सा कार्य करता है?
Answer:
चाँद रात के समय सभी को ठंडक भरी शीतल छाया देने का कार्य करता है। वह सभी पर समान रूप से चाँदनी बिखेरने का प्राकृतिक कार्य करता है।

Question 2.
फूल और काँटों पर समान रूप से क्या बहती है?
Answer:
फूल और काँटों पर समान रूप से हवाएँ बहती हैं। हवा किसी भी प्रकार का भेदभाव न करते हुए इन्हें एक-सी हवा देती है।

Question 3.
काँटों द्वारा उँगलियों को छेदने व कपड़े को फाड़ने से काँटों की किस वृत्ति का पता चलता है?
Answer:
काँटों द्वारा उँगलियों को छेदने व कपड़े को फाड़ने से काँटों की दूसरों से घृणा करने, दूसरों का तिरस्कार करने तथा दूसरों को जान-बुझकर तकलीफ देने की वृत्ति का पता चलता है।

Question 4.
‘फूल और काँटे’ कविता के माध्यम से ‘फूल’ हमें क्या संदेश देना चाहता है?
Answer:
‘फूल और काँटे’ कविता के माध्यम से ‘फूल’ हमें यह संदेश देना चाहता है कि हमें दूसरों के साथ प्रेमपूर्वक व्यवहार करना चाहिए तथा अपने अच्छे कर्मों से सबके मन को प्रसन्न व आनंदित रखना चाहिए। हमें अपने कर्मों से श्रेष्ठ बनना चाहिए।

Question 5.
मनुष्य महान कब और कैसे बनता है?
Answer:
मनुष्य महान तब बनता है, जब वह अपना कार्य स्वार्थ हेतु न करते हुए परमार्थ और जगत कल्याण के लिए करता है। वह कुल का बड़प्पन न देखकर स्वयं के बलबूते पर महान बनने का प्रयास करता है। इसलिए कहा गया है ‘कर्मप्रधान विश्व रचि राखा।’ अर्थात परोपकार व योग्य कर्म से मनुष्य को महानता प्राप्त होती है।

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के बहुवचन रूप लिखिए।

1. पौधा
2. आँख
3. भँवरा
4. हवा
5. तितली
6. उँगली

Answer:

1. पौधे
2. आँखें
3. भौरे
4. हवाएँ
5. तितलियाँ
6. उँगलियाँ

निम्नलिखित संज्ञा शब्दों की उचित विशेषण के साथ जोड़ियाँ मिलाइए।

(१) संज्ञा व सर्वनाम की विशेषता बतानेवाले शब्दों को ‘विशेषण’ कहते हैं। जैसे – सीमा सुंदर है।
विशेषण के मुख्य चार भेद होते हैं : गुणवाचक विशेषण: जो शब्द संज्ञा या सर्वनाम के रंगरूप, गुण-दोष, आकार-प्रकार व स्वभाव का बोध कराते हैं, वे गुणवाचक विशेषण कहलाते हैं। जैसे – गुलाबी चादर,
सुंदर नक्काशी, मीठे बेर आदि।
(२) संख्यावाचक विशेषण: जिस शब्द से संज्ञा या सर्वनाम की निश्चित या अनिश्चित संख्या का बोध होता हो, उन्हें ‘संख्यावाचक विशेषण’ कहते हैं।
(३) परिणामवाचक विशेषणः जिन विशेषण शब्दों से परिणाम की निश्चितता या अनिश्चितता का बोध होता है, वे ‘परिणामवाचक विशेषण’ कहलाते हैं।
(४) सार्वनामिक या संकेतवाचक विशेषण: जो सर्वनाम शब्द संज्ञा शब्द से पहले आकर विशेषण का काम करता है, उसे ‘सार्वनामिक विशेषण’ कहते हैं।
जैसे-

Answer:
(१) – चमकता
(२) – बरसता
(३) – श्याम
(४) – अनूठा
(५) – निराले
(६) – सुरीला

निम्नलिखित शब्दों में उचित स्थान पर अनुस्वार व अनुनासिक चिह्न का प्रयोग कीजिए।

1. चादनी
2. ढग
3. हवाए
4. सुगध
5. भवरा
6. तितलिया
7. हस
8. नदिया

Answer:

1. चाँदनी
2. ढंग
3. हवाएँ
4. सुगंध
5. भंवरा
6. तितलियाँ
7. हंस
8. नदियाँ

Hindi Sulabhbharti Class 7 Solutions पहली इकाई

• वाचन मेला Question Answer
• फूल और काँटे Question Answer
• दादी माँ का परिवार Question Answer
• देहात और शहर Question Answer
• बंदर का धंधा Question Answer
• ‘पृथ्‍वी’ से ‘अग्‍नि’ तक Question Answer
• जहॉं चाह, वहाँ राह Question Answer
• जीवन नहीं मरा करता है Question Answer

Class 7 Hindi Chapter 6 Prithvi Se Agni Tak Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 6 ‘पृथ्‍वी’ से ‘अग्‍नि’ तक Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 6 Prithvi Se Agni Tak Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 6 ‘पृथ्‍वी’ से ‘अग्‍नि’ तक Textbook Questions and Answers

स्वयं अध्ययन:

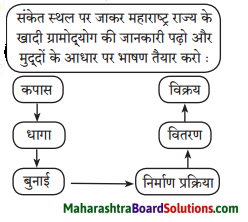
किसी महान विभूति क्रम जीवनक्रम वर्षानुसार बनाकर लाओ और पड़ो। जैसे: जन्म, शालेय शिक्षा आदि।

अंतरजाल के माध्यम से भारतीय वैज्ञानिकों और उनके कार्यों की सूची बनवाएँ।

डॉ. ए. पी. जे अब्दुल कलाम की जीवनी पढ़ने के लिए प्रेरित करें।

खोजबीन:

अंतरजाल से पद्मभूषण से विभूषित विभूतियों की जानकारी का संकलन करके सुनाओ।

सुनो तो जरा:

विज्ञान प्रदर्शनी के लिए बनाए गए उपकरण बनाने की विधि एवं उपयोग सुनो और सुनाओ।

जरा सोचो….. चर्चा करो:

“यदि मैं अंतरिक्ष यात्री बन जाऊँ तो…” विषय पर अपने विचार लिखिए। (कल्पनात्मक-लेखन)
Answer:
मेरे जीवन का एक सबसे बड़ा सपना है कि मैं एक अंतरिक्ष यात्री बने। अगर मैं अंतरिक्ष यात्री बन गया, तो मुझे स्वयं पर गर्व महसूस होगा क्योंकि यह मेरे जीवन का सबसे बड़ा लक्ष्य है। मैं भी आसमान में पक्षियों की भाँति उड़ जाऊँगा। ऊपर से हमारी सुंदर पृथ्वी का नजारा देखूगा। कई ग्रह, तारे, धूमकेतु इनका बारीकी से अवलोकन व अध्ययन करूँगा। कई प्रकार की नई बातें देश व देशवासियों के लिए खोज लाऊँगा। चंद्रमा के बारे में इसके पहले लोगों ने जो कथन किए हैं। मैं उनका प्रत्यक्ष अनुभव प्राप्त करूंगा। अपने यान से पृथ्वी, सूर्य, चंद्रमा और अन्य दूसरे दुर्लभ ग्रहों के चित्र संशोधन के लिए लूंगा। अपने अवलोकन व संशोधन से कई प्रकार का महत्त्वपूर्ण ज्ञान मैं देशवासियों और विश्व के लिए ले आऊँगा। मैं कुछ इस प्रकार के कारनामें करूँगा, जिससे विश्व में अपने देश का नाम ऊँचा हो। मैं सदैव एक सफल अंतरिक्ष यात्री बनकर लौटना चाहूँगा।

विचार मंथन:

“हम विज्ञान लोक के वासी’ विषय पर अपने विचार लिखिए। (विचारात्मक-लेखन)
Answer:
आज का युग विज्ञान का युग है। आज का कोई भी क्षेत्र विज्ञान से अछूता नहीं है। प्राचीन काल से असंभव समझे जानेवाले सभी कार्यों को विज्ञान ने संभव करके दिखाया है। छोटी सुई से लेकर आकाश की दूरी नापने वाले हवाई जहाज व रॉकेट इस विज्ञान की ही देन हैं। हम अपने प्रतिदिन के जीवन में विज्ञान निर्मित वस्तुओं का ही प्रयोग करते हैं। विद्युत की निर्मिती, कल-कारखाने, अंतरिक्ष की खोज, जीवन में बदलाव, आधुनिक खेती की सामग्री पूरा जीवन विज्ञान निर्मित वस्तुओं से घिरा हुआ है।

प्राचीन काल से हम कहते व सुनते आ रहे हैं कि मनुष्य “धरती का वासी है’, परंतु विज्ञान के इन चमत्कारों और मनुष्य द्वारा विज्ञान निर्मित वस्तुओं के उपयोग किए जाने पर हम अगर कहें कि ‘हम विज्ञान लोक के वासी’ हैं, तो यह गलत न होगा। विज्ञान ही है जिसने धरती के प्रत्येक असंभव कार्य को संभव करके दिखाया है। किंतु आज के इस आधुनिक युग में हमें इस बात का जरूर ध्यान रखना चाहिए कि विज्ञान से मनुष्य को कई हानियाँ भी हो रही हैं। इन सब बातों को ध्यान में रखते हुए हमें विज्ञान की तरक्की का उपयोग मानव जाति के भले के लिए ही करना चाहिए। तभी हम असल में ‘विज्ञान लोक के वासी’ कहलाएंगे।

मेरी कलम से:

निम्नलिखित संकेत बिंदुओं के आधार पर कहानी लिखिए। (कहानी-लेखन)

Answer:
शीर्षक बेगुसराय नाम का एक राज्य था। उस राज्य में विभूति नारायण नामक राजा राज्य करते थे। राजा बड़े ही कर्मठ, परोपकारी व न्यायी थे। उन्हें अपने दरबार के लिए एक ऐसे राजमंत्री की तलाश थी, जो परोपकारी व निस्वार्थी हो। एक दिन रामपुर नामक गाँव में एक मेला लगा। मेला देखने के लिए लोगों की भीड़ उमड़ पड़ी। राजा विभूतिनारायण ने अपने सैनिकों को बताया कि आज हम अपने राज्य के लिए राजमंत्री की खोज करेंगे। वे अपने सेवकों को सड़क के प्रवेशद्वार पर एक बड़ा-सा पत्थर रखवाने के लिए कहते हैं तथा वेश बदलकर स्वयं वहाँ खड़े हो जाते हैं। कई लोग उस रास्ते से जाते हैं। उस पत्थर से टकराते हैं, गिरते हैं, किंतु किसी ने भी उस पत्थर को उठाकर रास्ते से दूर नहीं किया। अजय नाम का एक लड़का बहुत रही थी।

कुछ देर बाद उससे न रहा गया। वह स्वयं उस बड़े भारी पत्थर के पास गया और पत्थर को ढंकेलकर रास्ते के किनारे से सरकाकर हटा दिया। राजा की नज़र इस लड़के पर पड़ी। राजा खुशी से प्रसन्न हो उठे। पर वे कुछ देर देखते रहे। अजय को उस पत्थर के नीचे एक चिट्ठी मिली। उसमें लिखा था “आज से तुम इस राज्य के राजमंत्री हो।” इतने में राजा विभूतिनारायण उसके समीप आए और उससे कहा कि “मैं तुम्हारी परोपकारी भावना व निस्वार्थ सेवा बृत्ति से प्रसन्न हूँ। आज से मैं तुम्हें इस राज्य का राजमंत्री घोषित करता हूँ।” अजय के लिए यही सबसे बड़ा पुरस्कार था। राजा ने अपनी ओर से हजार सुवर्ण मुद्राएँ देकर उसे सम्मानित किया और अपने दरबार में राजमंत्री का पद प्रदान किया।

सीख – इस कहानी से हमें यह सीख मिलती है कि हमें किसी भी कार्य को छोटा या बड़ा नहीं समझना चाहिए बल्कि परोपकारी भावना से प्रत्येक सामाजिक कार्य को हमें करना चाहिए। जो समाज व जनता के हित में हों।

शीर्षक – “जनसेवा ही सच्ची ईश्वर सेवा है।” अथवा
“कर भला तो हो भला।”

बताओ तो सही

वाचन जगत से :

गणतंत्र दिवस पर सम्मनित बच्चों के बहादुरी के प्रसंग पढ़ो और पसंदीदा किसी एक का वर्णन करो।

अध्ययन कौशल:

अपना दैनिक नियोजन बताओ तथा उसपर अमल करो।

सदैव ध्यान में रखो:

दैनिक जीवन में विज्ञान का उपयोग करना श्रेयस्कर होता है।

सही विकल्प चुनकर वाक्य फिर से लिखो:

(श्रीहरिकोटा, सेकंड्स, वैज्ञानिक, स्थगित, रॉकेट, चक्रवात, शोर, महानतम)

Question 1.
‘अग्नि’ टीम में पाँच सौ से अधिक …………” थे।
Answer:
अग्नि’ टीम में पाँच सौ से अधिक वैज्ञानिक थे।

Question 2.
‘पृथ्वी’ प्रक्षेपण के लिए ………….” अंतरिक्ष केंद्र में विशेष सुविधाएँ स्थापित की।
Answer:
‘पृथ्वी’ प्रक्षेपण के लिए श्रीहरिकोटा अंतरिक्ष केंद्र में विशेष सुविधाएँ स्थापित की।

Question 3.
यह मेरे जीवन के ………. क्षणों में से एक था।
Answer:
यह मेरे जीवन के महानतम क्षणों में से एक था।

Question 4.
सिर्फ छह सौ ………की भव्य उड़ान ने हमारी सारी
Answer:
सिर्फ छह सौ सेकंड्स की भव्य उड़ान ने हमारी सारी

Question 5.
थकान को एक पल में धो डाला। हमें प्रक्षेपण ……….करना पड़ा।
Answer:
थकान को एक पल में धो डाला। हमें प्रक्षेपण स्थगित करना पड़ा।

Question 6.
एक ………. का खतरा मँडरा रहा था।
Answer:
एक चक्रवात का खतरा मँडरा रहा था।

Question 7.
……… विज्ञान के क्षेत्र में इस तरह की चीजें बहुत आम
Answer:
रॉकेट विज्ञान के क्षेत्र में इस तरह की चीजें बहुत आम

Question 8.
ज्वार के कारण लहरें किनारों से टकराकर और अधिक ………….. मचा रही थीं।
Answer:
ज्वार के कारण लहरें किनारों से टकराकर और अधिक शोर मचा रही थीं।

तीन-चार वाक्यों में उत्तर लिखो:

Question 1.
भारत को चुनिंदा राष्ट्रों के समूह में किसने पहुँचा दिया?
Answer:
भारत को सामर्थ्यशील नागरिक अंतरिक्ष उद्योग और व्यवहार्य मिसाइल आधारित सुरक्षा प्रणालियों ने चुनिंदा राष्ट्रों के समूह में पहुंचा दिया।

Question 2.
टीम के साथ डॉ. कलाम ने कौन-सा अनुभव बाँटा?
Answer:
अपनी टीम के साथ डॉ. कलाम ने यह अनुभव बाँटा कि मेरा प्रक्षेपणयान तो गिरकर समुद्र में खो गया था, लेकिन उसकी वापसी सफलता के साथ हुई। आपकी मिसाइल तो अभी तक आपके सामने है। वास्तव में आपने कुछ भी ऐसा नहीं खोया है, जिसे एक-दो हफ्तों के काम से सुधारा न जा सके।

Question 3.
‘अग्नि’ का प्रक्षेपण पहले स्थगित क्यों करना पड़ा?
Answer:
कंप्यूटर द्वारा उपकरण ठीक ढंग से काम न करने के निर्देश तथा निचली रेंज केंद्र द्वारा ‘होल्ड’ करने के संकेत प्राप्त होने के कारण ‘अग्नि’ का प्रक्षेपण पहले स्थगित करना पड़ा।

Question 4.
रक्षामंत्री ने डॉ. कलाम जी से कब और क्या पूछा था?
Answer:
रक्षामंत्री महोदय ने डॉ. कलाम से ‘अग्नि’ के प्रक्षेपण करने की पहली रात पूछा, “अग्नि की कामयाबी का जश्न मनाने के लिए तुम मुझसे क्या उपहार चाहोगे?”

भाषा की ओर:

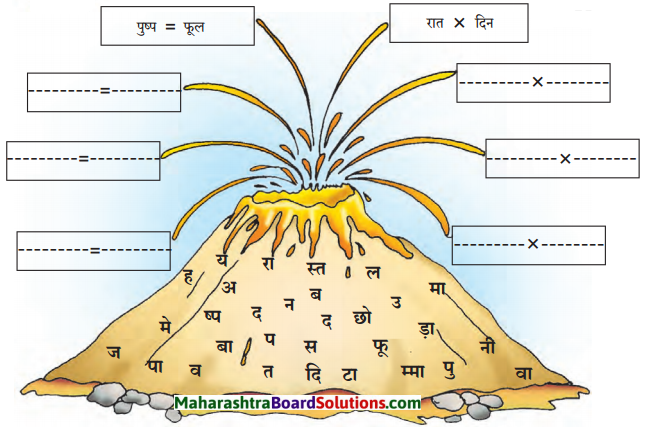
दाएँ पंख में उपसर्ग तथा बाएँ पंख में प्रत्यय लगाकर शब्द लिखो तथा उनके वाक्य बनाओ।

निम्नलिखित शब्दों में उपसर्ग व प्रत्यय लगाकर नए शब्द का निर्माण कीजिए तथा उनका वाक्य में प्रयोग कीजिए।
उपसर्ग (pefix): वे शब्दांश जो किसी शब्द के आगे लगकर उसके अर्थ में परिवर्तन लाते हैं तथा नया शब्द बनाते हैं उन्हें ‘उपसर्ग’ कहते है। जैसे – धन + वान = धनवान, मानव + ता = मानवता आदि।
प्रत्यय: वे शब्दांश जो किसी शब्द के पीछे जुड़कर उसके अर्थ को विशिष्ट बनाते हैं, उसे प्रत्यय (suffix) कहा जाता है।
जैसे = आवश्यक + ता = आवश्यकता

(१) दिन
उपसर्ग – प्रतिदिन प्रत्यय – दिनभर
Answer:
मैं प्रतिदिन खेलता हूँ।
दिनभर नहीं खेलना चाहिए।

(२) नम्र
उपसर्ग – विनम्र प्रत्यय – नम्रता
Answer:
सुनिल विनम्र लड़का है।
हमें सभी के साथ नम्रता से व्यवहार करना चाहिए।

(३) डर
उपसर्ग – निडर प्रत्यय – डरपोक
Answer:
मेरे पिताजी बड़े निडर है।
मोहन बड़ा डरपोक है।

(४) जल
उपसर्ग – निर्जल प्रत्यय – जलमय
Answer:
मेरी माँ निर्जल व्रत करती है।
पूरा तालाब जलमय है।

(५) साहस
उपसर्ग – दु:साहस प्रत्यय – साहसिक
उत्तरः
रावण के सभी कार्य दु:साहस से भरे थे।
राजन ने बड़ा साहसिक कार्य किया।

(६) सत्य
उपसर्ग – असत्य प्रत्यय – सत्यवादी
उत्तर :
गांधी जी कभी असत्य नहीं बोलते थे।
राजा हरिश्चंद्र बड़े सत्यवादी थे।

Hindi Sulabhbharti Class 7 Solutions Chapter 6 ‘पृथ्‍वी’ से ‘अग्‍नि’ तक Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।

Question 1.
देश के रॉकेट विज्ञान के इतिहास में कौन-सी युगांतरकारी घटना हुई।
Answer:
‘पृथ्वी’ उपग्रह को अंतरिक्ष में छोड़ना देश के रॉकेट विज्ञान के इतिहास में युगांतरकारी घटना हुई।

Question 2.
‘अग्नि’ टीम में कुल कितने वैज्ञानिक काम करते थे?
Answer:
‘अग्नि’ टीम में कुल पाँच सौ वैज्ञानिक काम करते थे।

Question 3.
डॉ. कलाम ने अपने टीम के सदस्यों को किस हालत में पाया?
Answer:
डॉ. कलाम ने अपने टीम के सदस्यों को सदमे और शोक की हालत में पाया।

Question 4.
प्रक्षेपणयान कहाँ खो गया था?
Answer:
प्रक्षेपणयान समुद्र में गिरकर कहीं खो गया था।

Question 5.
डॉ. कलाम व उनकी टीम को कौन-सा महान अवसर दिया गया था?
Answer:
डॉ. कलाम व उनकी टीम को ‘अग्नि’ जैसी प्रणाली विकसित करने का अवसर दिया गया था।

Question 6.
अंत में प्रक्षेपण कब निर्धारित किया गया?
Answer:
अंत में प्रक्षेपण बाईस मई उन्नीस सौ नवासी (२२ मई, १९८९) को निर्धारित किया गया।

Question 7.
रक्षामंत्री ने डॉ. कलाम से क्या पूछा?
Answer:
रक्षामंत्री ने डॉ. कलाम से यह पूछा कि “कलाम! कल ‘अग्नि’ की कामयाबी का जश्न मनाने के लिए तुम मुझसे क्या उपहार चाहोगे?”

Question 8.
डॉ. कलाम ने अपने उपहार के बदले में किस चीज़ की माँग की?
Answer:
डॉ. कलाम ने अपने उपहार के बदले में आर.सी.आई. में लगाने के लिए एक लाख पौधों की मांग की।

Question 9.
अगले दिन कितने बजे ‘अग्नि’ मिसाइल प्रज्वलित हो उठी?
Answer:
अगले दिन सुबह सात बजकर दस मिनट पर ‘अग्नि’ मिसाइल प्रज्वलित हो उठी।

Question 10.
डॉ. कलाम और उनके सदस्यों की थकान को किसने धो डाला?
Answer:
डॉ. कलाम और उनके सदस्यों की थकान को ‘अग्नि’ की सिर्फ छह सौ सेकंड्स की भव्य उड़ान ने धो डाला।

निम्नलिखित वाक्य सही है या गलत लिखिए।

Question 1.
डॉ. कलाम ने रक्षामंत्री से दस लाख रूपये की मांग की।
Answer:
गलत

Question 2.
‘अग्नि’ की उड़ान के लिए छह सौ सेकंड्स का समय लगा।
Answer:
सही

Question 3.
‘पृथ्वी’ उपग्रह २९ फरवरी १९२७ को छोड़ा गया।
Answer:
गलत

Question 4.
‘अग्नि’ का प्रक्षेपण ठीक ढंग से न होने पर डॉ. कलाम जी के टीम के सदस्य बहुत खुश हुए।
Answer:
गलत

Question 5.
समस्याओं को हमें हराने का मौका उन्हें नहीं देना चाहिए।
Answer:
सही

Question 6.
ज्वार के कारण लहरें शोर मचा रही थीं।
Answer:
सही

Question 7.
‘अग्नि’ की सफल उड़ान डॉ. कलाम के जीवन का एक महान क्षण था।
Answer:
सही

Question 8.
श्री हरिकोटा हमारे देश का एक प्रसिद्ध अंतरिक्ष केंद्र है।
Answer:
सही

डॉ. कलाम ने आर.डी.एल – आर.सी.आई परिवार के सदस्यों को संबोधित करते हुए क्या कहा?
Answer:
डॉ. कलाम ने आर.डी.एल व आर.सी.आई परिवार के सदस्यों को संबोधित करते हुए यह कहा कि स्वाभाविक रूप से बड़े अवसर अपने साथ बराबर की चुनौतियाँ लेकर आते हैं। हमें हिम्मत नहीं हारनी चाहिए, समस्याओं को हमें हराने का मौका नहीं देना चाहिए।

निम्नलिखित शब्दों का वाक्य में प्रयोग कीजिए।

Question 1.
उपग्रह
Answer:
हमारे देश ने आज तक कई उपग्रह अंतरिक्ष में भेजे हैं।

Question 2.
आत्मनिर्भर
Answer:
मनुष्य को हमेशा आत्मनिर्भर बनने का प्रयास करना चाहिए।

Question 3.
सदमा
Answer:
पिता के मृत्यु की खबर सुनकर मोहन को बड़ा सदमा पहुंचा।

Question 4.
हिम्मत
Answer:
मुसीबत के समय हमें अपनी हिम्मत नहीं हारनी चाहिए।

Question 5.
पूर्णिमा
Answer:
पूर्णिमा के दिन चाँद पूरा होता है।

Question 6.
प्रज्वलित
Answer:
साहित्यिक कार्यक्रम के पहले अतिथियों के हाथों से दीप प्रज्वलित किया गया।

Question 7.
नतीजा
Answer:
संजय की मेहनत का उसे शानदार नतीजा प्राप्त हुआ।

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों का विलोम शब्द लिखिए।

1. एक
2. कम
3. देश
4. भीतर
5. विशाल
6. दिन
7. सफलता
8. पूर्णिमा

Answer:

1. अनेक
2. ज्यादा
3. विदेश
4. बाहर
5. लघु
6. रात
7. असफलता
8. अमावस्या

निम्नलिखित संज्ञा शब्दों से विशेषण शब्दों की रचना कीजिए।

1. विज्ञान
2. इतिहास
3. संसार
4. व्यवहार
5. दिन
6. जोश
7. राष्ट्र
8. स्वभाव
9. भारत

Answer:

1. वैज्ञानिक
2. ऐतिहासिक
3. सांसारिक
4. व्यावहारिक
5. दैनिक
6. जोशीला
7. राष्ट्रीय
8. स्वाभाविक
9. भारतीय

निम्नलिखित शब्दों के समान अर्थवाले शब्द लिखिए।

1. समुद्र
2. रात
3. अवधि
4. विज्ञान
5. अवसर
6. अग्नि
7. मौसम
8. सवाल
9. नींद

Answer:

1. सागर
2. निशा
3. समय
4. शास्त्र
5. मौका
6. आग
7. ऋतु
8. प्रश्न
9. निद्रा

निम्नलिखित शब्दों का शुद्ध रूप लिखिए।

1. पृथवी
2. स्वदयेशी
3. सनगठन
4. सुरकक्षा
5. समुदर
6. परीवार
7. समबोधन
8. परिक्षा

Answer:

1. पृथ्वी
2. स्वदेशी
3. संगठन
4. सुरक्षा
5. समुद्र
6. परिवार
7. संबोधन
8. परीक्षा

पाठ में आए दस अनुस्वार व अनुनासिक शब्दों को ढूंढकर लिखिए।
Answer:
अनुस्वार – अंतरिम, संगठन, अंतरिक्ष, तुरंत, सेकंडों, केंद्र, संस्थान, लोगों, संचार, दिमागों, सुंदर, लंबी, रक्षामंत्री, श्रृंखला, सेकंड्स, क्षणों। अनुनासिक – पाँच, यहाँ, बाधाएँ, मैंडरा, आँकड़े, बाँटा, जाँच, चुनौतियाँ, बनाएँ, सुविधाएँ, दाँव, गतिविधियाँ।।

पाठ में आए सर्वनाम शब्दों को पहचानकर उनका भेद लिखिए तथा अपने वाक्यों में प्रयोग कीजिए।

Question 1.
मेरा (पुरुषवाचक सर्वनाम) (उत्तम पुरुष)
Answer:
मेरा प्रक्षेपणयान तो समुद्र में गिरकर कहीं खो गया था।

Question 2.
यह (निश्चयवाचक सर्वनाम)
Answer:
यह देश के रॉकेट विज्ञान के इतिहास में युगातरकारी घटना थी।

Question 3.
कुछ (अनिश्चयवाचक सर्वनाम)
Answer:
आने वाले कुछ पलों में जगह-जगह रूकने की जरूरत पड़ी।

क्या (प्रश्नवाचक)
Answer:
रक्षामंत्री ने कलाम से कहा, “तुम मुझसे क्या उपहार चाहोगे?”

Question 5.
जिस – उसी (संबंधवाचक सर्वनाम)
Answer:
जिस समय हम टी-१४ सेकंड पर थे, उसी समय कंप्यूटर ने संकेत दिया।

Question 6.
कोई (अनिश्चवाचक सर्वनाम)
Answer:
हमें संकेत मिला कि उपकरणों में से कोई एक ठीक काम नहीं कर रहा है।

Question 7.
हम (पुरुषवाचक सर्वनाम) (उत्तम पुरुष)
Answer:
हम पाँच साल की कड़ी मेहनत के बाद सफल हुए।

Hindi Sulabhbharti Class 7 Solutions पहली इकाई

• वाचन मेला Question Answer
• फूल और काँटे Question Answer
• दादी माँ का परिवार Question Answer
• देहात और शहर Question Answer
• बंदर का धंधा Question Answer
• ‘पृथ्‍वी’ से ‘अग्‍नि’ तक Question Answer
• जहॉं चाह, वहाँ राह Question Answer
• जीवन नहीं मरा करता है Question Answer

Class 7 Hindi Chapter 2 Beti Yug Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 2 बेटी युग Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 2 Beti Yug Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 2 बेटी युग Textbook Questions and Answers

जरा सोचो ….. लिखो

‘तुम्हें रुपयों से भरा बटुआ मिल जाए तो…’ इस विषय पर अपने विचार लिखिए। (कल्पनात्मक-लेखन)
Answer:
यदि मुझे रुपयों से भरा बटुआ मिल जाए तो सबसे पहले मैं यह जानना चाहूँगा कि वह बटुआ किसका है? यदि उस बटुए में उसके मालिक के बारे में कोई जानकारी मिल गई, तो मैं उस व्यक्ति को सूचित करूंगा। उसे विश्वास दिलाऊँगा कि आपका बटुआ मुझे मिला है और मैंने उसे संभाल कर रखा है। आप आकर अपनी अमानत ले जाइए। यदि बटुए में उसके मालिक के बारे में कोई जानकारी नहीं मिली, तो अपने विद्यालय के शिक्षकों को दूंगा। उनसे निवेदन करूंगा कि यह बटुआ मुझे मिला है आप इसके मालिक को इसे सुपुर्द करने की कृपा करें; क्योंकि जिसका बटुआ गायब हुआ होगा वह परेशान होगा।

स्वयं अध्ययन

Answer:
स्वयं: यदि स्त्री शिक्षित होगी, तो उसका जीवन स्तर अच्छा रहेगा। वह आत्मनिर्भर बनेगी। समाज में उसका सम्मान होगा। वह अपने देश और समाज के लिए अपना योगदान देने में समर्थ होगी। परिवार – यदि स्त्री शिक्षित होगी, तो वह अपने परिवार को भी शिक्षित बना सकती है। अपने परिवार को सही दिशा दिखा सकती है। अपने परिवार की आर्थिक मदद कर सकती है। सामाजिक कुरीतियों से बचा सकती है।
समाज – अक्सर देखा जाता है कि महिलाएँ तरह-तरह के अंधविश्वास एवं सामाजिक बुराइयों का शिकार हो जाती हैं। यदि स्त्री शिक्षित होगी, तो समाज में जागरूकता लाकर सामाजिक उत्थान कर सकती है। देश – यदि स्त्री शिक्षित होगी, तो देश में विकास की क्रांति आ सकती है। कहा जाता है कि देश पढ़ेगा तो देश आगे बढ़ेगा। शिक्षित स्वी देश में व्याप्त बुराइयों को दूर कर प्रगति पथ पर अग्रसर हो सकती है।

विचार मंथन

‘बेटी बचाओ, बेटी पढ़ाओ।’ विषय पर एक अनुच्छेद लिखिए। (अनुच्छेद-लेखन)
Answer:
हमारे देश में कालांतर से ही बेटा-बेटी में अंतर किया जाने लगा था। परिणाम यह हुआ कि लोग बेटी को विद्यालय ही नहीं भेजते थे। कुछ लोग उसे गर्भ में ही मार डालते थे। यह एक सामाजिक बुराई बन चुकी थी। इस बुराई को समाप्त करने के लिए प्रधानमंत्री नरेंद्र मोदी ने देश को एक नारा दिया। ‘बेटी बचाओ, बेटी पढ़ाओ।’ सरकार के प्रयास से लोगों में जारूकता आयी और सबने इस बात को स्वीकार किया कि हम बेटी को बचाएंगे और उसे पढ़ाएंगे भी। देश तभी आगे बढ़ेगा; जब बेटा-बेटी दोनों एक समान पढ़ेंगे। उनमें कोई भेद-भाव नहीं होगा। सर्वत्र समानता की लहर लहराएगी।

अध्ययन कौशल:

अपने विद्यालय के पाँचवीं से आठवीं तक कक्षाओं में पढ़ रहे छात्रों और छात्राओं की संख्या संयुक्त स्तंभालेख द्वारा दर्शाओ।

चर्चा करो:

‘लड़का – लड़की एक समान’ विषय पर चर्चा करो।

वाचन जगत से:

पुण्यश्लोक अहिल्याबाई होळकर के कार्य पढ़ो और प्रमुख मुद्दे बताओ।

सुनो तो जरा :

त्योहार मनाने के उद्देश्य की वैज्ञानिकता सुनो और सुनाओ।

कविता की पंक्तियाँ पूरी कीजिए।

Question 1.
बेटी युग में …………..
…………………………
…………………………गढेंगे।
Answer:
बेटी युग सम्मान पर्व है,
पुण्य पर्व है, ज्ञान पर्व है।
सब सबका सम्मान करें तो,
जन-जन का उत्थान पर्व है।

Question 2.
बेटी युग …………………..
…………………………….
………………………उत्थान पर्व है।
Answer:
बेटी युग में बेटा-बेटी,
सभी पढ़ेंगे, सभी बढ़ेंगे।
फौलादी ले नेक इरादे,
खुद अपना इतिहास गढ़ेंगे।

जानकारी लिखिए।

Question 1.
बेटी पर्व:
Answer:
भारत की संस्कृति उत्सव संस्कृति के रूप में जानी जाती है। यहाँ देवता ही नहीं प्रकृति की भी पूजा की जाती है। प्राचीन काल से यहाँ बेटियाँ लक्ष्मी, सरस्वती, सौता और सावित्री के रूप में पूजी जाती हैं। नवरात्र में तो कन्या पूजन का विशेष महत्त्व है। आधुनिक युग में इसमें कुछ कमी आई है जिसे शिक्षा द्वारा दूर करने के लिए सरकार प्रयास कर रही है। बेटी के जन्म पर उत्सव मनाकर, उसे पढ़ाकर हम बेटी पर्व मना सकते हैं और नए भारत के निर्माण में अपना योगदान दे सकते हैं।

Question 2.
शिक्षामय विश्व:
Answer:
‘शिक्षा’ शब्द संस्कृत भाषा के ‘शिक्ष्’ धातु से बना है जिसका अर्थ है – सिखना। मनुष्य जन्म से मृत्यु पर्यंत कुछन-कुछ सीखता रहता है। यह प्रक्रिया विश्वव्यापी है। दुनिया में कहीं भी जाएँ शिक्षा का महत्त्व सर्वोपरि है। कहा जाता है कि शिक्षा ही ऐसी वस्तु है; जिसे न तो चोर चुरा सकता है, न ही यह किसी को बाँटी जा सकती है, न ही राजा द्वारा छीनी जा सकती है और न ही भार लगने वाली है। इसे जितना खर्च किया जाए, उतनी ही बढ़ती है। इसके द्वारा दुनिया में प्रत्येक स्थान पर सम्मान प्राप्त किया जा सकता है। कहा गया है “स्वदेशे पूज्यते राजा, विद्वान सर्वत्र पूज्यते।”

Question 3.
‘लड़का-लड़की एक समान’ विषय पर आठ से दस वाक्य लिखिए।
Answer:
लड़का-लड़की आज के आधुनिक युग में एक समान हैं। जो कार्य एक लड़का करता है; उसे लड़की भी कर सकती है। आजकल लड़कियाँ सभी क्षेत्रों में लड़कों की बराबरी कर रही हैं। शिक्षा का क्षेत्र हो या उद्योग, राजनीति हो या प्रशासनिक कार्य लड़कियों ने दिखा दिया है कि वह लड़कों से कम नहीं हैं। आज लड़कियाँ पायलट बन कर हवाई जहाज उड़ा रही हैं। कल्पना चावला जैसी लड़कियाँ अंतरिक्ष की सैर कर रही हैं। यही नहीं वह राष्ट्रपति और प्रधानमंत्री बनकर देश का नेतृत्व कर रही हैं। आज की लड़की सबला बन गई है। आवश्यकता है कि उन्हें शिक्षा के द्वारा और सशक्त बनाया जाए।

भाषा की ओर

निम्नलिखित शब्दों के युग्म शब्द बताओ और वाक्यों में उचित शब्दयुग्म लिखो :

1. गाँव ……….
2. …. उधर
3. घूमना ………
4. धन ……….
5. …… पहचान
6. कूड़ा ………
7. ……….. फूल
8. घर …….

Answer:

1. गाँव
2. इधर
3. फिरना
4. दौलत
5. जान
6. करकट
7. फल
8. घर

Answer:
(१) धन – दौलत
(२) घूमना – फिरना
(३) घर – घर
(४) गाँव – गाँव
(५) फल – फूल
(६) कूड़ा – करकट
(७) जान – पहचान
(८) इधर – उधर

Hindi Sulabhbharti Class 7 Solutions Chapter 2 बेटी युग Additional Important Questions and Answers

निम्नलिखित प्रश्नों के एक शब्द में उत्तर लिखिए।

Question 1.
आज किसका युग है?
Answer:
बेटी का

Question 2.
किसकी कहानी सबको सुहानी लगती है?
Answer:
नानी की

Question 3.
अब कैसी जवानी दौड़ेगी?
Answer:
तरुण

Question 4.
सारे जग को कैसा करना है?
Answer:
शिक्षामय

Question 5.
सबके आँगन तक किसकी धारा पहुँचेगी?
Answer:
ज्ञानगंगा की

निम्नलिखित प्रश्नों के एक वाक्य में उत्तर लिखिए।

Question 1.
बेटी युग में कौन-कौन पढ़ेंगे?
Answer:
बेटी युग में बेटा-बेटी सभी पढ़ेंगे।

Question 2.
शिक्षा पूरी कब होगी?
Answer:
बेटा-बेटी जब दोनों शिक्षित होंगे, तब शिक्षा पूरी होगी।

Question 3.
अब कोई कैसा नहीं होगा?
Answer:
अब कोई अनपढ़ नहीं होगा।

Question 4.
बेटी युग किसका पर्व है?
Answer:
बेटी युग सम्मान, पुण्य और ज्ञान का पर्व है।

Question 5.
जन-जन का उत्थान पर्व कब होगा?
Answer:
जब सभी सबका सम्मान करेंगे, तब जन-जन का उत्थान पर्व होगा।

उचित जोड़ियाँ मिलाइए।

Answer:
१ – ग
२ – च
३ -घ
४ – ङ
५ – ख
६ – क

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए।

1. बेटा
2. बेटी
3. पर्व
4. अनपढ़
5. पुस्तक
6. कलम
7. समीक्षा
8. देश

Answer:

1. पुत्र
2. पुत्री
3. त्योहार
4. अशिक्षित
5. किताब
6. लेखनी
7. आलोचना
8. राष्ट्र

निम्नलिखित शब्दों के बहुवचन रूप लिखिए।

1. कहानी
2. इरादा
3. बढ़ेगा
4. पढ़ेगा
5. गढ़ेगा
6. बेटी
7. बेटा
8. चिड़िया

Answer:

1. कहानियाँ
2. इरादे
3. बढ़ेंगे
4. पढ़ेंगे
5. गढ़ेंगे
6. बेटियाँ
7. बेटे
8. चिड़ियाँ

निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए।

1. शिक्षा
2. आधी
3. जवानी
4. नई
5. शिक्षित
6. आना
7. तरुण

Answer:

1. अशिक्षा
2. पूरी
3. बुढ़ापा
4. पुरानी
5. अशिक्षित
6. जाना
7. वृद्ध

निम्नलिखित शब्दों के दो पर्यायवाची शब्द लिखिए।

1. पावन
2. हाथ
3. जग
4. गंगा
5. बेटा
6. बेटी
7. हवा
8. पावन

Answer:

1. पवित्र, शुचि, पुनीत
2. कर, हस्त, पाणि
3. संसार, विश्व, भव
4. सुरसरि, भागीरथी, देवनदी
5. सुत, आत्मज, नंदन
6. सुता, आत्मजा, पुत्री
7. मरुत्, वात, समीर
8. पवित्र, शुद्ध, पाक

Hindi Sulabhbharati 7th Standard Digest Guide दूसरी इकाई

• अस्‍पताल Question Answer
• बेटी युग Question Answer
• दाे लघुकथाएँ Question Answer
• शब्द संपदा Question Answer
• बसंत गीत Question Answer
• चंदा मामा की जय Question Answer
• रहस्‍य Question Answer
• हम चलते सीना तान के Question Answer

Class 7 Hindi Chapter 5 Bandar Ka Dhandha Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 5 बंदर का धंधा Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 5 Bandar Ka Dhandha Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 5 बंदर का धंधा Additional Important Questions and Answers

सही शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।

(कुरसी-मेज़, बूटी, जंगल, छू-मंतर, बुखार)

Question 1.
बंदर जड़ी-बूटियाँ ………. से लाता था।
Answer:
जंगल

Question 2.
बंदर ने पेड़ के नीचे …….. डाला।
Answer:
कुरसी-मेज़

Question 3.
पीपल की जड़ व तुलसी के पत्ते पानी में उबालकर पीने से खाँसी …………. हो जाती है।
Answer:
छू-मंतर

Question 4.
लोमड़ी सुंदर बनने की ……. चाहती थी।
Answer:
बूटी

Question 5.
बिल्ली को एक सौ चार ……आया था।
Answer:
बुखार

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।

Question 1.
भालू को क्या हो गया था?
Answer:
भालू को खाँसी और जुकाम हो गया था।

Question 2.
बिल्ली कहाँ जाना चाहती थी?
Answer:
बिल्ली शिकार पर जाना चाहती थी।

Question 3.
डॉ. बंदर ने बिल्ली को कौन-सा रस पीने के लिए कहा?
Answer:
डॉ. बंदर ने बिल्ली को गिलोय का रस पीने के लिए कहा।

Question 4.
लोमड़ी कैसी दिखना चाहती थी?
Answer:
लोमड़ी सबसे सुंदर दिखना चाहती थी।

Question 5.
घी कुँवार दो बार लगाने से लोमड़ी का चेहरा किसके समान चमकेगा?
Answer:
घी कुँवार दो बार लगाने से लोमड़ी का चेहरा कुंदन (सोने) के समान चमकेगा।

Question 6.
बंदर अभी मौज़ क्यों मनाने लगा था?
Answer:
बंदर अभी मौज़ इसलिए मनाने लगा था क्योंकि डॉक्टर बनने के बाद उसका धंधा चलने लगा था।

कविता में आए शब्द युग्मों को चुनकर लिखिए।

1. टूटा
2. कुरसी
3. सुबह
4. चिकना
5. अच्छी
6. जड़ी

Answer:

1. फूटा
2. मेज़
3. शाम
4. सुंदर
5. अच्छी
6. बूटियाँ

कविता में आए लयात्मक शब्द चनकर लिखिए।

1. जुकाम
2. बुखार
3. पीना
4. बनाओ
5. लगाओ
6. मनाता

Answer:

1. थाम
2. उतार
3. डीना, मीना, ईना
4. लाओ
5. दे जाओ
6. लाता

कविता के आधार पर उचित जोड़ियाँ मिलाइए।

Answer:
१ – ख
२ – ग
३ – घ
४ – क

निम्नलिखित पंक्तियों को कविता के आधार पर पूर्ण कीजिए।

Question 1.
झट बंदर ने पेड़ के नीचे,
………………………..ला डाला।
Answer:
कुरसी-मेज

Question 2.
…………………..”पर कैसे जाऊँ,
जल्दी इसे उतार।
Answer:
मैं शिकार

Question 3.
कल से ही तुम …………..
ईना, मीना, डीना।
Answer:
डांस करोगी

Question 4.
चमकेगा कुंदन-सा चेहरा,
…………जाओ।
Answer:
फीस मुझे दे

Question 5.
……………….” जड़ी-बूटियाँ,
जंगल से वह लाता।
Answer:
अच्छी-अच्छी

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों का बहुवचन लिखिए।

1. पत्ता
2. कुरसी
3. बिल्ली
4. बूटी
5. मेज़
6. एक

Answer:

1. पत्ते
2. कुरसियाँ
3. बिल्लियाँ
4. बूटियाँ
5. मेजें
6. अनेक

निम्नलिखित शब्दों के समान अर्थवाले शब्द लिखिए।

1. हाथ
2. जड़
3. बंदर
4. जंगल
5. सुबह
6. शाम

Answer:

1. हस्त, कर
2. मूल
3. कपि, मर्कट
4. वन, कानन
5. प्रातः, भोर
6. संध्या

लेखन विभाग

निम्नलिखित प्रश्नों के उत्तर संक्षेप में लिखिए।

Question 1.
जड़ी-बूटियों के उपयोग से क्या-क्या लाभ होते हैं?
Answer:
जड़ी-बूटियों के उपयोग से निम्नलिखित लाभ होते हैं

1. सर्दी, पेट दर्द, बुखार जैसी बीमारियों में संबंधित जड़ी बूटियाँ उबालकर या पानी में पीने से ये बीमारियाँ तुरंत दूर होती हैं।
2. संजीवनी बूटी का प्रयोग करने से पेट के रोग दूर होते हैं
3. तथा मनुष्य की लंबाई बढ़ाने में भी यह सहायक होती है।
4. पूदीने का सेवन करने से पेट दर्द में राहत मिलती है तथा मूर्छित व्यक्ति को उसके पत्तों को मसलकर सूंघाने से व्यक्ति की मूर्छा दूर हो जाती है।
5. गर्मी में बेल का शर्बत पीने से लू का खतरा नहीं होता व शरीर का तापमान योग्य रहता है।
6. मधुमेह में अश्वगंधा बूटी का सेवन अधिक फायदेमंद होता है।
7. अर्क मूल की छाल पानी में रखकर, पानी की बूंदें नेत्र में डालने से आँखों की लाली, दर्द व खुजली दूर होती है। इस प्रकार हमारी प्रकृति में ऐसी कई जड़ी-बूटियाँ हैं। जिनसे हमें कई लाभ होते हैं।

आकारिक मूल्यमापन

मौखिक कार्य
चर्चा करो:

1. कविता के प्रसंगों का नाटकीयकरण कराएँ।
2. घरेलू जड़ी-बूटी कौन-कौन-सी होती है? चर्चा करे।
3. विद्याथियों से कविता का साभिनय पाठ कराएँ।

Hindi Sulabhbharti Class 7 Solutions पहली इकाई

• वाचन मेला Question Answer
• फूल और काँटे Question Answer
• दादी माँ का परिवार Question Answer
• देहात और शहर Question Answer
• बंदर का धंधा Question Answer
• ‘पृथ्‍वी’ से ‘अग्‍नि’ तक Question Answer
• जहॉं चाह, वहाँ राह Question Answer
• जीवन नहीं मरा करता है Question Answer

Class 7 Hindi Chapter 7 Rahasya Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 7 रहस्‍य Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 7 Rahasya Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 7 रहस्‍य Textbook Questions and Answers

स्वयं अध्ययन

हिंदी मराठी के समानार्थी मुहावरे और कहावतें सुनिए और उनका द्विभाषी लघुकोश बनाइए।
Answer:

बताओ तो सही

Answer:
घर में – मेरे घर में मेरी दादी हमेशा कहा करती थी कि यदि तुम बाहर जा रहे हो और किसी ने रोक दिया, या किसी ने छींक दिया तो नहीं जाना चाहिए। परंतु जब मैंने विद्यालय में पढ़ा और समझा तो जाना कि यह अंधश्रद्धा है। तब से मैंने दादी को भी समझाकर उनका भ्रम तोड़ने की कोशिश की।

विद्यालय में – मेरा एक सहपाठी है; जिसका घर विद्यालय के पास में ही है। वह रोज विद्यालय देरी से आता है। मैंने कारण पूछा तो उसने बताया कि जब मैं निकलता हूँ, तो बिल्ली रास्ता काट देती है और मैं इंतजार करने लगता हूँ कि पहले कोई और रास्ता पार करे, तब मैं आगे जाऊँ। तब मैंने उसे समझाया कि ऐसा कुछ नहीं होता। यह अंधश्रद्धा है। अब वह रोज समय पर आता है। परिवेश में – मेरे पड़ोस में एक सज्जन रहते हैं। वे एक आँख से काने हैं। लोग किसी काम से जाते समय उनके सामने आने पर रुक जाते हैं। इससे वे बड़े दुखी रहते थे। मैंने लोगों से इस बारे में बात की और अब लोग उन्हें देखकर बुरा नहीं मानते। मुझे भी इस व्यवहारिक सुधार से सुख की अनुभूति हुई।

विचार मंथन

श्रद्धा और विज्ञान, जीवन के दो पक्ष महान ।(अनुच्छेद-लेखन)
Answer:
प्रत्येक सिक्के के दो पहलू होते हैं। इसी प्रकार जीवन के दो पक्ष हैं – श्रद्धा और विज्ञान। हम बाल्यकाल से अपने बड़े-बुजुर्गों से जो कुछ सीखते हैं; उसके प्रति हमारे मन में श्रद्धा होती है। हमारी संस्कृति प्राचीन है। प्राचीन काल से कुछ मान्यताएँ, रीति-रिवाज, परंपराएँ चली आ रही हैं। अशिक्षा के कारण इसमें कुछ कुरीतियाँ भी समाविष्ट हो गई हैं।

आधुनिक समय विज्ञान का युग है। ऐसे में बहुत सारी परंपराएँ, मान्यताएँ एवं रीति-रिवाज आज अपना मूल्य खोती जा रही हैं। अत: जीवन में भक्ति, ज्ञान, श्रद्धा का महत्त्व तो है; लेकिन वह विज्ञान सम्मत ही होनी चाहिए।आज हमें अंधश्रद्धा का निर्मूलन कर सही ज्ञान की आवश्यकता है जो कि विज्ञान की कसौटियों पर खरा उतर सके।

वाचन जगत से

टिपण्णी बनाने हेतु समाचार पत्र से बहादुरी के किस्से पढ़ो और संकलित करो।

निम्नलिखित प्रश्नों के उत्तर लिखिए।

Question 1.
आर्यन और कनिष्का द्वारा देखी हुई हवेली का वर्णन अपने शब्दों में लिखिए।
Answer:
आर्यन और कनिष्का जब हवेली पहुंचे तो वहाँ हँसी और कहकहों की आवाजें सुनाई पड़ी। वहाँ बीचोंबीच में एक बड़ा कमरा था। कमरे का दरवाजा अंदर से बंद था। खिडकियाँ नीचे से बंद थी; किंत ऊपर से खली थीं।

Question 2.
कनिष्का और आर्यन को ‘वीरता पुरस्कार’ घोषित होने का कारण बताइए।
Answer:
कनिष्का और आर्यन ने बहादुरी का काम किया था। जिन डाकुओं को पकड़ने के लिए पुलिस ने अपना खून-पसीना एक कर दिया था। उन्हें अपनी समझदारी से पकड़वा दिया था और डाकुओं के आतंक से गाँववालों को मुक्त
करा दिया था।

Question 3.
इस कहानी की किसी घटना को संवाद रूप में प्रस्तुत कीजिए।
Answer:
आर्यन – नमस्ते सर! क्या मैं अंदर आ सकता हूँ?
थानेदार – हाँ! कहिए आप सबकी मैं क्या मदद कर सकता हूँ।
आर्यन – सर! हमारे पास कुछ फोटो हैं। (फोटो दिखाते हुए)
थानेदार – अरे! तुम्हारे पास ये फोटो कहाँ से आए?
आर्यन – महोदय! यह कनिष्का है। यह मेरे मामा की लड़की है। इनके घर के पास एक हवेली है।
थानेदार – वो हवेली, जिसमें भूत रहते हैं।
कनिष्का- नहीं, नहीं, सर वहाँ कोई भूत-बूत नहीं रहते, हमने वही से कल रात ये फोटो खींची हैं।
थानेदार – शाबास! बच्चों! तुम दोनों ने बहादुरी का काम किया है।

कहानी के आधार पर प्रश्न निर्माण कीजिए।

Question 1.
कहानी से हमें क्या सीख मिलती है?
Answer:
अंधविश्वास से दूर रहकर वैज्ञानिक दृष्टिकोण अपनाने की सीख मिलती है।

Question 2.
कहानी के लिए कोई दूसरा शीर्षक बताइए।
Answer:
वीर बालक या अंधविश्वास का पर्दाफाश

Question 3.
आर्यन के मामा कहाँ रहते थे?
Answer:
आर्यन के मामा गाँव में रहते थे।

Question 4.
आर्यन के मामा का गाँव कैसा था?
Answer:
उनका गाँव समृद्ध था।

Question 5.
भारत के महामहिम राष्ट्रपति का नाम क्या है?
Answer:
महामहिम प्रणव मुखर्जी

सुनो तो जरा

पाठों में आए हुए मूल्यों को सुनो, तालिका बनाओ और सुनाओ।

सदैव ध्यान में रखो

बड़ों की आज्ञा का पालन करना चाहिए।

भाषा की ओर

चित्र के आधार पर सभी कारकों का प्रयोग करके वाक्य लिखो :


Answer:
(१) मछुआरे ने जाल फेंका।
(२) एक महिला नारियल को इकट्ठा कर रही है।
(३) एक व्यक्ति नाव से जा रहा है।
(४) एक लड़की मछलियों के लिए दाना डाल रही है।
(५) एक व्यक्ति पेड़ से नारियल तोड़ता है।
(६) महिला का पुत्र आ रहा है।
(७) मछुआरे की जाल में बहुत मछलियाँ हैं।
(८) अरे! तुम आ गए।

Hindi Sulabhbharti Class 7 Solutions Chapter 7 रहस्‍य Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए।

Question 1.
हवेली में पहले किसका परिवार रहता था?
Answer:
जमींदार का

Question 2.
एक बार हवेली में कौन गया था?
Answer:
घीसू

Question 3.
आर्यन गरमी की छुट्टियाँ बिताने किसके घर आया था?
Answer:
मामा के

Question 4.
मामाजी की लड़की का क्या नाम था?
Answer:
कनिष्का

Question 5.
फोटोग्राफर की दुकान कहाँ थी?
Answer:
नारायणपुर

Question 6.
आर्यन और कनिष्का को किस पुरस्कार से सम्मानित किया जाने वाला है?
Answer:
वीरता पुरस्कार

निम्नलिखित वाक्य सही है या गलत लिखिए।

Question 1.
चारों ओर सन्नाटा था।
Answer:
सही

Question 2.
सुबह होने वाली थी।
Answer:
गलत

Question 3.
हवेली में अंधेरा था।
Answer:
गलत

Question 4.
यह एक समृद्ध गाँव है।
Answer:
सही

Question 5.
मामाजी का एक लड़का था।
Answer:
गलत

Question 6.
मामाजी ने कैमरे की तारीफ की।
Answer:
सही

Question 7.
उस रात हवेली पर पुलिस ने छापा मारा।
Answer:
सही

Question 8.
दोनों ओर से गोलियाँ चलीं।
Answer:
सही

Question 9.
सवेरा होते-होते डाकू भाग गए।
Answer:
गलत

Question 10.
सभी डाकुओं के आतंक से मुक्त हो गए।
Answer:
सही

कोष्ठक में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।

(सलाह-मशविरा, रहस्य, भौंकने, करवटें, बहादुर, इंतजार, अँधेरा)

Question 1.
कभी-कभी कुत्तों के ……………………” की आवाज सुनाई पड़ती थी।
Answer:
भौंकने

Question 2.
आर्यन …………………..” बदलता रहा।
Answer:
करवटें

Question 3.
आर्यन ने कनिष्का से कुछ ………………. किया।
Answer:
सलाह-मशविरा

Question 4.
दोनों ………………. ।
Answer:
बहादुर

Question 5.
वे दोनों रात होने का ………………….” करने लगे।
Answer:
इंतजार

Question 6.
का पता लगाने का यह अच्छा अवसर था।
Answer:
रहस्य

Question 7.
…………………….. होते ही दोनों घर से निकल पड़े।
Answer:
अंधेरा

उचित जोड़ियाँ मिलाइए।

Answer:
फोटो की दुकान – नारायणपुर
भूत-वूत – कपोल कल्पना
हवेली – कहकहों की आवाज

निम्नलिखित प्रश्नों के उत्तर एक बाक्य में लिखिए।

Question 1.
मामाजी के पास कैसा कैमरा था?
Answer:
मामाजी के पास विदेशी डिजिटल कैमरा था।

Question 2.
आर्यन मन-ही-मन क्यों मुसकाने लगा?
Answer:
आर्यन मन-ही-मन मुसकाने लगा क्योंकि वह जानता था कि भूत-बूत कुछ नहीं होते।

Question 3.
हवेली के अंदर से कैसी आवाजें सुनाई पड़ रही थीं?
Answer:
हवेली के अंदर से हँसी और कहकों की आवाजें सुनाई पड़ रही थीं।

Question 4.
डाकुओं ने भूत होने की अफवाह क्यों फैलाई थी?
Answer:
डाकुओं ने भूत होने की अफवाह इसलिए फैलाई थी क्योंकि कोई हवेली की तरफ न जाए और उनका रहस्य न खुले।

व्याकरण और भाषाभ्यास

Question 1.
कहानी से बर्तमानकाल के वाक्य चुनकर लिखिए।
Answer:

• यह एक समृद्ध गाँव है।
• मामाजी के पास एक विदेशी डिजिटल कैमरा भी है।
• बिना फ्लैशगन के भी यह तस्वीर खींच लेता है।
• वहाँ कुछ फोटो लिए हैं।
• मुझे इस मामले में बहुत गड़बड़ी लगती है।

Question 2.
उपर्युक्त प्रश्नसंख्या ८ के वाक्यों को भूतकाल एवं भविष्यकाल में परिवर्तित कीजिए।
Answer:
भूतकाल –

• यह एक समृद्ध गाँव था।
• मामाजी के पास एक विदेशी डिजिटल कैमरा भी था।
• बिना फ्लैशगन के भी यह तस्वीर खींच लेता था।
• वहाँ कुछ फोटो लिए थे।
  मुझे इस मामले में बहुत गड़बड़ी लगती थी।

भविष्यकाल –

• यह एक समृद्ध गाँव होगा।
• मामाजी के पास एक विदेशी डिजिटल कैमरा भी होगा।
• बिना फ्लैशगन के भी यह तस्वीर खींच लेगा।
• वहाँ कुछ फोटो लेंगे।
• मुझे इस मामले में बहुत गड़बड़ी लगेगी।

निम्नलिखित वाक्यों में उचित कारक चिह्न लगाइए।

(को, ने, से, में, की, के, के लिए, का, के, से)

Question 1.
मामा जी …….. का था।
Answer:
ने

Question 2.
आर्यन ने खेतों ……. सरपट पार किया।
Answer:
को

Question 3.
हवेली ……… पिछले दस-पंद्रह सालों ………..”कोई नहीं रहता था।
Answer:
में, से

Question 4.
गरमी ……… छुट्टियाँ बिताने ……. वह मामाजी ……… घर आया था।
Answer:
की, के लिए, के

Question 5.
वह हवेली भूतों ………… डेरा है।
Answer:
का

Question 6.
सभी डाकुओं ……….. आतंक ………… मुक्त हो गए।
Answer:
के, से

निम्नलिखित शब्दों के विलोम शब्द बदलिए।

1. उजाला
2. बहादुर
3. तारीफ
4. सावधानी
5. पसंद
6. सम्मानित

Answer:

1. अंधेरा
2. कायर
3. निंदा
4. असावधानी
5. नापसंद
6. अपमानित

निम्नलिखित शब्दों के वचन बदलिए।

1. छुट्टी
2. आवाज
3. आँख
4. बंदूकें
5. तलवारें
6. खिड़की
7. रोटी
8. गोली

Answer:

1. छुट्टियाँ
2. आवाजें
3. आँखें
4. बंदूक
5. तलवार
6. खिड़कियाँ
7. रोटियाँ
8. गोलियाँ

निम्नलिखित मुहावरों का वाक्यों में प्रयोग कीजिए।

Question 1.
खाट पकड़ना
Answer:
रामू की माँ ने बीमारी में तीन महीने से खाट पकड़ी है।

Question 2.
करवटें बदलना
Answer:
चिंता के कारण पिता जी करवटें बदलते रहें।

Question 3.
कमर कसना
Answer:
हमारी सेना ने आतंकवाद को मिटाने के लिए कमर कस ली है।

Question 4.
तारीफ के पुल बाँधना
Answer:
कल हमारे शिक्षक शिवानी के शिष्टाचार की तारीफों के पुल बाँध रहे थे।

Question 5.
आँखें खुली की खुली रहना
Answer:
दुकानदार की मिलावट देखकर हमारी आँखें खुली की खुली रह गई।

Question 6.
खून-पसीना एक करना
Answer:
पुलिस ने चोरों को पकड़ने के लिए अपना खून-पसीना एक कर दिया था।

Question 7.
हथियार डालना
Answer:
हमारे फौज को देखते ही आतंकवादियों ने हथियार डाल दिए।

निम्नलिखित शब्दों के लिंग बदलिए।

1. मामा
2. शिक्षक
3. भाई
4. लड़का

Answer:

1. मामी
2. शिक्षिका
3. बहन
4. लड़की

निम्नलिखित शब्द युग्मों से विशेषण-विशेष्य अलग कीजिए।

• समृद्ध गाँव
• डिजिटल कैमरा
• वैज्ञानिक दृष्टिकोण
• खतरनाक काम
• वीरता पुरस्कार
• राष्ट्रपति कार्यालय

Answer:

निम्नलिखित शब्दों के तीन-तीन पर्यायवाची शब्द लिखिए।

1. आँख
2. रात
3. तलवार
4. दिन

Answer:

1. नेत्र, लोचन, नयन
2. रात्रि, निशा, रजनी
3. खड्ग, असि, कृपाण
4. दिवस, वार, वासर

Hindi Sulabhbharati 7th Standard Digest Guide दूसरी इकाई

• अस्‍पताल Question Answer
• बेटी युग Question Answer
• दाे लघुकथाएँ Question Answer
• शब्द संपदा Question Answer
• बसंत गीत Question Answer
• चंदा मामा की जय Question Answer
• रहस्‍य Question Answer
• हम चलते सीना तान के Question Answer

Class 7 Hindi Chapter 4 Dehat Aur Shahar Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 4 देहात और शहर Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 4 Dehat Aur Shahar Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 4 देहात और शहर Textbook Questions and Answers

खोजबीन

डाकघर से प्राप्त सेवाएँ बताइए और संकेत स्थलों से अन्य सेवाएँ ढूँढकर उनकी सूची बनाइए। सेवाओं के नाम कब ली जाती है?

Answer:
‘डाकघर’ को अंग्रेजी में (post office) कहते हैं, जो पत्रों को जमा करने, डाँटने, पहुँचाने आदि का काम करती है। लगभग ५०० साल पुरानी ‘भारतीय डाक व्यवस्था’ आज दुनिया की सबसे बेहतर डाक व्यवस्था है। आज भी हमारे देश में हर साल लगभग १०,००० करोड़ चिट्ठियाँ दरवाजे-दरवाजे तक पहुंचाई जाती हैं।
भारतीय डाक सेवाओं की सूची वी. पी. पी. पार्सल सेवा, पोस्टकार्ड, मनीऑर्डर सेवा, डाक जीवन बीमा, स्पीड पोस्ट (EME) सेवा, ग्रीटिंग पोस्ट सेवा, इलेक्ट्रॉनिक फंड ट्रान्सफर सेवा, इंटरनेट आधारित ट्रैक एवं टेक्स सेवा, बिल मेल सेवा, ई-पोस्ट सेवा।

विचार मंथन

“गाँव का विकास, देश का विकास” इस विषय पर दो मित्रों के बीच हुई बातचीत को संवाद के रूप में लिखिए। (संवाद-लेखन)
Answer:
राम – अरे! रतन कैसे हो?
रतन – ठीक हूँ। अभी-अभी अपने गाँव से आया हूँ।
राम – गाँव, अरे ! गाँवों में क्या रखा है?
रतन – नहीं राम। असली भारत तो गाँवों में ही बसता है।
राम – पर मुझे तो गाँव में अच्छा ही नहीं लगता। न वहाँ खेलने के साधन है, न खाने के तरह-तरह के पदार्थ हैं।
रतन – नहीं राम। तुम्हारी सोच गलत है। असली संस्कृति तो गाँवों में ही देखने को मिलती हैं।
रतन – गाँव की बातों को हम समझना ही नहीं चाहते हैं।
राम – क्या समझना है? सब कुछ तो वहाँ बेकार ही होता है। कुछ भी मज़ेदार नहीं।
रतन – राम! यह मत भूलो कि देश के लिए जितने भी वीर महापुरुष पैदा हुए वे गाँव में ही हुए हैं।
राम – हाँ ! रतन यह तो मैं भूल ही गया था।
रतन – सही कहा तुमने।
राम – मैं भूल गया था कि गाँवों से ही देश बनता है। इसलिए विकास की शुरुआत गाँवों से ही करनी होगी।
रतन – राम सही का तुमने। पर एक बात हमेशा ध्यान में रखो कि जब हम बदलेंगे, तब देश बदलेगा।
राम – हाँ, मित्र । मैं तुम्हारे विचार से सहमत हूँ। गाँव का विकास ही देश का विकास है।

बताओ तो सही

क्रिया के जिस रूप से उसके होने के समय का ज्ञान हो, उसे ‘काल’ कहते हैं। काल के मुख्य रूप से तीन भेद होते हैं :
(१) वर्तमानकाल
(२) भूतकाल
(३) भविष्यकाल

(१) वर्तमानकाल: क्रिया के जिस रूप से उसके वर्तमान समय में होने का बोध होता है, उसे ‘वर्तमानकाल’ कहते हैं। जैसे –
(१) माँ खाना बना रही है।
(२) ममता पड़ रही है।
(३) राजा पुस्तक पढ़ रहा है।

(२) भूतकाल : जिस क्रिया से उसके बीते हुए समय में होने का पता चलता है, उसे ‘भूतकाल’ कहते हैं। जैसे –
(१) चित्र देखकर राजा खुश हुए
(२) माँ दीदी को पढ़ा रही थी।

(३) भविष्यकालः ‘भविष्य’ यानी आनेवाला समय। जिस क्रिया से उनके आनेवाले समय में होने का पता लगे, उसे ‘भविष्यकाल’ कहते हैं। इसके अंत में गा, गी, गे जैसे शब्द होते हैं।
जैसे –
(१) हवा चलेगी।
(२) देश में अच्छे दिन आएंगे।

हिंदी की विभिन्न बोलियों के नाम लिखिए तथा उनसे संबंधित प्रदेशों के नाम लिखिए।
Answer:

हिंदी की बोलियाँ – संबंधित प्रदेश
(१) ब्रज – बुंदेलखंड, ग्वालियर, भरतपुर
(२) भोजपुरी – बिहार, उत्तर प्रदेश, झारखंड
(३) मारवाड़ी – राजस्थान, मध्यप्रदेश
(४) दक्खिनी – कर्नाटक, केरल, तमिलनाडु, आंध्रप्रदेश
(५) गढ़वाली – उत्तराखंड
(६) अवधी – उत्तर प्रदेश, अवध क्षेत्र
(७) बघेली – बघेलखंड
(८) हरियाणवी – मध्यप्रदेश, मालवा, हरियाणा

स्वयं अध्ययन

Answer:
सार्वजनिक यातायात साधन न होने पर देश की प्रगति पर गहरा असर पड़ सकता है। देश का प्रत्येक भाग एक-दूसरे से जुड़ा हुआ है। इन सबको मिलाकर तो देश बनता है और यातायात तो देश के आर्थिक व्यवहार की नींव है, इसके न होने से देश की प्रगति पर गहरा प्रभाव पड़ सकता है।

गाँव: गाँव में तैयार होने वाली चीजें वे बेचने के लिए शहर नहीं ले जा सकेंगे। बीमार पड़ने पर व्यक्ति को तुरंत आरोग्य सेवाएँ नहीं मिल सकेंगी। गाँव के बच्चे पढ़ने के लिए यातायात साधन के न होने के कारण शहर नहीं जा सकेंगे। शहरः शहर वासियों का आवागमन व व्यापार ठप्प हो जाएगा। सही समय पर अपने काम पर नहीं जा सकेंगे। ट्राफिक जैसी समस्याएँ निर्माण हो जाएंगी। लोग स्वयं के यातायात साधन का उपयोग करेंगे।

महानगर : महानगर में रहने वाले लोगों के जीवन की गति रूक जाएगी। सभी प्रकार के व्यापार व व्यवहार समय पर नहीं होंगे। बड़े पैमाने पर देश की हानि होगी। महानगर वासियों का जीवन थम-सा जाएगा।

देशः कई जगहों पर गाँवों, शहरों और महानगरों का संबंध एक-दूसरे से टूट जाएगा। देश के सारे महत्त्वपूर्ण शासकीय व न्यायालयीन कार्य समय पर नहीं होंगे। बड़े पैमाने पर देश की आर्थिक हानि होगी। यातायात साधन न होने से गाँवों, शहरों और महानगरों के बीच की दूरी बढ़ जाएगी। बाहरी देश से आनेवाली व जानेवाली कई साधन सामग्रियाँ समय पर न पहुंच पाने से देश का वैश्विक व्यापारिक स्तर डगमगा जाएगा।

अपने मित्र को निबंध प्रतियोगिता में प्रथम आने पर बधाई देते हुए अभिनंदन पत्र लिखिए।
Answer:

ए/१०२, नीलकमल अपार्टमेंट,
राहुल पार्क, एस. व्ही. रोड,
बोरीवली (पूर्व)
मुंबई : ४००५०१।
दिनांक : ०३ मई २०१७।
प्रिय मित्र विनोद,
सप्रेम नमस्ते!

तुम्हारा पत्र प्राप्त हुआ। पढ़कर अत्यंत हर्ष हुआ कि तुमने इस वर्ष अंतर शालेय निबंध प्रतियोगिता में प्रथम स्थान प्राप्त किया। मुझे तुमसे यही आशा थी। तुम बचपन से ही भाषा विषय में बहुत ही कुशल व निपुण हो। आशा करता हूँ कि तुम भविष्य में भी अपना यह प्रथम आने का प्रगतिशील दौर जारी रखोगे। मेरी हार्दिक शुभकामनाएँ सदैव तुम्हारे साथ हैं।

शुभकामनाओंसहित,
तुम्हारा अभिन्न मित्र,
विवेक

वाचन जगत से

गाँव संबंधी सरकारी योजनाओं की जानकारी पढ़ो और मुख्य बातें सुनाओ।
Answer:

गाँव संबंधी कुछ सरकारी योजनाएँ निम्नलिखित हैं:

१. प्रधानमंत्री ग्राम सड़क योजना (PMGSY)
२. सांसद आदर्श ग्राम योजना (SAGY)
३. दीनदयाल उपाध्याय ग्राम ज्योति योजना (DDUGJY)
४. प्रधानमंत्री फसल बीमा योजना (PMFBY)
५. प्रधानमंत्री उज्ज्वला योजना (PMUY)

अध्ययन कौशल

सुने हुए नए शब्दों की वर्णक्रमानुसार तालिका बनाकर संभाषण एवं लेखन में उनका प्रयोग करो ।
Answer:
१. चाचा जी प्रकल्प में मेरा मार्गदर्शन करते हैं।
२. विद्यालय में प्रत्येक विषय के लिए अलग-अलग अध्यापक होते हैं।
३. नाटक में अच्छा अभिनय करने पर गायत्री को सर्वश्रेष्ठ अभिनेत्री का पुरस्कार मिला।
४. सीमा ने मेले से एक सुंदर गुड्डा खरीदा।
५. ऊँटनी अपने बच्चे के साथ चारा खा रही थी।
६. सीमा अपनी सास का बहत सम्मान करती है।
७. चिड़ियाघर में प्राय: हंस देखने को मिल ही जाते हैं।
८. वह बालिका सुरीला गाना गाती है।

सदैव ध्यान में रखो

गाँव की समृद्धि में ही शहर की खुशहाली समाहित है।

निम्नलिखित वाक्य सही है था गालात लिजिए।

Question 1.
‘मोबाइल’ के माध्यम से नित-नवीन सुचनाएँ लोगों तक पहुँचती हैं।
Answer:
सही

Question 2.
महाविद्यालय गाँव में नहीं होते हैं।
Answer:
गलत

Question 3.
खेल ग्रामीण जीवन की आत्मा है।
Answer:
सही

Question 4.
आज भी कई गाँव प्रदूषण से मुक्त है।
Answer:
सही

Question 5.
बच्चों को सही मार्गदर्शन की आवश्यकता होती है।
Answer:
सही

Question 6.
आज का युवक वर्ग बुरी आदतों की और मुड़ रहा है।
Answer:
सही

Question 7.
हमें अपने गाँव को एक परिवार समझकर उसका विकास करना चाहिए।
Answer:
सही

Question 8.
गाँव में बीमारियाँ हैं पर पर्याप्त मात्रा में सुसज्ज और अच्छे अस्पताल हैं।
Answer:
गलत

कारण लिखो:

Question 1.
गाँवों में काम करने के लिए मज़दूर नहीं मिल रहे हैं।
Answer:
गाँवों में काम करने के लिए मज़दूर इसलिए नहीं मिल रहे हैं क्योंकि शहर की चमक-दमक व आधुनिक सुख सुविधाओं के कारण लोग उसकी ओर आकर्षित हो रहे हैं।

Question 2.
शहर परेशान हो उठा है।
Answer:
शहर में दिन-ब-दिन बढ़ती भीड़ के कारण शहर परेशान हो उठा है। बढ़ती आबादी के कारण उसे अब चिराग तले अँधेरा दिखाई दे रहा है।

Question 3.
गाँव बहुत उदास हो जाता है।
Answer:
गाँव बहुत उदास हो जाता है क्योंकि असुविधा, बेरोजगारी, आपसी झगड़े, गुटबाजी, अशांति जैसी समस्याओं से वह घिरता चला जा रहा है।

भाषा की ओर

निम्नलिखित शब्दों के लिंग बदलो और वाक्य बनाकर लिखो :

Question 1.
चाची- चाचा
Answer:
वाक्यः चाचा जी प्रकल्प में मेरा मार्गदर्शन करते हैं।

Question 2.
अध्यापिका – अध्यापक
Answer:
वाक्य: हमारे हिंदी के अध्यापक बहुत अच्छा पढ़ाते हैं।

Question 3.
अभिनेता – अभिनेत्री
Answer:
वाक्य: ऐश्वर्या राय एक कुशल अभिनेत्री है।

Question 4.
गुड़िया – गुड्डा
Answer:
वाक्य: मेरा गुड्डा बड़ा ही आकर्षक है।

Question 5.
ऊँट – ऊँटनी
Answer:
वाक्य: ऊँटनी अपने बच्चों को दूध पीला रही है।

Question 6.
ससुर – सास
Answer:
वाक्यः सास को अपनी बहू के साथ बेटी जैसा बर्ताव करना चाहिए।

Question 7.
हंसिनी – हंस
Answer:
वाक्य: हंस पक्षी सरस्वती देवी का वाहन है।

Question 8.
बालक – बालिका
Answer:
वाक्य: सीता नामक बालिका बड़ी होशियार है।

Hindi Sulabhbharti Class 7 Solutions Chapter 4 देहात और शहर Additional Important Questions and Answers

निम्नलिखित शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।

(दुखड़ा, शौचालय, रोजगार, इमारतों, अशिक्षा, मज़दूर)

Question 1.
………….. की तलाश में लोग शहर जा रहे हैं।
Answer:
रोजगार

Question 2.
अब मैं अपना ……….. क्या रोऊँ?
Answer:
दुखड़ा

Question 3.
शहर तो ………. के जंगल में बदल गए है।
Answer:
इमारतों

Question 4.
घर-घर में ……… जैसी सुविधा के प्रति लोग जागरूक हो रहे हैं।
Answer:
शौचालय

Question 5.
हमारे देश की सबसे बड़ी समस्या …. .. है।
Answer:
अशिक्षा

Question 6.
गाँव में काम के लिए .. …. नहीं मिलते।
Answer:
मज़दूर

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।

Question 1.
गाँवों पर किस क्रांति का असर दिखाई पड़ने लगा है?
Answer:
गाँवों पर ‘डिजिटल’ क्रांति का असर दिखाई पड़ने लगा है।

Question 2.
गाँवों मे कौन-सी योजना घर-घर तक पहुँच गई है?
Answer:
ङ्केलारा गाँवों में स्वच्छ गाम-स्वस्थ मामा’ परियोजना पर-घर तक पहुंच गई है।

Question 3.
शहर ने देहात को किसके उपलक्ष्य में बधाई दी?
Answer:
शहर ने देहात को ‘स्वतंत्रता दिवस के उपलक्ष्य में हार्दिक बधाई दी।

Question 4.
आज देशवासियों को कौन-सी बात समझ में आनी चाहिए?
Answer:
आज देशवासियों को ‘छोटा परिवार-सुखी परिवार’ की बात समझ में आनी चाहिए।

Question 5.
गाँव के लोगों को स्वयं कौन-सा महत्व समझना चाहिए?
Answer:
गाँव के लोगों को स्वयं सहकारिता का महत्त्व समझना चाहिए।

किसने, किससे कहा?

Question 1.
“तुम्हारी प्रगति के बारे में जानकर खुशी हुई! मित्र!”
Answer:
शहर ने देहात से कहा।

Question 2.
“मेरे सुख-दुख के संबंध में पूछा। धन्यवाद!”
Answer:
देहात ने शहर से कहा।

Question 3.
“मेरे यहाँ की दिन-ब-दिन बढ़ती भीड़ से मैं परेशान हो उठा हूँ।”
Answer:
शहर ने देहात से कहा।

Question 4.
“अरे देहात भाई! कितने भाग्यशाली हो कि तुम प्रदुषणमुक्त वातावरण में रहते हो।”
Answer:
शहर ने देहात से कहा।

निम्नलिखित प्रश्नों के उत्तर संक्षेप में लिखिए।

Question 1.
आजकल गाँव के लोग किन-किन बातों के बारे में जानने लगे हैं?
Answer:
आजकल गाँव के लोग ग्रामजन की शिक्षा, स्वास्थ्य, रोजगार, खेती के नए औजारों और आधुनिक खेती की पद्धतियों के बारे में जानने लगे हैं।

Question 2.
सहकारिता पर आधारित कौन-कौन से लघु उद्योग गाँव में शुरू किए जा सकते हैं?
Answer:
सहकारिता पर आधारित गाँव में छोटे-छोटे लघु व्यवसाय, फलोत्पादन, औषधीय वनस्पतियों की खेती, पशुपालन आदि जैसे उद्योग शुरू किए जा सकते हैं।

Question 3.
आज के युवक और बच्चों को लेखक ने ‘आशास्थान’ क्यों कहा है?
Answer:
आज के युवक और बच्चों को लेखक ने आशास्थान इसलिए कहा है क्योंकि आज के बच्चों को यदि उचित मार्गदर्शन दिया जाए, तो वे ही है; जो हमारी व्यथा को कम कर सकते हैं तथा देश को प्रगति के पथ पर अग्रसर कर सकते हैं। इसलिए ही युवाओं को राष्ट्र व भविष्य का निर्माता माना गया है।

निम्नलिखित प्रश्नों के उत्तर लिखिए।

Question 1.
आपके विचार से देहात और शहर में क्या-क्या अंतर होता है?
Answer:
हमारे विचार से देहात और शहर में निम्नलिखित अंतर है: देहात में लोगों को बिजली, पानी व यातायात के साधन मिलने में काफी कठिनाई होती है, शहर में बिजली, पानी व यातायात के साधन लोगों को सहज तरीके से प्राप्त होते हैं। देहात में आज भी लोग अपने बच्चों की शिक्षा व अपने परिवार कल्याण के प्रति उदासीन हैं, तो शहर में रहने वाले लोग अपने बच्चों की शिक्षा व अपने परिवार के कल्याण के प्रति जागरूक दिखाई देते हैं। देहात में लोगों को रोजगार प्राप्त नहीं होता किंतु शहर में आने वाला प्रत्येक व्यक्ति किसी-न-किसी प्रकार की नौकरी जरूर पाता है।

Question 2.
आपके विचार से आदर्श गाँव अथवा शहर में क्या क्या सुविधाएँ होनी चाहिए?
Answer:
आदर्श गाँव या शहर में निम्नलिखित सुविधाएँ होनी चाहिए :

• आदर्श गाँव या शहर में बिजली और पानी की आपूर्ति, शिक्षा की व्यवस्था योग्य रूप से होनी चाहिए।
• गाँव या शहर में रहने वाले सभी लोगों को गाँव या शहर की स्वच्छता व साफ-सफाई का ध्यान रखना चाहिए।
• गाँव या शहर में ही छोटे-छोटे लघु उद्योग निर्माण करने चाहिए ताकि गाँव या शहर का पढ़ा-लिखा युवक वर्ग बाहर रोजगार की तलाश में न जाए।
• आदर्श गाँव या शहर में सुसज्ज एवं अच्छे अस्पतालों की अच्छी व्यवस्था होनी चाहिए।
• आदर्श गाँव या शहरं में रहने वाले लोगों को विभिन्न व्यावसायिक कौशलों, कंप्यूटर का ज्ञान आदि संबंधित जानकारी होनी चाहिए।
• व इससे संबंधित सारी व्यवस्थाएँ गाँव में होनी चाहिए। आदर्श गाँव या शहर में अच्छे सरकारी यातायात साधनों की व्यवस्था होनी चाहिए। उनमें भाईचारे व एकता की भावना होनी चाहिए।

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के समानार्थी शब्द पाठ में से ढूँढ़कर लिखिए।

1. कठिनाई
2. सेहत
3. कृषि
4. प्रगति
5. अनपढ़
6. आज़ादी
7. प्रसिद्ध
8. बन
9. आकाश
10. पाठशाला

Answer:

1. समस्या
2. स्वास्थ्य
3. खेती
4. उन्नति
5. निरक्षर
6. स्वतंत्रता
7. विख्यात
8. जंगल
9. आसमान
10. विद्यालय

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. कठिन
2. दुर्लभ
3. आशा
4. गरीबी
5. सुख
6. शिक्षित
7. शांति
8. शहर

Answer:

1. सरल
2. सुलभ
3. निराशा
4. अमीरी
5. दुख
6. अशिक्षित
7. अशांति
8. गाँव

प्रस्तुत पाठ में आए युग्म शब्द को चुनकर लिखिए।
Answer:

• सुख – दुख
• नित – नवीन
• बड़े – बड़े
• कभी – कभी
• काम – धंधा
• चमक – दमक
• धीरे – धीरे
• रचा – बसा
• छोटे – छोटे
• रग – रग
• हरे-भरे
• खुला – खुला

निम्नलिखित वाक्यों को पढ़कर उनके काल का भेद लिखिए।

Question 1.
लोग पानी लेने के लिए दूर तक जाते थे।
Answer:
भूतकाल

Question 2.
हम गाँव में महविद्यालय बनाएँगे।
Answer:
भविष्यकाल

Question 3.
चारों तरफ हरियाली फैल रही है।
Answer:
वर्तमानकाल

Question 4.
गाँव से कई प्रसिद्ध खिलाड़ी बनेंगे।
Answer:
भविष्यकाल

Question 5.
शहर इमारतों के जंगल में बदल रहा है।
Answer:
वर्तमानकाल

Hindi Sulabhbharti Class 7 Solutions पहली इकाई

• वाचन मेला Question Answer
• फूल और काँटे Question Answer
• दादी माँ का परिवार Question Answer
• देहात और शहर Question Answer
• बंदर का धंधा Question Answer
• ‘पृथ्‍वी’ से ‘अग्‍नि’ तक Question Answer
• जहॉं चाह, वहाँ राह Question Answer
• जीवन नहीं मरा करता है Question Answer

Class 7 Hindi Chapter 1 Aspatal Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 1 अस्‍पताल Notes, Textbook Exercise Important Questions and Answers.

Std 7 Hindi Chapter 1 Aspatal Question Answer Maharashtra Board

Hindi Sulabhbharti Class 7 Solutions Chapter 1 अस्‍पताल Textbook Questions and Answers

Answer:
चित्रों का परिचय:

उपर्युक्त चित्र में अस्पताल से संबंधित जानकारी, सूचना व उनका पालन करने का वर्णन दिया गया है। यह अस्पताल है। यहाँ पर कुछ रोगी प्रतीक्षा कर रहे हैं। डॉक्टर बीमार व्यक्ति को देखने जा रहे हैं। एक परिचारिका (नर्स) एक रोगी को पहियेदार कुर्सी पर लेकर आ रही है। नेत्रदान और रक्तदान के प्रति लोगों को जागरूक करने के लिए ‘रक्तदान महादान’ और ‘नेत्रदान’ के घोषवाक्य लगाए गए हैं। रोगी से मिलने के लिए सुबह ८ से १० एवं शाम ४ से ७ बजे तक का समय निश्चित किया गया हैं। ‘छोटा परिवार-सुखी परिवार’ का आदर्श सूचना फलक पर लिखा गया है ताकि लोग छोटे परिवार के महत्त्व को समझें। अस्पताल में एक ओर कूड़ादान भी रखा हुआ है। चारों तरफ स्वच्छता है। रोगी से अधिक बात करके लोग उसे परेशान न करें इसलिए शांति व्यवस्थापन से संबंधित सूचना दी गई है। गहन चिकित्सा केंद्र (आई. सी. यू.) के पास एक पहरेदार खड़ा है। वार्ड के बाईं तरफ ‘बेटी बचाओ, बेटी पढ़ाओ’ का पोस्टर दिखाई पड़ रहा है। जिससे स्त्री-शिक्षा महत्त्व की स्थापना की गई है।

Hindi Sulabhbharti Class 7 Solutions Chapter 1 अस्‍पताल Additional Important Questions and Answers

पाठ्यपुस्तक पृष्ठ क्र. २७ पर दिए गए चित्रों को देखकर निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए।

Question 1.
उपर्युक्त चित्र में क्या दिख रहा है?
Answer:
अस्पताल

Question 2.
कितने रोगी प्रतीक्षा कर रहे हैं?
Answer:
तीन

Question 3.
चित्र में कितने कूड़ेदान दिख रहे हैं?
Answer:
एक

Question 4.
आई.सी.यू. के बाहर कौन खड़ा है?
Answer:
पहरेदार

Question 5.
चित्र में कितने डॉक्टर दिखाई दे रहे हैं?
Answer:
दो

निम्नलिखित बाक्यों के सामने सही (✓) अथवा गलत (✗) का निशान लगाइए।

Question 1.
अस्पताल में स्वच्छता है।
Answer:
(✓)

Question 2.
चित्र में जगह-जगह कूड़ादान रखा है।
Answer:
(✗)

Question 3.
काउन्टर पर लोग झगड़ा कर रहे हैं।
Answer:
(✗)

Question 4.
अस्पताल में शांति बनाए रखनी चाहिए।
Answer:
(✓)

Question 5.
रक्तदान को महादान कहा गया है।
Answer:
(✓)

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।

Question 1.
कौन-सा परिवार सुखी होता है?
Answer:
छोटा परिवार-सुखी परिवार होता है।

Question 2.
महादान किसे कहा गया है?
Answer:
रक्तदान को महादान कहा गया है।

Question 3.
अस्पताल में रोगी से मिलने का समय क्या रखा गया
Answer:
अस्पताल में रोगी से मिलने का समय सुबह ८ से १० और शाम ४ से ७ बजे तक रखा गया है।

Question 4.
रोगी से अधिक बातें क्यों नहीं करनी चाहिए?
Answer:
रोगी से अधिक बातें नहीं करनी चाहिए क्योंकि उसे आराम की जरूरत होती है।

Question 5.
अस्पताल में शांति क्यों बनाए रखनी चाहिए?
Answer:
अस्पताल में शोर करने से रोगियों को परेशानी होती है, इसलिए वहाँ शांति बनाए रखनी चाहिए।

निम्नलिखित शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।

(सुखी, शांति, रक्तदान, बातें, देखभाल)

Question 1.
रोगी से अधिक …………. न करें।
Answer:
बातें

Question 2.
छोटा परिवार ….. परिवार।
Answer:
सुखी

Question 3.
…….. बनाए रखें।
Answer:
शांति

Question 4.
…….. महादान।
Answer:
रक्तदान

Question 5.
अस्पताल में मरीजों की …… की जाती है।
Answer:
देखभाल

आकारिक मूल्यमापन

1. अस्पताल में जाकर वहाँ दी गई जानकारी, सूचना पढ़ने एवं पालन करने के लिए कहें।
2. अस्पताल में लगे हुए सूचना बोर्ड की सूची बनाएं।

Hindi Sulabhbharati 7th Standard Digest Guide दूसरी इकाई

• अस्‍पताल Question Answer
• बेटी युग Question Answer
• दाे लघुकथाएँ Question Answer
• शब्द संपदा Question Answer
• बसंत गीत Question Answer
• चंदा मामा की जय Question Answer
• रहस्‍य Question Answer
• हम चलते सीना तान के Question Answer