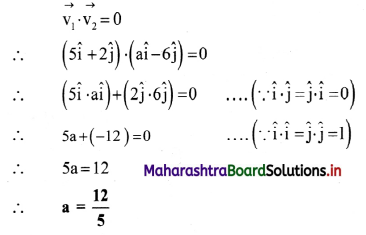Prasanna

11th Physics Chapter 2 Exercise Mathematical Methods Solutions Maharashtra Board

January 7, 2025January 6, 2025 by Prasanna

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 2 Mathematical Methods Textbook Exercise Questions and Answers.

Mathematical Methods Class 11 Exercise Question Answers Solutions Maharashtra Board

Class 11 Physics Chapter 2 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 2 Exercise Solutions

1. Choose the correct option.

Question 1.
The resultant of two forces 10 N and 15 N acting along + x and – x-axes respectively, is
(A) 25 N along + x-axis
(B) 25 N along – x-axis
(C) 5 N along + x-axis
(D) 5 N along – x-axis
Answer:
(D) 5 N along – x-axis

Question 2.
For two vectors to be equal, they should have the
(A) same magnitude
(B) same direction
(C) same magnitude and direction
(D) same magnitude but opposite direction
Answer:
(C) same magnitude and direction

Question 3.
The magnitude of scalar product of two unit vectors perpendicular to each other is
(A) zero
(B) 1
(C) -1
(D) 2
Answer:
(A) zero

Question 4.
The magnitude of vector product of two unit vectors making an angle of 60° with each other is
(A) 1
(B) 2
(C) \(\frac{3}{2}\)
(D) \(\frac{\sqrt{3}}{2}\)
Answer:
(D) \(\frac{\sqrt{3}}{2}\)

Question 5.
If \(\overrightarrow{\mathrm{A}}\), \(\overrightarrow{\mathrm{B}}\), and \(\overrightarrow{\mathrm{C}}\) are three vectors, then which of the following is not correct?
(A) \(\overrightarrow{\mathrm{A}}\) . (\(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{C}}\)) = \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{C}}\)
(B) \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) . \(\overrightarrow{\mathrm{A}}\)
(C) \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{A}}\)
(D) \(\overrightarrow{\mathrm{A}}\) × (\(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{C}}\)) = \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{C}}\)
Answer:
(C) \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{A}}\)

2. Answer the following questions.

Question 1.
Show that \(\overrightarrow{\mathrm{A}}\) = \(\frac{\hat{i}-\hat{j}}{\sqrt{2}}\) is a unit vector.
Solution:

Question 2.
If \(\overrightarrow{\mathbf{v}_{1}}\) = 3\(\hat{i}\) + 4\(\hat{j}\) + \(\hat{k}\) and \(\overrightarrow{\mathbf{v}_{2}}\) = \(\hat{i}\) – \(\hat{j}\) – \(\hat{k}\), determine the magnitude of \(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\).
Solution:
\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\) = (3\(\hat{i}\) + 4\(\hat{j}\) + \(\hat{k}\)) + (\(\hat{i}\) – \(\hat{j}\) – \(\hat{k}\))
= 3\(\hat{i}\) + 3\(\hat{i}\) + 4\(\hat{j}\) – \(\hat{j}\) + \(\hat{k}\) – \(\hat{k}\)
= 4\(\hat{i}\) + 3\(\hat{j}\)
∴ Magnitude of (\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\)),
|\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\)| = \(\sqrt{4^{2}+3^{2}}\) = \(\sqrt{25}\) = 5 units.
Answer:
Magnitude of \(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\) = 5 units.

Question 3.
For \(\overline{\mathrm{v}_{1}}\) = 2\(\hat{i}\) – 3\(\hat{j}\) and \(\overline{\mathrm{v}_{2}}\) = -6\(\hat{i}\) + 5\(\hat{j}\), determine the magnitude and direction of \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\).
Answer:
\(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\) = (2\(\hat{i}\) – 3\(\hat{j}\)) + (-6\(\hat{i}\) + 5\(\hat{j}\))
= (2\(\hat{i}\) – 6\(\hat{i}\)) + (-3\(\hat{j}\) + 5\(\hat{j}\))
= -4\(\hat{i}\) + 2\(\hat{j}\)
∴ |\(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\)| = \(\sqrt{(-4)^{2}+2^{2}}\) = \(\sqrt{20}\) = \(\sqrt{4 \times 5}\) = 2\(\sqrt{5}\)
Comparing \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\), with \(\overrightarrow{\mathrm{R}}\) = R_x\(\hat{i}\) + R_y\(\hat{j}\)
⇒ R_x = -4 and R_y = 2
Taking θ to be angle made by \(\overrightarrow{\mathrm{R}}\) with X-axis,

Answer:
Magnitude and direction of \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\), is
respectively 2\(\sqrt{5}\) and and tan^-1\(\left(-\frac{1}{2}\right)\) with X – axis.

Question 4.
Find a vector which is parallel to \(\overrightarrow{\mathrm{v}}\) = \(\hat{i}\) – 2\(\hat{j}\) and has a magnitude 10.
Answer:

Substituting for w_x in (i) using equation (ii),

Using equation (ii),

Answer:
Required vector is \(\frac{10}{\sqrt{5}} \hat{\mathbf{i}}\) – \(\frac{20}{\sqrt{5}} \hat{\mathbf{j}}\)

Alternate method:

When two vectors are parallel, one vector is scalar multiple of another,
i.e., if \(\overrightarrow{\mathrm{v}}\) and \(\overrightarrow{\mathrm{w}}\) are parallel then, \(\overrightarrow{\mathrm{w}}\) = n\(\overrightarrow{\mathrm{v}}\) where, n is scalar.

Question 5.
Show that vectors \(\vec{a}\) = 2\(\hat{\mathbf{i}}\) + 5\(\hat{\mathbf{j}}\) – 6\(\hat{\mathbf{k}}\) and \(\vec{b}\) = \(\hat{\mathbf{i}}\) + \(\frac{5}{2}\)\(\hat{\mathbf{j}}\) – 3\(\hat{\mathbf{k}}\) are parallel.
Answer:
Let angle between two vectors be θ.

⇒ Two vectors are parallel.

Alternate method:

\(\vec{a}\) = 2(\(\hat{\mathbf{i}}\) + \(\frac{5}{2}\)\(\hat{\mathbf{j}}\) + \(\hat{\mathbf{k}}\)) = 2\(\vec{b}\)
Since \(\vec{a}\) is a scalar multiple of \(\vec{b}\), the vectors are parallel.

3. Solve the following problems.

Question 1.
Determine \(\vec{a}\) × \(\vec{b}\), given \(\vec{a}\) = 2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) and \(\vec{b}\) = 3\(\hat{\mathbf{i}}\) + 5\(\hat{\mathbf{j}}\).
Answer:
Using determinant for vectors in two dimensions,

Answer:
\(\vec{a}\) × \(\vec{b}\) gives \(\hat{\mathbf{k}}\)

Question 2.
Show that vectors \(\overrightarrow{\mathbf{a}}\) = 2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) + 6\(\hat{\mathbf{k}}\), \(\overrightarrow{\mathbf{b}}\) = 3\(\hat{\mathbf{i}}\) – 6\(\hat{\mathbf{j}}\) + 2\(\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{c}}\) = 6\(\hat{\mathbf{i}}\) + 2\(\hat{\mathbf{j}}\) – 3\(\hat{\mathbf{k}}\) are mutually perpendicular.
Solution:
As dot product of two perpendicular vectors is zero. Taking dot product of \(\vec{a}\) and \(\vec{b}\)

Combining two results, we can say that given three vectors \(\vec{a}\), \(\vec{b}\), and \(\vec{c}\) are mutually perpendicular to each other.

Question 3.
Determine the vector product of \(\overrightarrow{\mathrm{v}_{1}}\) = 2\(\hat{i}\) + 3\(\hat{j}\) – \(\hat{k}\) and \(\overrightarrow{\mathrm{v}_{2}}\) = \(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\) are perpendicular to each other, determine the value of a.
Solution:

Answer:
Required vector product is -7\(\hat{i}\) + 5\(\hat{j}\) + \(\hat{k}\)

Question 4.
Given \(\bar{v}_{1}\) = 5\(\hat{i}\) + 2\(\hat{j}\) and \(\bar{v}_{2}\) = a\(\hat{i}\) – 6\(\hat{j}\) are perpendicular to each other, determine the value of a.
Solution:
As \(\bar{v}_{1}\) and \(\bar{v}_{2}\) are perpendicular to each other, θ = 90°

Answer:
Value of a is \(\frac{12}{5}\).

Question 5.
Obtain derivatives of the following functions:
(i) x sin x
(ii) x⁴ + cos x
(iii) x/sin x
Answer:
(i) x sin x
Solution:
\(\frac{d}{d x}\)[f₁(x) × f₂(x)] = f₁(x)\(\frac{\mathrm{df}_{2}(\mathrm{x})}{\mathrm{dx}}\) + \(\frac{\mathrm{df}_{1}(\mathrm{x})}{\mathrm{dx}}\)f₂(x)
For f₁(x) = x and f₂(x) = sin x
\(\frac{d}{d x}\)(x sin x) = x\(\frac{\mathrm{d}(\sin \mathrm{x})}{\mathrm{dx}}\) + \(\frac{d(x)}{d x}\) sin x
= x cos x + 1 × sin x
= sin x + x cos x

(ii) x⁴ + cos x
Solution:

(iii) \(\frac{\mathbf{x}}{\sin x}\)
Solution:

[Note: As derivative of (sin x) is cos x, negative sign that occurs in rule for differentiation for quotient of two functions gets retained in final answer]

Question 6.
Using the rule for differentiation for quotient of two functions, prove that \(\frac{d}{d x}\left(\frac{\sin x}{\cos x}\right)\) = sec²x
Solution:

Question 7.
Evaluate the following integral:
(i) \(\int_{0}^{\pi / 2} \sin x d x\)
(ii) \(\int_{1}^{5} x d x\)
Answer:
(i) \(\int_{0}^{\pi / 2} \sin x d x\)
Solution:

(ii) \(\int_{1}^{5} x d x\)
Solution:

11th Physics Digest Chapter 2 Mathematical Methods Intext Questions and Answers

Can you recall? (Textbook Page No. 16)

Question 1.
Define scalars and vectors.
Answer:

Physical quantities which can be completely described b their magnitude (a number and unit) are called scalars.
Physical quantities which need magnitude as well as direction for their complete description are called vectors.

Question 2.
Which of the following are scalars or vectors?
Displacements, distance travelled, velocity, speed, force, work done, energy
Answer:

Scalars: Distance travelled, speed, work done, energy.
Vectors: Displacement, velocity, force.

Question 3.
What is the difference between a scalar and a vector?
Answer:

No.	Scalars	Vectors
i.	It has magnitude only	It has magnitude as well as direction.
ii.	Scalars can be added or subtracted according to the rules of algebra.	Vectors are added or subtracted by geometrical (graphical) method or vector algebra.
iii.	It has no specific representation.	It is represented by symbol (→) arrow.
iv.	The division of a scalar by another scalar is valid.	The division of a vector by another vector is not valid.
	Example: Length, mass, time, volume, etc.	Example: Displacement, velocity, acceleration, force, etc.

Internet my friend (Textbook page no. 28)

1. hyperphysics.phy-astr.gsu.edu/hbase/vect. html#veccon
2. hyperphysics.phy-astr.gsu.edu/hbase/ hframe.html

Answer:
[Students can use links given above as reference and collect information about mathematical methods]

11th Std Physics Questions And Answers:

11th Biology Chapter 16 Exercise Skeleton and Movement Solutions Maharashtra Board

January 7, 2025January 6, 2025 by Prasanna

Balbharti Maharashtra State Board 11th Biology Textbook Solutions Chapter 16 Skeleton and Movement Textbook Exercise Questions and Answers.

Skeleton and Movement Class 11 Exercise Question Answers Solutions Maharashtra Board

Class 11 Biology Chapter 16 Exercise Solutions Maharashtra Board

Biology Class 11 Chapter 16 Exercise Solutions

1. Choose the correct option

Question (A).
The functional unit of striated muscle is …………..
a. cross bridges
b. myofibril
c. sarcomere
d. z-band
Answer:
c. sarcomere

Question (B).
A person slips from the staircase and breaks his ankle bone. Which bones are involved?
a. Carpals
b. Tarsal
c. Metacarpals
d. Metatarsals
Answer:
b. Tarsal

Question (C).
Muscle fatigue is due to accumulation of ……..
a. pyruvic acid
b. lactic acid
c. malic acid
d. succinic acid
Answer:
b. lactic acid

Question (D).
Which one of the following is NOT antagonistic muscle pair?
a. Flexo-extensor
b. Adductor-abductor
c. Levator-depressor
d. Sphinetro-suprinater
Answer:
d. Sphinetro-suprinater

Question (E).
Swelling of sprained foot is reduced by soaking in hot water containing a large amount of common salt,
a. due to osmosis
b. due to plasmolysis
c. due to electrolysis
d. due to photolysis
Answer:
a. due to osmosis

Question (F).
Role of calcium in muscle contraction is ……….
a. to break the cross bridges as a cofactor in the hydrolysis of ATP
b. to bind with troponin, changing its shape so that the actin filament is exposed
c. to transmit the action potential across the neuromuscular junction.
d. to re-establish the polarisation of the plasma membrane following an action potential
Answer:
b. to bind with troponin, changing its shape so that the actin filament is exposed

Question (G).
Hyper-secretion of parathormone can cause which of the following disorders?
a. Gout
b. Rheumatoid arthritis
c. Osteoporosis
d. Gull’s disease
Answer:
c. Osteoporosis

Question (H).
Select correct option between two nasal bones

Answer:
(c)

Question 2.
Answer the following questions

Question (A).
What kind of contraction occurs in your neck muscles while you are reading your class assignment?
Answer:

Isometric contractions occur in the neck muscles while reading class assignment.
These contractions are important for supporting objects in a fixed position.

Question (B).
Observe the diagram and enlist importance of ‘A’, ‘B’ and ‘C’.

Answer:

A – Posterior portion of vertebral foramen of atlas vertebrae; Importance – The spinal cord runs through this portion of vertebral foramen
B – Anterior portion of vertebral foramen of axis vertebrae; Importance – In this portion, the odontoid process of axis vertebrae forms ‘NO’ joint.
C – Inferior articular facet; Importance – It articulates with superior articular facet of axis and permits rotatory movement of head.

Question (C).
Raju intends to train biceps; while exercising using dumbbells, which joints should remain stationary and which should move?
Answer:
While performing exercise of biceps using dumbbells, the joint which should remain stationary are wrist joint or radiocarpal joint, ball and socket joint of shoulder. The only joint which should move is hinge joint of elbow.

Question (D).
In a road accident, Moses fractured his leg. One of the passers by, tied a wodden plank to the fractured leg while Moses
was rushed to the hospital Was this essential? Why?
Answer:

Fracture is a significant and traumatic injury which requires medical attention however, getting timely first aid is important.
If any bone is fractured, it is essential that the fractured part be immobilized to prevent further injury. It can be done with the help of any available wooden plank or batons or rulers. Thus, a wooden plank was tied to Moses’s fractured leg as a first aid for fracture.
A fractured bone is immobilized to prevent the sharp edges of the fractured bone from moving and cutting tissue, muscle, blood vessels and nerves. Immobilization can also help reduce pain or control shock.

Question (E).
Sprain is more painful than fracture. Why?
Answer:

A sprain is an injury that involves the ligaments (tissues that connect bones at joints), whereas a fracture is an injury that involves bones.
Sprains can be of three degree: 1^st degree: Mild with micro-tears, 2^nd degree: Partial with visible tear in ligament, 3^rd degree: Completely torn ligament.
If a sprain is 3^rd degree, it will be more painful than a fracture. It usually requires a surgery to fix this injury, while breaking a bone, most of the time does not require surgery.
Breaks or Fractures also vary greatly. Minor fractures (like stress/ hairline fractures) are much less painful than compound/ complex fractures in which the bone may be cracked into half.
Blood supply is essential for growth and regeneration. Bones are highly vascularized whereas, ligaments are not. This causes the bones to heal comparatively faster than severe sprains. Thus, the duration of enduring pain until the injury heals also differs.
Also, ligaments have a rich supply of sensory nerves, which may also be responsible for an elevated sense of pain during severe sprains.

[Note: 1^st and 2^nd degree sprains are not very serious and may be lesser painful than a fracture. Depending on the severity of the injury, intensity of pain will vary.]

Question (F).
Why a red muscle can work for a prolonged period whereas white muscle fibre suffers from fatigue after a shorter work? (Refer to chapter animal tissues.)
Answer:

Red muscle fibres contain large amount of myoglobin and mitochondria (site of aerobic respiration), whereas white muscles fibres contain lesser amount of myoglobin and mitochondria.
Myoglobin is an iron-containing pigment that carries oxygen molecules to muscle tissues. Abundance of these pigments in red muscle fibres supports higher rate of aerobic respiration, whereas white muscle fibres have less mitochondria and depend upon anaerobic respiration.
Anaerobic respiration in muscle white fibres leads to the production of lactic acid and accumulation of higher of levels lactic acid can result in fatigue in white muscle fibres.

Thus, red muscle fibres can perform prolonged work and show less fatigue due to accumulation of negligible amount loss or of lactic acid, whereas white muscle fibres suffer from fatigue after a shorter work due to accumulation of higher amount of lactic acid.

3. Answer the following questions in detail

Question (A).
How is the structure of sarcomere suitable for the contractility of the muscle? Explain its function according to sliding
filament theory. (Refer to chapter animal tissues.)
Answer:
i. Sarcomere is the functional unit of myofibril. It has specific arrangement of actin and myosin filaments. The components of sarcomere are organized into variety of bands and zones. Actin and myosin are referred as contractile proteins. Actin is called as thin filament whereas myosin in called as thick filament. The structure of sarcomere:

ii. ‘A’ band – dark bands present at the centre of sarcomere and contain myosin as well as actin.
‘H’ zone or Hensen’s zone – light area present at the centre of ‘A’ band
‘M’ line – present at the centre of ‘H’ zone
‘I’ band – light bands present on the either side of ‘A’ band containing only actin
Z’ line – adjacent ‘I’ bands are separated by ‘Z’ line.

iii. Sliding filament theory: It was put forth by H.E Huxley and A.F Huxley. It is also known as ‘Walk along theory’ or Ratchet theory.

According to the sliding filament theory, the interaction between actin and myosin filaments is the basic cause of muscle contraction. The actin filaments are interdigitated with myosin filaments.
The head of the myosin is joined to the actin backbone by a cross bridge forming a hinge joint. From this joint, myosin head cannot tilt forward or backward. This movement is an active process as it utilizes ATP.
Myosin head contains ATPase activity. It can derive energy by the breakdown of ATP molecule. This energy can be used for the movement of myosin head.
During contraction, the myosin head gets attached to the active site of actin filaments and pull them inwardly so that the actin filaments slide over the myosin filaments. This results in the contraction of muscle fibre.

Question (B).
Ragini, a 50 year old office goer, suffered hair-line cracks in her right and left foot in short intervals of time. She was worried about minor jerks leading to hair line cracks in bones. Doctor explained to her why it must be happening and prescribed medicines.

What must be the cause of Ragini’s problem? Why has it occurred? What precautions she should have taken earlier? What care she should take in future?
Answer:

Considering Ragini’s age, she may be undergoing menopause. After menopause, oestrogen level declines resulting in lower bone density.
Osteoporosis:
- In this disorder, bones become porous and hence brittle. It is primarily age related disease and is more common in women than men.
- Osteoporosis may be caused due to decreasing estrogen secretion after menopause, deficiency of vitamin D, low calcium diet, decreased secretion of sex hormones and thyrocalcitonin.
As age advances, bone resorption outpaces bone formation. Hence, the bones lose mass and become brittle. More calcium is lost in urine, sweat, etc., than it is gained through diet. Thus, prevention of disease is better than treatment by consuming adequate amount of calcium and exercise at young age.
A person with previous hairline fractures is more susceptible to reoccurrence of fractures. Hence, Ragini needs to take her medications and supplements properly, avoid jerky movements and maintain body weight.

Question (C).
How does structure of actin and myosin help muscle contraction?
Answer:
i. Myosin filament:

Each myosin filament is a polymerized protein.
Many meromyosins (monomeric proteins) constitute one thick filament.
Myosin molecule consists of two heavy chains (heavy meromyosin / HMM) coiled around each other forming a double helix. One end of each of these chains is projected outwardly is known as cross bridge. This end folds to form a globular protein mass called myosin head.
Two light chains are associated with each head forming 4 light chains/light meromyosin / LMM.
Myosin head has a special ATPase activity. It can split ATP to produce energy.
Myosin contributes 55% of muscle proteins.
In sarcomere, myosin tails are arranged to point towards the centre of the sarcomere and the heads point to the sides of the myofilament band.

ii. Actin filament: It is a complex type of contractile protein. It is made up of three components:

F actin: It forms the backbone of actin filament. F actin is made up of two helical strands. Each strand is composed of polymerized G actin molecules. One ADP molecule is attached to G actin molecule.
Tropomyosin: The actin filament contains two additional protein strands that are polymers of tropomyosin molecules. Each strand is loosely attached to an F actin. In the resting stage, tropomyosin physically covers the active myosin-binding site of the actin strand.
Troponin: It is a complex of three globular proteins, is attached approx. 2/3^rd distance along each tropomyosin molecule. It has affinity for actin, tropomyosin and calcium ions. The troponin complex is believed to attach the tropomyosin to the actin. The strong affinity of troponin for calcium ions is believed to initiate the contraction process.

Question (D).
Justify the structure of atlas and axis vertebrae with respect to their position and function.
Answer:
i. Atlas vertebrae:

Atlas is the ring-like, 1^st cervical vertebrae. It has anterior, posterior arches and large lateral masses.
It lacks centrum and spinous process. The superior surfaces of the lateral masses are concave and are known as superior articular facets.
These facets articulate with the occipital condyles of the occipital bone thereby forming atlanto-occipital joints. This articulation permits ‘YES movement’ or nodding movement.
The inferior surfaces of the lateral masses known as inferior articular facets articulate with axis vertebrae,

ii. Axis vertebrae:

It is the 2^ndcervical vertebrae.
A peg-like process called odontoid process projects superiorly through the anterior portion of the vertebral foramen of the atlas.
The odontoid process forms a pivot on which the atlas and head rotate. This arrangement allows ‘NO movement’ or side to side movement of the head.
The articulation formed between the anterior arch of atlas, the odontoid process of the axis and between their articular facets is called as atlanto-axial joint.

Question (E).
Observe the blood report given below and diagnose the possible disorder.

Answer:
On observing Report D, it is clear that the level of uric acid is more than normal, thus the patient must be suffering from gouty arthritis.

Also, the elevated blood urea nitrogen (BUN) indicates dysfunctional liver and/ or kidneys. It generally occurs due to decrease in GFR, caused by renal disease or obstruction of urinary tract.

Question 4.
Write short notes on following points

Question (A).
Actin filament
Answer:
Actin filament: It is a complex type of contractile protein. It is made up of three components:

F actin: It forms the backbone of actin filament. F actin is made up of two helical strands. Each strand is composed of polymerized G actin molecules. One ADP molecule is attached to G actin molecule.
Tropomyosin: The actin filament contains two additional protein strands that are polymers of tropomyosin molecules. Each strand is loosely attached to an F actin. In the resting stage, tropomyosin physically covers the active myosin-binding site of the actin strand.
Troponin: It is a complex of three globular proteins, is attached approx. 2/3rd distance along each tropomyosin molecule. It has affinity for actin, tropomyosin and calcium ions. The troponin complex is believed to attach the tropomyosin to the actin. The strong affinity of troponin for calcium ions is believed to initiate the contraction process.

Question (B).
Myosin filament
Answer:
i. Myosin filament:

Each myosin filament is a polymerized protein.
Many meromyosins (monomeric proteins) constitute one thick filament.
Myosin molecule consists of two heavy chains (heavy meromyosin / HMM) coiled around each other forming a double helix. One end of each of these chains is projected outwardly is known as cross bridge. This end folds to form a globular protein mass called myosin head.
Two light chains are associated with each head forming 4 light chains/light meromyosin / LMM.
Myosin head has a special ATPase activity. It can split ATP to produce energy.
Myosin contributes 55% of muscle proteins.
In sarcomere, myosin tails are arranged to point towards the centre of the sarcomere and the heads point to the sides of the myofilament band.

Question (C).
Role of calcium ions in contraction and relaxation of muscles.
Answer:
Calcium ions play a major role in contraction and relaxation of muscles.

Calcium ions are released from the sarcoplasm during muscle contraction and stored in sarcoplasmic reticulum during muscle relaxation.
When a skeletal muscle is excited and an action potential travels along the T tubule, the concentration of calcium ions increases.
These calcium ions bind to troponin which in turn undergoes a conformational change that causes tropomyosin to move away from the myosin-binding sites on actin. Once these binding sites are free, myosin heads bind to them to form cross-bridges and the muscle fiber contracts.
The decrease in calcium ion concentration in the sarcoplasmic reticulum causes tropomyosin to slide back and block the myosin binding sites on actin. This causes the muscle to relax.

Question 5.
Draw labelled diagrams

Question (A).
Synovial joint.
Answer:
i. Synovial joints / freely movable joints / diarthroses:

It is characterized by presence of a space called synovial cavity between articulating bones that renders free movement at the joint.
The articulating surfaces of bones at a synovial joint are covered by a layer of hyaline cartilage. It reduces friction during movement and helps to absorb shock.
Synovial cavity is lined by synovial membrane that forms synovial capsule. Synovial membrane secretes synovial fluid.
Synovial fluid is a clear, viscous, straw coloured fluid similar to lymph. It is viscous due to hyaluronic acid. The synovial fluid also contains nutrients, mucous and phagocytic cells to remove microbes.
Synovial fluid lubricates the joint, absorbs shocks, nourishes the hyaline cartilage and removes waste materials from hyaline cartilage cells (as cartilage is avascular). Phagocytic cells destroy microbes and cellular debris formed by wear and tear of the joint.
If the joint is immobile for a while, the synovial fluid becomes viscous and as joint movement starts, it becomes less viscous.
The joint is provided with capsular ligament and numerous accessory ligaments. The fibrous capsule is attached to periosteum of articulating bones. The ligament helps in avoiding dislocation of joint.
The types of synovial joints are on follows:

1. Pivot joint: In this type of joint, the rounded or pointed surface of one bone articulates with a ring formed partly by another bone and partly by the ligament. Rotation only around its own longitudinal axis is possible. e.g. in joint between atlas and axis vertebrae, head turns side ways to form ‘NO’ joint.

2. Ball and socket joint: The ball like surface of one bone fits into cup like depression of another bone forming a movable joint. Multi-axial movements are possible. This type of joint allows movements along all three axes and in all directions. e.g. Shoulder and hip joint.

3. Hinge joint: In a hinge joint, convex surface of one bone fits into concave surface of another bone. In most hinge joints one bone remains stationary and other moves. The angular opening and closing motion (like hinge) is possible. In this joint only mono-axial movement takes place like flexion and extension. e.g. Elbow and knee joint.

4. Condyloid joint: It is an ellipsoid joint. The convex oval shaped projection of one bone fits into oval shaped depression in another bone. it is a biaxial joint because it permits movement along two axes viz, flexion, extension, abduction, adduction and circumduction is possible. e.g. Metacarpophalangeal joint.

5. Gliding joint: It is a planar joint, where the articulating surfaces of bones are flat or slightly curved. These joints are non-axial because the motion they allow does not occur along an axis or a plane. e.g. Intercarpal and intertarsal joints.

6. Saddle joint: This joint is a characteristic of Homo sapiens. Here the articular surface of one bone is saddle-shaped and that of other bone fits into saddle (each bone forming this joint have both concave and convex areas). It is a modified condyloid joint in which movement is somewhat more free. It is a biaxial joint that allows flexion, extension, abduction, adduction and circumduction.
e.g. Carpometacarpellar joint between carpal (trapezium) and metacarpal of thumb.

Question (B).
Different cartilagenous joints.
Answer:
Cartilaginous / slightly movable joints / amphiarthroses:
These joints are neither fixed nor freely movable. Articulating bones are held together by hyaline or fibrocartilages. They are further classified as

a. Synchondroses: The two bones are held together by hyaline cartilage. They are meant for growth. On completion of growth, the joint gets ossified, e.g. Epiphyseal plate found between epiphysis and diaphysis of a long bone, Rib – Sternum junction.

b. Symphysis: In this type of joint, broad flat disc of fibrocartilage connects two bones. It occurs in mid-line of the body. e.g. Intervertebral discs, manubrium and sternum, pubic symphysis.

Practical / Project :

Identify the following diagrams and demonstrate the concepts in classroom.

Answer:
The diagrams A, B and C represent Class I, Class II and Class III lever respectively.
For description:

Class I lever: The joint between the first vertebra and occipital condyle of skull is an example of Class I lever. The force is directed towards the joints (fulcrum); contraction of back muscle provides force while the part of head that is raised acts as
Class II lever: Human body raised on toes is an example of Class II lever. Toe acts as fulcrum, contracting calf muscles provide the force while raised body acts as resistance.
Class III lever: Flexion of forearm at elbow exhibit lever of class III. Elbow joint acts as fulcrum and radius, ulna provides resistance. Contracting bicep muscles provides force for the movement.

[Students are expected to perform the given activity on their own]

12th Biology Digest Chapter 16 Skeleton and Movement Intext Questions and Answers

Movements And Locomotion (Textbook Page No. 193)

Question 1.
Streaming of protoplasm, peristalsis, walking, running, etc. Which of the above-mentioned movements are internal? Which are external? Can you add few more examples?
Answer:

Streaming of protoplasm, peristalsis are internal movements. Walking and running are external movements.
Examples of internal movement: Contraction and relaxation heart, inspiration and expiration, contraction of blood vessels, etc.
Examples of external movement: Swimming; movement tongue, jaws, snout, tentacles, movement of ear pinna, etc.

Can you recall? (Textbook Page No. 193)

Question 1.
Which are different types of muscular tissues?
Answer:

Smooth / non-striated / visceral / involuntary muscles
Cardiac muscles
Skeletal / straited / voluntary muscles.

Question 2.
Name the type of muscles which bring about running and speaking.
Answer:
Skeletal muscles (Voluntary muscles)

Question 3.
Name the muscles which do not contract as per our will.
Answer:
Involuntary muscles (smooth muscles and cardiac muscles)

Question 4.
Which type of muscles show rhythmic contractions?
Answer:
Cardiac muscles

Question 5.
Which type of muscle is present in the diaphragm of the respiratory system?
Answer:
Skeletal muscle

Question 6.
State the functions of:

Smooth muscles
Cardiac muscles
Striated muscles

Answer:

Smooth muscles: They bring about involuntary movements like peristalsis in the alimentary canal, constriction and dilation of blood vessels.
Cardiac muscles: They bring about contraction and relaxation of the heart.
Striated muscles: They control voluntary movements of limbs, head, trunk, eyes, etc.

Can you recall? (Textbook Page No. 193)

Question 1.
Name the part of human skeleton situated along the vertical axis.
Answer:
Axial skeleton

Question 2.
Give an account of bones of human skull.
Answer:
Skull is made up of 22 bones. It is located at the superior end of vertebral column. The bones of skull are
joined by fixed or immovable joints except for jaw.

Skull consists of cranium or brain box and facial bones.

i. Cranium: It is made up of four median bones and two paired bones.

Frontal bone: It is median bone (unpaired) forming forehead, roof of orbit (eye socket) and the most anterior part of cranium. It is connected to two parietals, sphenoid and ethmoid bone.
Parietal bones: These paired bones form the roof of cranium and greater portion of sides of the cranium.
Temporal bones: These paired bones are situated laterally just above the ear on either side. Each temporal bone gives out zygomatic process that joins zygomatic bone to form zygomatic arch. Just at the base of zygomatic process is mandibular fossa, a depression for mandibles (lower jaw bone) that forms the only movable joint of the skull. This bone harbors the ear canal that directs sound waves into the ear. The processes of temporal bones provide points for attachment for various muscles of neck and tongue.
Occipital bone: It is a single bone present at the back of the head. It forms the posterior part and most of the base of cranium. The inferior part of this bone shows foramen magnum, the opening through which medulla oblongata connects with spinal cord. On the either sides of foramen magnum are two prominent protuberances called occipital condyles. These fit into the corresponding depressions present in 1^st vertebra.
Sphenoid bone: Median bone present at the base of the skull that articulates with all other cranial bones and holds them together. This butterfly shaped bone has a saddle shaped region called sella turcica. In this hypophyseal fossa, the pituitary gland is lodged.
Ethmoid bone: This median bone is spongy in appearance. It is located anterior to sphenoid and posterior to nasal bones. It contributes to formation of nasal septum and is major supporting structure of nasal cavity.

ii. Facial Bones: Fourteen facial bones give a characteristic shape to the face. The growth of face stops of the
age of 16.
Following bones comprise the facial bones:

Nasals: These are paired bones that form the bridge of nose.
Maxillae: These form the upper jaw bones. They are paired bones that join with all facial bones except mandible. Upper row of teeth are lodged maxillae.
Palatines: These are paired bones forming the roof of buccal cavity or floor of the nasal cavity.
Zygomatic bones: They are commonly called as cheek bones.
Lacrimal bones: These are the smallest amongst the facial bones.
These bones form the medial wall of each orbit. They have lacrimal fossa that houses lacrimal sacs. These sacs gather tears and send them to nasal cavity.
Inferior nasal conchae: They form the part of lateral wall of nasal cavity. They help to swirl and filter air before it passes to lungs.
Vomer: The median, roughly triangular bone that forms the inferior portion of nasal septum.
Mandible: This median bone forms the lower jaw. It is the largest and strongest facial bone. It is the only movable bone of skull. It has curved horizontal body and two perpendicular branches i.e. rami. These help in attachment of muscles. It has lower row of teeth lodged in it.

Think about it. (Textbook Page No. 193)

Question 1.
Did you ever feel tickling in muscles?
Answer:
Yes, the tickling sensation in muscles can be felt and sometimes it is also accompanied by itching sensation.

Question 2.
What is locomotion?
Answer:
The change in locus of whole body of living organism from one place to another place is called locomotion.

Question 3.
State the four basic types of locomotory movements seen in animals.
Answer:
The four basic types locomotory movements seen in animals are:

Amoeboid movement: It is performed by pseudopodia, e.g. leucocytes.
Ciliary movement: It is performed by cilia, e.g. ciliated epithelium. In Paramoecium, cilia help in passage of food through cytopharynx.
Whirling movement: It is performed by flagella, e.g. sperms.
Muscular movement: It is performed by muscles, with the help of bones and joints.

Question 4.

Question 1.
Why do muscles show spasm after rigorous contraction?
Answer:

Rigorous contraction of muscles occurs during strenuous activities (swimming. running, cycling, aerobics. etc.)
Muscle contraction requires energy. Glucose in muscle cells breakdown during anerobic respiration resulting in accumulation of lactic acid.
This lactic acid buildup triggers muscle spasm around muscle cells.

Question 2.
Why do we shiver during winter?
Answer:

Humans are homeotherms as the can regulate their body temperature with respect to the surrounding temperature. During winter, when temperature falls, the thermoreceptors detect the change in temperature and send signals to the brain.
Shivering reflex i.e. rapid contraction of muscles is triggered by the brain to generate heat and raise the body temperature.

Can you tell? (Textbook Page No. 194)

Question 1.
Why are movement and locomotion necessary among animals?
Answer:

Movement is one of the important characteristics of all the living organisms. Animals exhibit wide range of
movements like rhythmic beating of heart, movement of diaphragm during respiration, ingestion of food,
movement of eyeballs, etc.
Locomotion results into change in place or location of an organism. Animals locomote in search of food, mate, shelter, breeding ground. while escaping from the enemy, etc.
Thus, locomotion and movement are necessary to support the living of animals.

Question 2.
All locomotions are movements but all movements are not locomotion. Justify
Answer:
Locomotion occurs when body changes its position, however all movements may not result in locomotion. Thus, all locomotions are movements but all movements are not locomotion.

Question 3.
Kriti was diagnosed with knee tendon injury. She asked the doctor whether she will be able to walk due to the injury? If not then state the reason.
Answer:
Knee tendon injury affects the ability to walk. Kriti may not be able to walk freely as the tendons attached to the bones help in the movement of the parts of skeleton.

Question 4.
What are antagonistic muscles? Explain with example.
Answer:

The muscles that work in pairs and produce opposite action are known as antagonistic muscles, e.g. biceps and triceps of upper arm.
The biceps (flexors) bring flexion (folding) and triceps (extensors) bring extension of the elbow joint.
One member from a pair is capable of bending the joint by pulling of bones the other member is capable of straightening the same joint by pulling.
In antagonistic pair of muscles, one member is stronger than the other, e.g. The biceps are stronger than the triceps.

Question 5.
Describe the antagonistic muscles in detail.
Answer:
Following are the important antagonistic muscles:

Flexor and extensor: Flexor muscle on contraction results into bending or flexion of joint, e.g. Biceps. Extensor muscle on contraction results in straightening or extension of a joint, e.g. Triceps.
Abductor and adductor: Abductor muscle moves a body part away from the body axis. e.g. Deltoid muscle of shoulder moves the arm away from the body. Adductor muscle moves a body part towards the body axis, e.g. Latissimus dorsi of shoulder moves the arm near the body.
Pronator and supinator: Pronator turns the palm downwards and supinator turns the palm upward.
Levator and depressor: Levator raises a body part and the depressors lower the body part.
Protractor and retractor: Protractor moves forward, whereas the retractor moves backward.
Sphincters: Circular muscles present in the inner walls of anus, stomach, etc., for closure and opening.

Question 6.
Differentiate between:
i. Flexor and extensor muscles
Answer:

	Flexor Muscles		Extensor Muscles
a.	Flexor muscles contract and bring about the bending or flexion of joint.	a.	Extensor muscles contract and bring about the straightening or extension of joint.
b.	These muscles decrease the angle between the bones on two sides of a joint.	b.	These muscles increase the angle between the components of limb.
e.g.	Biceps	e.g.	Triceps

ii. Pronator and supinator: Pronator turns the palm downwards and supinator turns the palm upward.

Can you recall? (Textbook Page No. 194)

Question 1.
Comment on contraction of skeletal muscles.
Answer:
Skeletal muscles show quick and strong voluntary contractions. They bring about voluntary movements of the body. For mechanism of muscle contraction:

When the muscles are relaxed, the active sites remain covered with tropomyosin and troponin complex. Due to this, myosin cannot interact with active site of actin and thus contraction cannot occur.

When an impulse (action potential) comes to muscle through motor end plate, it spreads throughout the sarcolemma of the myofibril.
The transverse tubules of sarcoplasmic reticulum release large number of Ca⁺⁺ ions into sarcoplasm. These calcium ions interact with the troponin molecules and the interaction inactivates troponin-tropomyosin complex. This causes change in the structure of tropomyosin.
As a result, tropomyosin gets detached from the active site of actin (F actin) filament, exposing the active site for actin.
The myosin head cleaves the ATP to derive energy and gets attached to the uncovered active site of actin. This results into the formation of acto-myosin complex.
The myosin heads are now tilted backwards and pull the attached actin filament inwardly. This results in contraction of the muscle fibres.

Do You Know How (Textbook Page No. 195)

Question 1.
Do skeletal muscles contract and bring about movement and locomotion?
Answer:
When the muscles are relaxed, the active sites remain covered with tropomyosin and troponin complex. Due to this, myosin cannot interact with active site of actin and thus contraction cannot occur.

When an impulse (action potential) comes to muscle through motor end plate, it spreads throughout the sarcolemma of the myofibril.
The transverse tubules of sarcoplasmic reticulum release large number of Ca⁺⁺ ions into sarcoplasm. These calcium ions interact with the troponin molecules and the interaction inactivates troponin-tropomyosin complex. This causes change in the structure of tropomyosin.
As a result, tropomyosin gets detached from the active site of actin (F actin) filament, exposing the active site for actin.
The myosin head cleaves the ATP to derive energy and gets attached to the uncovered active site of actin. This results into the formation of acto-myosin complex.
The myosin heads are now tilted backwards and pull the attached actin filament inwardly. This results in contraction of the muscle fibres.

Internet my friend. (Textbook Page No. 196)

Question 1.
Collect information about‘T’ tubules of sarcoplasmic reticulum.
Answer:

T tubules or the transverse tubules are invaginations of the sarcolemma penetrating into the myocyte interior, forming a highly branched and interconnected network that makes junctions with the sarcoplasmic reticulum.
These tubules are selectively enriched with specific ion channels and proteins crucial in the development of calcium transients necessary in excitation-contraction coupling, thereby facilitating a fast-synchronous contraction of the entire cell volume.
They are unique to straited muscle cells.
[Source: https://www. uniprot. org/locations]

Can you tell? (Textbook Page No. 197)

Question 1.
Explain the chemical changes taking place in muscle contraction.
Answer:
The muscle undergoes various chemical changes during contraction, they are as follows:

A nerve impulse arrives at the motor nerve. The neurotransmitter – acetylcholine is released at the neuromuscular junction (N-M junction or motor endplate) enters into the sarcomere.
This leads to inflow of Na+ inside the sarcomere and generates an action potential in the muscle fibre.
The action potential passes down the T tubules and activates calcium channels in the T tubular membrane. Activation of calcium channel allows calcium ions to pass into the sarcoplasm. These Ca⁺⁺ ions binds to the specific sites on troponin of actin filaments and a conformational change occurs in the troponin – tropomyosin complex, thereby removing the masking of active sites for myosin on the actin filament.
In the myosin head, the enzyme ATPase gets activated in the presence of Ca⁺⁺ and converts ATP into ADP and inorganic phosphate.
This energy from ATP hydrolysis is utilized by myosin bridges or myosin heads to bind with active sites of actin and form actomyosin complex pulling the actin filaments towards the centre of sarcomere. The myosin heads are now tilted backwards and pull the attached actin filament inwardly towards them. The actin filament slides over mysosin and contraction occurs.
Also, the ADP needs to be converted back to ATP immediately as they required for muscular contraction, This is achieved in the muscles by the presence of another high energy compound, creatine phosphate.
ADP combines with creatine phosphate to produce ATP and creatinine due to which the supply of ATP for muscle contraction is restored but the level of creatine phosphate keeps decreasing and the level of creatinine keeps on increasing.
The creatinine formed needs to be reconverted to creatine phosphate. This is done by ATP produced during oxidation of glycogen through glycolysis.

Question 2.
Why are muscle rich in creatine phosphate?
Answer:

Creatine phosphate or phosphocreatine is formed from ATP, when the muscle is in relaxed state. It is a phosphorylated form of creatine.
Muscle cells contain creatine phosphate which acts as energy reserve as this high energy compound acts as a phosphate donor for ATP formation.
ATP acts as an immediate source of energy for contraction

Question 3.
Explain the mechanism of muscle contraction and relaxation.
Answer:
Mechanism of muscle contraction:

When the muscles are relaxed, the active sites remain covered with tropomyosin and troponin complex. Due to this, myosin cannot interact with active site of actin and thus contraction cannot occur.

When an impulse (action potential) comes to muscle through motor end plate, it spreads throughout the sarcolemma of the myofibril.
The transverse tubules of sarcoplasmic reticulum release large number of Ca⁺⁺ ions into sarcoplasm. These calcium ions interact with the troponin molecules and the interaction inactivates troponin-tropomyosin complex. This causes change in the structure of tropomyosin.
As a result, tropomyosin gets detached from the active site of actin (F actin) filament, exposing the active site for actin.
The myosin head cleaves the ATP to derive energy and gets attached to the uncovered active site of actin. This results into the formation of actomyosin complex.
The myosin heads are now tilted backwards and pull the attached actin filament inwardly. This results in contraction of the muscle fibres.

Muscle relaxation: During relaxation, all the events occur in reverse direction as that of muscle contraction.

When the stimulation is terminated, the actomyosin complex is broken down and myosin head gets detached from actin filaments. This process utilizes ATP.
Also, the Ca⁺⁺ ions are pumped back into the sarcoplasmic reticulum. This process too is an energy dependent process and utilizes ATP.
As a result, the troponin-tropomyosin complex is restored again which covers the active sites of act in filament, due to disappearance of the Ca⁺⁺ ions. The interaction between actin and myosin ceases and the actin filaments return back to their original position.
This results in muscle relaxation.

Question 4.
What do you understand by muscle twitch?
Answer:
Single muscle twitch:

Single muscle twitch: It is a muscle contraction initiated by a single brief-stimulation. It occurs in 3 stages: a latent period of no contraction, a contraction period and a relaxation period.

The involuntary contraction of muscle fibers is known as muscle twitch.
Muscle twitch is also known as fasciculation.
It is caused due accumulation of lactic acid in muscles.

Do You Know How (Textbook Page No. 198)

Question 1.
Exoskeletal components change from lower to higher group of animals. These include chitinous structures, nails, horns, hooves, scales, hair, shell, plates, fur, muscular foot, tube feet, etc.

Question 1.
Do you know any of these exoskeletal structures help in movement and locomotion?
Answer:
Nails, hooves, scales, plates, muscular foot and tube feet help in movement and locomotion.

Question 2.
How do scales and plates help in movement and locomotion?
Answer:
Scales and plates in reptiles like snakes provide grip to move on rough edgy surfaces.

Question 3.
Are scales of a fish and that of snake similar?
Answer:
Fishes have dermal scales (bony scales), whereas reptiles like snakes have epidermal scales or scutes (horny, tough extensions of outer layer of skin i.e., stratum corneum).

Question 4.
Find out more information about exoskeletal structures and their role in movement and locomotion.
Answer:
Exoskeletal structures: Exoskeleton provide support, help in movement and also provides protection from predators. The exoskeletal structures vary from organism to organism. Echinoderms have tube feet for locomotion whereas molluscs (e.g. Chiton) have muscular foot for movement and locomotion

[Students are expected to find out more information about exoskeletal structures on their own.]

Question 2.
Name the tissues that form the structural framework of the body.
Answer:
Cartilage and bone

Do you remember? (Textbook Page No. 198)

Question 1.
What are the components of skeletal system?
Answer:
The components of skeletal system are bones, tendons, ligaments and joint.

Question 2.
What type of bones are present in our body?
Answer:
Long bones, short bones, flat bones, irregular bones and sesamoid bones.

Question 3.
How do bones help in various ways?
Answer:

Bones form the framework of our body and thus provide shape to the body.
They protect vital organs thus help in the smooth functioning of body.
The joints between the bones help in movement and locomotion.
They provide firm surface for attachment of muscles.
They are reservoirs of calcium and form important site for hemopoiesis.

Use your brain power. (Textbook Page No. 198)

Question 1.
Can you compare bone, muscle and joint which help in locomotion with any simple machines you have studied earlier?
Answer:
Bone, muscle and joint can be compared to the simple machines called levers. Joints act as fulcrum, respective muscle generates the force required to move the bone associated with joint.

Question 2.
Explain the three types of lever found in human body.
Answer:
The three types of lever are as follows:

Class I lever: The joint between the first vertebra and occipital condyle of skull is an example of Class I lever. The force is directed towards the joints (fulcrum); contraction of back muscle provides force while the part of head that is raised acts as resistance.
Class II lever: Human body raised on toes is an example of Class II lever. Toe acts as fulcrum, contracting calf muscles provide the force while raised body acts as resistance.
Class III lever: Flexion of forearm at elbow exhibit lever of class III. Elbow joint acts as fulcrum and radius, ulna provides resistance. Contracting bicep muscles provides force for the movement.

Use your brain power. (Textbook Page No. 199)

Question 1.
Why are long bones slightly bent and not straight?
Answer:

Long bones include tibia, fibula, femur, humerus, radius, ulna, etc.
They have greater length than width. They consist of a shaft and variable number of epiphysis.
They are slightly bent or curved to absorb the stress of the body’s weight and evenly distribute the body weight at several different points.
If long bones were straight, the weight of the body would be unevenly distributed and the bone would fracture more easily.

Identify and label. (Textbook Page No. 199)

Question 1.
Identify the different bones.
Answer:

Identify and label. (Textbook Page No. 200)

Question 1.
Name A, B, C and D from the given figure and discuss in group.

Answer:
A – Coronal suture,
B – Sagittal suture,
C – Lambdoidal suture,
D – Lateral / Squamous suture

Skull has many sutures (type of immovable joints) present, out of which four prominent ones are:

Coronal suture: Joins frontal bone with parietals.
Sagittal suture: Joins two parietal bones.
Lambdiodal suture: Joins two parietal bones with occipital bone.
Lateral/squamous sutures: Joins parietal and temporal bones on lateral side.

Can you tell? (Textbook Page No. 201)

Question 1.
Give schematic plan of human skeleton.
Answer:

[Note: Numbers in the bracket indicate the number of bones.]

Can you tell? (Textbook Page No. 201)

Question 1.
Enlist the bones of cranium.
Answer:
Cranium: It is made up of four median bones and two paired bones.

Frontal bone: It is median bone (unpaired) forming forehead, roof of orbit (eye socket) and the most anterior part of cranium. It is connected to two parietals, sphenoid and ethmoid bone.
Parietal bones: These paired bones form the roof of cranium and greater portion of sides of the cranium.
Temporal bones: These paired bones are situated laterally just above the ear on either side. Each temporal bone gives out zygomatic process that joins zygomatic bone to form zygomatic arch. Just at the base of zygomatic process is mandibular fossa, a depression for mandibles (lower jaw bone) that forms the only movable joint of the skull. This bone harbors the ear canal that directs sound waves into the ear. The processes of temporal bones provide points for attachment for various muscles of neck and tongue.
Occipital bone: It is a single bone present at the back of the head. It forms the posterior part and most of the base of cranium. The inferior part of this bone shows foramen magnum, the opening through which medulla oblongata connects with spinal cord. On the either sides of foramen magnum are two prominent protuberances called occipital condyles. These fit into the corresponding depressions present in 1st vertebra.
Sphenoid bone: Median bone present at the base of the skull that articulates with all other cranial bones and holds them together. This butterfly shaped bone has a saddle shaped region called sella turcica. In this hypophyseal fossa, the pituitary gland is lodged.
Ethmoid bone: This median bone is spongy in appearance. It is located anterior to sphenoid and posterior to nasal bones. It contributes to formation of nasal septum and is major supporting structure of nasal cavity.

Can you tell? (Textbook Page No. 201)

Question 1.
Write a note on structure and function of skull.
Answer:
i. Structure of skull:
Skull is made up of 22 bones. It is located at the superior end of vertebral column. The bones of skull are joined by fixed or immovable joints except for jaw.

Skull consists of cranium or brain box and facial bones.

i. Cranium: It is made up of four median bones and two paired bones.

Frontal bone: It is median bone (unpaired) forming forehead, roof of orbit (eye socket) and the most anterior part of cranium. It is connected to two parietals, sphenoid and ethmoid bone.
Parietal bones: These paired bones form the roof of cranium and greater portion of sides of the cranium.
Temporal bones: These paired bones are situated laterally just above the ear on either side. Each temporal bone gives out zygomatic process that joins zygomatic bone to form zygomatic arch. Just at the base of zygomatic process is mandibular fossa, a depression for mandibles (lower jaw bone) that forms the only movable joint of the skull. This bone harbors the ear canal that directs sound waves into the ear. The processes of temporal bones provide points for attachment for various muscles of neck and tongue.
Occipital bone: It is a single bone present at the back of the head. It forms the posterior part and most of the base of cranium. The inferior part of this bone shows foramen magnum, the opening through which medulla oblongata connects with spinal cord. On the either sides of foramen magnum are two prominent protuberances called occipital condyles. These fit into the corresponding depressions present in 1^st vertebra.
Sphenoid bone: Median bone present at the base of the skull that articulates with all other cranial bones and holds them together. This butterfly shaped bone has a saddle shaped region called sella turcica. In this hypophyseal fossa, the pituitary gland is lodged.
Ethmoid bone: This median bone is spongy in appearance. It is located anterior to sphenoid and posterior to nasal bones. It contributes to formation of nasal septum and is major supporting structure of nasal cavity.

ii. Facial Bones: Fourteen facial bones give a characteristic shape to the face. The growth of face stops of the age of 16.
Following bones comprise the facial bones:

Nasals: These are paired bones that form the bridge of nose.
Maxillae: These form the upper jaw bones. They are paired bones that join with all facial bones except mandible. Upper row of teeth are lodged maxillae.
Palatines: These are paired bones forming the roof of buccal cavity or floor of the nasal cavity.
Zygomatic bones: They are commonly called as cheek bones.
Lacrimal bones: These are the smallest amongst the facial bones. These bones form the medial wall of each orbit. They have lacrimal fossa that houses lacrimal sacs. These sacs gather tears and send them to nasal cavity.
Inferior nasal conchae: They form the part of lateral wall of nasal cavity. They help to swirl and filter air before it passes to lungs.
Vomer: The median, roughly triangular bone that forms the inferior portion of nasal septum.
Mandible: This median bone forms the lower jaw. It is the largest and strongest facial bone. It is the only movable bone of skull. It has curved horizontal body and two perpendicular branches i.e. rami. These help in attachment of muscles. It has lower row of teeth lodged in it.

ii. Functions of skull:

It protects the brain.
It provides sockets for ear, nasal chamber and eyes.
Mandible bone of the skull helps in opening and closing of the mouth.

Internet my friend. (Textbook Page No. 201)

Question 1.
Cleft palate and cleft lip
Answer:

Cleft palate and cleft lip are the birth defects that occur when a baby’s lip or mouth does develop properly.
Cleft palate happens when the tissue that forms the roof of the mouth does not join together completely during pregnancy.
Cleft lip happens when the tissue that makes up the lip does not join completely before birth. This leads to formation of an opening in the upper lip.

[Students are expected to find more information about Cleft Palate and lip on internet.]

Can you tell? (Textbook Page No. 202)

Question 1.
Why skull is important for us? Enlist few reasons.
Answer:
Functions of skull:

It protects the brain.
It provides sockets for ear, nasal chamber and eyes.
Mandible bone of the skull helps in opening and closing of the mouth.

Internet my friend. (Textbook Page No. 202)

Question 1.
Find out information about sinuses present in skull, functions of skull and disorder ‘sinusitis’.
Answer:
Sinuses are the hollow cavities present in the skull. They humidify the air we breathe.

i. The four types of sinuses present in the skull:

Frontal sinuses: They are located above each eye. There are right and left frontal sinuses.
Maxillary sinuses: They are the largest among all sinuses, located just behind the cheekbones near to upper jaws.
Sphenoid sinuses: These are present just behind the nose.
Ethmoid sinuses: These are present between the eyes.

ii. Functions of skull:

Functions of skull:

It protects the brain.
It provides sockets for ear, nasal chamber and eyes.
Mandible bone of the skull helps in opening and closing of the mouth.

iii. Sinusitis: It is the inflammation of tissue lining the sinuses. Healthy sinuses when get blocked with mucus and germs causing infection which may lead to sinusitis.

[Students are expected to find more information about sinusitis, using the internet.]

Something interesting. (Textbook Page No. 202)

Question 1.
If police suspect strangulation, they carefully inspect hyoid bone and cartilage of larynx. These get fractured during strangulation. V arious such investigations are done in case of suspicious death of an individual where ossification of sutures in skull, width of pelvic girdle, etc. are examined to find out approximate age of victim or gender of victim, etc. You may find out information about forensic science.
Answer:
Forensic science is an application of science which is used in the matter of criminal determination and civil law. It is generally used in investigation of crimes. Forensic scientists collect, preserve and analyze the evidence during the course of investigation.
[Students are expected to find more information about forensic science on internet.]

Try this. (Textbook Page No. 202)

Question 1.
Feel your spine (vertebral column). Is it straight or curved?
Answer:
Our spinc shows four slight curves which are visible when viewed from the sides.

Question 2.
Find information about slipped disc. (Textbook page no.202)
Answer:

The bones of vertebral column are supported by the intervertebral discs.
These intervertebral discs act as shock absorbers due to which they are constantly compressed.
The disc consists of two parts – soft gelatinous inner part (nucleus pulposus) and tough outer ring.

If the ligaments of the intervertebral discs become injured, the pressure developed in the nucleus pulposus protrudes posteriorly or into one of the adjacent vertebrae. This is known as slipped disc.

[Students are expected to find more information using the internet.]

Can you tell? (Textbook Page No. 204)

Question 1.
Write a note on curvatures of vertebral column and mention their importance.
Answer:

The four curvatures in human spine are cervical, lumbar, thoracic and sacral curvatures.
The cervical and lumbar curvatures are secondary and convex whereas the thoracic and sacral curvatures are
primary and concave.
Importance: Curvatures help in maintaining balance in upright position. They absorb shocks while walking
and also protect the vertebrae from fracture.

Question 2.
Explain the structure of typical vertebra.
Answer:

Each vertebra has prominent central body called centrum.
The centra of human vertebrae are flat in anterio-posterior aspect. Thus, human vertebrae are amphiplatyan.
From the either side of the centrum are two thick short processes which unite to form an arch like structure called neural arch, posterior to centrum.
Neural arch forms vertebral foramen which surrounds the spinal cord.
Vertebral foramina of all vertebrae form a continuous ‘neural canal’. Spinal cord along with blood vessels and protective fatty covering passes through neural canal.
The point where two processes of centrum meet, the neural arch is drawn into a spinous process called neural spine.
From the base of neural arch, two articulating processes called zygapophyses are given out on either side. The anterior is called superior zygapophyses and posterior called inferior zygapophyses.
In a stack of vertebrae, inferior zygapophyses of one vertebra articulates with superior zygapophyses of next vertebra. This allows slight movement of vertebrae without allowing them to fall.
At the junction of zygapophyses, a small opening is formed on either side of vertebra called intervertebral foramen that allows passage of spinal nerve.
From the base of neural arch, lateral processes are given out called transverse processes. Neural arch, neural spine and transverse processes are meant for attachment of muscles.

Question 2.
How will you identify a thoracic vertebra?
Answer:
Thoracic vertebrae can be identified on the basis of centrum, as the centrum of the thoracic vertebrae is heart shaped.

Can you recall? (Textbook Page No. 206)

Question 1.
How does humerus form ball and socket joint? Where is it located?
Answer:
The head of humerus fits into the glenoid cavity of scapula and forms ball and socket joint. it is located in shoulder and hips.

Can you tell? (Textbook Page No. 208)

Question 1.
Differentiate between the skeleton of palm and foot.
Answer:

	Skeleton of palm	Skeleton of foot
a.	It consists of metacarpals and phalanges	It consists of metatarsals and phalanges
b.	Saddle joints and condyloid joints are in the palm.	Condyloid or saddle joints are not present the foot.

Question 2.
Explain the longest bone in human body.
Answer:
Femur: The thigh bone is the longest bone in the body. The head is joined to shaft at an angle by a short neck. It forms ball and socket joint with acetabulum cavity of coxal bone. The lower one third region of shaft is triangular flattened area called popliteal surface. Distal end has two condyles that articulate with tibia and fibula.

Internet my friend. (Textbook Page No. 212)

Question 1.
Find out information about types of fractures and how they heal.
Answer:

Fractures are classified based on their severity, shape or position of the fracture line or the physician who first described them.
Types of fractures:
1. Open fractures: The broken ends of the bone protrude through skin.
2. Comminuted fractures: The bone is splintered, crushed or broken into pieces at the site of impact and smaller bone fragments lie between the two main fragments.
3. Greenstick fractures: A partial fracture in which one side of the bone is broken and the other side bends.
4. Impacted fractures: One end of the fractured bone is forcefully driven into the inferior of the other.
5. Pott fractures: Fracture of the distal end lateral leg bone with serious injury of the distal tibial articulation.
6. Codes fractures: Fracture of the distal end of the lateral forearm in which the distal fragment is displaced posteriorly.
A fractured bone heals in four phases viz, reactive phase, fibrocartilaginous formation phase, bony callus formation phase and bone remodeling phase.

[Source: Tortora, G., Derrickson, B. Principles of Anatomy and Physiology. 15^th Edition]

[Students are expected to find out more information about healing of fractures using the internet.]

Do you remember? (Textbook Page No. 208)

Question 1.
What are joints? What are the types?
Answer:
i. A point where two or more bones get articulated is called joint or articulation or athrosis.
They are classified based on degree of flexibility or movement they permit into lastly synovial or freely movable or diarthroses type of joints.

ii. Synarthroses / fibrous joints / movable joints:
In this joint, the articulating bones are held together by means of fibrous connective tissue. Bones do not exhibit movement. Hence, it is immovable or fixed type of joint. Synarthroses are further classified into sutures, syndesmoses and gomphoses.

Sutures: It is composed of thin layer of a dense fibrous connective tissue. Sutures are places of growth. They remain open till growth is complete. On completion of growth, they tend to ossify. Sutures may permit some moulding during childhood. Sutures are further classified into butt joint, scarf joint, lap joint and serrate joint.
Syndesmoses: It is present where there is greater distance between articulating bones. At such locations, fibrous connective tissue is arranged as a sheet or bundle, e.g. Distal tibiofibular joint, interosseous membrane between tibia and fibula and that between radius and ulna.
Gomphoses: In this type of joint, a cone shaped bone fits into a socket provided by other bone,
e. g. Tooth and jaw bones.

iii. Cartilaginous / slightly movable joints / amphiarthroses:
These joints are neither fixed nor freely movable. Articulating bones are held together by hyaline or
fibrocartilages. They are further classified as

Synchondroses: The two bones are held together by hyaline cartilage. They are meant for growth.
On completion of growth, the joint gets ossified, e.g. Epiphyseal plate found between epiphysis and diaphysis of a long bone, Rib – Sternum junction.
Symphysis: In this type of joint, broad flat disc of fibrocartilage connects two bones. It occurs in mid-line of the body. e.g. Intervertebral discs, manubrium and sternum, pubic symphysis.

iv. Synovial joints / freely movable joints / diarthroses:

It is characterized by presence of a space called synovial cavity between articulating bones that renders free movement at the joint.
The articulating surfaces of bones at a synovial joint are covered by a layer of hyaline cartilage. It reduces friction during movement and helps to absorb shock.
Synovial cavity is lined by synovial membrane that forms synovial capsule. Synovial membrane secretes synovial fluid.
Synovial fluid is a clear, viscous, straw coloured fluid similar to lymph. It is viscous due to hyaluronic acid. The synovial fluid also contains nutrients, mucous and phagocytic cells to remove microbes. Synovial fluid lubricates the joint, absorbs shocks, nourishes the hyaline cartilage and removes waste materials from hyaline cartilage cells (as cartilage is avascular). Phagocytic cells destroy microbes and cellular debris formed by wear and tear of the joint.
If the joint is immobile for a while, the synovial fluid becomes viscous and as joint movement starts, it becomes less viscous.
The joint is provided with capsular ligament and numerous accessory ligaments. The fibrous capsule is attached to periosteum of articulating bones. The ligament helps in avoiding dislocation of joint.

g. The types of synovial joints are on follows:

2. BaIl and socket joint: The ball like surface of one bone fits into cup like depression of another bone forming a movable joint. Multi-axial movements are possible. This type of joint allows movements along all three axes and in all directions. e.g. Shoulder and hip joint.

4. Condyloid joint: It is an ellipsoid joint. The convex oval shaped projection of one bone fits into oval shaped depression in another bone. It is a biaxial joint because it permits movement along two axes viz, flexion, extension, abduction, adduction and circumduction is possible. e.g. Metacarpophalangeal joint.

Saddle joint: This joint is a characteristic of Homo sapiens. Here the articular surface of one bone is saddle-shaped and that of other bone fits into saddle (each bone forming this joint have both concave and convex areas). It is a modified condyloid joint in which movement is somewhat more free. It is a biaxial joint that allows flexion, extension, abduction, adduction and circumduction. e.g. Carpometacarpellar joint between carpal (trapezium) and metacarpal of thumb.

Imagine. (Textbook Page No. 208)

Question 1.
If your elbow joint would be a fixed type of joint and joint between teeth and gum would be freely movable.
Answer:

If the elbow joint would be fixed the flexion and extension of the forearm won’t be possible. Also, rotation of the forearm and wrist would not be not possible.
Gomphoses is the type of joint that holds the teeth in the jaw bone. If this joint would be freely movable, we would not be able to chew and all our teeth would fall out.

Use your brain power. (Textbook Page No. 210)

Question 1.
Why are warming up rounds essential before regular exercise?
Answer:

Warming up before exercise stimulates the production and secretion of synovial fluid which reduces the stress on joints during exercise.
Also, if a joint is immobile for a while, the synovial fluid becomes viscous and as joint movement starts, it becomes less viscous.
Warming up increases the blood circulation, loosening the joints and increasing the blood flow. It also prepares the muscles for physical activity and prevents injuries.

Can you tell? (Textbook Page No. 211)

Question 1.
Classify various types of joints found in human body. Present the information in the form of chart. Give example of each type.
Answer:

i. A point where two or more bones get articulated is called joint or articulation or athrosis.
They are classified based on degree of flexibility or movement they permit into lastly synovial or freely movable or diarthroses type of joints.

Sutures: It is composed of thin layer of a dense fibrous connective tissue. Sutures are places of growth. They remain open till growth is complete. On completion of growth, they tend to ossify. Sutures may permit some moulding during childhood. Sutures are further classified into butt joint, scarf joint, lap joint and serrate joint.
Syndesmoses: It is present where there is greater distance between articulating bones. At such locations, fibrous connective tissue is arranged as a sheet or bundle, e.g. Distal tibiofibular joint, interosseous membrane between tibia and fibula and that between radius and ulna.
Gomphoses: In this type of joint, a cone shaped bone fits into a socket provided by other bone,
e. g. Tooth and jaw bones.

Synchondroses: The two bones are held together by hyaline cartilage. They are meant for growth.
On completion of growth, the joint gets ossified, e.g. Epiphyseal plate found between epiphysis and diaphysis of a long bone, Rib – Sternum junction.
Symphysis: In this type of joint, broad flat disc of fibrocartilage connects two bones. It occurs in mid-line of the body. e.g. Intervertebral discs, manubrium and sternum, pubic symphysis.

iv. Synovial joints / freely movable joints / diarthroses:

It is characterized by presence of a space called synovial cavity between articulating bones that renders free movement at the joint.
The articulating surfaces of bones at a synovial joint are covered by a layer of hyaline cartilage. It reduces friction during movement and helps to absorb shock.
Synovial cavity is lined by synovial membrane that forms synovial capsule. Synovial membrane secretes synovial fluid.
Synovial fluid is a clear, viscous, straw coloured fluid similar to lymph. It is viscous due to hyaluronic acid. The synovial fluid also contains nutrients, mucous and phagocytic cells to remove microbes.
Synovial fluid lubricates the joint, absorbs shocks, nourishes the hyaline cartilage and removes waste materials from hyaline cartilage cells (as cartilage is avascular). Phagocytic cells destroy microbes and cellular debris formed by wear and tear of the joint.
If the joint is immobile for a while, the synovial fluid becomes viscous and as joint movement starts, it becomes less viscous.
The joint is provided with capsular ligament and numerous accessory ligaments. The fibrous capsule is attached to periosteum of articulating bones. The ligament helps in avoiding dislocation of joint.

g. The types of synovial joints are on follows:

[Students are expected to prepare a chart on their own.]

Can you tell? (Textbook Page No. 211)

Question 1.
Human beings can hold an object in a better manner than monkeys. Why?
Answer:

Humans and monkeys both have five fingers including thumb, however humans can hold an object in better manner than monkeys because humans have highly developed opposable thumbs. The opposable thumb allows better grip.
The saddle joint in thumb allows free and independent movement to the thumb the carpometacarpellar joint between carpal (trapezium) and metacarpal of thumb makes the thumb opposable. It allows biaxial movements, i.e. flexion – extension and adduction – abduction but not rotation.

[Note: Gorillas, chimpanzees, orangutans and some other variants of apes have opposable thumb.]

Internet my friend. (Textbook Page No. 211)

Question 92.
Now a days we hear from many elderly people that they are undergoing knee replacement surgery. Find out why one has to undergo knee replacement; how it is carried out and how it can be prevented.
Answer:
Knee replacement is done in following cases:

Osteoarthritis: The cartilage in the knee undergoes degradation. It is caused by many factors such as muscle weakness, aging, obesity, etc.
Rheumatoid arthritis: It is characterised by inflammation of the synovial membrane, where it starts secreting excess of synovial fluid in the joint. This fluid exerts extensive pressure on the joint and causes severe pain.
Post-traumatic arthritis: This is caused due to breakage of ligament or cartilage. The breakage can be due to severe injury or accident. It causes severe pain and requires knee replacement.
Procedure:
The procedure involves removal of the damaged cartilage or ligament and replaces it with artificial implant made up of either metal, plastic or both. Metal or plastic knee caps are used to cover the knees. The implant is connected to the bone and an artificial knee joint is made between them.
Prevention: Maintaining body weight, exercising regularly, consuming appropriate medications and supplements, etc.

[Students are expected to find out more information about knee replacement on internet]

Find out. (Textbook Page No. 212)

Question 1.
You must have heard of Sachin Tendulkar suffering from ‘tennis elbow’, a cricketer suffering from a disorder named after another game. Can common people too suffer from this disorder? Find out more information about this disorder.
Answer:

Tennis elbow is caused due to inflammation of tendon which joins muscles of forearm to the bone of upper arm (humerus). It is known as lateral epicondylitis.
It causes severe pain in the elbow. It occurs due to extensive repetitive movement of hand. This damages the tendon and increases the tenderness of the elbow joint.
This disorder develops not only in athletes but also in other common people whose job involves extensive movement of hand such as carpenter, painter, plumber, etc.

[Students are expected to find more information about tennis elbow on their own.]

11th Std Biology Questions And Answers:

11th Physics Chapter 7 Exercise Thermal Properties of Matter Solutions Maharashtra Board

January 7, 2025January 6, 2025 by Prasanna

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 7 Thermal Properties of Matter Textbook Exercise Questions and Answers.

Thermal Properties of Matter Class 11 Exercise Question Answers Solutions Maharashtra Board

Class 11 Physics Chapter 7 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 7 Exercise Solutions

1. Choose the correct option.

Question 1.
Range of temperature in a clinical thermometer, which measures the temperature of human body, is
(A) 70 ºC to 100 ºC
(B) 34 ºC to 42 ºC
(C) 0 ºF to 100 ºF
(D) 34 ºF to 80 ºF
Answer:
(B) 34 ºC to 42 ºC

Question 2.
A glass bottle completely filled with water is kept in the freezer. Why does it crack?
(A) Bottle gets contracted
(B) Bottle is expanded
(C) Water expands on freezing
(D) Water contracts on freezing
Answer:
(C) Water expands on freezing

Question 3.
If two temperatures differ by 25 °C on Celsius scale, the difference in temperature on Fahrenheit scale is
(A) 65°
(B) 45°
(C) 38°
(D) 25°
Answer:
(B) 45°

Question 4.
If α, β and γ are coefficients of linear, area l and volume expansion of a solid then
(A) α: β:γ 1:3:2
(B) α:β:γ 1:2:3
(C) α:β:γ 2:3:1
(D) α:β:γ 3:1:2
Answer:
(B) α:β:γ 1:2:3

Question 5.
Consider the following statements-
(I) The coefficient of linear expansion has dimension K^-1
(II) The coefficient of volume expansion has dimension K^-1
(A) I and II are both correct
(B) I is correct but II is wrong
(C) II is correct but I is wrong
(D) I and II are both wrong
Answer:
(A) I and II are both correct

Question 6.
Water falls from a height of 200 m. What is the difference in temperature between the water at the top and bottom of a water fall given that specific heat of water is 4200 J kg^-1 °C^-1?
(A) 0.96 °C
(B) 1.02 °C
(C) 0.46 °C
(D) 1.16 °C
Answer:
(C) 0.46 °C

2. Answer the following questions.

Question 1.
Clearly state the difference between heat and temperature?
Answer:

	Heat	Temperature
i.	Heat is energy in transit. When two bodies at different temperatures are brought in contact, they exchange heat. OR Heat is the form of energy transferred between two (or more) systems or a system and its surroundings by virtue of their temperature difference.	Temperature is a physical quantity that defines the thermodynamic state of a system. OR Heat transfer takes place between the body and the surrounding medium until the body and the surrounding medium are at the same temperature.
ii.	Heat exchange can be measured with the help of a calorimeter.	Temperature is measured with the help of a thermometer.
iii.	Heat (being a form of energy) is a derived quantity.	Temperature is a fundamental quantity.

Question 2.
How a thermometer is calibrated?
Answer:

For the calibration of a thermometer, a standard temperature interval is selected between two easily reproducible fixed temperatures.
The fact that substances change state from solid to liquid to gas at fixed temperatures is used to define reference temperature called fixed point.
The two fixed temperatures selected for this purpose are the melting point of ice or freezing point of water and the boiling point of water.
This standard temperature interval is divided into sub-intervals by utilizing some physical property that changes with temperature.
Each sub-interval is called as a degree of temperature. Thus, an empirical scale for temperature is set up.

Question 3.
What are different scales of temperature? What is the relation between them?
Answer:

Celsius scale:
- The ice point (melting point of pure ice) is marked as O °C (lower point) and steam point (boiling point of water) is marked as 100 °C (higher point).
- Both are taken at one atmospheric pressure.
- The interval between these points is divided into two equal parts. Each of these parts is called as one degree celsius and it is ‘written as 1 °C.
Fahrenheit scale:
- The ice point (melting point of pure ice) is marked as 32 °F and steam point (boiling point of water) is marked as 212 °F.
- The interval between these two reference points is divided into 180 equal parts. Each part is called as degree fahrenheit and is written as 1 °F.
Kelvin scale:
- The temperature scale that has its zero at -273.15 °C and temperature intervals are same as that on the Celsius scale is called as kelvin scale or absolute scale.
- The absolute temperature, T and celsius temperature, T_C are related as, T = T_C + 273.15
  eg.: when T_C = 27 °C,
  T = 27+273.15 K = 300.15 K

Relation between different scales of temperature:
\(\frac{\mathrm{T}_{\mathrm{F}}-32}{180}=\frac{\mathrm{T}_{\mathrm{C}}-0}{100}=\frac{\mathrm{T}_{\mathrm{K}}-273.15}{100}\)
where,
T_F = temperature in fahrenheit scale,
T_C = temperature in celsius scale,
T_K = temperature in kelvin scale,
[Note: At zero of the kelvin scale, every substance in nature has the least possible activity.]

Question 4.
What is absolute zero?
Answer:

When the graph of pressure (P) against temperature T (°C) at constant volume for three ideal gases A, B and C is plotted, in each case, P -T graph is straight line indicating direct proportion between them. The slopes of these graphs are different.
The individual straight lines intersect the pressure axis at different values of pressure at O °C. but each line intersects the temperature axis at the same point, i.e., at absolute temperature (-273.15 °C).
Similarly graph at constant pressure for three different ideal gases A, B and C extrapolate to the same temperature intercept -273.15 °C i.e., absolute zero temperature.
It is seen that all the lines for different gases Cut the temperature axis at the same point at -273.15 °C.
This point is termed as the absolute zero of temperature.
It is not possible to attain a temperature lower than this value. Even to achieve absolute zero temperature is not possible in practice.
[Note: The point of zero pressure or zero volume does not depend on am specific gas.]

Question 5.
Derive the relation between three coefficients of thermal expansion.
Answer:
Consider a square plate of side l₀ at 0 °C and h at T °C.

l_T = l₀ (1 + αT)
If area of plate at 0 °C is A₀, A₀ = \(l_{0}^{2}\)
If area of plate at T °C is A_T,
A_T = \(l_{\mathrm{T}}^{2}=l_{0}^{2}\) (1 + αT)²
or A_T = A₀ (1 + αT)² …………… (1)
Also,
A_T = A₀(1 + βT)² …………… (2)
……………. [∵ β = \(\frac{\mathrm{A}_{\mathrm{T}}-\mathrm{A}_{0}}{\mathrm{~A}_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)]
Using Equations (1) and (2),
A₀ (1 + αT)² = A₀(1 + βT)
∴ 1 + 2αT + α²T² = 1 + βT
Since the values of a are very small, the term α²T² is very small and may be neglected,
∴ β = 2a
The result is general because any solid can be regarded as a collection of small squares.

Relation between coefficient of linear expansion (α) and coefficient of cubical expansion (γ).

Consider a cube of side l₀ at 0 °C and l_T at T °C.
∴ l_T = l₀(1 + αT)
If volume of the cube at 0 °C is V₀, V₀ = \(l_{0}^{3}\)
If volume of the cube at T °C is
V_T, V_T = \(l_{\mathrm{T}}^{3}=l_{0}^{3}\) (1 + αT)³
V_T = V₀ (1 + αT)³ ………. (1)
Also,
V_T = V₀(1 + γT) …………. (2)
…………. [∵ γ = \(\frac{\mathrm{V}_{\mathrm{T}}-\mathrm{V}_{0}}{\mathrm{~V}_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)]
Using Equations (1) and (2),
V₀(1 + αT)³ = V₀(1 + γT)
∴ 1 + 3αT + 3α²T² + α³T³ = 1 + γT
Since the values of a are very small, the terms with higher powers of a may be neglected,
∴ γ = 3α
The result is general because any solid can be regarded as a collection of small cubes.

Relation between α, β and γ is given by,
α = \(\frac{\beta}{2}=\frac{\gamma}{3}\)
where, α = coefficient of linear expansion.
β = coefficient of superficial expansion,
γ = coefficient of cubical expansion.

Question 6.
State applications of thermal expansion.
Answer:
Applications of thermal expansion:

The steel wheel is heated to expand. This expanded wheel can easily fit over axle. The wheel is then cooled quickly. Upon cooling, wheel contracts and fits tightly upon the axle.
An electric light bulb gets hot quickly when in use. The wire leads to the filament are sealed into the glass. 1f the glass of the bulbs has significantly different thermal expansivity from the wire leads, the glass and the wire would separate, breaking down the vacuum. To prevent this, wires are made of platinum or some suitable alloy with the same expansivity as ordinary glass.

Question 7.
Why do we generally consider two specific heats for a gas?
Answer:

A slight change in temperature causes considerable change in pressure as well as volume of the gas.
Therefore, two principal specific heats are defined for a gas viz., specific heat capacity at constant volume (S_V) and specific heat capacity at constant pressure (S_p).

Question 8.
Are freezing point and melting point same with respect to change of state ? Comment.
Answer:
Though freezing point and melting point mark same temperature (0°C or 32° F), state of change is different for the two points. At freezing point liquid gets converted into solid, whereas at melting point solid gets converted into its liquid state.

Question 9.
Define
(i) Sublimation
(ii) Triple point.
Answer:

The change from solid state to vapour stale without passing through the liquid state is called sublimation and the substance is said to sublime.
Examples: Dry ice (solid CO₂) and iodine.
The triple point of water is that point where water in a solid, liquid and gas state co-exists in equilibrium and this occurs only at a unique temperature and a pressure.

Question 10.
Explain the term ‘steady state’.
Answer:

When one end of a metal rod is heated, the heat flows by conduction from hot end to the cold end.
As a result, the temperature of every section of the rod starts increasing.
Under this condition, the rod is said to be in a variable temperature state.
After some time, the temperature at each section of the rod becomes steady i.e., does not change.
Temperature of each cross-section of the rod now becomes constant though not the same. This is called steady state condition.

Question 11.
Define coefficient of thermal conductivity. Derive its expression.
Answer:
Coefficient of thermal conductivity of a material is defined as the quantity of heat that flows in one second between the opposite faces of a cube of side 1 m, the faces being kept at a temperature difference of 1°C (or 1 K).

Expression for coefficient of thermal conductivity:

Under steady state condition, the quantity of heat ‘Q’ that flows from the hot face at temperature T₁ to the cold face at temperature T₂ of a cube with side x and area of cross- section A is
- directly proportional to the cross-sectional area A of the face. i.e.. Q ∝ A
- directly proportional to the temperature difference between the two faces i.e., Q ∝ (T₁ – T₂)
- directly proportional to time t (in seconds) for which heat flows i.e.. Q ∝ t
- inversely proportional to the perpendicular distance x between hot and cold faces i.e., Q ∝ 1/x
Combining the above four factors, we have the quantity of heat
Q ∝ \(\frac{\mathrm{A}\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right) \mathrm{t}}{\mathrm{x}}\)
∴ Q = \(\)
where k is a constant of proportionality and is called coefficient of thermal conductivity. Its value depends upon the nature of the material.

Question 12.
Give any four applications of thermal conductivity in every day life.
Answer:
Answer: Applications of thermal conductivity:

- Thick walls are used in the construction of cold storage rooms.
- Brick being a bad conductor of heat is used to reduce the flow of heat from the surroundings to the rooms.
- Better heat insulation is obtained by using hollow bricks.
- Air being a poorer conductor than a brick, it further avoids the conduction of heat from outside.
Street vendors keep ice blocks packed in saw dust to prevent them from melting rapidly.
The handle of a cooking utensil is made of a bad conductor of heat, such as ebonite, to protect our hand from the hot utensil.
Two bedsheets used together to cover the body help retain body heat better than a single bedsheet of double the thickness. Trapped air being a bad conductor of heat, the layer of air between the two sheets reduces thermal conduction better than a sheet of double the thickness. Similarly, a blanket coupled with a bedsheet is a cheaper alternative to using two blankets.

Question 13.
Explain the term thermal resistance. State its SI unit and dimensions.
Answer:

Consider expression for conduction rate,
P_cond = kA \(\frac{\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)}{\mathrm{x}}\)
⇒ \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{P}_{\text {cond }}}=\frac{\mathrm{x}}{\mathrm{kA}}\) ……………. (1)
Ratio \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{P}_{\text {cond }}}\) is called as thermal resistance (R_T) of material.

The SI unit of thermal resistance is °C s/kcal or °C s/J and its dimensional formula is [L^-2M^-1T³K¹].

Question 14.
How heat transfer occurs through radiation in absence of a medium?
Answer:

All objects possess thermal energy due to their temperature T(T > 0 K).
The rapidly moving molecules of a hot body emit EM waves travelling with the velocity of light. These are called thermal radiations.
These carry energy with them and transfer it to the low-speed molecules of a cold body on which they fall.
This results in an increase in the molecular motion of the cold body and its temperature rises.
Thus transfer of heat by radiation is a two fold process-the conversion of thermal energy into waves and reconversion of waves into thermal energy by the body on which they fall.

Question 15.
State Newton’s law of cooling and explain how it can be experimentally verified.
Answer:
The rate of loss of heat dT/dt of the both’ is directly proportional to the difference of temperature (T – T₀) of the body and the surroundings provided the difference in temperatures is small.

Mathematically, Newton’s law of cooling can be expressed as:
\(\frac{\mathrm{dT}}{\mathrm{dt}}\) ∝ (T – T₀)
∴ \(\frac{\mathrm{dT}}{\mathrm{dt}}\) ∝ C(T – T₀)
where, C is constant of proportionality. Experimental verification of Newton’s law of cooling:

Fill a calorimeter upto \(\frac{2}{3}\) of its capacity with a boiling water. Cover it with lid with a hole for passing the thermometer.
Insert the thermometer through the hole and adjust it so that the bulb of the thermometer is fully immersed in hot water.
Keep calorimeter vessel in constant temperature enclosure or just in open air since room temperature will not change much during the experiment.
Note down the temperature (T) on the thermometer at every one minute interval until the temperature of water decreases by about 25 °C.
Plot a graph of temperature (T) on Y-axis against time (t) on X-axis. This graph is called cooling curve as shown in figure (a).
Draw tangents to the curve at suitable points on the curve. The slope of each tangent is \(\lim _{\Delta t \rightarrow 0} \frac{\Delta \mathrm{T}}{\Delta \mathrm{t}}\) and gives the rate of fall of temperature at that temperature (T).
Now the graph of \(\left|\frac{\mathrm{dT}}{\mathrm{dt}}\right|\) on Y-axis against (T – T₀) on X-axis is plotted with (0, 0) origin. The graph is straight line and passes through origin as shown in figure (b), which verities Newton’s law of cooling.

(b) Graphical verification of Newton’s law of cooling

Question 16.
What is thermal stress? Give an example of disadvantages of thermal stress in practical use?
Answer:

Consider a metallic rod of length l₀ fixed between two rigid supports at T °C.
If the temperature of rod is increased by ∆T, length of rod would become,
l = l₀(1 + α∆T)
Where, α is the coefficient of linear expansion of material of the rod.
But the supports prevent expansion of rod. As a result, rod exerts stress on the supports. Such stress is termed as thermal stress.
Disadvantage: Thermal stress can lead to fracture or deformation in substance under certain conditions.
Railway tracks are made up of metals which expand upon heating. If no gap is kept between tracks, in hot weather, expansion of metal tracks may exert thermal stress on track. This may lead to bending of tracks which would be dangerous. Hence, railway track is not a continuous piece but is made up of segments separated by gaps.

Question 17.
Which materials can be used as thermal insulators and why?
Answer:

Substances such as glass, wood, rubber, plastic, etc. can be used as thermal insulators.
These substances do not have free electrons to conduct heat freely throughout the body. Hence, they arc poor conductors of heat.

3. Solve the following problems.

Question 1.
A glass flask has volume 1 × 10^-4 m³. It is filled with a liquid at 30 ºC. If the temperature of the system is raised to 100 ºC, how much of the liquid will overflow. (Coefficient of volume expansion of glass is 1.2 × 10^-5 (ºC)^-1 while that of the liquid is 75 × 10^-5 ºC^-1)
Solution:
Given: V₁ = 1 × 10^-4 m³ = 10^-4 m³, T₁ = 30°C,
T₂ = 100 °C
To find: Volume of liquid that overflows
Formula: γ = \(\frac{V_{2}-V_{1}}{V_{1}\left(T_{2}-T_{1}\right)}\)
Calculation: From formula,
Increase is volume = V₂ – V₁
= γV₁(T₂ – T₁)
increase in volume of beaker
= γ_glass × V₁ (T₂ – T₁)
= 1.2 × 10^-5 × 10^-4 × (100 – 30)
= 1.2 × 70 × 10^-9
= 4 × 10^-9 m³
∴ Increase in volume of beaker
= 84 × 10^-9 m³
Increase in volume of liquid
= γ_liquid × V₁ (T₂ – T₁)
= 75 × 10^-5 × 10 × (100 – 30)
= 75 × 70 × 10
= 5250 × 10^-9 m³
∴ Increase in volume of liquid = 5250 × 10^-9 m³
∴ Volume of liquid which overflows
= (5250 – 84) × 10^-9 m³
= 5166 × 10^-9 m³
= 0.5166 × 10^-7 m³
Volume of liquid that overflows is 0.5166 × 10^-7 m³.
[Note: The answer given above is presented considering standard conventions of writing number with its correct order of magnitude.]

Question 2.
Which will require more energy, heating a 2.0 kg block of lead by 30 K or heating a 4.0 kg block of copper by 5 K? (s_lead = 128 J kg^-1 K^-1, s_copper = 387 J kg^-1 K^-1)
Solution:
Given: m_lead = 2 kg, ∆T_lead = 30 K,
s_lead = 128 J/kg K,
m_Cu =4 kg, ∆T_Cu = 5 K,
s_Cu = 387 J/kg K
To find: Substance requiring more heat energy.
Formula: Q = ms ∆T
Calculation: From formula,
For lead, Q_lead = 2 × 128 × 30 = 7680J
For Copper, Q_Cu = 4 × 387 × 5 = 7740 J
Q_Cu > Q_lead, copper will require more heat energy.
Copper will require more heat energy.

Question 3.
Specific latent heat of vaporization of water is 2.26 × 10⁶ J/kg. Calculate the energy needed to change 5.0 g of water into steam at 100 ºC.
Solution:
Given: L_vap = 2.26 × 10⁶ J/kg
m = 5g = 5 × 10^-3 kg
In this case, no temperature change takes place only change of state occurs.
To find: Heat required to convert water into steam.
Formula: Heat required = mL_vap
Calculation: From formula,
Heat required = 5 × 10^-3 × 2.26 × 10⁶
= 11300J
= 1.13 × 10⁴ J
Heat required to convert water into steam is 1.13 × 10⁴ J
[Note: The answer given above is presented considering standard conventions of writing number with its correct order of magnitude.]

Question 4.
A metal sphere cools at the rate of 0.05 ºC/s when its temperature is 70ºC and at the rate of 0.025 ºC/s when its temperature is 50 ºC. Determine the temperature of the surroundings and find the rate of cooling when the temperature of the metal sphere is 40 ºC.
Solution:

∴ 2(50 – T₀) = 70 – T₀
∴ T₀ = 30 πC
Substituting value of T₀.
0.05 = C (70 – 30)
∴ C = \(\frac{0.05}{40}\) = 0.00125/s.
For T₃ = 40 °C
\(\left(\frac{\mathrm{d} \mathrm{T}}{\mathrm{dt}}\right)_{3}\) = C(T₃ – T₀)
= 0.00125 (40 – 30)
= 0.00125 × 10
= 0.0125°C/s.
i) Temperature of surrounding is 30 °C.
ii) Rate of cooling at 40 °C is 0.0125 °C/s.

Question 5.
The volume of a gas varied linearly with absolute temperature if its pressure is held constant. Suppose the gas does not liquefy even at very low temperatures, at what temperature the volume of the gas will be ideally zero?
Answer:
At temperature of -273.15 °C, the volume of the gas will be ideally zero.

Question 6.
In olden days, while laying the rails for trains, small gaps used to be left between the rail sections to allow for thermal expansion. Suppose the rails are laid at room temperature 27 ºC. If maximum temperature in the region is 45 ºC and the length of each rail section is 10 m, what should be the gap left given that α = 1.2 × 10^-5 K^-1 for the material of the rail section?
Solution:
Given. T₁ = 27 °C, T₂ = 45 °C,
L₁ = 10m.
α = 1.2 × 10^-5 K^-1
To find: Gap that should be left (L₂ – L₁)
Formula: L₂ – L₁ = L₁ α(T₂ – T₁)
Calculation: From formula,
L₂ – L₁ = 10 × 1.2 × 10^-5 × (45 – 27)
= 2.16 × 10^-3 m
= 2.16 mm
The gap that should be left between rail sections is 2.16 mm.

Question 7.
A blacksmith fixes iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the wooden rim and the iron ring are 1.5 m and 1.47 m respectively at room temperature of 27 ºC. To what temperature the iron ring should be heated so that it can fit the rim of the wheel (α_iron = 1.2 × 10^-5 K^-1).
Solution:
Given: d_w = 1.5 m, d = 1.47 m, T₁ = 27 °C.
α_i = 1.2 × 10^-5/ K
To find: Temperature (T₂)
Formula. α = \(\frac{\mathrm{d}_{\mathrm{w}}-\mathrm{d}_{\mathrm{i}}}{\mathrm{d}_{\mathrm{i}}\left(\mathrm{T}_{2}-\mathrm{T}_{1}\right)}\)
Calculation: From formula,
T₂ = \(\frac{\mathrm{d}_{\mathrm{w}}-\mathrm{d}_{\mathrm{i}}}{\mathrm{d}_{\mathrm{i}} \alpha}\) + T₁
= \(\frac{1.5-1.47}{1.47 \times 1.2 \times 10^{-5}}\) + 27
= 1700.7 + 27
= 1727.7 °C
Iron ring should be heated to temperature of 1727.7 °C.

Question 8.
In a random temperature scale X, water boils at 200 °X and freezes at 20 °X. Find the boiling point of a liquid in this scale if it boils at 62 °C.
Solution:
Here thermometric property P is temperature at some random scale X.
Using equation,
T = \(\frac{100\left(P_{T}-P_{1}\right)}{\left(P_{2}-P_{1}\right)}\)
For P₁ = 20 °X,
P₂ = 200 °X,
T = 62°C
∴ 62 = \(\frac{100\left(\mathrm{P}_{\mathrm{T}}-20\right)}{(200-20)}\)
∴ P_T = \(\frac{62 \times(200-20)}{100}\) + 20 = 111.6 + 20
= 131.6 °X
The boiling point of a liquid in this scale is 131.6 °X.

Question 9.
A gas at 900°C is cooled until both its pressure and volume are halved. Calculate its final temperature.
Solution:
Given: T₁ = 900 °C = 900 + 273.15 = 1173.15 K
V₂ = \(\frac{\mathrm{V}_{1}}{2}\), P₂ = \(\frac{\mathrm{P}_{1}}{2}\)
To find: Final temperature (T₂)
Formula: \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{\mathrm{I}}}=\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
Calculation: From formula.
\(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{1173.15}=\frac{\mathrm{P}_{1} \mathrm{~V}_{\mathrm{l}}}{4 \mathrm{~T}_{2}}\)
∴ T₂ = \(\frac{1173.15}{4}\) = 293.29 K
Final temperature of gas is 293.29 K.

Question 10.
An aluminium rod and iron rod show 1.5 m difference in their lengths when heated at all temperature. What are their lengths at 0 °C if coefficient of linear expansion for aluminium is 24.5 × 10^-6 /°C and for iron is 11.9 × 10^-6 /°C
Solution:
Given: (L_T)_i – (L_T)_al = 1.5 m, T₀ = 0 °C
α_al = 24.5 × 10^-6/°C
α_i = 11.9 × 10^-6 /°C
To find: Lengths of aluminium and iron rod (L₀)_al and (L₀)_i
Formula: L_T = L₀[(1 + α(T – T₀)]
Calculation: For T₀ = 0 °C
From formula,
L_T = L₀(1 + αT)
For aluminium,
(L₀)_al = (L₀)_al(1 + α_alT) ……………. (1)
For iron,
(L_T)_i = (L₀)_i (1 + α_iT) ………….. (2)
Subtracting equation (2) by (1),
(L_T)_i – (L_T)_al = [(L₀)_i + (L₀)_i α_iT] – [(L₀)_al + (L₀)_alα_alT]
= (L₀)_i – (L₀)_al + [(L₀)_i α_i – (L₀)_al α_al]T
∴ 1.5 = 1.5 + [(L₀)_i α_i – (L₀)_al α_al)]T
⇒ [(L₀)_iα_i – (L₀)_alα_al] T = 0
∴ (L₀)_alα_al = (L₀)_iα_i

Length of aluminium rod at 0 °C is 1.417 m and that of iron rod is 2.917 m.

Question 11.
What is the specific heat of a metal if 50 cal of heat is needed to raise 6 kg of the metal from 20°C to 62 °C ?
Solution:
Given: Q = 50 cal, m =6 kg,
∆T = 62 – 20 = 42 °C
To find: Specific heat (s)
Formula: Q = ms ∆T
Calculation: From formula,
s = \(\frac{\mathrm{Q}}{\mathrm{m} \Delta \mathrm{T}}=\frac{50}{6 \times 42}\) = 0.198 cal/kg °C
Specific heat of metal is copper 0.198 cal/kg °C.

Question 12.
The rate of flow of heat through a copper rod with temperature difference 30 °C is 1500 cal/s. Find the thermal resistance of copper rod.
Solution:
Given: ∆T = 30 °C, P_cond = 1500 cal/s
To find: Thermal resistance (R_T)
Formula: R_T = \(\frac{\Delta \mathrm{T}}{\mathrm{P}_{\text {cond }}}\)
Calculation: From formula,
R_T = \(\frac{30}{1500}\)
= 0.02 °C s/cal.
Thermal resistance of copper rod is 0.02 °C s/cal.

Question 13.
An electric kettle takes 20 minutes to heat a certain quantity of water from 0°C to its boiling point. It requires 90 minutes to turn all the water at 100°C into steam. Find the latent heat of vaporisation. (Specific heat of water = 1cal/g°C)
Solution:
Let heat supplied by kettle in 20 minutes be Q₁ and that in 90 min. be Q₂.
Using heat temperature of water is raised from O °C to 100 °C.
If mass of water in the kettle is ‘m’ then.
Q₁ = ms_water∆T m × 1 × (100 – 0)
= 100 m ………….. (i)
…………. (∵ S_water = 1 cal/g °C)
Similarly using heat Q₂ water is converted from liquid to gas,
∴ Q₂ = mL_vap ……………. (ii)
Given that heat Q₁, Q₂ are supplied to water in 20 min. (t₁) and 90 min (t₂) respectively.
Kettle being same its conduction rate (P_cond) is same.
Using P_cond = \(\frac{\mathrm{Q}_{1}}{\mathrm{t}_{1}}=\frac{\mathrm{Q}_{2}}{\mathrm{t}_{2}}\) …………… (iii)
From (i), (ii) and (iii),
\(\frac{100 \mathrm{~m}}{20}=\frac{\mathrm{mL}_{\text {vap }}}{90}\),
∴ L_vap = 5 × 90 = 450 cal/g
Latent heat of vaporisation for water is 450 cal/g.

Question 14.
Find the temperature difference between two sides of a steel plate 4 cm thick, when heat is transmitted through the plate at the rate of 400 k cal per minute per square metre at steady state. Thermal conductivity of steel is 0.026 kcal/m s K.
Solution:

Temperature difference between two sides is 10.26 K.
[Note: Above answer is expressed in K (‘kelvin considering that thermal conductivity is expressed in units of kcal / ms K, and not as kcal / m s °C. As 1 °C equivalent to 1 K. conceptually temperature difference of 10.26 K will correspond to 10.26 t]

Question 15.
A metal sphere cools from 80 °C to 60 °C in 6 min. How much time with it take to cool from 60 °C to 40 °C if the room temperature is 30°C?
Solution:
Given: T₁ = 80 °C, T₂ = 60 °C, T₃ = 40 °C, T₀ = 30 °C, (dt)₁ = 6 min.
To find: Time taken in cooling (dt)₂

Time taken in cooling is 10 min.

11th Physics Digest Chapter 7 Thermal Properties of Matter Intext Questions and Answers

Can you tell? (Textbook Page No. 125)

Question 1.
i) Why the metal wires for electrical transmission lines sag?
ii) Why a railway track is not a continuous piece but is made up of segments separated by gaps?
iii) How a steel wheel is mounted on an axle to fit exactly?
Answer:

In hot weather, metal wires get heated due to increased temperature of surrounding. As a result, they expand increasing the slack between transmission line structure, causing them to sag.
Railway tracks are made up of metals which expand upon heating. If no gap is kept between tracks, in hot weather, expansion of metal tracks may exert thermal stress on track. This may lead to bending of tracks which would be dangerous. Hence, railway track is not a continuous piece but is made up of segments separated by gaps.
The steel wheel is heated to expand. This expanded wheel can easily fit over axle. The wheel is then cooled quickly. Upon cooling, wheel contracts and fits tightly upon the axle.

Intext question. (Textbook Page No 124)

Question 1.
Can you now tell why the balloon bursts sometimes when you try to fill air in it?
Answer:

When balloon is blown, air that is blown inside makes the balloon expand.
A given size of balloon can expand upto certain limit.
Once that limit is reached and air is still blown inside the balloon, balloon cannot expand further.
As a result, air causes additional pressure on inner surface of balloon.
Since, pressure inside balloon is now greater than pressure outside balloon, balloon bursts equalizing the two pressures.

Can you tell? (Textbook Page No. 125)

Question 1.
Why lakes freeze first at the surface?
Answer:

In cold climate, temperature of water in ponds and lakes starts falling.
On getting colder, water contracts. As a result, density of water increases and it goes down. To replace it, warmer water from below rises up. This process continues till temperature of water at the bottom of pond becomes 4 °C.
Water, due to its anomalous behaviour possesses maximum density at 4 °C.
If the temperature lowers further, ice is formed at the surface of pond with water below it.
Ice being poor conductor of heat blocks the further heat exchange between atmosphere and water in the pond and maintains water below surface in liquid state.

Activity (Textbook Page No. 129)

Question 1.
To understand the process of change of state:
Take some cubes of ice in a beaker. Note the temperature of ice (0 °C). Start heating it slowly on a constant heat source. Note the temperature after every minute. Continuously stir the mixture of water and ice. Observe the change in temperature. Continue heating even after the whole of ice gets converted into water. Observe the change in temperature as before till vapours start coming out. Plot the graph of temperature (along Y-axis) versus time (along X-axis). Obtain a graph of temperature versus time.
Answer:
[Students are expected to attempt the activity on their own.]

Can you tell? (Textbook Page No. 130)

Question 1.
What is observed after point D in graph? Can steam be hotter than 100 °C?
Answer:
Beyond point D, thermometer again shows rise in temperature. This means, steam can be hotter than 100 °C and is termed as superheated steam.

Question 2.
Why steam at 100 °C causes more harm to our skin than water at 100 °C?
Answer:

Though steam and boiling water have same temperature, the heat contained in steam is more than that in boiling water.
Steam is formed when boiling water absorbs specific latent heat of vaporisation i.e.. 22.6 × 10⁵ J/kg.
As a result, when steam comes in contact with the skin of a person, it gives off additional 22.6 × 10⁵ joule per kilogram causing severe (more serious) burns.
Hence, burns caused from steam are more serious than those caused from boiling water at same temperature.

Activity (Textbook Page No. 130)

Activity to understand the dependence of boiling point on pressure:
Take a round bottom flask, more than half filled with water. Keep it over a burner and fix a thermometer and steam outlet through the cork of the flask as shown in figure. As water in the flask gets heated, note that first the air, which was dissolved in the water comes out as small bubbles. Later bubbles of steam form at the bottom but as they rise to the cooler water near the top, they condense and disappear. Finally, as the temperature of the entire mass of the water reaches 100 oc, bubbles of steam reach the surface and boiling is said to occur. The steam in the flask may not be visible hut as it comes out of the flask, It condenses as tiny droplets of water giving a foggy appearance.

If now the steam outlet is closed for a few seconds to increase the pressure in the flask, you will notice that boiling stops. More heat would be required to raise the temperature (depending on the increase in pressure) before boiling starts again. Thus, boiling point increases with increase in pressure. Let us now remove the burner. Allow water to cool to about 80°C. Remove the thermometers and steam outlet. Close the flask with a air tight cork. Keep the flask turned upside down on a stand. Pour icecold water on the flask. Water vapours in the flask condense reducing the pressure on the water surface inside the flask. Water begins to boil again, now at a lower temperature. Thus boiling point decreases with decrease in pressure and increases with increase in pressure.
Answer:
[Students are expected to attempt the activity an their own.]

Can you tell? (Textbook Page No. 131)

Question 1.
i) Why is cooking difficult at high altitude?
ii) Why is cooking faster in pressure cooker?
Answer:

- At high altitude density of air is low which causes reduction in atmospheric pressure.
- As pressure is less, boiling point of water lowers.
- Water, at high altitude, starts boiling below 100 OC.
- As food is cooked mostly through the water boiling, cooking of food becomes difficult.
- Pressure cooker operates by expelling air within the cooker and trapping steam produced from the liquid. (mostly water) boiling inside.
- Due to high internal pressure, boiling point of liquid increases and liquid boils at temperature higher than its boiling point.
- The increased boiling point allows more absorption of heat by liquid and steam formed is superheated.
- As a result, food gets cooked quickly.

Internet my friend (Textbook Page No. 139)

i) https ://hyperphysics. phy-astr.gsu.edul/base/hframe.html
ii) https://youtu.be/7ZKHc5J6R5Q
iii) https://physics. info/expansion
Answer:
[Students are expected to visit the above mentioned webs it es and collect more information about the thermal properties of matter.]

11th Std Physics Questions And Answers:

11th Physics Chapter 1 Exercise Units and Measurements Solutions Maharashtra Board

January 7, 2025January 6, 2025 by Prasanna

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 1 Units and Measurements Textbook Exercise Questions and Answers.

Units and Measurements Class 11 Exercise Question Answers Solutions Maharashtra Board

Class 11 Physics Chapter 1 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 1 Exercise Solutions

1. Choose the correct option.

Question 1.
[L¹M¹T^-2] is the dimensional formula for
(A) Velocity
(B) Acceleration
(C) Force
(D) Work
Answer:
(C) Force

Question 2.
The error in the measurement of the sides of a rectangle is 1%. The error in the measurement of its area is
(A) 1%
(B) \(\frac{1}{2}\)%
(C) 2%
(D) None of the above.
Answer:
(C) 2%

Question 3.
Light year is a unit of
(A) Time
(B) Mass
(C) Distance
(D) Luminosity
Answer:
(C) Distance

Question 4.
Dimensions of kinetic energy are the same as that of
(A) Force
(B) Acceleration
(C) Work
(D) Pressure
Answer:
(C) Work

Question 5.
Which of the following is not a fundamental unit?
(A) cm
(B) kg
(C) centigrade
(D) volt
Answer:
(D) volt

2. Answer the following questions.

Question 1.
Star A is farther than star B. Which star will have a large parallax angle?
Answer:

i). ‘b’ is constant for the two stars
∴ θ ∝ \(\frac{1}{D}\)

ii) As star A is farther i.e., D_A > D_B
⇒ θ_A < θ_B
Hence, star B will have larger parallax angle than star A.

Question 2.
What are the dimensions of the quantity l \(\sqrt{l / g}\), l being the length and g the acceleration due to gravity?
Answer:

[Note: When power of symbol expressing fundamental quantity appearing in the dimensional formula is not given, ills taken as 1.]

Question 3.
Define absolute error, mean absolute error, relative error and percentage error.
Answer:
Absolute error:
a. For a given set of measurements of a quantity, the magnitude of the difference between mean value (Most probable value) and each individual value is called absolute error (∆a) in the measurement of that quantity.
b. absolute error = |mean value – measured value|
∆a₁ = |a_mean – a₁|
Similarly, ∆a₂ = |a_mean – a₂|
. . . ..
. . . .
. . . .
∆a_n = |a_mean – a_n|

Mean absolute error:
For a given set of measurements of a same quantity the arithmetic mean of all the absolute errors is called mean absolute error in the measurement of that physical quantity.
∆a_mean = \(\frac{\Delta \mathrm{a}_{1}+\Delta \mathrm{a}_{2}+\ldots \ldots .+\Delta \mathrm{a}_{n}}{\mathrm{n}}=\frac{1}{\mathrm{n}} \sum_{\mathrm{i}=1}^{n} \Delta \mathrm{a}_{\mathrm{i}}\)

Relative error:
The ratio of the mean absolute error in the measurement of a physical quantity to its arithmetic mean value is called relative error.
Relative error = \(\frac{\Delta \mathrm{a}_{\mathrm{mean}}}{\mathrm{a}_{\mathrm{mean}}}\)

Percentage error:
The relative error represented by percentage (i.e., multiplied by 100) is called the percentage error.
Percentage error = \(\frac{\Delta \mathrm{a}_{\mathrm{mean}}}{\mathrm{a}_{\mathrm{mean}}}\) × 100%
[Note: Considering conceptual conventions question is modified to define percentage error and not mean percentage error.]

Question 4.
Describe what is meant by significant figures and order of magnitude.
Answer:
Significant figures:

Significant figures in the measured value of a physical quantity is the sum of reliable digits and the first uncertain digit.
OR
The number of digits in a measurement about which we are certain, plus one additional digit, the first one about which we are not certain is known as significant figures or significant digits.
Larger the number of significant figures obtained in a measurement, greater is the accuracy of the measurement. The reverse is also true.
If one uses the instrument of smaller least count, the number of significant digits increases.

Rules for determining significant figures:

All the non-zero digits are significant, for example if the volume of an object is 178.43 cm³, there are five significant digits which are 1,7,8,4 and 3.
All the zeros between two nonzero digits are significant, eg., m = 165.02 g has 5 significant digits.
If the number is less than 1, the zero/zeroes on the right of the decimal point and to the left of the first nonzero digit are not significant e.g. in 0.001405, significant. Thus the above number has four significant digits.
The zeroes on the right hand side of the last nonzero number are significant (but for this, the number must be written with a decimal point), e.g. 1.500 or 0.01500 both have 4 significant figures each.
On the contrary, if a measurement yields length L given as L = 125 m = 12500 cm = 125000 mm, it has only three significant digits.

Order of magnitude:
The magnitude of any physical quantity can be expressed as A × 10ⁿ where ‘A’ is a number such that 0.5 ≤ A < 5 then, ‘n’ is an integer called the order of magnitude.
Examples:

Speed of light in air = 3 × 10⁸ m/s
∴ order of magnitude = 8
Mass of an electron = 9.1 × 10^-31 kg
= 0.91 × 10³⁰ kg
∴ order of magnitude = -30

Question 5.
If the measured values of two quantities are A ± ∆A and B ± ∆B, ∆A and ∆B being the mean absolute errors. What is the maximum possible error in A ± B? Show that if Z = \(\frac{A}{B}\)
\(\frac{\Delta Z}{Z}=\frac{\Delta A}{A}+\frac{\Delta B}{B}\)
Answer:
Maximum possible error in (A ± B) is (∆A + ∆B).
Errors in divisions:
i) A
Suppose, Z = \(\frac{A}{B}\) and measured values of A and B are (A ± ∆A) and (B ± ∆B) then,

∴ Maximum relative error of \(\frac{\Delta Z}{Z}=\pm\left(\frac{\Delta \mathrm{A}}{\mathrm{A}}+\frac{\Delta \mathrm{B}}{\mathrm{B}}\right)\)

ii) Thus, when two quantities are divided, the maximum relative error in the result is the sum of relative errors in each quantity.

Question 6.
Derive the formula for kinetic energy of a particle having mass m and velocity v using dimensional analysis
Answer:
Kinetic energy of a body depends upon mass (m) and velocity (v) of the body.
Let K.E. ∝ m^x v^y
∴ K.E. = km^x v^y …….. (1)
where,
k = dimensionless constant of proportionality. Taking dimensions on both sides of equation (1),
[L²M¹T^-2] – [L⁰M¹T⁰]^x [L¹M⁰T^-1]^y
= [L⁰M^xT⁰] [L^yM⁰T^-y]
= [L^0+yM^x+0T^0-y]
[L²M¹T²] = [L^yM^xT^-y] …………. (2)
Equating dimensions of L, M, T on both sides of equation (2),
x = 1 and y = 2 ,
Substituting x, y in equation (1), we have
K.E. = kmv²

3. Solve numerical examples.

Question 1.
The masses of two bodies are measured to be 15.7 ± 0.2 kg and 27.3 ± 0.3 kg. What is the total mass of the two and the error in it?
Answer:
Given: A ± ∆A = 15.7 ± 0.2kg and
B ± ∆B = 27.3 ± 0.3 kg.
To find: Total mass (Z), and total error (∆Z)
Formulae: i. Z = A + B

ii) ±∆Z = ±∆A ± ∆B
Calculation: From formula (i),
Z = 15.7 + 27.3 = 43 kg
From formula (ii),
± ∆Z (± 0.2) + (± 0.3)
=±(0.2 + 0.3)
= ± 0.5 kg
Total mass is 43 kg and total error is ± 0.5 kg.

Question 2.
The distance travelled by an object in time (100 ± 1) s is (5.2 ± 0.1) m. What is the speed and it’s relative error?
Answer:
Given: Distance (D ± ∆D) = (5.2 ± 0.1) m,
time(t ± ∆t) = (100 ± 1)s.
To find: Speed (v), maximum relative error \(\left(\frac{\Delta \mathrm{v}}{\mathrm{v}}\right)\)

Formulae: i. v = \(\frac{\mathrm{D}}{\mathrm{t}}\)
ii. \(\frac{\Delta \mathrm{v}}{\mathrm{v}}=\pm\left(\frac{\Delta \mathrm{D}}{\mathrm{D}}+\frac{\Delta \mathrm{t}}{\mathrm{t}}\right)\)

Calculation: From formula (i),
v = \(\frac{5.2}{100}\) = 0.052 m/s
From formula (ii),
\(\frac{\Delta \mathrm{v}}{\mathrm{v}}=\pm\left(\frac{0.1}{5.2}+\frac{1}{100}\right)\)
= \(\pm\left(\frac{1}{52}+\frac{1}{100}\right)=\pm \frac{19}{650}\)
= ± 0.029 rn/s
The speed is 0.052 m/s and its maximum relative error is ± 0.029 m/s.
[Note: Framing of numerical is modified to make it specific and meaningful.]

Question 3.
An electron with charge e enters a uniform. magnetic field \(\vec{B}\) with a velocity \(\vec{v}\). The velocity is perpendicular to the magnetic field. The force on the charge e is given by
|\(\vec{F}\)| = Bev Obtain the dimensions of \(\vec{B}\).
Answer:
Given: |\(\vec{F}\)| = B e v
Considering only magnitude, given equation is simplified to,
F = B e v

∴ B = [L⁰M¹T^-2I^-1]
[Note: The answer given above is calculated in accordance with textual method considering the given data.]

Question 4.
A large ball 2 m in radius is made up of a rope of square cross section with edge length 4 mm. Neglecting the air gaps in the ball, what is the total length of the rope to the nearest order of magnitude?
Answer:
Volume of ball = Volume enclosed by rope.
\(\frac{4}{3}\) π (radius)³ = Area of cross-section of rope × length of rope.
∴ length of rope l = \(\frac{\frac{4}{3} \pi r^{3}}{A}\)
Given:
r = 2 m and
Area = A = 4 × 4 = 16 mm²
= 16 × 10^-6 m²
∴ l = \(\frac{4 \times 3.142 \times 2^{3}}{3 \times 16 \times 10^{-6}}\)
= \(\frac{3.142 \times 2}{3}\) × 10^-6 m
≈ 2 × 10⁶ m.
Total length of rope to the nearest order of magnitude = 10⁶ m = 10³ km

Question 5.
Nuclear radius R has a dependence on the mass number (A) as R = 1.3 × 10^-16 A^{\(\frac{1}{3}\)} m. For a nucleus of mass number A=125, obtain the order of magnitude of R expressed in metre.
Answer:
R= 1.3 × 10^-16 × A^{\(\frac{1}{3}\)} m
For A = 125
R= 1.3 × 10^-16 × (125)^{\(\frac{1}{3}\)}
= 1.3 × 10^-16 × 5
= 6.5 × 10^-16
= 0.65 × 10^-15 m
∴ Order of magnitude = -15
[Note: Taking the standard value of nuclear radius R = 1.3 × 10^-155 m, the order of magnitude comes to be 10^-14 m.]

Question 6.
In a workshop a worker measures the length of a steel plate with a Vernier callipers having a least count 0.01 cm. Four such measurements of the length yielded the following values: 3.11 cm, 3.13 cm, 3.14 cm, 3.14 cm. Find the mean length, the mean absolute error and the percentage error in the measured value of the length.
Answer:
Given: a₁ = 3.11 cm, a₂ = 3.13 cm,
a₃ = 3.14 cm. a₄ = 3.14cm
Least count L.C. = 0.01 cm.
To find.
i. Mean length (a_mean)
ii. Mean absolute error (∆a_mean)
iii. Percentage error.

Formulae: i. a_mean = \(\frac{a_{1}+a_{2}+a_{3}+a_{4}}{4}\)
ii. ∆a_n = |a_mean – a_n|
iii. ∆a_mean = \(\frac{\Delta \mathrm{a}_{1}+\Delta \mathrm{a}_{2}+\Delta \mathrm{a}_{3}+\Delta \mathrm{a}_{4}}{4}\)
iv. Percentage error = \(\frac{\Delta \mathrm{a}_{\mathrm{mean}}}{\mathrm{a}_{\text {mean }}}\) × 100

Calculation: From formula (i),
a_mean = \(\frac{3.11+3.13+3.14+3.14}{4}\)
= 3.13 cm
From formula (ii),
∆a₁ = |3.13 – 3.11| = 0.02 cm
∆a₂ = |3.13 – 3.13| = 0
∆a₃ = |3.13 – 3.14| = 0.01 cm
∆a₄ = |3.13 – 3.14| = 0.01 cm
From formula (iii),
∆a_mean = \(\frac{0.02+0+0.01+0.01}{4}\) = 0.01 cm
From formula (iii).
% error = \(\frac{0.01}{3.13}\) × 100
= \(\frac{1}{3.13}\)
= 0.3196
……..(using reciprocal table)
= 0.32%

i. Mean length is 3.13 cm.
ii. Mean absolute error is 0.01 cm.
iii. Percentage error is 0.32 %.
[Note: As per given data of numerical, percentage error calculation upon rounding off yields percentage error as 0.32%]

Question 7.
Find the percentage error in kinetic energy of a body having mass 60.0 ± 0.3 g moving with a velocity 25.0 ± 0.1 cm/s.
Answer:
Given: m = 60.0 g, v = 25.0 cm/s.
∆m = 0.3 g, ∆v = 0.1 cm/s
To find: Percentage error in E
Formula: Percentage error in E
\(\left(\frac{\Delta \mathrm{m}}{\mathrm{m}}+2 \frac{\Delta \mathrm{v}}{\mathrm{v}}\right)\) × 100%

Calculation: From formula,
Percentage error in E
= \(\left(\frac{0.3}{60.0}+2 \times \frac{0.1}{25.0}\right)\) × 100%
= 1.3%
The percentage error in energy is 1.3%.

Question 8.
In Ohm’s experiments, the values of the unknown resistances were found to be 6.12 Ω , 6.09 Ω, 6.22 Ω, 6.15 Ω. Calculate the mean absolute error, relative error and percentage error in these measurements.
Answer:
Given: a₁ = 6.12 Ω, a₂ = 6.09 Ω, a₃ = 6.22 Ω, a₄ = 6.15 Ω,

To find:

i) Absolute error (∆a_mean)
ii) Relative error
iii) Percentage error

Formulae:

i) a_mean = \(\frac{a_{1}+a_{2}+a_{3}+a_{4}}{4}\)
ii) ∆a_n = |a_mean – a_n|
iii) ∆a_mean = \(\frac{\Delta \mathrm{a}_{1}+\Delta \mathrm{a}_{2}+\Delta \mathrm{a}_{3}+\Delta \mathrm{a}_{4}}{4}\)
iv) Percentage error = \(\frac{\Delta \mathrm{a}_{\mathrm{mean}}}{\mathrm{a}_{\text {mean }}}\) × 100

From formula (ii),
∆a₁ = |6.145 – 6.12|= 0.025
∆a₂ = |6.145 – 6.09| = 0.055
∆a₃ = |6.145 – 6.22| = 0.075
∆a₄ = |6.l45 – 6.15| = 0.005
From formula (iii),
∆a_mean = \(\frac{0.025+0.055+0.075+0.005}{4}=\frac{0.160}{4}\)
= 0.04 Ω
From formula (iv),
Relative error = \(\frac{0.04}{6.145}\) = 0.0065 Ω
From formula (v).
Percentage error = 0.0065 \frac{0.04}{6.145} 100 = 0.65%

i. The mean absolute error is 0.04 Ω.
ii. The relative error is 0.0065 Ω.
iii. The percentage error is 0.65%.
[Note: Framing of numerical is modified to reach the answer given to the numerical.]

Question 9.
An object is falling freely under the gravitational force. Its velocity after travelling a distance h is v. If v depends upon gravitational acceleration g and distance, prove with dimensional analysis that v = k\(\sqrt{g h}\) where k is a constant.
Answer:
Given = v = k\(\sqrt{g h}\)

k being constant is assumed to be dimensionless.
Dimensions of L.H.S. = [v] = [L¹T^-1]
Dimension of R.H.S. = [latex]\sqrt{g h}[/latex]
= [L¹T^-2]^{\(\frac{1}{2}\)} × [L¹]^{\(\frac{1}{2}\)}
= [L²T^-2]^{\(\frac{1}{2}\)}
= [L¹T^-1]
As, [L.H.S.] = [R.H.S.],
=> v = k\(\sqrt{g h}\)is dimensionally correct equation.

Question 10.
v = at + \(\frac{b}{t+c}\) + v₀ is a dimensionally valid equation. Obtain the dimensional formula for a, b and c where v is velocity, t is time and v₀ is initial velocity.
Answer:
Solution: Given: y = at + \(\frac{b}{t+c}\) + + v₀

As only dimensionally identical quantities can be added together or subtracted from each other, each term on R.H.S. has dimensions of L.H.S. i.e., dimensions of velocity.

∴ [LH.S.] = [v] = [L¹T^-1]
This means, [at] = [v] = [L¹T^-1]
Given, t = time has dimension [T^-1]
∴ [a] = \(\frac{\left[\mathrm{L}^{1} \mathrm{~T}^{-1}\right]}{[\mathrm{t}]}=\frac{\left[\mathrm{L}^{1} \mathrm{~T}^{-1}\right]}{\left[\mathrm{T}^{1}\right]}\) = [L¹T^-2] = L¹M⁰T^-2]
Similarly, [c] = [t] = [T¹] = [L⁰M⁰T¹]
∴ \(\frac{[\mathrm{b}]}{\left[\mathrm{T}^{1}\right]}\) = [v] = [L¹T^-1]
∴ [b] = [L¹T^-1] × [T¹] = [L¹] = [L¹M⁰T⁰]

Question 11.
The length, breadth and thickness of a rectangular sheet of metal are 4.234 m, 1.005 m, and 2.01 cm respectively. Give the area and volume of the sheet to correct significant figures.
Answer:
Given: l = 4.234 m, b = 1.005 m,
t = 2.01 cm = 2.01 × 10^-2 m = 0.0201 m

To find:
i) Area of sheet to correct significant figures (A)
ii) Volume of sheet to correct significant figures (V)
Formulae: i. A = 2(lb + bt + tl)
iii) V = l × b × t

Calculation: From formula (i),
A = 2(4.234 × 1.005 + 1.005 × 0.0201 +0.0201 × 4.234)
= 2 |[antilog(log 4.234 + logl .005) + antiiog(log 1.005 + log0.0201) + antilog(log 0.0201 + log 4.234)]}
= 2{[antilog(0.6267 + 0.0021) + antilog(0.0021 + \(\overline{2}\) .3010) + antilog (\(\overline{2}\) .3010 + 0.6267)]}
= 2 {[antilog(0.6288) + antilog (\(\overline{2}[/latex .3031) +antilog([latex]\overline{2}\) .9277)]}
= 2 [4.254 + 0.02009 + 0.08467]
= 2 [4.35876]
= 8.71752m²

In correct significant figure,
A = 8.72 m2 From formula (ii),
V =4.234 × 1.005 × 0.0201
= antilog [log (4.234) + log (1.005) + log (0.0201)]
= antilog [0.6269 – 0.0021 – \(\overline{2}\).3032]
= antilog [0.6288 – \(\overline{2}\).3032]
= antilog [ 2 .9320]
= 8.551 × 10^-2
= 0.08551 m³
In correct significant figure (rounding off),
V = 0.086 m³

i.) Area of sheet to correct significant figures is 8.72 m².
ii) Volume of sheet to correct significant figures is 0.086 m³.
[Note: The given solution is arrived to by considering a rectangular sheet.]

Question 12.
If the length of a cylinder is l = (4.00 ± 0.001) cm, radius r = (0.0250 ± 0.001) cm and mass m = (6.25 ± 0.01) gm. Calculate the percentage error in the determination of density.
Answer:
Given: l = (4.00 ± 0.001) cm,
In order to have same precision, we use, (4.000 ± 0.001),
r = (0.0250 ± 0.00 1) cm,
In order to have same precision, we use, (0.025 ± 0.001)
m = (6.25 ± 0.01) g
To find: percentage error in density

Formulae:
i) Relative error in volume, \(\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{2 \Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta l}{l}\)
….(∵ Volume of cylinder, V = πr²l)

ii) Releative error \(\frac{\Delta \rho}{\rho}=\frac{\Delta m}{m}+\frac{\Delta V}{V}\)

iii) Percentage error= Relative error × 100%

Calculation.
From formulae (i) and (ii),
∴ \(\frac{\Delta \rho}{\rho}=\frac{\Delta \mathrm{m}}{\mathrm{m}}+\frac{2 \Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta l}{l}\)
= \(\frac{0.01}{6.25}+\frac{2(0.001)}{0.025}+\frac{0.001}{4.000}\)
= 0.00 16 + 0.08 + 0.00025
= 0.08 185
From formula (iii).
% error in density = \(\frac{\Delta \rho}{\rho}\) × 100
= 0.08185 × 100
= 8.185%
Percentage error in density is 8.185%.

Question 13.
When the planet Jupiter is at a distance of 824.7 million kilometers from the Earth, its angular diameter is measured to be 35.72″ of arc. Calculate the diameter of the Jupiter.
Answer:
Given: Angular diameter (a) = 35.72″
= 35.72″ × 4.847 × 10^-6 rad
1.73 × 10^-4 rad

Distance from Earth (D)
= 824.7 million km
= 824.7 × 10⁶ km
= 824.7 × 10⁹ m.

To find: Diameter of Jupiter (d)
Formula: d = α D
Calculation: From formula,
d = 1.73 × 10^-4 × 824.7 × 10⁹
= 1.428 × 10⁸ m
= 1.428 × 10⁵ km
Diameter of Jupiter is 1.428 × 10⁵ km.

Question 14.
If the formula for a physical quantity is X = \(\frac{a^{4} b^{3}}{c^{1 / 3} d^{1 / 2}}\) and if the percentage error in the measurements of a, b, c and d are 2%, 3%, 3% and 4% respectively. Calculate percentage error in X.
Answer:
Given X = \(\frac{a^{4} b^{3}}{c^{1 / 3} d^{1 / 2}}\)
Percentage error in a, b, c, d is respectively 2%, 3%, 3% and 4%.
Now, Percentage error in X

Question 15.
Write down the number of significant figures in the following: 0.003 m², 0.1250 gm cm^-2, 6.4 × 10⁶ m, 1.6 × 10^-19 C, 9.1 × 10^-31 kg.
Answer:

Question 16.
The diameter of a sphere is 2.14 cm. Calculate the volume of the sphere to the correct number of significant figures.
Answer:
Volume of sphere = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × 3.142 × (\(\frac{2.14}{2}\))³ ………….. (∵ r = \(\frac{d}{2}\))
= \(\frac{4}{3}\) × 3.142 × (1.07)³
= 1.333 × 3.142 × (1.07)³
= {antilog [log (1.333) + log(3.142)+3 log(1.07)]}
= {antilog [0.1249 + 0.4972 + 3 (0.0294)])
= {antilog [0.6221 + 0.0882]}
= {antilog [0.7103]}
= 5.133cm³
In multiplication or division, the final result should retain as many significant figures as there are in the original number with the least significant figures.
Volume in correct significant figures
∴ 5.13 cm³

11th Physics Digest Chapter 1 Units and Measurements Intext Questions and Answers

Can you recall (Textbook Page No. 1)

Question 1.
i) What is a unit?
ii) Which units have you used in the laboratory for measuring
a. length
b. mass
c. time
d. temperature?
iii. Which system of units have you used?
Answer:

The standard measure of any quantity is called the unit of that quantity.
MKS or SI system is used mostly. At times. even CGS system is used.

Can you tell? (Textbook Page No. 8)

Question 1.
If ten students are asked to measure the length of a piece of cloth upto a mm, using a metre scale, do you think their answers will be identical? Give reasons.
Answer:
Answers of the students are likely to be different. Length of cloth needs to be measured up to a millimetre (mm) length. Hence, to obtain accurate and precise reading one must use measuring instrument having least count smaller than 1 mm.

But least count of metre scale is 1 mm. As a result, even smallest uncertainty in reading would vary reading significantly. Also, skill of students doing measurement may also introduce uncertainty in observation.
Hence, their answers are likely to be different.

Activity (Textbook Page No. 10)

Perform an experiment using a Vernier callipers of least count 0.01cm to measure the external diameter of a hollow cylinder. Take 3 readings at different positions on the cylinder and find (i) the mean diameter (ii) the absolute mean error and (iii) the percentage error in the measurement of diameter.
Answer:
Given: L.C. = 0.01 cm
To measure external diameter of hollow cylinder readings are taken as follows:

[Note: The above table is made assuming zero error in Vernier callipers. If calliper has positive or negative zero error, the zero error correction needs to be introduced into observed reading.]

Internet my friend (Textbook Page No. 12)

i. ideoiectures.net/mit801f99_lewin_lec0l/
ii. hyperphysicsphy-astr.gsu.ed u/libase/hfra me. html

[Students can use links given above as reference and collect information about units and measurements]

Class 11 Physics Questions And Answers

11th Std Physics Questions And Answers:

11th Physics Chapter 10 Exercise Electrostatics Solutions Maharashtra Board

January 7, 2025January 6, 2025 by Prasanna

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 10 Electrostatics Textbook Exercise Questions and Answers.

Electrostatics Class 11 Exercise Question Answers Solutions Maharashtra Board

Class 11 Physics Chapter 10 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 10 Exercise Solutions

1. Choose the correct option.

Question 1.
A positively charged glass rod is brought close to a metallic rod isolated from ground. The charge on the side of the metallic rod away from the glass rod will be
(A) same as that on the glass rod and equal in quantity
(B) opposite to that on the glass of and equal in quantity
(C) same as that on the glass rod but lesser in quantity
(D) same as that on the glass rod but more in quantity
Answer:
(A) same as that on the glass rod and equal in quantity

Question 2.
An electron is placed between two parallel plates connected to a battery. If the battery is switched on, the electron will
(A) be attracted to the +ve plate
(B) be attracted to the -ve plate
(C) remain stationary
(D) will move parallel to the plates
Answer:
(A) be attracted to the +ve plate

Question 3.
A charge of + 7 µC is placed at the centre of two concentric spheres with radius 2.0 cm and 4.0 cm respectively. The ratio of the flux through them will be
(A) 1 : 4
(B) 1 : 2
(C) 1 : 1
(D) 1 : 16
Answer:
(C) 1 : 1

Question 4.
Two charges of 1.0 C each are placed one meter apart in free space. The force between them will be
(A) 1.0 N
(B) 9 × 10⁹ N
(C) 9 × 10^-9 N
(D) 10 N
Answer:
(B) 9 × 10⁹ N

Question 5.
Two point charges of +5 µC are so placed that they experience a force of 80 × 10^-3 N. They are then moved apart, so that the force is now 2.0 × 10^-3 N. The distance between them is now
(A) 1/4 the previous distance
(B) double the previous distance
(C) four times the previous distance
(D) half the previous distance
Answer:
(B) double the previous distance

Question 6.
A metallic sphere A isolated from ground is charged to +50 µC. This sphere is brought in contact with other isolated metallic sphere B of half the radius of sphere A. The charge on the two sphere will be now in the ratio
(A) 1 : 2
(B) 2 : 1
(C) 4 : 1
(D) 1 : 1
Answer:
(D) 1 : 1

Question 7.
Which of the following produces uniform electric field?
(A) point charge
(B) linear charge
(C) two parallel plates
(D) charge distributed an circular any
Answer:
(C) two parallel plates

Question 8.
Two point charges of A = +5.0 µC and B = -5.0 µC are separated by 5.0 cm. A point charge C = 1.0 µC is placed at 3.0 cm away from the centre on the perpendicular bisector of the line joining the two point charges. The charge at C will experience a force directed towards
(A) point A
(B) point B
(C) a direction parallel to line AB
(D) a direction along the perpendicular bisector
Answer:
(C) a direction parallel to line AB

2. Answer the following questions.

Question 1.
What is the magnitude of charge on an electron?
Answer:
The magnitude of charge on an electron is 1.6 × 10^-19 C

Question 2.
State the law of conservation of charge.
Answer:
In any given physical process, charge may get transferred from one part of the system to another, but the total charge in the system remains constant”
OR
For an isolated system, total charge cannot be created nor destroyed.

Question 3.
Define a unit charge.
Answer:
Unit charge (one coulomb) is the amount of charge which, when placed at a distance of one metre from another charge of the same magnitude in vacuum, experiences a force of 9.0 × 10⁹ N.

Question 4.
Two parallel plates have a potential difference of 10V between them. If the plates are 0.5 mm apart, what will be the strength of electric charge.
Answer:
V=10V
d = 0.5 mm = 0.5 × 10^-3 m
To find: The strength of electric field (E)
Formula: E = \(\frac {V}{d}\)
Calculation: From formula,
E = \(\frac {10}{0.5×10^{-3}}\)
20 × 10³ V/m

Question 5.
What is uniform electric field?
Answer:
A uniform electric field is a field whose magnitude and direction are same at all points. For example, field between two parallel plates as shown in the diagram.

Question 6.
If two lines of force intersect of one point. What does it mean?
Answer:
If two lines of force intersect of one point, it would mean that electric field has two directions at a single point.

Question 7.
State the units of linear charge density.
Answer:
SI unit of λ is (C / m).

Question 8.
What is the unit of dipole moment?
Answer:
i. Strength of a dipole is measured in terms of a quantity called the dipole moment.

ii. Let q be the magnitude of each charge and 2\(\vec{l}\) be the distance from negative charge to positive charge. Then, the product q(2\(\vec{l}\)) is called the dipole moment \(\vec{p}\).

iii. Dipole moment is defined as \(\vec{p}\) = q(2\(\vec{l}\))

iv. A dipole moment is a vector whose magnitude is q (2\(\vec{l}\)) and the direction is from the negative to the positive charge.

v. The unit of dipole moment is coulomb-metre (C m) or debye (D).

Question 9.
What is relative permittivity?
Answer:
i. Relative permittivity or dielectric constant is the ratio of absolute permittivity of a medium to the permittivity of free space.
It is denoted as K or ε_r.
i.e., K or ε_r = \(\frac {ε}{ε_0}\)

ii. It is the ratio of the force between two point charges placed a certain distance apart in free space or vacuum to the force between the same two point charges when placed at the same distance in the given medium.
i.e., K or ε_r = \(\frac {F_{vacuum}}{F_{medium}}\)

iii. It is also called as specific inductive capacity or dielectric constant.

3. Solve numerical examples.

Question 1.
Two small spheres 18 cm apart have equal negative charges and repel each other with the force of 6 × 10^-8 N. Find the total charge on both spheres.
Solution:
Given: F = 6 × 10^-8 N, r = 18 cm = 18 × 10^-2 m
To find: Total charge (q₁ + q₂)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation: From formula,

Taking square roots from log table,
∴ q = -4.648 × 10^-10 C
….(∵ the charges are negative)
Total charge = q₁ + q₂ = 2q
= 2 × (-4.648) × 10^-10
= -9.296 × 10^-10 C

Question 2.
A charge + q exerts a force of magnitude – 0.2 N on another charge -2q. If they are separated by 25.0 cm, determine the value of q.
Answer:
Given: q₁ = + q, q₂ = -2q, F = -0.2 N
r = 25 cm = 25 × 10^-2 m
To find: Charge (q)
Formula: F = \(\frac {1}{4πε_0}\) \(\frac {q_1q_2}{r^2}\)
Calculation: From formula,

[Note: The answer given above is calculated in accordance with textual method considering the given data]

Question 3.
Four charges of +6 × 10^-8 C each are placed at the corners of a square whose sides are 3 cm each. Calculate the resultant force on each charge and show in direction on a diagram drawn to scale.
Answer:
Given: q_A = q_B = q_C = q_D = 6 × 10^-8 C, a = 3 cm

∴ Resultant force on ‘A’
= F_AD cos 45 + F_AB cos 45 + F_AC
= (3.6 × 10^-2 × \(\frac {1}{√2}\)) + (3.6 × 10^-2 × \(\frac {1}{√2}\)) + 1.8 × 10^-2
= 6.89 × 10^-2 N directed along \(\vec{F_{AC}}\)

Question 4.
The electric field in a region is given by \(\vec{E}\) = 5.0 \(\hat{k}\) N/C Calculate the electric flux through a square of side 10.0 cm in the following cases
i. The square is along the XY plane
ii. The square is along XZ plane
iii. The normal to the square makes an angle of 45° with the Z axis.
Answer:
Given: \(\vec{E}\) = 5.0 \(\hat{k}\) N/C, |E| = 5 N/C
l = 10 cm = 10 × 10^-2 m = 10^-1 m
A = l² – 10^-2m²
To find: Electric flux in three cases.
(ø₁) (ø₂) (ø₃)
Formula: (ø₁) = EA cos θ
Calculation:
Case I: When square is along the XY plane,
∴ θ = 0
ø₁ = 5 × 10^-2 cos 0
= 5 × 10^-2 V m

Case II: When square is along XZ plane,
∴ θ = 90°
ø₁ = 5 × 10^-2 cos 90° = 0 V m

Case III: When normal to the square makes an angle of 45° with the Z axis.
∴ 0 = 45°
∴ ø₃ = 5 × 10^-2 × cos 45°
= 3.5 × 10^-2 V m

Question 5.
Three equal charges of 10 × 10^-8 C respectively, each located at the corners of a right triangle whose sides are 15 cm, 20 cm and 25 cm respectively. Find the force exerted on the charge located at the 90° angle.
Answer:
Given: q_A = q_B = q_C = 10 × 10^-8

Force on B due to A,

Question 6.
A potential difference of 5000 volt is applied between two parallel plates 5 cm apart. A small oil drop having a charge of 9.6 x 10-19 C falls between the plates. Find (i) electric field intensity between the plates and (ii) the force on the oil drop.
Answer:
Given: V = 5000 volt, d = 5 cm = 5 × 10^-2 m
q = 9.6 × 10^-19 C
To find:
i. Electric field intensity (E)
ii. Force (F)
Formula:
i. E = \(\frac {V}{d}\) \(\frac {q}{r}\)
ii. E = \(\frac {F}{q}\)
Calculation: From formula (i),
E = \(\frac {F}{q}\) = 10⁵ N/C
From formula (ii)
F = E x q
= 10⁵ × 9.6 × 10^-19
= 9.6 × 10^-14 N

Question 7.
Calculate the electric field due to a charge of -8.0 × 10^-8 C at a distance of 5.0 cm from it.
Answer:
Given: q = – 8 × 10^-8 C, r = 5 cm = 5 × 10^-2 m
To Find: Electric field (E)
Formula: E = \(\frac {1}{4πε_0}\) \(\frac {q}{r^2}\)
Calculation: From formula,
E = 9 × 10⁹ × \(\frac {(-8×10^{-8})}{(5×10^{-2})^2}\)
= -2.88 × 10⁵ N/C

11th Physics Digest Chapter 10 Electrostatics Intext Questions and Answers

Can you recall? (Textbookpage no. 188)

Question 1.
Have you experienced a shock while getting up from a plastic chair and shaking hand with your friend?
Answer:
Yes, sometimes a shock while getting up from a plastic chair and shaking hand with friend is experienced.

Question 2.
Ever heard a crackling sound while taking out your sweater in winter?
Answer:
Yes, sometimes while removing our sweater in winter, some crackling sound is heard and the sweater appears to stick to body.

Question 3.
Have you seen the lightning striking during pre-monsoon weather?
Answer:
Yes, sometimes lightning striking during pre-pre-monsoon weather seen.

Can you tell? (Textbook page no. 189)

i. When a petrol or a diesel tanker is emptied in a tank, it is grounded.
ii. A thick chain hangs from a petrol or a diesel tanker and it is in contact with ground when the tanker is moving.
Answer:
i. When a petrol or a diesel tanker is emptied in a tank, it is grounded so that it has an electrically conductive connection from the petrol or diesel tank to ground (Earth) to allow leakage of static and electrical charges.

ii. Metallic bodies of cars, trucks or any other big vehicles get charged because of friction between them and the air rushing past them. Hence, a thick chain is hanged from a petrol or a diesel tanker to make a contact with ground so that charge produced can leak to the ground through chain.

Can you tell? (Textbook page no. 194)

Three charges, q each, are placed at the vertices of an equilateral triangle. What will be the resultant force on charge q placed at the centroid of the triangle?
Answer:

Since AD. BE and CF meets at O, as centroid of an equilateral triangle.
∴ OA = OB = OC
∴ Let, r = OA = OB = OC
Force acting on point O due to charge on point A,
\(\overrightarrow{\mathrm{F}}_{\mathrm{OA}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}_{i}^{2}} \hat{\mathrm{r}}_{\mathrm{AO}}\)
Force acting on point O due to charge on point B,
\(\overrightarrow{\mathrm{F}}_{O \mathrm{~B}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}}_{\mathrm{BO}}\)
Force acting on point O due to charge on point C,
\(\overrightarrow{\mathrm{F}}_{\mathrm{OC}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}^{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}} \mathrm{co}\)
∴ Resultant force acting on point O,
F = \(\vec{F}\)_OA + \(\vec{F}\)_OB + \(\vec{F}\)_OC
On resolving \(\vec{F}\)_OB and \(\vec{F}\)_OC, we get –\(\vec{F}\)_OA
i.e., \(\vec{F}\)_OB + \(\vec{F}\)_OC = –\(\vec{F}\)_OA
∴ \(\vec{F}\) = \(\vec{F}\)_OA – \(\vec{F}\)_OA = 0
Hence, the resultant force on the charge placed at the centroid of the equilateral triangle is zero.

Can you tell? (Textbook page no. 197)

Why a small voltage can produce a reasonably large electric field?
Answer:

Electric field produced depends upon voltage as well as separation distance.
Electric field varies linearly with voltage and inversely with distance.
Hence, even if voltage is small, it can produce a reasonable large electric field when the gap between the electrode is reduced significantly.

Can you tell? (Textbook page no. 198)

Lines of force are imaginary; can they have any practical use?
Answer:
Yes, electric lines of force help us to visualise the nature of electric field in a region.

Can you tell? (Textbook page no. 204)

The surface charge density of Earth is σ = -1.33 nC/m². That is about 8.3 × 10⁹ electrons per square metre. If that is the case why don’t we feel it?
Answer:
The Earth along with its atmosphere acts as a neutral system. The atmosphere (ionosphere in particular) has nearly equal and opposite charge.

As a result, there exists a mechanism to replenish electric charges in the form of continual thunder storms and lightning that occurs in different parts of the globe. This makes average charge on surface of the Earth as zero at any given time instant. Hence, we do not feel it.

Internet my friend (Textbook page no. 205)

i. https://www.physicsclassroom.com/class
ii. https://courses.lumenleaming.com/physics/
iii. https://www,khanacademy.org/science
iv. https://www.toppr.com/guides/physics/
[Students are expected to visit the above mentioned websites and collect more information about electrostatics.]

11th Std Physics Questions And Answers:

11th Physics Chapter 5 Exercise Gravitation Solutions Maharashtra Board

January 7, 2025January 6, 2025 by Prasanna

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 5 Gravitation Textbook Exercise Questions and Answers.

Gravitation Class 11 Exercise Question Answers Solutions Maharashtra Board

Class 11 Physics Chapter 5 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 5 Exercise Solutions

1. Choose the correct option.

Question 1.
The value of acceleration due to gravity is maximum at
(A) the equator of the Earth .
(B) the centre of the Earth.
(C) the pole of the Earth.
(D) slightly above the surface of the Earth.
Answer:
(C) the pole of the Earth.

Question 2.
The weight of a particle at the centre of the Earth is _________
(A) infinite.
(B) zero.
(C) same as that at other places.
(D) greater than at the poles.
Answer:
(B) zero.

Question 3.
The gravitational potential due to the Earth is minimum at
(A) the centre of the Earth.
(B) the surface of the Earth.
(C) a points inside the Earth but not at its centre.
(D) infinite distance.
Answer:
(A) the centre of the Earth.

Question 4.
The binding energy of a satellite revolving around planet in a circular orbit is 3 × 10⁹ J. Its kinetic energy is _________
(A) 6 × 10⁹ J
(B) -3 × 10⁹ J
(C) -6 × 10⁺⁹ J
(D) 3 × 10⁺⁹J
Answer:
(D) 3 × 10⁺⁹J

2. Answer the following questions.

Question 1.
State Kepler’s law equal of area.
Answer:
The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.

Question 2.
State Kepler’s law of period.
Answer:
The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.

Question 3.
What are the dimensions of the universal gravitational constant?
Answer:
The dimensions of universal gravitational constant are: [L³M^-1T^-2].

Question 4.
Define binding energy of a satellite.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.

Question 5.
What do you mean by geostationary satellite?
Answer:
Some satellites that revolve around the Earth in equatorial plane have same sense of rotation as that of the Earth. The also have the same period of rotation as that of the Earth i.e.. 24 hours. Due to this, these satellites appear stationary from the Earth’s surface and are known as geostationary satellites.

Question 6.
State Newton’s law of gravitation.
Answer:
Statement:
Every particle of matter attracts every other particle of matter with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Question 7.
Define escape velocity of a satellite.
Answer:
The minimum velocity with which a both’ should he thrown vertically upwards from the surface of the Earth so that it escapes the Earth ‘s gravitational field, is called the escape velocity (v_e) of the body.

Question 8.
What is the variation in acceleration due to gravity with altitude?
Answer:
Variation in acceleration due to gravity due to altitude is given by, g_h = g\(\left(\frac{R}{R+h}\right)^{2}\)
where,
g_h = acceleration due to gravity of an object placed at h altitude
g = acceleration due to gravity on surface of the Earth
R = radius of the Earth
h = attitude height of the object from the surface of the Earth.
Hence, acceleration due to gravity decreases with increase in altitude.

Question 9.
On which factors does the escape speed of a body from the surface of Earth depend?
Answer:
The escape speed depends only on the mass and radius of the planet.
[Note: Escape velocity does not depend upon the mass of the body]

Question 10.
As we go from one planet to another planet, how will the mass and weight of a body change?
Answer:

As we go from one planet to another, mass of a body remains unaffected.
However, due to change in mass and radius of planet, acceleration due to gravity acting on the body changes as, g ∝ \(\frac{\mathrm{M}}{\mathrm{R}^{2}}\).
Hence, weight of the body also changes as, W ∝ \(\frac{\mathrm{M}}{\mathrm{R}^{2}}\)

Question 11.
What is periodic time of a geostationary satellite?
Answer:
The periodic time of a geostationary satellite is same as that of the Earth i.e., one day or 24 hours.

Question 12.
State Newton’s law of gravitation and express it in vector form.
Answer:

Statement:
Every particle of matter attracts every other particle of matter with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
In vector form, it can be expressed as,
\(\overrightarrow{\mathrm{F}}_{21}=\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\left(-\hat{\mathrm{r}}_{21}\right)\)
where, \(\hat{\mathbf{r}}_{21}\) is the unit vector from m₁ to m₂.
The force \(\overrightarrow{\mathrm{F}}_{21}\) is directed from m₂ to m₁.

Question 13.
What do you mean by gravitational constant? State its SI units.
Answer:

From Newton’s law of gravitation,
F = G \(\frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
where, G = constant called universal gravitational constant Its value is 667 X 10^-11 N m²/kg².
G = \(\frac{\mathrm{Fr}^{2}}{\mathrm{~m}_{1} \mathrm{~m}_{2}}\)
If m₁ = m₂ = 1 kg, r = 1 m thenF = G.
Hence, the universal gravitational constant is the force of gravitation between two particles of unit mass separated by unit distance.
Unit: N m²/kg² in SI system.

Question 14.
Why is a minimum two stage rocket necessary for launching of a satellite?
Answer:

For the projection of an artificial satellite, it is necessary for the satellite to have a certain velocity.
In a single stage rocket, when the fuel in first stage of rocket is ignited on the surface of the Earth, it raises the satellite vertically.
The velocity of projection of satellite normal to the surface of the Earth is the vertical velocity.
If this vertical velocity is less than the escape velocity (v_e), the satellite returns to the Earth’s surface. While, if the vertical velocity is greater than or equal to the escape velocity, the satellite will escape from Earth’s gravitational influence and go to infinity.
Hence, minimum two stage rocket, one to raise the satellite to desired height and another to provide required hori7ontal velocity, is necessary for launching of a satellite.

Question 15.
State the conditions for various possible orbits of a satellite depending upon the horizontal speed of projection
Answer:
The path of the satellite depends upon the value of horizontal speed of projection v_h relative to critical velocity v_c and escape velocity v_e.
Case (I) v_h < v_c:
The orbit of satellite is an ellipse with point of projection as apogee and Earth at one of the foci. During this elliptical path, if the satellite passes through the Earth’s atmosphere. it experiences a nonconservative force of air resistance. As a result it loses energy and spirals down to the Earth.
Case (II) v_h = v_c:
The satellite moves in a stable circular orbit around the Earth.
Case (III) v_c < v_h < v_e:
The satellite moves in an elliptical orbit round the Earth with the point of projection as perigee.
Case (IV) v_h = v_e
The satellite travels along parabolic path and never returns to the point of projection. Its speed will be zero at infinity.
Case (V) v_h > v_e:
The satellite escapes from gravitational influence of Earth traversing a hyperbolic path.

3. Answer the following questions in detail.

Question 1.
Derive an expression for critical velocity of a satellite.
Answer:
Expression for critical velocity:

Consider a satellite of mass m revolving round the Earth at height h above its surface. Let M be the mass of the Earth and R be its radius.
If the satellite is moving in a circular orbit of radius (R + h) = r, its speed must be equal to the magnitude of critical velocity v_c.
The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the satellite on the Earth.
∴ Centripetal force = Gravitational force

This is the expression for critical speed at the orbit of radius (R + h).
The critical speed of a satellite is independent of the mass of the satellite. It depends upon the mass of the Earth and the height at which the satellite is revolving or gravitational acceleration at that altitude.

Question 2.
State any four applications of a communication satellite.
Answer:
Applications of communication satellite:

For the transmission of television and radiowave signals over large areas of Earth’s surface.
For broadcasting telecommunication.
For military purposes.
For navigation surveillance.

Question 3.
Show that acceleration due to gravity at height h above the Earth’s surface is g_h = g(\(\frac{R}{R+h}\))²
Answer:
Variation of g due to altitude:

Let,
R = radius of the Earth,
M = mass of the Earth.
g = acceleration due to gravity at the surface of the Earth.
Consider a body of mass m on the surface of the Earth. The acceleration due to gravity on the Earth’s surface is given by,
The body is taken at height h above the surface of the Earth as shown in figure. The acceleration due to gravity now changes to,
g_h = \(\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}}\) …………. (2)
Dividing equation (2) by equation (1), we get,

We can rewrite,

This expression can be used to calculate the value of g at height h above the surface of the Earth as long as h<< R.

Question 4.
Draw a labelled diagram to show different trajectories of a satellite depending upon the tangential projection speed.
Answer:

v_h = horizontal speed of projection
v _c = critical velocity
v_e = escape velocity

Question 5.
Derive an expression for binding energy of a body at rest on the Earth’s surface.
Answer:

Let,
M = mass of the Earth
m = mass of the satellite
R = radius of the Earth.
Since the satellite is at rest on the Earth, v = 0
∴ Kinetic energy of satellite.
K.E = \(\frac{1}{2}\) mv² = 0
Gravitational potential at the Earth’s surface
= – \(\frac{\mathrm{GM}}{\mathrm{R}}\)
∴ Potential energy of satellite = Gravitational potential × mass of satellite
= –\(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Total energy of sitellite = T.E = P.E + K.E
∴ T.E. = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\) + 0 = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Negative sign in the energy indicates that the satellite is bound to the Earth, due to gravitational force of attraction.
For the satellite to be free form Earth’s gravitational influence, its total energy should become positive. That energy is the binding energy of the satellite at rest on the surface of the Earth.
∴ B.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\)

Question 6.
Why do astronauts in an orbiting satellite have a feeling of weightlessness?
Answer:

For an astronaut, in a satellite, the net force towards the centre of the Earth will always be, F = mg – N.
where, N is the normal reaction.
In the case of a revolving satellite, the satellite is performing a circular motion. The acceleration for this motion is centripetal, which is provided by the gravitational acceleration g at the location of the satellite.
In this case, the downward acceleration, a_d = g, or the satellite (along with the astronaut) is in the state of free fall.
Thus, the net force acting on astronaut will be, F = mg – ma_d i.e., the apparent weight will be zero, giving the feeling of total weightlessness.

Question 7.
Draw a graph showing the variation of gravitational acceleration due to the depth and altitude from the Earth’s surface.
Answer:

Question 8.
At which place on the Earth’s surface is the gravitational acceleration maximum? Why?
Answer:

Gravitational acceleration on the surface of the Earth depends on latitude of the place as well as rotation and shape of the Earth.
At poles, latitude θ = 90°.
∴ g’ = g
i.e., there is no reduction in acceleration due to gravity at poles.
Also, shape of the Earth is actually an ellipsoid, bulged at equator. The polar radius of the Earth is 6356 km which minimum. As g ∝ \(\frac{1}{\mathrm{R}^{2}}\), acceleration due to gravity is maximum at poles i.e., 9.8322 m/s².

Question 9.
At which place on the Earth surface the gravitational acceleration minimum? Why?
Answer:

Gravitational acceleration on the surface of the Earth depends on latitude of the place as well as rotation and shape of the Earth.
At equator, latitude θ = 0°.
∴ g’ = g – Rω²
i.e., the acceleration due to gravity ¡s reduced by amount Rω²(≈ 0.034 m/s²) at equator.
Also, shape of the Earth is actually an ellipsoid, bulged at equator. The equatorial radius of the Earth is 6378 km, which is maximum. As g ∝ \(\frac{1}{\mathrm{R}^{2}}\) acceleration due to gravity is minimum on equator i.e., 9.7804 m/s².

Question 10.
Define the binding energy of a satellite. Obtain an expression for binding energy of a satellite revolving around the Earth at certain attitude.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.
Expression for binding energy of satellite revolving in circular orbit round the Earth:

Consider a satellite of mass m revolving at height h above the surface of the Earth in a circular orbit. It possesses potential energy as well as kinetic energy.
Let M be the mass of the Earth, R be the Radius of the Earth, v_c be critical velocity of satellite, r = (R + h) be thc radius of the orbit.
Kinetic energy of satellite = \(\frac{1}{2} \mathrm{mv}_{\mathrm{c}}^{2}=\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\)
The gravitational potential at a distance r from the centre of the Earth is –\(\frac{\mathrm{GM}}{\mathrm{r}}\)
∴ Potential energy of satellite = Gravitational potential × mass of satellite
= –\(\frac{\mathrm{GMm}}{\mathrm{r}}\)
The total energy of satellite is given as T.E. = KF. + P.E.
= \(\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}-\frac{\mathrm{GMm}}{\mathrm{r}}=-\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\)
Total energy of a circularly orbiting satellite is negative. Negative sign indicates that the satellite is bound to the Earth, due to gravitational force of attraction. For the satellite to be free from the Earth’s gravitational influence its total energy should become zero or positive.
Hence the minimum energy to be supplied to unbind the satellite is +\(\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\). This is the binding energy of a satellite.

Question 11.
Obtain the formula for acceleration due to gravity at the depth ‘d’ below the Earth’s surface.
Answer:

The Earth can be considered to be a sphere made of large number of concentric uniform spherical shells.
When an object is on the surface of the Earth it experiences the gravitational force as if the entire mass of the Earth is concentrated at its centre.
The acceleration due to gravity on the surface of the Earth is, g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Assuming that the density of the Earth is uniform, mass of the Earth is given by
M = volume x density = \(\frac{4}{3}\) πR³ρ
∴ g = \(\frac{\mathrm{G} \times \frac{4}{3} \pi \mathrm{R}^{3} \rho}{\mathrm{R}^{2}}\) = \(\frac{4}{3}\) πRρG ………….. (1)
Consider a body at a point P at the depth d below the surface of the Earth as shown in figure.

Here the force on a body at P due to outer spherical shell shown by shaded region, cancel out due to symmetry.
The net force on P is only due to the inner sphere of radius OP = R – d.
Acceleration due to gravity because of this sphere is,

This equation gives acceleration due to gravity at depth d below the Earth’s surface.

Question 12.
State Kepler’s three laws of planetary motion.
Answer:

All planets move in elliptical orbits around the Sun with the Sun at one of the foci of the ellipse.
The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.

Question 13.
State the formula for acceleration due to gravity at depth ‘d’ and altitude ‘h’ Hence show that their ratio is equal to \(\left(\frac{R-d}{R-2 h}\right)\) by assuming that the altitude is very small as compared to the radius of the Earth.
Answer:

For an object at depth d, acceleration due to gravity of the Earth is given by,
g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) ………………. (1)
Also, the acceleration due to gravity at smaller altitude h is given by,
g_h = g(1 – \(\frac{2 \mathrm{~h}}{\mathrm{R}}\)) ……………. (2)
Hence, dividing equation (1) by equation (2),
we get,

Question 14.
What is critical velocity? Obtain an expression for critical velocity of an orbiting satellite. On what factors does it depend?
Answer:
The exact horizontal velocity of projection that must be given to a satellite at a certain height so that it can revolve in a circular orbIt round the Earth is called the critical velocity or orbital velocity (v_c).
Expression for critical velocity:

Consider a satellite of mass m revolving round the Earth at height h above its surface. Let M be the mass of the Earth and R be its radius.
If the satellite is moving in a circular orbit of radius (R + h) = r, its speed must be equal to the magnitude of critical velocity v_c.
The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the satellite on the Earth.
∴ Centripetal force = Gravitational force

This is the expression for critical speed at the orbit of radius (R + h).
The critical speed of a satellite is independent of the mass of the satellite. It depends upon the mass of the Earth and the height at which the satellite is revolving or gravitational acceleration at that altitude.

Question 15.
Define escape speed. Derive an expression for the escape speed of an object from the surface of the earth.
Answer:

The minimum velocity with which a both’ should he thrown vertically upwards from the surface of the Earth so that it escapes the Earth ‘s gravitational field, is called the escape velocity (v_e) of the body.
As the gravitational force due to Earth becomes zero at infinite distance, the object has to reach infinite distance in order to escape.
Let us consider the kinetic and potential energies of an object thrown vertically upwards with escape velocity v_e.
On the surface of the Earth,
K.E.= \(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}\)
P.E. = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Total energy = P.E. + K.E.
∴ T.E. = \(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}\) ………………. (1)
The kinetic energy of the object will go on decreasing with time as it is pulled back by Earth’s gravitational force. It will become zero when it reaches infinity. Thus, at infinite distance from the Earth,
K.E. = 0
Also,
P.E. = –\(\frac{\mathrm{GMm}}{\infty}\) = 0
∴ Total energy = P.E. + K.E. = 0
As energy is conserved
\(\frac{1}{2} \mathrm{mv}_{\mathrm{e}}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}=0\) ……[From(1)]
or, v_e = \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)

Question 16.
Describe how an artificial satellite using two stage rocket is launched in an orbit around the Earth.
Answer:

Launching of a satellite in an orbit around the Earth cannot take place by use of single stage rocket. It requires minimum two stage rocket.
With the help of first stage of rocket, satellite can be taken to a desired height above the surface of the Earth.
Then the launcher is rotated in horizontal direction i.e.. through 900 using remote control and the first stage of the rocket is detached.
With the help of second stage of rocket, a specific horizontal velocity (v_h) is given to satellite so that it can revolve in a circular path around the Earth.
The satellite follows different paths depending upon the horizontal velocity provided to it.

4. Solve the following problems.

Question 1.
At what distance below the surface of the Earth, the acceleration due to gravity decreases by 10% of its value at the surface, given radius of Earth is 6400 km.
Solution:
Given: g_d = 90% of g i.e., \(\frac{\mathrm{g}_{\mathrm{d}}}{\mathrm{g}}\) = 0.9,
R = 6400km = 6.4 × 10⁶ m
To find: Distance below the Earth’s surface (d)

At distance 640 km below the surface of the Earth, value of acceleration due to gravity decreases by 10%.

Question 2.
If the Earth were made of wood, the mass of wooden Earth would have been 10% as much as it is now (without change in its diameter). Calculate escape speed from the surface of this Earth.
Solution:

As, we know that the escape speed from surface of the Earth is 11.2 km/s, Substituting value of v_e = 11.2 km/s
V_e_w = 11.2 × \(\frac{1}{\sqrt{10}}=\frac{11.2}{3.162}\)
= 11.2 × \(\frac{1}{3.162}\)
…………… [Taking square root value]
= antilog {log(1 1.2) – Log(3.162)}
= antilog {1.0492 – 0.5000}
= antilog {0.5492} = 3.542
∴ V_e_w = 3.54km/s
The escape velocity from the surface of wooden Earth is 3.54 km/s.

Question 3.
Calculate the kinetic energy, potential energy, total energy and binding energy of an artificial satellite of mass 2000 kg orbiting at a height of 3600 km above the surface of the Earth.
Given:- G = 6.67 × 10^-11 Nm²/kg²
R = 6400 km
M = 6 × 10²⁴ kg
Solution:
Given:- m = 2000 kg, h = 3600 km = 3.6 × 10⁶ m,
G = 6.67 × 10^-11 Nm²/kg²
R = 6400 km
M = 6 × 10²⁴ kg

To find: i) Kninetic energy (K.E.)
ii) Potential Energy (P.E.)
iii) Total Energy (T.E.)
iv) Binding Energy (B.E.)

From formula (ii),
P.E. = -2 × 40.02 × 10⁹
= -80.04 × 10⁹ J
From formula (iii),
T.E. = (40.02 × 10⁹) + (-80.02 × 10⁹)
= -40.02 × 10⁹ J
From formula (iv),
B.E.= -(-40.02 × 10⁹)
= 40.02 × 10⁹ J
Kinetic energy of the satellite is 40.02 × 10⁹ J, potential energy is -80.04 × 10⁹ J, total energy is -40.02 × 10⁹ J and binding energy is 40.02 × 10⁹ J.
[Note: Total energy of orbiting satellite is negative.]

Question 4.
Two satellites A and B are revolving around a planet. Their periods of revolution are 1 hour and 8 hours respectively. The radius of orbit of satellite B is 4 × 10⁴ km. find radius of orbit of satellite A .
Solution:
Given: T_A = 1 hour, T_B = 8 hour,
r_B = 4 × 10⁴ km
To find: Radius of orbit of satellite A (r_A)

Radius of orbit of satellite A will be 1 × 10⁴ km.

Question 5.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 10³⁰ kg
Mass of the Earth = 5.98 × 10²⁴ kg
The average distance between the Earth and the Sun = 1.5 × 10¹¹ m.
Solution:
Given: M_S = 1.99 × 10³⁰ kg
M_E = 5.98 × 10²⁴ kg, R = 1.5 × 10¹¹ m.
To find: Gravitational force between the Sun and the Earth (F)
Formula: F = \(\frac{\mathrm{Gm}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
Calculation:As, we know, G = 6.67 × 10^-11 N m²/kg²
From formula,

= antilog {(log(6.67) + log( 1.99) + log(5.98) – log(2.25)} × 10²¹
= antilog {(0.8241) + (0.2989) + (0.7767) – (0.3522)} × 10²¹
= antilog {1.5475} × 10²¹
= 35.28 × 10²¹
= 3.5 × 10²² N
The gravitational force between the Sun and the Earth is 3.5 × 10²² N.

Question 6.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 10²⁴ kg, R = 6400 km).
Solution:
Given: h = 300 km = 0.3 × 10⁶ m,
M = 5.98 × 10²⁴ kg,
R = 6400km = 6.4 × 10⁶ m
G = 6.67 × 10^-11 Nm²/kg²
To find: Acceleration due to gravity at height (g_h)
Formula: g_h = \(\frac{G M}{(R+h)^{2}}\)

Calculation: From formula,
g_h = \(\frac{6.67 \times 10^{-11} \times 5.98 \times 10^{24}}{\left[\left(6.4 \times 10^{6}\right)+\left(0.3 \times 10^{6}\right)\right]^{2}}\)
= \(\frac{6.67 \times 5.98 \times 10^{13}}{(6.7)^{2} \times 10^{12}}\)
6.67 X 10” x 5.98 X iO
= antilog {log(6.67) + log(5.98) – 2log(6.7)} × 10
= antilog{0.8241 + 0.7767 – 2(0.8261)} × 10
= antilog {1.6008 – 1.6522} × 10
= antilog {\(\overline{1}\) .9486} × 10
= 0.8884 × 10 = 8.884 m/s²
Acceleration due to gravity at 300 km will be 8.884 m/s².

Question 7.
Calculate the speed of a satellite in an orbit at a height of 1000 km from the Earth’s surface. M_E = 5.98 × 10²⁴ kg, R = 6.4 × 10⁶ m.
Solution:
Given: h = 1000 km = 1 × 10⁶ m,
ME = 5.98 × 10²⁴ kg, R = 6.4 × 10⁶ m,
G = 6.67 × 10^-11 N m²/kg²
To find: Speed of satellite (v_c)

Speed of the satellite at height 1000 km is 7.34 × 10³ m/s.

Question 8.
Calculate the value of acceleration due to gravity on the surface of Mars if the radius of Mars = 3.4 × 10³ km and its mass is 6.4 × 10²³ kg.
Solution:
Given:
M = 6.4 × 10²³ kg
R = 3.4 × 10³ = 3.4 × 10⁶ m,
To find: Acceleration due to gravity on the surface of the Mars (g_M)
Formula: g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: As, G = 6.67 × 10^-11 N m²/kg²
From formula,
g_M = \(\frac{6.67 \times 10^{-11} \times 6.4 \times 10^{23}}{\left(3.4 \times 10^{6}\right)^{2}}=\frac{6.67 \times 6.4}{3.4 \times 3.4}\)
= antilog {log(6.67) + log(6.4) – log(3.4) – log(3.4)}
= antilog {(0.8241) + (0.8062) – (0.5315) – (0.53 15)}
= antilog {0.5673}
= 3.693 m/s²
Acceleration due to gravity on the surface of Mars is 3.693 m/s².

Question 9.
A planet has mass 6.4 × 10²⁴ kg and radius 3.4 × 10⁶ m. Calculate energy required to remove on object of mass 800 kg from the surface of the planet to infinity.
Solution:
Given: M = 6.4 × 10²⁴ kg, R = 3.4 × 10⁶ m, m = 800 kg
To find: Energy required to remove the object from surface of planet to infinity = B.E.
Formula: B.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Calculation: We know that,
G = 6.67 × 10^-11 N m²/kg²
From formula,

= antilog{log(6.67) + log(51.2) – log(3.4)} × 10⁹
= antilog{0.8241 + 1.7093 – 0.5315} × 10⁹
= antilog {2.0019} × 10⁹
= 1.004 × 10² × 10⁹
= 1.004 × 10¹¹ J
Energy required to remove the object from the surface of the planet is 1.004 × 10¹¹ J.
[Note: Answer calculated above ¡s in accordance with retual methods of calculation.]

Question 10.
Calculate the value of the universal gravitational constant from the given data. Mass of the Earth = 6 × 10²⁴ kg, Radius of the Earth = 6400 km and the acceleration due to gravity on the surface = 9.8 m/s²
Solution:
Given: M = 6 × 10²⁴ kg,
R = 6400km = 6.4 × 10⁶ m,
g = 9.8 m/s²
To find: Gravitational constant (G)
Formula. g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: From formula,
G = \(\frac{\mathrm{gR}^{2}}{\mathrm{M}}\)
G = \(\frac{9.8 \times\left(6.4 \times 10^{6}\right)^{2}}{6 \times 10^{24}}=\frac{401.4 \times 10^{12}}{6 \times 10^{24}}\)
∴ G = 6.69 × 10^-11 N m²/kg²
The value of gravitational constant is 6.69 × 10^-11 N m²/kg².

Question 11.
A body weighs 5.6 kg wt on the surface of the Earth. How much will be its weight on a planet whose mass is 1/7 times the mass of the Earth and radius twice that of the Earth’s radius.
Solution:
Given: W_E = 5.6 kg-wt.,
\(\frac{\mathrm{M}_{\mathrm{p}}}{\mathrm{M}_{\mathrm{E}}}=\frac{1}{7}, \frac{\mathrm{R}_{\mathrm{p}}}{\mathrm{R}_{\mathrm{E}}}\) = 2
To find: Weight of the body on the surface of planet (W_p)
Formula: W = mg = \(\frac{\mathrm{GMm}}{\mathrm{R}^{2}}\)
Calculation: From formula,

Weight of the body on the surface of a planet will be 0.2 kg-wt.
[Note: The answer given above is calculated in accordance with textual method considering the given data].

Question 12.
What is the gravitational potential due to the Earth at a point which is at a height of 2R_E above the surface of the Earth, Mass of the Earth is 6 × 10²⁴ kg, radius of the Earth = 6400 km and G = 6.67 × 10^-11 Nm² kg^-2.
Solution:
Given: M = 6 × 10²⁴ kg,
R_E = 6400km = 6.4 × 10⁶ m,
G = 6.67 × 10^-11 Nm²/kg²,
h = 2R_E
To find: Gravitational potential (V)
Formula: V = – \(\frac{\mathrm{GM}}{\mathrm{r}}\)
Calculation: From formula,

= -2.08 × 10⁷ J kg^-1
Negative sign indicates the attractive nature of gravitational potential.
Gravitational potential due to Earth will be 2.08 × 10⁷ J kg^-1 towards the centre of the Earth.
[Note: According lo definition of gravitational potential its SI unit is J/kg.]

11th Physics Digest Chapter 5 Gravitation Intext Questions and Answers

Can you recall? (Textbook Page No. 78)

Question 1.
i) What are Kepler’s laws?
ii)What is the shape of the orbits of planets?
Answer:

The Kepler’s laws are:
- Kepler’s first law: The orbit of a planet is an ellipse with the Sun at one of the foci.
- Kepler’s second law: The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
- Kepler’s third law: The square of orbital period of revolution of a planet around the Sun is directly proportional to the cube of the mean distance of the planet from the Sun.
The orbits of the planet are elliptical in shape.

Question 2.
When released from certain height why do objects tend to fall vertically downwards?
Answer:
When released from certain height, objects tend to fall vertically downwards because of the gravitational force exerted by the Earth.

11th Std Physics Questions And Answers:

11th Physics Chapter 6 Exercise Mechanical Properties of Solids Solutions Maharashtra Board

January 7, 2025January 6, 2025 by Prasanna

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 6 Mechanical Properties of Solids Textbook Exercise Questions and Answers.

Mechanical Properties of Solids Class 11 Exercise Question Answers Solutions Maharashtra Board

Class 11 Physics Chapter 6 Exercise Solutions Maharashtra Board

Physics Class 11 Chapter 6 Exercise Solutions

1. Choose the correct answer:

Question 1.
Change in dimensions is known as …………..
(A) deformation
(B) formation
(C) contraction
(D) strain.
Answer:
(A) deformation

Question 2.
The point on stress-strain curve at which strain begins to increase even without increase in stress is called…………
(A) elastic point
(B) yield point
(C) breaking point
(D) neck point
Answer:
(B) yield point

Question 3.
Strain energy of a stretched wire is 18 × 10^-3 J and strain energy per unit volume of the same wire and same cross section is 6 × 10^-3 J/m³. Its volume will be………….
(A) 3cm³
(B) 3 m³
(C) 6 m³
(D) 6 cm³
Answer:
(B) 3 m³

Question 4.
……………. is the property of a material which enables it to resist plastic deformation.
(A) elasticity
(B) plasticity
(C) hardness
(D) ductility
Answer:
(C) hardness

Question 5.
The ability of a material to resist fracturing when a force is applied to it, is called……………
(A) toughness
(B) hardness
(C) elasticity
(D) plasticity.
Answer:
(A) toughness

2. Answer in one sentence:

Question 1.
Define elasticity.
Answer:
If a body regains its original shape and size after removal of the deforming force, it is called an elastic body and the property is called elasticity.

Question 2.
What do you mean by deformation?
Answer:
The change in shape or size or both of u body due to an external force is called deformation.

Question 3.
State the SI unit and dimensions of stress.
Answer:

SI unit: N m^-2 or pascal (Pa)
Dimensions: [L^-1M¹T^-2]

Question 4.
Define strain.
Answer:
Strain:

Strain is defined as the ratio of change in dimensions of the body to its original dimensions.
Strain = \(\frac{\text { change in dimensions }}{\text { original dimensions }}\)
Types of strain:
- Longitudinal strain,
- Volume strain,
- Shearing strain.

Question 5.
What is Young’s modulus of a rigid body?
Answer:
Young’s modulus (Y): It is the modulus of elasticity related to change in length of an object like a metal wire, rod, beam, etc., due to the applied deforming force.

Question 6.
Why bridges are unsafe after a very long use?
Answer:
A bridge during its use undergoes recurring stress depending upon the movement of vehicles on it. When bridge is used for long time, it loses its elastic strength and ultimately may collapse. Hence, the bridges are declared unsafe after long use.

Question 7.
How should be a force applied on a body to produce shearing stress?
Answer:
A tangential force which is parallel to the top and the bottom surface of the body should be applied to produce shearing stress.

Question 8.
State the conditions under which Hooke’s law holds good.
Answer:
Hooke’s Taw holds good only when a wire/body is loaded within its elastic limit.

Question 9.
Define Poisson’s ratio.
Answer:
Within elastic limit, the ratio of lateral strain to the linear strain is called the Poisson‘s ratio.

Question 10.
What is an elastomer?
Answer:
A material that can be elastically stretched to a larger value of strain is called an elastomer.

Question 11.
What do you mean by elastic hysteresis?
Answer:

In case of some materials like vulcanized rubber, when the stress applied on a body decreases to zero, the strain does not return to zero immediately. The strain lags behind the stress. This lagging of strain behind the stress is called elastic hysteresis.
Below figure shows the stress-strain curve for increasing and decreasing load. It encloses a loop. Area of loop gives the energy dissipated during deformation of a material.

Question 12.
State the names of the hardest material and the softest material.
Answer:
Hardest material: Diamond
Softest material: Aluminium
[Note: Material with highest strength is steel whereas material with lowest strength is plasticine clay.]

Question 13.
Define friction.
Answer:
The property which resists the relative motion between two surfaces in contact is called friction.

Question 14.
Why force of static friction is known as ‘self-adjusting force?
Answer:
The force of static friction varies in accordance with applied force. Hence, it is called as self adjusting force.

Question 15.
Name two factors on which the coefficient of friction depends.
Answer:
Coefficient of friction depends upon:

the materials of the surfaces in contact.
the nature of the surfaces.

3. Answer in short:

Question 1.
Distinguish between elasticity and plasticity.
Answer:

No.	Elasticity	Plasticity
i.	Body regains its original shape or size after removal of deforming force.	Body does not regain its original shape or size after removal of deforming force.
ii.	Restoring forces are strong enough to bring the displaced molecules to their original positions.	Restoring forces are not strong enough to bring the molecules back to their original positions.
	Examples of elastic materials: metals, rubber, quartz, etc	Examples of plastic materials: clay, putty, plasticine, thick mud, etc

Question 2.
State any four methods to reduce friction.
Answer:
Friction can be reduced by using polished surfaces, using lubricants, using grease and using ball bearings.

Question 3.
What is rolling friction? How does it arise?
Answer:

Friction between two bodies in contact when one body is rolling over the other, is called rolling friction.
Rolling friction arises as the point of contact of the body with the surface keep changing continuously.

Question 4.
Explain how lubricants help in reducing friction?
Answer:

The friction between lubricant to surface is much less than the friction between two same surfaces. Hence using lubricants reduces the friction between the two surfaces.
When lubricant is applied to machine parts, it fills the depression present on the surface in contact. Thus, less friction is occurred between machine parts.
Application of lubricants also reduces wear and tear of machine parts which in turn reduces friction.
Advantage: Reduction in function reduces dissipation of energy in machines due to which efficiency of machines increases.

Question 5.
State the laws of static friction.
Answer:
Laws of static friction:

First law: The limiting force of static friction (F_L) is directly proportional to the normal reaction (N) between the two surfaces in contact.
F_L ∝ N
∴ F_L = µ_s N
where, µ_s = constant called coefficient of static friction.
Second law: The limiting force of friction is
independent of the apparent area between the surfaces in contact, so long as the normal reaction remains the same.
Third law: The limiting force of friction depends upon materials in contact and the nature of their surfaces.

Question 6.
State the laws of kinetic friction.
Answer:
Laws of kinetic friction:

First law: The force of kinetic friction (Fk) is directly proportional to the normal reaction (N) between two surfaces in contact.
F_k ∝ N
∴ F_k = µ_kN
where, µ_k = constant called coefficient of kinetic friction.
Second law: Force of kinetic friction is independent of shape and apparent area of the surfaces in contact.
Third law: Force of kinetic friction depends upon the nature and material of the surfaces in contact.
Fourth law: The magnitude of the force of kinetic friction is independent of the relative velocity between the object and the surface provided that the relative velocity is neither too large nor too small.

Question 7.
State advantages of friction.
Answer:
Advantages of friction:

We can walk due to friction between ground and feet.
We can hold object in hand due to static friction.
Brakes of vehicles work due to friction; hence we can reduce speed or stop vehicles.
Climbing on a tree is possible due to friction.

Question 8.
State disadvantages of friction.
Answer:
Disadvantages of friction:

Friction opposes motion.
Friction produces heat in different parts of machines. It also produces noise.
Automobile engines consume more fuel due to friction.

Question 9.
What do you mean by a brittle substance? Give any two examples.
Answer:

Substances which breaks within the elastic limit are called brittle substances.
Examples: Glass, ceramics.

4. Long answer type questions:

Question 1.
Distinguish between Young’s modulus, bulk modulus and modulus of rigidity.
Answer:

No	Young’s modulus	Bulk modulus	Modulus of rigidity
i.	It is the ratio of longitudinal stress to longitudinal strain.	It is the ratio of volume stress to volume strain.	It is the ratio of shearing stress to shearing strain.
ii.	It is given by, Y = \(\frac{\mathrm{MgL}}{\pi \mathrm{r}^{2} l}\)	It is given by, K = \(\frac{V d P}{d V}\)	It is given by, \(\eta=\frac{F}{A \theta}\)
iii.	It exists in solids.	It exists in solid, liquid and gases.	It exists in solids.
iv.	It relates to change in length of a body.	It relates to change in volume of a body.	It relates to change in shape of a body.

Question 2.
Define stress and strain. What are their different types?
Answer:
i) Stress:

The internal restoring force per unit area of a both is called stress.
Stress = \(\frac{\text { deforming force }}{\text { area }}=\frac{|\vec{F}|}{\mathrm{A}}\)
where \(\vec{F}\) is internal restoring force or external applied deforming force.
Types of stress:
- Longitudinal stress,
- Volume stress,
- Shearing stress.

ii. Strain:

Strain is defined as the ratio of change in dimensions of the body to its original dimensions.
Strain = \(\frac{\text { change in dimensions }}{\text { original dimensions }}\)
Types of strain:
- Longitudinal strain,
- Volume strain,
- Shearing strain.

Question 3.
What is Young’s modulus? Describe an experiment to find out Young’s modulus of material in the form of a long straight wire.
Answer:
Definition: Young ‘s modulus is the ratio of longitudinal stress to longitudinal strain.
It is denoted by Y.
Unit: N/m² or Pa in SI system.
Dimensions: [L^-1M¹T^-2]

Experimental description to find Young’s modulus:

i. Consider a metal wire suspended from a rigid support. A load is attached to the free end of the wire. Due to this, deforming force gets applied to the free end of wire in downward direction and it produces a change in length.
Let,
L = original length of wire,
Mg = weight suspended to wire,
l = extension or elongation,
(L + l) = new length of wire.
r = radius of the cross section of wire

ii. In its equilibrium position,

Question 4.
Derive an expression for strain energy per unit volume of the material of a wire.
Answer:
Expression for strain energy per unit volume;

i. Consider a wire of original length L and cross sectional area A stretched by a force F acting along its length. The wire gets stretched and elongation l is produced in it

ii. If the wire is perfectly elastic then,
Longitudinal stress = \(\frac{F}{A}\)
Longitudinal strain = \(\frac{l}{L}\)

iii. The magnitude of stretching force increases from zero to F during elongation of wire.
Let ‘f’ be the restoring force and ‘x’ be its corresponding extension at certain instant during the process of extension.
∴ f = \(\frac{\text { YAx }}{\mathrm{L}}\) ……………. (2)

iv. Let ‘dW’ be the work done for the further small extension ‘dx’.
Work = force × displacement
∴ dW = fdx
∴ dW= \(\frac{\text { YAx }}{L}\) dx …………..(3) [From (2)]

v. The total amount of work done in stretching the wire from x = 0 to x = l can be found out by integrating equation (3).

∴ Work done in stretching a wire,
W = \(\frac{1}{2}\) × load × extension

vi. Work done by stretching force is equal to strain energy gained by the wire.
∴ Strain energy = \(\frac{1}{2}\) × load × extension

vii. Work done per unit volume

∴ Strain energy per unit volume = \(\frac{1}{2}\) × stress × strain

viii. Other forms:

Question 5.
What is friction? Define coefficient of static friction and coefficient of kinetic friction. Give the necessary formula for each.
Answer:

The property which resists the relative motion between two surfaces in contact is called friction.
The coefficient of static friction is defined as the ratio of limiting force of friction to the normal reaction.
Formula: \(\mu_{\mathrm{S}}=\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}\)
The coefficient of kinetic friction is defined as the ratio of force of kinetic friction to the normal reaction between the two surfaces in contact.
Formula: \(\mu_{\mathrm{k}}=\frac{\mathrm{F}_{\mathrm{K}}}{\mathrm{N}}\)

Question 6.
State Hooke’s law. Draw a labelled graph of tensile stress against tensile strain for a metal wire up to the breaking point. In this graph show the region in which Hooke’s law is obeyed.
Answer:
i) Statement: Within elastic limit, stress is directly proportional to strain.
Explanation;

According to Hooke’s law,
Stress ∝ Strain

This constant of proportionality is called modulus of elasticity.
Modulus of elasticity of a material is the slope of stress-strain curve in elastic deformation region and depends on the nature of the material.
The graph of strain (on X-axis) and stress (on Y-axis) within elastic limit is shown in the figure.

ii)

iii) Hooke’s law is completely obeyed in the region OA.

5. Answer the following

Question 1.
Calculate the coefficient of static friction for an object of mass 50 kg placed on horizontal table pulled by attaching a spring balance. The force is increased gradually it is observed that the object just moves when spring balance shows 50N.
[Answer: µs = 0.102]
Solution:
Given: m = 50 kg, F_L = 50 N, g = 9.8 m/s²
To find: Coefficient of static friction (µ_s)
Formula: µ_s = \(\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}=\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{mg}}\)
µ_s = \(\frac{50}{50 \times 9.8}\) = 0.102
Answer:
The coefficient of static friction is 0.102.

Question 2.
A block of mass 37 kg rests on a rough horizontal plane having coefficient of static friction 0.3. Find out the least force required to just move the block horizontally.
[Answer: F= 108.8N]
Solution:
Given: m = 37 kg, µ_s = 0.3, g = 9.8 m /s²
To find: Limiting force (F_L)
Formula: F_L = µ_SN = µ_S mg
Calculation: From formula,
F_L = 0.3 × 37 × 9.8 = 108.8 N
Answer:
The force required to move the block is 108.8 N.

Question 3.
A body of mass 37 kg rests on a rough horizontal surface. The minimum horizontal force required to just start the motion is 68.5 N. In order to keep the body moving with constant velocity, a force of 43 N is needed. What is the value of
a) coefficient of static friction? and
b) coefficient of kinetic friction?
Asw:
a) µ_s = 0.188
b) µ_k = 0.118]
Solution:
Given:
F_L = 68.5 N, F_k = 43 N,
m = 37 kg, g = 9.8 m/s²

To find:

i. Coefficient of static friction (µ_s)
ii. Coefficient of kinetic friction (µ_k)

Formulae:

i. µ_s = \(\frac{F_{L}}{N}\) = \(\frac{F_{L}}{m g}\)
ii. µ_k = \(\frac{F_{k}}{N}\) = \(\frac{\mathrm{F}_{\mathrm{k}}}{\mathrm{mg}}\)

Calculation:
From formula (i),
∴ µ_s = \(\frac{F_{S}}{N}=\frac{68.5}{37 \times 9.8}\) = 0.1889
From formula (ii),
∴ µ_k = \(\frac{F_{k}}{N}=\frac{43}{37 \times 9.8}\) = 0.1186
Answer:

The coefficient of static friction is 0.1889.
The coefficient of kinetic friction is 0.1186.

[Note: Answers calculated above are in accordance with textual methods of calculation.]

Question 4.
A wire gets stretched by 4mm due to a certain load. If the same load is applied to a wire of same material with half the length and double the diameter of the first wire. What will be the change in its length?
Solution:
Given. l₁ = 4mm = 4 × 10^-3 m
L₂ = \(\frac{\mathrm{L}_{1}}{2}\), D₂ = 2D, r₂ = 2r₁
To find: Change in length (l₂)
Formula: Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} l}\)
Calculation: From formula,

= 0.5 × 10^-3 m
= 0.5 mm
The new change in length of the wire is 0.5 mm.

Question 5.
Calculate the work done in stretching a steel wire of length 2m and cross sectional area 0.0225mm² when a load of 100 N is slowly applied to its free end. [Young’s modulus of steel= 2 × 10¹¹ N/m²]
Solution:
Given. L = 2m, F = 100 N,
A = 0.0225 mm² = 2.25 × 10^-8 m²,
Y = 2 × 10^-11 N/m²,
To find: Work (W)
Formula: W = \(\frac{1}{2}\) × F × l
Claculation:

= antilog [log 10 – log 4.5]
= antilog [1.0000 – 0.6532 ]
= antilog [0.3468]
∴ W = 2.222 J
Answer:
The work done in stretching the steel wire is 2.222 J.

Question 6.
A solid metal sphere of volume 0.31m³ is dropped in an ocean where water pressure is 2 × 10⁷ N/m². Calculate change in volume of the sphere if bulk modulus of the metal is 6.1 × 10¹⁰ N/m²
Solution:
Given: V= 0.31 m³, dP = 2 × 10⁷ N/m²,
K = 6.1 × 10¹⁰ N/m²
To find: Change in volume (dV)
Formula: K = V × \(\frac{\mathrm{dP}}{\mathrm{dV}}\)
Calculation: From formula,
dV = \(\frac{\mathrm{V} \times \mathrm{dP}}{\mathrm{K}}\)
∴ dV = \(\frac{0.31 \times 2 \times 10^{7}}{6.1 \times 10^{10}}\) ≈ 10^-4 m³
The change in volume of the sphere is 10^-4 m³.

Question 7.
A wire of mild steel has initial length 1.5 m and diameter 0.60 mm is extended by 6.3 mm when a certain force is applied to it. If Young’s modulus of mild steel is 2.1 × 10¹¹ N/m², calculate the force applied.
Solution:
Given:
L = 1.5m, d = 0.60 mm,
r = \(\frac{d}{2}\) = 0.30 mm = 3 × 10^-4 m,
Y = 2.1 × 10¹¹ N/m²,
l = 6.3 mm = 6.3 × 10^-3 m
To find: Force (F)
Calculation:
From formula,

= 2.1 × 3.142 × 6 × 6.3
= antilog [log 2.1 + log 3.142 + log 6 + log 6.3]
= antilog [0.3222 + 0.4972 + 0.7782 + 0.7993]
= antilog [2.3969]
= 2.494 × 10²
≈ 250 N
The force applied on wire is 250 N.

Question 8.
A composite wire is prepared by joining a tungsten wire and steel wire end to end. Both the wires are of the same length and the same area of cross section. If this composite wire is suspended to a rigid support and a force is applied to its free end, it gets extended by 3.25mm. Calculate the increase in length of tungsten wire and steel wire separately.
[Given: Y_steel = 2 × 10¹¹ Pa, Y_Tungsten = 4.11 × 10¹¹ Pa]
Solution:
Given: l_s + l_T = 3.25 mm,
Y_T = 4.11 × 10¹¹ Pa
Y_s = 2 × 10¹¹ Pa
To find: Extension in tungsten wire (l_T)
Extension in steel wire (l_s)

But l_s + l_T = 3.25
l_s + 0.487 l_s = 3.25
l_s(1 + 0.487) = 3.25
l_s = 2.186 mm
∴ l_T = 3.25 – 2.186
= 1.064 mm
The extension in tungsten wire is 1.064 mm and the extension in steel wire is 2.186 mm.

[Note: Values of Young’s modulus of tungsten and steel considered above are standard values. Using them, calculation is carried out ¡n accordance with textual method.]

Question 9.
A steel wire having cross sectional area 1.2 mm² is stretched by a force of 120 N. If a lateral strain of 1.455 mm is produced in the wire, calculate the Poisson’s ratio.
Solution:
Given: A = 1.2 mm² = 1.2 × 10^-6 m²,
F = 120 N, Y_steel = 2 × 10¹¹ N/m²,
Lateral strain = 1.455 × 10^-4
To find: Poisson’s ratio (σ)

The Poisson’s ratio of steel is 0.291.
[Note: Lateral strain being ratio of two same physical quantities, is unitless. hence, value given in question ¡s modified to 1.455 × 10^-4 to reach the answer given in textbook.]

Question 10.
A telephone wire 125m long and 1mm in radius is stretched to a length 125.25m when a force of 800N is applied. What is the value of Young’s modulus for material of wire?
Solution:
Given: L = 125m,
r = 1 mm= 1 × 10^-3 m
l = 125.25 – 125 = 0.25 m,
F = 800N
To find: Young’s modulus (Y)
Formula: Y \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} l}\)
Calculation: From formula,
Y = \(\frac{800 \times 125}{3.142 \times 10^{-6} \times 0.25}\)
= {antilog [log 800 + log 125 – log 3.142 – log 0.25 ]} × 10⁶
= {antilog [2.9031 + 2.0969 – 0.4972 – \(\overline{1}\) .3979]} × 10⁶
= {antilog[5.1049]} × 10⁶
= 1.274 × 10⁵
= 1.274 × 10¹¹ N/m²
The Young’s modulus of telephone wire is 1.274 × 10¹¹ N/m².

Question 11.
A rubber band originally 30cm long is stretched to a length of 32cm by certain load. What is the strain produced?
Solution:
Given: L = 30 cm = 30 × 10 ^-2 m,
∆l = 32 cm – 30 cm = 2cm = 2 × 10 ^-2 m
To find. Strain
Formula: Strain = \(\frac{\Delta l}{\mathrm{~L}}\)
Calculation: From formula,
Strain = \(\frac{2 \times 10^{-2}}{30 \times 10^{-2}}\) = 6.667 × 10 ^-2
The strain produced in the wire is 6.667 × 10 ^-2.

Question 12.
What is the stress in a wire which is 50m long and 0.01cm² in cross section, if the wire bears a load of 100kg?
Solution:
Given: M = 100 kg, L 50 m, A = 0.01 × 10^-4 m
To find: Stress
Formula: Stress = \(\frac{\mathrm{F}}{\mathrm{A}}=\frac{\mathrm{Mg}}{\mathrm{A}}\)
Calculation: From formula,
Stress = \(\frac{100 \times 9.8}{0.01 \times 10^{-4}}\) = 9.8 × 10⁸ N/m²
The stress in the wire is 9.8 × 10⁸ N/m².

Question 13.
What is the strain in a cable of original length 50m whose length increases by 2.5cm when a load is lifted?
Solution:
Given: L = 50m, ∆l = 2.5cm = 2.5 × 10 ^-2 m
To find: Strain
Formula: Strain = \(\frac{\Delta l}{\mathrm{~L}}\)
Calculation: From formula,
Strain = \(\frac{2.5 \times 10^{-2}}{50}\) = 5 × 10^-4
The Strain produced in wire is 5 × 10^-4 .

11th Physics Digest Chapter 6 Mechanical Properties of Solids Intext Questions and Answers

Can you recall? (Textbook Page No. 100)

Question 1.

Can you name a few objects which change their shape and size on application of a force and regain their original shape and size when the force is removed?
Can you name objects which do not regain their original shape and size when the external force is removed?

Answer:

Objects such as rubber, metals, quartz, etc. change their shape and size on application of a force (within specific limit) and regain their original shape and size when the force is removed.
Objects such as putty, clay, thick mud. etc. do not regain their original shape and size when the external force is removed.

Can you tell? (Textbook Page No. 107)

Question 1.
Why does a rubber band become loose after repeated use?
Answer:

After repeated use of rubber band, its stress-strain curve does not remain linear.
In such case, since rubber crosses its elastic limit, there is a permanent set formed on the rubber due to which it becomes loose.

Can you tell? (Textbook Page No.111)

Question 1.
i. It is difficult to run fast on sand.
ii. It is easy to roll than pull a barrel along a road.
iii. An inflated tyre rolls easily than a flat tyre.
iv. Friction is a necessary evil.
Answer:
i.

The intermolecular space between crystals of sand is very large as compared to that in a rigid surface.
Thus, there are number of depressions at the points of contact of feet and sand surface.
Projections and depressions between sand and feet are not completely interlocked.
Thus, action and reaction force become unbalanced. The horizontal component of force helps to move forward and vertical component of the force resist to move.
Hence, it becomes difficult to run fast on sand.

ii.

When a barrel is pulled along a road, the friction between the tyres and road is kinetic friction, but when its rolls along the road it undergoes rolling friction.
The force of kinetic friction is greater than force of rolling friction.
Hence, it is easy to roll than pull a barrel along a road.

iii.

When the tyre is inflated, the pressure inside the tyre is reducing the normal force between tyre and the ground, and thus reducing the friction between the tyre and the road.
When the tyre gets deflated, it gets deformed during rolling, the supplied energy is used up in changing the shape and not overcoming the friction, and thus due to deformation, friction increases.
Hence, an inflated tyre rolls easily than a flat tyre.

iv.

Friction helps us to walk, hold objects in hand, lift objects and without friction we cannot walk, we cannot grip or hold objects with our hands,
Friction is responsible for wear and tear of various part of machines, it produces heat in different parts of machine and also produces noise but it also helps in ball bearing or connecting screws.
Hence, friction is said to be a necessary evil because it is useful as well as harmful.

Internet my friend (Textbook Page No. 111)

Question 1.
i. https ://opentextbc. ca/physicstestbook2/ chapter/friction/
ii. https://www.livescience.com/
iii. https://www.khanacademy.org/science/physics
iv. https://courses.lumenleaming.com/physics/ chapter/5-3-elasticity-stress-and-strain/
v. https://www.toppr.com/guides/physics/
Answer:
[Students are expected to visit the above mentioned websites and collect more information about mechanical properties of solid.]

11th Std Physics Questions And Answers:

11th Biology Chapter 15 Exercise Excretion and Osmoregulation Solutions Maharashtra Board

January 7, 2025January 6, 2025 by Prasanna

Balbharti Maharashtra State Board 11th Biology Textbook Solutions Chapter 15 Excretion and Osmoregulation Textbook Exercise Questions and Answers.

Excretion and Osmoregulation Class 11 Exercise Question Answers Solutions Maharashtra Board

Class 11 Biology Chapter 15 Exercise Solutions Maharashtra Board

Biology Class 11 Chapter 15 Exercise Solutions

1. Choose correct option

Question (A).
Which one of the following organisms would spend maximum energy in production of nitrogenous waste?
a. Polar bear
b. Flamingo
c. Frog
d. Shark
Answer:
b. Flamingo

Question (B).
In human beings, uric acid is formed due to metabolism of __________.
a. amino acids
b. fatty acids
c. creatinine
d. nucleic acids
Answer:
d. nucleic acids

Question (C).
Visceral layer : Podocytes :: PCT : _______
a. Cilliated cells
b. Squamous cells
c. Columnar cells
d. Cells with brush border
Answer:
d. Cells with brush border

Question (D).
Deproteinised plasma is found in __________.
a. Bowman’s capsule
b. Descending limb
c. Glomerular capillaries
d. Ascending limb
Answer:
a. Bowman’s capsule, b. Descending limb, d. Ascending limb

Question (E).
Specific gravity of urine would _______ if level of ADH increases.
a. remain unaffected
b. increases
c. decreases
d. stabilise
Answer:
b. increases

Question (F).
What is micturition?
a. Urination
b. Urine formation
c. Uremia
d. Urolithiasis
Answer:
a. Urination

Question (G).
Which one of the following organisms excrete waste through nephridia?
a. Cockroach
b. Earthworm
c. Crab
d. Liver Fluke
Answer:
c. Crab

Question (H).
Person suffering from kidney stone is advised not to have tomatoes as it has _______.
a. seeds
b. lycopene
c. oxalic acid
d. sour taste
Answer:
c. oxalic acid

Question (I).
Tubular secretion does not take place in ________.
a. DCT
b. PCT
c. collecting duct
d. Henle’s loop
Answer:
b. PCT

Question (J).
The minor calyx ____________.
a. collects urine
b. connects pelvis to ureter
c. is present in the cortex
d. receives column of Bertini
Answer:
a. collects urine

Question (K).
Which one of the followings is not a part of human kidney?
a. Malpighian body
b. Malpighian tubule
c. Glomerulus
d. Loop of Henle
Answer:
b. Malpighian tubule

Question (L).
The yellow colour of the urine is due to presence of ___________
a. uric acid
b. cholesterol
c. urochrome
d. urea
Answer:
c. urochrome

Question (M).
Hypotonic filtrate is formed in _______
a. PCT
b. DCT
c. LoH
d. CT
Answer:
a. PCT

Question (N).
In reptiles, uric acid is stored in _____
a. cloaca
b. fat bodies
c. liver
d. anus
Answer:
a. cloaca

Question (O).
The part of nephron which absorbs glucose and amino acid is______
a. collecting tubule
b. proximal tubule
c. Henle’s loop
d. DCT
Answer:
b. proximal tubule

Question (P).
Bowman’s capsule is located in kidney in the ________
a. cortex
b. medulla
c. pelvis
d. pyramids
Answer:
a. cortex

Question (Q).
The snakes living in desert are mainly__________
a. aminotelic
b. ureotelic
c. ammonotelic
d. uricotelic
Answer:
d. uricotelic

Question (R).
Urea is a product of breakdown of ___________
a. fatty acids
b. amino acids
c. glucose
d. fats
Answer:
b. amino acids

Question (S).
Volume of the urine is regulated by__________
a. aldosterone
b. ADH
c. both a and b
d. none
Answer:

Question 2.
Answer the following questions

Question (A).
Doctors say Mr. Shaikh is suffering from urolithiasis. How it could be explained in simple words?
Answer:
Urolithiasis is the condition of having calculi in the urinary tract (which also includes the kidneys), which may pass into urinary bladder.

Question (B).
Anitaji needs to micturate several times and feels very thirsty. This is an indication of change in permeability of certain part of nephron. Which is this part?
Answer:

Need to micturate several times (polyuria) and feeling very thirsty (polydipsia) is a symptom of diabetes insipidus (imbalance of fluids in the body).
ADH prevents diuresis and due to absence of ADH, large amount of dilute urine is excreted.
ADH stimulates reabsorption of water from last part of DCT and entire collecting duct by increasing the permeability of cells.
If the permeability of these cells changes, it will result in increase in urine volume (frequent micturition) and increase in the osmolarity of blood. An imbalance in volume and osmolarity of body fluids increases thirst.

[Note: Water is reabsorbed by osmosis in PCT, DCT and descending limb of loop of Henle)

Question (C).
Effective filtration pressure was calculated to be 20 mm Hg; where glomerular hydrostatic pressure was 70 mm of Hg. Which other pressure is affecting the filtration process? How much is it?
Answer:
The other pressure affecting the filtration process is osmotic pressure of blood and filtrate hydrostatic pressure. Commonly effective filtration pressure (EFP) is represented as;
EFP = Glomerular Hydrostatic pressure in glomerulus – (Osmotic pressure of blood + Filtrate Hydrostatic pressure)
If EFP = 20 mmHg and Glomerular Hydrostatic pressure = 70 mmHg
20 = 70 – (Osmotic pressure of blood + Filtrate hydrostatic pressure)
∴ (Osmotic pressure of blood + Filtrate hydrostatic pressure) = 70-20
Then (Osmotic pressure of blood + Filtrate Hydrostatic pressure) = 50 mmHg .

[Note: Given values are insufficient to calculate the exact osmotic pressure of blood and filtrate hydrostatic pressure. The sum of the two values can be calculated to be 50 mmHg ]

Question (D).
Name any one guanotelic organism.
Answer:
Spiders, scorpions and penguins are guanotelic organisms as they excrete guanine.

Question (E).
Why are kidneys called ‘retroperitoneal’?
Answer:
Kidneys are located in abdomen. Kidneys are not surrounded by peritoneum instead they are located posterior to it. Thus, kidneys are called retroperitoneal.

Question (F).
State role of liver in urea production.
Answer:

Ammonia formed during the breakdown of amino acids is converted into urea in the liver of ureotelic animals.
This conversion takes place by the help of the ornithine / urea cycle.
3 ATP molecules are used to produce one molecule of urea using the ornithine/ urea cycle. Since, the liver contains carrier molecules and enzymes necessary for urea cycle, it plays a major role in urea production.

Question (G).
Why do we get bad breath after eating garlic or raw onion?
Answer:

Raw onion and garlic contain volatile sulphur-containing compounds.
Sulphur-containing compounds have a distinctive odour which remain in the mouth after consumption of onion and garlic.
Also, volatile compounds (like certain sulphur containing compounds) in foodstuffs are generally excreted through the lungs and may result in bad breath.

3. Answer the following questions

Question (A).
John has two options as treatment for his renal problem : Dialysis or kidney transplants. Which option should he choose? Why?
Answer:

If John has two options of dialysis and kidney transplant, readily available he must opt for kidney transplant.
A kidney transplant, if successful, can improve the quality of life of a patient and reduce the risk of death.
The patient would not have to endure frequent dialysis procedures. Repeated visits for dialysis takes time and may not allow the patient to perform normal activities or go to office regularly.
Dialysis is regarded as a holding measure until kidney transplant can be performed or a supportive measure in those for whom a transplant would be inappropriate. However, dialysis cannot replace all the functions of a normal kidney such as production of hormones like erythropoietin, calcitriol and renin. Hence, if John has an option of kidney transplant, he must opt for it.

Question (B).
Amphibian tadpole can afford to be ammonotelic. Justify.
Answer:

Tadpole (larval stage of life cycle of amphibian) is aquatic. They are ammonotelic as they excrete nitrogenous waste in the form of ammonia.
Ammonia is very toxic and requires large amount of water for its elimination.
It is readily soluble in water and diffuses across the body surface and into the surrounding water.
Also, the water lost during excretion can be made up through the surrounding water in ammonotelic organisms.

Hence, amphibian tadpole can afford to be ammonotelic.

Question (C).
Birds are uricotelic in nature. Give reason.
Answer:

Birds are capable of converting ammonia into uric acid by ‘inosinic acid pathway’ in their liver.
Uric acid is least toxic and hence, it can be retained in the body for some time.
It is least soluble water hence, negligible amount of water is required for its elimination.
This mode of excretion can also help reduce body weight (an adaptation for flight) and those animals which
need to conserve more water follow uricotelism.

Hence, in order to conserve water as an adaptation for flight, birds are uricotelic in nature.

Question 4.
Write the explanation in your word

Question (A).
Nitya has been admitted to hospital after heavy blood loss. Till proper treatment could be given; how did Nitya’s body must have tackled the situation?
Answer:

Heavy blood loss is called haemorrhage. In case of haemorrhage or severe dehydration, the osmoreceptors stimulate Antidiuretic hormone (ADH) secretion.
ADH is important in regulating water balance through the kidneys. For detailed mechanism of reabsorption by ADH:

Regulating water reabsorption through ADH:
Hypothalamus in the midbrain has special receptors called osmoreceptors which can detect change in osmolarity (measure of total number of dissolved particles per liter of solution) of blood.

If osmolarity of blood increases due to water loss from the body (after eating namkeen or due to sweating), osmoreceptors trigger release of Antidiuretic hormone (ADH) from neurohypophysis (posterior pituitary). ADH stimulates reabsorption of water from last part of DCT and entire collecting duct by increasing the permeability of cells.

This leads to reduction in urine volume and decrease in osmolarity of blood.

Once the osmolarity of blood comes to normal, activity of osmoreceptor cells decreases leading to decrease in ADH secretion. This is called negative feedback.
In case of hemorrhage or severe dehydration too, osmoreceptors stimulate ADH secretion. ADH is important in regulating water balance through kidneys.

In absence of ADH, diuresis (dilution of urine) takes place and person tends to excrete large amount of dilute urine. This condition called as diabetes insipidus.

[Note: Hypothalamus is a part of forebrain]

Another regulatory mechanism that must have been activated is RAAS. For detailed mechanism of electrolyte reabsorption:

Electrolyte reabsorption through RAAS:
Another regulatory mechanism is RAAS (Renin Angiotensin Aldosterone System) by Juxta Glomerular Apparatus (JGA).

Whenever blood supply (due to change in blood pressure or blood volume) to afferent arteriole decreases (e.g. low BP/dehydration), JGA cells release Renin. Renin converts angiotensinogen secreted by hepatocytes in liver to Angiotensin I. ‘Angiotensin-converting enzyme’ further modifies Angiotensin I to Angiotensin II, the active form of hormone. It stimulates adrenal cortex to release another hormone called aldosterone that stimulates DCT and collecting ducts to reabsorb more Na⁺ and water, thereby increasing blood volume and pressure.

Question 5.
Complete the diagram / chart with correct labels / information. Write the conceptual details regarding it

Question (A).

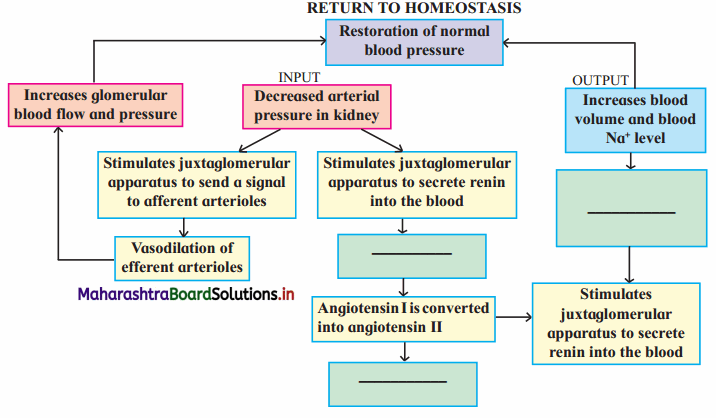
Answer:

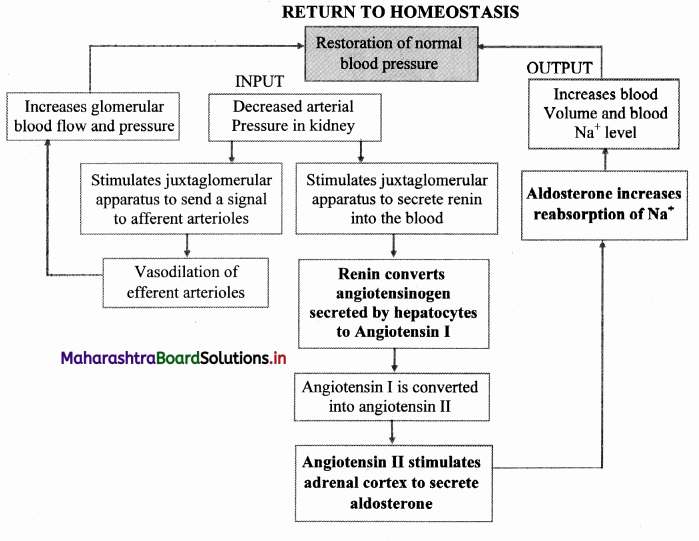
The composition of urine depends upon food and fluid consumed by an individual. There are two ways in which it the composition is regulated. They are as follows:

i. Regulating water reabsorption through ADH
ii. Electrolyte reabsorption though RAAS
iii. Atrial Natriuretic Peptide

In absence of ADH, diuresis (dilution of urine) takes place and person tends to excrete large amount of dilute urine. This condition called as diabetes insipidus.

[Note: Hypothalamus is a part of forebrain]

ii. Electrolyte reabsorption through RAAS:
Another regulatory mechanism is RAAS (Renin Angiotensin Aldosterone System) by Juxta Glomerular Apparatus (JGA).

Whenever blood supply (due to change in blood pressure or blood volume) to afferent arteriole decreases (e.g. low BP/dehydration), JGA cells release Renin. Renin converts angiotensinogen secreted by hepatocytes in liver to Angiotensin I. ‘Angiotensin converting enzyme’ further modifies Angiotensin I to Angiotensin II, the active form of hormone. It stimulates adrenal cortex to release another hormone called aldosterone that stimulates DCT and collecting ducts to reabsorb more Na⁺ and water, thereby increasing blood volume and pressure.

iii. Atrial natriuretic peptide (ANP): A large increase in blood volume and pressure stimulates atrial wall to produce atrial natriuretic peptide (ANP). ANP inhibits Na⁺ and Cl^– reabsorption from collecting ducts inhibits release of renin, reduces aldosterone and ADH release too. This leads to a condition called Natriuresis (increased excretion of Na⁺ in urine) and diuresis.

Question (B).

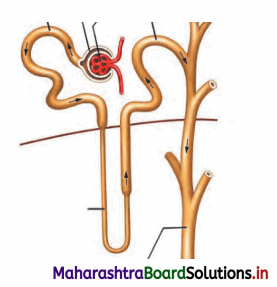
Answer:

Nephrons are structural and functional units of kidney.
Each nephron consists of a 4 – 6 cm long, thin-walled tube called the renal tubule and a bunch of capillaries known as the glomerulus.
The wall of the renal tubule is made up of a single layer of epithelial cells.
Its proximal end is wide, blind, cup-like and is called as Bowman’s capsule, whereas the distal end is open.
The nephron is divisible into Ilowman’s capsule, neck, proximal convoluted tubule (PCT), Loop of Henle (LoH), distal convoluted tubule (DCT) and collecting tubule (CT).
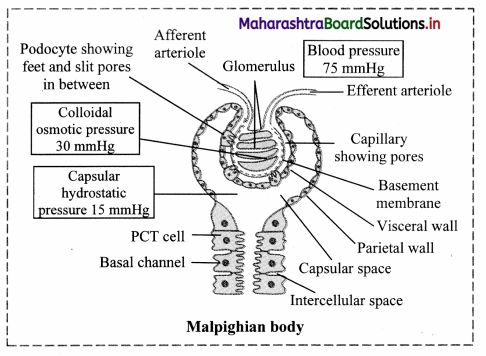
The glomerulus is present in the cup-like cavity of Bowman’s capsule and both are collectively known as renal corpuscle or Malpighian body.

Question (C)

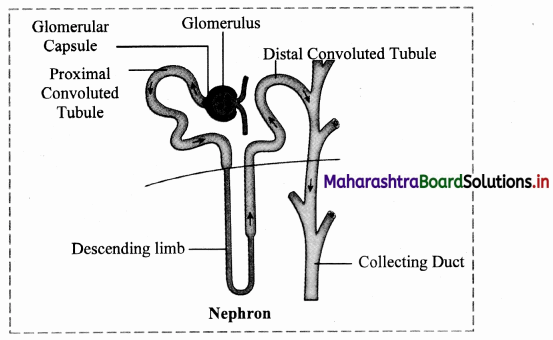
Answer:
Nephron is the structural and functional unit of kidney.
Structure of nephron:
A nephron (uriniferous tubule) is a thin walled, coiled duct, lined by a single layer of epithelial cells. Each nephron is divided into two main parts:

i. Malpighian body
ii. Renal tubule

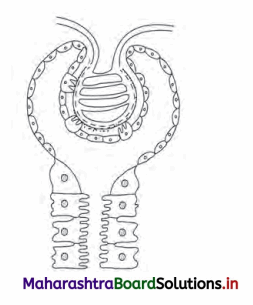
i. Malpighian body: Each Malpighian body is about 200pm in diameter and consists of a Bowman’s capsule and glomerulus.

a. Glomerulus:
Glomerulus is a bunch of fine blood capillaries located in the cavity of Bowman’s capsule.
A small terminal branch of the renal artery, called as afferent arteriole enters the cup cavity (Bowman capsule) and undergoes extensive fine branching to form network of several capillaries. This bunch is called as glomerulus.
The capillary wall is fenestrated (perforated).

All capillaries reunite and form an efferent arteriole that leaves the cup cavity.
The diameter of the afferent arteriole is greater than the efferent arteriole. This creates a high hydrostatic pressure essential for ultrafiltration, in the glomerulus.

b. Bowman’s capsule:
It is a cup-like structure having double walls composed of squamous epithelium.
The outer wall is called as parietal wall and the inner wall is called as visceral wall.
The parietal wall is thin consisting of simple squamous epithelium.
There is a space called as capsular space / urinary space in between two walls.
Visceral wall consists of special type of squamous cells called podocytes having a foot-like pedicel. These podocytes are in close contact with the walls of capillaries of glomerulus.
There are small slits called as filtration slits in between adjacent podocytes.

ii. Renal tubule:

a. Neck:
The Bowman’s capsule continues into the neck. The wall of neck is made up of ciliated epithelium. The lumen of the neck is called the urinary pole. The neck leads to proximal convoluted tubule.

b. Proximal Convoluted Tubule :
This is highly coiled part of nephron which is lined by cuboidal cells with brush border (microvilli) and surrounded by peritubular capillaries. Selective reabsorption occurs in PCT. Due to convolutions (coiling), filtrate flows slowly and remains in the PCT for longer duration, ensuring that maximum amount of useful molecules are reabsorbed.

c. Loop of Henle :
This is ‘U’ shaped tube consisting of descending and ascending limb.
The descending limb is thin walled and permeable to water and lined with simple squamous epithelium.
The ascending limb is thick walled and impermeable to water and is lined with simple cuboidal epithelium.
The LoH is surrounded by capillaries called vasa recta.
Its function is to operate counter current system – a mechanism for osmoregulation.
The ascending limb of Henle’s loop leads to DCT.

d. Distal convoluted tubule:
This is another coiled part of the nephron.
Its wall consists of simple cuboidal epithelium.
DCT performs tubular secretion / augmentation / active secretion in which, wastes are taken up from surrounding capillaries and secreted into passing urine.
DCT helps in water reabsorption and regulation of pH of body fluids.

e. Collecting tubule:
This is a short, straight part of the DCT which reabsorbs water and secretes protons.
The collecting tubule opens into the collecting duct.

Question (D).

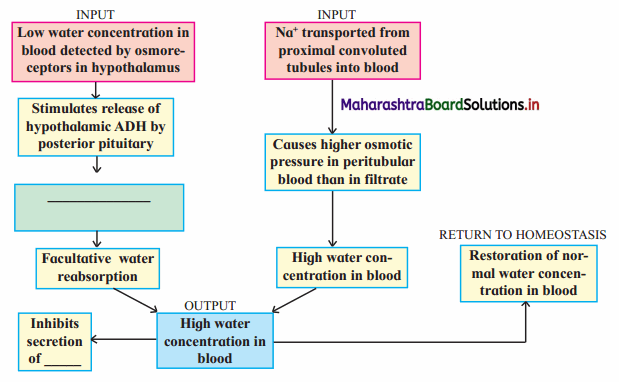
Answer:

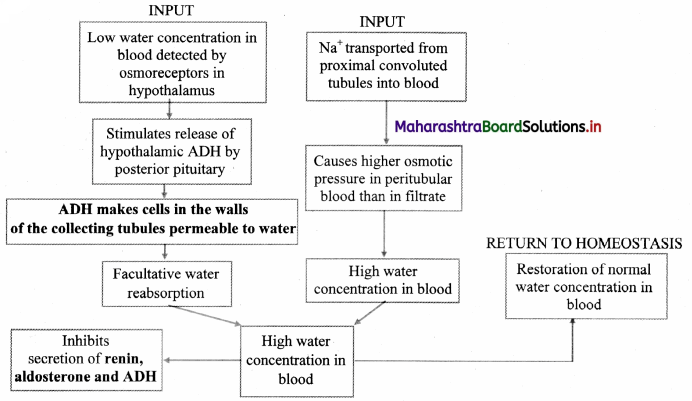
The composition of urine depends upon food and fluid consumed by an individual. There are two ways in which it the composition is regulated. They are as follows:

i. Regulating water reabsorption through ADH
ii. Electrolyte reabsorption though RAAS
iii. Atrial Natriuretic Peptide

In absence of ADH, diuresis (dilution of urine) takes place and person tends to excrete large amount of dilute urine. This condition called as diabetes insipidus.

[Note: Hypothalamus is a part of forebrain]

ii. Electrolyte reabsorption through RAAS:
Another regulatory mechanism is RAAS (Renin Angiotensin Aldosterone System) by Juxta Glomerular Apparatus (JGA).
Whenever blood supply (due to change in blood pressure or blood volume) to afferent arteriole decreases (e.g. low BP/dehydration), JGA cells release Renin. Renin converts angiotensinogen secreted by hepatocytes in liver to Angiotensin I. ‘Angiotensin-converting enzyme’ further modifies Angiotensin I to Angiotensin II, the active form of hormone. It stimulates adrenal cortex to release another hormone called aldosterone that stimulates DCT and collecting ducts to reabsorb more Na⁺ and water, thereby increasing blood volume and pressure.

Question (E).

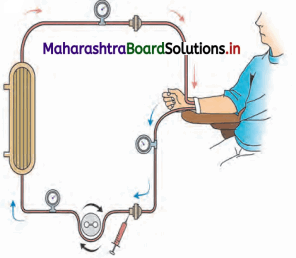
Answer:

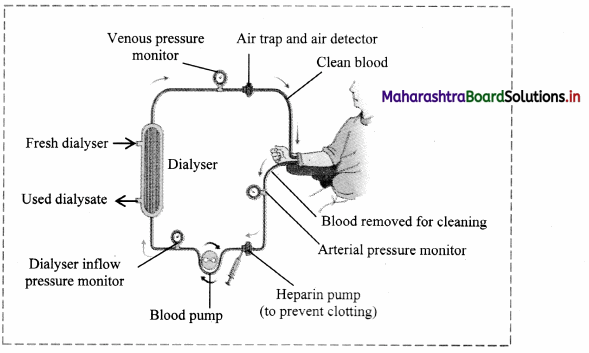
When renal function of a person falls below 5 – 7 %, accumulation of harmful substances in blood begins. In such a condition the person has to go for artificial means of filtration of blood i.e. haemodialysis.
In haemodialysis, a dialysis machine is used to filter blood. The blood is filtered outside the body using a dialysis unit.
In this procedure, the patients’ blood is removed; generally from the radial artery and passed through a cellophane tube that acts as a semipermeable membrane.
The tube is immersed in a fluid called dialysate which is isosmotic to normal blood plasma. Hence, only excess salts if present in plasma pass through the cellophane tube into the dialysate.
Waste substances being absent in the dialysate, move from blood into the dialyzing fluid.
Filtered blood is returned to vein.
In this process it is essential that anticoagulant like heparin is added to the blood while it passing through the tube and before resending it into the circulation, adequate amount of anti-heparin is mixed.
Also, the blood has to move slowly through the tube and hence the process is slow.

Question 6.
Prove that mammalian urine contains urea.
Answer:

Urea is a nitrogenous waste formed by breakdown of protein (deamination of amino acids).
During this process, amino groups are removed from the amino acids present in the proteins and converted to highly toxic ammonia. The ammonia is finally converted to area through ornithine cycle. Thus, the urea formed is passed to kidneys and excreted out of the body through urine.
Reabsorption of urea (proximal tubule, collecting ducts) and active secretion of urea (Henle loop) leads to a urea circulation (urea recycling) between the lumen of the nephron and renal medulla, which is an important element of the renal urine concentration.
About 54 g of urea is filtered per day in the glomerular capsule, of which approximately 30 g is excreted in the urine and 24 g is reabsorbed into blood (assuming GFR is 180 litres/day).
Urinalysis can help detect the amount of urea in urine (Urine urea nitrogen test, urease test, etc.).

Practical / Project :

Visit to a nearby hospital or pathological laboratory and collect detailed information about different blood and urine tests.
Answer:
Testing the urine is known as urinalysis. It generally has three parts:

Visual examination: Check sample colour and clearness.
Dipstick examination: Checks for abnormal amounts of glucose, protein, etc.
Microscopic examination: Check for presence of RBCs. WBCs, bacteria, crystals, etc.
Apart from routine urine examination, specific tests may also be done. They are as follows:
- BUN (Blood Urea Nitrogen) Test: It measures the amount of nitrogen in blood and evaluates kidney function.
- Urease Test/ Urea Nitrogen Test: It is done to check the amount of urea in urine sample.
- Urine albumin to creatine ratio (UACR) test: Estimates the amount of albumin in urine.

[Students are expected to collect more information and perform the given activity on their own]

12th Biology Digest Chapter 15 Excretion and Osmoregulation Intext Questions and Answers

Can you recall? (Textbook Page No. 174)

Question 1.
Why are various waste products produced in the body of an organism?
Answer:
Metabolism produces a variety of by-products, some of which need to be eliminated. Such by-produçts are called metabolic waste products.

Question 2.
How are these waste eliminated?
Answer:
Depending on the type of waste product, they are eliminated through various organs of the body:

The various excretory products produced by the human body are as follows:

Fluids such as water; gaseous wastes like CO₂ nitrogenous wastes like ammonia, urea and uric acid, creatinine; minerals; salts of sodium, potassium. calcium, etc. if present in body in excess are excreted through urine, faeces and sweat.
Pigments formed due to breakdown of haemoglobin like bilirubin (excreted through faeces) and urochrome (eliminated through urine).
The pigments present in consumed foodstuffs like beet root or excess of vitamins, hormones and drugs.
Volatile substances present in spices (eliminated through lungs).

Have you ever observed? (Textbook Page No. 174)

Question 1.
When does urine appear deeply coloured?
Answer:
Urine can appear deeply coloured due to various reasons:

Severe dehydration resulting in production of concentrated urine.
Consumption of foodstuff like beet root, which contain coloured pigments.
Some medications can also cause the urine to appear deeply coloured.

Think about it. (Textbook Page No. 174)

Question 1.
Do organisms differ in type of metabolic wastes they produce?
Answer:
Yes, organisms differ in the type of metabolic wastes they produce. Some organisms excrete ammonia while some excrete urea or uric acid as metabolic wastes.

Question 2.
Do environment or evolution have any effect on type of waste produced by an organism?
Answer:

The theory of evolution proposes that life started in an aquatic environment.
Aquatic organisms are generally ammonotelic. It is believed that the urea cycle evolved to adapt to a changing environment when terrestrial life forms evolved.
Arid conditions probably led to the evolution of the uric acid pathway as a means of conserving water.
However, the correlation between evolution and type of waste production is uncertain.

Question 3.
How do thermoregulation and food habits affect saste production?
Answer:

To generate heat. endotherms convert the food that they eat into energy through a process called metabolism. Hence, they consume more tì.od in order to meet their energy requirements.
Also, carnivorous diet contains more proteins than herbivores.
Consumption of high protein or more food containing proteins can result in production of large amount of nitrogenous waste
These animals would also require more energy to eliminate the high levels oF nitrogenous wastes which build up when animal protein is digested.

Use your brain power. (Textbookpage No. 175)

Question 1.
Why ammonia is highly toxic?
Answer:

Ammonia is basic in nature and its retention in the body would disturb the pH of the body.
An increase in pH would disturb all enzyme catalysed reactions in the body and also make the plasma membrane unstable.

Hence, ammonia is highly toxic to the body.

Find out. (Textbook page No. 175)

You will study about a type of arthritis called gouty arthritis caused due to accumulation of uric acid in joints. Where does uric acid come from in case of ureotelic human beings?
Answer:

Uric acid produced as a waste product during the normal breakdown of nucleic acids (purines) and certain naturally occurring substances found in foods such as mushrooms. Mackerel, dried beans. etc.
This uric acid is generally excreted out along with urine.
If uric acid is produced in excess or not excreted, it accumulates in joints causing gouty arthritis.

Think about it. (Textbook Page No.175)

Endotherms consume more food in order to meet energy requirements. Also, carnivorous diet contains more proteins than herbivorous. Does it affect excretion of nitrogenous waste?
Answer:

To generate heat, endotherms convert the food that they eat into energy through a process called metabolism. Hence, they consume more food in order to meet their energy requirements.
Also, carnivorous diet contains more proteins than herbivores.
Consumption of high protein or more food containing proteins can result in production of large amount of nitrogenous waste.
These animals would also require more energy to eliminate the high levels of nitrogenous wastes which build up when animal protein is digested.

Observe and Discuss (Textbook Page No. 176)

Question 1.
These are blood reports of patients undergoing investigations for kidney function. What is creatinine? What is your observation and opinion about the findings? Why is it used as an index of kidney function?

Answer:
i. Creatinine:

Plasma creatinine is produced from catabolism of creatinine phosphate during skeletal muscle contraction.
It provides a ready source of high energy phosphate.

ii. Observations and Opinion:
Report A indicates a value of creatinine which is higher than the normal range. This would indicate impaired kidney function.
Report B indicates high fasting blood sugar and detection of sugar in the blood is known as glucosuria. High fasting blood sugar (>126 mg/dL) is usually indicative of diabetes.

iii. Creatinine used as an index of kidney function:

Normally blood creatinine levels remain steady because the rate of production matches his excretion in urine.
Hence, plasma creatinine is used as an index of kidney function and its level above normal is an indication of poor renal function.

Think about it. (Textbook Page No. 176)

Question 1.
During summer, we tend to produce less urine, is it so?
Answer:

Generally, excess water containing wastes is lost from the body in the time of urine. sweat and faeces.
During summer when the surrounding temperature is high. we also lose a considerable amount of water in the form of sweat.

Thus, the kidneys retain water for maintaining the concentration of body fluids and reduce the amount of water lost through urine.

Question 2.
Marine birds like Albatross spend their life on the sea. That means the water the, drink is salty. how do they manage osnioregulation then?
Answer:

Marine birds like Albatross have special glands called salt glands near their nostrils.
These glands are capable of secreting salts by active transport and help to manage osmotic balance,

[Note: The salt glands in Albatross are located in or on the skull in the area of eyes.]

Question 3.
like ectothermic and endothermic animals, do organisms differ in the way they maintain salt balance?
Answer:
Yes, organisms differ in the way they maintain salt balance.

Animals can be either isosmotic to the surrounding (osmoconformers or control the internal environment independent of external environment (osmoregulators).
Marine organisms are mostly osmoconfòrmers because their body fluids and external environment are isosmotic in nature while fresh water forms and terrestrial organisms are osmoregulators,
Generally, most organisms can tolerate only a narrow range of salt concentrations. Such organism are known as stenohaline organisms.
Organisms which are capable of handling a wide change in salinity are called euryhaline organisms.e.g. Barnacles, clams etc.

Find out. (Textbook Page No 176)

Question 1.
How do freshwater fishes and marine fishes carry out osmoregulation?
Answer:
Osmoregulation is the process of maintaining an internal concentration of salt and water in the body of fishes.

i. Freshwater fishes:
The salt concentration inside the body of freshwater fishes is higher than their surrounding water. Due to this, water enters the body due to osmosis.
If the flow of water into the body is not regulated. fishes would swell and get bigger.
To compensate this, the kidneys produce a large amount of urine,
Excretion of large amounts of urine regulates the level of water in the body hut results in the loss of salts.
Thus, in order to maintain a sufficient salt level, special cells in the gills (chloride cells) take tip ions from
the water, which are then directly transported into the blood.

ii. Marine fishes:
Since the salt content in blood of marine fishes is much lower than that of seawater, they constantly tend to lose water and build up salt.
To replace the water loss, they continually need to drink seawater.
Since their small kidney can only excrete a relatively small amount of urine, salt is additionally excreted through gills, where chloride cells work in reverse as in freshwater fishes.

Make a table. (Textbook Page No. 178)

Question 1.
The details of modes of excretion of nitrogenous wastes.
Answer:
The three main modes of excretion in animals are as follows:

i. Ammonotelism
ii. Ureotelism
iii. Uricotelism

i. Ammonotelism:

Elimination of nitrogenous wastes in the form of ammonia is called as ammonotelism.
Ammonia is basic in nature and hence it can disturb the pH of the body, if not eliminated immediately.
Any change in pH would disturb all enzyme catalyzed reactions in the body and would also make the plasma membrane unstable.
Ammonia is readily soluble in water and needs large quantity of water to dilute and reduce its toxicity.
This is however an energy saving mechanism of excretion and hence all animals that have plenty of water available for dilution of ammonia, excrete nitrogenous wastes in the form of ammonia.
Animals that follow this mode of excretion are known as ammonotelic animals.
1 gm ammonia needs about 300 – 500 ml of water for elimination.
Ammonotelic animals excrete ammonia through general body surface (skin), gills and kidneys.
e.g. Ammonotelism is found in aquatic invertebrates, bony fishes, and aquatic / larval amphibians. Animals without excretory system (Protozoa) are also ammonotelic.

ii. Ureotelism:

Elimination of nitrogenous wastes in the form of urea is called as ureotelism.
Urea is comparatively less toxic and less water-soluble than ammonia. Hence, it can be concentrated to some extent in body.
The body requires less water for elimination.
Since it is less toxic and less water soluble, ureotelism is suitable for animals that need to conserve water to some extent. Hence, ureotelism is common in terrestrial animals, as they have to conserve water.
It takes about 50 ml H₂O for removal of 1 gm NH₂ in form of urea.
Ureotelic animals generally convert ammonia to urea in the liver by operating ornithine / urea cycle in which 3 ATP molecules are used to produce one molecule of urea.
e.g. Mammals, cartilaginous fishes (sharks and rays), many aquatic reptiles, most of the adult amphibians, etc. are ureotelic.

iii. Uricotelism:

Elimination of nitrogenous wastes in the form of uric acid is called as uricotelism.
Uric acid is least toxic and hence, it can be retained in the body for some time in concentrated form.
It is least soluble in water. Hence there is minimum (about 5 – 10 ml for 1 gm) or no need of water for its elimination.
Those animals which need to conserve more water follow uricotelism. However, these animals need to spend more energy.
Ammonia is converted into uric acid by ‘inosinic acid pathway’ in the liver of birds, e.g. Birds, some insects, many reptiles, land snails, are uricotelic.

No.	Ureotelism	Uricotelism
i.	It is the elimination of nitrogenous waste in the form of urea.	It is the elimination of nitrogenous waste in the form of uric acid.
ii.	Excretion of urea requires less (moderate ) amount of water.	Excretion of uric acid requires negligible amount of water.
iii.	Removal of 1 gm of urea requires 50 ml of water.	Removal of 1 gm of uric acid requires 5 – 10 ml of
iv.	rea is less toxic.	Uric acid is least toxic.
e.g.	It is generally seen in terrestrial animals. Mammals, cartilaginous fishes (sharks and rays), many aquatic reptiles, most adult amphibians, etc.	It is seen in birds, some insects, many reptiles, land snails, etc.

No.	Ammonotelism	Uricotelism
i.	It is the elimination of nitrogenous waste in the form of ammonia.	It is the elimination of nitrogenous waste in the form of uric acid.
ii.	Excretion of ammonia requires plenty of water.	Excretion of uric acid requires negligible amount of water.
iii.	Removal of 1 gm of ammonia requires 300 – 500 ml of water.	Removal of 1 gm of uric acid requires 10ml of water.
iv.	Ammonia is very toxic.	Uric acid is less toxic.
e.g.	It is found in aquatic invertebrates, bony fishes and aquatic/ larval amphibians, etc.	It is seen in birds, some insects, many reptiles, land snails, etc.

[Students can Refer these and make a chart on their own.]

Use your brain power. (Textbook Page No. 178)

Question 1.
Creatinine is considered as index of kidney function. Give reason.
Answer:

Plasma creatinine is produced from catabolism of creatinine phosphate during skeletal muscle contraction.
It provides a ready source of high energy phosphate.
Normally blood creatinine levels remain steady because the rate of production matches its excretion in urine.
Hence, plasma creatinine is used as an index of kidney function and its level above normal is an indication of poor renal function.

[Note: Plasma creatinine is a waste product produced by muscles from the breakdown of a compound called ‘creatine phosphate ’.]

Make a table. (Textbook Page No. 178)

Question 1.
The excretory organs found in various animal phyla.
Answer:

Sr. No.	Animal Phyla	Excretory organs
i.	Porifera	Lack excretory organ instead rely on water transport system/ Canal system
ii.	Coelenterata	Lack specialised excretory organs. Excretion takes place through simple diffusion or through the mouth.
iii.	Ctenophora	Lack specialised excretory organs
iv.	Platyhelminthes	Protonephridia or Flame cells
v.	Aschelminthes	Excretory tube and pore
vi.	Annelida	Nephridia
vii.	Arthropoda	Malpighian tubules
viii.	Mollusca	Organ of Bojanus
ix.	Echinodermata	Lack specialized excretory organs, waste materials directly diffuse into water or are excreted through tube feet
x.	Hemichordata	Proboscis gland
xi.	Chordata	Kidney

Observe and complete. (Textbook Page No. 178)

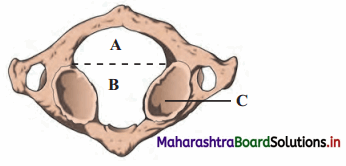
Question 1.
Label the diagram and complete following paragraphs.

i. Kidney: A pair of ____ shaped kidneys are present on either side of the ____ from 12^th thoracic to 3^rd lumbar vertebra. Kidneys are present behind ___. Hence are called retroperitoneal. Dimensions of
each kidney are 10 × ____ × ____ cms. Average weight is ___ g in males and 135 g in ____. Outer surface is ___ and inner is concave. Notch on the inner concave surface is called ___. Renal artery enters and renal vein as well as ureter leave the kidney through hilus. Each kidney has almost 1 million functional units called ___.

ii. Ureters: A pair of ureters arise from ___ of each kidney. Each ureter is a long muscular tube 25 – 30 cm in length. Ureters open into ___ by separate openings, which are not guarded by valves. They pass obliquely through the wall of urinary bladder. This helps in prevention of ___ of urine due to compression of ureters while bladder is filled.

iii. Urinary bladder: It is a median ___ sac. A hollow muscular organ, the bladder is situated in pelvic cavity posterior to pubic symphysis. At the base of the ___ there is a small inverted triangular area called trigone. At the apex of this triangle is opening of urethra. At the two points of the base of the triangle are openings of ureters. Urinary bladder is covered externally by peritoneum. Inner to peritoneum is muscular layer. It is formed by detrusor muscles which consist of three layers of smooth muscles. Longitudinal – circular – longitudinal respectively. Innermost layer is made up of transitional ___. It helps bladder to stretch.

iv. Urethra: It is a ___ structure arising from urinary bladder and opening to the exterior of the body.
There are ___ urethral sphincters between urinary bladder and urethra.
a. Internal sphincter: Made up of ___ muscles, involuntary in nature.
b. External sphincter: Made up of ___ muscles, voluntary in nature.
Answer:

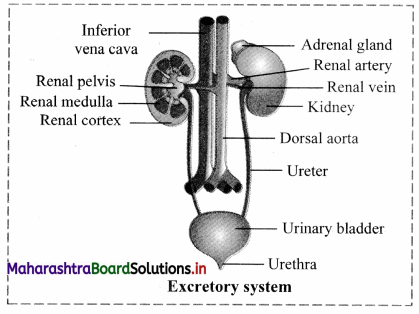
i. Kidney: A pair of bean shaped kidneys are present on either side of the backbone from 12^th thoracic to 3^rd lumbar vertebra. Kidneys are present behind peritoneum. Hence are called retroperitoneal. Dimensions of each kidney are 10 × 5 × 4 cms. Average weight is 150 g in males and 135 g in females. Outer surface is convex and inner is concave. Notch on the inner concave surface is called hilum. Renal artery enters and renal vein as well as ureter leave the kidney through hilus. Each kidney has almost 1 million functional units called nephron.

ii. Ureters: A pair of ureters arise from hilum of each kidney. Each ureter is a long muscular tube 25 – 30 cm in length. Ureters open into urinary bladder by separate openings, which are not guarded by valves. They pass obliquely through the wall of urinary bladder. This helps in prevention of backward flow of urine due to compression of ureters while bladder is filled.

iii. Urinary bladder: It is a median pear-shaped sac. A hollow muscular organ, the bladder is situated in pelvic cavity posterior to pubic symphysis. At the base of the urinary bladder there is a small inverted triangular area called trigone. At the apex of this triangle is opening of urethra. At the two points of the base of the triangle are openings of ureters. Urinary bladder is covered externally by peritoneum. Inner to peritoneum is muscular layer. It is formed by detrusor muscles which consist of three layers of smooth muscles. Longitudinal – circular – longitudinal respectively. Innermost layer is made up of transitional epithelial tissue. It helps bladder to stretch.

iv. Urethra: It is a fibromuscular tube-like structure arising from urinary bladder and opening to the exterior of the body. There are two urethral sphincters between urinary bladder and urethra.
a. Internal sphincter: Made up of detrusor muscles, involuntary in nature.
b. External sphincter: Made up of striated muscles, voluntary in nature.
If this valve is not functioning properly during inflammation of bladder, it can lead to kidney infection.

Internet is my friend. (Textbook Page No. 179)

Question 1.
Find out what is floating kidney.
Answer:

Floating kidney or nephroptosis, is an inferior displacement or dropping of the kidney.
This condition occurs when the kidney slips from its normal position because it is not held securely in place by the adjacent organs or its fat covering.
It generally develops in extremely thin people whose adipose capsule or renal fascia is deficient.
It may result in twisting of the ureter and cause blockage of urine flow. The resulting backup of urine would put pressure on the kidney and damage the tissues.
Twisting of the ureter may also cause pain and discomfort.
This condition is more common in females than males and happens commonly among one in four people.
Weakening of the fibrous bands that hold the kidney in place can predispose to floating kidney.

Can you recall? (Textbook Page No. 179)

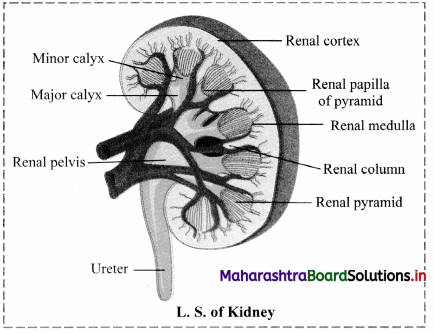
Question 1.
Observe the figure carefully and label various regions of L.S. of kidney.

Answer:

Can you tell? (Textbook Page No.182)

Question 1.
Why are kidneys called ‘retroperitoneal’?
Answer:
Kidneys are located in abdomen. Kidneys are not surrounded by peritoneum instead they are located posterior to it. Thus, kidneys are called retroperitoneal.

Question 2.
Why urinary tract infections are more common in females than males?
Answer:

The urethra in women (4 cm) is much shorter than that of males (20 cm).
This allows easy passage of bacteria into the urinary bladder.

Hence, urinary tract infections are more common in females than males.

Question 3.
What is nephron? Which are its main parts? Why are they important?
Answer:
Nephron is the structural and functional unit of kidney.
Structure of nephron:
A nephron (uriniferous tubule) is a thin walled, coiled duct, lined by a single layer of epithelial cells. Each nephron is divided into two main parts:

i. Malpighian body
ii. Renal tubule

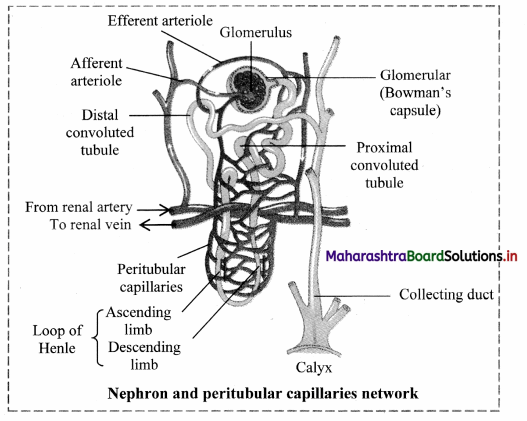
i. Malpighian body: Each Malpighian body is about 200pm in diameter and consists of a Bowman’s capsule and glomerulus.

ii. Renal tubule:

e. Collecting tubule:
This is a short, straight part of the DCT which reabsorbs water and secretes protons.
The collecting tubule opens into the collecting duct.

Think about ¡t. (Textbook Page No. 182)

Question 1.
How much blood ¡s supplied to kidney?
Answer:
Around 600 ml of blood passes through each kidney per minute.

Do this. (Textbook Page No. 183)

Question 1.
Check blood reports of patients and comment about possibility of glucosuria.
Answer:
Glucosuria is the presence of glucose sugar in urine. High glucose in urine is usually indicative of diabetes mellitus.

Condition	Glucose range in urine
Normal	0 to 15 mg/dL (0 to 0.8 mmol/L)
Prediabetes	100 to 125 mg/dL (5.6 to 6.9 mmol/L)
Diabetes	126 mg/dL (7 mmol/L)

[Students can get access to sample reports on the internet and refer the above table to comment on blood reports of patients on their own.]

Use your brain power. (Textbook Page No. 185)

Question 1.
In which regions of nephron the filtrate will he isotonic to blood?
Answer:
Filtrate leasing the proximal convoluted tubule (PCT) is isotonic to the blood plasma.

Can you tell? (Textbook Page No. 185)

Question 1.
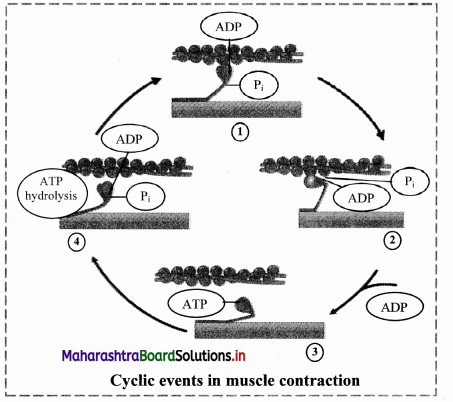
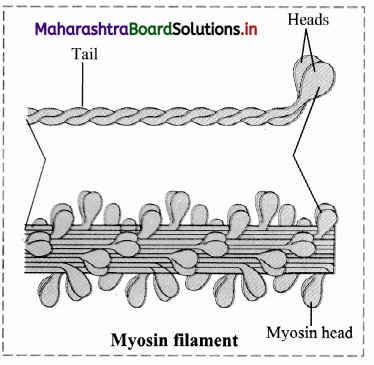
Explain the process of urine formation in details.
Answer:
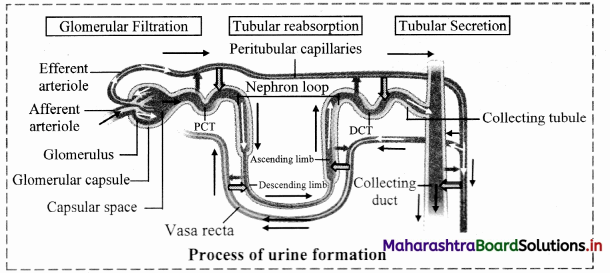
Process of urine formation is completed in three steps, namely;

i. Ultrafiltration/ Glomerular filtration,
ii. Selective reabsorption,
iii. Tubular secretion / Augmentation

i. Ultrafiltration / Glomerular filtration :
Diameter of afferent arteriole is greater than the efferent arteriole. The diameter of capillaries is still smaller than both arterioles. Due to the difference in diameter, blood flows with greater pressure through the glomerulus. This is called as glomerular hydrostatic pressure (GHP) and normally, it is about 55 mmHg. GIIP is opposed by osmotic pressure of blood (normally, about 30 mm Hg) and capsular pressure (normally, about 15 mm Hg).

Hence net / effective filtration pressure (EFP) is 10 mm Hg.
EFP = Hydrostatic pressure in glomerulus – (Osmotic pressure of blood + Filtrate Hydrostatic pressure)
= 55 – (30 + 15)
= 10 mm Hg

Under the effect of high pressure, the thin walls of the capillary become permeable to major components of blood (except blood cells and macromolecules like protein).
Thus, plasma except proteins oozes out through wall of capillaries.
About 600 ml blood passes through each kidney per minute.

The blood (plasma) flowing through kidney (glomeruli) is filtered as glomerular filtrate, at a rate of 125 ml / min. (180 L/d).
Glomerular filtrate / deproteinized plasma / primary urine is alkaline, contains urea, amino acids, glucose, pigments, and inorganic ions.
Glomerular filtrate passes through filtration slits into capsular space and then reaches the proximal convoluted tubule.

ii. Selective reabsorption :
Selective reabsorption occurs in proximal convoluted tubule (PCT). It is highly coiled so that glomerular filtrate passes through it very slowly. Columnar cells of PCT are provided with microvilli due to which absorptive area increases enormously.
This makes the process of reabsorption very effective.
These cells perform active (ATP mediated) and passive (simple diffusion) reabsorption.

Substances with considerable importance (high threshold) like – glucose, amino acids, vitamin C, Ca⁺⁺, K⁺, Na⁺, Cl^– are absorbed actively, against the concentration gradient. Low threshold substances like water, sulphates, nitrates, etc., are absorbed passively.
In this way, about 99% of glomerular filtrate is reabsorbed in PCT and DCT.

iii. Tubular secretion / Augmentation :
Finally filtrate reaches the distal convoluted tubule via loop of Henle. Peritubular capillaries surround DCT. Cells of distal convoluted tubule and collecting tubule actively absorb the wastes like creatinine and ions like K⁺, H⁺ from peritubular capillaries and secrete them into the lumen of DCT and CT, thereby augmenting the concentration of urine and changing its pH from alkaline to acidic.
Secretion of H⁺ ions in DCT and CT is an important homeostatic mechanism for pH regulation of blood. Tubular secretion is the only process of excretion in marine bony fishes and desert amphibians.

Question 2.
How does counter current mechanism help concentration of urine?
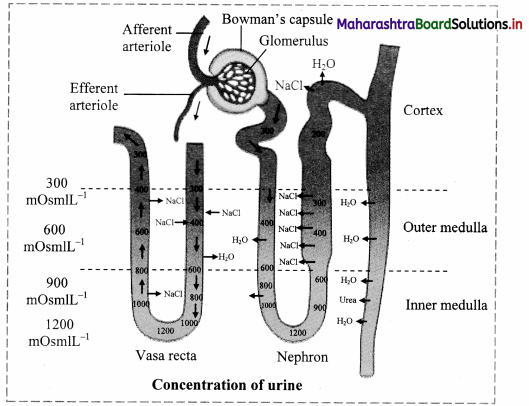
Answer:
Under the conditions like low water intake or high water loss due to sweating, humans can produce concentrated urine. This urine can be concentrated around four times i.e. 1200 mOsm/L than the blood (300 mOsm/L). Hence, a mechanism called countercurrent mechanism is operated in the human kidneys. The countercurrent mechanism operating in the Limbs of Henle’s loop of juxtamedullary nephrons and vasa recta is as follows:

It involves the passage of fluid from descending to ascending limb of Henle’s loop.
This mechanism is called countercurrent mechanism, since the flow of tubular fluid is in opposite direction through both limbs.
In case of the vasa recta, blood flows from ascending to descending parts of itself.
Wall of descending limb is thin and permeable to water, hence, water diffuses from tubular fluid into tissue fluid due to which, tubular fluid becomes concentrated.
The ascending limb is thick and impermeable to water. Its cells can reabsorb Na⁺ and Cl^– from tubular fluid and release into tissue fluid.
Due to this, tissue fluid around descending limb becomes concentrated. This makes more water to move out from descending limb into tissue fluid by osmosis.
Thus, as tubular fluid passes down through descending limb, its osmolarity (concentration) increases gradually due to water loss and on the other hand, progressively decreases due to Na⁺ and Cl^– secretion as it flows up through ascending limb.
Whenever retention of water is necessary, the pituitary secretes ADH. ADH makes the cells in the wall of collecting ducts permeable to water.
Due to this, water moves from tubular fluid into tissue fluid, making the urine concentrated.
Cells in the wall of deep medullar part of collecting ducts are permeable to urea. As concentrated urine flows through it, urea diffuses from urine into tissue fluid and from tissue fluid into the tubular fluid flowing through thin ascending limb of Henle’s loop.
This urea cannot pass out from tubular fluid while flowing through thick segment of ascending limb, DCT and cortical portion of collecting duct due to impermeability for it in these regions.
However, while flowing through collecting duct, water reabsorption is operated under the influence of ADII. Due to this, urea concentration increases in the tubular fluid and same urea again diffuses into tissue fluid in deep medullar region.
Thus, same urea is transferred between segments of renal tubule and tissue fluid of inner medulla. This is called urea recycling; operated for more and more water reabsorption from tubular fluid and thereby excreting small volumes of concentrated urine.
Osmotic gradient is essential in the renal medulla for water reabsorption by counter current multiplier system.
This osmotic gradient is maintained by vasa recta by operating counter current exchange system.
Vasa recta also have descending and ascending limbs. Blood that enters the descending limb of the vasa recta has normal osmolarity of about 300 mOsm/L.
As it flows down in the region of renal medulla where tissue fluid becomes increasingly concentrated, Na⁺, Cl^– and urea molecules diffuse from tissue fluid into blood and water diffuse from blood into tissue fluid.
Due to this, blood becomes more concentrated which now flows through ascending part of vasa recta. This part runs through such region of medulla where tissue fluid is less concentrated.
Due to this, Na⁺, Cl^– and urea molecules diffuse from blood to tissue fluid and water from tissue fluid to blood. This mechanism helps to maintain the osmotic gradient.

Try this. (Textbook Page No. 185)

Question 1.
Read the given urine report and prepare a note on composition of normal urine.

Answer:
The composition of normal urine is as follows:

A volume of 1 – 2 litres of urine in 24 hours is normal. This volume can however vary considerably as it depends on fluid intake, physical activity, temperature, etc.
The colour of normal urine is generally pale yellow due to urochrome (pigment produced by breakdown of bile). The colour of urine may vary slightly due to urochrome concentration and diet.
The appearance of urine is generally clear and transparent.
Any form of deposits (sediments/ crystals) is generally absent in normal urine.
The pH of normal urine is acidic and is generally around 6.0 (Range: 4.6 to 8.0). The pH varies considerably with the diet of a person.
The specific gravity of urine is an average of 1.02 ( Range : 1.001 to 1.035).
Albumin, sugar, bile salts bile pigments, ketone bodies and casts are absent in normal urine.
Occult blood is generally not seen in normal urine.

Think (Textbook Page No. 185)

Question 1.
What would happen if ADH secretion decreases due to any reason?
Answer:
In absence of ADH, diuresis (dilution of urine) takes place and person tends to excrete large amount of dilute urine. This condition called as diabetes insipidus. Frequent excretion of large amount of dilute urine may cause a person to feel thirsty.

Think and appreciate. (Textbook Page No. 185)

Question 1.
How do kidneys bring about homeostasis? Is there any role of neuro endocrine system in it?
Answer:
The composition of urine depends upon food and fluid consumed by an individual. There are two ways in which it the composition is regulated. They are as follows:

i. Regulating water reabsorption through ADH
ii. Electrolyte reabsorption though RAAS
iii. Atrial Natriuretic Peptide

i. Regulating water reabsorption through ADH:
Hypothalamus in the midbrain has special receptors called osmoreceptors which can detect change in osmolarity (measure of total number of dissolved particles per liter of solution) of blood.
If osmolarity of blood increases due to water loss from the body (after eating namkeen or due to sweating), osmoreceptors trigger release of Antidiuretic hormone (ADH) from neurohypophysis (posterior pituitary). ADH stimulates reabsorption of water from last part of DCT and entire collecting duct by increasing the permeability of cells.

This leads to reduction in urine volume and decrease in osmolarity of blood.
Once the osmolarity of blood comes to normal, activity of osmoreceptor cells decreases leading to decrease in ADH secretion. This is called negative feedback.
In case of hemorrhage or severe dehydration too, osmoreceptors stimulate ADH secretion. ADH is important in regulating water balance through kidneys.

In absence of ADH, diuresis (dilution of urine) takes place and person tends to excrete large amount of dilute urine. This condition called as diabetes insipidus.
[Note: Hypothalamus is a part of forebrain]

ii. Electrolyte reabsorption through RAAS:
Another regulatory mechanism is RAAS (Renin Angiotensin Aldosterone System) by Juxta Glomerular Apparatus (JGA).
Whenever blood supply (due to change in blood pressure or blood volume) to afferent arteriole decreases (e.g. low BP/dehydration), JGA cells release Renin. Renin converts angiotensinogen secreted by hepatocytes in liver to Angiotensin I. ‘Angiotensin converting enzyme’ further modifies Angiotensin I to Angiotensin II, the active form of hormone. It stimulates adrenal cortex to release another hormone called aldosterone that stimulates DCT and collecting ducts to reabsorb more Na and water, thereby increasing blood volume and pressure.

No. Both ADH and RAAS are essential for homeostasis.

Only ADH can lower blood Na⁺ concentration by way of water reabsorption in DCI and collecting duct. whereas RAAS stimulates Na⁺ reabsorption and maintains osmolarity of body fluid.
Action of ADH and RAAS leads to increase in blood volume and osmolarity.
For mechanism of Atrial natriuretic peptide:

Atrial natriuretic peptide (ANP): A large increase in blood volume and pressure stimulates atrial wall to produce atrial natriuretic peptide (ANP). ANP inhibits Na⁺ and Cl^– reabsorption from collecting ducts inhibits release of renin, reduces aldosterone and ADH release too. This leads to a condition called Natriuresis (increased excretion of Na⁺ in urine) and diuresis.

ADH is produced by the hypothalamus and is stored and released by the posterior pituitary or the neurohypophysis in response to appropriate trigger. Hence, there is a role of the neuroendocrine system in homeostasis.

Use your brain power. (Textbook Page No. 186)

Question 1.
Can we use this knowledge in treatment of high blood pressure? Why high BP medicines are many a times diuretics?
Answer:

Yes, the knowledge of homoeostasis is used in the treatment of high blood pressure.
Some commonly used theories for treatment of high blood pressure are as follows:
- Angiotensin II receptor blockers (ARBs) are used as medications to treat high blood pressure. These medications block the action of angiotensin II by preventing angiotensin II from binding to angiotensin II receptors on the muscles surrounding blood vessels. As a result, blood vessels enlarge (dilate), and blood pressure is reduced.
- Another method is the use of ‘Angiotensin converting enzyme’ ACE blockers. These inhibitors inhibit activity of ACE and therefore decrease the production of angiotensin II. As a result, these medications cause the blood vessels to enlarge or dilate, and this reduces blood pressure.
Vasodilation reduces arterial pressure. Reduced angiotensin II leads to natriuresis (increased excretion of Na⁺ in urine) and diuresis, thereby reducing blood pressure.
Too much salt can cause extra fluid to build up in the blood vessels, raising blood pressure. Diuretics are substances that slow renal absorption of water and thereby cause diuresis (elevated urine flow rate) which in turn reduces blood volume and blood pressure by flushing out salt and extra fluid. Hence, high BP medicines are many a times diuretics.

Can you tell? (Textbook page no. 186)
How do skin and lungs help in excretion?
OR
Can you tell? (Textbook page no. 187)
Explain role of lungs and skin in excretion.
Answer:
Yes, various organs other than the kidney participate in excretion. They are as follows:

i. Skin:

Skin acts as an accessory excretory organ. The skin of many organisms is thin and permeable. It helps in diffusion of waste products like ammonia.
Human skin however is thick and impermeable. It shows presence of two types of glands namely, sweat glands and sebaceous glands.

Sweat glands are distributed all over the skin. They are abundant in the palm and facial regions.
These simple, unbranched, coiled, tubular glands open on the surface of the skin through an opening called sweat pore. Sweat is primarily produced for thermoregulation but it also excretes substances like water, NaCl, lactic acid and urea.
Sebaceous glands are present at the neck of hair follicles. They secrete oily substance called sebum.
It forms a lubricating layer on skin making it softer. It protects skin from infection and injury.

ii. Lungs:

Lungs are the accessory excretory organs. They help in excretion of volatile substances like CO₂ and water vapour produced during cellular respiration. Along with CO₂, lungs also remove excess of H₂O in the form of vapours during expiration. They also excrete volatile substances present in spices and other food stuff.

Can you tell? (Textbook Page No. 187)

Question 1.
When does kidney produce renin? Where is it produced in kidney?
Answer:
Kidney produces renin whenever blood supply (due to change in blood pressure or blood volume) to afferent arteriole decreases (e.g. low BP/dehydration).
The juxtaglomerular Apparatus (JGA) cells secrete renin.

Question 2.
Explain how electrolyte balance of blood plasma maintained.
Answer:
The composition of urine depends upon food and fluid consumed by an individual. There are two ways in which it the composition is regulated. They are as follows:

i. Regulating water reabsorption through ADH
ii. Electrolyte reabsorption though RAAS
iii. Atrial Natriuretic Peptide

ii. Electrolyte reabsorption through RAAS:
Another regulatory mechanism is RAAS (Renin Angiotensin Aldosterone System) by Juxta Glomerular Apparatus (JGA).

Whenever blood supply (due to change in blood pressure or blood volume) to afferent arteriole decreases (e.g. low BP/dehydration), JGA cells release Renin. Renin converts angiotensinogen secreted by hepatocytes in liver to Angiotensin I. ‘Angiotensin converting enzyme’ further modifies Angiotensin I to Angiotensin II, the active form of hormone. It stimulates adrenal cortex to release another hormone called aldosterone that stimulates DCT and collecting ducts to reabsorb more Na and water, thereby increasing blood volume and pressure.

No. Both ADH and RAAS are essential for homeostasis.

Only ADH can lower blood Na⁺ concentration by way of water reabsorption in DCI and collecting duct. whereas RAAS stimulates Na⁺ reabsorption and maintains osmolarity of body fluid.
Action of ADH and RAAS leads to increase in blood volume and osmolarity.
For mechanism of Atrial natriuretic peptide:

Can you tell? (Textbook Page No. 187)

Question 1.
What is the composition of sweat?
Answer:
Sweat is composed of water, NaCl, lactic acid and urea.

Internet my friend. (Textbook Page No. 189)

Question 1.
Treatments other than surgical removal of kidney stone like Lithotripsy. (Breaking down of kidney stones using shock waves).
Answer:
a. Cystoscopy and ureteroscopy:
During cystoscopy, the doctor uses a cystoscope to look inside the urethra and bladder to find a stone in the urethra or bladder.
During ureteroscopy, the doctor uses a ureteroscope, which is longer and thinner than a cystoscope, to see detailed images of the lining of the ureters and kidneys.

The doctor inserts the cystoscope or ureteroscope through the urethra to see the rest of the urinary tract. Once the stone is found, the doctor can remove it or break it into smaller pieces.
The doctor performs these procedures in the hospital with anesthesia.

b. Percutaneous nephrolithotomy:
The doctor uses a thin viewing tool, called a nephroscope, to locate and remove the kidney stone.
The doctor inserts the tool directly into your kidney through a small cut made in your back.
For larger kidney stones, the doctor also may use a laser to break the kidney stones into small pieces. The doctor performs percutaneous nephrolithotomy in a hospital with anesthesia.

c. Generally for smaller stones doctors recommend drinking lots of water, consuming pain relievers and consuming medicines like alpha blocker to relax the ureter muscles, and help pass the kidney stones more quickly and with less pain

[Students are expected to find more information using the internet.]

Question 2.
Dietary restrictions suggested for kidney patients.
Dietary restrictions for kidney patients include the following:

Drinking large amounts of water.
Reduce consumption of oxalate rich food like rhubarb, beets, okra, spinach, Swiss chard, sweet potatoes, nuts, tea, chocolate and soy products.
Follow a diet low in salt and animal protein.
Reduce consumption of calcium supplements (if any) but consume appropriate amount of calcium in food.

[Students are expected to find more information using the internet.]

11th Std Biology Questions And Answers:

Heredity and Variation Class 9 Science Chapter 16 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 16 Heredity and Variation Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 16 Heredity and Variation Question Answer Maharashtra Board

Class 9 Science Chapter 16 Heredity and Variation Question Answer Maharashtra Board

1. Complete the following sentences by choosing the appropriate words from the brackets.
(Inheritance, sexual reproduction, asexual reproduction, chromosomes, DNA, RNA, gene)

a. Hereditary characters are transferred from parents to offsprings by …………………………….., hence they are said to be structural and functional units of heredity.
b. Organisms produced by …………………………….. show minor variations.
c. The component which is in the nuclei of cells and carries the hereditary characteristics is called ……………………………..
d. Chromosomes are mainly made up of ……………………………..
e. Organisms produced through …………………………….. show major variations.

2. Explain the following.

a. Explain Mendel’s monohybrid progeny with the help of any one cross.
Answer:

Mendel brought about a cross between two pea plants with only pair of contrasting characters. This type of cross is called a monohybrid cross.
Tall pea plants and dwarf pea plants were used in this cross. Hence this is parent generation (P₁).
All the plants produced in F₁ genration are tall, having genotype Tt. This indicates that the gene responsible for tallness in pea plants is dominant over the gene responsible for dwarfness.
When F₁ plants are self pollinated they produce second filial generation (F₂).
In F₂ generation both tall and dwarf plants appeared in the ratio 3:1.
Thus, the genotypic ratio of F₂ generation is 3 (Tall) : 1 (Dwarf) and the genotypic ratio is 1 TT : 2 Tt: 1 tt.

b. Explain Mendel’s dihybrid ratio with the help of any one cross.
Answer:

In dihybrid cross, Mendel considered two pairs of contrasting characters.
He made a cross between a pea plant producing rounded and yellow couloured seeds and a pea plant with wrinkled and green coloured seeds.
All the plants produced in F₁ generation had rounded yellow seeds. This is because in pea plants, round shape of seed is dominant over wrinkled shape and yellow colour of seed is dominant over green colour.
When F₁ plants are self pollinated, they produce four types of gamates – RY, Ry, rY, ry.
F₂ plants formed by the fusion of four types of male gametes and four types of female gametes, had phenotypes such as round yellow, wrinkled yellow, round green and wrinkled green.
Also, F₂ generation showed nine different types of genotypes such as RRYY, RRYy, RRyy, RrYY, RrYy, Rryy, rrYY, rrYy, rryy.
Phenotypic ratio of dihybrid cross is
The genotypic ratio of dihybrid cross is

c. Distinguish between monohybrid and dihybrid cross.
Answer:

Monohybrid cross	Dihybrid cross
(i) Cross involving a single pair of contrasting characters is called monohybrid cross.	(i) Cross involving two pairs of contrasting characters is called a dihybrid cross.
(ii) F₁ plants of monohybrid cross produce two types of gametes.	(ii) F₁ plants of dihybrid cross produce four types of gametes.
(iii) Monohybrid cross has a phenotypic ratio of 3 : 1 in F₂ generation.	(iii) Dihybrid cross has a phenotypic ratio of 9 : 3 : 3 : 1 in F₂ generation.

d. Is it right to avoid living with a person suffering from a genetic disorder?
Answer:

No, it is not right to avoid living with a person suffering from a genetic disorder.
Genetic disorders are transmitted from parents to offsprings only and they are non-contagious, i.e., they do not spread from one person to another through contact.

3. Answers the following questions in your own words.

a. What is meant by ‘chromosome’. Explain its types.
Answer:

The structure in the nucleus of cells that carries the hereditary characteristics is called the chromosome.
It is made up mainly of nucleic acids and proteins.
Depending upon the position of the centromere, there are four types of chromosomes.

(a) Metacentric: The centromere is exactly at the mid-point in this chromosome, and therefore, it looks like the English letter ‘V’. The arms of this chromosome are equal in length.

(b) Sub-metacentric: The centromere is somewhere near the mid-point in this chromosome which, therefore, looks like the English letter ‘U. One arm is slightly shorter than the other.

(c) Acrocentric: The centromere is near one end of this chromosome which therefore looks like the English letter One arm is much smaller than the other.

(d) Telocentric: The centromere is right at the end of this chromosome making the chromosome look like the English letter ‘i’. This chromosome consists of only one arm.

b. Describe the structure of the DNA molecule.
Answer:

In 1953, Watson and Crick proposed a model of the DNA molecule.
As per their model, two parallel threads (strands) of nucleotides are coiled around each other to form a double helix structure. This structure can be compared with a coiled and a flexible ladder.
Each strand of DNA is made up of many small molecules known as nucleotides.
Each nucleotide is made up of a molecule of nitrogen base and phosphoric acid joined to a molecule of sugar.
There are four types of nitrogen bases-adenine, guanine, cytosine and thymine. Adenine and guanine are called as purines while cytosine and thymine are called as pyrimidines.
Nucleotides are arranged like a chain in the DNA.
The two threads (strands) of the DNA are comparable to the two rails of the ladder and each rail is made up of alternately joined molecules of sugar and phosphoric acid.
Each rung of the ladder is a pair of nitrogenous bases joined by hydrogen bonds. Adenine always pairs with thymine and cytosine always pairs with guanine.

c. Express your opinion about the use of DNA fingerprinting.
Answer:

DNA fingerprinting is the technique in which the sequence of the genes in the DNA of a person, i.e., the genome of the person is identified.
This technique is useful to identify the lineage and to identify criminals because it is unique to every person.
It is also useful to identify paternity and maternity disputes etc.
This technique was developed by Professor of genetics Sir Alec Jeffreys.
A common method of collecting a reference sample, is in the use of a buccal swab. If this is not available, blood or saliva or hair sample may be used.
Just like your actual fingerprint, your DNA fingerprint is something that you are born with. It is unique to you.
DNA fingerprint is very useful in forensic science.

d. Explain the structure, function and types of RNA.
Answer:

Ribonucleic acid (RNA) is an important nucleic acid of the cell.
RNA is made up of ribose sugar, phosphate molecules and four types of nitrogenous bases adenine, guanine, cytosine and uracil.
The nucleotide i.e., smallest unit of the chain of the RNA molecule is formed by the combination of a ribose sugar, phosphate molecule and one of the nitrogen bases.
Large numbers of nucleotides are bonded together to form the macromolecule of RNA.
RNA performs the function of protein synthesis.
According to function, there are three types of RNA:
(a) Ribosomal RNA (rRNA): It is the component of cellular organelle ribosome. Ribosomes perform the function of protein synthesis.(b) Messenger RNA (mRNA): It carries the information for protein synthesis from genes (i.e. DNA segment in the cell nucleus) to ribosomes (in the cytoplasm) which produce the proteins.(c) Transfer RNA (tRNA): It carries the amino acid up to the ribosomes as per the message of the mRNA.

e. Why is it necessary for people to have their blood examined before marriage?
Answer:

If people have their blood examined before marriage, the partners will know about the possible genetic diseases that their children might inherit. So they may decide not to have children or not to get married.
Blood tests before marriage are also done to check for any contagious disease in the partners. This will help to protect the partners from contagious diseases like STDs.

4. Write a brief note on each.

a. Down syndrome
Answer:

Down syndrome is the disorder arising due to chromosomal abnormality.
This is the first discovered and described the chromosomal disorder in human beings.
This disorder is characterized by the presence of 47 chromosomes. It is described as the trisomy of the 21st pair.
Infants with this disorder have one extra chromosome with the 21st pair in every cell of the body. Therefore, they have 47 chromosomes instead of 46.
Children suffering from Down syndrome are usually mentally retarded and have a short lifespan. Mental retardation is the most prominent characteristic.
Other symptoms include short height, short wide neck, flat nose, short fingers, scanty hair, single horizontal crease on palm and a life expectancy of about 16-20 years.

b. Monogenic disorders
Answer:

Disorders occurring due to mutation in any single gene into a defective one are called monogenic disorders.
Approximately 4000 disorders of this type are now known.
Due to abnormal genes, their products are either produced in insufficient quantity or not produced at all.
It causes abnormal metabolism and may lead to death at a tender age.
Examples of monogenic disorders are Hutchinson’s disease, Tay-Sachs disease, galactosaemia, phenylketonuria, sickle cell anaemia, cyctic fibrosis, albinism, haemophilia, night blindness etc.

c. Sickle cell anaemia: symptoms and treatment.
Answer:

Sickle-cell anaemia is a hereditary disease caused due to mutation in a single gene. It is a monogenic disorder.
Normal haemoglobin has glutamic acid as the 6th amino acid in its molecular structure. However, if it is replaced by valine, the shape/structure of the haemoglobin molecule, changes.
Due to this, the erythrocytes (RBCs) which are normally biconcave become sickle-shaped. This condition is called sickle-cell anaemia. The oxygen-carrying capacity of haemoglobin in such individuals is very low.
In this condition, clumping and thereby, destruction of erythrocytes occurs most often. As a result, blood vessels are obstructed and the circulatory system, brain, lungs, kidneys, etc. are damaged.
Symptoms of sickle-cell anaemia are swelling of legs and hands, pain in joints, severe general body aches, frequent cold and cough, constant low-grade fever, exhaustion, pale face, low haemoglobin count.
A person suffering from sickle-cell anaemia should take a tablet of folic acid daily.

5. How are the items in groups A, B and C inter-releated?

6. Filling the blanks based on the given relationship.
a. 44 + X : Turner syndrome : : 44 + XXY: – ……………………………..
b. 3:1 Monohybrid : : 9:3:3:1 : ……………………………..
c. Women : Turner syndrome : : Men : ……………………………..
Answer:
a. Klinefelter syndrome
b. Dihybrid
c. Klinefelter syndrome

7. Complete the tree diagram below based on types of hereditary disorders.

Answer:

Class 9 Science Chapter 12 Study of Sound Intext Questions and Answers

Question 1.
How do specific traits or characteristics appear in organisms? (Can you tell; Textbook Page No. 180)
Answer:

Information necessary for synthesis of a particular protein is stored in the DNA.
The segment of DNA which contains all the information for synthesis of a particular protein is called a gene for that protein.
To understand how a specific trait is expressed, let us consider plant height as an example.
We know that there are growth hormones in plants. Increase in the height of plants depends upon the quantity of growth hormones.
The quantity of growth hormone produced by a plant depends upon the efficiency of the concerned enzyme.
Efficient enzymes produce a greater quantity of the hormone due to which the height of the plant increases.
However, if the enzymes are less efficient, a smaller quantity of hormone is produced leading to the stunting of the plant.
Thus, the expression of traits is controlled by the genes.

Question 2.
Show the monohybrid cross between (RR) and (rr) and write the phenotypic and genotypic ratio of F₂ generation. (Use your brain power; Textbook Page No. 187)
Answer:
Parental Generation (P₁)

Phenotypic ratio : 3 Round : 1 Wrinkled
Genotypic ratio : 1 RR : 2 Rr : 1 rr

Question 3.
Why did the characteristic of the Rounded- Yellow seeds alone appear in the Fj generation but not the characteristic of the wrinkled- green seeds? (Use your brain power; Textbook Page No. 187)
Answer:

Rounded-Yellow seeds is a dominant characteristic whereas wrinkled-green seeds is a recessive characteristic.
Therefore only the characteristic of Rounded- Yellow seeds appeared in the F1 generation.

Question 4.
Do all boys and girls of your class look alike? (Think about it; Textbook Page No. 179)
Answer:

No, all the boys and girls of my class do not look alike.
There is a lot of variation among them.

Question 5.
Carefully observe your classmate’s earlobes. (Observe; Textbook Page No. 179)
Answer:

Most of the classmates have free earlobes while very few have attached ear lobes.
This shows that in humans free earlobes is a dominant characteristic whereas attached earlobe is a recessive characteristic.

Question 6.
Irrespective of all of us being humans, what difference do you notice in our skin colour? (Observe; Textbook Page No. 179)
Answer:

Irrespective of all of us being humans, there is a lot of variation in our skin colour. Some people are light-skinned while some are dark-skinned.
The difference in skin colour is due to the gene responsible for the production of the pigment melanin.

Question 7.
All of you are in std. IX. Why then are some students tall and some short? (Observe; Textbook Page No. 179)
Answer:
Our height is decided by gene. People who are tall have genes for tallness whereas people who are short have genes for shortness and hence the variation.

Class 9 Science Chapter 12 Study of Sound Additional Important Questions and Answers

Choose and write the correct option:

Question 1.
The similarities and differences are all the effect of
(a) Heredity
(b) Fertilization
(c) Evolution
(d) Natural selection
Answer:
(a) Heredity

Question 2.
Each chromosome appears midway during cell division.
(a) Circular
(b) Rod-shaped
(c) Dumbbell-shaped
(d) Bottle-shaped
Answer:
(c) dumbbell-shaped

Question 3.
The chromosome in which the centromere is exactly at the mid-point is called chromosome.
(a) sub-metacentric
(b) metacentric
(c) acrocentric
(d) telocentric
Answer:
(b) metacentric

Question 4.
The chromosome in which the centromere is somewhere near the mid-point is called chromosome.
(a) metacentric
(b) acrocentric
(c) sub-metacentric
(d) telocentric
Answer:
(c) sub-metacentric

Question 5.
The chromosome in which the centromere is near one end of the chromosome is called chromosome.
(a) metacentric
(b) acrocentric
(c) sub-metacentric
(d) telocentric
Answer:
(d) telocentric

Question 6.
Sex chromosomes are called
(a) homologous chromosomes
(b) autosomes
(c) allosomes
(d) metacentric chromosomes
Answer:
(c) allosomes

Question 7.
Which of the following is absent in RNA?
(a) Adenine
(b) Uracil
(c) Cytosine
(d) Thymine
Answer:
(d) Thymine

Question 8.
DNA was discovered by
(a) Watson and Crick
(b) Frederick Miescher
(c) Gregor Johann Mendel
(d) Robert Brown
Answer:
(b) Frederick Miescher

Question 9.
The double helix model of DNA was produced by
(a) Watson and Crick
(b) Frederick Miescher
(c) Gregor Johann Mendel
(d) Robert Hooke
Answer:
(a) Watson and Crick

Question 10.
The molecule of RNA which is a component of the ribosome organelle is called a
(a) mRNA
(b) tRNA
(c) rRNA
(d) DNA
Answer:
(c) rRNA

Question 11.
In a monohybrid cross, the phenotypic ratio of F, generation is
(a) 1 tall: 3 dwarf
(b) 2 tall: 2 dwarf
(c) 3 tall: 1 dwarf
(d) 3 tall: 2 dwarf
Answer:
(c) 3 talhl dwarf

Question 12.
arises due to either inheritance of only X chromosome from parents or due to inactivation of the gender-related part of X-chromosomes.
(a) Down syndrome
(b) Turner syndrome
(c) Klinefelter syndrome
(d) Albinism
Answer:
(b) Turner syndrome

Question 13.
Progenies of normal man and sufferer woman for sickle-cell anaemia will be
(a) all normal
(b) 25% normal and 75% sufferer
(c) all carrier
(d) all sufferer
Answer:
(c) all carrier

Question 14.
is a mitochondrial disorder.
(a) Down syndrome
(b) Cleft palate
(c) Spina bifida
(d) Leber hereditary optic neuropathy
Answer:
(d) Leber hereditary optic neuropathy

Question 15.
is a monogenic disorder.
(a) Haemophilia
(b) Cleft palate
(c) Diabetes
(d) Spina bifida
Answer:
(a) Haemophilia

Question 16.
is a recessive character of pea plant.
(a) Round shape of seeds
(b) White colour of flowers
(c) Green colour of pods
(d) Inflated shape of pods
Answer:
(b) White colour of flowers

Question 17.
is a dominant character of pea plant.
(a) Dwarf height
(b) Yellow colour of pod
(c) Yellow colour of seeds
(d) Terminal position of flower
Answer:
(c) Yellow colour of seeds

Question 18.
is a dominant character in human beings.
(a) Non-rolling tongue
(b) Attached ear lobe
(c) Absence of hair on arms
(d) Free ear lobe
Answer:
(d) Free ear lobe

Question 19.
is a recessive character in human beings.
(a) Absence of hair on arms
(b) Black and curly hair
(c) Free earlobe
(d) Presence of hair on arms
Answer:
(a) Absence of hair on arms

Question 20.
If one parent is normal and one parent is carrier of sickle-cell anaemia, then the progenies will be
(a) all normal
(b) 50% normal and 50% carrier
(c) 50% carrier and 50% sufferer
(d) all carrier
Answer:
(b) 50% normal and 50% carrier

Question 21.
If one parent is carrier and one parent is a sufferer of sickle-cell anaemia, then the progenies will be
(a) 50% normal and 50% carrier
(b) all sufferers
(c) 50% carrier and 50% sufferer
(d) all carrier
Answer:
(c) 50% carrier and 50% sufferer

Find the odd man out:

Question 1.
Adenine, thymine, cytosine, uracil
Answer:
Adenine. It is a purine whereas the others are pyrimidines.

Question 2.
Axillary flower, green pod, green seed, inflated pod
Answer:
Green seed. It is a recessive character of pea plant whereas the others are dominant characters.

Question 3.
Constricted pod, purple flower, axillary flower, yellow seeds.
Answer:
Constricted pod. It is a recessive character of pea plant whereas the others are dominant characters.

Question 4.
Green seeds, wrinkled seeds, terminal flower, green pod.
Answer:
Green pod. It is a dominant character of pea plant whereas the others are recessive characters.

Question 5.
Attached ear lobes, brown and straight hair, non-rolling tongue, presence of hair on arms.
Answer:
Presence of hair on arms. It is a dominant characteristic of human beings whereas the others are recessive characters.

Question 6.
Cystic fibrosis, albinism, spina bifida, sicklecell anaemia.
Answer:
Spina bifida. It is a polygenic disorder whereas the others are monogenic disorders.

Question 7.
Fiutchinson’s disease, phenylketonuria, nightblindness, leber hereditary optic neuropathy.
Answer:
Leber hereditary optic neuropathy. It is a mitochondrial disorder whereas the others are monogenic disorders.

Complete the analogy:

a. Tall plant: Phenotype :: Tt:
b. Dominant trait : Axial position of flower :: Recessive trait:
c. Women : 44 + XX :: Men :
d. Adenine and Guanine : Purine :: Cytosine and Thymine :
Answer:
a. Genotype
b. Terminal position of flower
c. 44 + XY
d. Pyrimidine

Match the columns

Question 1.

Column 1	Column 2	Column 3
(1) Leber hereditary optic neuropathy	(a) 44 + XXY	(i) Pale skin, white hairs.
(2) Diabetes	(b) 45 + X	(ii) Men are sterile.
(3) Albinism	(c) Mitochondrial disorder	(iii) Women are sterile.
(4) Turner syndrome	(d) Polygenic disorder	(iv) This disorder arises during development of zygote.
(5) Klinefelter Syndrome	(e) Monogenic disorder	(v) Effect on blood- glucose level.

Answer:
(1 – c – iv),
(2 – d – v),
(3 – e – i),
(4-b- Hi),
(5 – a – ii)

Question 2.

Column ‘A’	Column ‘B’
(1) Yellow and rinkled	(a) yyrr
(2) Green and round	(b) YyRr
(3) Yellow and round	(c) YYrr
(4) Green and wrinkled	(d) yyRr

Answer:
(1 – c),
(2 – d),
(3 – b),
(4 – a)

Question 3.

Column ‘A’	Column ‘B’
(1) Tay-Sachs disease	(a) Multifactorial disorder
(2) Diabetes	(b) Destruction of erythrocytes
(3) Sickle-cell anaemia	(c) Absence of melanin
(4) Albinism	(d) Monogenic disorder

Answer:
(1 – d),
(2 – a),
(3 – b),
(4 – c)

State whether the following statements are true or false. Correct the false statement:

Question 1.
Offsprings produced through asexual reproduction show greater variations as compared to those produced through sexual reproduction.
Answer:
False. Offsprings produced through asexual reproduction show minor variations as compared to those produced through sexual reproduction.

Question 2.
Information necessary for protein synthesis is stored in the RNA.
Answer:
False. Information necessary for protein synthesis is stored in the DNA.

Question 3.
The quantity of growth hormone produced by a plant depends upon the efficiency of the concerned enzyme.
Answer:
True

Question 4.
The chromosome in which the centromere is exactly at the mid-point is called telocentric chromosome.
Answer:
False. The chromosome in which the centromere is exactly at the mid-point is called metacentric chromosome.

Question 5.
RNA molecules are called master molecules.
Answer:
False. DNA molecules are called master molecules.

Question 6.
The pair of sex chromosomes are called autosomes.
Answer:
False. The pair of sex chromosomes is called allosomes.

Question 7.
In DNA, Adenine always pairs with thymine and cytosine always pairs with guanine.
Answer:
True

Question 8.
In humans there are 23 pairs of autosomes and one pair of allosomes.
Answer:
False. In humans, there are 22 pairs of autosomes and one pair of allosomes.

Question 9.
The phenotypic and genotypic ratios are not same.
Answer:
True

Question 10.
Phenotype means the pairs of genes responsible for the visible characteristics of organisms.
Answer:
False. Phentotype means external appearance of visible characteristics of organisms.

Question 11.
During gamete formation, in Pj generation the pair of gametes separate independently.
Answer:
True

Question 12.
Down syndrome is caused due to monosomy of X chromosome.
Answer:
False. Down syndrome is caused due to trisomy of 21st chromosome.

Question 13.
In Klinefelter syndrome, women are sterile.
Answer:
False. In Klinefelter syndrome, men are sterile as this disorder arises in men due to abnormality in sex chromosome.

Question 14.
If the father and mother are both sufferers or carriers of sickle-cell anaemia, their offsprings are likely to suffer from this disease.
Answer:
True

Question 15.
During fertilization, mitochondria is contributed by the sperm cell and egg cell(ovum).
Answer:
False. During fertilization, mitochondria is contributed by the egg cell (ovum) alone.

Question 16.
Polygenic disorders strictly follow Mendel’s principles of heredity.
Answer:
False. Polygenic disorders do not strictly follow Mendel’s principles of heredity.

Question 17.
Genetic material is transferred in equal quantity from parents to progeny.
Answer:
True

Give scientific reasons:

Question 1.
DNA molecules are called as ‘Master molecules’.
Answer:

Molecules of DNA are present in all organisms from viruses and bacteria to human beings.
These molecules control the functioning, growth and division (reproduction) of the cell.
Genes present in the DNA are also responsible for transfer of hereditary characteristics from parents to offsprings.
Therefore, DNA molecules are called as ‘Master molecules’.

Question 2.
Phenotypic and genotypic ratios are different.
Answer:

Phenotype means external appearance or visible characteristics of organisms whereas the genotype is the pairs of genes responsible for the visible characteristics.
The genes responsible for any particular character are present in pairs.
Though, there are two genes, the phenotype
depends on the presence of the dominant gene, e.g. Genotype for tall height of the plant is TT or Tt.
Therefore, phenotypic and genotypic ratios are different.

Question 3.
A carrier or sufferer of sickle-cell anaemia should avoid marriage with another carrier or sufferer.
Answer:

Sickle-cell anaemia is a hereditary disease caused due to mutation of a single gene.
It is a monogenic disorder that occurs due to changes in a gene during conception.
If father and mother both are sufferers or carriers of sickle-cell anaemia, their offsprings are likely to suffer from the disease.
Therefore, a carrier or sufferer of sickle-cell anaemia should avoid marriage with another carrier or sufferer.

Question 3.
Mitochondrial disorders are inherited from the mother only.
Answer:

Mitochondrial DNA becomes defective due to mutation.
During fertilization, mitochondria are contributed by the egg cell (ovum) alone.
Hence, mitochondrial disorders are inherited from the mother only.

Question 4.
Tobacco smoking causes cancer.
Answer:

Tobacco smoke contains harmful chemicals like pyridine, ammonia, aldehyde furfural, carbon monoxide, nicotine, sulphur dioxide etc.
They cause uncontrolled cell division.
Tobacco smoke is full of minute carbon particles which cause normal tissue lining of the lung to transform into thickened black tissue. This leads to cancer.
Therefore, tobacco smoking causes cancer.

Define the following terms:

Question 1.
Gene
Answer:
The segment of DNA which contains all the information for synthesis of a particular protein is called a ‘gene’.

Question 2.
Chromosome
Answer:
The structure in the nucleus of the cells that carries the hereditary characteristics is called chromosome.

Question 3.
Genetics
Answer:
The branch of biology which studies the transfer of characteristics of organism from one generation to the next and genes in particular, is called genetics.

Question 4.
Heredity
Answer:
Transfer of characteristics from parents to offsprings is called heredity.

Question 5.
Homologous chromosomes
Answer:
If the pair consists of chromosomes are similar in shape and organization, they are called homologous chromosomes.

Question 6.
Heterologous chromosomes
Answer:
If the pair which consists of chromosomes are not similar in shape and organization, they are called heterologous chromosomes.

Question 7.
Genetic disorders
Answer:
Diseases or disorders occuring due to abnormalities in chromosomes and mutations in genes are called genetic disorders.

Distinguish between:

Question 1.
DNA and RNA
Answer:

DNA	RNA
(i) In DNA, the sugar present is deoxyribose.	(i) In RNA, the sugar present is ribose.
(ii) In DNA, the nitrogen bases are adenine, guanine, cytosine and thymine.	(ii) In RNA, the nitrogen base thymine is replaced by uracil.
(iii) DNA is double stranded.	(iii) RNA is single-stranded.
(iv) DNA carries hereditary information	(iv) RNA helps in protein synthesis.

Question 2.
Turner syndrome and Klinefelter syndrome.
Answer:

Turner syndrome	Kline fater syndrome
(i) It is due to monosomy of sex chromosome.	(i) It is due to felter of sex chromosome.
(ii) Disorder in sex chromosome results in 44 + X condition.	(ii) Disorder in sex chromosome results is 44 + XY condition.
(iii) Seen in women.	(iii) Seen in men
(iv) Women suffering from this syndrome are sexually sterile.	(iv) Men suffering from this syndrome are sexually sterile.
(v) There is presence of total 45 chromosomes instead of 46.	(v) There is presence of total 47 chromosomes instead of 46.

Write short notes on:

Question 1.
Albinism
Answer:

Albinism is a monogenic disorder.
Our eyes, skin and hair have colour due to the brown pigment melanin. In this disease, the body cannot produce melanin.
The skin becomes pale, hair are white and eyes are usually pink due to absence of melanin pigment in the retina and sclera.

Question 2.
Polygenic disorders.
Answer:

Polygenic disorders are caused due to mutations in more than one gene.
In most such cases, their severity increases due to effects of environmental factors on the foetus.’
Common examples of such disorders are cleft lip, cleft palate, constricted stomach, spina bifida (a defect of the spinal cord), etc. Besides diabetes, blood pressure, heart disorders, asthma and obesity are also polygenic disorders.
Polygenic disorders do not strictly follow Mendel’s principles of heredity.
These disorders arise from a complex interaction between environment, life style and defects in several genes.

Question 3.
Turner syndrome.
Answer:

Turner syndrome is a disorder arising in women due to abnormality in sex chromosomes.
Turner syndrome arises due to either inheritance of only one X chromosome from parents or due to inactivation of the gender- related part of X-chromosomes.
Instead of the normal 44 + XX condition, women suffering from Turner syndrome show a 44 + X condition.
Such women are sterile i.e. unable to have children due to improper growth of the reproductive organ.

Answer the following questions:

Question 1.
What are the main objectives of National Health Mission?
Answer:
The main objectives of National Health Mission are:

Strengthening of the rural and urban health facilities.
Controlling various diseases and illnesses.
Increasing public awareness about health.
Offering financial assistance to patients through various schemes.

Question 2.
Which were the seven pairs of contrasting characteristics studied by Mendel in pea plant?
Answer:
The seven pairs of contrasting characters studied by Mendel in pea plant were as follows:

Characters	Dominant	Recessive
Shape of the seed	Round(R)	Wrinkled (r)
Colour of the seed	Yellow (Y)	Green (y)
Colour of the flower	Purple (C)	White (c)
Shape of pod	Inflated (I)	Constricted (i)
Colour of pod	Green (G)	Yellow (g)
Position of flower	Axillary (A)	Terminal (a)
Height of the plant	Tall (T)	Dwarf (t)

Question 3.
Name some dominant and recessive characteristics seen in human beings.
Answer:
Some dominant and recessive characteristics of human beings.

Dominant	Recessive
Rolling tongue	Non-rolling tongue
Presence of hair on arms	Absence of hair on arms
Black and curly hair	Brown and straight hair
Free earlobe	Attached earlobe

Question 4.
What is Klinefelter syndrome?
Answer:

Klinefelter syndrome is a disorder arising in men due to abnormalities in sex chromosomes.
In this disorder, men have one extra X chromosome, hence their chromosomal condition becomes 44 + XXY.
Such men are usually sterile because their reproductive organs are not well developed.

Question 5.
How is the diagnosis for sickle-cell anaemia made?
Answer:

Under the National Health Mission scheme, the ‘Solubility Test’ for diagnosis of sickle-cell anaemia is available at all district hospitals.
Similarly, the confirmatory diagnostic test – ‘Electrophoresis’ is performed at rural and subdistrict hospitals.

Question 6.
Find out the Phenotypic ratio of the following:
(a) Round-Yellow
(b) Wrinkled-Yellow
(c) Round-Green
(d) Wrinkled-Green
Answer:
(a) Round-Yellow: 9
(b) Wrinkled-Yellow: 3
(c) Round-Green: 3
(d) Wrinkled-Green: 1
Phenotypic ratio: 9:3:3:1

Question 7.
Find out the Genotypic ratio of the following:
(a) RRYY
(b) RRYy
(c) RRyy
(d) RrYY
(e) RrYy
(f) Rryy
(g) rrYY
(h) rrYy
(i) rryy
Answer:
(a) RRYY -1
(b) RRYy-2
(c) RRyy-1
(d) RrYY-2
(e) RrYy-4
(f) Rryy-2
(g) rrYY – 1
(h) rrYy – 2
(i) rryy – 1
Genotypic ratio: 1:2:1:2:4:2:1:2:1

Draw neat and labelled diagrams of the following:

Question 1.
Structure of chromosome
Answer:

Question 2.
Types of RNA
Answer:

Answer the following questions:

Question 1.
What are the effects of tobacco consumption?
Answer:

Smoking of cigarettes and bidis adversely affects the process of digestion.
It causes a burning sensation in the throat and cough.
Excessive smoking causes instability and trembling of fingers.
It causes dry cough which leads to sleeplessness.
Tobacco consumption can lead to shortening of life span, chronic bronchitis, pericarditis, cancer of the lungs, mouth, larynx (voice box), pharynx, urinary bladder, lips or tongue.
The nicotine present in tobacco affects the central and peripheral nervous system. Arteries become hard i.e. it causes arteriosclerosis and hypertension.

Question 2.
Complete the table for number of chromosomes in different organisms.
Answer:

Organism	No. of Chromosomes
Crab	200
Maize	20
Frog	26
Roundworm	04
Potato	48
Human	46
Dog	78
Elephant	56
Fruit fly	08
Mango	40

9th Std Science Questions And Answers:

Energy Flow in an Ecosystem Class 9 Science Chapter 7 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 7 Energy Flow in an Ecosystem Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 7 Energy Flow in an Ecosystem Question Answer Maharashtra Board

Class 9 Science Chapter 7 Energy Flow in an Ecosystem Question Answer Maharashtra Board

1. Complete the following table (Carefully study the carbon, oxygen and nitrogen cycles).

Bio-geo-chemical cycles	Biotic processes	Abiotic processes
1. Carbon cycle
2. Oxygen cycle
3. Nitrogen cycle

2. Correct and rewrite the following statements and justify your corrections.
a. Carnivores occupy the second trophic level in the food chain.
b. The flow of nutrients in an ecosystem is considered to be a ‘one-way’ transport.
c. Plants in an ecosystem are called primary consumers.

3. Give reasons.
a. Energy flow through an ecosystem is ‘one way’.
Answer:

The Sun is the most important source of energy in any ecosystem.
Green plants of the ecosystem store some amount of solar energy in the form of food.
Before reaching the decomposers, this energy is passed on from one trophic level to the next.
Decomposers dissipate some amount of energy in the form of heat.
However, no part of the energy ever returns to the Sun. Hence, energy flow through an ecosystem is ‘one way’.

b. Equilibrium is necessary in the various bio-geo-chemical cycles.
Answer:

The cyclic flow of nutrients within an ecosystem is called bio-geo-chemical cycles.
Nutrients, necessary for the growth of organisms are continuously transferred from abiotic to biotic factors and biotic to abiotic factors within an ecosystem.
Any imbalance in the cycles will break the link between the biotic and abiotic factors.
Therefore, equilibrium is necessary between bio-geo-chemical cycles.

c. Flow of nutrients through an ecosystem is cyclic.
Answer:

All organisms need nutrients for their growth.
The nutrients carbon, oxygen, nitrogen, iron, calcium etc. are circulated and recycled from the biosphere to living organisms and after their death back to the biosphere.
Nutrients are taken up by plants and then passed on to the consumers.
Eventually, after their death, all types of consumers, are decomposed by decomposers like bacteria and fungi and the nutrients are again released into the biosphere and are, used again by living organisms.

Therefore, the flow of nutrients through an ecosystem is cyclic.

4. Explain the following cycles in your own words with suitable diagrams.
a. Carbon cycle.

Answer:

The circulation and recycling of carbon from the atmosphere to living organisms and after their death back to the atmosphere is called the carbon cycle.
Abiotic carbon atoms are circulated and recycled into biotic form mainly through photosynthesis and respiration.
Hence, the carbon cycle is one of the important bio-geochemical cycles.
Plants convert carbon dioxide into carbohydrates by the process of photosynthesis.
Similarly, they produce carbon compounds like proteins and fats, too.
Carnivores feed upon herbivores. In this way, biotic carbon is transported from plants to herbivores, from herbivores to carnivores and from carnivores to apex consumers.
Main processes in the carbon cycle
Eventually, after death, all types of consumers, are decomposed by decomposers like bacteria and fungi and carbon dioxide is released again into the atmosphere and is used again by living organisms.
In this way, carbon is continuously passed on from one living organism to another. After the death of living organisms, carbon goes to the atmosphere and is again taken up by living organisms.

b. Nitrogen cycle.
Answer:

Nitrogen forms 78% i.e. the maximum portion of the atmosphere. It is necessary for the maintenance of the cycle of nature.
The circulation and recycling of nitrogen gas into the form of different compounds through various biotic and abiotic processes in nature is called the nitrogen cycle.
All organisms participate in the nitrogen cycle. It is an important component of proteins and nucleic acids.
As compared to other elements, it is inactive and does not easily combine with other elements. Most organisms cannot use the free form of nitrogen.
Important processes of nitrogen cycle:
(a) Nitrogen fixation: Conversion of nitrogen into nitrates and nitrites through atmosphere, industrial and biological processes.
(b) Ammonification: Release of ammonia through the decomposition of dead bodies and excretory wastes of organisms.
(c) Nitrification: Conversion of ammonia into a nitrite and then nitrate.
(d) Denitrification: Conversion of nitrogen compounds into gaseous nitrogen.

c. Oxygen cycle.
Answer:

Oxygen forms 21% of the atmosphere. It is also present in the hydrosphere and lithosphere. The circulation and recycling of oxygen within the biosphere is called the oxygen cycle.
This cycle, includes both the biotic and abiotic components. Oxygen is continuously produced as well as used up in the atmosphere.
Oxygen is highly reactive and it readily reacts with other elements and compounds.
As oxygen is found in various forms like molecular oxygen (Oz), water (H,0), carbon dioxide (C02), inorganic compounds etc, the oxygen cycle of the biosphere is extremely complex.
Oxygen is released in the process of photosynthesis, whereas it is used up in processes like respiration, combustion, decomposition, corrosion, rusting, etc.

5. What would you do to help maintain the equilibrium in the various bio-geochemical cycles? Explain in brief.
Answer:

Bio-geo-chemical cycles always involve the achievement of equilibrium, i.e., a balance in the cycling of the nutrients between the spheres.
Human activities that are known to be environmentally unfriendly can disrupt this balance.
We should avoid deforestation as trees play an important role in maintaining the balance.
We should avoid overuse of fertilizers. The fertilizers get washed away in the nearby water bodies disrupting the balance.
Avoid burning of fossil fuels as these fuels release a large amount of carbon in the form of carbondioxide, thus disrupting the balance.
Vehicular emissions is another contributor to the disruption in balance of the various cycles.
These emissions release oxides of nitrogen and carbon and other hazardous air pollutants.
So, we must use better quality fuel like CNG or ethanol to reduce vehicular emissions.

6. Explain in detail the inter-relationship between the food chain and food web.
Answer:

Interaction go on continuously between producers, consumers and decomposers.
There is a definite sequence in these interactions which is called the food chain.
Each chain consists of four, five or more links.
An ecosystem consists of many food chains that are interconnected at various levels. Thus, a food web is formed.
An organism may be the prey for many other organisms.
For example, an insect feeds upon leaves of various plants but the same insect is the prey for different animals like frog, wall lizard, birds, etc.
Thus, many food chains interconnected together form an intricate web called as food web.

7. State the different types of bio-geochemical cycles and explain the importance of those cycles.
Answer:

The different types of bio-geo-chemical cycles are nitrogen, oxygen, carbon, water vapour, iron, calcium, phosphorus, etc.
Nutrients, necessary for the growth of the organisms are continuously transferred from abiotic to biotic factors and biotic to abiotic factors within an ecosystem.
These cycles operate continuously through the medium of the biosphere formed by the lithosphere, atmosphere and hydrosphere.
(iv) The recycling of biological, geological and chemical sources of nutrients takes place through these cycles.
Nutrients from the biosphere enter the bodies of plants and animals. Eventually, after death, all types of consumers are decomposed by decomposers like bacteria and fungi and they are again released into the biosphere and are used again by living organisms.
Therefore, these cycles help in maintaining the flow of nutrients and energy through ecosystem and maintaining the equilibrium in the ecosystem.

8. Explain the following with suitable examples.
a. What type of changes occur in the amount of energy during its transfer from plants to apex consumers?
Answer:

Plants of the ecosystem store some of the solar energy in the form of food.
Before reaching the decomposers, this energy is passed on from one trophic level to the next.
At every trophic level, some amount of energy is used by the organism for its own life processes and some amount of energy is lost to the surroundings.
Decomposers dissipate some amount of energy in the form of heat.
However, no part of the energy ever returns to the Sun. Hence, such passage of energy is referred to as ‘one way’ transport.
Therefore, energy is maximum at the base of the pyramid and is least at the apex, e.g.
phytoplanktons which form the base of the pyramid have 10,000 kcal of energy while humans at the apex have 10 kcal of energy.

b. What are the differences between flow of matter and of energy in an ecosystem? Why?
Answer:

Flow of matter	Flow of energy
(i) It involves the circulation and recycling of nutrients in a cyclic manner within the biosphere.	(i) It involves the flow of energy from one trophic level to another in a unidirectional or non-cyclic manner.
(ii) There is no dissipation of matter at any level.	(ii) There is the dissipation of energy at every level.
(iii) Biosphere is the source of nutrients.	(iii) The Sun is the most important source of energy.

Class 9 Science Chapter 7 Energy Flow in an Ecosystem Intext Questions and Answers

Can you recall?

7 Energy Flow In An Ecosystem Exercises Question 1.
What is meant by nitrogen fixation?
Answer:
The process of conversion of Nitrogen into nitrates and nitrites is called Nitrogen fixation.

Energy Flow In An Ecosystem Class 9 Questions And Answers Question 2.
Which microbes bring about the process of nitrogen fixation?
Answer:
Rhizobium present in the root nodules of the leguminous plant bring about the process of nitrogen fixation.

Class 9 Science Chapter 7 Energy Flow In An Ecosystem Question 3.
What is meant by ‘ecosystem’?
Answer:
An ecosystem includes all of the living things like plants, animals and other organisms in a given area, interacting with each other and also with non-living environmental factors like weather, earth, sun, soil, climate and atmosphere.

Energy Flow In An Ecosystem Class 9 Exercise 1Question 4.
Which are different types of ecosystems?
Answer:

Class 9 Science Chapter 7 Energy Flow In An Ecosystem Exercise Question 5.
How do interactions take place between biotic and abiotic factors of an ecosystem?
Answer:

Abiotic factors include non-living factors such as soil, water etc. and biotic factors include all living organisms.
Both these abiotic and biotic ecosystems are connected through various bio-geo-chemical cycles.
These connections/interactions are important for the flow of matter and flow of energy.

Class 9 Science Chapter 7 Energy Flow in an Ecosystem Additional Important Questions and Answers

Choose and write the correct option:

Question 1.
An intricate network of food chains is called
(a) Biosphere
(b) Food web
(c) Energy pyramid
(d) Ecosystem
Answer:
(b) food web

Question 2.
Fungi and other microbes are called
(a) Producers
(b) Consumers
(c) Decomposers
(d) Omnivores
Answer:
(c) decomposers

Question 3.
Oxygen forms of the atmosphere.
(a) 78%
(b) 21%
(c) 10%
(d) 90%
Answer:
(b) 21%

Question 4.
Microbes which do not need oxygen are called
(a) Producers
(b) Aerobes
(c) Anaerobes
(d) Decomposers
Answer:
(c) anaerobes

Question 5.
The pattern of energy exchange in an ecosystem is called a
(a) Food chain
(b) Food web
(c) Pyramid of energy
(d) Trophic levels
Answer:
(c) Pyramid of energy

Question 6.
Carbon atoms are circulated and recycled through
(a) Nitrification and denitrification
(b) Photosynthesis and respiration
(c) Respiration and nitrification
(d) Photosynthesis and ammonification
Answer:
(b) photosynthesis and respiration

Question 7.
Conversion of ammonia into a nitrite and then nitrate is called
(a) Nitrogen fixation
(b) Denitrification
(c) Nitrification
(d) Ammonification
Answer:
(c) nitrification

Question 8.
The conversion of nitrogen compounds into gaseous nitrogen is called
(a) Nitrogen fixation
(b) Denitrification
(c) Ammonification
(d) Nitrification
Answer:
(b) denitrification

Question 9.
is an important component of proteins and nucleic acids.
(a) Carbon
(b) Nitrogen
(c) Phosphorus
(d) Oxygen
Answer:
(b) Nitrogen

Question 10.
Amount of matter and energy from the lowest level to the highest level.
(a) decreases
(b) increases
(c) remains the same
(d) multiplies
Answer:
(a) decreases

Question 11.
is the most important source of energy in any ecosystem.
(a) The Sun
(b) The Moon
(c) Producers
(d) Decomposers
Answer:
(a) The Sun

Question 12.
Flow of energy in an ecosystem is
(a) cyclical
(b) two way transport
(c) o ne way transport
(d) to and fro transport
Answer:
(c) one way transport

Question 13.
The Indian Institute of Ecology and Environment, Delhi, has published
(a) Invasive species in a changing Environment
(b) Encyclopaedia of Ecology and Environment
(c) Environment and Ecology Magazine
(d) Biodiversity and Disaster Management
Answer:
(b) Encyclopaedia of Ecology and Environment

Question 14.
Oxygen is released in the process of
(a) Respiration
(b) Decomposition
(c) Combustion
(d) Photosynthesis
Answer:
(d) photosynthesis

Question 15.
cycle is a gaseous cycle.
(a) Carbon
(b) Phosphorus
(c) Calcium
(d) Iron
Answer:
(a) Carbon

Question 16.
is a sedimentary cycle.
(a) Carbon
(b) Nitrogen
(c) Oxygen
(d) Calcium
Answer:
(d) Calcium

Question 17.
is a primary consumer.
(a) Elephant
(b) Frog
(c) Owl
(d) Tiger
Answer:
(a) Elephant

Question 18.
is a secondary consumer.
(a) Grasshopper
(b) Elephant
(c) Frog
(d) Human
Answer:
(c) Frog

Question 19.
Tiger is a /an
(a) Producer
(b) Primary consumer
(c) Apex consumer
(d) Secondary consumer
Answer:
(c) apex consumer

Question 20.
Carbon dioxide is released into the atmosphere through
(a) burning of fossil fuels
(b) volcanic activity
(c) respiration
(d) all of these
Answer:
(d) all of these

Question 21.
in 1942 studied the food chain and energy flow through it
(a) Linderman
(b) Darwin
(c) Calypso
(d) Chu win lee
Answer:
(a) Linderman

Question 22.
fter the death of apex consumers, energy becomes available to.
(a) Decomposers
(b) Producers
(c) Herbivores
(d) Carnivores
Answer:
(a) Decomposers

Question 23.
Green plants of the ecosystem store in the form of food.
(a) Solar energy
(b) Chemical energy
(c) Thermal energy
(d) Electrical energy
Answer:
(a) Solar energy

Question 24.
Plants convert carbon dioxide into by the process of photosynthesis.
(a) Carbohydrates
(b) Proteins
(c) Fats
(d) Vitamins
Answer:
(a) Carbohydrates

Question 25.
Carnivores feed upon
(a) Decomposers
(b) Herbivores
(c) Producers
(d) Secondary producers
Answer:
(b) Herbivores

Question 26.
is used up in the processes like respiration, combustion, decomposition, corrosion, rusting, etc.
(a) Nitrogen
(b) Oxygen
(c) Argon
(d) Helium
Answer:
(b) Oxygen

Question 27.
Nitrogen forms % of the atmosphere.
(a) 79
(b) 78
(c) 21
(d) 2
Answer:
(b) 78

Question 28.
Most organisms cannot use the free form of
(a) Oxygen
(b) Nitrogen
(c) Carbon dioxide
(d) Carbon monoxide
Answer:
(b) Nitrogen

Question 29.
first proposed the concept of Ecological Pyramid in 1927.
(a) Darwin
(b) Newton
(c) Elton
(d) Edison
Answer:
(c) Elton

Question 30.
Ecological Pyramid is called
(a) Hills
(b) Mounts
(c) Eltonian
(d) Darwinism
Answer:
(c) Eltonian

Question 31.
is produced from oxygen through various atmospheric processes.
(a) Nitrogen dioxide
(b) Nitrites
(c) Ozone
(d) CFC
Answer:
(c) Ozone

Question 32.
Interactions between producers, consumers and saprophytes in a definite sequence is called
(a) Links
(b) Internet
(c) Food chain
(d) Connectors
Answer:
(c) Food chain

Question 33.
Many food chains interconnected at various levels is called
(a) Links
(b) Internet
(c) Connectors
(d) Food web
Answer:
(d) Food web

Question 34.
Decomposers dissipate some amount of energy in the form of
(a) Light
(b) Electricity
(c) Sound
(d) Heat
Answer:
(d) Heat

Question 35.
The flow of nutrients in an ecosystem is
(a) Non- cyclic
(b) Mono directional
(c) Reverse directional
(d) Cyclical
Answer:
(d) Cyclical

Question 36.
The cyclical flow of nutrients within an ecosystem is called
(a) Biological cycle
(b) Chemical cycle
(c) Solar cycle
(d) Bio-geo chemical cycle
Answer:
(d) Bio-geo chemical cycle

Question 37.
is an accumulation of the main abiotic gaseous nutrient materials found in the earth’s atmosphere.
(a) Gaseous cycle
(b) Water cycle
(c) Solar cycle
(d) Lunar cycle
Answer:
(a) Gaseous cycle

Question 38.
Oxygen is released into the atmosphere by the process of
(a) Photosynthesis
(b) Respiration
(c) Oxidation
(d) Decomposition
Answer:
(a) Photosynthesis

Question 39.
Charles Elton studied the of the Beer islands in England..
(a) Tundra ecosystem
(b) Mediterranean ecosystem
(c) Equatorial ecosystem
(d) Taiga ecosystem
Answer:
(a) Tundra ecosystem

Question 40.
in 1942 studied the food chain and energy flow through it.
(a) Charles Elton
(b) Lindeman
(c) Robert Whittaker
(d) Eichler
Answer:
(b) Lindeman

Question 41.
After the death of apex consumers, energy becomes available to
(a) Primary consumer
(b) Secondary consumer
(c) Decomposer
(d) Sun
Answer:
(c) Decomposer

Question 42.
Nitrogen forms % of the atmosphere.
(a) 28%
(b) 78%
(c) 48%
(d) 82%
Answer:
(b) 78%

Question 43.
first proposed the concept of the Ecological Pyramid in 1927.
(a) Charles Elton
(b) Lindeman
(c) Eichler
(d) John Muir
Answer:
(a) Charles Elton

Question 44.
Oxygen is released into the atmosphere by the process of
(a) respiration
(b) Photosynthesis
(c) Combustion
(d) All of these
Answer:
(b) Photosynthesis

Find the odd man out:

Question 1.
Photosynthesis, Respiration, Decomposition, Forest Fires
Answer:
Forest Fires

Question 2.
Combustion, Corrosion, rusting, formation of ozone, Photosynthesis
Answer:
Photosynthesis

Question 3.
Biological nitrogen fixation, ammonification, nitrification, denitrification, industrial nitrogen fixation
Answer:
Industrial nitrogen fixation

Question 4.
Frog, Owl, Squirrel, Fox
Answer:
Squirrel

Question 5.
Grasshopper, squirrel, elephant, lion
Answer:
Lion

Question 6.
Nitrogen cycle, oxygen cycle, carbon cycle, phosphorus cycle
Answer:
Phosphorus cycle

Question 7.
Photosynthesis, Nitrification, Ammonification, Denitrification
Answer:
Photosynthesis

Find out the correlation:

1. Grasshopper : Primary consumer :: Tiger : ………………..
2. Owl : Secondary consumer :: Squirrel : ………………..
3. Flow of energy : One way :: Flow of nutrients : ………………..
4. Plants : Producers :: Bacteria and Fungi : ………………..
5. Nitrogen : Gaseous cycle :: Phosphorus : ………………..
6. Oxygen : 21% :: Nitrogen : ………………..
7. Photosynthesis: Carbon cycle:: Ammonification : ………………..
8. Respiration : Oxygen cycle :: Nitrification : ………………..
9. Respiration : Biotic process :: Combustion : ………………..
10. Microbes using oxygen : Aerobes :: Microbes not using oxygen : ………………..
Answer:
(1) Apex consumer
(2) Primary consumer
(3) Cyclic
(4) Decomposers
(5) Sedimentary cycle
(6) 78%
(7) Nitrogen cycle
(8) Nitrogen cycle
(9) Abioticprocess
(10) Anaerobes

Q.l. (B) 3. Difference between:
(1) Azotobacter and Rhizobium
Answer:

Azotobacter	Rhizobium
Free-living nitrogen-fixing bacteria	Symbiotic nitrogen-fixing bacteria

(2) Biotic components and Abiotic component
Answer:

Biotic components	Abiotic component
Living component of an ecosystem	Physical/Chemical non-living components of an ecosystem

(3) Producers and Herbivores
Answer:

Producers	Herbivores
They are present in the 1^st trophic level	They are present in the 2^nd trophic level

(4) Carnivores and Herbivores
Answer:

Carnivores	Herbivores
They depend on Herbivores for nutrition	They depend on Producers for nutrition

(5) Phosphorus and Carbon
Answer:

Phosphorus	Carbon
It cycles through the Sedimentary cycle	It cycles through the Gaseous cycle

(6) Food chain and Food web
Answer:

Food chain	Food web
Interactions between producers, consumers and decomposers in a definite sequence is called as a food chain.	The interconnection among different food chains in an ecosystem at various levels is called as a food web

State whether the following statements are true or false. Correct the false statements:

(1) Herbivores occupy the third trophic level in a food chain.
(2) Apex consumers use herbivores and carnivores as their food.
(3) Humans are apex consumers.
(4) Omnivores feed only on carnivores.
(5) A food chain has two links.
(6) The number of consumers in a food web is fixed.
(7) The amount of matter and energy goes on increasing at every level in a food chain.
(8) Robert Brown first proposed the concept of Ecological Pyramid.
(9) After the death of apex consumers, the energy becomes available to decomposers.
(10) The gaseous cycle is a speedier cycle than the sedimentary cycle.
(11) Climatic changes and human activities seriously affect the speed, intensity and equilibrium of bio-geo-chemical cycles.
(12) Carbon dioxide is released in the atmosphere through photosynthesis.
(13) The equilibrium of oxygen and carbon dioxide gases is maintained by decomposers.
(14) The conversion of ammonia into a nitrite and then nitrate is called nitrogen fixation.
(15) Conversion of nitrogen compounds into gaseous nitrogen is called nitrogen fixation.
(16) Release of ammonia through decomposition of dead plants and excretory wastes of organisms is called ammonification.
(17) The cyclic flow of nutrients within an ecosystem is called Energy Pyramid.
Answer:
(1) False, herbivores occupy the second trophic level in a food chain as they are directly dependent on producers.
(2) True
(3) True
(4) False. Omnivores feed on both herbivores and carnivores.
(5) False. A food chain consists of four, five or more links.
(6) False. A food web can have many consumers.
(7) False. The amount of matter and energy goes on decreasing at every level in a food chain.
(8) False. Charles Elton first proposed the concept of Ecological Pyramid.
(9) True
(10) True
(11) True
(12) False. Carbon dioxide is released in the atmosphere through respiration, burning of fossil fuels and wood, forest fires and volcanic activity. (13) False. The equilibrium of oxygen and carbon dioxide gases is maintained by plants.
(14) False. The conversion of ammonia into a nitrite and then nitrate is called nitrification.
(15) False. Conversion of nitrogen compounds into gaseous nitrogen is called denitrification.
(16) True
(17) False. The cyclic flow of nutrients within an ecosystem is called bio-geochemical cycle.

Name the following:

Question 1.
The animals that feed on herbivores.
Answer:
Carnivores.

Question 2.
Organisms that feed on herbivores and carnivores.
Answer:
Omnivores.

Question 3.
Two examples of primary consumers.
Answer:
Grasshopper, squirrel.

Question 4.
Two examples of secondary consumers.
Answer:
Frog, owl.

Question 5.
Two examples of Apex consumers.
Answer:
Lion, tiger.

Question 6.
Levels in the food chain.
Answer:
Trophic level.

Question 7.
Organisms that decompose the dead bodies of plants and animals.
Answer:
Decomposers.

Question 8.
Process which releases oxygen.
Answer:
Photosynthesis.

Question 9.
Release of ammonia through decomposition of dead bodies and excretory wastes of organisms.
Answer:
Ammonification.

Question 10.
Conversion of nitrogen into nitrates and nitrites through atmospheric, industrial and biological processes.
Answer:
Nitrogen fixation.

One line answers:

Question 1.
What is Food chain?
Answer:
Interactions between producers, consumers and decomposers in a definite sequence is called as a food chain.

Question 2.
What is Food web?
Answer:
The interconnection among different food chains in an ecosystem at various levels is called as a food web.

Question 3.
What is Trophic level?
Answer:
A trophic level is the step at which the organism obtains its food in the chain.

Question 4.
What is Pyramid of energy?
Answer:
The pattern of energy exchange in an ecosystem is called a ‘Pyramid of energy’.

Question 5.
What is Bio-geo-chemical cycle?
Answer:
The cyclical flow of nutrients within an ecosystem is called bio-geo-chemical cycle.

Question 6.
What is Carbon cycle?
Answer:
The circulation and recycling of carbon from the atmosphere to living organisms and aher their death back to the atmosphere is called the carbon cycle.

Question 7.
What is Oxygen cycle?
Answer:
The circulation and recycling of oxygen within the biosphere is called as oxygen cycle.

Question 8.
What is Nitrogen cycle?
Answer:
The circulation and recycling of nitrogen gas into the form of different compounds through various biotic and abiotic processes in nature is called the nitrogen cycle.

Question 9.
What is Nitrogen fixation?
Answer:
The process of conversion of free nitrogen gas of the atmosphere into nitrogen compounds is called of nitrogen fixation.

Distinguish between:

Question 1.
Gaseous Cycle and Sedimentary Cycle.
Answer:

Gaseous Cycle

Sedimentary Cycle

(i) It is an accumulation of the main abiotic gaseous nutrient materials found in the earth’s atmosphere.

(ii) It includes nitrogen, oxygen, carbon dioxide, water vapour etc.

(i) It is an accumulation of the main abiotic nutrient materials found in the soil, sediment and sedimentary rocks, etc. of the earth.

(ii) It includes soil components like iron, calcium, phosphorus etc.

Question 2.
Carbon Cycle and Nitrogen Cyde.
Answer:

Carbon Cycle	Nitrogen Cycle
(i) The circulation and recycling of carbon from the atmosphere to living organisms and after their death back to the atmosphere is called the carbon cycle.	(i) The circulation and recycling of nitrogen into the form of different compounds through various biotic and abiotic processes in nature is called the nitrogen cycle.
(ii) Main processes involved in the carbon cycle are photosynthesis and respiration.	(ii) Main processes involved in the nitrogen cycle are nitrogen fixation, ammonification, nitrification and denitrification.
(iii) Carbon in the form of carbon dioxide is directly absorbed by plants for photosynthesis.	(iii) Nitrogen gas cannot be directly absorbed by plants. So nitrogen is fixed by the process of nitrogen fixation and then absorbed from the soil.

Complete the flow chart:

Question 1.
Energy Pyramid.

Question 3.
Nitrogen Cycle

Question 4.
Bio-Geo Chemical cycle

Write short notes on:

Question 1.
Trophic level.
Answer:

Each level in the food chain is called a trophic level.
A trophic level is the step at which the organism obtains its food in the chain.
The amount of matter and energy gradually decreases from producers at the lowest level to the top consumers at the highest level.

Question 2.
Food web.
Answer:

An ecosystem consists of many food chains that are interconnected at various levels. This is called food web.
An organism may be the prey for many other organisms.
For example, an insect feeds upon leaves of various plants but the same insect is the prey for different animals like wall lizards, birds etc.
This forms an intricate web instead of a linear food chain. Such an intricate network is called as food web.
Generally food webs are formed everywhere in nature.

Question 3.
Energy Pyramid.

Answer:

Each level in the food chain is called a trophic level.
The amount of matter and energy gradually decreases from producers at the lowest level to the top consumers at the highest level.
The initial quantity of energy goes on decreasing at every level of energy exchange.
Similarly, the number of organisms also decreases from the lowest level to the highest level.
This pattern of energy exchange in an ecosystem is called a Pyramid of energy.

Explain the following statements

Question 1.
justify the statements
(a) Producers form the first trophic level in the food chain. Herbivores depend directly on producers.
(b) The flow of nutrients in an ecosystem is cyclic.
(c) Plants in an ecosystem are called autotrophs.
Answer:

So herbivores form the second trophic level, whereas carnivores depend on herbivores, so they form the third trophic level in the food chain.
The nutrients are circulated and recycled from the biosphere to living organisms and after their death back to the biosphere.
They produce their own food by the process of photosynthesis. All animals in an ecosystem directly or indirectly depend on plants for food.

Explain the diagram

Question 1.
Food chain in a forest ecosystem:

Answer:

In a forest ecosystem, grass is eaten by a deer, which in turn is eaten by a tiger.
The grass, deer and tiger form a food chain.
In this food chain, energy flows from the grass (producer) to the deer (primary consumer) to the tiger (secondary consumer).

Question 2.
Food chain in an aquatic ecosystem (Pond)

Answer:

In a aquatic ecosystem algae are eaten by insects.
Insects are eaten by small fish, small fish are in turn eaten by big fish.
And the big fish are eaten by fish eating birds.
In this food chain, energy flows from the algae (producer) to the insects (primary consumers) to the small fish (secondary consumers) to the big fish (tertiary consumer) and to the fish eating birds (apex consumer).

Question 3.
Carbon cycle

Answer:

The circulation and recycling of carbon from the atmosphere to living organisms and after their death back to the atmosphere is called carbon cycle.
Main processes involved in carbon cycle are photosynthesis and respiration.
Carbon in the form of carbon dioxide is directly absorbed by plants for photosynthesis

Question 4.
Nitrogen cycle

Answer:
(i) The circulation and recycling of nitrogen into the form of different compounds through various biotic and abiotic processes in nature is called the nitrogen cycle.
(ii) Main processes involved in nitrogen cycle are nitrogen fixation, ammonification, nitrification and denitrification.
(iii) Nitrogen gas cannot be directly absorbed by plants. So nitrogen is fixed by the process of nitrogen fixation and then absorbed from the soil.

Question 5.
Oxygen cycle

Answer:

Oxygen forms 21% of the atmosphere. It is also present in the hydrosphere and lithosphere.
Circulation and recycling of oxygen within the biosphere is called the oxygen cycle.
This cycle, includes both the biotic and abiotic components.
Oxygen is continuously produced as well as used up in the atmosphere.
Oxygen is highly reactive and it readily reacts with other elements and compounds.
As oxygen is found in various forms like molecular oxygen (O₂), water (H₂O), carbon dioxide (CO₂), inorganic compounds etc, the oxygen cycle of the biosphere is extremely complex.
Oxygen is released in the process of photosynthesis, whereas it is used up in processes like respiration, combustion, decomposition, corrosion, rusting, etc.

Answers based on figures.

Question 1.
Nitrogen Cycle

Answer:

Oxygen forms 21% of the atmosphere. It is also present in the hydrosphere and lithosphere.
The circulation and recycling of oxygen within the biosphere is called the oxygen cycle.
This cycle, includes both the biotic and abiotic components.
Oxygen is continuously produced as well as used up in the atmosphere.
Oxygen is highly reactive and it readily reacts with other elements and compounds.
As oxygen is found in various forms like molecular oxygen (O₂), water (H₂O), carbon dioxide (CO₂), inorganic compounds etc, the oxygen cycle of the biosphere is extremely complex.
Oxygen is released in the process of photosynthesis, whereas it is used up in processes like respiration, combustion, decomposition, corrosion, rusting, etc.

Answers based on figures.

Question 1.
Nitrogen Cycle

(i) Is nitrogen a reactive gas?
Answer:
Nitrogen in its atmospheric state non-reactive gas

(ii) Name process of nitrogen conversion from atmosphere to green plants.
Answer:
Nitrogen fixation is the process of nitrogen conversion atmosphere to green plants

(iii) Name the process of converting usable nitrogenous products into atmospheric inert nitrogen.
Answer:
Denitrification is the process of converting usable nitrogenous products into atmospheric inert nitrogen

(iv) Animals produce which product of nitrogen?
Answer:
Animals produce ammonia as a product of nitrogen

(v) Name two nitrifying organisms.
Answer:
Azotobacter and Rhizobium are the two nitrifying organisms

(vi) Which type of bio-geo-chemical cycles does nitrogen follow?
Answer:
Nitrogen follows gaseous and sedimentary bio-geo-chemical cycles

Question 2.
Carbon cycle

(i) Is carbon dioxide gas freely available in the atmosphere?
Answer:
Carbon dioxide gas is freely available in the atmosphere

(ii) How is carbon found in water?
Answer:
Carbon is found in water in the form of carbonates

(iii) How are we using carbon as a fuel?
Answer:
Fossil fuels are a form of carbon which are used as fuel by us

(iv) How to plants use carbon as their food source?
Answer:
Plants take up carbon in photosynthesis and convert it into starch which is their food source

(v) How do animals use carbon?
Answer:
Animals use carbon in form of organic compounds and inorganic compounds

(vi) Which type of bio-geo-chemical cycles does carbon follow?
Answer:
Carbon follows gaseous and sedimentary bio-geo-chemical cycles

Question 3.
Oxygen cycle

(i) Is oxygen gas freely available in the atmosphere?
Answer:
Oxygen gas is freely available in the atmosphere

(ii) How is oxygen used by animals?
Answer:
Oxygen is used in respiration by the animals

(iii) How are we using carbon as a fuel?
Answer:
Fossil fuels are a form of carbon which are used as fuel by us

(iv) How to plants use carbon as their food source?
Answer:
Plants take up carbon in photosynthesis and convert it into starch which is their food source

(v) How do animals use carbon?
Answer:
Animals use carbon in form of organic compounds and inorganic compounds

(vi) Which type of bio-geo-chemical cycles does carbon follow?
Answer:
Carbon follows gaseous and sedimentary biogeo-chemical cycles

Question 4.
Food web

(i) What is the basic unit of food web?
Answer:
The basic unit of food web is food chain

(ii) Which organisms are on the 1st level of this food web?
Answer:
Producers are p. the 1st level of this food web

(iii) What are the animals which depend on producers directly for nutrition called?
Answer:
The animals which depend on producers directly for nutrition are called Herbivores

(iv) What are the animals which eat any type of food for nutrition called?
Answer:
The animals which eat any type of food for nutrition are called Omnivore

(v) What will happen if one animal in the food chain goes extinct?
Answer:
If one animal in the food chain goes extinct the entire food chain collapse

(vi) What are the factors badly affecting the food web?
Answer:
Factors like hunting, pollution, deforestation, human-animal conflicts etc. are the factors badly affecting the food web

Complete the paragraph

(1) Elemental oxygen is normally found in the form of a diatomic molecule. However, in the upper reaches of the atmosphere, a molecule containing three atoms of oxygen is found. This would mean a formula of 03 and this is called ozone. Unlike the normal diatomic molecule of oxygen, ozone is poisonous and we are lucky that it is not stable nearer to the Earth’s surface. But it performs an essential function where it is found. It absorbs harmful radiations from the Sun. This prevents those harmful radiations from reaching the surface of the Earth where they may damage many forms of life.

Recently it was discovered that this ozone layer was getting depleted. Various man-made compounds like CFCs (carbon compounds having both fluorine and chlorine) which are very stable and not degraded by any biological process) were found to persist in the atmosphere. Once they reached the ozone layer, they would react with the ozone molecules. This resulted in a reduction of the ozone layer and recently they have discovered a hole in the ozone layer above the Antarctica. It is difficult to imagine the consequences for life on Earth if the ozone layer dwindles further, but many people think that it would be better not to take chances. These people advocate working towards stopping all further damage to the ozone layer.

(2) The utilisation of glucose to provide energy to living things involves the process of respiration in which oxygen may or may not be used to convert glucose back into carbon dioxide. This carbon dioxide then goes back into the atmosphere. Another process that adds to the carbon dioxide in the atmosphere is the process of combustion where fuels are burnt to provide energy for various needs like heating, cooking, transportation and industrial processes.

In fact, the percentage of carbon dioxide in the atmosphere is said to have doubled since the industrial revolution when human beings started burning fossil fuels on a very large scale. Carbon, like water, is thus cycled repeatedly through different forms by the various physical and biological activities. Heat is trapped by glass, and hence the temperature inside a glass enclosure will be much higher than the surroundings. This phenomenon was used to create an enclosure where tropical plants could be kept warm during the winters in colder climates. Such enclosures are called greenhouses.

Greenhouses have also lent their name to an atmospheric phenomenon. Some gases prevent the escape of heat from the Earth. An increase in the percentage of such gases in the atmosphere would cause the average temperatures to increase worldwide and this is called the greenhouse effect. Carbon dioxide is one of the greenhouse gases. An increase in the carbon dioxide content in the atmosphere would cause more heat to be retained by the atmosphere and lead to global warming.

(3) Nitrogen gas makes up 78% of our atmosphere and nitrogen is also a part of many molecules essential to life like proteins, nucleic acids (DNA and RNA) and some vitamins. Nitrogen is found in other biologically important compounds such as alkaloids and urea too. Nitrogen is thus an essential nutrient for all life-forms and life would be simple if all these life-forms could use the atmospheric nitrogen directly. However, other than a few forms of bacteria, life-forms are not able to convert the comparatively inert nitrogen molecule into forms like nitrates and nitrites which can be taken up and used to make the required molecules.

These nitrogen-fixing bacteria may be free-living or be associated with some species of dicot plants. Most commonly, the nitrogenfixing bacteria are found in the roots of legumes (generally the plants which give us pulses) in special structures called root nodules. Other than these bacteria, the only other manner in which the nitrogen molecule is converted to nitrates and nitrites is by a physical process. During lightning, the high temperatures and pressures created in the air convert nitrogen into oxides of nitrogen. These oxides dissolve in water to give nitric and nitrous acids and fall on land along with rain. These are then utilised by various lifeforms.

Read the paragraph and answer the questions:

(1) Nitrogen cycle
The nitrogen cycle is the biogeochemical cycle by which nitrogen is converted into multiple chemical forms as it circulates among the atmosphere, terrestrial, and marine ecosystems. The conversion of nitrogen can be carried out through both biological and physical processes. Important processes in the nitrogen cycle include fixation, ammonification, nitrification, and denitrification, The majority of Earth’s atmosphere (78%) is atmosphere nitrogen, making it the largest source of nitrogen.

However, atmospheric nitrogen has limited availability for biological use, leading to a scarcity of usable nitrogen in many types of ecosystems. The nitrogen cycle is of particular interest to ecologists because nitrogen availability can affect the rate of key ecosystem processes, including primary production and decomposition, Human activities such as fossil fuel combustion, use of artificial nitrogen fertilizers, and release of nitrogen in wastewater have dramatically altered the global nitrogen cycle. Human modification of the global nitrogen cycle can negatively affect the natural environment system and also human health.

(i) Why nitrogen cycle is called bio-geochemical cycle?
Answer:
Nitrogen cycle is called bio-geochemical cycle as it undergoes biological as well as geochemical processes.

(ii) Why is nitrogen cycle important to us?
Answer:
Nitrogen cycle is important to us as nitrogen availability can affect the rate of key ecosystem processes, including primary production and decomposition.

(iii) Name important process of nitrogen cycle.
Answer:
Important processes in the nitrogen cycle include fixation, ammonification, nitrification, and denitrification.

(iv) What can affect the nitrogen cycle negatively?
Answer:
Human modification of the global nitrogen cycle can negatively affect the natural environment system and also human health.

(v) Which human activities change the nitrogen cycle?
Answer:
Human activities such as fossil fuel combustion, use of artificial nitrogen fertilizers, and release of nitrogen in wastewater have dramatically altered the global nitrogen cycle.

(2) Food web
A food chain is a linear network of links in a food i web starting from producer organisms (such asgrass or trees which use radiation from the Sun to make their food) and ending at apex predator species (like grizzly bears or killer whales), detritivores (like earthworms or woodlice), ordecomposer species (such as fungi or bacteria), A food chain also shows how the organisms are related with each other by the food they eat. Each level of a food chain represents a different trophiclevel. A food chain differs from a food web, because the complex network of different animal’s feeding relations are aggregated and the chain only follows a direct, linear pathway of one animal at a time.

Natural interconnections between food chains make it a food web. A common metric usedto the quantify food web trophic structure is foodi chain length. In its simplest form, the length of a chain is the number of links between a trophici consumer and the base of the web and the meanchain length of an entire web is the arithmetic average of the lengths of all chains in a food web. The food chain is an energy source diagram. Many food webs have a keystone species. A keystonespecies is a species that has a large impact on thei surrounding environment and can directly affectthe food chain.

If this keystone species dies off it can set the entire food chain off balance. Keystonespecies keep herbivores from depleting all of thei foliage in their environment and preventing ai mass extinction. Food chains were first introduced by the Arab scientist and philosopher Al-Jahiz inthe 10th century and later popularized in a book I published in 1927 by Charles Elton, which also i introduced the food web concept.

(i) What is a food web?
Answer:
Food web is a linear network of links of food chains.

(ii) In a food web which organism are called producers?
Answer:
In a food web which organism which can produce food by photosynthesis are called producers.

(iii) What is the role of keystone species?
Answer:
Keystone species keep herbivores from depleting all of the foliage in their environment and preventing a mass extinction.

(iv) What is a keystone species?
Answer:
A keystone species is a species that has a large impact on the surrounding environment and can directly affect the food chain.

(v) What does each level of food chain represent?
Answer:
Each level of a food chain represents a different trophic level.

(3) Carbon cycle
The carbon cycle is the biogeochemical cycle by which carbon is exchanged among the biosphere, pedosphere, geosphere, hydrosphere, and atmosphere of the Earth. Carbon is the main component of biological compounds as well as a major component of many minerals such as limestone. Along with the nitrogen cycle and the water cycle, the carbon cycle comprises a sequence of events that are key to make Earth capable of sustaining life. It describes the movement of carbon as it is recycled and reused throughout the biosphere, as well as long-term processes of carbon sequestration to and release from carbon sinks.

The carbon cycle was discovered by Antoine! Lavoisier and Joseph Priestley, and popularised by Humphry Davy. Carbon in the Earth’satmosphere exists in two main forms carbon dioxide and methane. Both of these gases absorb and retain heat in the atmosphere and are partially responsible for the greenhouse effect. Methane produces a larger greenhouse effect per volume as compared to carbon dioxide, but it exists in much lower concentrations and is more short-lived than carbon dioxide, making carbon dioxide the more important greenhouse gas of the two.

Carbon dioxide is removed from the atmosphere primarily through photosynthesis and enters the terrestrial and oceanic biospheres. Carbon dioxide also dissolves directly from the atmosphere into bodies of water (ocean, lakes, etc.), as well as dissolving in precipitation as raindrops fall through the atmosphere. When dissolved in water, carbon dioxide reacts with water molecules and forms carbonic acid, which contributes to ocean acidity. It can then be absorbed by rocks through weathering. It also can acidify other surfaces it touches or be washed into the ocean.

(i) Which gas has greener house effect as compared to CO₂?
Answer:
Methane gas CH₄ has greener house effect as compared to CO₂.

(ii) How does dissolved CO₂ affect oceans?
Answer:
When dissolved in water, carbon dioxide reacts with water molecules and forms carbonic acid, which contributes to ocean acidity.

(iii) Why is carbon cycle called bio-geochemical cycle?
Answer:
The carbon cycle is the biogeochemical cycle by which carbon is exchanged among the biosphere, pedosphere, geosphere, hydrosphere, and atmosphere of the Earth.

(iv) How is carbon dioxide removed from atmosphere?
Answer:
Carbon dioxide is removed from the atmosphere primarily through photosynthesis and enters the terrestrial and oceanic biospheres.

(v) Who discovered the carbon cycle?
Answer:
The carbon cycle was discovered by Antoine Lavoisier and Joseph Priestley.

Answer the questions in detail:

Question 1.
Write the important processes of the nitrogen cycle.
Answer:

Nitrogen fixation: Conversion of nitrogen into nitrates and nitrites through atmospheric, industrial and biological processes.
Ammonification: Release of ammonia through decomposition of dead bodies and excretory wastes of organisms.
Nitrification: Conversion of ammonia into a nitrite and then nitrate.
Denitrification: Conversion of nitrogen components into gaseous nitrogen.

Make a concept diagram and explain.

Question 1.
Food chain

Answer:
According to the mode of nutrition the organisms are classified into producers, consumers, saprotrophs (saprophytes) and decomposers. Primary consumers are directly dependent on autotrophs (producers), e.g.: Grasshopper, squirrel, elephant) Secondary consumers use herbivores as their food, e.g.: Frog, owl, fox, etc. Apex or top consumers use herbivores and carnivores as their food. No animals feed on top consumers, e.g.: Tiger, lion, etc. Omnivores feed on herbivores and carnivores, e.g.: Humans, bear, etc. A continuous interaction between producers, consumers and decomposers in a definite sequence is called as food chain.

Food chain, in ecology is the sequence of transfers of matter and energy in the form of food from organism to organism. Food chains intertwine locally into a food web because most organisms consume more than one type of animal or plant. Plants, which convert solar energy to food by photosynthesis, are the primary food source. In a predator chain, a plant-eating animal is eaten by a flesh-eating animal. In a parasite chain, a smaller organism consumes part of a larger host and may itself be parasitized by even smaller organisms. In a saprophytic chain, microorganisms live on dead organic matter.

Question 2.
Energy pyramid
Answer:

An energy pyramid is a model that shows the flow of energy from one trophic, or feeding, level to the next in an ecosystem. The model is a diagram that compares the energy used by organisms at each trophic level. The energy in an energy pyramid is measured in units of kilocalories (kcal). Energy pyramids are similar to biomass pyramids, another type of trophic pyramid that models the amount of biomass at each trophic level in an ecosystem, energy flow in ecosystems. The structure of an energy pyramid reflects the trophic structure of an ecosystem.

The pyramid is divided into trophic levels similar to those in a food chain. At the pyramid base are the producers, autotrophic organisms that make their own food from inorganic substances. All of the other organisms in the energy pyramid are consumers. These are heterotrophs, meaning that they get food energy by consuming other organisms. The consumers at each trophic level feed on organisms from the level below and are themselves consumed by organisms at the level above. Primary consumers are organisms that consume producers; thus, most primary consumers are herbivores, though some may be detrivores (organisms that feed on decaying organic matter).

Secondary consumers are carnivores that feed on primary consumers and tertiary consumers are carnivores that eat secondary consumers. In rare instances, an ecosystem may have an additional trophic level composed of quaternary consumers camivores that consume tertiary consumers’ energy pyramid. The shape of an energy pyramid shows that the amount of food energy that enters each trophic level is less than the amount that entered the level below. Approximately 90 percent of the food energy that enters a trophic level is “lost” as heat when it is used by organisms to power the normal activities of life such as breathing and digesting food the remaining 10 percent is stored in the various organisms’ tissues.

It is this latter energy that is available to be passed to the next trophic level. Thus, the higher the trophic level on the pyramid, the lower the amounts of available energy ecosystem energy transfer through an ecosystem. The number of organisms at each level decreases relative to the level below because there is less energy available to support those organisms. The top level of an energy pyramid has the fewest organisms because it has the least amount of energy. Eventually there is not enough energy left to support another trophic level; thus most ecosystems only have four trophic levels.

9th Std Science Questions And Answers: