Balbharti Maharashtra State Board Class 12 Sociology Important Questions Chapter 2 Segments of Indian Society Important Questions and Answers.
Maharashtra State Board 12th Sociology Important Questions Chapter 2 Segments of Indian Society
1A. Complete the following statements by choosing the correct alternative given in the brackets and rewrite it.
Question 1.
_____________ community comprises of non-agricultural sectors like industries and services. (Rural, Tribal, Urban)
Answer:
Urban
Question 2.
_____________ people marked by a distinct culture living in relative isolation. (Rural, Tribal, Urban)
Answer:
Tribal
![]()
Question 3.
The _____________ God is a prominent deity in the pantheon of gods in sacred groves in Maharashtra. (Tiger, Sun, Nature)
Answer:
Tiger
Question 4.
The term ‘____________’ is an umbrella term for a heterogeneous set of ethnic and tribal population of India. (adivasi, harijan, girijan)
Answer:
Adivasi
Question 5.
The occupations of _____________ community fall into the primary categories such as hunting, gathering, and agriculture. (rural, tribal, urban)
Answer:
tribal
Question 6.
_____________ labour is banned by Indian Law. (Bonded, Organised, Regular)
Answer:
Bonded
Question 7.
Article _____________ Prohibits discrimination against any citizen on the grounds of sex, religion, race, caste etc. (15, 14, 13)
Answer:
15
Question 8.
_____________ creates a cosmopolitan and tolerant approach. (Heterogeneity, Homogeneity, Alienation)
Answer:
Heterogeneity
Question 9.
Marketisation is an essential feature of _____________ centres today. (rural, tribal, urban)
Answer:
urban
![]()
Question 10.
Individualism has led to the increase in _____________ families. (nuclear, joint, traditional)
Answer:
joint
Question 11.
The _____________ refers to a community of people claiming descent from a common ancestor. (tribe, local, herd)
Answer:
tribe
Question 12.
_____________ community is one that is agrarian in nature. (Rural, Tribal, Urban)
Answer:
Rural
Question 13.
According to the 2011 census _____________ of Indian population lives in the rural areas. (68.84%, 70%, 65%)
Answer:
68.84%
Question 14.
The internal community issues are managed by the tribal through _____________ (law, judiciary, tribal panchayat)
Answer:
tribal panchayat
Question 15.
_____________ refers to a number of families who are related in blood and who trace their descent from a real or imagined person, object, or being. (Group, Family, Clans)
Answer:
Clan
Question 16.
Most tribes in India are divided into _____________ clans and lineages. (endogamous, exogamous, ritual)
Answer:
exogamous
Question 17.
After Independence, the Community Development Programme (CDP) was started in _____________ (1952, 1949, 1962)
Answer:
1952
![]()
Question 18.
_____________ is a situation in which too many people live in too little space. (Overcrowding, Beggary, Urban sprawl)
Answer:
Overcrowding
Question 19.
In Mumbai, beggary has been criminalised under the Bombay Prevention of Begging Act, _____________ (1940, 1959, 1905)
Answer:
1959
Question 20.
Urban society is _____________ in nature. (homogeneous, heterogeneous, informal)
Answer:
heterogeneous
Question 21.
About one-sixth of tribal population of India is found in the _____________ zone. (Western, Central, Southern)
Answer:
Southern
Question 22.
The tribal custom of worshipping a tree or any animal as the founding ancestor is known as _____________ (Animism, Naturism, Totemism)
Answer:
Totemism
1B. Correct the incorrect pair and rewrite it.
Question 1.
(a) Animism – Robert Marett
(b) Totemism – James Frazer
(c) Manaism – Robert Marett
(d) Naturism – Max Mueller
Answer:
(a) Animism – Edward Tylor
Question 2.
(a) Garo, Khasi, Jaintia – Himalayan region
(b) Gond, Santhal, Munda – Middle India Region
(c) Bhil, Katkari, Warli – Western Indian region
(d) Toda, Kota, Irula – The island region
Answer:
(d) Toda, Kota, Irula – South India region
![]()
Question 3.
(a) Swachh Bharat Mission (SBM) – Urban development
(b) Pradhan Mantri Gram Sadak Yojana – Rural development
(c) Village Grain Banks – Tribal development
(d) Panchsheel – Rural development
Answer:
(d) Panchsheel – Tribal development
Question 4.
(a) Worshipping the soul or ancestors – Manamism
(b) Worshipping any non-living body like stone or wood – Animatism
(c) Worshipping a tree or any animal as a founding ancestor – Totemism
(d) Worshipping elements of nature like a river, sun, forest – Naturism
Answer:
(a) Worshipping the soul or ancestors – Animism
1C. Identify the appropriate term from the given options in the box and rewrite it against the given statement.
Question 1.
The custom of worshipping the soul or ancestors.
Answer:
Animism
Question 2.
Shifting cultivation.
Answer:
Jhum
Question 3.
Tribal development guidelines were created by the first Prime Minister, Pandit Jawaharlal Nehru.
Answer:
Panchseel
Question 4.
Confers equal rights and opportunities to all.
Answer:
Article 14
![]()
Question 5.
A three-tier system of democratic functioning in villages.
Answer:
Panchayati Raj
Question 6.
Family is the unit of social responsibility.
Answer:
Familism
Question 7.
The inter-dependence among caste groups.
Answer:
Balutedari system
Question 8.
The root cause of urban problems.
Answer:
Urban sprawl
Question 9.
In mining areas, slums are known as Barack.
Answer:
Ghobara
![]()
Question 10.
Tribal people look upon this as the primordial source of all energy.
Answer:
Sun
1D. Correct underlined words and complete the statement.
Question 1.
The custom of worshipping elements of nature like a river stream, Sun, etc, is totemism.
Answer:
The custom of worshipping elements of nature like a river stream, Sun, etc, is naturism.
Question 2.
Urban economic activities are based on rudimentary technology.
Answer:
Tribal economic activities are based on rudimentary technology.
Question 3.
Article 330 states the Reservation of seats for Scheduled Castes and Scheduled Tribes in the Legislative.
Answer:
Article 332 states the Reservation of seats for Scheduled Castes and Scheduled Tribes in the Legislative.
Question 4.
The rural way of life revolves around an egalitarian value system.
Answer:
The rural way of life revolves around a traditional value system.
Question 5.
The population of the world is largely urban.
Answer:
The population of the world is largely rural.
Question 6.
The relationship is informal, personal, and inclusive in urban communities.
Answer:
The relationship is informal, personal, and inclusive in rural communities.
![]()
Question 7.
Education, law and legislation, police, and court are informal means of social control.
Answer:
Education, law and legislation, police, and court are formal means of social control.
2. Write short notes.
Question 1.
Characteristics of the rural community.
Answer:
The rural community has the following characteristics:
Community living in villages: The villages largely satisfy the needs of their residents.
They have a sense of togetherness. The development of villages is influenced considerably by the local needs.
Small size: It means that villages are comparatively smaller in size and population density. In the Indian context, a community with a population of about 5000 is designated as a “village”.
The dominance of agriculture: Agriculture is the major occupation in villages. However, it is not to be viewed as the only source of income but also as a way of life that needs to be ascertained. Almost 40% of our national income is obtained through agriculture and more than 60 % of the people still depend on agriculture. It was associated with various crafts like pottery, carpentry, smithy, basket-weaving, etc.
Primary relations: The impact of primary relations is still significant in Indian villages. The relationship is informal, personal, and inclusive. Community spirit prevails over individual interests. The ‘we feeling helps to build social cohesiveness.
Social homogeneity: Homogeneity is an underlying thread due to similarities in the ways of thinking, behaving, dressing, acting, and living. There is a tendency to conform to traditions and customs. Group feeling and mutual cooperation are evident among village dwellers. They cooperate with each other in times of exigencies.
![]()
Question 2.
Characteristics of Tribes.
Answer:
The basic characteristics of tribal communities in India:
Geographical isolation: They have usually a well-demarcated geographical territory. They live in clusters (called ‘padas’), which are generally located in remote forests and hilly areas. Today, however, many tribal people have migrated to rural villages and cities and in the course of time, they have mixed with non-tribal populations.
Economic life: They are engaged in varied occupations such as hunting, fishing, and food gathering of forest produce, basket making, weaving, iron-smith, etc. Besides, they also practice simple agriculture and shifting cultivation. Their economic activities are based on rudimentary technology, usually resulting in low productivity. They have a low level of literacy and poor health. In addition, their economic and infrastructural and marketing facilities are poor. Some tribes still depend on the barter system. These are among the few causes that leave them economically backward, at bare subsistence level, still leading a hand-to-mouth existence.
Sense of identity: Tribal folk nurture a sense of exclusive identity, which strongly binds them together as a community. This sense of identity is characterized by an awareness of territorial boundaries. The very existence of a tribe depends upon its sense of identity. Each tribe has a common name (e.g., Warli, Irula, Gond, Naga, Khasi) which adds to their sense of cohesion and solidarity.
Endogamous group: Tribal people generally do not marry outside their tribe. Marriage within the tribe is the usual norm. Marriage among tribals is based on the rule of tribal endogamy. It is viewed as a contract and usually, there are no taboos on divorce and remarriage. Recently, the increased mobility among the tribals has changed this condition and now, inter-tribal marriages are not uncommon.
![]()
Question 3.
Efforts towards Urban Development.
Answer:
Urbanization can be positively viewed as an engine of economic growth and an agent of socio-political transformation. But this is not sufficient, due to the high cost of living and partly and because of the growing economic disparity in urban areas. The rich are becoming richer and the poor are becoming poorer. Several steps have been initiated to meet the challenges posed by the urban crisis but with little or no success.
National Commission on Urbanisation (NCU) has, in its policy proposal of 1988, stressed the need for:
- The evolution of a spatial pattern of economic development and hierarchies of human settlements.
- Optimum distribution of population between rural and urban settlements and among towns and cities of various sizes.
- Distribution of economic activities in small and medium-sized growth centers.
- Dispersal of economic activities through the establishment of counter-magnets in the region.
- Provision of optimum levels of services in urban and rural areas.
The other major development programmes include:
- Urban Basic Services for the Poor (UBSP).
- Environmental Improvement of Urban Slums (EIUS) programme.
- Integrated Development of Small and Medium Towns (IDSMT).
- Various housing and infrastructure financing schemes e.g. Housing and Urban Development Corporation (HUDCO).
- Mega-Cities Project.
- Integrated Urban Poverty Eradication Programme (IUPEP).
Recent urban development programmes in India
- Smart Cities Mission.
- Atal Mission for Rejuvenation and Urban Transformation (AMRUT) Project.
- Pradhan Mantri Awas Yojana (Urban) or Housing for All by 2022 Mission.
- Heritage City Development and Augmentation Yojana (HRIDAY).
- Jawaharlal Nehru National Urban Renewal Mission.
- Urban transportation.
- Swachh Bharat Mission (SBM).
![]()
Question 4.
Efforts towards Tribal Development.
Answer:
‘Panchsheel’ Philosophy of Pandit Jawaharlal Nehru
Since Indian Independence, particularly with the inception of Five-Year Plans, the concern for tribal development has always been high on the government’s agenda. The first Prime Minister, Pandit Jawaharlal Nehru created long-term guidelines in this regard. This is evident from his views, on should take place at the cost of tribal development termed as ‘Panchsheel’.
Summary of ‘Panchsheel’
- People should develop along lines of their own genius and we should avoid imposing anything on them.
- Tribal rights to land and forests should be protected.
- We should try to train and build up a team of their own people to do the work of administration and development.
- We should not over-administer these areas with a multiplicity of schemes. We should rather work together and not in rivalry with our own social and cultural institutions.
- We should judge the results not by statistics or the amount of money spent on them, but by the quality of human life that is evolved.
A number of special schemes and programmes have evolved.in keeping with these broad Guidelines and the provisions of the Constitution.
Tribal Development Efforts after Independence
After Independence, the Government of India has taken various efforts for Tribal Development. The government made available, funding of Tribal Development Programmes i.e., State Plan.
Special Central Assistance, Sectorial Programmes of Central Ministries/Department, and Institutional Finance.
3. Write differences.
Question 1.
Tribal Community and Rural Community.
Answer:
| Tribal Community | Rural Community |
| (i) Size: The tribal population of Indian comes to constitutes about 8.6 percent of the total population. | (i) Size: The rural population of India constitutes about 68.84 percent of the total population. |
| (ii) Occupation: They are engaged in varied occupations such as hunting, fishing, and food gathering of forest produce, basket making, weaving, iron-smith, etc. | (ii) Occupation: Agriculture is the major occupation in villages. It is also associated with various crafts like pottery, carpentry, smithy, basket-weaving, etc. |
| (iii) Technology: Tribal communities make use of our moded techniques and rudimentary technology like a bow, arrow, spear, etc. | (iii) Technology: Rural community makes use of plough, animal power, fertilizers, pesticides, etc. |
| (iv) Nature of Social Control: Customs, traditions, religion, magic, tribal chief have effective social control over the members of the tribal community. | (iv) Nature of Social Control: In rural community caste council and village panchayat have effective social control. |
| (v) Cultural Background: They have independent traditions with respect to social customs, folklore, ecology, and a belief system. Each tribe has its own dialect. | (v) Cultural Background: There is social homogeneity in the rural community since their social and cultural background is the same. |
Question 2.
Rural Community and Urban Community.
Answer:
| Rural Community | Urban Community |
| (i) Size: The rural population constitutes about 68.84 percent of the total population. | (i) Size: The urban population constitutes about 31% percent of the total population. |
| (ii) Density: Villages are comparatively smaller in size and population density. | (ii) Density: An urban area is a human settlement with a high population density. |
| (iii) Occupation: Agriculture is the major occupation in villages. It was associated with various crafts like pottery, carpentry, smithy, basket-weaving, etc. | (iii) Occupation: The occupation in urban areas is mainly non-agricultural, i.e., based on manufacturing, trade, and commerce, professional and governance, services, etc. |
| (iv) Homogeneity/Heterogeneity: Rural areas are homogeneous in nature due to similarities in the ways of thinking, behaving, dressing, acting, and living. | (iv) Homogeneity/Heterogeneity: Urban areas are heterogeneous in nature, people belonging to diverse groups such as class, occupation, caste, language, and religion, etc., all reside in the same territory. |
| (v) Status of Women: In rural communities status of women is very low due to the impact of the patriarchal system of the family. | (v) Status of Women: The status of women is higher due to factors such as the spread of education, employment opportunities, etc. |
| (vi) Nature of Relations: The impact of primary relations is significant, in Indian villages. The relationship is informal, face to face Personal, and inclusive. | (vi) Nature of Relations: The impact of secondary relations is significant in urban areas characterized by formal interactions, and impersonal relationships. |
4. Explain the following concepts with examples.
Question 1.
Rural Development Programme
Answer:
Rural Development programme: Rural social change has been among the most important subjects of study in the ‘developing countries since the 1950s, partly because major national efforts in these countries have been directed towards economic development and such efforts have been located in predominantly agrarian social settings. We see changes in rural communities due to the efforts of the Government.
After Independence, the Community Development Programme (CDP) was started in 1952. It was an initiative meant for the all-around development of villages. The aim of CDP was to facilitate villages. The aim of CDP was to facilitate involvement and participation of the village community for its own welfare later on in 1957, Panchayati Raj (Local Self Government) was started. The Integrated Rural Development Programme (IRDP) replaced the CDP in 1979.
Examples: Some important recent schemes for Rural Development launched by the Government of India are Pradhan Mantri Gram Sadak Yojana, Deen Dayal Upadhyaya Grameen Kaushalya Yojana, Swarnjayanti Gram Swarozgar Yojana (SGSY)/ National Rural Livelihood Mission, Prime Minister Rural Development Fellows Scheme, Mahatma Gandhi National Rural Employment Guarantee Scheme (MGNREGS), Sampoorna Grameen Rozgar Yojana (SGRY), Sarva Shiksha Abhiyan (SSA).
![]()
Question 2.
Scheduled Tribe
Answer:
- Article 366 (25) of the Constitution of India refers to ‘Scheduled Tribes’ as those communities which are protected under a schedule, according to Article 342 of the Constitution.
- As per this, Scheduled Tribes are groups or communities that have been declared by the President of India, as possessing the following characteristics:
- Primitive traits
- Geographic isolation
- Distinct culture
- Shy of contact with the larger community
- Economic backwardness
- Scheduled Tribes’ can also be ascertained by the fact that they live apart in hills in isolation.
- Example – Schedule Tribes in Island region Andamanese, Jarawas Nicobarese Onges
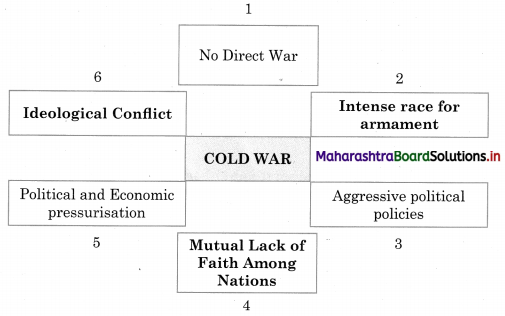
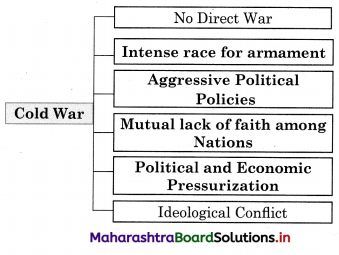
5A. Complete the concept map.
Question 1.

Answer:

Question 2.
Answer:

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

5B. State whether the following statements are True or False with reasons.
Question 1.
Urban society is characterized by Informal social control and Primary relations.
Answer:
This statement is False.
- Urban society is characterized by formal social control and secondary relations.
- In urban areas, interaction among people is largely based on anonymity and secondary contact.
- It is not personal nor face-to-face; rather cities are characterized by formal interactions and impersonal relationships that tend to become time-bound and based on vested interests.
- Cultural diversity, formal communication, friends’ circle are hallmarks of cities. For instance, people spend their leisure time at multiplexes, gardens, hotels, social clubs, and markets. Formal means of social control such as formal education, law, and legislation, police, and court are needed, in addition to informal means for regulating the behaviour of people.
- The traditional authority vested in figures such as family elders, religious leaders, and teachers has decreased greatly.
Question 2.
There are a large number of villages which suffer from major problems.
Answer:
This statement is True.
There are a large number of villages that suffer from major problems such as poverty, unemployment, illiteracy, indebtedness, superstition, and the like. Problems faced by the rural community are as follows:
![]()
Poverty: Poverty is a socio-economic phenomenon in which a section of rural society is not able to fulfill even its basic necessities of life. A vast majority of the rural population works in villages under the shadow of poverty, unemployment as well as pitiable economic conditions. Large portions of the rural poor are small and marginal farmers, agricultural laborers, and rural artisans.
Illiteracy: High illiteracy rates among children as well as adults continue even to this day because of inadequate budgetary provisions for rural education. The quality of education in rural areas is a matter of grave concern despite various programmes and provisions.
Traditionalism, conservatism, and superstitions: Rural India to date can be called a conservative society because it still holds on to traditional mindsets and beliefs. Conformity to traditional customs, religion, and ways of life is still rampant. There is usually a reluctance to change their way of life and outlook which have encouraged a fatalistic attitude.
Farmers’ suicides: A large percentage of farmers who take their own lives are financially indebted. Undoubtedly, there has been little positive impact of economic reforms in the agricultural sector in India
Question 2.
A majority of tribal people live below the poverty line.
Answer:
This statement is True.
A majority of tribal people live below the poverty line. The tribes practice simple occupations based on primitive technology. Most of the occupations fall into the primary categories such as hunting, gathering, and agriculture. There is no profit nor surplus making in such an economy.
Hence their per capita income is very low, far less compared to the national average. Most of them live in abject poverty and are steeped in debt. Local moneylenders and zamindars, take advantage of this situation and exploit the tribals. In order to repay the debts, they often have to mortgage or sell their land.
Though Bonded labour is banned by Indian Law, it still prevails in some tribal areas. Bonded labour is considered to be a serious problem, which started due to rampant poverty and lack of stable income among the tribals. In fact, land alienation, indebtedness, bonded labour, and poverty are problems that exist hand-in-hand.
Question 3.
The rapid growth of the urban population has put heavy pressure on public utilities and other social evils are rising.
Answer:
This statement is True.
Although India is one of the less urbanized countries of the world this country is, facing a serious crisis of urban growth at present. Poverty, unemployment, and under-employment among rural immigrants, beggars, theft, burglary and other social evils are on the rise.
The following urban problems are on rising:
Urban Sprawl: Urban sprawl or real expansion of the cities, both in population and geographical area, of rapidly growing cities is the root cause of urban problems. In most cities, the economic base is incapable of dealing with the problems created by their excessive size. Massive immigration from rural areas as well as from small towns into big cities has taken place almost consistently; thereby adding to the size of cities. The urban sprawl is taking place at the cost of valuable agricultural land.
![]()
Overcrowding: Overcrowding is a situation in which too many people live in too little space. Overcrowding is a logical consequence of over-population in urban areas. It is naturally expected that cities having a large size of population squeezed in a small space will suffer from] r overcrowding. This is well exhibited by almost all the big cities of India.
Beggary: For a majority of the urban poor, beggary has become a way of life, due to sheer lack of education and skill to find employability. Many people are pushed into beggary, due to reasons that range from abject poverty to beggary as a profession. There are organized gangs of beggars which are known to operate in big cities. Also, there are instances of children who are sold into beggary by their parents or are kidnapped and then coerced into begging by maiming them. In Mumbai, beggary has been criminalized under the Bombay Prevention of Begging Act, 1959.
6. Give your personal response.
Question 1.
Discuss, ‘The tribes have their own social problems.
Answer:
The tribes have their own social problems. They are traditional and bound by customs. Due to lack of education and development, they are superstitious and believe in outmoded and meaningless practices which can be harmful at times.
Child marriage, infanticide, homicide, animal sacrifice, exchange of wives, black magic, and other detrimental practices are still prevalent among them. They believe in supernatural powers and have a keen desire to maintain these practices. They don’t want to change their significant tribal character and hence it’s said that “tribes are the tribesmen first, the tribesmen last, and the tribesmen all the time.”
7. Answer the following question in detail. (about 150-200 words)
Question 1.
Though the urban community is in an advanced stage of development, it is not free from any problems. Using examples of your own, explain the major urban problems. Also, discuss any two recent urban development programmes in India.
Answer:
The rapid growth of the urban population, both natural and through migration, has put heavy pressure on public utilities like housing, sanitation, transport, water, electricity, health, education, and so on.
The following urban problems are highlighted:
Transport: With traffic congestion, almost all cities and towns of India are suffering from acute transportation problems. Today, we have reached a stage where practically no city in India gets sufficient water to meet the needs of the city-dwellers. In big cities like Mumbai, water is resourced from the rivers and lakes in Thane and Palghar, thereby causing hardship in the lives of those people.
Sewerage problems: Urban areas in India are almost invariably plagued with insufficient and inefficient sewage facilities. Insufficient resources faced by municipalities and the unauthorized growth of cities are two major causes of this. Most cities do not have proper arrangements for treating the sewerage waste and it is drained into nearby rivers.
Trash disposal: Huge quantities of garbage generated by our cities pose serious health hazards. Most cities do not have proper arrangements for garbage disposal and the existing landfills are full to the brim, which becomes hotbeds of disease and innumerable poisons into the environment. Also, a poisonous liquid called leachate is emitted, which contaminates groundwater.
![]()
Urban crime: Due to overcrowding poverty, unemployment many people in urban areas commit several types of crimes like thefts, robbery, cybercrime, gambling adulteration, corruption etc. Some criminals reach high political positions by using their money and muscle power.
Not only do the poor, deprived and slum dwellers take to crime; people from well-to-do families also resort to crime in order to make a fast wealth and to meet cravings for a lavish life.
Pollution: The intensity of air, water, and noise pollution has increased in the cities due to various factories and vehicles. Due to polluted air people suffer from various diseases like lung cancer, asthma, headache, etc., due to the polluted water, people suffer from various water-borne diseases.
Educational problems: Cities suffer from various educational problems like inadequate educational facilities, educational discrimination, costly education, indiscipline among the students.
Recent urban development programmes in India
(i) Swatch Bharat Abhiyan ( SBA ) or Swachh Bharat Mission (SBM) is a nationwide campaign in India for the period 2014 to 2019 that aims to clean up the streets, roads, and infrastructure of India’s cities, towns, urban and rural areas.to accelerate the efforts to achieve universal sanitation coverage and to put the focus on sanitation. The Prime Minister of India had launched the Swachh Bharat Mission on 2nd October 2014.
(ii) National Smart Cities Mission is an urban renewal program by the Government of India with the mission to develop smart cities across the country, making them citizen-friendly and sustainable The Union Ministry of Urban Development is responsible for implementing the mission in collaboration with the state governments of the respective cities. The mission initially included 100 cities, with the deadline for completion of the projects set between 2019 and 2023.