Class 10

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.3 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

10th Standard Maths 2 Practice Set 5.3 Chapter 5 Co-ordinate Geometry Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Practice Set 5.3 Chapter 5 Co-ordinate Geometry Questions With Answers Maharashtra Board

Practice Set 5.3 Geometry Class 10 Question 1. Angles made by the line with the positive direction of X-axis are given. Find the slope of these lines.
i. 45°
ii. 60°
iii. 90°
Solution:
i. Angle made with the positive direction of
X-axis (θ) = 45°
Slope of the line (m) = tan θ
∴ m = tan 45° = 1
∴ The slope of the line is 1.

ii. Angle made with the positive direction of X-axis (θ) = 60°
Slope of the line (m) = tan θ
∴ m = tan 60° = \(\sqrt { 3 }\)
∴ The slope of the line is \(\sqrt { 3 }\).

iii. Angle made with the positive direction of
X-axis (θ) = 90°
Slope of the line (m) = tan θ
∴ m = tan 90°
But, the value of tan 90° is not defined.
∴ The slope of the line cannot be determined.

Practice Set 5.3 Geometry Question 2. Find the slopes of the lines passing through the given points.
i. A (2, 3), B (4, 7)
ii. P(-3, 1), Q (5, -2)
iii. C (5, -2), D (7, 3)
iv. L (-2, -3), M (-6, -8)
v. E (-4, -2), F (6, 3)
vi. T (0, -3), s (0,4)
Solution:
i. A (x₁, y₁) = A (2, 3) and B (x₂, y₂) = B (4, 7)
Here, x₁ = 2, x₂ = 4, y₁ = 3, y₂ = 7

∴ The slope of line AB is 2.

ii. P (x₁, y₁) = P (-3, 1) and Q (x₂, y₂) = Q (5, -2)
Here, x₁ = -3, x₂ = 5, y₁ = 1, y₂ = -2

∴ The slope of line PQ is \(\frac { -3 }{ 8 } \)

iii. C (x₁, y₁) = C (5, -2) and D (x₂, y₂) = D (7, 3)
Here, x₁ = 5, x₂ = 7, y₁ = -2, y₂ = 3

∴ The slope of line CD is \(\frac { 5 }{ 2 } \)

iv. L (x₁, y₁) = L (-2, -3) and M (x₂,y₂) = M (-6, -8)
Here, x₁ = -2, x₂ = – 6, y₁ = – 3, y₂ = – 8

∴ The slope of line LM is \(\frac { 5 }{ 4 } \)

v. E (x₁, y₁) = E (-4, -2) and F (x₂, y₂) = F (6, 3)
Here,x₁ = -4, x₂ = 6, y₁ = -2, y₂ = 3

∴ The slope of line EF is \(\frac { 1 }{ 2 } \).

vi. T (x₁, y₁) = T (0, -3) and S (x₂, y₂) = S (0, 4)
Here, x₁ = 0, x₂ = 0, y₁ = -3, y₂ = 4

∴ The slope of line TS cannot be determined.

5.3.5 Practice Question 3. Determine whether the following points are collinear.
i. A (-1, -1), B (0, 1), C (1, 3)
ii. D (- 2, -3), E (1, 0), F (2, 1)
iii. L (2, 5), M (3, 3), N (5, 1)
iv. P (2, -5), Q (1, -3), R (-2, 3)
v. R (1, -4), S (-2, 2), T (-3,4)
vi. A(-4,4),K[-2,\(\frac { 5 }{ 2 } \)], N (4,-2)
Solution:


∴ slope of line AB = slope of line BC
∴ line AB || line BC
Also, point B is common to both the lines.
∴ Both lines are the same.
∴ Points A, B and C are collinear.

∴ slope of line DE = slope of line EF
∴ line DE || line EF
Also, point E is common to both the lines.
∴ Both lines are the same.
∴ Points D, E and F are collinear.

∴ slope of line LM ≠ slope of line MN
∴ Points L, M and N are not collinear.

∴ slope of line PQ = slope of line QR
∴ line PQ || line QR
Also, point Q is common to both the lines.
∴ Both lines are the same.
∴ Points P, Q and R are collinear.

∴ slope of line RS = slope of line ST
∴ line RS || line ST
Also, point S is common to both the lines.
∴ Both lines are the same.
∴ Points R, S and T are collinear.

∴ slope of line AK = slope of line KN
∴ line AK || line KN
Also, point K is common to both the lines.
∴ Both lines are the same.
∴ Points A, K and N are collinear.

Practice Set 5.3 Geometry 9th Standard Question 4. If A (1, -1), B (0,4), C (-5,3) are vertices of a triangle, then find the slope of each side.
Solution:

∴ The slopes of the sides AB, BC and AC are -5, \(\frac { 1 }{ 5 } \) and \(\frac { -2 }{ 3 } \) respectively.

Geometry 5.3 Question 5. Show that A (-4, -7), B (-1, 2), C (8, 5) and D (5, -4) are the vertices of a parallelogram.
Proof:


∴ Slope of side AB = Slope of side CD … [From (i) and (iii)]
∴ side AB || side CD
Slope of side BC = Slope of side AD … [From (ii) and (iv)]
∴ side BC || side AD
Both the pairs of opposite sides of ꠸ABCD are parallel.
꠸ABCD is a parallelogram.
Points A(-4, -7), B(-1, 2), C(8, 5) and D(5, -4) are the vertices of a parallelogram.

Question 6.
Find k, if R (1, -1), S (-2, k) and slope of line RS is -2.
Solution:
R(x₁, y₁) = R (1, -1), S (x₂, y₂) = S (-2, k)
Here, x₁ = 1, x₂ = -2, y₁ = -1, y₂ = k

But, slope of line RS is -2. … [Given]
∴ -2 = \(\frac { k+1 }{ -3 } \)
∴ k + 1 = 6
∴ k = 6 – 1
∴ k = 5

5.3 Class 10 Question 7. Find k, if B (k, -5), C (1, 2) and slope of the line is 7.
Solution:
B(x₁, y₁) = B (k, -5), C (x₂, y₂) = C (1, 2)
Here, x₁ = k, x₂ = 1, y₁ = -5, y₂ = 2

But, slope of line BC is 7. …[Given]
∴ 7 = \(\frac { 7 }{ 1-k } \)
∴ 7(1 – k) = 7
∴ 1 – k = \(\frac { 7 }{ 7 } \)
∴ 1 – k = 1
∴ k = 0

Question 8.
Find k, if PQ || RS and P (2, 4), Q (3, 6), R (3,1), S (5, k).
Solution:

But, line PQ || line RS … [Given]
∴ Slope of line PQ = Slope of line RS
∴ 2 = \(\frac { k-1 }{ 2 } \)
∴ 4 = k – 1
∴ k = 4 + 1
∴ k = 5

Class 10 Maths Digest

• Practice Set 4.1 Class 10 Answers
• Practice Set 4.2 Class 10 Answers
• Problem Set 4 Class 10 Answers
• Practice Set 5.1 Class 10 Answers
• Practice Set 5.2 Class 10 Answers
• Practice Set 5.3 Class 10 Answers
• Problem Set 5 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

10th Standard Maths 2 Practice Set 5.2 Chapter 5 Co-ordinate Geometry Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Practice Set 5.2 Chapter 5 Co-ordinate Geometry Questions With Answers Maharashtra Board

Question 1.
Find the co-ordinates of point P if P divides the line segment joining the points A (-1, 7) and B (4, -3) in the ratio 2:3.
Solution:
Let the co-ordinates of point P be (x, y) and A (x₁, y₁) B (x₂, y₂) be the given points.
Here, x₁ = -1, y₁ = 7, x₂ = 4, y₂ = -3, m = 2, n = 3
∴ By section formula,

∴ The co-ordinates of point P are (1,3).

Question 2.
In each of the following examples find the co-ordinates of point A which divides segment PQ in the ratio a : b.
i. P (-3, 7), Q (1, -4), a : b = 2 : 1
ii. P (-2, -5), Q (4, 3), a : b = 3 : 4
iii. P (2, 6), Q (-4, 1), a : b = 1 : 2
Solution:
Let the co-ordinates of point A be (x, y).
i. Let P (x₁, y₁), Q (x₂, y₂) be the given points.
Here, x₁ = -3, y₁ = 7, x₂ = 1, y₂ = -4, a = 2, b = 1
∴ By section formula,

∴ The co-ordinates of point A are (\(\frac { -1 }{ 3 } \),\(\frac { -1 }{ 3 } \)).

ii. Let P (x₁,y₁), Q (x₂, y₂) be the given points.
Here, x₁ = -2, y₁ = -5, x₂ = 4, y₂ = 3, a = 3, b = 4
By section formula,

∴ The co-ordinates of point A are (\(\frac { 4 }{ 7 } \),\(\frac { -11 }{ 7 } \))

iii. Let P (x₁, y₁), Q (x₂, y₂) be the given points.
Here,x₁ = 2,y₁ = 6, x₂ = -4, y₂ = 1, a = 1,b = 2
∴ By section formula,

∴ The co-ordinates of point A are (0,\(\frac { 13 }{ 3 } \))

Question 3.
Find the ratio in which point T (-1, 6) divides the line segment joining the points P (-3,10) and Q (6, -8).
Solution:
Let P (x₁, y₁), Q (x₂, y₂) and T (x, y) be the given points.
Here, x₁ = -3, y₁ = 10, x₂ = 6, y₂ = -8, x = -1, y = 6
∴ By section formula,

∴ Point T divides seg PQ in the ratio 2 : 7.

Question 4.
Point P is the centre of the circle and AB is a diameter. Find the co-ordinates of point B if co-ordinates of point A and P are (2, -3) and (-2,0) respectively.
Solution:
Let A (x₁, y₁), B (x₂, y₂) and P (x, y) be the given points.
Here, x₁ = 2, y₁ =-3,
x = -2, y = 0

Point P is the midpoint of seg AB.
∴ By midpoint formula,

∴ The co-ordinates of point B are (-6,3).

Question 5.
Find the ratio in which point P (k, 7) divides the segment joining A (8, 9) and B (1,2). Also find k.
Solution:
Let A (x₁, y₁), B (x₂, y₂) and P (x, y) be the given points.
Here, x₁ = 8, y₁ = 9, x₂ = 1, y₂ = 2, x = k, y = 7
∴ By section formula,

∴ Point P divides seg AB in the ratio 2 : 5, and the value of k is 6.

Question 6.
Find the co-ordinates of midpoint of the segment joining the points (22, 20) and (0,16).
Solution:
Let A (x₁, y₁) = A (22, 20),
B (x₂,y₂) = B (0, 16)
Let the co-ordinates of the midpoint be P (x,y).
∴ By midpoint formula,

The co-ordinates of the midpoint of the segment joining (22, 20) and (0, 16) are (11,18).

Question 7.
Find the centroids of the triangles whose vertices are given below.
i. (-7, 6), (2,-2), (8, 5)
ii. (3, -5), (4, 3), (11,-4)
iii. (4, 7), (8, 4), (7, 11)
Solution:
i. Let A (x₁, y₁) = A (-7, 6),
B (x₂, y₂) = B (2, -2),
C (x₃, y₃) = C(8, 5)
∴ By centroid formula,

∴ The co-ordinates of the centroid are (1,3).

ii. Let A (x₁ y₁) = A (3, -5),
B (x₂, y₂) = B (4, 3),
C(x₃, y₃) = C(11,-4)
∴ By centroid formula,

∴ The co-ordinates of the centroid are (6, -2).

iii. Let A (x₁, y₁) = A (4, 7),
B (x₂, y₂) = B (8,4),
C (x₃, y₃) = C(7,11)
∴ By centroid formula,

∴ The co-ordinates of the centroid are (\(\frac { 19 }{ 3 } \),\(\frac { 22 }{ 3 } \))

Question 8.
In ∆ABC, G (-4, -7) is the centroid. If A (-14, -19) and B (3, 5), then find the co-ordinates of C.
Solution:
G (x, y) = G (-4, -7),
A (x₁, y₁) = A (-14, -19),
B(x₂, y₂) = B(3,5)
Let the co-ordinates of point C be (x₃, y₃).
G is the centroid.
By centroid formula,

∴ The co-ordinates of point C are (-1, – 7).

Question 9.
A (h, -6), B (2, 3) and C (-6, k) are the co-ordinates of vertices of a triangle whose centroid is G (1,5). Find h and k.
Solution:
A(x₁,y₁) = A(h, -6),
B (x₂, y₂) = B(2, 3),
C (x₃, y₃) = C (-6, k)
∴ centroid G (x, y) = G (1, 5)
G is the centroid.
By centroid formula,

∴ 3 = h – 4
∴ h = 3 + 4
∴ h = 7

∴ 15 = -3 + k
∴ k = 15 + 3
∴ k = 18
∴ h = 7 and k = 18

Question 10.
Find the co-ordinates of the points of trisection of the line segment AB with A (2,7) and B (-4, -8).
Solution:
A (2, 7), B H,-8)
Suppose the points P and Q trisect seg AB.
∴ AP = PQ = QB

∴ Point P divides seg AB in the ratio 1:2.
∴ By section formula,

Co-ordinates of P are (0, 2).
Point Q is the midpoint of PB.
By midpoint formula,

Co-ordinates of Q are (-2, -3).
∴ The co-ordinates of the points of trisection seg AB are (0,2) and (-2, -3).

Question 11.
If A (-14, -10), B (6, -2) are given, find the co-ordinates of the points which divide segment AB into four equal parts.
Solution:
Let the points C, D and E divide seg AB in four equal parts.

Point D is the midpoint of seg AB.
∴ By midpoint formula,

∴ Co-ordinates of D are (-4, -6).
Point C is the midpoint of seg AD.
∴ By midpoint formula,

∴ Co-ordinates of C are (-9, -8).
Point E is the midpoint of seg DB.
∴ By midpoint formula,


∴ Co-ordinates of E are (1,-4).
∴ The co-ordinates of the points dividing seg AB in four equal parts are C(-9, -8), D(-4, -6) and E(1, – 4).

Question 12.
If A (20, 10), B (0, 20) are given, find the co-ordinates of the points which divide segment AB into five congruent parts.
Solution:
Suppose the points C, D, E and F divide seg AB in five congruent parts.
∴ AC = CD = DE = EF = FB

∴ co-ordinates of C are (16, 12).
E is the midpoint of seg CB.
By midpoint formula,

∴ co-ordinates of E are (8, 16).
D is the midpoint of seg CE.

∴ co-ordinates of F are (4, 18).
∴ The co-ordinates of the points dividing seg AB in five congruent parts are C (16, 12), D (12, 14), E (8, 16) and F (4, 18).

Maharashtra Board Class 10 Maths Chapter 5 Co-ordinate Geometry Intext Questions and Activities

Question 1.
A (15, 5), B (9, 20) and A-P-B. Find the ratio in which point P (11, 15) divides segment AB. Find the ratio using x and y co-ordinates. Write the conclusion. (Textbook pg. no. 113)
Solution:
Suppose point P (11,15) divides segment AB in the ratio m : n.
By section formula,

∴ Point P divides seg AB in the ratio 2 : 1.
The ratio obtained by using x and y co-ordinates is the same.

Question 2.
External division: (Textbook pg. no. 115)
Suppose point R divides seg PQ externally in the ratio 3:1.

Let the common multiple be k.
Let PR = 3k and QR = k
Now, PR = PQ + QR … [P – Q – R]
∴ 3k = PQ + k
∴ \(\frac { PQ }{ QR } \) = \(\frac { 2k }{ k } \) = \(\frac { 2 }{ 1 } \)
∴ Point Q divides seg PR in the ratio 2 : 1 internally.
Thus, we can find the co-ordinates of point R, when co-ordinates of points P and Q are given.

Class 10 Maths Digest

• Practice Set 4.1 Class 10 Answers
• Practice Set 4.2 Class 10 Answers
• Problem Set 4 Class 10 Answers
• Practice Set 5.1 Class 10 Answers
• Practice Set 5.2 Class 10 Answers
• Practice Set 5.3 Class 10 Answers
• Problem Set 5 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

10th Standard Maths 2 Practice Set 5.1 Chapter 5 Co-ordinate Geometry Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Practice Set 5.1 Chapter 5 Co-ordinate Geometry Questions With Answers Maharashtra Board

Practice Set 5.1 Geometry Class 10 Question 1. Find the distance between each of the following pairs of points.
i. A (2, 3), B (4,1)
ii. P (-5, 7), Q (-1, 3)
iii. R (0, -3), S (0,\(\frac { 5 }{ 2 } \))
iv. L (5, -8), M (-7, -3)
v. T (-3, 6), R (9, -10)
vi. W(\(\frac { -7 }{ 2 } \),4), X(11, 4)
Solution:
i. Let A (x₁, y₁) and B (x₂, y₂) be the given points.
∴ x₁ = 2, y₁ = 3, x₂ = 4, y₂ = 1
By distance formula,

∴ d(A, B) = 2\(\sqrt { 2 }\) units
∴ The distance between the points A and B is 2\(\sqrt { 2 }\) units.

ii. Let P (x₁, y₁ ) and Q (x₂, y₂) be the given points.
∴ x₁ = -5, y₁ = 7, x₂ = -1, y₂ = 3
By distance formula,

∴ d(P, Q) = 4\(\sqrt { 2 }\) units
∴ The distance between the points P and Q is 4\(\sqrt { 2 }\) units.

iii. Let R (x₁, y₁) and S (x₂, y₂) be the given points.
∴ x₁ = 0, y₁ = -3, x₂ = 0, y₂ = \(\frac { 5 }{ 2 } \)
By distance formula,

∴ d(R, S) = \(\frac { 11 }{ 2 } \) units
∴ The distance between the points R and S is \(\frac { 11 }{ 2 } \) units.

iv. Let L (x₁, y₁) and M (x₂, y₂) be the given points.
∴ x₁ = 5, y₁ = -8, x₂ = -7, y₂ = -3
By distance formula,

∴ d(L, M) = 13 units
∴ The distance between the points L and M is 13 units.

v. Let T (x₁,y₁) and R (x₂, y₂) be the given points.
∴ x₁ = -3, y₁ = 6,x₂ = 9,y₂ = -10
By distance formula,

∴ d(T, R) = 20 units
∴ The distance between the points T and R 20 units.

vi. Let W (x₁, y₁) and X (x₂, y₂) be the given points.

∴ d(W, X) = \(\frac { 29 }{ 2 } \) units
∴ The distance between the points W and X is \(\frac { 29 }{ 2 } \) units.

Practice Set 5.1 Geometry 10th Question 2. Determine whether the points are collinear.
i. A (1, -3), B (2, -5), C (-4, 7)
ii. L (-2, 3), M (1, -3), N (5, 4)
iii. R (0, 3), D (2, 1), S (3, -1)
iv. P (-2, 3), Q (1, 2), R (4, 1)
Solution:
i. By distance formula,


∴ d(A, B) = \(\sqrt { 5 }\) …(i)
On adding (i) and (iii),
d(A, B) + d(A, C)= \(\sqrt { 5 }\) + 5\(\sqrt { 5 }\) = 6\(\sqrt { 5 }\)
∴ d(A, B) + d(A, C) = d(B, C) … [From (ii)]
∴ Points A, B and C are collinear.

ii. By distance formula,

On adding (i) and (iii),
d(L, M) + d(L, N) = 3\(\sqrt { 5 }\) + 5\(\sqrt { 2 }\) ≠ \(\sqrt { 65 }\)
∴ d(L, M) + d(L, N) ≠ d(M, N) … [From (ii)]
∴ Points L, M and N are not collinear.

iii. By distance formula,

On adding (i) and (ii),
∴ d(R, D) + d(D, S) = \(\sqrt { 8 }\) + \(\sqrt { 5 }\) ≠ 5
∴ d(R, D) + d(D, S) ≠ d(R, S) … [From (iii)]
∴ Points R, D and S are not collinear.

iv. By distance formula,

On adding (i) and (ii),
d(P, Q) + d(Q, R) = \(\sqrt { 10 }\) + \(\sqrt { 10 }\) = 2\(\sqrt { 10 }\)
∴ d(P, Q) + d(Q, R) = d(P, R) … [From (iii)]
∴ Points P, Q and R are collinear.

Coordinate Geometry Class 10 Practice Set 5.1 Question 3. Find the point on the X-axis which is equidistant from A (-3,4) and B (1, -4).
Solution:
Let point C be on the X-axis which is equidistant from points A and B.
Point C lies on X-axis.
∴ its y co-ordinate is 0.
Let C = (x, 0)
C is equidistant from points A and B.
∴ AC = BC

∴ (x + 3)² + (-4)² = (x- 1)² + 4²
∴ x² + 6x + 9 + 16 = x² – 2x + 1 + 16
∴ 8x = – 8
∴ x = – \(\frac { 8 }{ 8 } \) = -1
∴ The point on X-axis which is equidistant from points A and B is (-1,0).

10th Geometry Practice Set 5.1 Question 4. Verify that points P (-2, 2), Q (2, 2) and R (2, 7) are vertices of a right angled triangle.
Solution:
Distance between two points

Consider, PQ² + QR² = 42 + 52 = 16 + 25 = 41 … [From (i) and (ii)]
∴ PR² = PQ² + QR² … [From (iii)]
∴ ∆PQR is a right angled triangle. … [Converse of Pythagoras theorem]
∴ Points P, Q and R are the vertices of a right angled triangle.

Question 5.
Show that points P (2, -2), Q (7, 3), R (11, -1) and S (6, -6) are vertices of a parallelogram.
Proof:
Distance between two points

PQ = RS … [From (i) and (iii)]
QR = PS … [From (ii) and (iv)]
A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent.
∴ □ PQRS is a parallelogram.
∴ Points P, Q, R and S are the vertices of a parallelogram.

Question 6.
Show that points A (-4, -7), B (-1, 2), C (8, 5) and D (5, -4) are vertices of rhombus ABCD.
Proof:
Distance between two points


∴ AB = BC = CD = AD …[From (i), (ii), (iii) and (iv)]
In a quadrilateral, if all the sides are equal, then it is a rhombus.
∴ □ ABCD is a rhombus.
∴ Points A, B, C and D are the vertices of rhombus ABCD.

Practice Set 5.1 Question 7. Find x if distance between points L (x, 7) and M (1,15) is 10.
Solution:
X₁ = x, y₁ = 7, x₂ = 1, y₂ = 15
By distance formula,

∴ 1 – x = ± 6
∴ 1 – x = 6 or l – x = -6
∴ x = – 5 or x = 7
∴ The value of x is – 5 or 7.

Geometry 5.1 Question 8. Show that the points A (1, 2), B (1, 6), C (1 + 2\(\sqrt { 3 }\), 4) are vertices of an equilateral triangle.
Proof:
Distance between two points

∴ AB = BC = AC … [From (i), (ii) and (iii)]
∴ ∆ABC is an equilateral triangle.
∴ Points A, B and C are the vertices of an equilateral triangle.

Maharashtra Board Class 10 Maths Chapter 5 Coordinate Geometry Intext Questions and Activities

Question 1.
In the figure, seg AB || Y-axis and seg CB || X-axis. Co-ordinates of points A and C are given. To find AC, fill in the boxes given below. (Textbook pa. no. 102)

Solution:
In ∆ABC, ∠B = 900
∴ (AB)² + (BC)² = [(Ac)² …(i) … [Pythagoras theorem]
seg CB || X-axis
∴ y co-ordinate of B = 2
seg BA || Y-axis
∴ x co-ordinate of B = 2
∴ co-ordinate of B is (2, 2) = (x₁,y₁)
co-ordinate of A is (2, 3) = (x₂, Y₂)
Since, AB || to Y-axis,
d(A, B) = Y₂ – Y₁
d(A,B) = 3 – 2 = 1
co-ordinate of C is (-2,2) = (x₁,y₁)
co-ordinate of B is (2, 2) = (x₂, y₂)
Since, BC || to X-axis,
d(B, C) = x₂ – x₁
d(B,C) = 2 – -2 = 4
∴ AC² = 12 + 42 …[From (i)]
= 1 + 16 = 17
∴ AC = \(\sqrt { 17 }\) units …[Taking square root of both sides]

Class 10 Maths Digest

• Practice Set 4.1 Class 10 Answers
• Practice Set 4.2 Class 10 Answers
• Problem Set 4 Class 10 Answers
• Practice Set 5.1 Class 10 Answers
• Practice Set 5.2 Class 10 Answers
• Practice Set 5.3 Class 10 Answers
• Problem Set 5 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 1 Similarity.

10th Standard Maths 2 Practice Set 1.2 Chapter 1 Similarity Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Practice Set 1.2 Chapter 1 Similarity Questions With Answers Maharashtra Board

Question 1.
Given below are some triangles and lengths of line segments. Identify in which figures, ray PM is the bisector of ∠QPR.

Solution:
In ∆ PQR,
\(\frac { PQ }{ PR } \) = \(\frac { 7 }{ 3 } \) (i)
\(\frac { QM }{ RM } \) = \(\frac { 3.5 }{ 1.5 } \) = \(\frac { 35 }{ 15 } \) = \(\frac { 7 }{ 3 } \) (ii)
∴ \(\frac { PQ }{ PR } \) = \(\frac { QM }{ RM } \) [From (i) and (ii)]
∴ Ray PM is the bisector of ∠QPR. [Converse of angle bisector theorem]

ii. In ∆PQR,
\(\frac { PQ }{ PR } \) = \(\frac { 10 }{ 7 } \) (i)
\(\frac { QM }{ RM } \) = \(\frac { 8 }{ 6 } \) = \(\frac { 4 }{ 3 } \) (ii)
∴ \(\frac { PQ }{ PR } \) ≠ \(\frac { QM }{ RM } \) [From (i) and (ii)]
∴ Ray PM is not the bisector of ∠QPR

iii. In ∆PQR,
\(\frac { PQ }{ PR } \) = \(\frac { 9 }{ 10 } \) (i)
\(\frac { QM }{ RM } \) = \(\frac { 3.6 }{ 4 } \) = \(\frac { 36 }{ 40 } \) = \(\frac { 9 }{ 10 } \) (ii)
∴ \(\frac { PQ }{ PR } \) = \(\frac { QM }{ RM } \) [From (i) and (ii)]
∴ Ray PM is the bisector of ∠QPR [Converse of angle bisector theorem]

Question 2.
In ∆PQR PM = 15, PQ = 25, PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason.

Solution:
PN + NR = PR [P – N – R]
∴ PN + 8 = 20
∴ PN = 20 – 8 = 12
Also, PM + MQ = PQ [P – M – Q]
∴ 15 + MQ = 25

∴ line NM || side RQ [Converse of basic proportionality theorem]

Question 3.
In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7, MQ = 2.5, then find QP.

Solution:
In ∆MNP, NQ is the bisector of ∠N. [Given]
∴\(\frac { PN }{ MN } \) = \(\frac { QP }{ MQ } \) [Property of angle bisector of a triangle]
∴\(\frac { 7 }{ 5 } \) = \(\frac { QP }{ 2.5 } \)
∴ QP = \(\frac { 7\times 2.5 }{ 5 } \)
∴ QP = 3.5 units

Question 4.
Measures of some angles in the figure are given. Prove that \(\frac { AP }{ PB } \) = \(\frac { AQ }{ QC } \)

Solution:
Proof
∠APQ = ∠ABC = 60° [Given]
∴ ∠APQ ≅ ∠ABC
∴ side PQ || side BC (i) [Corresponding angles test]
In ∆ABC,
sidePQ || sideBC [From (i)]
∴\(\frac { AP }{ PB } \) = \(\frac { AQ }{ QC } \) [Basic proportionality theorem]

Question 5.
In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, find BQ.

Solution:
side AB || side PQ || side DC [Given]
∴\(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \) [Property of three parallel lines and their transversals]
∴\(\frac { 15 }{ 12 } \) = \(\frac { BQ }{ 14 } \)
∴ BQ = \(\frac { 15\times 14 }{ 12 } \)
∴ BQ = 17.5 units

Question 6.
Find QP using given information in the figure.

Solution:
In ∆MNP, seg NQ bisects ∠N. [Given]
∴\(\frac { PN }{ MN } \) = \(\frac { QP }{ MQ } \) [Property of angle bisector of a triangle]
∴\(\frac { 40 }{ 25 } \) = \(\frac { QP }{ 14 } \)
∴ QP = \(\frac { 40\times 14 }{ 25 } \)
∴ QP = 22.4 units

Question 7.
In the adjoining figure, if AB || CD || FE, then find x and AE.

Solution:
line AB || line CD || line FE [Given]
∴\(\frac { BD }{ DF } \) = \(\frac { AC }{ CE } \) [Property of three parallel lines and their transversals]
∴\(\frac { 8 }{ 4 } \) = \(\frac { 12 }{ X } \)
∴ X = \(\frac { 12\times 4 }{ 8 } \)
∴ X = 6 units
Now, AE AC + CE [A – C – E]
= 12 + x
= 12 + 6
= 18 units
∴ x = 6 units and AE = 18 units

Question 8.
In ∆LMN, ray MT bisects ∠LMN. If LM = 6, MN = 10, TN = 8, then find LT.

Solution:
In ∆LMN, ray MT bisects ∠LMN. [Given]
∴\(\frac { LM }{ MN } \) = \(\frac { LT }{ TN } \) [Property of angle bisector of a triangle]
∴\(\frac { 6 }{ 10 } \) = \(\frac { LT }{ 8 } \)
∴ LT = \(\frac { 6\times 8 }{ 10 } \)
∴ LT = 4.8 units

Question 9.
In ∆ABC,seg BD bisects ∠ABC. If AB = x,BC x+ 5, AD = x – 2, DC = x + 2, then find the value of x.

Solution:
In ∆ABC, seg BD bisects ∠ABC. [Given]
∴\(\frac { AB }{ BC } \) = \(\frac { AD }{ CD } \) [Property of angle bisector of a triangle]
∴\(\frac { x }{ x+5 } \) = \(\frac { x-2 }{ x+2 } \)
∴ x(x + 2) = (x – 2)(x + 5)
∴ x2 + 2x = x2 + 5x – 2x – 10
∴ 2x = 3x – 10
∴ 10 = 3x – 2x
∴ x = 10

Question 10.
In the adjoining figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Solution:

Question 11.
In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB = seg AC, then prove that ED || BC.

Solution:
In ∆ABC, ray BD bisects ∠ABC. [Given]
∴\(\frac { AB }{ BC } \) = \(\frac { AE }{ EB } \) (i) [Property of angle bisector of a triangle]
Also, in ∆ABC, ray CE bisects ∠ACB. [Given]
∴\(\frac { AC }{ BC } \) = \(\frac { AE }{ EB } \) (ii) [Property of angle bisector of a triangle]
But, seg AB = seg AC (iii) [Given]
∴\(\frac { AB }{ BC } \) = \(\frac { AE }{ EB } \) (iv) [From (ii) and (iii)]
∴\(\frac { AD }{ DC } \) = \(\frac { AE }{ EB } \) [From (i) and (iv)]
∴ ED || BC [Converse of basic proportionality theorem]

Question 1.
i. Draw a ∆ABC.
ii. Bisect ∠B and name the point of intersection of AC and the angle bisector as D.
iii. Measure the sides.

iv. Find ratios \(\frac { AB }{ BC } \) and \(\frac { AD }{ DC } \)
v. You will find that both the ratios are almost equal.
vi. Bisect remaining angles of the triangle and find the ratios as above. Verify that the ratios are equal. (Textbook pg. no. 8)
Solution:

Note: Students should bisect the remaining angles and verify that the ratios are equal.

Question 2.
Write another proof of the above theorem (property of an angle bisector of a triangle). Use the following properties and write the proof.
i. The areas of two triangles of equal height are proportional to their bases.
ii. Every point on the bisector of an angle is equidistant from the sides of the angle. (Textbook pg. no. 9)

Given: In ∆CAB, ray AD bisects ∠A.
To prove: \(\frac { AB }{ AC } \) = \(\frac { BD }{ DC } \)
Construction: Draw seg DM ⊥ seg AB A – M – B and seg DN ⊥ seg AC, A – N – C.
Solution:
Proof:
In ∆ABC,
Point D is on angle bisector of ∠A. [Given]
∴DM = DN [Every point on the bisector of an angle is equidistant from the sides of the angle]
\(\frac{A(\Delta A B D)}{A(\Delta A C D)}=\frac{A B \times D M}{A C \times D N}\) [Ratio of areas of two triangles is equal to the ratio of the product of their bases and corresponding heights]
∴ \(\frac{A(\Delta A B D)}{A(\Delta A C D)}=\frac{A B}{A C}\) (ii) [From (i)]
Also, ∆ABD and ∆ACD have equal height.
∴ \(\frac{\mathrm{A}(\Delta \mathrm{ABD})}{\mathrm{A}(\Delta \mathrm{ACD})}=\frac{\mathrm{BD}}{\mathrm{CD}}\) (iii) [Triangles having equal height]
∴\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{DC}}\) [From (ii) and (iii)]

Question 3.
i. Draw three parallel lines.
ii. Label them as l, m, n.
iii. Draw transversals t₁ and t₂.
iv. AB and BC are intercepts on transversal t₁.
v. PQ and QR are intercepts on transversal t₂.
vi. Find ratios \(\frac { AB }{ BC } \) and \(\frac { PQ }{ QR } \). You will find that they are almost equal. Verify that they are equal.(Textbook pg, no. 10)
Solution:

(Students should draw figures similar to the ones given and verify the properties.)

Question 4.
In the adjoining figure, AB || CD || EF. If AC = 5.4, CE = 9, BD = 7.5, then find DF.(Textbook pg, no. 12)

Solution:

Question 5.
In ∆ABC, ray BD bisects ∠ABC. A – D – C, side DE || side BC, A – E – B, then prove that \(\frac { AB }{ BC } \) = \(\frac { AE }{ EB } \) (Textbook pg, no. 13)

Solution:

Class 10 Maths Digest

• Practice Set 1.1 Class 10 Answers
• Practice Set 1.2 Class 10 Answers
• Practice Set 1.3 Class 10 Answers
• Practice Set 1.4 Class 10 Answers
• Problem Set 1 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 1 Similarity.

10th Standard Maths 2 Practice Set 1.1 Chapter 1 Similarity Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Practice Set 1.1 Chapter 1 Similarity Questions With Answers Maharashtra Board

Question 1.
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
Solution:
Let the base, height and area of the first triangle be b₁, h₁, and A₁ respectively.
Let the base, height and area of the second triangle be b₂, h₂ and A₂ respectively.

[Since Ratio of areas of two triangles is equal to the ratio of the product of their bases and corresponding heights]
∴ The ratio of areas of the triangles is 3:4.

Question 2.
In the adjoining figure, BC ± AB, AD _L AB, BC = 4, AD = 8, then find \(\frac{A(\Delta A B C)}{A(\Delta A D B)}\)

Solution:
∆ABC and ∆ADB have same base AB.

[Since Triangles having equal base]

Question 3.
In the adjoining figure, seg PS ± seg RQ, seg QT ± seg PR. If RQ = 6, PS = 6 and PR = 12, then find QT.

Solution:
In ∆PQR, PR is the base and QT is the corresponding height.
Also, RQ is the base and PS is the corresponding height.
\(\frac{A(\Delta P Q R)}{A(\Delta P Q R)}=\frac{P R \times Q T}{R Q \times P S}\) [Ratio of areas of two triangles is equal to the ratio of the product of their bases and corresponding heights]
∴ \(\frac{1}{1}=\frac{P R \times Q T}{R Q \times P S}\)
∴ PR × QT = RQ × PS
∴ 12 × QT = 6 × 6
∴ QT = \(\frac { 36 }{ 12 } \)
∴ QT = 3 units

Question 4.
In the adjoining figure, AP ⊥ BC, AD || BC, then find A(∆ABC) : A(∆BCD).

Solution:
Draw DQ ⊥ BC, B-C-Q.

AD || BC [Given]
∴ AP = DQ   (i)  [Perpendicular distance between two parallel lines is the same]
∆ABC and ∆BCD have same base BC.

Question 5.
In the adjoining figure, PQ ⊥ BC, AD ⊥ BC, then find following ratios.

Solution:
i. ∆PQB and tPBC have same height PQ.

ii. ∆PBC and ∆ABC have same base BC.

iii. ∆ABC and ∆ADC have same height AD.

Question 1.
Find \(\frac{A(\Delta A B C)}{A(\Delta A P Q)}\)

Solution:
In ∆ABC, BC is the base and AR is the height.
In ∆APQ, PQ is the base and AR is the height.

Class 10 Maths Digest

• Practice Set 1.1 Class 10 Answers
• Practice Set 1.2 Class 10 Answers
• Practice Set 1.3 Class 10 Answers
• Practice Set 1.4 Class 10 Answers
• Problem Set 1 Class 10 Answers

Maharashtra State Board Class 10 Social Science Book Solutions

Maharashtra State Board Class 10 History Solutions Answers

• Chapter 1 Historiography Development in the West
• Chapter 2 Historiography Indian Tradition
• Chapter 3 Applied History
• Chapter 4 History of Indian Arts
• Chapter 5 Mass Media and History
• Chapter 6 Entertainment and History
• Chapter 7 Sports and History
• Chapter 8 Tourism and History
• Chapter 9 Heritage Management

Maharashtra State Board Class 10 Political Science Solutions Answers

• Chapter 1 Working of the Constitution
• Chapter 2 The Electoral Process
• Chapter 3 Political Parties
• Chapter 4 Social and Political Movements
• Chapter 5 Challenges faced by Indian Democracy

Maharashtra State Board Class 10 Geography Solutions Answers

• Chapter 1 Field Visit
• Chapter 2 Location and Extent
• Chapter 3 Physiography and Drainage
• Chapter 4 Climate
• Chapter 5 Natural Vegetation and Wildlife
• Chapter 6 Population
• Chapter 7 Human Settlements
• Chapter 8 Economy and Occupations
• Chapter 9 Tourism, Transport and Communication

Balbharti Maharashtra State Board Class 10 English Solutions Unit 1.3 On Wings of Courage Notes, Textbook Exercise Important Questions and Answers.

Class 10 English Chapter 1.3 Question Answer Maharashtra Board

On Wings of Courage Poem 10th Std Question Answer

Question 1.
The ranks of officers in Indian Army, Navy and Air Force are jumbled up. Discuss with your group and put them in the appropriate boxes.

Commander, Brigadier, Wing-Commander, Vice-Admiral, Squadron-Leader, Major, Colonel, Field Marshal, Air Marshal, Admiral of Fleet, Lieutenant-General, Flying Officer, Commodore, Rear Admiral, Air-Commodore.

ARMY	NAVY	AIR FORCE

Answer:

Army	Navy	Air Force
Brigadier,	Commander,	Wing-
Major, Colonel,	Vice-Admiral,	Commander,
Field Marshal,	Admiral	Squadron-
Lieutenant-	of Fleet,	Leader, Air
General	Commodore,	Marshal, Flying
	Rear Admiral	Officer, Air-Commodore

Question 2.
Homophones/ Homographs
(A) Make sentences to bring out the difference between-
(1) (a) wear ……………………………………..
(b) ware ……………………………………..
(2) (a) here ……………………………………..
(b) hear ……………………………………..
(3) (a) there ……………………………………..
(b) their ……………………………………..
(4) (a) cell ……………………………………..
(b) sell ……………………………………..
Answer:
(1) (a) wear: The little girl wanted to wear a pink, frilly dress.
(b) ware: The silver ware laid out on the King’s table was exquisite.

(2) (a) here: “You must sit here,” said the man to his guest.
(b) hear: The children could hear the sound of the planes quite clearly.

(3) (a) there: “I had kept my bag there,” said the woman to the policeman.
(b) their: The girls picked up their bags and went home.

(4) (a) cell: The prisoner sat in the dark cell without talking.
(b) sell: The hawker wanted to sell all his wares before evening.

(B) Write what the underlined Homographs in the following sentences mean.
(1) (a) A bear is an omnivorous animal. ……………………………………..
(b) She could not bear the injustice. ……………………………………..
(2) (a) A bat is the only bird which is a mammal. ……………………………………..
(b) His bat broke as it struck the ball. ……………………………………..
(3) (a) He had to pay a fine for breaking the traffic signal. ……………………………………..
(b) Use a fine cloth for the baby’s clothes. ……………………………………..
(4) (a) We enjoyed a lot at the temple fair. ……………………………………..
(b) She has a fair complexion. ……………………………………..
Answer:
(1) (a) A bear is an omnivorous animal.
bear – a large, heavy animal
(b) She could not bear the injustice,
bear – to tolerate

(2) (a) A bat is the only bird which is a mammal.
bat – a mammal that flies
(b) His bat broke as it struck the ball.
bat – a wooden implement used for hitting the ball in many games.

(3) (a) He had to pay a fine for breaking the traffic signal.
fine – penalty
(b) Use a fine cloth for the baby’s clothes,
fine – delicate, soft

(4) (a) We enjoyed a lot at the temple fair.
fair – a gathering of stalls and amusements for public entertainment
(b) She has a fair complexion, fair – light, not dark

Maharashtra Board Class 10 English Kumarbharati Unit 1.3 Questions and Answers

Question 1.
Read the text and fill in the flow chart of the promotions received by Arjan Singh.

Answer:

Question 2.
With the help of facts given in the text prepare a Fact file of Air Marshal Arjan Singh.
(a) Date of Birth
(b) Place of Birth
(c) Education
(d) First Assignments
(e) Important posts held
(a) In Air Force
(b) After retirement
(f) Awards
(g) Most outstanding contribution in IAF
(h) Retirement
Answer:
(a) Date of birth: April 15, 1919
(b) Place of birth: Lyalpur
(c) Education: at Montgomery; Empire Pilot Training Course at RAF (Cranwell)
(d) First Assignment: to fly Westland Wapiti biplanes in the North-Western Frontier Province as a member of the No. 1 RIAF Squadron
(e) Important posts held:
(1) In Air Force: Member of No. 1. RIAF, Flying Officer, Squadron Leader, Wing Commander, Group Captain, Air Commodore, Air Officer Commanding, Air Vice Marshal, Air Officer Commanding-in-Chief, Deputy Chief of Air Staff, Vice Chief of Air Staff, Chief of Air Staff, Air Chief Marshal.
(2) After retirement: Ambassador to Switzerland Lieutenant Governor of Delhi
(f) Awards: Distinguished Flying Cross (1944); Padma Vibhushan
(g) Most outstanding contribution in IAF: Transforming the IAF into one of the most potent air forces globally and the fourth biggest in the world.
(h) Retirement: in August 1969.

Question 3.
Fill in the web.

Answer:
(1) Singh had successfully led a young IAF during the 1965 Indo-Pak war.
(2) Singh played a major role in transforming the IAF into one of the most potent air forces globally and the fourth biggest in the world.
(3) Singh was honoured with the rank of Marshal on the Republic Day in 2002.
(4) Singh’s contribution was most outstanding during the 1965 Indo-Pak war.

Question 4.
Say what actions preceded the following promotions of Arjan Singh in his career in the IAF.
(a) Selected for Empire Pilot training course at RAF
(b) Promoted to Squadron Leader
(c) Leader of a flypast of over 100 aircraft at Red Fort, Delhi
(d) Awarded Padma Vibhushan
(e) First Air Chief Marshal of Indian Air Force
Answer:
(a) The authorities selected Singh for the Empire Pilot training course.
(b) He flew against the tribal forces and moved back to No. 1 Squadron as a Flying Officer to fly the Hawker Hurricane.
(c) On 15th August 1947, Arjan Singh achieved the unique honour of leading a fly-past of over a hundred IAF aircraft over the Red Fort in Delhi.
(d) He was awarded the Padma Vibhushan for his astute leadership of the Air Force and for inspiring the IAF to victory in the 1965 Indo-Pak war.
(e) He was a source of inspiration to all the personnel of the Armed Forces through the years.

Question 5.
Replace the underlined words/phrases with the appropriate ones, to retain the proper meaning.
(be the epitome of, gear up, a brief stint, play a major role, in recognition of, take over reins)
(a) He contributed notably in bringing up the school.
(b) Our school cricket team got ready for the final match against P. Q. R. High School.
(c) After a short period of working as a lecturer, Ravi took up an important post in a multi-national company.
(d) Our class monitor is a perfect symbol of duty and discipline.
(e) Accepting the great value of his research; they awarded him with a Ph.D. (degree)
(f) After the murder of King Duncan, Macbeth took over the control of Scotland.
Answer:
(a) He played a major role in bringing up the school.
(b) Our school cricket team geared up for the final match against P.Q.R.High School.
(c) After a brief stint as a lecturer, Ravi took up an important post in a multinational company.
(d) Our class monitor is the epitome of duty and discipline.
(e) In recognition of his research, they awarded him with a Ph.D. (degree)
(f) After the murder of King Duncan, Macbeth took over the reins of Scotland.

Question 6.
Build the word wall with the words related to ‘Military’.

Answer:

Question 7.
(A) State the different meanings of the following pairs of Homophones and make sentences of your own with each of them.

Word	Meaning	Sentence
(a) led lead(b) role roll(c) air heir(d) feat feet(e) reign rein rain	………………………….. ………………………………………………………… ……………………………………………………… ………………………………………………………. ………………………………………………………. …………………………..	………………………….. ………………………………………………………. ………………………………………………………. ………………………………………………………. ………………………………………………………. …………………………..

Answer:

Word	Meaning	Sentence
(a) led	past participle of lead (to guide or conduct)	The captain led his team to safety.
lead	graphite used as part of a pencil	Do you have a lead pencil?
(b) role	a part (in a play, film, etc.)	Marie got the leading role in the new movie.
roll	move in a particular direction by turning over and over	The boy wanted to roll in the mud while playing.
(c) air	the invisible gaseous substance surrounding the earth	There Is a lot of humidity in the air during the monsoon.
heir	successor or inheritor	The family did not know who the heir to the property was.
(d) feat	a great achievement	Climbing Mt. Everest is a feat.
feet	a unit of measurement	The girl saw to her shock that the lion was only a few feet away.
(e) reign	rule as king or queen	Queen Elizabeth’s reign has been a long one.
rein	a restraining influence	The new manager kept a tight rein on her employees.
rain	water that falls In drops from clouds in the sky	Children love to play in the rain.

(B) The following Homographs have the same spelling and pronunciation but can have different meanings. Make sentences of your own to show the difference.

Answer:
(a) firm: (i) My neighbour recently Joined an electronics firm as Sales Executive.
(ii) Many people feel that they must be firm with their children when they are growing.

(b) train: (i) The train left from platform 2 at seven p.m. sharp.
(ii) You must always train your pets to obey you.

(c) type: (i) The man asked his secretary to type the letter immediately.
(ii) Cows eat only a particular type of grass.

(d) post: (i) My aunt quit her job because she felt that the post was not suitable for her.
(ii) The little boy ran to the post office to post the letter to Santa Claus.

(e) current : (i) The minister was disturbed when he read about the current situation of unrest In the country.
(ii) It is a difficult task to row against the current in a river.

Question 8.
Glance through the text and prepare notes from the information that you get. Take only relevant points. Don’t use sentences. Arrange the points in the same order. You may use symbols or short forms. Present the points sequentially. Use highlighting techniques.
Answer:
Air Force Marshal Arjart Singh—Icon of India’s Military History

1. Date of Birth: 15 April, 1919
2. Qualifications: Empire Pilot Training Course at RAF (Cranwell)
3. Responsibilities:

• first assignment to fly Westland Wapiti biplanes in No.l RIAF Squadron
• brief stint in No.2 RIAF Squadron; moved back to No. 1 RIAF Squadron as Flying Officer
• overall commander of ‘Shiksha’
• led the IAF during the 1965 Indo-Pak war
• led a squadron against the Japanese during the Arakan Campaign; assisted the advance of Allied Forces to Yangoon
• led a fly-past on August 15, 1947
• commanded Ambala in the rank of Group Captain; took over as AOC of an operational command
• took over reins of the IAF
• ambassador to Switzerland; Lieutenant Governor of Delhi

(4) Achievements:

• selected for the Empire Pilot Training Course at RAF (Cranwell) in 1938, at age 19
• promoted to the rank of Squadron Leader in 1944
• led a fly-past over the Red Fort on August 15, 1947
• promoted to the rank of Wing Commander; promoted to the rank of Air Commodore in 1949
• longest tenure as AOC (1949-1952 and 19571961)
• appointed as Deputy Chief of Air Staff at the end of the 1962 war; appointed as Vice Chief of Air Staff in 1963
• rank of Air Marshal in August 1964; took over reins of IAF
• successfully led the IAF in 1965 Indo-Pak war
• promoted as Air Vice Marshal; appointed as AOC-in-C of an operational command
• first Air Chief to keep his flying currency till his CAS rank; has flown more than 60 different types of * aircraft
• first and only Air Chief Marshal of the IAF

(5) Awards:

– Distinguished Flying Cross (1944)
– Padma Vibhushan

(6) After retirement: Ambassador to Switzerland; Lieutenant Governor of Delhi
(Students can put these points attractively in boxes and use highlighting techniques.)

Question 9.
Develop a story suitable to the conclusion/end given below. Suggest a suitable title.
………………………………………………….. (Title)
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………..
………………………………………………………….. and so, with tears of joy and pride, the 10 year old Sanyogita More received the National Bravery Award from the Prime Minister.
Answer:
A WONDERFUL ACT OF BRAVERY
It was the 26th of July in Mumbai. It was raining cats and dogs. Ten-year-old Sanyogita More stood at the door of her hut. The street was flooded with water. Sanyogita was frightened. Her parents had not returned from work and she was all alone.

Suddenly, she saw two little boys, Rohan and Sohan, come out from the neighbouring hut to play in the water. As Sanyogita watched, there came a sudden gush of water and the boys were dragged towards an open manhole, which had been marked with a pole. They caught hold of the pole, but the pole began to tilt. It would soon fall—and the boys would go down the manhole!

Sanyogita ran as fast as she could towards the boys. Pulling a rope from a nearby door, she looped it around a large stone. She held onto the rope and extended her hand towards the boys. “Catch my hand, Sohan, Rohan,” she shouted. “Catch! Catch soon!”

The boys were in a panic but they did as they were told. Sohan held Rohan’s leg, Rohan held Sanyogita’s hand, and Sanyogita held onto the rope.

“Help! Help! she shouted, knowing that if the rope broke or the stone was dislodged, they would all go into the manhole.

She stood there shivering, her arms numb, for nearly 15 minutes before help arrived. Sanyogita collapsed after the incident. The news of her brave deed spread far and wide, and reached the ears of 1 the Prime Minister, who decided to honour her with an award. And so, with tears of joy and pride, the 10- I year-old Sanyogita More received the National Bravery ‘ Award from the Prime Minister.

Question 10.
You wish to join any one of the Indian Armed Forces. Fill in the following application form.
To
The Advertiser
N/AF Recruitment Service
Purangaon – 456 789

Affix recent
passport size
photograph

Application For Recruitment
Rect notice No 1234

1. Post applied for
2. Name and surname of Candidate (in Block letters)
3. Father’s Name ………………………………… Mother’s Name …………………………………
4. Date of Birth
5. Contact details :
Tel. No. (Res) ………………….. . Mobile No.
Email ID ………………….. .
6. Permanent Address :
House No./Street/Village ………………….. .
Post Office ………………….. .
District ………………….. State ………………….. .
Pincode ………………….. .
7. Educational Qualifications :

Serial Number	Qualification	Name of School/College	Name of Board/University	Percentage obtained

8. Whether registered at any employment exchange Yes/ No ………………….. (If yes, mention registration number and the name of the Employment Exchange.)

9. Outstanding achievements in extra-curricular activities/ sports/ games, etc.
………………………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………………………….

10. Why you wish to join Armed Forces. …………………………………………………………………
………………………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………………………….

Read More:

• Where the mind is Without fear Question Answers
• The Thief’s Story Question Answers
• On Wings of Courage Question Answers
• All the World’s a Stage Question Answers
• Joan of Arc Question Answers
• The Alchemy of Nature Question Answers

Balbharti Maharashtra State Board Class 10 History Solutions Chapter 5 Mass Media and History Notes, Textbook Exercise Important Questions and Answers.

Std 10 History Chapter 5 Question Answer Mass Media and History Maharashtra Board

Class 10 History Chapter 5 Mass Media and History Question Answer Maharashtra Board

History Class 10 Chapter 5 Question Answer Maharashtra Board

Mass Media And History Class 10 Question 1.
(A) Choose the correct option from the given options and complete the statement.

(1) The first English newspaper in India was started by ………………………….. .
(a) James Augustus Hickey
(b) John Marshall
(c) Allen Hume
Answer:
(a) James Augustus Hickey

(2) Television is an ………………………….. medium.
(a) visual
(b) audio
(c) audio-visual
Answer:
(c) audio-visual

(B) Identify and write the wrong pair in the following set.
(1) ‘Prabhakar’ – Acharya P.K. Atre
(2) ‘Darpan’ – Balshastri Jambhekar
(3) ‘Deenbandhu’ – Krishnarao Bhalekar
(4) ‘Kesari’ – Bal Gangadhar Tilak
Answer:
(1) Wrong Pair: ‘Prabhakar’ – Acharya P.K. Atre

Mass Media And History Class 10 Question 2.
Write short notes :
(1) The role of newspaper in the Indian struggle for independence
Answer:
Newspapers played an important role in the Indian independence struggle. It is as follows

• Newspapers served as an important medium to create awareness during those times.
• They described greatness of Indian culture and history to gather support of masses for the freedom movement.
• They supported social, political and religious movements and opposed imperialism.
• They discussed various social and political issues.
• The ideas of social reformers and various organisations active in independence struggle reached people through newspapers.

(2) Why do we need mass media?
Answer:
Mass media includes print and electronic and various new media.

• It facilitated free flow of information to all strata of the society and brought the world closer.
• Editorials, various columns and supplements are essential parts of newspapers.
• Readers also get a platform to voice their opinions. In fact, newspapers can help to make democracy stronger.
• Akashrani broadcasted various programmes of the government as well entertainment.
• Awareness creating programmes. It fulfill the need of the government to connect with people.
• Television is an Audio-Visual medium which has made it possible to cross the inherent limitations of newspapers.
• Radio to show the actual visuals of an event to people.
• Mass Media is very important as it plays an important role to strengthen democracy.

(3) Mass Media and professional opportunities.
Answer:
There are many professional opportunities available in printed, electronic and digital media.

• Writers, columnists, editors are required to write articles, columns and editorials in news-papers.
• Newspapers also require reporters to gather news and technicians to work in the press.
• There is requirement of actors and technicians in electronic media.
• Artists are required to present programmes on television, in the same way news presenters, anchors are required.
• If the articles, columns and programmes are based on history, an expert in history is required.

Mass Media And History Class 10 Question Answer Question 3.
Explain the following statements with reasons.
(1) Any information received through mass media needs to be reviewed critically.
Answer:

• Information provided in the media may not represent the exact truth. We need to scan it carefully.
• We have to understand idealistic and investigative motives of newspapers, government policies and prevailing social conditions behiid the newspiece.
• The information received through Mass Media might be prejudiced or give a one-sided idea.
• ‘Stern’, a German weekly magazine, purchased and published a number of so called handwritten diaries of Hitler.
• It then sold them to a number of publication companies.
• However, later it was proved that those diaries were forged. Hence it is essential to verily the information received through Mass Media.

(2) Knowledge of history is essential for newspaper articles.
Answer:

1. In order to unfold the background of an event in the news, we have to resort to history.
2. Some columns are based on historical events. These columns provide historical information about economical, social and political events in the past.
3. Newspapers publish supplements in addition to the regular edition or special issues to mark the completion of 50 or 100 years of an event. On such occasions, one has to review history of that particular event.
4. Even while writing columns like what happened in history on this day it is necessary to know past event. Hence, the knowledge of history is essential for writings of such type.

(3) Television is the most popular medium.
Answer:

• Television being an audio-visual medium brings us into contact with events in an exciting and clarifying way.
• It crossed the inherent limitations of newspapers and radio to show actual visuals.
• It becomes possible for people to watch all the national and international events sitting at home.
• Social problems, discussion on education and economics and political events are viewed by people.
• In 1991, Indian government granted permission to private, national and international channels to telecast in India.
• Television became a treasure house of entertainment.

Therefore, the television is the most popular medium.

Class 10 History Chapter 5 Questions And Answers Ssc Board Question 4.
Read the following extract and answer the questions.
Radio: ‘Indian Broadcasting Company’ (IBC), a private radio company was the first one to broadcast daily programmes. Later the same company was taken over by the British Government and named as, ‘Indian State Broadcasting Service (ISBS). On 8th June 1936 it was renamed, as ‘All India Radio (AIR)’.

After Independence, AIR became an integral part of the Ministry of Information and Broadcasting (India). Initially, it broadcasted Governmental programmes and schemes. It was named as ‘Akashvani’ on the suggestion of the famous poet Pandit Narendra Sharma. Akashvani broadcasts various entertainment, awareness creating and literary programmes. It also broadcasts special programmes for farmers, workers, the youth and women. The ‘Vividh Bharati’ programmes are broadcasted in 24 regional languages as well as 146 dialects of Indian languages. Lately, various new channels like ‘Radio Mirchi’ are providing radio services.

(1) Akashavani (AIR) is an integral part of which ministry?
Answer:

1. Indian Broadcasting Company, a private radio company was taken over by the British Government in 1927 and named ‘Indian State Broadcasting Service (ISBS)’. On 8th June 1936, it was renamed as ‘All India Radio (AIR)’.
2. AIR became integral part of the Ministry of Information and Broadcasting after independence. It was renamed Akashvani on the suggestion of Pandit Narendra Sharma.
3. Initially it used to broadcast Government’s programmes and schemes. Later it started broadcasting various entertainment, awareness creating and literary programmes.
4. Akashvani started ‘Vividh Bharati1 programmes. It broadcasts special programmes for farmers, workers, the youth and women.
5. Vividh Bharati Programmes are broadcast in 24 regional languages and 146 dialects.

(2) What was the new name of IBC?
Answer:
Indian Broadcasting Company (IBC) was taken over by the British Government. It was named as the Indian State Broadcasting Services. (ISBS). On 8th June 1936, it was renamed as ‘All India Radio’ (AIR).

(3) In how many regional languages and local dialects are ‘Vividh Bharati’ programmes broadcasted?
Answer:
People get access to news through social media like Twitter, Instagram, Facebook, YouTube and from web news portals, web channels. This information is available in English and many other languages.

(4) How AIR was named ‘Akashavani’?
Answer:
AIR was named as Akashvani on the suggestion of the famous poet Pandit Narendra Sharma.

Question 5.
Complete the following concept chart.

	Newspapers	Radio	Television
Beginning/Background
Nature of information/programmes
Functions

Answer:

	Newspapers	Radio	Television
Background/Beginning	James Augustus Hickey started Calcutta General Advertiser or Bengal Gazette on 29th January, 1780. It was the first newspaper in English.	A private radio station was started known as Indian Broadcasting Company.	First Doordarshan centre was started in Delhi.
Information Programmes	News, articles, columns, opinions of the people, editorials, advertisements etc. are published.	Along with entertainment programmes, have literary, informative programmes on farmers, women and educative values.	Events around the world, movies, music, information about environmental and historical places, sports are shown either live or recorded.
Functions	(1) Report daily news (2) Public awareness and mass education. (3) Provide information and strengthen democracy. (4) Oppose injustice and give publicity to developmental work.	(1) Provide news from different sectors. (2) Entertain through music, dramas, songs, etc. (3) Present social problems and educate the masses about it. (4) Conduct discussions on various issues ranging from the environment to culture.	(1) Telecast daily events and entertain. (2) Educate the masses. (3) Publicise programmes which are for social benefit. (4) Bring about social awakening opposing evil traditions and practices.

Project
Write a review of a historical serial that you have watched.

Memory Map

Question 6.
Complete the sentences by choosing a correct option:
(a) ………………….. is the first newspaper in Marathi.
(a) Deenbandhu
(b) Prabhakar
(c) Darpan
(d) Kesari
Answer:
(c) Darpan

(b) 6th January is celebrated as ………………….. day in Maharashtra.
(a) Periodical Day
(b) Newspaper Day
(c) Printing Day
(d) Journalist Day
Answer:
(d) Journalist Day

(c) The letters ‘Shatpatre1 published in Prabhakar were written by ………………….. .
(a) Lokmanya Tilak
(b) Lokhitvadi
(c) Mahatma Gandhi
(d) Justice Ranade
Answer:
(b) Lokhitvadi.

(d) The honour of printing illustrations for the first time in an Indian newspaper goes to ………………….. .
(a) Dnyanoday
(b) Darpan
(c) Prabhakar
(d) Kesari
Answer:
(a) Dnyanoday

(e) Deenbandhu was started by ………………….. who was a close associate of Mahatma Phule.
(a) Dr. Babasaheb Ambedkar
(b) Lokmanya Tilak %
(c) Narayan Meghaji Lokhande
(d) Krishnarao Bhalekar
Answer:
(d) Krishnarao Bhalekar

(f) ………………….. newspaper was started by Agarkar and Lokmanya Tilak.
(a) Deenbandhu and Induprakash
(b) Darpan and Prabhakar
(c) Dnyanoday and .Digdarshan
(d) Kesari and Maratha
Answer:
(d) Kesari and Maratha

(g) Balshastri Jambhekar started ………………….. the first monthly magazine in Marathi.
(a) Digdarshan
(b) Prabhakar
(c) Darpan
(d) Dnyanoday
Answer:
(a) Digdarshan

(h) ………………….. was acknowledged as the fourth pillar of democracy.
(a) Representatives
(b) Periodicals
(c) Newspaper
(d) Books
Answer:
(c) Newspaper.

(i) The first English news bulletin was broadcast on 23rd July, 1927 from the …………………… radio station.
(a) Kolkata
(b) Madras
(c) Mumbai
(d) Dblhi
Answer:
(c) Mumbai

(j) Dr. Rajendra Prasad, the first President of India inaugurated the …………………… Doordarshan centre.
(a) Mumbai
(b) Bangalore
(c) Lucknow
(d) Delhi
Answer:
(d) Delhi

(k) Newspapers published special supplements or a special issue to commemorate occasions like completion of seventy-five years of …………………… in 2017.
(a) Khilafat Movement
(b) Non Co-operation Movement
(c) Civil Disobedience Movement
(d) Quit India Movement
Answer:
(d) Quit India Movement

(l) ……………………, a German weekly magazine, had purchased a number of so called handwritten diaries that were later proved forged.
(a) Time Magazine
(b) Statesman
(c) Stern
(d) Reuters
Answer:
(c) Stern

(m) Akashvani has preserved recordings of all speeches delivered by the …………………… on 15th August.
(a) President
(b) Wee President
(c) Prime Minister
(d) Army General
Answer:
(c) Prime Minister

(n) Akashwani comes under the Ministry of …………………… of the Indian Government.
(a) Social welfare
(b) Human Resource and Development
(c) Information and Broadcasting
(d) Education Technology
Answer:
(c) Information and Broadcasting.

Question 7.
Identify the wrong pair in the following and write it:

Newspaper	Editor
(1)  Prabhakar (2)  Darpan (3)  Deenbandhu (4)  Kesari	(a)   Acharya R K. Atre (b)   Balshastri Jambhekar (c)  Krishnarao Bhalekar (d)   Bal Gangadhar Tilak

Answer:
Wrong pair: Prabhakar – Acharya R K. Atre

(2)

Newspaper	Issues
(1)  Prabhakar (2)  Induprakash (3)  Deenbandhu (4)  Kesari	(a)   History of French revolution (b)  Advocated widow re­marriage (c)  Information on Telegraph (d)   Voiced social and political problems.

Answer:
Wrong pair Deenbandhu – Information on Telegraph

(3)

Newspaper/Magazine/Book	Editor
(1) Pragati	(a) Tryambak Shankar Shejwalkar
(2) Digdarshan	(b) Narendra Sharma
(3) Deenbandhu	(c) Krishnarao Bhalekar
(4) Discovery of India	(d) Pandit Nehru

Answer:
Wrong pair: Digdarshan – Narendra Sharma

Question 8.
Do as directed:
(a) Complete the graphical description

Answer:

(2)

Answer:

(b) Show the progress of Indian television Time-line:

Answer:

Question 9.
Explain the following concepts:

(a) Electronic or Digital Journalism or Web Journalism.
Answer:

1. In the modem times, the computer and internet have become indispensable parts of printing and publishing process. Computer technology has led to the widespread practice of digital journalism.
2. Websites run by newspapers are basically extensions of newspapers themselves. Modern periodicals are part of electronic or digital journalism.
3. People get access to news through social media like Twitter, Instagram, Facebook, YouTube and from web news portals, web channels. This information is available in English and many other languages.
4. Journalists working in this area today have to have many more skills than in the past when writing was the only requirement. Information available on these mediums should be reviewed critically and used with utmost care.

(b) E-newspapers
Answer:

1. In recent times, e-newspapers have got prominent place in mass media.
2. E-newspaper is not exactly like the printed one. In e-newspapers, news comes in sequence and not based on the nature and the importance of the news, like in printed newspaper e.g.. Front page news. Headline or Last page news.
3. The news which we want to read has to be clicked and then it appears on the screen in detail.
4. There is space provided for opinion of readers. In 1992, the first edition of the e-newspaper was published by ‘Chicago Tribune1.
5. At present, almost all newspapers are available as e-newspapers and people can read them anytime, anywhere using the Internet or computer, tab, laptop or mobile.
6. In recent times many newspapers have introduced e-newspapers. The e-newspapers are being received well by the readers.
7. Learn to read e-newspapers with the help of your teachers.

Question 10.
Write short notes:
(a) Bengal Gazette:
Answer:

• Bengal Gazette is the first newspaper which was started in India.
• It was started by James Augustus Hickey, an Irish national.
• It was first published on 29th January, .1780. It was also called “Calcutta General Advertiser’.
• Bengal Gazette laid the foundation of newspaper in India.

(b) News printed in ‘Darpan’:
Answer:
The ‘Darpan newspaper started by Balshastri Jambhekar printed all types of news like political, economic, social and cultural. Some of them are mentioned below:

• The Accounts of Expenditure from the Three Administrative Divisions of the East India Company.
• The Danger of Russian Attack on the Nation.
• Appointment of a Committee for Cleanliness of the City.
• Remarriage of Hindu Widows.
• The Inception of Theatre at Calcutta.
• Achievements of Raja Ram Mohan Roy in England. All these reports published in the paper throw light on various situations/events of those days.

(c) Television:
Answer:

• The first President of India, Dr. Rajendra Prasad inaugurated Delhi Doordarshan Centre.
• Mumbai Doordarshan started to telecast its programmes on 2nd October, 1972.
• Colour television started on 15th August, 1982. The Indian government granted permission to private, national and international channels in 1991 to telecast in India.

Question 11.
Explain the following sentences with reason:
(a) Newspaper is an important medium of education and information.
Answer:

• Newspapers report events which are interesting to the public. But the importance of newspaper stretches far beyond a passing humari interest in events.
• It covers a miscellany of topical issues. News would involve matters of higher importance like war, global warming, education, national elections or trivial issues such as scandals, gossips and debates on minor controversies.
• Newspapers have contributed significantly to the spread of literacy and the concept of human rights and democratic freedoms.
• They are integral to the development of democracy. In fact, they can help in making the democracy stronger.
• Newspapers not only report the events but continue to shape opinions in the global village.

(b) 6th January is observed as ‘Patrakar Din’ or ‘Journalist Day’ in Maharashtra.
Answer:

• Balshastri Jambhekar started the first newspaper in Marathi on 6th January, 1832 in Mumbai.
• He is referred to as the ‘First Editor’ as he was the first editor.
• He laid the foundation of Marathi newspaper by starting Darpan. As 6th January is his birth date, it is observed as ‘Patrkar Din’ or ‘Journalists’ Day’ in Maharashtra.

(c) Television and history are closely related.
Answer:

1. Television plays a major role in developing interest in history. While producing shows and serials based on history and mythology, it is essential to have an accurate knowledge of history and know the minute details.
2. ‘Bharat Ek Khoj’, Raja Shivchhatrapati, Ramayana, Mahabharata are among the few popular serials based on history and mythology. While producing these serials.
3. It was essential to know the prevalent social conditions, outfits, lifestyle, weaponry, lingual expressions of the people. Historians who had knowledge on these subjects are required.
4. While making programmes, based on sportsmen, literature, war, historical events, forts and animal life, it is important to give history of their development in that particular period.
5. While conducting discussions on television on topics like social problems, education, economics, health, it is important to give references from the past.

This shows that the knowledge of history is required in the making many of programmes on Television. Hence Television and history are closely related.

Question 12.
Answer the following question in 25-30 words:
(a) Explain the objectives of newspapers.
Answer:
The main objectives of newspapers are as follows:

• Newspapers provide various local, national and international news to the people and inform them about daily events.
• They narrate political, economic, cultural and social history of the country.
• Newspapers fulfill their role as the fourth column of democracy by creating public awareness and becoming a medium of mass education.
• They even condemn the anti-social elements in the society and support the weaker section.

(b) How is history helpful in the planning of the Akashvani programmes ?
Answer:
Akashvani broadcasts all types of programmes from celebration of independence day to entertainment programmes. In planning these programmes, the knowledge of history is essential.

1. Akashvani invites historians as experts for discussions while presenting programmes on various occasions such as the anniversaries of births and deaths of national leaders, anniversaries of historical events; speeches of all Prime Ministers/Presidents.
2. Programmes like ‘On This Day in History’ is a daily programme which highlights importance of that day and date in history.
3. Information has to be verified by historians before it reaches the people. Lectures on the contributions of various national leaders need to be supported by historical information. In the following ways history is helpful in the planning of Akashvani programmes.

(c) How were the message conveyed to the people in olden days?
Answer:
The following were a few means used to convey messages to the people in olden days:

• A town crier would run on the streets beating drums and crying out important news according to the orders of the king.
• So, the news would spread among people by word of mouth.
• Inscriptions with royal decrees were placed at public places.

Question 13.
Read the following passages and answer the questions:”
(a) Which programmes are broadcasted by Akashvani?
Answer:

• Initially, Akashvani broadcasted government programmes and schemes.
• Later it broadcasted various entertainment and literary programmes.
• Akashvani presents various programmes for creating awareness.
• Special programmes are also broadcasted for farmers, workers, youth and women.

(a) On which book is the serial ‘Bharat Ek Khoj’ based on?
Answer:
The Serial Bharat Ek Khoj is based on ‘Discovery of India’, a book written by Pandit Jawaharlal Nehru.

(b) Who directed the serial ‘Bharat Ek Khoj’?
Answer:
The serial was directed by Shyam Benegal.

(c) Which factors/aspects of Indian history are depicted in ‘Bharat Ek Khoj’? OR Why was ‘Bharat Ek Khoj’ a serial telecasted by Doordarshan admired in all parts of India?
Answer:
The television serial ‘Bharat Ek Khoj’ presented social, political and economic life from ancient to the modem period in India.

1. It portrayed various aspects of Indian history like Harappan civilisation, Vedic history and the interpretation of epics like Mahabharata and Ramayana.
2. It used the technique of dramatisation effectively to recreate the Mauryan period and show the impact of Turk-Afghan invasions.
3. The Mughal period and their contributions which have long-lasting effect on social and cultural fabric of India is shown. The rise of Bhakti movement, role of Chhatrapati Shivaji Maharaj in getting swarajya is portrayed.
4. The last episodes (finale) of the serial narrate social movements and India’s freedom struggle in modem period.

Thus, the serial effectively portrayed the journey of India from Harappan civilisation to the modern period and therefore was admired in all parts of India.

Question 14.
Answer the following questions in detail:
(a) What were the different means of communication known around the world before the advent of newspaper?
Answer:
The following means of communication were used to convey news before the advent of newspaper:

1. Inscriptions with royal decrees placed at public places was a custom in Egypt. Emperor Ashoka followed the sam method to reach out to his subjects.
2. In the Roman Empire, roytil decrees were written on papers and those were distribute’d in all regions. It also contained information of various events taking place in the nation and its capital.
3. During, the reign of’ Julius Caesar ‘Acta Diurna’, meaning acts of everyday used to be placed at public places in Rome.
4. In the 7th century C.E., in China, royal dictates were distributed among people at public places.
5. In England handouts were distributed occasionally among people at public places giving information about war or any important events.
6. Travellers arriving from different faraway places would add spice to stories from those places and narrate the same to local people. The ambassadors of a king posted at various places would send back important news to the royal court.

(b) Write information on Periodicals based on its types.
Answer:
Magazines and journals which are published at regular intervals are known as Periodicals.
Types:

• They are categorised as weekly, biweekly, monthly, bimonthly, quarterly, six monthly and annual.
• There are some chronicles which are published at no fixed time.

Classification: Periodicals can be classified as popular and scholarly.

• If a periodical aims at specialists and researchers, it is a ‘journal1. Articles are generally written by experts in the subject.
• Popular periodicals are magazines published with variety of content. They can be on fashion, sports, entertainment and films.
• Bharatiya Itihas ani Sanskruti and Marathwada Itihas Parishad Patrika are periodicals of present times. Periodicals are an important source to study history.

(c) Write about the important role of newspaper in the freedom struggle.
Answer:

1. The press was the chief instrument for carrying out the political tasks and propagation of nationalist ideology.
2. Both English and Vernacular press started by prominent “leaders like Gopal Ganesh Agarkar and Lokmanya Tilak acted as catalyst to the freedom struggle. They started ‘Kesari’ and ‘Maratha’ in 1881.
3. Newspapers played a great role in building up an increasingly strong national sentiment and consciousness among people. It was an instrument to arouse, train, mobilise and consolidate nationalist public opinion.
4. The newspapers were an effective tool in the hands of social reformers. They exposed social evils such as child marriage, ban on remarriage of the widows, inhuman institution as untouchability, caste fetters, etc. It became a weapon in their hands to educate masses.
5. A comparative study was presented in newspaper on western education, knowledge and national education.
6. Newspapers also discussed political institutions in India and the west. The main aim of these newspapers was not to gain profit but to serve the people.

(d) Give a short account of the development of Indian television.
Answer:

1. Television service started in India in 1959. Dr. Rajendra Prasad, the first Indian President, inaugurated the Delhi Doordarshan centre.
2. Mumbai centre began to telecast its programmes on 2nd October 1972. Colour television was introduced in India on 15th August 1982.
3. The national telecast began in 1983. Doordarshan started Channels like DD Sports, DD Metro, news, etc. along with 10 regional channels.
4. In the year 1991, the Indian government gave permission to private, national and international channels to telecast in India.
5. Presently there are more than 800 national and regional channels. Some of them are exclusive news, sports, music, movies and religious channels which telecast programmes 24 hours a day.

(e) Distinguish between Newspapers and Magazines.
Answer:
Newspapers and magazines differ in their format, objectives and duration of getting published. The differences are noted below:

Newspapers	Magazines
1. Newspapers document the current events.	1. Magazines give no importance to current news.
2. News, articles, columns, editorials have importance in a newspaper.	2. Magazines give preferences to particular subject and publish articles on it.
3. Newspapers are also called ‘Dailies’ as they are published every day.	3. Duration of publication of magazine varies. Some are published weekly, fortnightly, monthly and annually.
4.. The main purpose of newspaper is to report local, national and international news.	4. Instead of providing news, their content is entertaining and knowledge-based.
5. Newspapers make the people aware of the events happening in the society. They do not stick to any one subject.	5. Magazines are about a specific topic. On the basis of their appearance, size, readability, content and audience, magazines differ from newspapers.
6. Newspapers mostly write about current news. Whatever happens in the world appears in the newspaper within a span of 24 hours. It shapes public opinion and keep people updated about the activities of the government.	6, As magazines have lot of detailed information on specific topics they are considered as historical source.

Brain Teaser

Across:

• Referred to as the ‘First Editor’.
• A newspaper representing masses of the Indian society (Bahujan Samaj).
• Tryambak Shankar Shejwalkar edited this journal.
• Letters by Lokhitvadi.

Down:

• The history of French Revolution was published in this newspaper.
• Newspaper started by James Augustus Hickey.
• First monthly magzine in Marathi.
• Pandit Narendra Sharma suggested this name for AIR.

10th Std History Questions And Answers:

• Historiography Development in the West Class 10 History Questions And Answers
• Historiography Indian Tradition Class 10 History Questions And Answers
• Applied History Class 10 History Questions And Answers
• History of Indian Arts Class 10 History Questions And Answers
• Mass Media and History Class 10 History Questions And Answers
• Entertainment and History Class 10 History Questions And Answers
• Sports and History Class 10 History Questions And Answers
• Tourism and History Class 10 History Questions And Answers
• Heritage Management Class 10 History Questions And Answers

Class 10 English Chapter 3.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 3.5 The Alchemy of Nature Notes, Textbook Exercise Important Questions and Answers.

The Alchemy of Nature Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.5 The Alchemy of Nature Textbook Questions and Answers

Warming up:
Chit-chat:

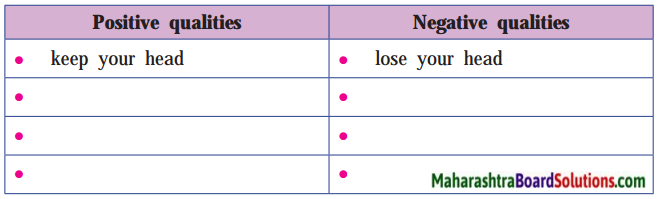
1. Divide the class into five groups. Discuss in the group the following topics. (One question for each group.)

Question (a)
Seeds regenerate from another seed.
Answer:
Regeneration is the renewal of germplasm accessions by sowing seeds which will possess the same characteristics as the original population.

Question (b)
Plants and flowers wilt and become one with the other.
Answer:
Wilting is the loss of rigidity of non- woody parts of plants if they do not get water to thrive and soil is too dry.

Question (c)
Cacti (-Pidgd ) thrive in the desert region.
Answer:
Cacti (plural of cactus) lack leaves, instead they have spines which help preventing the loss of water and mineral content in the desert plants.

Question (d)
Bare nature turns green in spring.
Answer:
As temperatures warm and days get longer, forest ecosystem begins the transition from winter to spring.

Question (e)
Caterpillar turns into butterfly.
Answer:
It is truly a fantastic mechanism developed by nature. For a caterpillar to turn into a butterfly, it digests itself using enzymes triggered by hormones.
(Each group will present their discussion in front of the class.)

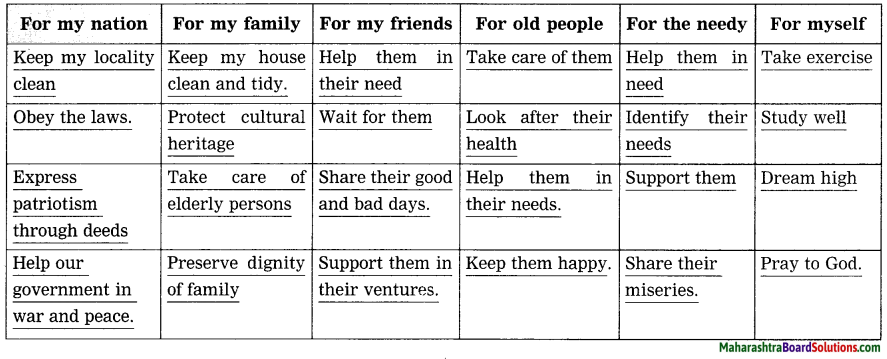
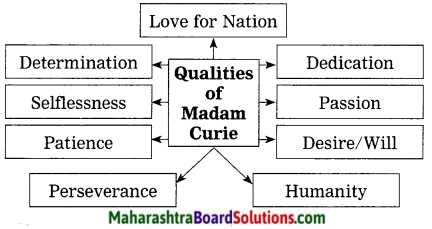
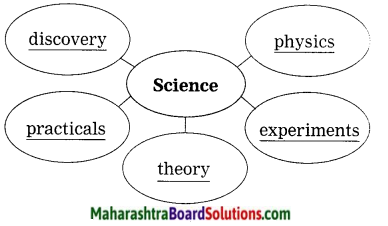
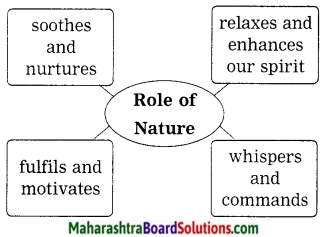
2. Role of Nature:

Question 1.
Role of Nature:
Discuss in pairs, the role played by nature and complete the web-diagram.

Answer:

3. Look at the following things. Discuss with your friend, what you learn from them.

Question 1.
Look at the following things. Discuss with your friend, what you learn from them.
(a) A bee …………………..
(b) An eagle ……………….
(c) A creeper ……………..
(d) The river ………………
(e) Rainfall ………………..
(f) Sun ………………………
Answer:
(a) A bee – teamwork and hard work
(b) An eagle – a strong vision/far-sightedness
(c) A creeper – perseverance
(d) The river – go with the flow/to face calamities
(e) Rainfall – dedication
(f) Sunlight up the lives of others/to give light and energy to others.

English Workshop:

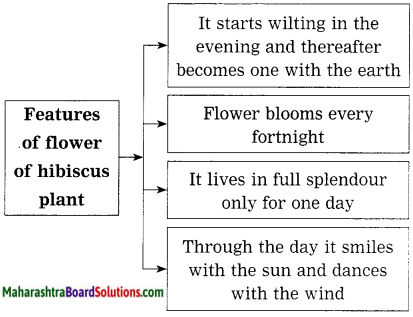
1. Go through the text again and complete the web that highlights the various features of flower of ‘hibiscus’ plant. One is done for you.

Question 1.
Go through the text again and complete the web that highlights the various features of flower of ‘hibiscus’ plant. One is done for you.

Answer:

2. The writer explains the contrast features of ‘water’ and ‘rock’ in the text. Write all the features of both water and rock in the given table:

Question 1.
The writer explains the contrast features of ‘water’ and ‘rock’ in the text. Write all the features of both water and rock in the given table:

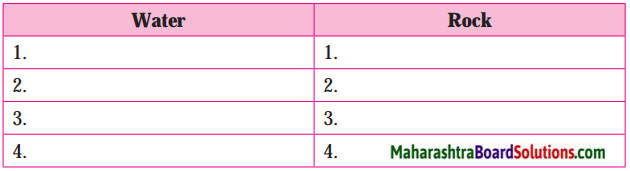
Answer:

Water	Rock
gentle	hard
command	gives in (humble)
flows over stone (perseverance)	takes the shape that water commands (obedient)

3. Impossible itself says ‘I M possible’. Do you agree? Justify your answer by citing some examples from the text and some that you have experienced or heard from someone.

Question 1.
Impossible itself says ‘I M possible’. Do you agree? Justify your answer by citing some examples from the text and some that you have experienced or heard from someone.
Answer:
Yes I agree, it is possible to do the most difficult of things, provided we have the will and conviction to do so. We can clearly know this from the passage. The bits of grass, the tree in the winter and the tiny ants, etc. are the examples from the passage.

The example that comes to my mind as justification is that of Sudha Chandran, the dancer. Though her leg was amputated below the knee, with great grit and determination, she restarted dancing and went on to become a famous dancer and actress. This shows that one can do things which seem to be impossible.

4. Find synonyms from the text for the following words/phrases.

Question 1.
Find synonyms from the text for the following words/phrases.
Answer:

1. a strong feeling of fear or respect – awe
2. to direct authoritatively – command
3. to peer through – peep
4. large and impressively beautiful – majestic
5. easily broken or damaged – delicate

5. How can you prove this maxim to be incorrect-’Too many cooks spoil the broth.’ Write a counterview on the given topic. (clue-teamwork)

Question 1.
How can you prove this maxim to be incorrect-’Too many cooks spoil the broth.’ Write a counterview on the given topic. (clue-teamwork)
Answer:
The maxim says when there are too many people involved in trying to do the same thing, the final result will not be good. But I believe that the teamwork is always good. We all know that unity is strength and it is of great value in every walk of life. If we come together and work, definitely our strength gets increased.

When there are a lot of people working on a project, then that project may not be completed to such a high standard because an individual can work better than many. It is the common perception of the people. But I think if a lot of people are working on a project, every one will use his talent, calibre, strength to take that project to higher level. So it will be completed on time with good standard.

Even when many cooks come together and try to make a single dish with their experience in different fields, it will become fantabulous. One dish will be prepared in variety of taste, colour and with varieties of combination. So it never gets spoiled. So I think the maxim too many cooks spoil the broth, is totally wrong in fact it adds flavour to that dish.

6. Make a list of all the words related to the word Ocean:

Question 1.
Make a list of all the words related to the word Ocean:
Answer:
Fishers, fish, salty, saline water, species, different water, high tide, low tide, pacific, gulf, bay, ships, pirates, piracy, warships, cruisers, oceanic currents.

7. The author has very positively described the different things in nature. Add the special features of each one of them:

Question 1.
The author has very positively described the different things in nature. Add the special features of each one of them. Add on the list.

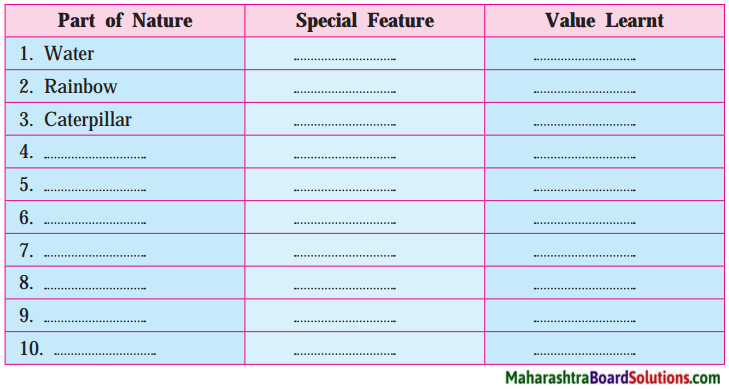
Answer:

Part of Nature	Special feature	Value learnt
1. Water	It gently flows every day and for years.	Keep on working gently for the well-being of the people.
2. Rainbow	Beauty	Add colours to the surroundings, make all happy.
3. Caterpillar	Sacrifice for creating new life.	Changing (turning) for better results.
4. Hibiscus	one day life.	We should live our life to its fullest.
5. Rocks	Though hard, it does not dominate or offer resistance.	Be humble and stay still and endure unpleasant things without complaining.
6. Grass	Evergreen	There is always an opening even when the things seem to be impossible.
7. Tree	Stands firmly in cold winter.	Wait resolutely in difficult times.
8. Ants	Organized	Teamwork and perseverance are always rewarded.
9. The wind	Flow	Make people happy with your activities and passion.
10. Spider webs	Delicate	Be strong in every situation and difficulty.

8. Your friend has his board exam. He studies for 14 hours a day, sitting at one place. Write a letter to him giving him tips to relax and be stress-free.

Question 1.
Your friend has his board exam. He studies for 14 hours a day, sitting at one place. Write a letter to him giving him tips to relax and be stress free.
Answer:
Vikas Shinde
16, Malhar Sankul,
Hadapsar,
Pune,
12th Jan., 2021.

Dear Mahesh,

I received a call from aunty telling about your preparations for forthcoming board examinations. I am shocked to hear that you study for 14 to 15 hours a day sitting at one place. I don’t understand how do you bear it?

You might have heard about “All work and no play makes Jack a dull boy.” It means without time off from work a person becomes both bored and dull. I know the board’s exams are around the corner, but if you work as usual with your tension, anxiety and pressure, it is going to be harmful to your health. Our body is not a machine. It needs some rest. It’s my advice to you to take some rest after certain l intervals. Watch T.V. for sometime, listen to music to refresh your mind, chat with your family members and friends, play with your friends. It will refresh your mind.

Take a break after 2-3 hours and give essential time to your mind and body. It will be good for you. I know you are a scholar and always get good marks in exam. But it doesn’t mean that you should ignore your health. Health is wealth. So concentrate on it, too. Hope you will try to understand what I mean to say and follow my tips rigorously.

Convey my regards to uncle and aunt and love to little Riya. Be in touch on mobile.

Your loving friend,
Vikas

9. You have an Environment Protection Week to be celebrated in your school. You have invited an environmentalist. You have to interview him/her about how to save environment. Frame about 10-12 questions for the interview.

Question 1.
You have an Environment Protection Week to be celebrated in your school. You have invited an environmentalist. You have to interview him/her about how to save environment. Frame about 10-12 questions for the interview.
Answer:
Good morning Sir/Madam. Happy to see you here in our school. I welcome you on behalf of our school.

1. Will you please tell us about your work in this field?
2. Were you really interested in this field from the beginning?
3. As an environmentalist, when did you start your work? What exactly do you do?
4. What do you think about diminishing percentage of trees and forest?
5. What is your ‘end of the world prediction’, If we don’t keep global temperature below 1.5°C?
6. What do you think the Government should do?
7. What will you tell the people who do not believe in widely discussed climate change?
8. Being a citizen of our country, what do you expect from every citizen about this intense problem?
9. If there’s one thing that everyone could do today to help protect the environment, what would that be?
10. What advice would you give to young generation at this moment?

10. Write a news report on ‘Environment Day’ celebrated in your school.

Question 1.
Write a news report on ‘Environment Day’ celebrated in your school.
Answer:
Environment Day Celebrations

Nagpur, June 7: ‘World Environment Day’ was celebrated in New Era School with great funfare on June 5. The main purpose of the celebration was to spread awareness among people and students about the need to protect the environment and the ways to do it.

The day was flagged off by a tree plantation drive in the locality. 300 quick-growing trees, which do not need much water on a daily basis, were planted near the school compound wall and in the surrounding area. An eminent environmentalist, Mr. A. T. Ali, spoke on the ways to protect the environment. He also judged the ‘Posters and Photographs’ exhibition organized by the school students and gave away prizes for the best entries.

Environment-friendly articles, like disposable plates and cups made from bamboo and banana stem, bags made from leaf wastes, etc. were on sale. Students gave continuous power-point presentations on the threats to the environment. Last but not the least, was the spirited debate on the topic. ‘Man: The worst enemy of the Environment’.

All in all, the day was a great success, and has certainly made a difference to the way people view our environment.

11. Develop a story with the given ending. Give a suitable title and moral.

Question 1.
Develop a story with the given ending. Give a suitable title and moral.
……………….. and so, Aditi decided to plant more trees.
Answer:
Save trees, save earth

It was the world earth day celebration in Aditi’s school. Aditi was attending it with a least interest as she was not interested in listening to such a boring subject from anybody. She was sitting forcefully for the guest’s lecture with her friends.

The chief guest, who was a renowned environmentalist started with a good slogan based on the earth and emphasised that the earth is the only known planet in this universe where we get all the necessary requisites of life, but the healthy survival is possible for years and years only when we take care and love our earth. Aditi suddenly became curious and started listening with apt attention.

He continued saying “because of the advancement in the life style, industrialization and deforestation; the condition of the earth is deteriorating day by day. It is being full of pollution, global warming and greenhouse gases. There is an urgent need to save our earth because it is the planet where we live. We need to do nothing more in order to maintain the greenery of the earth.

We just need to plant more trees, grow them well, to reduce the pollution level, to maintain the temperature level and to save our mother planet. We should understand our responsibility towards our mother earth and the future of the next generations. As they would not survive on this earth if there will not be a clean and natural climate.”

Aditi realised it and thought a lot and decided to take a positive step very seriously to save the earth. She thought seriously over the solution and that was planting more and more trees. She decided to create awareness among the people as well. She told everyone…

Save earth; save life
No earth… No life
No earth, No birth
Plant trees, Save mother earth

She understood that there will be no human beings on this earth if there will be no trees. If we have to save our lives, we have to plant more and more trees. So, Aditi decided to plant many trees after listening to that effective lecture of the chief, guest.

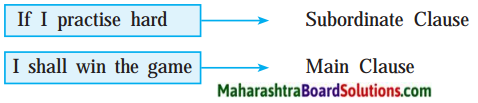
12. Just for laughs!

Question 1.
Divide the class into two groups : On 12 to 15 slips of paper, Group A writes 12 to 15 conditional clauses beginning with ‘if’.
(For example: If I work hard, I shall have a pizza. (Group B write 12 to 15 main clauses)
Now one student from Group ‘A’ reads the first conditional clause (possibility) and one student from Group ‘B’ reads the first main clause. It forms crazy sentences, just for laughter and fun. Enjoy.
Answer:

Group ‘A’	Group ‘B’
1. If I read a book,	my mother will shout at me.
2. If I do not study hard,	I will become the chief minister.
3. If you do not come to school,	teacher will come to your home.
4. If she gets a new mobile	she will run away from her home.
5. If the boys get freedom in the class,	they will keep silence in the class.

Language Study

Question 1.
Match the pairs of antonyms:

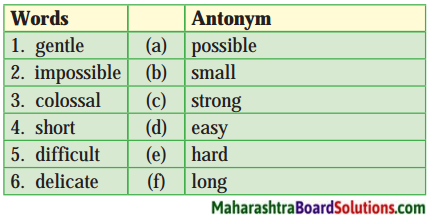
Answer:

1. gentle × hard
2. impossible × possible
3. colossal × small
4. short × long
5. difficult × easy
6. delicate × strong

Question 2.
Complete the table:

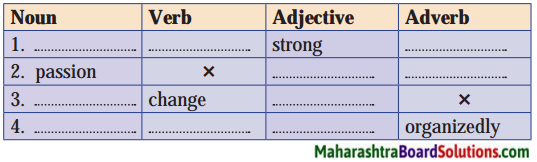
Answer:

Noun	Verb	Adjectives	Adverb
strongness, strength	strengthen	strong	strongly
passion	×	passionate	passionately
change	change	changeable	×
organization	organize	organizational	organizationally

Live English

Be a Netizen

Question (a)
Read the extract and underline the words which suggest that emails are fast, cheap and an easy communication tool.
Answer:
Email stands for electronic mail. Slowly and gradually email has replaced the old postal mails or snail mails. Having an email address is like having a postal address in a global village of internet. If you do not have one, you do not exist in today’s virtual world.

The reasons for popularity of emails are many. Emails can be achieved, saved, retrieved. Email is eco-friendly as people rarely take printouts of the mails. The main reason is its ease of access as anybody can access it on phone at the cost of cheap internet, anytime, anywhere.

Email writing is easy but it’s different from writing text messages. Text message is informal and rapid sharing of thoughts between two acquaintances. Emails are written and read by professionals, however, both arrive in inbox.

Like a citizen has his own home address, let’s sign up for the email and be a netizen. There are many free email service providers like Google, Yahoo, Outlook, Rediff, icloud, etc.

Question (b)
Follow these five simple steps to write an effective email. Click Compose to start writing email.
Answer:
Steps for Writing a Formal E-Mail:
1. Begin with a greeting.
Example: ‘Dear Sunil”, “Dear Sir/Madam”
2. Thank the recipient.
If you are replying, say Thank you for contacting”, If you got a reply, say Thank you for your prompt reply”
3. State your purpose.
For new email, begin by saying “I am writing in reference to..”
4. Add your closing remarks.
Example: Thank You for…”, I look forward to hearing from you.”
5. End with a closing.
Example: “Best Regards, Sincerely, Thanks and Regards etc.,”

Steps for sending an email:

Question 1.
Steps for sending an email:
1. Write proper mail ID in ‘To’
2. Use a short and accurate ‘subject’ line.
3. Click ‘Send’ button to send the email.
Answer:
1. Log in to your gmail account so that you are on the dashboard (main page) of your mail account.
2. Click ‘Compose’.
3. A new blank email window will open up in the
‘To’ box, type in the email address of the recipient.
4. Write the ‘Subject’.
5. Type your message in the main body field of your email.
6. Click the ‘Send’ button at the bottom of the composed window.
7. You will receive a message i.e. ‘Sent mail’.

Question (c)
Read the following sample email formats and prepare your own.
Sample Email formats
Answer:

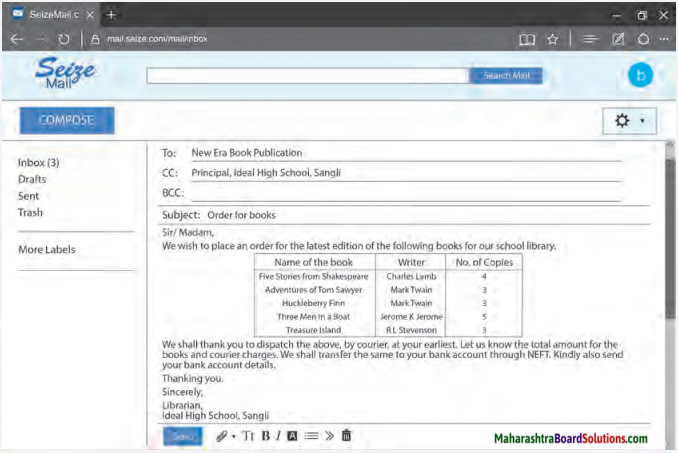
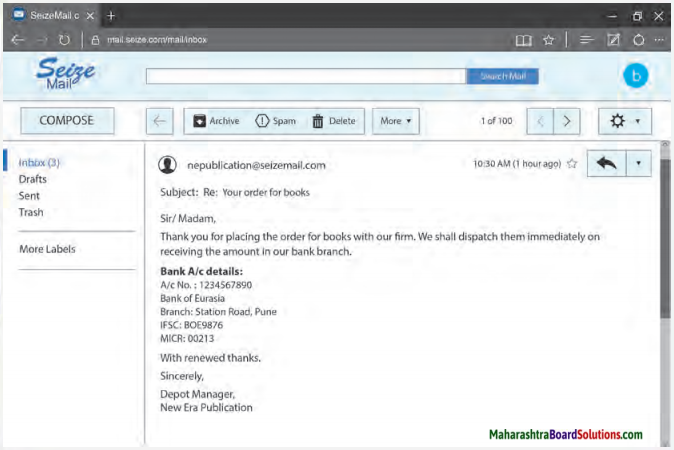
My English Coursebook 10th Digest Chapter 3.5 The Alchemy of Nature Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
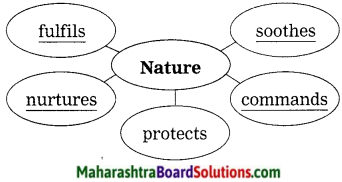
Complete the following web: (Answers are directly given.)
Answer:

Question 2.
State whether the following are True or False:
Answer:

1. On the rocky beach the writer found rocks curved and sculpted by the water – True
2. When we listen to the Nature, it leaves us in complete awe. – True
3. We should not live our life to its fullest. – False
4. The water was shaped by the rocks. – False

Question 3.
Choose the correct alternatives and complete the following sentences :
(Answers are directly given and underlined.)
Answer:
1. In the cold winter month, the tree was bare of all leaves.
(a) full
(b) withdrew
(c) bare
(d) short

2. We find innumerable stars in the infinite sky.
(a) clouds
(b) crowds
(c) stars
(d) moons.

3. There is always an opening even in impossible things.
(a) opening
(b) closing
(c) enjoying
(d) singing

4. Water without hint of ego, changes its form according to the dictates of the sun and the wind.
(a) the earth
(b) the sun
(c) the moon
(d) the horizon.

Question 4.
State who/what:
Answer:

1. Colours the entire sky. – Rainbow
2. Takes new shapes with every passing moment, – Clouds
3. Makes trees dance. – The wind
4. Changes its form according to the dictates of the sun and the wind. – Water

Question 5.
State whether you Agree or Disagree with the following statements:
Answer:

1. ‘There is always an opening even in impossible things’-we learn it from small bits of grass. – Agree
2. Our difficult time never changes. – Disagree
3. The team work and perseverance of the ants were impressive. – Agree
4. Clouds take new shapes with every passing moment. – Agree

Complex Factual Activities:

Question 1.
Complete the following sentences: (Answer is directly given.)
Answer:

1. Hibiscus flower smiles with the sun and dances with the wind.
2. ‘However short our life is, we should live to its fullest’ is the lesson we learn from the hibiscus plant.
3. The rock on the beach was curved, sculpted and shaped.
4. The poet William Blake tells us to hold infinity in the palm of our hand and eternity in an hour.

Question 2.
Complete the following web: (Answers are directly given.)
Answer:

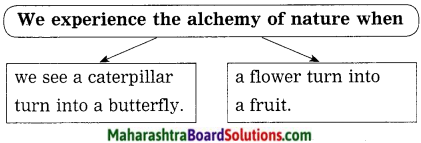
Question 3.
Who teaches us that hard times do not 1 last forever? How?
Answer:
Bits of grass peeping through small cracks in concrete pavement and the green leaves on a tree in spring teach us that hard times do not last forever.

The grass is destroyed by the concrete but comes to life again. The tree is bare all through the cold winter months, but when the spring sets in, it is full of leaves, regaining its green majesty.

Question 4.
What are the alchemies of nature mentioned in the extract?
Answer:
The alchemies of nature mentioned in the extract are-

1. Grass peeps through small cracks of a concrete pavement.
2. A rainbow colours the entire sky.
3. Oysters take in a grain of sand they open up with a pearl.
4. Innumerable stars shine across the infinite sky.
5. The wind makes trees dance with unhindered passion.
6. A caterpillar turns into a butterfly.

Activities based on Vocabulary:

Question 1.
Match the pairs of antonyms.
Answer:
1. remember × forget
2. persist × quit

Question 2.
Find out synonyms from the text for the following words/phrases:
Answer:
1. mysterious power – alchemy
2. drag with great efforts – lugging

Question 3.
Frame meaningful sentences by using the given words:
1. impressive
2. passion
Answer:
1.The show put up by the street children was really impressive.
2. One could see the passion and emotion in the artist’s work.

Question 4.
Find from the passage the antonyms of:
Answer:

1. weak × strong
2. easy × difficult
3. hot × cold
4. unimpressive × impressive

Activities based on Contextual Grammar:

1. Frame Wh-questions to get the underlined parts as answers:

Question 1.
The flower comes to life only for a day.
Answer:
How long does the flower come to life?

Question 2.
We saw the spread of the majestic ocean.
Answer:
What did we see of the majestic ocean?

Use ‘not only……….but also’.

Question 1.
Outdoor activities enhance and relax our well-being.
Answer:
Outdoor activities not only enhance but also relax our well-being.

Question 2.
Nature whispers and commands.
Answer:
Nature not only whispers but also commands.

Personal Response:

Question 1.
Explain the line ‘Nature whispers and commands.
Answer:
Nature is continually enticing us to spend time in her embrace; through the calling of birds, the babbling of brooks and streams, the fragrance of flowers and the whispers of trees as the wind blows through their branches. It commands us not to go against it otherwise it will curse us.

Question 2.
The rock is hard but is it dominating? Give reason for your answer.
Answer:
Even though the rock is hard, it is not dominating. I think water is stronger than rocks. It wears down the hard rock by its gentle patience, persistence and perseverance. Rock takes the shape that water commands. It shows that it is not dominating like water whereas it is ready to accept any change.

Question 3.
How can learning from nature help human beings?
Answer:

1. Limitless sky with trillions of galaxies reminds us how insignificant we humans are in this vast universe.
2. Water always flows from high to low in the same way knowledge should be transferred from the learned to ignorant.
3. Trees provide shade selflessly to everyone, we should be selfless in our life too.
4. Nature does not hurry; yet everything is accomplished.
5. Trees stand deeply rooted in the ground even though seasons change. We should face any difficulty in our life with patience.

Question 4.
‘Nature is our best teacher’ – Explain.
OR
According to the writer we learn many things from the nature. Do you agree with this sentence? Support your answer.
Answer:
Nature is a great teacher. No wonder our ancestors used to look up to nature to understand about life itself. The things like the sun, moon, trees, rivers, etc. all were treated as divine beings. We learn a lot from them and they teach us a lot about how to live happy life. Divinity exists in all aspects of life. When we are aware of ourselves, we become aware of God in everything big or small. We then learn to live life well and become complete. So Nature is always treated as our best teacher.

Do as directed:

Question 1.
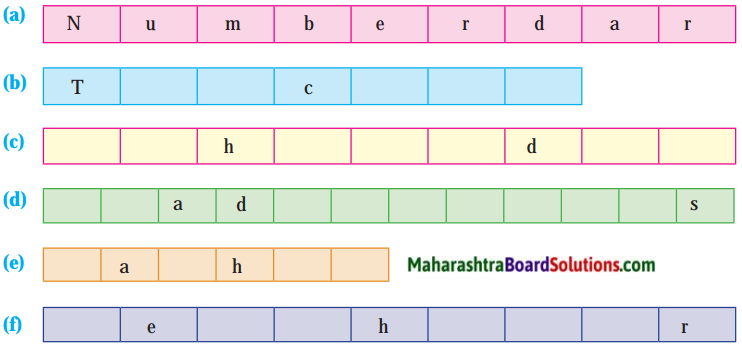
Complete the words by using correct letters:

1. d a _ c e
2. s h _ p e
3. f r u _ t
4. b i _ d s

Answer:

1. d a n c e
2. s h a p e
3. f r u i t
4. b i r d s

Question 2.
Put the words in alphabetical order:
1. splendour, colossal, alchemy, frail
2. consistent, caterpillar, command, complete.
Answer:
1. alchemy, colossal, frail, splendour.
2. caterpillar, command, complete, consistent

Question 3.
Punctuate the following sentences :
1. I asked my teachers why is he working outside
2. he asked me is the world so poor that it cannot give me a toy and a book, instead of forcing me to take a gun or a tool
Answer:
1. I asked my teachers, “Why is he working outside?”
2. He asked me, “Is the world so poor that it cannot give me a toy and a book, instead of forcing me to take a gun or a tool?”

Question 4.
Make four words each (minimum 3 letters) using the letters in the given word: “perseverance”
Answer:

1. reserve
2. presence
3. peer
4. seven

Question 5.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Question 6.
Complete the word-chain of ‘Nouns’. Add four words, each beginning with the last letter of ‘ the previous word:
Pavement, → t……….., ……….., ……….., ………..
Answer:
Pavement, → treasure, editor, roughness, sheep.

1. Attempt anyone:

Question (a)
Make a meaningful sentence by using the phrase: ‘in full splendour’
Answer:
The morning sun appeared in the sky, in its full splendour.

OR

Question (b)
Add a clause to expand the following sentence meaningfully: we saw a small tree …………….
Answer:
We saw a small tree which was full of flowers and fruits.

2. Attempt anyone:

Question (a)
Add prefix or suffix to make new words.
1. continue
2. pleasant
Answer:
1. discontinue, continuous
2. unpleasant, pleasantly

OR

Question (b)
Make a meaningful sentence using any one of the following words:
1. continue
2. pleasant
Answer:
1. This exhibition will continue till the end of this month.
2. The pleasant atmosphere in the morning attracts many birds.

Question 3.
Do as directed:
We saw an army of ants. (Choose the correct sentence of passive voice.)
(a) An army of ants was seen by us.
(b) An army of ants were seen by us
(c) An army of ants is seen by us.
(d) An army of ants are seen by us.
Answer:
(a) An army of ants was seen by us.

Question 4.
We touch it. (Rewrite the sentence in ‘Past Perfect Tense.)
Answer:
We had touched it.

Question 5.
Identify the tenses:
Answer:

1. We saw an army of ants – Simple Past Tense
2. We experience the alchemy of nature – Simple Present Tense
3. It will not remain so for ever – Simple Future Tense
4. Ants were lugging a fly. – Past Continuous Tense

My English Coursebook Standard Ten Digest Answers Pdf Unit 3

• If … Class 10 English Solutions
• A Lesson in Life from a Beggar Class 10 English Solutions
• Stopping by Woods on a Snowy Evening Class 10 English Solutions
• Let us March! Class 10 English Solutions
• The Alchemy of Nature Class 10 English Solutions

Class 10 English Chapter 1.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 1.4 Be SMART Notes, Textbook Exercise Important Questions and Answers.

Be SMART Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 1.4 Be SMART Textbook Questions and Answers

Warming up!

Chit-chat:

1. Planning your career is not an easy task. But we can reduce the distress by making a proper choice. If we do, what we love to do, the journey becomes smooth and leads to success.
The following diagram shows important factors to be considered while choosing a career. Discuss in your group, which factors you regard as important ones.

2. An Acroslic is a form of writing where the first letters in each of the lines form another word.
For example FRIEND

Prepare on your own such acrostics for-

• Your dearest family member
• Name of your best friend
• A quality or feeling
• Any profession

Question 1.
Prepare your own such acrostics for:
Your favourite family member.
Name of your best friend.
A quality or feeling.
Any profession.
Answer:
1. Best friend: TEJAL
True
Efficient
Jolly
Ambitious
Loving

2. Quality: Smart
Sober
Mannerly
Active
Radiant
Talented

3. Say whether the underlined words in the following sentences are used as a Noun or Verb or Adjective.

Question 1.
(a) I walk to school everyday. (………….)
(b) I go for a walk everyday. (………….)
(c) They gave me a gift everyday. (………….)
(d) You can gift her a story book. (………….)
(e) It was sold as a gift pack. (………….)
(f) They bought a new house on 10th street. (………….)
(g) The water – tanks leak a lot. (………….)
(h) The old-age home houses loo aging and homeless people. (………….)
Answer:
(a) I walk to school everyday. – Verb
(b) I go for a walk everyday – Noun
(e) They gave me a gift everyday – Noun
(d) You can gift her a story book – Verb
(e) It was sold as a gift pack – Adjective
(f) They bought a new house on 10th street – Noun
(g) The water-tanks leak a lot – Verb
(h) The old-age home houses 100 aging and homeless people. – Verb

English Workshop:

1. Complete the following web with the words associated with the passage and the given title :

Question 1.
Complete the following web with the words associated with the passage and the given title

Answer:

2. (A) Pick out examples from the text that support each of the following facts :

Question a.
Goals should be achievable.
Answer:
Example: We can’t become a President, a Prime Minister, but we can hope to hold the office of an important social worker and deliver results.

Question b.
A time-limit should be set to achieve goals.
Answer:
Example: To reduce weight we know how to go about it. But without consistent time-bound action, it never becomes a reality. It may be exercise, diet and stress-free thoughts. All these have to be practised and implemented within a deadline.

Question c.
A specific field/area has to be fixed to achieve goals.
Answer:
Example: If it is building a house, what exactly is the capacity required and how long can it stretch?

Question d.
Good results depend upon the quality and quantity of work put in.
Answer:
Example: Life is like a trumpet. If we don’t put anything in, we can’t get anything out.

Question e.
A benchmark is needed to track progress.
Answer:
Example: While playing football, a player’s exact role and position has to be clearly defined.

3. Complete the following sentences.

Question 1.
Complete the following sentences
(a) SMART goals are …………….
(b) Two valuable assets of setting goals are …………
Answer:
(a) SMART goals are a methodology of thinking I that helps people reach success.
(b) Two valuable assets of setting goals are-a ! sense of originality and a stepping stone to illuminate the path.

4. Read this quote.
‘If we don’t put anything in, we can’t get anything out.’ Guess the meaning. Discuss in pairs and find similar quotes that bring in the same meaning.
Question 1.
‘If we don’t put anything in, we can’t get anything out.’ Guess the meaning. Discuss in pairs and find similar quotes that bring in the same meaning.
(a) You reap as you sow
(b) Input is equal to output
(c) …………………………….
(d) …………………………….
(e) …………………………….
Answer:
(a) As you sow, so shall you reap.
(b) Input is equal to output.
(c) No pains, no gains.
(d) Nothing ventures, nothing have.
(e) The longer you work, the more you get.
(f) Well begun is half done.

5. Drafting a Speech. Discuss in groups each block and make notes about it.

Question 1.
Drafting a Speech. Discuss in groups each block and make notes about it.

Answer:
Do it yourself.

6. Speech development
(A) Content
(a) Greeting and introduction of the topic
(b) Exposition of main theme/clarity of message/organised thoughts and ideas.
(c) Moral and practical application with examples.
(d) Conclusion

(B) Speaking Presentation
(a) Verbal clarity – pronunciation of words, voice modulation and projection.
(b) Presentation/Speaking style – mannerism, audience eye contact, ability to keep the audience engaged.
(c) Confidence – gestures and expressions, stage courage

(C) Useful phrases and vocabulary
(a) It’s pleasure to see you all/I am happy to see you today/It’s good to see you all here.
(b) Today’s topic is ………../My talk is about………….. My topic is …………….
(c) The purpose/aim of this speech. …………
(d) I will focus on one/two/three major issues.
(e) If you have any question, feel free to ask me.
Answer:
Do it yourself.

7. Dos and Don’ts for delivering a speech. Add some more points.

Answer:

Dos	Don’ts
Talk slowly	Don’t mumble
Emphasize keywords	Don’t look up /down
Be confident	Don’t use too many hand gestures
Maintain a good posture	Don’t keep your speech too lengthy
Make eye contact with the entire audience	Don’t repeat the same words multiple times

8. You are going to participate in interschool elocution competition. The subject given to you is “How to achieve success in life.” Draft a speech to present it, in a competition.

Question 1.
You are going to participate in interschool elocution competition. The subject given to you is “How to achieve success in life.” Draft a speech to present it, in a competition.

Answer:
How to achieve success in life?
Honourable chairperson, respected headmaster, teachers and my dear friends. Today I am going to give my speech on “How to achieve success in life.” I request you to listen to me carefully. So my friends, success is very important in everyone’s life.

Everyone has a dream of becoming a successful human being in life. There is a good saying that, “Success is a journey and not a destination.” How true it is! If we look at the life of all successful people, we realize the truthfulness of the statement. The definition of success is different for every person. For a child, success is to solve a puzzle, for a S.S.C. student, success is to get good marks, for a businessman, success is to get a contract and for grandparents, success is to see the whole family live happily together.

Everyone wants to become rich and successful in life. To achieve ambition, there are many steps which are to be followed. First of all, we have to set our goal, means we have to decide what we are and what we want to be. So proper plan and execution of the plan are very important. The tragedy of life does not lie in not reaching the goal, the tragedy lies in having no goal to reach.

For a great success we need a lot of confidence, patience, knowledge, perseverance and hard work. We should not waste our time because time is money. Don’t compare yourself with any other person in the world. If you do so you are demeaning yourself. The main thing is that we should always think positively and never give up hope. Many of our failures are the people who did not realize how close they were to success when they gave up.

Always remember that the word “Impossible” means, I’m possible and if destiny is accompanied with the three D’s : determination, dedication and devotion, then everything becomes possible. We should learn from our own mistakes. We should always follow in the footsteps of great, successful people. Let’s take an example of Dhirubhai Ambani.

He was born in a poor family, but struggled a lot to achieve his ambition and never gave up hope because he knew that there is always a room at the top. He kept the hope alive in his heart and tried his level best and as you know he became one of the richest industrialists in the world. After all, no gains, without pains.

There is a great saying that successful people do not do different things, they do the things differently. So work hard, continuously. God’s blessings are always there with you. Thank you for listening to me carefully.
Jai Hind.

9. Project Work :
Your goal, this year, is to successfully pass out from secondary school. So let us be SMART and note down the following.
(a) Specific Area :
(Subjects) and number of units/lessons
1. English 4 units
2. ………………..
3. ………………..
4. ………………..
5. ………………..
6. ………………..

(b) Measurable :
Comparison of scores in previous examinations and in recent one.

(c) Achievable goal :
(Target scores/performance in SSC Exams.)
1. Good %
2. ……………
3. ……………
4. ……………
5. ……………
6. ……………

(d) Realisitc approach :
Plan of action that matches with your expertise/resources.
For example :
1. Make a study time table and follow it regularly.
2. ……………………………………………………..
3. ……………………………………………………..
4. ……………………………………………………..
5. ……………………………………………………..

(e) Time-bound Action :
Days required for revision

Answer:
Do it yourself.

Language Study:

Gerund:
When the – ‘ing’ form of a verb is used as a noun, it is known as a gerund a verbal noun. For example, The fighting went on. Here, we see that the – ‘ing’ form of the verb ‘fight’ is used as a subject in ‘The fighting went on’. It does a work of a noun.
Read the following examples of gerunds:

• Gardening is an art.
• Cooking is a science.
• I enjoy reading poems.
• I like reading more than writing.

Rewrite the above sentences using other appropriate gerunds in place of the given here.

Question 1.
Rewrite the above sentences using other appropriate gerunds in place of the given here.
Answer:

1. Painting is an art.
2. Banking is a science.
3. I enjoy acting.
4. I like riding more than swimming.

Infinitives:
Sometimes the form of a verb in a sentence names the action but does not change according to tense, number or person. Such a form is known as a non-finite form or an infinitive. An infinitive is used with or without ‘to’.
Examples: How did people first begin to drink tea? Can you name the beverage?
Underline the infinitive in the following sentences.
It was funny to read words that stood still.
Can I read the book?
To be or not to be – that is the question.

Question 1.
Underline the infinitive in the following sentences :
(The answers are directly given and underlined.)
Answer:

1. It was funny to read words that stood still.
2. Can I read the book?
3. To be or not to be – that is the question.

Finite:

Underline the verbs and choose the correct option from the brackets.

Thus, we see that verb forms show tense, number, etc. Here, the verb form changes according to the subject. A verb form which is decided by and changes according to the subject of the sentence is known as a Iuikite verb.
Example: ‘You are very kind.’ If the subject ‘you’ is changed to ‘she’, the sentence will be ‘She is very kind.’

Now change the verb form according to the change in the subject.

• I don’t know: Change ‘I’ to ‘She’ ……….
• My father knows: Change ‘My father’ to ‘We’ ……….
• I am following in your footsteps: Change ‘I’ to ‘He’ ……….

Underline the gerund/present participles/infinitive.
(a) Setting goal may appear easy, but it is quite challenging.
(b) Quantifying goals provide specific ways to track progress.
(c) It is important to create goals that are within a current skill set or area of expertise.
(d) We need to bring down life images down to earth and plan to execute our strategies.
(e) Finding the right footing, precisely mastering the skills and getting to the next place, all depend on how we approach and tackle the problem.

Classify the following words in their respective columns.
tackle, trumpet, directly, execute, aggressive, natural, absence, exactly, achieve, clearly, imagination, precisely, create, important, expert, specific. of, if, and, oh, from, we, but, it.

Changing word class:

Sometimes, the word class of a word changes without adding any prefix or suffix. For example, ‘run’ is used as a verb. So, ‘verb’ is its word class in ‘I can run faster than him.’ But when ‘run’ is used as a noun, its word class changes. For example, India has to score ten more runs to win the match.’ This is called a change of word class. Look at the following examples. Change of word class from verb to noun :
‘I doubt if I can write as fast as you can’ (verb). I have a doubt about this topic (noun). Similarly : laugh, walk, catch, throw, turn
Change of word class from noun to verb :
‘Remove the potato peels (noun). Peel the potato (verb).
‘She works as a nurse (noun). You have to nurse a patient till he/she recovers (verb).

Change the verb form according to the change in the subject.

• I don’t know: Change ‘I’ to ‘She’ ……….
• My father knows: Change ‘My father’ to ‘We’ ……….
• I am following in your footsteps: Change ‘I’ to ‘He’ ……….

Question 1.
I don’t know. (Change T to ‘She’.)
Answer:
She doesn’t know.

Question 2.
My father knows it. (Change ‘My father’ to ’We)
Answer:
We know it.

Question 3.
I am following in your footsteps.
(Change T to ‘He’)
Answer:
He is following in your footsteps.

Underline the gerund/present participles/infinitive.
(a) Setting goal may appear easy, but it is quite challenging.
(b) Quantifying goals provide specific ways to track progress.
(c) It is important to create goals that are within a current skill set or area of expertise.
(d) We need to bring down life images down to earth and plan to execute our strategies.
(e) Finding the right footing, precisely mastering the skills and getting to the next place, all depend on how we approach and tackle the problem.

Question 1.
Underline the gerund/present participles/infinitive.
(Answers are directly given.)
(a) Setting goal may appear easy, but it is quite challenging.
(b) Quantifying goals provide specific ways to track progress.
(c) It is important to create goals that are within a current skill set or area of expertise.
(d) We need to bring down life images down to earth and plan to execute our strategies.
(e) Finding the right footing, precisely mastering the skills and getting to the next place, all depend on how we approach and tackle the problem.

Classify the following words in their respective columns.

Question 1.
Classify the following words in their respective columns.
(Answers are directly given.)
vision, professional, natural, achieve, originality, 1 simply, failure, absence, expert, specific, easily, thrive, appear, five
Answer:

Nouns	Adjectives	Adverbs	Verbs
vision	natural	simply	achieve
professional	expert	easily	thrive
originality	specific		appear
failure	five
absence

Question 2.
Classify the following words in their respective columns.
(Answers are directly given.)
improvement, exactly, achievement, exact, clearly, important, create, aggressive, skill, help, hope, ability, defensive.
Answer:

Nouns	Adjectives	Adverbs	Verbs
improvement	exact	exactly	create
achievement	important	clearly	help
skill	aggressive		hope
help	defensive
hope
ability

Question 3.
Classify the following words in their respective columns.
(Answers are directly given.)
increase, consistent, imagination, execute, directly, tackle, reach, successful, expertise, unrealistic, reduce, precisely, hesitation, problem, valuable
Answer:

Nouns	Adjectives	Adverbs	Verbs
imagination	consistent	directly	increase
expertise	successful	precisely	execute
hesitation	unrealistic		tackle
problem	valuable		reach
			reduce

Question 4.
Classify the following words in their respective columns.
(Answers are directly given.)
ah, of, if, and, oh, from, we, but, it, hurrah
Answer:

Pronoun	Preposition	Conjunction	Interj­ection
we	of	if	oh
it	from	and	ah
		but	hurrah

My English Coursebook 10th Digest Chapter 1.4 Be SMART Additional Important Questions and Answers

Read the following passage and do the activities :

Simple Factual Activity :

Question 1.
Write whether the following statements are True or False :
Answer:

1. We won’t achieve our goals unless we take action to achieve them. – True
2. We all don’t have natural talents. – False
3. The skill must be stronger than will. – False
4. Goals help to steer a course of life. – True

Question 2.
Write whether the following sentences are True or False : (Board’s Model Activity Sheet)
Answer:

1. Quantifying goals provides specific ways to track progress against goals. – True
2. Setting goals that can’t be completed in the designated period of time. – False
3. It is important to create goals that are within one’s current skill set or area of expertise. – True
4. Being realistic will make it difficult to be successful at attaining goals. – False

Question 3.
Complete the following sentences with the help of the passage :
(Answers are directly given and underlined.)
Answer:

1. Specific goals make it easier to set parameters and work towards the goal.
2. Achievable goals may act like stepping stones to help meeting broader goals.
3. Expecting to become an expert in a short amount of time is unrealistic.

Question 4.
Complete the sentences with the help of the information in the passage :
(Answers are directly given and underlined.)
Answer:

1. For reducing weight, exercise, diet and stress- I free thoughts should be practised and implemented without hesitation.
2. Vision, wishes, intentions and dreams spark off imagination and encourage us to define where we want to reach.
3. The quality and quantity of energy we put forth, directly impact the results.
4. Success is a walk in the dark.

Complex Factual Activities:

Question 1.
Complete the web :
(Answer is directly given.)
Answer:

Question 2.
Complete the sentences using the information from the passage :
(Answers are directly given and underlined.)
Answer:

1. If we use our talent to set our goal in life, we can easily get success in life.
2. One has to decide what one wants to achieve in the end.
3. Setting goals sometimes appear easy but for some it is quite challenging.
4. We shall not achieve our goals if we do not take action to achieve them.

Question 3.
How does quantifying goals help us?
Answer:
Quantifying goals help us to provide detailed and exact ways to track progress against goals. This makes it easy to benchmark performance throughout the goal period, including areas to improve. In the game of football, the player’s exact role and position has to be clearly defined.

Question 4.
What factor is unreal, while setting goals?
Answer:
Expecting to become an expert in a short amount of time is an unreal factor, while setting goals. Building expertise always takes time.

Activities based on Vocabulary:

Question 1.
Find from the passage adjectives for :

1. nature
2. value
3. success
4. ease

Answer:

1. nature – natural
2. value – valuable
3. success – successful
4. ease – easy

Question 2.
Find from the passage adjectives for the following :

1. area
2. period
3. role
4. stones
5. picture

Answer:

1. specific – area
2. goal – period
3. exact – role
4. stepping – stones
5. clear – picture

Question 3.
Cross the odd man out:
(Answers are directly given.)
Answer:

Question 4.
Write from the passage noun forms of the following :
(Answers are directly given.)
Answer:

1. accountable – accountability
2. real – reality
3. imagine – imagination
4. hesitate – hesitation

Question 5.
Write from the passage words related to qualities required for success :
Answer:
accountability, consistent, vision, wish, intention, dream, imagination, execute, energy, skills, approach, strategy.

Activities based on Contextual Grammar :

Question 1.
Underline the gerund /present participles/ infinitives:
(Answers are directly given and underlined.)
Answer:

1. After all, one has to decide what one wants to achieve in the end.
2. If we use that talent to set in our Life, we call easily get success in Life.
3. They help to steer a course of our Life.

Question 2.
Underline the Present Participles/ Infinitives :
(Answers are directly given and underlined.)
Answer:

1. It makes it easier to set parameters.
2. These goals may act like stepping stones to help broader goals.
3. So expecting to become an expert in a short time is unrealistic.
4. Being realistic will make it easy to be successful at attaining goals.
5. You must have the ability to adhere to that picture.

Do as directed:

Question 1.
We all have natural talents,
(Add a question tag.)
Answer:
We all have natural talents, haven’t we?

Question 2.
The will must be stronger than the skill.
(Begin with-The skill must not be and change into positive degree.)
Answer:
The skill must not be as strong as the will.

Question 3.
It is important to create goals.
(Pick out the infinitive)
Answer:
to create.

Question 4.
These goals may act like stepping stones.
(Pick out the present participle)
Answer:
stepping.

Question 5.
Life is like a trumpet. (Frame a Wh-question to get the underlined word as answer.)
Answer:
What is life like?

Question 6.
Establish time parameters around each goal. (Rewrite the sentence beginning with ‘Let’and change the sentence into passive voice.)
Answer:
Let time parameters around each goal be established.

Question 7.
If we don’t put anything in, we can’t get anything out. (Rewrite the sentence using ‘unless’ in the beginning.)
Answer:
Unless we put anything in, we can’t get anything out.

Question 8.
It will help increase focus and accountability.
(Identify the Tense of the sentence.)
Answer:
Simple Future Tense

Question 9.
Complete the words by using correct

1. d r_a m
2. g o_l s
3. s m_r t
4. r i_h t

Answer:

1. dream
2. goals
3. smart
4. right

Question 10.
Put the following words in alphabetical order :
1. situation, some, specific, skill
2. stretch, involve, goal, rubric
Answer:
1. situation, skill, some, specific
2. goal, involve, rubric, stretch

Question 11.
Punctuate the following sentences :
1. Where are you going at this time said raja to smeeta
(2) The servant said what a kind nobleman he is
Answer:
1. “Where are you going at this time?” said Raja to Smeeta.
2. The servant said, “What a kind nobleman he is!”

Question 12.
Make four smaller words each (minimum 3 letters each) using the letters in the word : measurable
Answer:
meal, able, sure, marble

Question 13.
Write related words as shown in the example :
(Answer is directly given and underlined.)
Answer:

Question 14.
Complete the following word-chain based on nouns. Add four words, each beginning with the last letter of the previous word :
Tree → …………. → …………. → …………. → ………….
Answer:
Tree → egg → goat → team → mat.

1. Attempt any one :

a. Make your own meaningful sentence using the phrase ‘down to earth’ :
Answer:
He has achieved many awards but he remains down to earth all the time.
OR
b. Add a clause to the following sentence to expand it meaningfully :
I asked him
Answer:
I asked him if he was ready to come with me.

2. Attempt any one :
a. Add a prefix or suffix to make new words.
1. correct
2. fear
Answer:
1. incorrect
2. fearful/fearless
OR
b. Make meaningful sentence using any one of the following words :
1. correct
2. fear
Answer:
1. Whatever he said was correct.
2. The girl was shaking with fear.

Personal Response :

Question 1.
Do you have a goal in your life? What efforts will you make to achieve it?
Answer:
Yes, I do have decided my goal in my life. I aspire to be a top musician. To achieve my goal I will ‘ keep on trying and going ahead despite difficulties with the help of talent and hard work. I am sure that my faith in God, my perseverance, courage and , positive thinking will lead me to success.

Question 2.
Why do think that your goal should be achievable?
Answer:
I think, I must be very careful about choosing my goal. My goal must be achievable. That should be completed within the set deadline.
I should consider my talent and ability and then go for such a goal which will not remain incomplete and unsuccessful.

Question 3.
Why is it necessary to set our goals realistic?
Answer:
It is important to create goals that are within j your current skills limit. You must be expert in the area you have undertaken. Your approach towards your goal must be realistic and positive. You must have to work hard and know how and when you can | attain the goal.

Question 4.
Do you think, your attitude will change sifter your great success? Explain.
Answer:
No, I don’t think my great success will change my attitude towards the world. I shall be as humble as before. I shall not allow my success to go to my head. I shall be always down to earth. I will never trumpet my achievement and will express my views about my success without sounding boastful. Nothing will change in my life.

Question 5.
‘If we don’t put anything in, we can’t get anything out.’ Explain,
Answer:
When we wish to achieve something we must have to give time and put forth every quality and quantity of our energy. You have to prepare plan and execute it meticulously, concentrating on your goal. We will have to put everything at stake to get fruitful results. Efforts we put in the process wholeheartedly can only give us the output (success) we desire. The more you work in the direction of success, the more benefits you get.

Writing Skill:

Drafting a Speech :

Points: Understand the given topic for the speech – Collect all information from all sources – put your thoughts, ideas clearly, systematically in correct sequence – use good but – simple and impressive language – use slogans, quotes, maxims, proverbs, etc. – give examples to justify your points of view – emphasize your good points – conclude with thanks.

Delivering the Speech : Begin with greetings – introduce the topic – modulate your voice – be bold, straightforward and confident – look straight at the audience – speak slowly but loudly and clearly – avoid odd mannerisms or gestures – impress the audience – end the speech with thanks to audience.

Activities:

Question 1.
Your goal, this year, is to successfully pass from Secondary School to Higher Secondary School. So let us be SMART and note down the following :
(Note : Students should try to fill in their own ideas/information in the tables given on the coursebook pages 27 and 28.)
Points :
(a) Specific area : Note down the subjects and units.
(b) Measurable : Compare the scores of previous tests.
(c) Achievable goal: Set goals/target to be achieved.
(d) Realistic approach : Make action plans to get good marks.
(e) Time-bound Action : Study, Revision-required days

Language Study:

Question 1.
Change of word class from noun to verb :
Answer:
1. Remove the potato peels (noun). Peel the potato (verb).
2. She works as a nurse (noun). You have to nurse a patient till he/she recovers (verb).

My English Coursebook Standard Ten Guide Unit 1

• A Teenager’s Prayer Class 10 English Solutions
• An Encounter of a Special Kind Class 10 English Solutions
• Basketful of Moonlight Class 10 English Solutions
• Be SMART…! Class 10 English Solutions
• His First Flight Class 10 English Solutions