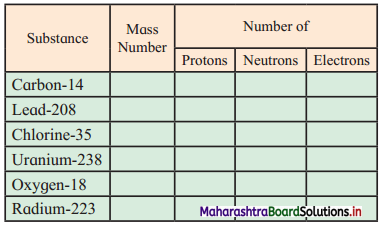
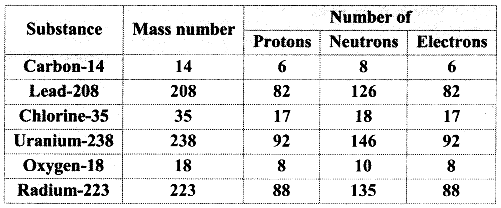
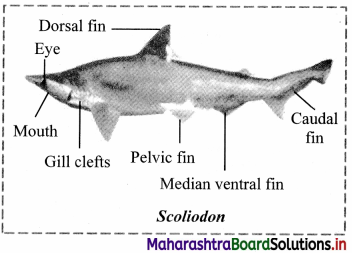
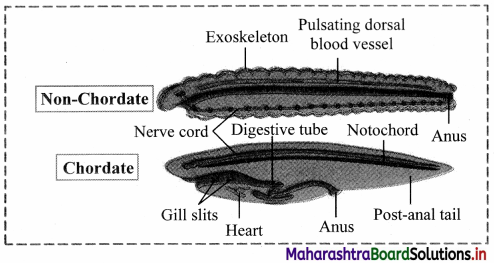
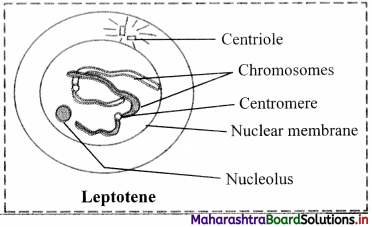
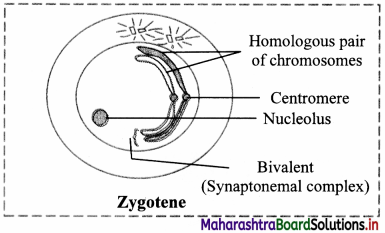
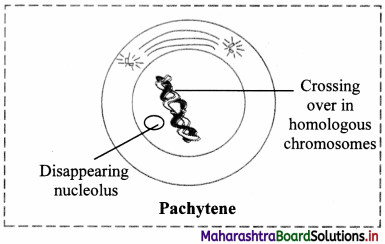
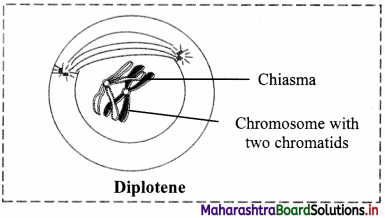
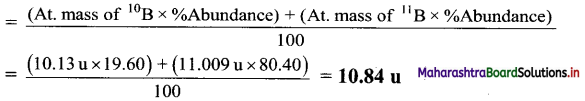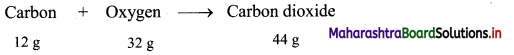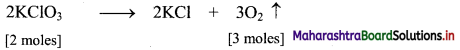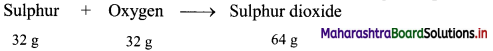Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 15 Hydrocarbons Textbook Exercise Questions and Answers.
Hydrocarbons Class 11 Exercise Question Answers Solutions Maharashtra Board
Class 11 Chemistry Chapter 15 Exercise Solutions Maharashtra Board
Chemistry Class 11 Chapter 15 Exercise Solutions
1. Choose correct options
Question A.
Which of the following compound has the highest boiling point?
a. n-pentane
b. iso-butane
c. butane
d. neopentane
Answer:
a. n-pentane
Question B.
Acidic hydrogen is present in :
a. acetylene
b. ethane
c. ethylene
d. dimethyl acetylene
Answer:
a. acetylene
Question C.
Identify ‘A’ in the following reaction:
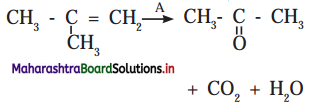
a. KMnO4/H+
b. alkaline KMnO4
c. dil. H2SO4/1% HgSO4
d. NaOH/H2O2
Answer:
a. KMnO4/H+
Question D.
Major product of chlorination of ethyl benzene is :
a. m-chlorethyl benzene
b. p-chloroethyl benzene
c. chlorobenzene
d. o-chloroethylbenzene
Answer:
b. p-chloroethyl benzene
Question E.
1 – chloropropane on treatment with alc. KOH produces :
a. propane
b. propene
c. propyne
d. propyl alcohol
Answer:
b. propene
![]()
2. Name the following :
Question A.
The type of hydrocarbon that is used as lubricant.
Answer:
Waxes
Question B.
Alkene used in the manufacture of polythene bags.
Answer:
Ethene
Question C.
The hydrocarbon said to possess carcinogenic property.
Answer:
Benzene
Question D.
What are the main natural sources of alkane?
Answer:
Crude petroleum and natural gas.
Question E.
Arrange the three isomers of alkane with malecular formula C5H12 in increasing order of boiling points and write their IUPAC names.
Answer:
The three isomers of alkane with molecular formula C5H12 are as follows:
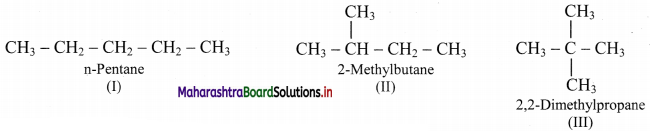
The increasing order of their boiling point is I > II > III.
![]()
Question F.
Write IUPAC names of the products obtained by the reaction of cold concentrated sulphuric acid followed by water with the following compounds.
a. propene
b. but-1-ene
Answer:
a. propene:
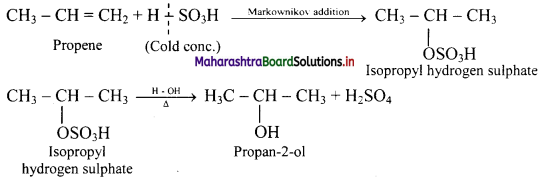
b. but-1-ene:
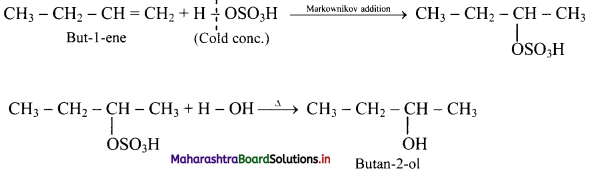
Question G.
Write the balanced chemical reaction for preparation of ethane from
a. Ethyl bromide
b. Ethyl magnesium iodide
Answer:
a. Preparation of ethane from ethyl bromide:

b. Preparation of ethane from ethyl magnesium iodide:

Question H.
How many monochlorination products are possible for
a. 2-methylpropane ?
b. 2-methylbutane ?
Draw their structures and write their IUPAC names.
Answer:
a. Possible monochlorination products for 2-methylpropane:
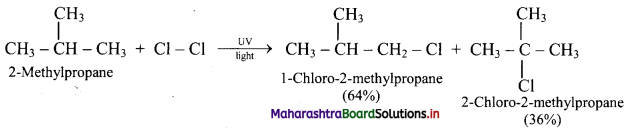
b. Possible monochlorination products for 2-methylbutane:

Question I.
Write all the possible products for pyrolysis of butane.
Answer:
Possible products for pyrolysis of butane are:
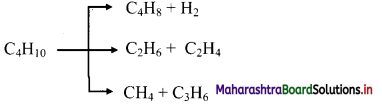
Question J.
Which of the following will exhibit geometical isomerism ?
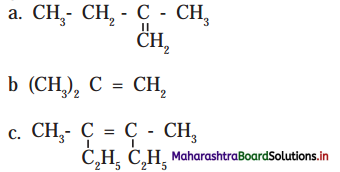
Answer:
Compound (c) will exhibit geometrical isomerism.
![]()
Question K.
What is the action of following on ethyl iodide ?
a. alc. KOH
b. Zn, HCl
Answer:
a. Action of alc. KOH on ethyl iodide:
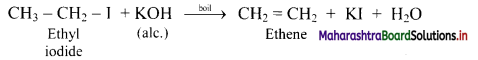
b. Action of Zn/HCl on ethyl iodide:

Question L.
An alkene ‘A’ an ozonolysis gives 2 moles of ethanal. Write the structure and IUPAC name of ‘A’.
Answer:
Structure of A: CH3 – CH = CH – CH3
IUPAC name of A: But-2-ene
Question M.
Acetone and acetaldehyde are the ozonolysis products of an alkene. Write the structural formula of an alkene and give IUPAC name of it.
Answer:
The structural formula of alkene:
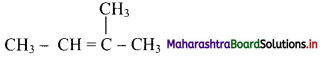
IUPAC name is 2-methylbut-2-ene.
Question N.
Write the reaction to convert
a. propene to n-propyl alcohol.
b. propene to isoproyl alcohol.
Answer:
a.
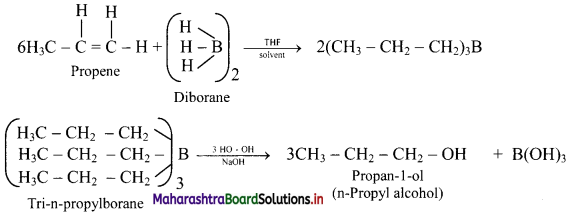
b.
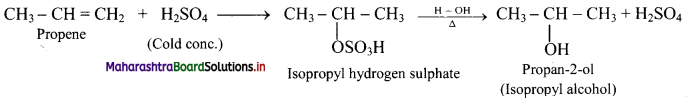
Question O.
What is the action of following on but-2-ene ?
a. dil alkaline KMnO4
b. acidic KMnO4
Answer:
a. Action of dil. alkaline KMnO4 on but-2-ene:
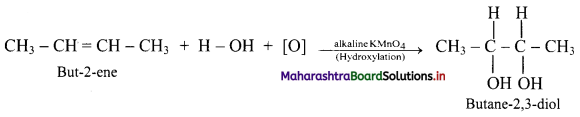
b. Action of acidic KMnO4 on but-2-ene:

Question P.
Complete the following reaction sequence :
![]()
Answer:
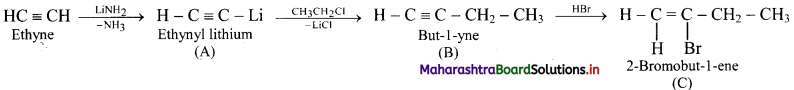
![]()
Question Q.
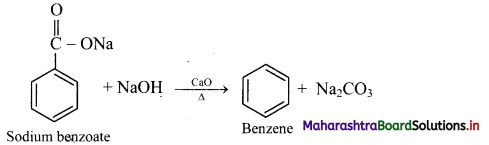
Write the balanced chemical reactions to get benzene from
a. Sodium benzoate.
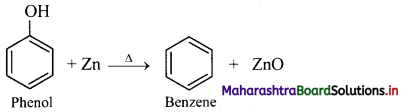
b. Phenol.
Answer:
a. Sodium benzoate:
When anhydrous sodium benzoate is heated with soda lime, it undergoes decarboxylation and gives benzene.
b. Phenol:
When vapours of phenol are passed over heated zinc dust, it undergoes reduction and gives benzene.
Question R.
Predict the possible products of the following reaction.
a. chlorination of nitrobenzene,
b. sulfonation of chlorobenzene,
c. bromination of phenol,
d. nitration of toluene.
Answer:
a. Nitro group is meta directing group. So, chlorination of nitrobenzene gives m-chloronitrobenzene.
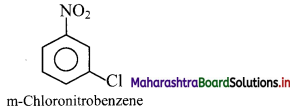
b. Chloro group is ortho and para directing group. So, sulphonation of chlorobenzene gives p-chlorobenzene sulphonic acid and o- chlorobenzene sulphonic acid.
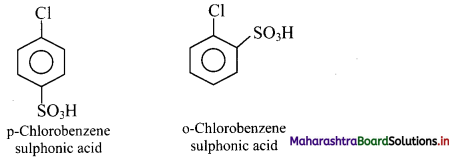
c. Phenolic -OH group is ortho and para directing group. So, bromination of phenol gives p-bromophenol and o-bromophenol.
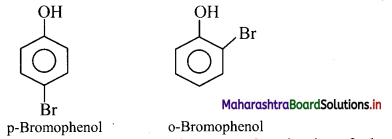
d. Methyl group is ortho and para directing group. So, nitration of toluene gives p-nitrotoluene and o-nitrotoluene.
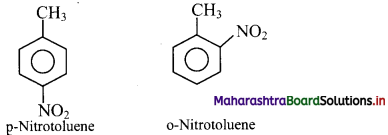
3. Identify the main product of the reaction
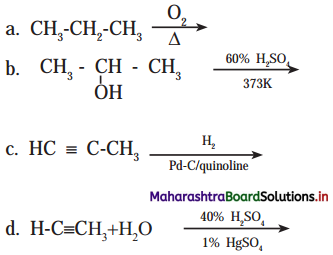
Answer:
a.
![]()
b.

c.
![]()
d.

4. Read the following reaction and answer the questions given below.
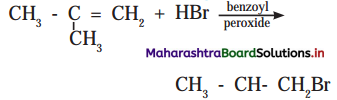
a. Write IUPAC name of the product.
b. State the rule that governs formation of this product.
Answer:
a. IUPAC name of the product: 1 -Bromo-2-methylpropane
b. Anti-Markownikov’s rule/Kharasch effect/peroxide effect: It states that, the addition of HBr to unsymmetrical alkene in the presence of organic peroxide (R-O-O-R) takes place in the opposite orientation to that suggested by Markovnikov’s rule.
![]()
5. Identify A, B, C in the following reaction sequence :
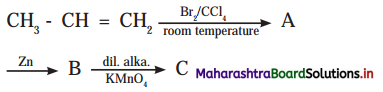
Answer:

6. Identify giving reason whether the following compounds are aromatic or not.
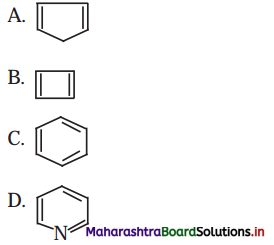
Answer:
A.

Compound is non-aromatic since it has 4π electrons and hence, does not obey Huckel rule of aromaticity.
B.
![]()
Compound is non-aromatic since it has 4π electrons and hence, does not obey Huckel rule of aromaticity.
C.

Compound is aromatic since it has 6π electrons and hence, obeys Huckel rule of aromaticity.
D.

Compound is aromatic since it has 6n electrons and hence, obeys Huckel rule of aromaticity.
7. Name two reagents used for acylation of benzene.
Answer:
The two reagents used for acylation of benzene are:
i. CH3COCl (acetyl chloride) and anhydrous AlCl3
ii. (CH3CO)2O (acetic anhydride) and anhydrous AlCl3
8. Read the following reaction and answer the questions given below.
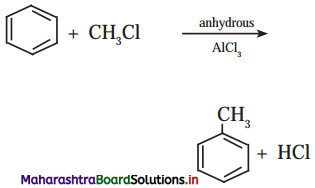
A. Write the name of the reaction.
B. Identify the electrophile in it.
C. How is this electrophile generated?
Answer:
A. The name of the reaction is Friedel-Craft’s alkylation reaction.
B. The electrophile in the reaction is +CH3.
C. The electrophile +CH3 is generated as follows:
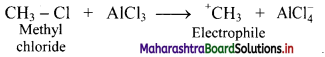
Activity:
Prepare chart of hydrocarbons and note down the characteristics.
Answer:
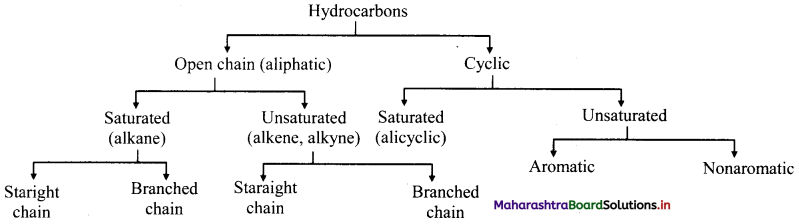
Characteristics of hydrocarbons:
- They are chemical compounds that are formed from only hydrogen and carbon atoms.
- Both ‘C’ and ‘H’ share an electron pair forming covalent bonds.
- One of the special properties of carbon is its ability to form double and triple bonds (unsaturation). Saturated hydrocarbons are alkanes and cycloalkanes while the unsaturated hydrocarbons are the aromatics, alkenes and alkynes.
- All hydrocarbons are insoluble in water, their boiling point increases as the size of alkane increases.
- All hydrocarbons can reach complete oxidation.
- Hydrocarbons are mainly used as fuel for transport and industry.
[Note: Students are expected to collect additional information on hydrocarbons on their own.]
![]()
11th Chemistry Digest Chapter 15 Hydrocarbons Intext Questions and Answers
Can you recall? (Textbook Page No. 233)
Question i.
What are hydrocarbons?
Answer:
The compounds which contain carbon and hydrogen as the only elements are called hydrocarbons.
Question ii.
Write structural formulae of the following compounds: propane, ethyne, cyclobutane, ethene, benzene.
Answer:
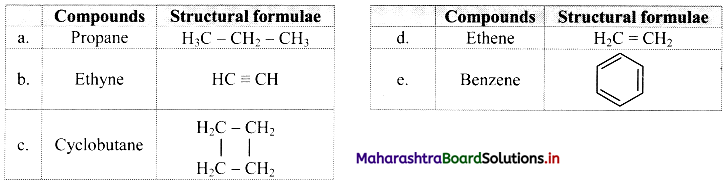
Do you know? (Textbook Page No. 233)
Question 1.
Why are alkanes called paraffins?
Answer:
i. Alkanes contain only carbon-carbon and carbon-hydrogen single covalent bonds.
ii. They are chemically less reactive and do not have much affinity for other chemicals.
Hence, they are called paraffins.
Internet my friend. (Textbook Page No. 233)
Question 1.
Collect information about hydrocarbon.
Answer:
- In organic chemistry, a hydrocarbon is an organic compound consisting of carbon and hydrogen as the only elements.
- They are examples of group 14 hydrides.
- Alkanes, cycloalkanes, aromatic hydrocarbons are different types of hydrocarbons.
- Most of the hydrocarbons found on earth occur naturally in crude oil.
- They mainly undergo substitution, addition or combustion reactions.
- Most hydrocarbons are flammable and toxic.
- They are the primary energy source in the form of combustible fuel source.
[Note: Students are expected to collect additional information on their own]
![]()
Use your brain power! (Textbook Page No. 234)
Question 1.
i. Write the structures of all the chain isomers of the saturated hydrocarbon containing six carbon atoms.
ii. Write IUPAC names of all the above structures.
Answer:
The structural formulae and names of all possible isomers having molecular formula C6H14 are as follows:
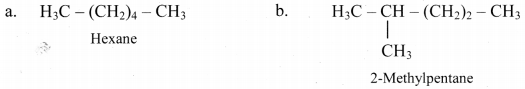

Note:
Alkanes and isomer number
| Number of Carbon | Alkane | Number of isomers |
| 1 | Methane | No structural isomer |
| 2 | Ethane | No structural isomer |
| 3 | Propane | No structural isomer |
| 4 | Butane | Two |
| 5 | Pentane | Three |
| 6 | Hexane | Five |
Can you recall? (Textbook Page No. 235)
Question i.
What is a catalyst?
Answer:
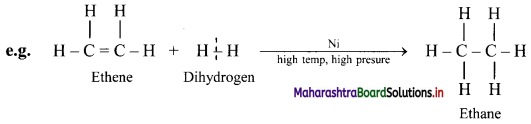
A catalyst is a substance that can be added to a reaction to increase the reaction rate without getting consumed in the process.
e.g. Ni is used as a catalyst in the catalytic hydrogenation of alkenes or alkynes.
Question ii.
What is addition reaction?
Answer:
When a compound combines with another compound to form a product that contain all the atoms in both the reactants, it is called an addition reaction.
Try this (Textbook Page No. 235)
Question 1.
Transform the following word equation into balanced chemical equation and write at least 3 changes that occur at molecular level during this chemical change.
\(\text { 2-Methylpropene + Hydrogen } \stackrel{\text { catalyst }}{\longrightarrow} \text { Isobutane }\)
Answer:

Three changes which occur at molecular level include:
Step 1: Adsorption of reactants: Reactants (alkene and hydrogen) get adsorbed on the catalytic surface.
Step 2: Formation of a product: Hydrogen atoms are added across the double bond of 2-methylpropene which results in the formation of product isobutane.
Step 3: Desorption: Product formed on the catalytic surface is readily desorbed making catalytic surface available for other molecules.
Use your brain power! (Textbook Page No. 236)
Question 1.
Why are alkanes insoluble in water and readily soluble in organic solvents like chloroform or ether?
Answer:
- The solubility of any substance is governed by the principle of like dissolves like. This means polar compounds are soluble in polar solvents while nonpolar compounds are soluble in nonpolar solvents.
- Alkanes consist of C – C and C – H nonpolar covalent bonds and thus, they are nonpolar in nature, whereas water is a polar solvent.
- The dipole-dipole forces that exist between water molecules is much stronger than the forces of attraction between alkane and water molecules.
Hence, alkanes are insoluble in water and readily soluble in organic solvents like chloroform or ether.
![]()
Can you recall? (Textbook Page No. 238)
Question 1.
What is the product which is poisonous and causes air pollution formed by incomplete combustion of alkane?
Answer:
When alkanes are subjected to incomplete combustion, it forms carbon monoxide and carbon (soot).
i. 2CH4(g) + 3O2(g) → 2CO(g) + 4H2O(g)
ii. CH4(g) + O2(g) → C(s) + 2H2O(l)
Can you recall? (Textbook Page No. 238)
Question i.
What are alkenes?
Answer:
Alkenes are unsaturated hydrocarbons containing at least one carbon-carbon double bond.
Question ii.
Calculate the number of sigma (σ) and pi (π) bonds in 2-methylpropene.
Answer:

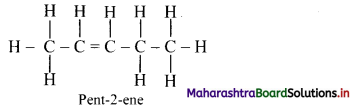
Question iii.
Write the structural formula of pent-2-ene.
Answer:
Can you tell? (Textbook Page No. 241)
Question i.
Explain by writing a reaction, the main product formed on heating 2-methylbutan-2-ol with concentrated sulphuric acid.
Answer:

Question ii.
Will the main product in the above reaction show geometrical isomerism?
Answer:
No, the major product, i.e., 2-methylbut-2-ene does not show geometrical (or cis-trans) isomerism.
Can you tell? (Textbook Page No. 244)
Question 1.
Propan-1-ol and 2-methypropan-1-ol are not prepared by hydration method. Why?
Answer:
Propan-1-ol and 2-methylpropan-1-ol cannot be prepared by hydration of propene and 2-methylprop-1-ene because the addition reaction follows Markovnikov’s rule.
![]()
Use your brainpower. (Textbook Page No. 244)
Question 1.
On ozonolysis, an alkene forms the following carbonyl compounds. Draw the structure of unknown alkene from which these compounds are formed: HCHO and CH3COCH2CH3
Answer:
The structure of alkene which produces a mixture of HCHO and CH3COCH2CH3 on ozonolysis is
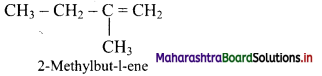
Use your brain power! (Textbook Page No. 245)
Question 1.
Write the structure of monomer from which each of the following polymers are obtained.
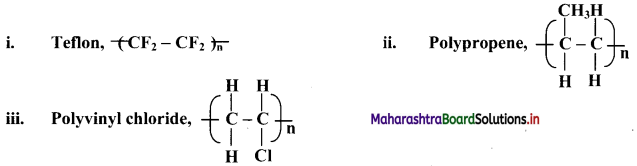
Answer:
| Polymer | Monomeric unit | |
| i. | Teflon | CF2 – CF2 Tetrafluoroethene |
| ii. | Polypropene | H3C – CH = CH2 Propene |
| iii. | Polyvinyl chloride | H2C = CHCl Vinyl chloride |
Can you tell? (Textbook Page No. 246)
Question i.
What are aliphatic hydrocarbons?
Answer:
Aliphatic hydrocarbons are hydrocarbons containing carbon and hydrogen joined together in straight chain or branched chain. They may be saturated (alkanes) or unsaturated (alkenes or alkynes).
Question ii.
Compare the proportion of carbon and hydrogen atoms in ethane, ethene and ethyne. Which compound is most unsaturated with hydrogen?
Answer:
Ethane
C : H = 2 : 6 = 1 : 3
Ethene
C : H = 2 : 4 = 1 : 2
Ethyne
C : H = 2 : 2 = 1 : 1
From the above proportion it is clear that ethyne with 1 : 1 ratio of C : H is most unsaturated with hydrogen (50%) as compared to ethane (25%) and ethene (33.33%).
Can you tell? (Textbook Page No. 247)
Question 1.
Why is sodamide used in dehydrohalogenation of vicinal dihalides to remove HX from alkenyl halide in place of alcoholic KOH?
Answer:
- Sodamide (NaNH2) is a strong base and hence, helps in complete conversion of alkenyl halide formed in the first step to form alkynes.
- The base (KOH or NaOH) used in first step gives alkynes in poor yield and hence, stronger bases such as NaNH2 on KNH2 are used in second step.
Use your brainpower! (Textbook Page No. 247)
Question 1.
Convert: 1-Bromobutane to hex-1-yne
Answer:

Can you tell? (Textbook Page No. 248)
Question 1.
Alkanes and alkenes do not react with lithium amide. Give reason.
Answer:
i. The sp hybrid carbon atom in terminal alkynes is more electronegative than the sp2 carbon in ethene or the sp3 carbon in ethane.
ii. Due to high electronegative character of carbon in terminal alkynes, hydrogen atom can be given away as proton (H+) to very strong base as shown in the reactions below.
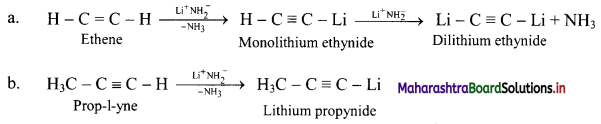
iii. Further, since s-character decreases from sp to sp2 to sp3 carbon atom, the relative acidity of alkanes, alkenes and alkynes is in the following order: H – C = C – H > H2C = CH2 > H3C – CH3
Hence, alkenes and alkanes do not react with lithium amide.
![]()
Use your brain power! (Textbook Page No. 248)
Question 1.
Arrange following hydrocarbons in the increasing order of acidic character: propane, propyne, propene.
Answer:
Propyne > propene > propane
Use your brain power! (Textbook Page No. 249)
Question 1.
Convert: 3-Methylbut-l-yne into 3-methylbutan-2-one
Answer:

Can you recall? (Textbook Page No. 249)
Question i.
What are aromatic hydrocarbons?
Answer:
Benzene and all compounds that have structures and chemical properties resembling benzene are called as aromatic hydrocarbons.
Question ii.
What are benzenoid and non-benzenoid aromatics?
Answer:
Benzenoid aromatics are compounds having at least one benzene ring in the structure.
e.g. Benzene, naphthalene, anthracene, phenol, etc.,
Non-benzenoid aromatics are compounds that contain an aromatic ring, other than benzene. e.g. Tropone, etc.
Can you recall? (Textbook Page No. 254)
Question 1.
What is decarboxylation?
Answer:
The reaction which involves removal of a carboxyl group (-COOH) in the form of carbon dioxide (CO2) is known as decarboxylation reaction.
R – COOH → R – H + CO2
11th Std Chemistry Questions And Answers:
- Elements of Group 13, 14 and 15 Class 11 Chemistry Questions And Answers
- States of Matter Class 11 Chemistry Questions And Answers
- Adsorption and Colloids Class 11 Chemistry Questions And Answers
- Chemical Equilibrium Class 11 Chemistry Questions And Answers
- Nuclear Chemistry and Radioactivity Class 11 Chemistry Questions And Answers
- Basic Principles of Organic Chemistry Class 11 Chemistry Questions And Answers
- Hydrocarbons Class 11 Chemistry Questions And Answers
- Chemistry in Everyday Life Class 11 Chemistry Questions And Answers


 Answer:
Answer: