Maharashtra Board Class 11 Chemistry Solutions Chapter 13 Nuclear Chemistry and Radioactivity

Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 13 Nuclear Chemistry and Radioactivity Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Chemistry Solutions Chapter 13 Nuclear Chemistry and Radioactivity

1. Choose correct option.

Question A.
Identify nuclear fusion reaction

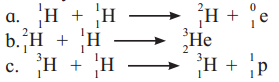
Answer:
Among the given options, reactions (i) and (ii) represent nuclear fusion reaction wherein lighter nuclei combine to form a heavy nucleus.

Question B.
The missing particle from the nuclear reaction is

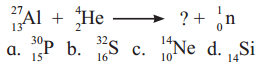
Answer:
(A) \({ }_{15}^{30} \mathrm{P}\)

Question C.
\({ }_{27}^{60} \mathrm{CO}\) decays with half-life of 5.27 years to produce \({ }_{28}^{60} \mathrm{Ni}\). What is the decay constant for such radioactive disintegration ?
a. 0.132 y^-1
b. 0.138
c. 29.6 y
d. 13.8%
Answer:
a. 0.132 y^-1

Question D.
The radioactive isotope used in the treatment of Leukemia is
a. ⁶⁰Co
b. ²²⁶Ra
c. ³²P
d. ¹³¹I
Answer:
c. ³²P

Question E.
The process by which nuclei having low masses are united to form nuclei with large masses is
a. chemical reaction
b. nuclear fission
c. nuclear fusion
d. chain reaction
Answer:
c. nuclear fusion

2. Explain

Question A.
On the basis of even-odd of protons and neutrons, what type of nuclides are most stable ?
Answer:

• Nuclides with even number of protons (Z) and even number of neutrons (N) are most stable.
• These nuclides tend to form proton-proton and neutron-neutron pairs.
• This impart stability to the nucleus.

Question B.
Explain in brief, nuclear fission.
Answer:
i. Nuclear fission: It is a process which involves splitting of the heavy nucleus of an atom into two nearly equal fragments accompanied by release of the large amount of energy.
e.g. Nuclear fission of ²³⁵U

ii. When a uranium nucleus absorbs neutron, it breaks into two lighter fragments and releases energy (heat), more neutrons, and other radiation. This can be given as,

iii. Characteristics of nuclear fission reactions:

• The mass of the fission products is less than the parent nucleus. A large amount of energy corresponding to the mass loss is released in each fission.
• When one uranium 235 nucleus undergoes fission, three neutrons are emitted, which subsequently disintegrate three more uranium nuclei and thereby produce nine neutrons. Such a chain continues by itself.
• In a very short time enormous amount of energy is liberated, which can be utilized for destructive or peaceful purposes.
• Energy released per fission is approximately 200 MeV.

Note:

• Each fission may lead to different products.
• There is no unique way for fission of ²³⁵U that produces Ba and Kr. There are 400 ways for fission of ²³⁵U leading to 800 fission products.
• Many of these fission products are radioactive which undergo spontaneous disintegrations giving rise to new elements in the periodic table.

Question C.
The nuclides with odd number of both protons and neutrons are the least stable. Why ?
Answer:

• The nuclides with odd number of both protons and neutrons are the least stable because, odd number of protons and neutrons results in the presence of two unpaired nucleons.
• These unpaired nucleons result in instability. Hence, such nuclides are the least stable.

Question D.
Referring the stabilty belt of stable nuclides, which nuclides are β^– and β⁺ emitters ? Why ?
Answer:

• Beta decay occurs when an unstable nucleus emits a beta particle and energy. A beta particle is either an electron or a positron. An electron is a negatively charged particle, and a positron is a positively charged electron (or anti-electron).
• When the beta particle is an electron, the decay is called beta-minus (β^–) decay. In beta-minus decay, a neutron breaks down to a proton and an electron, and the electron is emitted from the nucleus.
• When the beta particle is a positron, the decay is called beta-plus (β⁺) decay. In beta-plus decay, a proton breaks down to a neutron and a positron, and the positron is emitted from the nucleus.
• Thus, beta-minus decay occurs when a nucleus has too many neutrons relative to protons (i.e., N/Z > 1) and beta-plus decay occurs when a nucleus has too few neutrons relative to protons (i.e., N/Z < 1).
• By referring the stability belt of stable nuclides, nuclides with N/Z > 1 are to the left of the stability zone. Such nuclides are beta-minus emitters as they become stable when a neutron converts to a proton.
• Nuclides with N/Z < 1 are to the right of the stability zone. Such nuclides are beta-plus emitters as they become stable when a proton converts to a neutron.

Question E.
Explain with an example each nuclear transmutation and artifiacial radioactivity. What is the difference between them ?
Answer:
i. Nuclear transmutation: It involves transformation of a stable nucleus into another nucleus takes place which can be either stable or unstable.
ii. Artificial (induced) radioactivity: It is nuclear transmutation where the product nucleus is radioactive. The product nucleus decays spontaneously with emission of radiation and particles.

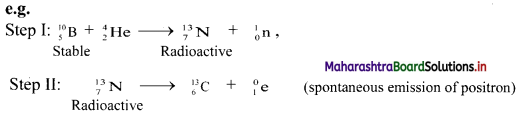
Step-I can be considered as nuclear transmutation as it produces a new nuclide \({ }_{7}^{13} \mathrm{~N}\).
However, the new nuclide is unstable (radioactive). Hence, step-I involves artificial (induced) radioactivity. Thus, in artificial transmutation, a stable element is collided with high speed particles to form another radioactive element.

Question F.
What is binding energy per nucleon ? Explain with the help of diagram how binding energy per nucleon affects nuclear stability ?
Answer:

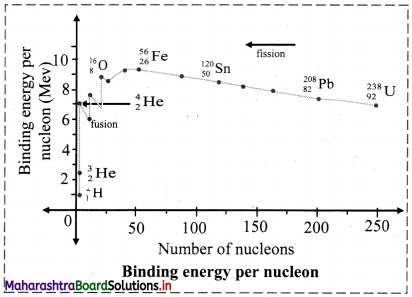
i. Binding energy per nucleon (\(\overline{\mathrm{B}}\)), for nucleus containing (A) nucleons with binding energy (B.E.) is given as,
\(\overline{\mathrm{B}}\) = B.E./A
ii. Mean binding energy per nucleon (\(\overline{\mathrm{B}}\)) for the most stable isotopes as a function of mass number is shown above. This plot leads to the following inferences:
a. Light nuclides: (A < 30)
The peaks with A values in multiples of 4. For example, \({ }_{2}^{4} \mathrm{He},{ }_{6}^{12} \mathrm{C},{ }_{8}^{16} \mathrm{O}\) are more stable.
b. Medium mass nuclides: (30 < A < 90)
\(\overline{\mathrm{B}}\) increases typically from 8 MeV for A = 16 to nearly 8.3 MeV for A between 28 and 32 and it remains nearly constant 8.5 MeV beyond this and shows a broad maximum. The nuclides falling on the maximum are most stable which turns possess high values. ⁵⁶Fe with \(\overline{\mathrm{B}}\) value of 8.79 MeV is the most stable.
c. Heavy nuclides (A > 90)
\(\overline{\mathrm{B}}\) decreases from maximum 8.79 MeV to 7.7 MeV for A ≅ 210, 209Bi is the stable nuclide. Beyond this, all nuclides are radioactive (α-emitters).

Question G.
Explain with example α-decay.
Answer:
i. The emission of α-particle from the nuclei of an radioelement is called α-decay.
ii. The charge on an α-particle is +2 with a mass of 4 u.
It is identical with helium nucleus and hence an α-particle is designated as \({ }_{2}^{4} \mathrm{He}\).
iii. In the α-decay process, the parent nucleus \({ }_{\mathrm{z}}^{\mathrm{A}} \mathrm{X}\) emits an α-particle and produces daughter nucleus Y. The parent nucleus thus loses two protons (charge +2) and two neutrons. The total mass lost is 4 u. The daughter nucleus will therefore, have mass 4 units less and charge 2 units less than its parent.
iv. General equation for α-decay process can be given as:

In α-decay process of radium, radon (daughter nuclei) is formed with loses of two protons (charge +2) and two neutrons. The total mass lost is 4 u.
Thus, radon has a mass of 4 units less and charge 2 units less than its parent radium.

Question H.
Energy produced in nuclear fusion is much larger than that produced in nuclear fission. Why is it difficult to use fusion to produce energy ?
Answer:

• Nuclear fusion involves the fusion of lighter nuclei to form a heavy nucleus which is accompanied by an enormous amount of energy (heat).
• Fusion reaction requires extremely high temperature typically of the order of 108 K.

Question I.
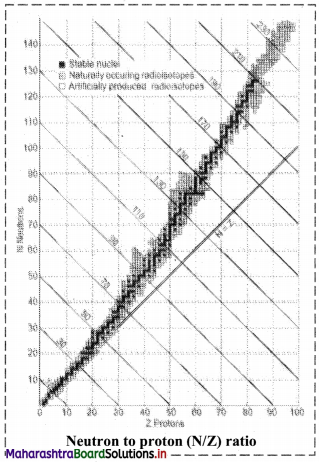
How does N/Z ratio affect the nuclear stability ? Explain with a suitable diagram.
Answer:

• When the graph of number of neutrons (N) against protons (Z) is drawn, and all the stable isotopes are plotted on it, there is quite a clear correlation between N and Z. This graph is shown in the adjacent figure.
• A large number of elements have several stable isotopes and hence, the curve appears as a belt or zone called stability zone. All stable nuclides fall with this zone and the nuclei that are to the left or to the right of the stability zone are unstable and exhibit radioactivity. Below the belt, a straight line which represents the ratio N/Z to be nearly unity (i.e., N = Z) is shown.
• For nuclei lighter than \({ }_{20}^{40} \mathrm{Ca}\), the straight line (N = Z) passes through the belt. The lighter nuclides are therefore stable (N/Z being 1).
• The N/Z ratio for the stable nuclides heavier than calcium gives a curved appearance to the belt with gradual increase of N/Z (> 1). The heavier nuclides therefore, need more number of neutrons than protons to attain stability. The heavier nuclides with increasing number of protons render large coulombic repulsions. With increased number of neutrons, the protons within the nuclei get more separated, which renders them stable.
• Thus, nuclear stability is linked to the number of nucleons (neutrons and protons). In general, the lighter stable nuclei have equal numbers of protons and neutrons while heavier stable nuclei have increasingly more neutrons than protons.

[Note: Atoms with unstable nuclei are radioactive (exhibit radioactivity). To become more stable, the nuclei undergo radioactive decay.]

Question J.
You are given a very old sample of wood. How will you determine its age ?
Answer:
The age of the wood sample can be determined by radiocarbon dating as ¹⁴C becomes a part of a plant due to the photosynthesis reaction (i.e., absorption of [¹⁴CO₂ + ¹²CO₂]).
i. The activity (N) of given wood sample and that of fresh sample of live plant (N₀) is measured, where, N₀ denotes the activity of the given sample at the time of death.
ii. The age of the given wood sample. can be determined by applying following Formulae:

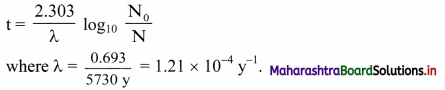
Note: The oldest rock found so far in Northern Canada is 3.96 billion years old.

3. Answer the following question

Question A.
Give example of mirror nuclei.
Answer:
Example of mirror nuclei: \({ }_{1}^{3} \mathrm{H}\) and \({ }_{2}^{3} \mathrm{He}\)

Question B.
Balance the nuclear reaction:

Answer:

Question C.
Name the most stable nuclide known. Write two factors responsible for its stability.
Answer:
The most stable nuclide known is lead (\({ }_{82}^{208} \mathrm{~Pb}\)).
Two factors responsible for its stability are as follows:

• It is a nuclide with even number of both protons (Z) and neutrons (N).
• It has two magic numbers i.e., 82 (for protons) and 126 (for neutrons).

Question D.
Write relation between decay constant of a radioelement and its half life.
Answer:
Relation between decay constant of a radioelement and its half-life is given as, λ = \(\frac{0.693}{\mathrm{t}_{1 / 2}}\)
Where, λ = Decay constant, t_1/2 = Half-life of a radioelement

Question E.
What is the difference between an α-particle and helium atom ?
Answer:

• Helium atom is composed of 2 protons and 2 neutrons (or 1 neutron) along with 2 electrons in the outer shell.
• On the other hand, α-particle constitutes 2 protons and 2 neutrons bound together to form a particle which is similar to helium (except presence of electrons).
• Helium is one of the inert gas which is stable (duplet complete) whereas α-particle is unstable and highly reactive.

Question F.
Write one point that differentiates nuclear reations from chemical reactions.
Answer:
Chemical reactions:

• Rearrangement of atoms by breaking and forming of chemical bonds.
• Different isotopes of an element have same behaviour.

Nuclear reactions:

• Elements or isotopes of one element are converted into another element in a nuclear reaction.
• Isotopes of an element behave differently.

Question G.
Write pairs of isotones and one pair of mirror nuclei from the following :

Answer:
Isotones: i. \({ }_{5}^{10} \mathrm{~B} \text { and }{ }_{6}^{11} \mathrm{C}\)
ii. \({ }_{13}^{27} \mathrm{Al} \text { and }{ }_{14}^{28} \mathrm{~S}\)
Mirror nuclei: Since there are no isobars the given set of nuclides does not contain a pair of mirror nuclei.

Question H.
Derive the relationship between half life and decay constant of a radioelement.
Answer:
Equation for the decay constant is given as,
λ = \(\frac{2.303}{t} \log _{10} \frac{\mathrm{N}_{0}}{\mathrm{~N}}\) …(i)
Where, λ = Decay constant
N = Number of nuclei (atoms) present at time t
At t = 0, N = N₀.
Hence, at t = t_1/2, N = N₀/2
Substitution of these values of N and t in equation (i) gives,

Question I.
Represent graphically log₁₀ (activity /dps) versus t/s. What is its slope ?
Answer:
Equation for a decay constant (λ) is given as,

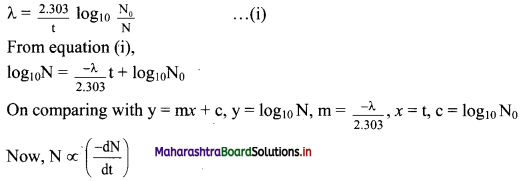
Hence, instead if log₁₀N versus t, log₁₀ \(\left(\frac{-\mathrm{d} \mathrm{N}}{\mathrm{dt}}\right)\) which is log₁₀ (activity) is plotted.
The graph of log₁₀ (activity/dps) versus t/s gives a straight line which can be represented as follows:

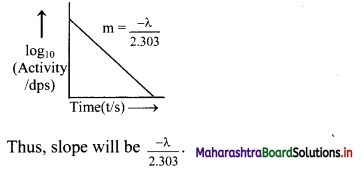
Question J.
Write two units of radioactivity. How are they interrelated ?
Answer:
The unit of radioactivity is curie (Ci).
1 Ci = 3.7 × 10¹⁰ dps
ii. Other unit of radioactivity is Becquerel (Bq).
1 Bq = 1 dps
Thus, 1 Ci = 3.7 × 10¹⁰ dps = 3.7 × 10¹⁰ Bq

Question K.
Half life of ²⁴Na is 900 minutes. What is its decay constant?
Answer:

Question L.
Decay constant of ¹⁹⁷Hg is 0.017 h^-1. What is its half life ?
Answer:

Question M.
The total binding energy of ⁵⁸Ni is 508 MeV. What is its binding energy per nucleon ?
Answer:
Given: B.E. of ⁵⁸Ni = 508 MeV,
A = 58
To find: Binding energy per nucleon \(\bar{B}\)

Question N.
Atomic mass of \({ }_{16}^{32} \mathrm{~S}\) is 31.97 u. If masses of neutron and H atom are 1.0087 u and 1.0078 u respectively. What is the mass defect ?
Answer:
Given: m = 31.97 u, Z = 16, A = 32
m_n = 1.0087 u
m_H = 1.0078 u
To find: Δm
Formula: Δm = Zm_H + (A – Z)m_n – m
Calculation: Δm = Zm_H + (A – Z)m_n – m
= 16 × 1.0078 + (16 × 1.0087) – 31.97
= [16.1248 + 16.1392] – 31.97
= 0.294 u
Ans: The mass defect is 0.294 u.

Question O.
Write the fusion reactions occuring in the Sun and stars.
Answer:
Fusion reactions occurring in the Sun and stars are can be represented as,

Question P.
How many α and β – particles are emitted in the trasmutation
\({ }_{90}^{232} \mathrm{Th} \longrightarrow{ }_{82}^{208} \mathrm{~Pb}\)
Answer:
\({ }_{90}^{232} \mathrm{Th} \longrightarrow{ }_{82}^{208} \mathrm{~Pb}\)
The emission of one α-particle decreases the mass number by 4 whereas the emission of β-particles has no effect on mass number.
Net decrease in mass number = 232 – 208 = 24.
This decrease is only due to α-particles. Hence, number of α-particles emitted = \(\frac {24}{4}\) = 6
Now, the emission of one α-particle decrease the atomic number by 2 and one β-particle emission increases it by 1.
The net decrease in atomic number = 90 – 82 = 8
The emission of 6 α-particles causes decrease in atomic number by 12. However, the actual decrease is only 8. Thus, atomic number increases by 4. This increase is due to emission of 4 β-particles.
Thus, 6 α and 4 β-particles are emitted.

Question Q.
A produces B by α- emission. If B is in the group 16 of periodic table, what is the group of A ?
Answer:

When α-emission occurs, atomic number decreases by 2 and atomic mass number by 4.
Thus, if ‘B’ belongs to group 16 of periodic table, that means outermost orbit will contain 6 electrons.
Thus, ‘A’ will have 8 electrons in its valence shell and it will belong to group 18 of the periodic table.

Question R.
Find the number of α and β- particles emitted in the process
\({ }_{86}^{222} \mathrm{Rn} \longrightarrow{ }_{84}^{214} \mathrm{PO}\)
Answer:
The emission of one α-particle decreases the mass number by 4 whereas the emission of β-particles has no effect on mass number.
Net decrease in mass number = 222 – 214 = 8. This decrease is only due to α-particle. Hence, number of α-particle emitted = 8/4 = 2
Now, the emission of one α-particle decreases the atomic number by 2 and one β-particle emission increases it by 1.
The net decrease in atomic number = 86 – 84 = 2
The emission of 2 α-particles causes decrease in atomic number by 4. However, the actual decrease is only 2. It means atomic number increases by 2. This increase is due to emission of 2 β-particles.
Thus, 2 α and 2 β-particles are emitted.

[Note: The above question is modified to include the final decay product so as to determine the number of α-particles and β-particles emitted in the process. Here, the final decay product is assumed to be Po-214.]

4. Solve the problems

Question A.
Half life of ¹⁸F is 110 minutes. What fraction of ¹⁸F sample decays in 20 minutes ?
Answer:
Given: t_1/2 = 110 min
t = 20 min
To find: Fraction of ¹⁸F simple that decays


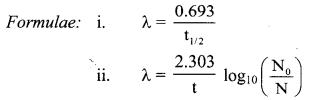
∴ Fraction of ¹⁸F sample that decays = 1 – 0.882 = 0.118
Ans: Fraction of ¹⁸F sample that decays in 20 minutes is 0.118.

Question B.
Half life of ³⁵S is 87.8 d. What percentage of ³⁵S sample remains after 180 d ?
Answer:
Given: t_1/2 = 87.8 d,
N₀ = 100,
t = 180 d
To find: % of ³⁵S that remains after 180 days

Question C.
Half life ⁶⁷Ga is 78 h. How long will it take to decay 12% of sample of Ga ?
Answer:
Given: t_1/2 = 78 h,
N₀ = 100,
N = 100 – 12 = 88
To find: t

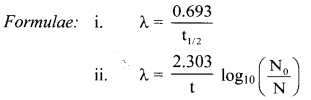
Question D.
0.5 g Sample of ²⁰¹Tl decays to 0.0788 g in 8 days. What is its half life ?
Answer:
Given: N₀ = 0.5 g,
N = 0.0788 g,
t = 8 days
To find: t_1/2

Question E.
65% of ¹¹¹In sample decays in 4.2 d. What is its half life ?
Answer:
Given: N₀ = 100,
N = 100 – 65 = 35,
t = 4.2d
To find: t_1/2

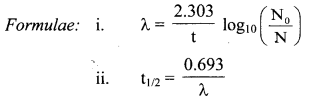
Question F.
Calculate the binding energy per nucleon of \({ }_{36}^{84} \mathrm{Kr}\) whose atomic mass is 83.913 u. (Mass of neutron is 1.0087 u and that of H atom is 1.0078 u).
Answer:
Given: A = 84, Z = 36,
m = 83.913 u
m_n = 1.0087 u
m_H = 1.0078 u
To find: Binding energy per nucleon \((\bar{B})\)

Question G.
Calculate the energy in Mev released in the nuclear reaction
\({ }_{77}^{174} \mathrm{Ir} \longrightarrow{ }_{75}^{170} \mathrm{Re}+{ }_{2}^{4} \mathrm{He}\)
Atomic masses : Ir = 173.97 u,
Re = 169.96 u and
He = 4.0026 u
Answer:
Given: m_Ir= 173.97 u
m_Re = 169.96 u
m_He = 4.0026 u
To find: Energy released
Formulae: i. Δm = (mass of ¹⁷⁴Ir) – (mass of ¹⁷⁰Re + mass of ⁴He)
ii. E = Δm × 931.4 MeV
Calculation:i. Δm = (mass of ¹⁷⁴Ir) – (mass of ¹⁷⁰Re + mass of ⁴He)
= 173.97 – (169.96 + 4.0026)
= 7.4 × 10^-3 u
ii. E = Δm × 931.4
= 7.4 × 10^-3 × 931.4
= 6.89236 MeV ≈ 6.892 MeV
Ans: The energy released in given nuclear reaction is 6.892 MeV.

Question H.
A 3/4 of the original amount of radioisotope decays in 60 minutes. What is its half life ?
Answer:

Question I.
How many – particles are emitted by 0.1 g of ²²⁶Ra in one year?
Answer:
Given: t = 1 y,
Amount of sample = 0.1 g
To find: Number of particles emitted

Activity = \(\frac{-\mathrm{d} \mathrm{N}}{\mathrm{dt}}\) = λN
= 4.28 × 10^-4 × 2.665 × 10²⁰ atoms
= 1.141 × 10¹⁷ particles/year
Ans: Particles emitted by 0.1 g of ²²⁶Ra in one year = 1.141 × 10¹⁷ particles/year.
[Note: The half-life of radium is 1620 years. In order to apply appropriate textual concept, we have used this value in calculation.]

Question J.
A sample of ³²P initially shows activity of one Curie. After 303 days the activity falls to 1.5× 10⁴ dps. What is the half life of ³²P ?
Answer:

Question K.
Half life of radon is 3.82 d. By what time would 99.9 % of radon will be decayed.
Answer:
Given: t_1/2 = 3.82 d,
N₀ = 100
N = 100 – 99.9 = 0.1
To find: t

Question L.
It has been found that the Sun’s mass loss is 4.34 × 10⁹ kg per second. How much energy per second would be radiated into space by the Sun ?
Answer:
Given: Sun’s mass loss = 4.34 × 10⁹ kg per second
To find: Energy radiated per second into space by Sun
calculation: Δm = 4.34 × 10⁹ kg per second
Now, 1.66 × 10^-27 kg = 1u
∴ Δm = \(\frac{4.34 \times 10^{9}}{1.66 \times 10^{-27}}\) u per second
= 2.614 × 10³⁶ u per second
Now, 1 u = 931.4 MeV
2.614 × 10³⁶ u per second = 2.614 × 10³⁶ × 931.4
= 2.435 × 10³⁹ MeV/s
Now, 1 MeV = 1.6022 × 10^-19 J and 1 eV = 1 × 10^-6 MeV
1 MeV = 1.6022 × 10^-13 J
= 1.6022 × 10^-16 LJ
E = 2.435 × 10³⁹ MeV/s × 1.6022 × 10^-16 kJ/MeV
= 3.901 × 10²³ kJ/s
Ans: Energy radiated per second into space by Sun is 3.901 × 10²³ kJ/s.

Question M.
A sample of old wood shows 7.0 dps/g. If the fresh sample of tree shows 16.0 dps/g, How old is the given sample of wood ? Half life of ¹⁴C 5730 y.
Answer:

Activity :

1. Discuss five applications of radioactivity for peaceful purpose.
Answer:

• Development in earth sciences: Like to understand various geographical changes occurring on earth.
• Development in space technology: To study nuclear reactions in stars which may lead to new discoveries.
• Development in medical sciences: Diagnosis and treatment of various diseases.
• Development in industries: As a potent source of electricity or a power generator.
• Development in agriculture: To study or monitor changes in soil like uptake of nutrients from the soil etc.

[Note: Students can use above points are reference to discuss topic in class].

2. Organize a trip to Bhabha Atomic Reasearch Centre, Mumbai to learn about nuclear reactor. This will have to be organized through your college.
Answer:
Students are expected to visit the place to understand more about nuclear reactors.

11th Chemistry Digest Chapter 13 Nuclear Chemistry and Radioactivity Intext Questions and Answers

Do you know? (Textbook Page no. 190)

Question 1.
How small is the nucleus in comparison to the rest of the atom?
Answer:
The radius of nucleus is of the order of 10^-15 m whereas that of the outer sphere is of the order of 10^-10 m. The size of outer sphere, is 10⁵ times larger than the nucleus i.e., if we consider the atom of size of football stadium then its nucleus will be the size of a pea.

(Textbook Page no. 191)

Question 1.
Identify the following nuclides as: isotopes, isobars and isotones.

Answer:

(Textbook Page No. 194)

Question 1.
i. What do you understand by the term rate of decay and give its mathematical expression.
ii. Why is minus sign required in the expression of decay rate?
Answer:
i. Rate of decay of a radioelement denotes the number of nuclei of its atoms which decay in unit time. It is also called activity of radioelement.
Rate of decay at any time t can be expressed as follows:
Rate of decay (activity) = \(-\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}\)
where, dN is the number of nuclei that decay within time interval dt.
ii. Minus sign in the expression indicates that the number of nuclei decreases with time. Therefore, dN is a negative quantity. But, the rate of decay is a positive quantity. The negative sign is introduced in the rate expression to make the rate positive.

Try this. (Textbook Page No. 194)

Question 1.
Prepare a chart of comparative properties of the above three types of radiations.
Answer:

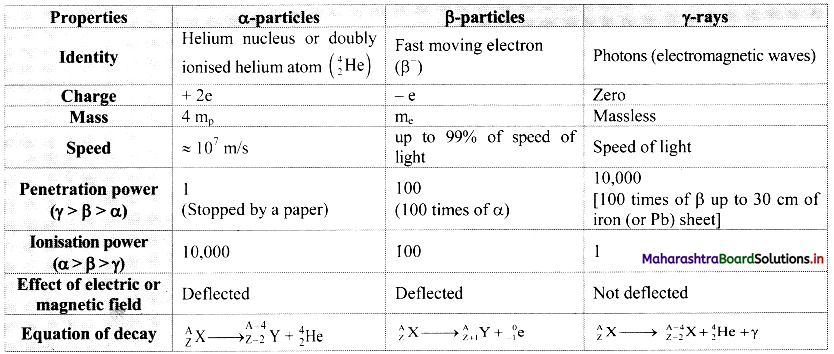
Just think (Textbook Page No. 195)

Question 1.
Does half-life increase, decrease or remain constant? Explain.
Answer:
Half-life of a particular radioelement remains constant at a given instant. A radioactive half-life refers to the amount of time it takes for half of the original isotope to decay. It is related to decay constant by the expression: t_1/2 = 0.693 / λ

From the expression, it is evident that half-life of a radio isotope is dependent only on the decay constant and is independent of the initial amount of the radio isotope. Each successive half-life in which the amount of radio isotope decreases to its half value is the same.

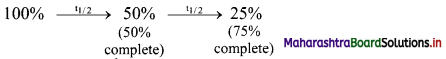
Thus, half-life remains constant.

Try this (Textbook Page No. 198)

Question 1.
²⁴Mg and ²⁷Al, both undergo (α, n) reactions and the products are radioactive. These emit β particles having positive charge (called positrons). Write balanced nuclear reactions in both.
Answer:

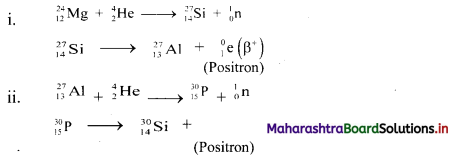
Do you know? (Textbook Page No. 198)

Question 1.
What is the critical mass of ²³⁵U?
Answer:
i. The critical mass is the minimum mass of uranium-235 required to achieve a self-sustaining fission chain reaction under stated conditions.
ii. The chain reaction in fission of U-235 becomes self-sustaining when the critical mass of uranium-235 is about 50 kilograms.

Activity (Textbook Page No. 200)

Question 1.
You have learnt in Std. 9th, medical, industrial and agricultural applications of radioisotopes. Write at least two applications each.
Answer:
i. The uses of radioactive isotopes in the field of medicine:
a. Polycythaemia: The red blood cell count increases in the disease polycythaemia. Phosphorus-32 is used in its treatment.
b. Bone cancer: Strontium-89, strontium-90, samarium-153 and radium-223 are used in the treatment of bone cancer.

ii. The uses of radioactive isotopes in the industrial field:
a. Luminescent paint and radioluminescence: The radioactive substances radium, promethium, tritium with some phosphorus are used to make certain objects visible in the dark.
e.g. Hands of a clock, krypton-85 is used in HID (High Intensity Discharge) lamps.
b. Use in ceramic articles:
1. Luminous colours are used to decorate ceramic tiles, utensils, plates, etc.
2. Uranium oxide was earlier used to colour ceramics.

iii. The uses of radioactive isotopes in the agriculture field:
a. The genes and chromosomes that give seeds its properties like fast growth, higher productivity, etc., can be modified by means of radiation.
b. Onions and potatoes are irradiated with gamma rays from cobalt-60 to prevent their sprouting.