Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 11 Adsorption and Colloids Textbook Exercise Questions and Answers.
Adsorption and Colloids Class 11 Exercise Question Answers Solutions Maharashtra Board
Class 11 Chemistry Chapter 11 Exercise Solutions Maharashtra Board
Chemistry Class 11 Chapter 11 Exercise Solutions
1. Choose the correct option.
Question A.
The size of colloidal particles lies between
a. 10-10 m and 10-9 m
b. 10-9 m and 10-6 m
c. 10-6 m and 10-4 m
d. 10-5 m and 10-2 m
Answer:
b. 10-9 m and 10-6 m
Question B.
Gum in water is an example of
a. true solution
b. suspension
c. lyophilic sol
d. lyophobic sol
Answer:
c. lyophilic sol
Question C.
In Haber process of production of ammonia K2O is used as
a. catalyst
b. inhibitor
c. promotor
d. adsorbate
Answer:
c. promotor
Question D.
Fruit Jam is an example of-
a. sol
b. gel
c. emulsion
d. true solution
Answer:
b. gel
![]()
2. Answer in one sentence :
Question A.
Name type of adsorption in which van der Waals focres are present.
Answer:
Physical adsorption or physisorption.
Question B.
Name type of adsorption in which compound is formed.
Answer:
Chemical adsoiption or chemisorption.
Question C.
Write an equation for Freundlich adsorption isotherm.
Answer:
Freundlich proposed the following empirical equation for adsorption of a gas on solid.
\(\frac{x}{\mathrm{~m}}\) = k P1/n (n > 1) ……(i)
where,
x = Mass of the gas adsorbed
m = Mass of the adsorbent
\(\frac{x}{\mathrm{~m}}\) = Mass of gas adsorbed per unit mass of adsorbent
P = Equilibrium pressure
k and n are constants which depend on the nature of adsorbate, adsorbent and temperature.
![]()
3. Answer the following questions:
Question A.
Define the terms:
a. Inhibition
b. Electrophoresis
c. Catalysis.
Answer:
a. Inhibition:
The phenomenon in which the rate of chemical reaction is reduced by an inhibitor is called inhibition.
b. Electrophoresis:
The movement of colloidal particles under an applied electric potential is called electrophoresis.
c. Catalysis:
The phenomenon of increasing the rate of a chemical reaction with the help of a catalyst is known as catalysis.
Question B.
Define adsorption. Why students can read blackboard written by chalks?
Answer:
- Adsorption is the phenomenon of accumulation of higher concentration of ‘one substance on the surface of another (in bulk) due to unbalanced/unsatisfied attractive forces on the surface.
- When we write on blackboard using chalk, the chalk particles get adsorbed on the surface of the blackboard.
Hence, students can read blackboard written by chalks.
Question C.
Write characteristics of adsorption.
Answer:
Following are the characteristics of adsorption:
- Adsorption is a surface phenomenon.
- It depends upon the surface area of the adsorbent.
- It involves physical forces (van der Waals forces) or chemical forces (chemical or covalent bonds).
- Adsorbate is always present in higher concentration on the surface of an adsorbent than in the bulk.
- Adsorption is dependent on temperature (of the surface) and pressure (of adsorbate gas).
- It takes place with the evolution of heat (with some exceptions).
Question D.
Distinguish between Lyophobic and Lyophilic sols.
Answer:
Lyophobic sols (colloids):
- Lyophobic sols are formed only by special methods.
- They are irreversible.
- These are unstable and hence, require traces of stabilizers.
- Addition of small amount of electrolytes causes precipitation or coagulation of lyophobic sols.
- Viscosity of lyophobic sol is nearly the same as the dispersion medium.
- Surface tension of lyophobic sol is nearly the same as the dispersion medium.
Lyophilic sols (colloids):
- Lyophilic sols are formed easily by direct mixing.
- They are reversible.
- These are self-stabilized.
- Addition of large amount of electrolytes causes precipitation or coagulation of lyophilic sols.
- Viscosity of lyophilic sol is much higher than that of the dispersion medium.
- Surface tension of lyophilic sol is lower than that of dispersion medium.
![]()
Question E.
Identify dispersed phase and dispersion medium in the following colloidal dispersions.
a. milk
b. blood
c. printing ink
d. fog
Answer:
| Colloidal dispersion | Dispersed phase | Dispersion medium |
| Milk | Liquid | Liquid |
| Blood | Solid | Liquid |
| Printing ink | Solid | Liquid |
| Fog | Liquid | Gas |
Question F.
Write notes on :
a. Tyndall effect
b. Brownian motion
c. Types of emulsion
d. Hardy-Schulze rule
Answer:
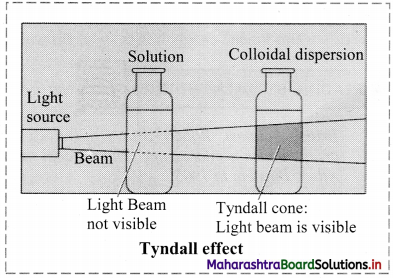
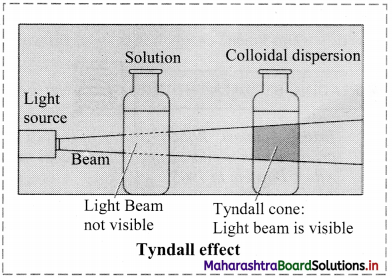
a. Tyndall effect:
i. Tyndall observed that when light passes through true solution, the path of light through it cannot be detected.
ii. However, if the light passes through a colloidal dispersion, the particles scatter some light in all directions and the path of the light through colloidal dispersion becomes visible to observer standing at right angles to its path.
iii. The phenomenon of scattering of light by colloidal particles and making path of light visible through the dispersion is referred as Tyndall effect and the bright cone of the light is called Tyndall cone.
iv. Tyndall effect is observed only when the following conditions are satisfied.
- The diameter of the dispersed particles is not much smaller than the wavelength of light used.
- The refractive indices of dispersed phase and dispersion medium differ largely.
v. Significance of Tyndall effect:
- It is useful in determining number of particles in colloidal system and their particle size.
- It is used to distinguish between colloidal dispersion and true solution.
b. Brownian motion:
i. The colloidal or microscopic particles undergo ceaseless random zig-zag motion in all directions in a fluid. This motion of dispersed phase particles is called Brownian motion.
ii. Cause of Brownian motion:
- Particles of the dispersed phase constantly collide with the fast-moving molecules of dispersion medium (fluid).
- Due to this, the dispersed phase particles acquire kinetic energy from the molecules of the dispersion medium.
- This kinetic energy brings about Brownian motion.
c. Types of emulsion:
iii. There are two types of emulsions:
a. Emulsion of oil in water (o/w type): An emulsion in which dispersed phase is oil and dispersion medium is water is called emulsion of oil in water.
e.g. 1. Milk consists of particles of fat dispersed in water.
2. Other examples include vanishing cream, paint, etc.
b. Emulsion of water in oil (w/o type): An emulsion in which dispersed phase is water and dispersion medium is oil is called emulsion of water in oil.
e.g. 1. Cod liver oil consists of particles of water dispersed in oil.
2. Some other examples of this type include butter, cream, etc.
d. Hardy-Schulze rule:
i. Generally, greater the valency of the flocculating ion added, greater is its power to cause precipitation. This is known as Hardy-Schulze rule.
ii. In the coagulation of negative sol, the flocculating power follows the following order:
Al3+ > Ba2+ > Na+
iii. Similarly, in the coagulation of positive sol, the flocculating power is in the following order:
[Fe (CN)6]4- > PO43- > SO42- > Cl–
Question G.
Explain Electrophoresis in brief with the help of diagram. What are its applications ?
Answer:
i. Electrophoresis: Electrophoresis set up is shown in the diagram below.
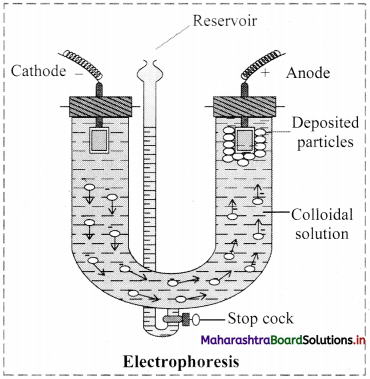
- The diagram shows U tube set up in which two platinum electrodes are dipped in a colloidal solution.
- When electric potential is applied across two electrodes, colloidal particles move towards one or other electrode.
- The movement of colloidal particles under an applied electric potential is called electrophoresis.
- Positively charged particles move towards cathode while negatively charged particles migrate towards anode and get deposited on the respective electrode.
ii. Applications of electrophoresis:
- On the basis of direction of movement of the colloidal particles under the influence of electric field, it is possible to know the sign of charge on the particles.
- It is also used to measure the rate of migration of sol particles.
- Mixture of colloidal particles can be separated by electrophoresis, since different colloidal particles in mixture migrate with different rates.
![]()
Question H.
Explain why finely divided substance is more effective as adsorbent?
Answer:
- Adsorption is a surface phenomenon and hence, the extent of adsorption depends upon surface area of the adsorbent.
- Adsorption increases with increase in surface area of the adsorbent.
- Finely divided powdered substances provide larger surface area for a given mass.
Hence, finely divided substance is more effective as adsorbent.
Question I.
What is the adsorption Isotherm?
Answer:
The relationship between the amount of a substance adsorbed per unit mass of adsorbent and the equilibrium pressure (in case of gas) or concentration (in case of solution) at a given constant temperature is called an adsorption isotherm.
Question J.
Aqueous solution of raw sugar, when passed over beds of animal charcoal, becomes colourless. Explain.
Answer:
- When aqueous solution of raw sugar is passed over beds of animal charcoal, charcoal adsorbs the coloured particles from the raw sugar.
- Thus, due to the adsorption of coloured particles, raw sugar becomes colourless when passed over beds of animal charcoal.
Question K.
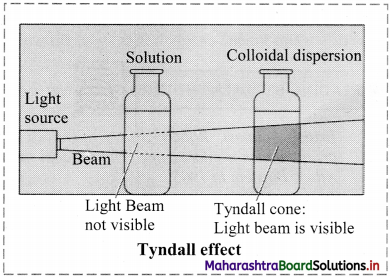
What happens when a beam of light is passed through a colloidal sol?
Answer:
i. When a beam of light is passed through colloidal sol, it is observed that the colloidal particles scatter some of the incident light in all directions.
ii. Because of this scattering of light, the path of light through the colloidal dispersion becomes visible to observer standing at right angles to its path and the phenomenon is known as Tyndall effect.
iii.
Question L.
Mention factors affecting adsorption of gas on solids.
Answer:
Adsorption of gases on solids depends upon the following factors:
- Nature of adsorbate (gas)
- Nature of solid adsorbent
- Surface area of adsorbent
- Temperature of the surface
- Pressure of the gas
![]()
Question M.
Give four uses of adsorption.
Answer:
i. Catalysis (Heterogeneous catalysis):
- The solid catalysts are used in many industrial manufacturing processes.
- For example, iron is used as a catalyst in manufacturing of ammonia, platinum in manufacturing of sulphuric acid, H2SO4 (by contact process) while finely divided nickel is employed as a catalyst in hydrogenation of oils.
ii. Gas masks:
- It is a device which consists of activated charcoal or mixture of adsorbents.
- It is used for breathing in coal mines to avoid inhaling of the poisonous gases.
iii. Control of humidity: Silica and alumina gels are good adsorbents of moisture.
iv. Production of high vacuum:
- Lowering of temperature at a given pressure, increases the rate of adsorption of gases on charcoal powder. By using this principle, high vacuum can be attained by adsorption.
- A vessel evacuated by vacuum pump is connected to another vessel containing coconut charcoal cooled by liquid air. The charcoal adsorbs the remaining traces of air or moisture to create a high vacuum.
Question N.
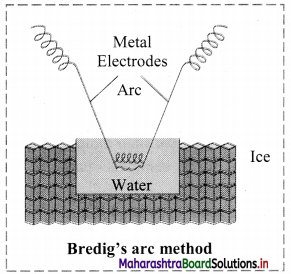
Explain Bredig’s arc method.
Answer:
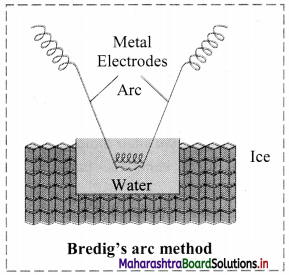
- Colloidal sols can be prepared by electrical disintegration using Bredig’s arc method.
- This process involves vaporization as well as condensation.
- Colloidal sols of metals such as gold, silver, platinum can be prepared by this method.
- In this method, electric arc is struck between electrodes of metal immersed in the dispersion medium.
- The intense heat produced vapourizes the metal which then condenses to form particles of colloidal sol.
Question O.
Explain the term emulsions and types of emulsions.
Answer:
i. A colloidal system in which one liquid is dispersed in another immiscible liquid is called an emulsion.
ii. There are liquid-liquid colloidal systems in which both liquids are either completely or partially immiscible.
iii. There are two types of emulsions:
a. Emulsion of oil in water (o/w type): An emulsion in which dispersed phase is oil and dispersion medium is water is called emulsion of oil in water.
e.g. 1. Milk consists of particles of fat dispersed in water.
2. Other examples include vanishing cream, paint, etc.
b. Emulsion of water in oil (w/o type): An emulsion in which dispersed phase is water and dispersion medium is oil is called emulsion of water in oil.
e.g. 1. Cod liver oil consists of particles of water dispersed in oil.
2. Some other examples of this type include butter, cream, etc.
![]()
4. Explain the following :
Question A.
A finely divided substance is more effective as adsorbent.
Answer:
- Adsorption is a surface phenomenon and hence, the extent of adsorption depends upon the surface area of the adsorbent.
- Adsorption increases with an increase in surface area of the adsorbent.
- Finely divided powdered substances provide a larger surface area for a given mass. Hence, a finely divided substance is more effective as an adsorbent.
Question B.
Freundlich adsorption isotherm, with the help of a graph.
Answer:
Graphical representation of the Freundlich adsorption isotherm:
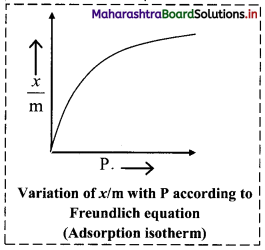
i. Freundlich proposed the following empirical equation for adsorption of a gas on solid.
\(\frac{x}{\mathrm{~m}}\) = k P1/n (n > 1) ………(i)
where,
x = Mass of the gas adsorbed
m = Mass of the adsorbent
\(\frac{x}{\mathrm{~m}}\) = Mass of gas adsorbed per unit mass of adsorbent
P = Equilibrium pressure
k and n are constants which depend on the nature of adsorbate, adsorbent and temperature.
ii. The graphical representation of Freundlich equation is as shown in the adjacent plot of x/m vs ‘P’.
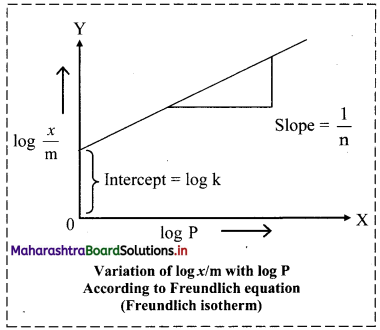
iii. In case of solution, P in the equation (i) is replaced by the concentration (C) and thus,
\(\frac{x}{\mathrm{~m}}\) = k C1/n ………(ii)
iv. By taking logarithm on both sides of the equation (ii),
we get
log \(\frac{x}{\mathrm{~m}}\) = log k + \(\frac{1}{n}\) log C ……..(iii)
v. On plotting a graph of log \(\frac{x}{\mathrm{~m}}\) against log C or log P, a straight line is obtained as shown in the adjacent plot. The slope of the straight line is and intercept on Y-axis is log k.
vi. The factor \(\frac{1}{n}\) ranges from 0 to 1. Equation (iii) holds good over limited range of pressures.
a. When \(\frac{1}{n}\) → 0, \(\frac{x}{\mathrm{~m}}\) → constant, the adsorption is independent of pressure.
b. When \(\frac{1}{n}\) = 1, \(\frac{x}{\mathrm{~m}}\) = k P, i.e., \(\frac{x}{\mathrm{~m}}\) ∝ P, the adsorption varies directly with pressure.
c. The experimental isotherms tend to saturate at high pressure.
5. Distinguish between the following :
Question A.
Adsorption and absorption. Give one example.
Answer:
Adsorption:
- Adsorption is a surface phenomenon as adsorbed matter is concentrated only at the surface and does not penetrate through the surface to the bulk of adsorbent.
- Concentration of the adsorbate is high only at the surface of the adsorbent.
- It is dependent on temperature and pressure.
- It is accompanied by evolution of heat known as heat of adsorption.
- It depends on surface area.
e.g. Adsoiption of a gas or liquid like acetic acid by activated charcoal.
Absorption:
- Absorption is a bulk phenomenon as absorbed matter is uniformly distributed inside as well as at the surface of the bulk of substance.
- Concentration of the absorbate is uniform throughout the bulk of the absorbent.
- It is independent of temperature and pressure.
- It may or may not be accompanied by any evolution or absorption of heat.
- It is independent of surface area.
e.g. Absorption of water by cotton, absorption of ink by blotting paper.
![]()
Question B.
Physisorption and chemisorption. Give one example.
Answer:
Physisorption:
- In physisorption, the forces operating are weak van der Waals forces.
- It is not specific in nature as all gases adsorb on all solids. For example, all gases adsorb on charcoal.
- The heat of adsorption is low and lies in the range 20-40 kJ mol-1.
- It occurs at low temperature and decreases with an increase of temperature.
- It is reversible.
- Physisorbed layer may be multimolecular layer of adsorbed particles under high pressure.
e.g. At low temperature N2 gas is physically adsorbed on iron.
Chemisorption:
- In chemisorption, the forces operating are of chemical nature (covalent or ionic bonds).
- It is highly specific and occurs only when chemical bond formation is possible between adsorbent and adsorbate. For example, adsorption of oxygen on tungsten, hydrogen on nickel, etc.
- The heat of adsorption is high and lies in the range 40-200 kJ mol-1.
- It is favoured at high temperature, however, the extent of chemical adsorption is lowered at very high temperature due to bond breaking.
- It is irreversible.
- Chemisorption forms monomolecular layer of adsorbed particles.
e.g. N2 gas chemically adsorbed on iron at high temperature forms a layer of iron nitride, which desorbs at very high temperature.
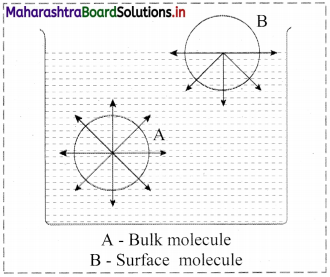
6. Adsorption is surface phenomenon. Explain.
Answer:
Consider a surface of a liquid or a solid.
- The molecular forces at the surface of a liquid are unbalanced or in unsaturation state.
- In solids, the ions or molecules at the surface of a crystal do not have their forces satisfied by the close contact with other particles.
- Because of the unsaturation, solid and liquid surfaces tend to attract gases or dissolved substances with which they come in close contact. Thus, the substance accumulates on the surface of solid or liquid i.e., the substance gets adsorbed on the surface.
Hence, adsorption is a surface phenomenon.
7. Explain how the adsorption of gas on solid varies with
a. nature of adsorbate and adsorbent
b. surface area of adsorbent
Answer:
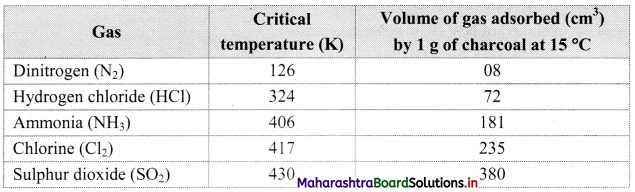
i. a. Nature of adsorbate:
1. All solids adsorb gases to some extent. It is observed that gases having high critical temperature liquify easily and can be readily adsorbed.
2. The gases such as SO2, Cl2, NH3 which are easily liquefiable are adsorbed to a larger extent as compared to gases such as N2, O2, H2, etc. which are difficult to liquify.
3. Thus, the amount of gas adsorbed by a solid depends on the nature of the adsorbate gas i.e., whether it is easily liquefiable or not.
b. Nature of adsorbent: Substances which provide large surface area for a given mass are effective as adsorbents and adsorb appreciable volumes of gases.
e.g. Silica gel and charcoal are effective adsorbents due to their porous nature.
ii. Surface area of the adsorbent:
- Adsorption is a surface phenomenon. Hence, the extent of adsorption increases with increase in surface area of the adsorbent.
- Finely divided substances, rough surfaces, colloidal substances are good adsorbents as they provide larger surface area for a given mass.
Note: Critical temperature of some gases and volume adsorbed.
8. Explain two applications of adsorption.
Answer:
i. Catalysis (Heterogeneous catalysis):
- The solid catalysts are used in many industrial manufacturing processes.
- For example, iron is used as a catalyst in manufacturing of ammonia, platinum in manufacturing of sulphuric acid, H2SO4 (by contact process) while finely divided nickel is employed as a catalyst in hydrogenation of oils.
ii. Gas masks:
- It is a device which consists of activated charcoal or mixture of adsorbents.
- It is used for breathing in coal mines to avoid inhaling of the poisonous gases.
![]()
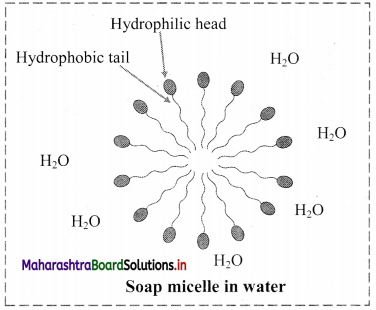
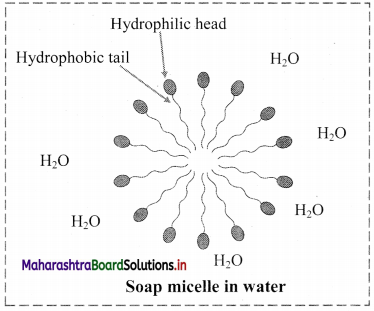
9. Explain micelle formation in soap solution.
Answer:
- Soap molecule has a long hydrophobic hydrocarbon chain called tail which is attached to hydrophilic ionic carboxylate group, called head.
- In water, the soap molecules arrange themselves to form spherical particles that are called micelles.
- In each micelle, the hydrophobic tails of soap molecules point to the centre and the hydrophilic heads lie on the surface of the sphere.
- As a result of this, soap dispersion in water is stable.
10. Draw labelled diagrams of the following :
a. Tyndall effect
b. Dialysis
c. Bredig’s arc method
d. Soap micelle
Answer:
a. Tyndall effect:
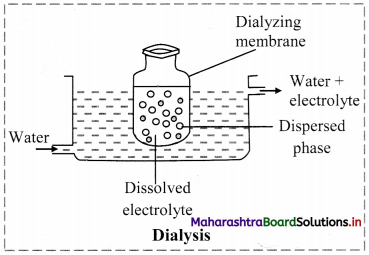
b. Dialysis:
c. Bredig’s arc method:
d. Soap micelle:
Activity :
Collect the information about methods to study surface chemistry.
Answer:
Following are the few methods that are employed to study surface chemistry.
i. X-ray photoelectron spectroscopy:
It is a surface-sensitive spectroscopic technique which is used to measure elemental composition of the surface, to determine elements that are present as contaminants on the surface, etc.
ii. Auger electron spectroscopy:
It is a common analytical technique which is used to study surfaces of materials.
iii. Temperature programmed desorption (TPD):
Adsorbed molecules get desorbed when the surface temperature is increased. TPD technique is used to observe these desorbed molecules and helps in providing information about binding energy between the adsorbate and adsorbent.
iv. Scanning Electron Microscopy:
In this technique, a scanning electron microscope is used to focus electron beam over the surface of the sample to be examined. The electron beam interacts with the sample and an image is obtained. This image provides information about surface structure and composition of the sample.
[Note: Students are expected to collect additional information about surface chemistry on their own.]
![]()
11th Chemistry Digest Chapter 11 Adsorption and Colloids Intext Questions and Answers
Can you tell? (Textbook Page No. 160)
Question 1.
What is adsorption?
Answer:
Adsorption is the phenomenon of accumulation of higher concentration of one substance on the surface of another (in bulk) due to unbalanced/unsatisfied attractive forces on the surface.
Try this. (Textbook Page No. 161)
Question 1.
Dip a chalk in ink. What do you observe?
Answer:
When a chalk is dipped in ink, it is observed that the ink molecules are adsorbed at the surface of chalk and the surface becomes coloured, while the solvent of the ink goes deeper into the chalk due to absorption.
Internet my friend. (Textbook Page No. 172)
Question i.
Brownian motion
Answer:
Students can search relevant videos on YouTube to visualize Brownian motion.
Question ii.
Collect information about Brownian motion.
Answer:
i. The colloidal or microscopic particles undergo ceaseless random zig-zag motion in all directions in a fluid. This motion of dispersed phase particles is called Brownian motion.
ii. Cause of Brownian motion:
- Particles of the dispersed phase constantly collide with the fast-moving molecules of dispersion medium (fluid).
- Due to this, the dispersed phase particles acquire kinetic energy from the molecules of the dispersion medium.
- This kinetic energy brings about Brownian motion.
![]()
Internet my friend. (Textbook Page No. 172)
Question 1.
Collect information about surface chemistry.
Answer:
- Surface or interface represents the boundary which separates two bulk phases.
e.g. Boundary between water and its vapour is a liquid-gas interface. - Certain properties of substances, particularly of solids and liquids, depend upon the nature of the surface.
- An interface usually has a thickness of a few molecules. However, its area depends on the size of the bulk phase particles.
- Commonly considered bulk phases may be pure compounds or solutions.
- A number of important phenomena, namely, dissolution, crystallization, heterogeneous catalysis, electrode processes and corrosion take place at an interface.
- Thus, study of chemistry of surfaces is critical to many applications in industry, analytical investigations and day-to-day activities such as cleaning and softening of water.
- The branch of chemistry which deals with the nature of surfaces and changes occurring on the surfaces is called surface chemistry.
- Study of surfaces requires a rigorously clean surface. An ultra-clean metal surface can be obtained under very high vacuum, of the order of 10-8 to 10-9 pascal.
- Adsorption, catalysis and colloids (such as emulsions and gels) are some of the important aspects of surface chemistry.
[Note: Students are expected to collect additional information about surface chemistry on their own.]
Activity. (Textbook Page No. 172)
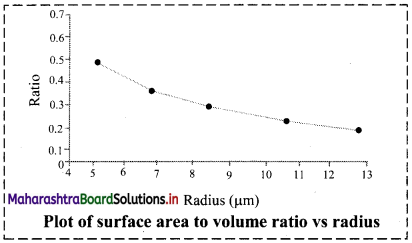
Question 1.
Calculate surface area to volume ratio of spherical particle. See how the ratio increases with the reduction of radius of the particle. Plot the ratio against the radius.
Answer:
The graph below shows that as the radius of the spherical particle decreases, the surface to volume ratio increases steadily.
11th Std Chemistry Questions And Answers:
- Elements of Group 13, 14 and 15 Class 11 Chemistry Questions And Answers
- States of Matter Class 11 Chemistry Questions And Answers
- Adsorption and Colloids Class 11 Chemistry Questions And Answers
- Chemical Equilibrium Class 11 Chemistry Questions And Answers
- Nuclear Chemistry and Radioactivity Class 11 Chemistry Questions And Answers
- Basic Principles of Organic Chemistry Class 11 Chemistry Questions And Answers
- Hydrocarbons Class 11 Chemistry Questions And Answers
- Chemistry in Everyday Life Class 11 Chemistry Questions And Answers
