Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 14 Basic Principles of Organic Chemistry Textbook Exercise Questions and Answers.
Basic Principles of Organic Chemistry Class 11 Exercise Question Answers Solutions Maharashtra Board
Class 11 Chemistry Chapter 14 Exercise Solutions Maharashtra Board
Chemistry Class 11 Chapter 14 Exercise Solutions
1. Answer the following :
Question A.
Write condensed formulae and bond line formulae for the following structures.
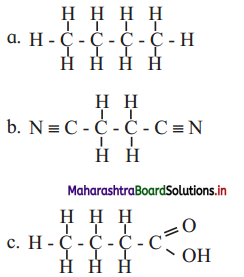
Answer:
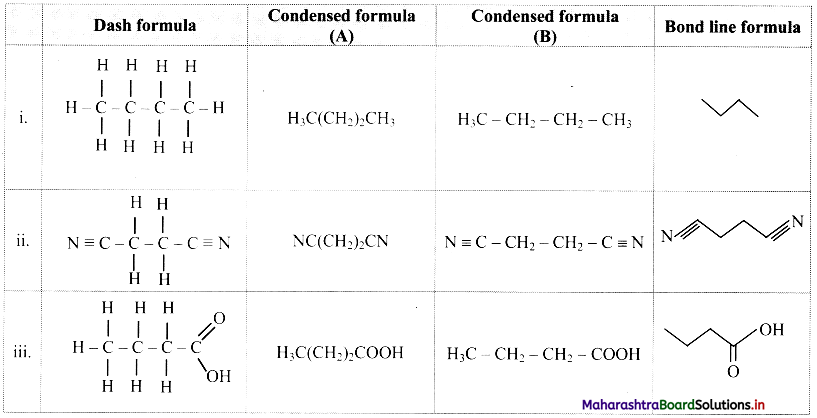
Question B.
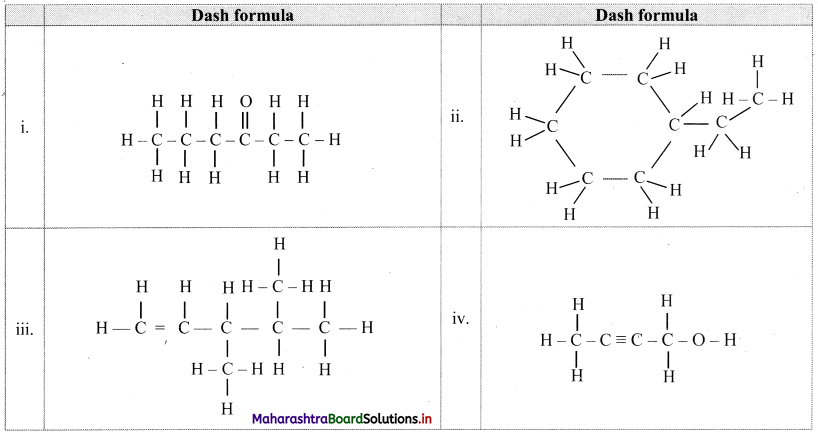
Write dash formulae for the following bond line formulae.
Answer:
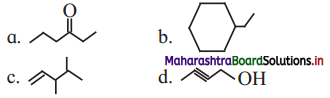
Question C.
Write bond line formulae and condensed formulae for the following compounds
a. 3-methyloctane
b. hept-2-ene
c. 2, 2, 4, 4- tetramethylpentane
d. octa-1,4-diene
e. methoxyethane
Answer:
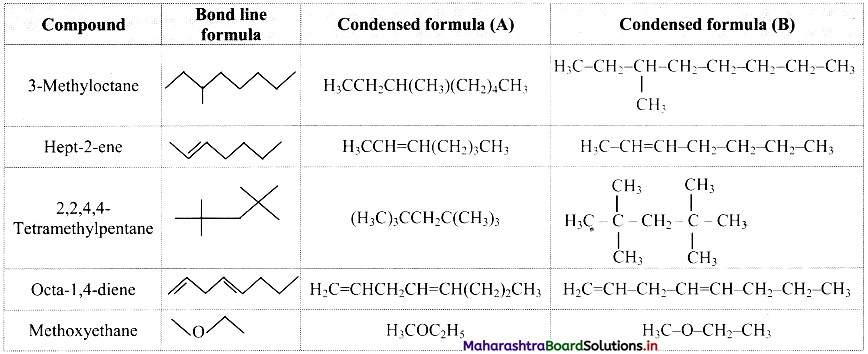
![]()
Question D.
Write the structural formulae for the following names and also write correct IUPAC names for them.
a. 5-ethyl-3-methylheptane
b. 2,4,5-trimethylthexane
c. 2,2,3-trimethylpentan-4-01
Answer:
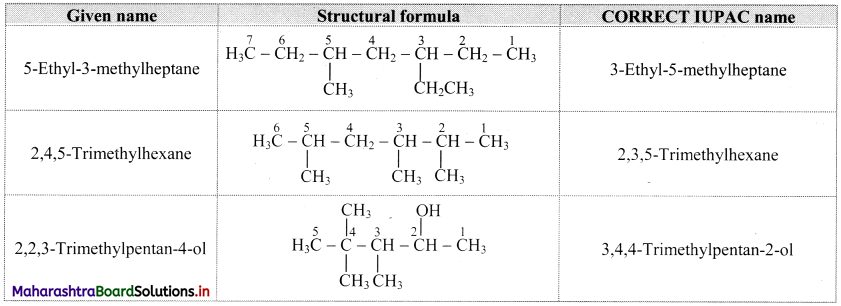
Question E.
Identify more favourable resonance structure from the following. Justify.
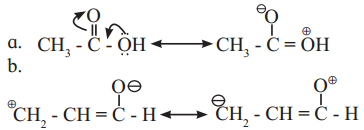
Answer:
a.
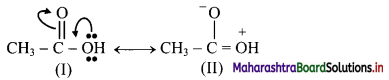
Structure (I) will be more favourable resonance structure as structure (II) involves separation of opposite charges and the electronegative oxygen atom has a positive charge.
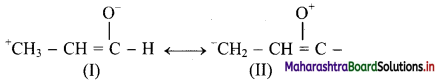
Both structures (I) and (II) involves separation of opposite charges, but structure (I) has a positive charge on the more electropositive ‘C’ and a negative charge on more electronegative ‘O’. Thus, structure (I) will be more favourable resonance structure.
Question F.
Find out all the functional groups present in the following polyfunctional compounds.
a. Dopamine a neurotransmitter that is deficient in Parkinson’s disease.
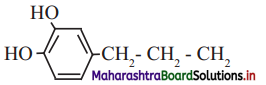
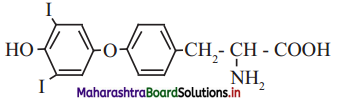
b. Thyroxine the principal thyroid hormone.
c. Penicillin G, a naturally occurring antibiotic

Answer:
i. Functional groups: Phenolic -OH group (Ar-OH) and primary amine (-NH2) group are present in dopamine.
ii. Functional groups: Phenolic -OH group (Ar-OH), halide (-I), ether (Ar-O-Ar), primary amine (-NH2) carboxylic acid (-COOH) groups are present in thyroxine.
iii. Functional groups: Secondary amide
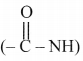 ,
,
carboxylic acid (-COOH), tertiary amide
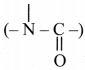 ,
,
thioether (R-S-R) groups are present in penicillin G.
![]()
Question G.
Find out the most stable species from the following. Justify.
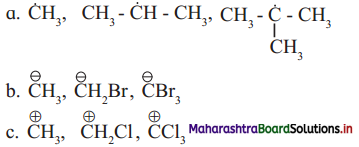
Answer:
a. The most stable species from the given species is \(\left(\mathrm{H}_{3} \mathrm{C}\right)_{3} \dot{\mathrm{C}}\) i.e., tert-butyl radical.
This is because it has greater number of alkyl groups attached to the C-atom having unpaired electron. More the number of the alkyl groups, the greater will be +1 inductive (electron releasing) effect, and thereby greater will be the stability of the free radical.
b. The most stable species from the given species is \(\mathrm{CBr}_{3}^{-}\).
This is because it contains 3 -Br atoms, which exhibits electron withdrawing inductive effect. Carbanions are stabilized by -I inductive (electron withdrawing) effect. Larger the number of -I groups attached to the negatively charged carbon atom, lower will be the electron density on the carbon atom and higher will be its stability.
c. The most stable species from the given species is \(\stackrel{+}{\mathbf{C}} \mathbf{H}_{3}\).
This because it does not contain Cl atom, which exhibits electron withdrawing inductive effect. Carbocations are destabilized by -I inductive (electron withdrawing) effect. When more number of-I groups are attached to the positively charged carbon atom, the positive charge on the carbon atom increases further, thus destabilizing the species. Hence, the species with no -I groups will be most stable.
Question H.
Identify the α-carbons in the following species and give the total number of α-hydrogen in each.
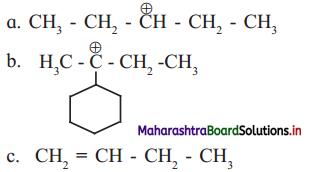
Answer:
a.
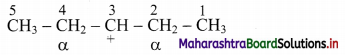
In structure (i), C-2 and C-4 are α-carbon atoms.
Hydrogen atoms(s) attached to α-C atoms is a α-H atom. Thus, structure (i) contains 4 α-H atoms.
b.
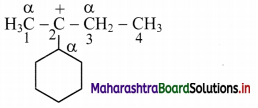
In structure (ii), carbon atoms adjacent to C-2 are α-carbon atoms (as shown in the structure).
Thus, structure (ii) contains 6 α-H atoms.
c.
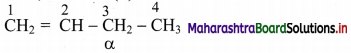
C-3 carbon atom, that is, C-atom next to (H2C=CH-) is a α-C atom.
Thus, structure (iii) contains 2 α-H atoms.
Question I.
Identify primary, secondary, tertiary and quaternary carbon in the following compounds.
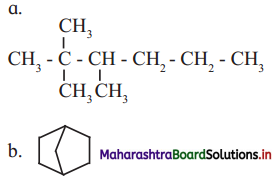
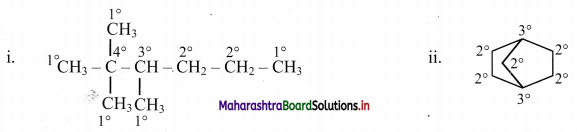
Answer:
2. Match the pairs
| Column ‘A’ | Column ‘B’ | ||
| i. | Inductive effect | a. | Delocalization of π electrons |
| ii. | Hyperconjugation | b. | Displacement of π electrons |
| iii. | Resonance effect | c. | Delocalization of σ electrons |
| d. | Displacement of σ electrons |
Answer:
i – d,
ii – c,
iii – a
![]()
3. What is meant by homologous series ? Write the first four members of homologous series that begins with
A. CH3CHO
B. H-C≡C-H
Also write down their general molecular formula.
Answer:
Homologous series: A series of compounds of the same family in which each member has the same type of carbon skeleton and functional group, and differs from the next member by a constant difference of one methylene group (-CH2-) in its molecular and structural formula is called as homologous series.
A. CH3CHO :
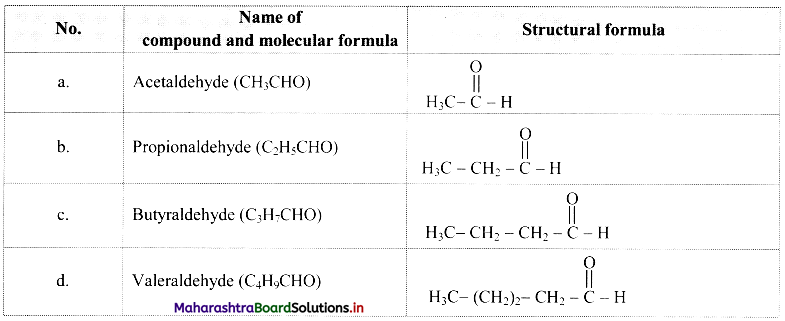
Comparing these molecular formulae and assigning the number of carbon atoms as ‘n’, the following general formula is deduced: CnH2nO/CnH2n-1CHO (where n = 1, 2, 3, …).
B. H-C≡C-H :

Comparing these molecular formulae and assigning the number of carbon atoms as ‘n’, the following general formula is deduced: CnH2n-2 (where n = 2, 3,4,….).
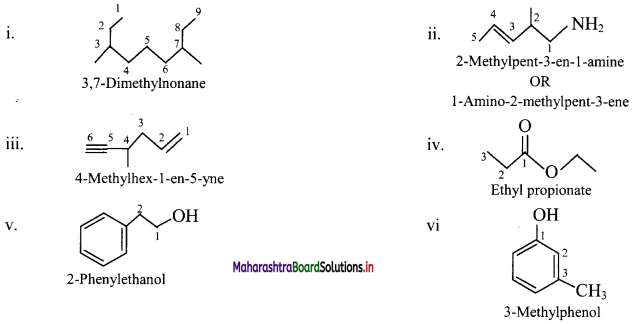
4. Write IUPAC names of the following

Answer:
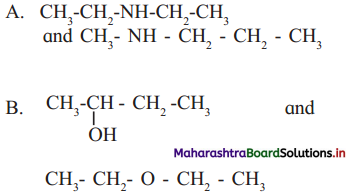
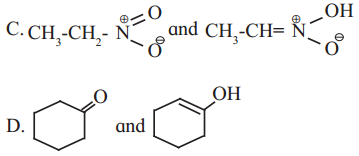
5. Find out the type of isomerism exhibited by the following pairs.
Answer:
A. Metamerism
B. Functional group isomerism
C. Tautomerism
D. Tautomerism
![]()
6. Draw resonance srtuctures of the following :
A. Phenol
B. Benzaldehyde
C. Buta-1,3-diene
D. Acetate ion
Answer:
A. Resonance structures for phenol:
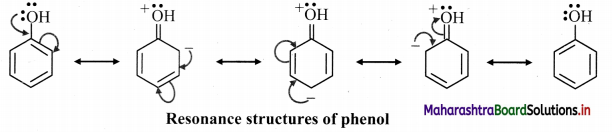
B. Resonance structures of benzaldehyde:
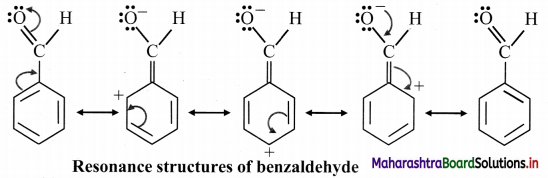
C. Resonance structures of Buta-1,3-diene:
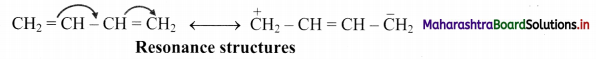
D. Resonance structures of acetate ion:
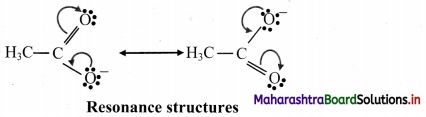
7. Distinguish :
Question A.
Inductive effect and resonance effect
Answer:
Inductive effect:
- Presence of polar covalent bond is required.
- The polarity is induced in adjacent carbon- carbon single (covalent) bond due to a presence of influencing group (more electronegative atom than carbon).
- Depending on the nature of influencing group it is differentiated as +I effect and -I effect.
- The direction of the arrow head denotes the direction of the permanent electron displacement.
Resonance effect:
- Presence of conjugated n electron system or species having an atom carrying p orbital attached to a multiple bond is required.
- The polarity is produced in the molecule by the interaction of conjugated π bonds (or that between π bond and p orbital on the adjacent atom).
- Depending on the nature of influencing group it is differentiated as +R and -R effect.
- The delocalisation of n electrons is denoted by using curved arrows.
Question B.
Electrophile and nucleophile
Answer:
Electrophile:
- Electrophile is an electron deficient species.
- It is attracted towards negative charge (electron seeking).
- It attacks a nucleophilic centre in the substrate and brings about an electrophilic reaction
- It is an electron pair acceptor. (Lewis acid)
- It can be a positively charged ion or a neutral species having a vacant orbital.
e.g. H+, Br , \(\mathrm{NO}_{2}^{+}\), BF3, AlCl3, etc.
Nucleophile:
- Nucleophile is an electron rich species.
- It is attracted towards positive charge (nucleus seeking).
- It attacks the electrophilic centre in the substrate and brings about a nucleophilic reaction.
- It is an electron pair donor. (Lewis base)
- It can be negatively charged ion or neutral species having at least one lone pair of electrons.
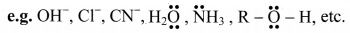
C. Carbocation and carbanion
Answer:
Carbocation:
- It is a species in which carbon carries a positive charge.
- Positively charged carbon is sp2 hybridized.
- It is electron-deficient.
- e.g. tert-Butyl carbocation, (CH3)3C+
Carbanion:
- It is a species in which carbon carries a negative charge.
- Negatively charged carbon is sp3/sp2 hybridized.
- It is electron-rich.
- e.g.Methyl carbanion,
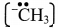
D. Homolysis and heterolysis
Answer:
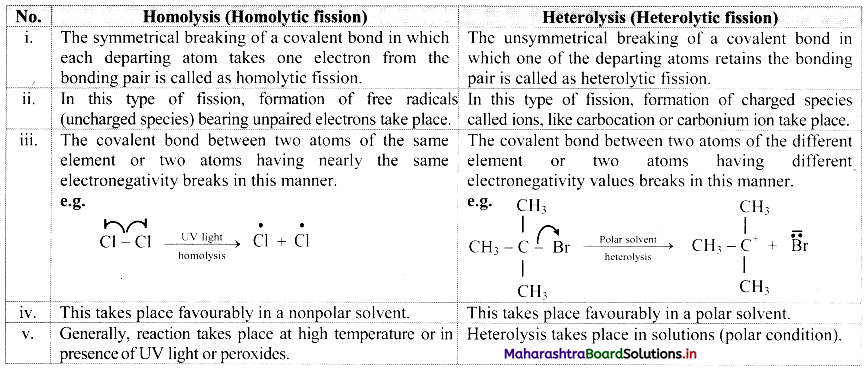
![]()
8. Write true or false. Correct the false stament
A. Homolytic fission involves unsymmetrical breaking of a covalent bond.
B. Heterolytic fission results in the formation of free radicals.
C. Free radicals are negatively charged species
D. Aniline is heterocyclic compound.
Answer:
A. False
Homolytic fission involves symmetrical breaking of a covalent bond.
B. False
Heterolytic fission results in the formation of charged ions like cation and anion.
C. False
Free radicals are electrically neutral/uncharged species.
D. False
Aniline is a homocyclic aromatic compound.
9. Phytane is naturally occuring alkane produced by the alga spirogyra and is a constituent of petroleum. The IUPAC name for phytane is 2, 6, 10, 14-tetramethyl hexadecane. Write zig-zag formula for phytane. How many primary, secondary, tertiary and quaternary carbons are present in this molecule.
Answer:
Zig-zag formula of phytane (2,6,10,14-tetramethyl hexadecane) is as follows:

Dash formula to represent types of C-atom:
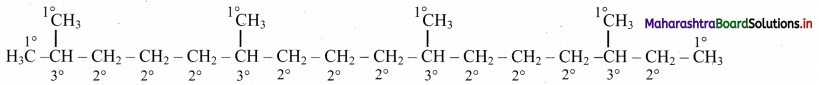
In phytane, six 1° C-atoms, ten 2° C-atoms, four 3° C-atoms are present. Phytane does not contain any quaternary carbon atom in its structure.
10. Observe the following structures and answer the questions given below.
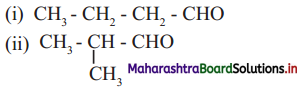
a. What is the relation between (i) and (ii) ?
b. Write IUPAC name of (ii).
c. Draw the functional group isomer of (i).
Answer:
a. (a) and (b) are chain isomers of each other.
b. IUPAC name of structure (b) is 2-methylpropanal.
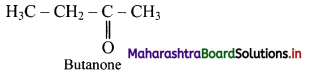
c. Functional group isomer of (a) is butanone.
11. Observe the following and answer the questions given below
![]()
a. Name the reactive intermediae produced
b. Indicate the movement of electrons by suitable arrow to produce this intermediate
c. Comment on stability of this intermediate produced.
Answer:
i. The reactive intermediates produced are methyl free radicals:
![]()
ii. Stability order of alkyl free radicals is: \(\dot{\mathrm{C}} \mathrm{H}_{3}\) < 1° <2° <3°
Hence, \(\dot{\mathrm{C}} \mathrm{H}_{3}\) produced in the above reaction is least stable and highly reactive.
![]()
12. An electronic displacement in a covalent bond is represented by following notation.
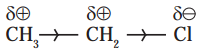
A. Identify the effect
B. Is the displacement of electrons in a covalent bond temporary or permanent.
Answer:
A. The electronic displacement represented above is inductive effect (-I effect).
B. Inductive effect is a permanent electronic effect as it depends on the electronegativity of the atoms. In the given example, the displacement of electrons is permanent as Cl is more electronegative than C.
13. Draw all the no-bond resonance structures of isopropyl carbocation.
Answer:
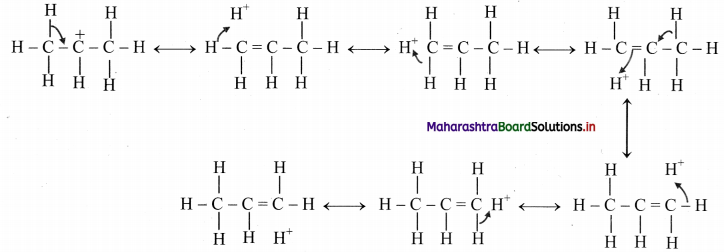
14. A covalent bond in tert-butyl bromide breaks in a suitable polat solvent to give ions.
A. Name the anion produced by this breaking of a covalent bond.
B. Indicate the type of bond breaking in this case.
C. Comment on geometry of the cation formed by such bond cleavage.
Answer:
A. The anion produced by breaking of the covalent C – Br bond is bromide
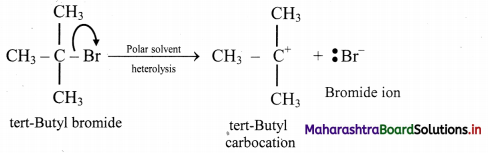
B. Heterolytic cleavage/fission takes place as charged ions are produced.
C. tert-Butyl carbocation formed in the given cleavage has trigonal planar geometry.
15. Choose correct options
A. Which of the following statements are true with respect to electronic displacement in covalent bond ?
a. Inductive effect operates through π bond
b. Resonance effect operates through σ bond
c. Inductive effect operates through σ bond
d. Resonance effect operates through π bond
i. a. and b
ii. a and c
iii. c and d
iv. b and c
Answer:
iii. c and d
B. Hyperconjugation involves overlap of …………. orbitals
a. σ – σ
b. σ – p
c. p – p
d. π – π
Answer:
b. σ – p
![]()
C. Which type of isomerism is possible in CH3CHCHCH3?
a. Position
b. Chain
c. Geometrical
d. Tautomerism
Answer:
a. Position
D. The correct IUPAC name of the compound
![]()
is ……………
a. hept-3-ene
b. 2-ethylpent-2-ene
c. hex-3-ene
d. 3-methylhex-3-ene
Answer:
d. 3-methylhex-3-ene
E. The geometry of a carbocation is …………
a. linear
b. planar
c. tetrahedral
d. octahedral
Answer:
b. planar
F. The homologous series of alcohols has general molecular formula ………..
a. CnH2n+1OH
b. CnH2n+2OH
c. CnH2n-2OH
d. CnH2nOH
Answer:
a. CnH2n+1OH
G. The delocaalization of electrons due to overlap between p-orbital and sigma bond is called …………….
a. Inductive effect
b. Electronic effect
c. Hyperconjugation
d. Resonance
Answer:
c. Hyperconjugation
11th Chemistry Digest Chapter 14 Basic Principles of Organic Chemistry Intext Questions and Answers
Can you recall? (Textbook Page No. 204)
Question i.
Which is the essential element in all organic compounds?
Answer:
Carbon is the essential element in all organic compounds.
Question ii.
What is the unique property of carbon that makes organic chemistry a separate branch of chemistry?
Answer:
- All organic compounds contain carbon.
- Carbon atoms show catenation property in which carbon atoms combine with other carbon atoms to form long chains and rings.
- Carbon atom can also form multiple bonds with other carbon atoms and with atoms of other elements.
- Due to this property of self-linking of carbon, a large number of organic compounds like proteins, DNA, sugar, oils, etc., are formed.
Thus, the unique property of catenation of carbon makes organic chemistry a separate branch of chemistry.
Question iii.
Which classes of organic compounds are often used in our daily diet?
Answer:
Carbohydrates (sugars), proteins (pulses), fats (edible plant and animal oil) and vitamins are the major classes of organic compounds often used in our daily diet.
![]()
Try this. (Textbook Page No. 204)
Question 1.
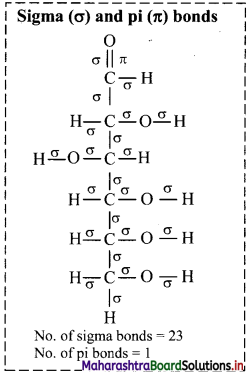
Find out the structures of glucose, vanillin, camphor and paracetamol using internet. Mark the carbon atoms present in them. Assign the hybridization state to each of the carbon and oxygen atom. Identify sigma (σ) and pi (π) bonds in these molecules.
Answer:
i. Structure of glucose:
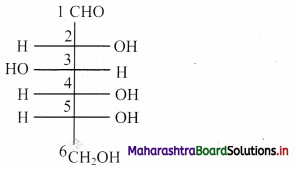
a. Hybridization of carbon: In glucose, only carbon at position C-1 is sp2 hybridized. On the other hand, carbons at C-2, C-3, C-4, C-5 and C-6 positions are sp3 hybridized.
b. Hybridization of oxygen: Oxygen atom attached to C-1 is sp2 hybridized, rest oxygen atoms attached to carbon at C-2, C-3, C-4, C-5 and C-6 are sp3 hybridized.
[Note: Here, the open chain structure of glucose is used to answer the given questions.]
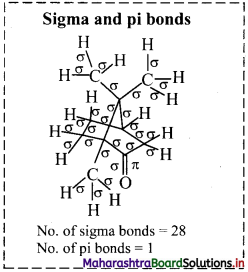
ii. Structure of vanillin:
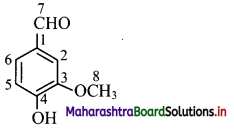
a. Hybridization of carbon: In vanillin, carbon atoms C-1 to C-7 are sp2 hybridized. Only C-8 carbon is sp3 hybridized.
b. Hybridization of oxygen: Oxygen atom bonded to C-7 sp2 hybridized whereas oxygen atom bonded to C-4 and C-8 are sp3 hybridized.
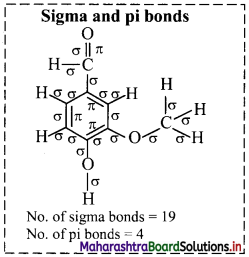
iii. Structure of camphor:
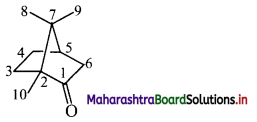
a. Hybridization of carbon: In camphor, all the carbons are sp3 hybridized except the carbonyl carbon which is sp2 hybridized.
b. Hybridization of oxygen: The carbonyl oxygen is sp2 hybridized.
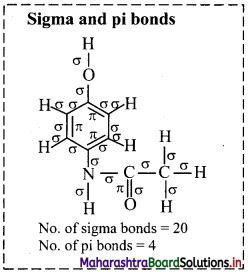
iv. Structure of paracetamol:

a. Hybridization of carbon: In paracetamol, carbons present in the ring and carbon at C-7 position are sp2 hybridized. Only C-8 carbon is sp3 hybridized.
b. Hybridization of oxygen: Oxygen atom attached to carbon at ,C-1 position is sp3 hybridized. Oxygen atom attached to carbon at C-7 position is sp2 hybridized.
![]()
Question 2.
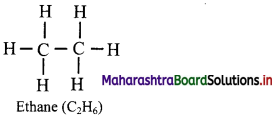
i. Draw the structural formula of ethane.
ii. Draw electron-dot structure of propane.
Ans:
i. Structural formula of ethane (C2H6) can be drawn as follows:
ii. Electron-dot structure of propane is given as,
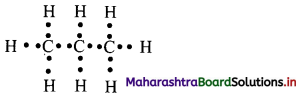
Where ‘•’ represents valence electrons of carbon and hydrogen.
Try this (Textbook Page No. 205)
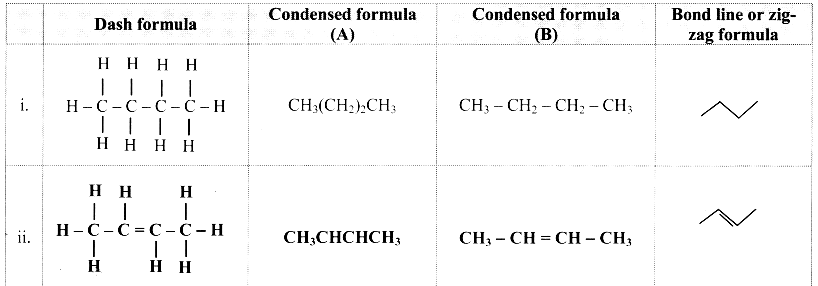
Complete the table:
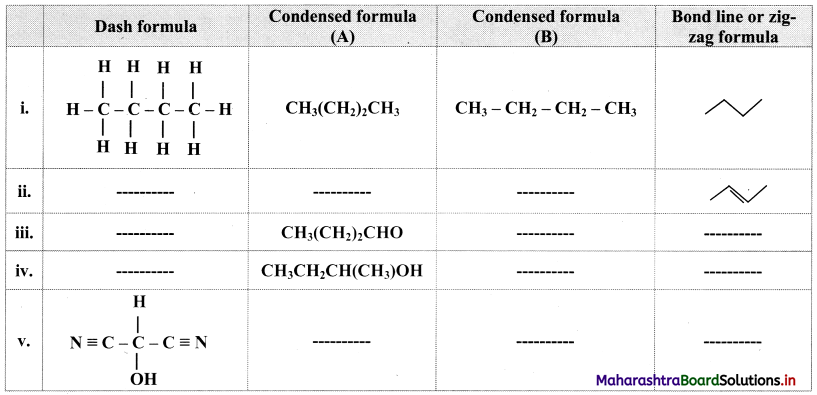
Answer:
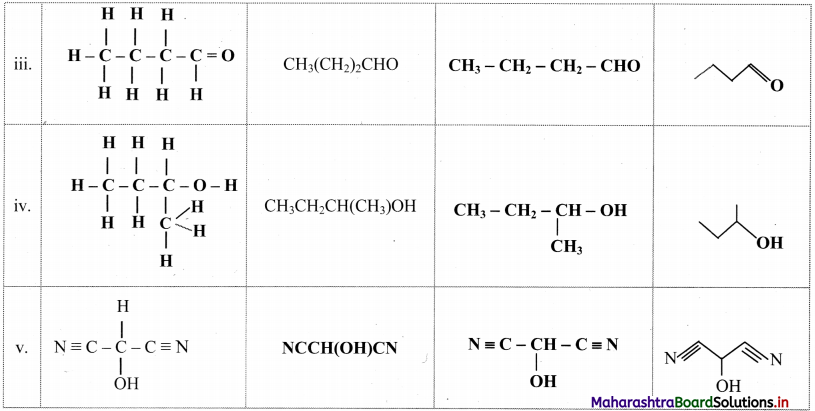
![]()
Try this. (Textbook Page No. 206)
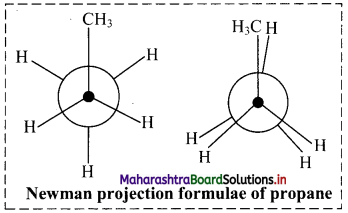
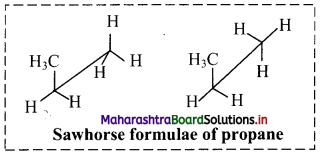
Question 1.
Draw two Newman projection formulae and two Sawhorse formulae for the propane molecule.
Answer:
Structural formula of propane is:

Structural formula of propane:
i. Newman projection formulae for propane molecule can be given as:
ii. Sawhorse formula for propane molecule can be given as:
Can you tell? (Textbook Page No. 208)
Question 1.
Consider the following reaction:
2CH3 – CH2 – CH2 – OH + 2Na → 2CH3 – CH2 – CH2 – ONa + H2
Compare the structure of the substrate propanol with that of the product sodium propoxide. Which part of the substrate, the carbon skeleton or the OH group has undergone a change during the reaction?
Answer:
In above reaction, the -OH group of the substrate molecule has undergone a change. The H-atom of hydroxyl group (-OH) is replaced by sodium forming the product.
Activity: (Textbook Page No. 219)

Observe the structural formulae (a) and (b).
i. Find out their molecular formulae.
ii. What is the difference between them?
iii. What is the relation between the two compounds represented by these structural formulae?
Answer:
i. Molecular formula of both (a) and (b) are same i.e., C3H6O.
ii. Compound (a), has a ketone (-CO-) functional group (i.e., acetone) and compound (b) has an aldehyde (-CHO) functional group (i.e., propionaldehyde). Both the compounds have different functional groups.
iii. Compound (a) and (b) are isomers of each other.
[Note: Aldehydes and ketones are the functional group isomers of each other.]
![]()
Can you tell? (Textbook Page No. 222)
Question 1.
Some bond fissions are described in the following table. For each of them, show the movement of electron/s using curved arrow notation. Classify them as homolysis or heterolysis and identify the intermediate species produced as carbocation, carbanion or free radical.
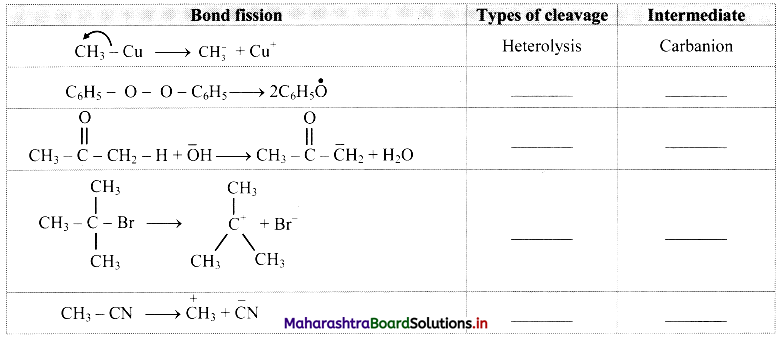
Answer:
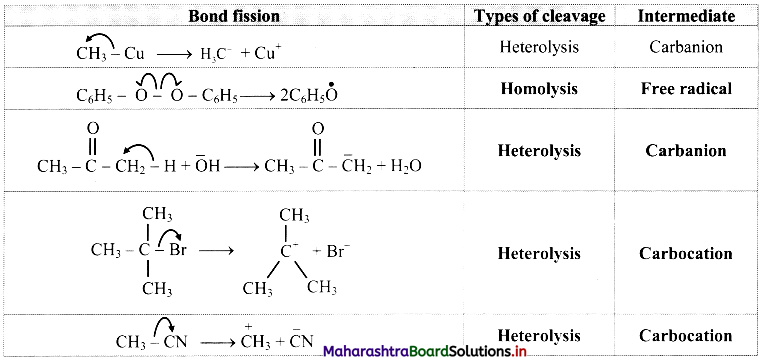
Can you recall? (Textbook Page No. 223)
i. What is meant by ‘reagent’?
ii. Identify the ‘reagent’, ‘substrate’, ‘product’ and ‘byproduct’ in the following reaction.
CH3COCl + NH3 → CH3CONH2 + HCl
Answer:
i. The reactant which reacts with a substrate to form corresponding products is known reagent.
ii.

Can you recall? (Textbook Page No. 224)
i. How is covalent bond formed between two atoms?
ii. Consider two covalently bonded atoms Q and R where R is more electronegative than Q. Will these atoms share the electron pair equally between them?
iii. Represent the above polar covalent bond between Q and R using fractional charges δ+ and δ–.
Answer:
i. A covalent bond is formed between two atoms by mutual sharing of electrons so as to complete their octets or duplets (in case of elements having only one shell).
ii. A covalent bond is formed between Q and R having different electronegativities, that is, R is more electronegative than Q. In such a case, the atom R with a higher value of electronegativity pulls the shared pair of electrons to a greater extent towards itself as compared to the atom Q with lower value of electronegativity. As a result of this, the shared pair of electrons will get shifted towards atom R. Thus, both the atoms Q and R will not share the electron pair equally between them.
iii. Polar covalent bond between Q and R can be represented as:
\(\mathrm{Q}^{\delta+}-\mathrm{R}^{\delta-}\)
![]()
Try this (Textbook Page No. 225)
i. Draw a bond line structure of benzene (C6H6).
ii. How many C – C and C = C bonds are there in this structure?
iii. Write down the expected values of the bond lengths of the carbon-carbon bonds in benzene (Refer chapter 5).
Answer:
i. Bond line structure of benzene:

ii. In benzene, there are three alternating C – C single bonds and C = C double bonds.
[Note: In benzene, there are six C – C sigma bonds and three C – C pi bonds.]
iii. The expected values of carbon-carbon bond lengths in benzene are:
| Bond | Bond length |
| C – C | 154 pm |
| C = C | 133 pm |
Can you recall? (Textbook Page No. 225)
i. Write down two Lewis structures for ozone. (Refer chapter 5)
ii. How are these two Lewis structures related to each other?
iii. What are these two Lewis structures called?
Answer:
i. Lewis structures of ozone can be shown as follows:

ii. In these two Lewis structures, the position of the atoms is same but the position of pair of electrons (or formal charge) is different. These two Lewis structures are considered equivalent to each other.
iii. These two Lewis structures are called as resonating or contributing or canonical structures.
Internet my friend (Textbook Page No. 229)
i. Basic principles of organic chemistry:
https://authors.library.caltech.edu/25034
ii. Collect information about isomerism.
Answer:
i. Students are expected to refer the book provided in the above link to collect additional information on the basic principles of organic chemistry.
ii. https://www.compoundchem.com/2014/05/22/typesofisomerism/
chemdictionary.org/structural-isomers/
https://en.wikipedia.org/wiki/Structural_isomer
[Note: Students can use the above links as reference and collect additonal information about isomerism on their own.]
11th Std Chemistry Questions And Answers:
- Elements of Group 13, 14 and 15 Class 11 Chemistry Questions And Answers
- States of Matter Class 11 Chemistry Questions And Answers
- Adsorption and Colloids Class 11 Chemistry Questions And Answers
- Chemical Equilibrium Class 11 Chemistry Questions And Answers
- Nuclear Chemistry and Radioactivity Class 11 Chemistry Questions And Answers
- Basic Principles of Organic Chemistry Class 11 Chemistry Questions And Answers
- Hydrocarbons Class 11 Chemistry Questions And Answers
- Chemistry in Everyday Life Class 11 Chemistry Questions And Answers
