Class 9

Balbharti Maharashtra State Board Class 9 Hindi Solutions Hindi Lokvani Chapter 7 छोटा जादूगर Notes, Textbook Exercise Important Questions and Answers.

Std 9 Hindi Chapter 7 Chota Jadugar Question Answer Maharashtra Board

Hindi Lokvani 9th Digest Chapter 7 छोटा जादूगर Questions And Answers

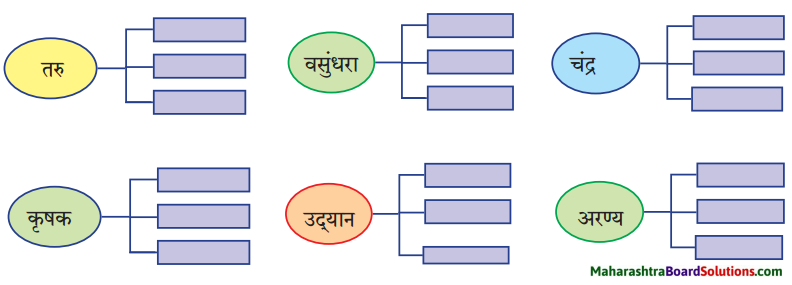
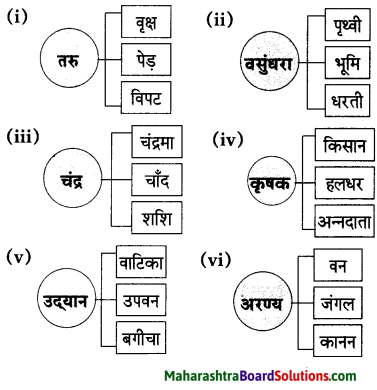
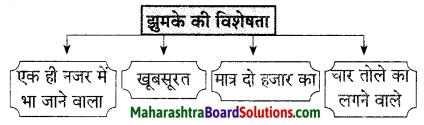
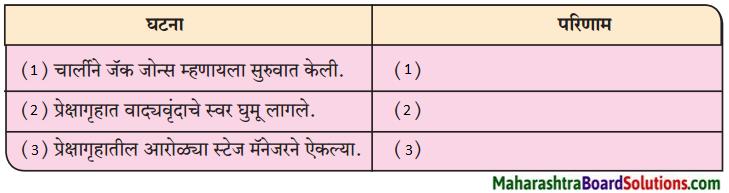
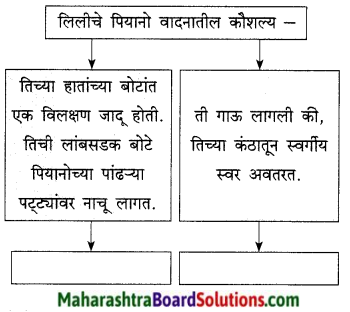
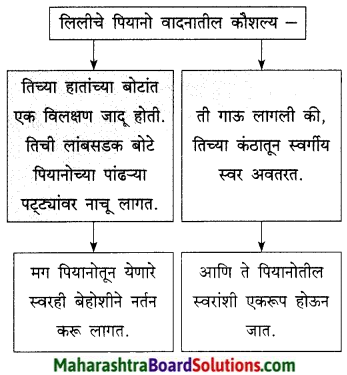
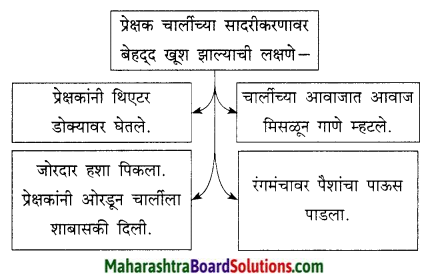
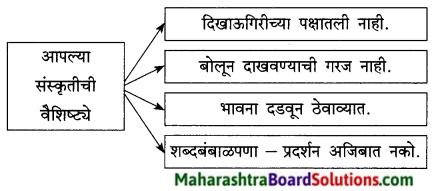
1. संजाल पूर्ण लिखिए 

प्रश्न 1.
संजाल पूर्ण लिखिए
उत्तर :

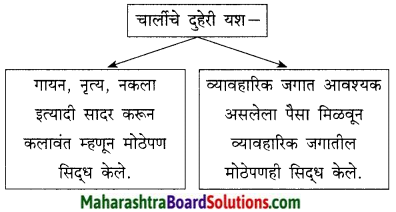
2. छोटा जादूगर कहानी में आए पात्रः

प्रश्न 1.
छोटा जादूगर कहानी में आए पात्रः
उत्तरः

3. ‘पात्र’ शब्द के दो अर्थ लिखिए।

प्रश्न 1.
‘पात्र’ शब्द के दो अर्थ लिखिए।
उत्तर :
i. अभिनेता
ii. बरतन

4. विधान को सही करके लिखिए। 

प्रश्न 1.
विधान को सही करके लिखिए।
i. ताश के सब पत्ते पीले हो गए।
ii. खेल हो जाने पर चीजें बटोरकर उसने भीड़ में मुझे देखा।
उत्तर :
i. ताश के सब पत्ते लाल हो गए।
ii. खेल हो जाने पर पैसा बटोरकर उसने भीड़ में मुझे देखा।

5. भाषाई कौशल पर आधारित पाठगत कृतियाँ।

भाषा बिंदु :

प्रश्न 1.
रिक्त स्थानों की पूर्ति अव्यय शब्दों से कीजिए और नया वाक्य बनाइए।
उत्तर:
i. जहाँ एक लड़का चुपचाप देख रहा था।
वाक्य:
मोहन नदी की लहरों को चुपचाप देख रहा था।

ii. मैं उसकी ओर न जाने क्यों आकर्षित हुआ।
वाक्य:
हिंसक शेर मेरी ओर चला आ रहा था।

iii. हाँ! मैं सच कहता हूँ बाबू जी।
वाक्य :
हाँ! मैं छोटा जादूगर हूँ।

iv. अकस्मात किसी ने ऊपर के हिंडोले से पुकारा।
वाक्य :
अकस्मात रमेश छत के ऊपर से कूद गया।

v. मैं बिना बुलाए भी कहीं जा पहुँचता हूँ।
वाक्य:
मैं बिना पढ़े परीक्षा नहीं देता हूँ।

vi. लेखकों और वक्ताओं की न जाने क्या दुर्दशा होती।
वाक्य :
मोहन और गणेश एक अच्छे मित्र हैं।

vii. वाह ! क्या बात।
वाक्य:
वाह ! आप मैच जीत गए।

viii. वह बाजार गया क्योंकि उसे किताब खरीदनी थी।
वाक्य :
मै प्रतिदिन पड़ता हूँ क्योंकि मुझे परीक्षा में अच्छे अंक लाने हैं।

6. रचनात्मकता की ओर संभाषणीय

प्रश्न 1.
माँ के लिए छोटे जादूगर के किए हुए प्रयास समावण बताइए।
उत्तर:
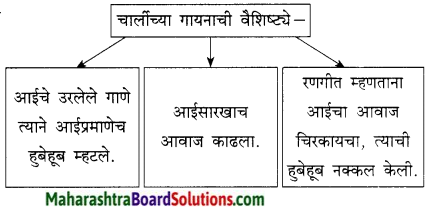
छोटा जादूगर अपनी माँ की दवा के लिए कार्निवाल के मैदान में जाता है, जहाँ पर उसकी मुलाकात लेखक से होती है। वह उन्हें अपनी माँ और पिता जी के बारे में बताता है। लेखक द्वारा शरबत पिलाने के बाद वह उनसे कहता है कि यदि आप मुझे शरबत न पिलाकर मेरा खेल देखकर कुछ पैसे दे देते तो माँ के लिए मैं पथ्य ले लेता। लेखक जब उसे निशानेबाजी के लिए ले गए तो उसने सभी बारह खिलौने जीत लिए।

लेखक फिर उससे कोलकाता के बोटेनिकल उद्यान में मिले जहाँ पर वह खिलौनों को लेकर तमाशा दिखाकर अपनी माँ के लिए एक सूती कंबल खरीदने की इच्छा लिए था। एक दिन लेखक जब मोटर से हावड़ा की ओर जा रहे थे तो वह छोटा जादूगर उन्हें एक झोंपड़ी के पास खड़ा मिला। उसने लेखक को बताया कि अस्पतालवालों ने उसकी माँ को निकाल दिया है। जब लेखक झोपड़ी के अंदर गए तो उन्होंने देखा कि छोटा जादूगर अपनी माँ के शरीर पर कंबल डाले उससे लिपट कर निरीह भाव से उसे निहार रहा है।

एक दिन छोटा जादूगर निर्मल धूप में सड़क के किनारे अपना तमाशा दिखा रहा था किंतु उसकी वाणी में प्रसन्नता न थी। लेखक द्वारा पूछने पर उसने बताया कि उसकी माँ का समय समीप है और उसने मुझे जल्दी घर बुलाया है। फिर वह पैसा बटोरकर लेखक के साथ अपने घर को चल दिया किंतु घर पहुँचकर पता चला कि उसकी माँ अब नहीं रही।

7. मौलिक सृजन :

प्रश्न 1.
‘माँ’ विषय पर स्वरचित कविता प्रस्तुत कीजिए।
उत्तर:
है साथ मेरे हरदम, बनकर एक साया,
उसने ही मेरा जीवन महकाया।

तकलीफ में भी मुस्काती है,
हर गम खुशी से सह जाती है।

मेरी राहों पर फूल बिछाती वो,
खुद काँटों पर सो जाती है।

ममता की सूरत है माँ,
भगवान की छवि कहलाती माँ ।

8. आसपास :

प्रश्न 1.
अपने विद्यालय के किसी समारोह का सूत्र संचालन कीजिए।
उत्तर:
सूत्र-संचालन (गणतंत्र दिवस)
आज के इस आज़ादी के जश्न में, मैं रामकुमार विद्यालय में पधारे हमारे अपने सभी खासो-ओ-आम का बहुत-बहुत स्वागत करता हूँ-जय हिंद कहता हूँ। मैं अपने सभी विशिष्ट अतिथियों, समाजसेवियों, हमारे गुरुजनों, सभी पधारे हुए आज़ादी के दीवानों और हमारे साथियों को हमारे विद्यालय की तरफ से गणतंत्र दिवस की शुभकामनाएँ देता हूँबधाइयाँ देता हूँ। शुभकामनाएँ इसलिए कि हमने लगभग 200 साल की परतंत्रता सहन करने के बाद यह अनमोल आज़ादी की फ़िज़ा पाई है।

और यह आज़ादी, यह अपनी पसंद से जीने का अधिकार हमें सदा प्राप्त हो ऐसी शुभकामनाओं के साथ मैं रामकुमार हमारे विद्यालय की तरफ से आप सब देशभक्तों का इस आज़ादी के जश्न में स्वागत करता हूँ-वंदे मातरम कहता हूँ। वतन पर मर-मिटने के ज़माने गुज़र गए, मज़ा तो अब इसके लिए जीने में है। अपनी आज़ादी अपनी संप्रभुता के लिए एक बार जोरदार तालियाँ बजा दीजिए।

धन्यवाद! जी हाँ साथियों, ये जो हमारे अमर शहीदों ने बलिदानों के बीज इस मातृभूमि पर रोपे थे, आज उनकी टहनियों पर महकते फूल खिल आए हैं। इन फूलों की महक इस देश में ही नहीं, सारे संसार में फैले, इस कामना के साथ आइए आज के इस महोत्सव का शुभारंभ करते हैं।

इक चमक ताब इक मदहोशी, हर आलम चंगा होता है, इक हूक चमकती आँखों में, हर कतरा गंगा होता है। दिल में मतवाली मौज पले, मन सात आसमाँ छूता है, जब-जब अपने इन हाथों में, लहराता तिरंगा होता है। तो आइए, मित्रों ! सर्वप्रथम हम अपनी आन-बान-शान के प्रतीक हमारे राष्ट्रीय ध्वज तिरंगे का ध्वज वंदन करें।

9. पाठ के आँगन में :

प्रश्न 1.
सियारामशरण गुप्त जी द्वारा लिखित ‘काकी’ पाठ के भावपूर्ण प्रसंग को शब्दांकित कीजिए।
उत्तर :
‘काकी’ शीर्षक कहानी में एक बच्चे के मन के भावों का वर्णन किया गया है। एक दिन श्यामू ने देखा कि उसकी माँ सिर से लेकर पैर तक कपड़ा ओढ़े हुए भूमि पर लेटी हुई है । घर के लोग उसे घेरे हुए रो रहे हैं, पर श्यामू को कुछ समझ में नहीं आ रहा था कि क्या हो रहा है? लोग जब उसकी माँ के मृत शरीर को उठाकर ले जाने लगे, तब उसने रो-रोकर तमाशा कर दिया। उसे बहुत समझाया गया फिर भी वह रोता रहा। कुछ दिन पश्चात् उसके मित्रों द्वारा पता चला कि उसकी माँ ऊपर राम के घर चली गई।

एक दिन श्यामू ने आकाश में पतंग उड़ते देखा। उसने सोचा,क्यों न वह एक पतंग आकाश में उड़ा दे और उसकी माँ पतंग के सहारे राम के घर से नीचे उतर आएगी। उसने पिता (काका) से पतंग दिलाने के लिए कहा, पर पिता ने पतंग नहीं दिलाई। एक दिन श्यामू ने अपने पिता की जेब से एक चवन्नी चुराई और अपने मित्र भोला से पतंग मँगवा ली। श्यामू ने सोचा पतंग पर ‘काकी’ लिखकर उड़ा देंगे और काकी इसे पकड़कर नीचे आ जाएगी।

भोला, श्यामू से अधिक समझदार था। उसने श्यामू को समझाया कि पतंग की डोर पतली है, काकी का भार सम्भाल नहीं पाएगी और टूट जाएगी। दूसरे दिन श्यामू ने अपने पिता की कोट से एक रूपया चुराया और मोटी रस्सी मँगवाई। जब श्यामू और भोला पतंग में रस्सी बाँध रहे थे, तभी श्यामू के पिता आ धमके और जब उन्हें पता चला कि श्याम ने उनकी जेब से पैसा निकाला है, तो उनको बहुत गुस्सा आया।

उन्होंने श्यामू को मारा और पतंग फाड़ दी। उनके डाँटने पर डर के कारण भोला ने बताया कि वह पतंग के सहारे अपनी काकी (माँ) को नीचे उतारना चाहता था। विश्वेश्वर ने जब भोला की बात सुनी तो उन्हें बहुत दुख हुआ। पतंग पर चिपके कागज पर ‘काकी’ लिखा देखकर वे हैरान रह गए। इस पाठ में बाल मन के निश्छल, निष्कपट प्रेम की मार्मिक अभिव्यक्ति की गई है।

Hindi Lokvani 9th Std Textbook Solutions Chapter 7 छोटा जादूगर Additional Important Questions and Answers

(क) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति क (1) : आकलन कृति

प्रश्न 1.
निम्नलिखित कश्चन सत्य है या असत्य लिखिए।

1. लड़के की जेब में पेड़ के कुछ पत्ते थे।
2. दोनों शरबत पीकर निशाना लगाने चले।
3. लड़के के स्वभाव में संपूर्णता थी।

उत्तर :

1. असत्य
2. सत्य
3. असत्य

कृति क (2) : शब्द संपदा

प्रश्न 2.
गद्यांश से समानार्थी शब्द ढूँढकर लिखिए।
i. दुख
ii. कारागार
उत्तर :
i. विषाद
ii. जेल

प्रश्न 3.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।
i. गरम × ……….
ii. बीमार × ………..
उत्तर :
i. ठंडा
ii. स्वस्थ

कृति क (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
अपने नगर में आयोजित किसी जादू के तमाशे का आँखों देखा वर्णन कीजिए।
उत्तर :
‘जीवन में जिस प्रकार खेलकूद और मनोरंजन के लिए अनेक प्रकार के साधन उपलब्ध हैं, उन्हीं में से एक है जादू का तमाशा। एक दिन हमारे शहर में भी जादू के तमाशे का समाचार अखबार में छपा। अगले ही दिन पिता जी हमें जादू का खेल दिखाने ले गए। हमने टिकटें खरीदी और अंदर गए। थोड़ी देर बाद जादूगर स्टेज पर आया। उसने जैसे ही सबको अभिवादन किया ऊपर से फूल बरसने लगे।

फिर उसने अपनी टोपी उतारकर दिखाई जो एकदम खाली थी लेकिन उसने उसमें हाथ डाला तो खरगोश बाहर निकला और भाग गया। उसने दोबारा हाथ डाला तो तितलियाँ निकलकर उड़ने लगीं। हम सब यह देखकर हैरान हो गए। इसके बाद अगले खेल में उसने अलग-अलग रंगों के कपड़ों की तीन-चार छोटी-छोटी पट्टियाँ मुँह में रख ली और हवा में हाथ घुमाया। फिर मुंह से पट्टियाँ बाहर निकाली तो रंग-बिरंगे रूमाल निकलते चले गए। ऐसा जादू हमने कभी नहीं देखा था और अंत में, हम सब आपस में चर्चा करते हुए खुशी-खुशी घर लौटे।

(ख) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

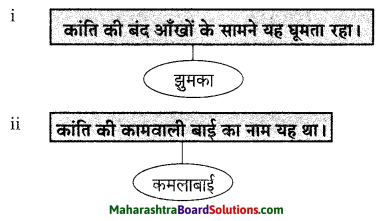
कृति ख (1) : आकलन कृति

प्रश्न 1.
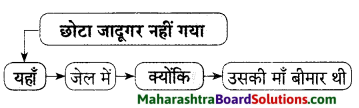
चौखट पूर्ण कीजिए।
उत्तर :

प्रश्न 2.
निम्नलिखित प्रश्नों के उत्तर लिखिए।
i. छोटा जादूगर को तब अधिक प्रसन्नता होती जब –
ii. देखने वाले इसलिए दंग रह गए क्योंकि –
उत्तर :
i. लेखक उसे शरबत न पिलाकर उसका खेल देखकर कुछ पैसे दे दिया होता।
ii. छोटा जादूगर पक्का निशानेबाज निकला। उसकी कोई गेंद खाली नहीं गई।

कृति ख (2) : शब्द संपदा

प्रश्न 1.
उचित प्रत्यय लगाकर नए शब्द बनाइए।
i. बीमार
ii. तमाशा
उत्तर :
i. बीमार + ई = बीमारी
ii. तमाशा + ई = तमाशाई

प्रश्न 2.
गद्यांश से विलोम शब्द ढूँढकर लिखिए।
i. झूठ × ……………
ii. नीचे × …………..
उत्तर :
i. सच
ii. ऊपर

कृति ख (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
जो व्यक्ति जीवन में अपना लक्ष्य हासिल करना चाहते हैं, वे बचपन से ही सपने देखा करते हैं। अपने विचार लिखिए।
उत्तर:
लक्ष्य को पाने के लिए व्यक्ति को बचपन से ही प्रयास करना पड़ता है। जो व्यक्ति दृढ़ निश्चयी होते हैं, वे बचपन से ही सपने देखते हैं। कल्पना चावला, न्यूटन, डॉ. अब्दुल कलाम आदि महापुरुषों ने बचपन से ही अपने लक्ष्य तक पहुंचने का सपना देखा था और उस दिशा में कोशिश एवं अथक परिश्रम करना शुरू कर दिया था। इसी कारण वे अपने लक्ष्य तक पहुँच सके थे।

(ग) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

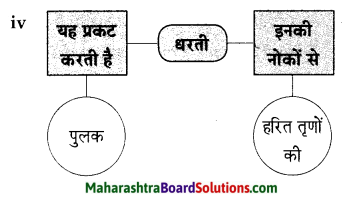
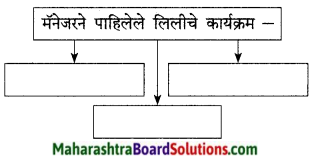
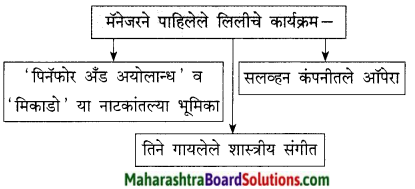
कृति ग (1) : आकलन कृति

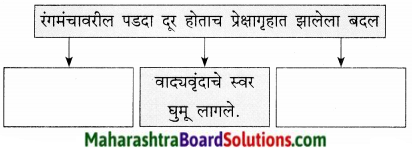
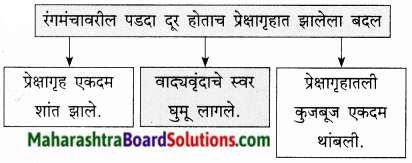
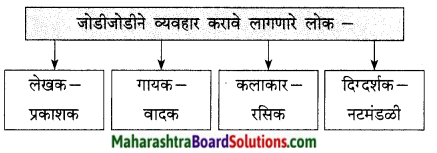
प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तर:

कृति ग (2) : शब्द संपदा

प्रश्न 1.
लिंग परिवर्तन कीजिए।
i. गुड़िया – ………….
ii. जादूगर – …………
उत्तर :
i. गुड्डा
ii. जादूगरनी

कृति ग (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘जीवन में माँ का महत्त्व’ पर अपने विचार व्यक्त कीजिए।
उत्तर:
हमारे जीवन में माँ का बहुत महत्त्व होता है। एक बालक का संपूर्ण संसार माँ ही होती है। माँ जीवन की प्रथम गुरु होती है। वह हमें चलना, बोलना और पढ़ना सिखाती है। उसके दिए संस्कारों से ही मनुष्य अपने चरित्र का निर्माण करता है। वह हमारे लिए पढ़ाई-लिखाई, भोजन, कपड़े आदि का इंतजाम करती है। सचमुच, माँ सेह, ममता, सद्भावना और कर्तव्य-पालन की जीवंत मूर्ति होती है।

(घ) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

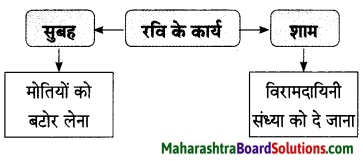
कृति घ (1) : आकलन कृति

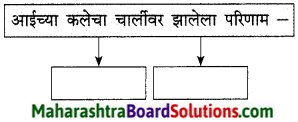
प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
सत्य या असत्य पहचानकर लिखिए।
i. गले की सूत की डोरी टुकड़े-टुकड़े होकर जुट गई।
ii. लेखक इडेन गार्डेन देखने के लिए चले।
उत्तर :
i. सत्य
ii. असत्य

प्रश्न 3.
समझकर लिखिए।
i. लेखक ने झोपड़ी में यह देखा –
उत्तर:
एक स्त्री चिथड़ो में लदी हुई काँप रही थी।

कृति घ (2) : शब्द संपदा

प्रश्न 1.
लिंग परिवर्तन कीजिए।
i. श्रीमती
ii. स्त्री
उत्तर :
i. श्रीमान
ii. पुरुष

प्रश्न 2.
गद्यांश से शब्द-युग्म ढूँडकर लिखिए।
उत्तर :
i. टुकड़े-टुकड़े
ii. धीरे-धीरे

कृति ग (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘अपने बचपन में नन्हें कलाकारों को अपना तमाशा दिखाते हुए देखा होगा…’ इस पर अपने विचार व्यक्त कीजिए।
उत्तर:
मैंने अपने बचपन में अनेक नन्हें कलाकारों को तमाशा दिखाते हुए देखा है। वे बाल कलाकार तमाशा दिखाते और उनके बदले कुछ पैसे या अनाज लेकर अपना पेट पालते हैं। यद्यपि उनके अंदर अनेक गुण होते हैं किंतु विषम परिस्थिति होने के कारण उनका वह गुण संपूर्ण दुनिया के सामने नहीं आ पाता है और वह जीवन पर्यंत सिर्फ अपना पेट ही पालते रह जाते हैं। सरकार और समाज को चाहिए कि वह इस प्रकार के बच्चों के लिए अलग से शिक्षा व्यवस्था करें तथा उन्हें आगे बढ़ने के लिए प्रोत्साहन और अवसर प्रदान करें; जिससे ये बच्चे भी दुनिया में अपनी अलग पहचान बना सकें।

(ङ) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति ङ (1) : आकलन कृति

प्रश्न 1.
उत्तर लिखिए।
i. लेखक का मन यहाँ से ऊब गया था –
ii. लेखक ने सड़क के किनारे यह देखा –
उत्तर :
i. कोलकाता से
ii. छोटे जादूगर का रंगमंच सजा हुआ।

प्रश्न 2.
विधानों को सही करके लिखिए।
i. तब भी तुम जादू दिखाने चले आए।
उत्तर :
i. तब भी तुम खेल दिखाने चले आए।

कृति ङ (2) : शब्द संपदा

प्रश्न 1.
उपसर्ग लगाकर शब्द बनाइए।
i. समय
ii. परिचित
उत्तर:
i. अ + समय = असमय
ii. अ+ परिचित – अपरिचित

प्रश्न 2.
गद्यांश से समानार्थी शब्द ढूँढकर लिखिए।
i. छुट्टी
ii. चेष्टा
उत्तर :
i. अवकाश
ii. प्रयत्न

प्रश्न 3.
गद्यांश से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तर:
i. चलते-चलते
ii. सुख-दुख

कृति छ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘माँ की ममता’ पर अपने विचार लिखिए।
उत्तर:
हमारे जीवन में सबसे महत्त्वपूर्ण इंसान ‘माँ’ होती है। वह हमेशा हमारे साथ रहती है और हर पल हमारा ध्यान रखती है। ढेर सारे दुख और पीड़ा सहकर वह हमें अपनी कोख में रखती है। वह अपने वास्तविक जीवन में हमेशा हमारे बारे में सोचकर खुश हो जाती है। एक माँ अपने बच्चों की खुशी के आगे अपनी खुशी को कुछ नहीं समझती। वह हमेशा हमारी हर क्रिया और हँसी में अपनी रुचि दिखाती है। उसके पास एक नि:स्वार्थ आत्मा है और प्यार तथा जिम्मेदारी से भरा दयालु दिल है।

छोटा जादूगर Summary in Hindi

लेखक-परिचय :

जीवन-परिचय :

जयशंकर प्रसाद का जन्म उत्तर प्रदेश के वाराणसी जिले के सरायगोवर्धन में हुआ था। प्रसाद जी की प्रारंभिक शिक्षा काशी में क्वींस कालेज में हुई, किंतु बाद में घर पर इनकी शिक्षा का व्यापक प्रबंध किया गया, जहाँ संस्कृत, हिंदी, उर्दू तथा फारसी का अध्ययन इन्होंने किया। प्रसाद जी हिंदी साहित्य के छायावादी कवियों के चार प्रमुख स्तंभों में से एक हैं। प्रसाद जी बहुमुखी प्रतिभा के धनी थे। ये हिंदी साहित्य में कवि, नाटककार, कथाकार, उपन्यासकार तथा निबंधकार के रूप में प्रसिद्ध हैं।

प्रमुख कृतियाँ :

• काव्य – ‘झरना’ , ‘आँसू’, ‘लहर’, आदि।
• महाकाव्य – ‘कामायनी’
• ऐतिहासिक नाटक – ‘स्कंदगुप्त’,’चंद्रगुप्त’, ‘धुवस्वामिनी।
• कहानी संग्रह – ‘प्रतिध्वनि’, ‘आकाशदीप’, ‘इंद्रजाल’ आदि।
• उपन्यास – ‘कंकाल’, ‘तितली,’ ‘इरावती’।

गद्य-परिचय :

संवादात्मक कहानी: किसी विशेष घटना की रोचक एवं आकर्षक ढंग से संवाद के रूप में प्रस्तुति ‘संवादात्मक कहानी’ कहलाती है।
प्रस्तावना : प्रस्तुत कहानी में लेखक ने एक लड़के के जीवन संघर्ष, बीमार माँ की देखभाल और उसके चातुर्यपूर्ण साहस को बड़े ही रोचक ढंग से प्रस्तुत किया है। मानवीय संवेदना की मार्मिक अभिव्यंजना ‘छोटे जादूगर’ के माध्यम से की गई है।

सारांश :

प्रस्तुत कहानी में लेखक ने एक लड़के के जीवन संघर्ष को उजागर किया है। इस कहानी में जयशंकर प्रसाद खुद एक पात्र हैं; जो एक लड़के के मन को पढ़ने का प्रयत्ल कर रहे हैं। उस समय के वातावरण का वर्णन करते हुऐ प्रसाद जी लिखते हैं कि कार्निवाल के मैदान में बिजली के जगमगाहट, हँसी और विनोद के कलनाद के बीच वे उस लड़के की तरफ आकर्षित हुए जिसके गले में फटे कुरते के ऊपर से एक मोटी सूत की रस्सी पड़ी थी और उसके जेब में कुछ ताश के पत्ते थे।

लेखक उसे खेल दिखाने ले गए। रास्ते में बातचीत के दौरान लेखक को पता चला कि लड़के के घर में उसके माँ और पिताजी भी हैं। उसके पिता जी देश के लिए जेल में बंद हैं और माँ बीमार है। लड़के ने लेखक को बताया कि उसकी माँ बीमार है और उसके दवा के लिए वह तमाशा दिखाकर कुछ पैसे इकट्ठा करना चाहता है। माँ के प्रति ममता देखकर लेखक उसे निशाना लगाने की जगह ले गए। जहाँ लड़के ने बारह खिलौने जीते और वहाँ से नौ-दो ग्यारह हो गया।

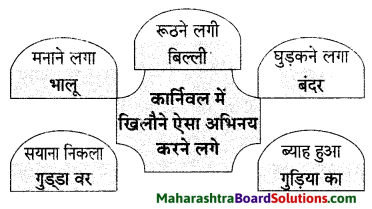
एक बार फिर लेखक को वह छोटा जादूगर कोलकाता के सुरम्य बोटेनिकल उद्यान में दिखाई दिया जहाँ लेखक अपनी मित्र मंडली के साथ जलपान कर रहे थे। लेखक के मना करने के बावजूद उनकी श्रीमती ने उस लड़के को तमाशा दिखाने के लिए कहा। लड़के ने अपना तमाशा दिखाया जिसे देखकर सब लोग प्रसन्न हुए और लेखक सोचता रहा कि ‘बालक को आवश्यकता ने कितना शीघ्र चतुर बना दिया है। यही तो संसार है।

एक दिन शाम के समय लेखक अपनी गाड़ी से हावड़ा की ओर जा रहे थे तो वह छोटा जादूगर उन्हें झोपड़ी के पास मिला और उनको बताया कि अस्पतालवालों ने उसकी माँ को निकाल दिया है। लेखक ने अंदर जाकर देखा तो उसकी माँ झोंपड़ी में चिथड़ों से लिपटी हुई पड़ी थी।

लेखक की जेहन में वह छोटा जादूगर घर कर गया। वह सोचता है कि छोटा जादूगर कितना निश्छल, कितना परिश्रमी, बाल-सुलभ चेष्टाएँ और बीमार माँ की जिम्मेदारी किस तरह वहन करता है।

एक दिन लेखक जब जा रहे थे तो उन्होंने छोटे जादूगर को तमाशा दिखाते हुए देखा किंतु उस जादूगर की वाणी में वह प्रसन्नता न देखकर उन्होंने कारण पूछा तो लड़के ने बताया कि उसकी माँ बहुत बीमार है और घर जल्दी आने को बोली है। लेखक उसे लेकर उसके घर पहुँचे तो उसकी बीमार माँ के मुख से सिर्फ ‘बे …’ शब्द निकलकर ही रह गया। जादूगर अपनी माँ से लिपटकर रोने लगा।

शब्दार्थ :

1. विषाद – दुख
2. हिंडोले – झूला
3. जलपान – नाश्ता
4. घुड़कना – डॉटना
5. वाचालता – अधिक बोलना
6. जीविका – रोजी-रोटी
7. ईर्ष्या – जलना, दवेष
8. चिथड़ा – फटा पुराना कपड़ा
9. बेष्टा – प्रयत्न
10. समीप – पास, निकट, नजदीक
11. अनुपात – प्रमाण, तुलनात्मक
12. समग्न – संपूर्ण
13. जगमगाना – चमकना
14. कलनाद – मधुर ध्वनि
15. गंभीर – गहरा, भारी
16. सहमत – एकमत, राजी
17. पथ्य – रोगी को दिया जाने वाला भोजन
18. सुरम्य – बहुत सुंदर, रमणीय
19. कमलिनी – छोटा कमल
20. सयाना – बुद्धिमान
21. बटोरना – समेटना, इकट्ठा करना
22. अस्ताचलगामी सूर्य – पश्चिम दिशा में भागता हुआ सूरज
23. स्मरण – स्मृति, याद
24. स्फूर्तिमान – सक्रिय
25. अविचल – स्थिर
26. स्तब्ध – संज्ञाहीन, स्थिर
27. विनोद – प्रसन्नता, खेल-कूद
28. फुहारा – फव्वारा
29. धैर्य – शांति
30. निकम्मा – जो कोई काम न करता हो
31. तिरस्कार – अपमान
32. व्यग्र – व्याकुल
33. उद्यान – बगीचा, फुलवारी
34. अभिनय – भावाभिव्यक्ति

मुहावरे :

• दंग रहना – चकित होना
• मन ऊब जाना – उकता जाना

Hindi Lokvani 9th Std Digest पहली इकाई

• नदी की पुकार Question Answer
• झुमका Question Answer
• निज भाषा (पठनार्थ) Question Answer
• मान जा मेरे मन Question Answer
• किताबें कुछ कहना चाहती हैं Question Answer
• ‘इत्यादि’ की आत्मकहानी (पठनार्थ) Question Answer
• छोटा जादूगर Question Answer
• जिंदगी की बड़ी जरूरत है हार..! Question Answer

Balbharti Maharashtra State Board Class 9 Hindi Solutions Hindi Lokvani Chapter 6 सागर और मेघ Notes, Textbook Exercise Important Questions and Answers.

Std 9 Hindi Chapter 6 Sagar Aur Megh Question Answer Maharashtra Board

Hindi Lokvani 9th Digest Chapter 6 सागर और मेघ Questions And Answers

1. स्वमत अभिव्यक्ति:

प्रश्न 1.
‘अगर न नभ में बादल होते’ इस पर अपने विचार लिखिए।
उत्तर:
अगर नभ में बादल न होते तो बारिश नहीं होती और यदि वर्षा नहीं होती तो हमारा जीवन संकट में पड़ जाता। क्योंकि जल ही जीवन है। वर्षा के माध्यम से हमें जल की प्राप्ति होती है। हमारा देश एक कृषि प्रधान देश है जहाँ ७०% आबादी कृषि पर निर्भर है अगर वर्षा न होती तो धरती बंजर रह जाती और हमें भोजन के लिए अन्न उपलब्ध नहीं होता। नदी, तालाब, जलाशय सब सूख जाते और प्राणियों का जीवन संकट में पड़ जाता क्योंकि बिना भोजन के हम कुछ दिन जीवित रह सकते हैं, लेकिन बिना पानी के हमारा एक-दो दिन जीना भी मुश्किल हो जाएगा।

अगर मेघ न होंगे, तो धरती का तापमान अत्यधिक बढ़ जाएगा और मनुष्य बेहाल हो जाएगा। बारिश के कारण धरती का तापमान नियंत्रित रहता है। बादल संसार को जल रूपी जीवन का दान करता है और अनुपजाऊ धरती को उपजाऊ बनाता है। किसान बड़ी आतुरता के साथ वर्षा का इंतजार करता है। इस प्रकार हम कह सकते हैं कि अगर न नभ में बादल होते, तो शायद यह जीवन ही संभव न हो पाता।

प्रश्न 2.
‘सागर और मेघ एक-दूसरे के पूरक हैं’ इस पर अपने विचार लिखिए।
उत्तर:
‘सागर और मेघ एक-दूसरे के पूरक हैं’ क्योंकि इन दोनों के बिना जलचक्र संभव नहीं हो सकता है। जब मेघ से पानी बरसता है तो वह वायुमंडल से भूमि तक पहुँचता है। फिर नदियों में जाकर मिलता है और वह नदियाँ अंत में जाकर सागर में मिल जाती हैं। सागर में वाष्पीकरण की क्रिया होती है और वह पानी वाष्प बनकर फिर बादल बन जाते हैं और पृथ्वी पर वर्षा होती है जिससे अनेक जीव-जंतु और वनस्पतियाँ उत्पन्न होती हैं। अत: हम कह सकते हैं कि सागर और मेघ के बिना प्राणी का जीवन संभव नहीं हो सकता। इसलिए वे दोनों एक-दूसरे के पूरक हैं।

2. उचित जोड़ियाँ मिलाइए।

प्रश्न 1.
उचित जोड़ियाँ मिलाइए।

‘अ’	‘ब’
1.  झूठी स्पर्धा करने वाला	(क) सागर
2. अपने हृदय में कंकड़ पत्थर, शंख-घोंघे	(ख) मेघ भरने वाला।
	(ग) मनुष्य

उत्तर:

‘अ’	‘ब’
1.  झूठी स्पर्धा करने वाला	(ग) मनुष्य
2. अपने हृदय में कंकड़ पत्थर, शंख-घोंघे	(क) सागर

3. समानार्थी शब्द बताइए।

प्रश्न 1.
समानार्थी शब्द बताइए।
1. संसार
2. विवेकहीन
उत्तर:
1. विश्व
2. बुद्धिहीन

भाषा बिंदु:

प्रश्न 1.
निम्न वाक्यों में से सर्वनाम एवं क्रिया छाँटकर भेदों सहित लिखिए।
उत्तर:

मौलिक सृजन:

प्रश्न 1.
‘परिवर्तन सृष्टि का नियम है’ इस संदर्भ में अपना मत व्यक्त कीजिए।
उत्तर:
परिवर्तन सृष्टि का नियम है। इस विषय पर हमें ध्यान देने की आवश्यकता है कि यह नियम क्या है। जैसे हमारे देश में ६ ऋतुएँ है इसी प्रकार संपूर्ण विश्व में भी कई प्रकार के मौसम हैं। जिस प्रकार गर्मी के बाद वसंत ऋतु आती है। यही प्रकृति का नियम हैं। उसी प्रकार हमारे मानव जीवन में भी कई परिवर्तन आते हैं जैसे जन्म से शिशु अवस्था, शैशव से किशोर अवस्था, युवा अवस्था और अंत में वृद्धावस्था और इसके बाद एक दिन सृष्टि के नियमानुसार हमें इस धराधाम को छोड़कर जाना पड़ता है। मानव जीवन में सुख और दुख भी होते हैं मगर हम मनुष्य हर परिवर्तन को सहन नहीं कर पाते; क्योंकि हर परिवर्तन हमारा मन चाहा नहीं होता है।

हम चाहते कुछ है और होता कुछ और है। ज्यादातर देखा गया है कि मनुष्य अगर इन परिवर्तनों को स्वीकार नहीं पाता है तो अधिक दुखी हो जाता है और इस दुख में इंसान अपने मन का संतुलन खो देता है और गलत कदम उठा लेता है। हमारे पूर्वजों के द्वारा हमें पता चलता है कि परमात्मा के दिए हुए हर परिवर्तन में कोई न कोई अच्छी दिशा, अच्छा और नया संदेश निहित होता है। अत: अगर हम परिवर्तन को ईश्वर का दिया हुआ वरदान मान लें; तो इसमें कोई नई आशा, नई दिशा तथा नया मार्ग मिले जो पहले से बेहतर हो इसलिए हमें यह समझने की जरूरत है कि परिवर्तन सृष्टि का नियम है।

पाठ के आँगन में:

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

पाठ से आगे:

प्रश्न 1.
‘मोती कैसे तैयार होता है?’ इस पर चर्चा कीजिए और दैनिक जीवन में मोती का उपयोग कहाँ -कहाँ होता हैं? स्पष्ट कीजिए।
उत्तर:
प्राचीन काल से ही मोती का उपयोग काफी प्रचलित था। रामायण तथा अन्य धार्मिक ग्रन्थों में भी मोती की चर्चा पाई गई है। अमेरिका के मूल निवासी रेड इंडियन मोती को काफी महत्त्व देते थे। प्राकृतिक मोती की उत्पत्ति प्राकृतिक ढंग से होती है। वराह मिहिर की वृहत्संहिता में बताया गया है कि प्राकृतिक मोती की उत्पत्ति सीप, सर्प के मस्तक, मछली, सुअर तथा हाथी से होती है। परंतु अधिकांश प्राचीन भारतीय विद्वानों ने मोती की उत्पत्ति सीप से बताई हैं। प्राचीन विद्वानों का मत है कि जब स्वाति नक्षत्र के दौरान वर्षा की बूंदे सीप में पड़ती हैं तो मोती का निर्माण होता है।

आधुनिक वैज्ञानिकों का मत है कि मोती निर्माण के लिए शरद ऋतु सबसे अनुकूल है क्योंकि इसी ऋतु में स्वाति नक्षत्र का आगमन होता है। इस समय जब वर्षा की बूंदें या वालू का कण किसी सीप के अंदर जाता है तो सीप एक तरल पदार्थ का स्राव करती है, यह तरल पदार्थ परत दर परत चढ़ता जाता है और मोती का रूप ले लेता है। 13 वीं शताब्दी से चीन में कृत्रिम मोती का उत्पादन भी होने लगा है। इसे मोती की खेती भी कहते हैं। 1961 से भारत में भी मोती की खेती की शुरूआत की गई। इसमें सबसे पहले सीपी का चुनाव किया जाता है फिर प्रत्येक सीपी में शल्य क्रिया करनी पड़ती है। इस शल्य क्रिया के बाद सीपी के भीतर एक छोटा-सा नाभिक तथा ऊतक रखा जाता है।

इसके बाद सीपी इस प्रकार बंद कर दिया जाता है कि उसकी सभी जैविक क्रियाएँ पहले की तरह चलती रहें। ऊतक से निकलने वाला पदार्थ नाभिक के चारों ओर जमने लगता है और अंत में मोती का रूप ले लेता है। आजकल नकली मोती भी बनाए जाते हैं। नकली मोती सीप से नहीं बनाए जाते बल्कि शीशे या आलाबास्टर के मनको पर मछली के शल्क के चूरे की परतें चढ़ाकर बनाए जाते हैं। इनकी आज बाजारों में बड़ी माँग है। ये कीमत में सस्ते भी होते हैं। मोती का उपयोग आभूषण बनाने में किया जाता है। इसके अलावा मोती औषधि बनाने के काम में भी आती है। जैसे मोती भस्म का उपयोग कब्ज नाशक के रूप में किया जाता है। इसके अलावा इन मोतियों से एक प्रकार की गोली बनती है, जो पेट की गैस तथा एलर्जी के लिए उपयोगी है।

आसपास:

प्रश्न 1.
दूरदर्शन पर प्रतिदिन दिखाए जानेवाली तापमान संबंधी जानकारी देखिए। संपूर्ण सप्ताह में तापमान में किस तरह का बदलाव पाया गया, इसकी तुलना करके टिप्पणी तैयार कीजिए।
उत्तर:
पिछले कई दिनों से मैं प्रतिदिन दूरदर्शन पर दिखाए जाने वाले तापमान संबंधी जानकारी को देख रहा हूँ। संपूर्ण सप्ताह का तापमान देखने के बाद मुझे ज्ञात हुआ कि महानगरों का तापमान कभी बहुत बढ़ जाता है तो कभी कम हो जाता है। पिछले कई सप्ताहों से मुंबई, दिल्ली,मद्रास, कोलकाता आदि महानगरों के तापमान में काफी बदलाव आ रहा है। वैज्ञानिकों का मानना है कि सारे बदलाव का कारण ग्लोबल वार्मिंग है। जिसे साधारण भाषा में भूमंडलीय तापमान में वृद्धि कहते हैं।

आज तापमानों में बदलाव का मुख्य कारण प्रदूषण है। जिससे कार्बन डाई आक्साईड की मात्रा बढ़ रही है। आधुनिकीकरण के कारण पेड़ों की कटाई और गाँवों का शहरीकरण बहुत तेजी से हो रहा है, जिसके कारण खुली और ताजी हवा या आक्सीजन का अभाव होता जा रहा है। पेड़ों तथा जंगलो की अंधाधुंध कटाई के कारण पर्यावरण का संतुलन बिगड़ता जा रहा है। जिससे कही ठंड बहुत ज्यादा हो रही है, तो कही गर्मी का प्रकोप बहुत ज्यादा हो रहा है।

वैज्ञानिकों का मत है कि आनेवाले समय में यह तापमान बदलाव बहुत भयानक रूप ले सकता है। यह फसलों के साथ-साथ जनजीवन के लिए भी नुकसानदायक है। ग्लोबल वार्मिंग के कारण अधिकतम तथा न्यूनतम पारे का अंतर बढ़ गया है। इसलिए हमें सावधान रहने की आवश्यकता है। हमें कोशिश करनी चाहिए कि जितनी जल्दी हो इस समस्या का समाधान प्राप्त कर लें।

Hindi Lokvani 9th Std Textbook Solutions Chapter 6 सागर और मेघ Additional Important Questions and Answers

(क) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति क (1): आकलन कृति

प्रश्न 1.
समझकर लिखिए।
1. नदियों के कर देने की निरंतरता इससे बनी रहती है –
2. सागर ने मेघ को इस पर ध्यान देने के लिए कहा –
उत्तर:
1. मेघ द्वारा दिया गया बहुत-सा दान जिसे नदियाँ पृथ्वी के पास धरोहर के रूप में रखे रहती हैं।
2. वाइव जो नित्य मुझे (सागर) जलाया करता है, फिर भी मैं उसे छाती से लगाए रहता हूँ।

प्रश्न 2.
उचित जोड़ियाँ मिलाइए।

‘अ’	‘ब’
1.  दूसरे की करतूत पर गर्व करनेवाला	(क) वाड़व
2. सागर को नित्य जलाने वाला	(ख) मेघ
	(ग) मनुष्य

उत्तर:

‘अ’	‘ब’
1.  झूठी स्पर्धा करने वाला	(ख) मेघ
2. अपने हृदय में कंकड़ पत्थर, शंख-घोंघे	(ग) मनुष्य

कृति (2): शब्द-संपदा

प्रश्न 1.
प्रत्यय अलग करके लिखिए।
1. निरंतरता
2. गरजकर
उत्तर:
1. निरंतर + ता (ता – प्रत्यय)
2. गरज + कर (कर – प्रत्यय)

प्रश्न 2.
वचन परिवर्तन कीजिए।
1. नदियाँ
2. पृथ्वी
उत्तर:
1. नदी
2. पृथ्वी

प्रश्न 3.
निम्नलिखित के समानार्थी शब्द लिखिए।
1. पृथ्वी
2. विश्राम
उत्तर:
1. धरती
2. आराम

(ख) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

कृति (2): शब्द-संपदा

प्रश्न 1.
उपसर्ग अलग करके लिखिए।
1. अस्थिरता
2. अचल
उत्तर:
1. अ + स्थिरता = अस्थिरता (अ – उपसर्ग)
2. अ+ चल = अचल (अ – उपसर्ग)

प्रश्न 2.
गद्यांश से विलोम शब्द ढूँढ़कर लिखिए।
1. अहिंसा × ……….
2. धरती × ………..
उत्तर:
1. हिंसा
2. आकाश

प्रश्न 3.
निम्नलिखित के समानार्थी शब्द लिखिए।
1. स्पर्धा
2. मेघ
उत्तर:
1. प्रतियोगिता
2. बादल

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘अगर सागर न होता तो ……..’ अपने विचार लिखिए।
उत्तर:
अगर सागर न होता, तो हमें बहुत सारी कठिनाइयों का सामना करना पड़ता । धरती के ७० प्रतिशत भू-भाग में सागर फैला हुआ है। अगर महासागरों में जैव विविधता का विशाल भंडार न होता, तो पृथ्वी पर जीवन ही संभव न होती। यदि समुद्र का पानी खारा न होता तो गर्म प्रदेश और गर्म हो जाते तथा ठंडे प्रदेश और ज्यादा ठंडे। यह सागर की विशाल जलराशि ही है जो सूर्य से आनेवाली उष्मा का एक बड़ा हिस्सा अपने भीतर समा लेती है। यह प्रक्रिया ही मौसम को संतुलित करती है।

सागर में मौजूद विविध जैविकी में कार्बन को अवशोषित करने की क्षमता होती है। इस क्षमता के कारण ही इन्हें पर्यावरण को संतुलित रखने का सबसे सशक्त माध्यम माना गया है। सागर का खारा पानी भले ही पीने लायक न हो लेकिन यह गर्म हवाओं को ठंडा करती है तथा इस खारेपन के कारण ही बारिश होती है, मौसमों में रंगों की विविधता है तथा जीवन है। जिस प्रकार समुद्र मंथन के दौरान भगवान शंकर विष को पीकर नीलकंठ कहलाए; उसी प्रकार कार्बन और नमक के जहर को पीकर सागर हमें सुरक्षित रखता है और पर्यावरण को संतुलित करता है। इसलिए अगर सागर न होता, तो शायद पृथ्वी में जीवन का अस्तित्व ही न होता।

(ग) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति ग (1): आकलन कृति

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
सत्य असत्य पहचानकर लिखिए।
1. क्रोध हमें विवेकहीन बना देता है।
2. मनुष्य सागर और मेघ पर निर्भर नहीं है।
उत्तर:
1. सत्य
2. असत्य

कृति ग (2): शब्द-संपदा

प्रश्न 1.
विलोम शब्द लिखिए।
1. स्वादिष्ट × ……………..
2. उन्नति × ……………..
उत्तर:
1. स्वादहीन
2. अवनति

प्रश्न 2.
निम्नलिखित शब्दों से प्रत्यय अलग करके लिखिए।
1. अपमानित
2. आतुरता
उत्तर:
1. ‘इत’ प्रत्यय
2. ‘ता’ प्रत्यय

भाषाई कौशल पर आधारित पाठगत कृतियाँ

भाषा बिंदु:

प्रश्न 1.
निम्न में से संज्ञा तथा विशेषण पहचानकर भेदों सहित लिखिए।
उत्तर:

सागर और मेघ Summary in Hindi

लेखक-परिचय:

जीवन-परिचय: राय कृष्णदास का जन्म उत्तर प्रदेश के वाराणसी जिले में हुआ था। ये हिंदी, अंग्रेजी, संस्कृत और बांग्लाभाषा के अच्छे जानकार थे। इन्होंने कविता, निबंध गद्यगीत, कहानी, कला, इतिहास आदि विषयों पर रचनाएँ की हैं। इनको ‘साहित्य वाचस्पति पुरस्कार’ तथा भारत सरकार दवारा ‘पद्म विभूषण’ की उपाधि मिली थी।

प्रमुख कृतियाँ: मौलिक ग्रंथ – ‘भारत की चित्रकला’, ‘भारत की मूर्तिकला’, कहानी संग्रह – ‘साधना आनाख्या’, ‘सुधांशु’, गद्यगीत – ‘प्रवाल’।

गद्य-परिचय:

संवाद: दो या दो से अधिक व्यक्तियों के बीच हुआ वार्तालाप, बातचीत या संभाषण ‘संवाद’ कहलाता है।

प्रस्तावना: प्रस्तुत संवाद ‘सागर और मेघ’ के द्वारा लेखक ने सागर एवं मेघ के गुणों को दर्शाया है और हमें विनम्र होने की सीख
देते हुए कहा है कि अपने गुणों पर इतराना और अहंकार करना एक बुराई है। अहंकार नाश का मूल है। अतः लेखक इससे बचने की सलाह देते हैं।

सारांश:

सागर और मेघ अपने गुणों का बखान करते हुए आपस में संवाद कर रहे हैं। सागर कहता है कि उसके हृदय में मोती भरे हैं। जवाब में मेघ कहता है कि तुमने मुझसे जल का हरण किया है। सागर कहता है कि मैं सदा अपना कर्म करता हूँ। अगर सागर न होते तो मेघ न बनते अर्थात तुम्हें जन्म देने वाला मैं हूँ। मेघ मुस्कुराकर कहता है कि अगर बरसात न होती, तो नदियाँ कहाँ से उमड़ती और तुम्हें भरती। सागर मेघ पर व्यंग्य करते हुए कहता है कि आकाश में इधर-उधर मारे-मारे फिरते हो। मेघ सागर को हँसकर जवाब देता है कि मैं घूम-फिर कर संसार का निरीक्षण करता हूँ और जहाँ आवश्यक होता है; वहाँ जीवन-दान करता हूँ। अगर मैं न रहूँ, तो यह धरती बंजर हो जाएगी।

फिर मेघ सागर को उलाहना देते हुए कहता है कि तुम्हारा हृदय कठोर है क्योंकि तुम्हारे दिल में कंकड़-पत्थर भरे हुए हैं। जवाब में सागर कहता है कि जिन्हें तुम कंकड़-पत्थर समझ रहे हो वो असल में रत्न हैं। सागर आगे कहता है कि तुम सिर्फ शोर मचाना जानते हो। मेघ तुरंत जवाब देता है कि वह गरजने के साथ बरसना भी जानता है। लेकिन वह सागर की तरह नहीं है कि केवल उत्पातियों और अपराधियों को जगह देता है। सागर मेघ की बातों से क्रोधित हो उठता है और कहता है कि हाँ, मैं शरण अवश्य देता हूँ लेकिन दंड उतना ही होना चाहिए कि दंडित सावधान हो जाए; उसे अपाहिज नहीं होना चाहिए।

सागर की बातों से मेघ भी गुस्से में आ जाता है और कहता है यह भी कोई नीति हुई कि राजा अपने राज्य की रक्षा के लिए हमेशा शस्त्र लिए खड़ा रहे अपनी राज्य की उन्नति न कर पाए। अब सागर को असली बात समझ में आती है और वह मेघ से कहता है कि अपना क्रोध शांत करो और आओ हम दोनों मिलकर जनकल्याण का कार्य करें।

मेघ का भी क्रोध शांत होता है और वह कहता है कि प्रति वर्ष किसान मेरी प्रतीक्षा करता है। इसलिए हे सागर भाई, हमें आपस में उलझना नहीं चाहिए। दोनों प्रतिज्ञा करते हैं कि अब हम घमंड में एक-दूसरे का अपमान नहीं करेंगे। बल्कि लोक कल्याण के लिए कार्य करेंगे। मेघ कहता है कि मैं नदियों को भर-भर कर तुम तक भेजूंगा और सागर कहता है कि मैं सहर्ष उन्हें उपकार सहित ग्रहण करूँगा।।

शब्दार्थ:

1. बुलंद – ऊँचा, उन्नत
2. वारि – जल
3. धरोहर – विरासत
4. निरंतरता – अविरामता
5. कायम रहना – बने रहना
6. विकार – गंदगी
7. तृप्त – संतुष्ट
8. करतूत – कार्य
9. हठात – हठपूर्वक
10. वाड़व – समुद्र जल के अंदर वाली अग्नि
11. मर्यादा. – सीमा
12. आयास – विस्तार (आयाम)
13. उच्छंखल – उदंड, उत्पाती
14. रसा – पृथ्वी
15. वंध्या – बंजर
16. निपात – गिरना
17. आततायियों – अत्याचारियों
18. चेत जाना – सावधान होना
19. शास्ता – राजा, शासक
20. आतुरता – उत्सुकता

Hindi Lokvani 9th Std Textbook Solutions दूसरी इकाई

• गागर में सागर Question Answer
• मैं बरतन माँगूँगा Question Answer
• ग्रामदेवता (पठनार्थ) Question Answer
• साहित्य की निष्कपट विधा है-डायरी Question Answer
• उम्मीद Question Answer
• सागर और मेघ Question Answer
• लघुकथाएँ (पठनार्थ) Question Answer
• झंडा ऊँचा सदा रहेगा Question Answer

Std 9 Hindi Chapter 1 Chandni Raat Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Hindi Solutions Lokbharti Chapter 1 चाँदनी रात Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 9th Digest Chapter 1 चाँदनी रात Questions And Answers

Hindi Lokbharti 9th Std Digest Chapter 1 चाँदनी रात Textbook Questions and Answers

1. सूचनानुसार कृतियाँ कीजिए :

(क) संजाल:

प्रश्न 1.
संजाल:

उत्तर:

(ख) चाँदनी रात की विशेषताएँ:

प्रश्न 1.
चाँदनी रात की विशेषताएँ:
उत्तर:

1. सुंदर चंद्रमा की झिलमिलाती किरणें जल और थल में फैली हुई हैं।
2. पृथ्वी और आकाश में स्वच्छ चाँदनी बिछी हुई है।
3. हरी-हरी घास की नोकों के माध्यम से पृथ्वी अपनी खुशी प्रकट कर रही है।
4. सभी वृक्ष मंद-मंद वायु के झोंकों से झूमते प्रतीत होते हैं।
5. दूर-दूर तक फैली चाँदनी बहुत ही साफ दिखाई दे रही है।
6. रात सन्नाटे से भरी है, कोई शोर नहीं हो रहा है।
7. वायु स्वच्छंद होकर मंद-मंद गति से बह रही है।
8. इस समय पूर्व, पश्चिम आदि सभी दिशाओं में आनंद ही आनंद व्याप्त है।

2. निम्नलिखित पंक्तियों का सरल अर्थ लिखिए :

प्रश्न च.
चारु चंद्र ……….. झोंकों से ।
उत्तर:
भावार्थ: गुप्त जी चाँदनी रात का वर्णन करते हुए कहते हैं कि सुंदर चंद्रमा की किरणें जल और थल में फैली हुई हैं। संपूर्ण पृथ्वी तथा आकाश में स्वच्छ चाँदनी बिछी हुई है। पृथ्वी हरी-हरी घास की नोकों के माध्यम से अपनी खुशी प्रकट कर रही है। ऐसा प्रतीत होता है, मानो वृक्ष भी मंद-मंद वायु के झोंकों से झूम रहे हैं।

प्रश्न छ.
क्या ही स्वच्छ ………. शांत और चुपचाप ।
उत्तर:
भावार्थ: पंचवटी में दूर-दूर तक चाँदनी फैली हुई है, वह बहुत ही साफ दिखाई दे रही है। रात सन्नाटे से भरी है। कोई शब्द नहीं हो रहा है। वायु स्वच्छंद होकर अपनी स्वतंत्र चाल से मंद-मंद बह रही है। इस समय कौन-सी दिशा है जो आनंद नहीं ले रही है? अर्थात सभी दिशाएँ इस सौंदर्य से आनंदित हो रही हैं। उत्तरपश्चिम आदि सभी दिशाओं में आनंद ही आनंद व्याप्त है। कोई भी दिशा आनंद-शून्य नहीं है। ऐसे समय में भी नियति नामक शक्ति-विशेष के समस्त कार्य संपन्न हो रहे हैं। कोई रुकावट नहीं। वह एक भाव से अर्थात् अकेले-अकेले और चुपचाप अपने कर्तव्यों का निर्वाह किए जा रही है।

पाठ से आगे

प्रश्न 1.

उत्तर:
आकाश केवल बिजली नहीं चमकाता
पर्वत केवल चोटियाँ नहीं दिखलाता
पृथ्वी केवल भूकंप नहीं लाती
तारे केवल टिमटिमाते नहीं
वैसे ही, हाँ वैसे ही
मन में सिर्फ विचार नहीं आते
बल्कि विश्वास,
आस्था, प्रकाश, उदासी की
एक पावन श्रृंखला भी आती है।
जो मनुष्य को मनुष्य से जोड़कर
मानवता के एकसूत्र में बाँधती है।

संभाषणीय :

शरद पूर्णिमा त्योहार के बारे में चर्चा कीजिए।

प्रश्न 1.
शरद पूर्णिमा त्योहार के बारे में चर्चा कीजिए।
उत्तरः

• गौरी – अरे राधिका, आज बहुत फूल-माला खरीद रही हो, क्या बात है?
• राधिका – गौरी तुम्हें मालूम नहीं कि आज शरद पूर्णिमा की रात होगी।
• गौरी – अरे! मैं तो भूल ही गई थी।
• राधिका – क्या तुम्हें मालूम है, यह त्योहार कब मनाया जाता है?
• गौरी – हाँ, मालूम है, शरदीय नवरात्र के बाद पड़ने वाली पूर्णिमा को यह त्योहार मनाते हैं। परंतु इस त्योहार की क्या मान्यता है?
• राधिका – ‘शरद पूर्णिमा’ हिंदुओं का प्रसिद्ध त्योहार है। ज्योतिष के अनुसार, पूरे साल में केवल इसी दिन चंद्रमा सोलह कलाओं से परिपूर्ण होता है। ऐसी मान्यता भी है कि आश्विन शुक्ल पक्ष में पड़ने वाली पूर्णिमा के दिन चंद्रमा से अमृत वर्षा होती है।
• गौरी – राधिका, इस त्योहार के दिन किसकी व्रत-पूजा होती है?
• राधिका – गौरी, इस दिन माँ लक्ष्मी का व्रत रखते हैं । पूरे वर्ष हम स्वस्थ और सुख-शांति से रहें, इसके लिए हम उनकी पूजा-अर्चना करते हैं।
• गौरी – इसकी पूजा की विधि क्या है , राधिका?
• राधिका – इस दिन मूर्ति बनाने वाले कारीगर के पास से एक लक्ष्मी की मूर्ति लाते हैं। पाँच तरह के फल व सब्जियों के साथ नारियल अर्पित कर उनकी पूजा करते हैं तथा उस मूर्ति को पूरे साल सँभाल कर रखते हैं। अगले वर्ष फिर शरद पूर्णिमा के दिन उस मूर्ति को विसर्जित कर नई प्रतिमा रखते हैं। इस दिन मंदिरों में भी विशेष पूजा-अर्चना होती है।
• गौरी – तुमसे मिलकर बहुत प्रसन्नता हुई। इतनी अच्छी जानकारी देने के लिए धन्यवाद!

भाषा बिंदु :

निम्नलिखित पद्यांश का भावार्थ लिखिए।

प्रश्न 1.
निम्नलिखित पद्यांश का भावार्थ लिखिए।

उत्तरः

Hindi Lokbharti 9th Answers Chapter 1 चाँदनी रात Additional Important Questions and Answers

पद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
एक शब्द में उत्तर लिखिए।
i. ये अपनी खुशी प्रकट कर रही है
ii. ये वायु के झोंकों से झूम रहे हैं
उत्तर:
i. पृथ्वी
ii. वृक्ष

प्रश्न 2.
चौखट पूर्ण कीजिए।
उत्तर:

प्रश्न 3.
चौखट पूर्ण कीजिए।
उत्तर:

प्रश्न 4.
समझकर लिखिए।
i. पंचवटी की छाया में बना है
ii. धनुर्धर इस पर बैठा हुआ है
उत्तर:
i. पर्णकुटीर
ii. स्वच्छ शिला पर

कृति (2) आकलन कृति

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
सही शब्द चुनकर वाक्य फिर से लिखिए।
i. क्या ही स्वच्छ/सुगंध चाँदनी है यह।
ii. नियति नदी/नटी के कार्य-कलाप।
उत्तरः
i. क्या ही स्वच्छ चाँदनी है यह।
ii. नियति नटी के कार्य-कलाप ।

प्रश्न 3.
आकृति पूर्ण कीजिए।
उत्तरः

प्रश्न 4.
सत्य या असत्य पहचानकर लिखिए।
i. पंचवटी में अंधेरी रात है।
ii. सभी दिशाओं में आनंद ही आनंद व्याप्त है।
उत्तर:
i. असत्य
ii. सत्य कृति

प्रश्न 5.
चौखट पूर्ण कीजिए।
उत्तर:

प्रश्न 6.
सत्य या असत्य पहचानकर लिखिए।
i. पृथ्वी मोतियों को समेट लेती है।
ii. सूर्य सबेरा होने पर मोतियों को बिखेर देता है।
उत्तर:
i. असत्य
ii. असत्य

प्रश्न 7.
एक-एक शब्द में उत्तर लिखिए।
i. सबके सो जाने पर मोती ये बिखेरती है
ii. सुबह होने पर मोतियों को ये बटोर लेता है
उत्तर:
i. वसुंधरा
ii. रवि

प्रश्न 8.
सत्य या असत्य पहचानकर लिखिए।
i. कुटीर पत्थरों का बना है।
ii. कुटीर में धौर-वीर निर्भीक मनवाला युवक बैठा है।
उत्तर:
i. असत्य
ii. असत्य

कृति (3) भावार्थ

निम्नलिखित पद्यांश का भावार्थ लिखिए ।

प्रश्न 1.
है बिखेर देती ……………………… छलकता है।।
भावार्थ:
चाँदनी रात में पृथ्वी सबके सो जाने पर ओस रूपी मोतियों को बिखेर देती है। सूर्य हमेशा सुबह होने पर उन मोतियों को अपनी किरणों से बटोर लेता है और अस्त होने से पहले ही वह आराम प्रदान करने वाली संध्या देकर चला जाता है। मानो आकाश को साँवला शरीर देकर वह अपना नया-सा रूप छलका जाता है।

प्रश्न 2.
पंचवटी की ………………………… होता है।।
भावार्थः
कवि कहता है कि पंचवटी की घनी छाया में पत्तों की एक सुंदर कुटिया बनी हुई है। इस कुटिया के सामने एक स्वच्छ तथा विशाल पत्थर पड़ा हुआ है और उस पत्थर के ऊपर धैर्यशाली, निर्भय मनवाला पुरुष बैठा हुआ है। सारा संसार सो रहा है परंतु यह धनुषधारी इस समय भी जाग रहा है। यह वीर ऐसा दिखाई पड़ता है जैसे भोग करनेवाला कामदेव यहाँ योगी बनकर आ बैठा हो।

लेखनीय :

प्रश्न 1.
प्रकृति मनुष्य की मित्र है’, स्पष्ट कीजिए।
उत्तरः
संदर्भ के लिए परिच्छेद (4) का स्वमत देखिए।

कल्पना पल्टन :

प्रश्न 1.
पुलक प्रगट करती है धरती हरित तणों की ‘नोकों से’ इस पंक्ति का कल्पना विस्तार कीजिए।
उत्तरः
चाँदनी रात में धरती से लेकर आकाश तक पूरी प्रकृति सुंदर और स्वच्छ किरणों में सराबोर है। धरती का कण-कण इन किरणों से दिप्त हो रहा है। धरती पर फैली हुई हरी-हरी घास की नोकों पर ओस की बूंदें पड़ी हैं, जिस पर चाँद की उज्ज्वल किरणें पड़ने से वे मोतियों की तरह चमक रही हैं। इनको देखकर ऐसा लगता है मानों धरती इन घास की नोकों पर चमकने वाली मोतियों के माध्यम से अपनी खुशी प्रकट कर रही हैं।

पद्य-विश्लेषण :

कविता का नाम – चाँदनी रात
कविता की विधा – खंडकाव्य
पसंदीदा पंक्ति – चारू चंद्र की चंचल किरणें खेल रही हैं जल-थल में। स्वच्छ चाँदनी बिछी हुई है अवनि और अंबर तल में।

पसंदीदा होने का कारण –
उपर्युक्त पंक्ति मेरी पसंदीदा पंक्ति है क्योंकि उसमें ‘च’ वर्ष की बार-बार पुनरावृत्ति होने से अनुमास अलंकार की छटा दिखलाई दे रही है। इस कारण कविता के सौंदर्य में वृद्धि हो गई है।

कविता से प्राप्त संदेश या प्रेरणा –
प्रस्तुत कविता से प्रेरणा यह मिलती है कि व्यक्ति को चाँदनी रात की तरह अपना जीवन सुंदर बनाना चाहिए। मनुष्य को प्रकृति के प्रति कृतज्ञ रहना चाहिए। प्रकृति मनुष्य के जीवन को शक्ति एवं आनंद प्रदान करती है। अत: उसे प्रकृति के साथ खिलवाड़ नहीं करना चाहिए। प्रकृति के संतुलन को बनाए रखने के लिए व्यक्ति को पेड़ लगाने चाहिए।

चाँदनी रात Summary in Hindi

कवि-परिचय:

जीवन-परिचय: मैथिलीशरण गुप्त जी खड़ी बोली के महत्त्वपूर्ण कवि हैं। इनका जन्म उत्तर प्रदेश में झाँसी जिले के चिरगाँव में हुआ। 12 वर्ष की अवस्था में उन्होंने ब्रजभाषा में कविता की रचना आरंभ की। उनकी रचनाएँ पवित्रता, नैतिकता, मानवीय संवेदनाओं और विशेषकर नारी के प्रति करुणा की भावना से ओतप्रोत हैं। उनकी रचनाओं से प्रसन्न होकर गाँधी जी ने उन्हें ‘राष्ट्रकवि’ की उपाधि दी। 12 दिसंबर 1964 ई. को दिल का दौरा पड़ने के कारण इनका निधन हो गया।
प्रमुख कृतियाँ: महाकाव्य – ‘साकेत’, खंडकाव्य – ‘यशोधरा’, ‘जयद्रथ वध’, ‘पंचवटी’, ‘भारत-भारती’, नाटक – ‘रंग में भंग’, ‘राजा-प्रजा’ आदि।

पद्य-परिचय:

खंडकाव्य: खंडकाव्य में मानव जीवन की किसी एक ही घटना की प्रधानता होती है। प्रासंगिक कथाओं को इसमें स्थान नहीं मिलता।
प्रस्तावना: प्रस्तुत कविता ‘चाँदनी रात’ पंचवटी खंडकाव्य से ली गई है। कवि मैथिलीशरण गुप्त जी ने इस कविता में प्रकृति की छटा का सुंदर रूप बड़े ही माधुर्य के साथ अभिव्यंजित किया है तथा चाँदनी रात का मनोहारी वर्णन सुंदर शब्दों में चित्रित किया है।

सारांश:

कवि चाँदनी रात का वर्णन करते हुए कहते हैं कि चंद्रमा की किरणें जल और थल में फैली हुई हैं। पृथ्वी से लेकर आकाश तक सर्वत्र चाँदनी बिछी हुई है। पूरी प्रकृति चाँदनी में सराबोर है। रात सन्नाटे में डूबी हुई है। वायु स्वच्छंद होकर मंद-मंद बह रही है। सभी दिशाओं में आनंद ही आनंद व्याप्त है। नियति चुपचाप अपने कर्तव्यों का पालन कर रही है। ऐसे में पंचवटी की छटा बहुत ही निराली प्रतीत होती है। उसकी घनी छाया में पत्तों की एक सुंदर कुटिया बनी हुई है। इसके सामने स्वच्छ शिला के ऊपर धैर्यशाली, निडर मनवाला एक पुरुष बैठा हुआ है। यह वीर ऐसा दिखाई पड़ता है जैसे कामदेव योगी बनकर बैठा है।

भावार्थ:

चारु चंद्र की …………………………. झोंकों से।।
गुप्त जी चाँदनी रात का वर्णन करते हुए कहते हैं कि सुंदर चंद्रमा की किरणें जल और थल में फैली हुई हैं। संपूर्ण पृथ्वी तथा आकाश में स्वच्छ चाँदनी बिछी हुई है। पृथ्वी हरी-हरी घास की नोकों के माध्यम से अपनी खुशी प्रकट कर रही है। ऐसा प्रतीत होता है, मानो वृक्ष भी
मंद-मंद वायु के झोंकों से झूम रहे हैं।

क्या ही स्वच्छ ………………………….. और चुपचाप।।
पंचवटी में दूर-दूर तक चाँदनी फैली हुई है, वह बहुत ही साफ दिखाई दे रही है। रात सन्नाटे से भरी है। कोई शब्द नहीं हो रहा है। वायु स्वच्छंद होकर अपनी स्वतंत्र चाल से मंद-मंद बह रही है । इस समय कौन-सी दिशा है जो आनंद नहीं ले रही है ? अर्थात सभी दिशाएँ इस सौंदर्य से आनंदित हो रही हैं। उत्तर-पश्चिम आदि सभी दिशाओं में आनंद ही आनंद व्याप्त है। कोई भी दिशा आनंद-शून्य नहीं है। ऐसे समय में भी नियति नामक शक्ति-विशेष के समस्त कार्य संपन्न हो रहे हैं। कोई रुकावट नहीं। वह एक भाव से अर्थात् अकेले-अकेले और चुपचाप अपने कर्तव्यों का निर्वाह किए जा रही है।

है बिखेर देती …………………………… छलकाता है।।
चाँदनी रात में पृथ्वी सबके सो जाने पर ओस रूपी मोतियों को बिखेर देती है। सूर्य हमेशा सुबह होने पर उन मोतियों को अपनी किरणों . से बटोर लेता है और अस्त होने से पहले ही वह आराम प्रदान करने वाली संध्या देकर चला जाता है। मानो आकाश को साँवला शरीर देकर वह अपना नया-सा रूप छलका जाता है।

पंचवटी की ……….. …………….. होता है।।
कवि कहते है कि पंचवटी की घनी छाया में पत्तों की एक सुंदर कुटिया बनी हुई है। इस कुटिया के सामने एक स्वच्छ तथा विशाल पत्थर पड़ा हुआ है और उस पत्थर के ऊपर धैर्यशाली, निर्भय मनवाला पुरुष बैठा हुआ है। सारा संसार सो रहा है परंतु यह धनुषधारी कौन है जो इस समय भी जाग रहा है? यह वीर ऐसा दिखाई पड़ता है जैसे भोग करनेवाला कामदेव यहाँ योगी बनकर आ बैठा हो।

शब्दार्थ:

1. चारु – सुंदर
2. थल – धरती
3. स्वच्छ – साफ, निर्मल
4. चाँदनी – चंद्रमा की किरणें
5. अवनि – धरती
6. अंबर – आकाश
7. पुलक – खुशी,रोमांच
8. तृण – घास
9. झूम – झूमना
10. तरु – पेड़
11. निस्तब्ध – सन्नाटे से भरी
12. निशा – रात
13. स्वच्छंद – स्वतंत्र
14. सुमंद – मंद-मंद
15. गंधवाह – वायु
16. निरानंद – आनंदरहित
17. नियति – नियतिरूपी
18. नटी – नर्तकी
19. कार्य-कलाप – क्रिया-कलाप, गतिविधि
20. एकांत – सुनसान, विरान
21. वसुंधरा – धरती
22. विरामदायिनी – आराम देने वाली
23. शून्य – आकाश
24. श्याम तनु – साँवला शरीर
25. पर्ण कुटीर – पत्तों की कुटिया
26. सम्मुख – सामने
27. शिला – चट्टान, पत्थर
28. निर्भीक मना – निडर मन वाला
29. भुवन – संपूर्ण संसार
30. भोगी – भोग करनेवाला
31. कुसुमायुध – कामदेव
32. योगी – तपस्वी
33. दृष्टिगत – जो दिखाई पड़ता है

Hindi Lokbharti 9th Digest Answers Pdf पहली इकाई

• चाँदनी रात Question Answer
• बिल्ली का बिलुंगड़ा Question Answer
• कबीर (पूरक पठन) Question Answer
• किताबें Question Answer
• जूलिया Question Answer
• ऐ सखि ! (पूरक पठन) Question Answer
• डाॅक्‍टर का अपहरण Question Answer
• वीरभूमि पर कुछ दिन Question Answer
• वरदान माँगूँगा नही Question Answer
• रात का चौकीदार (पूरक पठन) Question Answer
• निर्माणों के पावन युग में Question Answer

Balbharti Maharashtra State Board Class 9 Hindi Solutions Hindi Lokvani Chapter 2 झुमका Notes, Textbook Exercise Important Questions and Answers.

Std 9 Hindi Chapter 2 Jhumka Question Answer Maharashtra Board

Hindi Lokvani 9th Digest Chapter 2 झुमकाQuestions And Answers

1. आकृति पूर्ण कीजिए।

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए।
उत्तर:

प्रश्न 3.
आकृति पूर्ण कीजिए।
उत्तर:

2. निम्नलिखित घटनाओं को कालक्रमानुसार लिखिए। 

प्रश्न 1.
निम्नलिखित घटनाओं को कालक्रमानुसार लिखिए।
i. आलमारी के नीचे विछे कागज तक उलटकर देख लिए।
ii. कांति सिर से पाँव तक सिहर उठी।
iii. बिस्तर हटाकर दो-दो बार झाड़ डाला।
iv. कांति ने घर का कोना-कोना ढूँढ़ मारा।
उत्तर :
(iv), (i), (iii), (ii)

3. कारण लिखिए।

प्रश्न 1.
कारण लिखिए।
i. कांति को सर्वेश से झुमका खरीदवाने की हिम्मत नहीं हुई –
ii. कांति ने कमलाबाई को एक हजार रुपए दिए
उत्तर :
i. मार्च का महीना और इनकम टैक्स का टेंशन था इसलिए कांति को सर्वेश से झुमका खरीदवाने की हिम्मत नहीं हुई।
ii. एक झुमके की कीमत एक हजार रुपए थी।

4. निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए।

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए।

1. नीचे ………
2. खरीदना …………
3. अगला …………
4. खूबसूरत ……….
5. सुबह ……….
6. संकोच ………

उत्तर:

1. ऊपर
2. बेचना
3. पिछला
4. बदसूरत
5. शाम
6. नि:संकोच

5. सही विकल्प चुनकर पूर्ण वाक्य फिर से लिखिए । 

प्रश्न i.
कमलाबाई की लड़की दो महीने से ………….
(क) ससुराल में है।
(ख) ननिहाल में है।
(ग) मायके में है।
उत्तर:
(ग) मायके में है।

प्रश्न ii.
कमलाबाई ने भर आई आँखों की कोरों को ………….
(क) रूमाल से पोंछ डाला।
(ख) तौलिए से पोंछ डाला।
(ग) कोहनी से पोंछ डाला।
उत्तर:
(ग) कोहनी से पोंछ डाला।

6. निम्नलिखित शब्दों के समानार्थी शब्द लिखिए।

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए।

1. निद्रा
2. मुश्किल
3. रोजगार
4. आभूषण

उत्तर:

1. नींद
2. कठिनाई
3. नौकरी
4. गहना

7. ‘दहेज’ समाज के लिए एक कलंक है, इस पर अपने विचार लिखिए।

प्रश्न 1.
‘दहेज’ समाज के लिए एक कलंक है, इस पर अपने विचार लिखिए।
उत्तर :
दहेज आज कन्या-पक्ष के शोषण का माध्यम बन गया है। कहीं यह शोषण नगद धन-राशि के रूप में होता है, तो कहीं आभूषण, तो कहीं गाड़ी, मोटर-साइकिल, स्कूटर आदि के रूप में होता है। वधुओं को अनेक प्रकार की शारीरिक तथा मानसिक यातनाएँ दी जाती हैं। कभी वधु को जलाकर मार डाला जाता है तो कभी बहू को विष देकर मार डाला जाता है तो कभी इतना प्रताड़ित किया जाता है कि वह स्वयं आत्महत्या कर लेती है। सबसे बड़ा दुख तो इस बात का है कि हमारे समाज में शिक्षित वर्ग भी दहेज को अपना समर्थन दे रहा है।

8.  एक से दो शब्दों में उत्तर दीजिए। 

प्रश्न 1.
एक से दो शब्दों में उत्तर दीजिए।
i. कमलाबाई की पगार
ii. कमलाबाई ने नोट यहाँ रखे
उत्तर:
i. दौ सौ रुपए
ii. पल्लू में

9. ‘सौ’ शब्द का प्रयोग करके कोई दो कहावतें लिखिए।

प्रश्न 1.
‘सौ’ शब्द का प्रयोग करके कोई दो कहावतें लिखिए।
उत्तर:
i. सौ सुनार की, एक लोहार की।
ii. एक अनार, सौ बीमार।

10. अभिव्यक्ति

प्रश्न 1.
निम्न सामाजिक समस्याओं को लेकर आप क्या कर सकते है, बताइए। ।

उत्तर :
अशिक्षा और बेरोजगारी देश के सम्मुख प्रमुख समस्याएँ हैं जो प्रगति के मार्ग को तेजी से अवरुद्ध करती हैं। स्वतंत्रता के पचास वर्षों बाद भी सभी को रोजगार देने और शिक्षित करने के अपने लक्ष्य से हम मीलों दूर हैं। आज आवश्यकता इस बात की है कि बेरोजगारी और अशिक्षा के प्रमुख कारणों जैसे बढ़ती जनसंख्या, शिक्षा व्यवस्था, लघु उद्योगों का नष्ट होना आदि पर विशेष ध्यान दिया जाए और इसके निदान हेतु सार्थक उपाय किए जाएं।

इसके लिए सर्वप्रथम हमें अपने छात्र-छात्राओं तथा युवक-युवतियों की मानसिकता में परिवर्तन लाना होगा। यह तभी प्रभावी हो सकता है जब हम अपनी शिक्षा पद्धति में सकारात्मक परिवर्तन लाएँ। विद्यालयों में तकनीकी कार्य पर आधारित शिक्षा दें जिससे उनकी शिक्षा का प्रयोग उद्योगों व फैक्ट्रियों में हो सके और वे आसानी से नौकरी पा सकें।

11. एक-दो शब्दों में ही उत्तर लिखिए।

प्रश्न 1.
एक-दो शब्दों में ही उत्तर लिखिए।
(क) दुबली-पतली
(ख) कमजोर-सी
(ग) दो महीने से मायके में है-
(घ) दो महीने से यहीं है
उत्तर:
(क) कमलाबाई की लड़की
(ख) कमलाबाई की लड़की
(ग) कमलाबाई की लड़की
(घ) मायके में

12. अपने घरों में काम करने वाले नौकरों के साथ सौहार्दपूर्ण व्यवहार करना चाहिए। उस पर आधारित अपने विचार लिखिए।

प्रश्न 1.
अपने घरों में काम करने वाले नौकरों के साथ सौहार्दपूर्ण व्यवहार करना चाहिए। उस पर आधारित अपने विचार लिखिए।
उत्तर:
घर के नौकरों को अपने परिवार का ही एक सदस्य समझना चाहिए। उसके साथ हमेशा अच्छा व्यवहार करना चाहिए। नौकर घर के अन्य कामों के साथ ही घर के लोगों का भी ख्याल करता है । इसलिए घर के लोगों को भी उसका ख्याल करना चाहिए। नौकर के खाने, कपड़े तथा दवा आदि का ध्यान देना चाहिए। उसकी ईमानदारी पर हमें पूरा भरोसा होना चाहिए। उसे कभी भी पराया नहीं समझना चाहिए। सुख-दुख में उसका साथ देना चाहिए। उसके साथ अभद्र भाषा का प्रयोग नहीं करना चाहिए तथा अपनेपन का भाव रखना चाहिए।

13. भाषाई कौशल पर आधारित पाठगत कृतियाँ

भाषा बिंदु : 

प्रश्न 1.
रेखांकित शब्दों के विलोम शब्द लिखकर नए वाक्य बनाइए।
उत्तर:

	विलोम शब्द	वाक्य
1. कांति को कमला पर विश्वास था।	अविश्वास	सैनिकों के मन में राजा के प्रति अविश्वास फैल गया।
2. बड़ी मुश्किल से उसकी आँख लगी।	आसान	भारत से क्रिकेट मैच जीतना आसान नहीं है।
3. दुकानदार रमा का परिचित था।	अपरिचित	हम महात्मा की शक्तियों से अपरिचित हैं।
4. सोच समझकर व्यय करना चाहिए।	आय	हमें सरकार को अपनी आय का ब्यौरा देना चाहिए।
5. हमें सदैव अपने लिए किए गए कामों के प्रति कृतज्ञ होना चाहिए।	कृतघ्न	मैं कितना कृतघ्न हूँ कि माँ-बाप को ही भूला दिया।
6. पूर्व दिशा में सूर्योदय होता है।	सूर्यास्त	पश्चिम दिशा में सूर्यास्त होता है।

14. रचनात्मकता की ओर लेखनीय :

प्रश्न 1.
‘दहेज’ समाज के लिए एक कलंक है, इस पर अपने विचार लिखिए।
उत्तरः
दहेज आज कन्या-पक्ष के शोषण का माध्यम बन गया है। कहीं यह शोषण नगद धन-राशि के रूप में होता है, तो कहीं आभूषण, तो कहीं गाड़ी, मोटर-साइकिल, स्कूटर आदि के रूप में होता है। वधुओं को अनेक प्रकार की शारीरिक तथा मानसिक यातनाएँ दी जाती हैं। कभी वधु को जलाकर मार डाला जाता है तो कभी बहू को विष देकर मार डाला जाता है तो कभी इतना प्रताड़ित किया जाता है कि वह स्वयं आत्महत्या कर लेती है। सबसे बड़ा दुख तो इस बात का है कि हमारे समाज में शिक्षित वर्ग भी दहेज को अपना समर्थन दे रहा है।

15. मौलिक सृजन

प्रश्न 1.
हम समाज के लिए समाज हमारे लिए’ विषय पर अपने विचार व्यक्त कीजिए।
उत्तर:
हम एक सामाजिक प्राणी हैं जो आपस में मिल-जुलकर रहते हैं। हमें अपना जीवन सुचारु रूप से चलाने के लिए एक-दूसरे के सहयोग की आवश्यकता पड़ती है। व्यक्ति दूसरों के साथ जैसा व्यवहार करता है, दूसरे भी उसके साथ वैसा ही व्यवहार करते हैं। इसलिए हमें समाज के साथ अच्छा व्यवहार करना चाहिए। समाज-से अलग रहने वाला व्यक्ति पशु के समान माना जाता है। हम समाज को अच्छा-बुरा जो भी देते हैं. हमें भी वापस वही मिलता है। हम कह सकते हैं कि हम और समाज एक-दूसरे के पूरक हैं।

16. पाठ के आगे :

प्रश्न 1.
आभूषणों की सूची तैयार कीजिए और शरीर के किन अंगों पर पहने जाते हैं, बताइए।
उत्तरः
शरीर के विविध अंगों पर पहने जानेवाले आभूषण निम्नलिखित रूप में है: नाक-कील, पाँव-पायल, गला-हार, अंगुली-अंगूठी, कमरकरधनी, कलाई-चूड़ियाँ, कान-कुंडल आदि।

Hindi Lokvani 9th Std Textbook Solutions Chapter 2 झुमका Additional Important Questions and Answers

(क) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति क (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के लिंग पहचानिए।
i. झुमके
ii. दुकानदार
उत्तर:
i. पुल्लिंग
ii. पुल्लिंग

कृति क (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘मार्च महीना और इनकम टैक्स’ का तात्पर्य 8 से 10 पंक्तियों में लिखिए।
उत्तर:
सरकार द्वारा निर्धारित राशि से अधिक आय होने पर बढ़े हुए आय का कुछ अंश हमें सरकार के खाते में जमा करना पड़ता है। जिसे ‘टैक्स’ कहते हैं। यह टैक्स हर वर्ष मार्च महीने के अंत में भरना पड़ता है। सरकार की वित्तनीति के अनुसार यह टैक्स पिछले 12 महीने की आय का होता है। जिसकी समयावधि पिछले वर्ष के 1 अप्रैल से लेकर वर्तमान वर्ष के 31 मार्च तक के बीच की होती है।

(ख) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति ख (1) : आकलन कृति

प्रश्न 1.
घटनानुसार उचित क्रम लगाकर वाक्य फिर से लिखिए।

1. घर आकर कांति ने झुमके का पैकेट मेज़ पर रख दिया।
2. सुनार के यहाँ से तो दोनों झुमके लाई थी।
3. अभी चलकर ठीक करा ले।

उत्तर :

1. अभी चलकर ठीक करा ले।
2. घर आकर कांति ने झुमके का पैकेट मेज़ पर रख दिया।
3. सुनार के यहाँ से तो दोनों झुमके लाई थी।

प्रश्न 2.
सत्य या असत्य पहचानकर लिखिए।
i. कांति तुरंत ही रमा के साथ टैक्सी करके सुनार के यहाँ चली गई।
ii. घर आकर कांति ने झुमके का पैकेट आलमारी पर रख दिया।
उत्तर:
i. असत्य
ii. असत्य

प्रश्न 3.
उपर्युक्त गद्यांश से दो ऐसे प्रश्न तैयार कीजिए कि जिनके उत्तर निम्नलिखित शब्द हों –
i. मेज़
ii. झुमका
उत्तर:
i. घर आकर कांति ने झुमके का पैकेट कहाँ पर रख दिया?
ii. सुनार ने आधे घंटे में क्या ठीक करके दे दिया?

कृति ख (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के वचन बदलकर लिखिए ।
i. झुमके
ii. आलमारी
उत्तर:
i. झुमका
ii. आलमारियाँ

प्रश्न 2.
गद्यांश में आए शब्द-युग्म चुनकर लिखिए।
उत्तर :
काम-काज, छोटी-मोटी, मामूली-सी

कृति ख (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘स्त्री और आभूषण’ पर 8 से 10 पंक्तियों में अपने विचार लिखिए।
उत्तर:
स्त्री और आभूषण का संबंध प्राचीनकाल से ही चला आ रहा है। स्त्रियों को आभूषणों से गहरा प्रेम होता है और आभूषण पहनने से स्त्रियों की सुंदरता में चार चाँद लग जाता है। प्राचीन काल में सोने और चांदी के आभूषणों का प्रचलन कम होने के कारण उस समय की नारियाँ फूल और पत्तों से बने आभूषण पहनती थी, परंतु आधुनिक युग की स्त्रियाँ सोने, चाँदी, हीरे व मोती से बने आभूषणों का प्रयोग करती हैं। कुछ आभूषणों का अपना अलग महत्त्व है।

ये ग्रहों को प्रभावित करते हैं इसलिए ग्रहों को प्रभावशाली बनाने के लिए अलग-अलग धातु व रत्नों से बने गहने पहने जाते हैं। आज के युग में आभूषणों का प्रचलन बहुत अधिक होता जा रहा है। आधुनिक युग की स्त्रियाँ अपने वस्त्रों के अनुसार ही आभूषण धारण करती हैं।

(ग) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति ग (1) : आकलन कृति

प्रश्न 1.
एक-एक शब्द में उत्तर लिखिए ।

1. खाना खाकर दोपहर की नींद लेने के लिए कांति कहाँ पर लेटी?
2. कांति की बंद आँखों के सामने क्या घूमता रहा?
3. दरवाजे की घंटी किसने बजाई?
4. कमलाबाई की लड़की का घरवाला किस कंपनी में काम करता है?

उत्तर:

1. बिस्तर
2. झुमका
3. कमलाबाई
4. ट्रांसपोर्ट

प्रश्न 2.
आकृति पूर्ण कीजिए।
उत्तर:

कृति ग (2) : शब्द संपदा

प्रश्न 3.
गद्यांश से शब्द-युग्म ढूँढ़कर लिखिए ।
उत्तर :
i. दो-चार
ii. चौका-बासन

(घ) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति घ (1) : आकलन कृति

प्रश्न 1.
निम्नलिखित विधान सत्य है या असत्य लिखिए।
i. कमलाबाई अपनी पिछले महीने की पगार लेती जाना।
ii. कमलाबाई झुमका कहीं बेचने जाएगी तो कोई समझेगा कि चोरी का है।
उत्तर:
i. असत्य
ii. सत्य

कृति घ (2) : शब्द संपदा

प्रश्न 2.
गद्यांश में आए हुए शब्द-युग्म लिखिए।
उत्तर :
i. सौ-सौ
ii. हलका – फुलका

(ङ) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति ङ (1) : आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर :

कृति ङ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों विरुद्धार्थी शब्द लिखिए।
i. करीब ……….
ii. होश ………..
उत्तर:
i. दूर
ii. बेहोश

प्रश्न 2.
लिंग परिवर्तन कीजिए।
i. पति
ii. सुहाग
उत्तर:
i. पत्नी
ii. सुहागन

झुमका Summary in Hindi

लेखक-परिचय :

जीवन-परिचय : सुशील सरित जी आधुनिक हिंदी कथाकार हैं। आपकी कहानियाँ, निबंध विविध पत्र-पत्रिकाओं में प्राय: प्रकाशित होती रहती हैं।

गद्य-परिचय :

वर्णनात्मक कहानी : जीवन की किसी घटना का रोचक, प्रवाही वर्णन ही वर्णनात्मक कहानी है। इसमें वर्णन की प्रधानता होती है।
प्रस्तावना : प्रस्तुत कहानी के माध्यम से लेखक ने परोपकार, दया एवं अन्य मानवीय गुणों को दर्शाते हुए इन्हें अपनाने तथा नौकरों के साथ सौहार्दपूर्ण व्यवहार एवं उनकी मदद करने का मानवीय संदेश दिया है।

सारांश :

प्रस्तुत पाठ में लेखक ने बताया है कि कांति नाम की एक महिला का एक झुमका गायब हो गया जिसे वह पूरे घर में ढूँढ़ती रही पर वह नहीं मिला। उसने वह झुमका दो साल की बचत के बाद खरीदा था जिसके बारे में उसके पति सर्वेश को भी नहीं मालूम था। दरअसल झुमके का वह जोड़ा बहुत ही खूबसूरत था तथा सुनार ने परिचित होने के कारण चार तोले का लगनेवाले उस झुमके को सिर्फ दो हजार में दे दिया था।

वह झुमके को अपनी ‘मैरिज एनिवर्सरी’ पर पहनने वाली थी। झुमके में बगलवाला मोती टूटने के कारण वह सुनार के पास वापस गई तो सुनार ने उसे ठीक कर दिया। घर आकर उसने झुमके का पैकेट मेज़ पर रख दिया और घर के कार्यों में व्यस्त हो गई। घर का काम निपटाकर जब वह पैकेट देखने लगी तो उसमें से एक झुमका गायब था।

जिसके कारण उसे दोपहर की नींद नहीं आई। उसकी नौकरानी कमलाबाई के आने पर कांति ने दरवाजा खोला। कमलाबाई ने आकर बताया कि उनकी बेटी दो महीने से मायके में है क्योंकि उसके ससुराल वाले दहेज और गहने की माँग कर रहे हैं। गरीब होने के कारण वह इतना दहेज नहीं दे सकती। घर के कामों को निपटाकर जब वह जाने लगी तो कांति ने उसे उसकी दो सौ रुपए पगार दिया। कमलाबाई ने दरवाजे से वापस लौटकर कांति को एक झुमका देते हुए बताया कि उसे वह रास्ते में सड़क पर पड़ा मिला।

वह बेचेगी तो कोई समझेगा कि चोरी का है। वह झुमका बेचकर अपनी लड़की के लिए गहने बनवाना चाहती थी। अत: उसने कांति को झुमका बेचने के लिए कहा। कांति ने झुमका देखकर पहचान लिया कि वह उसी का है। किंतु कमलाबाई के लड़की के हालात को समझकर वह चुप रही तथा झुमके को आलमारी में रख दिया और कमलाबाई को एक हजार रुपया देते हुए कहा कि यदि झुमका बेचने पर अधिक पैसा मिलेगा तो वह उसे दे देगी। पैसा पाकर कमलाबाई कांति को आशीर्वाद देते हुए सुनार के पास अपनी लड़की के लिए गहने खरीदने चली गई।

शब्दार्थ :

1. कोना-कोना ढूँढ़ मारा – हर जगह ढूँढ़ना
2. झुमका – कान में पहने जाने वाला एक आभूषण, कुंडल
3. गनीमत – संकट में संतोष की बात
4. तसल्ली – धोरज
5. कोहनी – टिहुनी (बाँह के बीच का जोड़)
6. रकम – पैसा
7. इकट्ठा – एकत्रित, जमा
8. दरअसल – सच में, वास्तव में खूबसूरत
9. चार तोले – 40 ग्राम
10. परिचित – जाना-पहचाना, पहचान वाला
11. आग्रह – निवेदन
12. चौका-बासन – रसोई घर, बरतन साफ करना
13. इनकम टैक्स – आयकर
14. टेंशन – तनाव
15. मामूली-सी – छोटी-सी
16. नि:संकोच – जिना संकोच के
17. तसल्ली – दिलासा
18. पैकेट – थैली
19. ड्राइंग रूम – बैठक
20. तबीयत – सेहत
21. सफाई देना – ईमानदारी दर्शाना
22. मायके – माँ का घर
23. खबर – सूचना
24. घरवाला – पति
25. झबिया – छोटी टोकरी
26. भर आई आँखें – आँसूभरी आँखें
27. सहानुभूति – हमदर्दी
28. समेटकर – इकट्ठा कर
29. किचन – रसोई घर
30. सहम – डर
31. गंदुमी – गेहुँआ रंग
32. सुहाग सलामत रखे – पति बने रहें, पति दोधार्यु हो

मुहावरे :

1. सिहर उठना – भय से काँपना।
2. घर सर पर उठा लेना – शोर मचाना।
3. वादा करना – वचन देना।
4. आँख फटना – चकित हो जाना।
5. वादा करना – वचन देना।
6. आँख फटना – चकित हो जाना।

Hindi Lokvani 9th Std Digest पहली इकाई

• नदी की पुकार Question Answer
• झुमका Question Answer
• निज भाषा (पठनार्थ) Question Answer
• मान जा मेरे मन Question Answer
• किताबें कुछ कहना चाहती हैं Question Answer
• ‘इत्यादि’ की आत्मकहानी (पठनार्थ) Question Answer
• छोटा जादूगर Question Answer
• जिंदगी की बड़ी जरूरत है हार..! Question Answer

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 20.1 विश्वकोश Notes, Textbook Exercise Important Questions and Answers.

Class 9 Marathi Aksharbharati Chapter 20.1 विश्वकोश Question Answer Maharashtra Board

विश्वकोश Std 9 Marathi Chapter 20.1 Questions and Answers

1. टिपा लिहा:

प्रश्न 1.
विश्वकोशाचा उपयोग.
उत्तर:
शिक्षणाचा प्रसार खूप झपाट्याने झाला. औदयोगिकीकरणामुळे समाजाच्या वैज्ञानिक व तांत्रिक गरजा वाढल्या. विविध प्रकारचे शब्द अस्तित्वात आले व भाषा समृद्ध झाल्या. त्यामुळे आजच्या यंत्रयुगातील व विज्ञानयुगातील माणसाला आपले ज्ञान विश्वव्यापी व अदययावत करण्यासाठी विश्वकोशाची गरज निर्माण झाली. मानव्यविदया, विज्ञान व तंत्रज्ञान यांतील सर्वसंग्रहित विषयांची माहिती व ज्ञान विश्वकोशात समाविष्ट असते. मुख्य विषय व त्याच्या संलग्न विषयांचे ज्ञान मिळवण्यासाठी विश्वकोशाचा अत्यंत निकडीचा उपयोग आहे.

प्रश्न 2.
विश्वकोशाची निर्मिती प्रक्रिया.
उत्तर:
मानव्यविदया, विज्ञान व तंत्रज्ञान यांतील सर्व विषयांचे अययावत ज्ञान संकलित करण्यासाठी विश्वकोशाची निर्मिती झाली. प्रथम विषयवार तज्ज्ञांच्या समितीची रचना करण्यात आली. प्रत्येक विषयाच्या नोंदीची शीर्षके निश्चित करण्यात आली. नोंदीचे तीन प्रकार करण्यात आले – मुख्य, मध्यम व लहान नोंदी. त्यांतील मुद्द्यांची टाचणे करण्यात आली.

नोंदींच्या मर्यादा आखून टाचणांमध्ये तशा सूचना दिल्या. प्रत्येक विषयातील नोंदींच्या त्यांच्या प्रकारांनुसार यादया तयार करण्यात आल्या. अकारविल्यानुसार या यादया क्रमवार लावण्यात आल्या. अशा प्रकारे 1976 साली महाराष्ट्र राज्य साहित्य संस्कृती मंडळाने मराठी विश्वकोशाचा पहिला खंड प्रकाशित केला. आतापर्यंत विश्वकोशाचे अठरा खंड प्रकाशित झाले आहेत.

2. ‘शब्दकोडे सोडवल्यामुळे भाषिक कौशल्य वाढते,’ याविषयी तुमचे मत लिहा.

प्रश्न 1.
‘शब्दकोडे सोडवल्यामुळे भाषिक कौशल्य वाढते,’ याविषयी तुमचे मत लिहा.
उत्तर:
विविध मासिकांमधून व वर्तमानपत्रांमधून पुरवण्यांच्या द्वारे शब्दकोडी सर्रास दिली जातात. शब्दकोडे सोडवल्यामुळे अनेक जुने-नवे शब्द कळतात. आपली शब्दसंपत्ती वाढते. त्यामुळे बुद्धीत भर पडतेच पण आपल्याला शब्दांच्या अर्थछटा माहीत होऊन आपले ज्ञान वाढते. शब्दसमूहासाठी एक शब्द, एका शब्दांचे भिन्न अर्थ, प्रतिशब्द व विरुद्धार्थी शब्द यांचा बहुमोल खजिना लुटता येतो.

उदाहरणार्थ, जंगल या शब्दाला – अरण्य, रान, वन, कानन, विपीन असे पर्यायी शब्द कळल्यामुळे आपण शब्दसंपन्न होतो. शब्दकोडे सोडवताना गंमत येतेच, शिवाय बौद्धिक व मानसिक निर्मळ आनंद मिळतो. कालानुरूप शब्दांच्या अर्थकक्षा कशा रुंदावल्या व फैलावल्या यांची जाण शब्दकोड्यामुळे येते. अशा प्रकारे शब्दकोडे सोडवल्यामुळे भाषिक कौशल्य वाढते.

3. विश्वकोश पाहण्याचे तुमच्या लक्षात आलेले फायदे लिहा.

प्रश्न 1.
विश्वकोश पाहण्याचे तुमच्या लक्षात आलेले फायदे लिहा.
उत्तर:
आपल्याला माहीत नसलेल्या विषयांची सांगोपांग माहिती मिळवण्यासाठी विश्वकोश आपला मदतनीस होतो. त्या विषयाच्या अनुषंगाने असलेले संलग्न विषय कळतात व विषयसाखळीमुळे त्या त्या विषयाचे सखोल ज्ञान प्राप्त होते. आपले ज्ञानाविषयीचे कुतूहल शमवण्याचे विश्वकोश हे एक उत्तम साधन आहे. विश्वकोश पाहण्याने आपले जागतिक ज्ञानक्षेत्राचे क्षितिज विस्तारते. आपल्या अभिव्यक्तीला योग्य चालना मिळते. मराठी विश्वकोश हाताळल्यामुळे सर्व प्रकारचे प्रगल्भ व सूक्ष्म ज्ञान मराठी भाषेतून मिळते व आपल्या ज्ञानविषयक गरजा भागतात.

4. केशभूषेचे उद्देश सांगून, त्यात कोणत्या गोष्टींचा अंतर्भाव होतो, ते स्पष्ट करा.

प्रश्न 1.
केशभूषेचे उद्देश सांगून, त्यात कोणत्या गोष्टींचा अंतर्भाव होतो, ते स्पष्ट करा.
उत्तर:
मोकळे केस इतरांना दिसू नयेत, म्हणून पुरातन स्त्रियांनी केशबंधनाची कल्पना राबवली असावी. या कल्पनेतून केशभूषेचा उगम झाला असावा. लेण्यांमधल्या शिल्पकृतीत आढळणाऱ्या स्त्रियांनी केलेल्या प्राचीन केशरचनांचे अनुकरण भारतीय स्त्रिया करताना आढळतात. केशभूषेचा मुख्य उद्देश हा आकर्षकता व सौंदर्य वाढवणे हा आहे. सामाजिक संकेतानुसार प्रतीकात्मक केशभूषा करणे, हा केशभूषेचा सामाजिक उद्देश ठरतो. केशभूषेत केस कापणे, केस धुणे, नीट करणे, विंचरणे, कुरळे किंवा सरळ करणे या गोष्टींचा अंतर्भाव होतो.

5. विश्वकोशाचा उपयोग तुम्हांला मराठी भाषेतील ज्ञान प्राप्त करण्यासाठी कसा होऊ शकेल, ते लिहा.

प्रश्न 1.
विश्वकोशाचा उपयोग तुम्हांला मराठी भाषेतील ज्ञान प्राप्त करण्यासाठी कसा होऊ शकेल, ते लिहा.
उत्तर:
मराठी भाषेतील कोणत्याही विषयाचे ज्ञान मिळवण्यासाठी मराठी विश्वकोश हे अतिशय उत्तम साधन आहे. ज्ञान, विज्ञान, तंत्रज्ञान, तत्त्वज्ञान, क्रीडा व कला इत्यादी अनेक ज्ञानक्षेत्रांबद्दलचे आपले कुतूहल पूर्ण करण्याचे कार्य मराठी विश्वकोशातर्फे सुलभ झाले आहे. मराठी भाषेची व्युत्पत्ती, तिचा इतिहास, वेदांपासून ते अदययावत साहित्याविषयीची सर्वांगीण माहिती व ज्ञान मिळवणे विश्वकोशामुळे सहज झाले आहे. मराठी भाषा ही माझी मातृभाषा आहे. तिच्यावर माझे नितांत प्रेम आहे. मराठी भाषेतील प्राचीन काव्य, अनेकविध रचनाबंध समजून घेण्यासाठी मला मराठी विश्वकोशाचा उपयोग होईल. मराठी भाषेतील अद्ययावत ज्ञानाने माझे व्यक्तिमत्त्व संपन्न होण्यास मदत होईल.

भाषा सौंदर्य:

विश्वकोश अकारविल्ल्यानुसार (अनुज्ञेय) पाहाबा हे आपल्याला कळले. त्यासाठी संपूर्ण वर्णमाला (आता अँव ऑ हे स्वर धरून) आपल्याला क्रमाने मुखोद्गत असायला हवी. त्या योग्य वर्णाची आणि त्यांची उच्चारस्थाने, परिपूर्ण आकलनही असावयास हवे. (उदा., स्वर, स्वरादी, व्यंजन, महाप्राण, मृदू व्यंजने, कठोर व्यंजने, अनुनासिके).

प्रश्न 1.
पुढील कोडे सोडवा:

1. पैसे न देता, विनामूल्य.
2. पाणी साठवण्याचे मातीचे गोल भांडे.
3. जिच्यात रेतीचे प्रमाण खूप जास्त असते अशी जमिनीची जात.
4. रहस्यमय.
5. खास महाराष्ट्रीय पक्वान्न. पोळ्या, मोदक, करंज्या यांमध्ये हे भरतात.

उत्तर:

वरील कोडे वैशिष्ट्यपूर्ण आहे. त्याचे उत्तर तुम्हाला सोडवायचे आहे. हे कोडे सोडवल्यावर तुम्हांला निश्चितच भाषेचे सौंदर्य व गंमत लक्षात येईल. अशा कोड्यांचा अभ्यास करा. त्यातील भाषिक वैशिष्ट्ये समजून घ्या व अशी विविध वैशिष्ट्यांची कोडी तयार करण्याचा तुम्ही स्वतः प्रयत्न करा.

मैत्री तंत्रज्ञानाशी:

वडील: (सोनालीच्या आईशी बोलताना.) “अग, लाईटबिल भरण्याची अंतिम तारीख आजच आहे; पण आज माझी ऑफिसमध्ये महत्वाची मीटिंग आहे. काय करावं बरं?”

सोनाली: “बाबा, एवढी काळजी कशाला करता, लाईट बिलच भरायचय ना? आणा इकडे, मी भरते एका मिनिटांत, तेही उन्हातान्हात बाहेर न जाता, धावपळ न करता.”

सोनाली: “अग आई, एवढं आश्चर्यानं काय पाहतेस? आपल्याकडे संगणक आहे, आंतरजाल आहे. आता आपण ऑनलाईन बिल घरच्या घरी भरू शकतो. चल आई, मी तुला ऑनलाईन बिल कसे भरायचे ते दाखवते.”

आई: (मुलगी ऑनलाईन बिल भरते. आई-वडील तिच्या कृतींचे निरीक्षण करतात.) “शाबास बाळा! किती आत्मविश्वासाने संगणक हाताळतेस. बाजार करणं, बिलं भरणं, खरेदी करणं, वस्तू विकणं, असे ऑनलाईन व्यवहार मलाही शिकव.”

प्रश्न 1.
कमी वेळात, कमी कष्टात ऑनलाईन प्रक्रियेद्वारे तुम्ही कोणकोणती कामे करू शकता? त्यांची यादी करा.
उत्तर:

1. लाईट बिल भरणे
2. टेलिफोन बिल भरणे
3. गॅसचे बिल भरणे
4. आवश्यक वस्तू खरेदी करणे
5. वस्तू विकणे
6. गृहोपयोगी वस्तूंची मागणी करणे
7. प्रवासासाठी बस, रेल्वे, विमान किंवा खाजगी वाहन यांची बुकिंग करणे
8. भेटवस्तू पाठवणे.

उपक्रम:

प्रश्न 1.
ऑनलाईन व्यवहार करण्यासाठी उपलब्ध असलेले विविध अॅप्स कोणते?
त्यांचा वापर कसा करावा याविषयीची माहिती मिळवा.

विश्वकोश Summary in Marathi

पाठाचा परिचय:

या पाठात विश्वकोशाची ओळख करून दिली आहे. विश्वकोश का व कसा तयार झाला, वेगवेगळे संदर्भ मिळवण्याची आनंददायी प्रक्रिया, भाषासमृद्धी, तसेच एका विषयाच्या निमित्ताने अनेक संलग्न विषयांची माहिती मिळणे, ही विश्वकोशाची वैशिष्ट्ये आहेत.

पाठातील महत्त्वाचे मुद्दे:

1. आपल्या शाळेत, गावात, शहरात ग्रंथालय (वाचनालय) असते. मराठीतील विविध साहित्यसंपदा व अनेक विषयांची पुस्तके उपलब्ध होतात. मराठी विश्वकोश, मराठी चरित्रकोश, मराठी व्युत्पत्तिकोश इत्यादी ग्रंथसंपदा हा प्रत्येक ग्रंथालयाचा ‘मानबिंदू’ आहे.
2. मानव्यविदया (Social sciences), विज्ञान (Pure science) व तंत्रज्ञान (Technology) यांतील सर्व विषयांचे आजतागायतचे ज्ञान संकलित करण्यासाठी विश्वकोशाची निर्मिती झाली. मुख्य विषय व त्याच्या संलग्न विषयाचे ज्ञान मिळवण्यासाठी मराठी विश्वकोशाचा उपयोग होतो.
3. विश्वकोशाची गरज: भारतात शिक्षणाचा प्रसार वेगाने होऊ लागला. वाढत्या औदयोगिकीकरणामुळे समाजाच्या वैज्ञानिक व तांत्रिक गरजा वाढू लागल्या. अनेक शब्द अस्तित्वात येऊन भाषा समृद्ध होऊ लागली. त्यामुळे सर्वविषयसंग्राहक अशा विश्वकोशाची गरज निर्माण झाली.

उच्च शिक्षणाचे माध्यम म्हणून मराठी भाषेचा स्वीकार झाला. त्यामुळे मराठीमध्ये निर्माण झालेली संदर्भग्रंथांची तीव्र आवश्यकता, तसेच शासनव्यवहाराची भाषा म्हणून राज्यपातळीवर मराठीला मिळालेली मान्यता या पार्श्वभूमीवर मराठी भाषेतील सर्वविषयसंग्राहक विश्वकोशाची गरज निर्माण झाली. स्वातंत्र्यपूर्वकाळात ज्ञानकोशकार डॉ. श्रीधर व्यंकटेश केतकर यांनी विश्वकोशाची मुहूर्तमेढ रोवली.

1. विश्वकोश असा तयार झाला…

1. विषयवार तज्ज्ञांच्या समितीची रचना केली गेली.
2. प्रत्येक विषयाच्या नोंदीची शीर्षके निश्चित केली गेली.
3. मुख्य, मध्यम, लहान नोंदींतील मुद्द्यांची टाचणे तयार केली गेली.
4. नोंदींच्या मर्यादा आखून टाचणांमध्ये तशा सूचना दिल्या गेल्या.
5. प्रत्येक विषयातील मुख्य, मध्यम, लहान व नाममात्र नोंदींच्या यादया तयार केल्या गेल्या.
6. अकारविल्यानुसार या यादया लावण्यात आल्या.

1976 या वर्षी महाराष्ट्र राज्य साहित्य संस्कृती मंडळाने मराठी विश्वकोशाचा पहिला खंड प्रकाशित केला. सध्या विश्वकोशाचे अठरा खंड प्रसिद्ध आहेत.

2. विश्वकोश यासाठी पाहावा…

1. आपल्या ज्ञानविषयक गरजा मराठीतून भागवण्यासाठी.
2. जागतिक ज्ञानक्षेत्राचे क्षितिज विस्तारताना आपल्या विविध विषयांतील कुतूहलास इष्ट वळण लागण्यासाठी.
3. अभिव्यक्तीला योग्य चालना मिळण्यासाठी.
4. सर्व प्रकारचे प्रगल्भ व सूक्ष्म ज्ञान मराठी भाषेतून मिळण्यासाठी.

3. विश्वकोश असा पाहावा…
1. शब्द अकारविल्हे (अनुज्ञेय) नुसार पाहावेत.
2. बाराखडीतील स्वर व व्यंजन यांच्या स्थानानुसार अनुक्रमे दिलेला शब्द पाहावा.

4. मूलध्वनी (मराठी वर्णमाला):

5. व्यंजने (34)

स्वर + व्यंजने = अक्षरे/अर्थपूर्ण क्रमाने येणारी अक्षरे = शब्द/ अर्थपूर्ण शब्दांचा समूह = वाक्य.

चौदाखडी:

तुम्हांला आवडणारे कोणतेही शब्द… त्यांचे अर्थ… संदर्भ विश्वकोशातून शोधा व भाषेचे अनोखे अंग जाणून घ्या. विश्वकोश आता एका क्लिकवर – https://en.wikipedia.org/wiki/Marathi_Vishwakosh

1. मुलांना आवडणारी शब्दकोडी व फँशनपैकी केशरचना या ” शब्दांचे संदर्भ विश्वकोशाच्या आधारे दिले आहेत.

1. शब्दकोडी:

अशा कल्पनांवर आधारलेले अनेक प्रकार रूढ आहेत. संगणकीय खेळांमध्ये विविध प्रकारच्या शाब्दिक कोड्यांचा समावेश होतो.

1. प्रसिद्ध विधान अथवा अवतरण देऊन त्याचे लेखक ओळखण्यास सांगणे.

2. एका शब्दातील अक्षरे फिरवून नवीन शब्द तयार करणे.

3.  काही शब्दांतील रिकाम्या अक्षरांच्या जागा भरणे.

2. पुढील शब्दकोडे दिलेल्या वाक्यांच्या आधारे सोडवा:

1. ‘स्वेदगंगा’ या कवितासंग्रहाचे कवी.
2. एका साहित्यिकाचे आडनाव ‘श्रीपाद कृष्ण …’
3. तुरुंगात असतानादेखील ज्यांची काव्यप्रतिभा बहरून येई, असे साहित्यिक (देशभक्त).
4. ‘सुधारक’चे संपादक.
5. कवी यशवंत यांचे आडनाव.
6. एका विनोदी साहित्यिकाचे आडनाव.
7. मालतीबाई बेडेकर यांनी वापरलेल्या टोपणनावातील आडनाव.
8. कवी कुसुमाग्रज यांचे आडनाव.

उत्तरांसह कोड्याची आकृती : (पाठ्यपुस्तकानुसार)

2. केशभूषा:

आदिम लोक केसांना मातीचा लेप लावून आपला पराक्रम व गुणवैशिष्ट्ये दाखवण्याकरिता त्यात विजयचिन्हे आणि पदके लावत.
( केशभूषेचा उगम यातून झाला असावा. )
(केस इतरांना दिसू न देण्याच्या पुरातन स्त्रीच्या प्रयत्नातून केशबंधाची कल्पना पुढे आली असावी.)
अजिंठा, वेरूळ, कोणार्क, खजुराहो येथील शिल्पाकृतींत आढळणाऱ्या स्त्री-पुरुषांच्या केशरचना उल्लेखनीय आहेत. या प्राचीन केशरचनांचे अनुकरण भारतीय स्त्रिया करताना आढळतात.

9th Std Marathi Questions And Answers:

• वनवासी (कविता) Class 9 Question Answer
• ऑलिंपिक वर्तुळांचा गोफ Class 9 Question Answer
• हसरे दुःख Class 9 Question Answer
• प्रीतम Class 9 Question Answer
• आपुले जगणे…आपुली ओळख! (कविता) Class 9 Question Answer
• विश्वकोश (स्थूलवाचन) Class 9 Question Answer

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 1 सर्वात्मका शिवसुंदरा Notes, Textbook Exercise Important Questions and Answers.

Class 9 Marathi Aksharbharati Chapter 1 सर्वात्मका शिवसुंदरा Question Answer Maharashtra Board

सर्वात्मका शिवसुंदरा Std 9 Marathi Chapter 9 Questions and Answers

कवीचा परिचय :

नाव : विष्णु वामन शिरवाडकर
कालावधी : 1912 – 1999

ज्ञानपीठ पारितोषिक विजेते, प्रसिद्ध लेखक, कवी, नाटककार. ‘जीवनलहरी’, विशाखा’, ‘समिधा’, ‘स्वगत’, ‘हिमरेषा’, ‘वादळवेल’, ‘मारवा’, ‘किनारा’ इत्यादी काव्यसंग्रह; ‘वैजयंती’, ‘राजमुकुट’, ‘कौतेय’, ‘नटसम्राट’, ‘वीज महणाली धरतीला’, ‘विदूषक’ इत्यादी नाटके प्रसिद्ध.

प्रस्तावना :

‘सर्वात्मका शिवसुंदरा’ ही प्रार्थना कवी कुसुमाग्रज यांनी लिहिली आहे. या प्रार्थनेत परमेश्वरास वंदन करून अंधारातून उजेडाकडे नेण्याची, संकटातही सामना करण्याची शक्ती देण्याची विनंती कवीने केली आहे.

A famous poet Kusumagraj has written the prayer Sarvatmaka Shivsundara’. In this prayer, the poet is seeking guidance from the almighty God. He is asking the Lord to bestow upon him the strength to survive in all tough, difficult situations. He is asking the God to transport him from the darkness of everyday life to enlightenment

भावार्थ :

सर्वात्मका शिवसुंदरा …………………….. आमुच्या ने जीवना।।
हे सर्व प्राणीमात्रांच्या ठिकाणी असलेल्या शिवसुंदरा परमेश्वरा, तू आमचे वंदन स्वीकार कर. हे परमेश्वरा, तू आमच्या जीवनाला अंधाराकडून प्रकाशाकडे घेऊन जा. आमच्या जीवनाला योग्य मार्ग दाखव.

सुमनांत तू गगनात …………………….. चोहीकडे रूपे तुझी जाणीव ही माझ्या मना ।।
हे परमेश्वरा, सुमनात म्हणजेच प्रत्येक फुलात, गगनात तूच सामावलेला आहे. तान्यांमध्ये देखील तू फुललेला म्हणजेच भरलेला, व्यापलेला आहेस. या जगामध्ये जे जे सद्धमनि वागतात त्या सर्वांमध्ये तू राहतोस. या सृष्टीमध्ये चोहीकडे तुझीच रूपे आहेत, याची मला जाणीव आहे.

श्रमतोस तू शेतामधे ……………………. तिथे तुझे पद पावना ।।
हे परमेश्वरा, शेतामध्ये त्या कष्ट करणाऱ्या लोकांबरोबर तू स्वत: मेहनत करतोस. या जगामध्ये जे जे दुःखी, कष्टी जीवनाने त्रासलेले आहेत, त्या लोकांची आसवे तू पुसतोस. म्हणजेच या सर्वांचे दुःख, त्रास तू दूर करतोस. जिथे कोणत्याही स्वार्थाशिवाय तुझी सेवा केली जाते, तिथे तुझे पावन चरण पाहायला मिळतात. तिथे तुझे अस्तित्व जाणवते.

न्यायार्थ जे लढती रणी………………….मुनी होतोस त्यांची साधना।।
पुढे कवी सांगतात की, जे लोक अन्यायाविरुद्ध लढतात, न्यायासाठी तलवार हातात घेऊन रणांगणावर लवण्यासाठी जातात, त्यांच्या हातातल्या तलवारीमध्ये परमेश्वरा तू राहतोस. तसेच जे लोक ध्येयवेडे असतात. जे आपले ध्येय प्राप्त करण्यासाठी अंधारातून (संकटातून) ही मार्ग काढतात तू त्यांच्यामध्ये दीप बनून राहतोस. त्यांच्यात आत्मविश्वास, हिंमत निर्माण करतोस. म्हणजेच ध्येय प्राप्तीचा योग्य मार्ग तू त्यांना दाखवतोस. तसेच जे ज्ञानाची लालसा मनामध्ये धरून त्याची कास धरतात, त्यासाठी तप करतात, त्यांची ज्ञानसाधना तू होतोस.

करुणाकरा करुणा तुझी ………………. नित जगवि भीतीवाना।।
कवी परमेश्वराला सांगतो, हे करुणाकरा तुझा आशीर्वाद पाठीशी असताना मला कुठलीही भीती नाही. त्यामुळे आयुष्याच्या वाटेवर चालताना माझ्या प्रत्येक पावलाबरोबर तुझे पाऊल असेल, याची मला पक्की खात्री आहे. त्यामुळे माझ्याकडून नेहमीच सूजनत्व मणजेच नवनिर्मिती होईल. माझ्या मनात त्याविषयी कोणतीच भीती असणार नाही.

शब्दार्थ :

1. ज्ञानपीठ पुरस्कार – साहित्य क्षेत्रातील सर्वोत्कृष्ट पुरस्कार
2. सर्वात्मका – सर्व प्राणिमात्रांच्या ठिकाणी असलेला जीवात्मा, परमेश्वर (the soul of all, the entire self)
3. शिव – शंकर (God Shiva)
4. सुंदरा – सुंदर (beautiful)
5. स्वीकार – अंगीकार (acceptance)
6. अभिवादन – वंदन, नमन (salutation)
7. तिमिर – अंधार, काळोख (darkness)
8. तेज – प्रकाश, लकाकी (brightness)
9. प्रभु – ईश्वर, देव (God, Lord)
10. जीवन – आयुष्य (life)
11. सुमन – फूल (a flower)
12. गगन – आकाश, नभ (the sky)
13. तारा – चांदणी (star)
14. सद्धर्म – चांगला धर्म, सदाचार (good quality, good conduct)
15. जग – दुनिया, विश्व (the world, the universe)
16. वसणे – राहणे, वस्ती करणे (to establish, to stay)
17. चोहिकडे – सभोवार, सर्वत्र (everywhere, all round)
18. रूप – आकार (form, shape)
19. जाणीव – बोध, आकलन (consciousness, realization)
20. मन – चित्त, अंत:करण (the mind)
21. राबसी – राबतोस, भरपूर कष्ट करतोस (to work hard)
22. श्रमिक – कामकरी, कष्ट करणारा (a labour, a worker)
23. रंजले – त्रासले (to be harassed)
24. गांजणे – त्रासून जाणे, सतावले जाणे (to be harassed)
25. आसवे – अश्रू (tears)
26. स्वार्थ – स्वत:चा लाभ, मतलब (selfishness)
27. पद – पाय, पाऊल (a foot, a foot step)
28. न्याय – नीती (justice)
29. रण – रणभूमी, युद्धाची जागा, रणांगण (battlefield)
30. कर – हस्त, ह्यत (hand)
31. ध्येय – उद्दिष्ट, साध्य (a goal, an aim)
32. तमी – तम, अंधकार काळोख (darkness)
33. अंतरी – आतमध्ये (in interior)
34. ज्ञान – माहिती, प्रतिती (knowledge)
35. तपती – तपतात (experience burning, blazing, heat)
36. मुनि – ऋषी, साधू, तपस्वी (a holy sage)
37. साधना – तपश्चर्या (penance)
38. करुणा – दया (compassion, mercy)
39. भय – भीती, धास्ती (fear, fright)
40. मार्ग – रस्ता (way)
41. सदा – नेहमी (always)
42. तव – तुझे (yours)
43. पावले – पाऊले, पाय (feet)
44. सूजनत्व – नवनिर्मिती (creation)
45. नित – नेहमी, सदा (always, daily, everyday)
46. जगवि – जागव (to wake up)

9th Std Marathi Questions And Answers:

• सर्वात्मका शिवसुंदरा (प्रार्थना) Class 9 Question Answer
• संतवाणी (अ) भेटीलागी जीवा – संत तुकाराम Class 9 Question Answer
• संतवाणी (आ) संतकृपा झाली – संत बहिणाबाई Class 9 Question Answer
• ‘बेटा, मी ऐकतो आहे!’ Class 9 Question Answer
• जी. आय. पी. रेल्वे Class 9 Question Answer
• काझीरंगा (स्थूलवाचन) Class 9 Question Answer

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 18 हसरे दुःख Notes, Textbook Exercise Important Questions and Answers.

Class 9 Marathi Aksharbharati Chapter 18 हसरे दुःख Question Answer Maharashtra Board

हसरे दुःख Std 9 Marathi Chapter 18 Questions and Answers

1. आकृतीत दिलेल्या प्रसंगाबाबत माहिती लिहून आकृतिबंध पूर्ण करा:

प्रश्न 1.

उत्तर:

प्रश्न 2.

उत्तर:

2. खाली दिलेल्या घटनांचा परिणाम लिहा:

प्रश्न 1.
खाली दिलेल्या घटनांचा परिणाम लिहा:

उत्तर:

घटना	परिणाम
1. चार्लीने ‘जॅक जोन्स’ म्हणायला सुरुवात केली.	1. वादयवृंदही त्याला साथ देऊ लागला.
2. प्रेक्षागृहात वादयवृंदाचे स्वर घुमू लागले.	2. सारे थिएटर त्या स्वरांनी भरून गेले.
3. प्रेक्षागृहातील आरोळ्या स्टेज मॅनेजरने ऐकल्या.	3. स्टेज मॅनेजर धावतपळत आला आणि विंगेत. चार्लीच्या शेजारी उभा राहिला. गोंधळून जाऊन लिलीकडे बघत राहिला.

3. कंसातील वाक्प्रचारांचा खाली दिलेल्या वाक्यांत योग्य उपयोग करा:

प्रश्न (अ)
कंसातील वाक्प्रचारांचा खाली दिलेल्या वाक्यांत योग्य उपयोग करा: (अवेहलना करणे, चेहरा पांढरा फटफटीत पडणे, पदार्पण करणे, स्तिमित होणे)

1. आंब्याच्या झाडाचे मालक समोरून येताना दिसताच कैऱ्या पाडणाऱ्या मुलांच्या चेहऱ्यावर भीती पसरली.
2. शालेय स्नेहसंमेलनात प्राचीने स्टेजवर पहिले पाऊल टाकले.
3. दिव्यांग मुलांची प्रदर्शनातील चित्रे पाहून प्रमुख पाहुणे थक्क झाले.
4. गुणवान माणसांचा अनादर करू नये.

उत्तर:

1. आंब्याच्या झाडाचे मालक समोरून येताना दिसताच कैऱ्या पाडणाऱ्या मुलांचे चेहरे पांढरे फटफटीत पडले.
2. शालेय स्नेहसंमेलनात प्राचीने स्टेजवर पदार्पण केले.
3. दिव्यांग मुलांची प्रदर्शनातील चित्रे पाहून प्रमुख पाहुणे स्तिमित झाले.
4. गुणवान माणसांची अवहेलना करू नये.

प्रश्न (ब)
पुढील वाक्यांतील अधोरेखित शब्दांचे लिंग बदलून वाक्ये पुन्हा लिहा :

1. तिच्यावर आलेला वाईट प्रसंग या चिमुकल्याने सावरला.
2. तिच्या गोड गळ्याने कधीही दगा दिला नाही.
3. नर्तकीचे नृत्य प्रेक्षणीय होते.
4. सवाई गंधर्व महोत्सव प्रसिद्ध गायकाच्या गायनाने रंगला.

उत्तर:

1. तिच्यावर आलेला वाईट प्रसंग या चिमुकलीने सावरला.
2. त्याच्या गोड गळ्याने कधीही दगा दिला नाही.
3. नर्तकाचे नृत्य प्रेक्षणीय होते.
4. सवाई गंधर्व महोत्सव प्रसिद्ध गायिकेच्या गायनाने रंगला.

4. स्वमत:

प्रश्न 1.
चार्लीच्या तुम्हांला जाणवलेल्या गुणांचे वर्णन तुमच्या शब्दांत करा.
उत्तर:
चार्ली हा मुळातच गुणी कलावंत होता. आपली ही ओळख त्याने पदार्पणातच करून दिली. त्या दिवशी आई गात असताना तो एकाग्रतेने गाणे ऐकत होता. मला तर वाटते की, तो आईबरोबर मनातल्या मनात गाणे गातच असावा. यासाठी एकाग्रता राखण्याची व आपल्या आवडत्या विषयाशी एकरूप होण्याची क्षमता लागते. ती चार्लीकडे होती. रंगमंचावरून प्रत्यक्ष गाण्याची वेळ आली, तेव्हा चार्लीने ते यशस्वी रितीने गायले. याचे कारण त्याला कार्यक्रम सादर करायचा नव्हता. त्याला गायचे होते. त्याच्यात गायनाची ऊर्मी होती. तो त्या गाण्याशी एकरूप झाला होता. म्हणून तो गाऊ शकला.

पैशांचा पाऊस पडला, तेव्हा त्याने पैसे गोळा करायला सुरुवात केली. प्रेक्षकांनाही तसे सांगितले. हा त्याच्या मनाचा निरागसपणा, निष्पापपणा होता. तो कलावंतच होता. कलेची ऊर्मी त्याच्यात होती. म्हणून त्याने नाचून दाखवले. नकला करून दाखवल्या. हे सर्व त्याने निरीक्षणातून मिळवले होते. त्याची निरीक्षणक्षमता अफाट होती. एकंदरीत पदार्पणातच त्याने आपले कलावंतपण सिद्ध केले.

प्रश्न 2.
स्टेज मॅनेजरच्या जागी तुम्ही आहात अशी कल्पना करून त्या प्रसंगात तुम्ही कसे वागाल, ते सविस्तर लिहा.
उत्तर:
स्टेज मॅनेजरने चार्लीला गाणे सादर करायला सांगितले, हे योग्यच होते. तो निर्णय योग्यच होता, हे चालीने आपल्या कामगिरीने सिद्ध केलेच. मात्र, मॅनेजरची एक गोष्ट मला पटली नाही आणि आवडलीही नाही. लिलीवर अनवस्था प्रसंग ओढवला, तेव्हा मॅनेजर गोंधळून गेला. त्याने प्रेक्षकांना शांत करण्यासाठी काहीही केले नाही. मी त्याच्या जागी असतो, तर पुढे झालो असतो. प्रेक्षकांची क्षमा मागितली असती. घडलेल्या प्रसंगात लिलीची कोणतीही चूक नव्हती, तिच्यावर कोसळलेली ती नैसर्गिक आपत्ती होती, हे सर्व त्यांना समजावून सांगितले असते. पंधरा मिनिटांची विश्रांती जाहीर केली असती. या अवधीत विचारविनिमय केला असता. लिलीला धीर दिला असता. मला वाटते, असेच व्हायला हवे होते.

प्रश्न 3.
‘हसरे दुःख’ या शीर्षकाचा तुम्हांला समजलेला अर्थ तुमच्या शब्दांत लिहा.
उत्तर:
लिली हार्ले ही एक मोठी कलावंत होती. गायन, पियानो वादन, नर्तन यांत ती निष्णात होती. कलावंत म्हणून जे मोठेपण असते, ते तिने मिळवले होते. या सामर्थ्याच्या बळावर तिने पैसा, कीर्ती मिळवली होती. हे सर्व एके दिवशी अचानक लुप्त झाले. तिचा आवाज हरवला आणि तिचे सर्वस्वच गेले. ती रात्र तिच्या दृष्टीने काळरात्र होती. दुःखाचा कडेलोट होता.

त्याच रात्री लिलीचा पाच वर्षांचा हरहुन्नरी मुलगा या संकटात तिच्या मदतीला धावून आला. कोसळलेला कार्यक्रम त्याने पुन्हा उभारला. त्याने गायन, अभिनय व नर्तन या कौशल्यांचे डोळे दिपवणारे दर्शन घडवले. कोणत्याही आईला आभाळ ठेंगणे वाटावे, असे दृश्य होते ते. नवा कलावंत उदयाला आला. आपल्या मुलाचा हा उदयकाळ म्हणजे सुखाचा सर्वोच्च बिंदू होता. एका बाजूला सुख होते. त्याच क्षणी दुसऱ्या बाजूला दु:ख होते. म्हणून या पाठाचे शीर्षक आहे – ‘हसरे दुःख’.

5. हसरे दुःख’ या पाठातील पाठवंशाचे नाट्यीकरण करून वर्गात सादरीकरण करा.

प्रश्न 1.
हसरे दुःख’ या पाठातील पाठवंशाचे नाट्यीकरण करून वर्गात सादरीकरण करा.

अपठित गद्य आकलन:

1. खालील उतारा काळजीपूर्वक वाचून त्याखालील कृती का.

प्रश्न (अ)
चोकटी पूर्ण करा. अश्मयुगातील माणसाने दगडाचा उपयोग करून बनवलेल्या वस्तू – [ ] [ ] [ ] [ ]

आमयुगात माणसाने आपले जीवन सुखाचे काम येण्यासाठी चुलीसाठी तीन दगड मांडण्यापासून मृताचे थडगे बांधण्यापर्यंत दगडाला नानातहांनी वापरले. त्यांची भांडीकुंडी केली. औते-हत्यारे बनवली आणि त्याचे दागदागिने देखील घडवले. साठक कोरून किंवा दगडाच्या भिंती रचून आपल्या निवान्याची सोय केली. माणसाच्या प्राथमिक गरजा भागल्यानंतर त्याला आपल्या सृजनशीलतेला आणि पूजावृत्तीला वाट कान दिल्याशिवाय राहवले नाही.

फुरसद मिळाली तशी तो लेगी खोदू लागला; शिल्पे कोरू लागला, घरांना कलात्मक आकार देऊ लागला. शिल्प आणि स्थापत्य या दोन्ही कला प्रयाप्रमाणे अशा दाडातून फुटल्या आणि विज्ञानाचा उगम झाला. एक सबंध युग दशहाने माणसाचे जीवन परोपरीने सुखाचे केल्यामुळे आणि माणसाच्या सृजनशीलतेला कला आणि विज्ञान यांचे उमाळे आल्यामुळे त्याला दगडच देव वाटून त्याने तो पूजला.

प्रश्न (आ)
माणसाला दगडच देव वाटण्याचे कारण उताऱ्याच्या आधारे व तुमच्या मते स्पष्ट करा.

भाषाभ्यास:

अनुस्वार लेखनावावतचे नियम:

1. खालील शब्द वाचा.

‘रंग’, ‘का’, ‘पंचमी’, ‘पंडित’, ‘अंधुज हे शब्द तत्सम आहेत. हे आपण पर-सवर्णानसुया लिहू शकतो, म्हणजे अनुस्वारानंतर देणाऱ्या अक्षराच्या वर्गातील अनुनासिक वापरून लिहू शकतो. उदा., रा. पडकर, पञ्चमी, पण्डित, अन्धुन असे. विशेषतः जुने साहित्य वाचले तर असे लेखन दिसते. परंतु, आजकाल अशी पर-सवनि लिहिण्याची पद्धत जुनी झाली आहे. त्याऐवजी अनुस्वारच वापरले जातात. खालील शब्दया कसे दिसतात! ‘निबन्य’, ‘आम्बा’, ‘वन’, ‘सम्म’, ‘दल्या हे शब्द वयायला विचित्र वाटतात ना! कारण हे तत्सम नाहीत. पर-सवर्ग लिहिण्याची पद्यत का तत्सम शब्दांपुरती मर्यादित आहे. संस्कृत नसलेले मराठी शब्द शोविंद देऊनच लिहावेत.

मराठीत स्पष्टोच्यारित अनुनासिकाबद्दल शीविंदू दयावा.

2. खालील शब्द वाचा.

‘सिंह’, ‘संगम’, मांस’, ‘संहार’ या शब्दांचा उच्चार करे तर खूप शाळा आहे ना? या शब्दांचे ‘सिंह’, कम’, भांबा’, ‘संहार’ उच्चार असे होतात आणि तसेच ते कायचे असतात पण लिहिताना हे शब्द तसे लिहू नयेत.

इ.इ.स., स. प. म. रयांच्यापूर्वी येणाऱ्या अनुस्वारांबद्दल केवळ शीविंदू दयावा.

पर – सवर्णाने लिहा:
घंटा, मंदिर, चंपा, चंचल, मंगल

अनुस्वार वापसन लिहा:
जगाल, घेण्डू, सञ्च, गोन्धळ, बम्ब

Marathi Kumarbharati Textbook Std 9 Answers Chapter 18 हसरे दुःख Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
प्रेक्षागारात घडलेला तो विपरीत प्रसंग लिली कथन करीत आहे, अशी कल्पना करून लिहा.
उत्तर:
त्या दिवशी माझे गाणे रंगात आले होते. माझे खूप चाहते आले होते. त्यांना संगीताचा आनंद भरभरून दयावा, असे मलाच वाटत होते. आनंदाने फुललेले श्रोत्यांचे चेहेरे पाहण्यातले सुख मी अनेकदा अनुभवले आहे. त्या दिवशीसुद्धा मी भरभरून गात होते. श्रोते डोलत होते. त्यांच्या चेहेऱ्यांवरचा आनंद मला दिसत होता. मीसुद्धा खुशीत होते. आजसुद्धा मी यशाचा आणखी एक टप्पा गाठणार होते, अशी माझी खात्री झाली होती आणि घडले भलतेच.

मधुर स्वरविलास चालू असतानाच अचानक मध्येच माझा आवाज चिरकला. कंठातून आवाजच येईना. स्वर आतल्या आत विरून जाऊ लागले. स्वरांनी वादयवृंदाची साथसंगत सोडून दिली. काही केल्या काही होईना. मी घुसमटले. आतल्या आत कोसळले. इतकी लांच्छनास्पद स्थिती मी कधीच अनुभवली नव्हती. श्रोत्यांना तोंड दाखवण्याचीही मला लाज वाटू लागली. मी कशीबशी खाली मान घालून विंगेत परतले.

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
चंडोल पक्ष्याच्या उदाहरणाला अनुसरून आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
विपरीत घटनेचे श्रोत्यांवरील परिणाम लिहा.

1. ……………………………
2. …………………………..
3. …………………………..
4. …………………………..

उत्तर:

1. काही काळानंतर श्रोत्यांना दम धरवेना. त्यांच्यात कुजबूज सुरू झाली.
2. श्रोते आरडाओरडा करू लागले. आरडाओरड वाढू लागली.
3. काही श्रोते लिलीचे गाणे भसाड्या आवाजात म्हणू लागले.
4. श्रोत्यांच्या गायनाला शिट्ट्यांची व आरोळ्यांची साथ मिळाली.

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
यापूर्वीचा लिली हार्लेबाबतचा मॅनेजरचा अनुभव लिहा.
1. …………………….
2. ……………………
उत्तर:
1. लिली हार्ले एकदा रंगमंचावर गेली की, तिच्याकडे मॅनेजरला कधी बघावेच लागत नसे.
2. लिली रंगमंचावर उभी राहिली की, मॅनेजर निर्धास्तपणे दुसरीकडे बघायला मोकळा असे.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
लिली हार्लेच्या बाबतीत घडलेल्या प्रसंगासारखा तुम्ही अनुभवलेला किंवा तुम्हांला ठाऊक असलेला प्रसंग सांगा.
उत्तर:
माझ्या आयुष्यातला तो प्रसंग मी कधीही विसरणार नाही. प्रस्तुत पाठ वाचला त्या वेळी मला तो तीव्रपणे आठवला. लिलीची काय अवस्था झाली असेल, हे मला पूर्णपणे कळले. गेल्याच्या गेल्या वर्षीची गोष्ट आहे ही. मी सातवीत होतो. जिल्हास्तरीय वक्तृत्वस्पर्धा होती. आमच्या शाळेतून मी सहभागी झालो होतो. सभागृह पूर्ण भरलेले होते. एकेकाचे नाव घेतले जायचे, तो यायचा आणि तडाखेबंद भाषण करून जायचा. ते पाहून माझ्या छातीत धडधडायचे. माझा क्रमांक जवळ येऊ लागला तशी माझी भीती वाढू लागली. माझे नाव पुकारले गेले आणि मी आतून धडपडलोच. व्यासपीठावर गेलो. माझे हातपाय थरथरायला लागले.

परीक्षक मला, “घाबरू नकोस. बोल तू.’ असा धीर देऊ लागले. त्याबरोबर माझी भीती आणखी वाढू लागली. मी कशीबशी तीनचार वाक्ये बोललो आणि पुढचे काही आठवेच ना! खरे तर मी भाषण चोख पाठ केले होते. सरांनी माझ्याकडून घोटवून घेतले होते. कोणाचाही ऑफ पिरिअड असला की माझे भाषण ठेवायचे. भरपूर सराव झाला होता. आईबाबा आणि काकाकाकीसुद्धा खूश होते माझ्यावर. हे सगळे आठवले. पण भाषण आठवेना. मी तेच तेच शब्द पुन्हा पुन्हा म्हणू लागलो. शब्दसुद्धा थरथरत येऊ लागले. अखेरीस मला रडू आले. मी तसाच खाली उतरलो आणि टेबलावर डोके टेकून खूप वेळ तसाच बसून राहिलो.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढे दिलेल्या घटनांचे परिणाम लिहा:

घटना	परिणाम
लिली प्रहसनात काम करी, तेव्हा प्रेक्षागारात हास्यलहरी उठत.

उत्तर:

घटना	परिणाम
लिली प्रहसनात काम करी, तेव्हा प्रेक्षागारात हास्यलहरी उठत.	मग स्टेज मॅनेजर निर्धास्त होई. त्याला लिलीच्या कामाकडे लक्ष देण्याची गरज राहत नसे.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
मॅनेजरला घडलेले लिलीचे दर्शन.
उत्तर:
लिलीची मुद्रा पांढरी पडली होती. आजवर तिच्या गोड गळ्याने तिला दगा दिला नव्हता. तिची एवढी अवहेलना झाली नव्हती! अपमानित अवस्थेत ती मुकाट्याने विंगेत परतली.

प्रश्न 2.
अर्थ स्पष्ट करा:
विदयुल्लता चमकावी आणि क्षणार्धात घनदाट अंधकारात विलीन होऊन जावी, असा प्रकार घडला होता.
उत्तर:
वीज चमकते तेव्हा आसमंत झळाळून जातो. लख्ख प्रकाश पडतो. पण वीज चमकून गेली की, मिट्ट काळोख होतो. प्रकाशाचा टिपूसही दिसत नाही. लिलीच्या बाबतीत असेच घडले. तिची कारकीर्द झळाळत होती. तिला नाव मिळत होते. पैसा मिळत होता. तिचे हे तेज क्षणार्धात नष्ट झाले. तिच्या तेजाचा पुसटसा बिंदूही प्रकट झाला नाही. मिट्ट काळोख पसरावा तसे झाले.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
लिलीच्या या प्रसंगासंबंधात तिथे हजर असलेल्या एका रसिक श्रोत्याचे मनोगत लिहा.
उत्तर:
अरे देवा! काय घडले हे? विश्वासच बसत नाही. किती वेळा या लिलीचे कार्यक्रम मी पाहिले आहेत! किती वेळा गायन ऐकले आहे! प्रत्येक वेळी ती चार पावले पुढेच जात होती. तिची प्रगतीच होत होती. तिचे बहारदार नृत्य, रसाळ गायन, वातावरण प्रसन्न करणारा तिचा अभिनय! काय बोलावे त्याबद्दल? आता हा आनंद संपला. तिची अलौकिक कला लोप पावली.

असे कसे झाले? काय खाल्ले असेल तिने? तिच्या अन्नात कोणीतरी काहीतरी मिसळले नाही ना? एखादयाचे चांगले कोणाला पाहवत नाही. ते विनाकारण शत्रू बनतात आणि असा घात करतात. असा कोणी दुष्ट असेल, तर त्याला शोधलेच पाहिजे. छे, छे! अशी वेळ वैऱ्यावरसुद्धा येऊ नये. खरे म्हणजे हे फक्त लिलीचे नुकसान नाही. हे आम्हां रसिकांचेही नुकसान आहे. काय करणार? आलिया भोगासी…!

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढील वाक्यामागील भाव स्पष्ट करा:
मॅनेजरला ते माहीत का नव्हते?
उत्तर:
मॅनेजर लिलीला खूप आधीपासून ओळखत होता. तिचे अनेक कार्यक्रम त्याने जवळून पाहिले होते. कलावंत म्हणून असलेले तिचे मोठेपण त्याला माहीत होते. तिची असहायता, अगतिकता त्याला समजत होती. त्यामुळे तिने मॅनेजरजवळ दिलगिरी व्यक्त करण्याची गरज नव्हती. हा सर्व भाव त्या छोट्याशा एका वाक्यात आहे.

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
मॅनेजरने घेतलेल्या निर्णयावर तुमचे मत नोंदवा.
उत्तर:
मॅनेजरने खरे तर फार मोठा धोका पत्करला होता. कारण चार्ली त्या वेळी 5 वर्षांचा होता. 5 वर्षांच्या मुलाची समज ती काय असणार? कला म्हणजे काय हे समजून घेणे त्याच्या बुद्धीच्या पलीकडची गोष्ट होती. कलेच्या सादरीकरणातील खाचाखोचा त्याला कळणे शक्यच नव्हते. तो सतत आईसोबत असल्याने आईचे गाणे त्याच्या कानांवर सततच पडत होते. बालबुद्धीनुसार तो ते गाणे सतत गुणगुणत, गात राहिला असणार. आईच्या गायनाचे अनुकरण करीत करीत त्याने तिचे गायन आत्मसात केले. ते केवळ आईचे गायन नव्हते, तर ते उत्तम गायन होते. मॅनेजरने हे पाहिले होते, ऐकले होते. त्याला चार्लीचा अंतर्यामी विश्वास वाटत होता. म्हणून त्याने पाच वर्षांच्या चार्लीला स्टेजवर आणले, असे माझे मत आहे.

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढील उद्गार कोणी, कोणाला उद्देशून काढले ते लिहा:
1. याच्या आईची प्रकृती अचानक बिघडली… तेव्हा तिचं अपुरं राहिलेलं गाणं आता हा पुरं करील!
2. मी आधी पैसे गोळा करतो आणि मग राहिलेलं गाणं म्हणून दाखवतो.
उत्तर:
1. स्टेज मॅनेजर – रसिक श्रोत्यांना.
2. चार्ली – रसिक श्रोत्यांना.

कृती 2 : (आकलन)

प्रश्न 1.
का ते लिहा:
1. श्रोत्यांनी स्टेजवर पैशांची उधळण केली.
2. चार्लीने ताबडतोब स्टेज मॅनेजरचा पाठलाग केला.
उत्तर:
1. चार्लीच्या गाण्याने सारे श्रोते भारावून गेले.
2. श्रोत्यांनी चार्लीच्या गायनासाठी स्टेजवर उधळलेले पैसे गोळा करून स्टेज मॅनेजर निघून गेला.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यातून तुम्हांला जाणवणारे स्टेज मॅनेजरचे गुण लिहा.
उत्तर:
‘स्टेज मॅनेजर’ याला मराठीत ‘रंगमंच व्यवस्थापक’ म्हणतात. हा खरे तर व्यावसायिक. त्याचे काम खूप महत्त्वाचे असते. स्टेजवरचे पडदे, सर्व दिवे, ध्वनिव्यवस्था, वादयवृंदाची व्यवस्था, नेपथ्याची व्यवस्था वगैरे सर्व बाबी रंगमंच व्यवस्थापक सांभाळतो. हे काम करता करता त्याचे लिली व चार्ली यांच्याशी जिव्हाळ्याचे नाते निर्माण झाले आहे. लिलीच्या रंगमंच व्यवस्थापकाला मनुष्यस्वभावाची चांगली जाण आहे.

त्याला लिलीची कलेवरील निष्ठा आणि तिचे कलावंत म्हणून असलेले सामर्थ्य कळते. चार्लीची क्षमताही त्याने अचूक ओळखली. पाच वर्षांच्या चार्लीने पदार्पणातच आपली क्षमता सिद्ध केली. श्रोत्यांनी उधळलेले पैसे गोळा करून तो लिलीला नेऊन देतो. यात त्याचा प्रामाणिकपणा दिसतो. आलेल्या श्रोत्यांना-प्रेक्षकांना पूर्ण कार्यक्रम दाखवला पाहिजे, ही कर्तव्याची भावनाही त्याच्या मनात है असते. मुख्य म्हणजे व्यवहाराच्या पलीकडे जाऊन माणसांशी जिव्हाळ्याने वागण्याचा मोठा गुण त्याच्याकडे आहे.

उतारा क्र. 6

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
का ते लिहा:
1. चार्लीच्या जिवात जीव आला.
2. प्रेक्षकांनी थिएटर डोक्यावर घेतले.
उत्तर:
1. आपल्याला मिळालेले पैसे स्टेज मॅनेजर हडप करतो की काय, ही चार्लीला शंका आली. म्हणून त्याने त्याचा पाठलागही केला. पण मॅनेजरने ते पैसे चार्लीच्या आईकडे दिले. म्हणून चार्लीच्या जिवात जीव आला.
2. चार्लीच्या आईचा आवाज अचानक बसल्यामुळे तिचे गाणे अर्धवट राहिले. त्यामुळे श्रोत्यांचा विरस झाला होता. या पार्श्वभूमीवर चार्लीने उरलेले गाणे आईप्रमाणे हुबेहूब म्हटले. आणि चार्ली त्या वेळी अवघा पाच वर्षांचा होता. या सर्व बाबींमुळे श्रोते बेहद्द खूश झाले. त्यांनी आनंदाच्या भरात थिएटर डोक्यावर घेतले.

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यातून तुम्हांला जाणवणारे चार्लीचे स्वभावगुण लिहा.
उत्तर:
चार्लीचे वय पाच वर्षे होते. म्हणजे अज्ञानी बालकच तो. तो त्याच्या स्वभावाला अनुसरून नैसर्गिकपणे वागला. वास्तविक अशा समारंभाचे संकेत असतात. ते सर्वांनी पाळायचे असतात. पण चार्ली गाणे थांबवून पैसे गोळा करतो. पैसे घेऊन जाणाऱ्या मॅनेजरचा पाठलाग करतो. समारंभाचे संकेत मोडून तो बालसुलभ वृत्तीने वागतो. त्यामुळे गमतीदार विसंगती निर्माण होते. त्याची निरीक्षण शक्ती जबरदस्त आहे. म्हणून आईच्या गायनाची तो हुबेहूब नक्कल करतो. अन्य नकलाही करतो. रंगमंचावर वावरताना तो घाबरत नाही, गोंधळत नाही. कलावंताकडे असलेले हे महत्त्वाचे गुण त्याच्याकडे दिसतात.

उतारा क्र. 7

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
तक्ता भरा:
उत्तर:

सामासिक शब्द	विग्रह
1. दुःष्काळ	दुः (वाईट) असा काळ
2. आठवडा	आठ दिवसांचा समूह
3. नेआण	ने आणि आण
4. धर्माधर्म	धर्म किंवा अधर्म
5. पालापाचोळा	पाला, पाचोळा वगैरे

2. शब्दसिद्धी:

प्रश्न 1.
‘कार’ प्रत्यय असलेले चार शब्द लिहा.
उत्तर:

1. कथाकार
2. नाटककार
3. संगीतकार
4. शिल्पकार

3. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचा अर्थ सांगून वाक्यांत उपयोग करा:

1. नाचक्की होणे
2. भान हरपणे
3. लुप्त होणे
4. पाठ थोपटणे.

उत्तर:

1. नाचक्की होणे – अर्थ : अब्रू जाणे.
   वाक्य : सरांना उलट उत्तर देऊन सुरेशने स्वतःची नाचक्की केली.
2. भान हरपणे – अर्थ : जाणीव न उरणे.
   वाक्य: चित्र रंगवताना शालिनीचे भान हरपले.
3. लुप्त होणे – अर्थ : नाहीसे होणे.
   वाक्य: कडक उन्हाळ्यामुळे विहिरीतले पाणी लुप्त झाले.
4. पाठ थोपटणे – अर्थ : शाबासकी देणे.
   वाक्य : निबंधस्पर्धेत प्रथम क्रमांक पटकावणाऱ्या मालतीची सरांनी पाठ थोपटली.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
पुढील शब्दात लपलेले प्रत्येकी चार अर्थपूर्ण शब्द लिहा:

1. दुसरीकडे
2. लांबसडक
3. उदासवाण्या
4. पदन्यासात.

उत्तर:

प्रश्न 2.
विरुद्धार्थी शब्द लिहा:

1. बाहेर
2. गोड
3. धूसर
4. सुरेल
5. धाकटा
6. दूर.

उत्तर:

1. बाहेर × आत
2. गोड × कडू
3. धूसर × स्पष्ट
4. सुरेल × कर्कश
5. धाकटा × थोरला
6. दूर × जवळ.

2. लेखननियम:

प्रश्न 1.
अनुस्वार लेखनाबाबतचे नियम:
पुढील शब्द वाचा.
उत्तर:
‘रंग’, ‘पंकज’, ‘पंचमी’, ‘पंडित’, ‘अंबुज’ हे शब्द तत्सम आहेत. हे आपण पर-सवर्णानेसुद्धा लिहू शकतो. म्हणजे अनुस्वारानंतर येणाऱ्या अक्षराच्या वर्गातील अनुनासिक वापरून लिहू शकतो. उदा., रङ्ग, पङ्कज, पञ्चमी, पण्डित, अम्बुज असे. विशेषतः जुने साहित्य वाचले तर असे लेखन दिसते. परंतु, आजकाल अशी परसवर्णाने लिहिण्याची पद्धत जुनी झाली आहे. त्याऐवजी अनुस्वारच वापरले जातात. पुढील शब्द बघा कसे दिसतात!

‘निबन्ध’, ‘आम्बा’, ‘खन्त’, ‘सम्प’, ‘दगा’ हे शब्द बघायला विचित्र वाटतात ना! कारण हे तत्सम नाहीत. पर-सवर्ण लिहिण्याची पद्धत फक्त तत्सम शब्दांपुरती मर्यादित आहे. संस्कृत नसलेले मराठी शब्द शीर्षबिंदू देऊनच लिहावेत.

मराठीत स्पष्टोच्चारित अनुनासिकाबद्दल शीर्षबिंदू दयावा.

पुढील शब्द वाचा.

‘सिंह’, ‘संयम’, ‘मांस’, ‘संहार’ या शब्दांचा उच्चार खरे तर खूप वेगळा आहे ना? या शब्दांचे ‘सिंव्ह’, ‘संय्यम’, ‘मांव्स’, ‘संव्हार’ अनुस्वारांबद्दल केवळ शीर्षबिंदू दयावा.
असे उच्चार होत असले तरी लिहिताना हे शब्द तसे लिहू नयेत.

नियम : य्, र, ल, व्, श्, प्, स्, ह यांच्यापूर्वी येणाऱ्या अनुस्वारांबददल केवळ शीर्षबिंदू दयावा.

प्रश्न 1.
पुढील शब्द पर-सवर्णाने लिहा:

1. घंटा
2. मंदिर
3. चंपा
4. चंचल
5. मंगल.

उत्तर:

1. घण्टा
2. मन्दिर
3. चम्पा
4. चञ्चल
5. मङ्गल.

प्रश्न 2.
पुढील शब्द अनुस्वार वापरून लिहा:

1. जङ्गल
2. चेण्डू
3. सञ्च
4. गोन्धळ
5. बम्ब.

उत्तर:

1. जंगल
2. चेंडू
3. संच
4. गोंधळ
5. बंब.

प्रश्न 3.
पुढील शब्द लेखननियमांनुसार अचूक लिहा :

1. त्रिकालाबाधित
2. हास्यकल्लोळ
3. यत्किंचित
4. प्रकृती
5. कंठमाधुर्य.

उत्तर:

1. त्रीकाळाबाधीत
2. हस्यकलोल
3. यक्तिचीत
4. परक्रुती
5. कंठमाधूर्य.

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यात योग्य विरामचिन्हे वापरून वाक्य पुन्हा लिहा:
मॅनेजर म्हणाला छे छे तुम्ही आता स्टेजवर जाण्याची गरज नाही.
उत्तर:
मॅनेजर म्हणाला, “छे, छे! तुम्ही आता स्टेजवर जाण्याची गरज नाही.”

4. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द लिहा :
1. Children Theatre
2. Anniversary.
उत्तर:
1. बालरंगभूमी
2. वर्धापन दिन.

उपक्रम:

प्रश्न 1.
हसरे दु:ख’ या पाठातील पाठ्यांशाचे नाट्यीकरण करून वर्गात सादरीकरण करा.

हसरे दुःख Summary in Marathi

प्रस्तावना:

भा. द. खेर हे जुन्या पिढीतील एक सुप्रसिद्ध लेखक. त्यांनी विपुल लेखन केले आहे. त्यांचे काही लेखन पुढीलप्रमाणे:
कादंबऱ्या: ‘सुखाचा लपंडाव’, ‘प्रायश्चित्त’, ‘शुभमंगल’, ‘नंदादीप’, ‘वादळवारा’, ‘यज्ञ’, ‘अमृतपुत्र’.
अन्य लेखन: ‘आईन्स्टाईनचे नवे विश्व’, ‘गीताज्ञानदेवी’, ‘अपरोक्षानुभूती’, ‘अधांतरी’, ‘द प्रिन्सेस’ इत्यादी.

प्रस्तुत पाठात चार्ली चॅप्लिनचा कलेच्या प्रांतातील प्रवेशाचा प्रसंग चित्रित केला आहे. यातील दुर्दैवाचा भाग असा की, त्याच्या आईच्या कारकिर्दीचा दु:खद अंत झाला, त्या क्षणीच त्याची कलावंत म्हणून कारकीर्द सुरू झाली. एकच क्षण सुख आणि दु:ख यांनी भरलेला! म्हणून त्या प्रसंगातील भावनांना ‘हसरे दुःख’ असे नाव दिले आहे.

शब्दार्थ:

1. तेजोमय – तेजाने युक्त, तेजस्वी.
2. कंठमाधुर्य – कंठाचे माधुर्य, गळ्याचा गोडवा, म्हणजे आवाजाचा गोडवा.
3. विध – घायाळ.
4. विपरीत – उलट, विरुद्ध (वाईट या अर्थाने रूढ).
5. कावराबावरा – भीतीने बावरलेला, बुजलेला.
6. पदन्यास – पावलांची लयदार हालचाल.
7. अवहेलना – हेटाळणी.
8. नाचक्की – बदनामी.

वाक्प्रचार व त्यांचे अर्थ:

1. नजर खिळून राहणे – एकाग्रतेने पाहणे.
2. जिवाचा कान करणे – मन लावून ऐकणे.
3. भान हरपणे – गुंग होणे.
4. तंद्री लागणे – गुंग होणे.
5. रंगात येणे – तल्लीन होणे.
6. दम धरणे – धीर धरणे.
7. दम निघून जाणे – धीर सुटणे.

9th Std Marathi Questions And Answers:

• वनवासी (कविता) Class 9 Question Answer
• ऑलिंपिक वर्तुळांचा गोफ Class 9 Question Answer
• हसरे दुःख Class 9 Question Answer
• प्रीतम Class 9 Question Answer
• आपुले जगणे…आपुली ओळख! (कविता) Class 9 Question Answer
• विश्वकोश (स्थूलवाचन) Class 9 Question Answer

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 13 थोडं ‘आ’ भारनियमन करूया Notes, Textbook Exercise Important Questions and Answers.

Class 9 Marathi Aksharbharati Chapter 13 थोडं ‘आ’ भारनियमन करूया Question Answer Maharashtra Board

थोडं ‘आ’ भारनियमन करूया Std 9 Marathi Chapter 13 Questions and Answers

1. काय घडते ते पाठाच्या आधारे लिहून वाक्य पूर्ण करा:

प्रश्न 1.
काय घडते ते पाठाच्या आधारे लिहून वाक्य पूर्ण करा:
(अ) आदर मनात तुडुंब भरून असल्यास ………………..
(आ) खूप जवळच्या गहिऱ्या नात्यात शब्दांनी आभार मानल्यास ……………………….
(इ) मित्रमैत्रिणीने आभार मानल्यास ………………………………….
(ई) लेखिकांच्या मते ‘आ’भारनियमन केल्यास ……………….
उत्तर:
(अ) आदर मनात तुडुंब भरून असल्यास तो कृतीत सहजासहजी उतरतो.
(आ) खूप जवळच्या गहिऱ्या नात्यात शब्दांनी आभार मानल्यास उभयपक्षी अवघडलेपणा येतो. गहिरेपणा उणावून नुसती औपचारिकता उरते.
(इ) मित्रमैत्रिणीने आभार मानल्यास आपल्या पाठीत एक सणसणीत धपाटा मिळतो आणि ‘जादा आगाऊपणा केलास तर याद राख’ अशी धमकीही मिळते.
(ई) लेखिकांच्या मते, ‘आ’भारनियमन केल्यास त्या शब्दांमधला जिव्हाळा आणि भावनांची ऊब संपून जाणार नाही.

2. पाठातील उदाहरणे शोधा:

प्रश्न 1.
पाठातील उदाहरणे शोधा:

उत्तर:

शब्दांशिवाय मानलेले आभार	स्पर्शाने	कटाक्षाने
	ऑपरेशनच्या गुंगीतून नुकताच बाहेर आलेला रुग्ण डॉक्टरांचे हात घट्ट धरतो.	आईच्या आजारपणात  खूप मदत करणाऱ्या मित्रमैत्रिणींकडे कृतज्ञतेने टाकलेला कटाक्ष.

3. चूक की बरोबर ते ओळखा:

प्रश्न 1.
चूक की बरोबर ते ओळखा:
(अ) आभार आणि अभिनंदन या शब्दांत माणसं अनेकदा गल्लत करतात.
(आ) भारतीय संस्कृतीत भावनांचे प्रदर्शन करणे आदर्श मानले जाते.
(इ) ममनात आदर असेल तर तो कृतीत दिसतो.
(ई) लआभार मानण्याचा अतिरेक चांगला नव्हे.
उत्तर:
(अ) बरोबर
(आ) चूक
(इ) मबरोबर.
(ई) लबरोबर

4. कारणे लिहा.

प्रश्न 1.
कारणे लिहा.

उत्तर:

5. पाठातील विनोद निर्माण करणारी वाक्ये शोधा.

प्रश्न 1.
पाठातील विनोद निर्माण करणारी वाक्ये शोधा.
उत्तर:

1. साधं घोटभर पेय दिलं तरी हातभर बैंक्यू म्हणतात.
2. बैंक्यू म्हणता येणं हा सुसंस्कृतपणाचा कडेलोट आहे, असं काही काळ वाटून गेलं.
3. तू कसली ग माझी ऑक्यू? मीच तुझी बैंक्यू.
4. त्याला बैंक्यू दिलेस का पण?
5. तुला कितीही बँक्यू केलं तरी कमीच.
6. आभार न मानण्याचा मॅनरलेसपणा त्याच्या खाती रुजू होणार नव्हता.
7. जन्मल्या जन्मल्या आईबापांचे आभार मानणारे कार्ड आणि वर गेल्यावर खालून वेळच्या वेळी आपल्याला नीट वर पोचवणाऱ्यांचे आभार कार्ड अजून माझ्या पाहण्यात आलेलं नाही.
8. बँक्स फॉर मॅरिंग हं. लग्न केल्याबद्दल मनःपूर्वक आभार.

6. खाली दिलेल्या शब्दांसाठी मराठी भाषेतील शब्द लिहा:

प्रश्न 1.
खाली दिलेल्या शब्दांसाठी मराठी भाषेतील शब्द लिहा:

1. कॅप्शन
2. टेन्शन
3. आर्किटेक्ट
4. ऑपरेशन.

उत्तर:

1. षवाक्य
2. ताणतणाव
3. वास्तुविशारद
4. शस्त्रक्रिया.

7. खाली दिलेल्या शब्दांचा तुम्हांला समजलेला अर्थ लिहा:

प्रश्न 1.
सुसंस्कृतपणाचा कडेलोट.
उत्तर:
शिष्टाचार पाळणे हे सुसंस्कृतपणाचे लक्षण मानले जाते. इंग्रज आपल्यापेक्षा श्रेष्ठच आहेत, असे मनोमन मानणारे खूप लोक आहेत. इंग्रज म्हणजे सुसंस्कृतच; ते जे जे करतात, ते ते सर्व सुसंस्कृतपणाचे लक्षणच होय; असे या लोकांना वाटते. इंग्रज लोक उठता-बसता बैंक्यू म्हणतात, म्हणून त्यांचे आंधळे अनुकरण करणारेही सतत बैंक्यू म्हणतात. या लोकांच्या मते, बँक्यू म्हणणे हा सुसंस्कृतपणाचा अत्युच्च बिंदू होय. हा सर्व भाव ‘सुसंस्कृतपणाचा कडेलोटच’ या शब्दांतून व्यक्त होतो.

प्रश्न 2.
घाऊक आभार
उत्तर:
सर्व व्यक्तींचे सर्व बाबींसाठी एकदाच एकत्रित आभार मानणे म्हणजे ‘घाऊक आभार’ मानणे होय.

8. स्वमत:

प्रश्न (अ)
‘आभार मानणे,’ या शिष्टाचाराविषयीचे तुमचे मत लिहा.
उत्तर:
आपण अनेक कामे पार पाडतो. ही कामे आपण पूर्णांशाने केलेली नसतात. त्या कामांना अनेकांचा हातभार लागलेला असतो. तरी कामाचे श्रेय आपल्याला मिळते. त्याचे फायदेही आपल्याला मिळतात. वास्तविक आपल्या एकट्याचा तो अधिकार नसतो. त्यावर इतरांचाही अधिकार असतो. पण श्रेय व फायदे मात्र आपण एकटेच घेतो. हे अनुचित होय. इतरांच्या सहकार्याशिवाय आपण काहीही करू शकत नाही. म्हणून इतरांच्या सहकार्याबद्दल, त्यांच्या मदतीबद्दल कृतज्ञता व्यक्त केली पाहिजे. आभार मानणे हा कृतज्ञता व्यक्त करण्याचाच प्रकार आहे.

लेखिका मंगला गोडबोले म्हणतात, तेही खरेच आहे. आभाराचा अतिरेक चालू आहे. क्षुल्लक कारणासाठीसुद्धा आभार मानले जातात. बऱ्याच वेळा समोरच्या व्यक्तीबद्दल कृतज्ञता व्यक्त करण्याऐवजी आपण स्वतः सुसंस्कृत आहोत, असे दाखवण्यासाठी आभार मानले जातात. असे होते तेव्हा आभाराचा मूळ उद्देशच नष्ट होतो. म्हणून है आभार मानताना तारतम्य बाळगले पाहिजे. मुख्य म्हणजे अत्यंत प्रामाणिकपणे आभार मानले पाहिजेत.

प्रश्न (आ)
पाठाच्या शीर्षकातून तुम्हांला समजलेला विनोद तुमच्या शब्दांत स्पष्ट करा.
उत्तर:
भारनियमन म्हणजे विजेच्या पुरवठ्यात केलेली काटकसर. भारनियमन, काटकसर हे गोंडस शब्द झाले. वस्तुस्थिती अत्यंत विदारक आहे. मुंबईसारख्या शहरात 24 तास वीजपुरवठा चालू असतो. पण ग्रामीण भागात मात्र 10-10, 15-15 तास वीजपुरवठा बंद असतो. ग्रामीण जनतेला यामुळे अनेक हालअपेष्टांना तोंड दयावे लागते. शासन या हालअपेष्टा कमी करीत नाही, मात्र या हालअपेष्टांना गोंडस नाव देते – ‘भारनियमन’!

उलटी परिस्थिती दुसऱ्या ठिकाणी दिसते. लोक सुसंस्कृतपणाच्या कल्पनेच्या ओझ्याखाली ‘आभार’, ‘सॉरी’ वगैरे शब्दांचा वारेमाप वापर करतात. अत्यंत क्षुल्लक कारणासाठीसुद्धा या शब्दांची उधळमाधळ केली जाते. अनेकदा ही उधळण हास्यास्पद पातळीवर जाऊन पोहोचते. म्हणून लग्न करणाऱ्या नवऱ्या मुलाचे ‘लग्न केल्याबद्दल आभार’ मानले जातात. खरे तर ‘आभारा’ची काटकसर करणे आवश्यक आहे. वीजपुरवठ्यातील अपुरेपणा, ‘आभार’ इत्यादी शब्दांची उधळण या दोन विपरीत स्थितींचा निर्देश करण्यासाठी आणि ‘आभार’ मानण्याबाबत लोकांनी विवेक बाळगावा म्हणून ‘भार’ – ‘आभार’ या शब्दांची कोटी करीत लेखिकांनी ‘आभारनियमन’ हा शब्द घडवला आणि त्यावरून पाठाचे शीर्षक तयार केले आहे.

उपक्रम:

प्रश्न 1.
दैनंदिन व्यवहारात शब्दांच्या रचनेमुळे निर्माण होणाऱ्या विनोदाची उदाहरणे शोधा व वर्गात त्यांचे सादरीकरण करा.

भाषाभ्यास:

अक्षरगणवृत्ते यापूर्वी आपण पाहिली आहेत. आता आपण काही मात्रावृत्तांचा परिचय करून घेऊया.

1. दिंडी: पहिल्या चरणात 9, दुसऱ्या चरणात 10 मात्रा असतात. तेही 3-2-2-2, 3-3-2-2 असे मात्रागणांचे गट पडतात. ‘दिंडी’ हे मराठीतील जुने वृत्त आहे.
उदा., घोष होता ग्यानबा तुकाराम
राऊळाची ही वाट सखाराम
करी भक्ती चित्तात नृत्यलीला
पहा दिंडी चालली पंढरीला
12 22 212 2122
= 9 = 10

2. आर्या: आर्या हे देखील जुने वृत्त आहे. मोरोपंतांच्या आर्या प्रसिद्ध आहेत. आर्या वृत्तात 30 मात्रा असून 12+18 असे गट पडतात.
उदा., सुश्लोक वामनाचा अभंगवाणी प्रसिद्ध तुकयाची
ओवी ज्ञानेशाची किंवा आर्या मयूरपंताची
22 2222 22 22 121222
= 12 = 18
चार चरण असतील तर पहिल्या आणि तिसऱ्या चरणात 12 मात्रा; दुसऱ्या आणि चौथ्या चरणात 18 मात्रा असतात.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 13 थोडं ‘आ’ भारनियमन करूया Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
चूक की बरोबर ते लिहा:
1. आभार अनेकदा कृत्रिम झाल्याने खोटे वाटू लागतात.
उत्तर:
1. बरोबर.

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
रोजच्या व्यवहारात आभाराचे अति झालेले प्रकार:
1. क्षुल्लक कारणांसाठी ……………………
2. नुकतं बोलायला लागलेल्या मुलालाही ………………………..
उत्तर:
1. क्षुल्लक कारणांसाठी माणसे एकमेकांचे आभार मानताना दिसतात.
2. नुकतं बोलायला लागलेल्या मुलालाही ‘बँक्स-र्थंक्यू’ वगैरे बोलायला शिकवतात.

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
संकल्पना स्पष्ट करा:
1. आभारबाज.
उत्तर:
1. लहानमोठ्या सर्व कारणांसाठी, अगदी क्षुल्लक कारणांसाठीसुद्धा, सतत आभार मानण्याची चटक लागलेली व्यक्ती म्हणजे ‘आभारबाज’ होय.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
अजूनही तयार न झालेली आभाराची कार्डे:
1. ………………………………..
2. ………………………………..
उत्तर:
अजूनही तयार न झालेली आभाराची कार्डे :
1. जन्मल्या जन्मल्या आई-बापांचे आभार मानणारे कार्ड.
2. मरण पावल्यावर खालून वेळच्या वेळी वर पोहोचवणाऱ्यांचे आभार मानणारे कार्ड.

प्रश्न 2.
का ते लिहा:
1. अलीकडच्या लहान मुलाच्या खात्यावर ‘मॅनरलेसपणा’ रुजू होणार नाही.
2. आभार मानणे दिवसेंदिवस कृत्रिम होत आहे.
उत्तर:
1. अलीकडच्या लहान मुलाच्या खात्यावर ‘मॅनरलेसपणा’ रुजू होणार नाही; कारण अगदी लहानपणापासून शिकवल्याप्रमाणे तो वेळच्या वेळी सर्वांचे न विसरता आभार मानतो.
2. आभार मानणे दिवसेंदिवस कृत्रिम होत आहे; कारण सर्व नात्यांना, सर्व निमित्तांना लागू होतील अशी छापील कार्डे सर्रास वापरली जातील. आभाराचे छापील कार्ड हाच कृत्रिमतेचा नमुना आहे.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
शुभेच्छा कार्डे, आभार कार्डे, अभिनंदन कार्डे इत्यादींबद्दल तुमचे मत लिहा.
उत्तर:
शुभेच्छा कार्डे आकर्षक रितीने छापलेली असतात. कागद छान असतो. एकूण मांडणी सुरेख असते. शब्दांची रचनाही लक्षवेधक असते. पण तरीही मला मात्र ही कार्डे परकी परकी वाटत राहतात. याचे महत्त्वाचे कारण हे की ते शब्द माझे नसतात. त्यामुळे त्यांतून व्यक्त होणारी भावना मला माझी वाटत नाही. मला माझ्या आईबद्दल, बाबांबद्दल, माझ्या ताईबद्दल जे वाटते, ते त्या शब्दांत नसतेच. माझ्या माणसांशी असलेले माझे संबंध मलाच माहीत आहेत. कोणत्या गोष्टी आमच्यामध्ये महत्त्वाच्या आहेत, हे मलाच माहीत आहे. मला माझ्या ताईने पहिल्यांदा सायकल शिकवली.

मी तिच्याकडून फक्त सायकल चालवायला नाही शिकलो. मला आत्मविश्वास मिळाला. रस्त्यावर मागून-पुढून जाणाऱ्या गाड्या, मोटरसायकली, सायकली, रस्त्यावरून वाकडेतिकडे चालणारे लोक, रस्त्यावरील खड्डे या सगळ्यांना चुकवून सायकल चालवताना मनात जे काही चालते, ते शब्दांत सांगता येणार नाही. ताईशी बोलताना, ताईबद्दल बोलताना, माझ्या दृष्टीने ही गोष्ट महत्त्वाची असते. ती छापील कार्डामध्ये मिळूच शकत नाही. ही छापील कार्डे मला माझी वाटतच नाहीत.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
अर्थ लिहा:
तोंड उघडल्याबद्दल आणि योग्य वेळी ते बंद केल्याबद्दल धन्यवाद.
उत्तर:
अनेकांना आपली छबी दूरचित्रवाणीवर दिसते, यातच धन्यता वाटत असते. संबंधित क्षेत्रात या लोकांचे काही योगदान नसते किंवा त्या क्षेत्राचा काही अभ्यासही नसतो. त्यामुळे दूरचित्रवाणीवरील कार्यक्रमात या लोकांना काही मौलिक विचार मांडता येत नाहीत. ते तोंड मिटून गप्प बसतात. काहीजण अकारण बडबड करून प्रेक्षकांचा वेळ वाया घालवतात. या दोघांवरही टीका करण्यासाठी लेखिका ‘तोंड उघडल्याबद्दल व योग्य वेळी ते बंद केल्याबद्दल’ त्यांना धन्यवाद देतात.

प्रश्न 2.
का ते लिहा:
1. नटवणाऱ्यांचे व नटवल्यामुळे ते सुंदर दिसत होते, असे मानणाऱ्यांचे आभार.
2. ज्यांनी किमान तीस सेकंद आमचा चॅनेल पाहिला त्यांना कोटी कोटी प्रणाम.
उत्तर:
1. दूरचित्रवाणीवरील काही कार्यक्रमांत सूत्रसंचालकांची गरज असते. संपूर्ण कार्यक्रम प्रवाहीपणे सुरळीत पार पाडणे हे सूत्रसंचालकांचे काम असते. पण अनेक सूत्रसंचालकांना स्वत:च्या नटण्यात जास्त रस असतो. मेकअपमनही त्यांना नटवण्यात गढून जातो. इतर अनेक जण सूत्रसंचालकांच्या कामापेक्षा त्यांच्या सुंदर दिसण्याचेच कौतुक अधिक करतात. लोकांच्या या हास्यास्पद वृत्तीची खिल्ली उडवण्यासाठी लेखिकांनी सूत्रसंचालकांना नटवणाऱ्यांचे व नटल्यामुळे ते सुंदर दिसत होते असे मानणाऱ्यांचे आभार मानले आहेत.

2. दूरचित्रवाणीवरील बहुतांश कार्यक्रम निर्बुद्ध असतात. त्यांत मध्ये मध्ये जाहिरातींचा धुमाकूळ असतो. त्यामुळे प्रेक्षक कोणताही कार्यक्रम मनापासून सलग पाहत नाहीत. जाहिराती व प्रायोजक मिळवण्यासाठी आपली वाहिनी लोकप्रिय आहे, हे दाखवण्याची वाहिन्यावाल्यांची धडपड चालू असते. वाहिन्यावाल्यांचा हा केविलवाणेपणा दाखवून देण्यासाठी, प्रेक्षकांना कोटी कोटी प्रणाम केले जातात, असे लेखिका म्हणतात.

कृती 2 : (आकलन)

प्रश्न 1.
पुढील वाक्याच्या आधारे लेखिका कशावर टीका करतात, ते लिहा:
आजच्या दिवसभरात ज्यांनी ज्यांनी मुलाखती दिल्या आणि हुकमी ‘मागे वळून पाहिलं’ त्यांचे आम्ही ऋणी आहोत. त्यांच्या दुखऱ्या मानांचे शतशः आभार.
उत्तर:
साधारणपणे वेगवेगळ्या क्षेत्रांत महत्त्वपूर्ण कामगिरी करणाऱ्यांच्या मुलाखती प्रसारित करण्यामागे त्यांच्या अनुभवाचा फायदा इतरांना मिळावा, ही अपेक्षा असते. हे मुलाखतदाते विशिष्ट शब्दप्रयोग करतात. त्यांपैकी एक असा : ‘इतक्या वर्षांनी आता मागे वळून पाहताना.’ दूरचित्रवाणीवर येणाऱ्या बऱ्याच मुलाखतदात्यांकडे सांगण्यासारखे काहीही नसते. पण मुलाखतीची ऐट दाखवण्यासाठी ‘मागे वळून पाहताना’ यांसारखे शब्दप्रयोग ते हमखास करतात. त्यांची खिल्ली उडवण्यासाठी लेखिका वरील वाक्य लिहितात.

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
दूरचित्रवाणीच्या विविध वाहिन्यांवरील कार्यक्रमांविषयी तुमचे मत लिहा.
उत्तर:
दूरचित्रवाणीवरचे बहुतेक कार्यक्रम मनोरंजनाचे असतात. प्रायोजक व जाहिराती मिळवण्यासाठी प्रेक्षकसंख्या जास्त असावी लागते. म्हणून मग हे कार्यक्रम लोकप्रिय करण्याचा प्रयत्न होतो. त्यातून लोकानुनय केला जातो. साहजिकच पारंपरिक विचारांची चिकित्सा नसते. उलट त्यांचा प्रसारच केला जातो. तसेच, देवदेवतांच्या, बुवाबापूंच्या कार्यक्रमांची रेलचेल असते. चमत्कार दृश्यांची त्यात भर पडते. त्यामुळे अंधश्रद्धा बळकट होतात. वाहिनी लोकप्रिय करण्याच्या नादात अनिष्ट वृत्ती वाढीला लागत आहेत. हे सर्वच वाहिन्यांबाबत घडत आहे. हे भयंकर आहे. समाजाच्या सांस्कृतिक आरोग्याच्या दृष्टीने ही परिस्थिती धोक्याची आहे.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढील घटनांचे परिणाम लिहा:

घटना	परिणाम
1. ऑपरेशनच्या गुंगीमधून नुकता नुकता बाहेर येणारा रुग्ण डॉक्टरांचा हात घट्ट धरतो.
2. खूप जवळच्या माणसाचे आभार मानायची वेळ येते, तेव्हा ‘यात नव्याने काय सांगायचं?’ असे मनात येतं.

उत्तर:

घटना	परिणाम
1. ऑपरेशनच्या गुंगीमधून नुकता नुकता बाहेर येणारा रुग्ण डॉक्टरांचा हात घट्ट धरतो.	स्पर्शातून कृतज्ञता व्यक्त होते.
2. खूप जवळच्या माणसाचे आभार मानायची वेळ येते, तेव्हा ‘यात नव्याने काय सांगायचं?’ असे मनात येतं.	आभाराच्या शब्दांतली ताकद निघून जाते.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यात लेखिकांनी मांडलेल्या विचाराबाबत तुमचे मत लिहा.
उत्तर:
‘बैंक्यू/सॉरी’चा खूपच अतिरेक झाला आहे, यात शंकाच नाही. अनेकजण उठताबसता ‘बैंक्यू’ म्हणतात. लेखिकांच्या या मताशी मी पूर्ण सहमत आहे. तरीही मी थोडीशी जोड देऊ इच्छितो. बैंक्यूचा वापर केव्हा घडतो? जेव्हा व्यक्तींमधले संबंध औपचारिक असतात तेव्हा. औपचारिक संबंध नसतात, तेव्हा आईबाबा-मुले, मित्रमैत्रिणी यांच्यात उपचार नसतो. प्रेमाचा हक्क असतो. आम्हां मित्रांमध्ये असेच घडते. आम्ही प्रेमाने एकमेकांना काही देतो आणि हक्काने हवे ते मागून घेतो. अशा वेळी प्रेमाचा जोर जास्त असतो.

पण सार्वजनिक ठिकाणी मात्र उपचार पाळलेच पाहिजेत. बसमध्ये एखादयाच्या पायावर आपला पाय पडला, तर विनाविलंब ‘सॉरी’ म्हटलेच पाहिजे. आपण समोरच्या माणसाच्या वेदनेकडे सहानुभूतीने पाहतो, हे अशा वेळी सिद्ध होते. आपण बेदरकार नाही, हेही सिद्ध होते. लेखिका म्हणतात तसा अतिरेक करूच नये, हे खरे आहे. पण तारतम्याने या सॉरी/बैंक्यूचा वापर केला पाहिजे, असे मला वाटते.

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
चूक की बरोबर ते ओळखा:
1. अंतिम उत्पादन, कलाकृती उत्तम व्हायला हवी असेल, तर आर्थिक लाभ ज्याचा जास्त, त्याने जास्त निष्ठेने काम केले पाहिजे.
उत्तर:
1. चूक.

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
कोण ते लिहा:

1. ‘आमचा’ सिनेमा, ‘आपलं’ पुस्तक, ‘आमचं’ नाटक असे शब्दप्रयोग करतात.
2. आपली निष्ठा कृतीने सिद्ध करील.
3. “बँक्स फॉर मॅरिंग हं,” असे बोलणारा.

उत्तर:

1. ‘आमचा’ सिनेमा : दिग्दर्शक – नटमंडळी
   1. ‘आपलं’ पुस्तक : लेखक – प्रकाशक
   2. ‘आमचं’ नाटक : लेखक – दिग्दर्शक.
2. लेखक.
3. नवऱ्या मुलाचा मित्र.

प्रश्न 2.
जोडीजोडीने व्यवहार करावे लागणाऱ्या तुम्हाला माहीत असलेल्या दोन जोड्या लिहा.
उत्तर:
1. शिक्षक – विदयार्थी
2. वक्ता – श्रोते.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
‘प्रत्येकाने आपापली भूमिका चोख बजवावी लागते. तो अलिखित नियम असतो,’ या विधानावर तुमचे मत लिहा.
उत्तर:
जोडीजोडीने व्यवहार कराव्या लागणाऱ्या काहीजणांबद्दल लेखिकांचे हे मत आहे. जोडीतील दोघांपैकी एकाकडे व्यवहाराची सूत्रे असतात. अनेकदा ही सूत्रे ज्याच्याकडे अधिक घट्ट असतात, त्याच व्यक्तीला व्यवहाराचे फायदे अधिक असतात. हे सर्व खरे आहे. पण म्हणून जास्त फायदा असलेल्यानेच जास्त कष्ट घेऊन व जास्त निष्ठेने काम केले पाहिजे, असा नियम करता येणार नाही. असे केल्यास दोघांनाही तोटाच होईल. कोणी एकाने दुर्लक्ष केल्यास अंतिम फळ उत्तम असणार नाही. त्याचा तोटा दोघांनाही भोगावा लागेल.

नावाडी पैसे घेऊन लोकांना नदीपार करतो. नाव मध्यावर गेल्यावर दुर्दैवाने नावाड्याचा हात लचकला आणि त्याला होडी वल्हवता आली नाही तर? नावाड्याने पैसे घेतले आहेत. आम्ही त्याला मदत करणार नाही, अशी प्रवाशांनी भूमिका घेतली, तर प्रवाशांचा जीव धोक्यात येऊ शकतो. म्हणून दोघांनीही जास्तीत जास्त निष्ठेने काम केले पाहिजे; तरच अंतिम फळ उत्तम होईल. त्याचा दोघांनाही फायदा होईल.

उतारा क्र. 6

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
काय घडते ते पाठाच्या आधारे लिहून वाक्य पूर्ण करा:
1. कामाच्या मोबदल्यात पैसे देत असल्यास …………………
उत्तर:
1. कामाच्या मोबदल्यात पैसे देत असल्यास लोक आभाराची काटकसर करतात.

प्रश्न 2.
पुढील सेवादात्यांचे दुर्गुण लिहा:
1. प्लंबर, इलेक्ट्रिशियन मंडळी.
2. इस्त्रीवाला.
उत्तर:
1. प्लंबर, इलेक्ट्रिशियन मंडळी सांगितलेल्या वेळेला घरी काम करायला येत नाहीत आणि जुने काम करताना नवीन काम निर्माण करून ठेवतात.
2. इस्त्रीवाला दिलेल्या तारखेला कपडे आणून देत नाही.

कृती 2 : (आकलन)

प्रश्न 1.
ठरलेल्या वेळी काम न करणाऱ्या तुम्हाला माहीत असलेल्या चार सेवादात्यांची नावे लिहा.
उत्तर:
वेळेवर काम न करणारे सेवादाते : गवंडी, सुतार, रंगारी, शिंपी.

प्रश्न 2.
लेखिकांनी सांगितलेली विविध सेवादात्यांची वृत्ती सांगा.
उत्तर:
विविध सेवादात्यांचा सर्वांत मोठा दुर्गुण म्हणजे ते कधीच ठरलेल्या वेळी येत नाहीत. दुसरे म्हणजे ते प्रामाणिकपणे काम करीत नाहीत. ते काम करून गेल्यावर काम चोख झाले असेल, अशी मनाला खात्री वाटत नाही. विविध सेवादात्यांची ही वृत्ती लेखिकांनी या उताऱ्यात अधोरेखित केली आहे.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यात लेखिकांनी सांगितलेले सामाजिक व्यंग स्पष्ट करून सांगा.
उत्तर:
या उताऱ्यात काही सेवादात्यांच्या उणिवा लेखिकांनी सांगितल्या आहेत. ते ठरवलेल्या वेळी कामावर येत नाहीत. निष्ठापूर्वक काम करीत नाहीत. आपण आपले काम चोख करावे, अशी त्यांची इच्छाच नसते. त्यामुळे त्यांनी केलेले काम परिपूर्ण असेल, अशी खात्री बाळगता येत नाही. लेखिकांनी सांगितलेल्या या उणिवा आपल्या समाजाच्या प्रत्येक व्यक्तीत दिसून येतात. कोणत्याही पदावरील कोणाही व्यक्तीला उत्तम काम करण्याची इच्छाच नसते. विदयार्थी उत्तम काम करू इच्छित नाहीत. दुकानदार उत्तम वस्तू वाजवी भावात ग्राहकाला देण्याची इच्छा बाळगत नाही.

शासकीय कार्यालयातील कर्मचारी लोकांची कामे रेंगाळत ठेवण्यात धन्यता मानतात. अशी शेकडो उदाहरणे देता येतील. या वृत्तीमुळे समाजात पार पडणारे कोणतेही कार्य परिपूर्ण होत नाही. रस्ता बांधला की अल्पावधीतच खड्डे पडतात. घरे कोसळतात. या सर्व बाबींमुळे आपल्या समाजातील बांधवांचेच नुकसान होते. त्यांना उत्तम दर्जाच्या सेवा वा वस्तू मिळत नाहीत. साहजिकच त्यांना उत्तम दर्जाचे जीवन जगण्याची संधी मिळत नाही. आपली वृत्ती सुधारली तर देश सुधारेल, असे मला वाटते. कारण हे सर्व देशाच्या प्रगतीशी निगडित आहे.

उतारा क्र. 7

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
पाठाच्या आधारे गाळलेल्या जागा भरून विधाने पूर्ण करा:
1. अपत्याची टॉन्सिलची शस्त्रक्रिया किरकोळ होती; पण आईच्या ———
2. ऑपरेशननंतर त्रासाचा लोप व्हावा, म्हणून
उत्तर:
1. अपत्याची टॉन्सिलची शस्त्रक्रिया किरकोळ होती; पण आईच्या दृष्टीने मुलाचं कोणतंच ऑपरेशन किरकोळ असूच शकत नाही..
2. ऑपरेशननंतर त्रासाचा लोप व्हावा, म्हणून पंधरा दिवस आइस्क्रीमचा उतारा होता.

प्रश्न 2.
काय केले ते लिहा:
1. डॉक्टरांचे आभार मानण्यासाठी ………………………
2. पाहुणचार करण्यासाठी आल्यागेलेल्या सर्वांना ………………
उत्तर:
1. डॉक्टरांचे आभार मानण्यासाठी लेखिकांनी त्यांना फोन केला.
2. पाहुणचार करण्यासाठी आल्यागेलेल्या सर्वांना आइस्क्रीम दिले जात होते.

कृती 2 : (आकलन)

प्रश्न 1.
पुढील घटनांचे परिणाम लिहा:
1. घटना : लेखिकांनी डॉक्टरांना फोन केला.
परिणाम : ……………………………
2. घटना : डॉक्टरांनी फोनबद्दल आपली नाराजी व्यक्त केली.
परिणाम : ……………………………..
उत्तर:
1. परिणाम: काहीतरी विपरीत घडले असावे, या कल्पनेने डॉक्टर हादरले.
2. परिणाम: लेखिकांना डॉक्टरांचा राग न येता त्यांची दया आली.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
‘परि तू जागा चुकलासी’ या उक्तीबद्दल तुमचे मत लिहा.
उत्तर:
आभार व्यक्त करणे वा आदर दाखवणे यांसारख्या उपचारांचा अतिरेक होऊ लागला आहे. असे उपचार पाळणे हे सुसंस्कृतपणाचे लक्षण मानले जाऊ लागल्यामुळे विपरीत प्रसंग उद्भवू लागले आहेत. आभार कोणाचे मानावेत, कधी मानावेत व कसे मानावेत यांबाबत कोणता धरबंदच राहिलेला नाही. ही एक भ्रामक गरज निर्माण झालेली आहे.

व्यापाऱ्यांचे याकडे लक्ष न जाते, तर नवलच! यातून शुभेच्छांची कृत्रिम कार्डे निर्माण झाली आहेत. काहीही करून आभार मानायचेच, असा अट्टहास बाळगल्याने हास्यास्पद प्रसंग घडताना दिसतात. लग्न होत असताना अभिनंदन करायचे सोडून आभार मानण्याचा प्रसंग पाठात आलेलाच आहे. म्हणून आभार कोणाचे मानू नयेत, केव्हा मानू नयेत, तसेच, ते कसे मानू नयेत याचे भान बाळगणे गरजेचे बनले आहे. कारण ‘परी तू जागा चुकलासी’ असे सांगण्याचे प्रसंग वारंवार येऊ लागले आहेत.

भाषाभ्यास:

(अ) अव्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
जोड्या लावा:

सामासिक शब्द	उत्तरे	विग्रह
1. महात्मा	– महान असा आत्मा	वादळ, वारा वगैरे
2. सप्तसिंधू	– सात समुद्रांचा समूह	दक्षिण आणि उत्तर
3. दक्षिणोत्तर	– दक्षिण आणि उत्तर	महान असा आत्मा
4. दहाबारा	– दहा किंवा बारा	सात समुद्रांचा समूह
5. वादळवारा	– वादळ, वारा वगैरे	दहा किंवा बारा

2. शब्दसिद्धी:

प्रश्न 1.
‘सु’ उपसर्ग असलेले चार शब्द लिहा.
उत्तर:

1. सुविचार
2. सुवचन
3. सुसंस्कृत
4. सुगंध.

3. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचे अर्थ सांगून वाक्यांत उपयोग करा:

1. चोख असणे
2. चारीमुंड्या चीत करणे
3. काटकसर करणे.

उत्तर:

1. चोख असणे – अर्थ : व्यवस्थित असणे.
   वाक्य: गावामध्ये ग्रामपंचायतीचा कारभार अगदी चोख होता.
2. चारीमुंड्या चीत करणे – अर्थ : पराभव करणे.
   वाक्य: कारगिल युद्धात भारतीय जवानांनी शत्रूला चारीमुंड्या चीत केले.
3. काटकसर करणे – अर्थ : बचत करणे.
   वाक्य: महिन्याच्या पगारातून कामगारांनी थोडी काटकसर करणे आवश्यक आहे.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
विरुद्धार्थी शब्द लिहा:

1. थोडे
2. घट्ट
3. लवकर
4. विशिष्ट.

उत्तर:

1. थोडे × जास्त
2. घट्ट × सैल
3. लवकर × उशिरा
4. विशिष्ट × सामान्य.

प्रश्न 2.
वचन ओळखा:

1. गाणी
2. विमाने
3. घड्याळ
4. वादय.

उत्तर:

1. गाणी – अनेकवचन
2. विमाने – अनेकवचन
3. घड्याळ – एकवचन
4. वादय – एकवचन.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:

1. निरिक्षण, निरीक्षण, निरीकराण, निरीक्षन.
2. अलिखीत, अलिखित, अलीखित, अलीखीत.
3. क्षुल्लक, क्षुलक, र्लक्क, क्षुल्लक.
4. सूसंस्कृत, सुसंस्कृत, सुसंस्कृत, सुसंक्त.
5. उत्पादन, ऊत्पादन, उप्तादन, उत्पादण.
6. शिष्ठाचार, शीष्टाचार, शिष्टाचार, शीष्ठाचार.

उत्तर:

1. निरीक्षण
2. अलिखित
3. क्षुल्लक
4. सुसंस्कृत
5. उत्पादन
6. शिष्टाचार.

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यांत योग्य विरामचिन्हे घालून वाक्ये पुन्हा लिहा:
1. आमच्या पिढीवर गोऱ्यांचे शिष्टाचार या गोष्टीची अंमळ जास्तच मुद्रा उमटली
2. लेखक आणि प्रकाशक गायक वादक कलाकार रसिक दिग्दर्शक आणि नटमंडळी ही जोडीजोडीने काम करीत असतात
उत्तर:
1. आमच्या पिढीवर ‘गोऱ्यांचे शिष्टाचार’ या गोष्टीची अंमळ जास्तच मुद्रा उमटली.
2. लेखक आणि प्रकाशक, गायक-वादक, कलाकार-रसिक, दिग्दर्शक आणि नटमंडळी ही जोडीजोडीने काम करीत असतात.

4. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द दया:
1. Humanism
2. Honorable.
उत्तर:
1. मानवतावाद
2. माननीय.

थोडं ‘आ’ भारनियमन करूया Summary in Marathi

प्रस्तावना:

मराठीतील एक लोकप्रिय व अग्रेसर विनोदी लेखिका. त्यांच्या लेखनाच्या केंद्रस्थानी मध्यमवर्गीय मराठी माणूस प्राधान्याने असतो. त्या मध्यमवर्गीय माणसाच्या जीवनातील विसंगती खेळकरपणे चित्रित करतात. त्यांची लेखनशैली प्रसन्न आहे. त्यांचा भर मुख्यतः वक्रोक्तीवर असतो. त्यांचा विनोद कधीही बोचरा, जखम करणारा नसतो. त्या हसतखेळत विसंगती दाखवून देतात. सामाजिक व्यंगांकडेही त्यांचे खास लक्ष असते. त्यांचे लेखन हे नेहमीच आधुनिकतेचा पुरस्कार करणारे असते. पारंपरिक मागासलेल्या विचारांना त्या सहजगत्या हास्यविषय करतात. अतिरेकी आधुनिक विचारांवरही त्या हसतखेळत टीका करतात. त्यांचे लेखन सदैव वाचनीय ठरले आहे.

मंगला गोडबोले यांनी गंभीर स्वरूपाचे कथालेखन व कादंबरीलेखनही केले आहे. आपण आधुनिक बनत जाण्याच्या प्रयत्नात पाश्चिमात्य लोकांचे आंधळेपणाने अनुकरण करतो आणि हास्यास्पद बनत जातो, ही वस्तुस्थिती प्रस्तुत पाठात लेखिकांनी अत्यंत खेळकरपणे दाखवून दिली आहे. आपण इंग्रजांच्या अनुकरणातून ‘बँक्यू’, ‘प्लीज’ हे शब्द उचलले आहेत आणि त्यांचा अतिरेकी वापर करतो. ‘बँक यू’, ‘बँक्यू’ (I thank you) हे पूर्ण वाक्य आहे. हे लक्षात न घेता ‘बैंक्यू = आभार’ असा अर्थ घेऊन ‘तू कसली ग माझी बँक्यू?’ ‘मीच तुझी बँक्यू’ असले हास्यास्पद शब्दप्रयोग आपण करतो. आपल्या समाजातील या विसंगतीचे मजेदार दर्शन या पाठात लेखिका घडवतात आणि आपल्याला अंतर्मुख करतात.

शब्दार्थ:

1. धसमुसळे – दांडगे, अडाणी, पशुतुल्य, रानवट, वाटेल तसे , वागणारा.
2. सुमार – मर्यादा, अंदाज, सान्निध्य.
3. अस्थानी – चुकीच्या ठिकाणी.
4. आभारबाज – लहानमोठ्या सर्व कारणांसाठी, अगदी क्षुल्लक कारणासाठीसुद्धा, सतत आभार मानण्याची चटक लागलेली व्यक्ती.
5. घाऊक आभार – सर्व व्यक्तींचे सर्व बाबींसाठी एकदाच एकगठ्ठा आभार मानणे.
6. तुडुंब – काठोकाठ, भरपूर.
7. दिखाऊगिरी – इतरांसमोर अकारण जाहीर व सातत्याने प्रदर्शन करीत राहणे.
8. बासन – एखादी वस्तू गुंडाळून ठेवण्याचा कापडाचा खास तुकडा.
9. शब्दबंबाळ – (समुदाय, मोठा नाद) शब्दांचा समुदाय ज्यात जाणवतो ते, आशयापेक्षा ज्यात केवळ शब्दच जाणवतात (शब्दांचा
10. फक्त आवाज जाणवतो) ते लेखन. सणसणीत – उष्ण, तीव्र, जबर, भक्कम.
11. उणावून – कमी होऊन.
12. कटाक्ष – डोळ्यांच्या कोपऱ्यातून टाकलेली एक नजर.
13. प्रौढ – पोक्त, निष्णात, धीट (तरुण व वृद्ध यांच्या मधल्या अवस्थेत असलेली व्यक्ती).
14. वट्ट – चोख, एकत्रित, एकूण.
15. अश्राप – गरीब, बिचारे, सभ्य, निर्व्याज, अभिजात.

टिपा:

1. निष्ठा – (नि + स्था) निग्रहाने एका जागी स्थिर राहणे. काही माणसे आयुष्यभर एखादा विचार, मूल्य उराशी बाळगतात; त्यापासून ढळत नाहीत. यावरून त्या विचाराला, मूल्याला, दृष्टिकोनाला त्या माणसांची निष्ठा म्हणतात.

2. मॅनरलेसपणा – मॅनर (manner = शिष्टाचार). मॅनरलेस म्हणजे शिष्टाचार न पाळणारा, असंस्कृत, उद्धट. ‘mannerless पणा’ यात इंग्रजी शब्दाला मराठी प्रत्यय जोडलेला आहे. येथे इंग्रजी शब्द वापरण्याची केवळ हौस दिसते. अशा सवयीमुळे धेडगुजरी शब्द तयार होतात.

वाक्प्रचार व त्यांचे अर्थ:

1. मुद्रा उमटणे – ठसा उमटणे, प्रभाव दिसून येणे.
2. जप करणे – एकच बाब पुन्हा पुन्हा बोलणे.
3. गुण गाणे – स्तुती करणे.
4. चारी मुंड्या चीत करणे – पूर्णपणे पराभूत करणे.
5. तोंड उघडणे – थोडे तरी बोलणे, (कधी कधी) नको ते र बोलणे.
6. तोंड बंद करणे – गप्प बसणे.
7. मुखर करणे – शब्दरूप देणे, शब्दांत व्यक्त करणे.
8. दाबून फिया घेणे – मोठ्या प्रमाणात अवास्तव शुल्क आकारणे.
9. आरती ओवाळणे – कौतुक करणे, स्तुती करणे (बहुतेक वेळा अवास्तव).
10. पुष्पहार घालणे – आभार मानणे, कृतज्ञता व्यक्त करणे, स्वागत करणे.

9th Std Marathi Questions And Answers:

• मातीची सावली Class 9 Question Answer
• महाराष्ट्रावरूनी टाक ओवाळून काया (पोवाडा) Class 9 Question Answer
• थोडं ‘आ’ भारनियमन करूया Class 9 Question Answer
• आदर्शवादी मुळगावकर Class 9 Question Answer
• निरोप (कविता) Class 9 Question Answer
• ‘बिग ५’ च्या सहवासात (स्थूलवाचन) Class 9 Question Answer

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 9 मी वाचवतोय Notes, Textbook Exercise Important Questions and Answers.

Class 9 Marathi Aksharbharati Chapter 9 मी वाचवतोय Question Answer Maharashtra Board

मी वाचवतोय Std 9 Marathi Chapter 9 Questions and Answers

1. कोष्टक पूर्ण करा:

प्रश्न 1.
कोष्टक पूर्ण करा:

उत्तर:

पूर्वीचे व्यवसाय	पूर्वीचे खेळ
1. लोहारकाम	1. विटीदांडू
2. कुंभार (मडकी बनवणे)	2. लगोरी
3. भांड्यांना कल्हई करणे	3. आट्यापाट्या

2. आकृती पूर्ण करा:

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

3. सकारण लिहा:

प्रश्न 1.
सकारण लिहा:

उत्तर:

जुन्या गोष्टींपैकी वाचाव्यात अशा वाटणाऱ्या गोष्टी	त्या गोष्टी वाचवण्याची तुमच्या मते कारणे
1. कविता	1. मन समृद्ध होते
2. आई	2. प्रेम, माया, जिव्हाळा लाभतो
3. बोली	3. विचार व्यक्त करता येतात
4. भूमी	4. मूल्यांवर निष्ठा असते

4. कव्यसौंदर्य.

प्रश्न (अ)
तुम्हांला जाणवलेली कवीच्या मनातली खंत स्पष्ट करा.
उत्तर:
जुन्या जमान्यातील काही चांगल्या गोष्टी हरवत व दुरावत चालल्या आहेत, यांची खंत कवीला वाटते. बदलत चाललेल्या समाजातील वास्तव कवीच्या मनाला खटकते. आपण आईला ‘आई’ अशी साद घालत नाही. वासरासाठी गोठ्यात गायही हंबरत नाही. मॉलच्या नवीन झगमगीत संस्कृतीमुळे किराणा व भुसार हरवत चाललेयत. गावगाड्यातील व्यवसाय लोप पावतायत. मुले मातीतले खेळ खेळत नाहीत. कुणी लेखन करीत नाही. मातृभाषेत कुणी या भूमीतली संस्कृती जपत नाही. अशा प्रकारे सांस्कृतिक वैभव नष्ट होण्याची खंत कवीला बोचते आहे.

प्रश्न (आ)
‘शब्द बापुडे केवळ वारा’ या काव्यपंक्तीतील आशयसौंदर्य शब्दबद्ध करा.
उत्तर:
पूर्वीच्या कविता किंवा साहित्य उच्च सांस्कृतिक मूल्य जपणारे होते. जीवनानुभूतीतून आदर्श व प्रेरणा जनमानसाला मिळत होत्या. परंतु आता लिहिणाऱ्या हातातून सकस साहित्यनिर्मिती होत नाही, हे कवीला सांगायचे आहे. जो शब्दपसारा दिसतो तो भावनाशून्य व पोकळ आहे, असे कवीला म्हणायचे आहे. शाश्वत राहणारे अभिजात साहित्य निर्माण होत नाही, याची खंत व्यक्त करताना कवी म्हणतात की, आताचे शब्द केविलवाणे झाले आहेत व ते वाऱ्यावर विरून जात आहेत. आता लिहिल्या जाणाऱ्या शब्दांची नश्वरता व तात्कालिकता कवीला या ओळीतून सांगायची आहे.

प्रश्न (इ)
सामाजिक बदलाबद्दल कवितेतून व्यक्त झालेला विचार स्पष्ट करा.
उत्तर:
पूर्वी गावगाडा होता. नैतिक मूल्ये जपणारी गावची संस्कृती होती. हळूहळू समाज बदलत गेला. शहरे वाढू लागली. सगळ्या वस्तू झगमगीत मॉलमध्ये, सुपरमार्केटमध्ये मिळू लागल्या. त्यामुळे छोटी छोटी किराणा, भुसार मालाची दुकाने हरवून गेली. लोहाराचा भाता बंद पडला. कुंभाराचे चाक फिरायचे थांबले. तांब्या-पितळेच्या भांड्यांचा वापर लयाला गेल्यामुळे कल्हईची झिलई निघून गेली. चुलीची जागा गॅसच्या शेगड्यांनी घेतली. आधुनिक समाजव्यवहारांमुळे मायेची माणसे दुरावली. अशा प्रकारे या कवितेत सामाजिक बदलाविषयी कवीने सांगितले आहे.

5. स्वमत:

प्रश्न (अ)
‘माझी बोली’ या संकल्पनेतून तुम्हांला समजलेला कवीचा दृष्टिकोन स्वभाषेत मांडा.
उत्तर:
‘माझी बोली’ म्हणजे मायबोली किंवा मातृभाषा होय. वेगाने बदलत जाणाऱ्या समाजात जी नवीन पिढी शिकते आहे; त्यांच्यावर शिशुवर्गापासूनच इंग्रजीचे संस्कार होत आहे. पूर्वीचे घरचे मराठमोळे वातावरण झपाट्याने बदलत आहे. आधुनिकीकरणामुळे नवीन पिढीच्या तोंडी इंग्रजी रुळत जाते आहे. आईची जागा ‘मम्मी’ने घेतली आहे. मातृभाषेतून दिले जाणारे शिक्षण हळूहळू मंदावत आहे. मातृभाषा हेच विचार व भावना मांडण्याचे नैसर्गिक माध्यम असते. ते माध्यम बंद पडत चालल्यामुळे कवीने खंत व्यक्त केली आहे. अशा प्रकारे ‘माझी बोली’ या संकल्पनेतून कवींची खेदजनक भावना व्यक्त झाली आहे.

प्रश्न (आ)
‘मॉलच्या अतिक्रमणामुळे छोट्या दुकानदारांना फटका बसतो,’ याबाबत तुमचे मत स्पष्ट करा.
उत्तर:
शहरे वाढली तसतसे लोकांच्या गरजा पुरवणारे ‘मॉल’ वाढले. पूर्वी शहरामध्येसुद्धा छोटे छोटे दुकानदार होते. विशिष्ट प्रकारच्या वस्तू विशिष्ट दुकानांत मिळायच्या. मॉलमध्ये सर्व वस्तूंची दुकाने एकत्र असतात. शिवाय खादयपान सेवेची हॉटेल्स व सिनेमागृहेही असतात. मॉलच्या एकंदर झगमगाटाचे आकर्षण माणसांच्या ठायी निर्माण झाले. महागड्या वस्तू म्हणजे दर्जेदार वस्तू असा गैरसमज फोफावला. त्यातच आकर्षक जाहिरातींची भर पडल्यामुळे लोकांना मॉलचे आकर्षण निर्माण झाले. साहजिकच माणसांचा मॉलमध्ये राबता सुरू झाला आणि त्यांनी छोट्या दुकानांकडे पाठ फिरवली. अर्थात मॉलच्या अतिक्रमणामुळे छोट्या दुकानदारांना फटका बसतो, हे खरे आहे.

उपक्रम:

तुमच्या अवतीभवती घडणाऱ्या सामाजिक बदलांची पुढील मुद्द्यांच्या आधारे नोंद करा व कोष्टक तयार करा:

1. बदल
2. परिणाम
3. तुमचे मत

Marathi Kumarbharati Textbook Std 9 Answers Chapter 9 मी वाचवतोय Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
शब्दजाल पूर्ण करा:

उत्तर:
1. हाकेतून हद्दपार होत आहे.
(1) हंबरायच्या थांबल्या आहेत.
2. लोहाराचा भाता
(1) कुंभाराचा आवा

प्रश्न 3.
चौकटी पूर्ण करा:

उत्तर:

1. (i) किराणा (ii) भुसार
2. रटरटणारी आमटी
3. कल्हईची झिलई
4. आईची बोली
5. बापुडे शब्द
6. परकरी मुली

कृती 3 : (दोन ओळींचा सरळ अर्थ)

प्रश्न 1.
हरवत चाललाय किराणा आणि भुसार सुपर मार्केटच्या झगमगाटात झरझर
उत्तर:
बदलत चाललेल्या परिस्थितीचा आढावा घेताना कवी सतीश काळसेकर म्हणतात की, शहरात मोठमोठे मॉल व सुपर मार्केट निर्माण झाल्यामुळे पूर्वीची किराणामालाची व भुसारीची दुकाने भूतकाळात जमा झाली आहेत.

कृतिपत्रिकेतील प्रश्न 2 (आ) साठी……

प्रश्न 1.
पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:
कविता – मी वाचवतोय.
उत्तर:
मी वाचवतोय.
1. प्रस्तुत कवितेचे कवी/कवयित्री → सतीश काळसेकर.

2. कवितेचा विषय → वेगाने बदलत जाणाऱ्या महानगरीय समाजाचे वास्तव चित्रण हा कवितेचा विषय आहे.

3. कवितेतील दोन शब्दांचे अर्थ →

1. हाक = साद
2. आई = माता
3. विस्तव = आग
4. राख = रक्षा
5. वारा = वात.

4. कवितेतून मिळणारा संदेश → चांगली जुनी संस्कारक्षम मूल्ये हरवू नयेत; आईची बोली पारखी होऊ नये; भौतिक सुखामध्ये नैतिक मूल्यांची पायमल्ली होता कामा नये; हा संदेश प्रस्तुत कविता देते.

5. कवितेची भाषिक वैशिष्ट्ये → जुन्या मूल्यांविषयीची आस्था व नवीन महानगरीय बदलते वास्तव यांतील अंतर्विरोध कवींनी चपखल शब्दांत मांडला आहे. कवितेची भाषा हृदयाला भिडेल अशी थेट व स्पष्टोक्तीपूर्ण आहे. यातील भावनांची आवाहकता प्रशंसनीय आहे. मुक्त गदय शैली आशयाला पूरक आहे. कवितेतील अंतर्गत यमक व सूचक शब्दांची मांडणी आशयाला उठाव देणारी आहे. कवितेचा शेवट परिणामकारक झाल्यामुळे रसिक चिंतनशील होतात.

6. कवितेतून व्यक्त होणारा विचार → यंत्रयुगातील नवीन बदलांमुळे जुनी मूल्ये ढासळत चाललीयत. ती वाचवणे व सुरक्षित ठेवणे गरजेचे आहे.

7. कवितेतील दोन ओळींचा सरळ अर्थ:
हाकेतून हद्दपार होतेय आई
हंबरायच्या थांबल्यायत गोठ्यातल्या गाई
→ बदलत जाणाऱ्या वास्तवामध्ये ममी-डॅडी या परकीय शब्दांमुळे
आईची मायेची हाक आता ऐकू येत नाही. गोठ्यातल्या गाईसुद्धा 3 आता नैसर्गिक हंबरणे विसरत चालल्या आहेत.

8. कविता आवडण्याची वा न आवडण्याची कारणे → जुनी मूल्ये नामशेष होण्याची खंत कवींनी आर्तपणे व तेवढ्याच परखडपणे मांडली आहे. नवीन पिढीचा निरुद्देश चंगळवाद अधोरेखित केला आहे. आई, आईची बोली, भूमी आणि कविता वाचवण्याचा दृढनिश्चय व्यक्त केला आहे. या सर्व कारणांमुळे ही कविता मला खूप आवडली.

कृतिपत्रिकेतील प्रश्न 2 (इ) साठी…

प्रश्न 1.
पुढील ओळीचे रसग्रहण तुमच्या शब्दांत करा:
‘हाकेतून हद्दपार होतेय आई
हंबरायच्या थांबल्यायत गोठ्यातल्या गाई.’
उत्तर:
आशयसौंदर्य: यंत्रवत असलेल्या महानगरीय जीवनात जुनी जीवनमूल्ये नष्ट होत आहेत. क्रय वस्तूंच्या बेगडी झगमगाटात जुनी चूल, जुने खेळ, बोली व संस्कृती यांचा नवीन पिढीला विसर पडत चालला आहे, या वास्तववादी आशयाचे विदारक चित्रण कवी सतीश काळसेकर यांनी ‘मी वाचवतोय’ या कवितेत केले आहे.

काव्यसौंदर्य: बदलत जाणाऱ्या समाजाचे वास्तव शब्दांत चितारताना प्रस्तुत ओळींमध्ये कवी म्हणतात की ‘मम्मी-डॅडी’ या उसन्या परिभाषेमुळे ‘आई’. अशी हाक आता ऐकू येत नाही. जणू ती हाक सीमेबाहेर गेली आहे. गोठ्यातल्या मायेचा वारसा असलेल्या गाईसुद्धा आता नैसर्गिक हंबरणे विसरल्या आहेत. त्या आता आपल्या वासरांसाठी हंबरत नाहीत. म्हणजेच आई-लेकरांचे संबंध मायाममतेचे राहिले नाहीत, ही खंत कवींनी व्यक्त केली आहे. भौतिक सुखामध्ये नैतिक मूल्यांची पायमल्ली होते, याची बोचणी प्रस्तुत ओळींमध्ये स्पष्टपणे दर्शवली आहे.

भाषिक वैशिष्ट्ये: जुन्या मूल्यांविषयीची आस्था व नवीन महानगरीय बदलते वास्तव यांतील अंतर्विरोध कवीने चपखल शब्दांत मांडला आहे. कवितेची भाषा हृदयाला भिडेल अशी थेट व स्पष्टोक्तीपूर्ण आहे. यातील भावनांची आवाहकता प्रशंसनीय आहे. मुक्त गदय शैली आशयाला पूरक आहे. कवितेतील अंतर्गत यमक व सूचक शब्दांची मांडणी आशयाला उठाव देणारी आहे. योग्य परिणामकारकता शब्दाशब्दांत अभिव्यक्त झाल्यामुळे रसिक चिंतनशील होतात.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
पुढील सामासिक शब्दांचे समास ओळखा :

1. सत्यासत्य
2. सप्तसागर
3. पूर्वपश्चिम
4. रक्तचंदन

उत्तर:

1. वैकल्पिक द्वंद्व
2. द्विगू
3. इतरेतर द्वंद्व
4. कर्मधारय.

2. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचे अर्थ सांगून वाक्यात उपयोग करा:
1. दंग असणे
2. दुरावणे.
उत्तर:
1. दंग असणे – अर्थ : मग्न असणे.
वाक्य: जेव्हा बघावे तेव्हा मंदार खेळामध्ये दंग असतो.

2. दुरावणे – अर्थ : लांब जाणे.
वाक्य : परदेशी गेल्यामुळे ममताला आईवडिलांची संगत दुरावली.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
शब्दसमूहाबद्दल एक शब्द लिहा:
1. लिहिता-वाचता येणारा → …………………..
2. लिहिता-वाचता न येणारा → ………………..
उत्तर:
1. साक्षर
2. निरक्षर.

प्रश्न 2.
अनेकवचन लिहा:

1. गाय
2. खेळ
3. कविता
4. सुट्टी.

उत्तर:

1. गाई
2. खेळ
3. कविता
4. सुट्ट्या

प्रश्न 3.
पुढील शब्दांतील अक्षरांपासून दोन अर्थपूर्ण शब्द लिहा:
1. वाचवतोय
2. समाजाचे
उत्तर:
1. चव, वय
2. मास सजा

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:
1. बोलचाली, बोलाचाली, बोलाचालि, बोलचालि.
2. दूरर्दशन, दुरदर्शन, दूर्रदर्शन, दूरदर्शन.
उत्तर:
1. बोलाचाली
2. दूरदर्शन.

3. पारिभाषिक शब्द:

प्रश्न 1.
मराठी प्रतिशब्द लिहा:

1. Lyric
2. Magazine
3. Category
4. Index

उत्तर:

1. भावगीत
2. मासिक-पत्रिका
3. प्रवर्ग
4. अनुक्रमणिका.

मी वाचवतोय Summary in Marathi

कवितेचा आशय:

समाजाचे वास्तव वेगाने बदलत चालले आहे. जुने व्यवसाय, जुने खेळ काळाच्या पडद्याआड गेले आहेत. यंत्रयुगाच्या आधुनिक झगमगाटात आईची बोली कोणी बोलत नाही. नवीन पिढी यांत्रिक वस्तूंच्या आहारी गेली आहे. या सर्व बदलांची खंत या कवितेत कवींनी व्यक्त केली आहे. जुन्या काही चांगल्या गोष्टी या बदलातून वाचवणे गरजेचे झाले आहे.

शब्दार्थ:

1. वाचवतोय – बचाव करतोय.
2. मुकाट – शांतपणे, निमूट.
3. विस्तव – निखारे.
4. धग – ऊब.
5. रटरटणारी – शिजणारी.
6. सहित – सोबत, बरोबर, संगती.
7. बोलाचाली – संभाषण.
8. बोली – भाषा.
9. दंगा – (इथे अर्थ) गोंधळ, आरडाओरडा.
10. परकऱ्या – परकर घालणाऱ्या (मुली).
11. लिहिते हात – लेखनाचा सराव.
12. बापुडे – गरीब, केविलवाणे.
13. भूमी – धरती.

टिपा:

1. हंबरणे – गाईचा आवाज (ओरडणे).
2. किराणा-भुसार – अन्नधान्याच्या वस्तू.
3. सुपर मार्केट – अन्नधान्य, भाजीपाला, खाण्याचे तयार पदार्थ, तसेच अन्य अगणित वस्तू एका छपराखाली मिळतील असे, भव्य दुकान ; मोठमोठाले मॉल.
4. लोहाराचा भाता – लोखंडी वस्तू बनवण्यासाठी लोहार वापरत असलेल्या भट्टीला वारा घालण्याचे साधन.
5. कुंभाराचा आवा – ओल्या मातीच्या गोळ्याला मडक्यांचा आकार देण्यासाठी कुंभार वापरत असलेले लाकडी गोल चाक.
6. गावगाडा – गावची जुनी संस्कृती व्यवहार.
7. कल्हईची झिलई – तांब्या-पितळेची भांडी कळकू नयेत म्हणून कथिलाची तार तापवून त्याच्या रसापासून तयार केलेलामुलामा.
8. आईची बोली – मातृभाषा.
9. विटीदांडू – लाकडाची छोटी विटी व मोठा दांडू यांचा जुना मैदानी खेळ.
10. लगोऱ्या – दगडांच्या चकत्या एकावर एक रचून चेंडूने फोडण्याचा जुना मैदानी खेळ.
11. आट्यापाट्या – जमिनीवर आडव्या-उभ्या रेघा आखून खेळता येणारा सांघिक खेळ.
12. पिंगा – मान गोल गोल फिरवून घुमण्याचा खेळ.
13. क्राइम-थ्रिलर – गुन्हेगारी जीवनाचे चित्रण करणाऱ्या दूरदर्शनवरील मालिका.

वाक्प्रचार व त्यांचे अर्थ:

1. हद्दपार होणे – सीमेबाहेर सोडणे (जीवनातून निघून जाणे).
2. दुरावत जाणे – लांब जाणे.
3. दंग असणे – गुंगणे, मग्न असणे.
4. विरून जाणे – विरघळून जाणे, नाहीसे होणे.

कवितेचा भावार्थ:

बदलत जाणाऱ्या समाजाचे वास्तव शब्दांत चितारताना कवी म्हणतात – ‘आई’ अशी हाक आता ऐकू येत नाही. जणू ती सीमेबाहेर गेली आहे. गोठ्यातल्या गाईसुद्धा आता हंबरणे विसरल्या आहेत. त्या आता वासरासाठी हंबरत नाहीत. (आई-लेकरांचे संबंध मायेचे राहिले नाहीत.)

मोठमोठे मॉल्स व सुपर मार्केट निर्माण झाल्यामुळे त्यांच्या झगमगाटी दुनियेत आता पूर्वीच्या किराणा व भुसाराची दुकाने हरवून जात आहेत. पूर्वीच्या गावच्या संस्कृतीत (गावगाड्यात) असलेले (जुने व्यावसायिक) लोहार, कुंभार नि त्यांचे भाते व चाके गावगाड्याबरोबरच निमूटपणे नाहीशी झाली आहेत. पूर्वीच्या भांड्यांची कल्हईची झिलई विस्तवासोबत निघून गेली आहे. चुलीच्या जाळावर शिजत असलेली आमटी राखेसकट दूर गेली. आता धुराशिवाय ती गॅस शेगडीवर शिजत असलेली दिसते.संभाषणातून-संवादातून हल्ली (माझी) मातृभाषा (आईची बोली) निघून चालली आहे.

आता मुले सुट्ट्यांमध्ये पूर्वीसारखी विटीदांडू आणि लगोरीचे खेळ खेळत नाहीत. त्यांचा गिल्ला आता थांबलाय. आता आट्यापाट्या किंवा पिंगा असले जुने खेळ नाहीसे झाले आहेत. परकर घालणाऱ्या लहान मुली आता पूर्वीचे मातीतले खेळ खेळताना दिसत नाहीत. आता मुले दूरदर्शनच्या स्पोर्ट चॅनेलवर क्रिकेटची मॅच पाहण्यात रमून जातात किंवा गुन्हेगारी विश्वातील मालिका बघत राहतात. आता कुणाकडूनही पूर्वीसारख्या गोष्टी लिहिल्या जात नाहीत. लिहिणाऱ्या हातांचा सराव थांबलाय. शब्द केविलवाणे होऊन फक्त वाऱ्यासारखे विरून जातात.

अशा या बदलत्या भयानक वास्तवात मी माझी कविता सांभाळतोय आणि कवितेसोबतच माझी आई, माझी भाषा नि माझी भूमी यांचा { मी या आधुनिक वास्तवापासून बचाव करतो आहे.

9th Std Marathi Questions And Answers:

• या झोपडीत माझ्या (कविता) Class 9 Question Answer
• दुपार Class 9 Question Answer
• अभियंत्यांचे दैवत-डॉ. विश्वेश्वरय्या Class 9 Question Answer
• मी वाचवतोय (कविता) Class 9 Question Answer
• यंत्रांनी केलं बंड Class 9 Question Answer
• इंग्लंडचा हिवाळा (स्थूलवाचन) Class 9 Question Answer

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 14 आदर्शवादी मुळगावकर Notes, Textbook Exercise Important Questions and Answers.

Class 9 Marathi Aksharbharati Chapter 14 आदर्शवादी मुळगावकर Question Answer Maharashtra Board

आदर्शवादी मुळगावकरStd 9 Marathi Chapter 14 Questions and Answers

1. योग्य उदाहरण लिहा:

प्रश्न 1.

उत्तर:

प्रश्न 2.
योग्य उदाहरण लिहा:

उत्तर:

2. आकृती पूर्ण करा:

प्रश्न 1.

उत्तर:

प्रश्न 2.

उत्तर:

3. खाली काही उदाहरणे दिली आहेत. या उदाहरणावरून मुळगावकरांच्या व्यक्तिमत्त्वाचे तुम्हांला जाणवलेले पैलू लिहा:

प्रश्न (अ)

उत्तर:

प्रश्न (आ)

उत्तर:

4. वैशिष्ट्ये लिहा:

प्रश्न 1.
वैशिष्ट्ये लिहा:
(अ) लंडनच्या स्थापत्य विषयाची पदवी –
(आ) टेल्कोचा पुण्यातील कारखाना –
(इ) टेल्कोची परंपरा –
(ई) टेल्कोची मालमोटार –
उत्तर:
(अ) लंडनच्या पदवी परीक्षेच्या अभ्यासक्रमात पुस्तकी शिक्षण होतेच; शिवाय, प्रत्यक्ष कारखान्यात काम करावे लागे. मगच पदवी मिळत असे.
(आ) टेल्कोचा पुण्यातील कारखाना : उत्पादन व व्यवस्थापन या दोन्ही दृष्टींनी कारखाना पहिल्या दर्जाचा आहे, हा लौकिक मिळाला.
(इ) टेल्कोची परंपरा : सर्व दर्जाचे व्यवस्थापक कारखान्यात रोज फेरी मारत असत, ही टेल्कोची परंपरा होती.
(ई) टेल्कोची मालमोटार : टेल्कोची मालमोटार पहिल्या दर्जाची बनली व त्यात सतत सुधारणा होत गेली.

5. खालील वाक्यांतील अधोरेखित शब्दांचे विरुद्धार्थी शब्द लिहून, अर्थ न बदलता वाक्य पुन्हा लिहा.

(अ) मुळगावकर अबोल प्रवृत्तीचे होते.
(आ) मुळगावकर पदवी घेऊन आले, तेव्हा भारतात मंदीची लाट होती.
(इ) मुळगावकरांचे जीवन असमाधानी नव्हते.

6. अधोरेखित केलेल्या अर्थाचा वाक्प्रचार पाठातून शोधून लिहा.

(अ) प्रकृतीकडे दुर्लक्ष केल्यामुळे यश वारंवार आजारी पडत होता.
(आ) शेतीत खूप कष्ट केल्यामुळे यावर्षी रामरावांच्या कष्टाला चांगले फळ मिळाले.
(इ) आवाक्याबाहेरचे काम समीरने सन्मार्गाने पूर्ण केले.
(ई) स्वत:च्या तत्त्वांशी समझोता करणे योग्य नव्हे.
(अ) पाठात उल्लेख असलेल्या चिनी म्हणीतील विचार तुमच्या शब्दांत स्पष्ट करा. (आ) टेल्कोच्या मालमोटारीच्या ड्रायव्हरशी संवाद साधण्यामागे मुळगावकरांचे कोणते हेतू असावेत, असे तुम्हांस वाटते?

7. स्वमत.

प्रश्न (अ)
पाठात उल्लेख असलेल्या चिनी म्हणीतील विचार तुमच्या शब्दांत स्पष्ट करा.
उत्तर:
माणसे आपल्या भविष्याची तरतूद करून ठेवतात. ही तरतूद वेगवेगळ्या स्वरूपांत असते. पैशाच्या स्वरूपातील मदत फार मुळगावकरांनी सामाजिक कार्ये केलेली क्षेत्रे – उपयोगाला येत नाही. झाडे लावली, तर दरवर्षी फळाफुलांचे उत्पन्न मिळते. लाकूडही निर्माण होते. झाडांचा हा असा दरवर्षी नियमितपणे शेती शिक्षण आरोग्य फायदा होतो. मात्र, कोणत्या झाडांचा कधी, कसा व किती फायदा घ्यायचा, हे माणूसच ठरवतो. म्हणून माणूस चांगला घडलेला असेल, मुळगावकरांचे छंद – तर त्याला स्वत:ला या गोष्टीचा फायदा होतोच; शिवाय त्याच्या कुटुंबालाही होतो.

अशी व्यक्ती खूप कर्तबगार निघाली, तर त्या छायाचित्रण कला झाडे लावणे व्यक्तीचा अखंड समाजालाही फायदा होतो. म्हणून पैसे साठवून मुळगावकरांच्या छंदांची फलश्रुती ठेवण्यापेक्षा झाडेझुडपे लावली, तर त्यांचा माणसांना उपयोग होणारच. पण त्याहीपेक्षा माणसे घडवली, तर त्याचा खूप उपयोग होतो. म्हणजे त्यांनी काढलेली त्यांनी लावलेल्या माणसे तयार करणे, हा मानवी समाज घडवण्याचा मार्ग आहे. चिनी छायाचित्रे इतकी सुंदर आहेत झाडांनी पुण्याचा परिसर ई म्हणीमध्ये नेमके हेच सांगितले आहे. की त्यांची प्रदर्शने भरू अत्यंत नयनमनोहर शकतात.

प्रश्न (आ)
टेल्कोच्या मालमोटारीच्या ड्रायव्हरशी संवाद साधण्यामागे मुळगावकरांचे कोणते हेतू असावेत, असे तुम्हांस वाटते ?
उत्तर:
मालमोटारीचा ड्रायव्हर देशभर विविध प्रदेशांत हिंडत असतो. तो कधी जंगलातून प्रवास करतो, तर कधी वाळवंटी प्रदेशातून. उंचसखल प्रदेश, सपाट प्रदेश, दलदलीचा प्रदेश, अतिथंडीचा प्रदेश, प्रचंड पाऊस कोसळणारा प्रदेश अशा विविध प्रकारच्या परिसरांतून आपली मालमोटार प्रवास करीत असते.

अशा वेगवेगळ्या प्रकारच्या परिसरांतील वातावरणात आपली मालमोटार कशी चालत असेल? काही अडचणी निर्माण होत असतील का? मोटारीच्या स्वरूपात उणिवा राहिल्या असतील का? अशा प्रश्नांची उत्तरे ड्रायव्हरांशी केलेल्या संवादातून मिळतात. गाडीत काही उणिवा असतील तर त्या दूर करता येतात. आपली मोटार अधिकाधिक निर्दोष करण्याची संधी मिळते.

उपक्रम:

प्रश्न 1.
तुमच्या परिसरातील लघुउद्योजकांची मुलाखत घ्या.

भाषाभ्यास:

हस्व दीर्घ लेखनाबाबतचे नियम:

प्रश्न 1.
खालील शब्द वाचा.
कुस्ती, मुक्काम, पुष्कळ, शिस्त, दुष्काळ, पुस्तक, चिठ्ठी, डुक्कर, बिल्ला, चिक्की.
वरील प्रत्येक उदाहरणात एक जोडाक्षर आहे. या जोडाक्षरयुक्त अक्षरापूर्वीच्या अक्षराचे नीट निरीक्षण करा. काय आढळले? या अक्षरांतील उकार, इकार हे -हस्व आहेत.

मराठी शब्दांत जोडाक्षर असल्यास जोडाक्षरापूर्वीचे इकार, उकार, सामान्यतः हस्य असतात.

लक्षात ठेवा: तत्सम शब्दांतील जोडाक्षरापूर्वीचे इकार व उकार न्हस्व व दीर्घ अशा दोन्ही प्रकारचे आढळतात.
उदा., पुण्य, तीक्ष्ण, पूज्य

वर दिलेल्या वर्णनानुसार किमान दहा शब्द लिहा.

प्रश्न 2.
खालील शब्द वाचा.

चिंच, लिंबू, बिंदू, तुरुंग, उंच, लिंग, अरविंद, अरुंधती, दिंडी, पिंड, किंकाळी, चिंता, पिंड, पुरचुंडी, पुंगी, धुंद, चिंधी
वरील शब्द अनुस्वारयुक्त आहेत. यांतील अनुस्वारयुक्त अक्षराकडे नीट पाहिल्यास काय जाणवते ?
शब्द मराठी असो वा तत्सम. अनुस्वारयुक्त अक्षरे -हस्व आहेत.

मराठी व तत्सम शब्दांतील इकारयुक्त व उकारयुक्त अक्षरांवर अनुस्वार असल्यास सामान्यत: ती हस्य असतात, म्हणजेच ह्या अनुस्वारयुक्त अक्षरातील इकार, उकार -हस्व असतात. वर दिलेल्या वर्णनानुसार किमान दहा शब्द लिहा.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 14 आदर्शवादी मुळगावकर Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

प्रश्न 2.
कोण ते लिहा:
1. होऊन गेलेल्या बातमीवर अथवा घडामोडीवर परखड भाष्य करणारा.
2. समाजमनावर आपल्या कार्यकर्तृत्वाचा ठसा उमटवणारा.
उत्तर:
1. संपादक
2. समाजमनस्क व्यक्तिमत्त्व.

कृती 2 : (आकलन)

प्रश्न 1.
उत्तर लिहा:
संपादकाचे आवश्यक गुण:

1. बहुश्रुतता
2. ………………..
3. ………………..

उत्तर:

1. संपादकाचे आवश्यक गुण:
2. बहुश्रुतता
3. चिकित्सक विचार

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
‘फॅक्ट्स आर् सेक्रेड बट कॉमेंट्स आर् फ्री’ या उक्तीचा तुम्हांला कळलेला अर्थ लिहा.
उत्तर:
वृत्तपत्रांनी बातमी देणे हे त्यांचे मूळ कर्तव्य आहे. वाचकांना आपल्या अवतीभवती, देशविदेशात घडणाऱ्या घडामोडी जाणून घेण्यात रस असतो. वृत्तपत्रांनी बातमीच्या रूपात या घडामोडींची माहिती दयायची असते. ही बातम देताना घटना जशी घडली तशी बातमीत ती आली पाहिजे. बातमीदाराने स्वत:चे विचार, कल्पना बातमीत मिसळू नयेत, अशी अपेक्षा असते. बातमीदाराने आपल्या आवडत्या राजकीय पक्षाची बातमी भरभरून दिली, तर तो त्या पक्षाचा प्रचार होईल. वाचकांना मात्र संबंधित घटना खऱ्या स्वरूपात कळणार नाहीत. हे गैर आहे.

थोडक्यात बातमीदाराने, पत्रकारांनी बातमीत भेसळ करता कामा नये. यालाच ‘फॅक्ट्स आर् सेक्रेड’ असे म्हटले आहे. पत्रकारांना स्वत:चे विचार, मते मांडायची असतील, तर ती त्यांनी अग्रलेखात मांडावीत. स्वतंत्र लेख लिहून मांडावीत. मात्र ही मतेसुद्धा तटस्थपणे व परखडपणे मांडली पाहिजेत. पत्रकारांना ते स्वातंत्र्य पूर्णपणे बहाल केलेले असते. यालाच ‘कॉमेंट्स आर फ्री’ असे म्हटले आहे.

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
कोष्टक पूर्ण करा:

कृती	तुम्हांला जाणवलेले गुण
पहिले 6 महिने विनावेतन काम केले आणि नंतर काही काळ अत्यल्प वेतनावर काम केले.

उत्तर:

कृती	तुम्हांला जाणवलेले गुण
पहिले 6 महिने विनावेतन काम केले आणि नंतर काही काळ अत्यल्प वेतनावर काम केले.	चिकाटी व कामावरील निष्ठा

कृती 2 : (आकलन)

प्रश्न 1.
वैशिष्ट्ये लिहा:
1. मंदीच्या काळातील नोकऱ्या.
उत्तर:
1. मंदीच्या काळातील नोकरीत सुरुवातीला काही महिने विनावेतन काम करावे लागे व नंतर काही काळ अत्यल्प वेतन मिळत असे.

प्रश्न 2.
कोण ते लिहा:
1. टाटा कंपनीत येण्याचे मुळगावकरांना आमंत्रण देणारे.
2. ध्येयाच्या बाबतीत अजिबात तडजोड न करणारे.
उत्तर:
1. जे. आर. डी. टाटा
2. सुमंत मुळगावकर.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
तुम्हांला जाणवलेले मुळगावकरांचे मोठेपण समजावून सांगा.
उत्तर:
मुळगावकरांनी शास्त्र शाखेची पदवी घेतली होती. पुढे ते लंडनला गेले आणि त्यांनी स्थापत्यशास्त्राची पदवी घेतली. त्या काळाचा विचार करता, हे खूप उच्च दर्जाचे शिक्षण त्यांनी मिळवले होते. लेखकांनी सांगितलेला आदर्शवाद जोपासण्याचा मुळगावकरांचा गुण यातून दिसून येतो. जे करायचे ते उत्तमच, हा त्यांचा ध्यास या कृतीतून दिसतो. उच्च शिक्षण घेतलेले असूनही त्यांना सुरुवातीला 6 महिने विनावेतन काम करावे लागले. या परिस्थितीने ते खचले नाहीत. निराश झाले नाहीत. अत्यल्प वेतनावरही त्यांनी काम केले. यातून त्यांची चिकाटी दिसते. आपल्या ध्येयाकडे जाताना येईल त्या संकटाला तोंड दयायची त्यांची तयारी होती.

या सर्व काळात मुळगावकरांनी आपली योग्यता सिद्ध केली होती. म्हणूनच सिमेंटचे अधिक कारखाने उभारण्याची जबाबदारी त्यांच्यावर सोपवली गेली. दुसऱ्या महायुद्धाच्या काळात युरोप-अमेरिकेत तंत्रज्ञांचे एक मंडळ तत्कालीन सरकारने पाठवले. त्यात मुळगावकरांचा समावेश होता. लक्षात घेण्यासारखी गोष्ट म्हणजे त्या मंडळात जे. आर. डी. टाटांसारखा दूरदृष्टीचा उदयोजकही होता. टाटांनी त्या प्रवासातच मुळगावकरांना टाटा कंपनीत येण्याचे आमंत्रण दिले. या घटनांवरून मुळगावकरांच्या मोठेपणाची सहज कल्पना येऊ शकेल.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
उत्तर लिहा:
सलग बारा वर्षे मालमोटारींचे उत्पादन न करण्यामागील रहस्य:
उत्तर:
सलग बारा वर्षे मालमोटारींचे उत्पादन न करण्यामागील रहस्य: मुळगावकरांना केवळ कारखाना उभारायचा नव्हता; तर त्यांना एक उदयोग उभारायचा होता.

कृती 3 : (स्वमत अभिव्यक्ती)

प्रश्न 1.
मुळगावकरांची दिसून येणारी व्यवस्थापनातील दूरदृष्टी व कौशल्य समजावून सांगा.
उत्तर:
साधारणपणे बहुसंख्य उदयोजक भराभर उत्पादन तयार करतात आणि बाजारात आणतात. या घाईमुळे उत्पादनात दोष राहतात. कर्मचाऱ्यांना व अधिकाऱ्यांनाही एक वाईट सवय लागते. उत्पादनात उणिवा दिसल्या तरी तिकडे दुर्लक्ष करण्याची सवय लागते. अचूक काम करण्याची, काटेकोरपणे काम करण्याची इच्छा राहत नाही. उत्तम दर्जा हवा, हा आग्रहही हळूहळू राहत नाही. अशी कंपनी कधीही पहिल्या दर्जाची होऊ शकत नाही. म्हणून मुळगावकरांनी प्रथम उत्पादनावर भर दिला नाही. मूलभूत बाबी निर्माण करण्यावर भर दिला. याचा टेल्को कंपनीला फार मोठा फायदा झाला. यातच मुळगावकरांची दूरदृष्टी होती व कौशल्य होते.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
मुळगावकरांचे स्वभावविशेष लिहा.

1. ………………………..
2. ………………………..
3. ………………………..
4. ………………………..

उत्तर:
मुळगावकरांचे स्वभावविशेष:

1. सौम्य प्रवृत्ती
2. मोजके बोलणे
3. आस्थेवाईकपणा
4. टापटीपपणा.

प्रश्न 3.
विधाने पूर्ण करा:
1. आपल्या कारखान्याला आदर्श करायचे असेल, तर …………………………….
2. आपल्या कारखान्याचे हित कशात आहे, हे लक्षात घेतले, तर ………………………….
उत्तर:
1. आपल्या कारखान्याला आदर्श करायचे असेल, तर कठोरपणे निर्णय घेणे आवश्यक असते.
2. आपल्या कारखान्याचे हित कशात आहे, हे लक्षात घेतले, तर कठोर निर्णय घेणे सोपे जाते.

कृती 2 : (आकलन)

प्रश्न 1.
पुढील घटनांचा परिणाम लिहा:

घटना	परिणाम
1. मुळगावकर दौऱ्यावर असताना टेल्कोची मालमोटार दिसल्यास ते ती थांबवत आणि ड्रायव्हरशी बोलत.
2. कारखान्याचे अध्यक्ष व अन्य अधिकारी कामगारांत मिसळत.

उत्तर:

घटना	परिणाम
1. मुळगावकर दौऱ्यावर असताना टेल्कोची मालमोटार दिसल्यास ते ती थांबवत आणि ड्रायव्हरशी बोलत.	मोटार चांगली चालते का, काही अडचणी येतात का, इत्यादी माहिती मिळे.
2. कारखान्याचे अध्यक्ष व अन्य अधिकारी कामगारांत मिसळत.	विचारांची देवाण-घेवाण होत असे.

प्रश्न 2.
विधाने पूर्ण करा:
1. ………………….. ही मोटार उदयोगाला मुळगावकरांनी दिलेली देणगी होय.
2. आपले उत्पादन अधिकाधिक सरस व्हावे, म्हणून ……………………….
उत्तर:
1. अनेक तंत्रज्ञ शिकून तयार झाले, ही मोटार उद्योगाला मुळगावकरांनी दिलेली देणगी होय.
2. आपले उत्पादन अधिकाधिक सरस व्हावे, म्हणून मुळगावकरांनी संशोधन विभागावर लक्ष केंद्रित केले.

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती :

1. समास:

प्रश्न 1.
पुढील विग्रहावरून समास ओळखा:
उत्तर:

1. हळद, कुंकू वगैरे → समाहार वंद्व समास
2. पाच मुखांचा समूह → द्विगू समास
3. राव किंवा रंक → वैकल्पिक द्वंद्व समास
4. ऋषीसारखा राजा → कर्मधारय समास
5. देव आणि दानव → इतरेतर द्वंद्व समास

2. शब्दसिद्धी:

प्रश्न 1.
‘उपसर्गघटित, प्रत्ययघटित व अभ्यस्त’- प्रत्येकी दोन है शब्द लिहा.
उत्तर:

उपसर्गघटित	प्रत्ययघटित	अभ्यस्त
नि:पक्षपाती	पत्रकार	हळूहळू
प्रक्रिया	दयावान	लालेलाल

प्रश्न 2.
‘ज्ञ’ प्रत्यय लागलेले चार शब्द लिहा : जसे-तंत्रज्ञ.
उत्तर:

1. शास्त्रज्ञ
2. तत्त्वज्ञ
3. शिल्पज्ञ
4. मनोज्ञ

प्रश्न 3.
‘सद् (सत्)’ उपसर्ग लागलेले चार शब्द लिहा: जसे-सद्वर्तन.
उत्तर:

1. सद्विचार
2. सद्विवेक
3. सदाचार
4. सद्गुणी

3. वाक्प्रचार:

प्रश्न 1.
अधोरेखित केलेल्या अर्थाचा वाक्प्रचार पाठातून शोधून लिहा:

1. यशने आहाराकडे दुर्लक्ष केल्यामुळे तो वारंवार आजारी पडत होता.
2. शेतीत खूप कष्ट केल्यामुळे या वर्षी रामरावांच्या कष्टाला चांगले फळ मिळाले.
3. आवाक्याबाहेरचे काम समीरने सन्मार्गाने पूर्ण केले.
4. स्वत:च्या तत्त्वांशी समझोता करणे योग्य नव्हे.

उत्तर:

1. यशने आहाराची हेळसांड केल्यामुळे तो वारंवार आजारी पडत होता.
2. शेतीत खूप राबल्यामुळे या वर्षी रामरावांच्या कष्टाला चांगले फळ मिळाले.
3. आटोक्यात नसलेले काम समीरने सन्मार्गाने पूर्ण केले.
4. स्वत:च्या तत्त्वांशी तडजोड करणे योग्य नव्हे.

प्रश्न 2.
पुढील वाक्प्रचारांचा अर्थ सांगून वाक्यात उपयोग करा:

1. वाखाणणे
2. गाजावाजा करणे
3. प्रेरणा देणे.

उत्तर:

1. वाखाणणे – अर्थ : प्रशंसा करणे.
   वाक्य: सुधीरच्या चित्राची सरांनी खूप वाखाणणी केली.
2. गाजावाजा करणे – अर्थ : स्वत:ची टिमकी वाजवणे.
   वाक्य: आपल्या कर्तृत्वाचा गाजावाजा करणे अयोग्य आहे.
3. प्रेरणा देणे — अर्थ : स्फूर्ती देणे.
   वाक् : राजूच्या समाजसेवेच्या कार्याला आईने खूप प्रेरणा दिली.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
पुढील वाक्यांतील अधोरेखित शब्दांचे विरुद्धार्थी शब्द लिहून, अर्थ न बदलता वाक्य पुन्हा लिहा:

1. सौम्य प्रकृतीच्या मुळगावकरांना प्रसंगी कठोर निर्णय घेणे शक्य होत असे.
2. मुळगावकर अबोल प्रवृत्तीचे होते.
3. मुळगावकर पदवी घेऊन आले, तेव्हा भारतात मंदीची लाट होती.
4. मुळगावकरांचे जीवन असमाधानी नव्हते.

उत्तर:

1. सौम्य प्रकृतीच्या मुळगावकरांना प्रसंगी सौम्य निर्णय घेणे शक्य होत नसे. सौम्य प्रकृतीच्या मुळगावकरांना प्रसंगी सौम्य निर्णय घेणे अशक्य होत असे.
2. मुळगावकर बोलक्या प्रवृत्तीचे नव्हते.
3. मुळगावकर पदवी घेऊन आले, तेव्हा भारतात भरभराटीची लाट नव्हती.
4. मुळगावकरांचे जीवन समाधानी होते.

प्रश्न 2.
तक्ता भरा:

एकवचन	पदवी		देणगी
अनेकवचन		कारखाने		मोटारी

उत्तर:

एकवचन	पदवी	कारखाना	देणगी	मोटार
अनेकवचन	पदव्या	कारखाने	देणग्या	मोटारी

प्रश्न 3.
कंसांतील योग्य विरुद्धार्थी शब्द निवडून लिहा:

1. सरस × …………………. (विरस, निरस, सुरस)
2. सचोटी × ………………. (लबाडी, गुणवान, दुर्गुणी)
3. अवाढव्य × …………….. (प्रचंड, विशाल, चिमुकले)
4. सुदैव × ………………… (सदैव, एकमेव, दुर्दैव)

उत्तर:

1. सरस × निरस
2. सचोटी × लबाडी
3. अवाढव्य × चिमुकले
4. सुदैव × दुर्दैव.

2. लेखननियम:

प्रश्न 1.
नियम 1 मध्ये दिलेल्या वर्णनानुसार किमान दहा शब्द लिहा.
उत्तर:

1. उल्लेख
2. मुद्दाम
3. किल्ला
4. जिल्हा
5. झिम्मा
6. कुत्रा
7. पुत्र
8. चित्र
9. दुर्जन
10. दिल्ली.

प्रश्न 2.
नियम 2 मध्ये दिलेल्या वर्णनानुसार किमान दहा शब्द लिहा.
उत्तर:

1. इंच
2. भिंत
3. कुंडी
4. शिंग
5. बिंब
6. बुंदी
7. रुंदी
8. उंदीर
9. टिंब
10. पिंप.

प्रश्न 3.
अचूक शब्द ओळखा:

1. प्रर्दशन, प्रदर्शन, परदर्शन, प्रदशर्न.
2. केंद्रित, केद्रीत, केद्रित, केंद्रीत.
3. सलागार, सल्लागर, सल्लागार, सलागर.
4. चिकीत्सक, चीकीत्सक, चिकिस्तक, चिकित्सक.
5. बहुश्रुतता, बहुश्रुतता, बहूश्रूतता, बहुश्रूतता.
6. व्यक्तीमत्त्व, व्यक्तिमत्व, व्यक्तिमत्त्व, व्यक्तीमत्व.

उत्तर:

1. प्रदर्शन
2. केंद्रित
3. सल्लागार
4. चिकित्सक
5. बहुश्रुतता
6. व्यक्तिमत्त्व.

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यातील चुकीची विरामचिन्हे दुरुस्त करून योग्य ती विरामचिन्हे घालून वाक्ये लिहा:
1. तो म्हणाला. मी! तिथे मुळीच येणार नाही,
2. छे, छे, मला नकोच हा वेगळा छंद.
उत्तर:
1. तो म्हणाला, “मी तिथे मुळीच येणार नाही.”
2. “छे! छे! मला नकोच हा वेगळा छंद!”

4. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द दया:

1. Plumber
2. Comedy
3. Magazine
4. Orientation.

उत्तर:

1. नळ-कारागीर
2. सुखात्मिका
3. मासिक-पत्रिका
4. उद्बोधन, निदेशन.

उपक्रम:

प्रश्न 1.
तुमच्या परिसरातील लघुउदयोजकाची मुलाखत घ्या.

आदर्शवादी मुळगावकर Summary in Marathi

प्रस्तावना:

गोविंद तळवलकर हे मराठीतील व इंग्रजीतील एक श्रेष्ठ संपादक. आंतरराष्ट्रीय घडामोडींचे चिकित्सक अभ्यासक, सामाजिक व राजकीय घडामोडींवर अधिकारवाणीने भाष्य करणारे व्यासंगी पत्रकार. इंग्रजी वाङ्मय, जागतिक राजकारण, विशेषतः रशियन राज्यक्रांती व रशियाची जडणघडण यांचा सखोल अभ्यास हे गोविंद तळवलकरांचे खास वैशिष्ट्य. पुरोगामी दृष्टिकोन, खोलवर चिकित्सा, नि:पक्षपाती भूमिका व धारदार लेखणी यांमुळे वृत्तपत्रसृष्टीत त्यांचा जबरदस्त दरारा निर्माण झाला होता. राजकारणी लोकांना त्यांचा खूप धाक वाटत असे. त्यांनी राजकारण्यांवर नैतिक अंकुश ठेवण्याचे काम केले.

गोविंद तळवलकरांनी विविध प्रकारचे लेखन केले आहे. अनेक कर्तृत्ववान व्यक्तींच्या कार्याचा परिचय करून देणारे लेखही त्यांनी लिहिले आहेत. प्रस्तुत ‘आदर्शवादी मुळगावकर’ हा पाठ अशाच प्रकारातला आहे. श्री. सुमंत मुळगावकर हे टाटा समूहातील टेल्को या कंपनीचे व्यवस्थापकीय संचालक होते. एखादी कंपनी स्थापन करायची आणि तिला नफा मिळवून दयायचा, एवढाच मर्यादित हेतू त्यांनी मनात बाळगला नाही. जे काही करायचे ते सर्वोत्तम, आदर्शच असले पाहिजे, असा त्यांचा ध्यास होता.

कंपनीच्या इमारतीची रचना कशी करायची, कर्मचाऱ्यांना कसे घडवायचे, उत्पादन प्रक्रिया कशी आखायची, अंतिम उत्पादन ग्राहकस्नेही कसे करायचे या सर्व बाबतीत ते आदर्शवादीच होते. यामुळे टेल्को कंपनीने संपूर्ण भारतात एक उत्कृष्ट कंपनी म्हणून लौकिक मिळवलाच; शिवाय, जागतिक पातळीवरही ‘उत्कृष्ट कंपनी’ असा शिक्का प्राप्त केला. अशा या सुमंत मुळगावकर या व्यक्तिमत्त्वाच्या कार्याचा व स्वभावगुणांचा परिचय या पाठात गोविंद तळवलकरांनी करून दिला आहे.

शब्दार्थ:

1. परखड – स्पष्ट, कोणाच्या दडपणाखाली न येता व कोणालाही खूश करण्याचा हेतू न बाळगता व्यक्त केलेले (मत, विचार इत्यादी).
2. बहुश्रुतता – खूप ऐकलेले, पाहिलेले, वाचलेले असणे.
3. समाजमनस्क – समाजाविषयी जागरूक मन असलेला.
4. आदर्श – आरसा; एखादी गोष्ट, तत्त्व, विचार यांची सर्वोत्कृष्ट अवस्था.
5. सचोटी – प्रामाणिकपणा, प्रांजळपणा.
6. निकडीचे – (निकडतातडी, ताबडतोबीची गरज) तातडीचे.
7. अवाढव्य – प्रचंड.
8. सौम्य – मृदू, कोमल.
9. हेळसांड – हयगय, दुर्लक्ष.

टिपा:

1. फॅक्ट्स आर् सेक्रेड, बट कॉमेंट्स आर् फ्री: ‘गार्डियन’ या जगप्रसिद्ध वर्तमानपत्राचे हे घोषवाक्य. फॅक्ट्स म्हणजे घटना, घडलेली गोष्ट. वर्तमानपत्राने घटना घडली, तशीच तिची बातमी दिली पाहिजे. बातमीत स्वत:ची मते, पूर्वग्रह, हेतू मिसळता कामा नयेत. जसे घडले तसे शोधून काढून प्रसिद्ध केले पाहिजे. वर्तमानपत्राची ही नीती असली पाहिजे. भगवद्गीता, बायबल, कुराण यांसारख्या धर्मग्रंथांतील वचने, त्यांतील शब्द हे पवित्र मानले जातात. त्यांत बदल करता कामा नये. त्यांची मोडतोड करून वेगळी रचना करता कामा नये. त्या ग्रंथांत मुळात जसे आहे, तसेच उद्धृत केले पाहिजे, असा दंडक असतो. या अर्थाने बातमीसुद्धा पवित्र असते. तिच्या पावित्र्याला धक्का लावता कामा नये. मात्र त्या बातमीवर, बातमीतील घटनांवर भाष्य करण्याचा संपादकांना अधिकार असतो. असा एकूण त्या घोषवाक्याचा अर्थ आहे.

2. मंदीची लाट: कोणत्या तरी कारणाने एखादे उत्पादन खपत नाही किंवा त्याचे पुरेसे उत्पादन होत नाही. त्यामुळे नफा कमी होतो. साहजिकच पगारकपात केली जाते किंवा नोकरभरती होत नाही किंवा नोकरकपात केली जाते. याचा परिणाम म्हणून लोकांच्या हातात कमी पैसा येतो. पैसा कमी असल्याने बाजारात मालाचा उठाव होत नाही. त्यामुळे संबंधित उदयोगाचा नफा कमी होतो. नोकरकपात होते. पुन्हा मागणी कमी होते… अशा रितीने हेच चक्र वेगाने चालू होते. बेकारी येते. उत्पादन थंडावते. समाजाची आर्थिक स्थिती डबघाईला येते. या स्थितीला ‘मंदी’ म्हणतात.

वाक्प्रचार व त्यांचे अर्थ:

1. कस लागणे – सामर्थ्य सिद्ध होणे, गुणवत्ता सिद्ध होणे.
2. मानवंदना देणे – आदरपूर्वक सन्मान करणे.
3. कटाक्ष असणे – आग्रह असणे.
4. जीव तोडून काम करणे – शरीराला कितीही त्रास झाला तरी त्याची पर्वा न करता कष्ट करणे, पराकोटीचे कष्ट करणे.
5. गाजावाजा होणे – अवाजवी प्रसिद्धी होणे.

9th Std Marathi Questions And Answers:

• मातीची सावली Class 9 Question Answer
• महाराष्ट्रावरूनी टाक ओवाळून काया (पोवाडा) Class 9 Question Answer
• थोडं ‘आ’ भारनियमन करूया Class 9 Question Answer
• आदर्शवादी मुळगावकर Class 9 Question Answer
• निरोप (कविता) Class 9 Question Answer
• ‘बिग ५’ च्या सहवासात (स्थूलवाचन) Class 9 Question Answer