Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 14 Biomolecules Textbook Exercise Questions and Answers.
Biomolecules Class 12 Exercise Question Answers Solutions Maharashtra Board
Class 12 Chemistry Chapter 14 Exercise Solutions Maharashtra Board
Chemistry Class 12 Chapter 14 Exercise Solutions
1. Select the most correct choice.
Question i.
CH2OH-CO-(CHOH)4-CH2OH is an example of
a. Aldohexose
b. Aldoheptose
c. Ketotetrose
d. Ketoheptose
Answer:
(d) Ketoheptose
![]()
Question ii.
Open chain formula of glucose does not contain
a. Formyl group
b. Anomeric hydroxyl group
c. Primary hydroxyl group
d. Secondary hydroxyl group
Answer:
(b) Anomeric hydroxyl group
Question iii.
Which of the following does not apply to CH2NH2 – COOH
a. Neutral amino acid
b. L – amino acid
c. Exists as zwitterion
d. Natural amino acid
Answer:
(d) Natural amino acid
Question iv.
Tryptophan is called essential amino acid because
a. It contains an aromatic nucleus.
b. It is present in all the human proteins.
c. It cannot be synthesized by the human body.
d. It is an essential constituent of enzymes.
Answer:
(c) It cannot be synthesised by human body.
Question v.
A disulfide link gives rise to the following structure of protein.
a. Primary
b. Secondary
c. Tertiary
d. Quaternary
Answer:
(c) Tertiary
Question vi.
RNA has
a. A – U base pairing
b. P – S – P – S backbone
c. double helix
d. G – C base pairing
Answer:
(a) A – U base pairing
2. Give scientific reasons :
Question i.
The disaccharide sucrose gives negative Tollens test while the disaccharide maltose gives positive Tollens test.
Answer:
(1) In disaccharide sucrose, the reducing groups of glucose and fructose are involved in glycosidic bond formation, sucrose is a nonreducing sugar. As there is no free aldehyde group, it does not reduce Tollen’s reagent to metallic silver. Hence, sucrose gives negative Tollen’s test.
(2) While the disaccharide maltose is a reducing sugar because a free aldehyde group can be produced at C1 of second sugar molecule. It is a reducing sugar. It reduces Tollen’s reagent to shining silver mirror. Hence, Maltose gives positive Tollen’s test.
![]()
Question ii.
On complete hydrolysis DNA gives equimolar quantities of adenine and thymine.
Answer:
On complete hydrolysis DNA yields 2-deoxy-D-ribose, adenine, thymine, guanine, cystosine and phosphoric acid. Since adenine always forms two hydrogen bonds with thymine, the hydrolysis of DNA gives equimolar quantities of adenine and thymine.
Question iii.
α – Amino acids have high melting points compared to the corresponding amines or carboxylic acids of comparable molecular mass.
Answer:

α-Amino acids have high melting points compared to the corresponding amines or carboxylic acids of comparable molecular mass due to the presence of both acidic (carboxylic group) and basic (amino group) groups in the same molecule. In aqueous solution, proton transfer from acidic group to amino (basic) group of amino acid forms a salt, which is a dipolar ion called zwitter ion.
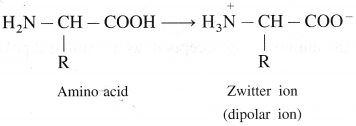
Question iv.
Hydrolysis of sucrose is called inversion.
Answer:

Sucrose is dextro rotatory. On hydrolysis it gives equimolar mixture of D – ( + ) glucose and D – ( -) fructose. Since the laevorotation of fructose (- 92.4°) is more than dextrorotation of glucose ( + 52.7°), the hydrolysis product has net laevorotation. Thus, hydrolysis of sucrose brings about a change in the sign of rotation, from dextro ( + ) to laevo (-) and the product is called as invert sugar and so the hydrolysis of sucrose is called inversion.
![]()
Question v.
On boiling, egg albumin becomes opaque white.
Answer:
Upon boiling the egg, denaturation αcurs. During denaturation, secondary and tertiary structures are destroyed, but primary structure remains intact. Egg contains soluble globular proteins, which forms insoluble fibrous proteins (opque) on boiling egg.
3. Answer the following
Question i.
Some of the following statements apply to DNA only, some to RNA only and some to both. Lable them accordingly.
a. The polynucleotide is double stranded. ( …………… )
b. The polynucleotide contains uracil. ( …………… )
c. The polynucleotide contains D-ribose ( …………… ).
d. The polynucleotide contains Guanine ( …………… ).
Answer:
(1) The polynucleotide is double stranded. (DNA)
(2) The polynucleotide contains uracil. (RNA)
(3) The polynucleotide contain D-ribose (RNA)
(4) Thc polynucleotide contains Guanine (DNA, RNA)
Question ii.
Write the sequence of the complementary strand for the following segments of a DNA molecule.
a. 5′ – CGTTTAAG – 3′
b. 5′ – CCGGTTAATACGGC – 3′
Answer:
(1) DNA molecule : 5′ – CGTTTAAG – 3′
The complementary strand runs in opposite direction from the 3′ end to the 5′ end. It has the base sequence decided by complementary base pairs A – T and C – G.

(2) DNA molecule : 5′ – CCGGTTAATACGGC – 3′
The complementary strand runs in opposite direction from the 3′ end to the 5′ end. It has the base sequence decided by complementary base pairs A – T and C – G.

Question iii.
Write the names and schematic representations of all the possible dipeptides formed from alanine, glycine and tyrosine.
Answer:
(1) Dipeptide formed from alanine and glycine
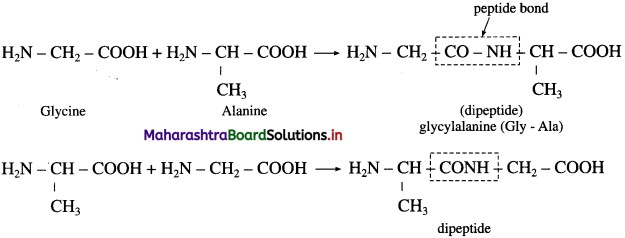
(2) Dipeptide formed from alanine and tyrosine

(3) Dipeptide formed from glycine and tyrosine.

Question iv.
Give two pieces of evidence for the presence of the formyl group in glucose.
Answer:
(1) Glucose reacts with hydroxyl amine in an aqueous solution to form glucose oxime. This indicates the presence of – CHO (formyl group) in glucose.

(2) Glucose on oxidation with mild oxidising agent like bromine water gives gluconic acid which shows carbonyl group in glucose is aldehyde (formyl group) group.

![]()
4. Draw a neat diagram for the following:
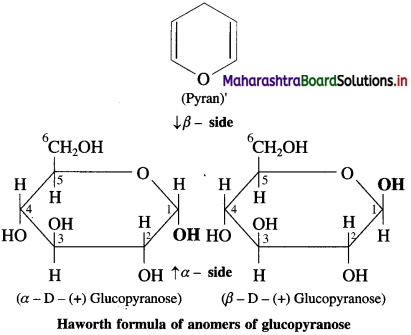
Question i.
Haworth formula of glucopyranose
Answer:
Question ii.
Zwitter ion
Answer:
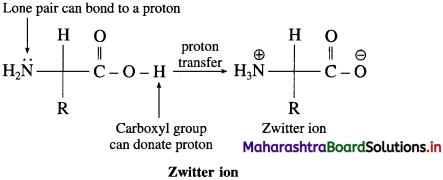
Question iii.
Haworth formula of maltose
Answer:
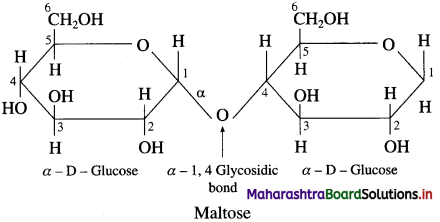
Question iv.
Secondary structure of the protein
Answer:
The structure of proteins can be studied at four different levels i.e. primary, secondary, tertiary and quaternary levels. Each level is more complex than the previous one.
(1) Primary structure of proteins :
(a) Representation by structural formula

(b) Representation with amino acid symbols
![]()
Primary structure of proteins is the sequence of constituent a-amino acid residues linked by peptide bonds. Any change in the sequence of amino acid residue creates different protein molecule. Primary structure of proteins is represented by writing the three letter symbols of amino acid residues as per their sequence in the concerned protein. The symbols are separated by dashes. According to the convention, the N-terminal amino acid residue as written at the left end and the C-terminal amino acid residue at the right end.
![]()
(2) Secondary structure of proteins : The three-dimensional arrangement of lαalized regions of a long polypeptide chain is called the secondary structure of protein. Hydrogen bonding between N-H proton of one amide linkage and C = O oxygen of another gives rise to the secondary structure. There are two different types of secondary structures i.e. α-helix and β-pleated sheet.
α-Helix : In a-helix structure, a polypeptide chain gets coiled by twisting into a right handed or clαkwise spiral known as a-helixn. The characteristic features of α-helical structure of protein are :
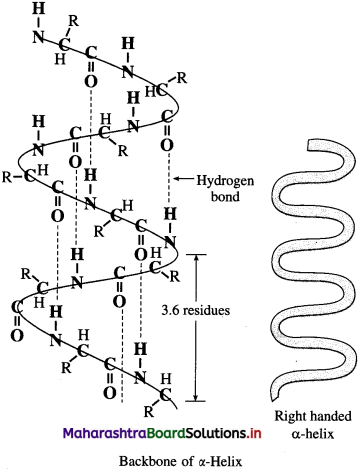
(1) Each turn of the helix has 3.6 amino acids.
(2) A C = O group of one amino acid is hydrogen bonded to N – H group of the fourth amino acid along the chain.
(3) Hydrogen bonds are parallel to the axis of helix while R groups extend outward from the helix core.
Myosin in muscle and a-keratin in hair are proteins with almost entire a-helical secondary structure.
β-Pleated sheet : In secondary structure, when two or more polypeptide chains (strands) line up side-by-side is called β-pleated sheets. The β-picate sheet structure of protein consists of extended strands of polypeptide chains held together by intermolecular hydrogen bonding. The characteristics of β-pleated sheet structure are :
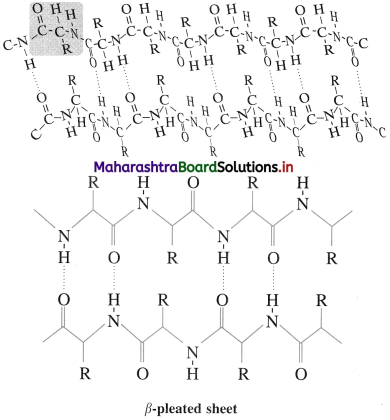
- The C = O and N – H bonds lie in the planes of the sheet.
- Hydrogen bonding occurs between the N – H and C = O groups of nearby amino acid residues in the neighbouring chains.
- The R groups are oriented above and below the plane of the sheet.
The β-pleated sheet arrangement is favoured by amino acids with small R groups.
(3) Tertiary structure of proteins :

The three-dimensional shape acquired by the entire polypeptide chain of a protein is called its tertiary structure. The structure is stabilized and has attractive interaction with the aqueous environment of the cell due to the folding of the chain in a particular manner. Tertiary structure gives rise to two major molecular shapes i.e. globular and fibrous proteins. The main forces which stabilize a particular tertiary structure include hydrogen bonding, dipole-dipole attraction (due to polar bonds in the side chains), electrostatic attraction (due to the ionic groups like -COO–, \(\mathrm{NH}_{3}^{+}\) in the side chain) and also London dispersion forces. Finally, disulfide bonds formed by oxidation of nearby – SH groups (in cysteine residues) are the covalent bonds which stabilize the tertiary structure.
![]()
(4) Quaternary structure of proteins The two or more polypeptide chains with folded tertiary structures forms complex protein. The spatial arrangements of these polypeptide chains with respect to each other is known as quaternary structure. Each individual polypeptide chain is called a subunit of the overall protein. For example: Haemoglobin consists of four subunits called haeme held together by intermolecular forces in a compact three dimensional shape. Haemoglobin can do its function of oxygen transport only when all the four subunits are together.

Question v.
AMP
Answer:

![]()
Question vi.
dAMP
Answer:

Question vii.
One purine base from nucleic acid
Answer:

Question viii.
Enzyme catalysis
Answer:
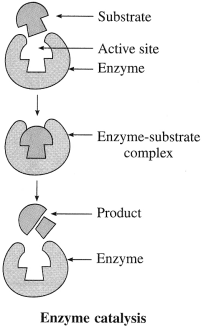
Activity :
- Draw the structure of a segment of DNA comprising at least ten nucleotides on a big chart paper.
- Make a model of DNA double stranded structure as group activity.
12th Chemistry Digest Chapter 14 Biomolecules Intext Questions and Answers
Try ….. this (Textbook Page No 298)
Question 1.
Observe the following structural formulae carefully and answer the questions.

(1) How many OH groups are present in glucose, fructose and ribose respectively?
(2) Which other functional groups are present in these three compounds?
Answer:
(1) Glucose contains five hydroxyl (- OH) groups.
Fructose contains five hydroxyl ( – OH) groups.
Ribose contains four hydroxyl ( – OH) groups.
(2) Glucose contains aldehyde ( – CHO) as other functional group.
Fructose contains ketonic group ![]() as other functional group.
as other functional group.
Ribose contains aldehyde ( – CHO) as other functional group.
![]()
Use your brain power! (Textbook Page No 299)
Question 1.
Give IUPAC names to the following monosaccharides.

Answer:
(1) Aldotriose
(2) Aldopentose
(3) Ketoheptose
Problem 14.1 : (Textbook Page No 300)
Question 1.
An alcoholic compound was found to have molecular mass of 90 u. It was acetylated. Molecular mass of the acetyl derivative was found to be 174 u. How many alcoholic (- OH) groups must be present in the original compound?
Solution :
In acetylation reaction H atom of an (- OH) group is replaced by an acetyl group (- COH3).
This results in an increase in molecular mass by [(12 + 16 + 12 + 3 x 1) – 1] that has, 42 u. In the given alcohol, increase in molecular mass = 174 u – 90 u = 84 u
∴ Number of – OH groups \(=\frac{84 \mathrm{u}}{42 \mathrm{u}}=2\)
Use your brain power! (Textbook Page No 301)
(1) Write structural formula of glucose showing all the bonds in the molecule.
(2) Number all the carbons in the molecules giving number 1 to the ( – CHO) carbon.
(3) Mark the chiral carbons in the molecule with asterisk (*).
(4) How many chiral carbons are present in glucose?
Answer:
Refer structural formula of glucose for (1) (2) and (3).

(4) There are 4 chiral carbon atoms present in glucose.
Use your brain power! (Textbook Page No 306)
Question 1.
(1) Is galactose an aldohexose or a ketohexose?
(2) Which carbon in galactose has different configuration compared to glucose?
(3) Draw Haworth formulae of α-D-galactose and β-D-galactose.
(4) Which disaccharides among sucrose, maltose and lactose is/are expected to give positive Fehling test?
(5) What are the expected products of hydrolysis of lactose?
Answer:
- Galactose is an aldohexose.
- Fourth carbon in galactose has different configuration compared to glucose.

- Maltose and lactose are expected to give positive Fehling solution test.
- The expected products of hydrolysis of lactose are D – ( +) glucose and D – ( +) galactose.
![]()
Can you think? (Textbook Page No 307)
Question 1.
When you chew plain bread, chapati or bhaakari for long time, it tastes sweet. What could be the reason?
Answer:
When chapati, bread or bhakari are chewed for long time the pulp mixes with saliva and carbohydrate component in them diseminates and gives the sweet taste.
Use your brain power! (Textbook Page No 309)
Question 1.
Tryptophan and histidine have the structures (I) and (II) respectively. Classify them into neutral? acidic/basic &amino acids and justify your answer. (Hint: Consider învolvement of lone pair in resonance).
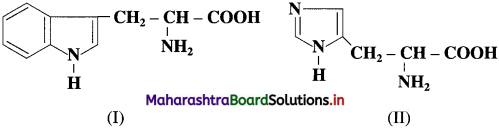
Answer:

In tryptophan, nitrogen atom present in cyclic structure cannot donate pair of electrons as it is stabilized by resonance. The other amino group and carboxylic group present in the side chain neutralize each other. Tryptophan has equal number of amino and carboxylic groups. Hence, tryptophan is a neutral amino acid.
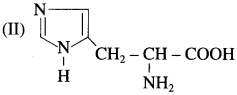
In histidine, amino groups are more in number than carboxyl groups therefore histidine ¡s basic in nature.
Can you think? (Textbook Page No 309)
Question 1.
Compare the molecular masses of the following compounds and explain the observed melting points.

Answer:
Above compounds have same molecular masses but they have different melting points, a-amino acids have higher melting points compared to the corresponding amines or carboxylic acids of comparable masses. This property is due to the presence of both carboxylic group (acidic) and amino group (basic) in the molecule. In aqueous solution, protons transfer from acidic group to amino (basic) group of amino acid forms a salt, which is a dipolar ion called – Zwitter ion.

![]()
Use your brain power! (Textbook Page No 310)
Question 1.
(1) Write the structural formula of dipeptide formed by combination of carboxyl group of alanine and amino group of glycine.
(2) Name the resulting dipeptide.
(3) Is this dipeptide same as glycyalanine or its structural isomer?
Answer:

(2) ala-glycine. OR ala-gly
(3) It is a structural isomer.
Question 54.
Write the names and schematic representations of all the possible dipeptides formed from alanine, glycine and tyrosine.
Problem 14.3 : (Textbook Page No 311)
Question 1.
Chymotrypsin is a digestive enzyme that hydrolyzes those amide bonds for which the carbonyl group comes from phenylalanine, tyrosine or tryptophan. Write the symbols of the amino acids and peptides smaller than pentapeptide formed by hydrolysis of the following hexapeptide with chymotrypsin. Gly-Tyr-Gly-Ala-Phe-Val
Solution :
In the given hexapeptide hydroylsis by chymotripsin can take place at two points, namely, Phe and Tyr. The carbonyl group of these residues is towards the right side, that is, toward the C-terminal. Therefore the hydrolysis products in required range will be :
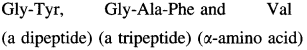
Problem 14.4 : (Textbook Page No 311)
Question 1.
Write down the structures of amino acids constituting the following peptide.

Solution :
The given peptide has two amide bonds linking three amino acids. The structures of these amino acids are obtained by adding one H2O molecule across the amide bond as follows :

![]()
Use your brain power! (Textbook Page No 313)
A protein chain has the following amino acid residues. Show and label the interactions that can be present in various pairs from these giving rise to tertiary level structure of protein.

Answer:
Tertiary level structure from amino residues.

Can you tell? (Textbook Page No 313)
Question 1.
What is the physical change observed when (a) egg is boiled, (b) milk gets curdled on adding lemon juice?
Answer:
(a) When egg is boiled, coagulation of eggwhite (insoluble fibrous proteins) takes place. This is a common example of denaturation.
(b) When lemon juice is added to milk, it gets curdled due to the formation of lactic acid. This is another example of denaturation.
Can you tell? (Textbook Page No 315)
Question 1.
What is the single term that answers all the following questions?
(1) What decides whether you are blue eyed or brown eyed?
(2) Why does wheat grain germinate to produce wheat plant and not rice plant?
(3) Which acid molecules are present in nuclei of living cells?
Answer:
(1) Nucleic acid (DNA)
(2) Nucleic acid (DNA)
(3) Nucleic acid (DNA + RNA)
![]()
Use your brain power! (Textbook Page No 317)
Question 1.
Draw structural formulae of nucleosides formed from the following sugars and bases.
(1) D – ribose and guanine
(2) D – 2 – deoxyribose and thymine
Answer:
(1) D-ribose and guanine
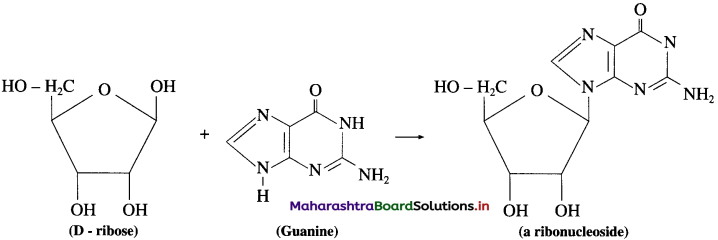
(2) D – 2 – deoxyribose and thymine

Problem 14.5 (Textbook Page No 318)
Queston 1.
Draw a schematic representaion of trinucicotide segment ACT of a DNA molecule.
Solution :
In DNA molecule sugar is deoxyribose. The base ‘A’ in the given segment is at 5 end while the base T at the 3’ end. I-fence the schematic representation of the given segment of DNA is

Problem 14.6 : (Textbook Page No 320)
![]()
Question 1.
Write the sequence of the complementary strand of the following portion of a DNA molecule : 5 -ACGTAC-3
Solution :
The complementary strand runs in opposite direction from the 3′ end to the 5′ end. It has the base sequence decided by complementary base pairs A – T and C – G.

Problem 14.2 : (Text Page No 303)
Question 1.
Assign D/L configuration to the following monosaccharides.

Solution :
D/L configuration is assigned to Fischer projection formula of monosaccharide on the basis of the lowest chiral carbon.

Threose has two chiral carbons C-2 and C-3. The given Fischer projection formula of threose has OH groups at the lowest C -3 chiral carbon on the right side.
∴ It is D-threose.

Ribose has three chiral carbons C – 2, C – 3 and C -4.
The given Fischer projection formula of ribose has – OH group at the lowest C -4 chiral carbon on the left side.
∴ It is L-ribose
12th Std Chemistry Questions And Answers:
- Coordination Compounds Class 12 Chemistry Questions And Answers
- Halogen Derivatives Class 12 Chemistry Questions And Answers
- Alcohols, Phenols and Ethers Class 12 Chemistry Questions And Answers
- Aldehydes, Ketones and Carboxylic Acids Class 12 Chemistry Questions And Answers
- Amines Class 12 Chemistry Questions And Answers
- Biomolecules Class 12 Chemistry Questions And Answers
- Introduction to Polymer Chemistry Class 12 Chemistry Questions And Answers
- Green Chemistry and Nanochemistry Class 12 Chemistry Questions And Answers





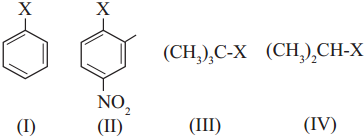




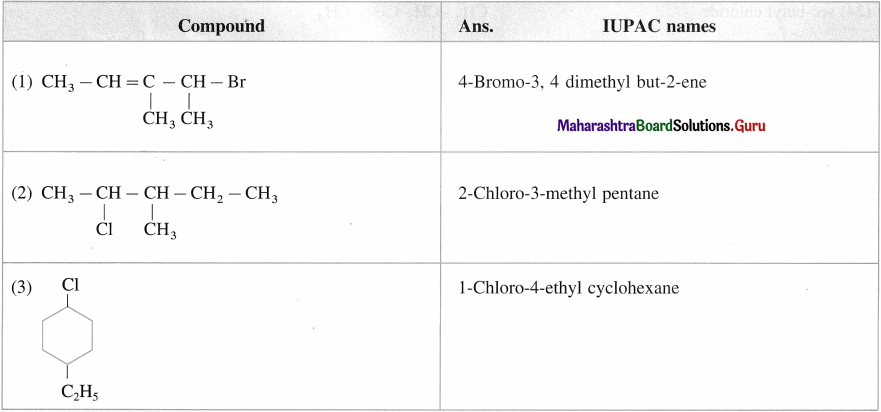

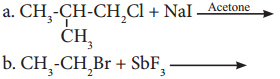




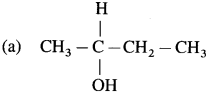
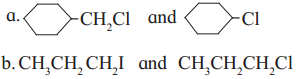
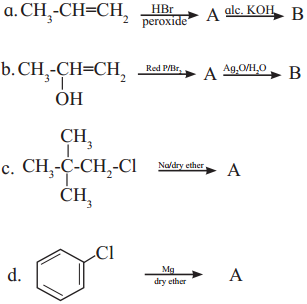
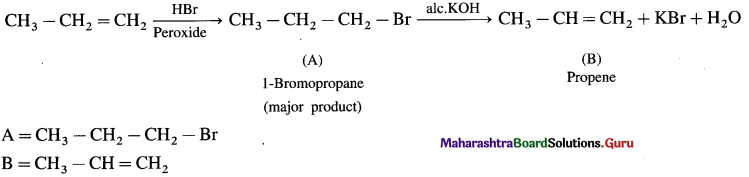
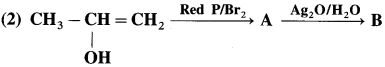
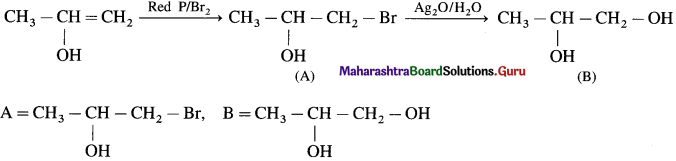
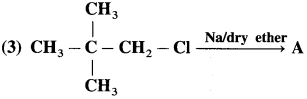
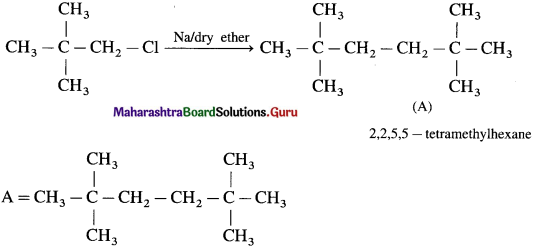
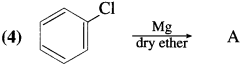
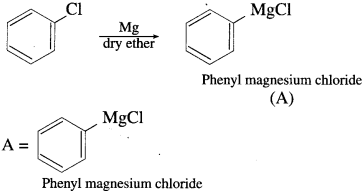
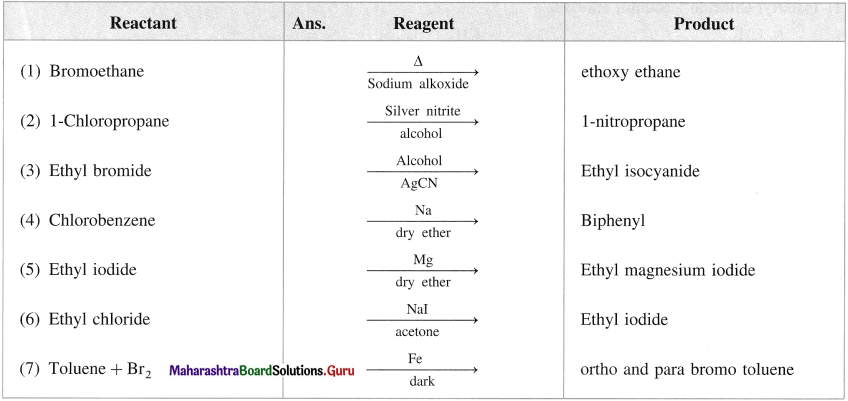

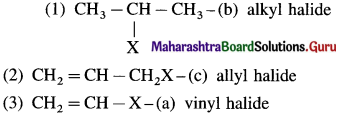




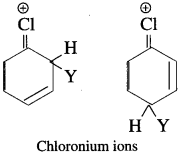
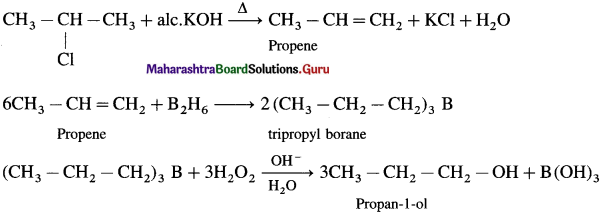
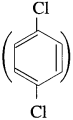 has mp. higher than those of o-and rn-isomers.
has mp. higher than those of o-and rn-isomers.
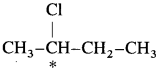 carbon atom (the starred carbon atom) which is attached to four different groups, i.e., ethyl (-CH2 – CH3), methyl (CH3), chloro (Cl) and hydrogen (H) groups.
carbon atom (the starred carbon atom) which is attached to four different groups, i.e., ethyl (-CH2 – CH3), methyl (CH3), chloro (Cl) and hydrogen (H) groups.






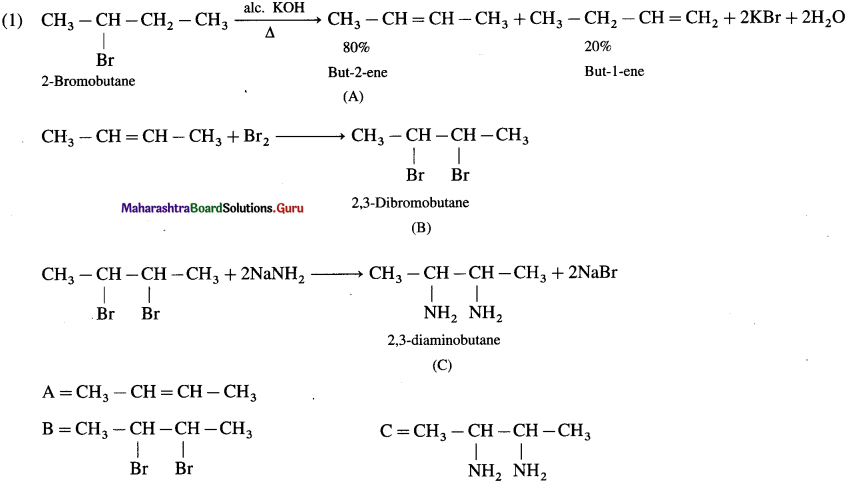
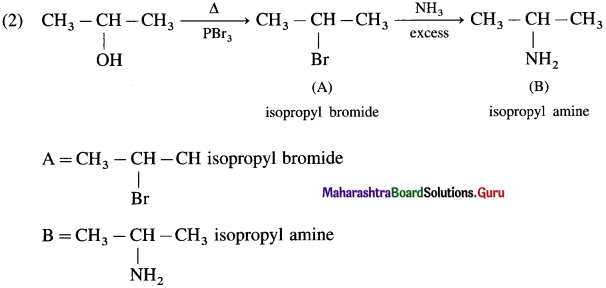
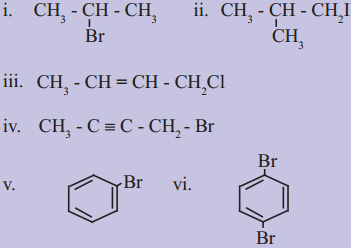
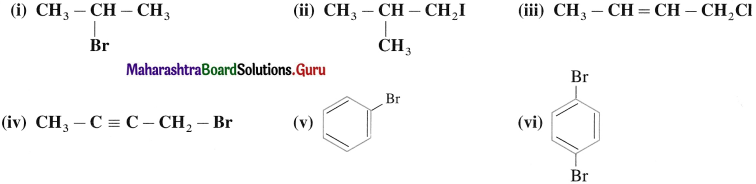
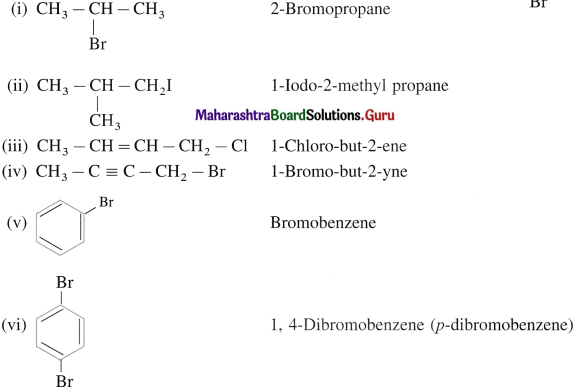



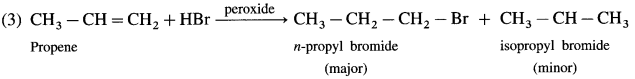
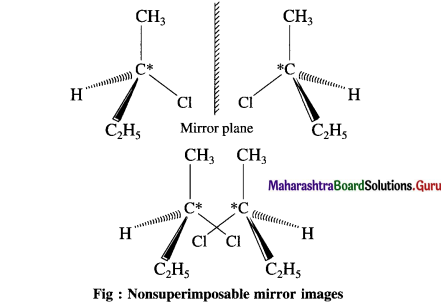
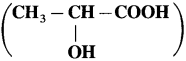 using Fischer projection formulae.
using Fischer projection formulae.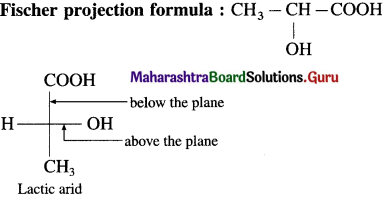

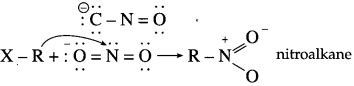
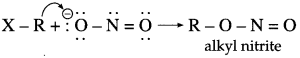

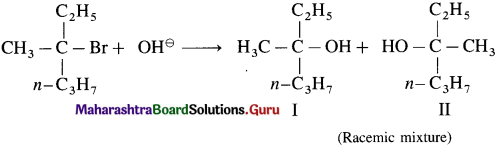












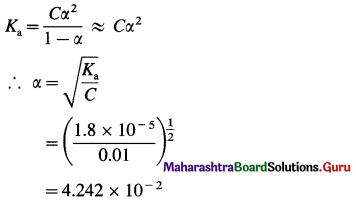
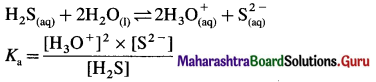
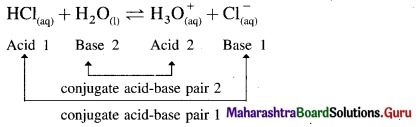
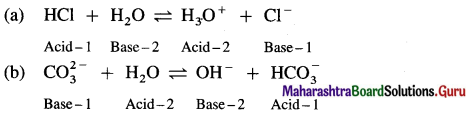
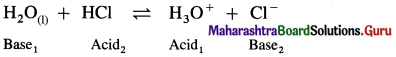

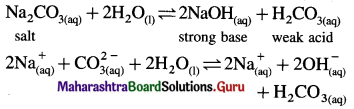
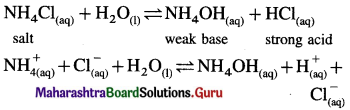


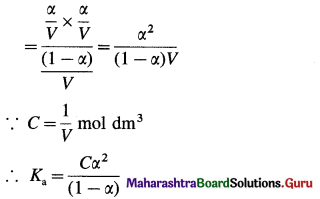
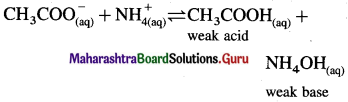

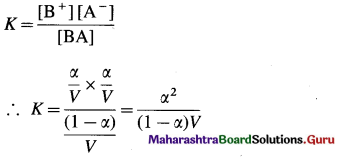

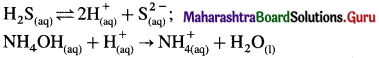
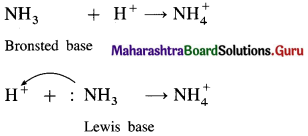
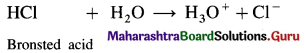

















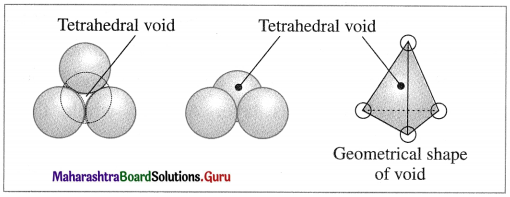

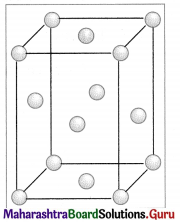
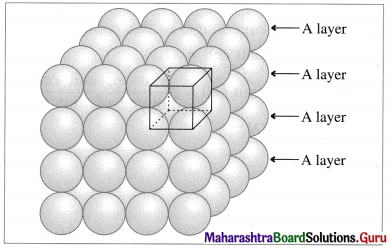
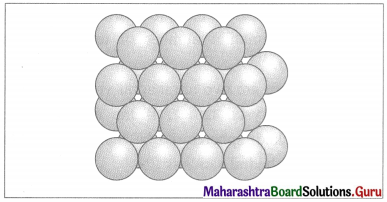



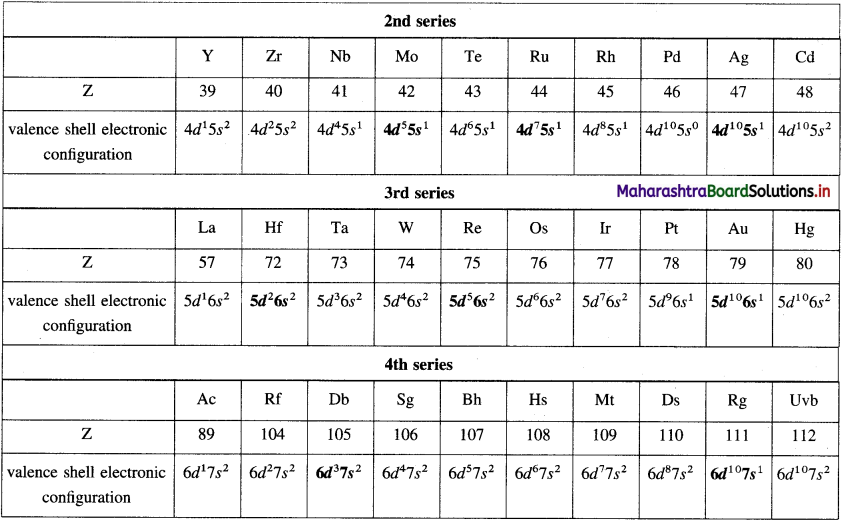
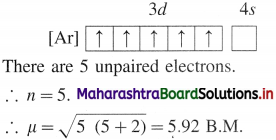
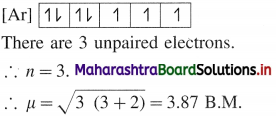

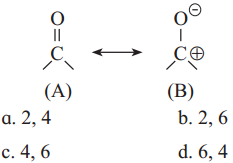
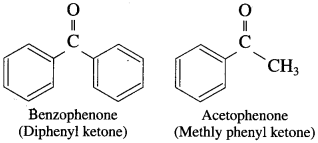
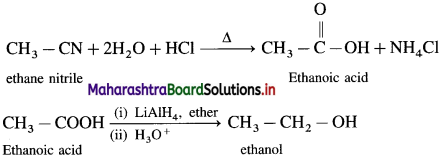

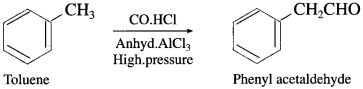

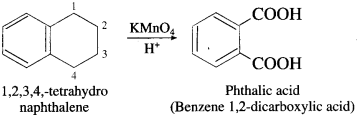



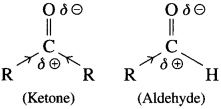
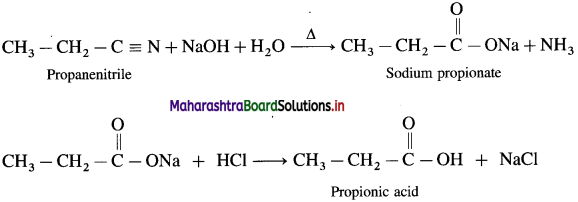

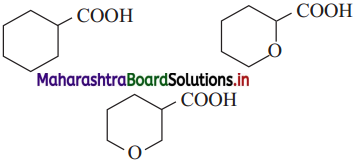
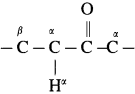
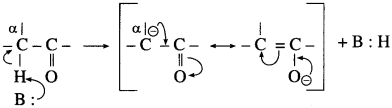
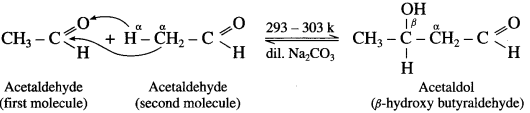



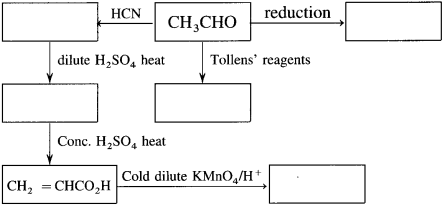
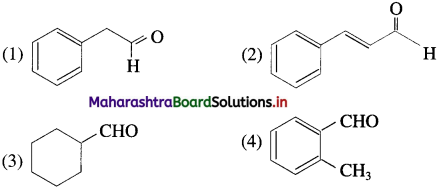




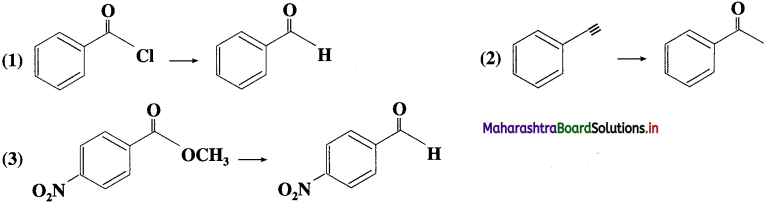
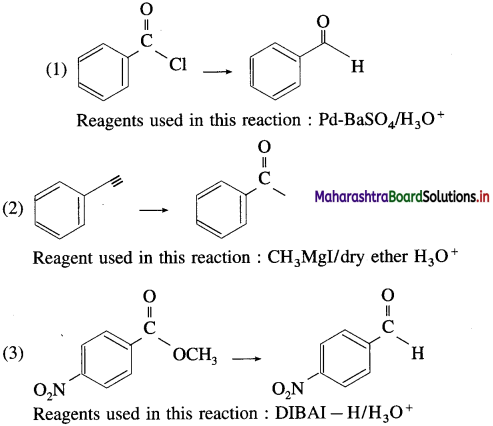

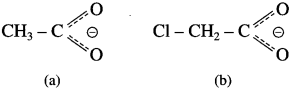
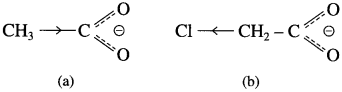
 The acetate ion formed gets destabilised due to electron releasing effect of methyl group
The acetate ion formed gets destabilised due to electron releasing effect of methyl group
 The dichloroacetate ion formed gets stabilised due electron-withdrawing effect of two chlorine atoms. (- 1 effect)
The dichloroacetate ion formed gets stabilised due electron-withdrawing effect of two chlorine atoms. (- 1 effect)

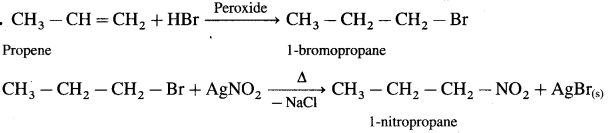
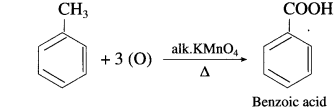
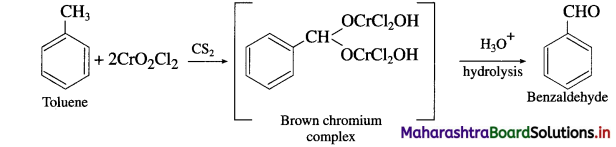
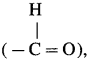 , an aldehyde is oxidised to carboxylic acid
, an aldehyde is oxidised to carboxylic acid  which is not possible in case of ethers, ketones, alcohols and hydrocarbons.
which is not possible in case of ethers, ketones, alcohols and hydrocarbons. can’t be broken easily.
can’t be broken easily.
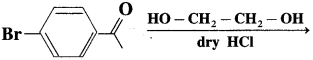
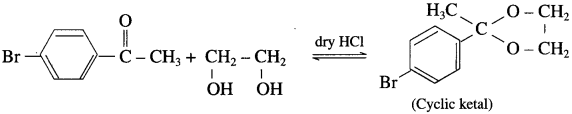



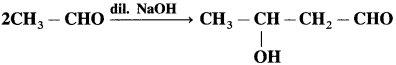
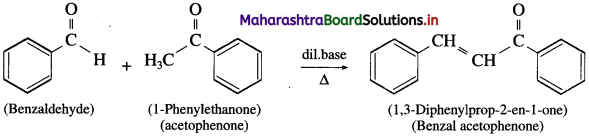
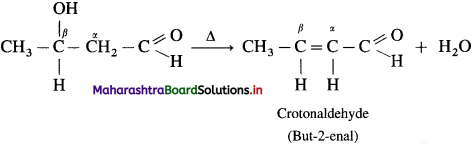
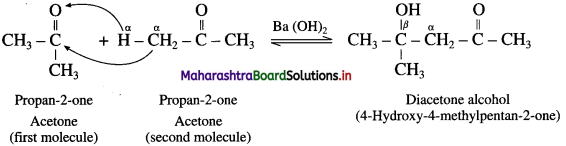
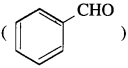 does not have a-hydrogen atom, it will not undergo self aldol condensation.
does not have a-hydrogen atom, it will not undergo self aldol condensation. contains a-carbon atom, it cannot undergo Cannizzaro reaction.
contains a-carbon atom, it cannot undergo Cannizzaro reaction.