Class 11

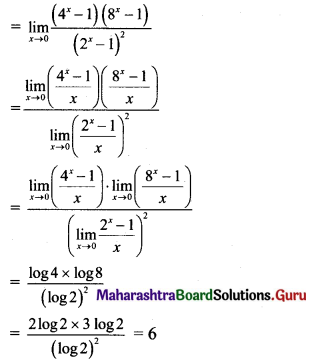
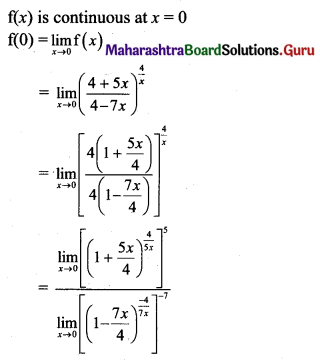
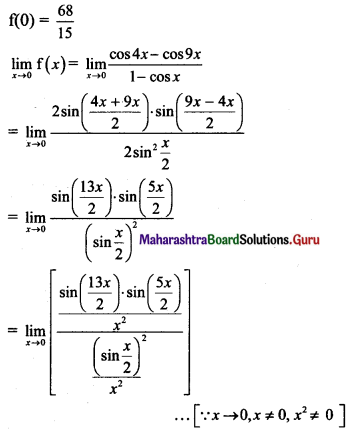
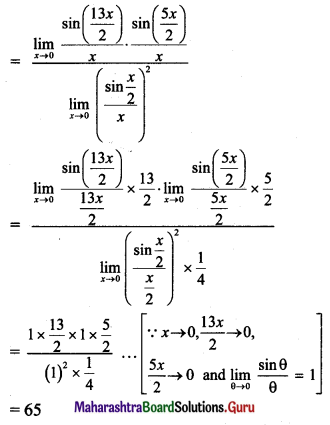
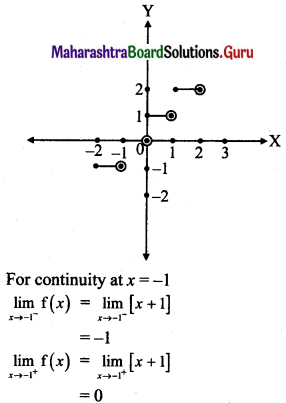
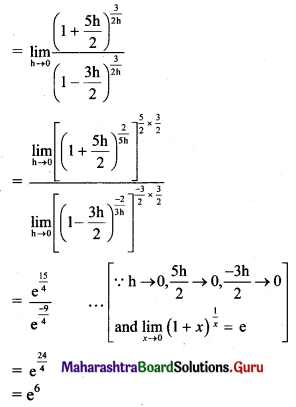
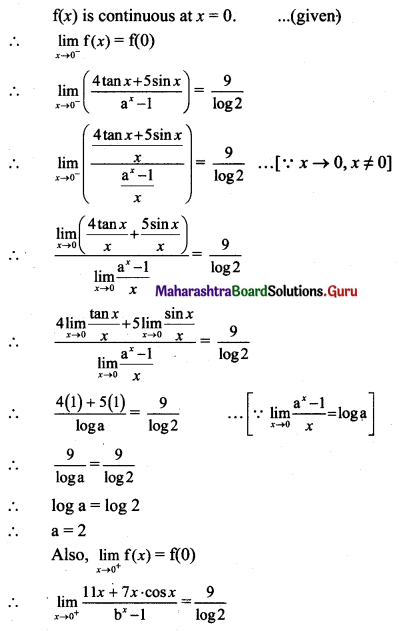
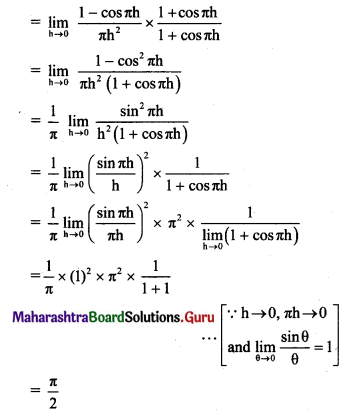
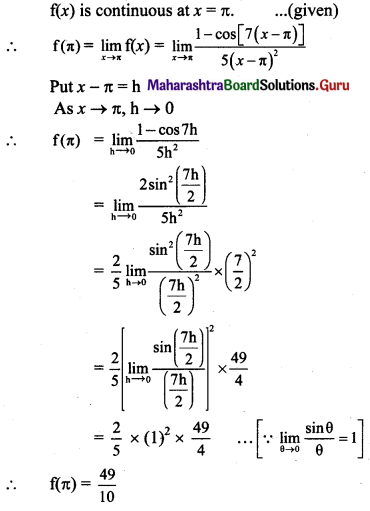
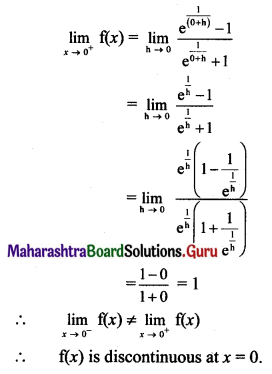
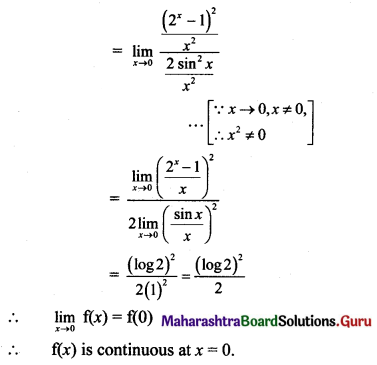
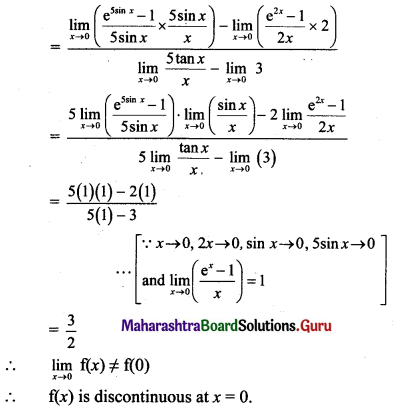
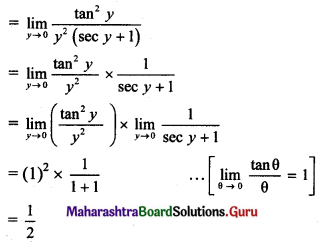
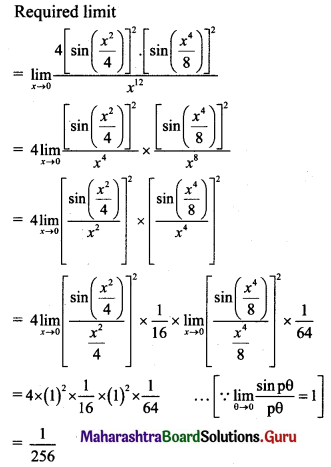
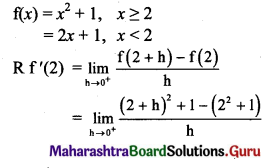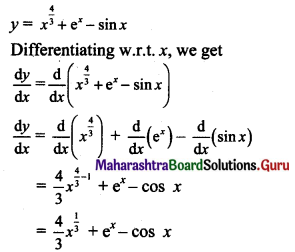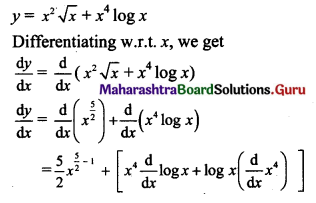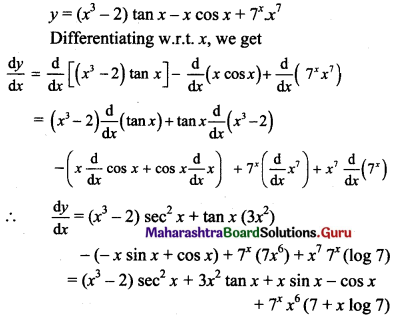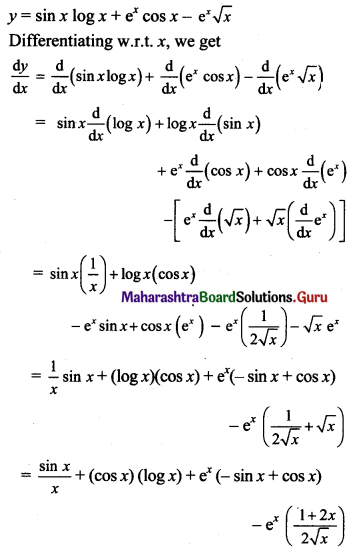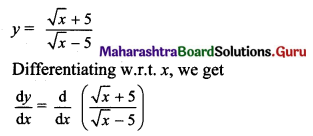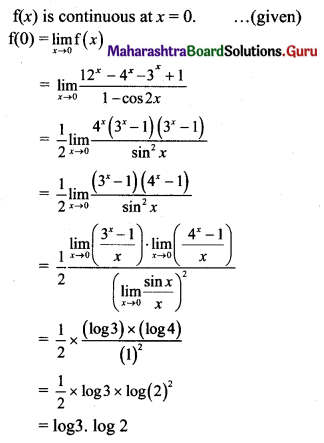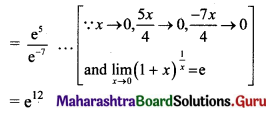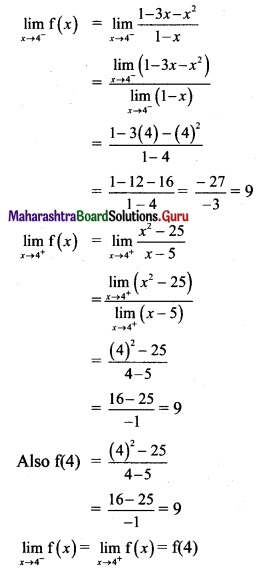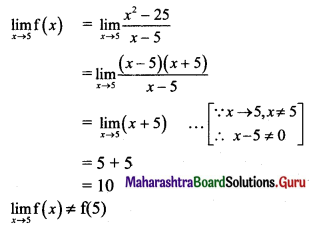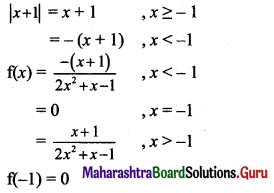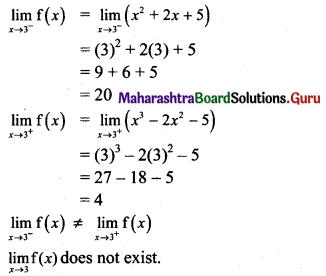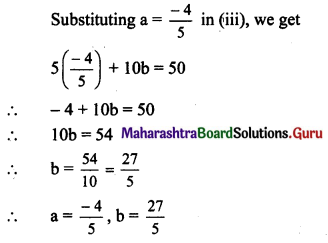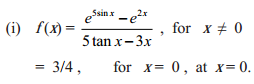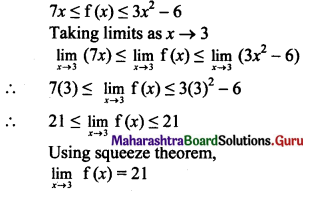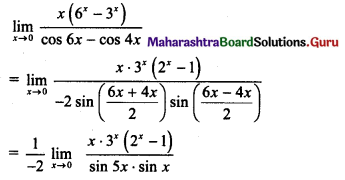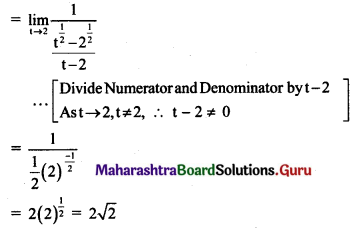Psychology Class 11 Chapter 3 Self Question Answers Maharashtra Board

Balbharti Maharashtra State Board Class 11 Psychology Solutions Chapter 3 Self Textbook Exercise Questions and Answers.

Self Class 11 Psychology Chapter 3 Questions and Answers

1A. Complete the following statements.

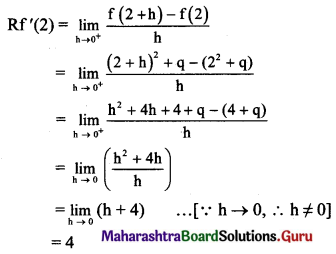
Question 1.
The self-concept begins to form when ___________
a. a one and half-year-old child recognizes her image in the mirror
b. an infant is able to distinguish his body from the rest in his surrounding
c. a child recognizes his/herself as a boy or a girl
Answer:
b. an infant is able to distinguish his body from the rest in his surrounding

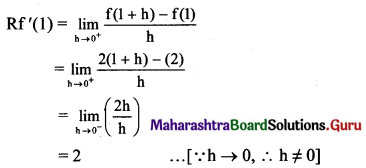
Question 2.
According to Carl Rogers, every individual strives for ___________
a. achievement
b. self-actualization
c. status in society
Answer:
b. self-actualisation

Question 3.
Self-esteem is a sense of self-worth that depends upon ___________
a. actual performance of an individual
b. self-perception of one’s own performance
c. other people’s performance perception of one’s
Answer:
b. self-perception of one’s own performance

Question 4.
Ability to monitor our actions and feelings, is called ___________
a. self-regulation
b. self-awareness
c. self-efficacy
Answer:
a. self-regulation

1B. State whether the following statements are true or false and give a reason for your answer.

Question 1.
Congruence between the real self and ideal self is an indicator of good mental health.
Answer:
True
Explanation: Congruence between the real self and ideal self leads to a greater sense of self-worth and thereby, indicates good mental health.

Question 2.
Namrata aspires to become a pilot but she should not be encouraged because one must choose a profession appropriate to their gender.
Answer:
False
Reason: It is wrong to think that profession should be chosen based on one’s gender. Gender roles are diluting in modern times.

Question 3.
People with high self-esteem are not necessarily the ones who are always successful.
Answer:
True
Explanation: People with high self-esteem may not always succeed. But they have high self-worth even when they encounter failure.

Question 4.
Accepting mistakes helps improving self-esteem.
Answer:
True
Explanation: Accepting mistakes enables a person to take steps to correct them in the future and thereby, improve self-esteem.

Question 5.
Self-awareness is a necessary attribute to have a healthy self-concept.
Answer:
True
Explanation: Self-awareness enables a person to have realistic perception of oneself and thereby, helps in the formation of healthy self-concept.

1C. Identify the odd item from the following.

Question 1.
Goal-orientation, Internal values, Feeling of superiority, Positivity
Answer:
Feeling of superiority

Question 2.
Fear of risks, Fear of uncertainty, Self-confidence, Impression management
Answer:
Self-confidence

Question 3.
Self-indulgence, Self-awareness, Self-efficacy, Self-esteem
Answers:
Self-indulgence

1D. Match the following pairs.

Question 1.

A	B
1. Rentsch and Heffener model	a. A sense of self-worth
2. Carl Rogers	b. Monitoring one’s own actions
3. Congruence between ideal and real self	c. Confidence in one’s own abilities to complete a task
4. Self-esteem	d. Categories of self-concept
5. Self-regulation	e. Fully functioning person
6. Self-efficacy	f. Good mental health

Answer:

A	B
1. Rentsch and Heffener model	d. Categories of self-concept
2. Carl Rogers	e. Fully functioning person
3. Congruence between ideal and real self	f. Good mental health
4. Self-esteem	a. A sense of self-worth
5. Self-regulation	b. Monitoring one’s own actions
6. Self-efficacy	c. Confidence in one’s own abilities to complete a task

2. Answer the following questions in around 35-40 words each.

Question 1.
How do we develop a concept of our ‘self’ as we grow?
Answer:

• Till six months: A child is unaware of himself.
• As the child grows, he develops a distinction between ‘me’ and ‘what is not me’.
• By the age of two: The child becomes aware of general expectations.
• By the age of three: The child starts recognizing himself and others as boys or girls.
• At the age of five-six: The child begins to compare himself to others.
• Between the age of three-twelve: Self-concept is based on developing talents and skills.
• Adolescence: It involves perspective taking, i.e. understanding other’s points of view.

Question 2.
Explain the sex identity and sex role as a part of the self-concept.
Answer:

• Gender identity is the perception of oneself as male or female. It is the biological aspect of self-concept.
• Gender role is psycho-social in nature as it is determined by the family atmosphere and cultural influences through which the child learns. It is an acquired attribute of self-concept.

Question 3.
What are the ways in which we can achieve congruence between the ideal self and the real self?
Answer:
Some of the ways in which we can achieve congruence between the ideal self and the real self are:

• Recognizing one’s own potential
• Taking steps to achieve one’s full potential
• Having trust in one’s own competence
• Being positive and rational

Question 4.
Why is the congruence between the ideal self and the real self is very significant to enjoy psychological well-being?
Answer:

• High congruence between the real self and ideal self leads to the formation of accurate self-concept.
• It also results in a greater sense of self-worth and contributes to a healthy productive life.
• Hence, congruence between the ideal self and the real self is significant to enjoy psychological well-being.

Question 5.
What is meant by self-esteem?
Answer:

• Self-esteem is a general evaluation of an individual along a dimension. It is the respect one has for himself.
• According to Seligman, ‘self-esteem is your overall evaluation of your worth as a person, high or low, based on all positive and negative self-perceptions.

Question 6.
Describe the characteristics of individuals with high self-esteem.
Answer:
Some characteristics of individuals with high self-esteem are as follows:

• Positive
• Responsible
• Committed to goals
• Strong internal values
• Genuine and forgiving
• Desire for self-improvement

Question 7.
What are the ways to improve one’s self-esteem? Give example.
Answer:

1. Some ways to improve one’s self-esteem are as follows:
   • Eliminate negative self-talk
   • Recognize your strengths
   • Recognize self-worth
   • Accept mistakes
   • Accept rejection
2. e.g. When Neha accepted rejection in interviews as a part of life, she started looking at it in a positive way. This improved her self-esteem.

Question 8.
What are the characteristics of individuals with self-efficacy? Give examples.
Answer:

• Individuals with high self-efficacy have accurate self-evaluation and are willing to take risks. They are confident and experience a sense of accomplishment. e.g. Emerging entrepreneurs often have high self-efficacy.
• Individuals with low self-efficacy fear uncertainty and failure. They are afraid to take risks. e.g. After losing five games in a row, players in the football team suffered from low self-efficacy.

Question 9.
What is self-image?
Answer:

• Self-image is a personal view or mental picture that we have of ourselves. It is a collection of an individual’s assets (strengths) and liabilities (weaknesses).
• Body image, i.e. how we think, feel, and react to our physical attributes, is also a part of self-image.

Question 10.
What are the ways to regulate self? Give examples.
Answer:

1. Some ways to regulate self are as follows:
   • Being aware of one’s own actions
   • Being able to evaluate the impact of one’s actions
   • Being able to predict others’ reactions
2. e.g. When Aditya realized that his anger outbursts scare his toddler, he felt guilty and decided to stop it. He used anger management techniques to regulate himself during such situations.

3. Compare and contrast

Question 1.
Ideal self — Real self
Answer:

• The ideal self is what we want to be while the real self is what we actually are.
• The ideal self represents our dynamic ambitions and goals. It comprises of some goals which are beyond our reach. On the other hand, the real self is our inner personality. It may not be perfect but it is our real part.

Question 2.
Private self — Objective self-awareness
Answer:

• The development of the private self takes place between the age of five to six while objective self-awareness develops during adolescence.
• Private self begins to develop when children learn that they can lie and keep secrets. There is the hidden side of the self which includes thoughts, feelings, and desires which parents are unaware of. On the other hand, objective self-awareness develops when adolescents seek to become the center of attraction and popularity. To achieve this, they accept a group’s mannerisms and behavioural patterns.

Question 3.
People with high self-esteem and People with low self-esteem
Answer:

• People with high self-esteem are positive, responsible, genuine, and committed to their goals. On the other hand, people with low self-esteem are negative, need externally oriented goals, and are impatient with themselves as well as others.
• People with high self-esteem have strong internal values and forgiving nature. They continuously seek to improve themselves. Conversely, those with low self-esteem are unhappy and experience anxiety. They may also have a superiority or inferiority complex.

4. How will you deal with the following situations if it were you in those situations?

Question (a).
Grishma thinks she is extremely good-looking – which is not true in reality – she aspires to become a star model.
Answer:
I feel few important characteristics to become a star model are confidence, physical fitness, gracefulness, and determination.

I will talk to Grishma about the incongruence between her ‘real self’ (self-image) and ‘ideal self. I will also make her understand that even though she is not extremely good-looking, she can actualize her potential by taking efforts to sharpen her other positive attributes.

Question (b).
Harshad is avoiding places where he has to meet many people as he wears spectacles and he has got lot of pimples.
Answer:

• I will make Harshad realize that his pimples or spectacles do not define ‘who he is’ or, determine his worth as a person. So, he should not let it impact him in a negative manner.
• I will also highlight his strengths to make him understand that his ‘self-concept’ should be based on a broader range of aspects than just a body image. I will also encourage him to engage in diverse social interactions to improve his sense of self-worth.

Question (c).
Sushma is too short so she does not mix with others.
Answer:

• I will talk to Sushma that being short is not something she should be ashamed of. Her height is just one aspect of her personality. She should not let it come in the way of her social interactions.
• I will also motivate Sushma to interact with others so that she can build strong and long-lasting social connections. It will make her feel positive and happy.

5. Write short notes in 50-60 words each.

Question 1.
Gender role
Answer:

• Gender role is an acquired attribute of self-concept which is psycho-social by nature.
• It is determined by the family atmosphere as well as cultural influences where the child learns through observation and imitation.
• e.g. if a girl is assertive and practical, she may be considered to be ‘masculine. This is because these attributes are usually associated with boys.
• However, gender-based roles are diluting in modern times. Society is approving and accepting these changes with an open mind.
• e.g. Pt. Birjoo Maharaj, Sanjeev Kapoor, Vikram Gaikwad are famous in female-dominated areas while Phogat sisters, Kalpana Chawla, Kiran Bedi are successful in male-dominated areas.

For your understanding

• Due to societal expectations, both males and females are expected to behave in certain ways, e.g. men are taught that they should be strong. If they cry, it is considered to be ‘girl’.
• However, now people have begun to realize that there is nothing wrong if a man takes up a feminine role or a woman behaves in a masculine way.

Question 2.
Carl Rogers’ theory of self
Answer:

• According to Carl Rogers, every individual has a tendency to actualize himself.
• Two important concepts related to Roger’s theory are the real self and the ideal self.
• The real self is what we actually are while the ideal self is what we want to be. The real self has a tendency to actualize himself. But the ideal self may consist of some goals which are beyond our reach.
• High congruence between the real self and ideal self leads to healthy productive life while a large gap or incongruence between them leads to maladjustment.
• By trying to achieve our full potential, we strive to be fully functioning individuals, i.e. achieve self-actualization.
• People who achieve self-actualization are well-balanced, well-adjusted, and interesting.

Question 3.
Self-efficacy
Answer:

• Self-efficacy is a person’s belief in his ability to accomplish some specific goal or a task.
• It depends on his trust in his own competency. Competence can vary between different situations, e.g. a person’s self-efficacy may be high in painting but low in cooking.
• Self-efficacy is based on ‘Social cognitive theory. The theory holds that humans actively shape their lives rather than passively reacting to the environment.
• Maddux defined self-efficacy as ‘what I believe I can do with my skills under certain conditions.
• Two factors related to efficacy are outcome expectancies (skills required to complete the goal) and efficacy expectancies (person’s analysis about whether he has those capacities).
• Self-efficacy can be improved by reinforcing oneself, developing one’s own skillset, choosing a role model for a particular activity and following him, seeking constructive feedback from others, and learning techniques to control one’s own emotional arousal.

Question 4.
Self-awareness
Answer:

• Self-awareness is the quality or trait that involves conscious awareness of one’s thoughts, feelings, behaviours, and traits.
• In order to have a proper self-concept, one must have some level of self-awareness, i.e. understanding that a person has a separate identity from others.
• According to Piaget, self-consciousness starts emerging between 15-24 months.
• Self-awareness is necessary before the child becomes aware of being a focus of attention. It enables him to understand what others are feeling. It also enables him to identify what belongs to him and what belongs to others.

Question 5.
Self-esteem
Answer:

• According to Seligman, ‘self-esteem is your overall evaluation of your worth as a person, high or low, based on all positive and negative self-perceptions. It is the respect one has for himself.
• A person may have various levels of self-esteem, e.g. a girl may have high self-esteem about her intelligence but may have low self-esteem about her looks.
• People with high self-esteem are positive, responsible, genuine, and committed to their goals. They have strong internal values and forgiving nature. They continuously seek to improve themselves.
• On the other hand, people with low self-esteem are negative, need externally oriented goals, and are impatient with themselves as well as others. They are unhappy and experience anxiety. They may also have a superiority or inferiority complex.
• Some of the ways to improve one’s self-esteem are as follows:
  • Eliminate negative self-talk
  • Recognize your strengths
  • Recognise self-worth
  • Accept mistakes
  • Accept rejection

Question 6.
Self-regulation
Answer:

• Self-regulation is being able to control our own thoughts, feelings, and actions for our own benefit.
• It involves monitoring one’s own actions and reactions. When one engages in self-regulation, he avoids impulsive reactions.
• It also involves predicting the consequences of our behaviour and avoiding behavioural patterns which can negatively affect ourselves or others in the future.
• Self-regulation also involves focusing on certain parts of life and ignoring some other parts for the time being, e.g. as exams approach, a person will stop spending time on Netflix and focus on studies.
• Higgins’ research on regulatory focus showed that people either have promotion regulatory focus or prevention regulatory focus.
• It means people either focus on achieving positive outcomes or don’t do anything in order to prevent negative outcomes.
• Self-regulation has crucial implications in our life.

6. Answer the following questions in 150-200 words.

Question 1.
Give a detailed account of the development of an individual’s self-concept through the stages of life.
Answer:

• On average, till the age of six months, the child is unaware of himself. As the child grows, he starts making distinctions between his own body and everything else.
• In normal children, face recognition with a mirror occurs at the average age of one and half years. They are capable of pretend play. They also start using personal pronouns, (I, me, mine).
• By the age of two, the child becomes aware of general expectations (what is good/ bad behaviour). They smile when people smile at them and frown when others get angry. They also develop a sense of self by comparing themselves with the standard role model (beginning of self-esteem).
• By the age of three, children start recognizing themselves and others as boys or girls.
• Between the age of three to twelve, the self-concept is defined mainly in terms of sex, age, family, and what the child believes he or she can or can’t do.
• When schooling starts at the age of five-six, a child begins to compare himself to others (beginning of social comparison). Also, the development of the private self-concept takes place during this stage.
• The final unfolding of self-concept during adolescence involves perspective taking, i.e. thinking and understanding other’s point of view. They might even enter into the stage of objective self-awareness.

Question 2.
Explain the theory of the self as proposed by Carl Rogers.
Answer:

• According to Carl Rogers, every individual has a tendency to actualize himself.
• Rogers also asserted that mentally healthy individuals have congruence between their experience and their self-concept while neurotic individuals deny awareness of their sensory and emotional experience.
• Two important concepts related to Roger’s theory are the real self and the ideal self.
• The real self (self-image) is what we actually are while the ideal self is what we want to be. The real self is our inner personality while the ideal self represents our dynamic ambitions and goals.
• The real self has a tendency to actualize himself. But the ideal self may consist of some goals which are beyond our reach. This may result in the gap between the real self and the ideal self.
• High congruence between the real self and ideal self leads to a greater sense of self-worth and healthy productive life while a large gap or incongruence between them leads to maladjustment.
• By trying to achieve our full potential, we strive to be fully functioning individuals, i.e., achieve self-actualization.
• Self-actualization means recognizing and exploring one’s full potential. People who achieve self-actualization are well-balanced, well-adjusted, and interesting.

Congruent

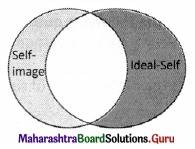
The self-image is similar to the ideal self.
There is more overlap.
This person can self-actualize.

Incongruent

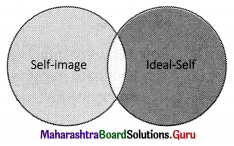
The self-image is different from the ideal self.
There is only a little overlap.
Here self-actualization will be difficult.

Class 11 Psychology Textbook Solutions Digest

• Psychology Class 11 Chapter 1 Question Answers
• Psychology Class 11 Chapter 2 Question Answers
• Psychology Class 11 Chapter 3 Question Answers
• Psychology Class 11 Chapter 4 Question Answers
• Psychology Class 11 Chapter 5 Question Answers
• Psychology Class 11 Chapter 6 Question Answers
• Psychology Class 11 Chapter 7 Question Answers
• Psychology Class 11 Chapter 8 Question Answers

Psychology Class 11 Chapter 2 Branches of Psychology Question Answers Maharashtra Board

Balbharti Maharashtra State Board Class 11 Psychology Solutions Chapter 2 Branches of Psychology Textbook Exercise Questions and Answers.

Branches of Psychology Class 11 Psychology Chapter 2 Questions and Answers

1A. Complete the following statements.

Question 1.
The branches of Psychology that explore relationships among different variables and human behaviour are known as ___________ Psychology.
a. Theoretical
b. Applied
c. Common
Answer:
a. Theoretical

Question 2.
The study of human behaviour at the workplace is the concern of ___________ Psychology.
a. Social
b. Industrial
c. Experimental
Answer:
b. Industrial

Question 3.
One can study the problems of adolescence in ___________
a. Developmental
b. Social
c. Cognitive
Answer:
a. Developmental

Question 4.
___________ Psychology is concerned with diagnosis and treatment of psychological disorders.
a. Counselling
b. Cognitive
c. Clinical
Answer:
c. Clinical

1B. Identify the odd item from the following.

Question 1.
Experimental Psychology, Social Psychology, Industrial Psychology, Cognitive Psychology
Answer:
Industrial Psychology

Question 2.
Clinical psychology, Industrial Psychology, Sports Psychology, Abnormal Psychology
Answer:
Abnormal Psychology

1C. Match the following pairs.

Question 1.

A	B
1. Developmental Psychology	a) Studies organisations, human factor design, and employee training
2. Criminal Psychology	b) Studies how people become who they are from conception to death
3. Educational Psychology	c) Studies thinking process
4. Industrial Psychology	d) Helps educators to promote learning
5. Social Psychology	e) Studies criminal behaviour
6. Cognitive Psychology	f) Studies the influence of other people upon an individual’s behaviour

Answer:

A	B
1. Developmental Psychology	b) Studies how people become who they are from conception to death
2. Criminal Psychology	e) Studies criminal behaviour
3. Educational Psychology	d) Helps educators to promote learning
4. Industrial Psychology	a) Studies organisations, human factor design, and employee training
5. Social Psychology	f) Studies the influence of other people upon an individual’s behaviour
6. Cognitive Psychology	c) Studies thinking process

2. Compare and contrast.

Question 1.
Theoretical and applied branches of Psychology.
Answer:
In theoretical branches, psychologists concentrate on carrying out research and forming theories while applied branches help individuals to use the knowledge gained from research to solve their problems.

The main aim of theoretical branches is to develop principles and establish laws in order to explain behaviour of human beings while the main objective of applied branches is to put knowledge into practice by helping individuals to adjust to their real-life situations.

Some theoretical branches are Developmental Psychology, Child Psychology, Social Psychology, Cognitive Psychology, Experimental Psychology, Abnormal Psychology while some applied branches are Educational Psychology, Clinical Psychology, Counselling Psychology, Criminal Psychology, Sports Psychology, Industrial Psychology.

For your understanding
The activities of applied psychology range from conducting field studies for finding practical solutions to problems to directly providing services to concerned individuals or organizations.

Question 2.
Abnormal Psychology and Clinical Psychology
Answer:
Abnormal Psychology is a theoretical branch that studies the unusual behavioural, emotional, and thinking patterns in individuals while Clinical Psychology is an applied branch that studies diagnoses and treats emotional and behavioural problems.

Abnormal Psychology aims to study the causes and factors leading to abnormal reactions like excessive suspiciousness, mental retardation, extreme mood swings, etc. On the other hand, Clinical Psychology deals with the diagnosis and treatment of mental illness, marital and familial conflicts, drug addiction, depression, delinquency, etc.

3. Write Short Notes.

Question 1.
Clinical Psychology
Answer:

• Clinical Psychology is an applied branch that studies, diagnoses, and treats emotional and behavioural problems in individuals like mental illness, marital and familial conflict, drug addiction, severe depression, alcoholism, delinquency, etc.
• For diagnosis, clinical psychologists collect detailed information regarding the client through psychological tests and by conducting interviews of clients as well as their family and friends.
• Once the problem is diagnosed, they use appropriate psychotherapy to help the client overcome his problem.
• Clinical psychologists usually work in hospitals and community health centers or they may have their private practice.
• Clinical Psychology is the largest subfield of Psychology.

Question 2.
Cognitive Psychology
Answer:

• Cognitive Psychology concentrates on higher mental processes such as thinking, reasoning, and decision making.
• It is concerned with the study of attention, perception, language development, thinking, memory, and problem-solving.
• It also answers questions related to the disruption of memory, different types of learning styles and disorders, causes of speech impairment as well as the functioning of decision-making mechanisms.

Question 3.
Developmental Psychology
Answer:

• Developmental Psychology studies changes in behaviour from conception to death.
• It is the scientific study of how and why human beings change over the course of their life.
• It examines changes across three major dimensions, viz. physical, cognitive, and social development.
• It aims to explain how thinking, feeling, and behaviour change throughout life.
• It may study a specific period of life like childhood, adolescence, adulthood, and old age.

Question 4.
Industrial Psychology
Answer:

• Industrial Psychology is concerned with behaviour of people working in an organization.
• Industrial psychologists play a crucial role in selection and placement, workforce motivation, and job satisfaction as well as appraisals and grievances.
• They help to enhance motivation, group morale, and leadership skills among the employees.
• Consumer Psychology is a branch of Industrial Psychology that deals with consumer behaviour, quality of products, brand loyalty, and influence of advertisement on purchasing.

4. Suggest an appropriate branch of psychology related to the following situations.

Question 1.
A husband and wife do not understand each other so they keep fighting.
Answer:
Counselling Psychology

Question 2.
My friend’s father lost his job and he is in depression.
Answer:
Clinical Psychology

Question 3.
A 5th standard student is unable to concentrate.
Answer:
Educational Psychology

Question 4.
I want to study the process of thinking and learning.
Answer:
Cognitive Psychology

Question 5.
I want proper information about attitude, prejudice, or conflicts in a group.
Answers:
Social Psychology

5. Answer the following questions in detail.

Question 1.
Explain any five theoretical branches of Psychology.
Answer:
Some theoretical branches of Psychology are as follows:

Child Psychology: It deals with the biological, psychological, and emotional changes that occur during childhood. These changes occur as the individual progresses from being dependent to becoming independent. Child psychologists study problems related to children such as lying, bunking school, stealing, bedwetting. They also conduct researches on effective child-rearing practices and the role of reinforcement in motivating children.

Social Psychology: It studies how an individual influences other people and gets influenced by them. According to Myers, Social Psychology is the scientific study of how an individual’s behaviour is affected by others. The primary focus of Social Psychology is to understand how individuals are affected by other people. It examines issues such as co-operation or conflicts within groups, attitudes, prejudices, friendliness, and leadership qualities of an individual.

Experimental Psychology: It attempts to understand the fundamental causes of behaviour. It studies how people learn, remembers, reason, and respond emotionally. It deals with problems related to sensation, perception, learning and memory. Experimental psychologists conduct laboratory experiments to study how people react to sensory stimuli and perceive the world.

Cognitive Psychology: It concentrates on higher mental processes such as thinking, reasoning, and decision making. It also answers questions related to the disruption of memory, different types of learning styles and disorders, causes of speech impairment as well as the functioning of decision-making mechanisms.

Abnormal Psychology: It studies unusual patterns of behaviour, emotions, and thinking. It aims to study the causes and factors leading to abnormal reactions such as excessive suspiciousness, extreme mood swings, perceiving objects or situations which are not real, mental retardation, extreme fear of objects, animals, or situations, etc.

Question 2.
Describe any five applied branches of Psychology.
Answer:
Some applied branches of Psychology are as follows:

Educational Psychology: It studies all factors related to education. It is concerned with increasing the efficiency of the teaching and learning process. It also focuses on the learning difficulties of slow learners, exceptional as well as average children. Educational psychologists are primarily associated with schools, colleges, and universities. They try to design intervention programs to develop motivation, effective study habits, and a better classroom environment. They also deal with behavioral issues of children such as learning disorders, hyperactivity, lack of concentration, ADHD.

Counselling Psychology: It deals with milder behavioural problems. Counselling psychologists offer guidance about adjustment issues faced by a person, e.g. difficulties experienced by a person in studies, personal life issues, or workplace issues. Counselling psychologists are also involved in vocational and career guidance.

Criminal Psychology: It deals with the motives behind criminal behaviour. Criminal psychologists are concerned with identifying the causes of crime, studying the personality of criminals, suggesting preventive measures to control criminal behaviour, and implementing plans for criminal rehabilitation. They play a significant role in the forensic department to uncover the scene of the crime. They generally work with the law enforcement department or the criminal investigation department or social organisations working for rehabilitation.

Sports Psychology: It helps sportspersons to maintain their motivation and stamina during the actual performance. It also aids sportspersons to maintain themselves when they are not on the field. Sports psychologists help players to maintain composure when they are under pressure, maintain emotional balance when they go through a bad patch, and maintain wellness when they are recovering from personal injuries.

Industrial Psychology: It is concerned with the behaviour of people working in an organisation. Industrial psychologists play a crucial role in selection and placement, workforce motivation, and job satisfaction as well as appraisals and grievances. Consumer Psychology is a branch of Industrial Psychology that deals with consumer behaviour.
applied branch of Psychology. The development of aviation and space exploration programmes has accelerated growth in Engineering Psychology.

Question 3.
Write any five career opportunities in Psychology.
Answer:
Counselling Psychology: An individual can become an educational counsellor or vocational counsellor or marriage counsellor and help people to solve career-related or personal problems.

Social Psychology: An individual can become a public relations officer or social welfare officer or labour welfare officer.
These officers attempt to solve various social problems.

Sports Psychology: An individual can become a sports counsellor and work in gyms, schools, or professional sports teams. These counsellors help to improve the confidence, concentration, and morale of players.

Military Psychology: An individual can become an army mental health specialist or army psychologist, navy psychologist, air force psychologist, or marine psychologist. These psychologists play a role in the selection of army officers. They also improve the morale of people in defense services.

Rehabilitation Psychology: An individual can become a special educator or rehabilitation psychologist or disaster management and rehabilitation officer. A special educator works for specially-abled persons while a rehabilitation psychologist works in remand homes. A disaster management and rehabilitation officer helps in disaster management and rehabilitation.

Activities

Activity 3. (Textbook Page No. 14)

Try to find at least one example that can fit into each of the above sub-branches of theoretical Psychology.
Answer:

• Developmental Psychology: Mr. Mehta conducted a comparative study of physical and cognitive development during early childhood and late childhood.
• Child Psychology: Mr. Singh studied the impact of parental divorce on the social behaviour of a child.
• Social Psychology: Mrs. Joshi examined the effect of peer pressure on a person’s dressing style.
• Cognitive Psychology: Mr. Dsouza studied factors influencing the attention span of students during lectures.
• Experimental Psychology: Mr. Iyer studied the reactions of individuals in a laboratory to disgusting events.
• Abnormal Psychology: Mrs. Ajmera conducted a study on the genetic factors influencing depression.

Activity 4. (Textbook Page No. 15)

Can you think of at least one problem that educational psychologists can find solutions to, concerning the following areas?

1. Behaviour of the student
2. Teaching methods
3. Teacher’s behaviour in the class

Answer:

1. Why do students bunk lectures?
2. Do interactions with students during lectures improve learning outcomes?
3. Is it possible to use reward and punishment techniques to motivate students?

Activity 6. (Textbook Page No. 16)

Can you think of at least one problem that a counselling psychologist can find solutions to, concerning the following areas?

1. Adjusting with peers
2. Adjusting with parents and siblings
3. Making decisions about a career

Answer:

1. How conflict with peers affects an individual’s mood?
2. How generation gap may lead to a difference of opinion?
3. How to choose a career that matches one’s interests and aptitude?

Activity 8. (Textbook Page No. 16)

Think of at least one problem that a sports psychologist can find solutions to, concerning the following areas.

1. Improving team spirit
2. Emotional management
3. Improving self-confidence

Answer:

1. How to build healthy relations with team members?
2. How to remain calm and composed even after a failure?
3. How to believe in one’s capabilities during challenging tournaments?

Activity 9. (Textbook Page No. 17)

1. Talk to your parents/teachers and enlist the factors that give them satisfaction at their work.
2. While buying something from the market, which factors affect your desires? Enlist these factors that influence your choice. For example advertisements, brands, etc.

Answer:

1. Some of the factors that are associated with job satisfaction are the extent to which one enjoys his work, relation with superiors and colleagues, rate of remuneration and other incentives as well as the scope of growth in the future.
2. Some of the factors that influence consumer choices are quality of the product, price of the product, price of substitute and complementary products, the income of a person, latest trends, personal choices, habits, and opinions of significant others.

Class 11 Psychology Textbook Solutions Digest

• Psychology Class 11 Chapter 1 Question Answers
• Psychology Class 11 Chapter 2 Question Answers
• Psychology Class 11 Chapter 3 Question Answers
• Psychology Class 11 Chapter 4 Question Answers
• Psychology Class 11 Chapter 5 Question Answers
• Psychology Class 11 Chapter 6 Question Answers
• Psychology Class 11 Chapter 7 Question Answers
• Psychology Class 11 Chapter 8 Question Answers

Psychology Class 11 Chapter 1 Story of Psychology Question Answers Maharashtra Board

Balbharti Maharashtra State Board Class 11 Psychology Solutions Chapter 1 Story of Psychology Textbook Exercise Questions and Answers.

Story of Psychology Class 11 Psychology Chapter 1 Questions and Answers

1A. Complete the following statements.

Question 1.
Psychology is a study of ______________
(A) mind
(B) behaviour
(C) soul
Answer:
(B) behaviour

Question 2.
processes include thinking, memory, emotions, etc.
(A) Mental
(B) Cognitive
(C) Spiritual
Answer:
(B) Cognitive

1B. Match the following pairs.

Question 1.

A	B
1. Tri-Doshas	a. First laboratory of Psychology
2. Tri-Gunas	b. Study of unconscious
3. Wilhelm Wundt	c. Perception, thinking, memory, etc.
4. Sigmund Freud	d. Sattva, Rajas, Tamas
5. Cognitive processes	e. Ashtanga Yog
6. Patanjali	f. Kapha, Vata and Pitta

Answer:
1 – f, 2 – d, 3 – a, 4 – b, 5 – c, 6 – e

1C. State whether the following statements are true or false.

Question 1.
Psychology is a study of the mind.
Answer:
False

Question 2.
The first mental hospital in India was established in Mumbai.
Answer:
False

Question 3.
There was no study of mental processes in India till the formal discipline of Psychology was recognized as a science.
Answer:
False

Question 4.
Dr. Sigmund Freud proposed the concept of the unconscious.
Answer:
True

Question 5.
Control is one of the objectives of Psychology.
Answer:
True

1D. Identify the odd item from the following and give reasons for the same.

Question 1.
Soul, Mind, Feeling, Consciousness, Behaviour.
Answer:
Feeling
Reason: Rest is the term used in the definition of Psychology.

Question 2.
Walking, dancing, playing, thinking, eating.
Answer:
Thinking
Reason: The rest are overt behaviours.

Question 3.
Yam, Niyam, Karya, Aasana, Pratyahar.
Answer:
Karya
Reason: The rest are the aspects of Ashtanga Yoga.

Question 4.
Feeling, memory, attention, perception
Answer:
Feeling
Reason: The rest are the processes in the study of cognition.

1E. Complete the following table.

Question 1.

Answer:
1. Greek word: Psyche – Soul
2. John Locke – Empty slate
3. First Psychological Laboratory
4. Sigmund Freud – Founder of Psychoanalysis
5. John Watson OR Organism’s response to stimuli – Behaviour

2. Explain the following concepts.

Question 1.
Psychology
Answer:
The word Psychology is derived from Greek words – ‘Psyche’ and ‘Logos’. It is denoted by the Greek Alphabet “Psi” and the symbol is 4L Wilhelm Wundt defined it as “the study of consciousness”. Dr. Sigmund Freud defined it as “the study of unconsciousness”. John B. Watson defined it as “the science of human behaviour”. The latest definition of Psychology is ‘The study of human behaviour and mental processes.

For your understanding

• Conscious mind: It is the level of mind that someone is aware of at any particular point in time.
• Unconscious mind: It contains thoughts, memories, and desires that are buried deep in us. Although we are not aware of their existence, they exert great influence on our behaviour.

Question 2.
Behaviour
Answer:
In general, behaviour is an organism’s response to various internal and external stimuli.
John Watson defined behaviour as ‘anything that can be observed, recorded and studied in human beings and animals.’ Behaviour is either overt (seen) or covert (hidden).

Question 3.
Overt behaviour
Answer:
Overt behaviour is that behaviour that is directly noticeable or observable. It includes responses such as walking, talking, dancing.

Question 4.
Covert behaviour
Answer:
Covert behaviour is that which is not directly noticeable but can be inferred from behaviour like thinking, feeling. It basically includes mental processes.

Question 5.
Stimulus
Answer:
Stimulus is defined as any physical event or condition that gives rise to a reaction. It can be external or internal.
In simple words, it is an object or event that elicits a sensory or behavioural response in an organism.

Question 6.
Response
Answer:
A response is defined as a reaction of the organism to a given stimulus. All organisms respond differently to the same stimulus.
Example:
Stimulus (S): A teacher asks students to prepare a presentation.
Organism (O): All students present in class.
Response (R):

• Some students actively participate in presentations.
• Some students remain silent as they are scared to talk in front of the entire class.

3. Answer the following questions in 35-40 words.

Question 1.
Psychology is a science: explain why?
Answer:

• Psychology is the scientific study of human behaviour and mental processes.
• Through experiments and observations, Psychologists try to analyze and predict human behaviour. This shows the empirical nature of Psychology.
• Wilhelm Wundt used scientific methods to study fundamental psychological processes. John Watson also conducted scientific research on animal behaviour and child-rearing.

Ques 2.
Explain the S-O-R model, with your own experience.
Answer:

• The S-O-R model explains how organisms respond differently to the same stimulus. It can be explained as follows:
  
• Example: Suppose Neha is an excellent orator while her friend Seema is afraid of public speaking.
  • Stimulus: The teacher asks Neha and Seema to give speeches.
  • Organism: Neha and Seema.
  • Response: Neha will confidently give her speech.
    Seema is likely to get cold feet and become nervous.
• This shows that different organisms (Neha and Seema) react differently to the same situation.

Question 3.
Explain the goals of Psychology.
Answer:

1. Describe
   • To precisely identify and classify behaviours and mental processes
   • Involves recording behaviour using various tools
2. Explain
   • To understand the causes of behaviour through meaningful explanation of facts
   • Involves the use of standardized tests
   • Behaviour observed in most people can be generalized
3. iii. Predict
   • To predict how given conditions will lead to a particular behaviour and mental processes.
   • b. Involves knowledge of possible outcomes
4. Control
   • To mould behaviour in a particular direction
   • Involves the use of psychological principles and psychotherapeutic techniques

4. Give a historical account of the emergence of Psychology as a science.
Answer:

• Psychology is a vast field studying behavioural aspects of mankind and it started as a branch of Philosophy. It evolved as a separate branch in the 19th century.
• The first attempt to define Psychology was made based on the terminology. The word ‘Psychology’ is derived from two Greek words: ‘Psyche’ (soul or mind) and ‘Logos’ (science or branch of knowledge).
• Rational sciences establish facts based on observation and experimentation. However, neither soul nor mind can be observed. Hence, the definition of Psychology changed over time.
• In the late 19th century, Wilhelm Wundt established the first psychological laboratory at Leipzig University. He defined Psychology as the study of consciousness.
• Sigmund Freud defined Psychology as the study of the unconscious while John Watson defined it as ‘Science of human behaviour’.
• The latest definition of Psychology is the ‘Study of human behaviour and processes.’
• Psychology as a discipline evolved over time.

5. Describe the goals of Psychology.
Answer:

1. Describe
   • To precisely identify and classify behaviours and mental processes
   • Involves recording behaviour using various tools
2. Explain
   • To understand the causes of behaviour through meaningful explanation of facts
   • Involves the use of standardized tests
   • Behaviour observed in most people can be generalized
3. Predict
   • To predict how given conditions will lead to a particular behaviour and mental processes.
   • Involves knowledge of possible outcomes
4. Control
   • To mould behaviour in a particular direction
   • Involves the use of psychological principles and psychotherapeutic techniques

Activities

Activity 2. (Textbook Page No. 3)

Do you agree with the definition of Psychology as the Science which deals with the soul? If yes why? If no, why?
Answer:

• No, I don’t agree with this definition since the soul refers to the spiritual part of a person; which is believed to exist in some form even after death.
• Psychology is not a spiritual science. Since it studies the mental activities and behaviour of living beings, this definition seems to be incorrect.

Activity 3 (Textbook Page No. 3)

Collect information about Bahinabai Chaudhari: Mana (description of Mind)
Answer:

• Bahinabai Chaudhari (11 Aug 1880 – 3 Dec 1951) was an illiterate cotton farmer from the Jalgaon district in Maharashtra.
• She was a famous Marathi poet. Her poems captured the essence of her life, reflect the culture of the village and farming life, and present her wisdom.
• She has beautifully compared the mind with different aspects of nature such as wind, waves, butterflies, small particles, etc. The poet stressed that the mind is a unique creation of God and nothing in this world compares to it.

Activity 5 (Textbook Page No. 4)

Do you agree with the definition that Psychology is the study of the unconscious? What could be the limitations of this definition?
Answer:
I agree with the above definition because Psychology studies unconscious behaviour. A person himself may not be aware of unconscious aspects of his personality even when it may have a significant impact on his thoughts and behaviour. Psychology enables us to understand this unconscious side of human beings and hence, I agree with this definition. However, the limitation of the definition is the unconscious mind. It can’t be observed directly and hence is difficult to study it. Furthermore, Psychology is also concerned with the study of the conscious mind.

Activity 6 (Textbook Page No. 5)

Make a note of how your friends react to the same stimulus in a different way. Example: examination.
Answer:

• Nisha and Seema are two of my friends. During the examination, Seema gets extremely tensed. She is not able to concentrate. She even fails to sleep and eat peacefully.
• She needs the constant emotional support of her parents and friends to overcome her fear.
• Conversely, Nisha views the exam as a challenge. She does not get worked up.
• Instead, her moderate tension motivates her to study sincerely.
• She also knows that failure is a part and parcel of life and tries to learn from each mistake.
• Hence, she remains calm and confident even during the exam period.

Activity 8 (Textbook Page No. 6)

Find out more attributes of Vata, Kapha, and Pitta.
Answer:
Vata:

• Elements: Air + Space
• Body Type: Slim, lean
• Properties: Energetic, Moody, Creative

Kapha:

• Elements: Earth + Water
• Body Type: Average build, moderate weight
• Properties: Strong build, Affectionate, Cool

Pitta:

• Elements: Fire + Water
• Body Type: Large frame, heavy
• Properties: Smart, Fiery nature

Activity 9 (Textbook Page No. 6)

Find out different characteristics of Rajas, Tamas, and Sattva Guna.
Answer:
Rajas represent passion, action, energy, and motion. Tamas manifests itself as impurity, laziness, and darkness. Sattva manifests itself as purity, knowledge, and harmony.

Activity 10 (Textbook Page No. 7)

Look at the statements given below. Analyze each one of them and come up with goats of Psychology or the role that Psychology plays in real life.

Question 1.
A group of Psychologists observed 1000 individuals and recorded their behaviour and reactions.
Answer:
The goal of description (What): Describing what happens in a particular situation

Question 2.
After analyzing their responses, they tried to understand the reasons behind their behaviours.
Answer:
The goal of explanation (Why): Explaining why a particular instance happened

Question 3.
These observations can be generalized to the entire population. Therefore behaviour of an individual under stressful situations can be predicted.
Answer:
The goal of prediction (Anticipate): Predicting how people will behave under a given situation

Question 4.
The Psychologists came up with some conclusions so that people can change their responses to stressful situations for the better.
Answer:
The goal of control (Modify): Controlling actions of human beings with the help of psychological techniques.

Activity 11 (Textbook Page No. 8)

Find more examples of each of the above goals of Psychology. They could be real examples that you know or you have read about or they could be fictional examples.
Answer:

Goal	Example	Explanation
i. Describe	Recording how different students behave during exam period	Neha is confident while Reena gets anxious.
ii. Explain	Analyzing why different students behave in different ways during exam	Neha has always done well in exams while Reena gets tensed due to over-expectations from her parents.
iii. Predict	Anticipating how students will react in other stressful situations	Neha is likely to handle stressful situations calmly than Reena
iv. Control	Enabling anxious students to control their anxiety level during exams and other stressful situations	Reena could take counselling to improve her abilities to deal with examinations and other stressful situations.

 

Class 11 Psychology Textbook Solutions Digest

• Psychology Class 11 Chapter 1 Question Answers
• Psychology Class 11 Chapter 2 Question Answers
• Psychology Class 11 Chapter 3 Question Answers
• Psychology Class 11 Chapter 4 Question Answers
• Psychology Class 11 Chapter 5 Question Answers
• Psychology Class 11 Chapter 6 Question Answers
• Psychology Class 11 Chapter 7 Question Answers
• Psychology Class 11 Chapter 8 Question Answers

Sets and Relations Class 11 Commerce Maths 1 Chapter 1 Exercise 1.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 1 Sets and Relations Ex 1.1 Questions and Answers.

Std 11 Maths 1 Exercise 1.1 Solutions Commerce Maths

Question 1.
Describe the following sets in Roster form:
(i) {x / x is a letter of the word ‘MARRIAGE’}
(ii) {x / x is an integer, –\(\frac{1}{2}\) < x < \(\frac{9}{2}\)}
(iii) {x / x = 2n, n ∈ N}
Solution:
(i) Let A = {x / x is a letter of the word ‘MARRIAGE’}
∴ A = {M, A, R, I, G, E}

(ii) Let B = {x / x is an integer, –\(\frac{1}{2}\) < x < \(\frac{9}{2}\)}
∴ B = {0, 1, 2, 3, 4}

(iii) Let C = {x / x = 2n, n ∈ N}
∴ C = {2, 4, 6, 8, ….}

Question 2.
Describe the following sets in Set-Builder form:
(i) {0}
(ii) {0, ±1, ±2, ±3}
(iii) \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
Solution:
(i) Let A = {0}
0 is a whole number but it is not a natural number.
∴ A = {x / x ∈ W, x ∉ N}

(ii) Let B = {0, ±1, ±2, ±3}
B is the set of elements which belongs to Z from -3 to 3.
∴ B = {x / x ∈ Z, -3 ≤ x ≤ 3}

(iii) Let C = \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
∴ C = {x / x = \(\frac{n}{n^{2}+1}\), n ∈ N, n ≤ 7}

Question 3.
If A = {x / 6x² + x – 15 = 0}, B = {x / 2x² – 5x – 3 = 0}, C = {x / 2x² – x – 3 = 0}, then find (i) (A ∪ B ∪ C) (ii) (A ∩ B ∩ C)
Solution:
A = {x / 6x² + x – 15 = o}
∴ 6x² + x – 15 = 0
∴ 6x² + 10x – 9x – 15 = 0
∴ 2x(3x + 5) – 3(3x + 5) = 0
∴ (3x + 5) (2x – 3) = 0
∴ 3x + 5 = 0 or 2x – 3 = 0
∴ x = \(\frac{-5}{3}\) or x = \(\frac{3}{2}\)
∴ A = \(\left\{\frac{-5}{3}, \frac{3}{2}\right\}\)

B = {x / 2x² – 5x – 3 = 0}
∴ 2x² – 5x – 3 = 0
∴ 2x² – 6x + x – 3 = 0
∴ 2x(x – 3) + 1(x – 3) = 0
∴ (x – 3)(2x + 1) = 0
∴ x – 3 = 0 or 2x + 1 = 0
∴ x = 3 or x = \(\frac{-1}{2}\)
∴ B = {\(\frac{-1}{2}\), 3}

C = {x / 2x² – x – 3 = 0}
∴ 2x² – x – 3 = 0
∴ 2x² – 3x + 2x – 3 = 0
∴ x(2x – 3) + 1(2x – 3) = 0
∴ (2x – 3) (x + 1) = 0
∴ 2x – 3 = 0 or x + 1 = 0
∴ x = \(\frac{3}{2}\) or x = -1
∴ C = {-1, \(\frac{3}{2}\)}

(i) A ∪ B ∪ C = \(\left\{-\frac{5}{3}, \frac{3}{2}\right\} \cup\left\{\frac{-1}{2}, 3\right\} \cup\left\{-1, \frac{3}{2}\right\}\) = \(\left\{\frac{-5}{3},-1, \frac{-1}{2}, \frac{3}{2}, 3\right\}\)

(ii) A ∩ B ∩ C = { }

Question 4.
If A, B, C are the sets for the letters in the words ‘college’, ‘marriage’ and ‘luggage’ respectively, then verify that [A – (B ∪ C)] = [(A – B) ∩ (A – C)].
Solution:
A = {c, o, l, g, e}
B = {m, a, r, i, g, e}
C = {l, u, g, a, e}
B ∪ C = {m, a, r, i, g, e, l, u}
A – (B ∪ C) = {c, o}
A – B = {c, o, l}
A – C = {c, o}
∴ [(A – B) ∩ (A – C)] = {c, o} = A – (B ∪ C)
∴ [A – (B ∪ C)] = [(A – B) ∩ (A – C)]

Question 5.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8} and universal set X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then verify the following:
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(iii) (A ∪ B)’ = A’ ∩ B’
(iv) (A ∩ B)’ = A’ ∪ B’
(v) A = (A ∩ B) ∪ (A ∩ B’)
(vi) B = (A ∩ B) ∪ (A’ ∩ B)
(vii) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Solution:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8}, X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(i) B ∩ C = {4, 5, 6}
∴ A ∪ (B ∩ C) = {1, 2, 3, 4, 5, 6} ……(i)
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
∴ (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5, 6} ……(ii)
From (i) and (ii), we get
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

(ii) B ∪ C = {3, 4, 5, 6, 7, 8}
∴ A ∩ (B ∪ C) = {3, 4} …..(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) ∪ (A ∩ C) = {3, 4} …..(ii)
From (i) and (ii), we get
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

(iii) A ∪ B = {1, 2, 3, 4, 5, 6}
∴ (A ∪ B)’ = {7, 8, 9, 10} …….(i)
A’ = {5, 6, 7, 8, 9, 10}, B’ = {1, 2, 7, 8, 9, 10}
∴ A’ ∩ B’ = {7, 8, 9, 10} ……(ii)
From (i) and (ii), we get
(A ∪ B)’ = A’ ∩ B’

(iv) A ∩ B = {3, 4}
∴ (A ∩ B)’ = {1, 2, 5, 6, 7, 8, 9, 10} ……(i)
A’ = {5, 6, 7, 8, 9, 10}
B’ = {1, 2, 7, 8, 9, 10}
∴ A’ ∪ B’ = {1, 2, 5, 6, 7, 8, 9, 10} ……(ii)
From (i) and (ii), we get
(A ∩ B)’ = A’ ∪ B’

(v) A = {1, 2, 3, 4} …..(i)
A ∩ B = {3, 4}
B’ = {1, 2, 7, 8, 9, 10}
A ∩ B’ = {1, 2}
∴ (A ∩ B) ∪ (A ∩ B’) = {1, 2, 3, 4} ……(ii)
From (i) and (ii), we get
A = (A ∩ B) ∪ (A ∩ B’)

(vi) B = {3, 4, 5, 6} …..(i)
A ∩ B = {3, 4}
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ (A ∩ B) ∪ (A’ ∩ B) = {3, 4, 5, 6} …..(ii)
From (i) and (ii), we get
B = (A ∩ B) ∪ (A’ ∩ B)

(vii) A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
A ∩ B = {3, 4}, A ∪ B = {1, 2, 3, 4, 5, 6}
∴ n(A) = 4, n(B) = 4,
n(A ∩ B) = 2,
n(A ∪ B) = 6 …..(i)
∴ n(A) + n(B) – n(A ∩ B) = 4 + 4 – 2
∴ n(A) + n(B) – n(A ∩ B) = 6 …..(ii)
From (i) and (ii), we get
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Question 6.
If A and B are subsets of the universal set X and n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5, find
(i) n(A ∪ B)
(ii) n(A ∩ B)
(iii) n(A’ ∩ B)
(iv) n(A ∩ B’)
Solution:
n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5
(i) n(A ∪ B) = n(X) – [n(A ∪ B)’]
= n(X) – n(A’ ∩ B’)
= 50 – 5
= 45

(ii) n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 35 + 20 – 45
= 10

(iii) n(A’ ∩ B) = n(B) – n(A ∩ B)
= 20 – 10
= 10

(iv) n(A ∩ B’) = n(A) – n(A ∩ B)
= 35 – 10
= 25

Question 7.
Out of 200 students, 35 students failed in MHT-CET, 40 in AIEEE and 40 in IIT entrance, 20 failed in MHT-CET and AIEEE, 17 in AIEEE and IIT entrance, 15 in MHT-CET and IIT entrance, and 5 failed in all three examinations. Find how many students
(i) did not fail in any examination.
(ii) failed in AIEEE or IIT entrance.
Solution:
Let A = set of students who failed in MHT-CET
B = set of students who failed in AIEEE
C = set of students who failed in IIT entrance
X = set of all students
∴ n(X) = 200, n(A) = 35, n(B) = 40, n(C) = 40,
n(A ∩ B) = 20, n(B ∩ C) = 17, n(A ∩ C) = 15, n(A ∩ B ∩ C) = 5

(i) n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
= 35 + 40 + 40 – 20 – 17 – 15 + 5
= 68
∴ No. of students who did not fail in any exam = n(X) – n(A ∪ B ∪ C)
= 200 – 68
= 132

(ii) No. of students who failed in AIEEE or IIT entrance = n(B ∪ C)
= n(B) + n(C) – n(B ∩ C)
= 40 + 40 – 17
= 63

Question 8.
From amongst 2000 literate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read
(i) at least one of the newspapers.
(ii) neither Marathi nor English newspaper.
(iii) only one of the newspapers.
Solution:
Let M = set of individuals who read Marathi newspapers
E = set of individuals who read English newspapers
X = set of all literate individuals
∴ n(X) = 2000,
n(M) = \(\frac{70}{100}\) × 2000 = 1400
n(E) = \(\frac{50}{100}\) × 2000 = 1000
n(M ∩ E) = \(\frac{32.5}{2}\) × 2000 = 650
n(M ∪ E) = n(M) + n(E) – n(M ∩ E)
= 1400 + 1000 – 650
= 1750

(i) No. of individuals who read at least one of the newspapers = n(M ∪ E) = 1750.
(ii) No. of individuals who read neither Marathi nor English newspaper = n(M’ ∩ E’)
= n(M ∪ E)’
= n(X) – n(M ∪ E)
= 2000 – 1750
= 250
(iii) No. of individuals who read only one of the newspapers = n(M ∩ E’) + n(M’ ∩ E)
= n(M ∪ E) – n(M ∩ E)
= 1750 – 650
= 1100

Question 9.
In a hostel, 25 students take tea, 20 students take coffee, 15 students take milk, 10 students take both tea and coffee, 8 students take both milk and coffee. None of them take tea and milk both and everyone takes atleast one beverage, find the number of students in the hostel.
Solution:
Let T = set of students who take tea
C = set of students who take coffee
M = set of students who take milk
∴ n(T) = 25, n(C) = 20, n(M) = 15,
n(T ∩ C) = 10, n(M ∩ C) = 8, n(T ∩ M) = 0, n(T ∩ M ∩ C) = 0

∴ Number of students in the hostel = n(T ∪ C ∪ M)
= n(T) + n(C) + n(M) – n(T ∩ C) – n(M ∩ C) – n(T ∩ M) + n(T ∩ M ∩ C)
= 25 + 20 + 15 – 10 – 8 – 0 + 0
= 42

Question 10.
There are 260 persons with skin disorders. If 150 had been exposed to the chemical A, 74 to the chemical B, and 36 to both chemicals A and B, find the number of persons exposed to
(i) Chemical A but not Chemical B
(ii) Chemical B but not Chemical A
(iii) Chemical A or Chemical B.
Solution:
Let A = set of persons exposed to chemical A
B = set of persons exposed to chemical B
X = set of all persons
∴ n(X) = 260, n(A) = 150, n(B) = 74, n(A ∩ B) = 36

(i) No. of persons exposed to chemical A but not to chemical B = n(A ∩ B’)
= n(A) – n(A ∩ B)
= 150 – 36
= 114

(ii) No. of persons exposed to chemical B but not to chemical A = n(A’ ∩ B)
= n(B) – n(A ∩ B)
= 74 – 36
= 38

(iii) No. of persons exposed to chemical A or chemical B = n(A ∪ B)
= n(A) + n(B) – n(A ∩ B)
= 150 + 74 – 36
= 188

Question 11.
If A = {1, 2, 3}, write the set of all possible subsets of A.
Solution:
A = {1, 2, 3}
∴ { }, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3} and {1, 2, 3} are all the possible subsets of A.

Question 12.
Write the following intervals in set-builder form:
(i) (-3, 0)
(ii) [6, 12]
(iii) (6, 12)
(iv) (-23, 5)
Solution:
(i) (-3, 0) = {x / x ∈ R, -3 < x < 0}
(ii) [6, 12] = {x / x ∈ R, 6 ≤ x ≤ 12}
(iii) (6, 12) = {x / x ∈ R, 6 < x < 12}
(iv) (-23, 5) = {x / x ∈ R, -23 < x < 5}

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 1.1 Solutions
• 11th Commerce Maths Exercise 1.2 Solutions
• 11th Commerce Maths Miscellaneous Exercise 1 Solutions

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 9 Differentiation Miscellaneous Exercise 9 Questions and Answers.

11th Maths Part 2 Differentiation Miscellaneous Exercise 9 Questions And Answers Maharashtra Board

(I) Select the appropriate option from the given alternatives.

Question 1.
If y = \(\frac{x-4}{\sqrt{x+2}}\), then \(\frac{d y}{d x}\) is
(A) \(\frac{1}{x+4}\)
(B) \(\frac{\sqrt{x}}{\left(\sqrt{x+2)^{2}}\right.}\)
(C) \(\frac{1}{2 \sqrt{x}}\)
(D) \(\frac{x}{(\sqrt{x}+2)^{2}}\)
Answer:
(C) \(\frac{1}{2 \sqrt{x}}\)
Hint:

Question 2.
If y = \(\frac{a x+b}{c x+d}\),then \(\frac{d y}{d x}\) =
(A) \(\frac{a b-c d}{(c x+d)^{2}}\)
(B) \(\frac{a x-c}{(c x+d)^{2}}\)
(C) \(\frac{a c-b d}{(c x+d)^{2}}\)
(D) \(\frac{a d-b c}{(c x+d)^{2}}\)
Answer:
(D) \(\frac{a d-b c}{(c x+d)^{2}}\)
Hint:

Question 3.
If y = \(\frac{3 x+5}{4 x+5}\), then \(\frac{d y}{d x}\) =
(A) \(-\frac{15}{(3 x+5)^{2}}\)
(B) \(-\frac{15}{(4 x+5)^{2}}\)
(C) \(-\frac{5}{(4 x+5)^{2}}\)
(D) \(-\frac{13}{(4 x+5)^{2}}\)
Answer:
(C) \(-\frac{5}{(4 x+5)^{2}}\)
Hint:

Question 4.
If y = \(\frac{5 \sin x-2}{4 \sin x+3}\), then \(\frac{d y}{d x}\) =
(A) \(\frac{7 \cos x}{(4 \sin x+3)^{2}}\)
(B) \(\frac{23 \cos x}{(4 \sin x+3)^{2}}\)
(C) \(-\frac{7 \cos x}{(4 \sin x+3)^{2}}\)
(D) \(-\frac{15 \cos x}{(4 \sin x+3)^{2}}\)
Answer:
(B) \(\frac{23 \cos x}{(4 \sin x+3)^{2}}\)
Hint:

Question 5.
Suppose f(x) is the derivative of g(x) and g(x) is the derivative of h(x).
If h(x) = a sin x + b cos x + c, then f(x) + h(x) =
(A) 0
(B) c
(C) -c
(D) -2(a sin x + b cos x)
Answer:
(B) c
Hint:
h(x) = a sin x + b cos x + c
Differentiating w.r.t. x, we get
h'(x) = a cos x – b sin x = g(x) …..[given]
Differentiating w.r.t. x, we get
g'(x) = -a sin x – b cos x = f(x) …..[given]
∴ f(x) + h(x) = -a sin x – b cos x + a sin x + b cos x + c
∴ f(x) + h(x) = c

Question 6.
If f(x) = 2x + 6, for 0 ≤ x ≤ 2
= ax² + bx, for 2 < x ≤ 4
is differentiable at x = 2, then the values of a and b are
(A) a = \(-\frac{3}{2}\), b = 3
(B) a = \(\frac{3}{2}\), b = 8
(C) a = \(\frac{1}{2}\), b = 8
(D) a = \(-\frac{3}{2}\), b = 8
Answer:
(D) a = \(-\frac{3}{2}\), b = 8
Hint:
f(x) = 2x + 6, 0 ≤ x ≤ 2
= ax² + bx, 2 < x ≤ 4
Lf'(2) = 2, Rf'(2) = 4a + b
Since f is differentiable at x = 2,
Lf'(2) = Rf'(2)
∴ 2 = 4a + b …..(i)
f is continuous at x = 2.
∴ \(\lim _{x \rightarrow 2^{+}} f(x)=f(2)=\lim _{x \rightarrow 2^{-}} f(x)\)
∴ 4a + 2b = 2(2) + 6
∴ 4a + 2b = 10
∴ 2a + b = 5 …..(ii)
Solving (i) and (ii), we get
a = \(-\frac{3}{2}\), b = 8

Question 7.
If f(x) = x² + sin x + 1, for x ≤ 0
= x² – 2x + 1, for x ≤ 0, then
(A) f is continuous at x = 0, but not differentiable at x = 0
(B) f is neither continuous nor differentiable at x = 0
(C) f is not continuous at x = 0, but differentiable at x = 0
(D) f is both continuous and differentiable at x = 0
Answer:
(A) f is continuous at x = 0, but not differentiable at x = 0
Hint:

Question 8.
If f(x) = \(\frac{x^{50}}{50}+\frac{x^{49}}{49}+\frac{x^{48}}{48}+\ldots .+\frac{x^{2}}{2}+x+1\), then f'(1) =
(A) 48
(B) 49
(C) 50
(D) 51
Answer:
(C) 50
Hint:

(II).

Question 1.
Determine whether the following function is differentiable at x = 3 where,
f(x) = x² + 2, for x ≥ 3
= 6x – 7, for x < 3.
Solution:
f(x) = x² + 2, x ≥ 3
= 6x – 7, x < 3
Differentiability at x = 3


Here, Lf'(3) = Rf'(3)
∴ f is differentiable at x = 3.

Question 2.
Find the values of p and q that make function f(x) differentiable everywhere on R.
f(x) = 3 – x, for x < 1
= px² + qx, for x ≥ 1.
Solution:
f(x) is differentiable everywhere on R.
∴ f(x) is differentiable at x = 1.
∴ f(x) is continuous at x = 1.

f(x) is differentiable at x = 1.
∴ Lf'(1) = Rf'(1)
∴ -1 = 2p + q …..(ii)
Subtracting (i) from (ii), we get
p = -3
Substituting p = -3 in (i), we get
p + q = 2
∴ -3 + q = 2
∴ q = 5

Question 3.
Determine the values of p and q that make the function f(x) differentiable on R where
f(x) = px³, for x < 2
= x² + q, for x ≥ 2
Solution:
f(x) is differentiable on R.
∴ f(x) is differentiable at x = 2.
∴ f(x) is continuous at x = 2.
Continuity at x = 2:
f(x) is continuous at x = 2.


f(x) is differentiable at x = 2.
∴ Lf'(2) = Rf'(2)
∴ 12p = 4
∴ p = \(\frac{1}{3}\)
Substituting p = \(\frac{1}{3}\) in (i), we get
8(\(\frac{1}{3}\) – q = 4
∴ q = \(\frac{8}{3}\) – 4 = \(\frac{-4}{3}\)

Question 4.
Determine all real values of p and q that ensure the function
f(x) = px + q, for x ≤ 1
= tan(\(\frac{\pi x}{4}\)), for 1 < x < 2
is differentiable at x = 1.
Solution:
f(x) is differentiable at x = 1.
∴ f(x) is continuous at x = 1.
Continuity at x= 1:
f(x) is continuous at x = 1.

Question 5.
Discuss whether the function f(x) = |x + 1| + |x – 1| is differentiable ∀ x ∈ R.
Solution:


Here, Lf'(1) ≠ Rf'(1)
∴ f is not differentiable at x = 1.
∴ f is not differentiable at x = -1 and x = 1.
∴ f is not differentiable ∀ x ∈ R.

Question 6.
Test whether the function
f(x) = 2x – 3, for x ≥ 2
= x – 1, for x < 2
is differentiable at x = 2.
Solution:

Question 7.
Test whether the function
f(x) = x² + 1, for x ≥ 2
= 2x + 1, for x < 2
is differentiable at x = 2.
Solution:

Question 8.
Test whether the function
f(x) = 5x – 3x², for x ≥ 1
= 3 – x, for x < 1
is differentiable at x = 1.
Solution:

Here, Lf'(1) = Rf'(1)
∴ f(x) is differentiable at x = 1.

Question 9.
If f(2) = 4, f'(2) = 1, then find \(\lim _{x \rightarrow 2}\left[\frac{x f(2)-2 f(x)}{x-2}\right]\)
Solution:

Question 10.
If y = \(\frac{\mathbf{e}^{x}}{\sqrt{x}}\), find \(\frac{d y}{d x}\) when x = 1.
Solution:

Class 11 Maharashtra State Board Maths Solution 

• Exercise 8.1 Class 11 Maths 2
• Miscellaneous Exercise 8 Class 11 Maths 2
• Exercise 9.1 Class 11 Maths 2
• Exercise 9.2 Class 11 Maths 2
• Miscellaneous Exercise 9 Class 11 Maths 2

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 9 Differentiation Ex 9.2 Questions and Answers.

11th Maths Part 2 Differentiation Exercise 9.2 Questions And Answers Maharashtra Board

(I) Differentiate the following w.r.t. x

Question 1.
y = \(x^{\frac{4}{3}}+e^{x}-\sin x\)
Solution:

Question 2.
y = √x + tan x – x³
Solution:

Question 3.
y = log x – cosec x + \(5^{x}-\frac{3}{x^{\frac{3}{2}}}\)
Solution:

Question 4.
y = \(x^{\frac{7}{3}}+5 x^{\frac{4}{5}}-\frac{5}{x^{\frac{2}{5}}}\)
Solution:

Question 5.
y = 7^x + x⁷ – \(\frac{2}{3}\) x√x – log x + 7⁷
Solution:

Question 6.
y = 3 cot x – 5e^x + 3 log x – \(\frac{4}{x^{\frac{3}{4}}}\)
Solution:

(II) Diffrentiate the following w.r.t. x

Question 1.
y = x⁵ tan x
Solution:

Question 2.
y = x³ log x
Solution:

Question 3.
y = (x² + 2)² sin x
Solution:

Question 4.
y = e^x log x
Solution:

Question 5.
y = \(x^{\frac{3}{2}} e^{x} \log x\)
Solution:

Question 6.
y = \(\log e^{x^{3}} \log x^{3}\)
Solution:

(III) Diffrentiate the following w.r.t. x

Question 1.
y = x²√x + x⁴ log x
Solution:

Question 2.
y = e^x sec x – \(x^{\frac{5}{3}}\) log x
Solution:

Question 3.
y = x⁴ + x√x cos x – x² e^x
Solution:

Question 4.
y = (x³ – 2) tan x – x cos x + 7^x . x⁷
Solution:

Question 5.
y = sin x log x + e^x cos x – e^x √x
Solution:

Question 6.
y = e^x tan x + cos x log x – √x 5^x
Solution:

(IV) Diffrentiate the following w.r.t.x.

Question 1.
y = \(\frac{x^{2}+3}{x^{2}-5}\)
Solution:

Question 2.
y = \(\frac{\sqrt{x}+5}{\sqrt{x}-5}\)
Solution:

Question 3.
y = \(\frac{x e^{x}}{x+e^{x}}\)
Solution:

Question 4.
y = \(\frac{x \log x}{x+\log x}\)
Solution:
y = \(\frac{x \log x}{x+\log x}\)

Question 5.
y = \(\frac{x^{2} \sin x}{x+\cos x}\)
Solution:

Question 6.
y = \(\frac{5 e^{x}-4}{3 e^{x}-2}\)
Solution:

(V).

Question 1.
If f(x) is a quadratic polynomial such that f(0) = 3, f'(2) = 2 and f'(3) = 12, then find f(x).
Solution:
Let f(x) = ax² + bx + c …..(i)
∴ f(0) = a(0)² + b(0) + c
∴ f(0) = c
But, f(0) = 3 …..(given)
∴ c = 3 …..(ii)
Differentiating (i) w.r.t. x, we get
f'(x) = 2ax + b
∴ f'(2) = 2a(2) + b
∴ f'(2) = 4a + b
But, f'(2) = 2 …..(given)
∴ 4a + b = 2 …..(iii)
Also, f'(3) = 2a(3) + b
∴ f'(3) = 6a + b
But, f'(3) = 12 …..(given)
∴ 6a + b = 12 …..(iv)
equation (iv) – equation (iii), we get
2a = 10
∴ a = 5
Substituting a = 5 in (iii), we get
4(5) + b = 2
∴ b = -18
∴ a = 5, b = -18, c = 3
∴ f(x) = 5x² – 18x + 3

Check:
If f(0) = 3, f'(2) = 2 and f'(3) = 12, then our answer is correct.
f(x) = 5x² – 18x + 3 and f'(x) = 10x – 18
f(0) = 5(0)² – 18(0) + 3 = 3
f'(2) = 10(2) – 18 = 2
f'(3) = 10(3) – 18 = 12
Thus, our answer is correct.

Question 2.
If f(x) = a sin x – b cos x, f'(\(\frac{\pi}{4}\)) = √2 and f'(\(\frac{\pi}{6}\)) = 2, then find f(x).
Solution:
f(x) = a sin x – b cos x
Differentiating w.r.t. x, we get
f'(x) = a cos x – b (- sin x)
∴ f'(x) = a cos x + b sin x


Now, f(x) = a sin x – b cos x
∴ f(x) = (√3 + 1) sin x + (√3 – 1) cos x

VI. Fill in the blanks. (Activity Problems)

Question 1.
y = e^x . tan x
Diff. w.r.t. x

Solution:

Question 2.
y = \(\frac{\sin x}{x^{2}+2}\)
diff. w.r.t. x

Solution:

Question 3.
y = (3x² + 5) cos x
Diff. w.r.t. x

Solution:

Question 4.
Differentiate tan x and sec x w.r.t. x using the formulae for differentiation of \(\frac{u}{v}\) and \(\frac{1}{v}\) respectively.
Solution:

Class 11 Maharashtra State Board Maths Solution 

• Exercise 8.1 Class 11 Maths 2
• Miscellaneous Exercise 8 Class 11 Maths 2
• Exercise 9.1 Class 11 Maths 2
• Exercise 9.2 Class 11 Maths 2
• Miscellaneous Exercise 9 Class 11 Maths 2

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 9 Differentiation Ex 9.1 Questions and Answers.

11th Maths Part 2 Differentiation Exercise 9.1 Questions And Answers Maharashtra Board

Question 1.
Find the derivatives of the following w.r.t. x by using the method of the first principle.
(a) x² + 3x – 1
Solution:
Let f(x) = x² + 3x – 1
∴ f(x + h) = (x + h)² + 3(x + h) – 1
= x² + 2xh + h² + 3x + 3h – 1
By first principle, we get

(b) sin(3x)
Solution:
Let f(x) = sin 3x
f(x + h) = sin3(x + h) = sin(3x + 3h)
By first principle, we get

(c) e^2x+1
Solution:

(d) 3^x
Solution:

(e) log(2x + 5)
Solution:
Let f(x) = log(2x + 5)
∴ f(x + h) = log[2(x + h) + 5] = log (2x + 2h + 5)
By first principle, we get

(f) tan(2x + 3)
Solution:
Let f(x) = tan(2x + 3)
∴ f(x + h) = tan[2(x + h) + 3] = tan(2x + 2h + 3)
By first principle, we get

(g) sec(5x – 2)
Solution:
Let f(x) = sec(5x – 2)
f(x + h) = sec[5(x + h) – 2] = sec(5x + 5h – 2)
By first principle, we get

(h) x√x
Solution:

Question 2.
Find the derivatives of the following w.r.t. x. at the points indicated against them by using the method of the first principle.
(i) \(\sqrt{2 x+5}\) at x = 2
Solution:

(ii) tan x at x = \(\frac{\pi}{4}\)
Solution:

(iii) 2^3x+1 at x = 2
Solution:

(iv) log(2x + 1) at x = 2
Solution:
Let f(x) = log(2x + 1)
∴ f(2) = log [2(2) + 1] = log 5 and
f(2 + h) = log [2(2 + h) + 1] = log(2h + 5)
By first principle, we get

(v) e^3x-4 at x = 2
Solution:

(vi) cos x at x = \(\frac{5 \pi}{4}\)
Solution:

Question 3.
Show that the function f is not differentiable at x = -3,
where f(x) = x² + 2 for x < -3
= 2 – 3x for x ≥ -3
Solution:


∴ L f'(-3) ≠ R f'(-3)
∴ f is not differentiable at x = -3.

Question 4.
Show that f(x) = x² is continuous and differentiable at x = 0.
Solution:

Question 5.
Discuss the continuity and differentiability of
(i) f(x) = x |x| at x = 0
Solution:

(ii) f(x) = (2x + 3) |2x + 3| at x = \(-\frac{3}{2}\)
Solution:

Question 6.
Discuss the continuity and differentiability of f(x) at x = 2.
f(x) = [x] if x ∈ [0, 4). [where [ ] is a greatest integer (floor) function]
Solution:
Explanation:
x ∈ [0, 4)
∴ 0 ≤ x < 4
We will plot graph for 0 ≤ x < 4
not for x < 0 and upto x = 4 making on X-axis.

f(x) = [x]
∴ Greatest integer function is discontinuous at all integer values of x and hence not differentiable at all integers.
∴ f is not continuous at x = 2.
∵ f(x) = 1, x < 2
= 2, x ≥ 2
x ∈ neighbourhood of x = 2.
∴ L.H.L. = 1, R.H.L. = 2
∴ f is not continuous at x = 2.
∴ f is not differentiable at x = 2.

Question 7.
Test the continuity and differentiability of
f(x) = 3x + 2 if x > 2
= 12 – x² if x ≤ 2 at x = 2.
Solution:

Question 8.
If f(x) = sin x – cos x if x ≤ \(\frac{\pi}{2}\)
= 2x – π + 1 if x > \(\frac{\pi}{2}\)
Test the continuity and differentiability of f at x = \(\frac{\pi}{2}\).
Solution:

Question 9.
Examine the function
f(x) = x² cos(\(\frac{1}{x}\)), for x ≠ 0
= 0, for x = 0
for continuity and differentiability at x = 0.
Solution:

Class 11 Maharashtra State Board Maths Solution 

• Exercise 8.1 Class 11 Maths 2
• Miscellaneous Exercise 8 Class 11 Maths 2
• Exercise 9.1 Class 11 Maths 2
• Exercise 9.2 Class 11 Maths 2
• Miscellaneous Exercise 9 Class 11 Maths 2

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 8 Continuity Miscellaneous Exercise 8 Questions and Answers.

11th Maths Part 2 Continuity Miscellaneous Exercise 8 Questions And Answers Maharashtra Board

(I) Select the correct answer from the given alternatives.

Question 1.
f(x) = \(\frac{2^{\cot x}-1}{\pi-2 x}\), for x ≠ \(\frac{\pi}{2}\)
= log √2, for x = \(\frac{\pi}{2}\)
(A) f is continuous at x = \(\frac{\pi}{2}\)
(B) f has a jump discontinuity at x = \(\frac{\pi}{2}\)
(C) f has a removable discontinuity
(D) \(\lim _{x \rightarrow \frac{\pi}{2}} f(x)=2 \log 3\)
Answer:
(A) f is continuous at x = \(\frac{\pi}{2}\)
Hint:

Question 2.
If f(x) = \(\frac{1-\sqrt{2} \sin x}{\pi-4 x}\), for x ≠ \(\frac{\pi}{4}\) is continuous at x = \(\frac{\pi}{4}\), then f(\(\frac{\pi}{4}\)) =
(A) \(\frac{1}{\sqrt{2}}\)
(B) \(-\frac{1}{\sqrt{2}}\)
(C) \(-\frac{1}{4}\)
(D) \(\frac{1}{4}\)
Answer:
(D) \(\frac{1}{4}\)
Hint:

Question 3.
If f(x) = \(\frac{(\sin 2 x) \tan 5 x}{\left(e^{2 x}-1\right)^{2}}\), for x ≠ 0 is continuous at x = 0, then f(0) is
(A) \(\frac{10}{e^{2}}\)
(B) \(\frac{10}{e^{4}}\)
(C) \(\frac{5}{4}\)
(D) \(\frac{5}{2}\)
Answer:
(D) \(\frac{5}{2}\)
Hint:

Question 4.
f(x) = \(\frac{x^{2}-7 x+10}{x^{2}+2 x-8}\), for x ∈ [-6, -3]
(A) f is discontinuous at x = 2
(B) f is discontinuous at x = -4
(C) f is discontinuous at x = 0
(D) f is discontinuous at x = 2 and x = -4
Answer:
(B) f is discontinuous at x = -4
Hint:
f(x) = \(\frac{x^{2}-7 x+10}{x^{2}+2 x-8}\), for x ∈ [-6, -3]
= \(\frac{x^{2}-7 x+10}{(x+4)(x-2)}\)
Here f(x) is a rational function and is continuous everywhere except at the points Where denominator becomes zero.
Here, denominator becomes zero when x = -4 or x = 2
But x = 2 does not lie in the given interval.
∴ x = -4 is the point of discontinuity.

Question 5.
If f(x) = ax² + bx + 1, for |x – 1| ≥ 3 and
= 4x + 5, for -2 < x < 4
is continuous everywhere then,
(A) a = \(\frac{1}{2}\), b = 3
(B) a = \(-\frac{1}{2}\), b = -3
(C) a = \(-\frac{1}{2}\), b = 3
(D) a = \(\frac{1}{2}\), b = -3
Answer:
(A) a = \(\frac{1}{2}\), b = 3
Hint:
f(x) = ax² + bx + 1, |x – 1| ≥ 3
= 4x + 5; -2 < x < 4
The first interval is
|x – 1| ≥ 3
∴ x – 1 ≥ 3 or x – 1 ≤ -3
∴ x ≥ 4 or x ≤ -2
∴ f(x) is same for x ≤ -2 as well as x ≥ 4.
∴ f(x) is defined as:
f(x) = ax² + bx + 1; x ≤ -2
= 4x + 5; -2 < x < 4
= ax² + bx + 1; x ≥ 4
f(x) is continuous everywhere.
∴ f(x) is continuous at x = -2 and x = 4.
As f(x) is continuous at x = -2,
\(\lim _{x \rightarrow-2^{-}} f(x)=\lim _{x \rightarrow-2^{+}} f(x)\)
∴ \(\lim _{x \rightarrow-2}\left(a x^{2}+b x+1\right)=\lim _{x \rightarrow-2}(4 x+5)\)
∴ a(-2)² + b(-2) + 1 = 4(-2) + 5
∴ 4a – 2b + 1 = -3
∴ 4a – 2b = -4
∴ 2a – b = -2 …..(i)
∵ f(x) is continuous at x = 4,
\(\lim _{x \rightarrow 4^{-}} \mathrm{f}(x)=\lim _{x \rightarrow 4^{+}} \mathrm{f}(x)\)
∴ \(\lim _{x \rightarrow 4}(4 x+5)=\lim _{x \rightarrow 4}\left(a x^{2}+b x+1\right)\)
4(4) + 5 = a(4)² + b(4) + 1
16a + 4b + 1 = 21
16a + 4b = 20
4a + b = 5 …..(ii)
Adding (i) and (ii), we get
6a = 3
∴ a = \(\frac{1}{2}\)
Substituting a = \(\frac{1}{2}\) in (ii), we get
4(\(\frac{1}{2}\)) + b = 5
∴ 2 + b = 5
∴ b = 3
∴ a = \(\frac{1}{2}\), b = 3

Question 6.
f(x) = \(\frac{\left(16^{x}-1\right)\left(9^{x}-1\right)}{\left(27^{x}-1\right)\left(32^{x}-1\right)}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, then ‘k’ =
(A) \(\frac{8}{3}\)
(B) \(\frac{8}{15}\)
(C) \(-\frac{8}{15}\)
(D) \(\frac{20}{3}\)
Answer:
(B) \(\frac{8}{15}\)
Hint:

Question 7.
f(x) = \(\frac{32^{x}-8^{x}-4^{x}+1}{4^{x}-2^{x+1}+1}\), for x ≠ 0
= k, for x = 0,
is continuous at x = 0, then value of ‘k’ is
(A) 6
(B) 4
(C) (log 2) (log 4)
(D) 3 log 4
Answer:
(A) 6
Hint:

Question 8.
If f(x) = \(\frac{12^{x}-4^{x}-3^{x}+1}{1-\cos 2 x}\), for x ≠ 0 is continuous at x = 0 then the value of f(0) is
(A) \(\frac{\log 12}{2}\)
(B) log 2 . log 3
(C) \(\frac{\log 2 \cdot \log 3}{2}\)
(D) None of these
Answer:
(B) log 2 . log 3
Hint:

Question 9.
If f(x) = \(\left(\frac{4+5 x}{4-7 x}\right)^{\frac{4}{x}}\), for x ≠ 0 and f(0) = k, is continuous at x = 0, then k is
(A) e⁷
(B) e³
(C) e¹²
(D) \(e^{\frac{3}{4}}\)
Answer:
(C) e¹²
Hint:

Question 10.
If f(x) = \(\lfloor x\rfloor\) for x ∈ (-1, 2), then f is discontinuous at
(A) x = -1, 0, 1, 2
(B) x = -1, 0, 1
(C) x = 0, 1
(D) x = 2
Answer:
(C) x = 0, 1
Hint:
f(x) = \(\lfloor x\rfloor\), x ∈ (-1, 2)
This function is discontinuous at all integer values of x between -1 and 2.
∴ f(x) is discontinuous at x = 0 and x = 1.

II. Discuss the continuity of the following functions at the point(s) or on the interval indicated against them.

Question 1.
f(x) = \(\frac{x^{2}-3 x-10}{x-5}\), for 3 ≤ x ≤ 6, x ≠ 5
= 10, for x = 5
= \(\frac{x^{2}-3 x-10}{x-5}\), for 6 < x ≤ 9
Solution:

Question 2.
f(x) = 2x² – 2x + 5, for 0 ≤ x ≤ 2
= \(\frac{1-3 x-x^{2}}{1-x}\), for 2 < x < 4
= \(\frac{x^{2}-25}{x-5}\), for 4 ≤ x ≤ 7 and x ≠ 5
= 7, for x = 5
Solution:
The domain of f(x) is [0, 7].
(i) For 0 ≤ x ≤ 2
f(x) = 2x² – 2x + 5
It is a polynomial function and is Continuous at all point in [0, 2).

(ii) For 2 < x < 4
f(x) = \(\frac{1-3 x-x^{2}}{1-x}\)
It is a rational function and is continuous everwhere except at points where its denominator becomes zero.
Denominator becomes zero at x = 1
But x = 1 does not lie in the interval.
f(x) is continuous at all points in (2, 4).

(iii) For 4 ≤ x ≤ 7, x ≤ 5
f(x) = \(\frac{x^{2}-25}{x-5}\)
It is a rational function and is continuous everywhere except at points where its denominator becomes zero.
Denominator becomes zero at x = 5
But x = 5 does not lie in the interval.
∴ f(x) is continuous at all points in (4, 7] – {5}.

(iv) For continuity at x = 2:

∴ f(x) is continuous at x = 2.

(v) For continuity at x = 4:

∴ f(x) is continuous at x = 4.

(vi) For continuity at x = 5.
f(5) = 7

∴ f(x) is discontinuous at x = 5.
Thus, f(x) is continuous at all points on its domain except at x = 5.

Question 3.
f(x) = \(\frac{\cos 4 x-\cos 9 x}{1-\cos x}\), for x ≠ 0
f(0) = \(\frac{68}{15}\), at x = 0 on \(-\frac{\pi}{2}\) ≤ x ≤ \(\frac{\pi}{2}\)
Solution:
The domain of f(x) is [\(-\frac{\pi}{2}\), \(\frac{\pi}{2}\)]
(i) For [\(-\frac{\pi}{2}\), \(\frac{\pi}{2}\)] – {0}:
f(x) = \(\frac{\cos 4 x-\cos 9 x}{1-\cos x}\)
It is a rational function and is continuous everywhere except at points where its denominator becomes zero.
Denominator becomes zero when cos x = 1,
i.e., x = 0
But x = 0 does not lie in the interval.
∴ f(x) is continuous at all points in [\(-\frac{\pi}{2}\), \(\frac{\pi}{2}\)] – {0}

(ii) For continuity at x = 0:


∴ \(\lim _{x \rightarrow 0} f(x) \neq f(0)\)
∴ f(x) is discontinuous at x = 0.

Question 4.
f(x) = \(\frac{\sin ^{2} \pi x}{3(1-x)^{2}}\), for x ≠ 1
= \(\frac{\pi^{2} \sin ^{2}\left(\frac{\pi x}{2}\right)}{3+4 \cos ^{2}\left(\frac{\pi x}{2}\right)}\), for x = 1, at x = 1
Solution:

Question 5.
f(x) = \(\frac{|x+1|}{2 x^{2}+x-1}\), for x ≠ -1
= 0, for x = -1, at x = -1
Solution:

Question 6.
f(x) = [x + 1] for x ∈ [-2, 2)
Where [*] is greatest integer function.
Solution:
f(x) = [x + 1], x ∈ [-2, 2)
∴ f(x) = -1, x ∈ [-2, -1)
= 0, x ∈ [-1, 0)
= 1, x ∈ [0, 1)
= 2, x ∈ [1, 2)

∴ \(\lim _{x \rightarrow-1^{-}} \mathrm{f}(x)=\lim _{x \rightarrow-1^{+}} \mathrm{f}(x)\)
∴ f(x) is discontinuous at x = -1.
Similarly, f(x) is discontinuous at the points x = 0 and x = 1.

Question 7.
f(x) = 2x² + x + 1, for |x – 3| ≥ 2
= x² + 3, for 1 < x < 5
Solution:
|x – 3| ≥ 2
∴ x – 3 ≥ 2 or x – 3 ≤ -2
∴ x ≥ 5 or x ≤ 1
∴ f(x) = 2x² + x + 1, x ≤ 1
= x² + 3, 1 < x < 5
= 2x² + x + 1, x ≥ 5
Consider the intervals
x < 1 , i.e., (-∞, 1)
1 < x < 5, i.e., (1, 5) x > 5, i.e., (5, ∞)
In all these intervals, f(x) is a polynomial function and hence is continuous at all points.
For continuity at x = 1:

∴ f(x) is discontinuous at x = 5.
∴ f(x) is continuous for all x ∈ R, except at x = 5.

III. Identify discontinuities if any for the following functions as either a jump or a removable discontinuity on their respective domains.

Question 1.
f(x) = x² + x – 3, for x ∈ [-5, -2)
= x² – 5, for x ∈ (-2, 5]
Solution:
f(-2) has not been defined.
\(\lim _{x \rightarrow-2^{-}} f(x)=\lim _{x \rightarrow-2^{-}}\left(x^{2}+x-3\right)\)
= (-2)² + (-2) – 3
= 4 – 2 – 3
= -1
\(\lim _{x \rightarrow-2^{+}} f(x)=\lim _{x \rightarrow-2^{+}}\left(x^{2}-5\right)\)
= (-2)² – 5
= 4 – 5
= -1
∴ \(\lim _{x \rightarrow-2^{-}} f(x)=\lim _{x \rightarrow-2^{+}} f(x)\)
∴ \(\lim _{x \rightarrow-2} f(x) \text { exists. }\)
But f(-2) has not been defined.
∴ f(x) has a removable discontinuity at x = -2.

Question 2.
f(x) = x² + 5x + 1, for 0 ≤ x ≤ 3
= x³ + x + 5, for 3 < x ≤ 6
Solution:
\(\lim _{x \rightarrow 3^{-}} f(x)=\lim _{x \rightarrow 3^{-}}\left(x^{2}+5 x+1\right)\)
= (3)² + 5(3) + 1
= 9 + 15 + 1
= 25
\(\lim _{x \rightarrow 3^{+}} f(x)=\lim _{x \rightarrow 3^{+}}\left(x^{3}+x+5\right)\)
= (3)³ + 3 + 5
= 27 + 3 + 5
= 35
∴ \(\lim _{x \rightarrow 3^{-}} f(x) \neq \lim _{x \rightarrow 3^{+}} f(x)\)
∴ \(\lim _{x \rightarrow 3} f(x)\) does not exist.
∴ f(x) is discontinuous at x = 3.
∴ f(x) has a jump discontinuity at x = 3.

Question 3.
f(x) = \(\frac{x^{2}+x+1}{x+1}\), for x ∈ [0, 3)
= \(\frac{3 x+4}{x^{2}-5}\), for x ∈ [3, 6]
Solution:


∴ f(x) is continuous at x = 3.

IV. Discuss the continuity of the following functions at the point or on the interval indicated against them. If the function is discontinuous, identify the type of discontinuity and state whether the discontinuity is removable. If it has a removable discontinuity, redefine the function so that it becomes continuous.

Question 1.
f(x) = \(\frac{(x+3)\left(x^{2}-6 x+8\right)}{x^{2}-x-12}\)
Solution:
f(x) = \(\frac{(x+3)\left(x^{2}-6 x+8\right)}{x^{2}-x-12}\)
= \(\frac{(x+3)(x-2)(x-4)}{(x-4)(x+3)}\)
∴ f(x) is not defined at x = 4 and x = -3.
∴ The domain of function f = R – {-3, 4}.
For x ≠ -3 and 4,

f(x) is discontinuous at x = 4 and x = -3.
This discontinuity is removable.
∴ f(x) can be redefined as
f(x) = \(\frac{(x+3)\left(x^{2}-6 x+8\right)}{x^{2}-x-12}\), for x ≠ 4, x ≠ -3
= -5, for x ∈ R – {-3, 4}, x = -3
= 2, for x ∈ R – {-3, 4}, x = 4

Question 2.
f(x) = x² + 2x + 5, for x ≤ 3
= x³ – 2x² – 5, for x > 3
Solution:

∴ f(x) is discontinuous at x = 3.
This discontinuity is irremovable.

V. Find k if the following functions are continuous at the points indicated against them.

Question 1.
f(x) = \(\left(\frac{5 x-8}{8-3 x}\right)^{\frac{3}{2 x-4}}\), for x ≠ 2
= k, for x = 2 at x = 2.
Solution:
f(x) is continuous at x = 2. …..(given)

Question 2.
f(x) = \(\frac{45^{x}-9^{x}-5^{x}+1}{\left(k^{x}-1\right)\left(3^{x}-1\right)}\), for x ≠ 0
= \(\frac{2}{3}\), for x = 0, at x = 0
Solution:
f(x) is continuous at x = 0 …..(given)

VI. Find a and b if the following functions are continuous at the points or on the interval indicated against them.

Question 1.
f(x) = \(\frac{4 \tan x+5 \sin x}{a^{x}-1}\), for x < 0
= \(\frac{9}{\log 2}\), for x = 0
= \(\frac{11 x+7 x \cdot \cos x}{b^{x}-1}\), for x < 0
Solution:

Question 2.
f(x) = ax² + bx + 1, for |2x – 3| ≥ 2
= 3x + 2, for \(\frac{1}{2}\) < x < \(\frac{5}{2}\)
Solution:

VII. Find f(a), if f is continuous at x = a where,

Question 1.
f(x) = \(\frac{1+\cos (\pi x)}{\pi(1-x)^{2}}\), for x ≠ 1 and at a = 1.
Solution:

Question 2.
f(x) = \(\frac{1-\cos [7(x-\pi)]}{5(x-\pi)^{2}}\), for x ≠ π and at a = π.
Solution:

VIII. Solve using intermediate value theorem.

Question 1.
Show that 5^x – 6x = 0 has a root in [1, 2].
Solution:
Let f(x) = 5^x – 6x
5^x and 6x are continuous functions for all x ∈ R.
∴ 5^x – 6x is also continuous for all x ∈ R.
i.e., f(x) is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
f(1) = 5¹ – 6(1) = -1 < 0
f(2) = (5)² – 6(2) = 13 > 0
∴ f(1) < 0 and f(2) > 0
∴ By intermediate value theorem, there has to be a point ‘c’ between 1 and 2 such that f(c) = 0.
∴ There is a root of the given equation in [1, 2].

Question 2.
Show that x³ – 5x² + 3x + 6 = 0 has at least two real roots between x = 1 and x = 5.
Solution:
Let f(x) = x³ – 5x² + 3x + 6
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
Here, we have been asked to show that f(x) has at least two roots between x = 1 and x = 5.
f(1) = (1)³ – 5(1)² + 3(1) + 6
= 5 > 0
f(2) = (2)³ – 5(2)² + 3(2) + 6
= 8 – 20 + 6 + 6
= 0
∴ x = 2 is a root of f(x).
Also, f(3) = (3)³ – 5(3)² + 3(3) + 6
= 27 – 45 + 9 + 6
= -3 < 0
f(4) = (4)³ – 5(4)² + 3(4) + 6
= 64 – 80 + 12 + 6
= 2 > 0
∴ f(3) < 0 and f(4) > 0
∴ By intermediate value theorem, there has to be a point ‘c’ between 3 and 4 such that f(c) = 0.
∴ There are two roots, x = 2 and a root between x = 3 and x = 4.
Thus, there are at least two roots of the given equation between x = 1 and x = 5.

Class 11 Maharashtra State Board Maths Solution 

• Exercise 8.1 Class 11 Maths 2
• Miscellaneous Exercise 8 Class 11 Maths 2
• Exercise 9.1 Class 11 Maths 2
• Exercise 9.2 Class 11 Maths 2
• Miscellaneous Exercise 9 Class 11 Maths 2

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 8 Continuity Ex 8.1 Questions and Answers.

11th Maths Part 2 Continuity Exercise 8.1 Questions And Answers Maharashtra Board

Question 1.
Examine the continuity of
(i) f(x) = x³ + 2x² – x – 2 at x = -2
Solution:
Given, f(x) = x³ + 2x² – x – 2
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
∴ f(x) is continuous at x = -2.

(ii) f(x) = sin x, for x ≤ \(\frac{\pi}{4}\)
= cos x, for x > \(\frac{\pi}{4}\), at x = \(\frac{\pi}{4}\)
Solution:

(iii) f(x) = \(\frac{x^{2}-9}{x-3}\), for x ≠ 3
= 8 for x = 3, at x = 3.
Solution:
f(3) = 8 ….(given)

∴ f(x) is discontinuous at x = 3.

Question 2.
Examine whether the function is continuous at the points indicated against them.
(i) f(x) = x³ – 2x + 1, if x ≤ 2
= 3x – 2, if x > 2, at x = 2.
Solution:

(ii) f(x) = \(\frac{x^{2}+18 x-19}{x-1}\), for x ≠ 1
= 20, for x = 1, at x = 1.
Solution:

(iii) f(x) = \(\frac{x}{\tan 3 x}+2\), for x < 0
= \(\frac{7}{3}\), for x ≥ 0, at x = 0.
Solution:

Question 3.
Find all the points of discontinuities of f(x) = [x] on the interval (-3, 2).
Solution:
f(x) = [x], x ∈ (-3, 2)
i.e., f(x) = -3, x ∈ (-3, -2)
= -2, x ∈ [-2, -1)
= -1, x ∈ [- 1, 0)
= 0, x ∈ [0, 1)
= 1, x ∈ [1, 2)

Similarly, f(x) is discontinuous at the points x = -1, x = 0, x = 1.
Thus all the integer values of x in the interval (-3, 2),
i.e., the points x = -2, x = -1, x = 0 and x = 1 are the required points of discontinuities.

Question 4.
Discuss the continuity of the function f(x) = |2x + 3|, at x = \(\frac{-3}{2}\).
Solution:

Question 5.
Test the continuity of the following functions at the points or intervals indicated against them.


Solution:

Question 6.
Identify discontinuities for the following functions as either a jump or a removable discontinuity.
(i) f(x) = \(\frac{x^{2}-10 x+21}{x-7}\)
Solution:
Given, f(x) = \(\frac{x^{2}-10 x+21}{x-7}\)
It is a rational function and is discontinuous if
x – 7 = 0, i.e., x = 7
∴ f(x) is continuous for all x ∈ R, except at x = 7.
∴ f(7) is not defined.

Thus, \(\lim _{x \rightarrow 7} \mathrm{f}(x)\) exist but f(7) is not defined.
∴ f(x) has a removable discontinuity.

(ii) f(x) = x² + 3x – 2, for x ≤ 4
= 5x + 3, for x > 4.
Solution:
f(x) = x² + 3x – 2, x ≤ 4
= 5x + 3, x > 4
f(x) is a polynomial function for both the intervals.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = 4.

∴ f(x) is discontinuous at x = 4.
∴ f(x) has a jump discontinuity at x = 4.

(iii) f(x) = x² – 3x – 2, for x < -3 = 3 + 8x, for x > -3.
Solution:
f(x) = x² – 3x – 2, x < -3 = 3 + 8x, x > -3
f(x) is a polynomial function for both the intervals.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = -3.

∴ f(x) is discontinuous at x = -3.
∴ f(x) has a jump discontinuity at x = -3

(iv) f(x) = 4 + sin x, for x < π = 3 – cos x for x > π.
Solution:
f(x) = 4 + sin x, x < π = 3 – cos x, x > π
sin x and cos x are continuous for all x ∈ R.
4 and 3 are constant functions.
∴ 4 + sin x and 3 – cos x are continuous for all x ∈ R.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = π.

But f(π) is not defined.
∴ f(x) has a removable discontinuity at x = π.

Question 7.
Show that the following functions have a continuous extension to the point where f(x) is not defined. Also, find the extension.
(i) f(x) = \(\frac{1-\cos 2 x}{\sin x}\), for x ≠ 0.
Solution:
f(x) = \(\frac{1-\cos 2 x}{\sin x}\), for x ≠ 0
Here, f(0) is not defined.
Consider,

But f(0) is not defined.
∴ f(x) has a removable discontinuity at x = 0.
∴ The extension of the original function is
f(x) = \(\frac{1-\cos 2 x}{\sin x}\) for x ≠ 0
= 0 for x = 0
∴ f(x) is continuous at x = 0.

(ii) f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), for x ≠ 0.
Solution:
f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), for x ≠ 0
Here, f(0) is not defined.
Consider,

But f(0) is not defined.
∴ f(x) has a removable discontinuity at x = 0.
∴ The extension of the original function is
f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), x ≠ 0
= \(\frac{7}{2}\), x = 0
∴ f(x) is continuous at x = 0.

(iii) f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), for x ≠ -1
Solution:
f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), for x ≠ -1
Here, f(-1) is not defined.
Consider,

But f(-1) is not defined.
∴ f(x) has a removable discontinuity at x = -1.
∴ The extension of the original function is
f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), x ≠ -1
= \(-\frac{2}{3}\), x = -1
∴ f(x) is continuous at x = \(-\frac{2}{3}\)

Question 8.
Discuss the continuity of the following functions at the points indicated against them.

Solution:

Question 9.
Which of the following functions has a removable discontinuity? If it has a removable discontinuity, redefine the function so that it becomes continuous.


Solution:

Question 10.
(i) If f(x) = \(\frac{\sqrt{2+\sin x}-\sqrt{3}}{\cos ^{2} x}\), for x ≠ \(\frac{\pi}{2}\), is continuous at x = \(\frac{\pi}{2}\) then find f(\(\frac{\pi}{2}\)).
Solution:
f(x) is continuous at x = \(\frac{\pi}{2}\), …..(given)

(ii) If f(x) = \(\frac{\cos ^{2} x-\sin ^{2} x-1}{\sqrt{3 x^{2}+1}-1}\) for x ≠ 0, is continuous at x = 0 then find f(0).
Solution:
f(x) is continuous at x = 0, …..(given)

(iii) If f(x) = \(\frac{4^{x-\pi}+4^{\pi-x}-2}{(x-\pi)^{2}}\) for x ≠ π, is continuous at x = π, then find f(π).
Solution:
f(x) is continuous at x = π, …..(given)

Question 11.
(i) If f(x) = \(\frac{24^{x}-8^{x}-3^{x}+1}{12^{x}-4^{x}-3^{x}+1}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, then find k.
Solution:
f(x) is continuous at x = 0 …..(given)

(ii) If f(x) = \(\frac{5^{x}+5^{-x}-2}{x^{2}}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, then find k.
Solution:
f(x) is continuous at x = 0 …..(given)

(iii) If f(x) = \(\frac{\sin 2 x}{5 x}\) – a, for x > 0
= 4 for x = 0
= x² + b – 3, for x < 0
is continuous at x = 0, find a and b.
Solution:
f(x) is continuous at x = 0 ……(given)

(iv) For what values of a and b is the function
f(x) = ax + 2b + 18, for x ≤ 0
= x² + 3a – b, for 0 < x ≤ 2 = 8x – 2, for x > 2,
continuous for every x?
Solution:
f(x) is continuous for every x …..(given)
∴ f(x) is continuous at x = 0 and x = 2.
As f(x) is continuous at x = 0,
\(\lim _{x \rightarrow 0^{-}} \mathrm{f}(x)=\lim _{x \rightarrow 0^{+}} \mathrm{f}(x)\)

∴ (2)² + 3a – b = 8(2) – 2
∴ 4 + 3a – b = 14
∴ 3a – b = 10 …….(ii)
Subtracting (i) from (ii), we get
2a = 4
∴ a = 2
Substituting a = 2 in (i), we get
2 – b = 6
∴ b = -4
∴ a = 2 and b = -4

(v) For what values of a and b is the function
f(x) = \(\frac{x^{2}-4}{x-2}\), for x < 2
= ax² – bx + 3, for 2 ≤ x < 3
= 2x – a + b, for x ≥ 3
continuous for every x on R?
Solution:
f(x) is continuous for every x on R …..(given)
∴ f(x) is continuous at x = 2 and x = 3.
As f(x) is continuous at x = 2,

∴ a(3)² – b(3) + 3 = 2(3) – a + b
∴ 9a – 3b + 3 = 6 – a + b
∴ 10a – 4b = 3 …..(ii)
Multiplying (i) by 2, we get
8a – 4b = 2 ….(iii)
Subtracting (ii) from (iii), we get
-2a = -1
∴ a = \(\frac{1}{2}\)
Substituting a = \(\frac{1}{2}\) in (i), we get
4(\(\frac{1}{2}\)) – 2b = 1
∴ 2 – 2b = 1
∴ 1 = 2b
∴ b = \(\frac{1}{2}\)
∴ a = \(\frac{1}{2}\) and b = \(\frac{1}{2}\)

Question 12.
Discuss the continuity of f on its domain, where
f(x) = |x + 1|, for -3 ≤ x ≤ 2
= |x – 5|, for 2 < x ≤ 7
Solution:

Question 13.
Discuss the continuity of f(x) at x = \(\frac{\pi}{4}\) where,
f(x) = \(\frac{(\sin x+\cos x)^{3}-2 \sqrt{2}}{\sin 2 x-1}\), for x ≠ \(\frac{\pi}{4}\)
= \(\frac{3}{\sqrt{2}}\), for x = \(\frac{\pi}{4}\)
Solution:

Question 14.
Determine the values of p and q such that the following function is continuous on the entire real number line.
f(x) = x + 1, for 1 < x < 3
= x² + px + q, for |x – 2| ≥ 1.
Solution:
|x – 2| ≥ 1
∴ x – 2 ≥ 1 or x – 2 ≤ -1
∴ x ≥ 3 or x ≤ 1
∴ f(x) = x² + px + q for x ≥ 3 as well as x ≤ 1
Thus, f(x) = x² + px + q; x ≤ 1
= x + 1; 1 < x < 3 = x² + px + q; x > 3
f(x) is continuous for all x ∈ R.
∴ f(x) is continuous at x = 1 and x = 3.
As f(x) is continuous at x = 1,

Subtracting (i) from (ii), we get
2p = -6
∴ p = -3
Substituting p = -3 in (i), we get
-3 + q = 1
∴ q = 4
∴ p = -3 and q = 4

Question 15.
Show that there is a root for the equation 2x³ – x – 16 = 0 between 2 and 3.
Solution:
Let f(x) = 2x³ – x – 16
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
f(2) = 2(2)³ – 2 – 16 = -2 < 0
f(3) = 2(3)³ – 3 – 16 = 35 > 0
∴ f(2) < 0 and f(3) > 0
∴ By intermediate value theorem,
there has to be point ‘c’ between 2 and 3 such that f(c) = 0.
∴ There is a root of the given equation between 2 and 3.

Question 16.
Show that there is a root for the equation x³ – 3x = 0 between 1 and 2.
Solution:
Let f(x) = x³ – 3x
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
f(1) = (1)³ – 3(1) = -2 < 0
f(2) = (2)³ – 3(2) = 2 > 0
∴ f(1) < 0 and f(2) > 0
∴ By intermediate value theorem,
there has to be point ‘c’ between 1 and 2 such that f(c) = 0.
There is a root of the given equation between 1 and 2.

Question 17.
Let f(x) = ax + b (where a and b are unknown)
= x² + 5 for x ∈ R
Find the values of a and b, so that f(x) is continuous at x = 1.

Solution:
f(x) = x² + 5, x ∈ R
∴ f(1) = 1 + 5 = 6
If f(x) = ax + b is continuous at x = 1, then
f(1) = \(\lim _{x \rightarrow 1}(a x+b)\) = a + b
∴ 6 = a + b where, a, b ∈ R
∴ There are infinitely many values of a and b.

Question 18.
Activity: Suppose f(x) = px + 3 for a ≤ x ≤ b
= 5x² – q for b < x ≤ c
Find the condition on p, q, so that f(x) is continuous on [a, c], by filling in the boxes.

Solution:

Class 11 Maharashtra State Board Maths Solution 

• Exercise 8.1 Class 11 Maths 2
• Miscellaneous Exercise 8 Class 11 Maths 2
• Exercise 9.1 Class 11 Maths 2
• Exercise 9.2 Class 11 Maths 2
• Miscellaneous Exercise 9 Class 11 Maths 2

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Miscellaneous Exercise 7 Questions and Answers.

11th Maths Part 2 Limits Miscellaneous Exercise 7 Questions And Answers Maharashtra Board

I. Select the correct answer from the given alternatives.

Question 1.
\(\lim _{x \rightarrow 2}\left(\frac{x^{4}-16}{x^{2}-5 x+6}\right)=\)
(A) 23
(B) 32
(C) -32
(D) -16
Answer:
(C) -32
Hint:

Question 2.
\(\lim _{x \rightarrow-2}\left(\frac{x^{7}+128}{x^{3}+8}\right)=\)
(A) \(\frac{56}{3}\)
(B) \(\frac{112}{3}\)
(C) \(\frac{121}{3}\)
(D) \(\frac{28}{3}\)
Answer:
(B) \(\frac{112}{3}\)
Hint:

Question 3.
\(\lim _{x \rightarrow 3}\left(\frac{1}{x^{2}-11 x+24}+\frac{1}{x^{2}-x-6}\right)=\)
(A) \(-\frac{2}{25}\)
(B) \(\frac{2}{25}\)
(C) \(\frac{7}{25}\)
(D) \(-\frac{7}{25}\)
Answer:
(A) \(-\frac{2}{25}\)
Hint:

Question 4.
\(\lim _{x \rightarrow 5}\left(\frac{\sqrt{x+4}-3}{\sqrt{3 x-11-2}}\right)=\)
(A) \(\frac{-2}{9}\)
(B) \(\frac{2}{7}\)
(C) \(\frac{5}{9}\)
(D) \(\frac{2}{9}\)
Answer:
(D) \(\frac{2}{9}\)
Hint:

Question 5.
\(\lim _{x \rightarrow \frac{\pi}{3}}\left(\frac{\tan ^{2} x-3}{\sec ^{3} x-8}\right)=\)
(A) 1
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{3}\)
(D) \(\frac{1}{4}\)
Answer:
(C) \(\frac{1}{3}\)
Hint:

Question 6.
\(\lim _{x \rightarrow 0}\left(\frac{5 \sin x-x \cos x}{2 \tan x-3 x^{2}}\right)=\)
(A) 0
(B) 1
(C) 2
(D) 3
Answer:
(C) 2
Hint:

Question 7.
\(\lim _{x \rightarrow \frac{\pi}{2}}\left[\frac{3 \cos x+\cos 3 x}{(2 x-\pi)^{3}}\right]=\)
(A) \(\frac{3}{2}\)
(B) \(\frac{1}{2}\)
(C) \(-\frac{1}{2}\)
(D) \(\frac{1}{4}\)
Answer:
(C) \(-\frac{1}{2}\)
Hint:

Question 8.
\(\lim _{x \rightarrow 0}\left(\frac{15^{x}-3^{x}-5^{x}+1}{\sin ^{2} x}\right)=\)
(A) log 15
(B) log 3 + log 5
(C) log 3 . log 5
(D) 3 log 5
Answer:
(C) log 3 . log 5
Hint:

Question 9.
\(\lim _{x \rightarrow 0}\left(\frac{3+5 x}{3-4 x}\right)^{\frac{1}{x}}=\)
(A) e³
(B) e⁶
(C) e⁹
(D) e^-3
Answer:
(A) e³
Hint:

Question 10.
\(\lim _{x \rightarrow 0}\left[\frac{\log (5+x)-\log (5-x)}{\sin x}\right]=\)
(A) \(\frac{3}{2}\)
(B) \(-\frac{5}{2}\)
(C) \(-\frac{1}{2}\)
(D) \(\frac{2}{5}\)
Answer:
(D) \(\frac{2}{5}\)
Hint:

Question 11.
\(\lim _{x \rightarrow \frac{\pi}{2}}\left(\frac{3^{\cos x}-1}{\frac{\pi}{2}-x}\right)=\)
(A) 1
(B) log 3
(C) \(3^{\frac{\pi}{2}}\)
(D) 3 log 3
Answer:
(B) log 3
Hint:

Question 12.
\(\lim _{x \rightarrow 0}\left[\frac{x \cdot \log (1+3 x)}{\left(e^{3 x}-1\right)^{2}}\right]=\)
(A) \(\frac{1}{\mathrm{e}^{9}}\)
(B) \(\frac{1}{\mathrm{e}^{3}}\)
(C) \(\frac{1}{9}\)
(D) \(\frac{1}{3}\)
Answer:
(D) \(\frac{1}{3}\)
Hint:

Question 13.
\(\lim _{x \rightarrow 0}\left[\frac{\left(3^{\sin x}-1\right)^{3}}{\left(3^{x}-1\right) \cdot \tan x \cdot \log (1+x)}\right]=\)
(A) 3 log 3
(B) 2 log 3
(C) (log 3)²
(D) (log 3)³
Answer:
(C) (log 3)²
Hint:

Question 14.
\(\lim _{x \rightarrow 3}\left[\frac{5^{x-3}-4^{x-3}}{\sin (x-3)}\right]=\)
(A) log 5 – 4
(B) log \(\frac{5}{4}\)
(C) \(\frac{\log 5}{\log 4}\)
(D) \(\frac{\log 5}{4}\)
Answer:
(B) log \(\frac{5}{4}\)
Hint:

Question 15.
\(\lim _{x \rightarrow \infty}\left[\frac{(2 x+3)^{7}(x-5)^{3}}{(2 x-5)^{10}}\right]=\)
(A) \(\frac{3}{8}\)
(B) \(\frac{1}{8}\)
(C) \(\frac{1}{6}\)
(D) \(\frac{1}{4}\)
Answer:
(B) \(\frac{1}{8}\)
Hint:

(II) Evaluate the following.

Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{(1-x)^{5}-1}{(1-x)^{3}-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0}[x]\) ([*] is a greatest integer function.)
Solution:

Question 3.
If f(r) = πr² then find \(\lim _{h \rightarrow 0}\left[\frac{f(r+h)-f(r)}{h}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 0}\left[\frac{x}{|x|+x^{2}}\right]\)
Solution:

Question 5.
Find the limit of the function, if it exists, at x = 1
\(f(x)=\left\{\begin{array}{lll}
7-4 x & \text { for } & x<1 \\
x^{2}+2 & \text { for } & x \geq 1
\end{array}\right.\)
Solution:

Question 6.
Given that 7x ≤ f(x) ≤ 3x² – 6 for all x. Determine the value of \(\lim _{x \rightarrow 3} f(x)\)
Solution:

Question 7.
\(\lim _{x \rightarrow 0}\left[\frac{\sec x^{2}-1}{x^{4}}\right]\)
Solution:

Question 8.
\(\lim _{x \rightarrow 0}\left[\frac{e^{x}+e^{-x}-2}{x \cdot \tan x}\right]\)
Solution:

Question 9.
\(\lim _{x \rightarrow 0}\left[\frac{x\left(6^{x}-3^{x}\right)}{\cos (6 x)-\cos (4 x)}\right]\)
Solution:

Question 10.
\(\lim _{x \rightarrow 0}\left[\frac{a^{3 x}-a^{2 x}-a^{x}+1}{x \cdot \tan x}\right]\)
Solution:

Question 11.
\(\lim _{x \rightarrow a}\left[\frac{\sin x-\sin a}{x-a}\right]\)
Solution:

Question 12.
\(\lim _{x \rightarrow 2}\left[\frac{\log x-\log 2}{x-2}\right]\)
Solution:

Question 13.
\(\lim _{x \rightarrow 1}\left[\frac{a b^{x}-a^{x} b}{x^{2}-1}\right]\)
Solution:

Question 14.
\(\lim _{x \rightarrow 0}\left[\frac{\left(5^{x}-1\right)^{2}}{\left(2^{x}-1\right) \log (1+x)}\right]\)
Solution:

Question 15.
\(\lim _{x \rightarrow \infty}\left[\frac{(2 x+1)^{2}(7 x-3)^{3}}{(5 x+2)^{5}}\right]\)
Solution:

Question 16.
\(\lim _{x \rightarrow a}\left[\frac{x \cos a-a \cos x}{x-a}\right]\)
Solution:

Question 17.
\(\lim _{x \rightarrow \frac{\pi}{4}}\left[\frac{(\sin x-\cos x)^{2}}{\sqrt{2}-\sin x-\cos x}\right]\)
Solution:

Question 18.
\(\lim _{x \rightarrow 1}\left[\frac{2^{2 x-2}-2^{x}+1}{\sin ^{2}(x-1)}\right]\)
Solution:

Question 19.
\(\lim _{x \rightarrow 1}\left[\frac{4^{x-1}-2^{x}+1}{(x-1)^{2}}\right]\)
Solution:

Question 20.
\(\lim _{x \rightarrow 1}\left[\frac{\sqrt{x}-1}{\log x}\right]\)
Solution:

Question 21.
\(\lim _{x \rightarrow 0}\left(\frac{\sqrt{1-\cos x}}{x}\right)\)
Solution:

Question 22.
\(\lim _{x \rightarrow 1}\left(\frac{x+3 x^{2}+5 x^{3}+\cdots \cdots \cdots \cdots \cdots+(2 n-1) x^{n}-n^{2}}{x-1}\right)\)
Solution:

Question 23.
\(\lim _{x \rightarrow 0} \frac{1}{x^{12}}\left[1-\cos \left(\frac{x^{2}}{2}\right)-\cos \left(\frac{x^{4}}{4}\right)+\cos \left(\frac{x^{2}}{2}\right) \cdot \cos \left(\frac{x^{4}}{4}\right)\right]\)
Solution:

Question 24.
\(\lim _{x \rightarrow \infty}\left(\frac{8 x^{2}+5 x+3}{2 x^{2}-7 x-5}\right)^{\frac{4 x+3}{8 x-1}}\)
Solution:

Class 11 Maharashtra State Board Maths Solution 

• Exercise 7.1 Class 11 Maths 2
• Exercise 7.2 Class 11 Maths 2
• Exercise 7.3 Class 11 Maths 2
• Exercise 7.4 Class 11 Maths 2
• Exercise 7.5 Class 11 Maths 2
• Exercise 7.6 Class 11 Maths 2
• Exercise 7.7 Class 11 Maths 2
• Miscellaneous Exercise 7 Class 11 Maths 2