Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 9 Differentiation Ex 9.1 Questions and Answers.
11th Maths Part 2 Differentiation Exercise 9.1 Questions And Answers Maharashtra Board
Question 1.
Find the derivatives of the following w.r.t. x by using the method of the first principle.
(a) x2 + 3x – 1
Solution:
Let f(x) = x2 + 3x – 1
∴ f(x + h) = (x + h)2 + 3(x + h) – 1
= x2 + 2xh + h2 + 3x + 3h – 1
By first principle, we get

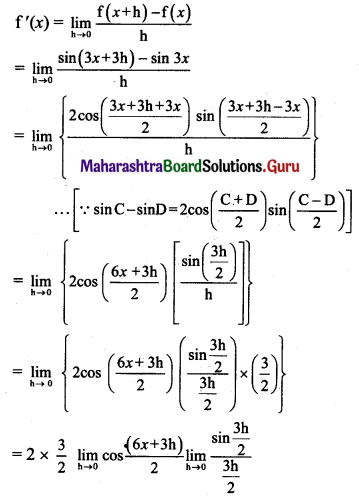
(b) sin(3x)
Solution:
Let f(x) = sin 3x
f(x + h) = sin3(x + h) = sin(3x + 3h)
By first principle, we get

![]()
(c) e2x+1
Solution:

(d) 3x
Solution:

(e) log(2x + 5)
Solution:
Let f(x) = log(2x + 5)
∴ f(x + h) = log[2(x + h) + 5] = log (2x + 2h + 5)
By first principle, we get


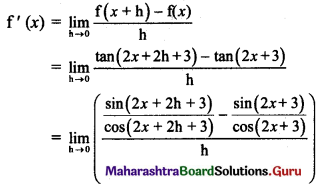
(f) tan(2x + 3)
Solution:
Let f(x) = tan(2x + 3)
∴ f(x + h) = tan[2(x + h) + 3] = tan(2x + 2h + 3)
By first principle, we get

(g) sec(5x – 2)
Solution:
Let f(x) = sec(5x – 2)
f(x + h) = sec[5(x + h) – 2] = sec(5x + 5h – 2)
By first principle, we get


![]()
(h) x√x
Solution:

Question 2.
Find the derivatives of the following w.r.t. x. at the points indicated against them by using the method of the first principle.
(i) \(\sqrt{2 x+5}\) at x = 2
Solution:

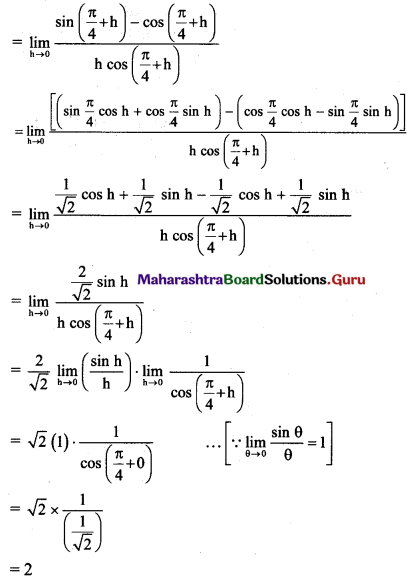
(ii) tan x at x = \(\frac{\pi}{4}\)
Solution:

(iii) 23x+1 at x = 2
Solution:

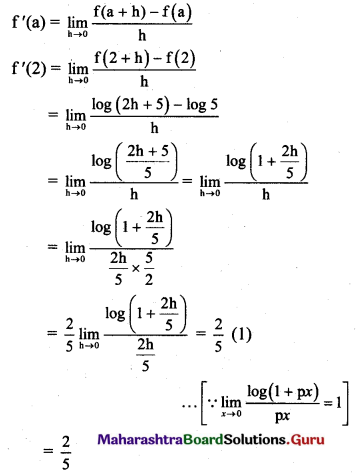
(iv) log(2x + 1) at x = 2
Solution:
Let f(x) = log(2x + 1)
∴ f(2) = log [2(2) + 1] = log 5 and
f(2 + h) = log [2(2 + h) + 1] = log(2h + 5)
By first principle, we get
(v) e3x-4 at x = 2
Solution:

(vi) cos x at x = \(\frac{5 \pi}{4}\)
Solution:
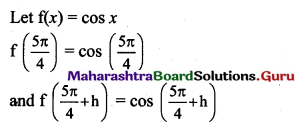


![]()
Question 3.
Show that the function f is not differentiable at x = -3,
where f(x) = x2 + 2 for x < -3
= 2 – 3x for x ≥ -3
Solution:


∴ L f'(-3) ≠ R f'(-3)
∴ f is not differentiable at x = -3.
Question 4.
Show that f(x) = x2 is continuous and differentiable at x = 0.
Solution:

Question 5.
Discuss the continuity and differentiability of
(i) f(x) = x |x| at x = 0
Solution:

(ii) f(x) = (2x + 3) |2x + 3| at x = \(-\frac{3}{2}\)
Solution:
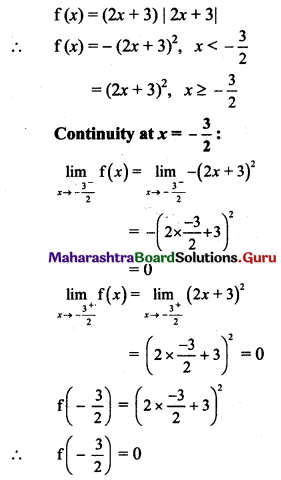


Question 6.
Discuss the continuity and differentiability of f(x) at x = 2.
f(x) = [x] if x ∈ [0, 4). [where [ ] is a greatest integer (floor) function]
Solution:
Explanation:
x ∈ [0, 4)
∴ 0 ≤ x < 4
We will plot graph for 0 ≤ x < 4
not for x < 0 and upto x = 4 making on X-axis.
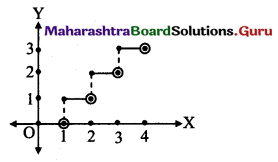
f(x) = [x]
∴ Greatest integer function is discontinuous at all integer values of x and hence not differentiable at all integers.
∴ f is not continuous at x = 2.
∵ f(x) = 1, x < 2
= 2, x ≥ 2
x ∈ neighbourhood of x = 2.
∴ L.H.L. = 1, R.H.L. = 2
∴ f is not continuous at x = 2.
∴ f is not differentiable at x = 2.
![]()
Question 7.
Test the continuity and differentiability of
f(x) = 3x + 2 if x > 2
= 12 – x2 if x ≤ 2 at x = 2.
Solution:
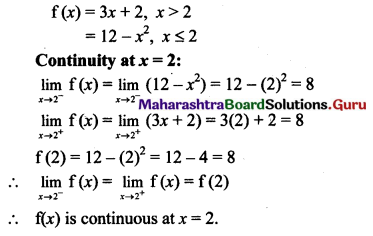

Question 8.
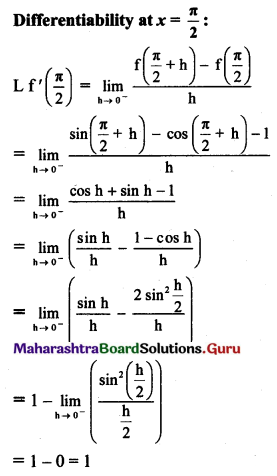
If f(x) = sin x – cos x if x ≤ \(\frac{\pi}{2}\)
= 2x – π + 1 if x > \(\frac{\pi}{2}\)
Test the continuity and differentiability of f at x = \(\frac{\pi}{2}\).
Solution:
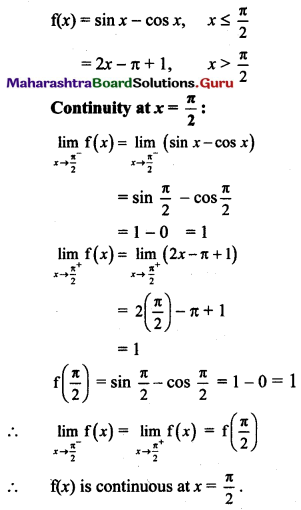

![]()
Question 9.
Examine the function
f(x) = x2 cos(\(\frac{1}{x}\)), for x ≠ 0
= 0, for x = 0
for continuity and differentiability at x = 0.
Solution:

Class 11 Maharashtra State Board Maths Solution