Sets and Relations Class 11 Commerce Maths 1 Chapter 1 Miscellaneous Exercise 1 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 1 Sets and Relations Miscellaneous Exercise 1 Questions and Answers.
Std 11 Maths 1 Miscellaneous Exercise 1 Solutions Commerce Maths
Question 1.
Write the following sets in set builder form:
(i) {10, 20, 30, 40, 50}
(ii) {a, e, i, o, u}
(iii) {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
Solution:
(i) Let A = {10, 20, 30, 40, 50}
∴ A = {x / x = 10n, n ∈ N and n ≤ 5}
(ii) Let B = {a, e, i, o, u}
∴ B = {x / x is a vowel of English alphabets}
(iii) Let C = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
∴ C = {x / x represents days of a week}
![]()
Question 2.
If U = {x / x ∈ N, 1 ≤ x ≤ 12}, A = {1, 4, 7, 10}, B = {2, 4, 6, 7, 11}, C = {3, 5, 8, 9, 12}.
Write the sets
(i) A ∪ B
(ii) B ∩ C
(iii) A – B
(iv) B – C
(v) A ∪ B ∪ C
(vi) A ∩ (B ∪ C)
Solution:
U = {x / x ∈ N, 1 ≤ x ≤ 12} = {1, 2, 3, …., 12}
A = {1, 4, 7, 10}, B = {2, 4, 6, 7, 11}, C = {3, 5, 8, 9, 12}
(i) A ∪ B = {1, 2, 4, 6, 7, 10, 11}
(ii) B ∩ C = { }
(iii) A – B = {1, 10}
(iv) B – C = {2, 4, 6, 7, 11}
(v) A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
(vi) B ∪ C = {2, 3, 4, 5, 6, 7, 8, 9, 11, 12}
∴ A ∩ (B ∪ C) = {4, 7}
Question 3.
In a survey of 425 students in a school, it was found that 115 drink apple juice, 160 drink orange juice, and 80 drink both apple as well as orange juice. How many drinks neither apple juice nor orange juice?
Solution:
Let A = set of students who drink apple juice
B = set of students who drink orange juice
X = set of all students
∴ n(X) = 425, n(A) = 115, n(B) = 160, n(A ∩ B) = 80
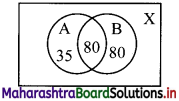
No. of students who neither drink apple juice nor orange juice
n(A’ ∩ B’) = n(A ∪ B)’
= n(X) – n(A ∪ B)
= 425 – [n(A) + n(B) – n(A ∩ B)]
= 425 – (115 + 160 – 80)
= 230
![]()
Question 4.
In a school, there are 20 teachers who teach Mathematics or Physics. of these, 12 teach Mathematics and 4 teach both Physics and Mathematics. How many teachers teach Physics?
Solution:
Let A = set of teachers who teach Mathematics
B = set of teachers who teach Physics
n(A ∪ B) = 20, n(A) = 12, n(A ∩ B) = 4
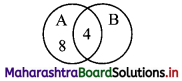
Since, n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 20 = 12 + n(B) – 4
∴ n(B) = 12
∴ Number of teachers who teach physics = 12
Question 5.
(i) If A = {1, 2, 3} and B = {2, 4}, state the elements of A × A, A × B, B × A, B × B, (A × B) ∩ (B × A).
(ii) If A = {-1, 1}, find A × A × A.
Solution:
(i) A = {1, 2, 3} and B = {2, 4}
A × A = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
A × B = {(1, 2), (1, 4), (2, 2), (2, 4), (3, 2), (3, 4)}
B × A = {(2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3)}
B × B = {(2, 2), (2, 4), (4, 2), (4, 4)}
(A × B) ∩ (B × A) = {(2, 2)}
(ii) A = {-1, 1}
∴ A × A × A = {(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1),(1, 1, 1)}
Question 6.
If A = {1, 2, 3}, B = {4, 5, 6}, which of the following are relations from A to B.
(i) R1 = {(1, 4), (1, 5), (1, 6)}
(ii) R2 = {(1, 5), (2, 4), (3, 6)}
(iii) R3 = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
(iv) R4 = {(4, 2), (2, 6), (5, 1), (2, 4)}
Solution:
A = {1, 2, 3}, B = {4, 5, 6}
∴ A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(i) R1 = {(1, 4), (1, 5), (1, 6)}
Since, R1 ⊆ A × B
∴ R1 is a relation from A to B.
(ii) R2 = {(1, 5), (2, 4), (3, 6)}
Since, R2 ⊆ A × B
∴ R2 is a relation from A to B.
(iii) R3 = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
Since, R3 ⊆ A × B
∴ R3 is a relation from A to B.
(iv) R4 = {(4,2), (2, 6), (5,1), (2, 4)}
Since, (4, 2) ∈ R4, but (4, 2) ∉ A × B
∴ R4 ⊄ A × B
∴ R4 is not a relation from A to B.
![]()
Question 7.
Determine the domain and range of the following relation.
R = {(a, b) / a ∈ N, a < 5, b = 4}
Solution:
R = {(a, b) / a ∈ N, a < 5, b = 4}
∴ Domain (R) = {a / a ∈ N, a < 5} = {1, 2, 3, 4}
Range (R) = {b / b = 4} = {4}
11th Commerce Maths Digest Pdf