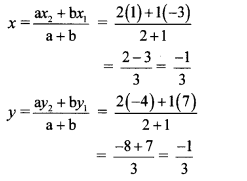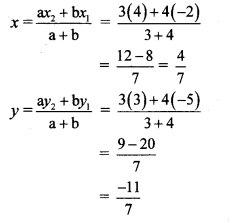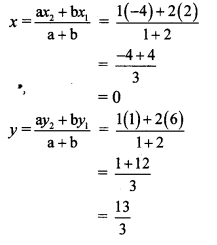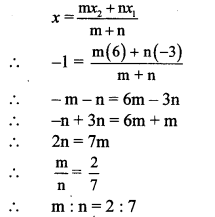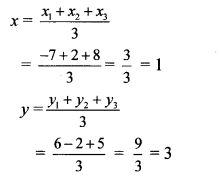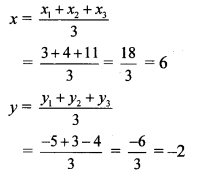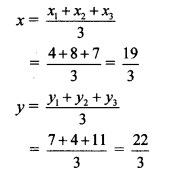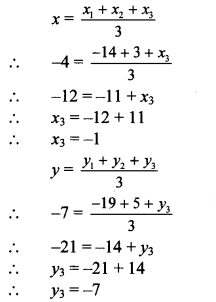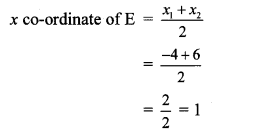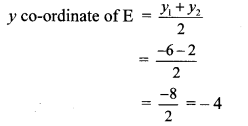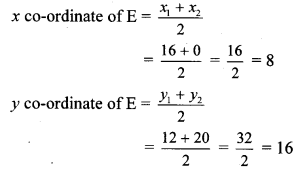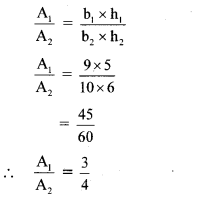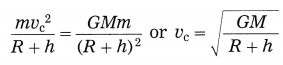Balbharti Maharashtra State Board Class 10 Science Solutions Part 1 Chapter 10 Space Missions Notes, Textbook Exercise Important Questions and Answers.
Std 10 Science Part 1 Chapter 10 Space Missions Question Answer Maharashtra Board
Class 10 Science Part 1 Chapter 10 Space Missions Question Answer Maharashtra Board
Question 1.
Fill in the blanks and explain the statements with reasoning:
a. If the height of the orbit of a satellite from the earth’s surface is increased, the tangential velocity of the satellite will ………………
Answer:
If the height of the orbit of a satellite from the earth’s surface, is increased, the tangential velocity of the satellite will decrease.
Explanation: The gravitational force (F) exerted by the earth on the satellite will decrease if the height of the orbit of the satellite from the earth’s surface is increased. Hence, the tangential velocity of the satellite will decrease.
The formula
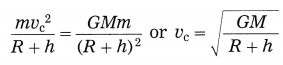
shows that υc decreases with increasing h.
b. The initial velocity (during launching) of the Mangalyaan must be greater than ………… from the earth.
Answer:
The initial velocity (during launching) of the Mangalyaan must be greater than the escape velocity from the earth.
Explanation: If a satellite is to travel beyond the gravitational pull of the earth, its velocity must be more than the escape velocity from the earth.
[Note: The velocity must be atleast equal to the escape velocity. Refer the definition of escape velocity.]

Question 2.
State with reasons whether the following statements are true or false.
a. If a spacecraft has to be sent away from the influence of the earth’s gravitational field, its velocity must be less than the escape velocity.
Answer:
False.
Explanation: The escape velocity of a body is the minimum velocity with which it should be projected from the earth’s surface, so that it can escape the influence of the earth’s gravitational field. This clearly shows that the given statement is false.
b. The escape velocity on the moon is less than that on the earth.
Answer:
True.
Explanation: Escape velocity of an object from the earth,

c. A satellite needs a specific velocity to revolve in a specific orbit.
Answer:
True.
Explanation:
Centripetal force on the satellite \(\frac{m v_{c}^{2}}{R+h}\) = gravitational force exerted by the earth on the satellite \(\frac{G M m}{(R+h)^{2}}\)
where,
m: mass of the satellite
υc: critical velocity of the satellite
h: height of the satellite from the surface of the earth
M: mass of the earth
R: radius of the earth
G: gravitational constant
∴ \(v_{\mathrm{c}}^{2}=\frac{G M}{R+h}\)
∴ \(v_{\mathrm{c}}=\sqrt{\frac{G M}{R+h}}\)
Thus, if the value of h changes, the value of υc also changes. It means a satellite needs to be given a specific velocity (in the tangential direction) to keep it revolving in a specific orbit.
d. If the height of the orbit of a satellite increases, its velocity must also increase.
Answer:
False.
Explanation:
Centripetal force on the satellite \(\frac{m v_{c}^{2}}{R+h}\) = gravitational force exerted by the earth on the satellite \(\frac{G M m}{(R+h)^{2}}\)
where,
m : mass of the satellite
υc : critical velocity of the satellite
h : height of the satellite from the surface of the earth
M : mass of the earth
R : radius of the earth
G : gravitational constant
∴ \(v_{\mathrm{c}}^{2}=\frac{G M}{R+h}\)
∴ \(v_{\mathrm{c}}=\sqrt{\frac{G M}{R+h}}\)
Thus, if the value of h changes, the value of υc also changes. It means a satellite needs to be given a specific velocity (in the tangential direction) to keep it revolving in a specific orbit.
As per the formula υc = \(\sqrt{\frac{G M}{R+h}}\) , if the value of h increases, the value of υc decreases. Hence, if the height of the satellite from the surface of the earth increases, its velocity decreases.

Question 3.
Answer the following questions:
a. What is meant by an artificial satellite? How are the satellites classified based on their functions?
(OR)
Write the importance of artificial satellites in your words. (Practice Activity Sheet – 3)
Answer:
A manmade object orbiting the earth or any other planet is called an artificial satellite. Satellites work on solar energy and hence photovoltaic panels are attached on both sides of the satellite, which look like wings. Satellites are also installed with various transmitters and other equipment to receive and transmit signals between the earth and the satellites.
Classification of satellites depending on their functions:
(1) Weather satellites: weather satellites collect the information regarding weather conditions of the region. It records temperature, air pressure, wind direction, humidity, cloud cover, etc. this information is sent to the space research station on the earth and then with this information weather forecast is made.
(2) Communication satellites: In order to establish communication between different places on the earth through mobile phones or computer assisted internet, communication satellites are used. Many artificial satellites placed at various locations in the earth’s orbit are well interconnected and help us to have communication with any place, from anywhere, at any time and in any form including voicemail, email, photographs, audio mail, etc.
(3) Broadcasting satellites: Broadcasting satel¬lites are used to transmit various radio and television programs and even live programs from any place on the earth to any other place. As a result, one can have access to information about current incidents, events, programs, sports and other events right from his drawing room with these satellites.
(4) Navigational satellites: Navigational satel¬lites assist the surface, water and air transportation and coordinate their busy schedule. These satellites also assist the user with current live maps as well as real time traffic conditions.
(5) Military satellites: Every sovereign nation needs to keep the real time information about the borders. Satellites help to monitor all movements of neighboring countries or enemy countries. Military satellites also help to guide the missiles effectively.
(6) Earth observation satellites: These satellites observe and provide the real time information about the earth. These satellites also help us to collect information about the resources, their management, continuous observation about a natural phenomenon and the changes within it.
(7) Other satellites: Apart from these various satellites, certain satellites for specific works or purposes are also sent in the space. E.g. India has sent EDUSAT for educational purpose; CARTOSAT for surveys and map making. Similarly, satellites with telescopes, like Hubble telescope or a satellite like International Space Station help to explore the universe. In fact, ISS (International Space Station) provides a temporary residence where astronauts can stay for a certain short or long period and can undertake the research and study space activities.
The various functions listed above show the importance of artificial satellites.
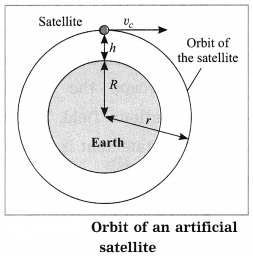
b. What is meant by the orbit of a satellite? On what basis and how are the orbits of artificial satellites classified?
Answer:
Orbit of a satellite is its path around the earth.
Orbits of artificial satellites can be classified on various basis.
(1) On the basis of the angle of the orbital plane: Orbital plane of a satellite can be the equatorial plane of the earth or it can be at an angle to it.
(2) On the basis of the nature of the orbit: Orbital plane can be circular or elliptical in shape.
(3) On the basis of the height of the satellite: Orbit of a satellite can be HEO, MEO or LEO.
(i) High Earth Orbit (HEO) satellite: A satellite orbiting at a height equal to or greater than 35780 km above the earth’s surface is called a High Earth Orbit satellite. The critical velocity (υc) of a satellite revolving in an orbit at 35780 km above the earth surface is 3.08 km/s. Such a satellite will take about 23 hours 54 minutes to complete one revolution around the earth. The earth completes one rotation about its axis in the same time. The orbital plane of such a satellite is the equatorial plane of the earth. The satellite’s relative position appears stationary with respect to a place on the earth. This satellite is, therefore, called a geostationary satellite or geosynchronous satellite.
(ii) Medium Earth Orbit (MEO) satellite: A satellite orbiting at a height between 2000 km and 35780 km above the earth’s surface is called a Medium Earth Orbit satellite. The orbital path of such a satellite is normally elliptical and passes through the North and the South polar regions. These satellites take about 12 hours to complete one revolution around the earth.
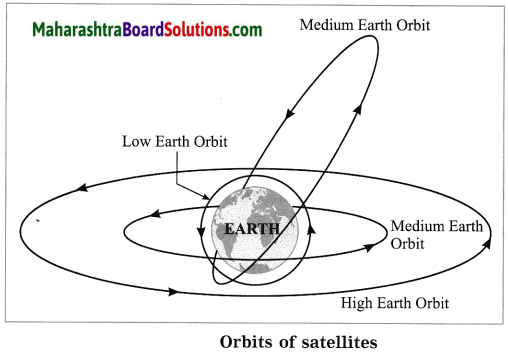
(iii) Low Earth Orbit (LEO) satellite:
A satellite orbiting at a height between 180 km and 2000 km above the earth’s surface is called a Low Earth Orbit satellite. Normally, these satellites take 90 minutes to complete one revolution around the earth. Weather satellites, space telescopes and International Space Station are Low Earth Orbit satellites.
c. Why are geostationary satellites not useful for studies of polar regions? (Practice Activity Sheet – 4)
(OR)
Explain the following statement. A geostationary satellite is not useful in the study of polar regions. (Practice Activity Sheet – 1)
Answer:
Geostationary satellites have two distinct characteristics:
(1) Geostationary satellites are HEO satellites and are placed at 35780 km above the earth’s surface.
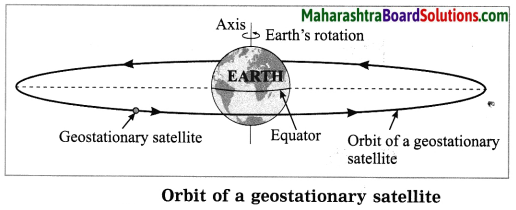
(2) A geostationary satellite revolves in the equatorial plane of the earth, and thus, it can never fly above the polar regions.
Hence, geostationary satellites are not useful for studies of polar regions.
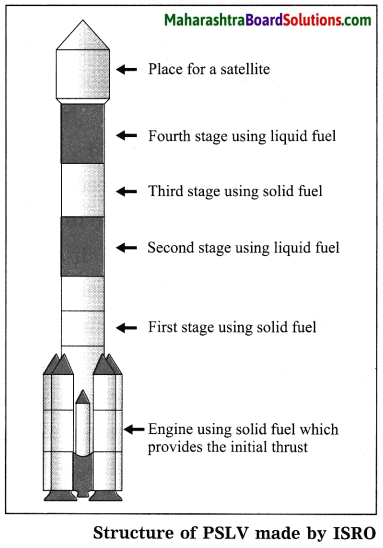
d. What is meant by a satellite launch vehicle? Explain the satellite launch vehicle developed by ISRO with the help of a schematic diagram.
Answer:
A rocket used to carry an artificial satellite to a desired height above the earth’s surface and then project it with a proper velocity so that the satellite orbits the earth in the desired orbit is called a launch vehicle. A satellite launch vehicle needs a specific velocity as well as a thrust to reach the desired height above the earth’s surface. The velocity and the thrust of a satellite launch vehicle depend on the weight and orbital height of the satellite.
Accordingly, the structure of the launch vehicle is decided and designed. The weight of the fuel also contributes a major portion in the total weight of the launch vehicle. This also influences the structure of the launch vehicle. In order to use the fuel optimally, multiple stage launch vehicles are now designed and used.
The Polar Satellite Launch Vehicle (PSLV) developed by ISRO is shown below in a schematic diagram.
e. Why is it beneficial to use a satellite j launch vehicle made up of more than one stage?
Answer:
Earlier Satellite Launch Vehicles (SLV) used to be of a single stage vehicles. Such SLVs used to be very heavy as well as expensive in terms of its fuel consumption. As a result, SLVs with multiple stages were developed.
In multistage SLVs, as the journey of the launch vehicle progresses and the vehicle achieves a specific velocity and a certain height, the fuel of the first stage is exhausted and the empty fuel tank gets detached from the main body of the launch vehicle and falls back into a sea or on unpopulated land. As the fuel in the first stage is exhausted, the engine in the second stage is Ignited. However, the weight of the launch vehicle is now less than what it was earlier and hence it can move with higher velocity, Thus, it saves fuel consumption. Hence, it is beneficial to use a multistage satellite launch vehicle.

Question 4.
Complete the following table:
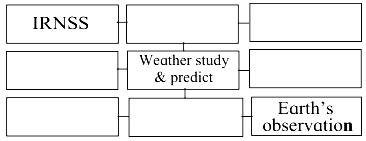
Answer:
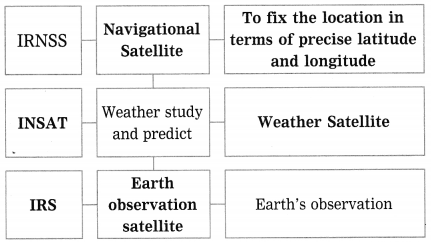
Question 5.
Solve the following problems:
a. If the mass of a planet is eight times the mass of the earth and its radius is twice the radius of the earth, what will be the escape velocity for that planet?
Answer:
Given:
(1) The mass of the planet (M) is eight times the mass of the earth, i.e., 8 × 6 × 1024 kg
(2) The radius of the planet (R) is twice the radius of the earth, i.e., 2 × 6.4 × 106 km
(3) G = 6.67 × 10-11 N·m2/kg2
Escape velocity for that planet
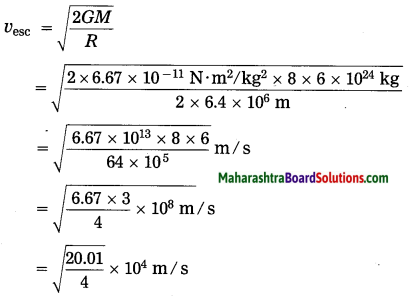
= 2.237 × 104 m/s
= 22.37 km/s
b. How much time would a satellite in an orbit at a height of 35780 km above the earth’s surface take to complete one revolution around the earth, if the mass of the earth were four times its original mass?
Answer:
Given: R (Earth) = 6400 km = 6.4 × 106 m,
M (Earth) = 6 × 1024 kg
∴ M’ = 4M = 4 × 6 × 1024 kg
h = 35780 km = 3.578 × 107 m = 35.78 × 106 m,
G = 6.67 × 10-11 N·m2/kg2, T = ?
The time that the satellite would take to complete one revolution around the earth,

= Approx 4.303 × 104 s
= Approx 11.95 h
or 11 hours 57 minutes 10 seconds.

c. If the height of a satellite completing one revolution around the earth in T seconds is h1 meters, then what would be the height of a satellite taking 2\(\sqrt{2}\) T seconds for one revolution?
Answer:
Given:
(1) Time: T seconds
(2) Height: h1
Let us assume the height of the satellite completing one revolution in 2\(\sqrt{2}\) T seconds as h2.

∴ R + h2 = 2R + 2h1
∴ h2 = R + 2h1
Project:
Project 1.
Collect information about the space missions undertaken by Sunita Williams.
Hints:
The following sources can be used to get the information on the above topic:
(1) Google Search Engine
(2) YouTube
(3) E-books on Sunita Williams
(4) English and other regional language books on Sunita Williams available in your library
(5) Newspaper clippings
Based on the information you have collected from the above sources, complete the project in about 5 pages. You can do value addition to your project with the help of suitable photos, clippings, charts, graphs and sketches.
Project 2.
Assume that you are interviewing Sunita Williams. Prepare a questionnaire and also the answers.
Answer:
Points to make a list of a questionnaire for the interview of Sunita Williams :
(1) Primary and higher education
(2) The source of inspiration to become an astronaut
(3) Information about her mentor
(4) General and specific training
(5) Initial experience of being an astronaut
(6) First space mission, its nature, duration and experience
(7) Natureofresearchcarriedoutinspace
(8) Some special memories
(9) Future plans
(10) Tips and guidance for the younger generation.

Can you recall? (Text Book Page No. 135)
Question 1.
What is the difference between space and sky?
Answer:
- The visible portion of the atmosphere and outer space seen by simple eyes, without any equipment from the earth, is known as the sky.
- The infinite three-dimensional expanse in which the Solar system, stars, celestial bodies, galaxies and the endless Universe exist is known as space.
- Both sky and space lack a definite boundary. However, the sky is a very tiny part of space.
Question 2.
What are different objects in the Solar system?
Answer:
- Our Solar system is a very tiny part of a huge Galaxy-Milky Way.
- The Sun is at the centre of the Solar system. Sun is a star.
- Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus and Neptune are planets in our Solar system. These planets revolve around the Sun. Some of these planets have their own natural satellites.
- Besides, there are asteroids, meteoroids, comets and meteors in the Solar system.
Question 3.
What is meant by a satellite?
Answer:
- An astronomical object orbiting any planet of our Solar system is called a satellite.
- Mercury and Venus have no satellites.
- Some planets have more than one satellite. E.g. Jupiter has 69 satellites.
Question 4.
How many natural satellites does the earth have?
Answer:
The earth has one natural satellite called the moon.
Question 5.
Which type of telescopes are orbiting around the earth? Why is it necessary to put them in space?
Answer:
(1) The following three types of telescopes are orbiting around the earth:
- Optical Refracting Telescope.
- Optical Reflecting Telescope.
- Radio Telescope.
(2) Visible light and radio waves emitted by celestial bodies in space pass through the atmosphere before reaching the earth’s surface. During this journey, some light is absorbed by the atmosphere. Hence, the intensity of the light reaching the earth’s surface decreases. Besides, temperature and air pressure cause the atmospheric turbulence. Hence, light rays change their path, resulting in a change in the position of the image of a celestial body.
City lights during night, and bright sunlight during day also put limitations on usage of optical telescopes on the earth. To minimize these problems, optical telescopes are situated on mountain top, away from inhabited places. However, limitations caused by the atmosphere still persist.
To get rid of these problems scientists have successfully launched telescopes in space. Images obtained by these telescopes are brighter and clearer than those obtained by the telescopes located on the earth’s surface.
Can you recall? (Text Book Page No. 135)
Question 1.
Where does the signal in your cellphone come from?
Answer:
In nearby area of our residence, many mobile towers are installed at various places. Cellphones receive signals from one of these mobile towers.
Question 2.
Where from does it come to mobile towers?
Answer:
All mobile towers are connected to satellites. Cellphone signal reaching the nearest mobile tower in our vicinity is first transmitted to the satellite. The satellite transmits the signal to the mobile tower near the destination.
Question 3.
Where does the signal to your TV set come from?
Answer:
(1) Television Centre or Studio transmits the TV program which first reaches the satellite. The dish antenna of the cable operator in our area receives these signals. The TV programs reach our TV set through a cable connected between the cable operator’s receiving station and our TV set.
(2) Alternatively, a small portable dish antenna fixed on the rooftop is also used to receive the TV signals directly from the satellites. Finally, a cable connected to the dish antenna and TV set brings the programme to our TV set.

Question 4.
You may have seen photographs showing the position of monsoon clouds over the country in the newspaper. How are these images obtained?
Answer:
Weather satellites take photographs of the sky above the earth’s surface at regular intervals. Some satellites, capable of receiving radio signals, also collect the information of weather conditions and finally images of the sky are built with computers. Territorial boundaries of the states and the country are drawn later on these images. Such satellite images with imposed boundaries are printed in media or shown on the television.
Fill in the blanks:
Question 1.
A man-made object revolving around the earth in a fixed orbit is called …………..
Answer:
A man-made object revolving around the earth in a fixed orbit is called an artificial satellite.
Question 2.
Chandrayaan-I discovered the presence of ………….. on the moon.
Answer:
Chandrayaan-I discovered the presence of water on the moon.
Question 3.
Apart from launching a satellite around the earth, India has been able to launch a satellite around ……………
Answer:
Apart from launching a satellite around the earth, India has been able to launch a satellite around Mars.
Question 4.
All satellites work on …………… energy.
Answer:
All satellites work on solar energy.
Question 5.
……………. are used to carry and place a satellite in a specific orbit.
Answer:
Satellite launchers are used to carry and place a satellite in a specific orbit.
Question 6.
USA has developed ……………. as an alternative to space launch vehicles.
Answer:
USA has developed space shuttles as an alternative to space launch vehicles.
Question 7.
Hubble telescope is a ………….. satellite.
Answer:
Hubble telescope is a Low Earth Orbit (LEO) satellite.
Question 8.
……………. executed the first ever mission to the moon in the world.
Answer:
Russia executed the first ever mission to the moon in the world.

Question 9.
………… executed the first manned mission to the moon in the world.
Answer:
USA executed the first manned mission to the moon in the world.
Select the appropriate answer from given options:
Question 1.
Which one of the following is a Low Earth Orbit (LEO) satellite?
(a) Navigational satellite
(b) Geostationary satellite
(c) International Space Station
(d) All of the above
Answer:
(c) International Space Station
Question 2.
Which of the following satellite launchers is developed by India?
(a) INSAT
(b) IRNSS
(c) EDUSAT
(d) PSLV
Answer:
(d) PSLV
Question 3.
Which of the following astronauts travelled through space shuttle ‘Discovery’ first time? (Practice Activity Sheet – 4)
(a) Kalpana Chawla
(b) Rakesh Sharma
(c) Sunita Williams
(d) Neil Armstrong
Answer:
(c) Sunita Williams
Considering the correlation between the words of the first pair, pair the third word accordingly with proper answer. (OR) Considering the first correlation, complete the second.
Question 1.
IRNSS : Direction showing satellite :: INSAT :………… (Practice Activity Sheet – 1)
Answer:
IRNSS : Direction showing satellite :: INSAT : Weather satellite
Question 2.
Hubble telescope : 569 km high from the earth’s surface :: Revolving orbit of Hubble telescope :………. (Practice Activity Sheet – 2; March 2019)
Answer:
Hubble telescope : 569 km high from the earth’s surface :: Revolving orbit of Hubble telescope : Low Earth Orbit.
Match the column:
Question 1.
| Column A |
Column B |
| (1) Clouds over India |
(a) Low Earth Orbit |
| (2) Global communication |
(b) PSLV |
| (3) Launch vehicle made by ISRO |
(c) Communication satellite |
| (4) International Space Station |
(d) EDUSAT |
| (5) Navigational satellite |
(e) Weather satellite |
|
(f) Medium Earth Orbit |
Answer:
(1) Clouds over India – Weather satellite
(2) Global communication – Communication satellite
(3) Launch vehicle made by ISRO – PSLV
(4) International Space Station – Low Earth Orbit
(5) Navigational satellite – Medium Earth Orbit.

Answer the following questions in one sentence each:
Question 1.
What do you mean by the orbit of a satellite?
Answer:
Orbit of a satellite is its path around the earth.
Question 2.
Which factor decides the orbit of a satellite?
Answer:
The function of a satellite decides the orbit of the satellite.
Question 3.
What is a High Earth Orbit satellite?
Answer:
A satellite orbiting at a height equal to or greater than 35780 km above the earth’s surface is called a High Earth Orbit satellite.
Question 4.
Give two examples of Low Earth Orbit satellites.
Answer:
Weather satellite and International Space Station are Low Earth Orbit satellites.
Question 5.
What is a launch vehicle?
Answer:
A rocket used to carry an artificial satellite to a desired height above the earth’s surface and then project it with a proper velocity so that the satellite orbits the earth in the desired orbit is called a launch vehicle.
Question 6.
Name the launch vehicle developed by India.
Answer:
The launch vehicle developed by India is known as PSLV, i.e., Polar Satellite Launch Vehicle.
Answer the following questions:
Question 1.
Write the proper name of the orbits of satellites shown in the following figure with their height from the earth’s surface. (Practice Activity Sheet – 4)
Answer:
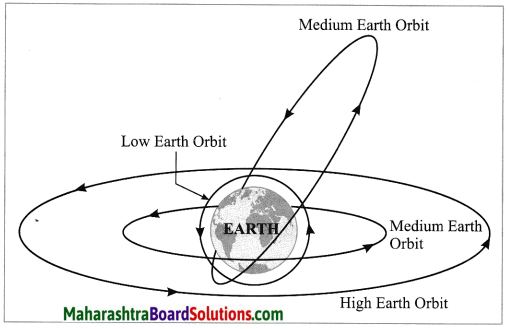
(a) Low earth orbits: height above the earth’s surface: 180 km to 2000 km
(b) Medium earth orbits: height above the earth’s surface: 2000 km to 35780 km
(c) High earth orbits: height from the earth’s surface > 35780 km

Question 2.
Explain the need and importance of space missions.
Answer:
Man has always been curious about the sun, moon, stars and the world beyond the earth. Initially, man tried to observe space with the help of telescopes. However, later he dreamt to fly into space and finally succeeded to reach into space.
Space missions are now essential to understand the origin and evolution of our solar system as well as to study the Universe beyond the Solar system.
Space missions have given us many benefits and made our life simpler. It is because of space missions that the real-time immediate communication and exchange of information across the globe is now possible. We can receive the abundant information at the desk at our home or office. We also get information about any topic at any time and anywhere at fingertips through the Internet. Besides, the advanced alerts about some natural calamities like cyclones or storms are received through satellites sent as a part of space missions. Satellites have also helped us in entertainment. Programmes, sports events, etc., can be telecast live and can reach millions at a time throughout the world.
Satellite surveillance of the enemy, exploring the reserves of various minerals resources, access to various activities like trade, tourism and navigation, and easy global reach to make world a global village is all possible due to the space missions. Thus, space missions are extremely important in defence, communication, weather forecast, observation, direction determination, etc.
Question 3.
What are space expeditions? Explain their need and importance in your words. (Practice Activity Sheet – 2)
Answer:
A mission planned (i) for establishing artificial satellites in the earth’s orbit, using them for research or for the benefit of life, or (ii) for sending a spacecraft to the various components of the solar system or outside is called a space expedition.
Man has always been curious about the sun, moon, stars and the world beyond the earth. Initially, man tried to observe space with the help of telescopes. However, later he dreamt to fly into space and finally succeeded to reach into space. Space missions are now essential to understand the origin and evolution of our solar system as well as to study the Universe beyond the Solar system.
Space missions have given us many benefits and made our life simpler. It is because of space missions that the real-time immediate communication and exchange of information across the globe is now possible. We can receive the abundant information at the desk at our home or office. We also get information about any topic at any time and anywhere at fingertips through the Internet. Besides, the advanced alerts about some natural calamities like cyclones or storms are received through satellites sent as a part of space missions. Satellites have also helped us in entertainment. Programmes, sports events, etc., can be telecast live and can reach millions at a time throughout the world.
Satellite surveillance of the enemy, exploring the reserves of various minerals resources, access to various activities like trade, tourism and navigation, and easy global reach to make world a global village is all possible due to the space missions. Thus, space missions are extremely important in defence, communication, weather forecast, observation, direction determination, etc.
Question 4.
What are the objectives of the space mission?
Answer:
Man initially tried to satisfy his curiosity to know the world and universe beyond the earth with the help of telescopes. However, it has some obvious limitations and to overcome these limitations, man later ventured into space missions.
Space missions carried out by man were aimed at four specific objectives:
- To launch artificial satellites in the earth’s orbit for study and research.
- To launch artificial satellites in the earth’s orbit for various purposes like telecommunication, weather forecast, radio and TV programme transmission, etc.
- To send artificial satellites beyond the earth’s orbit to observe, study and collect the information from other planets, meteors, meteoroids, asteroids and comets.
- To sense and understand space beyond the solar system.

Question 5.
Write on significant space missions carried out by man.
Answer:
Man has carried out many space missions within and beyond the earth’s orbit. Significant space missions are as follows:
(1) Space missions within the earth’s orbit: Man has so far sent many artificial satellites of various types in the earth’s orbit. These satellites have made the life of man simpler. Besides, it has also helped us in resource management, communication, disaster management, etc.
(2) Moon missions : Moon is the natural satellite , of the earth and it is the nearest celestial body to us. Naturally, our initial space missions were directed to the moon. As of now, only Russia, USA, European Union, China, Japan and India have successfully undertaken . moon missions. Russia executed 15 moon missions between 1959 and 1976. Of these, last 4 missions brought the stone samples from the moon for study and analysis. However all these missions were unmanned. USA executed moon missions between 1962 and 1972. Some of these missions were unmanned.
However, the historic moon mission took place on 20th July, 1969, when American astronaut Neil Armstrong became the first human to step on the moon. India has undertaken the moon mission. Indian Space Research Organisation (ISRO) successfully launched Chandrayaan-I and placed it in orbit of the moon. It sent useful information to the earth for about a year. The most important discovery made during the mission was the presence of water on moon’s surface. India was the first country to discover this.
(3) Mars mission: The second nearest celestial object to the earth is Mars and many nations sent spacecraft towards it. But only few of them have been successful. However, the performance of Mangalyaan, the Indian spacecraft sent by ISRO towards Mars, was remarkable. Mangalyaan was launched in November 2013 and was placed in the orbit of Mars successfully in September 2014. It has obtained useful information about the surface and atmosphere of Mars.
(4) Space missions to other planets: Other than moon and Mars missions, many other space missions were undertaken for studying other planets. Some spacecraft orbited the planets, some landed on some planets, and some just observed the planets, passed near them and went further to study other celestial bodies. Some spacecraft were sent specifically to study asteroids and comets. Some spacecraft’s have brought dust and stone samples from asteroids for the study.
All these space missions are very useful in getting information and helping us in clarifying our concepts about the origin of the earth and the Solar system.
Question 6.
Bring out the contribution of India’s space missions.
Answer:
Successful space missions as well as scientific and technological accomplishments by India in space technology have made a significant contribution in the national and social development of our country.
India has indigenously built various launchers and these launchers can put the satellites having the mass up to 2500 kg in orbit.
Indian Space Research Organisation (ISRO) has designed and built two important launchers: Polar Satellite Launch Vehicle (PSLV) and Geosynchronous Satellite Launch Vehicle (GSLV).
Many satellites in INS AT and GSAT series are active in telecommunication, television broadcasting, meteorological services, disaster management and in monitoring and management of natural resources. EDUSAT is used specifically for education while satellites in IRNSS series are used for navigation. Thumba, Sriharikota and Chandipur are Indian satellite launch centers.
Vikram Sarabhai Space Centre at Thiruvananthapuram, Satish Dhawan Space Research Centre at Sriharikota and Space Application Centre at Ahmedabad are space research organizations of India.

Question 7.
What is meant by space debris? Why is there need to manage the debris? (March 2019)
Answer:
In a space nonessential objects such as the parts of launchers and satellites, revolving around the earth are called the debris in space.
The debris can be harmful to the artificial satellites. It can collide with the satellite or spacecrafts and damage them. Therefore the future of artificial satellites or spacecrafts are in danger.
Hence, it is necessary to manage the debris.
Solve the following examples/numerical problems:
[Note: See the textbook for the relevant data.]
Problem 1.
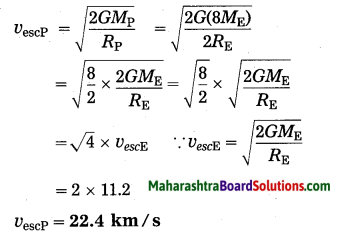
If the mass of a planet is 8 times that of the earth and its radius is twice the radius of the earth, what will be the escape velocity for that planet? (Escape velocity for the earth = 11.2 km/s) (Practice Activity Sheet – 2)
Answer:
Given:
Mass of the planet = 8ME radius of the planet, Rp = 2RE,
escape velocity for the earth, υescE = 11.2 km/s
escape velocity for the planet, υescP = ?

Problem 2.
Calculate the critical velocity (υc) of the satellite to be located at 35780 km above the surface of the earth.
Answer:
Given:
G: 6.67 × 10-11 N·m2/kg2,
M(Earth): 6 × 1024 kg,
R(Earth): 6.4 × 106 m,
h: 35780 km = 35780 × 103 m,
υc = ?
Critical velocity of the satellite

= 3.08 × 103 m/s
= 3.08 Km/s.
Problem 3.
In the above example (2) how much time will the satellite take to complete one revolution around the earth?
Answer:
Given:
R: 6400mkm = 6.4 × 106 m
h: 35780 km = 3.5780 × 107 m
v: 3.08 km/s = 3.08 × 103 m/s
T = ?
The time required for the satellite to complete one revolution around the earth,

= Approx 86060 s
= 23 hours 54 minutes 20 seconds
Problem 4.
Calculate the critical velocity (υc) of the satellite to be located at 2000 km above the surface of the earth.
Answer:
Refer to the example (2) above.
Here,h = 2 × 106 m
υc = 6902 m/s

Problem 5.
In the above example (4), how much time will the satellite take to complete one revolution around the earth?
Answer:
Refer to example (3) above.
Approx 7647 s
= 2 hours 7 minutes 27 seconds.
[Note: For more solved problems and problems for practice, refer Chapter 1 (Gravitation)]
![]()