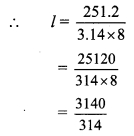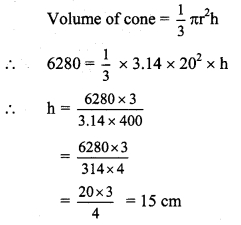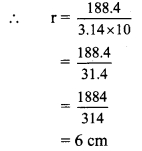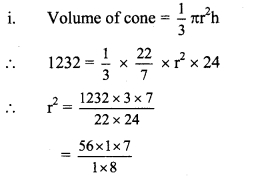Prasanna

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.2 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Parallel Lines and Transversals Class 8 Maths Chapter 2 Practice Set 2.2 Solutions Maharashtra Board

Std 8 Maths Practice Set 2.2 Chapter 2 Solutions Answers

Question 1.
Choose the correct alternative.
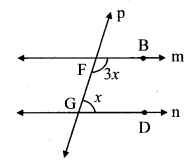
i. In the given figure, if line m || line n and line p is a transversal, then find x.

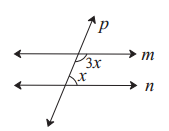
(A) 135°
(B) 90°
(C) 45°
(D) 40°
Solution:
(C) 45°

Hint:

line m || line n and line p is a transversal.
∴ m∠BFG + m∠FGD = 180°
…[Interior angles]
∴ 3x + x = 180°
∴ 4x = 180°
∴ x = \(\frac { 180 }{ 4 }\)
∴ x = 45°

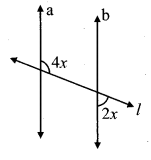
ii. In the given figure, if line a || line b and line l is a transversal, then find x.

(A) 90°
(B) 60°
(C) 45°
(D) 30°
Solution:
(D) 30°

Hint:

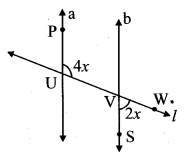
line a || line b and line l is a transversal.
∴ m∠UVS = m∠PUV
…[Alternate angles]
= 4x
m∠UVS + m∠WVS = 180°
… [Angles in a linear pair]
∴ 4x + 2x = 180°
∴ 6x = 180°
∴ x = \(\frac { 180 }{ 6 }\)
∴ x = 30°

Question 2.
In the given figure, line p || line q. Line t and line s are transversals. Find measure of ∠x and ∠y using the measures of angles given in the figure.

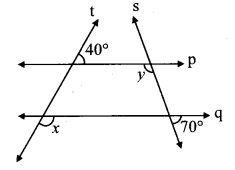
Solution:

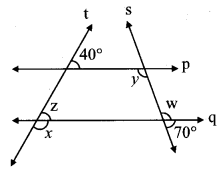
i. Consider ∠z as shown in figure.
line p || line q and line t is a transversal.
∴ m∠z = 40° …(i) [Corresponding angles]
m∠x + m∠z = 180° …[Angles in a linear pair]
∴ m∠x + 40o = 180° …[From(i)]
∴ m∠x= 180° – 40°
∴ m∠x = 140°

ii. Consider ∠w as shown in the figure.
m∠w + 70° = 180° …[Angles in a linear pair]
∴ m∠w = 180° – 70°
∴ m∠w = 110° …(ii)
line p || line q and line s is a transversal.
∴ m∠y = m∠w …[Alternate angles]
∴ m∠y =110° …[From (ii)]
∴ m∠x = 140°, m∠y = 110°

Question 3.
In the given figure, line p || line q, line l || line m. Find measures of ∠a, ∠b and ∠c, using the measures of given angles. Justify your answers.

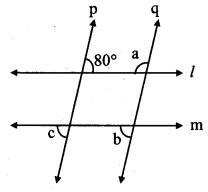
Solution:
i. line p || line q and line l is a transversal.
∴ m∠a + 80° = 180° …[Interior angles]
∴ m∠a= 180° – 80°
∴ m∠a= 100°

ii. line l || line m and line p is a transversal.
∴ m∠c = 80° …(i) [Exterior alternate angles]

iii. line p || line q and line m is a transversal.
∴ m∠b = m∠c … [Corresponding angles]
m∠b = 80° …[From (i)]
∴ m∠a = 100°, m∠b = 80°, m∠c = 80°

Question 4.
In the given figure, line a || line b, line l is a transversal. Find the measures of ∠x, ∠y, ∠z using the given information.

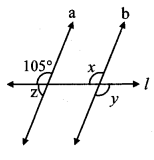
Solution:
line a || line b and line l is a transversal.
∴ m∠x = 105° …(i) [Corresponding angles]

ii. m∠y = m∠x … [Vertically opposite angles]
∴ m∠y = 105° …[From (i)]

iii. m∠z + 105° = 180° …[Angles in a linear pair]
∴ m∠z = 180°- 105°
∴ m∠z = 75°
∴ m∠x = 105°, m∠y = 105°, m∠z = 75°

Question 5.
In the given figure, line p || line l || line q. Find ∠x with the help of the measures given in the figure.

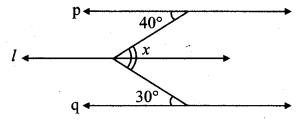
Solution:

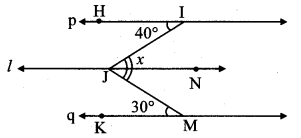
line p || line l and line IJ is a transversal.
m∠IJN = m∠JIH … [Alternate angles]
∴ m∠IJN = 40° …(i)
line l || line q and line MJ is a transversal.
m∠MJN = m∠JMK … [Alternate angles]
∴ m∠MJN = 30° …(ii)
Now, m∠x = m∠IJN + m∠MJN
…[Angle addition property]
= 40° + 30° …[From (i) and (ii)]
∴ m∠x = 70°

Maharashtra Board Class 8 Maths Chapter 2 Parallel Lines and Transversals Practice Set 2.2 Intext Questions and Activities

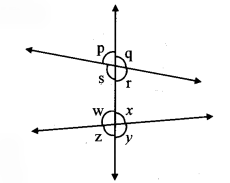
Question 1.
When two parallel lines are intersected by a transversal eight angles are formed. If the measure of one of these eight angles is given, can we find measures of remaining seven angles? (Textbook pg, no. 9)
Solution:
Yes, we can find the measures of the remaining angles.

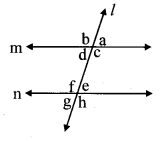
In the given figure, line m || line n and line l is a transversal.
m∠a = 60°(say) …(i)
i. m∠a + m∠b = 180° …[Angles in a linear pair]
∴ 60° + m∠b =180° … [From (i)]
∴ m∠b = 180° – 60°
∴ m∠b = 120° …(ii)

ii. m∠c = m∠b …[Vertically opposite angles]
∴ m∠c = 120° .. .(iii) [From (ii)]

iii. m∠d = m∠a …[Vertically opposite angles]
∴ m∠d = 60° …(iv) [From (i)]

iv. m∠e = m∠d …[Alternate angles]
∴ m∠e = 60° … [From (iv)]

v. m∠f = m∠c …[Alternate angles]
∴ m∠f = 120° …[From (iii)]

vi. m∠g = m∠d …[Corresponding angles]
∴ m∠g = 60° … [From (iv)]

vii. m∠h = m∠c … [Corresponding angles]
∴ m∠h = 120° …[From (iii)]

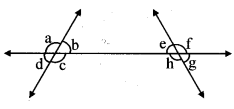
Question 2.
As shown in the figure (A), draw two parallel lines and their transversal on a paper. Draw a copy of the figure on another blank sheet using a trace paper, as shown in the figure (B). Colour part Land part II with different colours. Cut out the two parts with a pair of scissors. Place, part I and part II on each angle in the figure A and answer the following questions. (Textbook pg. no. 9)

1. Which angles coincide with part I?
2. Which angles coincide with part II?

Solution:

1. ∠d, ∠f and ∠h coincide with part I.
2. ∠c, ∠e and ∠g coincide with part II.

Std 8 Maths Digest

• Practice Set 1.1 Class 8 Answers
• Practice Set 1.2 Class 8 Answers
• Practice Set 1.3 Class 8 Answers
• Practice Set 1.4 Class 8 Answers
• Practice Set 2.1 Class 8 Answers
• Practice Set 2.2Class 8 Answers
• Practice Set 2.3 Class 8 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.1 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Parallel Lines and Transversals Class 8 Maths Chapter 2 Practice Set 2.1 Solutions Maharashtra Board

Std 8 Maths Practice Set 2.1 Chapter 2 Solutions Answers

Question 1.
In the given figure, each angle is shown by a letter. Fill in the boxes with the help of the figure

Corresponding angles:
i. ∠p and __
ii. ∠q and __
iii. ∠r and __
iv. ∠s and __

Interior alternate angles:
v. ∠s and __
vi. ∠w and __
Solution:
i. ∠w
ii. ∠x
iii. ∠y
iv. ∠z
v. ∠x
vi. ∠r

Question 2.
Observe the angles shown in the figure and write the following pair of angles.

1. Interior alternate angles
2. Corresponding angles
3. Interior angles

Solution:

1. ∠c and ∠e; ∠b and ∠h
2. ∠a and ∠e; ∠b and ∠f; ∠c and ∠g; ∠d and ∠h
3. ∠c and ∠h; ∠b and ∠e

Std 8 Maths Digest

• Practice Set 1.1 Class 8 Answers
• Practice Set 1.2 Class 8 Answers
• Practice Set 1.3 Class 8 Answers
• Practice Set 1.4 Class 8 Answers
• Practice Set 2.1 Class 8 Answers
• Practice Set 2.2 Class 8 Answers
• Practice Set 2.3 Class 8 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.4 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Rational and Irrational Numbers Class 8 Maths Chapter 1 Practice Set 1.4 Solutions Maharashtra Board

Std 8 Maths Practice Set 1.4 Chapter 1 Solutions Answers

Question 1.
The number √2 is shown on a number line. Steps are given to show √3 on the number line using √2. Fill in the boxes properly and complete the activity.

The point Q on the number line shows the number ……….
A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line.
Right angled ∆OQR is obtained by drawing seg OR.
l(OQ) = √2, l(QR) = 1
∴By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²

Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3
Solution:
The point Q on the number line shows the number √2
A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line.
Right angled ∆OQR is obtained by drawing seg OR.
l(OQ) = √2, l(QR) = 1
∴By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²

.. .[Taking square root of both sides]
Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3.

Question 2.
Show the number √5 on the number line.
Solution:
Draw a number line and take a point Q at 2
such that l(OQ) = 2 units.
Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.
Draw seg OR.
∆OQR formed is a right angled triangle.
By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
= 2² + 1²
= 4 + 1
= 5
∴l(OR) = √5 units
…[Taking square root of both sides]
Draw an arc with centre O and radius OR. Mark the point of intersection of the number line and arc as C. The point C shows the number √5.

Question 3.
Show the number √7 on the number line.
Solution:
Draw a number line and take a point Q at 2 such that l(OQ) = 2 units.
Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.
Draw seg OR.
∆OQR formed is a right angled triangle.
By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
= 2² + 1²
= 4 + 1
= 5
∴ l(OR) = √5 units
… [Taking square root of both sides]
Draw an arc with centre O and radius OR.
Mark the point of intersection of the number line and arc as C. The point C shows the number √5.
Similarly, draw a line CD perpendicular to the number line through the point C such that l(CD) = 1 unit.
By Pythagoras theorem,
l(OD) = √6 units
The point E shows the number √6 .
Similarly, draw a line EP perpendicular to the number line through the point E such that l(EP) = 1 unit.
By Pythagoras theorem,
l(OP) = √7 units
The point F shows the number √7.

Std 8 Maths Digest

• Practice Set 1.1 Class 8 Answers
• Practice Set 1.2 Class 8 Answers
• Practice Set 1.3 Class 8 Answers
• Practice Set 1.4 Class 8 Answers
• Practice Set 2.1 Class 8 Answers
• Practice Set 2.2Class 8 Answers
• Practice Set 2.3 Class 8 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.2 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Rational and Irrational Numbers Class 8 Maths Chapter 1 Practice Set 1.2 Solutions Maharashtra Board

Std 8 Maths Practice Set 1.2 Chapter 1 Solutions Answers

Question 1.
Compare the following numbers.
i. 7, -2
ii. 0, \(\frac { -9 }{ 5 }\)
iii. \(\frac { 8 }{ 7 }\), 0
iv. \(-\frac{5}{4}, \frac{1}{4}\)
v. \(\frac{40}{29}, \frac{141}{29}\)
vi. \(-\frac{17}{20},-\frac{13}{20}\)
vii. \(\frac{15}{12}, \frac{7}{16}\)
viii. \(-\frac{25}{8},-\frac{9}{4}\)
ix. \(\frac{12}{15}, \frac{3}{5}\)
x. \(-\frac{7}{11},-\frac{3}{4}\)
Solution:
i. 7, -2
If a and b are positive numbers such that a < b, then -a > -b.
Since, 2 < 7 ∴ -2 > -7

ii. 0, \(\frac { -9 }{ 5 }\)
On a number line, \(\frac { -9 }{ 5 }\) is to the left of zero.
∴ 0 > \(\frac { -9 }{ 5 }\)

iii. \(\frac { 8 }{ 7 }\), 0
On a number line, zero is to the left of \(\frac { 8 }{ 7 }\) .
∴ \(\frac { 8 }{ 7 }\) > 0

iv. \(-\frac{5}{4}, \frac{1}{4}\)
We know that, a negative number is always less than a positive number.
∴ \(-\frac{5}{4}<\frac{1}{4}\)

v. \(\frac{40}{29}, \frac{141}{29}\)
Here, the denominators of the given numbers are the same.
Since, 40 < 141
∴ \(\frac{40}{29}<\frac{141}{29}\)

vi. \(-\frac{17}{20},-\frac{13}{20}\)
Here, the denominators of the given numbers are the same.
Since, 17 < 13
∴ -17 < -13
∴ \(-\frac{17}{20}<-\frac{13}{20}\)

vii. \(\frac{15}{12}, \frac{7}{16}\)
Here, the denominators of the given numbers are not the same.
LCM of 12 and 16 = 48

Alternate method:
15 × 16 = 240
12 × 7 = 84
Since, 240 > 84
∴ 15 × 16 > 12 × 7

viii. \(-\frac{25}{8},-\frac{9}{4}\)
Here, the denominators of the given numbers are not the same.
LCM of 8 and 4 = 8

ix. \(\frac{12}{15}, \frac{3}{5}\)
Here, the denominators of the given numbers are not the same.
LCM of 15 and 5 = 15

x. \(-\frac{7}{11},-\frac{3}{4}\)
Here, the denominators of the given numbers are not the same.
LCM of 11 and 4 = 44

Maharashtra Board Class 8 Maths Solutions Chapter 1 Rational and Irrational Numbers Practice Set 1.2 Questions and Activities

Question 1.
Verify the following comparisons using a number line. (Textbook pg. no, .3)
i. 2 < 3 but – 2 > – 3
ii. \(\frac{5}{4}<\frac{7}{4}\) but \(\frac{-5}{4}<\frac{-7}{4}\)
Solution:

We know that, on a number line the number to the left is smaller than the other.
∴ 2 < 3 and -3 < -2
i.e. 2 < 3 and -2 > -3

Std 8 Maths Digest

• Practice Set 1.1 Class 8 Answers
• Practice Set 1.2 Class 8 Answers
• Practice Set 1.3 Class 8 Answers
• Practice Set 1.4 Class 8 Answers
• Practice Set 2.1 Class 8 Answers
• Practice Set 2.2Class 8 Answers
• Practice Set 2.3 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.

9th Standard Maths 2 Practice Set 9.1 Chapter 9 Surface Area and Volume Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 9.1 Chapter 9 Surface Area and Volume Questions With Answers Maharashtra Board

Question 1.
Length, breadth and height of a cuboid shape box of medicine is 20 cm, 12 cm and 10 cm respectively. Find the surface area of vertical faces and total surface area of this box.
Given: For cuboid shape box of medicine,
length (l) = 20 cm, breadth (b) = 12 cm and height (h) = 10 cm.
To find: Surface area of vertical faces and total surface area of the box
Solution:
i. Surface area of vertical faces of the box
= 2(l + b) x h
= 2(20+ 12) x 10
= 2 x 32 x 10
= 640 sq.cm.

ii. Total surface area of the box
= 2 (lb + bh + lh)
= 2(20 x 12+ 12 x 10 + 20 x 10)
= 2(240 + 120 + 200)
= 2 x 560
= 1120 sq.cm.
∴ The surface area of vertical faces and total surface area of the box are 640 sq.cm, and 1120 sq.cm, respectively.

Question 2.
Total surface area of a box of cuboid shape is 500 sq.unit. Its breadth and height is 6 unit and 5 unit respectively. What is the length of that box?
Given: For cuboid shape box,
breadth (b) = 6 unit, height (h) = 5 unit Total surface area = 500 sq. unit.
To find: Length of the box (l)
Solution:
Total surface area of the box = 2 (lb + bh + lh)
∴ 500 = 2 (6l + 6 x 5 + 5l)
∴ \(\frac { 500 }{ 2 }\) = (11l + 30)
∴ 250= 11l + 30
∴ 250 – 30= 11l
∴ 220 = 11l
∴ 220 = l
∴ \(\frac { 220 }{ 11 }\) = l
∴ l = 20 units
∴ The length of the box is 20 units.

Question 3.
Side of a cube is 4.5 cm. Find the surface area of all vertical faces and total surface area of the cube.
Given: Side of cube (l) = 4.5 cm
To find: Surface area of all vertical faces and the total surface area of the cube
Solution:
i. Area of vertical faces of cube = 4l²
= 4 (4.5)² = 4 x 20.25 = 81 sq.cm.
ii. Total surface area of the cube = 6l²
= 6 (4.5)²
= 6 x 20.25
= 121.5 sq.cm.
∴ The surface area of all vertical faces and the total surface area of the cube are 81 sq.cm, and 121.5 sq.cm, respectively.

Question 4.
Total surface area of a cube is 5400 sq. cm. Find the surface area of all vertical faces of the cube.
Given: Total surface area of cube = 5400 sq.cm.
To find: Surface area of all vertical faces of the cube
Solution:
i. Total surface area of cube = 6l²
∴ 5400 = 6l²
∴ \(\frac { 5400 }{ 6 }\) = l²
∴ l² = 900
ii. Area of vertical faces of cube = 4l²
= 4 x 900 = 3600 sq.cm.
∴ The surface area of all vertical faces of the cube is 3600 sq.cm.

Question 5.
Volume of a cuboid is 34.50 cubic metre. Breadth and height of the cuboid is 1.5 m and 1.15 m respectively. Find its length.
Given: Breadth (b) = 1.5 m, height (h) = 1.15 m
Volume of cuboid = 34.50 cubic metre
To find: Length of the cuboid (l)
Solution:
Volume of cuboid = l x b x h
∴ 34.50 = l x b x h
∴ 34.50 = l x 1.5 x 1.15

= 20
∴ The length of the cuboid is 20 m.

Question 6.
What will be the volume of a cube having length of edge 7.5 cm ?
Given: Length of edge of cube (l) = 7.5 cm
To find: Volume of a cube
Solution:
Volume of a cube = l²
= (7.5)³
= 421.875 ≈ 421.88 cubic cm
∴The volume of the cube is 421.88 cubic cm.

Question 7.
Radius of base of a cylinder is 20 cm and its height is 13 cm, find its curved surface area and total surface area, (π = 3.14)
Given: Radius (r) = 20 cm, height (h) = 13 cm
To find: Curved surface area and
the total surface area of the cylinder
Solution:
i. Curved surface area of cylinder = 2πrh
= 2 x 3.14 x 20 x 13
= 1632.8 sq.cm

ii. Total surface area of cylinder = 2πr(r + h)
= 2 x 3.14 x 20(20 + 13)
= 2 x 3.14 x 20 x 33 = 4144.8 sq.cm
∴ The curved surface area and the total surface area of the cylinder are 1632.8 sq.cm and 4144.8 sq.cm respectively.

Question 8.
Curved surface area of a cylinder is 1980 cm² and radius of its base is 15 cm. Find the height of the cylinder. (π = \(\frac { 22 }{ 7 }\))
Given: Curved surface area of cylinder = 1980 sq.cm., radius (r) = 15 cm
To find: Height of the cylinder (h)
Solution:
Curved surface area of cylinder = 2πrh
∴ 1980 = 2 x \(\frac { 22 }{ 7 }\) x 15 x h
∴ \(h=\frac{1980 \times 7}{2 \times 22 \times 15}\)
∴ h = 21 cm
∴ The height of the cylinder is 21 cm.

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.

9th Standard Maths 2 Practice Set 9.2 Chapter 9 Surface Area and Volume Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 9.2 Chapter 9 Surface Area and Volume Questions With Answers Maharashtra Board

Question 1.
Perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
Given: Height (h) = 12 cm, length (l) = 13 cm
To find: Radius of the base of the cone (r)
Solution:
l² = r² + h²
∴ 13² = r² + 12²
∴ 169 = r² + 144
∴169 – 144 = r²
∴ r² = 25
∴ r = √25 … [Taking square root on both sides]
= 5 cm
∴ The radius of base of the cone is 5 cm.

Question 2.
Find the volume of a cone, if its total surface area is 7128 sq.cm and radius of base is 28 cm. ( π = \(\frac { 22 }{ 7 }\))
Given: Radius (r) = 28 cm,
Total surface area of cone = 7128 sq.cm
To find: Volume of the cone
Solution:
i. Total surface area of cone = πr (l + r)
∴ 7128= y x 28 x (l + 28)
∴ 7128 = 22 x 4 x(l +28)
∴ l + 28 = \(\frac { 7128 }{ 22\times 4 }\)
∴ l + 28 = 81
∴ l = 81 – 28
∴ l = 53cm

ii. Now, l² = r² + h²
∴ 53² = 28²+ h²
∴ 2809 = 784 + h²
∴ 2809 – 784 = h²
∴ h² = 2025
∴ h = \(\sqrt { 2025 }\) …… [Taking square root on both sides]
= 45 cm

= 22 x 4 x 28 x 15
= 36960 cubic.cm
∴ The volume of the cone is 36960 cubic.cm.

Question 3.
Curved surface area of a cone is 251.2 cm² and radius of its base is 8 cm. Find its slant height and perpendicular height, (π = 3.14)
Given: Radius (r) = 8 cm, curved surface area
of cone = 251.2 cm²
To find: Slant height (l) and the perpendicular height (h) of the cone
Solution:
i. Curved surface area of cone = πrl
∴ 251.2 = 3.14 x 8 x l

∴ l= 10 cm

ii. Now, l² = r² + h²
∴ 10² = 8² + h²
∴ 100 = 64 + h²
∴ 100 – 64 = h²
∴ h² = 36
∴ h = √36 … [Taking square root on both sides]
= 6 cm
∴ The slant height and the perpendicular height of the cone are 10 cm and 6 cm respectively.

Question 4.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is ₹ 10 per sq.m?
Given: Radius (r) = 6 m, length (l) = 8 m
To find: Total cost of making the cone
Solution:
i. To find the total cost of making the cone of tin sheet, first we need to find the total surface area of the cone.
Total surface area of the cone = πr (l + r)
= \(\frac { 22 }{ 7 }\) x 6 x (8 + 6)
= \(\frac { 22 }{ 7 }\) x 6 x 14
= 22 x 6 x 2 = 264 sq.m

ii. Rate of making the cone = ₹ 10 per sq.m
∴ Total cost = Total surface area x Rate of making the cone
= 264 x 10
= ₹ 2640
∴ A The total cost of making the cone of tin sheet is ₹ 2640.

Question 5.
Volume of a cone is 6280 cubic cm and base radius of the cone is 20 cm. Find its perpendicular height, (π = 3.14)
Given: Radius (r) = 20 cm,
Volume of cone = 6280 cubic cm
To find: Perpendicular height (h) of the cone
Solution:

∴ The perpendicular height of the cone is 15 cm.

Question 6.
Surface area of a cone is 188.4 sq.cm and its slant height is 10 cm. Find its perpendicular height (π = 3.14).
Given: Length (l) =10 cm, curved surface area of the cone = 188.4 sq.cm
To find: Perpendicular height (h) of the cone
Solution:
i. Curved surface area of the cone = πrl
∴ 188.4 = 3.14 x r x 10

ii. Now, l² = r² + h²
∴ 10² = 6² + h²
∴ 100 = 36 + h²
∴ 100 – 36 = h²
∴ h² = 64
∴ h = \(\sqrt { 64 }\) … [Taking square root on both sides]
= 8 cm
∴ The perpendicular height of the cone is 8 cm.

Question 7.
Volume of a cone is 1232 cm³ and its height is 24 cm. Find the surface area of the cone. (π = \(\frac { 22 }{ 7 }\))
Given: Height (h) = 24 cm,
Volume of cone = 1232 cm³
To find: Surface area of the cone
Solution:

∴ r² = 49
∴ r = \(\sqrt { 49 }\) … [Taking square root on both sides]
= 7 cm

ii. Now, l² = r² + h²
∴ l² = 7² + 24²
= 49 + 576 = 625
∴ l = \(\sqrt { 625 }\) … [Taking square root on both sides]
= 25

iii. Curved surface area of cone = πrl
= \(\frac { 22 }{ 7 }\) x 7 x 25
= 22 x 25
= 550 sq.cm
∴The surface area of the cone is 550 sq.cm.

Question 8.
The curved surface area of a cone is 2200 sq.cm and its slant height is 50 cm. Find the total surface area of cone. (π = \(\frac { 22 }{ 7 }\))
Given: Length (l) = 50 cm, curved surface area of cone = 2200 sq.cm
To find: Total surface area of the cone
Solution:
i. Curved surface area of cone = πrl

ii. Total surface area of cone = πr (l + r)
= \(\frac { 22 }{ 7 }\) x 14 x (50 + 14)
= \(\frac { 22 }{ 7 }\) x 14 x 64
= 22 x 2 x 64
= 2816 sq.cm
∴ The total surface area of the cone is 2816 sq.cm.

Question 9.
There are 25 persons in a tent which is conical in shape. Every person needs an area of 4 sq.m, of the ground inside the tent. If height of the tent is 18 m, find the volume of the tent.
Given: For the tent,
height (h) = 18m,
number of people in the tent = 25,
area required for each person = 4 sq.m
To find: Volume of the tent
Solution:
i. Every person needs an area of 4 sq.m, of the ground inside the tent.
Surface area of the base of the tent = number of people in the tent × area required for each person
= 25 × 4
= 100 sq.m

ii. Surface area of the base of the tent = πr²
∴ 100 = πr²
∴ πr² = 100

iii. Volume of the tent= \(\frac { 1 }{ 3 }\) πr²h
= \(\frac { 1 }{ 3 }\) x 100 x 18 …….[∵ πr² = 100]
= 100 x 6
= 600 cubic metre
∴ The volume of the tent is 600 cubic metre.

Question 10.
In a field, dry fodder for the cattle is heaped in a conical shape. The height of the cone is 2.1 m and diameter of base is 7.2 m. Find the volume of the heap of the fodder. If it is to be covered by polythene in rainy se&son then how much minimum polythene
sheet is needed? (π = \(\frac { 22 }{ 7 }\) and \(\sqrt { 17.37 }\) = 4.17 ]
Given: Height of the heap (h) = 2.1 m.
diameter of the base (d) = 7.2 m
∴Radius of the base (r) = \(\frac { d }{ 2 }\) = \(\frac { 7.2 }{ 2 }\) = 3.6 m
To find: Volume of the heap of the fodder and polythene sheet required
Solution:
i. Volume of the heap of fodder = \(\frac { 1 }{ 3 }\)πr²h
= \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x (3.6)² x 2.1
= \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x 3.6 x 3.6 x 2.1
= 1 x 22 x 1.2 x 3.6 x 0.3
= 28.51 cubic metre

ii. Now, l² = r² + h²
= (3.6)² + (2.1)²
= 12.96 + 4.41
∴ l² =17.37
∴ l² = \(\sqrt { 17.37 }\) .. .[Taking square root on both sides]
= 4.17 m

iii. Area of the polythene sheet needed to cover the heap of the fodder = Curved surface area of the conical heap
= πrl
= \(\frac { 22 }{ 7 }\) x 3.6 x 4.17
= 47.18 sq.m
∴ The volume of the heap of the fodder is 28.51 cubic metre and a polythene sheet of 47.18 sq.m will be required to cover it.

Maharashtra Board Class 9 Maths Solutions

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.

9th Standard Maths 2 Practice Set 9.3 Chapter 9 Surface Area and Volume Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 9.3 Chapter 9 Surface Area and Volume Questions With Answers Maharashtra Board

Question 1.
Find the surface areas and volumes of spheres of the following radii
i. 4 cm
ii. 9 cm
iii. 3.5 cm (π = 3.14)
i. Given: Radius (r) = 4 cm
To find: Surface area and volume of sphere
Solution:
Surface area of sphere = 4πr²
= 4 x 3.14 x 4²
∴ Surface area of sphere = 200.96 sq.cm
Volume of sphere = \(\frac { 4 }{ 3 }\)πr³
= \(\frac { 4 }{ 3 }\) x 3.14 x 4²
∴ Volume of sphere = 267.95 cubic cm

ii. Given: Radius (r) = 9 cm
To find: Surface area and volume of sphere
Solution:
Surface area of sphere = 4πr²
= 4 x 3.14 x 9²
∴ Surface area of sphere = 1017.36 sq.cm

∴ Volume of sphere = 3052.08 cubic cm

iii. Given: Radius (r) = 3.5 cm
To find: Surface area and volume of sphere
Solution:
Surface area of sphere = 4πr²
= 4 x 3.14 x (3.5)²
∴ Surface area of sphere = 153.86 sq.cm
Volume of sphere = \(\frac { 4 }{ 3 }\) πr³
= \(\frac { 4 }{ 3 }\) x 3.14 x (3.5)³
∴ Volume of sphere = 179.50 cubic cm

Question 2.
If the radius of a solid hemisphere is 5 cm, then find its curved surface area and total surface area, (π = 3.14)
Given: Radius (r) = 5 cm
To find: Curved surface area and total surface area of hemisphere
Solution:
i. Curved surface area of hemisphere = 2πr²
= 2 x 3.14 x 5²
= 2 x 3.14 x 25
= 50 x 3.14
= 157 sq.cm.

ii. Total surface area of hemisphere = 3πr²
= 3 x 3.14 x 5²
= 235.5 sq.cm.
∴ The curved surface area and totai surface area of hemisphere are 157 sq.cm, and 235.5 sq.cm, respectively.

Question 3.
If the surface area of a sphere is 2826 cm² then find its volume. (π = 3.14)
Given: Surface area of sphere = 2826 sq.cm.
To find: Volume of sphere
Solution:
i. Surface area of sphere = 4πr²
∴ 2826 = 4 x 3.14 x r²
2826 = 282600 = 900
∴ \( r^{2}=\frac{2826}{4 \times 3.14}=\frac{282600}{4 \times 314}=\frac{900}{4}\)
∴ r² = 225
∴ r = \(\sqrt { 225 }\) … [Taking square root on both sides]
= 15 cm

ii. Volume of sphere = \(\frac { 4 }{ 3 }\) πr³
= \(\frac { 4 }{ 3 }\) x 3.14 x 15³
= \(\frac { 4 }{ 3 }\) x 3.14 x 15 x 15 x 15
= 4 x 3.14 x 5 x 15 x 15
= 14130 cubic cm.
∴ The volume of the sphere is 14130 cubic cm.

Question 4.
Find the surface area of a sphere, if its volume is 38808 cubic cm. (π = \(\frac { 22 }{ 7 }\))
Given: Volume of sphere = 38808 cubic cm.
To find: Surface area of sphere
Solution:

∴ r³ = 441 x 21 = 21 x 21 x 21
∴ r = 21 cm … [Taking cube root on both sides]
ii. Surface area of sphere = 4πr²
= 4 x \(\frac { 22 }{ 7 }\) x 21
= 4 x \(\frac { 22 }{ 7 }\) x 21 x 21
= 4 x 22 x 3 x 21
= 5544 sq.cm.
∴ The surface area of sphere is 5544 sq.cm.

Question 5.
Volume of a hemisphere is 18000π cubic cm. Find its diameter.
Given: Volume of hemisphere = 1 8000π cubic cm.
To find: Diameter of the hemisphere
Solution:
i. Volume of hemisphere = \(\frac { 2 }{ 3 }\) πr³

= 9000 x 3
∴ r³ = 27000
∴ r = \(\sqrt [ 3 ]{ 27000 }\) … [Taking cube root on both sides]
= 30 cm

ii. Diameter = 2r
= 2 x 30 = 60 cm
∴ The diameter of the hemisphere is 60 cm.

Maharashtra Board Class 9 Maths Solutions

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 17.2 8th Std Maths Answers Solutions Chapter 17 Circle: Chord and Arc.

Circle: Chord and Arc Class 8 Maths Chapter 17 Practice Set 17.2 Solutions Maharashtra Board

Std 8 Maths Practice Set 17.2 Chapter 17 Solutions Answers

Question 1.
The diameters PQ and RS of the circle with centre C are perpendicular to each other at C. State, why arc PS and arc SQ are congruent. Write the other arcs which are congruent to arc PS.

Solution:
diameter PQ ⊥ diameter RS … [Given]
∴ m∠PCS = m∠SCQ = m∠PCR = m∠RCQ = 90°
The measure of the angle subtended at the centre by an arc is the measure of the arc.
∴ m(arc PS) = m∠PCS = 90° …(i)
m (arc SQ) = m∠SCQ = 90° …(ii)
∴ m(arc PS) = m(arc SQ) … [From (i) and (ii)]
∴ arc PS ≅ arc SQ … [If the measures of two arcs of a circle are same, then the two arcs are congruent]
m(arc PR) = m∠PCR = 90° .. .(iii)
m (arc RQ) = m∠RCQ = 90° … (iv)
∴ m(arc PS) = m(arc PR) = m(arc RQ) … [From (i), (iii) and (iv)]
∴ arc PS ≅ arc PR ≅ arc RQ
… [If the measures of two arcs of a circle are same, then the two arcs are congruent]
∴ arc PR and arc RQ are congruent to arc PS.

Question 2.
In the given figure, O is the centre of the circle whose diameter is MN. Measures of some central angles are given in the figure.
i. m∠AOB and m∠COD
ii. Show that arc AB ≅ arc CD
iii. Show that chord AB ≅ chord CD

Solution:
i. Seg MN is the diameter of the circle. … [Given]
∴ m∠AOM + m∠AON = 180° … [Angles in a linear pair]
∴ m∠AOM + (m∠AOB + m∠BON) = 180° … [Angle addition property]
∴ 100° + m∠AOB + 35° = 180°
…[∵ m∠AOM = 100°, m∠BON = 35°]
∴ m∠AOB + 135° = 180°
∴ m∠AOB = 180°- 135°
∴m∠AOB = 45° …(i)
Also, m∠DOM + m∠DON = 180° … [Angles in a linear pair]
∴ m∠DOM + (m∠COD + m∠CON) = 180° … [Angle addition property]
∴ 100° +m∠COD + 35°= 180°
…[∵ m∠DOM = 100°, m∠CON = 35° ]
∴ m∠COD + 135° = 180°
∴ m∠COD = 180°- 135°
∴ m∠COD = 45° …(ii)

ii. m(arc AB) = m∠AOB = 45° … [From (i)]
m(arc DC) = m∠DOC = 45° .. .[From (ii)]
∴ m(arc AB) = m(arc DC) …[From (i) and (ii)]
∴ arc AB ≅ arc CD
… [If the measures of two arcs of a circle are same, then the two arcs are congruent]

iii. arc AB ≅ arc CD
∴ chord AB ≅ chord CD ….[The chords corresponding to congruent arcs are congruent]

Maharashtra Board Class 8 Maths Chapter 17 Circle: Chord and Arc Practice Set 17.2 Intext Questions and Activities

Question 1.
If the measures of two arcs of a circle are same, then two arcs are congruent. Verify this property using tracing paper. (Textbook pg. no. 117)
Solution:
[Students should attempt the above activities on their own.]

Question 2.
With the help of following activity find out the properties of the chord and the corresponding arc.
i. a. Draw a circle with centre O.
b. Draw ∠COD and ∠AOB of same measure.
You will find that the arc AXB and arc CYD are congruent.
c. Draw chords AB and CD.
d. Using compass experience that the length of chord AB and chord CD is also same.
(Textbook pg. no. 117)

Solution:
[Students should attempt the above activities on their own.]

ii. a. Draw a circle with centre C.
b. Draw the congruent chords AB and DE of the circle. Draw the radii CA, CB, CD and CE.
c. Check that ∠ACB and ∠DCE are congruent.
d. Hence show that measure of arc AB and arc DE is equal. Hence these arcs are congruent. (Textbook pg. no. 117)

Solution:
[Students should attempt the above activities on their own.]

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.

9th Standard Maths 2 Practice Set 9 Chapter 9 Surface Area and Volume Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 9 Chapter 9 Surface Area and Volume Questions With Answers Maharashtra Board

Question 1.
If diameter of a road roller is 0.9 m and its length is 1.4 m, how much area of a field will be pressed in its 500 rotations? ( π = \(\frac { 22 }{ 7 }\))
Given: For road roller,
diameter (d) = 0.9 m, length (h) = 1.4 m
To find: Area of a field pressed in 500 rotations
Solution:
i. Since, area of field pressed in 1 rotation of road roller = curved surface area of road roller
∴ Curved surface area of the road roller = 2πrh
= πdh ,..[∵ d = 2r]
= \(\frac { 22 }{ 7 }\) x 0.9 x 1.4 7
= 22 x 0.9 x 0.2
= 3.96 sq.m.

ii. Area of land pressed in 1 rotation = 3.96 sq.m.
∴Area of land pressed in 500 rotations = 500 x 3.96
= 1980 sq.m.
∴ 1980 sq.m, land will be pressed in 500 rotations of the road roller.

Question 2.
To make an open fish tank, a glass sheet of 2 mm gauge is used. The outer length, breadth and height of the tank are 60.4 cm, 40.4 cm and 40.2 cm respectively. How much maximum volume of water will be contained in it ?
Given: Thickness of the glass = 2 mm,
outer length of the tank = 60.4 cm,
outer breadth of the tank = 40.4 cm,
outer height of the tank = 40.2 cm
To find: Volume of water fish tank contains
Solution:

i. Thickness oldie glass = 2 mm.
= \(\frac { 2 }{ 10 }\) cm
= 0.2 cm
Outerlengthofthetank = 60.4 cm
∴ Inner length oldie tank (l) = Outer length – thickness oldie glass on both sides
= 60.4 – 0.2 – 0.2
= 60cm
Outer breadth oldie tank = 40.4 cm
∴ Inner breadth of the tank (b) = 40.4 – 0.2 – 0.2
= 40 cm
Outer height of the tank = 40.2 cm
∴Inner height of the tank (h) = 40.2 – 0.2
= 40 cm

ii. Maximum volume of water that can be contained in the tank = volume of the tank
= l x b x h
= 60 x 40 x 40
= 96000 cubic cm.
∴ The fishtank can contain maximum of 96000 cubic cm. water in it.

Question 3.
If the ratio of radius of base and height of a cone is 5 : 12 and its volume is 314 cubic metre. Find its perpendicular height and slant height (π = 3.14).
Given: Ratio of radius of base and height of a cone = 5 : 12,
Volume = 314 cubic metre
To find: Perpendicular height (h) and slant height (l)
Solution:
i. The ratio of radius and height of cone is 5 : 12
Let the common multiple be x.
∴ Radius of base (r) = 5x
Perpendicular height (h) = 12x

∴ x³ = 1
∴ x = 1 … [Taking cube root on both sides]
∴ r = 5x = 5(1) = 5m
h = 12x = 12(1) = 12 m

ii. Now, l² = r² + h²
= 5² + 12²
= 25 + 144
∴l² = 169
∴ l = \(\sqrt { 169 }\) … [Taking square root on both sides]
= 13 m
The perpendicular height and slant height of the cone are 12 m and 13 m respectively.

Question 4.
Find the radius of a sphere if its volume is 904.32 cubic cm. (π = 3.14)
Given: Volume of sphere = 904.32 cubic cm.
To find: Radius of a sphere
Solution:
Volume of sphere = \(\frac { 4 }{ 3 }\) πr³
∴ 904.32 = \(\frac { 4 }{ 3 }\) x 3.14 x r³

= 216
∴ r = \(\sqrt [ 3 ]{ 216 }\) … [Taking cube root on both sides]
= 6 cm
∴ The radius of the sphere is 6 cm.

Question 5.
Total surface area of a cube is 864 sq.cm. Find its volume.
Given: Total surface area of cube = 864 sq. cm
To find: Volume of cube
Solution:
i. Total surface area of cube = 6l²
∴ 864 = 6l²
∴ l²= \(\sqrt [ 864 ]{ 6 }\)
∴ l² = 144
∴ l = \(\sqrt { 144 }\) … [Taking square root on both sides]
= 12 cm

ii. Volume of cube = l²
= 12³
= 1728 cubic cm.
∴ The volume of cube is 1728 cubic cm.

Question 6.
Find the volume of a sphere, if its surface area is 154 sq.cm.
Given: Surface area of sphere = 154 sq. cm.
To find: Volume of sphere
Solution:
i. Surface area of sphere = 4πr²


∴ The volume of sphere is 179.67 cubic cm.

Question 7.
Total surface area of a cone is 616 sq.cm. If the slant ‘height of the cone Is three times the radius of its base, find its slant height.
Given: Total surface area of a cone = 616 sq.cm., slant height of the cone is three times the radius of its base
To find: Slant height (l)
Solution:
i. Let the radius of base be r cm.
∴ Slant height (l) = 3r cm
Total surface area of cone = πr (l + r)
∴ 616 = πr(l + r)
∴ 616 = \(\sqrt [ 22 ]{ 7 }\) x r x (3r + r)
∴ 616 = \(\sqrt [ 22 ]{ 7 }\) x 4r²

∴ r² = 49
∴ r = \(\sqrt { 49 }\) … [Taking square root on both sides]
= 7

ii. Slant height (l) = 3r = 3 x 7 = 21 cm
∴ The slant height of the cone is 21 cm.

Question 8.
The inner diameter of a well is 4.20 metre and its depth is 10 metre. Find the inner surface area of the well. Find the cost of plastering it from inside at the rate ₹ 52 per sq.m.
Given: Inner diameter (d) = 4.2 m,
To find: depth (h) = 10 m,
rate of plastering = ₹ 52 per sq.m.
Inner surface area and total cost of plastering
Solution:
i. Inner curved surface area of the well = 2πrh
= πdh …[∵ d = 2r]
= \(\sqrt [ 22 ]{ 7 }\) x 4.2 x 10
= \(\sqrt [ 22 ]{ 7 }\) x 42
= 22 x 6
= 132 sq.m.

ii. Rate of plastering = ₹52 per sq.m.
∴ Total cost = Curved surface area x Rate of plastering
= 132 x 52 = ₹6864
∴ The cost of plastering the well from inside is ₹6864.

Question 9.
The length of a road roller is 2.1 m and its diameter is 1.4 m. For levelling a ground 500 rotations of the road roller were required. How much area of ground was levelled by the road roller? Find the cost of levelling at the rate of ₹ 7 per sq.m.
Given: For road roller,
diameter (d) = 1.4 m,
length (h) = 2.1 m
number of rotations required for levelling the ground = 500,
rate of levelling = ₹ 7 per sq. m.
To find: Area of ground leveled by the road roller and cost of levelling
Solution:
i. Since, area of ground levelled in 1 rotation of road roller = curved surface area of road roller
∴Curved surface area of the road roller = 2πrh
= πdh …[∵ d = 2r]
= \(\frac { 22 }{ 7 }\) x 1.4 x 2.1
= 22 x 0.2 x 2.1
= 9.24 sq.m.

ii. Area of ground levelled in 1 rotation = 9.24 sq.m.
∴Area of ground levelled in 500 rotations = 9.24 x 500
= 4620 sq.m.

iii. Rate of levelling ₹ 7 per sq.m.
∴Total cost = Area of ground levelled x Rate of levelling
= 4620 x 7
= ₹32340
∴ The road roller levels 4620 sq.m. land in 500 rotation, and the cost of levelling is ₹32340.

Maharashtra Board Class 9 Maths Chapter 9 Surface Area and Volume Practice Set 9 Intext Questions and Activities

Question 1.
Curved surface area of cone. (Textbook pg. no. 116)

Circumference of base of the cone = 2πr
As shown in the figure (c), make pieces of the net as small as possible. Join them as shown in the figure (d),. By joining the small pieces of net of the cone, we get a rectangle ABCD approximately.
Total length of AB and CD is 2πr.
∴ length of side AB of rectangle ABCD is πr and length of side CD is also πr.
Length of side BC of rectangle = slant height of cone = l.
Curved surface area of cone is equal to the area of the rectangle.
∴ curved surface area of cone = Area of rectangle = AB x BC = πr x l = πrl

Question 2.
Prepare a cylinder of a card sheet, keeping one of its faces open. Prepare an open cone of card sheet which will have the same base-radius and the same height as that of the cylinder. Pour fine sand in the cone till it just fills up the cone. Empty the cone in the cylinder. Repeat the procedure till the cylinder is just filled up with sand. Note how many coneful of sand is required to fill up the cylinder. (Textbook pg, no 117)

Answer:
To fill the cylinder, three coneful of sand is required.

Question 3.
Finding total surface area of sphere. (Textbook pg, no 120)

i. Take a sweet lime (Mosambe), Cut it into two equal parts.

ii. Take one of the parts. Place its circular face on a paper. Draw its circular border. Copy three more such circles. Again, cut each half of the sweet lime into two equal parts.

iii. Now you get 4 quarters of sweet lime. Separate the peel of a quarter part. Cut it into pieces as small as possible. Try to cover one o’f the circles drawn, by the small pieces. Observe that the circle gets nearly covered.
The activity suggests that,
Curved surface area of a sphere = 4πr²

∴ Curved surface area of a sphere = 4 x Area of a circle

Question 4.
Make a cone and a hemisphere of cardsheet such that radii of cone and hemisphere are equal and height of cone is equal to radius of the hemisphere.
Fill the cone with fine sand. Pour the sand in the hemisphere. How many cones are required to fill the hemisphere completely ? (Textbook pg. no. 121)

Answer:
To fill the hemisphere, two coneful of sand is required.

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers