Practice Set 15.5 Class 8 Answers Chapter 15 Area Maharashtra Board

by

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.5 8th Std Maths Answers Solutions Chapter 15 Area.

Area Class 8 Maths Chapter 15 Practice Set 15.5 Solutions Maharashtra Board

Std 8 Maths Practice Set 15.5 Chapter 15 Solutions Answers

Question 1.
Find the areas of given plots. (All measures are in meters.)
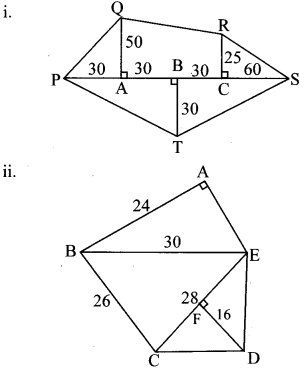
Maharashtra Board Class 8 Maths Solutions Chapter 15 Area Practice Set 15.5 1
Solution:
i. Here, ∆QAP, ∆RCS are right angled triangles and ☐QACR is a trapezium.
In ∆QAP, l(AP) = 30 m, l(QA) = 50 m
A(∆QAP)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(AP) x l(QA)
= \(\frac { 1 }{ 2 }\) x 30 x 50
= 750 sq. m
In ☐QACR, l(QA) = 50 m, l(RC) = 25 m,
l(AC) = l(AB) + l(BC)
= 30 + 30 = 60 m
A(☐QACR)
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
= \(\frac { 1 }{ 2 }\) x [l(QA) + l(RC)] x l(AC)
= \(\frac { 1 }{ 2 }\) x (50 + 25) x 60
= \(\frac { 1 }{ 2 }\) x 75 x 60
= 2250 sq.m
In ∆RCS, l(CS) = 60 m, l(RC) = 25 m A(∆RCS)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(CS) x l(RC)
= \(\frac { 1 }{ 2 }\) x 60 x 25
= 750 sq. m
In ∆PTS, l(TB) = 30 m,
l(PS) = l(PA) + l(AB) + l(BC) + l(CS)
= 30 + 30 + 30 + 60
= 150m
A(∆PTS) = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x l(PS) x l(TB)
= \(\frac { 1 }{ 2 }\) x 150 x 30
= 2250 sq. m
∴ Area of plot QPTSR = A(∆QAP) + A(☐QACR) + A(∆RCS) + A(∆PTS)
= 750 + 2250 + 750 + 2250
= 6000 sq. m
∴ The area of the given plot is 6000 sq.m.

ii. In ∆ABE, m∠BAE = 90°, l(AB) = 24 m, l(BE) = 30 m
∴ [l(BE)]² = [l(AB)]² + [l(AE)]²
…[Pythagoras theorem]
∴ (30)² = (24)² + [l(AE)]²
∴ 900 = 576 + [l(AE)]²
∴ [l(AE)]² = 900 – 576
∴ [l(AE)]² = 324
∴ l(AE) = √324 = 18 m
…[Taking square root of both sides]
A(∆ABE)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(AE) x l(AB)
= \(\frac { 1 }{ 2 }\) x 18 x 24
= 216 sq. m
In ∆BCE, a = 30m, b = 28m, c = 26m
Maharashtra Board Class 8 Maths Solutions Chapter 15 Area Practice Set 15.5 2
∴ Area of plot ABCDE
= A(∆ABE) + A(∆BCE) + A(∆EDC)
= 216 + 336 + 224
= 776 sq. m
∴ The area of the given plot is 776 sq.m.
[Note: In the given figure, we have taken l(DF) = 16 m]

Std 8 Maths Digest