Practice Set 15.3 Class 8 Answers Chapter 15 Area Maharashtra Board

by

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.3 8th Std Maths Answers Solutions Chapter 15 Area.

Area Class 8 Maths Chapter 15 Practice Set 15.3 Solutions Maharashtra Board

Std 8 Maths Practice Set 15.3 Chapter 15 Solutions Answers

Question 1.
In the given figure, ☐ABCD is a trapezium, side AB || side DC, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area ☐ABCD.
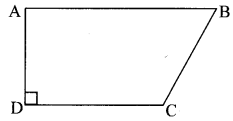
Maharashtra Board Class 8 Maths Solutions Chapter 15 Area Practice Set 15.3 1
Solution:
☐ABCD is a trapezium, side AB || side DC,
l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm,
Area of a trapezium = \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A (☐ABCD) = \(\frac { 1 }{ 2 }\) x [l(AB) + l(DC)] x l(AD)
= \(\frac { 1 }{ 2 }\) x (13 + 9) x 8
= \(\frac { 1 }{ 2 }\) x 22 x 8
= 11 x 8
= 88 sq.cm
∴ The area of ☐ABCD is 88 sq. cm.
[Note: The question is modified.]

Question 2.
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
Solution:
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm and its height is 4.2 cm.
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
= \(\frac { 1 }{ 2 }\) x (8.5 + 11.5) x 4.2
= \(\frac { 1 }{ 2 }\) x 20 x 4.2
= 10 x 4.2
= 42 sq. cm
∴ The area of the trapezium is 42 sq. cm.

Question 3.
☐PQRS is an isosceles trapezium. l(PQ) = 7 cm, seg PM ⊥ seg SR, l(SM) = 3 cm. Distance between two parallel sides is 4 cm, find the area of ☐PQRS.
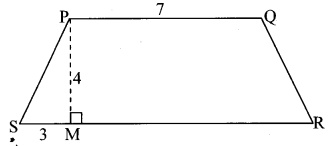
Maharashtra Board Class 8 Maths Solutions Chapter 15 Area Practice Set 15.3 2
Solution:
☐PQRS is an isosceles trapezium.
l(PQ) = 7 cm, seg PM ⊥ seg SR,
l(SM) = 3 cm, l(PM) = 4cm
Draw seg QN ⊥ seg SR.
In ☐PMNQ,
seg PQ || seg MN
∠PMN = ∠QNM = 90°
∴ ☐PMNQ is a rectangle.
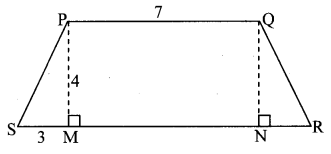
Maharashtra Board Class 8 Maths Solutions Chapter 15 Area Practice Set 15.3 3
Opposite sides of a rectangle are congruent.
∴ l(PM) = l(QN) = 4 cm and
l(PQ) = l(MN) = 7 cm
In ∆PMS, m∠PMS = 90°
∴ [l(PS)]² = [l(PM)]² + [l(SM)]² … [Pythagoras theorem]
∴ [l(PS)]² = (4)² + (3)²
∴ [l(PS)]² = 16 + 9 = 25
∴ l(PS) = √25 = 5 cm
…[Taking square root of both sides]
☐PQRS is an isosceles trapezium.
∴ l(PS) = l(QR) = 5 cm
In ∆QNR, m ∠QNR = 90°
∴ [l(QR)]² = [l(QN)]² + [l(NR)]²
… [Pythagoras theorem]
∴ (5)² = (4)² + [l(NR)]²
∴ 25 = 16 + [l(NR)]²
∴ [l(NR)]² = 25 – 16 = 9
∴ l(NR) = √9 = 3 cm
…[Taking square root of both sides]
l(SR) = l(SM) + l(MN) + l(NR)
= 3 + 7 + 3
= 13 cm
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A(☐PQRS) = \(\frac { 1 }{ 2 }\) x [l(PQ) + l(SR)] x l(PM)
= \(\frac { 1 }{ 2 }\) x (7+ 13) x 4
= \(\frac { 1 }{ 2 }\) x 20 x 4
= 40 sq.cm
∴ The area of ☐PQRS is 40 sq. cm.

Std 8 Maths Digest