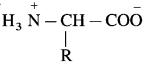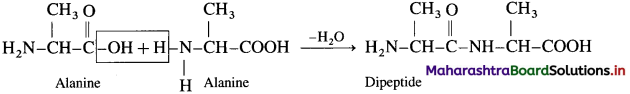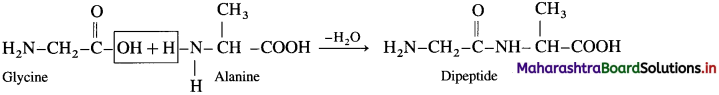Balbharti Maharashtra State Board Class 11 Geography Important Questions Chapter 2 Weathering and Mass Wasting Important Questions and Answers.
Maharashtra State Board 11th Geography Important Questions Chapter 2 Weathering and Mass Wasting
Complete the chain
Question 1.
| Types of Mass | Wasting Characteristics | Regions |
| (1) Creep | (1) Rapid fall | (1) Periglacial or alpine region |
| (2) Rockfall | (2) Slowest moving | (2) Hillsides in a humid region |
| (3) Earth flow | (3) Slow downhill creep | (3) Rocky areas |
| (4) Solifluction | (4) Rapid or slow | (4) Tops and basal portions of hills |
Answer:
| Types of Mass | Wasting Characteristics | Regions |
| (1) Creep | (1) Slowest moving | (1) Tops and basal portions of hills |
| (2) Rock fall | (2) Rapid fall | (2) Rocky areas |
| (3) Earth flow | (3) Rapid or slow | (3) Hill sides in humid region |
| (4) Solifluction | (4) Slow downhill creep | (4) Periglacial or alpine region |
![]()
Question 2.
| Types of weathering | Factors | Resultant |
| (1) Physical | (1) Heat | (1) Oxidation |
| (2) Chemical | (2) Explosion | (2) Granular weathering |
| (3) Anthropological | (3) Water (H2O) | (3) Exfoliation |
| (4) Pressure | (4) Mining |
Answer:
| Types of weathering | Factors | Resultant |
| (1) Physical | (1) Heat Pressure | (1) Exfoliation, Granular weathering |
| (2) Chemical | (2) Water (H2O) | (2) Oxidation |
| (3) Anthropological | (3) Explosion | (3) Mining |
Choose the correct option by identifying the correct correlation in the sentences.
Question 1.
Rocks can break because of …………….
(a) water, pressure, heat, etc.
(b) gravity
(c) deposition
(d) sedimentation
Answer:
(a) water, pressure, heat, etc.
Question 2.
In rocks such as granite which have joints, heat can cause weathering ………………….
(a) by breaking the rock into two halves
(b) by breaking the rock along the joints into blocks
(c) by breaking the rock into pieces
(d) by shattering
Answer:
(b) by breaking the rock along the joints into blocks
Question 3.
Chemical weathering is effective and rapid in …………………
(a) cold climate
(b) hot climate
(c) humid climate
(d) dry climate
Answer:
(c) humid climate
![]()
Question 4.
Erosion involves the application of ………………
(a) kinetic energy to the surface along which the material moves
(b) gravitational force to the surface along which the material moves
(c) tensional force to the surface along which the material moves
(d) compressional force to the surface along which the material moves
Answer:
(a) kinetic energy to the surface along which the material moves
Question 5.
The salts of calcium, sodium etc., present in rocks have a tendency to expand, this leads to ………………..
(a) breaking of rocks
(b) dissolving the salts
(c) formation of cracks in rocks
(d) crystallization of salts
Answer:
(d) crystallization of salts
Question 6.
Water molecules react with minerals present in the rocks. This process is called ………………..
(a) solution
(b) hydrolysis
(c) oxidation
(d) carbonation
Answer:
(b) hydrolysis
Question 7.
The calcium present in ………………. reacts with the water and air to form carbonic acid.
(a) limestone
(b) marble
(c) granite
(d) slate
Answer:
(a) limestone
Question 8.
During ………………., the calcium and carbonate in limestone detach from each other, thereby decomposing the limestone.
(a) oxidation
(b) solution
(c) desilication
(d) carbonation
Answer:
(d) carbonation
Question 9.
When rocks break along joints due to heat, it is called ……………….
(a) block disintegration
(b) cracks
(c) shattering
(d) granular weathering
Answer:
(a) block disintegration
Question 10.
Mining, blasting of hills and ridges is a type of …………….. weathering.
(a) physical
(b) chemical
(c) biological
(d) anthropogenic
Answer:
(d) anthropogenic
Question 11.
Mass movements occur continuously on all …………………
(a) plains
(b) plateau
(c) slopes
(d) rivers
Answer:
(c) slopes
![]()
Question 12.
The ……………….. plays a big role in stabilizing slopes.
(a) gravity
(b) water
(c) slope
(d) vegetation
Answer:
(d) vegetation
Question 13.
Slow downhill creep of soil in periglacial or alpine regions is known as ………………..
(a) rock fall
(b) solifluction
(c) earth flow
(d) landslide
Answer:
(b) solifluction
Identify the correct correlation
Question 1.
A – Mass wasting is effective on slopes that are made up of clay and shale.
R – Mass wasting determines the material of the slope.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.
Question 2.
A – Microscopic organisms like algae, moss, lichens cause biological weathering.
R – They produce chemicals on the outer layer of the rocks.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.
Question 3.
A – Quartzite, a metamorphic rock, is harder than steel.
R – It does not easily react physically but is easily fractured by chemical weathering.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A..
Question 4.
A – In mass movements, the materials come down the slope without the aid of a transporting medium like running water, ice or wind.
R – Anthropogenic weathering is responsible for mass movement.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(a) Only A is correct
Question 5.
A – Steeper slope will also have higher possibility of slow mass movement.
R – Gentle slopes will have slow mass movement.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(b) Only R is correct.
![]()
Question 6.
A – Mass movement is based on how quickly the rock and weathered material moves due to friction, gravity, load of material.
R – The rock and material move because of running water.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A.
Identify the incorrect factor.
Question 1.
The factors that affect mechanical weathering.
(a) Water
(b) Heat
(c) Pressure
(d) Microscopic organism
Answer:
(d) Microscopic organism
Question 2.
The factors that affect biological weathering.
(a) Mining
(b) Microscopic organism
(c) Barrowing animals
(d) Roots of trees
Answer:
(a) Mining
Question 3.
The reasons for anthropogenic weathering.
(a) Mining
(b) Pressure
(c) Road construction
(d) Quarrying for building material
Answer:
(b) Pressure
Question 4.
The factors responsible for mass movements.
(a) Gravity
(b) Water
(c) Heat
(d) Relief and slope
Answer:
(c) Heat
Question 5.
The mass movements can be divided into four main classes.
(a) Creep
(b) Fall or topple
(c) Flows
(d) Weak material and structure
Answer:
(d) Weak material and structure
![]()
Question 6.
The types of mass wasting.
(a) Fall or topple
(b) Landslide
(c) Solifluction
(d) Rock fall
Answer:
(a) Fall or topple
Identify the correct group
Question 1.
| A | B | C | D |
| (1) Algae | (1) Rock fall | (1) Relief and slope | (1) Shattering |
| (2) Roots and plants | (2) Landslide | (2) Gravity | (2) Block disintegration |
| (3) Lichens | (3) Earth flow | (3) Water | (3) Exfoliation |
| (4) Moss | (4) Exfoliation | (4) Vegetation | (4) Burrowing |
Answer:
A
Give geographical reasons
Question 1.
Many times, rocks break.
Answer:
Rocks break because-
- Rocks which are exposed are affected by the climate of that region in various ways.
- Rocks can break because of water, pressure, heat, etc. in various ways.
- Those rocks which have joints or layers, break easily than rocks which are homogeneous.
- The rocks which have vertical strata are easily loosened and break, due to changes in temperature, water, wind or frost action.
- If there are larger grains in the rocks, there is ample space in the rocks for water to enter and they get weathered easily and break.
- Some rocks are very hard and resistant to chemical weathering but they are easily fractured by physical weathering.
- Generally, sedimentary rocks break easily than igneous rocks and metamorphic rocks.
Question 2.
Water plays an important role in weathering.
Answer:
Water plays an important role in weathering because-
- In areas where diurnal range of temperature is high, water inside the crack’s freezes. During daytime, it again becomes water.
- When water freezes, its volume increases due to the pressure exerted on the walls of the rock, the cracks in the rocks widen and finally rock breaks down due to freeze and thaw weathering.
- Water also breaks down the rocks chemically. The water molecules react with minerals present in the rocks. This is called hydrolysis.
- Another way by which water can cause chemical weathering is by solution. Minerals like calcium, magnesium dissolves in water.
- Oxygen present in air and water reacts with iron or aluminium present in rock and as a result rock rusts and ultimately breaks.
Question 3.
Biological weathering is the disintegration of rocks as a result of action by living organisms.
Answer:
Biological weathering is the disintegration of rocks as a result of action by living organisms because-
- Roots of trees and other plants penetrate into the soil and grow in size. Thus, they exert pressure on rocks and make the cracks wider and deeper.
- Some plants grow within fissures and lead to disintegration.
- Microscopic organisms such as algae, moss, lichens and bacteria grow on rock surface and produce chemicals, they react on outer layers the rocks and break them.
- Man known for his economic and technological development becomes the most powerful weathering and erosion agent. Mining, blasting, construction of roads, railways etc., result in fast disintegration of rocks.
- There are some barrowing animals like rats, when they barrow, rocks are broken.
Question 4.
Vegetation plays a big role in stabilizing slopes.
Answer:
Vegetation plays a big role in stabilizing slopes because-
- The strong root system of trees and other plants help to hold the soil in place.
- When these trees are removed, the soil becomes loose and can be easily washed away.
- This is why, when there is dense forest cover there is stabilization of slopes but deforested areas are likely to be sites of mass wasting.
![]()
Differentiate between.
Question 1.
Physical weathering ad Chemical weathering.
Answer:
| Physical weathering | Chemical weathering |
| (i) Physical weathering may be defined as the disintegration or breaking of rocks without changing the properties of the rock. | (i) Chemical weathering is the process by which the internal structures of a mineral is altered by the addition or renewal of elements. |
| (ii) This type of weathering occurs mainly by temperature and pressure changes. | (ii) This type of weathering occurs when water activates several types of chemical reactions within the rocks. |
| (iii) In general, cold dry climate accelerates physical weathering. | (iii) Hot wet climate accelerates chemical weathering. |
| (iv) E.g. Exfoliation | (iv) E.g. Oxidation |
Question 2.
Landslides and Earth flow.
Answer:
| Landslides | Earth flow |
| (i) All types of mass movements of rock, debris, including soils and ice are collectively called landslides. | (i) Diagonal down slope movement of rock fragments and fine-grained material along sliding plane with enough water is called earth flow. |
| (ii) Landslides occur on steep or gentle slope gradient, from mountain range to coastal cliffs. | (ii) Earth flow is more common or hillsides or valley sides having rich minerals. |
| (iii) Gravity is primary force for the landslide to occur, others are slope stability, heavy rainfall or earthquake. | (iii) The primary reason for Earth flow is continuous heavy rainfall which saturates the ground and increases the pour water pressure, and earth flow starts. |
Question 3.
Rockfall and Solifluction.
Answer:
| Rockfall | Solifluction |
| (i) Rapid fall of rock material down or rock travel downwards bouncing and rolling is termed as rock fall. | (i) Solifluction is the name for the slow downhill creep of soil. |
| (ii) Rockfalls occur mainly in rocky areas. | (ii) Solifluction occurs mainly in periglacial or alpine regions. |
| (iii) The size of rockfall blocks can range from one cubic centimetre to ten thousand cubic meters. | (iii) The size of material in solifluction is very small since it contains particles of soil. |
Write short notes on
Question 1.
Types of Mass Wasting
Answer:
Mass wasting or mass movement is the down slope movement of loose mixture of soil, land and rock particles by force of gravity.
Following are different types of mass wasting:
Creep:
- Very slow imperceptible down slope movement of materials is called creep.
- It occurs along top and basal portions of hills.
Rock fall:
- Rock falls are relatively small landslides confined to the removal of individual and superficial blocks down a cliff base.
- It mainly occurs in rocky areas.
Earth flow:
- Earth flow is promoted by excessive water received mostly through rainfall so that the materials are oversaturated.
- It typically occurs on hill sides in humid regions.
Solifluction:
- Solifluction is the name for the slow downhill creep of soil, which occurs in a variety of climatic conditions.
- It occurs in periglacial or alpine regions.
- It occurs very slowly, so it is measured in millimetres or centimetres.
- As permafrost is impermeable to water, soil overlying may become oversaturated and the slides slope down under the pull of gravity.
Landslide:
- It may be mentioned that generally all types of mass movements of rock wastes including soils and ice are collectively called landslides.
- It occurs on moderately steep slopes.
- Gravity is primary force for the landslide to occur, others are slope stability, heavy rainfall or earthquake.
![]()
Question 2.
Biological Weathering:
Answer:
Flora : Roots of trees penetrate into the soil in search of minerals. Sometimes the plants grow within the fissures in the rock leading to widening of the fissures and eventually rocks disintegrate.
Fauna : Microscopic organisms such as algae, moss, lichens and bacteria grow on rock surface and produce chemicals, which react with the rock surface and create weathering. Burrowing animals like moles, mice, rats, reptiles, like snakes etc., dig holes in the soil and speed up disintegration.
Draw a neat diagram and labelled for:
Question 1.
Exfoliation
Answer:

Answer in Details
Question 1.
Explain different types of mass wasting.
Answer:
Mass wasting is the down slope movement of loose mixture of soil, land and rock particles by force of gravity.
Following are different types of mass wasting:
Creep:
- Very slow imperceptible down slope movements of materials is called creep.
- It occurs along tops and basal portions of hills.
Rock fall:
- Rock falls are relatively small landslides confined to the removal of individual and superficial blocks from cliff base.
- It mainly occurs in rocky areas.
Earth flow:
- Earth flow is promoted by excessive water received mostly through rainfall so that the materials are oversaturated.
- It typically occurs on hill slides in humid regions.
Solifluction:
- Solifluction is the name for the slow downhill creep of soil, which occurs in variety of climatic conditions.
- It occurs in periglacial or alpine regions.
- As permafrost is impermeable to water, soil overlying may become oversaturated and slide slope down under the pull of gravity.
Landslide:
- It may be mentioned that generally all types of mass movements of rock wastes including soils and ice are collectively called landslides.
- It occurs on moderately steep slopes.
Question 2.
What is weathering? Explain different types of weathering.
Answer:
Weathering refers to the break down or disintegration and decomposition of rocks in situ through mechanical and chemical changes in the rocks and their minerals affected by water temperature, wind, different atmospheric gases and organisms. Following are the types of weathering-
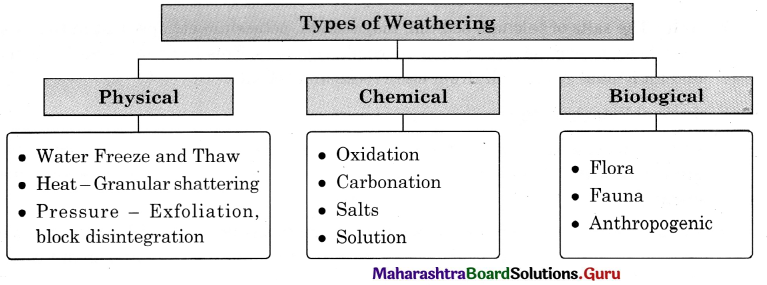
Let us study the types in details:
Physical Weathering:
(i) Water:
- In areas where diurnal temperature range is high, water inside the crack’s freezes during night and melts during daytime.
- Due to this continuous freezing and thawing, the cracks widen and disintegration of rocks takes place. This is called freeze and thaw weathering.
(ii) Heat:
- In hot deserts the temperature increases during the day. The minerals present in the rock react differently to the increased temperature.
- The minerals within the rock expand leading to stress and the rock breaks into individual mineral grains. This is called as granular disintegration.
- In the similar process, in the deserts during day time the rock surface gets heated and shatters. It may produce a breaking sound. This is called shattering.
- In rocks such as granite which have joints, heat can cause weathering by breaking the rocks along the joints into blocks. This is called block disintegration.
Pressure:
- Due to overlying rocks, the rocks beneath the surface experience a lot of pressure.
- When the underlying rock gets exposed to the surface, they are subjected to low pressure. As a result of pressure differences, the rock mass expands outwards.
- The expansion causes outer layer to separate from lower layer. It is called dislodgement which happens due to pressure release. It is mainly observed in igneous rocks which are more homogeneous. The continuous removal of outer layer of the rock is called exfoliation.
Chemical Weathering:
- Oxidation: When oxygen from air and water reacts with iron or bauxite present in the rocks, iron and aluminium oxides are formed. The colour of the rock changes and it is called rusting.
- Carbonation: When carbon-dioxide reacts with the minerals in the soil, carbonation takes place. The decomposition of dead produces C02, which reacts with minerals in the rocks.
- Solution: When some minerals in the rocks reacts with water in the rock or moisture in the air and gets dissolved, it is called solution. For example, chalk dissolves in water.
- Salt: The salts of calcium, sodium, magnesium, potassium etc., present in the rocks have a tendency to expand due to their thermal properties. This leads to crystallization of salts and individual grains spilt from main rocks and fall off at the end.
Biological Weathering:
Flora : Roots of trees penetrate into the soil in search of minerals. Sometimes the plants grow within the fissures in the rock leading to widening of the fissures and eventually disintegrating.
Fauna : Microscopic organisms such as algae, moss, lichens and bacteria grow on rock surface and produce chemicals, which react with the rock surface and create weathering. Burrowing animals like moles, mice, rats, reptiles, like snakes etc., dig holes in the soil and speeds up disintegration.
Anthropogenic weathering:
Man is responsible for weathering as he constructs roads, railways, do mining etc.
- Man being a biological agent affects weathering.
- With economic and technological development, man has become the most powerful weathering and erosion agent.
- Mining, blasting of hills and ridges for road and dam construction, quarrying for industrial and building materials, etc result in a fast rate of disintegration of rocks.
- This may be accomplished by natural weathering processes in thousands to millions of years.
- Man accelerates the rate of weathering on hill slopes through activities like deforestation.
![]()
Question 3.
Classify and explain mass movement on basis of weathered material.
Answer:

- Fall or topple: It happens when rocks have a free fall and land at the bottom of a slope.
- Flows: A mixture of water, rock and weathered material. They move very quickly. Large flows can bury an entire village. Small flows can block roads.
- Slide: A slide happens when section of soil or rock suddenly gives way and moves down a slope. The material moves as a single mass along a slippery zone.
- Creep: It is a very slow mass movement that goes on for years or even centuries.
Question 4.
What are the factors affecting mass movement?
Answer:
The factors responsible for mass movement are:
Relief and slope:
- There should be considerable elevation in an area for down slope movement to occur.
- Such movements will not occur in plain areas.
- Hilly, mountainous and plateau areas are more vulnerable to such movements.
- The steeper the slope, higher are the chances of occurrence of mass movements. Gentle slopes will have slow movements while steep slopes will have rapid movements.
Gravity:
- It is the main force responsible for mass movements.
- It is a force that acts everywhere on the surface of the earth, pulling everything down.
Water:
- Although water is not always directly involved as transporting medium but it plays an important role.
- Addition of water from rainfall or snowfall or melting of snow makes the material on the slope heavier.
- Water can reduce the friction along a sliding surface.
Weak material and structures:
- Some rocks are weaker than others. Rocks which have joints break easily.
- In particular, rocks containing calcium or clay minerals tend to have a low strength.
- Such areas will be more susceptible to mass wasting.
![]()
Question 5.
Complete the following flow chart.
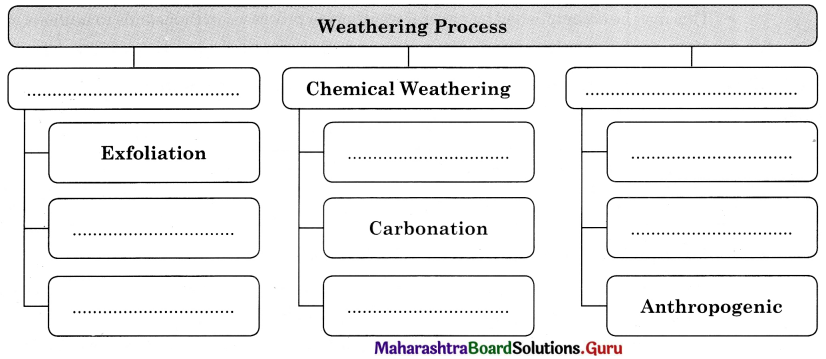
Answer:
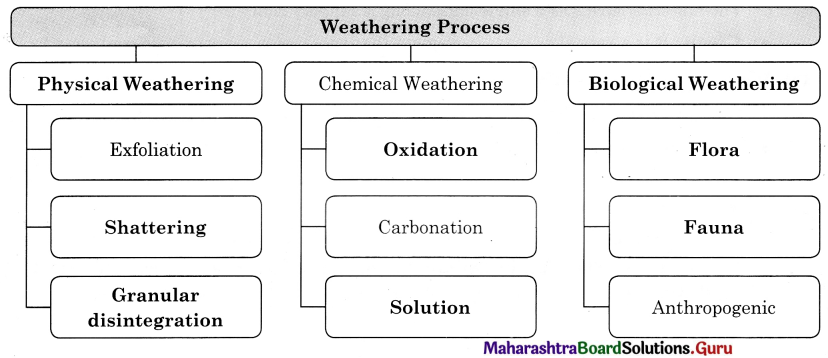
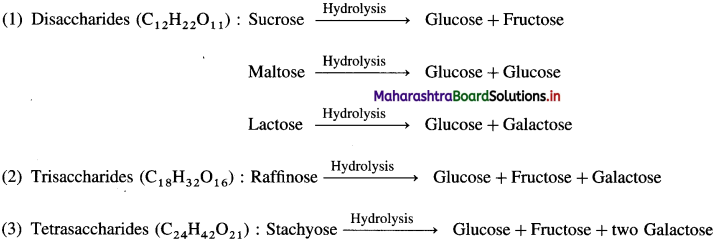
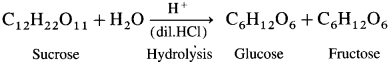

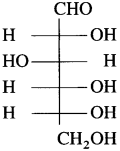
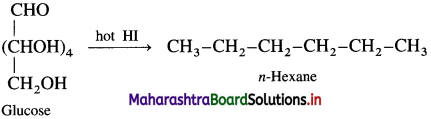
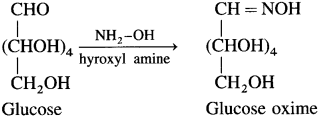
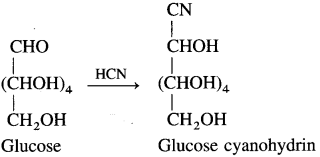
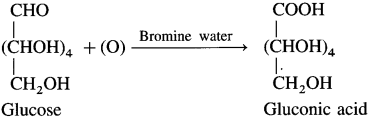
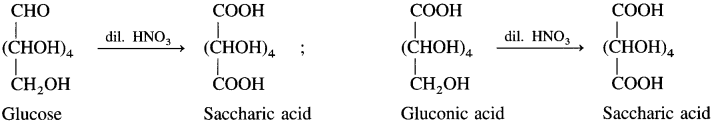


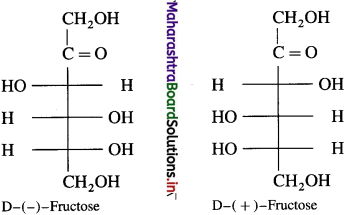
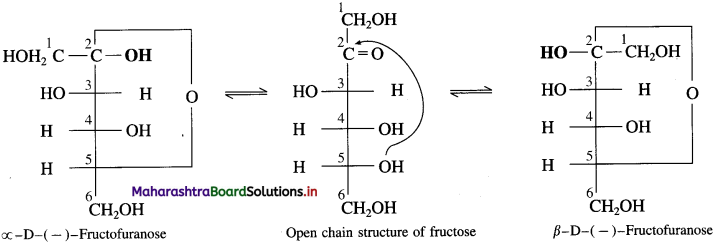
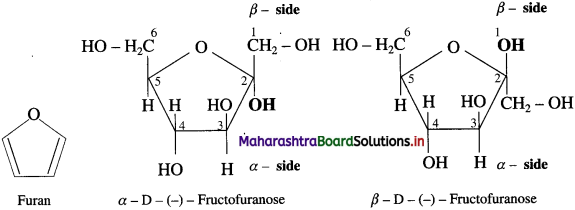
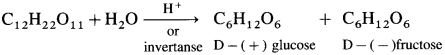

 (where R is an alkyl group or aryl group).
(where R is an alkyl group or aryl group).