Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Vectors Ex 5.5 Questions and Answers.
12th Maths Part 1 Vectors Exercise 5.5 Questions And Answers Maharashtra Board
Question 1.
Find \(\bar{a}\)∙(\(\bar{b}\) × \(\bar{c}\)), if \(\bar{a}\) = \(3 \hat{i}-\hat{j}+4 \hat{k}\), \(\bar{b}\) = \(2 \hat{i}+3 \hat{j}-\hat{k}\) and \(\bar{c}\) = \(-5 \hat{i}+2 \hat{j}+3 \hat{k}\)
Solution:
\(\bar{a}\)∙(\(\bar{b}\) × \(\bar{c}\)) = \(\left|\begin{array}{rrr}
3 & -1 & 4 \\
2 & 3 & -1 \\
-5 & 2 & 3
\end{array}\right|\)
= 3(9 + 2) + 1 (6 – 5) + 4(4 + 15)
= 33 + 1 + 76
= 110.
Question 2.
If the vectors \(3 \hat{i}+5 \hat{k}, 4 \hat{i}+2 \hat{j}-3 \hat{k}\) and \(3 \hat{i}+\hat{j}+4 \hat{k}\) are to co-terminus edges of the parallelo piped, then find the volume of the parallelopiped.
Solution:
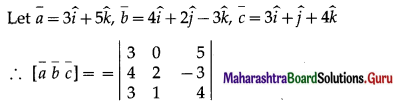
= 3(8 + 3) – 0(16 + 9) + 5(4 – 6)
= 33 – 0 – 10 = 23
∴ volume of the parallelopiped = \([\bar{a} \bar{b} \bar{c}]\)
= 23 cubic units.
![]()
Question 3.
If the vectors \(-3 \hat{i}+4 \hat{j}-2 \hat{k}, \hat{i}+2 \hat{k}\) and\(\hat{i}-p \hat{j}\) are coplanar, then find the value of p.
Solution:
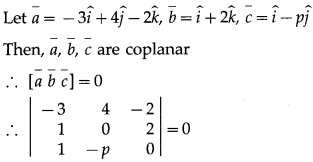
∴ -3(0 + 2p) – 4(0 – 2) – 2(-p – 0) = 0
∴ -6p + 8 + 2p = 0
∴ -4p = -8
P = 2.
Question 4.
Prove that :
(i) [latex]\bar{a} \bar{b}+\bar{c} \bar{a}+\bar{b}+\bar{c}[/latex] = 0
Solution:
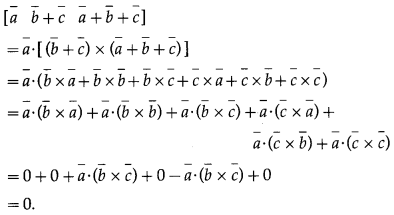
![]()
(ii) (\(\bar{a}\) – \(2 \bar{b}\) – \(\bar{c}\))∙[(\(\bar{a}\) – \(\bar{b}\)) × \(\bar{a}\) – \(\bar{b}\) – \(\bar{c}\)] = 3[\(\bar{a}\) – \(\bar{b}\) – \(\bar{c}\)]
Question is modified.
(\(\bar{a}\) – \(2 \bar{b}\) – \(\bar{c}\)) [(\(\bar{a}\) – \(\bar{b}\)) × \(\bar{a}\) – \(\bar{b}\) – \(\bar{c}\)] = 3[\(\bar{a}\) \(\bar{b}\) \(\bar{c}\)]
Solution:

Question 5.
If \(\bar{c}\) =3\(\bar{a}\) – 2\(\bar{b}\) prove that [\(\bar{a}\) \(\bar{b}\) \(\bar{c}\)] = 0
Solution:
We use the results :\(\bar{b}\) × \(\bar{b}\) = 0 and if in a scalar triple product, two vectors are equal, then the scalar triple product is zero.

![]()
Question 6.
If u = \(\hat{\mathbf{i}}-2 \hat{\mathbf{j}}+\hat{k}\), \(\bar{v}\) = \(3 \hat{\mathbf{i}}+\hat{k}\) and \(\bar{w}\) = \(\hat{\mathrm{j}}-\hat{\mathrm{k}}\) are given vectors, then find
(i) [\(\bar{u}\) + \(\bar{w}\)]∙[(\(\bar{w}\) × \(\bar{r}\)) × (\(\bar{r}\) × \(\bar{w}\))]
Question is modified.
If \(\bar{u}\) = \(\hat{\mathbf{i}}-2 \hat{\mathbf{j}}+\hat{k}\), \(\bar{r}\) = \(3 \hat{\mathbf{i}}+\hat{k}\) and \(\bar{w}\) = \(\hat{\mathrm{j}}-\hat{\mathrm{k}}\) are given vectors, then find [\(\bar{u}\) + \(\bar{w}\)]∙[(\(\bar{u}\) × \(\bar{r}\)) × (\(\bar{r}\) × \(\bar{w}\))]
Solution:

= 1(6 – 18) + 1 (-6 + 6) + 0
= -12 + 0 + 0 = -12.
Question 7.
Find the volume of a tetrahedron whose vertices are A( -1, 2, 3) B(3, -2, 1), C (2, 1, 3) and D(-1, -2, 4).
Solution:
The position vectors \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d }\) of the points A, B, C and D w.r.t. the origin are \(\bar{a}\) = \(-\hat{i}+2 \hat{j}+3 \hat{k}\), \(\bar{b}\) = \(3 \hat{i}-2 \hat{j}+\hat{k}\), \(\bar{c}\) = \(2 \hat{i}+\hat{j}+3 \hat{k}\) and

![]()
Question 8.
If \(\bar{a}\) = \(\hat{i}+2 \hat{j}+3\), \(\bar{b}\) = \(3 \hat{i}+2 \hat{j}\) and \(\bar{c}\) = ,\(2 \hat{i}+\hat{j}+3\) then verify that \(\bar{a}\) × (\(\bar{b}\) × \(\bar{c}\)) = (\(\bar{a}\) ⋅ \(\bar{c}\))\(\bar{b}\) – (\(\bar{a}\) ⋅ \(\bar{b}\))\(\bar{c}\)
Solution:
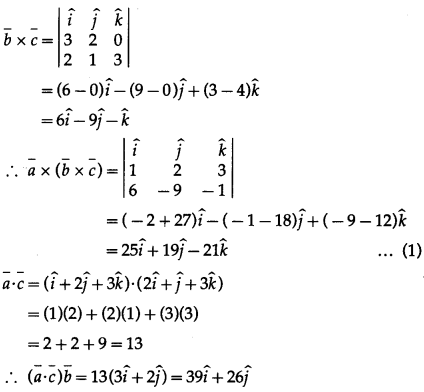

From (1) and (2), we get
\(\bar{a}\) × (\(\bar{b}\) × \(\bar{c}\)) = (\(\bar{a}\) ⋅ \(\bar{c}\))\(\bar{b}\) – (\(\bar{a}\) ⋅ \(\bar{b}\))\(\bar{c}\)
Question 9.
If, \(\bar{a}\) = \(\hat{i}-2 \hat{j}\), \(\bar{b}\) = \(\hat{i}+2 \hat{j}\) and \(\bar{c}\) =\(2 \hat{i}+\hat{j}-2\) then find
(i) \(\bar{a}\) × (\(\bar{b}\) × \(\bar{c}\))
Solution:
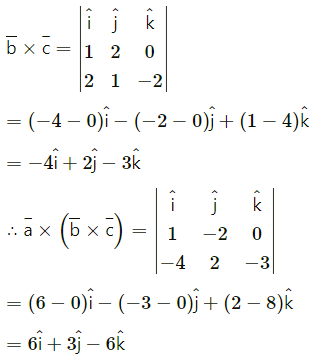
(ii) (\(\bar{a}\) × \(\bar{b}\)) × \(\bar{c}\) Are the results same? Justify.
Solution:
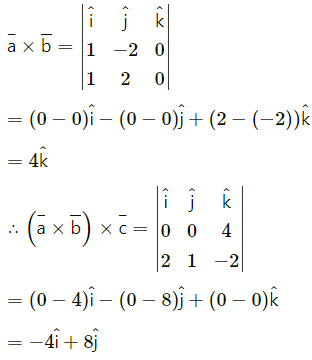
\(\bar{a}\) × (\(\bar{b}\) × \(\bar{c}\)) ≠ (\(\bar{a}\) × \(\bar{b}\)) × \(\bar{c}\)
![]()
Question 10.
Show that \(\bar{a}\) × (\(\bar{b}\) × \(\bar{c}\)) + \(\bar{b}\) × (\(\bar{c}\) × \(\bar{a}\)) + \(\bar{c}\) × (\(\bar{a}\) × \(\bar{b}\)) = 0
Solution:
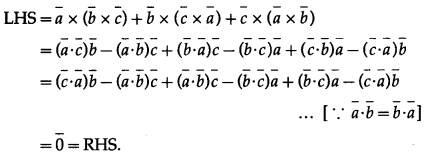
Class 12 Maharashtra State Board Maths Solution