Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Vectors Ex 5.2 Questions and Answers.
12th Maths Part 1 Vectors Exercise 5.2 Questions And Answers Maharashtra Board
Question 1.
Find the position vector of point R which divides the line joining the points P and Q whose position vectors are \(2 \hat{i}-\hat{j}+3 \hat{k}\) and \(-5 \hat{i}+2 \hat{j}-5 \hat{k}\) in the ratio 3 : 2
(i) internally
Solution:
It is given that the points P and Q have position vectors \(\bar{p}\) = \(2 \hat{i}-\hat{j}+3 \hat{k}\) and \(\bar{p}\) = \(-5 \hat{i}+2 \hat{j}-5 \hat{k}\) respectively.
(i) If R(\(\bar{r}\)) divides the line segment PQ internally in the ratio 3 : 2, by section formula for internal division,

(ii) externally.
Solution:
If R(\(\bar{r}\)) divides the line segment joining P and Q externally in the ratio 3 : 2, by section formula for external division,
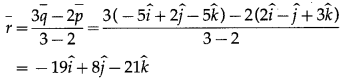
∴ coordinates of R = (-19, 8, -21).
Hence, the position vector of R is \(-19 \hat{i}+8 \hat{j}-21 \hat{k}\) and coordinates of R are (-19, 8, -21).
![]()
Question 2.
Find the position vector of midpoint M joining the points L (7, -6, 12) and N (5, 4, -2).
Solution:
The position vectors \(\bar{l}\) and \(\bar{n}\) of the points L(7, -6, 12) and N (5, 4, -2) are given by
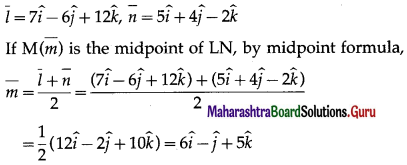
∴ coordinates of M = (6, -1, 5).
Hence, position vector of M is \(6 \hat{i}-\hat{j}+5 \hat{k}\) and the coordinates of M are (6, -1, 5).
Question 3.
If the points A(3, 0, p), B (-1, q, 3) and C(-3, 3, 0) are collinear, then find
(i) The ratio in which the point C divides the line segment AB.
Solution:
Let \(\bar{a}\), \(\bar{b}\) and \(\bar{c}\) be the position vectors of A, B and C respectively.
Then \(\bar{a}\) = \(3 \hat{i}+0 \cdot \hat{j}+p \hat{k}\), \(\bar{b}\) = \(-\hat{i}+q \hat{j}+3 \hat{k}\) and \(\bar{c}\) = \(-3 \hat{i}+3 \hat{j}+0 \hat{k}\).
As the points A, B, C are collinear, suppose the point C divides line segment AB in the ratio λ : 1.
∴ by the section formula,
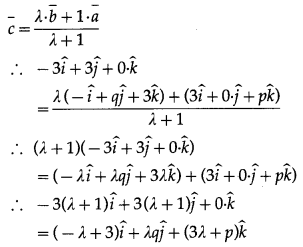
By equality of vectors, we have,
-3(λ + 1) = -λ + 3 … (1)
3(λ + 1 ) = λ q … (2)
0 = 3λ + p … (3)
From equation (1), -3λ – 3 = -λ + 3
∴ -2λ = 6 ∴ λ = -3
∴ C divides segment AB externally in the ratio 3 : 1.
![]()
(ii) The values of p and q.
Solution:
Putting λ = -3 in equation (2), we get
3(-3 + 1) = -3q
∴ -6 = -3q ∴ q = 2
Also, putting λ = -3 in equation (3), we get
0 = -9 + p ∴ p = 9
Hence p = 9 and q = 2.
Question 4.
The position vector of points A and B are 6\(\bar{a}\) + 2\(\bar{b}\) and \(\bar{a}\) – 3\(\bar{b}\). If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is 3\(\bar{a}\) – \(\bar{b}\).
Solution:
Let \(\bar{c}\) be the position vector of C.
Since C divides AB in the ratio 3 : 2,

Hence, the position vector of C is 3\(\bar{a}\) – \(\bar{b}\).
![]()
Question 5.
Prove that the line segments joining mid-point of adjacent sides of a quadrilateral form a parallelogram.
Solution:
Let ABCD be a quadrilateral and P, Q, R, S be the midpoints of the sides AB, BC, CD and DA respectively.
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\), \(\bar{d}\), \(\bar{p}\), \(\bar{q}\), \(\bar{r}\) and s be the position vectors of the points A, B, C, D, P, Q, R and S respectively.
Since P, Q, R and S are the midpoints of the sides AB, BC, CD and DA respectively,
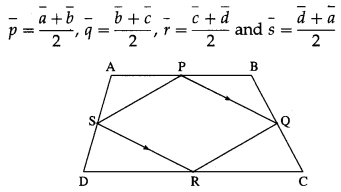
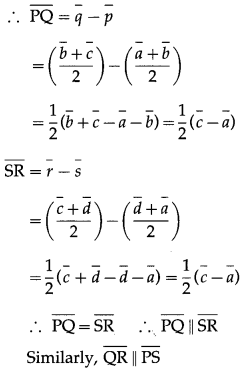
∴ □PQRS is a parallelogram.
Question 6.
D and E divide sides BC and CA of a triangle ABC in the ratio 2 : 3 respectively. Find the position vector of the point of intersection of AD and BE and the ratio in which this point divides AD and BE.
Solution:
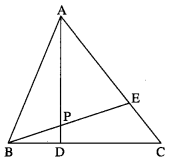
Let AD and BE intersect at P.
Let A, B, C, D, E, P have position vectos \(\bar{a}\), \(\bar{b}\), \(\bar{c}\), \(\bar{d}\), \(\bar{e}\), \(\bar{p}\) respectively.
D and E divide segments BC and CA internally in the ratio 2 : 3.
By the section formula for internal division,

LHS is the position vector of the point which divides segment AD internally in the ratio 15 : 4.
RHS is the position vector of the point which divides segment BE internally in the ratio 10 : 9.
But P is the point of intersection of AD and BE.
∴ P divides AD internally in the ratio 15 : 4 and P divides BE internally in the ratio 10 : 9.
Hence, the position vector of the point of interaction of
AD and BE is \(\bar{p}\) = \(\frac{15 \bar{d}+4 \bar{a}}{19}=\frac{10 \bar{e}+9 \bar{b}}{19}\) and it divides AD internally in the ratio 15 : 4 and BE internally in the ratio 10 : 9.
![]()
Question 7.
Prove that a quadrilateral is a parallelogram if and only if its diagonals bisect each other.
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) be respectively the position vectors of the vertices A, B, C and D of the parallelogram ABCD. Then AB = DC and side AB || side DC.
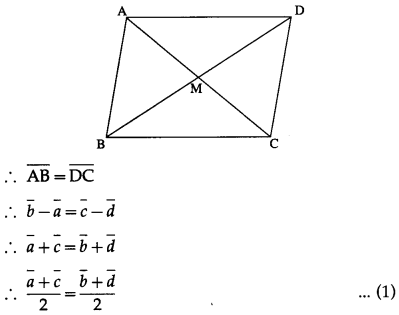
The position vectors of the midpoints of the diagonals AC and BD are (\(\bar{a}\) + \(\bar{c}\))/2 and (\(\bar{b}\) + \(\bar{d}\))/2. By (1), they are equal.
∴ the midpoints of the diagonals AC and BD are the same.
This shows that the diagonals AC and BD bisect each other.
(ii) Conversely, suppose that the diagonals AC and BD
of □ ABCD bisect each other,
i. e. they have the same midpoint.
∴ the position vectors of these midpoints are equal.
∴ \(\frac{\bar{a}+\bar{c}}{2}=\frac{\bar{b}+\bar{d}}{2}\) ∴ \(\bar{a}+\bar{c}=\bar{b}+\bar{d}\)
∴ \(\bar{b}\) – \(\bar{a}\) = \(\bar{c}\) – \(\bar{d}\) ∴ \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{DC}}\)
∴ \(\overline{\mathrm{AB}}\) ||\(\overline{\mathrm{DC}}\) and \(|\overline{\mathrm{AB}}|\) = \(|\overline{\mathrm{DC}}|\)
∴ side AB || side DC and AB = DC.
∴ □ ABCD is a parallelogram.
![]()
Question 8.
Prove that the median of a trapezium is parallel to the parallel sides of the trapezium and its length is half the sum of parallel sides.
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) be respectively the position vectors of the vertices A, B, C and D of the trapezium ABCD, with side AD || side BC.
Then the vectors \(\overline{\mathrm{AD}}\) and \(\overline{\mathrm{BC}}\) are parallel.
∴ there exists a scalar k,
such that \(\overline{\mathrm{AD}}\) = k∙\(\overline{\mathrm{BC}}\)
∴ \(\overline{\mathrm{AD}}\) + \(\overline{\mathrm{BC}}\) = k∙\(\overline{\mathrm{BC}}\) + \(\overline{\mathrm{BC}}\)
= (k + 1)BC …(1)
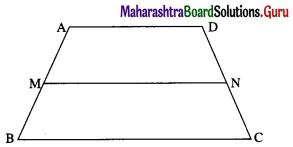
Let \(\bar{m}\) and \(\bar{n}\) be the position vectors of the midpoints M and N of the non-parallel sides AB and DC respectively.
Then seg MN is the median of the trapezium.
By the midpoint formula,
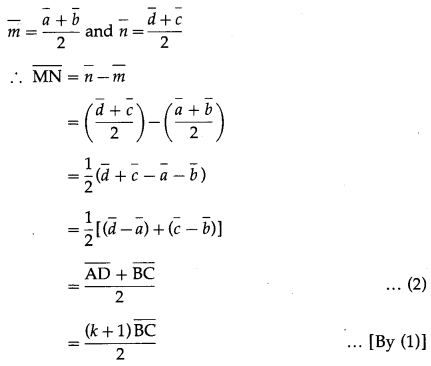
Thus \(\overline{\mathrm{MN}}\) is a scalar multiple of \(\overline{\mathrm{BC}}\)
∴ \(\overline{\mathrm{MN}}\) and \(\overline{\mathrm{BC}}\) are parallel vectors
∴ \(\overline{\mathrm{MN}}\) || \(\overline{\mathrm{BC}}\) where \(\overline{\mathrm{BC}}\) || \(\overline{\mathrm{AD}}\)
∴ the median MN is parallel to the parallel sides AD and BC of the trapezium.
Now \(\overline{\mathrm{AD}}\) and \(\overline{\mathrm{BC}}\) are collinear
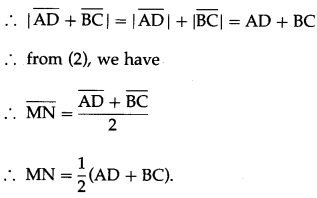
Question 9.
If two of the vertices of the triangle are A(3, 1, 4) and B(-4, 5, -3) and the centroid of a triangle is G(-1, 2, 1), then find the coordinates of the third vertex C of the triangle.
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{g}\) be the position vectors of A, B, C and G respectively.
Then \(\bar{a}\) = \(3 \hat{i}+\hat{j}+4 \hat{k}\), \(\bar{b}\) = \(-4 \hat{i}+5 \hat{j}-3 \hat{k}\) and \(\bar{g}\) = \(-\hat{i}+2 \hat{j}+\hat{k}\).
Since G is the centroid of the ∆ABC, by the centroid formula,
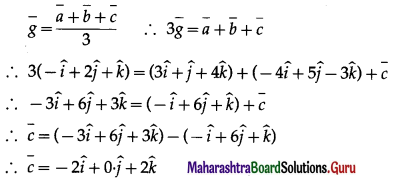
∴ the coordinates of third vertex C are (-2, 0, 2).
![]()
Question 10.
In∆OAB, E is the mid-point of OB and D is the point on AB such that AD : DB = 2 : 1.
If OD and AE intersect at P, then determine the ratio OP : PD using vector methods.
Solution:
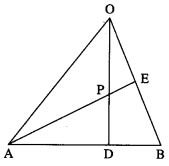
Let A, B, D, E, P have position vectors \(\bar{a}\), \(\bar{b}\), \(\bar{d}\), \(\bar{e}\), \(\bar{p}\) respectively w.r.t. O.
∵ AD : DB = 2 : 1.
∴ D divides AB internally in the ratio 2 : 1.
Using section formula for internal division, we get

LHS is the position vector of the point which divides OD internally in the ratio 3 : 2.
RHS is the position vector of the point which divides AE internally in the ratio 4 : 1.
But OD and AE intersect at P
∴ P divides OD internally in the ratio 3 : 2.
Hence, OP : PD = 3 : 2.
Question 11.
If the centroid of a tetrahedron OABC is (1, 2, -1) where A = (a, 2, 3), B = (1, b, 2), C = (2, 1, c) respectively, find the distance of P (a, b, c) from the origin.
Solution:
Let G = (1, 2, -1) be the centroid of the tetrahedron OABC.
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\), \(\bar{g}\) be the position vectors of the points A, B, C, G respectively w.r.t. O.

By equality of vectors
a + 3 = 4, b + 3 = 8, c + 5= -4
∴ a = 1, b = 5, c = -9
∴ P = (a, b, c) = (1, 5, -9)
Distance of P from origion = \(\sqrt{1^{2}+5^{2}+(-9)^{2}}\)
= \(\sqrt{1+25+81}\)
= \(\sqrt{107}\)
![]()
Question 12.
Find the centroid of tetrahedron with vertices K(5, -7, 0), L(1, 5, 3), M(4, -6, 3), N(6, -4, 2) ?
Solution:
Let \(\bar{p}\), \(\bar{l}\), \(\bar{m}\), \(\bar{n}\) be the position vectors of the points K, L, M, N respectively w.r.t. the origin O.

Hence, the centroid of the tetrahedron is G = (4, -3, 2).
Class 12 Maharashtra State Board Maths Solution