Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Vectors Ex 5.3 Questions and Answers.
12th Maths Part 1 Vectors Exercise 5.3 Questions And Answers Maharashtra Board
Question 1.
Find two unit vectors each of which is perpendicular to both
\(\bar{u}\) and \(\bar{v}\), where \(\bar{u}\) = \(2 \hat{i}+\hat{j}-2 \hat{k}\), \(\bar{v}\) = \(\hat{i}+2 \hat{j}-2 \hat{k}\)
Solution:
Let \(\bar{u}\) = \(2 \hat{i}+\hat{j}-2 \hat{k}\)
\(\bar{v}\) = \(\hat{i}+2 \hat{j}-2 \hat{k}\)
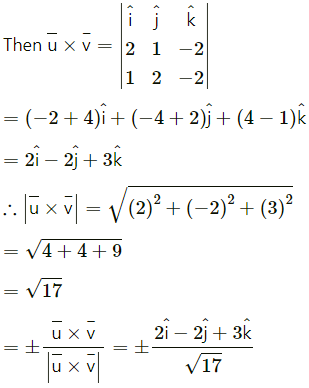
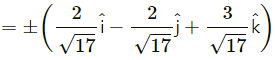
Question 2.
If \(\bar{a}\) and \(\bar{b}\) are two vectors perpendicular to each other, prove that (\(\bar{a}\) + \(\bar{b}\))2 = (\(\bar{a}\) – \(\bar{b}\))2
Solution:
\(\bar{a}\) and \(\bar{b}\) are perpendicular to each other.

∴ LHS = RHS
Hence, (\(\bar{a}\) + \(\bar{b}\))2 = (\(\bar{a}\) – \(\bar{b}\))2.
![]()
Question 3.
Find the values of c so that for all real x the vectors \(x c \hat{i}-6 \hat{j}+3 \hat{k}\) and \(x \hat{i}+2 \hat{j}+2 c x \hat{k}\) make an obtuse angle.
Solution:
Let \(\bar{a}\) = \(x c \hat{i}-6 \hat{j}+3 \hat{k}\) and \(\bar{b}\) = \(x \hat{i}+2 \hat{j}+2 c x \hat{k}\)
Consider \(\bar{a}\)∙\(\bar{b}\) = \((x c \hat{i}-6 \hat{j}+3 \hat{k}) \cdot(x \hat{i}+2 \hat{j}+2 c x \hat{k})\)
= (xc)(x) + (-6)(2) + (3)(2cx)
= cx2 – 12 + 6cx
= cx2 + 6cx – 12
If the angle between \(\bar{a}\) and \(\bar{b}\) is obtuse, \(\bar{a}\)∙\(\bar{b}\) < 0.
∴ cx2 + 6cx – 12 < 0
∴ cx2 + 6cx < 12
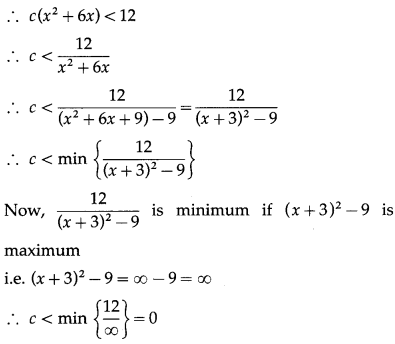
∴ c < 0.
Hence, the angle between a and b is obtuse if c < 0.
Question 4.
Show that the sum of the length of projections of \(\hat{p} \hat{i}+q \hat{j}+r \hat{k}\) on the coordinate axes, where p = 2, q = 3 and r = 4, is 9.
Solution:
Let \(\bar{a}\) = \(\hat{p} \hat{i}+q \hat{j}+r \hat{k}\)
Projection of \(\bar{a}\) on X-axis
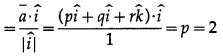
Similarly, projections of \(\bar{a}\) on Y- and Z-axes are 3 and 4 respectively.
∴ sum of these projections = 2 + 3 + 4 = 9.
![]()
Question 5.
Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular.
Solution:
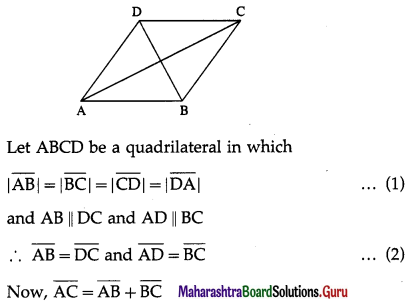
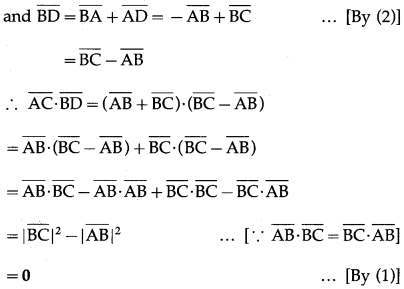
∵ \(\overline{\mathrm{AC}}\), \(\overline{\mathrm{BD}}\) are non-zero vectors
∴ \(\overline{\mathrm{AC}}\) is perpendicular to \(\overline{\mathrm{BD}}\)
Hence, the diagonals are perpendicular.
Question 6.
Determine whether \(\bar{a}\) and \(\bar{b}\) are orthogonal, parallel or neither.
(i) \(\bar{a}\) = \(-9 \hat{i}+6 \hat{j}+15 \hat{k}\), \(\bar{b}\) = \(6 \hat{i}-4 \hat{j}-10 \hat{k}\)
Solution:
\(\bar{a}\) = \(-9 \hat{i}+6 \hat{j}+15 \hat{k}\) = -3\((3 \hat{i}-2 \hat{j}-5 \hat{k})\)
= \(-\frac{3}{2}(6 \hat{i}-4 \widehat{j}-19 \hat{k})\)
∴ \(\bar{a}\) = \(-\frac{3}{2} \bar{b}\)
i.e. \(\bar{a}\) is a non-zero scalar multiple of \(\bar{b}\)
Hence, \(\bar{a}\) is parallel to \(\bar{b}\).
![]()
(ii) \(\bar{a}\) = \(2 \hat{i}+3 \hat{j}-\hat{k}\), \(\bar{b}\) = \(5 \hat{i}-2 \hat{j}+4 \hat{k}\)
Solution:
\(\bar{a} \cdot \bar{b}\) = \((2 \hat{i}+3 \hat{j}-\hat{k}) \cdot(5 \hat{i}-2 \hat{j}+4 \hat{k})\)
= (2)(5) + (3)(-2) + (-1)(4)
= 10 – 6 – 4 = 0
Since, \(\bar{a}\), \(\bar{b}\) are non-zero vectors and \(\bar{a} \cdot \bar{b}\) = 0, \(\bar{a}\) is orthogonal to \(\bar{b}\).
(iii) \(\bar{a}\) = \(-\frac{3}{5} \hat{i}+\frac{1}{2} \hat{j}+\frac{1}{3} \hat{k}\), \(\bar{b}\) = \(5 \hat{i}+4 \hat{j}+3 \hat{k}\).
Solution:
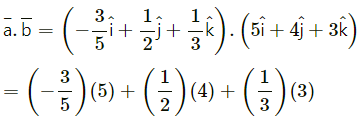
= -3 + 2 + 1
= 0
Since, \(\bar{a}\), \(\bar{b}\) are non-zero vectors and \(\bar{a} \cdot \bar{b}\) = 0
\(\bar{a}\) is orthogonal to \(\bar{b}\).
(iv) \(\bar{a}\) = \(4 \hat{i}-\hat{j}+6 \hat{k}\), \(\bar{a}\) = \(5 \hat{i}-2 \hat{j}+4 \hat{k}\)
Solution:
\(\bar{a} \cdot \bar{b}\) = \((4 \hat{i}-\hat{j}+6 \hat{k}) \cdot(5 \hat{i}-2 \hat{j}+4 \hat{k})\)
= (4)(5) + (-1)(-2) + (6)(4)
= 20 + 2 + 24
= 46 ≠ 0
∴ \(\bar{a}\) is not orthogonal to \(\bar{b}\).
It is clear that \(\bar{a}\) is not a scalar multiple of \(\bar{b}\).
∴ \(\bar{a}\) is not parallel to \(\bar{b}\).
Hence, \(\bar{a}\) is neither parallel nor orthogonal to \(\bar{b}\).
![]()
Question 7.
Find the angle P of the triangle whose vertices are P(0, -1, -2), Q(3, 1, 4) and R(5, 7, 1).
Solution:
The position vectors \(\bar{p}\), \(\bar{q}\) and \(\bar{r}\) of the points P(0, -1, -2), Q(3, 1, 4) and R(5, 7, 1) are

∴ P = 45°
Question 8.
If\(\hat{p}\), \(\hat{q}\), and \(\hat{r}\) are unit vectors, find
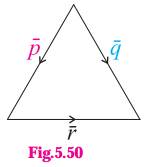
(i) \(\hat{p} \cdot \hat{q}\)
Solution:
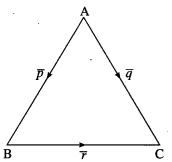
Let the triangle be denoted by ABC,
where \(\overline{\mathrm{AB}}\) = \(\bar{p}\), \(\overline{\mathrm{AC}}\) = \(\bar{q}\) and \(\overline{\mathrm{BC}}\) = \(\bar{r}\)
∵ \(\bar{p}\), \(\bar{r}\), \(\bar{r}\) are unit vectors.
∴ l(AB) = l(BC) = l(CA) = 1
∴ the triangle is equilateral
∴ ∠A = ∠B = ∠C = 60°
(i) Using the formula for angle between two vectors,
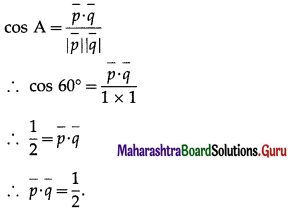
(ii) \(\hat{p} \cdot \hat{r}\)
Solution:
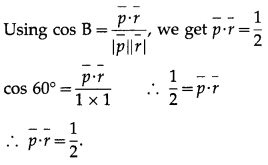
![]()
Question 9.
Prove by vector method that the angle subtended on semicircle is a right angle.
Solution:
Let seg AB be a diameter of a circle with centre C and P be any point on the circle other than A and B. Then ∠APB is an angle subtended on a semicircle.
Let \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{CB}}\) = \(\bar{a}\) and \(\overline{\mathrm{CP}}\) = \(\bar{r}\).
Then|\(\bar{a}\)| = |\(\bar{r}\)| …(1)
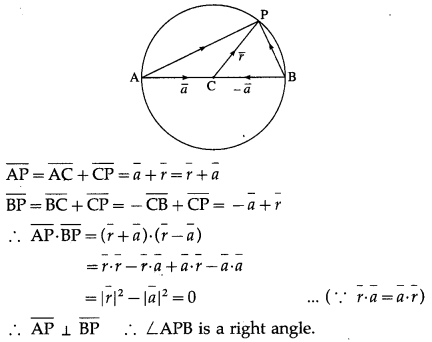
Hence, the angle subtended on a semicircle is the right angle.
Question 10.
If a vector has direction angles 45ºand 60º find the third direction angle.
Solution:
Let α = 45°, β = 60°
We have to find γ.
∴ cos2α + cos2β + cos2γ = 1
∴ cos245° + cos260° + cos2γ = 1
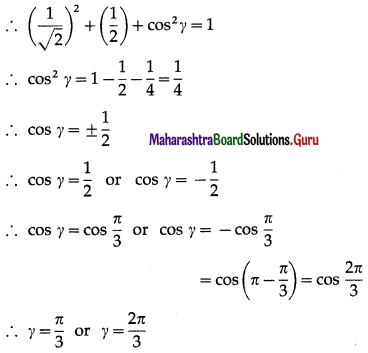
Hence, the third direction angle is \(\frac{\pi}{3}\) or \(\frac{2 \pi}{3}\).
![]()
Question 11.
If a line makes angles 90º, 135º, 45º with the X, Y and Z axes respectively, then find its direction cosines.
Solution:
Let l, m, n be the direction cosines of the line.
Then l = cos α, m = cos β, n = cos γ
Here, α = 90°, β = 135° and γ = 45°
∴ l = cos 90° = 0
m = cos 135° = cos (180° – 45°) = -cos 45° = \(-\frac{1}{\sqrt{2}}\) and n = cos 45° = \(\frac{1}{\sqrt{2}}\)
∴ the direction cosines of the line are 0, \(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\).
Question 12.
If a line has the direction ratios, 4, -12, 18 then find its direction cosines.
Solution:
The direction ratios of the line are a = 4, b = -12, c = 18.
Let l, m, n be the direction cosines of the line.
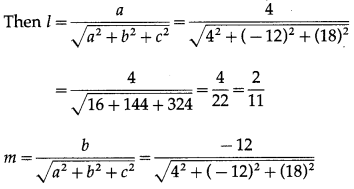

![]()
Question 13.
The direction ratios of \(\overline{A B}\) are -2, 2, 1. If A = (4, 1, 5) and l(AB) = 6 units, find B.
Solution:
The direction ratio of \(\overline{A B}\) are -2, 2, 1.
∴ the direction cosines of \(\overline{A B}\) are
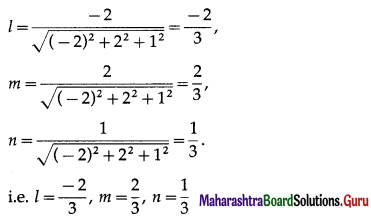
The coordinates of the points which are at a distance of d units from the point (x1, y1, z1) are given by (x1 ± ld, y1 ± md, z1 ± nd)
Here x1 = 4, y1 = 1, z1 = 5, d = 6, l = \(-\frac{2}{3}\), m = \(\frac{2}{3}\), n = \(\frac{1}{3}\)
∴ the coordinates of the requited points are
(4 ± \(\left(-\frac{2}{3}\right)\)6, 1 ± \(\frac{2}{3}\)(6), 5 ± \(\frac{1}{3}\)(6))
i.e. (4 – 4, 1 + 4, 5 + 2) and (4 + 4, 1 – 4, 5 – 2)
i.e. (0, 5, 7) and (8, -3, 3).
Question 14.
Find the angle between the lines whose direction cosines l, m, n satisfy the equations 5l + m + 3n = 0 and 5mn – 2nl + 6lm = 0.
Solution:
Given, 5l + m + 3n = 0 …(1)
and 5mn – 2nl + 6lm = 0 …(2)
From (1), m = -(51 + 3n)
Putting the value of m in equation (2), we get,
-5(5l + 3n)n – 2nl – 6l(5l + 3n) = 0
∴ -25ln – 15n2 – 2nl – 30l2 – 18ln = 0
∴ – 30l2 – 45ln – 15n2 = 0
∴ 2l2 + 3ln + n2 = 0
∴ 2l2 + 2ln + ln + n2 = 0
∴ 2l(l + n) + n(l + n) = 0
∴ (l + n)(2l + n) = 0
∴ l + n = 0 or 2l + n = 0
l = -n or n = -2l
Now, m = -(5l + 3n), therefore, if l = -n,
m = -(-5n + 3n) = 2n
∴ -l = \(\frac{m}{2}\) = n
∴ \(\frac{l}{-1}=\frac{m}{2}=\frac{n}{1}\)
∴ the direction ratios of the first line are
a1 = -1, b1 = 2, c1 = 1
If n = -2l, m = -(5l – 6l) – l
∴ l = m = \(\frac{n}{-2}\)
∴ \(\frac{l}{1}=\frac{m}{1}=\frac{n}{-2}\)
∴ the direction ratios of the second line are
a2 = -1, b2 = 1, c2 = -2
Let θ be the angle between the lines.
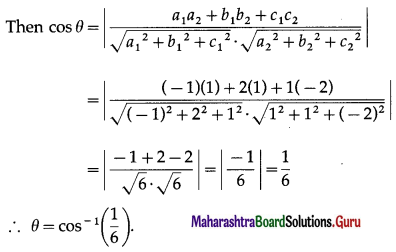
Class 12 Maharashtra State Board Maths Solution