Maharashtra Board 12th Maths Solutions Chapter 5 Vectors Ex 5.4

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Vectors Ex 5.4 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 5 Vectors Ex 5.4

Question 1.
If \(\bar{a}\) = \(2 \hat{i}+3 \hat{j}-\hat{k}\), \(\bar{b}\) = \(\hat{i}-4 \hat{j}+2 \hat{k}\) find (\(\bar{a}\) + \(\bar{b}\)) × (\(\bar{a}\) – \(\bar{b}\))
Solution:

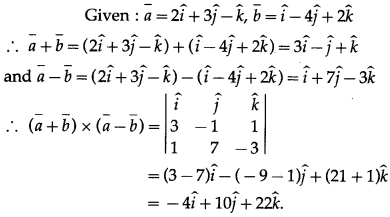
Question 2.
Find a unit vector perpendicular to the vectors \(\hat{j}+2 \hat{k}\) and \(\hat{i}+\hat{j}\).
Solution:
Let \(\bar{a}\) = \(\hat{j}+2 \hat{k}\), \(\bar{b}\) = \(\hat{i}+\hat{j}\)

Question 3.
If \(\bar{a} \cdot \bar{b}\) = \(\sqrt {3}\) and \(\bar{a} \times \bar{b}\) = \(2 \hat{i}+\hat{j}+2 \hat{k}\), find the angle between \(\bar{a}\) and \(\bar{b}\).
Solution:
Let θ be the angle between \(\bar{a}\) and \(\bar{b}\)

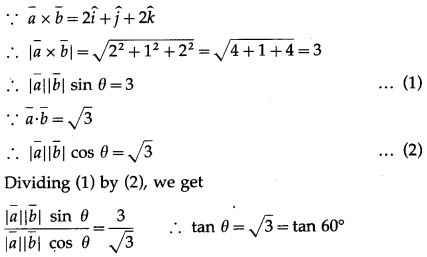
∴ θ = 60°.

Question 4.
If \(\bar{a}\) = \(2 \hat{i}+\hat{j}-3 \hat{k}\) and \(\bar{b}\) = \(\hat{i}-2 \hat{j}+\hat{k}\), find a vector of magnitude 5 perpendicular to both \(\bar{a}\) and \(\bar{b}\).
Solution:
Given : \(\bar{a}\) = \(2 \hat{i}+\hat{j}-3 \hat{k}\) and \(\bar{b}\) = \(\hat{i}-2 \hat{j}+\hat{k}\)

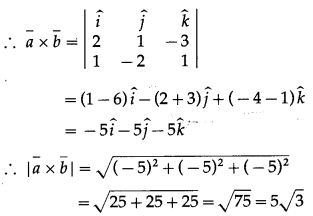
∴ unit vectors perpendicular to both the vectors \(\bar{a}\) and \(\bar{b}\).

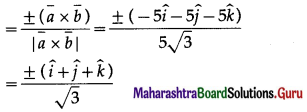
∴ required vectors of magnitude 5 units
= ±\(\frac{5}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})\)

Question 5.
Find
(i) \(\bar{u}\)∙\(\bar{v}\) if \(|\bar{u}|\) = 2, \(|\vec{v}|\) = 5, \(|\bar{u} \times \bar{v}|\) = 8
Solution:
Let θ be the angle between \(\bar{u}\) and \(\bar{v}\).
Then \(|\bar{u} \times \bar{v}|\) = 8 gives
\(|\bar{u}||\bar{v}|\) sin θ = 8
∴ 2 × 5 × sin θ = 8

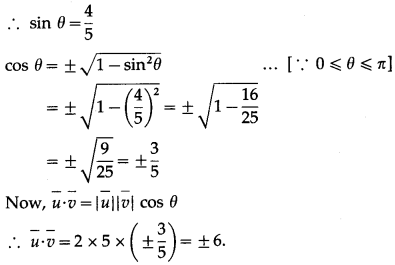
(ii) \(|\bar{u} \times \bar{v}|\) if \(|\bar{u}|\) = 10, \(|\vec{v}|\) = 2, \(\bar{u} \cdot \bar{v}\) = 12
Solution:
Let θ be the angle between \(\bar{u}\) and \(\bar{v}\).
Then \(\bar{u} \cdot \bar{v}\) = 12 gives
\(|\bar{u} \| \bar{v}|\)cos θ = 12
∴ 10 × 2 × cos θ = 12

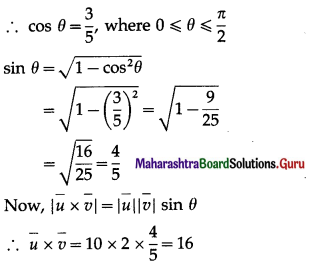
Question 6.
Prove that 2(\(\bar{a}\) – \(\bar{b}\)) × 2(\(\bar{a}\) + \(\bar{b}\)) = 8(\(\bar{a}\) × \(\bar{b}\))
Solution:

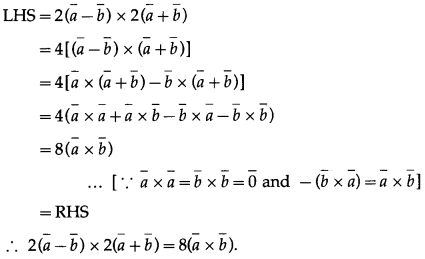
Question 7.
If \(\bar{a}\) = \(\hat{i}-2 \hat{j}+3 \hat{k}\), \(\bar{b}\) = \(4 \hat{i}-3 \hat{j}+\hat{k}\), and \(\bar{c}\) = \(\hat{i}-\hat{j}+2 \hat{k}\), verify that \(\bar{a}\) × (\(\bar{b}\) + \(\bar{c}\)) = \(\bar{a}\) × \(\bar{b}\) + \(\bar{a}\) × \(\bar{c}\)
Solution:
Given : \(\bar{a}\) = \(\hat{i}-2 \hat{j}+3 \hat{k}\), \(\bar{b}\) = \(4 \hat{i}-3 \hat{j}+\hat{k}\), \(\bar{c}\) = \(\hat{i}-\hat{j}+2 \hat{k}\)

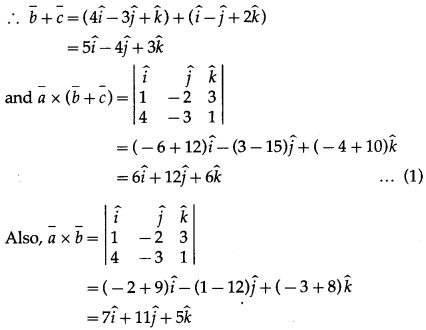
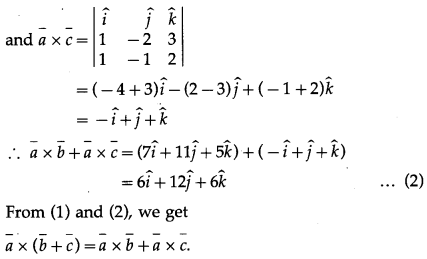
Question 8.
Find the area of the parallelogram whose adjacent sides are the vectors \(\bar{a}\) = \(2 \hat{i}-2 \hat{j}+\hat{k}\) and \(\bar{b}\) = \(\hat{i}-3 \hat{j}-3 \hat{k}\).
Solution:
Given : \(\bar{a}\) = \(2 \hat{i}-2 \hat{j}+\hat{k}\), \(\bar{b}\) = \(\hat{i}-3 \hat{j}-3 \hat{k}\)

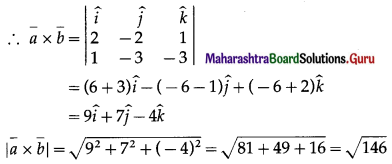
Area of the parallelogram whose adjacent sides are \(\bar{a}\) and \(\bar{b}\) is \(|\bar{a} \times \bar{b}|\) =\(\sqrt {146}\) sq units.

Question 9.
Show that vector area of a quadrilateral ABCD is \(\frac{1}{2}\) (\(\overline{A C}\) × \(\overline{B D}\)), where AC and BD are its diagonals.
Solution:
Let ABCD be a parallelogram.
Then \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{AB}}\) + \(\overline{\mathrm{BC}}\)

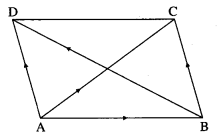
Question 10.
Find the area of parallelogram whose diagonals are determined by the vectors \(\bar{a}\) = \(3 i-\hat{j}-2 \hat{k}\), and \(\bar{b}\) = \(-\hat{i}+3 \hat{j}-3 \hat{k}\)
Solution:
Given: \(\bar{a}\) = \(3 i-\hat{j}-2 \hat{k}\), \(\bar{b}\) = \(-\hat{i}+3 \hat{j}-3 \hat{k}\)

Question 11.
If \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) are four distinct vectors such that \(\bar{a} \times \bar{b}=\bar{c} \times \bar{d}\) and \(\bar{a} \times \bar{c}=\bar{b} \times \bar{d}\), prove that \(\bar{a}\) – \(\bar{d}\) is parallel to \(\bar{b}\) – \(\bar{c}\).
Solution:
\(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) are four distinct vectors

Question 12.
If \(\bar{a}\) = \(\hat{i}+\hat{j}+\hat{k}\) and, \(\bar{c}\) = \(\hat{j}-\hat{k}\), find a vector \(\bar{b}\) satisfying \(\bar{a}\) × \(\bar{b}\) = \(\bar{c}\) and \(\bar{a} \cdot \bar{b}\) = 3
Solution:
Given \(\bar{a}\) = \(\hat{i}+\hat{j}+\hat{k}\), \(\bar{c}\) = \(\hat{j}-\hat{k}\)

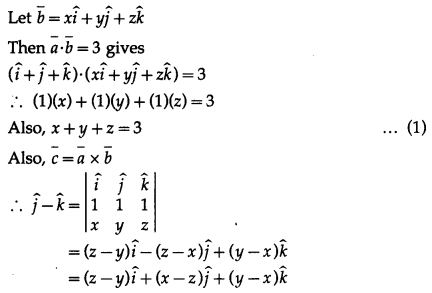
By equality of vectors,
z – y = 0 ….(2)
x – z = 1 ……(3)
y – x = -1 ……(4)
From (2), y = z.
From (3), x = 1 + z
Substituting these values of x and y in (1), we get
1 + z + z + z = 3 ∴ z = \(\frac{2}{3}\)
∴ y = z = \(\frac{2}{3}\)
∴ x = 1 + z =1 + \(\frac{2}{3}=\frac{5}{3}\)

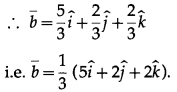
Question 13.
Find \(\bar{a}\), if \(\bar{a} \times \hat{i}+2 \bar{a}-5 \hat{j}=\overline{0}\).
Solution:

By equality of vectors
2x = 0 i.e. x = 0
2y + z – 5 = 0 … (1)
2z – y = 0 … (2)
From (2), y = 2z
Substituting y = 2z in (1), we get
4z + z = 5 ∴ z = 1
∴ y = 2z = 2(1) = 2
∴ x = 0, y = 2, z = 1
∴ \(\bar{a}=2 \hat{j}+\hat{k}\)

Question 14.
If \(|\bar{a} \cdot \bar{b}|\) = \(|\bar{a} \times \bar{b}|\) and \(\bar{a} \cdot \bar{b}\) < 0, then find the angle between \(\bar{a}\) and \(\bar{b}\)
Solution:
Let θ be the angle between \(\bar{a}\) and \(\bar{b}\).
Then \(|\bar{a} \cdot \bar{b}|\) = \(|\bar{a} \times \bar{b}|\) gives

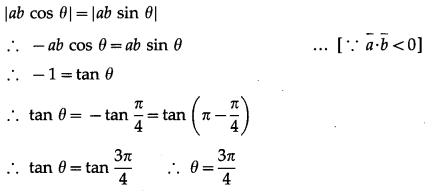
Hence, the angle between \(\bar{a}\) and \(\bar{b}\) is \(\frac{3 \pi}{4}\).

Question 15.
Prove by vector method that sin (α + β) = sinα∙cosβ+cosα∙sinβ.
Solution:

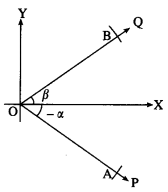
Let ∠XOP and ∠XOQ be in standard position and m∠XOP = -α, m∠XOQ = β.
Take a point A on ray OP and a point B on ray OQ such that
OA = OB = 1.
Since cos (-α) = cos α
and sin (-α) = -sin α,
A is (cos (-α), sin (-α)),
i.e. (cos α, – sin α)
B is (cos β, sin β)

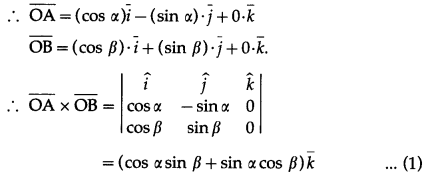
The angle between \(\overline{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\) is α + β.
Also \(\overline{\mathrm{OA}}\), \(\overline{\mathrm{OB}}\) lie in the XY-plane.
∴ the unit vector perpendicular to \(\overline{\mathrm{OA}}\) and \(\overline{\mathrm{OB}}\) is \(\bar{k}\).
∴ \(\overline{\mathrm{OA}}\) × \(\overline{\mathrm{OB}}\) = [OA∙OB sin (α + β)]\(\bar{k}\)
= sin(α + β)∙\(\bar{k}\) …(2)
∴ from (1) and (2),
sin (α + β) = sin α cos β + cos α sin β.

Question 16.
Find the direction ratios of a vector perpendicular to the two lines whose direction ratios are
(i) -2, 1, -1 and -3, -4, 1
Solution:
Let a, b, c be the direction ratios of the vector which is perpendicular to the two lines whose direction ratios are -2, 1, -1 and -3, -4, 1
∴ -2a + b – c = 0 and -3a – 4b + c = 0

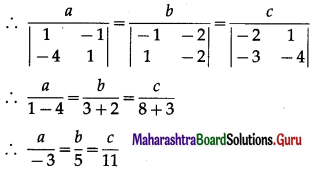
∴ the required direction ratios are -3, 5, 11
Alternative Method:
Let \(\bar{a}\) and \(\bar{b}\) be the vectors along the lines whose direction ratios are -2, 1, -1 and -3, -4, 1 respectively.
Then \(\bar{a}\) = \(-2 \hat{i}+\hat{j}-\hat{k}\) and \(\bar{b}\) = \(-3 \hat{i}-4 \hat{j}+\hat{k}\)
The vector perpendicular to both \(\bar{a}\) and \(\bar{b}\) is given by

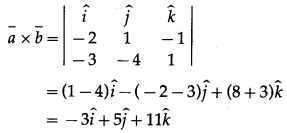
Hence, the required direction ratios are -3, 5, 11.

(ii) 1, 3, 2 and -1, 1, 2
Solution:

Question 17.
Prove that two vectors whose direction cosines are given by relations al + bm + cn = 0 and fmn + gnl + hlm = 0 are perpendicular if \(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}\) = 0
Solution:
Given, al + bm + cn = 0 …(1)
and fmn + gnl + hlm = 0 …..(2)
From (1), n = \(-\left(\frac{a l+b m}{c}\right)\) …..(3)
Substituting this value of n in equation (2), we get
(fm + gl)∙[latex]-\left(\frac{a l+b m}{c}\right)[/latex] + hlm = 0
∴ -(aflm + bfm² + agl² + bglm) + chlm = 0
∴ agl² + (af + bg – ch)lm + bfm² = 0 … (4)
Note that both l and m cannot be zero, because if l = m = 0, then from (3), we get
n = 0, which is not possible as l² + m² + n² = 1.
Let us take m # 0.
Dividing equation (4) by m², we get
ag\(\left(\frac{l}{m}\right)^{2}\) + (af + bg – ch)\(\left(\frac{l}{m}\right)\) + bf = 0 … (5)
This is quadratic equation in \(\left(\frac{l}{m}\right)\).
If l₁, m₁, n₁ and l₂, m₂, n₂ are the direction cosines of the two lines given by the equation (1) and (2), then \(\frac{l_{1}}{m_{1}}\) and \(\frac{l_{2}}{m_{2}}\) are the roots of the equation (5).
From the quadratic equation (5), we get

i.e. if \(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}\) = 0.

Question 18.
If A(1, 2, 3) and B(4, 5, 6) are two points, then find the foot of the perpendicular from the point B to the line joining the origin and point A.
Solution:

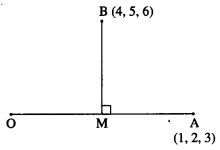
Let M be the foot of the perpendicular drawn from B to the line joining O and A.
Let M = (x, y, z)
OM has direction ratios x – 0, y – 0, z – 0 = x, y, z
OA has direction ratios 1 – 0, 2 – 0, 3 – 0 = 1, 2, 3
But O, M, A are collinear.
∴ \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) = k …(Let)
∴ x = k, y = 2k, z = 3k
∴ M = (k, 2k, 3k)
∵ BM has direction ratios
k – 4, 2k – 5, 3k – 6
BM is perpendicular to OA
∴ (l)(k – 4) + 2(2k – 5) + 3(3k – 6)
∴ = k – 4 + 4k – 10 + 9k – 18 = 0
∴ 14k = 32
∴ k = \(\frac{16}{7}\)
∴ M = (k, 2k, 3k) = (\(\frac{16}{7}, \frac{32}{7}, \frac{48}{7}\))