Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 7 Conic Sections Ex 7.2 Questions and Answers.
11th Maths Part 1 Conic Sections Exercise 7.2 Questions And Answers Maharashtra Board
Question 1.
Find the
(i) lengths of the principal axes
(ii) co-ordinates of the foci
(iii) equations of directrices
(iv) length of the latus rectum
(v) distance between foci
(vi) distance between directrices of the ellipse:
(a) \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
(b) 3x2 + 4y2 = 12
(c) 2x2 + 6y2 = 6
(d) 3x2 + 4y2 = 1
Solution:
(a) Given equation of the ellipse is \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 25 and b2 = 9
a = 5 and b = 3
Since a > b,
X-axis is the major axis and Y-axis is the minor axis.
(i) Length of major axis = 2a = 2(5) = 10
Length of minor axis = 2b = 2(3) = 6
Lengths of the principal axes are 10 and 6.
(ii) We know that e = \(\frac{\sqrt{a^{2}-b^{2}}}{a}\)
= \(\frac{\sqrt{25-9}}{5}\)
= \(\frac{\sqrt{16}}{5}\)
= \(\frac{4}{5}\)
Co-ordinates of the foci are S(ae, 0) and S'(-ae, 0),
i.e., S(5(\(\frac{4}{5}\)), 0) and S'(-5(\(\frac{4}{5}\)), 0)
i.e., S(4, 0) and S'(-4, 0)
(iii) Equations of the directrices are x = ±\(\frac{\mathrm{a}}{\mathrm{e}}\)
= \(\pm \frac{5}{\frac{4}{5}}\)
= \(\pm \frac{25}{4}\)
(iv) Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(3)^{2}}{5}=\frac{18}{5}\)
(v) Distance between foci = 2ae
= 2(5)(\(\frac{4}{5}\))
= 8
(vi) Distance between directrices = \(\frac{2 \mathrm{a}}{\mathrm{e}}\)
= \(\frac{2(5)}{\frac{4}{5}}\)
= \(\frac{25}{2}\)
![]()
(b) Given equation of the ellipse is 3x2 + 4y2 = 12
\(\frac{x^{2}}{4}+\frac{y^{2}}{3}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 4 and b2 = 3
a = 2 and b = √3
Since a > b,
X-axis is the major axis and Y-axis is the minor axis.
(i) Length of major axis = 2a = 2(2) = 4
Length of minor axis = 2b = 2√3
Lengths of the principal axes are 4 and 2√3.
(ii) We know that e = \(\frac{\sqrt{a^{2}-b^{2}}}{a}\)
= \(\frac{\sqrt{4-3}}{2}\)
= \(\frac{1}{2}\)
Co-ordinates of the foci are S(ae, 0) and S'(-ae, 0),
i.e., S(2(\(\frac{1}{2}\)), 0) and S'(-2(\(\frac{1}{2}\)), 0)
i.e., S(1, 0) and S'(-1, 0)
(iii) Equations of the directrices are x = ±\(\frac{\mathrm{a}}{\mathrm{e}}\)
= \(\pm \frac{2}{\frac{1}{2}}\)
= ±4
(iv) Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(\sqrt{3})^{2}}{2}=3\)
(v) Distance between foci = 2ae = 2(2)(\(\frac{1}{2}\)) = 2
(vi) Distance between directrices = \(\frac{2 \mathrm{a}}{\mathrm{e}}\)
= \(\frac{2(2)}{\frac{1}{2}}\)
= 8
(c) Given equation of the ellipse is 2x2 + 6y2 = 6
\(\frac{x^{2}}{3}+\frac{y^{2}}{1}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 3 and b2 = 1
a = √3 and b = 1
Since a > b,
X-axis is the major axis and Y-axis is the minor axis.
(i) Length of major axis = 2a = 2√3
Length of minor axis = 2b = 2(1) = 2
Lengths of the principal axes are 2√3 and 2.
(ii) We know that e = \(\frac{\sqrt{a^{2}-b^{2}}}{a}\)
= \(\frac{\sqrt{3-1}}{\sqrt{3}}\)
= \(\frac{\sqrt{2}}{\sqrt{3}}\)
Co-ordinates of the foci are S(ae, 0) and S'(-ae, 0),
i.e., S(√3(\(\frac{\sqrt{2}}{\sqrt{3}}\)), o) and S'(-√3(\(\frac{\sqrt{2}}{\sqrt{3}}\)), 0)
i.e., S(√2, 0) and S'(-√2, 0)
(iii) Equations of the directrices are x = ±\(\frac{a}{e}\),
= \(\pm \frac{\sqrt{3}}{\frac{\sqrt{2}}{\sqrt{3}}}\)
= \(\pm \frac{3}{\sqrt{2}}\)
(iv) Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2(1)^{2}}{\sqrt{3}}=\frac{2}{\sqrt{3}}\)
(v) Distance between foci = 2ae
= \(2(\sqrt{3})\left(\frac{\sqrt{2}}{\sqrt{3}}\right)\)
= 2√2
(vi) Distance between directrices = \(\frac{2 \mathrm{a}}{\mathrm{e}}\)
= \(\frac{2 \sqrt{3}}{\frac{\sqrt{2}}{\sqrt{3}}}\)
= \(\frac{2 \times 3}{\sqrt{2}}\)
= 3√2
(d) Given equation of the ellipse is 3x2 + 4y = 1.
\(\frac{x^{2}}{\frac{1}{3}}+\frac{y^{2}}{\frac{1}{4}}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = \(\frac{1}{3}\) and b2 = \(\frac{1}{4}\)
a = \(\frac{1}{\sqrt{3}}\) and b = \(\frac{1}{2}\)
Since a > b,
X-axis is the major axis and Y-axis is the minor axis.
(i) Length of major axis = 2a = 2(\(\frac{1}{\sqrt{3}}\)) = \(\frac{2}{\sqrt{3}}\)
Length of minor axis = 2b = 2(\(\frac{1}{2}\)) = 1
Lengths of the principal axes are \(\frac{2}{\sqrt{3}}\) and 1.
(ii) We know that e = \(\frac{\sqrt{a^{2}-b^{2}}}{a}\)
e = \(\frac{\sqrt{\frac{1}{3}-\frac{1}{4}}}{\frac{1}{\sqrt{3}}}=\frac{\sqrt{\frac{1}{12}}}{\frac{1}{\sqrt{3}}}=\sqrt{\frac{3}{12}}=\sqrt{\frac{1}{4}}=\frac{1}{2}\)
Co-ordinates of the foci are S(ae, 0) and S'(-ae, 0),
i.e., S\(\left(\frac{1}{\sqrt{3}}\left(\frac{1}{2}\right), 0\right)\) and S’\(\left(-\frac{1}{\sqrt{3}}\left(\frac{1}{2}\right), 0\right)\)
i.e., S(\(\frac{1}{2 \sqrt{3}}\), 0) and S'(-\(\frac{1}{2 \sqrt{3}}\), 0)
(iii) Equations of the directrices are x = ±\(\frac{a}{e}\),
= \(\pm \frac{\frac{1}{\sqrt{3}}}{\frac{1}{2}}\)
= \(\pm \frac{2}{\sqrt{3}}\)
(iv) Length of latus rectum = \(\frac{2 b^{2}}{a}\)
= \(\frac{2\left(\frac{1}{2}\right)^{2}}{\frac{1}{\sqrt{3}}}\)
= \(\frac{\sqrt{3}}{2}\)
(v) Distance between foci = 2ae
= \(2\left(\frac{1}{\sqrt{3}}\right)\left(\frac{1}{2}\right)\)
= \(\frac{1}{\sqrt{3}}\)
(vi) Distance between directrices = \(\frac{2 a}{e}\)
= \(\frac{2\left(\frac{1}{\sqrt{3}}\right)}{\frac{1}{2}}\)
= \(\frac{4}{\sqrt{3}}\)
![]()
Question 2.
Find the equation of the ellipse in standard form if
(i) eccentricity = \(\frac{3}{8}\) and distance between its foci = 6.
(ii) the length of the major axis is 10 and the distance between foci is 8.
(iii) distance between directrices is 18 and eccentricity is \(\frac{1}{3}\).
(iv) minor axis is 16 and eccentricity is \(\frac{1}{3}\).
(v) the distance between foci is 6 and the distance between directrices is \(\frac{50}{3}\).
(vi) the latus rectum has length 6 and foci are (±2, 0).
(vii) passing through the points (-3, 1) and (2, -2).
(viii) the distance between its directrices is 10 and which passes through (-√5, 2).
(ix) eccentricity is \(\frac{2}{3}\) and passes through (2, \(\frac{-5}{3}\)).
Solution:
(i) Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
Given, eccentricity (e) = \(\frac{3}{8}\)
Distance between foci = 2ae
Given, distance between foci = 6
2ae = 6

The required equation of ellipse is \(\frac{x^{2}}{64}+\frac{y^{2}}{55}=1\).
(ii) Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
Length of major axis = 2a
Given, length of major axis = 10
2a = 10
a = 5
a2 = 25
Distance between foci = 2ae
Given, distance between foci = 8
2ae = 8
2(5)e = 8

The required equation of ellipse is \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\).
(iii) Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
Given, eccentricity (e) = \(\frac{1}{3}\)
Distance between directrices = \(\frac{2a}{e}\)
Given, distance between directrices = 18

The required equation of ellipse is \(\frac{x^{2}}{9}+\frac{y^{2}}{8}=1\)
(iv) Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
Length of minor axis = 2b
Given, length of minor axis = 16
2b = 16
b = 8
b2 = 64
Given, eccentricity (e) = \(\frac{1}{3}\)
Now, b2 = a2 (1 – e2)
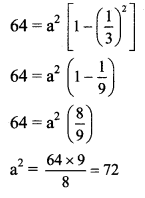
The required equation of ellipse is \(\frac{x^{2}}{72}+\frac{y^{2}}{64}=1\).
(v) Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
Distance between foci = 2ae
Given, distance between foci = 6
2ae = 6
ae = 3
a = \(\frac{3}{e}\) …….(i)
Distance between directrices = \(\frac{2a}{e}\)
Given, distance between directrices = \(\frac{50}{3}\)

The required equation of ellipse is \(\frac{x^{2}}{25}+\frac{y^{2}}{16}=1\).
![]()
(vi) Given, the length of the latus rectum is 6, and co-ordinates of foci are (±2, 0).
The foci of the ellipse are on the X-axis.
Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
Length of latus rectum = \(\frac{2 b^{2}}{a}\)
\(\frac{2 b^{2}}{a}\) = 6
b2 = 3a …..(i)
Co-ordinates of foci are (±ae, 0)
ae = 2
a2e2 = 4 …..(ii)
Now, b2 = a2 (1 – e2)
b2 = a2 – a2 e2
3a = a2 – 4 …..[From (i) and (ii)]
a2 – 3a – 4 = 0
a2 – 4a + a – 4 = 0
a(a – 4) + 1(a – 4) = 0
(a – 4) (a + 1) = 0
a – 4 = 0 or a + 1 = 0
a = 4 or a = -1
Since a = -1 is not possible,
a = 4
a2 = 16
Substituting a = 4 in (i), we get
b2 = 3(4) = 12
The required equation of ellipse is \(\frac{x^{2}}{16}+\frac{y^{2}}{12}=1\).
(vii) Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
The ellipse passes through the points (-3, 1) and (2, -2).
Substituting x = -3 and y = 1 in equation of ellipse, we get
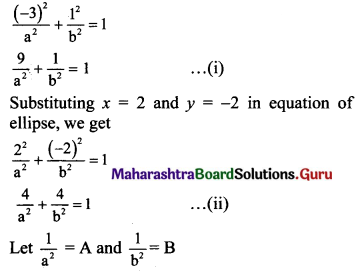
Equations (i) and (ii) become
9A + B = 1 …..(iii)
4A + 4B = 1 …..(iv)
Multiplying (iii) by 4, we get
36A + 4B = 4 …..(v)
Subtracting (iv) from (v), we get
32A = 3
A = \(\frac{3}{32}\)
Substituting A = \(\frac{3}{32}\) in (iv), we get
4(\(\frac{3}{32}\)) + 4B = 1
\(\frac{3}{8}\) + 4B = 1
4B = 1 – \(\frac{3}{8}\)
4B = \(\frac{5}{8}\)
B = \(\frac{5}{32}\)

(viii) Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
Distance between directrices = \(\frac{2 a}{e}\)
Given, distance between directrices = 10
\(\frac{2 a}{e}\) = 10
a = 5e …..(i)
The ellipse passes through (-√5, 2).
Substituting x = -√5 and y = 2 in equation of ellipse, we get

b2 = 15(\(\frac{2}{5}\))
b2 = 6
The required equation of ellipse is \(\frac{x^{2}}{15}+\frac{y^{2}}{6}=1\).
(ix) Let the required equation of ellipse be \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), where a > b.
Given, eccentricity (e) = \(\frac{2}{3}\)
The ellipse passes through (2, \(\frac{-5}{3}\)).
Substituting x = 2 and y = \(\frac{-5}{3}\) in equation of ellipse, we get

The required equation of ellipse is \(\frac{x^{2}}{9}+\frac{y^{2}}{5}=1\).
![]()
Question 3.
Find the eccentricity of an ellipse, if the length of its latus rectum is one-third of its minor axis.
Solution:
Let the equation of ellipse be \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), where a > b.
Length of latus rectum = \(\frac{2 b^{2}}{a}\)
Length of minor axis = 2b
According to the given condition,
Length of latus rectum = \(\frac{1}{3}\) (Minor axis)

Question 4.
Find the eccentricity of an ellipse, if the distance between its directrices is three times the distance between its foci.
Solution:
Let the required equation of ellipse be \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), where a > b.
Distance between directrices = \(\frac{2 \mathrm{a}}{\mathrm{e}}\)
Distance between foci = 2ae
According to the given condition,
distance between directrices = 3(distance between foci)
\(\frac{2 \mathrm{a}}{\mathrm{e}}\) = 3(2ae)
\(\frac{1}{\mathrm{e}}\) = 3e
\(\frac{1}{3}\) = e2
e = \(\frac{1}{\sqrt{3}}\) ……[∵ 0 < e < 1]
Eccentricity of the ellipse is \(\frac{1}{\sqrt{3}}\)
![]()
Question 5.
Show that the product of the lengths of the perpendicular segments drawn from the foci to any tangent line to the ellipse \(\frac{x^{2}}{25}+\frac{y^{2}}{16}=1\) is equal to 16.
Solution:
Given equation of the ellipse is \(\frac{x^{2}}{25}+\frac{y^{2}}{16}=1\).
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 25, b2 = 16
a = 5, b = 4


Question 6.
A tangent having slope \(\left(-\frac{1}{2}\right)\) the ellipse 3x2 + 4y2 = 12 intersects the X and Y axes in the points A and B respectively. If O is the origin, find the area of the triangle AOB.
Solution:
Given equation of the ellipse is 3x2 + 4y2 = 12.
\(\frac{x^{2}}{4}+\frac{y^{2}}{3}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 4, b2 = 3
Equations of tangents to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
Here, m = \(-\frac{1}{2}\)
Equations of the tangents are
y = \(\frac{-1}{2} x \pm \sqrt{4\left(-\frac{1}{2}\right)^{2}+3}=\frac{-1}{2} x \pm 2\)
2y = -x ± 4
x + 2y ± 4 = 0
Consider the tangent x + 2y – 4 = 0
Let this tangent intersect the X-axis at A(x1, 0) and Y-axis at B(0, y1).
x1 + 0 – 4 = 0 and 0 + 2y1 – 4 = 0
x1 = 4 and y1 = 2
A = (4, 0) and B = (0, 2)
l(OA) = 4 and l(OB) = 2
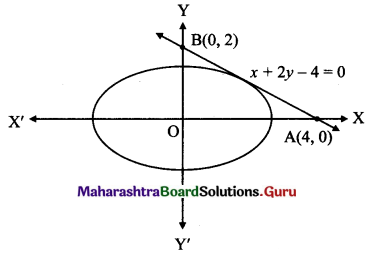
Area of ∆AOB = \(\frac{1}{2}\) × l(OA) × l(OB)
= \(\frac{1}{2}\) × 4 × 2
= 4 sq.units
Question 7.
Show that the line x – y = 5 is a tangent to the ellipse 9x2 + 16y2 = 144. Find the point of contact.
Solution:
Given equation of the ellipse is 9x2 + 16y2 = 144
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 16 and b2 = 9
Given equation of line is x – y = 5, i.e., y = x – 5
c2 = a2 m2 + b2
Comparing this equation with y = mx + c, we get
m = 1 and c = -5
For the line y = mx + c to be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=\)1, we must have
c2 = a2 m2 + b2
c2 = (-5)2 = 25
a2 m2 + b2 = 16(1)2 + 9 = 16 + 9 = 25 = c2
The given line is a tangent to the given ellipse and point of contact
= \(\left(\frac{-\mathrm{a}^{2} \mathrm{~m}}{\mathrm{c}}, \frac{\mathrm{b}^{2}}{\mathrm{c}}\right)\)
= \(\left(\frac{(-16)(1)}{-5}, \frac{9}{-5}\right)\)
= \(\left(\frac{16}{5}, \frac{-9}{5}\right)\)
![]()
Question 8.
Show that the line 8y + x = 17 touches the ellipse x2 + 4y2 = 17. Find the point of contact.
Solution:
Given equation of the ellipse is x2 + 4y2 = 17.
\(\frac{x^{2}}{17}+\frac{y^{2}}{\frac{17}{4}}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 17 and b2 = \(\frac{17}{4}\)
Given equation of line is 8y + x = 17,
y = \(\frac{-1}{8} x+\frac{17}{8}\)
Comparing this equation with y = mx + c, we get
m = \(\frac{-1}{8}\) and c = \(\frac{17}{8}\)
For the line y = mx + c to be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=\)1, we must have

Question 9.
Determine whether the line x + 3y√2 = 9 is a tangent to the ellipse \(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\). If so, find the co-ordinates of the point of contact.
Solution:
Given equation of the ellipse is \(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 9 and b2 = 4
Given equation of line is x + 3y√2 = 9,
i.e., y = \(\frac{-1}{3 \sqrt{2}} x+\frac{3}{\sqrt{2}}\)
Comparing this equation with y = mx + c, we get
m = \(\frac{-1}{3 \sqrt{2}}\) and c = \(\frac{3}{\sqrt{2}}\)
For the line y = mx + c to be a tangent to the ellipse \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=\)1, we must have

Question 10.
Find k, if the line 3x + 4y + k = 0 touches 9x2 + 16y2 = 144.
Solution:
Given equation of the ellipse is 9x2 + 16y2 = 144.
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 16 and b2 = 9
Given equation of line is 3x + 4y + k = 0,
i.e., y = \(-\frac{3}{4} x-\frac{k}{4}\)
Comparing this equation with y = mx + c, we get
m = \(\frac{-3}{4}\) and c = \(\frac{-\mathrm{k}}{4}\)
For the line y = mx + c to be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=\)1, we must have
c2 = a2 m2 + b2
\(\left(\frac{-k}{4}\right)^{2}=16\left(\frac{-3}{4}\right)^{2}+9\)
\(\frac{\mathrm{k}^{2}}{16}\) = 9 + 9
\(\frac{\mathrm{k}^{2}}{16}\) = 18
k2 = 288
k = ±12√2
![]()
Question 11.
Find the equations of the tangents to the ellipse:
(i) \(\frac{x^{2}}{5}+\frac{y^{2}}{4}=1\) passing through the point (2, -2).
(ii) 4x2 + 7y2 = 28 from the point (3, -2).
(iii) 2x2 + y2 = 6 from the point (2, 1).
(iv) x2 + 4y2 = 9 which are parallel to the line 2x + 3y – 5 = 0.
(v) \(\frac{x^{2}}{25}+\frac{y^{2}}{4}=1\) which are parallel to the line x + y + 1 = 0.
(vi) 5x2 + 9y2 = 45 which are ⊥ to the line 3x + 2y + 1 = 0.
(vii) x2 + 4y2 = 20 which are ⊥ to the line 4x + 3y = 7.
Solution:
(i) Given equation of the ellipse is \(\frac{x^{2}}{5}+\frac{y^{2}}{4}=1\).
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 5 and b2 = 4
Equations of tangents to the ellipse \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
Since (2, -2) lies on both the tangents,
-2 = 2m ±\(\sqrt{5 m^{2}+4}\)
-2 – 2m = ±\(\sqrt{5 m^{2}+4}\)
Squaring both the sides, we get
4m2 + 8m + 4 = 5m2 + 4
m2 – 8m = 0
m(m – 8) = 0
m = 0 or m = 8
These are the slopes of the required tangents.
By slope point form y – y1 = m(x – x1),
the equations of the tangents are
y + 2 = 0(x – 2) and y + 2 = 8(x – 2)
y + 2 = 0 and y + 2 = 8x – 16
y + 2 = 0 and 8x – y – 18 = 0
(ii) Given equation of the ellipse is 4x2 + 7y2 = 28.
\(\frac{x^{2}}{7}+\frac{y^{2}}{4}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 7 and b2 = 4
Equations of tangents to the ellipse \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
Since (3, -2) lies on both the tangents,
-2 = 3m ± \(\sqrt{7 \mathrm{~m}^{2}+4}\)
-2 – 3m = ±\(\sqrt{7 \mathrm{~m}^{2}+4}\)
Squaring both the sides, we get
9m2 + 12m + 4 = 7m2 + 4
2m2 + 12m = 0
2m(m + 6) = 0
m = 0 or m = -6
These are the slopes of the required tangents.
By slope point form y – y1 = m(x – x1),
the equations of the tangents are
y + 2 = 0(x – 3) and y + 2 = -6(x – 3)
y + 2 = 0 and y + 2 = -6x + 18
y + 2 = 0 and 6x + y – 16 = 0
![]()
(iii) Given equation of the ellipse is 2x2 + y2 = 6.
\(\frac{x^{2}}{3}+\frac{y^{2}}{6}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 3 and b2 = 6
Equations of tangents to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
Since (2, 1) lies on both the tangents,
1 = 2m ± \(\sqrt{3 m^{2}+6}\)
1 – 2m = ±\(\sqrt{3 m^{2}+6}\)
Squaring both the sides, we get
1 – 4m + 4m2 = 3m2 + 6
m2 – 4m – 5 = 0
(m – 5)(m + 1) = 0
m = 5 or m = -1
These are the slopes of the required tangents.
By slope point form y – y1 = m(x – x1),
the equations of the tangents are
y – 1 = 5(x – 2) and y – 1 = -1(x – 2)
y – 1 = 5x – 10 and y – 1 = -x + 2
5x – y – 9 = 0 and x + y – 3 = 0
(iv) Given equation of the ellipse is x2 + 4y2 = 9.
\(\frac{x^{2}}{9}+\frac{y^{2}}{\frac{9}{4}}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 9 and b2 = \(\frac{9}{4}\)
Slope of the line 2x + 3y – 5 = 0 is \(\frac{-2}{3}\).
Since the given line is parallel to the required tangents, slope of the required tangents is
m = \(\frac{-2}{3}\)
Equations of tangents to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) having slope m are

(v) Given equation of the ellipse is \(\frac{x^{2}}{25}+\frac{y^{2}}{4}=1\).
Comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 25 and b2 = 4
Slope of the given line x + y + 1 = 0 is -1.
Since the given line is parallel to the required tangents,
the slope of the required tangents is m = -1.
Equations of tangents to the ellipse
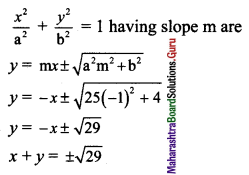
(vi) Given equation of the ellipse is 5x2 + 9y2 = 45.
\(\frac{x^{2}}{9}+\frac{y^{2}}{5}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 9 and b2 = 5
Slope of the given line 3x + 2y + 1 = 0 is \(\frac{-3}{2}\)
Since the given line is perpendicular to the required tangents, slope of the required tangents is
m = \(\frac{2}{3}\)
Equations of tangents to the ellipse
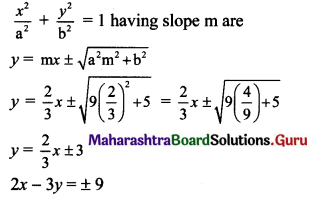
(vii) Given equation of the ellipse is x2 + 4y2 = 20.
\(\frac{x^{2}}{20}+\frac{y^{2}}{5}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 20 and b2 = 5
Slope of the given line 4x + 3y = 7 is \(\frac{-4}{3}\).
Since the given line is perpendicular to the required tangents,
slope of the required tangents is m = \(\frac{3}{4}\).
Equations of tangents to the ellipse \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
y = \(\frac{3}{4} x \pm \sqrt{20\left(\frac{3}{4}\right)^{2}+5}\)
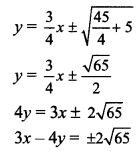
![]()
Question 12.
Find the equation of the locus of a point, the tangents from which to the ellipse 3x2 + 5y2 = 15 are at right angles.
Solution:
Given equation of the ellipse is 3x2 + 5y2 = 15.
\(\frac{x^{2}}{5}+\frac{y^{2}}{3}=1\)
Comparing this equation with \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\), we get
a2 = 5 and b2 = 3
Equations of tangents to the ellipse \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{y^{2}}{\mathrm{~b}^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
y = mx ± \(\sqrt{5 m^{2}+3}\)
y – mx =±\(\sqrt{5 m^{2}+3}\)
Squaring both the sides, we get
y2 – 2mxy + m2x2 = 5m2 + 3
(x2 – 5) m2 – 2xym + (y2 – 3) = 0
The roots m1 and m2 of this quadratic equation are the slopes of the tangents.
m1m2 = \(\frac{y^{2}-3}{x^{2}-5}\)
Since the tangents are at right angles,
m1m2 = -1
\(\frac{y^{2}-3}{x^{2}-5}=-1\)
y2 – 3 = -x2 + 5
x2 + y2 = 8, which is the required equation of the locus.
Alternate method:
The locus of the point of intersection of perpendicular tangents is the director circle of an ellipse.
The equation of the director circle of an ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) is x2 + y2 = a2 + b2
Here, a2 = 5 and b2 = 3
x2 + y2 = 5 + 3
x2 + y2 = 8, which is the required equation of the locus.
Question 13.
Tangents are drawn through a point P to the ellipse 4x2 + 5y2 = 20 having inclinations θ1 and θ2 such that tan θ1 + tan θ2 = 2. Find the equation of the locus of P.
Solution:
Given equation of the ellipse is 4x2 + 5y2 = 20.
\(\frac{x^{2}}{5}+\frac{y^{2}}{4}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 5 and b2 = 4
Since inclinations of tangents are θ1 and θ2,
m1 = tan θ1 and m2 = tan θ2
Equation of tangents to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
y = mx ± \(\sqrt{5 \mathrm{~m}^{2}+4}\)
y – mx = ± \(\sqrt{5 \mathrm{~m}^{2}+4}\)
Squaring both the sides, we get
y2 – 2mxy + m2x2 = 5m2 + 4
(x2 – 5)m2 – 2xym + (y2 – 4) = 0
The roots m1 and m2 of this quadratic equation are the slopes of the tangents.
m1 + m2 = \(\frac{-(-2 x y)}{x^{2}-5}=\frac{2 x y}{x^{2}-5}\)
Given, tan θ1 + tan θ2 = 2
m1 + m2 = 2
\(\frac{2 x y}{x^{2}-5}\) = 2
xy = x2 – 5
x2 – xy – 5 = 0, which is the required equation of the locus of P.
![]()
Question 14.
Show that the locus of the point of intersection of tangents at two points on an ellipse, whose eccentric angles differ by a constant, is an ellipse.
Solution:
Let P(θ1) and Q(θ2) be any two points on the given ellipse such that θ1 – θ2 = k, where k is a constant.
The equation of the tangent at point P(θ1) is
\(\frac{x \cos \theta_{1}}{\mathrm{a}}+\frac{y \sin \theta_{1}}{\mathrm{~b}}=1\) ……(i)
The equation of the tangent at point Q(θ2) is
\(\frac{x \cos \theta_{2}}{\mathrm{a}}+\frac{y \sin \theta_{2}}{\mathrm{~b}}=1\) ……(ii)
Multiplying equation (i) by cos θ2 and equation (ii) by cos θ1 and subtracting, we get
\(\frac{y}{b}\) (sin θ1 cos θ2 – sin θ2 cos θ1) = cos θ2 – cos θ1


Question 15.
P and Q are two points on the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) with eccentric angles θ1 and θ2. Find the equation of the locus of the point of intersection of the tangents at P and Q if θ1 + θ2 = \(\frac{\pi}{2}\).
Solution:
Given equation of the ellipse is \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\).
θ1 and θ2 are the eccentric angles of a tangent.
Equation of tangent at point P is
\(\frac{x}{a} \cos \theta_{1}+\frac{y}{b} \sin \theta_{1}=1\) ……(i)
Equation of tangent at point Q is
\(\frac{x}{a} \cos \theta_{2}+\frac{y}{b} \sin \theta_{2}=1\) ………(ii)
θ1 + θ2 = \(\frac{\pi}{2}\) …..[Given]

i.e., points P and Q coincide, which is not possible, as P and Q are two different points.
cos θ1 – sin θ1 ≠ 0
Dividing equation (iii) by (cos θ1 – sin θ1), we get
\(\frac{x_{1}}{a}=\frac{y_{1}}{b}\)
bx1 – ay1 = 0
bx – ay = 0, which is the required equation of locus of point M.
Question 16.
The eccentric angles of two points P and Q of the ellipse 4x2 + y2 = 4 differ by \(\frac{2 \pi}{3}\). Show that the locus of the point of intersection of the tangents at P and Q is the ellipse 4x2 + y2 = 16.
Solution:
Given equation of the ellipse is 4x2 + y2 = 4.
\(\frac{x^{2}}{1}+\frac{y^{2}}{4}=1\)
Let P(θ1) and Q(θ2) be any two points on the given ellipse such that
θ1 – θ2 = \(\frac{2 \pi}{3}\)
The equation of the tangent at point P(θ1) is
\(\frac{x \cos \theta_{1}}{1}+\frac{y \sin \theta_{1}}{2}=1\) ……(i)
The equation of the tangent at point Q(θ2) is
\(\frac{x \cos \theta_{2}}{1}+\frac{y \sin \theta_{2}}{2}=1\)
Multiplying equation (i) by cos θ2 and equation (ii) by cos θ1 and subtracting, we get
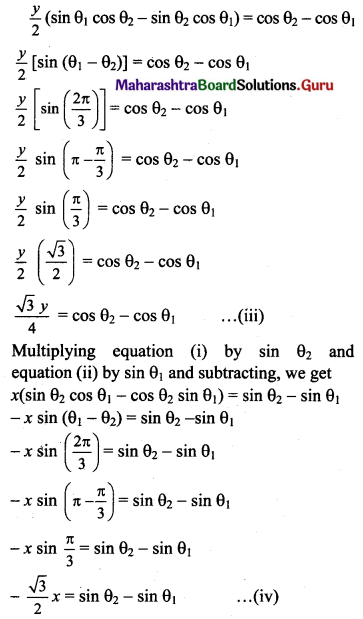

![]()
Question 17.
Find the equations of the tangents to the ellipse \(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\), making equal intercepts on co-ordinate axes.
Solution:
Given equation of the ellipse is \(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 16 and b2 = 9
Since the tangents make equal intercepts on the co-ordinate axes,
m = -1.
Equations of tangents to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) having slope m are
y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
y = -x ± \(\sqrt{16(-1)^{2}+9}\)
y = -x ± \(\sqrt{25}\)
x + y = ±5
Question 18.
A tangent having slope \(\left(-\frac{1}{2}\right)\) to the ellipse 3x2 + 4y2 = 12 intersects the X and Y axes in the points A and B respectively. If O is the origin, find the area of the triangle AOB.
Solution:
The equation of the ellipse is 3x2 + 4y2 = 12
\(\frac{x^{2}}{4}+\frac{y^{2}}{3}=1\)
Comparing with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\), we get
a2 = 4, b2 = 3
The equation of tangent with slope m is
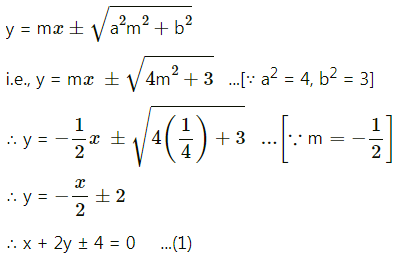
It meets X axis at A
∴ for A, put y = 0 in equation (1), we get,
x = ±4
∴ A = (±4, 0)
Similarly, B = (0, ±2)
∴ OA = 4, OB = 2
∴ Area of ΔOAB = \(\frac{1}{2}\) × OA × OB
= \(\frac{1}{2}\) × 4 × 2
= 4 sq. units
Class 11 Maharashtra State Board Maths Solution