Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 6 Circle Ex 6.3 Questions and Answers.
11th Maths Part 1 Circle Exercise 6.3 Questions And Answers Maharashtra Board
Question 1.
Write the parametric equations of the circles:
(i) x2 + y2 = 9
(ii) x2 + y2 + 2x – 4y – 4 = 0
(iii) (x – 3)2 + (y + 4)2 = 25
Solution:
(i) Given equation of the circle is
x2 + y2 = 9
⇒ x2 + y2 = 32
Comparing this equation with x2 + y2 = r2, we get r = 3
The parametric equations of the circle in terms of θ are
x = r cos θ and y = r sin θ
⇒ x = 3 cos θ and y = 3 sin θ
(ii) Given equation of the circle is
x2 + y2 + 2x – 4y – 4 = 0
⇒ x2 + 2x + y2 – 4y – 4 = 0
⇒ x2 + 2x + 1 – 1 + y2 – 4y + 4 – 4 – 4 = 0
⇒ (x2 + 2x + 1 ) + (y2 – 4y + 4) – 9 = 0
⇒ (x + 1)2 + (y – 2)2 = 9
⇒ (x + 1)2 + (y – 2)2 = 32
Comparing this equation with (x – h)2 + (y – k)2 = r2, we get
h = -1, k = 2 and r = 3
The parametric equations of the circle in terms of θ are
x = h + r cos θ and y = k + r sin θ
⇒ x = -1 + 3 cos θ and y = 2 + 3 sin θ
(iii) Given equation of the circle is
(x – 3)2 + (y + 4)2 = 25
⇒ (x – 3)2 + (y + 4)2 = 52
Comparing this equation with (x – h)2 + (y – k)2 = r2, we get
h = 3, k = -4 and r = 5
The parametric equations of the circle in terms of θ are
x = h + r cos θ and y = k + r sin θ
⇒ x = 3 + 5 cos θ and y = -4 + 5 sin θ
![]()
Question 2.
Find the parametric representation of the circle 3x2 + 3y2 – 4x + 6y – 4 = 0.
Solution:
Given equation of the circle is 3x2 + 3y2 – 4x + 6y – 4 = 0
Dividing throughout by 3, we get

Comparing this equation with (x – h)2 + (y – k)2 = r2, we get
h = \(\frac{2}{3}\), k = -1 and r = \(\frac{5}{3}\)
The parametric representation of the circle in terms of θ are
x = h + r cos θ and y = k + r sin θ
⇒ x = \(\frac{2}{3}\) + \(\frac{5}{3}\) cos θ and y = -1 + \(\frac{5}{3}\) sin θ
Question 3.
Find the equation of a tangent to the circle x2 + y2 – 3x + 2y = 0 at the origin.
Solution:
Given equation of the circle is x2 + y2 – 3x + 2y = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -3, 2f = 2, c = 0
⇒ g = \(-\frac{3}{2}\), f = 1, c = 0
The equation of a tangent to the circle
x2 + y2 + 2gx + 2fy + c = 0 at (x1, y1) is xx1 +yy1 + g(x + x1) + f(y + y1) + c = 0
The equation of the tangent at (0, 0) is
x(0) + y(0) + (\(-\frac{3}{2}\)) (x + 0) + 1(y + 0) + 0 = 0
⇒ \(-\frac{3}{2}\)x + y = 0
⇒ 3x – 2y = 0
![]()
Question 4.
Show that the line 7x – 3y – 1 = 0 touches the circle x2 + y2 + 5x – 7y + 4 = 0 at point (1, 2).
Solution:
Given equation of the circle is x2 + y2 + 5x – 7y + 4 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = 5, 2f = -7, c = 4
⇒ g = \(\frac{5}{2}\), f = \(\frac{-7}{2}\), c = 4
The equation of a tangent to the circle x2 + y2 + 2gx + 2fy + c = 0 at (x1, y1) is
xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
The equation of the tangent at (1, 2) is
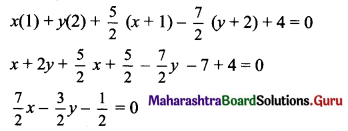
7x – 3y – 1 = 0, which is same as the given line.
The line 7x – 3y – 1 = 0 touches the given circle at (1, 2).
Question 5.
Find the equation of tangent to the circle x2 + y2 – 4x + 3y + 2 = 0 at the point (4, -2).
Solution:
Given equation of the circle is x2 + y2 – 4x + 3y + 2 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -4, 2f = 3, c = 2
g = -2, f = \(\frac{3}{2}\), c = 2
The equation of a tangent to the circle x2 + y2 + 2gx + 2fy + c = 0 at (x1, y1) is
xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
The equation of the tangent at (4, -2) is
x(4) + y(-2) – 2(x + 4) + \(\frac{3}{2}\)(y – 2) + 2 = 0
⇒ 4x – 2y – 2x – 8 + \(\frac{3}{2}\) y – 3 + 2 = 0
⇒ 2x – \(\frac{1}{2}\)y – 9 = 0
⇒ 4x – y – 18 = 0
Class 11 Maharashtra State Board Maths Solution