Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 6 Circle Ex 6.2 Questions and Answers.
11th Maths Part 1 Circle Exercise 6.2 Questions And Answers Maharashtra Board
Question 1.
Find the centre and radius of each of the following circles:
(i) x2 + y2 – 2x + 4y – 4 = 0
(ii) x2 + y2 – 6x – 8y – 24 = 0
(iii) 4x2 + 4y2 – 24x – 8y – 24 = 0
Solution:
(i) Given equation of the circle is x2 + y2 – 2x + 4y – 4 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -2, 2f = 4 and c = -4
⇒ g = -1, f = 2 and c = -4
Centre of the circle = (-g, -f) = (1, -2)
and radius of the circle
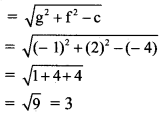
(ii) Given equation of the circle is x2 + y2 – 6x – 8y – 24 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -6, 2f = -8 and c = -24
⇒ g = -3, f = -4 and c = -24
Centre of the circle = (-g, -f) = (3, 4)
and radius of the circle
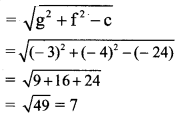
![]()
(iii) Given equation of the circle is 4x2 + 4y2 – 24x – 8y – 24 = 0
Dividing throughout by 4, we get x2 + y2 – 6x – 2y – 6 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -6, 2f = -2 and c = -6
⇒ g = -3, f = -1 and c = -6
Centre of the circle = (-g, -f) = (3, 1)
and radius of the circle
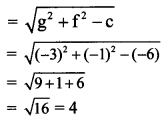
Question 2.
Show that the equation 3x2 + 3y2 + 12x + 18y – 11 = 0 represents a circle.
Solution:
Given equation is 3x2 + 3y2 + 12x + 18y – 11 = 0
Dividing throughout by 3, we get
x2 + y2 + 4x + 6y – \(\frac{11}{3}\) = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = 4, 2f = 6, c = \(\frac{-11}{3}\)
⇒ g = 2, f = 3, c = \(\frac{-11}{3}\)
Now, g2 + f2 – c = (2)2 + (3)2 – (\(\frac{-11}{3}\))
= 4 + 9 + \(\frac{11}{3}\)
= \(\frac{50}{3}\) > 0
∴ The given equation represents a circle.
![]()
Question 3.
Find the equation of the circle passing through the points (5, 7), (6, 6), and (2, -2).
Solution:
Let C(h, k) be the centre of the required circle.
Since the required circle passes through points A(5, 7), B(6, 6), and D(2, -2),
CA = CB = CD = radius
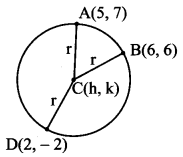
Consider, CA = CD
By distance formula,
\(\sqrt{(\mathrm{h}-5)^{2}+(\mathrm{k}-7)^{2}}=\sqrt{(\mathrm{h}-2)^{2}+[\mathrm{k}-(-2)]^{2}}\)
Squaring both the sides, we get
⇒ (h – 5)2 + (k – 7)2 = (h – 2)2 + (k + 2)2
⇒ h2 – 10h + 25 + k2 – 14k + 49 = h2 – 4h + 4 + k2 + 4k + 4
⇒ -10h – 14k + 74 = -4h + 4k + 8
⇒ 6h + 18k – 66 = 0
⇒ h + 3k – 11 = 0 …..(i)
Consider, CB = CD
By distance formula,
\(\sqrt{(h-6)^{2}+(k-6)^{2}}=\sqrt{(h-2)^{2}+[k-(-2)]^{2}}\)
Squaring both the sides, we get
⇒ (h – 6)2 + (k – 6)2 = (h – 2)2 + (k + 2)2
⇒ h2 – 12h + 36 + k2 – 12k + 36 = h2 – 4h + 4 + k2 + 4k + 4
⇒ -12h – 12k + 72 = -4h + 4k + 8
⇒ 8h + 16k – 64 = 0
⇒ h + 2k – 8 = 0 ……(ii)
By (i) – (ii), we get k = 3
Substituting k = 3 in (i), we get
h + 3(3) – 11 = 0
⇒ h + 9 – 11 = 0
⇒ h = 2
Centre of the circle is C(2, 3).
radius (r) = CD
= \(\sqrt{(2-2)^{2}+(3+2)^{2}}\)
= \(\sqrt{0+5^{2}}\)
= √25
= 5
The equation of a circle with centre at (h, k) and radius r is given by (x – h)2+ (y – k)2 = r2
Here, h = 2, k = 3
The required equation of the circle is
(x – 2)2 + (y – 3)2 = 52
⇒ x2 – 4x + 4 + y2 – 6y + 9 = 25
⇒ x2 + y2 – 4x – 6y + 4 + 9 – 25 = 0
⇒ x2 + y2 – 4x – 6y – 12 = 0
![]()
Question 4.
Show that the points (3, -2), (1, 0), (-1, -2) and (1, -4) are concyclic.
Solution:
Let the equation of the circle passing through the points (3, -2), (1, 0) and (-1, -2) be
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
For point (3, -2),
Substituting x = 3 and y = -2 in (i), we get
9 + 4 + 6g – 4f + c = 0
⇒ 6g – 4f + c = -13 ….(ii)
For point (1, 0),
Substituting x = 1 andy = 0 in (i), we get
1 + 0 + 2g + 0 + c = 0
⇒ 2g + c = -1 ……(iii)
For point (-1, -2),
Substituting x = -1 and y = -2, we get
1 + 4 – 2g – 4f + c = 0
⇒ 2g + 4f – c = 5 …….(iv)
Adding (ii) and (iv), we get
8g = -8
⇒ g = -1
Substituting g = -1 in (iii), we get
-2 + c = -1
⇒ c = 1
Substituting g = -1 and c = 1 in (iv), we get
-2 + 4f – 1 = 5
⇒ 4f = 8
⇒ f = 2
Substituting g = -1, f = 2 and c = 1 in (i), we get
x2 + y2 – 2x + 4y + 1 = 0 ……….(v)
If (1, -4) satisfies equation (v), the four points are concyclic.
Substituting x = 1, y = -4 in L.H.S of (v), we get
L.H.S. = (1)2 + (-4)2 – 2(1) + 4(-4) + 1
= 1 + 16 – 2 – 16 + 1
= 0
= R.H.S.
Point (1, -4) satisfies equation (v).
∴ The given points are concyclic.
Class 11 Maharashtra State Board Maths Solution