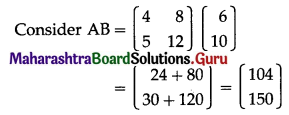
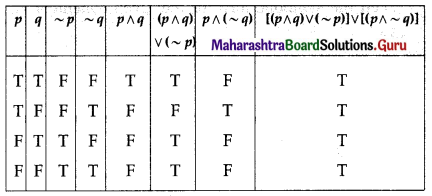
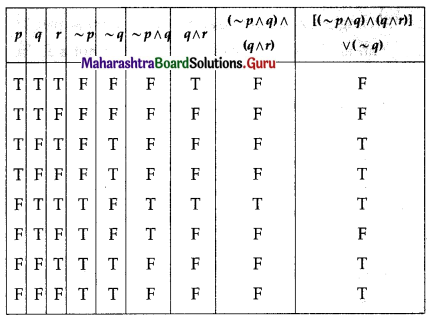
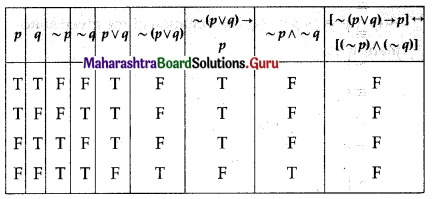
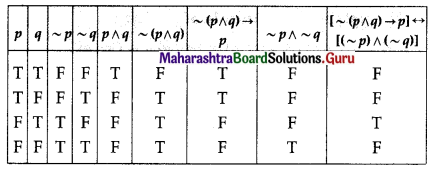
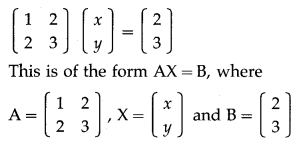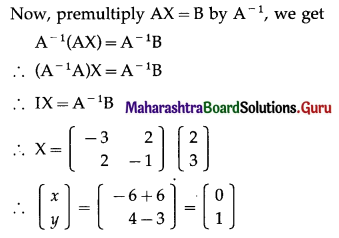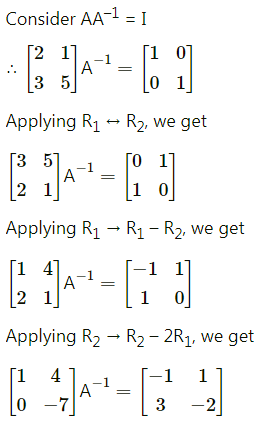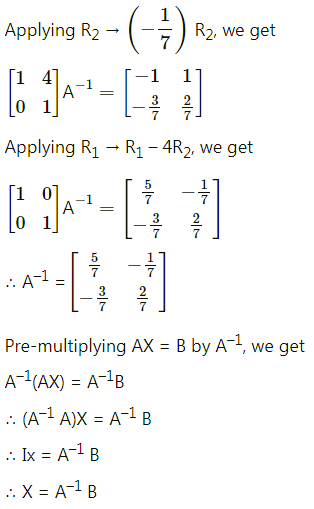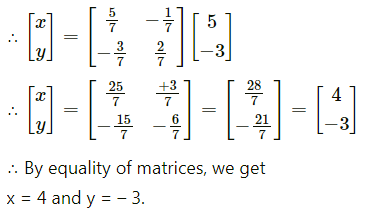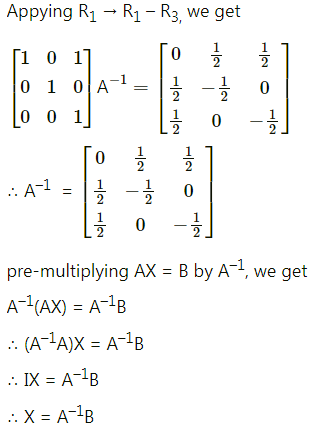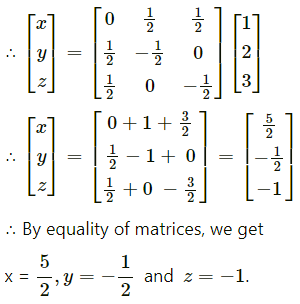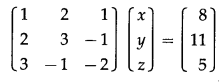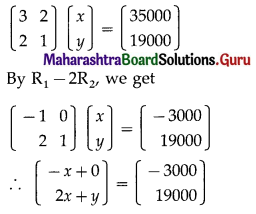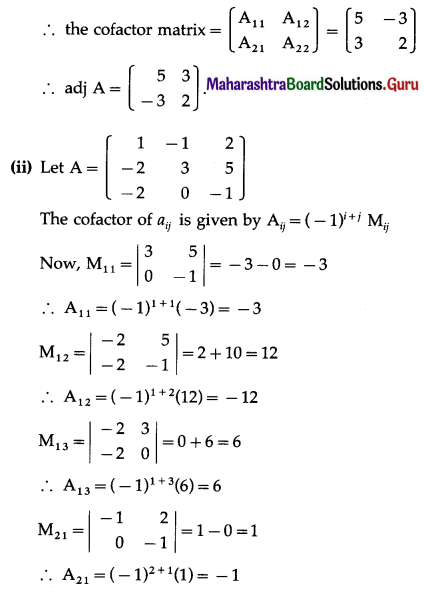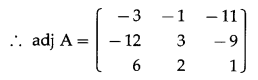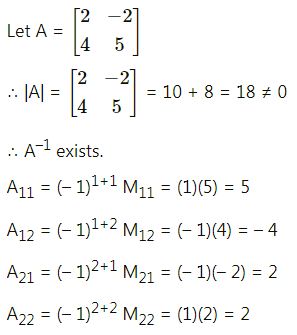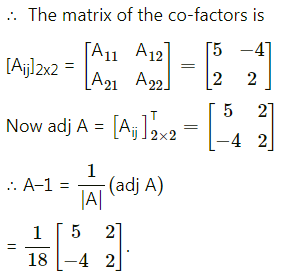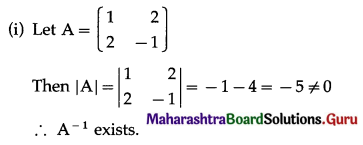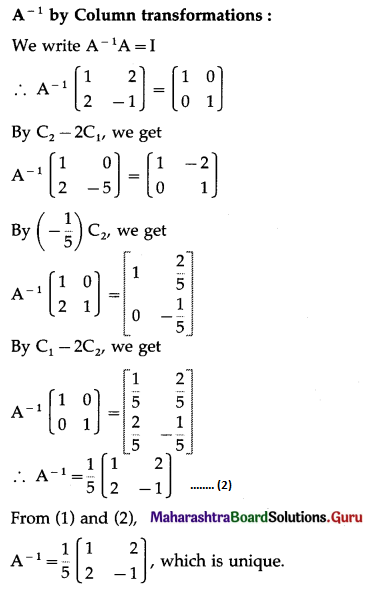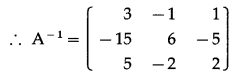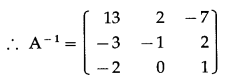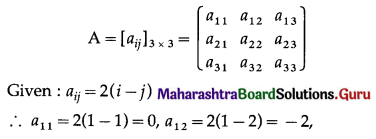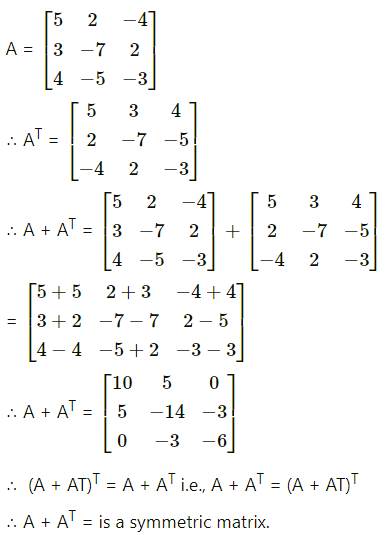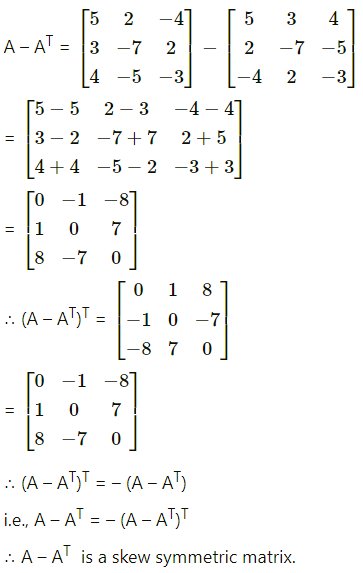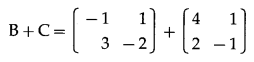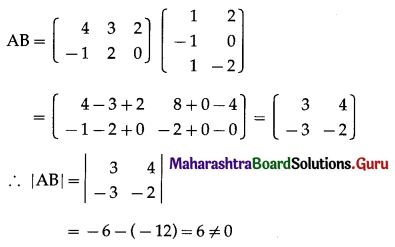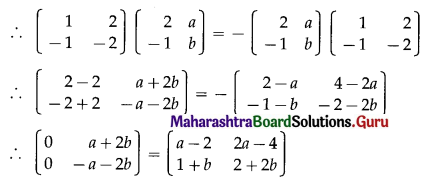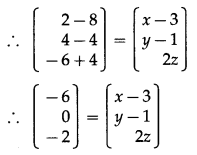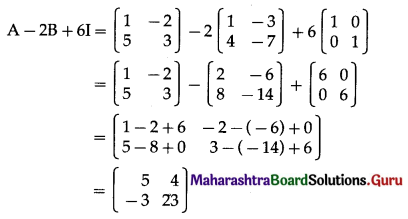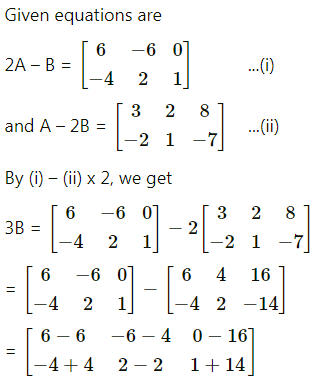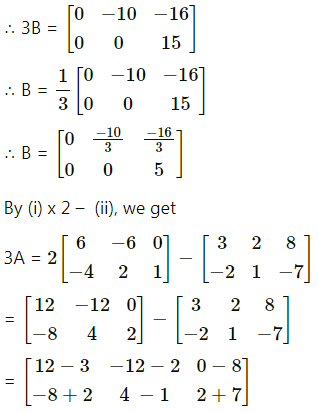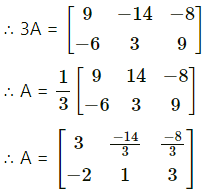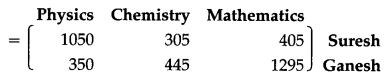Matrices Class 12 Commerce Maths 1 Chapter 2 Miscellaneous Exercise 2 Answers Maharashtra Board
Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Miscellaneous Exercise 2 Questions and Answers.
Std 12 Maths 1 Miscellaneous Exercise 2 Solutions Commerce Maths
(I) Choose the correct alternative.
Question 1.
If AX = B, where A = \(\left[\begin{array}{cc}
-1 & 2 \\
2 & -1
\end{array}\right]\), B = \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\) then X = ___________
(a) \(\left[\begin{array}{l}
\frac{3}{5} \\
\frac{3}{7}
\end{array}\right]\)
(b) \(\left[\begin{array}{l}
\frac{7}{3} \\
\frac{5}{3}
\end{array}\right]\)
(c) \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\)
(d) \(\left[\begin{array}{l}
1 \\
2
\end{array}\right]\)
Answer:
(c) \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\)
Question 2.
The matrix \(\left[\begin{array}{lll}
8 & 0 & 0 \\
0 & 8 & 0 \\
0 & 0 & 8
\end{array}\right]\) is ___________
(a) identity matrix
(b) scalar matrix
(c) null matrix
(d) diagonal matrix
Answer:
(b) scalar matrix
![]()
Question 3.
The matrix \(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\) is ___________
(a) identity matrix
(b) diagonal matrix
(c) scalar matix
(d) null matrix
Answer:
(d) null matrix
Question 4.
If A = \(\left[\begin{array}{lll}
a & 0 & 0 \\
0 & a & 0 \\
0 & 0 & a
\end{array}\right]\), then |adj A| = ___________
(a) a12
(b) a9
(c) a6
(d) a-3
Answer:
(c) a6
Hint:
adj A = \(\left[\begin{array}{ccc}
a^{2} & 0 & 0 \\
0 & a^{2} & 0 \\
0 & 0 & a^{2}
\end{array}\right]\)
∴ |adj A| = a2(a4 – 0) = a6
Question 5.
Adjoint of \(\left[\begin{array}{ll}
2 & -3 \\
4 & -6
\end{array}\right]\) is ___________
(a) \(\left[\begin{array}{ll}
-6 & 3 \\
-4 & 2
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
6 & 3 \\
-4 & 2
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
-6 & -3 \\
4 & 2
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
-6 & 3 \\
4 & -2
\end{array}\right]\)
Answer:
(a) \(\left[\begin{array}{ll}
-6 & 3 \\
-4 & 2
\end{array}\right]\)
Question 6.
If A = diag. [d1, d2, d3, …, dn], where d1 ≠ 0, for i = 1, 2, 3, …….., n, then A-1 = ___________
(a) diag [1/d1, 1/d2, 1/d3, …, 1/dn]
(b) D
(c) I
(d) O
Answer:
(a) diag [1/d1, 1/d2, 1/d3, …, 1/dn]
![]()
Question 7.
If A2 + mA + nI = O and n ≠ 0, |A| ≠ 0, then A-1 = ___________
(a) \(\frac{-1}{m}\)(A + nI)
(b) \(\frac{-1}{n}\)(A + mI)
(c) \(\frac{-1}{m}\)(I + mA)
(d) (A + mnI)
Answer:
(b) \(\frac{-1}{n}\)(A + mI)
Hint:
A2 + mA + nI = 0
∴ (A2 + mA + nI) . A-1 = 0 . A-1
∴ A(AA-1) + m(AA-1) + nIA-1 = 0
∴ AI + mI + nA-1 = 0
∴ nA-1 = -A – mI
∴ A-1 = \(\frac{-1}{n}\)(A + mI)
Question 8.
If a 3 × 3 matrix B has its inverse equal to B, then B2 = ___________
(a) \(\left[\begin{array}{lll}
0 & 1 & 1 \\
0 & 1 & 0 \\
1 & 0 & 1
\end{array}\right]\)
(b) \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 0 & 1
\end{array}\right]\)
(c) \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right]\)
(d) \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
Answer:
(d) \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
Hint:
B-1 = B
∴ B2 = B.B-1 = I
Question 9.
If A = \(\left[\begin{array}{cc}
\alpha & 4 \\
4 & \alpha
\end{array}\right]\) and |A3| = 729 then α = ___________
(a) ±3
(b) ±4
(c ) ±5
(d) ±6
Answer:
(c ) ±5
Hint:
|A|= \(\left|\begin{array}{ll}
\alpha & 4 \\
4 & \alpha
\end{array}\right|\) = α2 – 16
∴ |A3| = |A|3 = (α2 – 16)3 = 729
∴ α2 – 16 = 9
∴ α2 = 25
∴ α = ±5
![]()
Question 10.
If A and B square matrices of order n × n such that A2 – B2 = (A – B)(A + B), then which of the following will be always true?
(a) AB = BA
(b) either A or B is a zero matrix
(c) either of A and B is an identity matrix
(d) A = B
Answer:
(a) AB = BA
Hint:
A2 – B2 = (A – B)(A + B)
∴ A2 – B2 = A2 + AB – BA – B2
∴ 0 = AB – BA
∴ AB = BA
Question 11.
If A = \(\left[\begin{array}{ll}
2 & 5 \\
1 & 3
\end{array}\right]\) then A-1 = ___________
(a) \(\left[\begin{array}{rr}
3 & -5 \\
1 & 2
\end{array}\right]\)
(b) \(\left[\begin{array}{rr}
3 & -5 \\
-1 & 2
\end{array}\right]\)
(c) \(\left[\begin{array}{rr}
3 & 5 \\
-1 & 2
\end{array}\right]\)
(d) \(\left[\begin{array}{ll}
3 & -5 \\
1 & -2
\end{array}\right]\)
Answer:
(b) \(\left[\begin{array}{rr}
3 & -5 \\
-1 & 2
\end{array}\right]\)
Question 12.
If A is a 2 × 2 matrix such that A(adj A) = \(\left[\begin{array}{ll}
5 & 0 \\
0 & 5
\end{array}\right]\), then |A| = ___________
(a) 0
(b) 5
(c) 10
(d) 25
Answer:
(b) 5
Hint:
A(adj A) = |A|.I
Question 13.
If A is a non-singular matrix, then det(A-1) = ___________
(a) 1
(b) 0
(c) det(A)
(d) 1/det(A)
Answer:
(d) 1/det(A)
Hint:
AA-1 = I
∴ |A|.|A-1| = 1
∴ |A-1| = \(\frac{1}{|\mathrm{~A}|}\)
![]()
Question 14.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
-3 & -1
\end{array}\right]\), B = \(\left[\begin{array}{rr}
-1 & 0 \\
1 & 5
\end{array}\right]\) then AB = ___________
(a) \(\left[\begin{array}{rr}
1 & -10 \\
1 & 20
\end{array}\right]\)
(b) \(\left[\begin{array}{rr}
1 & 10 \\
-1 & 20
\end{array}\right]\)
(c) \(\left[\begin{array}{ll}
1 & 10 \\
1 & 20
\end{array}\right]\)
(d) \(\left[\begin{array}{rr}
1 & 10 \\
-1 & -20
\end{array}\right]\)
Answer:
(c) \(\left[\begin{array}{ll}
1 & 10 \\
1 & 20
\end{array}\right]\)
Question 15.
If x + y + z = 3, x + 2y + 3z = 4, x + 4y + 9z = 6, then (y, z) = ___________
(a) (-1, 0)
(b) (1, 0)
(c) (1, -1)
(d) (-1, 1)
Answer:
(b) (1, 0)
(II) Fill in the blanks:
Question 1.
A = \(\left[\begin{array}{l}
3 \\
1
\end{array}\right]\) is ___________ matrix.
Answer:
column
Question 2.
Order of matrix \(\left[\begin{array}{lll}
2 & 1 & 1 \\
5 & 1 & 8
\end{array}\right]\) is ___________
Answer:
2 × 3
Question 3.
If A = \(\left[\begin{array}{ll}
4 & x \\
6 & 3
\end{array}\right]\) is a singular matrix, then x is ___________
Answer:
2
![]()
Question 4.
Matrix B = \(\left[\begin{array}{ccc}
0 & 3 & 1 \\
-3 & 0 & -4 \\
p & 4 & 0
\end{array}\right]\) is a skew-symmetric, then value of p is ___________
Answer:
-1
Question 5.
If A = [aij]2×3 and B = [bij]m×1, and AB is defined, then m = ___________
Answer:
3
Question 6.
If A = \(\left[\begin{array}{cc}
3 & -5 \\
2 & 5
\end{array}\right]\), then cofactor of a12 is ___________
Answer:
-2
Question 7.
If A = [aij]m×m is non-singular matrix, then A-1 = \(\frac{1}{\ldots \ldots}\) adj (A).
Answer:
|A|
Question 8.
(AT)T = ___________
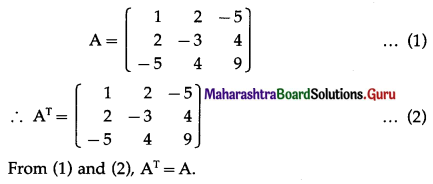
Answer:
A
Question 9.
If A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & 1
\end{array}\right]\) and A-1 = \(\left[\begin{array}{cc}
1 & -1 \\
x & 2
\end{array}\right]\), then x = ___________
Answer:
-1
![]()
Question 10.
If a1x+ b1y = c1 and a2x + b2y = c2, then matrix form is \(\left[\begin{array}{cc}
\cdots & \ldots \\
\cdots & \ldots
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
\ldots \\
\cdots
\end{array}\right]\)
Answer:
\(\left[\begin{array}{ll}
a_{1} & b_{1} \\
a_{2} & b_{2}
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
c_{1} \\
c_{2}
\end{array}\right]\)
(III) State whether each of the following is True or False:
Question 1.
Single element matrix is row as well as a column matrix.
Answer:
True
Question 2.
Every scalar matrix is unit matrix.
Answer:
False
Question 3.
A = \(\left[\begin{array}{ll}
4 & 5 \\
6 & 1
\end{array}\right]\) is non-singular matrix.
Answer:
True
Question 4.
If A is symmetric, then A = -AT.
Answer:
False
![]()
Question 5.
If AB and BA both exist, then AB = BA.
Answer:
False
Question 6.
If A and B are square matrices of same order, then (A + B)2 = A2 + 2AB + B2.
Answer:
False
Question 7.
If A and B are conformable for the product AB, then (AB)T = ATBT.
Answer:
False
Question 8.
Singleton matrix is only row matrix.
Answer:
False
Question 9.
A = \(\left[\begin{array}{cc}
2 & 1 \\
10 & 5
\end{array}\right]\) is invertible matrix.
Answer:
False
Question 10.
A(adj A) = |A| I, where I is the unit matrix.
Answer:
True.
(IV) Solve the following:
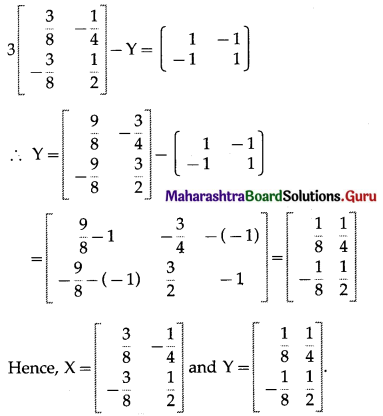
Question 1.
Find k, if \(\left[\begin{array}{ll}
7 & 3 \\
5 & k
\end{array}\right]\) is a singular matrix.
Solution:
Let A = \(\left[\begin{array}{ll}
7 & 3 \\
5 & k
\end{array}\right]\)
Since, A is singular matrix, |A| = 0
∴ \(\left|\begin{array}{ll}
7 & 3 \\
5 & k
\end{array}\right|\) = 0
∴ 7k – 15 = 0
∴ k = \(\frac{15}{7}\)
![]()
Question 2.
Find x, y, z if \(\left[\begin{array}{lll}
2 & x & 5 \\
3 & 1 & z \\
y & 5 & 8
\end{array}\right]\) is a symmetric matrix.
Solution:

By equality of matrices,
x = 3, y = 5 and z = 5.
Question 3.
If A = \(\left[\begin{array}{ll}
1 & 5 \\
7 & 8 \\
9 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 4 \\
1 & 5 \\
-8 & 6
\end{array}\right]\), C = \(\left[\begin{array}{cc}
-2 & 3 \\
1 & -5 \\
7 & 8
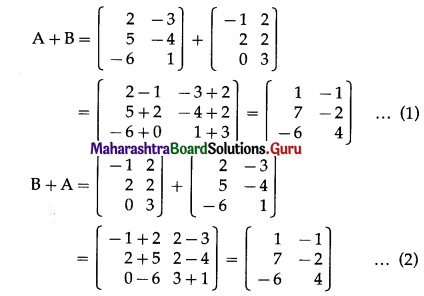
\end{array}\right]\) then show that (A + B) + C = A + (B + C).
Solution:
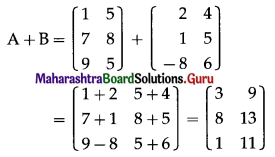

From (1) and (2),
(A + B) + C = A + (B + C).
Question 4.
If A = \(\left[\begin{array}{ll}
2 & 5 \\
3 & 7
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 7 \\
-3 & 0
\end{array}\right]\), find the matrix A – 4B + 7I, where I is the unit matrix of order 2.
Solution:

![]()
Question 5.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
3 & -2 \\
-1 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-3 & 4 & 1 \\
2 & -1 & -3
\end{array}\right]\) verify
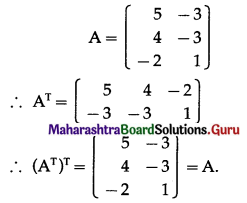
(i) (A + 2BT)T = AT + 2B
(ii) (3A – 5BT)T = 3AT – 5B
Solution:
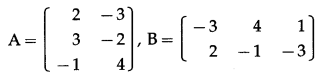



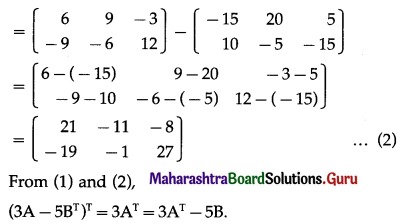
Question 6.
If A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 6 \\
1 & 2 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
-3 & 2 & -1 \\
-2 & 1 & 0
\end{array}\right]\) thenshow that AB and BA are both singular matrices.
Solution:

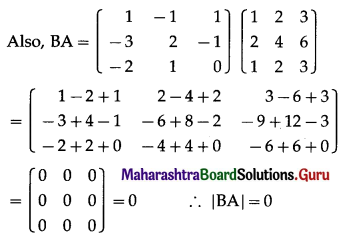
∴ BA is also a singular matrix.
Hence, AB and BA are both singular matrices.
Question 7.
If A = \(\left[\begin{array}{ll}
3 & 1 \\
1 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 2 \\
5 & -2
\end{array}\right]\), verify |AB| = |A| |B|.
Solution:

Question 8.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
-1 & 2
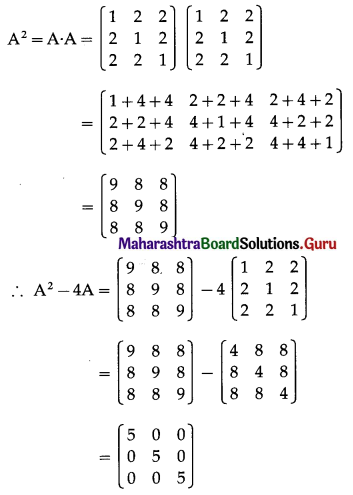
\end{array}\right]\), then show that A2 – 4A + 3I = 0.
Solution:

Question 9.
If A = \(\left[\begin{array}{cc}
-3 & 2 \\
2 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & a \\
b & 0
\end{array}\right]\) and (A + B)(A – B) = A2 – B2, find a and b.
Solution:
(A + B)(A – B) = A2 – B2
∴ A2 – AB + BA – B2 = A2 – B2
∴ -AB + BA = 0
∴ AB = BA
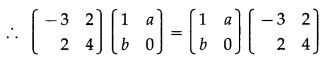

By equality of matrices,
-3 + 2b = -3 + 2a ……..(1)
-3a = 2 + 4a ……..(2)
2 + 4b = -3b ……..(3)
2a = 2b ……..(4)
From (2), 7a = -2
∴ a = \(\frac{-2}{7}\)
From (3), 7b = -2
∴ b = \(\frac{-2}{7}\)
These values of a and b also satisfy equations (1) and (4).
Hence, a = \(\frac{-2}{7}\) and b = \(\frac{-2}{7}\)
![]()
Question 10.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 3
\end{array}\right]\), then find A3.
Solution:

Question 11.
Find x, y, z if \(\left\{5\left[\begin{array}{ll}
0 & 1 \\
1 & 0 \\
1 & 1
\end{array}\right]-\left[\begin{array}{cc}
2 & 1 \\
3 & -2 \\
1 & 3
\end{array}\right]\right\}\left[\begin{array}{l}
2 \\
1
\end{array}\right]=\left[\begin{array}{c}
x-1 \\
y+1 \\
2 z
\end{array}\right]\)
Solution:
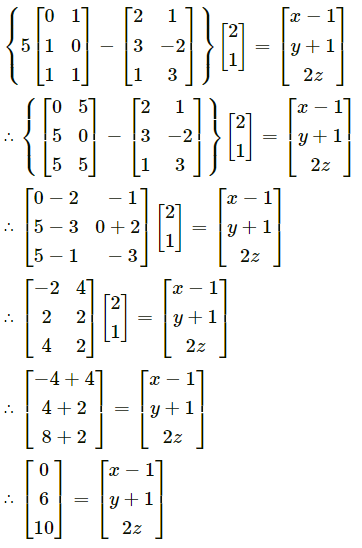
∴ By equality of matrices, we get
x – 1 = 0 ∴ x = 1
y + 1 = 6 ∴ y = 5
2z = 10 ∴ z = 5
Question 12.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
3 & -2 \\
0 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 1 & 0
\end{array}\right]\) then showthat(AB)T = BTAT.
Solution:

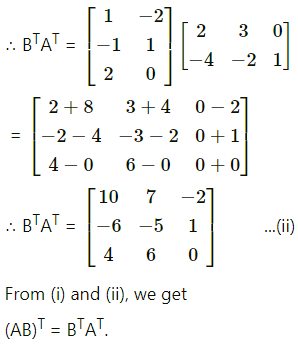
Question 13.
If A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\), then reduce it to unit matrix by row tranformation.
Solution:

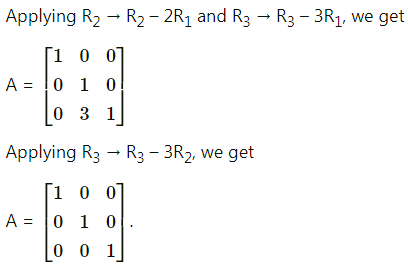
![]()
Question 14.
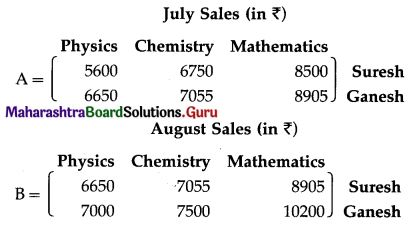
Two farmers Shantaram and Kantaram cultivate three crops rice, wheat, and groundnut. The sale (in ₹) of these crops by both the farmers for the month of April and May 2016 is given below:
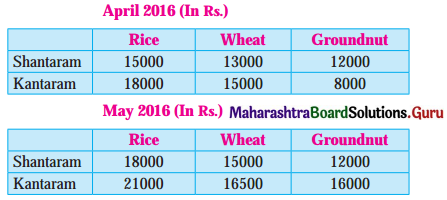
Find (i) the total sale in rupees for two months of each farmer for each crop.
(ii) the increase in sales from April to May for every crop of each farmer.
Solution:
The given information can be written in matrix form as:
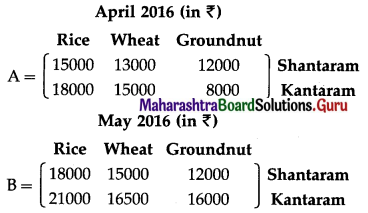
(i) The total sale in ₹ for two months of each farmer for each crop can be obtained by the addition A + B.
Now, A + B

∴ total sale in ₹ for two months of each farmer for each crop is given by

Hence, the total sale for Shantaram are ₹ 33000 for Rice, ₹ 28000 for Wheat, ₹ 24000 for Groundnut, and for Kantaram are ₹ 39000 for Rice, ₹ 31500 for Wheat, ₹ 24000 for Groundnut.
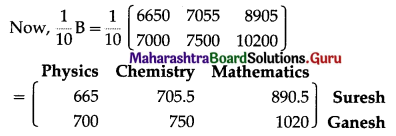
(ii) The increase in sales from April to May for every crop of each farmer can be obtained by the subtraction of A from B.
Now, B – A

Hence, the increase in sales from April to May of Shantam is ₹ 3000 in Rice, ₹ 2000 in Wheat, nothing in Groundnut and of Kantaram are ₹ 3000 in Rice, ₹ 1500 in Wheat, ₹ 8000 in Groundnut.
Question 15.
Check whether following matrices are invertible or not:
(i) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Then |A| = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\)
= 1 – 0
= 1 ≠ 0
∴ A is a non-singular matrix.
Hence, A-1 exists.
(ii) \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Then |A| = \(\left|\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right|\)
= 1 – 1
= 0
∴ A is a singular matrix.
Hence, A-1 does not exist.
![]()
(iii) \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Then |A| = \(\left|\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right|\)
= 3(5 – 0) – 4(5 – 0) + 3(4 – 1)
= 15 – 20 + 9
= 4 ≠ 0
∴ A is a non-singular matrix.
Hence, A-1 exists.
(iv) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 5 \\
2 & 4 & 6
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 5 \\
2 & 4 & 6
\end{array}\right]\)
Then |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 5 \\
2 & 4 & 6
\end{array}\right|\)
= 1(24 – 20) – 2(12 – 10) + 3(8 – 8)
= 4 – 4 + 0
= 0
∴ A is a singular matrix.
Hence, A-1 does not exist.
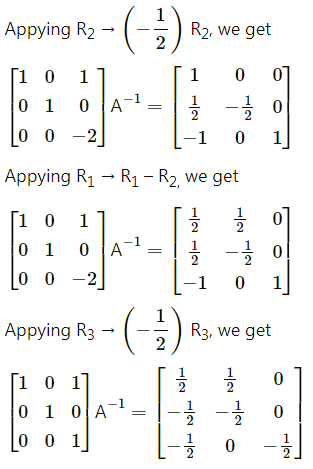
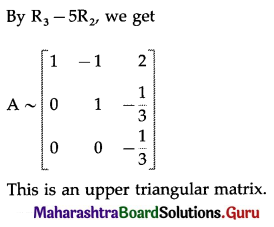
Question 16.
Find inverse of the following matrices (if they exist) by elementary transformation:
(i) \(\left[\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right]\)
Solution:
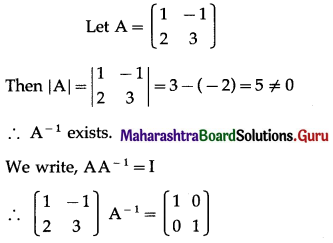
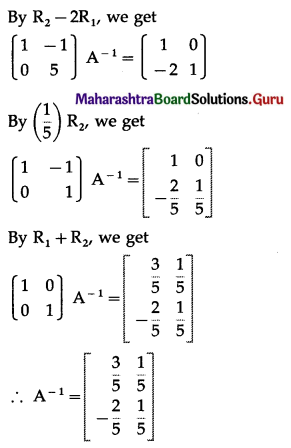
(ii) \(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{ccc}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
Solution:


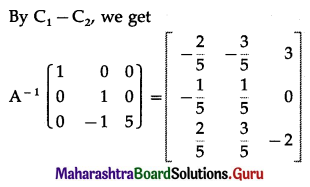

![]()
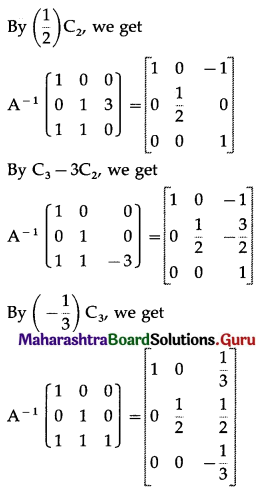
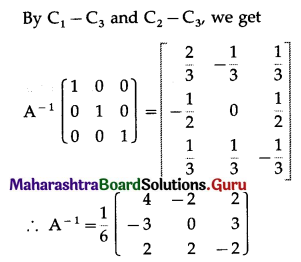
(iv) \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:



Question 17.
Find the inverse of \(\left[\begin{array}{lll}
3 & 1 & 5 \\
2 & 7 & 8 \\
1 & 2 & 5
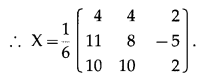
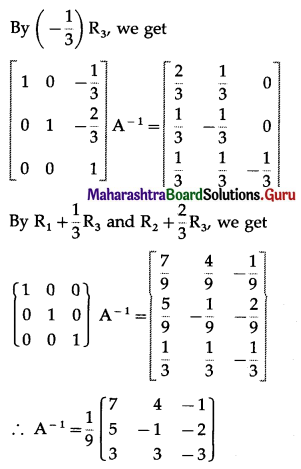
\end{array}\right]\) by adjoint method.
Solution:



Question 18.
Solve the following equations by method of inversion:
(i) 4x – 3y – 2 = 0, 3x – 4y + 6 = 0
Solution:
The given equations are
4x – 3y = 2
3x – 4y = -6
These equations can be written in matrix form as:



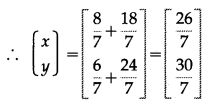
By equality of matrices,
x = \(\frac{26}{7}\), y = \(\frac{30}{7}\) is the required solution.
(ii) x + y – z = 2, x – 2y + z = 3 and 2x – y – 3z = -1
Solution:
The given equations can be written in matrix form as:



By equality of matrices,
x = 3, y = 1, z = 2 is the required solution.
(iii) x – y + z = 4, 2x + y – 3z = 0 and x + y + z = 2
Solution:


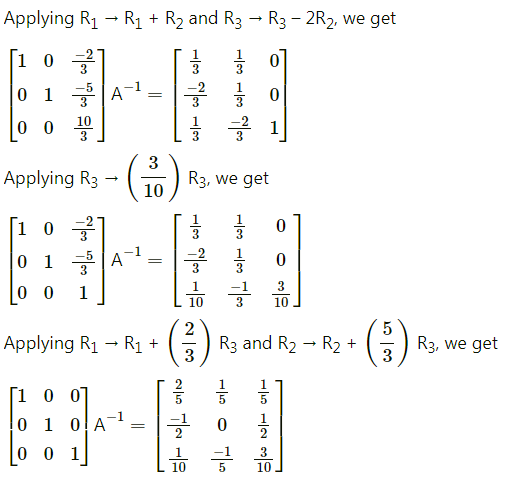
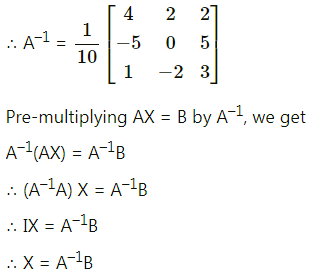
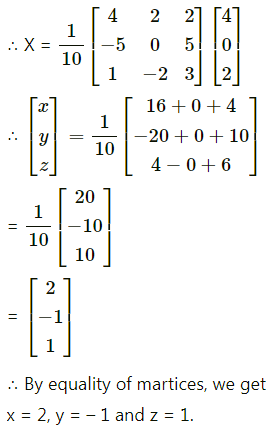
![]()
Question 19.
Solve the following equations by method of reduction:
(i) 2x + y = 5, 3x – 5y = -3
Solution:
The given equation can be written in matrix form as:
\(\left[\begin{array}{ll}
2 & 1 \\
3 & 5
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{r}
5 \\
-3
\end{array}\right]\)
By R2 – 5R1, we get
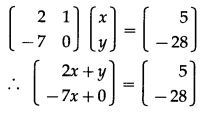
By equality of matrices,
2x + y = 5 …….(1)
-7x = -28 ……(2)
From (2), x = 4
Substituting x = 4 in (1), we get
2(4) + y = 5
∴ y = -3
Hence, x = 4 and y = -3 is the required solution.
(ii) x + 2y + z = 3, 3x – y + 2z = 1 and 2x – 3y + 3z = 2
Solution:
The given equations can be written in matrix form as:

By equality of matrices,
x + 2y + z = 3 …….(1)
-7y – z = -8 …….(2)
2z = 4 …….(3)
From (3), z = 2
Substituting z = 2 in (2), we get
-7y – 2 = -8
∴ -7y = -6
∴ y = \(\frac{6}{7}\)
Substituting y = \(\frac{6}{7}\), z = 2 in (1), we get
x + 2(\(\frac{6}{7}\)) + 2 = 3
x = 3 – 2 – \(\frac{12}{7}\) = \(\frac{-5}{7}\)
Hence, x = \(\frac{-5}{7}\), y = \(\frac{6}{7}\) and z = 2 is the required solution.
(iii) x – 3y + z = 2, 3x + y + z = 1 and 5x + y + 3z = 3.
Solution:


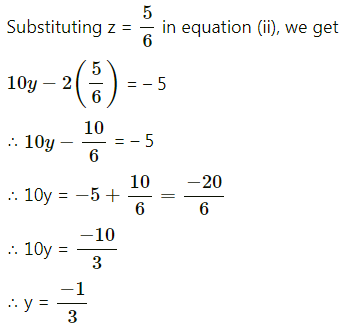
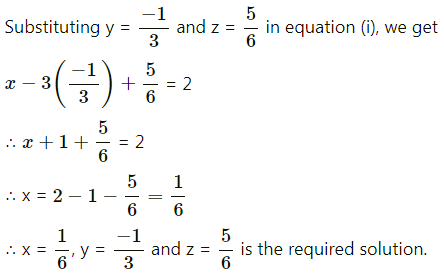
![]()
Question 20.
The sum of three numbers is 6. If we multiply the third number by 3 and add it to the second number, we get 11. By adding first and third numbers we get a number that is double the second number. Use this information and find a system of linear equations. Find the three numbers using matrices.
Solution:
Let the three numbers be x, y, and z.
According to the given condition,
x + y + z = 6
3z + y = 11, i.e. y + 3z = 11
and x + z = 2y, i.e. x – 2y + z = 0
Hence, the system of linear equations is
x + y + z = 6
y + 3z = 11
x – 2y + z = 0
These equations can be written in matrix form as:

By equality of matrices,
x + y + z = 6 …….(1)
y + 3z = 11 ………(2)
-3y = -6 ………(3)
From (3), y = 2
Substituting y = 2 in (2), we get
2 + 3z = 11
∴ 3z = 9
∴ z = 3
Substituting y = 2, z = 3 in (1), we get
x + 2 + 3 = 6
∴ x = 1
∴ x = 1, y = 2, z = 3
Hence, the required numbers are 1, 2 and 3.
12th Commerce Maths Digest Pdf
- 12th Commerce Maths Exercise 2.1 Solutions
- 12th Commerce Maths Exercise 2.2 Solutions
- 12th Commerce Maths Exercise 2.3 Solutions
- 12th Commerce Maths Exercise 2.4 Solutions
- 12th Commerce Maths Exercise 2.5 Solutions
- 12th Commerce Maths Exercise 2.6 Solutions
- 12th Commerce Maths Exercise Miscellaneous Exercise 2 Solutions