Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Ex 2.2 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 2 Matrices Ex 2.2
Question 1.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
5 & -4 \\
-6 & 1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
-1 & 2 \\
2 & 2 \\
0 & 3
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
4 & 3 \\
-1 & 4 \\
-2 & 1
\end{array}\right]\) show that
(i) A + B = B + A
(ii) (A + B) + C = A + (B + C)
Solution:
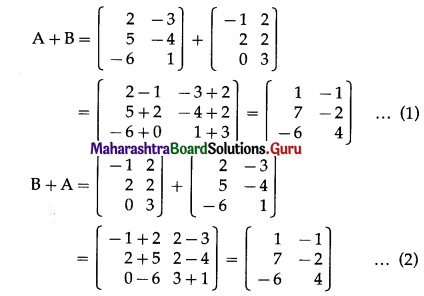

From (1) and (2), we get
(A + B) + C = A + (B + C).
Question 2.
If A = \(\left[\begin{array}{cc}
1 & -2 \\
5 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & -3 \\
4 & -7
\end{array}\right]\), then find the matrix A – 2B + 6I, where I is the unit matrix of order 2.
Solution:
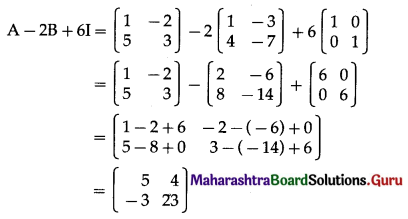
![]()
Question 3.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -3 \\
-3 & 7 & -8 \\
0 & -6 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
9 & -1 & 2 \\
-4 & 2 & 5 \\
4 & 0 & -3
\end{array}\right]\), then find the matrix C such that A + B + C is a zero matrix.
Solution:
A + B + C = 0
∴ C = -A – B

Question 4.
If A = \(\left[\begin{array}{cc}
1 & -2 \\
3 & -5 \\
-6 & 0
\end{array}\right]\), B = \(\left[\begin{array}{cc}
-1 & -2 \\
4 & 2 \\
1 & 5
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
2 & 4 \\
-1 & -4 \\
-3 & 6
\end{array}\right]\), find the matrix X such that 3A – 4B + 5X = C.
Solution:
3A – 4B + 5X = C
∴ 5X = C – 3A + 4B

Question 5.
If A = \(\left[\begin{array}{ccc}
5 & 1 & -4 \\
3 & 2 & 0
\end{array}\right]\), find (AT)T.
Solution:
A = \(\left[\begin{array}{ccc}
5 & 1 & -4 \\
3 & 2 & 0
\end{array}\right]\)
∴ AT = \(\left[\begin{array}{rr}
5 & 3 \\
1 & 2 \\
-4 & 0
\end{array}\right]\)
∴ (AT)T = \(\left[\begin{array}{ccc}
5 & 1 & -4 \\
3 & 2 & 0
\end{array}\right]\) = A
![]()
Question 6.
If A = \(\left[\begin{array}{ccc}
7 & 3 & 1 \\
-2 & -4 & 1 \\
5 & 9 & 1
\end{array}\right]\), find (AT)T.
Solution:
A = \(\left[\begin{array}{ccc}
7 & 3 & 1 \\
-2 & -4 & 1 \\
5 & 9 & 1
\end{array}\right]\)
∴ AT = \(\left[\begin{array}{rrr}
7 & -2 & 5 \\
3 & -4 & 9 \\
1 & 1 & 1
\end{array}\right]\)
∴ (AT)T = \(\left[\begin{array}{ccc}
7 & 3 & 1 \\
-2 & -4 & 1 \\
5 & 9 & 1
\end{array}\right]\) = A
Question 7.
Find a, b, c if \(\left[\begin{array}{ccc}
1 & \frac{3}{5} & a \\
b & -5 & -7 \\
-4 & c & 0
\end{array}\right]\) is a symetric matrix.
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & \frac{3}{5} & a \\
b & -5 & -7 \\
-4 & c & 0
\end{array}\right]\)
Since, A is a symmetric matrix, aij = aji for all i and j

Question 8.
Find x, y, z if \(\left[\begin{array}{ccc}
0 & -5 i & x \\
y & 0 & z \\
\frac{3}{2} & -\sqrt{2} & 0
\end{array}\right]\) is a skew symmetric matrix.
Solution:
Let A = \(\left[\begin{array}{ccc}
0 & -5 i & x \\
y & 0 & z \\
\frac{3}{2} & -\sqrt{2} & 0
\end{array}\right]\)
Since, A is skew-symmetric matrix,


![]()
Question 9.
For each of the following matrices, find its transpose and state whether it is symmetric, skew-symmetric or neither:
(i) \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\)
Then AT = \(\left[\begin{array}{rrr}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\)
Since, A = AT, A is a symmetric matrix.
(ii) \(\left[\begin{array}{ccc}
2 & 5 & 1 \\
-5 & 4 & 6 \\
-1 & -6 & 3
\end{array}\right]\)
Solution:
Let B = \(\left[\begin{array}{ccc}
2 & 5 & 1 \\
-5 & 4 & 6 \\
-1 & -6 & 3
\end{array}\right]\)
Then BT = \(\left(\begin{array}{rrr}
2 & -5 & -1 \\
5 & 4 & -6 \\
1 & 6 & 3
\end{array}\right)\)
∴ B ≠ BT
Also,
-BT = \(\left(\begin{array}{rrr}
2 & -5 & -1 \\
5 & 4 & -6 \\
1 & 6 & 3
\end{array}\right)=\left(\begin{array}{rrr}
-2 & 5 & 1 \\
-5 & -4 & 6 \\
-1 & -6 & -3
\end{array}\right)\)
∴ B ≠ -BT
Hence, B is neither symmetric nor skew-symmetric matrix.
(iii) \(\left[\begin{array}{ccc}
0 & 1+2 i & i-2 \\
-1-2 i & 0 & -7 \\
2-i & 7 & 0
\end{array}\right]\)
Solution:

Hence, C is a skew-symmetric matrix.
Question 10.
Construct the matrix A = [aij]3×3, where aij = i – j. State whether A is symmetric or skew-symmetric.
Solution:
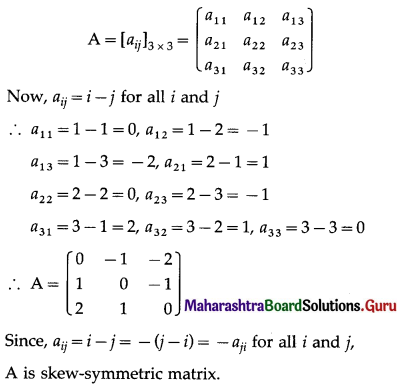
![]()
Question 11.
Solve the following equations for X and Y, if 3X – Y = \(\left[\begin{array}{cc}
1 & -1 \\
-1 & 1
\end{array}\right]\) and X – 3Y = \(\left[\begin{array}{ll}
0 & -1 \\
0 & -1
\end{array}\right]\)
Solution:

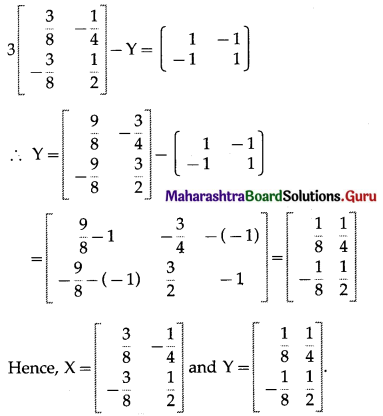
Question 12.
Find matrices A and B, if 2A – B = \(\left[\begin{array}{ccc}
6 & -6 & 0 \\
-4 & 2 & 1
\end{array}\right]\) and A – 2B = \(\left[\begin{array}{ccc}
3 & 2 & 8 \\
-2 & 1 & -7
\end{array}\right]\)
Solution:
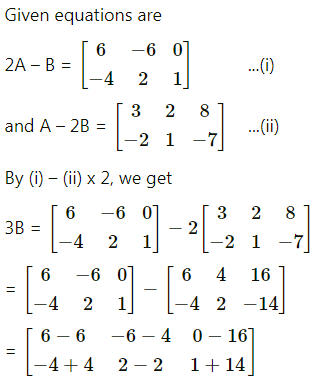
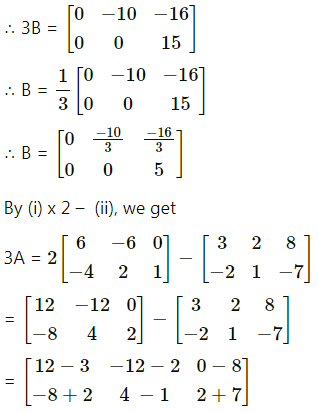
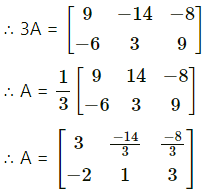
Question 13.
Find x and y, if \(\left[\begin{array}{ccc}
2 x+y & -1 & 1 \\
3 & 4 y & 4
\end{array}\right]+\left[\begin{array}{ccc}
-1 & 6 & 4 \\
3 & 0 & 3
\end{array}\right]=\left[\begin{array}{ccc}
3 & 5 & 5 \\
6 & 18 & 7
\end{array}\right]\)
Solution:

By equality of matrices, we get
2x + y – 1 = 3 ……..(1)
and 4y = 18 ……….(2)
From (2), y = \(\frac{9}{2}\)
Substituting y = \(\frac{9}{2}\) in (1), we get
2x + \(\frac{9}{2}\) – 1 = 3
∴ 2x = 3 – \(\frac{7}{2}\) = \(\frac{-1}{2}\)
∴ x = \(\frac{-1}{4}\)
Hence, x = \(\frac{-1}{4}\) and y = \(\frac{9}{2}\).
![]()
Question 14.
If \(\left[\begin{array}{cc}
2 a+b & 3 a-b \\
c+2 d & 2 c-d
\end{array}\right]=\left[\begin{array}{cc}
2 & 3 \\
4 & -1
\end{array}\right]\), find a, b, c and d.
Solution:
\(\left[\begin{array}{cc}
2 a+b & 3 a-b \\
c+2 d & 2 c-d
\end{array}\right]=\left[\begin{array}{cc}
2 & 3 \\
4 & -1
\end{array}\right]\)
By equality of matrices,
2a + b = 2 ….. (1)
3a – b = 3 …… (2)
c + 2d = 4 …… (3)
2c – d = -1 …… (4)
Adding (1) and (2), we get
5a = 5
∴ a = 1
Substituting a = 1 in (1), we get
2(1) + b = 2
∴ b = 0
Multiplying equation (4) by 2, we get
4c – 2d = -2 …… (5)
Adding (3) and (5), we get
5c = 2
∴ c = \(\frac{2}{5}\)
Substituting c = \(\frac{2}{5}\) in (4), we get
2(\(\frac{2}{5}\)) – d = -1
∴ d = \(\frac{4}{5}\) + 1 = \(\frac{9}{5}\)
Hence, a = 1, b = 0, c = \(\frac{2}{5}\) and d = \(\frac{9}{5}\).
![]()
Question 15.
There are two book shops owned by Suresh and Ganesh. Their sales (in Rupees) for books in three subjects – Physics, Chemistry and Mathematics for two months, July and August 2017 are given by two matrices A and B:
July sales (in Rupees), Physics, Chemistry, Mathematics
A = \(\left[\begin{array}{lll}
5600 & 6750 & 8500 \\
6650 & 7055 & 8905
\end{array}\right]\) First Row Suresh / Second Row Ganesh
August Sales (in Rupees), Physics, Chemistry, Mathematics
B = \(\left[\begin{array}{ccc}
6650 & 7055 & 8905 \\
7000 & 7500 & 10200
\end{array}\right]\) First Row Suresh / Second Row Ganesh
(i) Find the increase in sales in Z from July to August 2017.
(ii) If both book shops get 10% profit in the month of August 2017,
find the profit for each bookseller in each subject in that month.
Solution:
The sales for July and August 2017 for Suresh and Ganesh are given by the matrices A and B as:
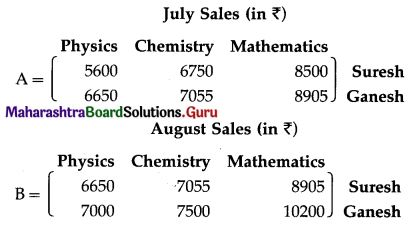
(i) The increase in sales (in ₹) from July to August 2017 is obtained by subtracting the matrix A from B.

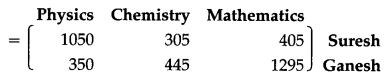
Hence, the increase in sales (in ₹) from July to August 2017 for:
Suresh book shop: ₹ 1050 in Physics, ₹ 305 in Chemistry, and ₹ 405 in Mathematics.
Ganesh book shop: ₹ 350 in Physics, ₹ 445 in Chemistry, and ₹ 1295 in Mathematics.
(ii) Both the book shops get 10% profit in August 2017,
the profit for each bookseller in each subject in August 2017 is obtained by the scalar multiplication of matrix B by 10%,
i.e. \(\frac{10}{100}=\frac{1}{10}\)
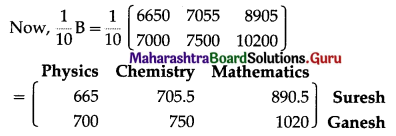
Hence, the profit for Suresh book shop are ₹ 665 in Physics, ₹ 705.50 in Chemistry and ₹ 890.50 in Mathematics and for Ganesh book shop are ₹ 700 in Physics, ₹ 750 in Chemistry and ₹ 1020 in Mathematics.