Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.4 Answers Maharashtra Board
Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.4 Questions and Answers.
Std 12 Maths 1 Exercise 1.4 Solutions Commerce Maths
Question 1.
Write the following statements in symbolic form:
(i) If the triangle is equilateral, then it is equiangular.
Solution:
Let p : Triangle is equilateral.
q : It is equiangular.
Then the symbolic form of the given statement is p → q.
(ii) It is not true that ‘i’ is a real number.
Solution:
Let p : ‘i’ is a real number.
Then the symbolic form of the given statement is ~p.
(iii) Even though it is not cloudy, it is still raining.
Solution:
Let p : It is cloudy.
q : It is still raining.
Then the symbolic form of the given statement is ~p ∧ q.
![]()
(iv) Milk is white if and only if the sky is not blue.
Solution:
Let p : Milk is white.
q : Sky is blue.
Then the symbolic form of the given statement is p ↔ (~q).
(v) Stock prices are high if and only if stocks are rising.
Solution:
Let p : Stock prices are high.
q : stocks are rising.
Then the symbolic form of the given statement is p ↔ q
(vi) If Kutub-Minar is in Delhi, then Taj Mahal is in Agra.
Solution:
Let p : Kutub-Minar is in Delhi.
q : Taj Mahal is in Agra.
Then the symbolic form of the given statement is p → q
Question 2.
Find the truth value of each of the following statements:
(i) It is not true that 3 – 7i is a real number.
Solution:
Let p : 3 – 7i be a real number.
Then the symbolic form of the given statement is ~p.
The truth value of p is F.
∴ the truth value of ~p is T. ….[~F ≡ T]
![]()
(ii) If a joint venture is a temporary partnership, then a discount on purchase is credited to the supplier.
Solution:
Let p : Joint venture is a temporary partnership.
q : Discount on purchases is credited to the supplier.
Then the symbolic form of the given statement is p → q.
The truth values of p and q are T and F respectively.
∴ the truth value of p → q is F. …..[T → F ≡ F]
(iii) Every accountant is free to apply his own accounting rules if and only if machinery is an asset.
Solution:
Let p : Every accountant is free to apply his own accounting rules.
q : Machinery is an asset.
Then the symbolic form of the given statement is p ↔ q.
The truth values of p and q are F and T respectively.
∴ the truth value of p ↔ q is F. ….[F ↔ T ≡ F]
(iv) Neither 27 is a prime number nor divisible by 4.
Solution:
Let p : 27 is a prime number.
q : 27 is divisible by 4.
Then the symbolic form of the given statement is ~p ∧ ~q.
The truth values of both p and q are F.
∴ the truth value of ~p ∧ ~q is T. …..[~F ∧ ~F ≡ T ∧ T ≡ T]
![]()
(v) 3 is a prime number and an odd number.
Solution:
Let p : 3 be a prime number.
q : 3 is an odd number.
Then the symbolic form of the given statement is p ∧ q
The truth values of both p and q are T.
∴ the truth value of p ∧ q is T. …..[T ∧ T ≡ T]
Question 3.
If p and q are true and r and s are false, find the true value of each of the following statements:
(i) p ∧ (q ∧ r)
Solution:
Truth values of p and q are T and truth values of r and s are F.
p ∧ (q ∧ r) ≡ T ∧ (T ∧ F)
≡ T ∧ F
≡ F
Hence, the truth value of the given statement is false.
(ii) (p → q) ∨ (r ∧ s)
Solution:
(p → q) ∨ (r ∧ s) ≡ (T → T) ∨ (F ∧ F)
≡ T ∨ F
≡ T
Hence, the truth value of the given statement is true.
(iii) ~[(~p ∨ s) ∧ (~q ∧ r)]
Solution:
~[(~p ∨ s) ∧ (~q ∧ r)] ≡ ~[(~ T ∨ F) ∧ (~T ∧ F)]
≡ ~[(F ∨ F) ∧ (F ∧ F)]
≡ ~(F ∧ F)
≡ ~F
≡ T
Hence, the truth value of the given statement is true.
![]()
(iv) (p → q) ↔ ~(p ∨ q)
Solution:
(p → q) ↔ ~(p ∨ q) = (T → T) ↔ ~(T ∨ T)
≡ T ↔ ~ (T)
≡ T ↔ F
≡ F
Hence, the truth value of the given statement is false.
(v) [(p ∨ s) → r] ∨ [~(p → q) ∨ s]
Solution:
[(p ∨ s) → r] ∨ ~[~(p → q) ∨ s]
≡ [(T ∨ F) → F] ∨ ~[ ~(T → T) ∨ F]
≡ (T → F) ∨ ~(~T ∨ F)
≡ F ∨ ~ (F ∨ F)
≡ F ∨ ~F
≡ F ∨ T
≡ T
Hence, the truth value of the given statement is true.
(vi) ~[p ∨ (r ∧ s)] ∧ ~[(r ∧ ~s) ∧ q]
Solution:
~[p ∨ (r ∧ s)] ∧ ~[(r ∧ ~s) ∧ q]
≡ ~[T ∨ (F ∧ F)] ∧ ~[(F ∧ ~F) ∧ T]
≡ ~[T ∨ F] ∧ ~[(F ∧ T) ∧ T]
≡ ~T ∧ ~(F ∧ T)
≡ F ∧ ~F
≡ F ∧ T
≡ F
Hence, the truth value of the given statement is false.
Question 4.
Assuming that the following statements are true:
p : Sunday is a holiday.
q : Ram does not study on holiday.
Find the truth values of the following statements:
(i) Sunday is not holiday or Ram studies on holiday.
Solution:
The symbolic form of the statement is ~p ∨ ~q.
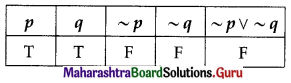
∴ the truth value of the given statement is F.
(ii) If Sunday is not a holiday, then Ram studies on holiday.
Solution:
The symbolic form of the given statement is ~p → ~q.
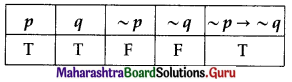
∴ the truth value of the given statement is T.
(iii) Sunday is a holiday and Ram studies on holiday.
Solution:
The symbolic form of the given statement is p ∧ q.
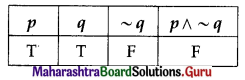
∴ the truth value of the given statement is F.
Question 5.
If p : He swims.
q : Water is warm.
Give the verbal statements for the following symbolic statements:
(i) p ↔ ~q
Solution:
p ↔ ~ q
He swims if and only if the water is not warm.
(ii) ~(p ∨ q)
Solution:
~(p ∨ q)
It is not true that he swims or water is warm.
![]()
(iii) q → p
Solution:
q → p
If water is warm, then he swims.
(iv) q ∧ ~p
Solution:
q ∧ ~p
The water is warm and he does not swim.
12th Commerce Maths Digest Pdf
- 12th Commerce Maths Exercise 1.1 Solutions
- 12th Commerce Maths Exercise 1.2 Solutions
- 12th Commerce Maths Exercise 1.3 Solutions
- 12th Commerce Maths Exercise 1.4 Solutions
- 12th Commerce Maths Exercise 1.5 Solutions
- 12th Commerce Maths Exercise 1.6 Solutions
- 12th Commerce Maths Exercise 1.7 Solutions
- 12th Commerce Maths Exercise 1.8 Solutions
- 12th Commerce Maths Exercise 1.9 Solutions
- 12th Commerce Maths Exercise 1.10 Solutions
- 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions