Matrices Class 12 Commerce Maths 1 Chapter 2 Exercise 2.5 Answers Maharashtra Board
Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Ex 2.5 Questions and Answers.
Std 12 Maths 1 Exercise 2.5 Solutions Commerce Maths
Question 1.
Apply the given elementary transformation on each of the following matrices:
(i) \(\left[\begin{array}{cc}
3 & -4 \\
2 & 2
\end{array}\right]\), R1 ↔ R2
(ii) \(\left[\begin{array}{cc}
2 & 4 \\
1 & -5
\end{array}\right]\), C1 ↔ C2
(iii) \(\left[\begin{array}{ccc}
3 & 1 & -1 \\
1 & 3 & 1 \\
-1 & 1 & 3
\end{array}\right]\) 3R2 and C2 → C2 – 4C1
Solution:

Question 2.
Transform \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
2 & 1 & 3 \\
3 & 2 & 4
\end{array}\right]\) into an upper triangularmatrix by suitable row transformations.
Solution:

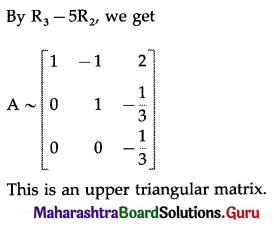
![]()
Question 3.
Find the cofactor matrix of the following matrices:
(i) \(\left[\begin{array}{cc}
1 & 2 \\
5 & -8
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
5 & 8 & 7 \\
-1 & -2 & 1 \\
-2 & 1 & 1
\end{array}\right]\)
Solution:




Question 4.
Find the adjoint of the following matrices:
(i) \(\left[\begin{array}{cc}
2 & -3 \\
3 & 5
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
Solution:

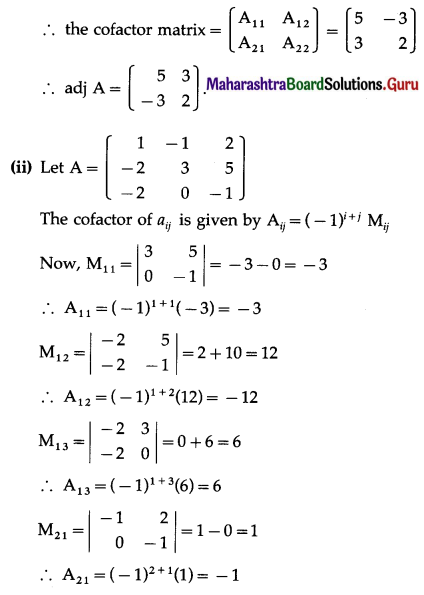

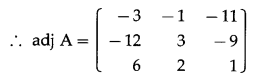
![]()
Question 5.
Find the inverses of the following matrices by the adjoint mathod:
(i) \(\left[\begin{array}{rr}
3 & -1 \\
2 & -1
\end{array}\right]\)
(ii) \(\left[\begin{array}{cc}
2 & -2 \\
4 & 5
\end{array}\right]\)
(iii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
Solution:

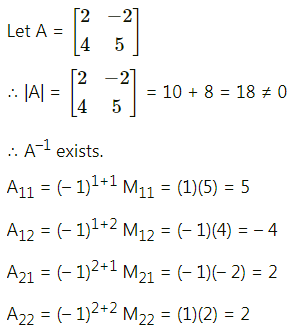
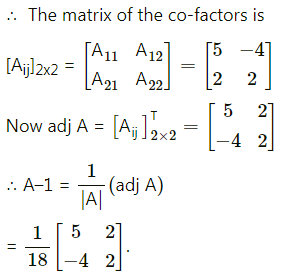



Question 6.
Find the inverses of the following matrices by the transformation method:
(i) \(\left[\begin{array}{cc}
1 & 2 \\
2 & -1
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:
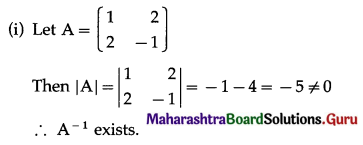

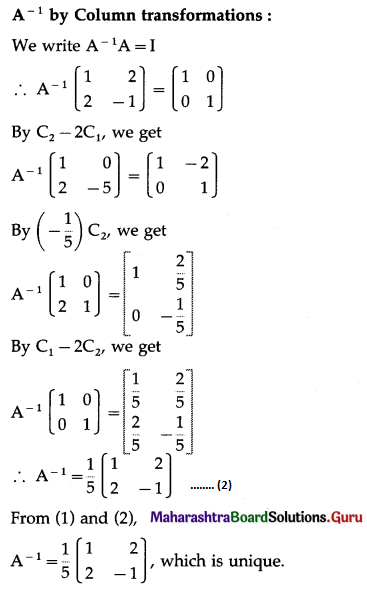


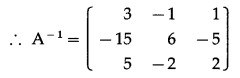
![]()
Question 7.
Find the inverse of A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) by elementary column transformations.
Solution:

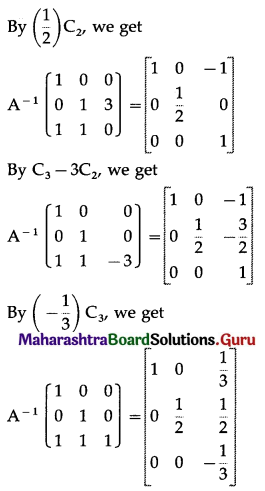
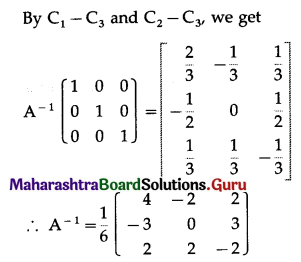
Question 8.
Find the inverse of \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\) by the elementary row transformations.
Solution:


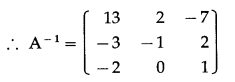
![]()
Question 9.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\), then find matrix X such that XA = B.
Solution:


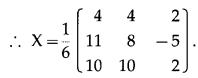
Question 10.
Find matrix X, if AX = B, where A = \(\left[\begin{array}{ccc}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\)
Solution:


12th Commerce Maths Digest Pdf
- 12th Commerce Maths Exercise 2.1 Solutions
- 12th Commerce Maths Exercise 2.2 Solutions
- 12th Commerce Maths Exercise 2.3 Solutions
- 12th Commerce Maths Exercise 2.4 Solutions
- 12th Commerce Maths Exercise 2.5 Solutions
- 12th Commerce Maths Exercise 2.6 Solutions
- 12th Commerce Maths Exercise Miscellaneous Exercise 2 Solutions