Class 12

Balbharti Yuvakbharati English 12th Digest Chapter 1.3 The Cop and the Anthem Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 1.3 The Cop and the Anthem

12th English Digest Chapter 1.3 The Cop and the Anthem Textbook Questions and Answers

Question 1.
Suppose you have gone to a place where the winter season is very severe. Discuss with your partner the ways in which you would protect yourself in the cold climate. (The answer is given and underlined.)

Answer:

Question 2.
When you see a cop approaching, you feel either ‘relieved’ or ‘scared’. Discuss with your partner and write down the situations when you feel ‘relieved’ or ‘scared’.
Answer:
Relieved:
(a) You are walking alone in a dark street.
(b) There is a fight taking place near you.
(c) A group of rough-looking people are coming towards you on a lonely road.
Scared:
(a) You are riding a bike without a valid driving licence.
(b) You have broken a traffic signal.
(c) You have been involved in a fight.

Question 3.
Discuss some of the motivating things that can change a person’s life :
Answer:
(a) Listening to an inspiring speech
(b) Reading motivating books and biographies of great people
(c) Reading epics and religious books
(d) Observing successful/happy people or watching biopics of their lives.

(A1)

Question (i)
Discuss with your partner and find out the different ways in which Soapy tried ; to get arrested. The first one is given.
Answer:
(a) Tried to enter a luxurious cafe.
(b) Threw a stone and broke a shop window.
(c) Ate heartily at a restaurant and then said he had no money.
(d) Shouted and howled and raved and danced on the sidewalk.
(e) Stole an umbrella.

Question (ii)
Describe the atmosphere when Soapy reached near the Church.
Answer:
(a) A soft light glowed through the violet-stained window.
(b) Sweet music drifted out of the quaint, old church.
(c) There was a full, radiant moon, and few vehicles and pedestrians.
(d) Sparrows twittered sleepily in the eaves.

(A2)

Question (i)
Read the story and match the incidents given in Column A with the consequences given in Column B.

Answer:

1. Soapy tried to enter a cafe – Strong and ready hands of the head waiter turned him around.
2. Soapy broke a glass window – The cop ran after another man.
3. Two waiters pitched Soapy on the callous pavement – He stood up slowly beating the i dust from his clothes.
4. Soapy heard the anthem being played in the Church – Suddenly a wonderful change came in his heart.
5. Cop arrests Soapy for hanging around. – Dream of turning around in life was shattered.

Question (ii)
Give reasons and complete the following: (The answers are given directly and underlined.)
Answer:
(a) Soapy had confidence in himself because he was shaven, his coat was trim and he had a neat, black bow. The portion of him that showed above the table looked respectable and would raise no doubt in the waiter’s mind.
(b) The head waiter of the luxurious cafe did not allow Soapy to enter because he saw Soapy’s tattered trousers and old, worn out shoes, and knew that Soapy would not have money to pay for a meal.
(c) The cop did not arrest Soapy for breaking the glass window because Soapy was standing calmly and talking to him. The policeman felt that men who smash glass windows do not remain to chat with the police.
(d) The cop did not arrest Soapy for shouting and dancing because it was the time of celebrations for the local college boys. They were generally noisy but harmless, and he had been told by his superiors to let them be.

(iii) Pick out the lines from the text which show that:

Question (a)
Soapy wants to enter the cafe for two reasons.
Answer:
1. A roasted mallard duck, thought Soapy, would be about the thing with a bottle of wine and then some cheese, a cup of coffee and a cigar.
2. The meat would leave him filled and happy for the journey to his winter island.

Question (b)
Soapy was afraid that he won’t be able to enter the prison.
Answer:
It seemed that his route to the coveted island was not to be an easy one. Some other way of entering the limbo must be devised.

Question (c)
Soapy was not caught by the cop for throwing stones at the glass.
Answer:
1. The policeman refused to accept Soapy even as a clue.
2. The policeman saw a man half-way down the block running to catch a car. With drawn club he joined in the pursuit.

Question (d)
Soapy actually did not want the umbrella.
Answer:
He hurled the umbrella angrily into the excavation.

Question (e)
Listening to the anthem, Soapy remembered his good old days.
Answer:
He had known it well in the days when his life contained such things as mothers and roses and ambitions and friends and immaculate thoughts and collars.

Question (iv)
‘He would make a man of himself again’ – The word ‘man’ in the sentence means ……………….. .
Answer:
‘He would make a man of himself again’ – The word ‘man’ in the sentence means a responsible and worthy human being.

Question (v)
Soapy’s earlier life was much different from his present life. Complete the table to show this contrast. One is done for you.

Answer:

Earlier life	Present life
(a) contained friends and roses	(a) unworthy desires
(b) eager ambitions	(b) dead hopes, degraded days
(c) clean thoughts and clothes	(c) wrecked faculties and base motives

Question (vi)
After listening to the sweet and solemn organ notes, Soapy decides to:
Answer:
1. pull himself out of the mire, conquer the evil that had enslaved him and make a man of himself again
2. resurrect his old eager ambitions and pursue them without faltering
3. go into the roaring downtown district and find work

Question (vii)
Write an incident in which you did something wrong and repented for it later. Give reasons.
Answer:
A lady who stayed in my building used to shout at me for playing noisily under her window. One day, she shouted at me as usual from her window and went inside. I suddenly got angry and threw a stone at her window. The stone hit the glass which broke. I heard a loud shout of pain and ran away. I later came to know that she had been badly injured by the shattered glass. I repented for what I had done. Though I did not tell her that I was the culprit, I was very good to her after that.

(A3)

Question (i)
O’Henry has used different words to indicate prison where Soapy wants to reach. Make a list of those words from the extract.
Answer:
the island

Question (ii)
Find out the words used for the ‘degraded state of Soapy’.
Answer:

1. the pit into which he had tumbled
2. the degraded days
3. unworthy desires
4. dead hopes
5. wrecked faculties
6. base motives
7. mire
8. evil that had enslaved him.

Question (iii)
The specific meaning of word ‘anthem’ in the content of the story is:
Answer:
Anthem – a rousing or uplifting song.

(A4)

Question (i)
Convert the following sentences into the negative without changing their meanings:
(a) The policeman refused to accept Soapy even as a clue.
(b) Soapy drifted along, twice unsuccessful.
(c) Soapy stopped his unavailing racket.
(d) The island seemed very far away.
(e) The island seemed an unattainable Arcadia.
Answer:
(a) The policeman did not accept Soapy even as a clue.
(b) Soapy drifted along, twice not successful.
(c) Soapy stopped his racket which was not successful.
(d) The island seemed not at all near.
(e) The island seemed an Arcadia which was not attainable.

Question (ii)
Convert the following sentences into the affirmative without changing their meanings :
(a) Men who smash windows do not remain to chat with the police.
(b) On the opposite side of the street was a restaurant of no great pretensions.
(c) Why don’t you call a cop?
(d) Noisy; but no harm.
(e) They seemed to regard him as a King who could do no wrong.
Answer:
(a) Men who smash windows refrain from remaining to chat with the police.
(b) On the opposite side of the street was a very ordinary restaurant.
(c) Please call a cop.
(d) Noisy; but harmless.
(e) They seemed to regard him as a King who was always right.

(A5)

Question (i)
‘Forgiveness is often better than punishment’. Write two paragraphs – one for and another against this notion.
Answer:
1. To err is human, to forgive is divine.

We all make mistakes. Nobody is perfect. That is why we are human. However, mistakes should be forgiven if there is sufficient repentance. Forgiveness will make the guilty person feel ashamed of his conduct and he will not repeat it. It is easy to punish but very difficult to forgive someone. It needs a big heart and a lot of kindness. If we punish the guilty person we will only make him more defiant. If punishing someone could have solved the problem, criminals who have been jailed would never have repeated the crime. But this is not found to be so. Just as God forgives us our mistakes, we should forgive others their mistakes too.

2. Punishment is the only answer

Forgiveness may work in certain cases, but there are hardened criminals who will not respond to forgiveness. They will only be stopped by punishment. If a person has murdered another in cold blood, will he improve by forgiveness? Never. He has to be punished severely so that he does not repeat it and society feels safe.

People only fear punishment. It can be easily seen at traffic signals – if there is no policeman to punish you, most people will break the signal. Then there will be chaos. If there is no punishment and no prisons, people will do whatever they want – rob, kill, etc. – and go off freely. No, in a society where it is not possible to expect everyone to have high values, punishment for misdeeds is the only solution.

Question (ii)
You are the class representative and you have been asked by the Principal to conduct an interview of a cop. Frame 8-10 questions with the help of the following points, give introduction and conclusion.

• reasons for joining the department
• special trainings
• developing the skill to identify and locate criminals
• dealing with criminals
• achievements and awards

Answer:
Good morning, Mr. Pawar. Congratulations on your excellent work in finding the bank robbers. May I ask you a few questions about your life? Thank you.

1. When did you join the police department?
2. Which examinations did you have to clear for the post?
3. What were your reasons for joining the department?
4. Did you have to go through any special training sessions?
5. What type of criminals do you come across most in this area-thieves, killers, molesters,
   etc?
6. How do you identify or locate criminals?
7. Once you catch the culprit-say a thief-how do you deal with him?
8. Can you tell me something about your achievements and awards?
9. How can you motivate others to join the force?
10. Any message to college students?

Thank you, Sir, for sparing the time for this interview. It will be published in our school magazine. Good day.

(A6)

Question (i)
Make a list of jobs which would give you an opportunity to help the society or serve the country. Also mention the different ways in which they can be beneficial to the people and also the country,

Question (ii)
Go to your school/college library and read some other stories by O’Henry like, ‘The Gift of the Magi’, ‘The Last Leaf and ‘After Twenty years’. Write the stories in short in your notebook.

Yuvakbharati English 12th Digest Chapter 1.3 The Cop and the Anthem Additional Important Questions and Answers

Read the extract and complete the activities given below:

Global Understanding:

Question 1.
Name the following:
Answer:

1. This is where Soapy stopped at a luxurious cafe
2. This had been a gift to Soapy: a neat, black bow
3. This is what Soapy wanted to eat: a roasted mallard duck, some cheese a bottle of wine, a cup of coffee
4. This is what Soapy wanted to drink: Soapy’s tattered
5. This is what the head waiter noticed:trousers and old shoes
6. This is where Soapy was left by the head: on the sidewalk

Question 1.
Write if the following sentences are True or False. Correct the False sentences:
1. Soapy broke the glass of the shop window.
2. Nobody heard the breaking of the window.
3. The policeman chased Soapy.
4. Soapy did not run away from the place.
5. The restaurant Soapy entered was an ordinary one.
6. The policeman ate beefsteak, flapjacks, doughnuts and pie.
Answer:
True sentences:
1. Soapy broke the glass of the shop window.
4. Soapy did not run away from the place.
5. The restaurant Soapy entered was an ordinary one.

False sentences:
2. Nobody heard the breaking of the window.
3. The policeman chased Soapy.
6. The policeman ate beefsteak, flapjacks, doughnuts and pie.

Corrected sentences:
1. A policeman as well as some people heard the breaking of the window.
2. The policeman chased a man running to catch a car.
3. Soapy ate beefsteak, flapjacks, doughnuts and pie.

Question 2.
Complete the table:
(The answers is given directly and underlined.)
Answer:

The Words	mo said	To whom
1. Noisy, but no harm	A policeman	A citizen
2. I took it.	Soapy	The umbrella man
3. You know how these mistakes occur.	The umbrella man	Soapy
4. Of course it’s mine!	Soapy	The umbrella man
5. We’ve instructions to let them be.	A policeman	A citizen
6. I hope you’ll excuse me.	The umbrella man	Soapy

Question 3.
Rearrange the following sentences according to their occurrence in the extract:

1. Soapy decided to go into the downtown district and find work.
2. A policeman caught Soapy’s arm.
3. Soapy saw a quaint old church.
4. Soapy’s ears caught sweet music.

Answer:

1. Soapy saw a quaint old church.
2. Soapy’s ears caught sweet music.
3. Soapy decided to go into the downtown district and find work.
4. A policeman caught Soapy’s arm.

Question 4.
Complete the following:
(The answers are given directly and underlined.)
Answer:

1. A soft light glowed through one violet-stained window.
2. Soapy came to a standstill on an unusually quiet corner.
3. Soapy stood without moving near the iron fence listening to the anthem that the organist played.
4. Soapy planned to resurrect his old eager ambitions.

Answer the following in a few words each:

Question 1.
Who was lighting a cigar?
Answer:
A well-dressed man

Question 2.
Who twirled his club?
Answer:
A policeman

Question 3.
Who grabbed the umbrella?
Answer:
Soapy

Question 4.
Whom did the policeman help?
Answer:
A tall blonde

Complex Factual:

Question 1.
Give reasons and complete the following:
(The answers are given directly and underlined.)
Answer:
Soapy was disgusted with the policeman because he refused to accept that Soapy had broken the window, and he rushed off to chase another man.

Question 2.
Complete the web:
(The answers are given directly and underlined.)
Answer:

Question 3.
Describe Soapy’s behaviour on the sidewalk.
Answer:
On the sidewalk Soapy began to yell drunken meaningless things at the top of his harsh voice. He danced, howled, spoke wildly and made a big disturbance.

Question 4.
Describe the wonderful change in Soapy’s soul.
Answer:
After listening to the anthem, Soapy remembers his earlier life, and is horrified to realize that he has indeed become a degraded person. He decides to pull himself out of the pit into which he has fallen and make a man of himself again. He determines to bring back to his life his old eager ambitions and pursue them. He makes up his mind to take up a job.

Question 5.
Describe the end of the story in your own words.
Answer:
Initially Soapy had felt that he would like to pass the winter months in prison, and he makes several efforts to get himself arrested. The notes of anthem transform him from within and he decides to give up his evil ways and become a man again. He resolves to work hard. At that very moment, ironically, a policeman arrests him for loitering and he is sent to prison for three months. Soapy faces the irony of fate as the moment he realizes that real freedom lies in a virtuous life, he is taken into confinement.

Question 6.
Complete the following:
Soapy was angry because ………..
Answer:
Soapy was angry because when he wanted to fall into the clutches of the policemen. In order to be arrested, they seemed to regard him as a king who could do nothing wrong.

Inference/Interpretation/Analysis:

Question 1.
Complete the following:
(The answers are given directly and underlined.)
Answer:
Soapy took a stone because he wanted to break the glass of the shop window. This would result in a policeman arresting him for this act, and he would be imprisoned for the winter, which was exactly what he wanted.

Discuss the hidden meaning in the expressions/sentences.

Question 1.
It catered to large appetites and modest purses.
Answer:
The restaurant prepared food for ordinary workers who had large appetites but very little money.

Question 2.
He told the waiter the fact that the minutest coin and himself were total strangers.
Answer:
He told the waiter that he did not have any money.

Question 3.
A voice like butter cakes and an eye like the cherry in the Manhattan cocktail.
Answer:
A very smooth voice and a hard, stony eye (a tough person).

Question 4.
Discuss the meaning in the context:
He caught at the immediate straw of ‘disorderly conduct’.
Answer:
Soapy wanted to be arrested by a policeman and imprisoned. However, his efforts towards this end had been unsuccessful, and he was worried that he would continue to be unsuccessful. When he suddenly came upon a policeman lounging in front of a theatre, an idea struck him. He felt that if he shouted and screamed and made a lot of noise, he would be arrested for behaving in a dangerous and disturbing way in public, and would be imprisoned, which was what he wanted.

Question 5.
Complete the following:
(The answer is given directly and underlined.)
Answer:
Soapy was angry because even after he had stolen a man’s umbrella, the man did not report him to the police, but instead apologized and said that perhaps he (the umbrella man) had made a mistake.

Question 6.
The umbrella man did not call a policeman. Give reasons for this.
Answer:
The umbrella man had himself probably stolen the umbrella from somewhere. When Soapy picked up the umbrella, the man first thought that he could get it back. But when Soapy spoke about calling a policeman, the man thought that the umbrella was actually Soapy’s, and Soapy would hand him over to the police. Hence, he apologized quickly and walked away without calling a policeman.

Personal Response:

Question 1.
Give your opinion about Soapy’s desire to enter prison.
Answer:
I find it very strange that a person can actually want to enter prison, whatever be the reason. At least, from what I know of prisons, they are terrible places, and one has a very difficult time there. However, Soapy has obviously been to prison before, and probably enjoys the free food and protection from the winter that he gets there.

Question 2.
Have you ever bought/eaten something and then found that you did not have enough money to pay for it? Describe your feeling at that time.
Answer:
Yes, it happened to me once. I went to a mall and bought a jacket for myself. I had been looking at a lot of jackets and I got confused with the prices. Finally, when the cashier was making the bill, I found that the jacket I had chosen was very expensive and I did not have enough money to pay for it. I was very embarrassed to tell the cashier this, but I had to. He gave me an angry look.

Question 3.
Have you ever stolen/wanted to steal anything? Narrate in brief.
Answer:
Yes, when I was about 12 years old, I stole my friend’s remote-controlled toy car, which his uncle had sent him from abroad. It was a beautiful car. However, when I was playing with it at home my mother saw me, and she made me return the car. I later felt very ashamed of myself, but fortunately my friend forgave me.

Language Study.

Question 1.
If only he could reach a table in the restaurant unsuspected, success would be his.
(Rewrite using ‘unless’.)
Answer:
Unless he could reach a table in the restaurant unsuspected, success would not be his.

Question 2.
One dollar for the cigar would be enough.
(Add a question tag.)
Answer:
One dollar for the cigar would be enough, wouldn’t it?

Question 3.
Some other way of entering the limbo must be devised.
(Use an infinitive in place of a gerund.)
Answer:
Some other way to enter the limbo must be devised.

Question 4.
He had set his silk umbrella by the door on entering. (Rewrite using the verb form of the underlined word.)
Answer:
He had set his silk umbrella by the door when he entered.

Question 5.
At length Soapy reached one of the avenues to the east. (Rewrite using another adverb phrase with the same meaning as the underlined phrase.)
Answer:
After a long time Soapy reached one of the avenues to the east.

Question 6.
On an unusually quiet corner, Soapy came to a standstill. (Rewrite using ‘that’.)
Answer:
Soapy came to a standstill on a corner that was unusually quiet.

Vocabulary:

Question 1.
Guess the meaning of the following in the context:
1. winter island
2. eye fell upon
Answer:
1. winter island – prison.
2. eye fell upon – saw or noticed.

Question 2.
O’Henry has used different words to indicate prison, where Soapy wants to reach. Make a list of those words from the extract.
Answer:

1. winter island
2. coveted island
3. limbo

Question 3.
Make sentences using the following words/expressions :
1. eye fell upon
2. strolled
Answer:
1. My eye fell upon the clock, and I sat up with shock.
2. Seema strolled along the beach, enjoying the breeze.

Question 4.
Guess the meaning of:

1. napery
2. betook
3. brass buttons

Answer:

1. napery – table linen.
2. betook – to cause oneself to go.
3. brass buttons – the police.

Question 5.
O’Henry has used different words to indicate prison where Soapy wants to reach. Make a list of those words from the extract:
Answer:
the island

Question 6.
Fill in the blanks with the correct nouns from the extract:

1. friendly
2. electric
3. large
4. callous

Answer:

1. friendly voice
2. electric lights
3. large appetites
4. callous pavement

Question 7.
O’Henry has used different words to indicate prison where Soapy wants to reach. Make a list of those words from the extract.
Answer:
the island, Arcadia

Question 8.
Pick out four verbs in the simple past tense from the extract.
Answer:
danced, howled, raved, disturbed

Question 9.
Match the words in Column A with the meanings in Column B :
Answer:

1. disconsolate – very unhappy
2. sauntered – walked in a relaxed manner
3. raved – spoke wildly
4. rendered – made

Non-Textual Grammar

Do as directed:

Question 1.
Shivani found a small box and dropped her bangles inside.
(Rewrite the sentence, beginning ‘Finding …)
Answer:
Finding a small box, Shivani dropped her bangles inside.

Question 2.
Sunlight from the window made her black hair appear brown. (Rewrite using ‘that’.)
Answer:
Sunlight that came from the window made her black hair appear brown.

Question 3.
On the day the school closed for the summer, no student was more delighted than Rithik.
(Change the degree.)
Answer:
1. On the day the school closed for the summer, Rithik was the most delighted student. – Superlative degree
2. On the day the school closed for the summer, Rithik was more delighted than any other student. – Comparative degree

Spot the error in the following sentences and rewrite them correctly:

Question 1.
There is room for much boxes in this cupboard.
Answer:
There is room for many boxes in this cupboard.

Question 2.
If I requires help for him in public places, I was not embarrassed to seek it from people around.
Answer:
If I required help for him in public places, I was not embarrassed to seek it from people around.

Balbharti Maharashtra State Board Class 12 Psychology Solutions Chapter 5 Emotions Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Psychology Solutions Chapter 5 Emotions

1. Choose the correct option and complete the following statements.

Question 1.
…………… is a combination of bodily arousal, expressive behavior, thoughts, and feelings.
(a) Response
(b) Reaction
(c) Emotions
Answer:
(c) Emotions

Question 2.
According to James Lange we first experience ……………….. then emotions.
(a) physical arousal
(b) feelings
(c) thoughts
Answer:
(a) physical arousal

Question 3.
Emotion is used as a …………….. to control others.
(a) weapon
(b) measure
(c) opportunity
Answer:
(a) weapon

Question 4.
When you allow another person to exploit you, you are a victim of ………….. abuse.
(a) physical
(b) emotional
(c) social
Answer:
(b) emotional

Question 5.
Exercising releases ………………… which makes you feel good as a stress buster.
(a) endorphins
(b) thyroxin
(c) insulin
Answer:
(a) endorphins

2. Identify the odd items from the following and write a suitable reason for your choice

Question 1.
admiration, disgust, acceptance, trust

Question 2.
kicking, ignoring, shoving, screaming

Question 3.
Reassess, React, Respond, Relax

Question 4.
meditation, social work, compassion, engage in hobbies

3. Match the pair.

Question 1.

Group A	Group B
(1) Happiness	(a) basic emotion
(2) Paul Ekman	(b) fight and flight
(3) Anger	(c) surprise
(4) Fear	(d) sadness
(5) Grief	(e) triggers
(6) Anger management technique	(f) powerful emotion

Answer:

Group A	Group B
(1) Happiness	(c) surprise
(2) Paul Ekman	(a) basic emotion
(3) Anger	(f) powerful emotion
(4) Fear	(b) fight and flight
(5) Grief	(d) sadness
(6) Anger management technique	(e) triggers

4. State whether the following statements are true or false.

Question 1.
Emotional well-being is not easily observable.
Answer:
True

Question 2.
Positive emotions energise you.
Answer:
True

Question 3.
You should feel guilty for standing up for yourself.
Answer:
false

Question 4.
Anger is a basic negative emotion.
Answer:
True

5. Answer the following questions in 35 – 40 words each.

Question 1.
Explain the term facial feedback hypothesis.
Answer:
According to the facial feedback hypothesis, our facial expressions provide feedback to our brain about our emotions. Facial expressions are not only the result of our emotions, e.g., smiling in happiness, but they are also capable of influencing emotions, e.g. laughter can actually make us feel happier. The same might hold true for other emotions as well. In the 1840’s, William James presented the idea that awareness of our bodily experiences is the basis of emotion.

Question 2.
When does an individual face social rejection?
Answer:
Social rejection occurs when an individual is deliberately excluded from a social relationship or interaction. This can be done by a person or a group. It includes rejection of the person by family/ peers/ colleagues or even in intimate relationships. Rejection may be active, i.e., by ridiculing, bullying, etc., or passive, i.e., ‘silent treatment’. Social rejection may be faced due to individual differences e.g., attractiveness, shyness or due to intergroup exclusion on the basis of prejudice, e.g., in case of Dalits or ethnic minorities.

Question 3.
With the help of an example write the non-verbal triggers of anger.
Answer:
Anger is a common emotion that everybody experiences in life from time to time. Anger is a normal response to some real or perceived threat. It is a protective emotion that help us to defend ourselves against physical or psychological harm.

Triggers of Anger refer to any event that signals the brain to activate the body’s anger system. The triggers of anger may be (i) verbal, for e.g., being blamed, disrespected or abused (ii) non¬verbal, for e.g., being ignored unappreciated or rejected, (iii) physical such as physical threats, sexual/ physical assault, etc.

Non-verbal triggers of anger are feelings of being neglected, disregarded, disappointed, unloved or frequently spurned. It is expressed through gestures such as pointing a finger, shrugging the shoulders; by facial expressions such as sneering, frowning and also by behaviours such as groaning/sighing/whining or speaking in a mocking tone.

There are three factors involved in the experience of anger : A trigger (causes of anger) → individual’s personality → particular interpretation of that situation.

Question 4.
What are the aspects of emotional well-being?
Answer:
Emotional well-being means managing our emotions, both positive and negative ones, so that we can lead a healthy and productive life. It is the absence of negative affect as well as general satisfaction with life. A person who experiences emotional well-being is positively engaged with the world.
The aspects of emotional well-being are at three levels viz. physical, emotional and social.

1. Physical level, i.e., well balanced diet, exercise.
2. Emotional level, i.e., practise mindfulness, raising levels of motivation and optimism.
3. Social level, i.e., engaging in prosocial behaviour, meaningful relationships.

6. Compare and Contrast

Question 1.
Happiness and Sadness

Question 2.
James Lange theory and Cannon Bard’s Theory

7. Write short notes on the following in 50 – 60 words each.

Question 1.
Measures of dealing with Emotional Abuse
Answer:
Emotional abuse is any kind of abuse that is emotional rather than physical in nature. It occurs when one person subjects or exposes another person to intentionally harmful behaviour that may result in anxiety, depression and psychological trauma to the victim.
The types of emotional abuse may be-

1. verbal abuse such as blaming, insulting, labeling, threatening, swearing, etc.
2. non verbal abuse such as ignoring, rejection, bullying, spying, etc.

The most important technique is to break the silence and stand up for yourself.

1. Accept that emotional abuse is not because of you, i.e., don’t justify the actions of the abuser.
2. Respond assertively to the abuser but seek distance from him.
3. Give yourself time to heal.
4. Prioritize your self-care, e.g., eating right, exercise, etc.
5. Mobilise support from family and friends. If needed, seek professional help.

Question 2.
Plutchiks’s Model of Emotions
Answer:

Robert Plutchik presented the wheel of emotions,

1. there are 8 basic emotions viz. joy, trust, fear, surprise, sadness, anticipation, anger and disgust.
2. each primary emotion has its polar opposite such as fear is opposite of anger.
3. primary emotions combine to produce complex emotions, for e.g., love (complex) is a combination of joy and trust.
4. intensity of emotions increases as we move toward the centre and decreases as we move outward. For e.g., apprehension (weak) → fear (basic) → terror (strongest).

This model is important from the perspective of emotional literacy, i.e., understanding emotional levels, complexity and change as well as appropriate emotional labelling

Question 3.
Anger -A powerful emotion
Answer:
Anger is a common emotion that everybody experiences in life from time to time. Anger is a normal response to some threat. It is a protective emotion that helps us to defend ourselves against physical/ psychological harm. However, anger may also be unwanted, irrational and destructive. When we experience anger, our amygdala goes into action and overrides the cerebral cortex which is in control of thinking and evaluation. Triggers of anger refer to any event that signals the brain to activate the body’s anger system. The triggers may be (i) verbal, for e.g., being blamed, disrespected or abused (ii) non-verbal, for e.g., being ignored unappreciated or rejected, (iii) physical such as physical threats, sexual/ physical assault, etc.

There are three factors involved in the experience of anger: A trigger (causes of anger) → individual’s personality → particular interpretation of that situation. As the experience of anger is subjective, it can be controlled too. If we understand the triggers of anger, we can anticipate potential anger episodes and provide an intentional/ acceptable response such as it may energize us towards solving problems. As anger is a powerful emotion, it must be kept in check to avoid it’s destructive out comes.

Question 4.
Managing Emotions
Answer:
The word emotion is derived from the latin word ‘emovere’, which means to stir up or to move. An emotion refers to an involuntary, aroused state of an organism involving physical, cognitive and behavioural components. It is described as a combination of bodily arousal, e.g., increased heartrate, thoughts and feelings, i.e. emotional tone and expressive behaviour, i.e., facial expression.

Managing of emotions is an important life skill. Managing emotions can be defined as, ‘the ability to be open to feelings and modulate them in oneself and in others, so as to promote personal understanding and growth. It is the ability to be aware and constructively handle both positive and challenging emotions.

Sometimes, our emotions hijack our thinking due to which we act impulsively. This is because the limbic system (emotional section) developed before the prefrontal cortex (thinking part) and is hence, an extremely strong part of the brain. Emotional management is an art as it is a form of expression as well as a science as it is a skill that needs to be learnt and practiced If a person ignores of suppresses his/her emotions it leads to anxiety. The best way of manage emotions is to acknowledge the emotions, find out what is the cause of that emotion in you, chose how to respond in that situation.

Question 5.
Benefits of Emotional Well-being
Answer:
Emotional well-being means managing our emotions, both positive and negative ones, so that we can lead a healthy and productive life.
Persons who have high emotional well-being experience benefits such as- (i) better able to deal with stress (ii) better self-regulation (iii) increased productivity in tasks undertaken (iv) increased creativity (v) life satisfaction due to meaningful activities and relationship.

1. Coping with stress – It helps to deal with stress using healthy methods such as exercise, social support, etc.
2. Better self-regulation – It enables the person to label how they feel and accept negative emotions life fear, anger, etc.
3. Increases productivity in tasks undertaken – The ability to focus is enhanced, the person feels positive and energized.
4. Increases creativity – The person indulges in divergent thinking, shows curiosity is open to new experiences.
5. Life satisfaction – The individual is able to have meaningful interactions and relationships, show empathy, altruism and engage in activities like volunteer work.

8. Answer the following 50 – 60 words.

Question 1.
Using the 3 R model of Anger Management present a case study of your own experience.
Answer:
Anger management is an intervention programme to prevent anger from turning into a habit or obstacle. It enables the person to create an awareness of and responsibility for his/her emotions. This involves two aspects (i) managing one’s own anger (ii) learning to respond effectively to anger in others.

The 3 R’s in anger management a Relax, Reassess and Respond.
1. Relaxation – Relaxation and connection with the inner self helps to enhance thinking and concentration so that we ‘respond’ rather than ‘react’ impulsively.
2. Reassess – This helps the person to revisit the situation objectively. It involves

• taking complete responsibility for your emotion
• developing empathy for the person you perceive has wronged you
• conduct a reality check e.g., is your anger justified given the facts of what happened.

The feeling’s thermometer helps to focus on the extent of anger we are experiencing and helps in the process of reassessment.

3. Respond – It entails re-engaging with the other person/situation. Responding involves

• consulting a trustworthy person to get another perspective
• engage in talks with the other party in a calm respectful manner with a willingness to sort out the situation.
• active listening and assertive speaking – Allow the person to express their viewpoint. However, we should stand up for our feeling while exhibiting the same for the other person. The right approach is a practical, positive communication style.
• cage your rage i.e. establish boundaries and moderate your anger – We must guard against escalation of our own anger which may lead us to provoke the other person. Moderation of anger and establishing clear boundaries of interaction with each other is essential.

CASE STUDY – 1 was in the passenger seat and my brother was driving the car. Suddenly, a cyclist swerved right in front after he had failed to observe the red light. This led me to get enraged at this uncalled-for action. Using the 3R technique. I tried to breathe for a few seconds to give me recovery time, i.e. Relaxation. I revisited the situation – Is my anger justified? Was it a genuine error? Is the cyclist hurt? Did the incident cause injury to us or damage to the car.? Is the anger worth my time/effort? Reassess. I allowed my elder brother to handle the situation but also assertively cautioned the teenage cyclist about the dangers of riding in a rash manner, i.e. Respond.

Question 2.
How does the brain work when angry?
Answer:
Anger is a common emotion that everybody experiences in life from time to time. Anger is a normal response to some threat. It is a protective emotion that help us to defend ourselves against physical/ psychological harm. However, anger may also be unwanted, irrational and destructive. When we experience anger, our amygdala goes into action and overrides the cerebral cortex which is in control of thinking and evaluation.

Triggers of anger refer to any event that signals the brain to activate the body’s anger system. The triggers may be (i) verbal, for e.g., being blamed, disrespected or abused (ii) non-verbal, for e.g., being ignored unappreciated or rejected, (iii) physical such as physical threats, sexual/ physical assault, etc.

There are three factors involved in the experience of anger: A trigger (causes of anger) → individual’s personality → particular interpretation of that situation. As the experience of anger is subjective, it can be controlled too. If we understand the triggers of anger, we can anticipate potential anger episodes and provide an intentional / acceptable response.

The emotional center of the brain is the Limbic system and is more primitive than the cerebral cortex. It is located in the lower section of the brain. Hence when a person is experiencing and expressing anger, he or she is not using the cortex (thinking section) but primarily functioning from the limbic system. In the limbic system, a small structure called Amygdala which is a storehouse of emotional memories plays an important role in the emotional outbursts. The data coming in from the world around us passes through the amygdala where the decision is made whether to send the data to the limbic or cortex area of the brain.

If the incoming data triggers enough of an emotional charge, the amygdala can override the cortex, which means the data will be sent to the limbic system causing the person to react using the lower part of the brain. During an overriding event, the amygdala goes into action without much regard for the consequences (since this area of the brain is not involved in judging, thinking, or evaluating).

Eg. You are waiting patiently in the queue at the bank, a person comes and cuts the line and moves ahead of you, you scream at them and ask them to go back. On an average, it can take 20 minutes for a person who has experienced an angry state of arousal to calm, to move from functioning from the emotional area to the thinking area of the brain.

Question 3.
After having realised you are emotionally abused by your best friend, write the steps you will take to deal with it.
Answer:
Emotional abuse is any kind of abuse that is emotional rather than physical in nature. It occurs when one person subjects or exposes another person to intentionally harmful behaviour that may result in anxiety, depression and psychological trauma.
The types of emotional abuse may be (i) verbal abuse such as blaming, insulting, labeling, threatening, swearing, etc. (ii) non verbal abuse such as ignoring, rejection, bullying, spying, etc. Some of the techniques to deal with emotional abuse are-

1. Accept that emotional abuse is not because of you i.e. don’t justify the actions of the abuser.
2. Respond assertively to the abuser but seek distance from him/her.
3. Give yourself time to heal.
4. Prioritize your self-care, e.g., eating right, exercise, etc.
5. Mobilise support from family and friends. If needed, seek professional help.

If I realize that I have been emotionally abused by my good friend I will adopt the following steps-

1. Disengage from the friendship and set personal boundaries
2. Understand that I am not the cause of abuse and so respond assertively to the abuser
3. Practice self care and give myself time to heal
4. If necessary seek guidance from other friends or my family / teachers.

9. Analyse the situations presented below and
a. Write the Emotion/s you experience.
b. What will be your response to this situation?

Question 1.
Anish was scolded by his boss. He came home and in a fit of rage hit his son. You are Anish’s friend who witnessed this outburst.
Answer:
I will feel anger as well as disgusted on witnessing this outbust. I will try to calm Anish and make him realise the harm that his anger can cause.

Question 2.
You helped your friend with study notes during his illness. But when your friend got better he did not respond nor show any sense of appreciation.
Answer:
I will feel disappointment as well as sadness. I will meet the friend and tell him that his lack of courtesy has hurt me.

Question 3.
Though you are a good friend of Anushka, she has not invited you to her new year’s party.
Answer:
I will feel disappointed and hurt. I will (if possible) try to find out if the action was deliberate or an oversight.

Question 4.
It’s your Birthday and you wake up that morning to find yourself surrounded with beautiful gifts.
Answer:
I will obviously feel immense happiness.

Question 5.
You have had a hectic day at college when you come home you find the door locked. You forgot your keys at home that day and your parents have not informed you of their plans.
Answer:
I will be angry at my at myself and my parents also. But since I forgot the keys, I will take full responsibility and wait it out some family member returns.

Question 6.
You have planned a surprise day out for your best friend and she tells you she is not interested and has other plans
Answer:
I will be a little sad and disappointed but will accept my friend’s decision sportingly.

Class 12 Psychology Chapter 5 Emotions Intext Questions and Answers

ACTIVITIES (Textbook Page. No. 44)

Activity 1

THINK AND ANALYSE
Think of the following situations and note down what will be the experience of each person in that situation.

1. It’s Mira’s Std. 12th result today. She comes to know that she has topped in the college.
2. Rahul’s mother passed away just few days before his 18th birthday.
3. Suchita was ridiculed by her classmate for wearing old fashioned clothes.
4. Yash had a fight at home because his parents were not allowing him to go for a late night party.

Answer:

1. Mira will experience happiness due to her success.
2. Rahul will experience grief and loneliness.
3. Suchita will experience a sense of helplessness and shame.
4. Yash will be angry with his parents and feel they are doing him an injustice.

Activity 2 (Textbook Page. No. 46)

Observe each figure carefully and write the emotion that corresponds to each in the blank spaces provided below. Can you identify which among these is a positive and negative emotion?

Answer:
(A) = Surprise (positive), (B) = Anger (negative), (C) = Disgust (negative), (D) = Sadness (negative),
(E) = Joy (positive), (F) = Fear (negative).

Activity 3 (Textbook Page. No. 46, 47)

Check whether you can name the emotions accurately from the following examples-

1. It’s Riya’s 18th birthday today and her friends have given her a surprise party.
2. Rohan recently had a break up with his long time girlfriend with whom he was in love deeply.
3. Sameer had a disagreement with his best friend over where to go for a picnic and the situation got heated up.
4. Sumi has come to know that she has failed in her exam and she is figuring out how she will convey this to her parents.
5. Ashmeet suddenly saw his school best friend across the street after many years.
6. Amy opened today’s newspaper and read the news of a 5 year old getting gang raped.

Answer:

1. Happiness
2. Surprise
3. Anger
4. Fear
5. Surprise
6. Disgust

Activity 4 (Textbook Page. No. 48)

THINK, REFLECT, ANALYSE AND DISCUSS
State what will you feel and how will /did you behave in the given following situations:-

1. You are crossing the road and suddenly find a car breaking the signal and speeding up towards you.
2. You reach home and find the table laid with your favourite dish cooked by your mother.
3. You receive a phone call telling you that your best friend is undergoing an operation and needs blood.
4. Recall an incident in your childhood when you were insulted by an adult.

Answer:

1. I will feel angry but also afraid. I will jump out of the way
2. I will feel happy and surprised.
3. I will fear but feel concerned and be motivated to arrange for the blood.
4. Students are expected to answer this question by themselves.

Activity 5 (Textbook Page. No. 49)

THINK, ANALYSE AND ACT

You see a snake ….. with reference to the above given components fill the process with your interpretations, feelings and actions.
Answer:

Balbharti Maharashtra State Board Class 12 Psychology Solutions Chapter 2 Intelligence Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Psychology Solutions Chapter 2 Intelligence

1. Choose the correct option and complete the following statements.

Question 1.
……………………. has given formula of I.Q.
(a) Binet
(b) Stern
(c) Wechsler
Answer:
(b) Stern

Question 2.
…………………. has given the concepts of fluid intelligence and crystallized intelligence.
(a) Cattell
(b) Thorndike
(c) Salovey
Answer:
(a) Cattell

Question 3.
…………………. is an individual test of intelligence.
(a) Army Alpha Test
(b) Army Beta Test
(c) Block Building Test
Answer:
(c) Block Building Test

2. State whether the following statements are true or false.

Question 1.
Verbal tests of intelligence can be given easily to illiterate people.
Answer:
False

Question 2.
It is possible to increase emotional intelligence.
Answer:
True

Question 3.
There are certain limitations to Artificial Intelligence.
Answer:
True

Question 4.
Group tests of intelligence are less expensive.
Answer:
True

3. Answer the following in one sentence each.

Question 1.
What is meant by intelligence?
Answer:
David Wechsler defines intelligence as, “the aggregate or global capacity of an individual to act purposefully, to think rationally and to deal effectively with his environment.”

Question 2.
Who is considered as the father of intelligence test?
Answer:
Alfred Binet is considered as the father of intelligence tests.

Question 3.
What is meant by verbal tests of intelligence?
Answer:
Verbal tests of intelligence make use of words and numbers to measure intelligence and subjects respond verbally to the test items, for e.g., WAIS, Army Alpha Test, etc.

Question 4.
What is meant by individual test of intelligence?
Answer:
Individual tests of intelligence are tests which can be administered to a single person at a time, for e.g., Stanford Binet Scales, WAIS, Koh’s Block Design Test, etc.

4. Define / Explain the concepts in 25 – 30 words each.

Question 1.
Mental Age
Answer:
Alfred Binet introduced the concept of Mental Age. It is defined as the age at which the person successfully performs on all items of the test prepared for that age level. Mental Age need not correspond to Chronological Age. If Mental Age (MA) is the same as Chronological Age (CA), the person has average intelligence. For e.g., Sumit aged 10 years has successfully performed all items on the test for age 12. Hence, his Mental Age will be 12 years, i.e., he has above average intelligence.

Question 2.
Social Intelligence
Answer:
E.L. Thorndike proposed the term Social Intelligence. Howard Gardner included ‘interpersonal intelligence’in the Multiple Intelligences Theory. According to Karl Albrecht, ‘Social intelligence . is the ability to get along well with others and to get them to cooperate with oneself.’

A continued pattern of nourishing behaviour indicates a high level of social intelligence. Such persons are skilled at interacting with and understanding people around them. They respect and encourage others. They effectively comprehend social dynamics.

Question 3.
Emotional Intelligence
Answer:
The term Emotional Intelligence was used for the first time by John Mayer and Peter Salovey. The concept of emotional intelligence was popularized by Daniel Goleman. It is defined as “the ability to perceive and monitor one’s own and others emotions, to discriminate among them and to use this information to guide one’s thinking and actions.” Emotional Intelligence refers to a set of cognitive abilities such as perceiving emotions, using emotions to facilitate thought, understanding emotions and managing (regulating) emotions. Persons with high emotional intelligence tend to be emotionally stable, patient, optimistic, enthusiastic and calm.

5. Write short notes on the following.

Question 1.
Intelligence Quotient
Answer:
Intelligence is the highest attribute of human beings. Different psychologists have defined intelligence differently. Lewis Terman explains intelligence as, “an ability to think on an abstract level.”

David Wechsler defines intelligence as, “the aggregate or global capacity of an individual to act purposefully, to think rationally and to deal effectively with his environment.”

Intelligence Quotient refers to a measurement of intelligence.. In 1912, William Stern introduced the concept of intelligence quotient (IQ). Terman, refined the formula for calculating IQ, which is as stated below-
IQ = \(\frac {MA}{CA}\) × 100
Example: Ankush who is 10 years old has a Mental Age of 11 years. Let us calculate his IQ.
MA = 11 years CA = 10 years IQ = ?
IQ = \(\frac {MA}{CA}\) × 100 = \(\frac {11}{10}\) × 100 = 110
Ankush has an IQ of 110.

Question 2.
Charles Spearman’s theory of intelligence
Answer:
Intelligence is the highest attribute of human beings. Different psychologists have defined intelligence differently. Lewis Terman explains intelligence as, “an ability to think on an abstract level.”
David Wechsler defines intelligence as, “the aggregate or global capacity of an individual to act purposefully, to think rationally and to deal effectively with his environment.”
In 1927, Charles Spearman with the help of a statistical method called factor analysis separated and identified two different factors of intelligence viz. General factor (g) and Specific factor (s).

1. General factor is the minimum competence required to carry out daily work.
2. Specific factor includes abilities which are required to solve problems in specific areas.

Question 3.
Verbal tests of intelligence
Answer:
Intelligence is the highest attribute of human beings. Different psychologists have defined intelligence differently. Lewis Terman explains intelligence as, “an ability to think on an abstract level.”
David Wechsler defines intelligence as, “the aggregate or global capacity of an individual to act purposefully, to think rationally and to deal effectively with his environment.”

On the basis of material used in the tests, intelligence tests can be classified as Verbal tests and Non-verbal tests of intelligence. Intelligence tests that use language (words or numbers) for measuring intelligence are called verbal tests of intelligence. In these tests subjects are required to respond verbally to test items. Army Alpha Test, Wechsler’s Adult Intelligence Scale (WAIS), etc., are some of the examples of verbal tests of intelligence. These tests are language and culture bound and hence cannot be used with children, illiterates etc. However, they are useful in measuring higher mental abilities.

Question 4.
Non-verbal tests of intelligence
Answer:
Intelligence is the highest attribute of human beings. Different psychologists have defined intelligence differently. Lewis Terman explains intelligence as, “an ability to think on an abstract level.”
David Wechsler defines intelligence as, “the aggregate or global capacity of an individual to act purposefully, to think rationally and to deal effectively with his environment.”
On the basis of material used in the tests, intelligence tests can be classified as Verbal tests and Non-verbal tests of intelligence.

Intelligence tests that use pictures, designs, material objects, etc., to measure intelligence are called non-verbal tests of intelligence. In these tests language is not used to measure intelligence. In these tests subjects are not required to respond verbally to test items. Non-verbal tests are of two types viz.

1. Performance tests for e.g., Koh’s Block Design test, Dr. Bhatia’s Non Verbal test, Alexander’s Pass-along test, etc. and
2. Paper-pencil tests for e.g., Raven’s Standard Progressive Matrices.

Question 5.
Artificial Intelligence
Answer:
The term Artificial Intelligence was suggested by John McCarthy. Artificial intelligence is an innovation created by human intelligence. It is a field of study that combines computer science, algorithms, psychology, etc. It refers to enabling software programmes and computer systems to perform tasks that normally require human intelligence, such as visual perception, speech recognition, weather forecasting, language translation, etc.

Artificial intelligence can take decisions only on the basis of stored information and so cannot be an alternative to human intelligence. Artificial intelligence has immense applications in daily life as well as to solve critical problems. Artificial intelligence is used in devices like robots, computers, self-driving cars, automatic missiles, smart phones, medical diagnostic tools, etc.

6. Answer the following questions with the help of the given points.

Question 1.
Write in brief about individual tests of intelligence
(i) Meaning
(ii) Advantages
(iii) Disadvantages
Answer:

(i) Meaning – Intelligence tests that can be administered to a single person at a time are called individual tests of intelligence, for e.g., Stanford Binet Scales, Koh’s Block Design Test, etc.

(ii) Advantages-

1. The test administrator can establish a rapport with the client.
2. The test administrator can get additional information about the client’s feelings, moods and expressions during testing.
3. Individual tests are more capable of measuring creative thinking, compared to group tests.

(iii) Disadvantages-

1. Individual tests are time consuming and costly to administer.
2. Individual tests require a trained and skillful examiner to administer, score and interpret them.
3. These tests cannot be used for mass testing.

Question 2.
Write in brief about group tests of intelligence
(i) Meaning
(ii) Advantages
(iii) Disadvantages
Answer:

(i) Meaning – Group test of intelligence are tests that can be administered to more than one person at a time, i.e., for mass testing, for e.g., Army Alpha and Army Beta Test, OTIS self¬administrating tests, etc.

(ii) Advantages-

1. Group tests are less time consuming and more economical to administer.
2. In administrating of group tests, the role of the examiner is minimal. So, he/she need not go through any specialised training.
3. These tests can be used in cases where mass testing is needed.

(iii) Disadvantages-

1. The test administrator has much less opportunity to establish rapport, obtain cooperation and maintain interest of the clients.
2. Compared to individual tests, group tests are less capable of measuring the creative aspect of intelligence.

7. Answer the following questions in Detail.

Question 1.
Write in detail about the history of intelligence testing.
Answer:
Intelligence is the highest attribute of human beings. Different psychologists have defined intelligence differently. Lewis Terman explains intelligence as, “an ability to think on an abstract level.”

David Wechsler defines intelligence as, ‘the aggregate or global capacity of an individual to act purposefully, to think rationally and to deal effectively with his environment’. Many psychologists have contributed to the measurement of Intelligence.

Sir Francis Galton thought that he could determine intelligence by measuring the size of the human skull. He administered a battery of tests to measure variables such as head size, reaction time, visual acuity, etc. However, these tests did not prove useful to measure intelligence.

Raymond Cattell, used the term ‘mental test’ for the first time. Like his mentor, Sir Galton, Cattell also believed that intelligence is best measured by sensory tasks. However, be emphasized that test administration must be standardized.

In 1905, Alfied Binet in collaboration with Theodor Simon, published the First Scale of Intelligence. This scale was revised in 1908 and 1911. In 1916, Lewis Terman revised the scale, i.e., adapted few items, established new age norms etc. This came to be called ‘Stanford Binet Test’. Binet also introduced the concept of Mental Age. It is defined as the age at which the person successfully performs on all items of the test prepared for that age level.

In 1917, Robert Yerkes and his colleagues developed the Army Alpha (verbal test) and Army Beta (performance test) intelligence tests. These two tests were used to recruit soldiers. In 1939, during World War II also, to recruit army personnel, the Army General Classification Test was used.

In 1939, David Wechsler published the Wechsler-Bellevue Intelligence Test. In 1955, the test was revised and then called Wechsler Adult Intelligence Scale (WAIS). It has a verbal scale and performance scale. Wechsler also developed a test to measure intelligence of children, i.e., Wechsler Intelligence Scale for Children (WISC).

Mental Age – Alfred Binet introduced the concept of Mental Age. It is defined as the age at which the person successfully performs on all items of the test prepared for that age level. Mental Age need not correspond to Chronological Age. It Mental Age (MA) is the same as Chronological Age (CA), the person has average intelligence.

Intelligence Quotient – In 1912, William Stern introduced the concept of Intelligence Quotient (IQ). Terman, refined the formula for calculating IQ which is as stated below-
IQ = \(\frac {MA}{CA}\) × 100 IQ made it possible to compare the intelligence of individuals of different age CA groups.

Question 2.
‘Intelligence testing has a wide usage in various areas’. Justify with examples.
Answer:
David Wechsler defines intelligence as, ‘the aggregate or global capacity of an individual to act purposefully, to think rationally and to deal effectively with his environment.’
Types of Intelligence Tests-
(i) Individual tests of intelligence-
Individual tests of intelligence are tests which can be administered to a single person at a time, for e.g., Stanford Binet Scales, WAIS, Koh’s Block Design Test, etc.

(ii) Group tests of intelligence-
Group test of intelligence are tests that can be administered to more than one person at a time, i.e., for mass testing, for e.g., Army Alpha and Army Beta Test, OTIS self-administrating tests, etc.

(iii) Verbal tests of intelligence-
Verbal tests of intelligence make use of words and numbers to measure intelligence and subjects respond verbally to the test items, for e.g., WAIS, Army Alpha Test, etc.

(vi) Non-verbal tests of intelligence-
Non-verbal tests of intelligence do not use language to measure intelligence. They make use of pictures, designs, objects, etc. Such tests may be (i) Performance tests, e.g., Koh’s Block Design Test or (ii) Paper-pencil test e.g., Raven’s Standard Progressive Matrices.

Application of Intelligence Testing

1. Effective Schooling – On the basis of intelligence test scores, teachers can classify students into intellectual categories and devise special instructional programmes suited to their mental development.
2. Aids Mental Health Personnel – Intelligence tests are helpful to Mental Health personnel such as psychologists, etc., for diagnosis purposes and therapy.
3. Effective Parenting – Parents can provide appropriate educational facilities to their children based on their IQ scores.
4. Career Counselling – Scores obtained on intelligence tests help the student to select the right educational options/ courses.
5. Vocational Counselling – Individuals can choose a suitable career and achieve job satisfaction when they make a realistic choice of vocation based on IQ scores.

Question 3.
Explain the characteristics of people having high social intelligence.
Answer:
E.L. Thorndike proposed the term Social Intelligence. Howard Gardner included ‘interpersonal intelligence’ in the Multiple Intelligences Theory. According to Karl Albrecht, “Social intelligence is the ability to get along well with others and to get them to cooperate with oneself’.

According to Karl Albrecht our behaviour towards others falls somewhere on a spectrum between toxic behaviour and nourishing behaviour. Devaluing others, refusing cooperation to others, negative talking, discouraging others, etc., are some of the examples of toxic behaviours. A continued pattern of toxic behaviour indicates a low level of social intelligence. Respecting others, cooperating with others, positive talking, encouraging others, etc., are some of the examples of nourishing behaviour. A continued pattern of nourishing behaviour indicates a high level of social intelligence.

The following are some of the characteristics of people having high social intelligence:

1. They are good at understanding and interacting with other people.
2. They have ability to monitor their verbal and non-verbal expressions while communicating with others.
3. They are good speakers and good listeners.
4. They are skilled at assessing the emotions, motivations, desires, and intentions of those around them.
5. They understand social dynamics in an effective way.
6. They are flexible in their approach while dealing with others.
7. They are goal orientated, persistent and self- confident.
8. They can resolve conflicts in social contexts.
9. They are successful negotiators.
10. They enhance personal and professional relationships with others.

Class 12 Psychology Chapter 2 Intelligence Intext Questions and Answers

ACTIVITY (Textbook Page. No. 12)

Activity 1
Read the following sentences and decide whether the given sentences are the facts or just beliefs about intelligence :
(i) Intelligence is something that is inborn.
(ii) Students who are intelligent can get good marks in examinations.
(iii) Students who do not get good marks in examinations are less intelligent.
(iv) People who are intelligent are very smart.
(v) Intelligent people can impress anyone by their talk.
Answer:
[All the statements are just beliefs, not facts.]

Activity 2 (Textbook Page. No. 15)
Read the following examples. Using the formula, calculate the I.Q. of the following students:
(i) Aabha is a genius girl. Her chronological age is 8 years and her mental age is 14 years. Find out her I.Q.
(ii) Mayur has learning disabilities. His chronological age is 8 years and his mental age is 6 years. Find out his I.Q.
Answer:
(i) In case of Aabha – Mental Age (MA) = 14 years
Chronological Age (CA) = 8 years, IQ = ?
IQ = \(\frac {MA}{CA}\) × 100 = \(\frac {14}{10}\) × 100 = 175
IQ = 175.

(ii) In case of Mayur – Mental Age (MA) = 6 years.
Chronological Age (CA) = 8 years, IQ = ?
MA 6
IQ = \(\frac {MA}{CA}\) × 100 = \(\frac {6}{10}\) × 100 = 75
IQ = 75.

Activity 3 (Textbook Page. No. 16)

Make a chart listing the advantages and disadvantages of individual tests of intelligence.
Answer:
(i) Advantages-

1. The test administrator can establish a rapport with the client.
2. The test administrator can get additional information about the client’s feelings, moods and expressions during testing.
3. Individual tests are more capable of measuring creative thinking, compared to group tests.

(ii) Disadvantages-

1. Individual tests are time consuming and costly to administer.
2. Individual tests require a trained and skillful examiner to administer, score and interpret them.
3. These tests cannot be used for mass testing.

Activity 4 (Textbook Page. No. 16)

Make a chart listing the advantages and disadvantages of group tests of intelligence.
Answer:
(i) Advantages-

1. Group tests are less time consuming and economical to administer.
2. In administrating group tests, the role of the examiner is minimal. So, he/she need not go through any specialized training.
3. These tests can be used in cases where mass testing is needed.

(ii) Disadvantages-

1. The test administrator has much less opportunity to establish rapport, obtain cooperation and maintain interest of the clients.
2. Compared to individual tests, group tests are less capable of measuring creative aspect of intelligence.

Activity 5 (Textbook Page. No. 17)

Verbal test of intelligence Choose the correct option:
(i) Shoe – Foot : : Hat – ……………..
(a) Kitten
(b) Head
(c) Knife
Answer:
Shoe – Foot: : Hat – Head

(ii) Eye – Head : : Window – ………………
(a) Key
(b) Floor
(c) Room
Answer:
Eye – Head : : Window – Room

Activity 6 (Textbook Page. No. 19)

Read the examples given in Activity 6 on textbook page no. 18 and decide the positions of Chetan, Sagar and Anil on the following spectrum of behaviour:

Answer:

Activity 7 (Textbook Page. No. 20)

Study the differences between the characteristics of people having high emotional intelligence and low emotional intelligence and think about what you can do to develop your emotional intelligence?

Characteristics of people having high emotional intelligence	Characteristics of people having low emotional intelligence
Emotionally stable, Patient	Emotionally unstable, Impatient
Optimistic, Independent	Pessimistic, Dependent
Happy, Enthusiastic	Sad, Apathetic
Calm, Satisfied	Restless, Dissatisfied

Answer:
I will try to develop emotional intelligence by adopting the following ways-

1. active listening skills .and effective style of communication.
2. practice self-evaluation and self-awareness.
3. respond instead of reacting in conflict situations.
4. stay motivated, rational and have a positive outlook.
5. show empathy, be approachable.
6. adopt effective stress management techniques.

Activity 8 (Textbook Page. No. 20)

Discuss how the following devices use Artificial Intelligence:
(i) Computers
(ii) Self-driving cars
(iii) Robots
(iv) Medical diagnostic tools
(v) Translation devices
(vi) Automatic Missiles
(vii) Chatbots, etc.
Answer:
(i) Computers – AI is the ability of a computer programme to think and learn. It makes computers smart, i.e., work without being encoded with commands.

(ii) Self-driving cars – Autonomous driving is a key application of AI. Self-driving cars are equipped with multiple sensors such as cameras, radars, etc., which generate massive amount of data and simulate human perceptual and decision making processes in driving.

(iii) Robots – AI gives robots the computer vision to navigate, sense and calculate their reaction accordingly. Robots learn to perform tasks from humans through machine learning which is a part of computer programming and AI.

(iv) Medical diagnostic tools – Abnormalities in body fluids and tissue can be automatically detected using AI in medical diagnosis solutions. AI can help to speed up process of diagnosis, i.e., biomarkers.

(v) Translation devices-AI uses Neural Machine Translation (NMT), i.e., an electronic, neural network trained to recognize patterns in the input data set and translate it into desired output data, for e.g., a sentence in Japanese into English. It is more accurate than simple machine translation.

(vi) Automatic Missiles – AI is leading the world towards a battlefield that has no boundaries, may not even have humans involved and will be impossible to control across the human ecosystem in Cyberspace, Geospace and Space (CGS). It refers to the weaponisation of AI, i.e., a weapon system that can select human/ non-human targets without further intervention by a human operator.

(vii) Chatbots – AI makes it possible for chatbots to ‘learn’ by discovering patterns in data. A chatbot is a computer programme that imitates spoken and written conversation, i.e., voice commands and texts, for e.g., Siri.

Balbharti Maharashtra State Board Class 12 Psychology Solutions Chapter 8 Positive Psychology Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Psychology Solutions Chapter 8 Positive Psychology

1. Choose the correct option and complete the following statements.

Question 1.
……………. is the father of positive psychology.
(a) Carver
(b) Masten
(c) Seligman
Answer:
(c) Seligman

Question 2.
Barbara Fredrickson introduced the Broaden and ………………. theory.
(a) Build
(b) Emotion
(c) Learning
Answer:
(a) Build

Question 3.
The belief that good things will happen is called as ………………..
(a) pessimism
(b) resilience
(c) optimism
Answer:
(c) optimism

Question 4.
The capacity to understand what the other person is experiencing is………………
(a) sympathy
(b) empathy
(c) emotion
Answer:
(b) empathy

2. Answer the following questions in 35 – 40 words each.

Question 1.
Explain the theories of happiness
Answer:
Happiness is a positive emotional state that is subjective to each person, for e.g., people feel happy when they are successful or surprised or loved, etc.
The main theories of happiness are-

1. Need/ goal satisfaction theories – Happiness is experienced when some need or goal is satisfied, e.g., Rohit feels happiness when he clears IIT-JEE exams.
2. Process/ activity theories – Happiness is experienced when one engages in a particular activity, e.g., Sumit enjoys trekking.
3. Genetic/ personality theories – Genetic and personality characteristics are involved in the experience of happiness.

Question 2.
What is mindfulness?
Answer:
Mindfulness is the basic human ability to be fully aware of where we are and what we are doing. It means that we should not be overly reactive or overwhelmed by what’s going on around us. Mindfulness refers to mental awareness that helps to focus on the ‘Here and Now’. It helps to increase self-regulation, which results in growth and happiness. Mindfulness is maintaining moment by moment awareness of our bodily sensations, environment, thoughts and feelings.

Question 3.
What is resilience?
Answer:
According to the American Psychological Association, resilience is the process of adapting well in the face of adversity, trauma, tragedy, threats or significant sources of stress such as family and relationships, health, work and finances, etc. It is the act of ‘bouncing back’ inspite of barriers or set backs.

Resilience helps the person to recover form setbacks with the least negative consequences. Individuals high on resilience exhibit the following characteristics-

1. they regain their confidence after a period of emotional disturbance
2. they are able to maintain their psychological well-being.

The types of resilience are physical, psychological, emotional and community resilience.

3. Write short notes on the following in 50 – 60 words each.

Question 1.
Life above zero
Answer:
Traditional psychology focused on life at and below zero. Zero is the line that divides illness form
health. Hence, life below zero indicates a life that is full of problems stress, diseases, etc. Positive psychology emphasizes the study of life above zero.

-1 to +1 indicates neutral charactristics while below 0 indicates disorders, dysfunction or illness. Life above zero covers a large area of positive aspects of behaviour such as mindfulness, resilience, happiness, hope, trust and empathy. It acknowledges elements of living that enrich and meaningfully sustain what is referred to as “the good life” in positive psychology.

Question 2.
Determinants of happiness
Answer:
Happiness is a positive emotional state. Factors like health, prestige, income, success, etc., contribute to only a small portion of our total happiness.
Some factors are predictors of long lasting happiness-

1. Strong, intimate social relationships, positive contacts and good support system.
2. Optimism leads to less of negative emotions like stress.
3. Self-esteem enhances our confidence level and ability to approach challenges in a constructive manner.
4. Achieving challenging goals- If the goals are too easy, it leads to boredom and if they are too difficult, it leads to frustration. Moderately challenging goals, increase the chance of success, leading to happiness.
5. Perceiving meaning and purpose in life, without which we will experience frustration, boredom, etc.
6. Looking at life’s challenges as an opportunity rather than a threat helps to develop our potential.

Question 3.
Characteristics of an optimist
Answer:
Optimism is a mental attitude that includes feelings of hopefulness and a belief that the future will be positive and favourable. It is the belief that negative events are merely setbacks that are temporary and can be overcome.
The characteristics of optimists are:

1. they try to choose the best options available
2. they tend to be high on self confidence
3. they face difficulties positively as they view them as a challenge for a person to become strong
4. they are hopeful about the future and do not generalize present failure to future events.

Question 4.
Methods to promote empathy
Answer:
Empathy is the capacity to understand and feel what another person is experiencing from within their frame of reference i.e. capacity to place oneself in another’s position.

According to Simon Baron-Cohen there are three components of empathy viz. cognitive empathy emotional reactivity and social skills. Empathy builds a sense of security and trust. It is closely related to emotional intelligence and is a key to successful relationships.
Empathy can be promoted by using the following methods-

1. Increase social interactions – Especially with people who need help in order to understand their perspectives and motives.
2. Connecting through similarities – With others, e.g., those having same hobbies/ work/ goals, etc.
3. Understanding what you are feeling – Those who are able to accurately judge their own motives, can empathize better.
4. Challenge yourself – Tasks that are challenging lead to the person struggling to achieve a goal. This lead to humility which enables empathy.
5. Cultivate a sense of curiosity – This leads to open-mindedness and a better understanding of those around us.
6. Widen our social circle – Contact with people of different races, cultures, viewpoints helps to increase empathy towards them at a neurological level.

4. Explain the Following concepts.

Question 1.
Positive Psychology
Answer:
Positive Psychology is a newly emerging branch of psychology. Martin Seligman officially introduced Positive Psychology as a subfield of psychology. It is the science of happiness, human strength and growth. Positive Psychology focuses on building of character strengths like courage, happiness, perseverance, etc., rather than on anxiety, conflict, avoidance, etc. According to Seligman, positive psychology is “the scientific study of positive human functioning and flourishing on multiple levels that include the biological, personal, relational, institutional, cultural and global dimensions of life.”

Question 2.
Half glass full and half glass empty.
Answer:
Optimism is a mental attitude that includes feelings of hopefulness. It is a belief that the future will be positive and favourable and that negative events are merely setbacks that are temporary and can be overcome. Seligman explained about optimism in the book ‘Learned Optimism’. Our perspective determines whether or not we will show optimism.

A glass which has water upto its mid level may be perceived as half full (optimism) or as half empty (pessimism). This is described as ‘Half glass full and half glass empty’.

Question 3.
Empathy
Answer:
Empathy is the capacity to understand and feel what another person is experiencing from within their frame of reference, i.e., capacity to place oneself in another’s position. According to Simon Baron-Cohen, there are three components of empathy viz. cognitive empathy i.e., perspective taking, emotional reactivity (connecting in an intimate bond with another person) and social skills (moved to help the other). Empathy builds a sense of security and trust. It is closely related to emotional intelligence and is a key to successful relationships.

Question 4.
Mindfulness
Answer:
Mindfulness is the basic human ability to be fully aware of where we are and what we are doing. It means that we should not be overly reactive or overwhelmed by what’s going on around us. Mindfulness refers to mental awareness that helps to focus on the ‘Here and Now’. It helps to increase self-regulation, which results in growth and happiness. Mindfulness is maintaining moment by moment awareness of our bodily sensations, environment, thoughts and feelings.

Question 5.
Social resilience
Answer:
According to the American Psychological Association, resilience is the process of adapting well in the face of adversity, trauma, tragedy, threats or significant sources of stress such as family, health, etc. It is the act of ‘bouncing back’ inspite of barriers or set backs.

Social resilience is also called community resilience. It is the ability of groups of people to respond to and recover from adverse situations such as natural disasters, epidemics, war and socio-economic challenges to their community. This is mainly due to strong connections or bonds that the community members have with each other.

5. Answer the following question in 150 – 200 words each.

Question 1.
What are the essential building blocks of resilience?
Answer:
According to the American Psychological Association, resilience is the process of adapting well in the face of adversity, trauma, tragedy, threats or significant sources of stress such as family, health, etc. It is the act of ‘bouncing back’ inspite of barriers or set backs. Resilience helps the person to recover form setbacks with the least negative consequences. Individuals who are resilience tend to-

1. regain their confidence after a period of emotional disturbance
2. they are able to maintain their psychological well-being.

6. The types of resilience are physical, psychological, emotional and community resilience.

According to Ann Masten, building blocks is ‘ordinary magic’, which involves behaviour that can be easily learnt. The 7 C’s of reilience are-

1. Competence – Competence is the ability or know-how to handle situations effectively. Competence is acquired through actual experience.
2. Confidence – True confidence is a strong belief in one’s own abilities. Confidence is gained by demonstrating competence in real life situations.
3. Connection – Family is the central force in an individual’s life. Connections with other people, schools and communities gives the individual a sense of security that allows him/her to be independent and develop creative solutions.
4. Character – It refers to a clear sense of right and wrong and a commitment to integrity. An individual with character has a strong sense of self-worth and confidence.
5. Contribution – An individual who understands the importance of personal contribution develops a sense of purpose that can motivate him/her, further leading to him/her psychological well-being.
6. Coping – A person who learns to cope effectively with stress is better prepared to overcome life’s challenges.
7. Control – When an individual realizes that he can control the outcomes of his decisions and actions, he is more likely to know that he has the ability to bounce back.

Question 2.
Recollect the most challenging situation you faced in your life till now and the way you dealt with it. With reference to the 7 C’s of Resilience, which qualities helped you to overcome the challenge? For each of the C’s write the process you adopted to deal with the situation.
Answer:
[Students are expected to answer this question by themselves.]

7. Find out the positive aspects of behaviour from the example given below and answer in one word.

Question 1.
Mahesh studies so attentively that he never gets distracted.
Answer:
Mindfulness

Question 2.
Sujata lost her hands in an accident. Now she has learned to write with her leg.
Answer:
Resilience

Question 3.
Vasanta’s daughter died by cancer. He has opened a rehabilitation center for cancer patients.
Answer:
Empathy

8. Case Study

Anurag was a software engineer working in one of the leading company’s in the USA for almost 5 years. He was in a stable relationship and he had plans to start a family and to settle there. Unfortunately due to the poor economy in USA he lost his job and had to return back to India. He felt distressed as he realized that he had lost everything he had worked so hard to build. This made him feel like a failure.

1. How do you think Anurag can apply the 7 C’s of resilience to overcome the difficult situation he is in?
2. As Anurag’s friend how will you empathise with him and help him deal with this challenge?
3. Anurag has developed a very pessimistic approach after these setbacks, how will you guide him to stay happy and optimistic?

Answer:
According to the American Psychological Association, resilience is the process of adapting well in the face of adversity, trauma, tragedy, threats or significant sources of stress such as family, health, etc. It is the act of ‘bouncing back’ inspite of barriers or set backs. Resilience helps the person to recover form setbacks. Individuals who are resilient tend to-
(i) regain their confidence after a period of emotional disturbance
(ii) maintain their psychological well-being.

Anurag can apply the 7 C’s of resilience as follows-
1. He has already worked in a reputed firm successfully. Hence he has the Competence and Confidence in his own abilities. Although he is feeling a sense of hopelessness and failure, he must live in the ‘Here and Now’ by taking stock of the situation. Character will provide Anurag self worth and provide a sense of purpose and motivation, i.e., Contribution. When he realizes that he can still succeed in life by applying for a similar job here and accepting the situation, i.e., Control he can use effective Coping mechanisms. Besides, he should not forget social support of family and friends, i.e., Connection.

2. As Anurag’s friend, I can understand and feel what he is going through, from his frame of reference. Since, he is feeling distressed and like a failure due to loss of job, I will empathize with him by being encouraging and supportive. I will try to make him understand that with his own competence and experience, he can easily find a well paying job in India. I will also encourage him to improve his professional skills and seek social support from family and friends.

3. It seems natural for a person who was in a good job, stable relationship and successful position to feel pessimistic and like a failure when all of these no longer exist in his life. I will help Anurag to have a positive approach towards the challenges and difficulties in his life, i.e., view all setbacks i.e. loss of job, being sent back from the USA, etc., as opportunities not as obstacles. This will help him to gain a better perspective.

Class 12 Psychology Chapter 8 Positive Psychology Intext Questions and Answers

ACTIVITY (Textbook Page. No. 99)

Activity 4

(a) Meera scored poor marks in the examination.
(b) Suresh’s scholarship application got rejected.
(c) Mahesh lost his job.
Imagine yourself in their position and answer the following questions-
(i) How does being in their situation make you feel?
(ii) What do you think about yourself and your future being in their position?
Answer:
(i) You may feel

• Hopeless and so you might think that your future is dark.
• Helpless and so you might think that you cannot do anything to get out of the situation.
• Worthless and so you might think that you are a failure.

(ii) In contrast you may also feel

• Hopeful and think that the current adverse situation can change in the future.
• Challenged and think that you have the ability to overcome the adversity.
• Confident and think that one failure does not define you

Activity 5 (Textbook Page. No. 100)

What would your feeling be in the following situations?
(i) After a long struggle your friend got a job.
(ii) You see a person who just met with an accident and is bleeding profusely.
(iii) Your cousin is awarded a PhD. degree.
Answer:
In all the above examples I would feel empathy i.e., feel what these persons are experiencing.
(i) I will also feel happy and hopeful.
(ii) I will also feel concerned and helpless,
(iii) I will feel elated and proud.

Activity 8 (Textbook Page. No. 104)

Think of someone you know who has faced a challenging situation in their life and were successfully able to deal with it. This situation may have been emotionally difficult to deal with like death of a loved one, loss of a job, dealing with chronic illness, failure etc. Answer the following questions and discuss the answers in class.

1. How did they handle the adverse situation?
2. Which obstacles did they have to overcome?
3. In your opinion which specific attitudes and skills helped them cope with the situation?
4. Do you think they received help and support from others?

Answer:
Sundari, a professor in a reputed college was diagnosed with cancer at age 35 years.

1. Initially, she was overcome by feelings of intense fear and hopelessness. However, she decided that she would not give up the fight against cancer.
2. She had to overcome obstacles such as intense pain, fear of chemotherapy, pity shown by some ‘well wishers’, financial constraints, etc.
3. Specific attitudes that helped her to cope with this trauma were Resilience, fighting spirit interacting with other cancer survivors and good coping skills.
4. Yes, she received immense support from family, colleagues, friends and support groups like CPAA and Cancer Aid Foundation.

Activity 9 (Textbook Page. No. 105)

Read about the life of Indian boxer Mary Kom. Discuss in class the struggles she faced and how she overcame them to win multiple medals for the country.
Answer:
Mary Kom was born in Kangathei in the north-east state of Manipur. She grew up in a humble surroundings in an agricultural family. She is the eldest of three siblings. Her father had been a keen wrestler. Since a young age, Mary exhibited an inclination towards sports, like athletics and football. She was inspired by Dingko Singh, (a fellow Manipur who won a gold medal in 1998 Asian games ) to take up boxing. She was unable to pass her matriculation exam but still cleared X Std., from NIOS, Imphal. When she was 15, she left home to study at the Sports Academy in Imphal.

Her first coach K. K. Meitei recalls her as being hard working, dedicated, a quick learner with a strong will power. She has won many accolades such as 6 World Championships, Bronze medal at London Olympics (2012), 1 gold medal each at Asian Games (2014) and at Commonwealth Games (2018). She has been awarded the Padma Shri, Padma Bhushan and Padam Vibushan.

Her life story exhibits how Mary overcome obstacles of poverty, family opposition, gender bias to become the undisputed Queen of Boxing. Even at age 37, she still has the hunger to compete and win medals for India. Mary showed resilience as she has returned to the very demanding sport of boxing, after the birth of each child and has exceeded all expectations.

Activities 1, 2, 3, and 6
Answer:
[These are personal response questions.]

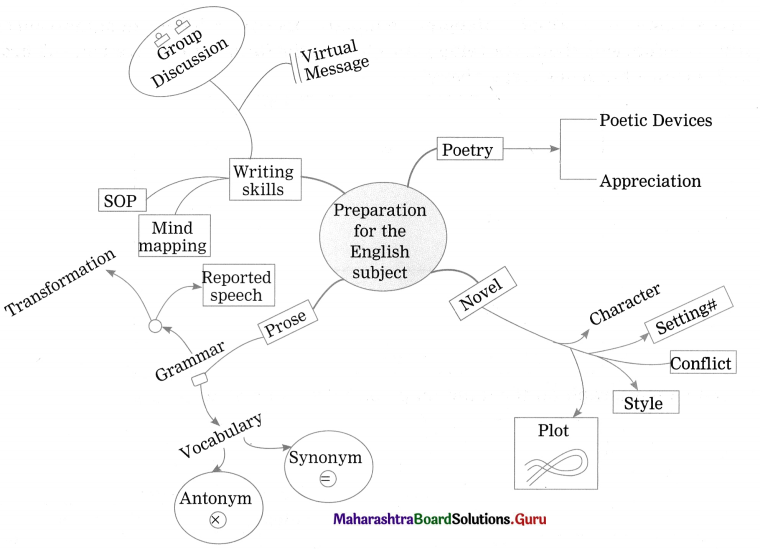
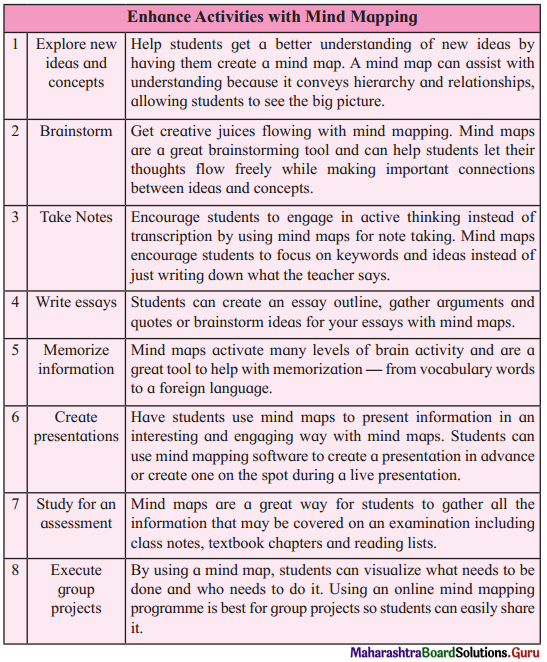
Balbharti Yuvakbharati English 12th Digest Chapter 1.4 Big Data-Big Insights Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 1.4 Big Data-Big Insights

12th English Digest Chapter 1.4 Big Data-Big Insights Textbook Questions and Answers

Question 1.
Give business suggestions to the respective industry/company for the following situations. You have received data that –
Answer:
(a) Many passengers prefer morning flights between 7 am and 9 am from Mumbai to Delhi.
Suggestion: Increase the number of flights between 7 am and 9 am.

(b) Many students are opting for UPSC/ MPSC Exams.
Suggestion: Increase the number of examination centres as well as job opportunities.

(c) Many people go for a morning walk to Kamla Nehru Park.
Suggestion: Open the gates of the Park earlier and close them only at noon. Also, clean the Park the previous night before closing or very early in the morning. Keep security guards in the mornings to maintain discipline.

(d) Many people buy clothes from miracle.com an online shopping site.
Suggestion: Increase the variety and brands in clothes. Give discounts and incentives to new and regular customers. Start various schemes.

(e) The viewership on television is more between 8 pm and 10 pm.
Suggestion: Telecast serials with the highest TRPs and socially important ads (like eye donation, polio drops, etc.) at this time.

Question 2.
People get information from various sources: Can you name a few?

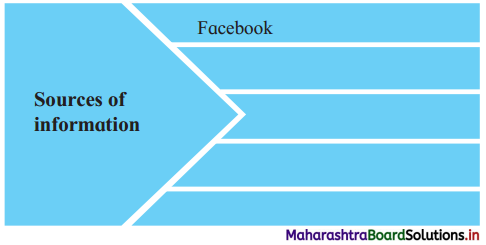
Answer:
Sources of Information:

1. Facebook
2. Internet
3. WhatsApp
4. Dictionary
5. Encyclopedia

(A1)

Question 1.
YouTube has many videos on various things. Listen to the uses and health benefits of ‘Lemon’ and share them with your friends.

(A2)

(i) Make pointwise notes from the lesson regarding the uses of Big Data in the following application. Do not write complete sentences.

Question (a)
‘Location Tracking’.
Answer:

1. Used by Google Maps and GPS to identify and track location of a place.
2. Geographic positioning, radio frequency identification sensors data about traffic conditions on particular route.
3. Can plan route according to travel time, transportation of the goods.
4. Companies reduce risks in transport improves speed, reliability in delivery.

Question (b)
Health Care Industry.
Answer:
Uses of Big Data:
Various apps, smartwatches, gadgets, etc. collect data about various functions of our body.

1. Data analyzed and feedback provided.
2. Doctors can have a better diagnosis of any ailment effects of any drug.
3. Past data of patients maintained suggestions, solutions for their problems given.
4. Helps in monitoring the outbreaks of epidemics, diseases.

Question (c)
Education Industry.
Answer:

1. Get information about the study patterns of students – can now prepare customized and dynamic learning programmes according to need of individual students.
2. Every student’s comprehension level is different – course material designed to cater to different requirements of the students. One-size-fits-all pitfall avoided.
3. Students’ choices, difficulties, results, etc. are available.
4. Strengths and weaknesses gauged -guidance while choosing career.

Question (ii)
When you are asked for personal details on social media, mention precautions that you will take.
Answer:
When I am asked for personal details on social media, I first try to find out who wants them and why. I never reveal credit/ debit card pin numbers, even if it is a bank asking me. I never give my mobile/adhaar card numbers either. I also keep my social media accounts private and visible only to friends. Only after checking and re-checking do I give any details, for I know that there are many cases of exploitation going on.

Question (iii)
Do you think all the data we receive is used for positive things? If ‘No’, make a list of the negative things which can be done with the help of Big Data.
Answer:
Negative things which can be done with the help of Big Data:

1. Loss of privacy-Big Data has all information about us.
2. Misuse of personal information
3. Leaking of information-this leads to thefts, blackmail, cheating, and so on.
4. Data may fall into wrong hands, and a person may be harassed.
5. Unsolicited calls and emails based on your internet history.

(A3)

Question 1.
Guess the meaning of the following idioms and phrases and use them in sentences of your own. One is done for you.
One-size-fits-all – suitable for or used in all circumstances
The wrist watches have adjustable belts, so one – size – fits – all.

Question (a)
‘Once in a blue moon’:
Answer:
Meaning: very rarely.
Sentence: Our English teacher is very strict and smiles only once in a blue moon.

Question (b)
‘One man army’ :
Answer:
Meaning: A ‘one-man army’ is someone who can do, or thinks he can do, everything by himself and without assistance.

(A4)

Do as directed.

Question (a)
Advertisers are one of the biggest players in Big Data.
1. Begin the sentence with ‘Very few ……………’
2. Use ‘bigger than’ and rewrite the sentence.
Answer:
1. Very few players in Big data are as big as advertisers.
2. Very few players in Big Data are bigger than advertisers.

Question (b)
No other diagnosis is as good as the diagnosis done with the help of Big Data.
1. Use ‘best’ and rewrite the sentence.
2. Use ‘better than’ and rewrite the sentence.
Answer:
1. The diagnosis done with the help of Big data is the best diagnosis.
2. No other diagnosis is better than the diagnosis done with the help of Big Data.

Question (c)
These internet giants provide the greatest data about people.
1. Begin the sentence with ‘No other ……………’
2. Use ‘greater than’ and rewrite the sentence.
Answer:
1. No other networking services provide greater data about people than these internet giants.
2. No other networking services provide greater data about people than these internet giants. OR These internet giants provide greater data about people than any other networking services.

Question (ii)
Read the sentence from the text.
New insights have enabled the banks and finance companies to come up with suitable plans.
Answer:
New insights have enabled either the banks or the finance companies to come up with suitable plans.

Question (a)
New insights have enabled the banks and finance companies to come up with suitable plans. (Rewrite using ‘either … or’.)
Answer:
New insights have enabled either the banks or the finance companies to come up with suitable plans.

Question (b)
Whatever activity we do online is recorded, monitored and analysed. (Rewrite using ‘either … or’.)
Answer:
Whatever activity we do online is either recorded, monitored or analysed.

Question (c)
Weather sensors and satellites help us to understand the weather and help in weather forecasting. (Rewrite using ‘either … or’.)
Answer:
Weather sensors and satellites help us to either understand the weather or help in weather forecasting.

(A5)

Question (i)
Interview the students of your class regarding the career they would like to pursue and the reason for selecting that particular career. Collect the data and analyse the information you have collected. Answer:
(Sample questions)
Hi, Rohan. I would like to ask you a few questions regarding the career you would like to pursue and the reason for selecting that particular career. Are you ready? Thanks.

1. Which are your favourite subjects?
2. Have you decided on the career you would like to pursue?
3. Why have you selected that particular career?
4. What are the exams you have to pass or the qualifications you must have to pursue this career?
5. What type of work does it involve?
6. What are the job opportunities?
7. Will you have chances of business travel?
8. Is the salary structure good?
9. Is your family happy with your choice?
10. Is this your final choice, or are you still in the process of deciding?

Thanks, Rohan. I have learnt a lot from this interview today. Bye.

Question (ii)
To listen well is as powerful a means of influence as to talk well and is essential to all true conversations.
Form a group and have a group discussion on the topics:
(a) Social Media – Curse or Boon (If used carefully and judiciously, a boon if misused, or people become addicts, then a curse)
(b) Women Empowerment and Equality (very important today-gender equality a must-the hand that rocks the cradle rules the world-however, women must not take advantage of this change-must be judicious in the use of the powers given)
(c) Climate Change (one of the biggest problems of today-must be taken very seriously-must change lifestyles-reduce consumption- recycle-carbon footprint)

(A6)

Question 1.
Find out job opportunities in the following areas and the skills required for them.
(a) Clinical Data Management
(b) Network Operations
(c) Data Processing
(d) Data Operations and Research
(e) Data Entry Operation

Yuvakbharati English 12th Digest Chapter 1.4 Big Data-Big Insights Additional Important Questions and Answers

Global Understanding:

Question 1.
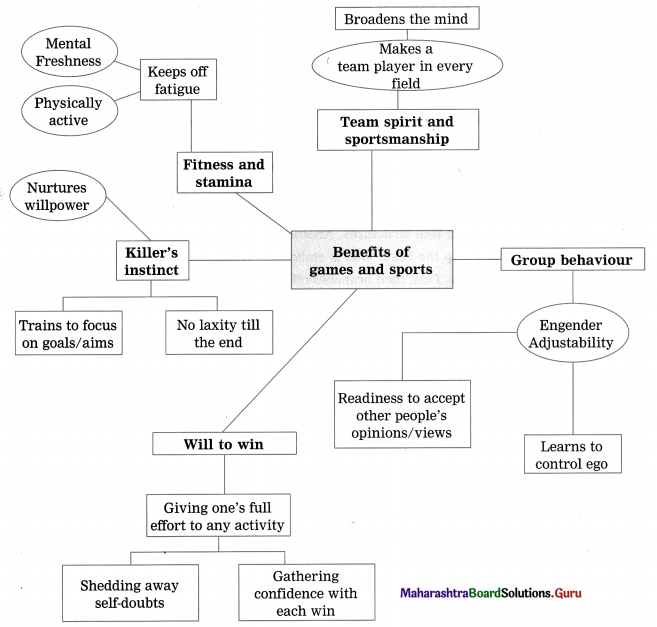
Complete the web:
(The answers are given directly and underlined.)
Answer:

Question 2.
Complete the following:
Answer:

1. Big Data analytics is used to give insights that were previously incomprehensible.
2. Big Data is so massive that it challenges the current computing technologies.
3. It’s not the amount of data that is important but what the [organizations do with the data is what matters.
4. Big Data analytics is the complex process of examining large and varied data sets or Big Data to uncover information.

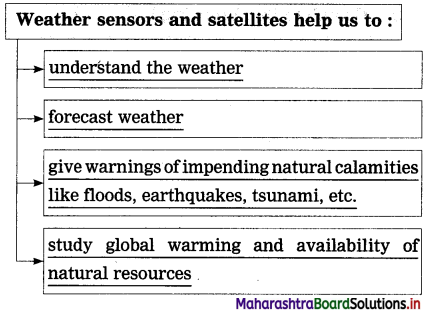
Question 3.
Complete the web:
(The answers are given directly and underlined.)
Answer:

Question 4.
Complete the following:
(The answers are given directly and underlined.)
Answer:

Question 5.
Write whether you agree or disagree with the following statements:

1. Today, the majority of equity trading takes place via data algorithms.
2. Big Data analytics cannot help in studying the investment patterns of people.
3. Big Data is useful in High-Frequency Trading.
4. Big Data cannot predict possible spikes on servers.

Answer:

1. Agree
2. Disagree
3. Agree
4. Disagree

Question 6.
Describe the ways used to create a huge database in sports.
Answer:
A huge data has been created over a period of time from the recording of matches, training sessions and workouts.

Question 7.
The database collected can help a sportsperson. Explain how.
Answer:
The data enables a sportsperson to study his own performance as well as that of the other players worldwide. It also helps in improving individual as well as team performance.

Question 8.
State the use of video analytics.
Answer:
Video analytics help one to see each and every performance minutely.

Question 9.
Name the Internet Giants mentioned in the extract.
Answer:
Facebook, Google, Twitter.

Question 10.
Pick out the False sentences, if any, and correct them:
1. Every student’s level of understanding is the same.
2.Big Data has brought about a big negative change in the education industry.
3. Designing the course material to cater to different requirements of the students is a good idea.
4. Big Data has provided a solution to the ‘one-size-fits-all’ pitfall.
Answer:
False sentences:
1. Every student’s level of understanding is the same.
2. Big Data has brought about a big negative change in the education industry.
Corrected sentences:
1. Every student’s level of understanding is different.
2. Big data has brought about a big positive change in the education industry.

Complex Factual:

Question 1.
Complete the following describing the sources of the collection of data:
(The answers are given directly and underlined.)
Answer:

Question 2.
Mention the ways to reduce risk in transport.
Answer:
Big Data has been useful in identifying and tracking the exact location of a place. GPS and Google Maps make use of Big Data. With geographic positioning and radio frequency identification sensors we get the up-to-date data about traffic, congestion on a particular route, information if the route is closed or if it is a one-way route, understanding accident prone areas, etc. Thus, we can plan our own route according to the travel time and the transportation of goods.

If we have ordered something online we can track the location of our goods in transit, we can also track the condition of the goods. All this has immensely helped the logistics companies to reduce risks in transport, improve speed and reliability in delivery.

Question 3.
Complete the following:
(The answers are given directly and underlined.)
Answer:

1. Big Data helps to predict and prevent cybercrimes, card fraud detection, archival of audit trails, etc.
2. Banks can predict future attempts of frauds by analyzing the past data of their customers and the data on previous brute force attacks.
3. SEC is using Big Data to monitor financial markets for possible illegal trades and suspicious activities.
4. Big Data algorithms are used to make trading decisions.

Question 4.
List the ways in which sensors help a person.
Answer:
Sensors help a person:

1. to understand the game from close quarters
2. to understand field conditions
3. to understand the weather conditions
4. to understand individual performances

Inference/Interpretation/ Analysis:

Question 1.
Discuss and write how Big data is increasing in volume, variation, velocity, veracity and value.
Answer:
When we like a post on Facebook or share a post on WhatsApp, visit any website, make online purchases, or watch videos, the variety of activity we do online is recorded, monitored and analysed. So a huge amount of data is collected. Data is also collected swiftly from different sources, for example web, sales, customer contact centre, social media, mobile data and so on.

Big Data analytics is used to give insights that were previously incomprehensible. As more and more people use the Internet, social media, make online purchases, use mobile phones, and are generally more active online, Big data is increasing in volume, variation, velocity, veracity and value in leaps and bounds.

Question 2.
Do you think Big Data has improved the quality of life? Give reasons for your answer.
Answer:
Big Data has certainly improved the quality of life. Through various apps, we can maintain our body weight and exercise levels, and remain healthy. Our heart rate, sleep patterns, etc. can be monitored and any changes can be immediately reported to the doctor, who can then prescribe the correct treatment as soon as possible.

Age-related diseases like diabetes and arteriosclerosis can be treated at the early stages. Thus, we can lead healthier and more active lives. Big Data is also being used to. predict and monitor epidemics, thus ensuring that they affect as few people as possible.

Question 3.
Write some ways of the condition of the goods.
Answer:
When we order something online, we are given a tracking number. By logging into the website of the company and entering this tracking number in the given slot, we can find out the location and condition of the goods.

Question 4.
Can we understand the economy of the country by the data on Banking and Finance? Explain.
Answer:
Yes, we can. With the Big Data analytics the study of investment patterns of the people can be done. We can analyse the bank deposits made, the loans taken and the equity trading.

We can find out the business across borders. We can find out how many industries have come up, and what the industrial economy is. From all this information, we understand the economy of the country.

Question 5.
Explain, giving an example, the technique used by Netflix and YouTube to increase viewership.
Answer:
Netflix and YouTube know through Big Data just what a person has viewed and his/her behaviour online. Based on this information, the person will be shown different recommendations. For example, if a person has viewed a couple of horror films from start to end, Netflix will know that the viewer is interested in horror films.

Accordingly, Netflix will recommend a few more horror films. The viewer is pleased with this easy access to his/her favourite genre, and continues to be a customer, thus increasing Netflix revenue.

Question 6.
Discuss a solution provided by Big Data.
Answer:
Through Big Data we have information about the study patterns of students, and we can now prepare customized and dynamic learning programmes according to the need of an individual student.

Personal Response:

Question 1.
Industries can be benefited from data. Explain with an example.
Answer:
Industries can benefit from the huge amount of data available. For example, in the tourism industry, through Big Data travel agencies and hotels can identify the times when there are more crowds and hence more demand for a certain tourist spot.

They can accordingly make arrangements for more flights, trains, buses, tours, labour, essential items, etc. Hotels can use big data to compile and analyse information about their main competitors so that they are aware of what other hotels or businesses are offering customers.

Question 2.
Do you have any app on your phone that monitors your health? Describe it in brief.
Answer:
Yes, I have an app that helps me to measure the calories I have eaten and I can thus plan my meals. It also records my weight and tells me whether it has gone up or down. There is a very clear graph too which gives me complete information of the ups and downs in my weight. I have managed to lose a few kilos with the help of this app and feel much healthier now.

Question 3.
Do you use GPS and Google Maps? If so, where and when?
Answer:
I drive a two-wheeler. If I have to go to a new shop/hotel or some other place, I find out the route through GPS and follow this route. I used Google Maps when I went to Goa with my family and wanted to calculate distances and use the best routes.

Question 4.
Do you spend a lot of time on Facebook, Netflix, etc.? Do you think it is addictive?
Answer:
Yes, I do spend a lot of time on Facebook. I have a large number of friends, and hence the news feed is quite a lot. I like to know what my friends are doing, where they have gone, etc. It is addictive, and since I have Facebook on my mobile phone too, I can check it at any time. This is what most of my friends do too. I know it is not good, and I am trying to control screen time. I do not subscribe to Netflix.

Question 5.
Do you think Big Data will help to bring improvements in students? Give reasons for your answer.
Answer:
Yes, Big Data will certainly help to bring improvements in students. Students can learn topics/subj ects. according to their abilities and capacity. They can choose their careers after knowing their strengths and weaknesses, their mental make-up and abilities. Thus, there will be fewer drop-outs, and students will be happy in the careers they have chosen..

Language Study:

Question 1.
Whatever activity we do online is recorded, monitored and analysed. (Rewrite using ‘as well as’….)
Answer:
Whatever activity we do online is recorded, monitored, as well as analysed.

Question 2.
The massive data available with us can really work wonders. (Rewrite using the noun form of the underlined word.)
Answer:
The availability of massive data with us can really work wonders.

Question 3.
Big Data analytics is the complex process of examining large and varied data sets or Big Data to uncover information. (Frame a wh-question to get the underlined part as the answer.)
Answer:
What is Big Data analytics?

Question 4.
Big Data helps in monitoring the outbreaks of epidemics and diseases. (Rewrite using ‘as well as …’)
Answer:
Big Data helps in monitoring the outbreaks of epidemics as well as diseases.

Question 5.
Big Data helps in monitoring the outbreaks of epidemics and diseases. (Rewrite using ‘either …or’.)
Answer:
Big Data helps in monitoring the outbreaks of either epidemics or diseases.

Question 6.
Big Data has been useful in identifying and tracking the exact location of a place. (Rewrite using ‘as well as’.)
Answer:
Big Data has been useful in identifying as well as tracking the exact location of a place.

Question 7.
Big Data has been useful in identifying and tracking the exact location of a place. (Rewrite using ‘either … or’.)
Answer:
Big Data has been useful in either identifying or tracking the exact location of a place.

Question 8.
Weather sensors and satellites help us to understand the weather and help in weather forecasting. (Rewrite using ‘as well as’.)
Answer:
Weather sensors and satellites help us to understand the weather as well as help in weather forecasting.

Question 9.
Huge amount of data is continuously being I received from them. (Change the voice.)
Answer:
We continuously receive a huge amount of data from them.

Question 10.
Big Data has enabled smooth functioning of these agencies and institutions. (Rewrite as an interrogative question.)
Answer:
Hasn’t Big Data enabled smooth functioning of these agencies and institutions?

Question 11.
Here, Big Data algorithms are used to make trading decisions. (Rewrite using a gerund in place of the underlined word.)
Answer:
Here, Big Data algorithms are used for making trading decisions.

Question 12.
Every student’s comprehension level is different. (Add a question tag.)
Answer:
Every student’s comprehension level is different, isn’t it?

Question 13.
This will also help in guiding the student regarding the best career for him. (Rewrite using the noun form of the underlined word.)
Answer:
This will also help in providing guidance to the student regarding the best career for him.

Question 14.
This would, in general, enhance progress of all students. (Rewrite beginning ‘Progress….)
Answer:
Progress of all students, would in general, be enhanced.

Vocabulary:

Question 1.
From the extract, find the antonyms of the following words :

1. understandable
2. tiny
3. sales
4. simple

Answer:

1. understandable × incomprehensible
2. tiny × massive (huge)
3. sales × purchase
4. simple × complex

Question 2.
From the words given below, write down the ones that have been formed using prefixes:
industries, increasing, incomprehensible, unknown, examining, uncover, information, innumerable, important
Answer:
incomprehensible, unknown, uncover, innumerable

Question 3.
Find the meanings of:
1. petabytes
2. exabytes
Answer:
1. petabytes – units of information equal to one thousand million 1000 tetrabytes.
2. exabytes – units of information equal to one quintillion 1000 petabytes

Question 4.
Pick out 4 words ending in ‘ing’ from the extract.
Answer:
identifying, tracking, positioning, understanding

Question 5.
Pick out 4 nouns ending in ‘tion’ from the extract.
Answer:
location, identification, congestion, information

Question 6.
Complete the following, giving the meanings.
(The answers are given directly and underlined.)
Answer:
e.g. new insights: insights that are new.

1. health-conscious people: people who are conscious of their health.
2. smartwatches: watches that are smart.
3. heart rate: the rate at which heart beats.
4. blood pressure: the pressure of the blood.
5. necessary precautions: precautions that are necessary.
6. unnecessary guesswork: guesswork that is unnecessary.

Question 7.
Find adjectives from the extract having the following suffixes :
(-able, -ible, -ial, -ious, -al)
Answer:

1. -able – suitable;
2. -ible – possible;
3. -ial – financial, social;
4. -ious – suspicious, previous;
5. -al-natural.

Question 8.
Match the words in Column A with the words in Column B to make collocations found in the extract:
Answer:

A	B	Answer
new	crimes	new insights
cyber	seconds	cyber crimes
future	insights	future attempts
split	attempts	split seconds

Question 9.
Give the adjective forms of the following words:

1. giant
2. interest
3. create
4. behaviour

Answer:

1. giant – gigantic
2. interest – interesting
3. create – creative
4. behaviour – behavioural

Question 10.
Match the words in Box A with the meanings in Box B:
Answer:

1. revenue – earnings
2. gigantic – huge
3. enables – allows
4. embedded – implanted

Question 11.
Make sentences of your own using the following expressions/words :

1. leaps and bounds
2. enhance
3. to make optimum use of

Answer:

1. leaps and bounds: Suman’s progress in studies increased by leaps and bounds after her health improved.
2. enhance: We can enhance our looks by having a pleasant expression on our faces.
3. to make optimum use of: Saurav decided to make optimum use of the Diwali vacation to catch up with his studies.

Oral Work:

Question 1.
Do you think people click consciously on Facebook? Discuss.
Answer:
[Points: in general, most people just press ‘like’ button on friends’ posts, many times not even reading the post-sometimes some only repeat the comment above theirs-some forwards and videos are not even seen-with so many posts and information many times there is no time to read everything]

Non-Textual Grammar

Do as directed:

Question 1.
Her family and their well-being were her highest priority. (Rewrite as an interrogative sentence.)
Answer:
Weren’t her family and their well-being her highest priority?

Question 2.
The shadows were lengthening when Smita arrived at the college. (Identify the clauses.)
Answer:
The shadows were lengthening – Main Clause
when Smita arrived at the college – Subordinate Adverb Clause of Time

Question 3.
He had to find the books and read them before the day ended.
(Rewrite using ‘not only…but also’.)
Answer:
He had not only to find the books but also read them before the day ended.

Spot the error in the following sentences and rewrite them correctly:

Question 1.
I was either scared of people’s curious looks nor their awkward questions.
Answer:
I was neither scared of people’s curious looks nor their awkward questions.

Question 2.
He was unable to participate due to a health problems.
Answer:
He was unable to participate due to a health problem.

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 11 India Transformed Part 1 Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 History Solutions Chapter 11 India Transformed Part 1

1A. Choose the correct alternative and rewrite the statement.

Question 1.
A legal agreement was signed in Geneva which is known as ____________
(a) SEATO
(b) NATO
(c) GATT
(d) SAARC
Answer:
(c) GATT

Question 2.
An act similar to ‘Right to Information’ was first applied in ____________ in 1776.
(a) Sweden
(b) France
(c) England
(d) India
Answer:
(a) Sweden

Question 3.
The birth anniversary of Swami Vivekananda is observed as ____________
(a) National Education Day
(b) National Youth Day
(c) National Integration Day
(d) National Science Day
Answer:
(b) National Youth Day

2A. Write the names of historical places/persons/events.

Question 1.
In 2004, this became the biggest firm in Asia providing software services –
Answer:
Tata Consultancy Services

Question 2.
In 2002, the Metro railway was flagged off –
Answer:
The Delhi Metro Railway

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
India became member of World Trade Organisation, because ____________
(a) India want to compete with other nations
(b) India cannot stay aloof from the global economy
(c) India adopted the policy of liberalisation
(d) India wanted to be in the leading position at the global level
Answer:
(c) India adopted the policy of liberalisation

3. Complete the following concept map.

Question 1.

Answer:

4. Write short notes.

Question 1.
The Youth Policy of Government of India.
Answer:

• India is a country with a maximum proportion of young people. Individuals in the age group of 15-29 are considered as ‘youth’.
• Youth, if provided with opportunities, for education and skill training, can contribute significantly to the development of India.
• A number of centers of‘Nehru Yuva Kendra Sangathan’ were established in 1972 for the training of young people in various skills.
• The programmes run by these centers were eventually merged in the ‘National Youth Empowerment Programme’. This programme put a thrust on topics like literacy, education, health and hygiene, family welfare, preservation and conservation of the environment, awareness of social issues, rural development, and self-employment.
• 12th January the birth anniversary of Swami Vivekanand is celebrated as ‘National Youth Day. National Youth Festival is also celebrated in the month of January. This festival is designed to provide a platform for the artistic talents of young individuals.
• ‘Youth Hostels Association of India’ has established youth hostels in various parts of the country which works for encouraging adventure skills among young people.
• Training programmes are arranged by this association through ‘Bharat Scout and Guides, National Service Scheme and National Cadet Corps’.

Question 2.
‘Pradhan Mantri Gram Sadak Yojana’.
Answer:

• The Government of India knows the importance of having roads in good condition in the interior areas started ‘Pradhan Mantri Gram Sadak Yojana’ in 2000.
• Initially, the work of building roads began by linking the villages of population strength up to 1000. In 2001 this programme was merged in ‘Pradhan Mantri Gramoday Yojana’.
• The roads measuring about 75000 km. were completed till 2005. The purpose of this work was to extend the benefits of the country’s economic growth to people living in rural areas and to bring transformation in their lives.
• It aimed at providing amenities for good health, education, drinking water, dwellings, roads, and electricity.

5. State your opinion.

Question 1.
India is a leading country in the field of space research.
Answer:

• In 2007, India entered a new field of space research. It commercially launched the Italian satellite.
• Other countries had submitted tenders quoting very high rates, to get this contract. However, India got this contract by quoting reasonable rates.
• Before entering this field on a commercial basis, India had already successfully launched the satellite of Argentina, Belgium, South Korea, Indonesia, and Germany.
• In 2008, India launched ‘Chandrayaan-1’, the first lunar probe. India could collect evidence for the presence of water on the moon through this satellite.
• After that India also launched ‘Chandrayaan-2’ and ‘Mangalyaan’.
• All these achievements proved that India is a leading country in the field of space research.

6. Answer the following questions in detail.

Question 1.
Which programmes were launched in India for making the opportunities of wage-earning?
Answer:
Creating employment opportunities for an ever-increasing population is a major challenge for the government. There are several programmes launched by the government of India for wage earners.
These programs are as follows:

• Pradhan Mantri Rojgar Yojana and ‘Rojgar Hami Yojana’: To create job opportunities for educated youth the ‘Ministry of Commerce and Industry of the Government of India started this plan on 2nd October 1993 on the birth anniversary of Mahatma Gandhi.
• Rojgar Hami Yojana was to assure daily wages to the unemployed agricultural labourers. The objective of this plan was to provide wage-earning opportunity, who was in search. This programme was launched in 257 districts in India. A goal was to provide work to two young laborers in each family below the poverty line. In 2001, this plan was merged in ‘Gramin Rojgar Yojana’.
• In 1998, to provide support to farmers in difficult times “Kisan Credit Card” plan was started. It helps the farmer to avail funds for essential equipments and seeds for cultivation. Later, an insurance facility was also offered to farmers, who were Kisan Credit Card holders.
• Suvarnajayanti Gramin Svayam Rojgar Yojana: This plan was launched in 1999 by merging various plans together namely ‘Ekatmik Gramin Vikas Yojana’, Self-employment training programmes, ‘Ganga Kalyan Yojana’ etc.
• Jawahar Gram Samruddhi Yojana: In 1999, a new plan was implemented with the intention to provide adequate employment for unemployed men and women. It was merged in ‘Sampoorna Gramin Rojgar Yojana’ in 2001.
• Sampoorna Gramin Rojgar Yojana: This plan made provision for creating opportunities in rural areas of earning wages, to provide food grains in exchange for work, etc. This scheme was started in 150 economically backward districts in the country. In 2006, this scheme was merged in ‘Rashtriya Gramin Rojgar Hami Yojana’.
• Rashtriya Gramin Rojgar Hami Yojana: Under this scheme, each family in rural areas were given assurance of at least 100 days of work.

7. Answer the following question with the help of the given points.

Question 1.
Give information about the ‘Right to Information Act.
(a) Background of the act and the beginning of this movement in India.
(b) Definition of ‘Information’.
(c) The rights of citizens under this act.
Answer:
(a) Background of the act and the beginning of this movement in India:

• This kind of Act was first implemented in Sweden in 1776. In 1946, ‘United Nations’ declared the ‘Right to Information to be the fundamental human right.
• In 1982, L.K. Kulwant, a resident of Jaipur in Rajasthan, a social activist initiated the process by applying to know the Jaipur Municipal Corporation’s work for cleaning the city.
• The High Court gave a clear verdict stating that ‘Right to Information is a fundamental right of all citizens.
• In 1990, Aruna Roy started the movement called ‘Majdoor Kisan Shakti Sanghatan’. A need for ‘Right to Information was started through this movement.
• Harsh Mander, the Divisional Commissioner of Bilaspur showed courage to disclose official information while serving as a bureaucrat.
• The struggle of Anna Hazare in 2001, had a decisive role in Maharashtra in this matter. The Act was implemented in Maharashtra on 12th October 2005.

(b) Definition of ‘Information’:
The definition of term ‘Information’ includes official records, documents, memoranda, emails, comments, consultations, press notes, circulars, orders, logbooks, tenders, reports, correspondence, formats, models, electronic data, the information of a private institution or an individual that is available in the records of any public establishment.

(c) The rights of citizens under this act:

• Right to information grants access to official documents, records, permission to obtain their copies, to take notes, to extract passages, to get samples of authorised material and prints of data stored in CDs, Floppy discs, tapes, video cassettes, or in any other form, or stored on computers.
• Citizens can get the desired information after submitting an application to the ‘Information officer’ of a ‘Public Authority.

Class 12 History Chapter 11 India Transformed Part 1 Intext Questions and Answers

Collect information of following schemes: (Textbook Page No. 92)

National Pension Scheme, Pradhan Mantri Suraksha Vima Yojana, Pradhan Mantri Jeevan Jyoti Vima Yojana, Atal Pension Yojana, Indian Post Payments Bank.
Answer:
(A) National Pension Scheme:

• The National Pension Scheme is a voluntary contribution of the pension system in India which is sponsored by the government of India.
• This scheme was started by the Government of India in 2004 for all government employees.
• The scheme was made open to all citizens in 2009. It is a voluntary and long-term retirement scheme. It is regulated by Pension Fund Regulatory and Development Authority (PFRDA) and the central government.
• Any employee from the public, private, and even the unorganized sectors can opt for this.
• Personnel from the armed forces are not allowed. The scheme is open to all across industries and locations.

(B) Pradhan Mantri Suraksha Vima Yojana:

• The scheme is available to people in the age group 18 to 70 years with a bank account who give their consent to join/enable auto-debit on or before 31st May for the coverage period 1st June to 31st May on an annual renewal basis.
• Aadhar would be the primary KYC for the bank account. The risk coverage under the scheme is ₹ 2 lakh for accidental death and full disability and ₹ 1 lakh for partial disability.
• The premium of 112 per annum is to be deducted from the account holder’s bank account through ‘auto-debit facility in one installment.

(C) Pradhan Mantri Jeevan Jyoti Vima Yojana:

• Pradhan Mantri Jeevan Jyoti Vima Yojana is available to people between 18 and 50 years of age with a bank account.
• This scheme was launched on 9th May 2015 by Prime Minister Narendra Modi in Kolkata.
• It has an annual premium of ₹ 330. In case of death due to any cause, the payment to the nominee will be ₹ 2 lakh.
• As of 31st March 2019, 5.92 crore people have already enrolled for this scheme.

(D) Atal Pension Yojana:

• Atal Pension Yojana is a pension scheme under the Government of India.
• This scheme replaces the Swavalamban Yojana and was established to provide old age income security to the workers belonging to the unorganized sector.
• The Atal Pension Yojana was launched by Prime Minister Narendra Modi on 9th May 2015 in Kolkata.
• The scheme focuses on encouraging workers of the unorganized sectors to save for their future (Age limit 18-40 years).

(E) Indian Postal Payments Bank :

• The Indian Postal Payment Bank was launched on September 1, 2018, by Prime Minister Narendra Modi that aims at making banking services available at people’s doorstep.
• This is a 100% Government-owned public sector bank, operating with the Department of Posts under the Ministry of Communications.
• IPPB would be like any other bank but it will operate at a smaller scale without involving any credit risks and can’t issue advance loans or issue credit cards.

Let us know: (Textbook Page No. 92)

Collect information with the help of the internet about the ‘Rafi Ahmad Kidwai National Postal Academy (Gaziabad).

Answer:

• Rafi Ahmad Kidwai National Postal Academy, recently called Postal Staff College India (PSCI) is the apex training institution of Indian postal services.
• It was set up in the year 1977. Initially, the college functioned from Sanchar Bhavan and later from Dak Bhavan in Delhi.
• It was shifted to its present location in Gaziabad in the year 1990. It is a central training institute and has the primary role of training and grooming the young officers who get recruited to the Indian Postal Service.
• It also conducts various in-service training programmes on postal management for Postal Service officers in India and other foreign postal administrations.
• Its goal is to make the officers of the department of posts professionally competent to handle the ever-changing communication market.
• Training Program:
  • Advanced Development Program
  • Executive Development Program
  • Technology Management Program
  • Postal Life Insurance
  • Leadership Development for postmasters and mangers
  • Quality Management

Let us collect information (Textbook Page No. 92)

Collect information about various services like ‘Sarvabhaum Suvarn Rokhe’ (Gold Bonds issued by the Government), ‘Electronic Indian Postal Order’, ‘E-Dakghar’, ‘E-Payment Portal’, ‘Mobile App’ etc. by interviewing the Postmaster of any branch.
Answer:
(A) Sarvabhaum Suvarn Rokhe:

• This scheme was launched by Government in November 2015, under Gold Monetisation Scheme. The issues are made open for subscription in tranches by RBI in consultation with GOI.
• As per RBI instructions, every application must be accompanied by the PAN number issued by the income tax department to the investors as the PAN number of the first/ sole applicant is mandatory.
• SGBs are government securities denominated in grams of gold. They are substitutes for holding physical gold. Investors have to pay the issue price in cash and the bonds will be redeemed in cash on maturity. The bond is issued by Reserve Bank on behalf of the government of India.
• The SGB offers a superior alternative to holding gold in physical form. The quantity of gold for which the investor pays is protected since he receives the ongoing market price at the time of redemption /premature redemption.

(B) Electronic Indian Postal Order:

• The Department of Personnel and Training and Department of Posts have launched a service called e-IPO (Electronic Indian Postal Order) to enable the Indian citizens abroad to purchase an Indian Postal Order electronically by paying fee on-line through the e-post Office portal i.e., http://www.epostoffice.gov.in.
• It also facilitates them to file the Right to Information (RTI) application. Registration is mandatory to avail of this facility. Options for new account creation, user verification, search e-IPO, etc are available.

(C) e-Payment portal:

• e-Payment is a smart option for businesses and organizations to collect their bills or other payments through post office networks.
• When businesses require the collection of bills and other payments from customers across the country, Post offers them a simple and convenient solution in the form of e-payment.
• e-Payment is a many-to-one solution that allows the collection of money (telephone bills, electricity bills, examination fees, taxes, university fees, school fees, etc) on behalf of any organization. The collection is consolidated electronically using web-based software and payment is made centrally through cheque from a specified Post Office of billers choice.
• The information and MIS regarding the payment can be seen by the biller online. The MIS will contain the five fields of billers choice like name, telephone number, application number, etc. The services are currently available through more than 14,000 Post offices across the country.
• There is an agency in the market today with a large reach and establishing trust as the Post Office where the public can comfortably deposit all their bills in their neighbourhood.

(D) e-Dak Ghar:
The e-Post Office of India post offers a variety of online Postal services to the users. One can avail services-philately (purchase of stamps), PLI/RPLI (payment of the premium), and IPO (purchase order for RTI).

(E) Mobile app:

• The IPPB app is available on both Android and iOS platforms. This app, however, can only be used by those individuals who have an account in a core banking-enabled post office. KYC of the account should also be completed in advance.
• Internet banking and mobile banking services should also be completed in advance.
• Using the mobile app, account holders can also view account balances and statements, transfer funds, request a checkbook, stop payment on a cheque, use sweep-in-sweep-out facilities, and pay utility bills.

Project (Textbook Page No. 98)

Collect information about the States of India and Union Territories, as well as the names of their capital cities, with the help of the internet.
Answer:
The states of India and its capitals are as follows:

States	Capital
1. Andhra Pradesh	Hyderabad
2. Arunachal Pradesh	Itanagar
3. Assam	Dispur
4. Bihar	Patna
5. Chhattisgarh	Raipur
6. Goa	Panaji
7. Gujrat	Gandhinagar
8. Haryana	Chandigarh
9. Himachal Pradesh	Shimla
10. Jharkhand	Ranchi
11. Karnataka	Bengaluru
12. Kerala	Thiruvananthapuram
13. Madhya Pradesh	Bhopal
14. Maharashtra	Mumbai
15. Manipur	Imphal
16. Meghalaya	Shillong
17. Mizoram	Aizawl
18. Nagaland	Kohima
19. Odisha	Bhubaneswar
20. Punjab	Chandigarh
21. Rajasthan	Jaipur
22. Sikkim	Gangtok
23. Telangana	Hyderabad
24. Tamil Nadu	Chennai
25. Tripura	Agartala
26. Uttar Pradesh	Lucknow
27. West Bengal	Kolkata
28. Uttarakhand	Dehradun

Union Territories and its Capitals:

Union Territories	Capitals
1. Anadaman and Nicobar Island	Port Blair
2. Chandigarh	Chandigarh
3. Dadra and Nagar Haveli and Daman and Diu	Daman
4. Delhi	New Delhi
5. Lakshadweep	Kavaratti
6. Puducherry	Pondicherry
7. Ladakh	Leh (summer), Kargil (winter)
8. Jammu and Kashmir	Srinagar (summer) Jammu (winter)

 

Balbharti Maharashtra State Board Class 12 Political Science Solutions Chapter 5 Contemporary India: Good Governance Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Political Science Solutions Chapter 5 Contemporary India: Good Governance

1. (A) Complete the following statements by selecting the appropriate option.

Question 1.
The concept of Lokpal is taken from
(a) United States
(b) United Kingdom
(c) Sweden
(d) Russia
Answer:
(c) Sweden

Question 2.
The Right to Information was passed in the year
(a) 1950
(b) 1976
(c) 2016
(d) 2005
Answer:
(d) 2005

(B) State the appropriate concept for the given statements.

Question 1.
Person investigating complaints against government officials.
Answer:
Ombudsman

2. (A) Complete the concept map.

Question 1.

Answer:

(B) State whether the following statements are true or false with reason.

Question 1.
Lokayukta can investigate complaints against political executives.
Answer:
This statement is True.

1. Lokayuktas were created by the Lokpal and Lokayuktas Act, 2013 to look into allegations of corruption against public functionaries in the States.
2. A member of the public can file specific allegations with the Lokayukta for inquiry against any public servant including legislators, political executives, local bodies, public enterprises.

Question 2.
Good Governance aims at efficient use of natural resources.
Answer:
This statement is True.

1. One of the core values of good governance is effectiveness and efficiency.
2. It refers to sustainable human development in the context of efficient use of natural resources and the protection of the environment.

3. Explain the correlation between the following.

Question 1.
Good Governance and E-Governance.
Answer:
Good Governance aims to replace traditional public administration riddled with corruption and redtapism and to make it more citizen-centric, responsible and responsive. The core values of good governance include efficiency, inclusiveness, being consensus-oriented, transparency, accountability, etc. Specific programmes aimed at good governance include setting up of Lokpal and Lokayuktas, Creating of Citizen’s Charters, Right to Information Act, institutional mechanisms like NHRC, NCW, etc.

E-Governance is one of the most important aspects of good governance. It involves the employment of Information and Communications Technology (I.C.T) to facilitate efficient and instant transmission and processing of information as well as storing and retrieval of data. Thus, e-governance helps to implement core values of good governance such as transparency, effectiveness, accountability and participation of citizens.

4. Express your opinion of the following.

Question 1.
E-governance speeds up governmental processes.
Answer:
I agree with this statement.
E-governance refers to the use of Information and Communications Technology (I.C.T) to carry out the varied and complex aspects of governance and of citizen’s expectations. E-governance facilitates instantaneous transmission and processing of information as well as efficient storing and retrieval of data. This helps in speeding up governmental processes and taking decisions expeditiously. Large scale digitisation of records enables easy and reliable access over the internet.

Question 2.
E-governance brought administration closer to people.
Answer:
I agree with this statement.
E-governance refers to the use of Information and Communications Technology (I.C.T) to carry out the varied and complex aspects of governance and of citizen’s expectations. Large scale digitisation of records enables easy and reliable access over the internet.

E-governance helps in increasing the geographical and demographical reach of the government. Efforts have been made at various levels to improve the delivery of public services and simplify the process of accessing them. The objective of National e-Governance Plan is to bring public services closer to the people i.e., make them citizen centric.

5. Answer the following question in 80 to 100 words.

Question 1.
Explain various institutions protecting rights of different sections in India.
Answer:
The core values of good governance include administration being consensus-oriented based on principles of inclusiveness and equity as well as responsiveness to the needs of citizens.

The benefits of good governance must be available to all the sections of the society. The constitution provides for socio-economic and political safeguards to certain disadvantaged sections of the society. Besides the safeguards, provided for them the government has created several commissions to safeguard the rights of different sections of the society. These include the following:
1. National Commission for Scheduled Castes – Deals with matters related to the safeguards provided in the constitution for the Scheduled Castes and inquire into specific complaints relating to deprivation of rights of the Schedule Castes.

2. National Commission for Scheduled Tribes – Deals with matters related to the safeguards provided in the constitution for the Scheduled Tribes and inquire into specific complaints relating to deprivation of rights of the Schedule Tribes.

3. National Human Rights Commission – It deals with protection of rights relating to life, liberty, equality and dignity guaranteed by the constitution.

4. National Commission for Women – This was created to facilitate the redressal of grievances and accelerate socio-economic development of women.

5. National Commission for the Protection of Child Rights – It seeks to protect, promote and defend child rights in the country. The Commission defines a child as a person in the 0 to 18 years of age group.

6. National Commission for Backward Classes – The focus is welfare of socially and economically backward classes.

7. National Commission for Minorities – It monitors the working of the safeguards for minorities provided in the Constitution and by laws enacted by the Parliament and the State Legislatures. The National Commission for Minorities recognises the following religious communities as minority communities: Muslim, Sikh, Christian, Buddhist, Parsis and Jain.

8. National Consumer Disputes Redressal Commission – This provides for a consumer disputes redressal mechanism e.g.,consumer courts are set up.

6. Answer the following question with reference to the given points.

Question 1.
Explain in detail the following values of Good Governance.
(a) participation
(b) transparency
(c) responsiveness
(d) accountability
Answer:
In development administration, not only the government but also citizens and NGO’s play a vital role. The term ‘governance’ is used to describe this cooperative effort of the government and non-governmental bodies in public administration. Governance is broader than government as

1. it includes formal institutions of government e.g., legislature, bureaucracy as well as informal institutions e.g., NGO’s.
2. it aims to improve the performance of public institutions with focus on values like accountability, transparency, citizen feedback, etc.

The Good Governance approach aims at the following-

1. to reform the traditional, huge-sized public administration which was riddled with red tape and corruption.
2. to replace the archaic systems with responsible, participative and equitable systems.
3. to look at interlinkages between government and civil society.
4. to make the administration citizen-centered and not rule bound.

a. Participation – The effective functioning of any democratic system requires that people get an opportunity to participate in the process of decision making and its implementation.

b. Transparency – This value of good governance enables people to keep the government under scrutiny for e.g., Right to Information Act (2005) provides citizens access to information about public policies and actions.

c. Responsiveness – The government must be prompt and sensitive while designing policies to serve all stake holders within a reasonable time frame.

d. Accountability – This cannot be enforced without the rule of law and transparency. Any organization is accountable to those who will be affected by it’s decisions and actions, i.e. to stakeholders. Governmental institutions, private sector and civil society institutions must be accountable.

Activity

Question 1.
Find out the information regarding State level commissions working for safeguarding rights of various sections of society (Text Book Page No. 58)
Answer:
The State Level Commissions are-
1. State Information Commission was constituted with the objective to fulfill the mandate assigned in the RTI Act 2005. It consists of State Information Commissioners headed by the State Chief Information Commissioner.

2. State Commission for Women was constituted on 25th January 1993. It consists of a chair person, 6 nonofficial members, a member secretary and a DGP as ex-officio member. It aims to investigate into practices derogatory to women and suggest remedial measures. It also advises the government on matters related to upliftment to the status of women.

3. State Commission for Scheduled Castes and Scheduled Tribes was established by the Social Justice and Special Assistance Department dated 1st March 2005. It’s role is to study existing socio-economic, political and educational situation of Scheduled Castes and Tribes and to suggest measures to improve the same. It also investigates grievances raised by members of Scheduled Castes and Schedules Tribes.

4. State Human Rights Commission (MSHRC) was established on 6th March 2001 to protect, promote and enforce human rights. It can inquire suo motu (of its own accord) or on petition presented to it, into complaints of violation of human rights.

5. State Commission for Protection of Child’s Rights was set up in July 2007 to protect and defend child rights in the State.

6. State Commission for Minorities – was set up to safeguard the interests of religious and linguistic minorities.

Question 2.
Find out information about Ombudsman. (Text Book Page No. 58)
Answer:
Ombudsman is a Swedish term. In general, it means “a legal representative” or an official appointed to investigate complaints especially against public officials. The first country to set up ombudsman institution in 1809 was Sweden. In India, the Lokpal (for centre) and Lokayuktas (for States) are the ombudsman. The ARC (1966-70) headed by Morarji Desai recommended the institution of Lokpal and the Bill was first introduced in Parliament in 1968. Orissa was the first State to constitute institution of Lokayukta.

After the India Against Corruption Movement led by Anna Hazare, the Lokpal and Lokayuktas Bill, 2013 was passed in Parliament and came into force on 16th January 2014. The Lokpal is a multimember body, consisting of a chairperson and a maximum of 8 members. The Lokpal and Lokayuktas inquire into allegations of corruption / maladministration against public functionaries.

Class 12 Political Science Chapter 5 Contemporary India: Good Governance Intext Questions and Answers

ACTIVITY (Text Book Page No. 48)

Question 1.
Identify NGO’s that are working in your Area/City/State. Look at the issues and work done by them. In which NGO would you like to work?
Answer:
1. For environmental causes

• Bombay Natural History Society (BNHS)
• Vanshakti
• Earth5R
• Bombay Environmental Action Group (BEAG)
• Vasundhara
• PETA

2. For child welfare

• Child Right and You (CRY)
• Prerana
• Helen Keller Institute
• Bal Asha Trust
• Salaam Baalak Trust
• Akansha Foundation
• Apnalaya

3. For educational purposes

• Teach for India
• Door step School
• Magic Bus India Foundation
• Pratham Education Foundation
• VIDYA .
• Abhilasha Foundation

4. For women’s welfare

• Society for Nutrition, Education and Health Action (SNEHA)
• Apne Aap Women’s Collective (AAWC)
• Women’s India Trust (WIT)
• MAJLIS

5. For the disabled/ill/aged

• AASRA
• National Association for the Blind (NAB)
• ALERT-India (leprosy patients)
• Cancer Patients Aid Association (CPAA)
• Committed Action for Relief and Education (CARE)
• Cheshire Homes India

Question 2.
Find out E-governance initiatives of Government of Maharashtra (Text Book Page No. 54)
Answer:
Maharashtra is a pioneer in citizen centric e-governance initiatives such as

1. SARITA (Stamps and Registration Information Technology based Administration) for registration of 67 different types of documents over the entire State.
2. SETU (Integrated Citizen Facilitation Centres) act as one stop service centre for people who have to visit government offices for permits/affidavits, etc. The Society for promotion of Excellence and Transparency for better Understanding of the requirements of citizen in interface with government.
3. E-validity for caste/minority status certificates.
4. Online Disability certificates.
5. SEVARTH – integrated system to provide electronic salary payment to all government personnel.
6. SARTHI – Computerisation of driving license and vehicle registration.
7. Rojgar Wahini – to provide free services like vocational guidance, job opportunities, self-employment guidance, etc.

Question 3.
Consumer Protection Act (1986) (Text Book Page No. 56)
Answer:
The Consumer Protection Act was enacted by Parliament in 1986 to protect the interests of consumers in India. It is replaced by the Consumer Protection Act 2019.
It aims to check unfair trade practices, ‘defects in goods’, and ‘deficiencies in services’ and has led to a widespread network of consumer fora and appellate courts all over the country. The Act provided six rights to consumers:

• Right to seek redressal against unfair trade practices.
• Right to be heard and be assured that their interests receive due consideration at an appropriate forum.
• Right to be assured wherever possible, access to a variety of goods and services at competitive prices.
• Right to be informed about the quality, standard, price of goods and services.
• Right to be protected against marketing of goods and services which are hazardous to life and property.
• Right to consumer education.

To ensure consumer rights, Consumer Disputes Redressal System included a three-tier level i.e.,

• National Consumer Commission (set up by the central government).
• State Consumer Commission (set up by each State).
• District Consumer Forum (in each district of the State).

The redressal agencies (consumer courts) set up were. Central Consumer Protection Council and State Consumer Councils. Consumer courts are special-purpose courts dealing with cases involving consumer disputes, conflicts and grievances.

Balbharti Maharashtra State Board Class 12 History Solutions Chapter 10 Cold War Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 History Solutions Chapter 10 Cold War

1. Choose the correct alternative and rewrite the statement.

Question 1.
The headquarters of SEATO were located at ___________
(a) Thailand
(b) the Philippines
(c) Pakistan
(d) the United Kingdom
Answer:
(a) Thailand

Question 2.
A fund named ‘Africa Fund’ was raised at ___________ for providing necessary aid to neighbouring nations of South Africa.
(a) Jakarta
(b) Harare
(c) Namibia
(d) Indonesia
Answer:
(b) Harare

2A. Write the names of historical places/persons/events.

Question 1.
On 30th June 1977, this organisation ceased to exist –
Answer:
SEATO

Question 2.
The idea of Commonwealth games was introduced by –
Answer:
Reverend Astley Cooper

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
No country was included in the ANZUS treaty except Australia, New Zealand, and the United States of America ___________
(a) they did not want to let the United Kingdom and France have an upper hand
(b) it was a military pact
(c) it was a secret pact
(d) it was a pact only among countries with friendly relations
Answer:
(a) they did not want to lot the United Kingdom and France to have an upper hand

3. Complete the concept map.

Question 1.

Answer:

4. Write short notes.

Question 1.
Cold War.
Answer:

• Definition: The tussle between Capitalist nations and Communist nations for power and ideological influence, which began after the Second World War is referred to as the ‘Cold War.
• Walter Lippmann, an American political columnist was the first to use the term ‘Cold War’.
• ‘Cold War’ is characterized by the following factors –
  • No Direct War.
  • The intense race for armament.
  • Aggressive Political Policies.
  • Mutual lack of Faith among Nations.
  • Political and Economic Pressurisation.
  • Ideological Conflict.
• The aftermath of the Second World War created conditions leading to the Cold War.
• England and France lost their primary positions in world politics.
• During the world war, Russia gained prominence in Eastern Europe while America, England, and France gained prominence in Western Europe.
• The Eastern European nations under the influence of Soviet Russia adopted communist ideology while the Western European nations under the influence of America adopted capitalist ideology and democratic system. This situation caused the emergence of the ‘Cold War.

Question 2.
Non- Alignment Movement.
Answer:

• After the Second World War, India decided not to join either Russia or America. India adopted the policy of development by its own efforts and shape its own strategies leading towards peace. This policy is known as the ‘NAM-Non Alignment Policy’.
• Pandit Jawaharlal Nehru, Dr. Sukarno (Indonesia), Nkrumah (Ghana), Gamal Abdel Nasser (Egypt), and Marshal Tito (Yugoslavia) were the architects of the concept ‘NAM’.
• The nations, which adopt an independent foreign policy based on the concept of peaceful co-existence, support other nations in their independence struggle, and do not involve themselves in the military agreements or bilateral treaties with the superpowers is known as ‘Non-Aligned Nations’.
• Non-Alignment is a concept concerned more with progress and peace than war and poverty, so it is positive.

5. Explain the following statements with reasons.

Question 1.
CENTO became non-operational.
Answer:

• CENTO stands for Central Treaty Organisation.
• CENTO earlier known as the ‘Baghdad Pact’ or Middle East Treaty Organisation (METO) is a treaty among four nations namely, Turkey, Pakistan, Iran, and England.
• This treaty was signed on 24th February 1955. Iraq joined later.
• America started providing the member nations of CENTO economic and military aid.
• America feared that if Soviet Russia attacked any of the member nations, then all member nations should fight it collectively.
• But in reality, none of the member nations had the military capacity to fight.
• Except for the United Kingdom, the rest of the three were in need of military and technological aid but America was too involved to pay attention to their need.
• Hence, the other members of CENTO were not satisfied. They wanted to withdraw from the treaty and act independently.
• Iran and Pakistan withdrew from the treaty and hence CENTO became non-operational.

Question 2.
SAARC has achieved success in some fields.
Answer:

• SAARC has achieved success in some fields for e.g. a centre for the dissemination of agro-related information was started in Bangladesh and it has also been used as a platform for research related to seeds, animal husbandry, and fisheries.
• A SAARC center for meteorological research was established in Dhaka.
• In Kathmandu, an orthopedic center was established.
• Efforts are being made to promote tourism in SAARC countries.
• SAARC is also working to eliminate poverty in South Asia with the help of the Economic and Social Commission for Asia and Pacific (ESCAP).
• An inter-Governmental group was established to formulate an agreement (SAFTA- South Asia Free Trade Area) for promoting free trade and economic cooperation among SAARC nations.
• The SAARC Documentation Centre was established in Delhi for the dissemination of information.
• SAARC Human Resources Development Centre was established in Islamabad (Pakistan).
• Agreements were signed to counter the smuggling of narcotic drugs. Committees were appointed for development in the fields of postal services and transportation.

6. State your opinion.

Question 1.
The Cold War began between America and Soviet Russia.
Answer:

• The tussle between the Capitalist nations and Communist nations for power and ideological influence which began after the second world war is referred to as the ‘Cold War.
• During the world war, Russia gained prominence in Eastern Europe while America, France, and England gained prominence in Western Europe.
• The Eastern European nations under the influence of Soviet Russia adopted Communist ideology.
• The Western European nations under the influence of America adopted a Capitalist ideology and democratic system.
• This situation caused the emergence of the ‘Cold War’ between Soviet Russia and America.

Question 2.
India has always opposed colonialism.
Answer:

• India is acknowledged as a great democracy in the world.
• After independence, India adopted the policy of active non-alignment in international politics.
• India would always strive to establish global peace.
• India would not tolerate foreign intervention in her internal matters. India shall respect the regional unity and sovereignty of other countries.
• India emphasizes the principle of ‘live and let live’ supported by peaceful co-existence.
• For e.g. in the post-independence period in 1949, a conference was held in Delhi in which support was declared to the issue of Indonesia’s independence. It was demanded that the Dutch should leave Indonesia before 1950 and grant its independence.
• The position India took in the case of Africa, is also very important. India took a strong initiative in demanding independence of African countries especially the protectorates of European nations.
• India insisted that the foreign rulers (colonialist European countries) should leave the colonies.
• India cared about Africa because of its long-standing relations with African countries.
• Mahatma Gandhi showed Africa the path to satyagraha for independence.
• Thus, India had been at the forefront of the struggle against colonialism.

Class 12 History Chapter 10 Cold War Intext Questions and Answers

Try to do this (Textbook Page No. 77)

Collect information about the ‘United Nations’ with the help of the internet. Create groups of students in the class and let them compile the information of various specialized agencies of the United Nations.
Answer:
The United Nations was established after World War II with the aim of preventing any war in the future and establishing peace in the world. UN is the largest and most powerful intergovernmental organisation in the world. It was established on 24th October 1945. Currently, 193 countries in the world are members of the UN. The headquarter of the UN is located in New York, USA. Since its establishment UN has been working for maintaining world peace and avoiding conflict among nations, it also works for remoting sustainable development, protection and preservation of the environment, and protecting human rights.

The important agencies of the UN are as follows:
(i) International Labour Organisation (ILO):
Established in – 1919 to improve the conditions and living standards of workers.
Headquarters – Geneva.

(ii) International Monetary Fund (IMF):
Established in – 1945 to promote international monetary cooperation.

(iii) Food and Agricultural Organisation:
Established in – 1945

(iv) United National Educational, Scientific and Cultural Organization (UNESCO):
Established in – 1945.

(v) World Health Organisation:
Established in – 1948

(vi) International Atomic Energy Agency (IAEA):
Established in – 1957

(vii) United Nations Development Programme (UNDP):
Established in – 1965

(viii) World Trade Organisation (WTO):
Established in – 1995

(ix) UN Women:
Established in – 2010

(x) United Nation Office on Drugs and Crime (UNODC):
Established in – 1997

(xi) United Nation Environmental Programme (UNEP):
Established in – 1972

(xii) International Development Association (IDA):
Established in – 1960

(xiii) United Nations International Children’s Emergency Fund (UNICEF):
Established in – 1946

(xiv) International Telecommunication Union (ITU):
Established in – 1865

Try to do this (Textbook Page No. 83)

Review the proceedings of NAM conferences held during the period from 1992 to the Venezuela conference of 2016.
Answer:
NAM was established in 1961 in Belgrade, SR Serbia, Yugoslavia through an initiative of the Indian Prime Minister Pandit Jawaharlal Nehru. The Non-Aligned Movement (NAM) is an organization of Redeveloping nations that are not formally aligned, with any major power flex. Here is the list of NAM summits:

• 10th NAM Summit: 1-6 September 1992 – Jakarta, Indonesia.
• 11th NAM Summit: 18-20 October 1995 – Cartagena, Colombia.
• 12th NAM Summit: 2-3 September 1998, Durban, South Africa.
• 13th NAM Summit: 20-25 Feb 2003, Kuala Lumpur, Malaysia.
• 14th NAM Summit: 15-16 September 2006, Havana, Cuba.
• 15th NAM Summit: 11-16 July 2009, Sharm-El-Sheikh, Egypt.
• 16th NAM Summit: 26-31 August 2012, Tehran, Iran.
• 17th NAM Summit: 13-18 September 2016, Porlamar, Venezuela.

Try to do this (Textbook Page No. 85)

Collect information about SAARC conferences till 2014, with the help of the internet.
Answer:
SAARC also known as The South Asian Association for Regional Cooperation is the regional intergovernmental organisation in South Asia. Total 8 countries are members of SAARC.

1. Nepal
2. Bhutan
3. India
4. the Maldives
5. Sri Lanka
6. Pakistan
7. Bangladesh
8. Afghanistan.

• The First Summit was held in Dhaka, Bangladesh on 7-8 December 1985, signed the SAARC charter on 8 December 1985 thereby establishing the regional association and study groups on the problems of terrorism, drug trafficking, etc.
• Second Summit India: Date – 17-18 November 1986 in Bangalore.
  Appointment of Ambassador Abdul Ahsan of Bangladesh as the first Secretary-General of South Asian Association of Regional Cooperation.
• 3rd Summit: 2-4 November 1987 in Kathmandu, Nepal.
• 4th Summit: 29-31 December 1988 in Islamabad, Pakistan.
• 5th Summit: 21-23 November 1990 in Male, Maldives.
• 6th Summit: 21 December 1991 in Colombo, Sri Lanka
• 7th Summit: 10-11 April 1992, Dhaka, Bangladesh.
• 8th Summit: 2-4 May 1995, New Delhi, India
• 9th Summit: 12-14 May 1997, Male, Maldives.
• 10th Summit: 29-31 July 1998, Colombo, Sri Lanka
• 11th Summit: 4-6 January 2002, Kathmandu, Nepal.
• 12th Summit: 4-6 January 2004, Islamabad, Pakistan.
• 13th Summit: 12-13 November 2005, Dhaka, Bangladesh
• 14th Summit: 3-4 April 2007, New Delhi, India
• 15th Summit: 1-3 August 2008, Colombo, Sri Lanka.
• 16th Summit: 28-29 April 2010, Thimphu, Bhutan
• 17th Summit: 10-11 November 2011, Addu City, Maldives.
• 18th Summit: 26-27 November 2014, Kathmandu, Nepal.

Project (Textbook Page No. 87)

Collect information about the ‘Commonwealth Games’ with the help of the internet.
Answer:
The Commonwealth Games is an international multi-sport event involving athletes from the Commonwealth of Nations. The event was first held in 1930, and, with the exception of 1942 and 1946, has taken place every four years since then. The Commonwealth Games were known as the British Empire Games from 1930 to 1950, the British Empire and Commonwealth Games from 1954 to 1966, and British Commonwealth Games from 1970 to 1974. Athletes with a disability are also included as full members of their national teams, making the Commonwealth Games the first fully inclusive international multi-sport event. It is also the world’s first multi-sport event that inducts an equal number of women’s and men’s medal events and was implemented recently in the 2018 Commonwealth Games. With such unique features, the World Economic Forum called the event inspiring and significant.

Their creation was inspired by the Inter-Empire Championships, as a part of the Festival of Empire, which was held in London, England in 1911. Melville Marks Robinson founded the games as the British Empire Games which were first hosted in Hamilton, Canada in 1930. During the 20th and 21st centuries, the evolution of the movement of the game has resulted in several changes to the Commonwealth Games. Some of these adjustments include the creation of the Commonwealth Winter Games for snow and ice sports for the commonwealth athletes, the Commonwealth Paraplegic Games for commonwealth athletes with a disability, and the Commonwealth Youth Games for commonwealth athletes aged 14 to 18. The first edition of the winter games and paraplegic games were held in 1958 and 1962 respectively, with their last edition held in 1966 and 1974 respectively and the first youth games were held in 2000. The 1942 and 1946 Commonwealth Games were canceled because of the Second World War.

Balbharti Maharashtra State Board Class 12 Psychology Solutions Chapter 7 First Aid in Mental Health Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Psychology Solutions Chapter 7 First Aid in Mental Health

1. Choose the correct option and complete the following statements.

Question 1.
One of the major obstacles to getting help from a mental health professional is the ………………… attached to mental illness.
(a) policy
(b) stigma
(c) society
Answer:
(b) stigma

Question 2.
Friends and family are not a substitute for …………………..
(a) solving problems
(b) giving solutions
(c) professional help
Answer:
(c) professional help

Question 3.
In our culture the ………………….. of an individual is considered to be the reflection of one’s family.
(a) intelligence
(b) behaviour
(c) status
Answer:
(b) behaviour

Question 4.
Individuals who experience ………………… commonly have a negative thinking style.
(a) depression
(b) phobia
(c) acute stress
Answer:
(a) depression

2. Answer the following questions in 35 – 40 words each.

Question 1.
Describe the term Mental Health First Aid?
Answer:
Mental Health First Aid (MHFA) is an internationally recognized training programme designed to teach people how to identify the signs and symptoms of mental health problems and to provide assistance on a first aid basis. MHFA was originally developed by Betty Kitchener and Anthony Jorm.

First Aid in Mental Health is a concept based on the idea of ‘prevention is better than cure’. If the early signs of mental illness are recognized, it can help in the following ways.

1. Diagnosis – timely diagnosis at the onset of mental illness helps to prevent it from developing into a more severe form.
2. Intervention – early intervention helps to get professional help.
3. Relapse prevention – it prevent reoccurrence of symptom of the mental illness.

Question 2.
What are the stigmas attached to mental illness?
Answer:
One of the major obstacles to getting help from a mental health professional is the stigma that is attached to mental illness. We fear things that we do not understand. In the same way, our lack of understanding of mental illness makes us fear it.
This lack of knowledge and awareness makes us-

1. Blame the individual, i.e., think that mental illness is a personal failing or weakness.
2. Think that mental illness is caused as punishment for our sins.
3. Think that the person is intentionally behaving in an inappropriate way.

Question 3.
Anxiety disrupts day to day functioning of an individual : State two predispositional factors contributing to anxiety.
Answer:
Anxiety that is excessive or persists after the anxiety creating situation has subsided leads to anxiety disorders such as phobias, acute stress disorder, etc.
Predispositional factors in anxiety are-

1. Genetic factors – if anyone in the family has anxiety issues, then the person will be at a higher risk of exhibiting high levels of anxiety as compared to other persons.
2. Childhood trauma such as physical or mental neglect or abuse, death of a loved one, parental divorce, etc.

Question 4.
Your friend confided in you that he is suffering from anxiety.
Suggest two self- help strategies to help him deal with this issue.
Answer:
The self help strategies that can be suggested to help him deal with excessive anxiety are-

1. Engage in some activity that he always wanted to pursue for e.g., pottery, writing, sketching or voluntary social service.
2. Indulge in physical activity like exercise, outdoor games or trekking.
3. Relaxation techniques like laughter therapy, meditation and breathing techniques.

3. Answer the following in 80 – 100 words based on the given points.

Question 1.
Explain the reasons why First Aid in Mental Health is required.
(a) Stigma associated with mental health
(b) Shame
(c) People do not always know how to respond
(d) People may not always seek professional help
Answer:
MHFA is an internationally recognized training programme whose objective is to teach people how to identify the signs and symptoms of mental health problems and to provide assistance on a first aid basis.
(a) Stigma associated with mental health:
Lack of understanding about mental illness makes us fear it. This lack of awareness leads us to blame the person for behaving inappropriately or showing personal failing.

(b) Shame:
Often, a person who has been diagnosed with a mental illness is ridiculed or blamed. He/she experiences shame, withdraws from social interaction and does not reach out to others or seek help. Hence, it is beneficial to show understanding and provide support.

(c) People do not always know how to respond:
Most people may not respond in an adequate way to a mentally ill person who reaches out to them. Sometimes, their advice/help may do more harm than good. However, MHFA programme can help friends/family to identify early signs of mental illness and help the person to get professional help.

(d) People may not always seek professional help:
The main reasons for this is-

1. Culture – Stigma attached to mental illness prevents people from seeking professional help as it may hurt the reputation of the family.
2. Advice from elders – A mentally ill person may incorrectly believe that advice of elders alone is sufficient to cure his illness.
3. Superstitions – If the person is convinced that his//her mental illness is caused due to sins/curses etc., they will not want to visit a mental health professional. Hence, they will be deprived of the benefits of early intervention.

Question 2.
Explain the ALGEE Model in your own words.
(a) Approach, Assess and Assist in any crisis
(b) Listen non-judgmentally
(c) Give support and information
(d) Encourage the person to get professional help
(e) Encourage self-help and other support strategies
Answer:
ALGEE is an action plan to carry out First Aid in Mental Health.
(a) Approach, Assess and Assist in any crisis – An attempt is made to understand the situation and observe if there are behavioural changes in the person whom we are concerned about.

(b) Listen non-judgmentally – We should listen to the other person without letting our opinions influence us. We should not judge/ criticise but listen with acceptance and empathy. It does not imply that we agree with what the other person is saying but it ensures that the person feels supported.

(c) Give support and information – This helps the person to feel more in control of the situation since they have emotional and informational support.

(d) Encourage the person to get professional help – Persons suffering from mental illness may hesitate to seek help due to lack of knowledge or due to stigma attached. Others may not know how to respond to someone showing ‘red flags’ of mental illness and may do more harm than good. Mental health professionals are trained to help the person to identify the problem and cope with the situation.

(e) Encourage self-help and other support strategies – Self-help strategies are tasks that help to increase our resources to deal with stress and to maintain mental health such as exercise, adequate sleep, having hobbies, etc.

Question 3.
Enumerate the various symptoms that are exhibited by an individual with anxiety disorders.
(a) Physical Symptoms
(b) Psychological Symptoms
(c) Behavioural Symptoms
Answer:
Anxiety is an emotion characterised by feelings of tension, hopelessness, etc. Excessive level of anxiety which persists even after the anxiety producing situation has gone away, can lead to anxiety disorders.
(a) Physical Symptoms

1. Heart palpitations and rapid heart rate
2. Shortness of breath
3. Dizziness or headaches
4. Restlessness, tremors and shaking

(b) Psychological Symptoms

1. Mind racing or going blank
2. Difficulty in concentration
3. Forgetfulness
4. Problems in decision making
5. Irritability, impatience and anger

(c) Behavioural Symptoms

1. Avoiding people and situations
2. Repetitive checking
3. Strong urge to escape the situation

Question 4.
Explain excessive dependence on the internet.
(a) Meaning
(b) Four C’s to identify excessive internet usage
(c) Red flags that indicate internet addiction.
Answer:
(a) Meaning
The amount of time as well as reason for using the internet may become a matter of concern for e.g., online gambling, gaming, etc. The person may socialise more online with friends than real life socialising. Spending excess time online may cause the person to neglect family, relationships, work etc. Virtual world enables games/gambling almost continuously. This leads to the person neglecting personal hygiene, real life relationships and become withdrawn and irresponsible. The person may feel guilty or defensive about internet use. He/ she may panic in the absence of internet service. A growing dependence on internet refers to an inability to stop and down down.

(b) Four C’s to identify excessive internet usage
Excessive internet usage is characterised by extensive, problematic addiction to the use of computer and internet. It signifies poorly controlled preoccupations or behaviour regarding such usage. Excessive internet usage leads to personal distress and social impairment.
The four C’s to identify excessive internet usage are as follows-

1. Craving – Do you have an intense desire to use the internet?
2. Control – Do you have an inability to control your self using the internet?
3. Compulsion – Do you find it difficult to stop using the internet? Even though you know you should not spend so much time on it?
4. Consequence – Have you ever experienced any physical or psychological ill effects as a result of excessive use of the internet? If you answer a ‘yes’ for at least three of the C’s, it can be a matter of concern.

(c) Red flags that indicate internet addiction
The Red Flags that indicate over dependence on internet are-

1. Feelings of euphoria while using the internet.
2. Physical symptoms like headache, dry eyes, etc.
3. Inability to keep to schedules and boredom with routine tasks.
4. Poor personal hygiene and nutrition to remain online.

4. Analysis the following case study.

Sujata is now a sad and lonely girl. She has cut off herself from all her relatives and family friends. She doesn’t participate in any college programmes nor family functions. She is mostly found in the library all by herself. She has lost her self-confidence. At home she prefers eating in the bedroom and mostly indulges in television or mobile activities. Apply the ALGEE model and help Sujata to evolve in her mental health.
Answer:
Sujata is showing symptoms of depression and anxiety such as sadness, withdrawing from family/ friends and social activities. The ALGEE model can be used.

1. Approach, assess and assist in any crisis – Behavioural changes are very noticeable in Sujata. I can voice my concern to the teachers/ counsellor of the school or to her family members.
2. Listen in a non-judgemental manner -1 will try to meet Sujata in the library or any place where she feels comfortable. I will explain my concerns to her about not interacting with others and overuse of mobile phones. I will listen patiently and compassionately.
3. Give support and information – Let Sujata know that she has emotional support of her friends. There is nothing to feel guilty or ashamed of. She should hence be forthcoming about her problems.
4. Encourage her to get professional help – I will encourage her to meet the college counsellor who will be able to help her professionally.
5. Encourage self-help strategies – This will help Sujata to regain control over her life. Some positive measures include breathing exercises, yoga, laughter therapy, etc.

Balbharti Maharashtra State Board Class 12 Geography Solutions Chapter 1 Population Part 1 Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Geography Solutions Chapter 1 Population Part 1

1. Identify the correct correlation.

A – Assertion R – Reasoning
Question 1.
A – Areas which have fertile soil have dense population.
R – Fertile soils are good for agriculture.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 2.
A – Population of a region does not change.
R – Birth rate, death rate and migration affect the population of a region.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(b) Only R is correct.

Question 3.
A – In stage 2, death rate reduces but birth rate is constant.
R – Population increases rapidly in stage 2.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 4.
A – In stage 5 death rate is more than birth rate.
R – Population is declining in stage 5.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 5.
A – In stage 1 both death rate and birth rate are high.
R – Population growth is stable in stage 1.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

2. Write short notes on.

Question 1.
Impact of relief on population distribution.
Answer:
1. Relief is one of the most important factors influencing the distribution of population.

2. Generally, mountains are thinly populated, plains are thickly populated and plateaus are moderately populated.

3. The mountains and hilly areas are less populated because of limited means of livelihood; agriculture is poorly developed and transportation facilities are limited. For example, north eastern states of India have less population due to hilly and mountainous relief.

4. On the other hand, plains are densely populated because of fertile soil and well-developed agriculture. Due to plain relief, it is easy to construct roads and develop industries. Better employment facilities attract people in these areas. For example, Ganga plains are thickly populated.

5. In short, we can say plains are densely populated and mountains and plateaus are sparsely populated.

Question 2.
Correlation between birth rate and death rate.
Answer:

• Birth rate and death rate are the important components of population change.
• Birth rate is the number of live births in a year per thousand population.
• Death rate is the number of deaths in a year per thousand population.
• Population growth depends upon birth rate and death rate in a year.
• Population growth occurs not only by increasing birth rate but also because of decreasing death rate.
• When birth rate is more than death rate, population increases.
• When birth rate is less than death rate, population decreases.
• If both, birth rate and death rate is same then population is said to remain stable. However, the birth rate and death rate being same is only a hypothetical situation.

Question 3.
Stage 3 of Demographic Transition Theory.
Answer:
1. Stage 3 of Demographic Transition Theory is the stage of expanding population.

2. From second stage to this stage, death rates are decreasing. Birth rates are also decreasing. Decrease in both birth rates and death rates, reduces the rate of growth of population. But actually, population is growing because the birth rates are higher than death rates.

3. In this stage, since the country is making progress, the income of the people is above the subsistence level and there is an improvement in the standard of living of the people. Poverty is also reducing.

4. There is development of technology as a result secondary and tertiary activities develop.

5. Due to increase in education level, people understand the importance of family planning so size of family reduces.

6. In short in stage 3 countries are moving from developing stage to developed stage.

3. Give geographical reasons.

Question 1.
India is passing through Stage 3 of demographic transition.
Answer:

• In India, since there is a decrease in the birth rates and death rates, the growth rate of population is also decreasing.
• Due to the development in the country, income of the people has reached above subsistence level, standard of living is improved, poverty is decreasing, technology is developing.
• Number of people engaged in secondary and tertiary activities are increasing.
• Due to increase in the literacy rate, people have understood the importance of family planning. Therefore, there is a decrease in the size of family.
• Hence, India is passing through Stage 3 of demographic transition.

Question 2.
Population distribution is uneven.
Answer:
1. Distribution of population in the world is very uneven because distribution of population depends upon many physical factors such as relief, climate, availability of water supply, soil etc.

2. For example, if you consider relief factor, mountains and hilly areas are thinly populated. Plateau regions are moderately populated and plains are densely populated. The Himalayan region in India is thinly populated but the Gangatic plains are thickly populated and Deccan plateau region are moderately populated.

3. The distribution of population also depends upon human factors such as agriculture, mining, transportation, urbanisation etc.

4. For example, agriculture or mining activities support large population since they provide source of living to many people.

5. Sometimes government policies also affect population distribution. For example, government provided land, water, electricity at concessional rate in New Mumbai area to attract people and to reduce pressure of population in Mumbai city.

Question 3.
Population increases because of transportation facilities.
Answer:
1. The development of roads and railways makes the region more accessible.

2. Such areas provide favourable conditions for the development and manufacturing industries, which generate employment. Therefore, people from different areas migrate in search of jobs. Thus, such areas become densely populated. For example, Gangetic plain of India, where the density of roads and railways is highest in India.

3. Population increases in port cities due to availability of sea transport for the development of trade. Therefore, the coastal region is densely populated. For example, many port cities like Chennai, Mumbai are developed on the east and west coast of India.

4. Thus, population increases because of transportation facilities.

Question 4.
Secondary and tertiary activities increase in the third stage of demographic transition.
Answer:

• In Stage 3 of demographic transition theory, growth rate of population decreases.
• As a result, the income of the people in the country reaches above subsistence level. Poverty rate decreases and standard of living increases. Therefore, the use of technology increases and this generates an employment in secondary and tertiary activities.
• Due to increase in education level and development of health facilities there is increase in employment in tertiary sector.
• Thus, secondary and tertiary activities increase in the third stage of demographic transition.

Question 5.
Population may increase though birth rates are low.
Answer:
The growth of population depends upon the difference between number of live births in a year per thousand population and number of deaths in a year per thousand population. Therefore, growth of population depends upon both birth rate and death rate.

When birth rate is low and death rate is also low, then though the number of live births per thousand population are less, but due to a smaller number of deaths per thousand population, there is increase in population of the country.

Question 6.
Population density is a function of population and area of a region.
Answer:
The number of people living in any area or country is called total population of the area or country.

Density of population is the ratio between total population and a total area of that region or country.

For example, as per the census of 2011, Density of population in India is 325 persons per sq. km. It is a ratio between total population in India and total area of India in sq. kms.

In some countries total population may be less but the density of population is high due to small area of the country. For example, Bangladesh’s total population is less but area of country is small therefore, density of population is high.

In some countries total population may be more but the density of population is low due to very large area of the country. For example, Brazil has more total population but area of country is also large therefore, density of population is low.

Thus, population density is a function of population and area of a region.

4. Answer the following questions in detail.

Question 1.
Explain the physical factors affecting distribution of population.
Answer:
Physical factors affecting distribution of population are:
(i) Relief
(ii) Climate
(iii) Availability of water
(iv) Soils

(i) Relief

• Distribution of population is greatly affected by relied features.
• Generally, flat plains or gently sloping lands are densely populated.
• Plains are suitable for agricultural activities.
• In these areas it is easier to construct roads and railways and development of industries and trade. As a result, many people are attracted to plains and they become densely populated. For example, Ganga plains are thickly populated.
• On the other hand, in mountainous and hilly areas density of population is low. This is because in such areas agricultural development is difficult.
• The construction and development of transport facilities is very difficult and costly too. Such areas are inaccessible.
• Due to inaccessibility, movement of goods and people are restricted. Therefore, mountainous and hilly areas are thinly populated. For example, north eastern states of India have less population due to hilly and mountainous relief.

(ii) Climate

• Climate is the most important factor of all the factors influencing the distribution of population.
• Areas having very hot or very cold climate, heavy rainfall are very uncomfortable for human settlement. Such areas are thinly populated.
• For example, polar regions where Eskimos and Lapps live are sparsely populated due to extreme cold climate. Sahara Desert is sparsely populated due to extreme hot climate.
• On the other hand, areas with equable climate, that is climate having not much seasonal variation attract people. People feel comfortable to stay in these areas.
• For example, coastal areas have dense population because of equable climate and wide scope for the development of agriculture, industries and trade.

(iii) Availability of water

• Water is the most important factor affecting distribution of population. It is the most essential factor for all human activities.
• Therefore, more people live in areas where potable and sufficient water is available. As a result of this most of the river valleys are densely populated i.e. Nile river valley.
• Even in desert areas there is more population near oasis due to availability of water.

(iv) Soil

• Fertile soils are most important for the development of agriculture.
• The areas having fertile alluvial soil have developed intensive agriculture and support large number of people and hence they are densely populated, e.g., Gangetic Plain, Plains of Mississippi, Irrawaddy and Yangtze etc.
• Similarly, in the areas having very fertile black cotton soil or regur soil, agriculture is well developed and hence such areas are densely populated.
• The volcanic soil is very fertile hence, it supports agriculture. Therefore, slopes of volcanic mountains have dense population. For example, volcanic mountain slopes of Java island.

Question 2.
In the first and fifth stage of the demographic transition, population growth is almost nil. What is the difference between the two stages then?
Answer:

• In the stage 1 both birth rates and death rates are high. The difference between the two is very less and therefore, population is stable.
• In stage 1 birth rates are high due to limited educational opportunities, people feel having many children is good. Therefore, families are big.
• In stage 1, due to lack of sanitation facilities, medical facilities, spread of contagious diseases, malnutrition, etc., death rate is high.
• In stage 5 birth rates and death rates are very low. Birth rates are almost equal to death rates.
• As a result, the population growth is almost minimal or very low or even negative in case of some countries.
• In stage 5, death rate is low because of improved medical facilities, eradication of contagious diseases and healthy environment.
• In stage 5, due to increase in awareness among the people, birth rate is low.

Question 3.
Discuss the problems faced by counties in stage 4 and stage 5.
Answer:
Problems faced by stage 4 countries are as under:

• The death rate is very low and going down as the medical facilities have improved and pandemic like plague, cholera, small pox, etc., are eradicated.
• Birth rate is the same as death rate so population growth is minimal.
• Problems faces by stage 5 countries are as under:
• In this stage the birth rate is very low and death rate is high. Therefore, the growth of population is slow or negative growth of population is seen.
• Due to large number of old people the death rate is high and due to a smaller number of young people birth rate is low.
• Due to large number of old people, dependent population is high.
• Due to less young age population, working population is limited.
• As a result, the size of dependant population is larger than active population and it has adverse effect on economy of the country.

5. Draw a neat labelled diagram for demographic transition theory and its various stages.
Answer:

6. Mark and name the following on the outline map of the world with suitable index.

(a) Highly populated region in Australia.
(b) Sparsely populated region in India.
(c) Any 2 countries in stage 5 of demography transition theory.
(d) Any 2 countries in stage 2 of demographic transition theory.
Answer:

Class 12 Geography Chapter 1 Population Part 1 Intext Questions and Answers

Try These

Question 1.
Observe the pie charts shown in the figure and answer the following questions. (Text book pg.no – 1)

1. Which continent has least population?
2. Which continent has the least landmass and also least population?
3. Which continent has the most land mass as well as most of the population?
4. Which continent is missing in one of the pie charts? Why?

Answer:

1. The continent which has the least population is Australia.
2. The continent which has the least land mass and also least population is Australia.
3. The continent which has the most land mass and also most population is Asia.
4. The continent of Antarctica is missing in population distribution chart, because it has no permanent human settlement.

Question 2.
Look at the below figure and answer the questions that follow:

1. What does the image show?
2. What happens to the population when the deaths are more than births?
3. What happens to the population when births are more than deaths?
4. What happens when both are same? Is it possible?

Answer:

1. The image shows balance between birth rate and death rate.
2. Population growth may be less or in some countries there may be negative growth.
3. When births are more than deaths, then population growth is faster.
4. When both births and deaths are same, population will be stagnant. This is not possible for any country.

Give it a try

Question 1.
The below table shows the 10 most populated countries in the world in 2018 with their areas. Calculate their population densities and complete the table. (Text book pg.no – 1)

Answer:

Question 2.
The satellite image given in Fig. They show the same area from two different periods. (Text book pg.no – 6)

1. What difference do you see?
2. What might have caused these changes?

Answer:
1. The satellite image ‘A’ is image of the year 2005 and satellite image ‘B’ is of the year 2019. That means there is a difference of 14 years in these two images.

2. In image ‘A’ you can see that there are a few roads, limited settlements and most of the areas are covered by agricultural fields, and there is thin population.

3. When we compare the image ‘A’ with the image ‘B’, we find that in image ‘B’ the number of major roads (highway) and minor roads have increased. As a result, the area has become more accessible and thickly populated.

Due to development of industries and employment opportunities there is development of transport.

Question 3.
1. Can you calculate the death rate if the total number of deaths in the above city was 2,986 in the same year?
2. On the basis of the birth rates given in earlier and death rates calculated, what change in population do you observe?
Answer:
1. Total population of a city is 223000 and total deaths in the city are 2986 in that year.
Death Rate = \(\frac {Total number of deaths in a year}{Total population in that year}\) × 1000
Death Rate = \(\frac {2896}{223000}\) × 1000 = 13.39
Therefore, the death rate is 13.39.

2. In earlier example birth rate was 14.57 and the death rates calculated is 13.39. It means death rate have decreased by 1.8. It means the population has increased.

Question 4.
Look at the graph in Fig. carefully. Answer the following questions: (Text book pg.no – 9)

1. What do the blue and black lines indicate?
2. What does the green part in the graph show?
3. What does the blue part in the graph show?
4. In which stages is the birth rate more than the death rate?
5. In which stages is the birth rate same as the death rate?
6. In which stage is the death rate being more than birth rate?

Answer:

1. Blue lines indicate birth rate and black lines indicate death rate.
2. Green part in the graph shows the natural increase of population.
3. Blue part in the graph shows the natural decrease of population.
4. In stage 2 and 3 birth rates is more than death rate.
5. In stage 4 the birth rate is same as the death rate.
6. In stage 5 the death rate is more than birth rate.

Make friends with maps!

Question 1.
Look at the map in Fig. Compare it with the physical map of the world given in Textbook Page No. 83. Try to understand the impact of physical factors on population distribution. Complete the table accordingly. (Text book pg.no – 2)


Answer:

Continent	Physical factors responsible for High population	Physical factors responsible for less population
North America	Coastal Areas	Forest, deserts, snow covered land
Asia	Coastal areas and Fertile Plains	Mountains and deserts
Europe	Coastal areas and fertile Plains	Mountains, snow covered areas
Africa	Coastal Areas	Dense forest, mountains and deserts
South America	Coastal Areas	Mountains, dense forest and deserts
Australia	Coastal Areas	Hilly regions and deserts
Antarctica	–	Snow covered areas

Question 2.
Refer to the map showing rice producing regions of the world in Fig. Relate it with the population map of the world in Fig. Write the conclusions in your own words. (Text book pg.no – 5)


Answer:
Areas of high density of population in Fig 1.2 if we compare with world map Fig 1.4 showing major rice producing areas in the world, we found that the areas of major rice production and areas of high density / thick population are the same areas.
Conclusion:
Rice cultivation is possible only in those areas where there is fertile alluvial soil and assured supply of water.
Rice producing areas and areas of dense population in the world are the river flood plains and delta of rivers like Kaveri, Krishna, Godavari and Ganga in India, Brahmaputra in Bangladesh, Irrawaddy in Myanmar, Yangtze and Yellow in China, Mekong in Laos and Cambodia etc. These areas are high density areas in the world.

Can you tell?

Question 1.
Can you think of the factors besides physiography which affect the distribution of population? Make a list. (Text book pg.no – 3)
Answer:

Physical / Human factors	High density of population	Low density of population
Availability of potable water	River valleys	Deserts
Climate	Equable climate – coastal areas	Extreme climate – polar regions
Availability of resources	Minerals, fertile soil	Limited resources
Economic	Transportation, employment opportunities, urbanisation	Less employment opportunities, poor economic growth
Social	Migration from different parts of India in Mumbai	Out migration from Konkan to Mumbai
Government Policy	Favourable government policies to attract people	Unfavourable government policies

Question 2.
Observe the table 1.4. Arrange data in ascending order for birth rate and death rates respectively. (Text book pg.no – 8)

Country	Crude BR (2017)	Crude DR (2017)
Sweden	11.5	9.1
India	18.1	7.2
Greece	8.2	11.6
China	12.4	7.1
USA	11.8	8.5
Niger	46.5	8.5

Answer:

Question 3.
Look at the Fig. and answer the following questions. (Text book pg.no – 9)

1. If the crude birth rate is 7 and crude death rate is 8 then which stage of demographic transition is the country in?
2. If a country has crude death rate of 20 and crude birth rate of 24, then which stage of demographic transition is the country in? [Text book pg.no – 10]

Answer:

1. The country is in stage 5 of demographic transition.
2. The country is in stage 3 of demographic transition.

Find out.

Question 1.
(i) Are Eskimos still living in their conventional ways?
(ii) What changes can be seen in their lifestyle now? (Text book pg.no – 4)
Answer:
(i) No, Eskimos are not living in their conventional way due to the changing environment as a result of increased contacts with societies to the south.

(ii) Eskimo life has changed greatly because of increased contacts with societies to the south.

• They were using harpoons for hunting, now they are using rifles. They were using dogs for land transport, now they are using snowmobiles.
• Outboard motors, store-bought clothing and many other manufactured products have entered into their culture.
• Women are taking salaried jobs to earn currency for store-bought products. As a result, women are losing their knowledge of traditional skills such as sewing animal skin.
• Many Eskimos are not doing nomadic hunting which was their main activity. Now they are living in northern towns and cities and working in mines and oil fields.
• Some Eskimos in Canada have formed cooperative societies for marketing their handicrafts, fish catches, tourism ventures etc.

Use your brain power!

Question 1.
(i) Can lakes be a factor for concentration of population? Find examples.
(ii) Which water bodies are surrounded by dense population in Maharashtra? (Text book pg.no – 4)
Answer:
(i) Man always likes to settle near a waterbody. People are attracted towards lakes.

Lakes are not only a source of fresh water but also a source of fish. They also provide water supply for industries, agriculture and provide water transport. They provide good sites to develop tourism due to greenery of trees surrounding the lake, scope for boating, cool breeze and pleasant atmosphere.

For example, Lake Victoria in Africa, supports 40 million people, with population density 250 persons per sq. km. The growth rate of the population is 3.5 percent each year, which is among the highest growth rates in the world.

The Victoria lake supports the largest freshwater fishery in the world. The fish catch from the lake is more than one million and it employs two lakh people in direct fishing and supports livelihood to four million people.

Five Great lakes in USA – Superior, Huron, Michigan, Erie and Ontario make up the largest body of freshwater on earth. They support more than 30 million people. This equates to 10 percent of USA residents and 30 percent Canadian residents.

The lakes have been a major source for transportation, trade, fishing, tourism, power, recreation etc.

(ii)

• In Maharashtra the following water bodies are surrounded by dense populations.
• Rankala lake around which dense population of Kolhapur city.
• Powai lake around which dense population of Mumbai city.
• Ambazari lake around which dense population of Nagpur city.
• Pashan lake around which dense population of Pune city.
• Dense population on the bank of Mula-Mutha river of Pune city.
• Dense population on the bank of Nag river – Nagpur city.
• Dense population on the bank of Tapi river – Bhusaval and other cities.
• Dense population on the bank of Godavari river – Nasik city.
• Dense population on the bank of Krishna- Koyana rivers – Karad, Sangli cities.
• Dense population along the coastline of Arabian sea- Mumbai city.

Question 2.
In which stage do you think India is passing right now? (Text book pg.no – 10)
Answer:
India is passing through stage 3 right now.

Question 3.
Find out in what multiples has population increased in the following timeline and write down your findings. For example, in the initial phase, the population took 6 centuries (1000 to 1600 A.D.) to double itself. (Text book pg.no – 11)

Answer:
(i) 1000 to 1600 population increase 2 times in 6 hundred years.
(ii) 1600 to 1900 population increased 3 times in 3 hundred years.
(iii) 1900 to 1960 population increased 2 times in 6 hundred years.
(iv) 1960 to 2000 population increased 2 times in 4 hundred years.

Let’s recall.

Question 1.
Which policy did the Brazilian government promote with respect to decentralisation? (Text book pg.no – 7)
Answer:

1. Last two decades there is highly centralised military rule in Brazil so there was demand for local autonomy. Brazil sought to decentralised government authority and promote citizen participation to establish democracy.
2. Brazil became decentralised federation when it undertook transformation of governance.
3. As result authoritarian military regime came to an end.