Class 12

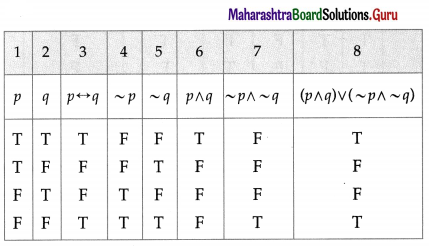
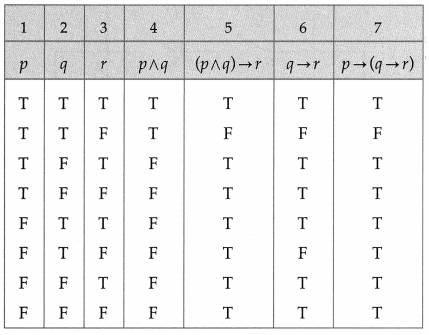
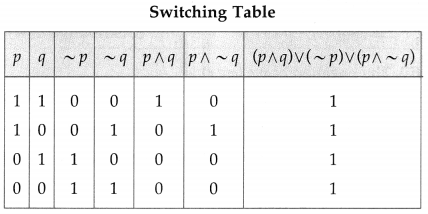
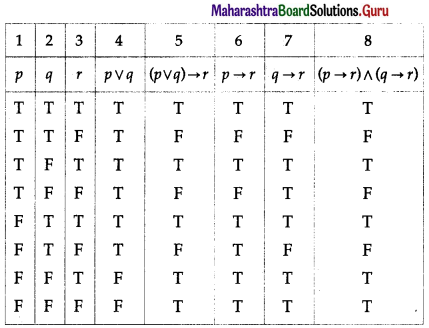
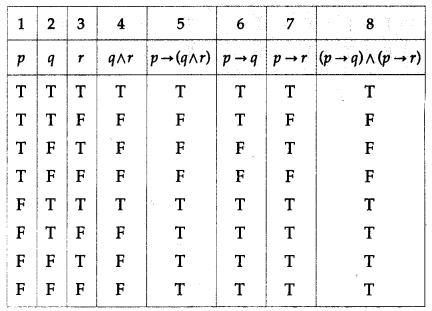
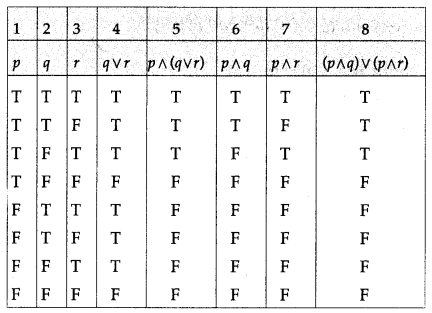
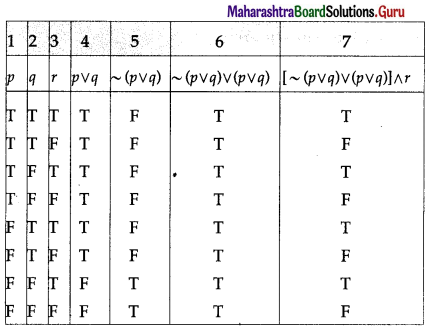
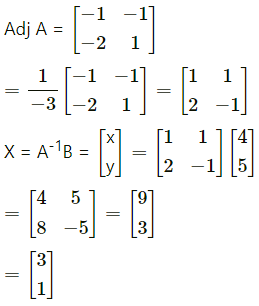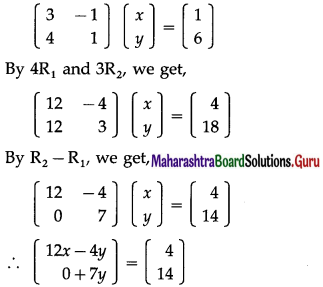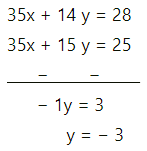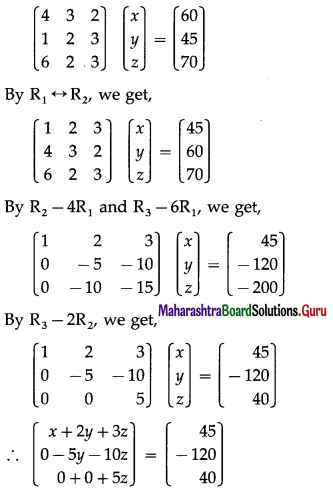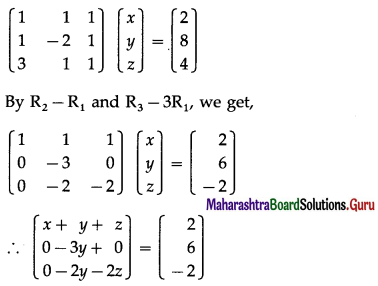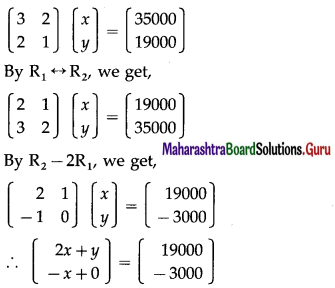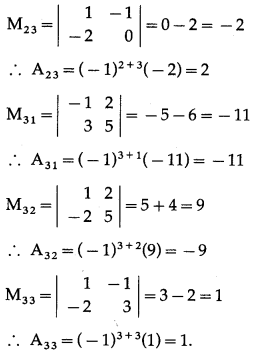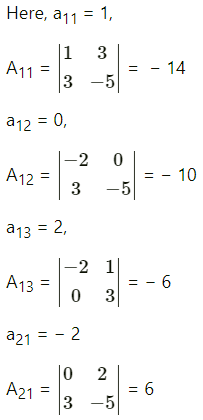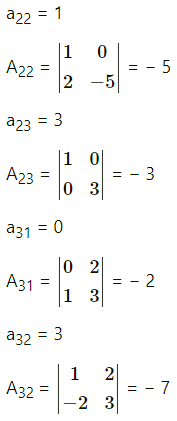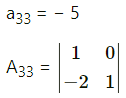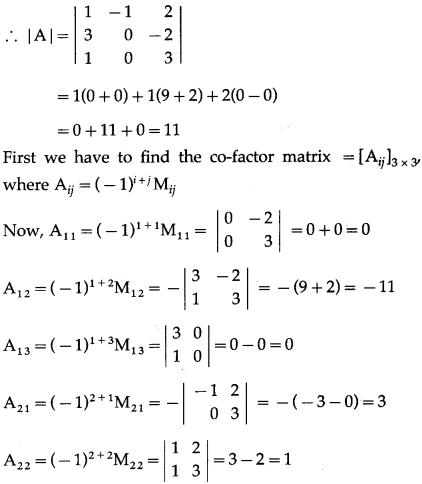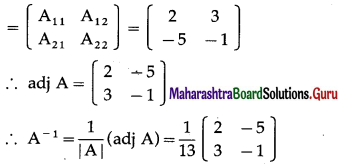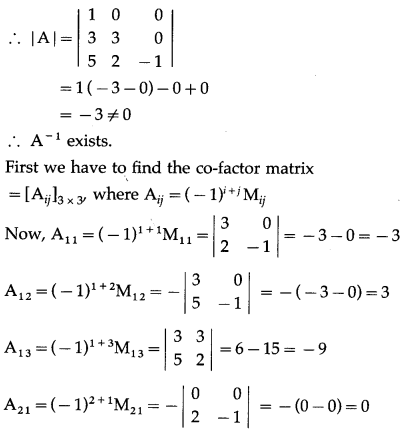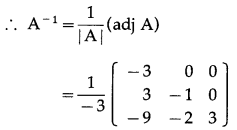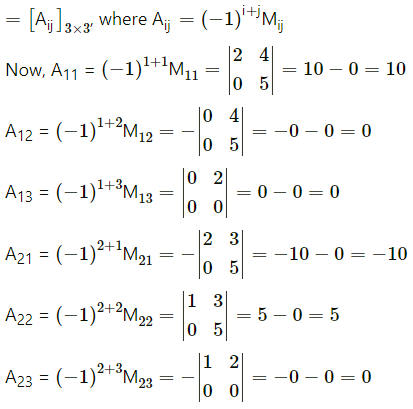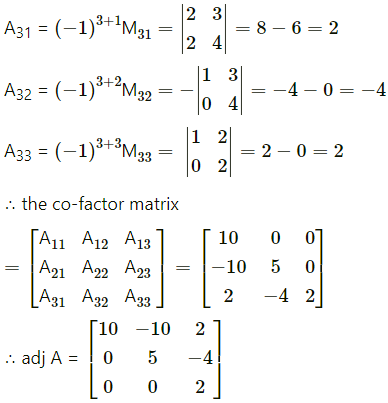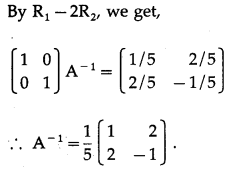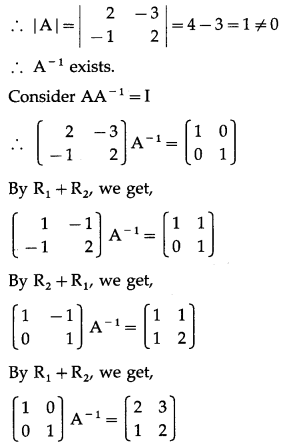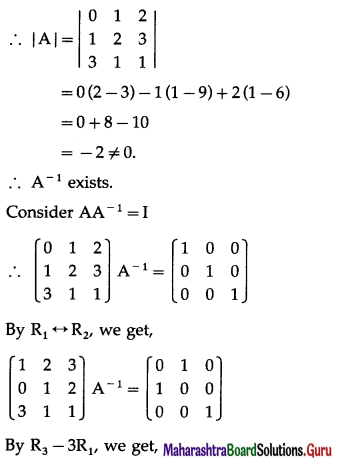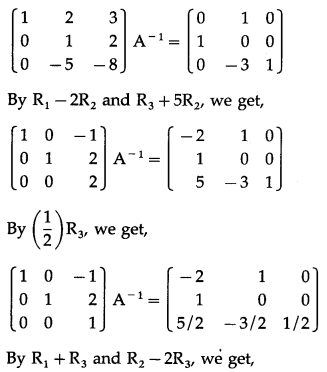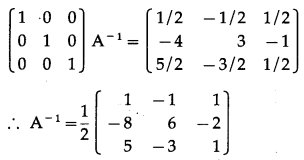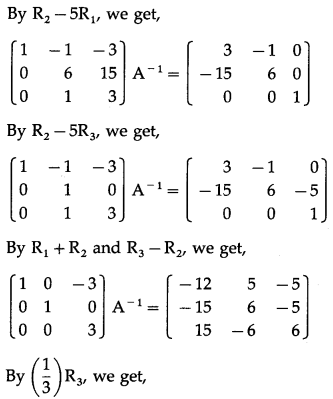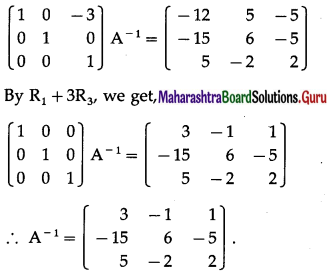Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Miscellaneous Exercise 2A Questions and Answers.

12th Maths Part 1 Matrices Miscellaneous Exercise 2A Questions And Answers Maharashtra Board

Question 1.
If A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\) then reduce it to I₃ by using column transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right|\)
= 1(1 – 0) – 0 + 0 = 1 ≠ 0
∴ A is a non-singular matrix.
Hence, the required transformation is possible.
Now, A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\)
By C₁ – 2C₂, we get, A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
-3 & 3 & 1
\end{array}\right]\)
By C₁ + 3C₃ and C₂ – 3C₃, we get,
A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) = I₃.

Question 2.
If A = \(\left[\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right]\), then reduce it to I₃ by using row transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right|\)
= 2 (0 – 1) – 1(1 – 1) + 3 (1 – 0)
= -2 – 0 + 3 = 1 ≠ 0
∴ A is a non-singular matrix.
Hence, the required transformation is possible.
Now, A = \(\left[\begin{array}{lll}
2 & 1 & 3 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right]\)
By R₁ – R₂, we get,

By R₁ – R₃ and By R₂ – R₃, we get
A ~ \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) = I₃.

Question 3.
Check whether the following matrices are invertible or not:
(i) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1 – 0 = 1 ≠ 0.
∴ A is a non-singular matrix.
Hence, A^-1 exists.

(ii) \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right|\) = 1 – 1 = 0.
∴ A is a singular matrix.
Hence, A^-1 does not exist.

(iii) \(\left[\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
1 & 2 \\
3 & 3
\end{array}\right|\) = 3 – 6 = -3 ≠ 0.
∴ A is a non-singular matrix.
Hence, A^-1 exist.

(iv) \(\left[\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll}
2 & 3 \\
10 & 15
\end{array}\right|\) = 30 – 30 = 0.
∴ A is a singular matrix.
Hence, A^-1 does not exist.

(v) \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{cc}
\sec \theta & \tan \theta \\
\tan \theta & \sec \theta
\end{array}\right|\)
= sec²θ – tan²θ = 1 ≠ 0.
∴ A is a non-singular matrix.
Hence, A^-1 exist.

(vii) \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Solution:
let A = \(\left[\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
3 & 4 & 3 \\
1 & 1 & 0 \\
1 & 4 & 5
\end{array}\right|\)
= 3(5 – 0) – 4(5 – 0) + 3(4 – 1)
= 15 – 20 + 9 = 4 ≠ 0
∴ A is a non-singular matrix.
Hence, A^-1 exist.

(viii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & -1 & 3 \\
1 & 2 & 3
\end{array}\right|\)
= 1 (-3 -6) – 2 (6 – 3) + 3 (4 + 1)
= -9 – 6 + 15 = 0
∴ A is a singular matrix.
Hence, A^-1 does not exist.

(ix) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right]\)
Then, |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
3 & 4 & 5 \\
4 & 6 & 8
\end{array}\right|\)
= 1(32 – 30) – 2(24 – 20) + 3(18 – 16)
= 2 – 8 + 6 = 0
∴ A is a singular matrix.
Hence, A^-1 does not exist.

Question 4.
Find AB, if A = \(\left[\begin{array}{ccc}
1 & 2 & 3 \\
1 & -2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & -1 \\
1 & 2 \\
1 & -2
\end{array}\right]\) Examine whether AB has inverse or not.
Solution:

∴ A is a non-singular matrix.
Hence, (AB)^-1 exist.

Question 5.
If A = \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\) is a nonsingular matrix then find A^-1 by elementary row transformations.
Hence, find the inverse of \(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\)
Solution:
Since A is a non-singular matrix, then find A^-1 by using elementary row transformations.
We write AA^-1 = I

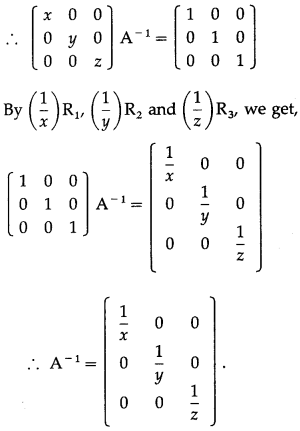
Comparing \(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) with \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\),
we get, x = 2, y = 1, z = -1
∴ \(\frac{1}{x}\) = \(\frac{1}{2}\), \(\frac{1}{y}\) = \(\frac{1}{1}\) = 1, \(\frac{1}{z}\) = \(\frac{1}{-1}\) = -1
\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) is \(\left(\begin{array}{rrr}
\frac{1}{2} & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right)\).

Question 6.
if A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\) and X is a 2 × 2 matrix such that AX = I , then find X.
Solution:
We will reduce the matrix A to the identity matrix by using row transformations. During this pro¬cess, I will be converted to the matrix X.
We have AX = I.

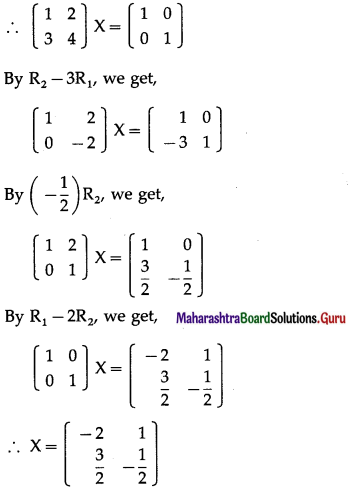
Question 7.
Find the inverse of each of the following matrices (if they exist).
(i) \(\left[\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
1 & -1 \\
2 & 3
\end{array}\right|\) = 3 + 2 = 5 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

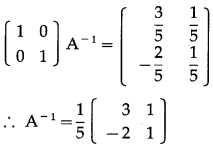
(ii) \(\left[\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & 1 \\
1 & -1
\end{array}\right|\) = -2 – 1 = -3 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

(iii) \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right|\) = 7 – 6 = 1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

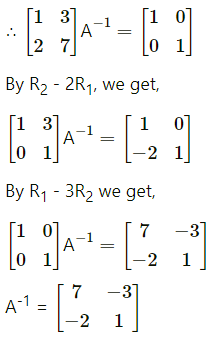
(iv) \(\left[\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & -3 \\
5 & 7
\end{array}\right|\) = 14 + 15 = 29 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

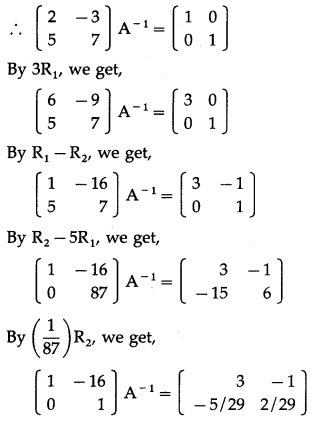
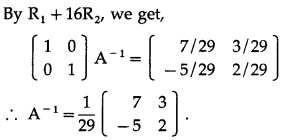
(v) \(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right|\) = 8 – 7 = 1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

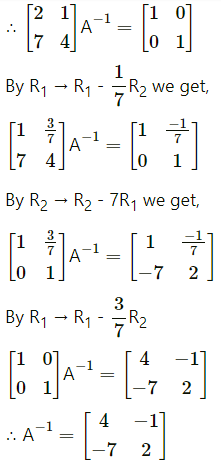
(vi) \(\left[\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
3 & -10 \\
2 & -7
\end{array}\right|\) = -21 + 20 = -1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

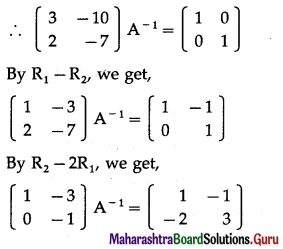
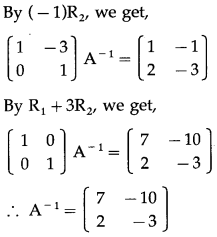
(vii) \(\left[\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right|\)
= 2(4 + 6) +3(4 – 9) + 3(-4 – 6)
= 20 – 15 – 30 = -25 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

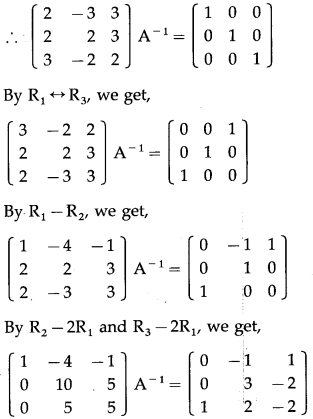
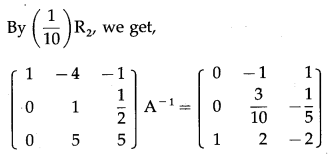
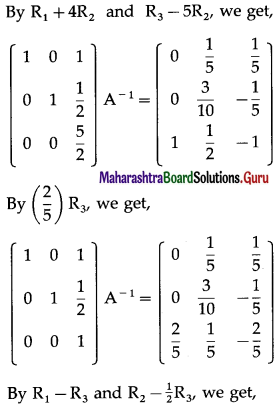
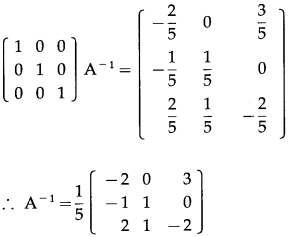
(viii) \(\left[\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right|\)
= 1(0 + 25) + 3(0 + 10) + 2(-15 – 0)
= 25 + 30 -30
= 25 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

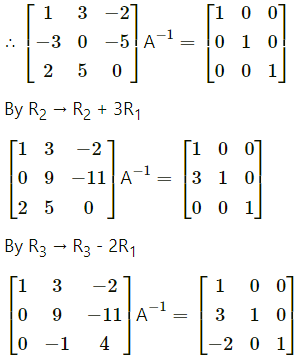
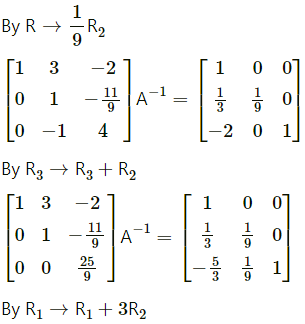
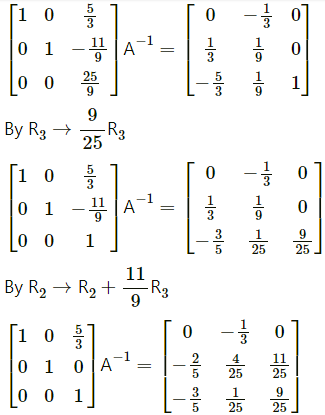
(ix) \(\left[\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:
Let A =\(\left[\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right|\)
= 2(3 – 0) – 0 – 1(5 – 0)
= 6 – 0 – 5 = 1 ≠ 0
∴ A^-1 exists.
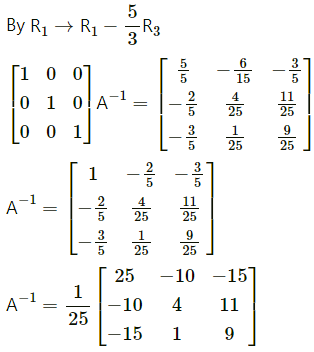
Consider AA^-1 = I


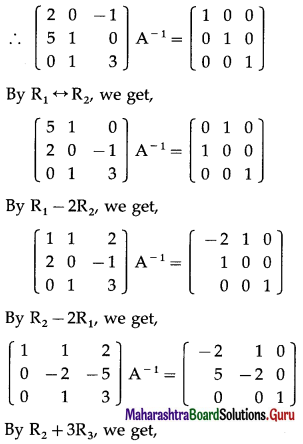
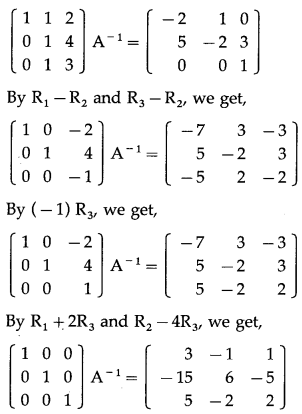
∴ A^-1 = \(\left[\begin{array}{lll}
3 & -1 & 1 \\
-15 & 6 & -5 \\
5 & -2 & 2
\end{array}\right]\)

(x) \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
∴ A^-1 = \(\left[\begin{array}{lll}
1 & 2 & -2 \\
0 & -2 & 1 \\
-1 & 3 & 0
\end{array}\right]\)
= 1\(\left|\begin{array}{ll}
-2 & 1 \\
3 & 0
\end{array}\right|\) – 2\(\left|\begin{array}{ll}
0 & 1 \\
-1 & 1
\end{array}\right|\) – 2\(\left|\begin{array}{ll}
0 & -2 \\
-1 & 3
\end{array}\right|\)
|A| = 1(0 – 3) – 2(0 + 1) – 2(0 – 2)
= -3 – 2 + 4
= -1 ≠ 0
∴ A^-1 exists.
We have
AA^-1 = I


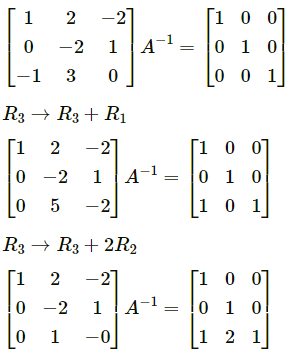
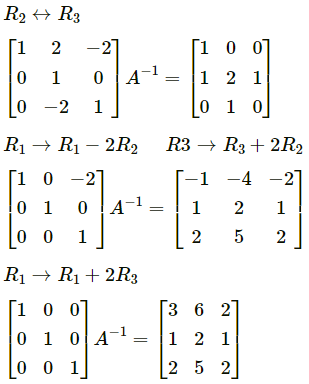
∴ A^-1 = \(\left[\begin{array}{lll}
3 & 6 & 2 \\
1 & 2 & 1 \\
2 & 5 & 2
\end{array}\right]\)

Question 8.
Find the inverse of A = \(\left[\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right]\) by
(i) elementary row transformations
Solution:
|A| = \(\left|\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right|\)
= cosθ (cosθ – 0) + sinθ (sinθ – 0) + 0
= cos²θ + sin²θ = 1 ≠ 0
∴ A^-1 exists.
(i) Consider AA^-1 = I

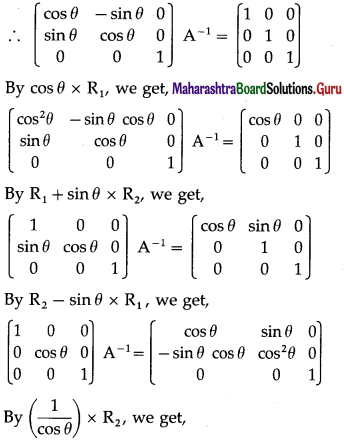
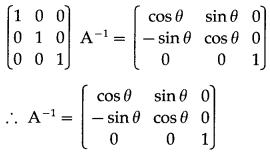
(ii) elementary column transformations
Solution:
Consider A^-1A = I

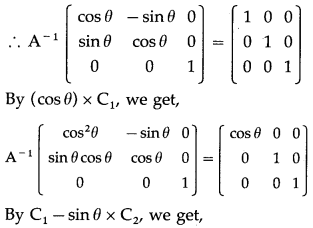
Question 9.
If A = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & 0 \\
3 & 1
\end{array}\right]\) find AB and (AB)^-1. Verify that (AB)^-1 = B^-1A^-1
Solution:
AB = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\) \(\left[\begin{array}{ll}
1 & 0 \\
3 & 1
\end{array}\right]\)




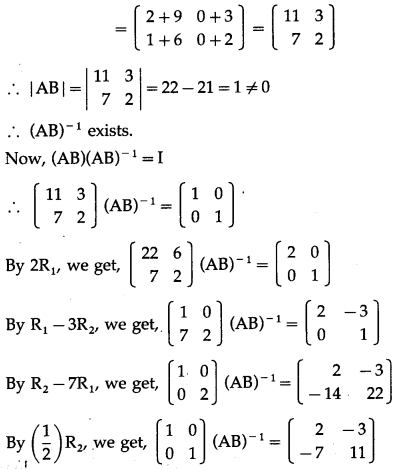
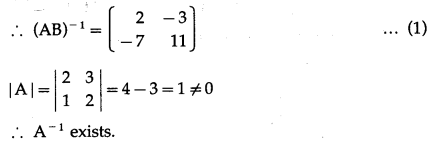
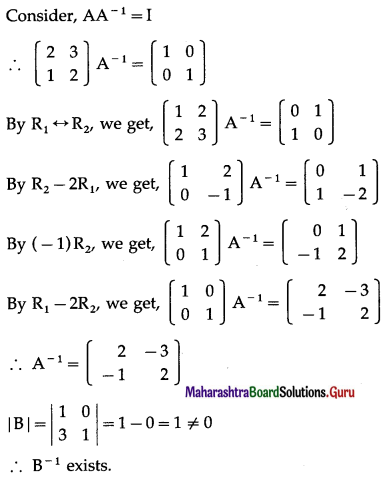
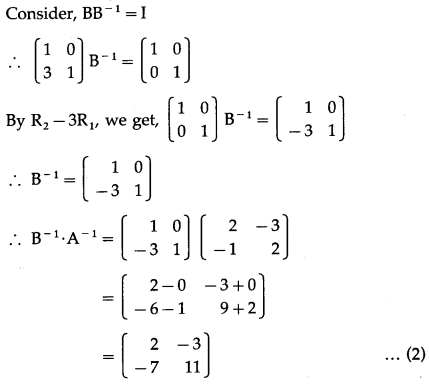
From (1) and (2), (AB)^-1 = B^-1 ∙ A^-1.

Question 10.
If A = \(\left[\begin{array}{ll}
4 & 5 \\
2 & 1
\end{array}\right]\), then show that A^-1 = \(\frac{1}{6}\)(A – 5I)
Solution:
|A| = \(\left|\begin{array}{ll}
4 & 5 \\
2 & 1
\end{array}\right|\) = 4 – 10 = -6 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

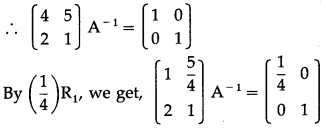
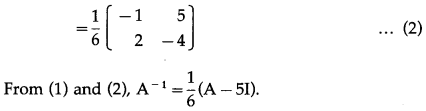
Question 11.
Find matrix X such that AX = B, where A = \(\left[\begin{array}{ll}
1 & 2 \\
-1 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
0 & 1 \\
2 & 4
\end{array}\right]\)
Solution:
AX = B

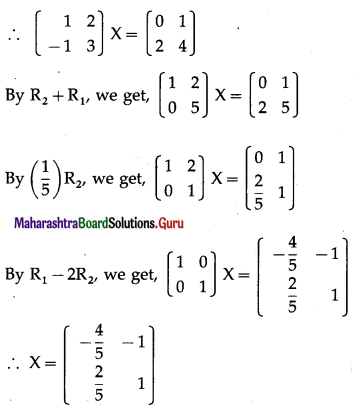
Question 12.
Find X, if AX = B where A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\).
Solution:
AX = B

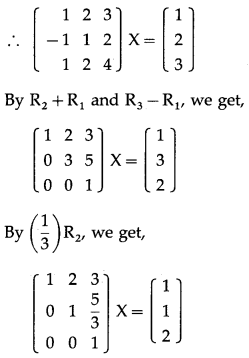
Question 13.
If A = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{ll}
4 & 1 \\
3 & 1
\end{array}\right]\) and C = \(\left[\begin{array}{ll}
24 & 7 \\
31 & 9
\end{array}\right]\) then find matrix X such that AXB = C.
Solution:
AXB = C
∴ \(\left(\begin{array}{ll}
1 & 1 \\
1 & 2
\end{array}\right)(\mathrm{XB})\) =\(\left[\begin{array}{ll}
24 & 7 \\
31 & 9
\end{array}\right]\)
First we perform the row transformations.

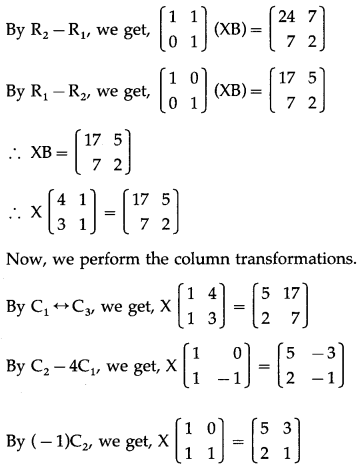
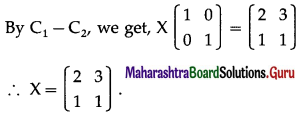
Question 14.
Find the inverse of \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\) by adjoint method.
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right|\)
= 1(7 – 20) – 2(7 – 10) + 3(4 – 2)
= -13 + 6 + 6 = -1 ≠ 0
∴ A^-1 exists.
First we have to find the cofactor matrix
= [A_ij]_3×3 where A_ij = (-1)^i+jM_ij
Now, A₁₁ = (-1)¹⁺¹M₁₁ = \(\left|\begin{array}{ll}
1 & 5 \\
4 & 7
\end{array}\right|\) = 7 – 20 = -13
A₁₂ = (-1)¹⁺²M₁₂ = \(\left|\begin{array}{ll}
1 & 5 \\
2 & 7
\end{array}\right|\) = -(7 – 10) = 3

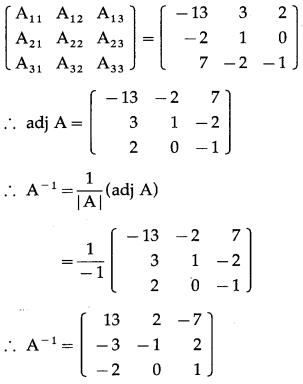
Question 15.
Find the inverse of \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) by adjoint method.
Solution:
where A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\)
|A| = 1(2 – 6) – 0(0 – 3) + 1(0 – 2)
|A| = -4 – 2
|A| = -6 ≠ 0
∴ A^-1 exists.
First we have to find the cofactor matrix
= [A_ij]3×3, where A_ij = (-1)^i+jM_ij

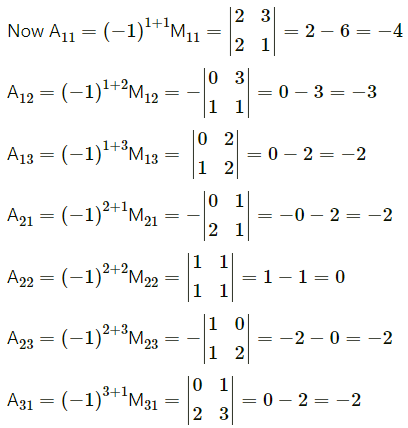
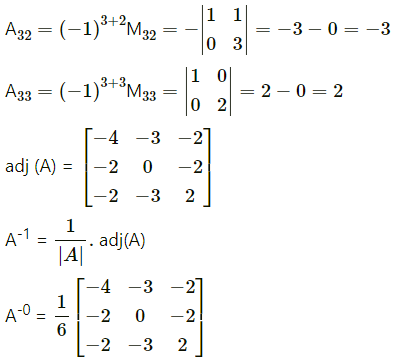
Question 16.
Find A^-1 by adjoint method and by elementary transformations if A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right]\)
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
-1 & 1 & 2 \\
1 & 2 & 4
\end{array}\right|\)
= 1(4 – 4) – 2(-4 – 2) + 3(-2 – 1)
= 0 + 12 – 9 = 3 ≠ 0
∴ A^-1 exists.
A^-1by adjoint method :
We have to find the cofactor matrix
= [A_ij]_3×3, where A_ij = (-1)^i+j M_ij

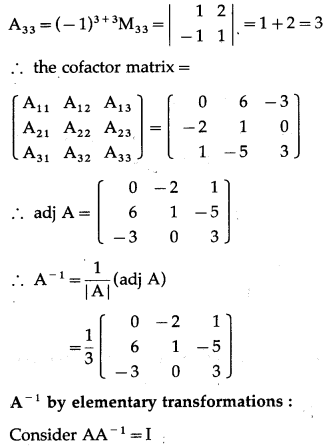
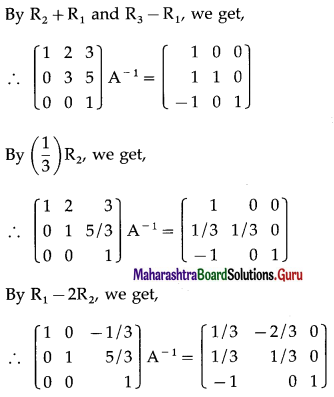
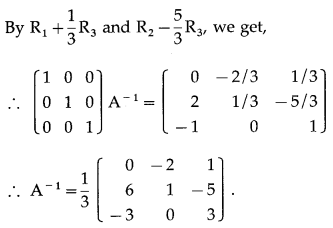
Question 17.
Find the inverse of A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) by elementary column transformations.
Solution:
|A| = \(\left|\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right|\)
= 1 (2 – 6) – 0 + 1 (0 – 2)
= -4 – 2= -6 ≠ 0
∴ A^-1 exists.
Consider A^-1A = I
∴ A^-1\(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
By C₃ – C₁, we get,

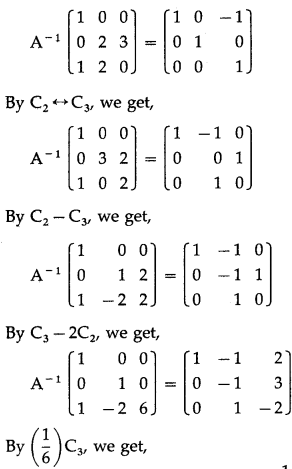
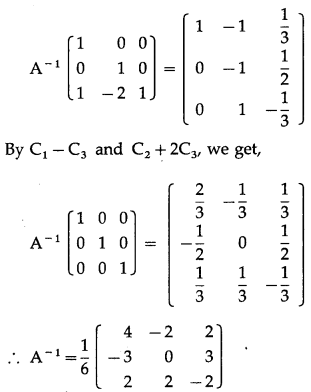
Question 18.
Find the inverse of \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\) by elementary row transformations.
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right|\)
= 1(7 – 20) – 2(7 – 10) + 3(4 – 2)
= -13 + 6 + 6 = -1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

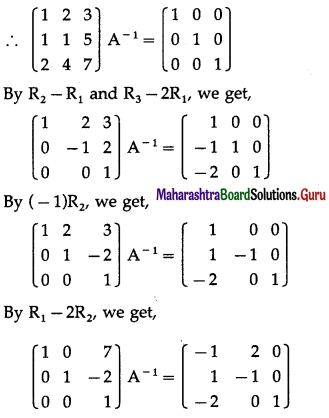
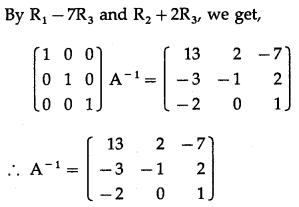
Question 19.
Show with usual notations that for any matrix A = [a_ij]_3×3
(i) a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃ = 0
Solution:
A = [a_ij]_3×3 = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\)
(i) A₂₁ = (-1)²⁺¹M₂₁ = \(-\left|\begin{array}{ll}
a_{12} & a_{13} \\
a_{32} & a_{33}
\end{array}\right|\)
= -(a₁₂a₃₃ – a₁₃a₃₂)
= -a₁₂a₃₃ + a₁₃a₃₂
A₂₂ = (-1)²⁺²M₂₂ = \(\left|\begin{array}{ll}
a_{11} & a_{13} \\
a_{31} & a_{33}
\end{array}\right|\)
= a₁₁a₃₃ – a₁₃a₃₁
A₂₃ = (-1)²⁺³M₂₃ = \(-\left|\begin{array}{ll}
a_{11} & a_{12} \\
a_{31} & a_{32}
\end{array}\right|\)
= -(a₁₁a₃₂ – a₁₂a₃₁)
= -a₁₁a₃₂+ a₁₂a₃₁
∴ a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃
= a₁₁(-a₁₂₃₃ + a₁₃a₃₂) + a₁₂(a₁₁a₃₃ – a₁₃a₃₁) + a₁₃(-a₁₁a₃₂ + a₁₂a₃₁)
= -a₁₁a₁₂a₃₃ + a₁₁a₁₃a₃₂ + a₁₁a₁₂a₃₃ – a₁₂a₁₃a₃₁ – a₁₁a₁₃a₃₂ + a₁₂a₁₃a₃₁
= 0

(ii) a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ = |A|
Solution:

Question 20.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 2 & 3 \\
1 & 2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
1 & 1 & 5 \\
2 & 4 & 7
\end{array}\right]\), then find a matrix X such that XA= B.
Solution:
Consider XA = B

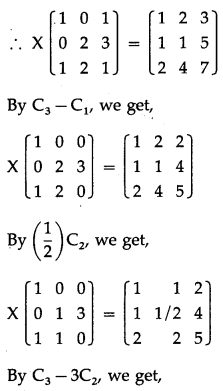
Class 12 Maharashtra State Board Maths Solution 

• Exercise 2.1 Class 12 Maths 1
• Exercise 2.2 Class 12 Maths 1
• Exercise 2.3 Class 12 Maths 1
• Miscellaneous Exercise 2A Class 12 Maths 1
• Miscellaneous Exercise 2B Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Ex 2.3 Questions and Answers.

12th Maths Part 1 Matrices Exercise 2.3 Questions And Answers Maharashtra Board

Question 1.
Solve the following equations by the inversion method.
(i) x + 2y = 2, 2x + 3y = 3
Solution:
The given equations can be written in the matrix form as :
\(\left[\begin{array}{ll}
1 & 2 \\
2 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\)
This is of the form AX = B, where

∴ A^-1 = \(\left[\begin{array}{rr}
-3 & 2 \\
2 & -1
\end{array}\right]\)
Now, premultiply AX = B by A^-1, we get,
A^-1(AX) = A^-1B
∴ (A^-1A)X = A^-1B
∴ IX = A^-1B
∴ X = \(=\left[\begin{array}{rr}
-3 & 2 \\
2 & -1
\end{array}\right]\left[\begin{array}{l}
2 \\
3
\end{array}\right]\)
∴ \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(=\left[\begin{array}{r}
-6+6 \\
4-3
\end{array}\right]\) = \(=\left[\begin{array}{l}
0 \\
1
\end{array}\right]\)
By equality of matrices,
x = 0, y = 1 is the required solution.

(ii) x + y = 4, 2x – y = 5
Solution:
x + y = 4, 2x – y = 5
The given equations can be written in the matrix form as:
\(\left[\begin{array}{cc}
1 & 1 \\
2 & -1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
4 \\
5
\end{array}\right]\)
This is of the form AX = B ⇒ X ⇒ A^-1B
A = \(\left[\begin{array}{cc}
1 & 1 \\
2 & -1
\end{array}\right]\)
|A| = -1 – 2 = -3 ≠ 0

By equality of matrices.
x = 3, y = 1

(iii) 2x + 6y = 8, x + 3y = 5
Solution:
The given equations can be written in the matrix form as :
\(\left[\begin{array}{ll}
2 & 6 \\
1 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
8 \\
5
\end{array}\right]\)
This is of the form AX = B, where
A = \(\left[\begin{array}{ll}
2 & 6 \\
1 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
8 \\
5
\end{array}\right]\)
Let us find A^-1.
|A| = \(\left|\begin{array}{ll}
2 & 6 \\
1 & 3
\end{array}\right|\) = 6 – 6 = 0
∴ A^-1 does not exist.
Hence, x and y do not exist.

Question 2.
Solve the following equations by reduction method.
(i) 2x + y = 5, 3x + 5y = -3
Solution:
The given equations can be written in the matrix form as :

By equality of matrices,
2x + y = 5 …(1)
7y = -21 …(2)
From (2), y = -3
Substituting y = -3 in (1), we get,
2x – 3 = 5
∴ 2x = 8 ∴ x = 4
Hence, x = 4, y = -3 is the required solution.

(ii) x + 3y = 2, 3x + 5y = 4.
Solution:
The given equations can be written in the matrix form as :
\(\left[\begin{array}{ll}
1 & 3 \\
3 & 5
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
4
\end{array}\right]\)
By R₂ – 3R₁, we get
\(\left[\begin{array}{rr}
1 & 3 \\
0 & -4
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left(\begin{array}{r}
2 \\
-2
\end{array}\right)\)
∴ \(\left[\begin{array}{l}
x+3 \\
0-4 y
\end{array}\right]\) = \(\left[\begin{array}{r}
2 \\
-2
\end{array}\right]\)
By equality of matrices,
x + 3y = 2 …(1)
-4y = -2
From (2), y = \(\frac{1}{2}\)
Substituting y = \(\frac{1}{2}\) in (1), we get,
x + \(\frac{3}{2}\) = 2
∴ x = 2 – \(\frac{3}{2}=\frac{1}{2}\)
Hence, x = \(\frac{1}{2}\), y = \(\frac{1}{2}\) is the required solution.

(iii) 3x – y = 1, 4x + y = 6
Solution:
The given equations can be written in the matrix form as :

By equality of matrices,
12x – 4y = 4 … (1)
7y = 14 … (2)
From (2), y = 2
Substituting y = 2 in (1), we get,
12x – 8 = 4
∴ 12x = 12 ∴ x = 1
Hence, x = 1, y = 2 is the required solution.

(iv) 5x + 2y = 4, 7x + 3y = 5
Solution:
5x + 2y = 4 ………..(1)
7x + 3y = 5 …………(2)
Multiplying Eq. (1) with 7 and Eq. (2) with 5

Put y = -3 into Eq. (1)
5x + 2y = 4
5x + 2(-3) = 4
5x – 6 = 4
5x = 4 + 6
5x = 10
x = \(\frac{10}{5}\)
x = 2
Hence, x = 2, y = -3 is the required solution.

Question 3.
The cost of 4 pencils, 3 pens and 2 erasers is ₹ 60. The cost of 2 pencils, 4 pens and 6 erasers is ₹ 90, whereas the cost of 6 pencils, 2 pens and 3 erasers is ₹ 70. Find the cost of each item by using matrices.
Solution:
Let the cost of 1 pencil, 1 pen and 1 eraser be ₹ x, ₹ y and ₹ z respectively.
Then, from the given conditions,
4x + 3y + 2z = 60
2x + 4y + 6z = 90, i.e., x + 2y + 3z = 45
6x + 2y + 3z = 70
These equations can be written in the matrix form as :

By equality of matrices,
x + 2y + 3z = 45 …….(1)
– 5y – 10z = – 120 …….(2)
5z = 40
From (3), z = 8
Substituting z = 8 in (2), we get,
– 5y – 80 = -120
∴ – 5y = -40 ∴ y = 8
Substituting y = 8, z = 8 in (1), we get,
x + 16 + 24 = 45
∴ x + 40 = 45 ∴ x = 5
∴ x = 5, y = 8, z = 8
Hence, the cost is ₹ 5 for a pencil, ₹ 8 for a pen and ₹ 8 for an eraser.

Question 4.
If three numbers are added, their sum is 2. If 2 times the second number is subtracted from the sum of first and third numbers, we get 8 and if three times the first number is added to the sum of second and third numbers, we get 4. Find the numbers using matrices.
Solution:
Let the three numbers be x, y and z. According to the given conditions,
x + y + z = 2
x + z – 2y = 8, i.e., x – 2y + 2 = 8
and y + z + 3x = 4, i.e., 3x + y + z = 4
Hence, the system of linear equations is
x + y + z = 2
x – 2y + z = 8
3x + y + z = 4
These equations can be written in the matrix form as :

By equality of matrices,
x + y + z = 2 ……(1)
-3y = 6 ……(2)
– 2y – 2z = -2 ……..(3)
From (2), y = -2
Substituting y = -2 in (3), we get,
-2(-2) – 2z = -2
∴ -2z = -6 ∴ z = 3
Substituting y = -2, z = 3 in (1), we get,
x – 2 + 3 = 2 ∴ x = 1
Hence, the required numbers are 1, -2 and 3.

Question 5.
The total cost of 3 T.V. sets and 2 V.C.R.s is ₹ 35000. The shop-keeper wants profit of ₹ 1000 per television and ₹ 500 per V.C.R. He can sell 2 T. V. sets and 1 V.C.R. and get the total revenue as ₹ 21,500. Find the cost price and the selling price of a T.V. sets and a V.C.R.
Solution:
Let the cost of each T.V. set be ₹ x and each V.C.R. be ₹ y. Then the total cost of 3 T.V. sets and 2 V.C.R.’s is ₹ (3x + 2y) which is given to be ₹ 35,000.
∴ 3x + 2y = 35000
The shopkeeper wants profit of ₹ 1000 per T.V. set and of ₹ 500 per V.C.R.
∴ the selling price of each T.V. set is ₹ (x + 1000) and of each V.C.R. is ₹ (y + 500).
∴ selling price of 2 T.V. set and 1 V.C.R. is
₹ [2(x + 1000) + (y + 500)] which is given to be ₹ 21,500.
∴ 2(x + 1000) + (y + 500) = 21500
∴ 2x + 2000 + y + 500 = 21500
∴ 2x + y = 19000
Hence, the system of linear equations is
3x + 2y = 35000
2x + y = 19000
These equations can be written in the matrix form as :

By equality of matrices,
2x + y = 19000 ……….(1)
-x = -3000 ……….(2)
From (2), x = 3000
Substituting x = 3000 in (1), we get,
2(3000) + y = 19000
∴ y = 13000
∴ the cost price of one T.V. set is ₹ 3000 and of one V.C.R. is ₹ 13000 and the selling price of one T.V. set is ₹ 4000 and of one V.C.R. is ₹ 13500.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 2.1 Class 12 Maths 1
• Exercise 2.2 Class 12 Maths 1
• Exercise 2.3 Class 12 Maths 1
• Miscellaneous Exercise 2A Class 12 Maths 1
• Miscellaneous Exercise 2B Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Ex 2.2 Questions and Answers.

12th Maths Part 1 Matrices Exercise 2.2 Questions And Answers Maharashtra Board

Question 1.
Find the co-factors of the elements of the following matrices
(i) \(\left[\begin{array}{cc}
-1 & 2 \\
-3 & 4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
-1 & 2 \\
-3 & 4
\end{array}\right]\)
Here, a₁₁ = -11, M₁₁ = 4
∴ A₁₁ = (-1)¹⁺¹(4) = 4
a₁₂ = 2, M₁₂ = -3
∴ A₁₂ = (-1)¹⁺²(- 3) = 3
a₂₁ = – 3, M₂₁ = -2
∴ A₂₁ = (- 1)²⁺¹(2) = -2
a₂₂ = 4, M₂₂ = -1
∴ A₂₂ = (-1)²⁺²(-1) = -1.

(ii) \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
The co-factor of a_ij is given by A_ij = (-1)^i+jM_ij

Question 2.
Find the matrix of co-factors for the following matrices
(i) \(\left[\begin{array}{rr}
1 & 3 \\
4 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rr}
1 & 3 \\
4 & -1
\end{array}\right]\)
Here, a₁₁ = 1, M₁₁ = -1
∴ A₁₁ = (-1)¹⁺¹(-1) = -1
a₁₂ = 3, M₁₂ = 4
∴ A₁₂ = (-1)¹⁺²(4) = -4
a₂₁ = 4, M₂₁ = 3
∴ A₂₁ = (-1)²⁺¹(3) = -3
a₂₂ = -1, M₂₂ = 1
∴ A₂₂ = (-1)²⁺¹(1) = 1
∴ the co-factor matrix = \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\)
= \(\left(\begin{array}{rr}
-1 & -4 \\
-3 & 1
\end{array}\right)\)

(ii) \(\left[\begin{array}{rrr}
1 & 0 & 2 \\
-2 & 1 & 3 \\
0 & 3 & -5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rrr}
1 & 0 & 2 \\
-2 & 1 & 3 \\
0 & 3 & -5
\end{array}\right]\)



A₁₁ = -14, A₁₂ = -10, A₁₃ = -6,
A₂₁ = 6, A₂₂ = -5, A₂₃ = -3,
A₃₁ = -2, A₃₂ = -7, A₃₃ = 1.
∴ the co-factor matrix
= \(\left[\begin{array}{lll}
A_{11} & A_{12} & A_{13} \\
A_{21} & A_{22} & A_{23} \\
A_{31} & A_{32} & A_{33}
\end{array}\right]\) = \(\left[\begin{array}{rrr}
-14 & -10 & -6 \\
6 & -5 & -3 \\
-2 & -7 & 1
\end{array}\right]\)

Question 3.
Find the adjoint of the following matrices.
(i) \(\left[\begin{array}{cc}
2 & -3 \\
3 & 5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -3 \\
3 & 5
\end{array}\right]\)
Here, a₁₁ = 2, M₁₁= 5
∴ A₁₁ = (-1)¹⁺¹(5) = 5
a₁₂ = -3, M₁₂ = 3
∴ A₁₂ = (-1)¹⁺²(3) = -3
a₂₁ = 3, M₂₁ = -3
∴ A A₂₁ = (-1)²⁺¹(-3) = 3
a₂₂ = 5, M₂₂ = 2
∴ A₂₂ = (-1)²⁺¹ = 2
∴ the co-factor matrix = \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\)
= \(\left[\begin{array}{rr}
5 & -3 \\
3 & 2
\end{array}\right]\)
∴ adj A = \(\left(\begin{array}{rr}
5 & 3 \\
-3 & 2
\end{array}\right)\)

(ii) \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
Solution:


A₁₁ = -3, A₁₂ = -12, A₁₃ = 6,
A₂₁ = -1, A₂₂ = 3, A₂₃ = 2,
A₃₁ = -11, A₃₂ = -9, A₃₃ = 1
∴ the co-factor matrix = \(\left[\begin{array}{lll}
\mathrm{A}_{11} & \mathrm{~A}_{12} & \mathrm{~A}_{15} \\
\mathrm{~A}_{21} & \mathrm{~A}_{22} & \mathrm{~A}_{23} \\
\mathrm{~A}_{31} & \mathrm{~A}_{32} & \mathrm{~A}_{33}
\end{array}\right]\)
= \(\left[\begin{array}{rrr}
-3 & -12 & 6 \\
-1 & 3 & 2 \\
-11 & -9 & 1
\end{array}\right]\)
∴ adj A = \(\left[\begin{array}{rrr}
-3 & -1 & -11 \\
-12 & 3 & -9 \\
6 & 2 & 1
\end{array}\right]\)

Question 4.
If A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\), verify that A (adj A) = (adj A) A = | A | ∙ I
Solution:
A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\)




From (1), (2) and (3), we get,
A(adj A) = (adj A)A = |A|∙I.
Note: This relation is valid for any non-singular matrix A.

Question 5.
Find the inverse of the following matrices by the adjoint method
(i) \(\left[\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right|\) = -2 + 15 = 13 ≠ 0
∴ A^-1 exists.
First we have to find the co-factor matrix
= [A_ij]_2×2, where A_ij = (-1)^i+jM_ij
Now, A₁₁ = (-1)¹⁺¹M₁₁ = 2
A₁₂ = (-1)¹⁺²M₁₂ = -(-3) = 3
A₂₁ = (-1)²⁺¹M₂₁ = -5
A₂₂ = (-1)²⁺²M₂₂ = -1
Hence, the co-factor matrix

(ii) \(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)
|A| = \(\) = 6 + 8 = 14 ≠ 0
∴ A^-1 exist
First we have to find the co-factor matrix
= [A_ij] _2×2 where A_ij = (-1)^i+jM_ij
Now, A₁₁ = (-1)¹⁺¹M₁₁ = 3
A₁₂ = (-1)¹⁺²M = -4
A₂₁ = (-2)²⁺¹M₂₁ = (-2) = 2
A₂₂ = (-1)²⁺²M₂₂ = 2
Hence the co-factor matrix
= \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\) = \(\left[\begin{array}{cc}
3 & -4 \\
2 & 2
\end{array}\right]\)
∴ adj A = \(\left[\begin{array}{cc}
3 & 2 \\
-4 & 2
\end{array}\right]\)
∴ A^-1 = \(\frac{1}{|\mathrm{~A}|}\) (adj A) = \(\frac{1}{14}\left(\begin{array}{cc}
3 & 2 \\
-4 & 2
\end{array}\right)\)

(iii) \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)



∴ A^-1 = \(\frac{1}{3}\left[\begin{array}{rrr}
3 & 0 & 0 \\
-3 & 1 & 0 \\
9 & 2 & -3
\end{array}\right]\)

(iv) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
∴ |A| = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
= 1(10 – 0) – 0 + 0
= 1(10) – 0 + 0
= 10 ≠ 0
∴ A^-1 exists.
First we have to find the co-factor matrix


∴ A^-1 = \(\frac{1}{|\mathrm{~A}|}\) (adj A)
= \(\frac{1}{10}\left(\begin{array}{rrr}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right)\)
∴ A^-1 = \(\frac{1}{10}\left(\begin{array}{rrr}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right)\)

Question 6.
Find the inverse of the following matrices
(i) \(\left[\begin{array}{cc}
1 & 2 \\
2 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
1 & 2 \\
2 & -1
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right]\)

∴ A^-1 = \(\left(\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right)\)

(iii) \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\)

(iv) \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)

Class 12 Maharashtra State Board Maths Solution 

• Exercise 2.1 Class 12 Maths 1
• Exercise 2.2 Class 12 Maths 1
• Exercise 2.3 Class 12 Maths 1
• Miscellaneous Exercise 2A Class 12 Maths 1
• Miscellaneous Exercise 2B Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Ex 2.1 Questions and Answers.

12th Maths Part 1 Matrices Exercise 2.1 Questions And Answers Maharashtra Board

Question 1.
Apply the given elementary transformation on each of the following matrices.
A = \(\left[\begin{array}{cc}
1 & 0 \\
-1 & 3
\end{array}\right]\), R₁ ↔ R₂
Solution:
A = \(\left[\begin{array}{cc}
1 & 0 \\
-1 & 3
\end{array}\right]\)
By R₁ ↔ R₂, we get,
A ~ \(\left[\begin{array}{rr}
-1 & 3 \\
1 & 0
\end{array}\right]\)

Question 2.
B = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 5 & 4
\end{array}\right]\), R₁ → R₁ → R₂
Solution:
B = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 5 & 4
\end{array}\right]\),
R₁ → R₁ → R₂ gives,
B ~ \(\left[\begin{array}{rrr}
-1 & -6 & -1 \\
2 & 5 & 4
\end{array}\right]\)

Question 3.
A = \(\left[\begin{array}{ll}
5 & 4 \\
1 & 3
\end{array}\right]\), C₁ ↔ C₂; B = \(\left[\begin{array}{ll}
3 & 1 \\
4 & 5
\end{array}\right]\), R₁ ↔ R₂. What do you observe?
Solution:
A = \(\left[\begin{array}{ll}
5 & 4 \\
1 & 3
\end{array}\right]\)
By C₁ ↔ C₂, we get,
A ~ \(\left[\begin{array}{ll}
4 & 5 \\
3 & 1
\end{array}\right]\) …(1)
B = \(\left[\begin{array}{ll}
3 & 1 \\
4 & 5
\end{array}\right]\)
By R₁ ↔ R₂, we get,
B ~ \(\left[\begin{array}{ll}
4 & 5 \\
3 & 1
\end{array}\right]\) …(2)
From (1) and (2), we observe that the new matrices are equal.

Question 4.
A = \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & 1 & 3
\end{array}\right]\), 2C₂
B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 4 & 5
\end{array}\right]\), -3R₁
Find the addition of the two new matrices.
Solution:
A = \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & 1 & 3
\end{array}\right]\)
By 2C₂, we get,
A ~ \(\left[\begin{array}{rrr}
1 & 4 & -1 \\
0 & 2 & 3
\end{array}\right]\)
B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 4 & 5
\end{array}\right]\)
By -3R₁, we get,
B ~ \(\left[\begin{array}{rrr}
-3 & 0 & -6 \\
2 & 4 & 5
\end{array}\right]\)
Now, addition of the two new matrices

Question 5.
A = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\), 3R₃ and then C₃ + 2C₂.
Solution:
A = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right]\)
By 3R₃, we get
A ~ \(\left[\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
9 & 9 & 3
\end{array}\right]\)
By C₃ + 2C₂, we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 3+2(-1) \\
2 & 1 & 0+2(1) \\
9 & 9 & 3+2(9)
\end{array}\right)\)
∴ A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
9 & 9 & 21
\end{array}\right)\)

Question 6.
A = \(\left(\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right)\), C₃ + 2C₂ and then 3R₃. What do you conclude from Ex. 5 and Ex. 6 ?
Solution:
A = \(\left(\begin{array}{rrr}
1 & -1 & 3 \\
2 & 1 & 0 \\
3 & 3 & 1
\end{array}\right)\)
By C₃ + 2C₂, we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 3+2(-1) \\
2 & 1 & 0+2(1) \\
3 & 3 & 1+2(3)
\end{array}\right)\)
∴ A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
3 & 3 & 7
\end{array}\right)\)
By 3R₃, we get
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 1 \\
2 & 1 & 2 \\
9 & 9 & 21
\end{array}\right)\)
We conclude from Ex. 5 and Ex. 6 that the matrix remains same by interchanging the order of the elementary transformations. Hence, the transformations are commutative.

Question 7.
Use suitable transformation on \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\) into an upper triangular matrix.
Solution:
Let A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
By R₂ – 3R₁, we get,
A ~ \(\left[\begin{array}{rr}
1 & 2 \\
0 & -2
\end{array}\right]\)
This is an upper triangular matrix.

Question 8.
Convert \(\left[\begin{array}{rr}
1 & -1 \\
2 & 3
\end{array}\right]\) into an identity matrix by suitable row transformations.
Solution:
Let A = \(\left[\begin{array}{rr}
1 & -1 \\
2 & 3
\end{array}\right]\)
By R₂ – 2R₁, we get,
A ~ \(\left[\begin{array}{rr}
1 & -1 \\
0 & 5
\end{array}\right]\)
By \(\left(\frac{1}{5}\right)\)R₂, we get,
A ~ \(\left[\begin{array}{rr}
1 & -1 \\
0 & 1
\end{array}\right]\)
By R₁ + R₂, we get,
A ~ \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
This is an identity matrix.

Question 9.
Transform \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 1 & 3 \\
3 & 2 & 4
\end{array}\right]\) into an upper triangular matrix by suitable row transformations.
Solution:
Let A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 1 & 3 \\
3 & 2 & 4
\end{array}\right]\)
By R₂ – 2R₁ and R₃ – 3R₁, we get
A ~ \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
0 & 3 & -1 \\
0 & 5 & -2
\end{array}\right]\)
By R₃ – \(\left(\frac{5}{3}\right)\)R₂, we get,
A ~ \(\left(\begin{array}{rrr}
1 & -1 & 2 \\
0 & 3 & -1 \\
0 & 0 & -\frac{1}{3}
\end{array}\right)\)
This is an upper triangular matrix.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 2.1 Class 12 Maths 1
• Exercise 2.2 Class 12 Maths 1
• Exercise 2.3 Class 12 Maths 1
• Miscellaneous Exercise 2A Class 12 Maths 1
• Miscellaneous Exercise 2B Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Miscellaneous Exercise 1 Questions and Answers.

12th Maths Part 1 Mathematical Logic Miscellaneous Exercise 1 Questions And Answers Maharashtra Board

Question 1.
Select and write the correct answer from the given alternatives in each of the following questions:
i) If p ∧ q is false and p ∨ q is true, the ________ is not true.
(A) p ∨ q
(B) p ↔ q
(C) ~p ∨ ~q
(D) q ∨ ~p
Solution:
(b) p ↔ q.

(ii) (p ∧ q) → r is logically equivalent to ________.
(A) p → (q → r)
(B) (p ∧ q) → ~r
(C) (~p ∨ ~q) → ~r
(D) (p ∨ q) → r
Solution:
(a) p → (q → r) [Hint: Use truth table.]

(iii) Inverse of statement pattern (p ∨ q) → (p ∧ q) is ________.
(A) (p ∧ q) → (p ∨ q)
(B) ~(p ∨ q) → (p ∧ q)
(C) (~p ∧ ~q) → (~p ∨ ~q)
(D) (~p ∨ ~q) → (~p ∧ ~q)
Solution:
(c) (~p ∧ ~q) → (~p ∨ ~ q)

(iv) If p ∧ q is F, p → q is F then the truth values of p and q are ________.
(A) T, T
(B) T, F
(C) F, T
(D) F, F
Solution:
(b) T, F

(v) The negation of inverse of ~p → q is ________.
(A) q ∧ p
(B) ~p ∧ ~q
(C) p ∧ q
(D) ~q → ~p
Solution:
(a) q ∧ p

(vi) The negation of p ∧ (q → r) is ________.
(A) ~p ∧ (~q → ~r)
(B) p ∨ (~q ∨ r)
(C) ~p ∧ (~q → ~r)
(D) ~p ∨ (~q ∧ ~r)
Solution:
(d) ~p ∨ (q ∧ ~r)

(vii) If A = {1, 2, 3, 4, 5} then which of the following is not true?
(A) Ǝ x ∈ A such that x + 3 = 8
(B) Ǝ x ∈ A such that x + 2 < 9
(C) Ɐ x ∈ A, x + 6 ≥ 9
(D) Ǝ x ∈ A such that x + 6 < 10
Solution:
(c) Ǝ x ∈ A, x + 6 ≥ 9.

Question 2.
Which of the following sentences are statements in logic? Justify. Write down the truth
value of the statements :
(i) 4! = 24.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(ii) π is an irrational number.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(iii) India is a country and Himalayas is a river.
Solution:
It is a statement which is false, hence its truth value is ‘F’. ….[T ∧ F ≡ F]

(iv) Please get me a glass of water.
Solution:
It is an imperative sentence, hence it is not a statement.

(v) cos²θ – sin²θ = cos2θ for all θ ∈ R.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(vi) If x is a whole number the x + 6 = 0.
Solution:
It is a statement which is false, hence its truth value is ‘F’.

Question 3.
Write the truth values of the following statements :
(i) \(\sqrt {5}\) is an irrational but \(3\sqrt {5}\) is a complex number.
Solution:
Let p : \(\sqrt {5}\) is an irrational.
q : \(3\sqrt {5}\) is a complex number.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]

(ii) Ɐ n ∈ N, n² + n is even number while n² – n is an odd number.
Solution:
Let p : Ɐ n ∈ N, n² + n is an even number.
q : Ɐ n ∈ N, n² – n is an odd number.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F].

(iii) Ǝ n ∈ N such that n + 5 > 10.
Solution:
Ǝ n ∈ N, such that n + 5 > 10 is a true statement, hence its truth value is T.
(All n ≥ 6, where n ∈ N, satisfy n + 5 > 10).

(iv) The square of any even number is odd or the cube of any odd number is odd.
Solution:
Let p : The square of any even number is odd.
q : The cube of any odd number is odd.
Then the symbolic form of the given statement is p ∨ q.
The truth values of p and q are F and T respectively.
∴ the truth value of p ∨ q is T. … [F ∨ T ≡ T].

(v) In ∆ ABC if all sides are equal then its all angles are equal.
Solution:
Let p : ABC is a triangle and all its sides are equal.
q : Its all angles are equal.
Then the symbolic form of the given statement is p → q
If the truth value of p is T, then the truth value of q is T.
∴ the truth value of p → q is T. … [T → T ≡ T].

(vi) Ɐ n ∈ N, n + 6 > 8.
Solution:
Ɐ n ∈ N, 11 + 6 > 8 is a false statement, hence its truth value is F.
{n = 1 ∈ N, n = 2 ∈ N do not satisfy n + 6 > 8).

Question 4.
If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}, determine the truth value of each of the following statement :
(i) Ǝ x ∈ A such that x + 8 = 15.
Solution:
True

(ii) Ɐ x ∈ A, x + 5 < 12.
Solution:
False

(iii) Ǝ x ∈ A, such that x + 7 ≥ 11.
Solution:
True

(iv) Ɐ x ∈ A, 3x ≤ 25.
Solution:
False

Question 5.
Write the negations of the following :
(i) Ɐ n ∈ A, n + 7 > 6.
Solution:
The negation of the given statements are :
Ǝ n ∈ A, such that n + 7 ≤ 6.
OR Ǝ n ∈ A, such that n + 7 ≯ 6.

(ii) Ǝ x ∈ A, such that x + 9 ≤ 15.
Solution:
Ɐ x ∈ A, x + 9 > 15.

(iii) Some triangles are equilateral triangle.
Solution:
All triangles are not equilateral triangles.

Question 6.
Construct the truth table for each of the following :
(i) p → (q → p)
Solution:

(ii) (~p ∨ ~q) ↔ [~(p ∧ q)]
Solution:

(iii) ~(~p ∧ ~q) ∨ q
Solution:

(iv) [(p ∧ q) ∨ r] ∧ [~r ∨ (p ∧ q)]
Solution:

(v) [(~p ∨ q) ∧ (q → r)] → (p → r)
Solution:

Question 7.
Determine whether the following statement patterns are tautologies contradictions or contingencies :
(i) [(p → q) ∧ ~q)] → ~p
Solution:

All the entries in the last column of the above truth table are T.
∴ [(p → q) ∧ ~q)] → ~p is a tautology.

(ii) [(p ∨ q) ∧ ~p] ∧ ~q
Solution:

All the entries in the last column of the above truth table are F.
∴ [(p ∨ q) ∧ ~p] ∧ ~q is a contradiction.

(iii) (p → q) ∧ (p ∧ ~q)
Solution:

All the entries in the last column of the above truth table are F.
∴ (p → q) ∧ (p ∧ ~q) is a contradiction.

(iv) [p → (q → r)] ↔ [(p ∧ q) → r]
Solution:

All the entries in the last column of the above truth table are T.
∴ [p → (q → r)] ↔ [(p ∧ q) → r] is a tautology.

(v) [(p ∧ (p → q)] → q
Solution:

All the entries in the last column of the above truth table are T.
∴ [(p ∧ (p → q)] → q is a tautology.

(vi) (p ∧ q) ∨ (~p ∧ q) ∨ (p ∨ ~q) ∨ (~p ∧ ~q)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p ∧ q) ∨ (~p ∧ q) ∨ (p ∨ ~q) ∨ (~p ∧ ~q) is a tautology.

(vii) [(p ∨ ~q) ∨ (~p ∧ q)] ∧ r
Solution:

The entries in the last column are neither T nor all F.
∴ [(p ∨ ~q) ∨ (~p ∧ q)] ∧ r is a contingency.

(viii) (p → q) ∨ (q → p)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p → q) ∨ (q → p) is a tautology.

Question 8.
Determine the truth values ofp and q in the following cases :
(i) (p ∨ q) is T and (p ∧ q) is T
Solution:

Since p ∨ q and p ∧ q both are T, from the table the truth values of both p and q are T.

(ii) (p ∨ q) is T and (p ∨ q) → q is F
Solution:

Since the truth values of (p ∨ q) is T and (p ∨ q) → q is F, from the table, the truth values of p and q are T and F respectively.

(iii) (p ∧ q) is F and (p ∧ q) → q is T
Solution:

Since the truth values of (p ∧ q) is F and (p ∧ q) → q is T, from the table, the truth values of p and q are either T and F respectively or F and T respectively or both F.

Question 9.
Using truth tables prove the following logical equivalences :
(i) p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Solution:

The entries in the columns 3 and 8 are identical.
∴ p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q).

(ii) (p ∧ q) → r ≡ p → (q → r)
Solution:

The entries in the columns 5 and 7 are identical.
∴ (p ∧ q) → r ≡ p → (q → r).

Question 10.
Using rules in logic, prove the following :
(i) p ↔ q ≡ ~ (p ∧ ~q) ∧ ~(q ∧ ~p)
Solution:
By the rules of negation of biconditional,
~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p)
∴ ~ [(p ∧ ~ q) ∨ (q ∧ ~p)] ≡ p ↔ q
∴ ~(p ∧ ~q) ∧ ~(q ∧ ~p) ≡ p ↔ q … (Negation of disjunction)
≡ p ↔ q ≡ ~(p ∧ ~ q) ∧ ~ (q ∧ ~p).

(ii) ~p ∧ q ≡ (p ∨ q) ∧ ~p
Solution:
(p ∨ q) ∧ ~ p
≡ (p ∧ ~p) ∨ (q ∧ ~p) … (Distributive Law)
≡ F ∨ (q ∧ ~p) … (Complement Law)
≡ q ∧ ~ p … (Identity Law)
≡ ~p ∧ q …(Commutative Law)
∴ ~p ∧ q ≡ (p ∨ q) ∧ ~p.

(iii) ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p
Solution:
~ (p ∨ q) ∨ (~p ∧ q)
≡ (~p ∧ ~q) ∨ (~p ∧ q) … (Negation of disjunction)
≡ ~p ∧ (~q ∨ q) … (Distributive Law)
≡ ~ p ∧ T … (Complement Law)
≡ ~ p … (Identity Law)
∴ ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p.

Question 11.
Using the rules in logic, write the negations of the following :
(i) (p ∨ q) ∧ (q ∨ ~r)
Solution:
The negation of (p ∨ q) ∧ (q ∨ ~ r) is
~ [(p ∨ q) ∧ (q ∨ ~r)]
≡ ~ (p ∨ q) ∨ ~ (q ∨ ~r) … (Negation of conjunction)
≡ (~p ∧ ~q) ∨ [~q ∧ ~(~r)] … (Negation of disjunction)
≡ {~ p ∧ ~q) ∨ (~q ∧ r) … (Negation of negation)
≡ (~q ∧ ~p) ∨ (~q ∧ r) … (Commutative law)
≡ (~ q) ∧ (~ p ∨ r) … (Distributive Law)

(ii) p ∧ (q ∨ r)
Solution:
The negation of p ∧ (q ∨ r) is
~ [p ∧ (q ∨ r)]
≡ ~ p ∨ ~(q ∨ r) … (Negation of conjunction)
≡ ~p ∨ (~q ∧ ~r) … (Negation of disjunction)

(iii) (p → q) ∧ r
Solution:
The negation of (p → q) ∧ r is
~ [(p → q) ∧ r]
≡ ~ (p → q) ∨ (~ r) … (Negation of conjunction)
≡ (p ∧ ~q) ∨ (~ r) … (Negation of implication)

(iv) (~p ∧ q) ∨ (p ∧ ~q)
Solution:
The negation of (~ p ∧ q) ∨ (p ∧ ~ q) is
~ [(~p ∧ q) ∨ (p ∧ ~q)]
≡ ~(~p ∧ q) ∧ ~ (p ∧ ~q) … (Negation of disjunction)
≡ [~(~p) ∨ ~q] ∧ [~p ∨ ~(q)] … (Negation of conjunction)
≡ (p ∨ ~ q) ∧ (~ p ∨ q) … (Negation of negation)

Question 12.
Express the following circuits in the symbolic form. Prepare the switching table :
(i)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q: the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given circuit is :
(p ∧ q) ∨ (~p) ∨ (p ∧ ~q).

(ii)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed.
Then the symbolic form of the given statement is : (p ∨ q) ∧ (p ∨ r).

Question 13.
Simplify the following so that the new circuit has minimum number of switches. Also, draw the simplified circuit.

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p: the switch S₁‘ is closed or the switch S₁ is open
~ q: the switch S₂‘ is closed or the switch S₂ is open.
Then the given circuit in symbolic form is :
(p ∧ ~q) ∨ (~p ∧ q) ∨ (~p ∧ ~q)
Using the laws of logic, we have,
(p ∧ ~q) ∨ (~p ∧ q) ∨ (~p ∧ ~ q)
= (p ∧ ~q) ∨ [(~p ∧ q) ∨ (~p ∧ ~q) …(By Complement Law)
= (p ∧ ~q) ∨ [~p ∧ (q ∨ ~q)} (By Distributive Law)
= (p ∧ ~q) ∨ (~p ∧ T) …(By Complement Law)
= (p ∧ ~q) ∨ ~ p …(By Identity Law)
= (p ∨ ~p) ∧ (~q ∨ ~p) …(By Distributive Law)
= ~q ∨ ~p …(By Identity Law)
= ~p ∨ ~p …(By Commutative Law)
Hence, the simplified circuit for the given circuit is :

(ii)

Solution:
(ii) Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
s : the switch S₄ is closed
t : the switch S₅ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open
~ r : the switch S₃‘ is closed or the switch S₃ is open
~ s : the switch S₄‘ is closed or the switch S₄ is open
~ t : the switch S₅‘ is closed or the switch S₅ is open.
Then the given circuit in symbolic form is
[(p ∧ q) ∨ ~r ∨ ~s ∨ ~t] ∧ [(p ∧ q) ∨ (r ∧ s ∧ t)]
Using the laws of logic, we have,
[(p ∧ q) ∨ ~r ∨ ~s ∨ ~ t] ∧ [(p A q) ∨ (r ∧ s ∧ t)]
= [(p∧ q) ∨ ~(r ∧ s ∧ t)] ∧ [(p ∧ q) ∨ (r ∧ s ∧ t)] … (By De Morgan’s Law)
= (p ∧ q) ∨ [ ~(r ∧ s ∧ t) ∧ (r ∧ s ∧ t)] … (By Distributive Law)
= (p ∧ q) ∨ F … (By Complement Law)
= p ∧ q … (By Identity Law)
Hence, the alternative simplified circuit is :

Question 14.
Check whether the following switching circuits are logically equivalent – Justify.
(A)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
(A) The symbolic form of the given switching circuits are
p ∧ (q ∨ r) and (p ∧ q) ∨ (p ∧ r) respectively.
By Distributive Law, p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Hence, the given switching circuits are logically equivalent.

(B)

Solution:
The symbolic form of the given switching circuits are
(p ∨ q) ∧ (p ∨ r) and p ∨ (q ∧ r)
By Distributive Law,
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
Hence, the given switching circuits are logically equivalent.

Question 15.
Give alternative arrangement of the switching following circuit, has minimum switches.

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~p : the switch S₁‘ is closed, or the switch S₁ is open
~q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form Of the given circuit is :
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r)
Using the laws of logic, we have,
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r)
≡ (p ∧ ~p ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) y (p ∧ ~q ∧ r) …(By Commutative Law)
≡ (F ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Complement Law)
≡ F ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ [(~p ∨ p) ∧ (q ∧ r)] ∨ (p ∧ ~q ∧ r) … (By Distributive Law)
≡ [T ∧ (q ∧ r)] ∨ (p ∧ ~q ∧ r) = (q ∧ r) ∨ (p ∧ ~q ∧ r) …(By Complement Law)
≡ (q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ [q ∨ (p ∧ ~q)] ∧ r … (By Distributive Law)
≡ [q ∨ p) ∧ ((q ∨ ~q)] ∧ r … (By Distributive Law)
≡ [(q ∨ p) ∧ T] ∧ r …(By Complement Law)
≡ (q ∨ p) ∧ r … (By Identity Law)
≡ (p ∨ q) ∧ r …(By Commutative Law)
∴ the alternative arrangement of the new circuit with minimum switches is :

Question 16.
Simplify the following so that the new circuit circuit.

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given switching circuit is :
(~p ∨ q) ∨ (p ∨ ~q) ∨ (p ∨ q)
Using the laws of logic, we have,
(~p ∨ q) ∨ (p ∨ ~q) ∨ (p ∨ q)
≡ (~p ∨ q ∨ p ∨ ~q) ∨ (p ∨ q)
≡ [(~p ∨ p) ∨ (q ∨ ~q)] ∨ (p ∨ q) … (By Commutative Law)
≡ (T ∨ T) ∨ (p ∨ q) … (By Complement Law)
≡ T ∨ (p ∨ q) … (By Identity Law)
≡ T … (By Identity Law)
∴ the current always flows whether the switches are open or closed. So, it is not necessary to use any switch in the circuit.
∴ the simplified form of given circuit is :

Question 17.
Represent the following switching circuit in symbolic form and construct its switching table. Write your conclusion from the switching table.

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~ q : the switch S₂‘ is closed or the switch S₂ is open
~ r : the switch S₃‘ is closed or the switch S₃ is open.
Then, the symbolic form of the given switching circuit is : [p ∨ (~ q) ∨ (~ r)] ∧ [p ∨ (q ∧ r)]

From the table, the’ final column’ and the column of p are identical. Hence, the given circuit is equivalent to the simple circuit with only one switch S₁.
the simplified form of the given circuit is :

Class 12 Maharashtra State Board Maths Solution 

• Exercise 1.1 Class 12 Maths 1
• Exercise 1.2 Class 12 Maths 1
• Exercise 1.3 Class 12 Maths 1
• Exercise 1.4 Class 12 Maths 1
• Exercise 1.5 Class 12 Maths 1
• Miscellaneous Exercise 1 Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.5 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.5 Questions And Answers Maharashtra Board

Question 1.
Express the following circuits in the symbolic form of logic and write the input-output table.
(i)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~p : the switch S₁‘ is closed or the switch S₁is open
~q : the switch S₂‘ is closed or the switch S₂ is open
~r : the switch S₃‘ is closed or the switch S₃ is open
l : the lamp L is on
(i) The symbolic form of the given circuit is : p ∨ (q ∧ r) = l
l is generally dropped and it can be expressed as : p ∨ (q ∧ r).

(ii)

Solution:
The symbolic form of the given circuit is : (~ p ∧ q) ∨ (p ∧ ~ q).

(iii)

Solution:
The symbolic form of the given circuit is : [p ∧ (~q ∨ r)] ∨ (~q ∧ ~ r).

(iv)

Solution:
The symbolic form of the given circuit is : (p ∨ q) ∧ q ∧ (r ∨ ~p).

(v)

Solution:
The symbolic form of the given circuit is : [p ∨ (~p ∧ ~q)] ∨ (p ∧ q).

(vi)

Solution:
The symbolic form of the given circuit is : (p ∨ q) ∧ (q ∨ r) ∧ (r ∨ p)

Question 2.
Construct the switching circuit of the following :
(i) (~p∧ q) ∨ (p∧ ~r)
Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open
~ r : the switch S₃‘ is closed or the switch S₃ is open.
Then the switching circuits corresponding to the given statement patterns are :

(ii) (p∧ q) ∨ [~p ∧ (~q ∨ p ∨ r)]
Solution:

(iii) [(p ∧ r) ∨ (~q ∧ ~r)] ∧ (~p ∧ ~r)
Solution:

(iv) (p ∧ ~q ∧ r) ∨ [p ∧ (~q ∨ ~r)]
Solution:

(v) p ∨ (~p ) ∨ (~q) ∨ (p ∧ q)
Solution:

(vi) (p ∧ q) ∨ (~p) ∨ (p ∧ ~q)
Solution:

Question 3.
Give an alternative equivalent simple circuits for the following circuits :
(i)

Solution:
(i) Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch Si is open Then the symbolic form of the given circuit is :
p ∧ (~p ∨ q).
Using the laws of logic, we have,
p ∧ (~p ∨ q)
= (p ∧ ~ p) ∨ (p ∧ q) …(By Distributive Law)
= F ∨ (p ∧ q) … (By Complement Law)
= p ∧ q… (By Identity Law)
Hence, the alternative equivalent simple circuit is :

(ii)

Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~q : the switch S₂‘ is closed or the switch S₂ is open
~r : the switch S₃‘ is closed or the switch S₃ is open.
Then the symbolic form of the given circuit is :
[p ∧ (q ∨ r)] ∨ (~r ∧ ~q ∧ p).
Using the laws of logic, we have
[p ∧ (q ∨ r)] ∨ (~r ∧ ~q ∧ p)
≡ [p ∧ (q ∨ r)] ∨ [ ~(r ∨ q) ∧ p] …. (By De Morgan’s Law)
≡ [p ∧ (q ∨ r)] ∨ [p ∧ ~(q ∨ r)] … (By Commutative Law)
≡ p ∧ [(q ∨ r) ∨ ~(q ∨ r)) … (By Distributive Law)
≡ p ∧ T … (By Complement Law)
≡ p … (By Identity Law)
Hence, the alternative equivalent simple circuit is :

Question 4.
Write the symbolic form of the following switching circuits construct its switching table and interpret it.
i)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given circuit is :
(p ∨ ~q) ∨ (~p ∧ q)

Since the final column contains all’ 1′, the lamp will always glow irrespective of the status of switches.

ii)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~p : the switch S₁ is closed or the switch S₁ is open.
~q : the switch S₂‘ is closed or the switch S₂ is open.
Then the symbolic form of the given circuit is : p ∨ (~p ∧ ~q) ∨ (p ∧ q)

Since the final column contains ‘0’ when p is 0 and q is ‘1’, otherwise it contains ‘1′.
Hence, the lamp will not glow when S₁ is OFF and S₂ is ON, otherwise the lamp will glow.

iii)

Solution:
Let p : the switch S₁ is closed
q : the switch S₂ is closed
r : the switch S₃ is closed
~q : the switch S₂‘ is closed or the switch S₂ is open
~r: the switch S₃‘ is closed or the switch S₃ is open.
Then the symbolic form of the given circuit is : [p ∨ (~q) ∨ r)] ∧ [p ∨ (q ∧ r)]

From the switching table, the ‘final column’ and the column of p are identical. Hence, the lamp will glow which S₁ is ‘ON’.

Question 5.
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
(i) p ∨ (q ∧ ~ q)
Solution:
Using the laws of logic, we have, p ∨ (q ∧ ~q)
≡ p ∨ F … (By Complement Law)
≡ p … (By Identity Law)
Hence, the simple logical expression of the given expression is p.
Let p : the switch S₁ is closed
Then the corresponding switching circuit is :

(ii) (~p ∧ q) ∨ (~p ∧ ~q) ∨ (p ∧ ~q)]
Solution:
Using the laws of logic, we have,
(~p ∧ q) ∨ (~p ∨ ~q) ∨ (p ∧ ~q)
≡ [~p ∧ (q ∨ ~q)] ∨ (p ∧ ~ q)… (By Distributive Law)
≡ (~p ∧ T) ∨ (p ∧ ~q) … (By Complement Law)
≡ ~p ∨ (p ∧ ~q) … (By Identity Law)
≡ (~p ∨ p) ∧ (~p ∧~q) … (By Distributive Law)
≡ T ∧ (~p ∧ ~q) … (By Complement Law)
≡ ~p ∨ ~q … (By Identity Law)
Hence, the simple logical expression of the given expression is ~ p ∨ ~q.
Let p : the switch S₁ is closed
q : the switch S₂ is closed
~ p : the switch S₁‘ is closed or the switch S₁ is open
~ q : the switch S₂‘ is closed or the switch S₂ is open,
Then the corresponding switching circuit is :

(iii) [p (∨ (~q) ∨ ~r)] ∧ (p ∨ (q ∧ r)
Solution:
Using the laws of logic, we have,
[p ∨ (~ (q) ∨ (~r)] ∧ [p ∨ (q ∧ r)]
= [p ∨ { ~(q ∧ r)}] ∧ [p ∨ (q ∧ r)] … (By De Morgan’s Law)
= p ∨ [~(q ∧ r) ∧ (q ∧ r) ] … (By Distributive Law)
= p ∨ F … (By Complement Law)
= p … (By Identity Law)
Hence, the simple logical expression of the given expression is p.
Let p : the switch S₁ is closed
Then the corresponding switching circuit is :

(iv) (p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) ∨ (p ∧ q ∧ r)
Question is Modified
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r)∨ (p ∧ q ∧ r)
Solution:
Using the laws of logic, we have,
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r)
= (p ∧ ~p ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Commutative Law)
= (F ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Complement Law)
= F ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Identity Law)
= (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) … (By Identity Law)
= (~ p ∨ p) ∧ (q ∧ r) … (By Distributive Law)
= T ∧ (q ∧ r) … (By Complement Law)
= q ∧ r … (By Identity Law)
Hence, the simple logical expression of the given expression is q ∧ r.
Let q : the switch S₂ is closed
r : the switch S₃ is closed.
Then the corresponding switching circuit is :

Class 12 Maharashtra State Board Maths Solution 

• Exercise 1.1 Class 12 Maths 1
• Exercise 1.2 Class 12 Maths 1
• Exercise 1.3 Class 12 Maths 1
• Exercise 1.4 Class 12 Maths 1
• Exercise 1.5 Class 12 Maths 1
• Miscellaneous Exercise 1 Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.4 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.4 Questions And Answers Maharashtra Board

Question 1.
Using rules of negation write the negations of the following with justification.
(i) ~q → p
Solution:
The negation of ~q → p is
~(~q → p) ≡ ~ q ∧ ~p…. (Negation of implication)

(ii) p ∧ ~q
Solution:
The negation of p ∧ ~q is
~(p ∧ ~q) ≡ ~p ∨ ~(~q) … (Negation of conjunction)
≡ ~ p ∨ q … (Negation of negation)

(iii) p ∨ ~q
Solution:
The negation of p ∨ ~ p is
~ (p ∨ ~(q) ≡ ~p ∧ ~(~(q) … (Negation of disjunction)
≡ ~ p ∧ q … (Negation of negation)

(iv) (p ∨ ~q) ∧ r
Solution:
The negation of (p ∨ ~ q) ∧ r is
~[(p ∨ ~q) ∧ r] ≡ ~(p ∨ ~q) ∨ ~r … (Negation of conjunction)
≡ [ ~p ∧ ~(~q)] ∨ ~ r… (Negation of disjunction)
≡ (~ p ∧ q) ∧ ~ r … (Negation of negation)

(v) p → (p ∨ ~q)
Solution:
The negation of p → (p ∨ ~q) is
~ [p → (p ∨ ~q)] ≡ p ∧ ~ (p ∧ ~p) … (Negation of implication)
≡ p ∧ [ ~ p ∧ ~ (~(q)] … (Negation of disjunction)
≡ p ∧ (~ p ∧ q) (Negation of negation)

(vi) ~(p ∧ q) ∨ (p ∨ ~q)
Solution:
The negation of ~(p ∧ q) ∨ (p ∨ ~q) is
~[~(p ∧ q) ∨ (p ∨ ~q)] ≡ ~[~(p ∧ q)] ∧ ~(p ∨ ~q) … (Negation of disjunction)
≡ ~[~(p ∧ q)] ∧ [ p ∧ ~(~q)] … (Negation of disjunction)
≡ (p ∧ q) ∧ (~ p ∧ q) … (Negation of negation)

(vii) (p ∨ ~q) → (p ∧ ~q)
Solution:
The negation of (p ∨ ~q) → (p ∧ ~q) is
~[(p ∨ ~q) → (p ∧ ~q)]
≡ (p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of implication)
≡ (p ∨ ~q) ∧ [ ~p ∨ ~(~q)] … (Negation of conjunction)
≡ (p ∨ ~q) ∧ (~p ∨ q) … (Negation of negation)

(viii) (~ p ∨ ~q) ∨ (p ∧ ~q)
Solution:
The negation of (~ p ∨ ~q) ∨ (p ∧ ~ q) is
~ [(~p ∨ ~q) ∨ (p ∧ ~ q)]
≡ ~(~p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of disjunction)
≡ [~(~p) ∧ ~(~q)] ∧ [~p ∨ ~(~q)] … (Negation of disjunction and conjunction)
≡ (p ∧ q) ∧ (~p ∨ q) … (Negation of negation)

Question 2.
Rewrite the following statements without using if .. then.
(i) If a man is a judge then he is honest.
Solution:
Since p → ≡ ~p ∨ q, the given statements can be written as :
A man is not a judge or he is honest.

(ii) It 2 is a rational number then \(\sqrt {2}\) is irrational number.
Solution:
2 is not a rational number or \(\sqrt {2}\) is irrational number.

(iii) It f(2) = 0 then f(x) is divisible by (x – 2).
Solution:
f(2) ≠ 0 or f(x) is divisible by (x – 2).

Question 3.
Without using truth table prove that :
(i) p ↔ q ≡ (p∧ q) ∨ (~ p ∧ ~q)
Solution:
LHS = p ↔ q
≡ (p ↔ q) ∧ (q ↔ p) … (Biconditional Law)
≡ (~p ∨ q) ∧ (~q ∨ p) … (Conditional Law)
≡ [~p ∧ (~q ∨ p)] ∨ [q ∧ (~q ∨ p)] … (Distributive Law)
≡ [(~p ∧ ~q) ∨ (~p ∧ p)] ∨ [(q ∧ ~q) ∨ (q ∧ p)] … (Distributive Law)
≡ [(~p ∧ ~q) ∨ F] ∨ [F ∨ (q ∧ p)] … (ComplementLaw)
≡ (~ p ∧ ~ q) ∨ (q ∧ p) … (Identity Law)
≡ (~ p ∧ ~ q) ∨ (p ∧ q) … (Commutative Law)
≡ (p ∧ q) ∨ (~p ∧ ~q) … (Commutative Law)
≡ RHS.

(ii) (p ∨ q) ∧ (p ∨ ~q) ≡ p
Solution:
LHS = (p ∨ q) ∧ (p ∨ ~q)
≡ p ∨ (q ∧ ~q) … (Distributive Law)
≡ p ∨ F … (Complement Law)
≡ p … (Identity Law)
≡ RHS.

(iii) (p ∧ q) ∨ (~ p ∧ q) ∨ (p ∧ ~q) ≡ p ∨ q
Solution:
LHS = (p ∧ q) v (~p ∧ q) ∨ (p ∧ ~q)
≡ [(p ∨ ~p) ∧ q] ∨ (p ∧ ~q) … (Distributive Law)
≡ (T ∧ q) ∨ (p ∧ ~q) … (Complement Law)
≡ q ∨ (p ∧ ~q) … (Identity Law)
≡ (q ∨ p) ∧ (q ∨ ~q) … (Distributive Law)
≡ (q ∨ p) ∧ T .. (Complement Law)
≡ q ∨ p … (Identity Law)
≡ p ∨ q … (Commutative Law)
≡ RHS.

(iv) ~[(p ∨ ~q) → (p ∧ ~q)] ≡ (p ∨ ~q) ∧ (~p ∨ q)
Solution:
LHS = ~[(p ∨ ~q) → (p ∧ ~q)]
≡ (p ∨ ~q) ∧ ~(p ∧ ~q) … (Negation of implication)
≡ (p ∨ ~q) ∧ [~p ∨ ~(~q)] … (Negation of conjunction)
≡ (p ∨ ~ q) ∧ (~p ∨ q)… (Negation of negation)
≡ RHS.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 1.1 Class 12 Maths 1
• Exercise 1.2 Class 12 Maths 1
• Exercise 1.3 Class 12 Maths 1
• Exercise 1.4 Class 12 Maths 1
• Exercise 1.5 Class 12 Maths 1
• Miscellaneous Exercise 1 Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.3 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.3 Questions And Answers Maharashtra Board

Question 1.
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of each of the following.
(i) Ǝ x ∈ A such that x – 8 = 1
Solution:
Clearly x = 9 ∈ A satisfies x – 8 = 1. So the given statement is true, hence its truth value is T.

(ii) Ɐ x ∈ A, x² + x is an even number
Solution:
For each x ∈ A, x² + x is an even number. So the given statement is true, hence its truth value is T.

(iii) Ǝ x ∈ A such that x² < 0
Solution:
There is no x ∈ A which satisfies x² < 0. So the given statement is false, hence its truth value is F.

(iv) Ɐ x ∈ A, x is an even number
Solution:
x = 3 ∈ A, x = 5 ∈ A, x = 7 ∈ A, x = 9 ∈ A, x = 11 ∈ A do not satisfy x is an even number. So the given statement is false, hence its truth value is F.

(v) Ǝ x ∈ A such that 3x + 8 > 40
Solution:
Clearly x = 11 ∈ A and x = 12 ∈ A satisfies 3x + 8 > 40. So the given statement is true, hence its truth value is T.

(vi) Ɐ x ∈ A, 2x + 9 > 14
Solution:
For each x ∈ A, 2x + 9 > 14. So the given statement is true, hence its truth value is T.

Question 2.
Write the duals of each of the following.
(i) p ∨ (q ∧ r)
Solution:
The duals of the given statement patterns are :
p ∧ (q ∨ r)

(ii) p ∧ (q ∧ r)
Solution:
p ∨ (q ∨ r)

(iii) (p ∨ q) ∧ (r ∨ s)
Solution:
(p ∧ q) ∨ (r ∧ s)

(iv) p ∧ ~q
Solution:
p ∨ ~q

(v) (~p ∨ q) ∧ (~r ∧ s)
Solution:
(~p ∧ q) ∨ (~r ∨ s)

(vi) ~p ∧ (~q ∧ (p ∨ q) ∧ ~r)
Solution:
~p ∨ (~q ∨ (p ∧ q) ∨ ~r)

(vii) [~(p ∨ q)] ∧ [p ∨ ~(q ∧ ~s)]
Solution:
[ ~(p ∧ q)] ∨ [p ∧ ~(q ∨ ~s)]

(viii) c ∨ {p ∧ (q ∨ r)}
Solution:
t ∧ {p ∧ (q Ar)}

(ix) ~p ∨ (q ∧ r) ∧ t
Solution:
~p ∧ (q ∨ r) ∨ c

(x) (p ∨ q) ∨ c
Solution:
(p ∧ q) ∧ t

Question 3.
Write the negations of the following.
(i) x + 8 > 11 or y – 3 = 6
Solution:
Let p : x + 8 > 11, q : y — 3 = 6.
Then the symbolic form of the given statement is p ∨ q.
Since ~(p ∨ q) ≡ ~p ∧ ~q, the negation of given statement is :
‘x + 8 > 11 and y – 3 ≠ 6’ OR
‘x + 8 ≮ 11 and y – 3 ≠ 6’

(ii) 11 < 15 and 25 > 20
Solution:
Let p: 11 < 15, q : 25 > 20.
Then the symbolic form of the given statement is p ∧ q.
Since ~(p ∧ q) ≡ ~p ∨ ~q, the negation of given statement is :
’11 ≮ 15 or 25 > 20.’ OR
’11 ≯ 15 or 25 ≮ 20.’

(iii) Qudrilateral is a square if and only if it is a rhombus.
Solution:
Let p : Quadrilateral is a square.
q : It is a rhombus.
Then the symbolic form of the given statement is p ↔ q.
Since ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p), the negation of given statement is :
‘ Quadrilateral is a square but it is not a rhombus or quadrilateral is a rhombus but it is not a square.’

(iv) It is cold and raining.
Solution:
Let p : It is cold.
q : It is raining.
Then the symbolic form of the given statement is p ∧ q.
Since ~(p ∧ q) ≡ ~p ∨ ~q, the negation of the given statement is :
‘It is not cold or not raining.’

(v) If it is raining then we will go and play football.
Solution:
Let p : It is raining.
q : We will go.
r : We play football.
Then the symbolic form of the given statement is p → (q ∧ r).
Since ~[p → (q ∧ r)] ≡ p ∧ ~(q ∧ r) ≡ p ∧ (q ∨ ~r), the negation of the given statement is :
‘It is raining and we will not go or not play football.’

(vi) \(\sqrt {2}\) is a rational number.
Solution:
Let p : \(\sqrt {2}\) is a rational number.
The negation of the given statement is
‘ ~p : \(\sqrt {2}\) is not a rational number.’

(vii) All natural numbers are whole numers.
Solution:
The negation of the given statement is :
‘Some natural numbers are not whole numbers.’

(viii) Ɐ n ∈ N, n² + n + 2 is divisible by 4.
Solution:
The negation of the given statement is :
‘Ǝ n ∈ N, such that n² + n + 2 is not divisible by 4.’

(ix) Ǝ x ∈ N such that x – 17 < 20
Solution:
The negation of the given statement is :
‘Ɐ x ∈ N, x – 17 ≯ 20.’

Question 4.
Write converse, inverse and contrapositive of the following statements.
(i) If x < y then x² < y² (x, y ∈ R)
Solution:
Let p : x < y, q : x² < y².
Then the symbolic form of the given statement is p → q.
Converse : q → p is the converse of p → q.
i.e. If x² < y², then x < y.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If x ≯ y, then x² ≯ y². OR
If x ≮ y, then x² ≮ y².
Contrapositive : ~q → p is the contrapositive of
p → q i.e. If x² ≯ y², then x ≯ y. OR
If x² ≮ y², then x ≮ y.

(ii) A family becomes literate if the woman in it is literate.
Solution:
Let p : The woman in the family is literate.
q : A family become literate.
Then the symbolic form of the given statement is p → q
Converse : q → p is the converse of p → q.
i.e. If a family become literate, then the woman in it is literate.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If the woman in the family is not literate, then the family does not become literate.
Contrapositive : ~q → ~p is the contrapositive of p → q. i e. If a family does not become literate, then the woman in it is not literate.

(iii) If surface area decreases then pressure increases.
Solution:
Let p : The surface area decreases.
q : The pressure increases.
Then the symbolic form of the given statement is p → q.
Converse : q → p is the converse of p→ q.
i.e. If the pressure increases, then the surface area decreases.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If the surface area does not decrease, then the pressure does not increase.
Contrapositive : ~q → ~p is the contrapositive of p → q.
i.e. If the pressure does not increase, then the surface area does not decrease.

(iv) If voltage increases then current decreases.
Solution:
Let p : Voltage increases.
q : Current decreases.
Then the symbolic form of the given statement is p → q.
Converse : q →p is the converse of p → q.
i.e. If current decreases, then voltage increases.
Inverse : ~p → ~q is the inverse of p → q.
i.e. If voltage does not increase, then current does not decrease.
Contrapositive : ~q → ~p, is the contrapositive of p → q.
i.e. If current does not decrease, then voltage doesnot increase.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 1.1 Class 12 Maths 1
• Exercise 1.2 Class 12 Maths 1
• Exercise 1.3 Class 12 Maths 1
• Exercise 1.4 Class 12 Maths 1
• Exercise 1.5 Class 12 Maths 1
• Miscellaneous Exercise 1 Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.2 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.2 Questions And Answers Maharashtra Board

Question 1.
Construct the truth table for each of the following statement patterns:
(i) [(p → q) ∧ q] → p
Solution :
Here are two statements and three connectives.
∴ there are 2 × 2 = 4 rows and 2 + 3 = 5 columns in the truth table.

(ii) (p ∧ ~q) ↔ (p → q)
Solution:

(iii) (p ∧ q) ↔ (q ∨ r)
Solution:

(iv) p → [~(q ∧ r)]
Solution:

(v) ~p ∧ [(p ∨ ~q ) ∧ q]
Solution:

(vi) (~p → ~q) ∧ (~q → ~p)
Solution:

(vii) (q → p) ∨ (~p ↔ q)
Solution:

(viii) [p → (q → r)] ↔ [(p ∧ q) → r]
Solution:

(ix) p → [~(q ∧ r)]
Solution:

(x) (p ∨ ~q) → (r ∧ p)
Solution:

Question 2.
Using truth tables prove the following logical equivalences.
(i) ~p ∧ q ≡ (p ∨ q) ∧ ~p
Solution:

The entries in the columns 4 and 6 are identical.
∴ ~p ∧ q ≡ (p ∨ q) ∧ ~p.

(ii) ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p
Solution:

The entries in the columns 3 and 7 are identical.
∴ ~(p ∨ q) ∧ (~p ∧ q) = ~p.

(iii) p ↔ q ≡ ~[(p ∨ q) ∧ ~(p ∧ q)]
Solution:

The entries in the columns 3 and 8 are identical.
∴ p ↔ q ≡ ~[(p ∨ q) ∧ ~(p ∧ q)].

(iv) p → (q → p) ≡ ~p → (p → q)
Solution:

The entries in the columns 4 and 7 are identical.
∴ p → (q → p) ≡ ~p → (p → q).

(v) (p ∨ q ) → r ≡ (p → r) ∧ (q → r)
Solution:

The entries in the columns 5 and 8 are identical.
∴ (p ∨ q ) → r ≡ (p → r) ∧ (q → r).

(vi) p → (q ∧ r) ≡ (p → q) ∧ (p → r)
Solution:

The entries in the columns 5 and 8 are identical.
∴ p → (q ∧ r) ≡ (p → q) ∧ (p → r).

(vii) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Solution:

The entries in the columns 5 and 8 are identical.
∴ p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r).

(viii) [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
Solution:

The entries in the columns 3 and 7 are identical.
∴ [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r.

(ix) ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p)
Solution:

The entries in the columns 6 and 9 are identical.
∴ ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p).

Question 3.
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
(i) (p ∧ q) → (q ∨ p)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p ∧ q) → (q ∨ p) is a tautology.

(ii) (p → q) ↔ (~p ∨ q)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p → q) ↔ (~p ∨ q) p is a tautology.

(iii) [~(~p ∧ ~q)] ∨ q
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ [~(~p ∧ ~q)] ∨ q is a contingency.

(iv) [(p → q) ∧ q)] → p
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ [(p → q) ∧ q)] → p is a contingency

(v) [(p → q) ∧ ~q] → ~p
Solution:

All the entries in the last column of the above truth table are T.
∴ [(p → q) ∧ ~q] → ~p is a tautology.

(vi) (p ↔ q) ∧ (p → ~q)
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ (p ↔ q) ∧ (p → ~q) is a contingency.

(vii) ~(~q ∧ p) ∧ q
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ ~(~q ∧ p) ∧ q is a contingency.

(viii) (p ∧ ~q) ↔ (p → q)
Solution:

All the entries in the last column of the above truth table are F.
∴ (p ∧ ~q) ↔ (p → q) is a contradiction.

(ix) (~p → q) ∧ (p ∧ r)
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ (~p → q) ∧ (p ∧ r) is a contingency.

(x) [p → (~q ∨ r)] ↔ ~[p → (q → r)]
Solution:

All the entries in the last column of the above truth table are F.
∴ [p → (~q ∨ r)] ↔ ~[p → (q → r)] is a contradiction

Class 12 Maharashtra State Board Maths Solution 

• Exercise 1.1 Class 12 Maths 1
• Exercise 1.2 Class 12 Maths 1
• Exercise 1.3 Class 12 Maths 1
• Exercise 1.4 Class 12 Maths 1
• Exercise 1.5 Class 12 Maths 1
• Miscellaneous Exercise 1 Class 12 Maths 1

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.1 Questions and Answers.

12th Maths Part 1 Mathematical Logic Exercise 1.1 Questions And Answers Maharashtra Board

Question 1.
State which of the following sentences are statements. Justify your answer. In case of the statement, write down the truth value :
(i) 5 + 4 = 13.
Solution:
It is a statement which is false, hence its truth value is ‘F’.

(ii) x – 3 = 14.
Solution:
It is an open sentence, hence it is not a statement.

(iii) Close the door.
Solution:
It is an imperative sentence, hence it is not a statement.

(iv) Zero is a complex number.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(v) Please get me breakfast.
Solution:
It is an imperative sentence, hence it is not a statement.

(vi) Congruent triangles are also similar.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(vii) x² = x.
Solution:
It is an open sentence, hence it is not a statement,

(viii) A quadratic equation cannot have more than two roots.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(ix) Do you like Mathematics ?
Solution:
It is an interrogative sentence, hence it is not a statement.

(x) The sun sets in the west.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xi) All real numbers are whole numbers.
Solution:
It is a statement which is false, hence its truth value is ‘F’.

(xii) Can you speak in Marathi ?
Solution:
It is an interrogative sentence, hence it is not a statement.

(xiii) x² – 6x – 7 = 0, when x = 7.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xiv) The sum of cuberoots of unity is zero.
Solution:
It is a statement which is true, hence its truth value is ‘T’.

(xv) It rains heavily.
Solution :
It is an open sentence, hence it is not a statement.

Question 2.
Write the following compound statements symbolically:
(i) Nagpur is in Maharashtra and Chennai is in Tamil Nadu.
Solution:
Let p : Nagpur is in Maharashtra.
q : Chennai is in Tamil Nadu.
Then the symbolic form of the given statement is P∧q.

(ii) Triangle is equilateral or isosceles,
Solution:
Let p : Triangle is equilateral.
q : Triangle is isosceles.
Then the symbolic form of the given statement is P∨q.

(iii) The angle is right angle if and only if it is of measure 90°.
Solution:
Let p : The angle is right angle.
q : It is of measure 90°.
Then the symbolic form of the given statement is p↔q

(iv) Angle is neither acute nor obtuse.
Solution:
Let p : Angle is acute.
q : Angle is obtuse.
Then the symbolic form of the given statement is
~p ∧ ~q.

(v) If ∆ ABC is right angled at B, then m∠A + m∠C = 90°.
Solution:
Let p : ∆ ABC is right angled at B.
q : m∠A + m∠C = 90°.
Then the symbolic form of the given statement is p → q

(vi) Hima Das wins gold medal if and only if she runs fast.
Solution:
Let p : Hima Das wins gold medal
q : She runs fast.
Then the symbolic form of the given statement is p ↔ q.

(vii) x is not irrational number but it is a square of an integer.
Solution:
Let p : x is not irrational number
q : It is a square of an integer
Then the symbolic form of the given statement is p ∧ q
Note : If p : x is irrational number, then the symbolic form of the given statement is ~p ∧ q.

Question 3.
Write the truth values of the following :
(i) 4 is odd or 1 is prime.
Solution:
Let p : 4 is odd.
q : 1 is prime.
Then the symbolic form of the given statement is p∨q.
The truth values of both p and q are F.
∴ the truth value of p v q is F. … [F ∨ F = F]

(ii) 64 is a perfect square and 46 is a prime number.
Solution:
Let p : 64 is a perfect square.
q : 46 is a prime number.
Then the symbolic form of the given statement is p∧q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]

(iii) 5 is a prime number and 7 divides 94.
Solution:
Let p : 5 is a prime number.
q : 7 divides 94.
Then the symbolic form of the given statement is p∧q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]

(iv) It is not true that 5 – 3i is a real number.
Solution:
Let p : 5 – 3i is a real number.
Then the symbolic form of the given statement is ~ p.
The truth values of p is F.
∴ the truth values of ~ p is T. … [~ F ≡ T]

(v) If 3 × 5 = 8, then 3 + 5 = 15.
Solution:
Let p : 3 × 5 = 8.
q : 3 + 5 = 15.
Then the symbolic form of the given statement is p → q.
The truth values of both p and q are F.
∴ the truth value of p → q is T. … [F → F ≡ T]

(vi) Milk is white if and only if sky is blue.
Solution:
Let p : Milk is white.
q : Sky is blue
Then the symbolic form of the given statement is p ↔ q.
The truth values of both p and q are T.
∴ the truth value of p ↔ q is T. … [T ↔ T ≡ T]

(vii) 24 is a composite number or 17 is a prime number.
Solution :
Let p : 24 is a composite number.
q : 17 is a prime number.
Then the symbolic form of the given statement is p ∨ q.
The truth values of both p and q are T.
∴ the truth value of p ∨ q is T. … [T ∨ T ≡ T]

Question 4.
If the statements p, q are true statements and r, s are false statements, then determine the truth values of the following:
(i) p ∨ (q ∧ r)
Solution:
Truth values of p and q are T and truth values of r and s are F.
p ∨ (q ∧ r) ≡ T ∨ (T ∧ F)
≡ T ∧ F ≡ T
Hence the truth value of the given statement is true.

(ii) (p → q) ∨ (r → s)
Solution:
(p → q) ∨ (r → s) ≡ (T → T) ∨ (F → F)
≡ T ∨ T ≡ T
Hence the truth value of the given statement is true.

(iii) (q ∧ r) ∨ (~p ∧ s)
Solution:
(q ∧ r) ∨ (~p ∧ s) ≡ (T ∧ F) ∨ (~T ∧ F)
≡ F ∨ (F ∧ F)
≡ F ∨ F ≡ F
Hence the truth value of the given statement is false.

(iv) (p → q) ∧ (~ r)
Solution:
(p → q) ∧ (~ r) ≡ (T → T) ∧ (~ F)
≡ T ∧ T ≡ T
Hence the truth value of the given statement is true.

(v) (~r ↔ p) → (~q)
Solution:
(~r ↔ p) → (~q) ≡ (~F ↔ T) → (~T)
≡ (T ↔ T) → F
≡ T → F ≡ F
Hence the truth value of the given statement is false.

(vi) [~p ∧ (~q ∧ r) ∨ (q ∧ r) ∨ (p ∧ r)]
Solution:
[~p ∧ (~q ∧ r)∨(q ∧ r)∨(p ∧ r)]
≡ [~T ∧ (~T ∧ F)] ∨ [(T ∧ F) V (T ∧ F)]
≡ [F ∧ (F ∧ F)] ∨ [F V F]
≡ (F ∧ F) ∨ F
≡ F ∨ F ≡ F
Hence the truth value of the given statement is false.

(vii) [(~ p ∧ q) ∧ (~ r)] ∨ [(q → p) → (~ s ∨ r)]
Solution:
[(~ p ∧ q) ∧ (~ r)] ∨ [(q → p) → (~ s ∨ r)]
≡ [(~T ∧ T) ∧ (~F)] ∨ [(T → T) → (~F ∨ F)]
≡ [(F ∧ T) ∧ T] ∨ [T → (T ∨ F)]
≡ (F ∧ T) ∨ (T → T)
≡ F ∨ T ≡ T
Hence the truth value of the given statement is true.

(viii) ~ [(~p ∧ r) ∨ (s → ~q)] ↔ (p ∧ r)
Solution :
~ [(~p ∧ r) ∨ (s → ~q)] ↔ (p ∧ r)
≡ ~ [(~T ∧ F) ∨ (F → ~T)] ↔ (T ∧ F)
≡ ~ [(F ∧ F) ∨ (F → F)] ↔ F
≡ ~ (F ∨ T) ↔ F
≡ ~T ↔ F
≡ F ↔ F ≡ T
Hence the truth value of the given statement is true.

Question 5.
Write the negations of the following :
(i) Tirupati is in Andhra Pradesh.
Solution:
The negations of the given statements are :
Tirupati is not in Andhra Pradesh.

(ii) 3 is not a root of the equation x² + 3x – 18 = 0.
Solution:
3 is a root of the equation x² + 3x – 18 = 0.

(iii) \(\sqrt {2}\) is a rational number.
Solution:
\(\sqrt {2}\) is not a rational number.

(iv) Polygon ABCDE is a pentagon.
Solution:
Polygon ABCDE is not a pentagon.

(v) 7 + 3 > 5.
Solution :
7 + 3 > 5.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 1.1 Class 12 Maths 1
• Exercise 1.2 Class 12 Maths 1
• Exercise 1.3 Class 12 Maths 1
• Exercise 1.4 Class 12 Maths 1
• Exercise 1.5 Class 12 Maths 1
• Miscellaneous Exercise 1 Class 12 Maths 1