Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Miscellaneous Exercise 2B Questions and Answers.
12th Maths Part 1 Matrices Miscellaneous Exercise 2B Questions And Answers Maharashtra Board
I. Choose the correct answer from the given alternatives in each of the following questions:
Question 1.
If A = \(\left(\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right)\), adj = \(\left(\begin{array}{ll}
4 & a \\
-3 & b
\end{array}\right)\) then the values of a and b are,
(a) a = – 2, b = 1
(b) a = 2, b = 4
(c) a = 2, b = –1
(d) a = 1, b = –2
Solution:
(a) a = – 2, b = 1
Question 2.
The inverse of \(\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\) is

Solution:
\(\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\)
Question 3.
If A = \(\left(\begin{array}{ll}
1 & 2 \\
2 & 1
\end{array}\right)\) and A(adj A) = k 1, then the value of k is
(a) 1
(b) -1
(c) 0
(d) -3
Solution:
(d) -3 [Hint : A(adj A) = |A| ∙ I]
![]()
Question 4.
If A = \(\left(\begin{array}{ll}
2 & -4 \\
3 & 1
\end{array}\right)\), then the adjoint of matrix A is
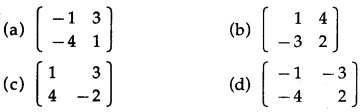
Solution:\(\left(\begin{array}{ll}
1 & 4 \\
-3 & 2
\end{array}\right)\)
Question 5.
If A = \(\left(\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right)\) and A(adj A) = kI, then the value of k is
(a) 2
(b) -2
(c) 10
(d) -10
Solution:
(b) -2
Question 6.
If A = \(\left(\begin{array}{rr}
\lambda & 1 \\
-1 & -\lambda
\end{array}\right)\), then A-1 does not exist if λ = ………..
(a) 0
(b) ± 1
(c) 2
(d) 3
Solution:
(b) ± 1
![]()
Question 7.
If A = \(\left[\begin{array}{ll}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) then A-1 = ….
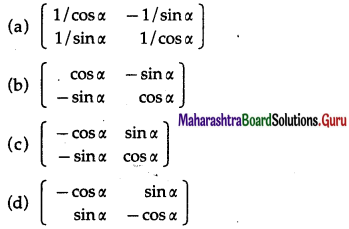
Solution:
\(\left[\begin{array}{rr}
\cos \alpha & -\sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\)
Question 8.
If F (∝) = \(\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\) where ∝ ∈ R then [F(∝)]-1 is =
(a) F(-∝)
(b) F(∝-1)
(c) F(2∝)
(d) None of these
Solution:
(a) F(-∝)
Question 9.
The inverse of A = \(\left[\begin{array}{lll}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\)
(a) I
(b) A
(c) A’
(d) -I
Solution:
(b) A
![]()
Question 10.
The inverse of a symmetric matrix is
(a) Symmetric
(b) Non-symmetric
(c) Null matrix
(d) Diagonal matrix
Solution:
(a) Symmetric
Question 11.
For a 2 × 2 matrix A, if A(adjA) = \(\left(\begin{array}{ll}
10 & 0 \\
0 & 10
\end{array}\right)\) then determinant A equals
(a) 20
(b) 10
(c) 30
(d) 40
Solution:
(b) 10
Question 12.
If A2 = \(-\frac{1}{2}\left[\begin{array}{cc}
1 & -4 \\
-1 & 2
\end{array}\right]\) then A =
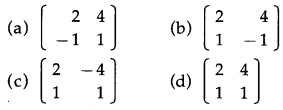
Solution:
\(-\frac{1}{2}\left[\begin{array}{cc}
2 & 4 \\
1 & 1
\end{array}\right]\)
II. Solve the following equations by the methods of inversion.
(i) 2x – y = -2 , 3x + 4y = 5
Solution:
The given equations can be written in the matrix form as :

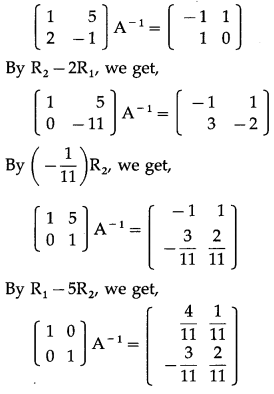
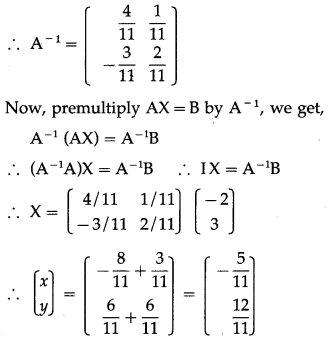
By equality of matrices,
x = \(-\frac{5}{11}\), y = \(\frac{12}{11}\) is the required solution.
![]()
(ii) x + y + z = 1, 2x + 3y + 2z = 2 and ax + ay + 2az = 4, a ≠ 0.
Solution:
The given equations can be written in the matrix form as :

= 1(6a – 2a) – 1(4a – 2a) + 1(2a – 3a)
= 4a – 2a – a = a ≠ 0 ∴ A-1 exists.
Consider AA-1 = I
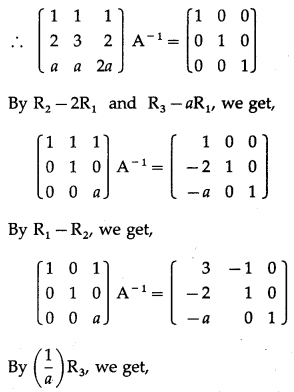
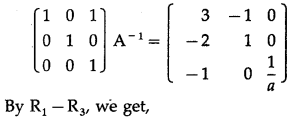

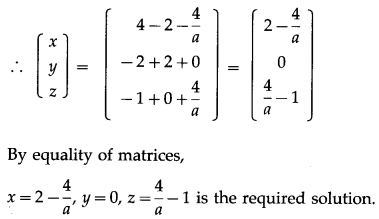
(iii) 5x – y +4z = 5, 2x + 3y + 5z = 2 and 5x – 2y + 6z = -1
Solution:
The given equations can be written in the matrix form as :
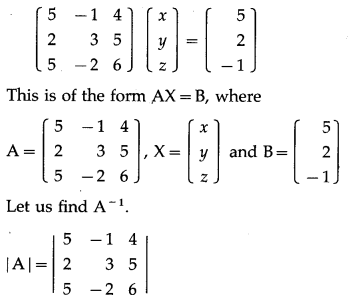
= 5(18 + 10) + 1 (12 – 25) + 4( -4 – 15)
= 140 – 13 – 76 = 51 #0
∴ A-1 exists.
Now, we have to find the cofactor matrix

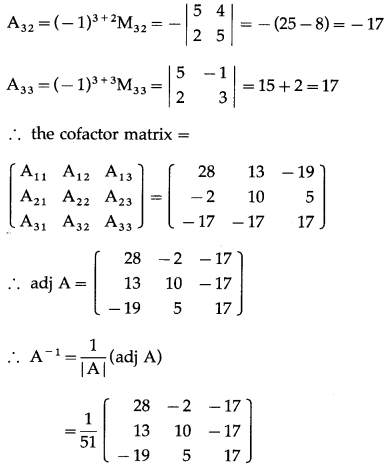
Now, premultiply AX = B by A-1, we get,
A-1(AX) = A-1B
∴ (A-1A)X = A-1B
∴ IX = A-1B
∴ X = \(\frac{1}{51}\left[\begin{array}{rrr}
28 & -2 & -17 \\
13 & 10 & -17 \\
-19 & 5 & 17
\end{array}\right]\left[\begin{array}{r}
5 \\
2 \\
-1
\end{array}\right]\)
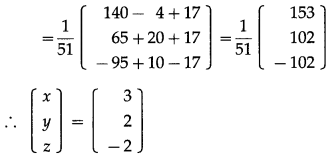
By equality of matrices,
x = 3, y = 2, z = -2 is the required solution.
![]()
(iv) 2x + 3y = -5, 3x + y = 3
Solution:
(v) x + y + z = -1, y + z = 2 and x + y – z = 3
Solution:
The given equations can be written in the matrix form as :

= 1(-1 – 1) – 1 (0 – 1) + 1(0 – 1)
= -2 + 1 – 1 = -2 ≠ 0 ∴ A-1 exists.
Consider AA-1 = I
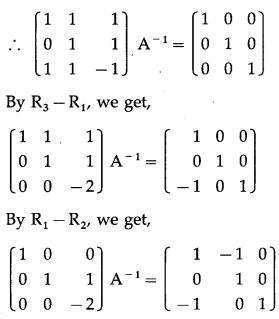
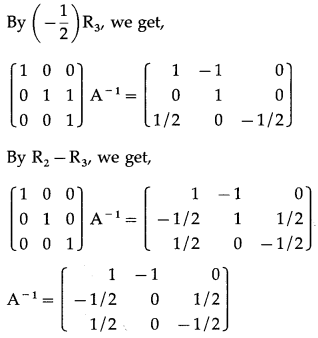
Now, premultiply AX = B by A-1, we get,
A-1(AX) = A-1B
∴ (A-1A)X = A-1B
∴ IX = A-1B
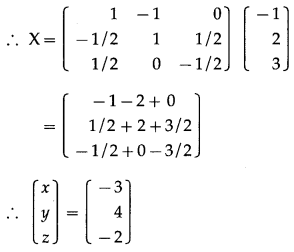
∴ by equality of the matrices, x= -3, y = 4, z = -2 is the required solution.
Question 2.
Express the following equation in matrix from and solve them by the method of reduction.
(i) x – y + z = 1, 2x – y = 1, 3x + 3y – 4z = 2
Solution:
The given equations can be written in the matrix form as :
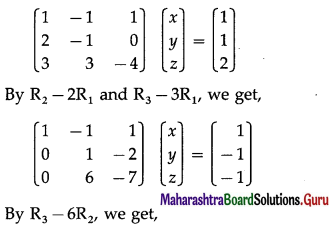
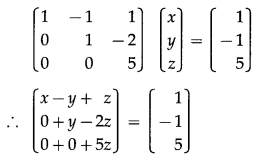
By equality of matrices,
x – y + z = 1 ……(1)
y – 2z = -1 …..(2)
5z = 5 ….(3)
From (3), z = 1
Substituting z = 1 in (2), we get,
y – 2 = -1 ∴ y = 1
Substituting y = 1, z = 1 in (1), we get,
x – 1 + 1 = 1
∴ x = 1
Hence, x = 1, y = 1, z = 1 is the required solution.
![]()
(ii) x + y = 1, y + z = \(\frac{5}{3}\), z + x = \(\frac{4}{3}\).
Solution:
The given equations can be written in the matrix form as :

By equality of matrices,
x + y = 1 ……(1)
y + z = \(\frac{5}{3}\) …(2)
2z = 2 ……..(3)
From (3), z = 1
Substituting z = 1 in (2), we get,
y + 1 = \(\frac{5}{3}\) ∴ y = \(\frac{2}{3}\)
Substituting y = \(\frac{2}{3}\) in (1), we get,
x + \(\frac{2}{3}\) = 1 ∴ x = \(\frac{1}{3}\)
Hence, x = \(\frac{1}{3}\), y = \(\frac{2}{3}\), z = 1 is the required solution.
(iii) 2x – y + z = 1, x + 2y + 3z = 8 and 3x + y – 4z = 1
Solution:
The given equations can be written in the matrix form as :

∴ \(\left[\begin{array}{r}
x+2 y+3 z \\
0-5 y-5 z \\
0+0-8 z
\end{array}\right]\) = \(\left[\begin{array}{r}
8 \\
-15 \\
-8
\end{array}\right]\)
By equality of matrices,
x + 2y + 3z = 8 …..(1)
-5y – 5z = -15 ….(2)
-8z = -8 …..(3)
From (3), z = 1
Substituting z = 1 in (2), we get,
-5y – 5 = -15
-5y = -10
∴ y = 2
Substituting y = 2, z = 1 in (1), we get,
x + 4 + 3 = 8 ∴ x = 1
Hence, x = 1, y = 2, z = 1 is the required solution.
![]()
(iv) x + y + z = 6, 3x – y + 3z =10 and 5x + 5y – 4z = 3.
Solution:
(v) x + 2y + z = 8, 2x + 3y – z =11 and 3x – y – 2z = 5
Solution:
The given equations can be written in the matrix form as :

By equality of matrices,
x + 2y + z = 8 … (1)
-y – 3z = -5 … (2)
16z = 16 … (3)
From (3), z = 1
Substituting z = 1 in (2), we get,
-y – 3 = -5, ∴ y = 2
Substituting y = 2, z = 1 in (1), we get,
x + 4 + 1 = 8 ∴ x = 3
Hence, x = 3, y = 2, z = 1 is the required solution.
(vi) x + 3y + 2z = 6, 3x – 2y + 5z =5 and 2x – 3y + 6z = 7.
Solution:
The given equations can be written in the matrix form as :
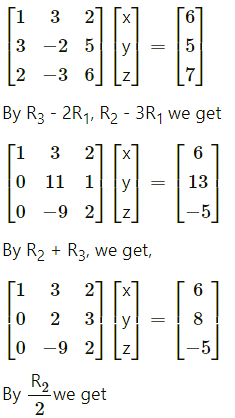
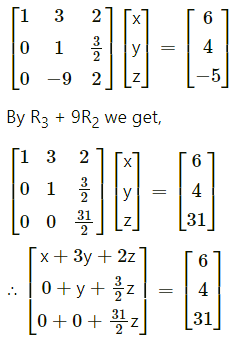
By equality of matrices,
x + 3y + 2z = 6 …(1)
y + \(\frac{3}{2}\) z = 4 …(2)
\(\frac{31}{2}\)z = 31 …..(3)
From (3), z = 2
Substituting z = 2 in (2), we get,
y + \(\frac{3}{2}\)z = 4
y + \(\frac{3}{2}\)(2) = 4
y + 3 = 4
y = 1
Substituting y = 1, z = 2 in (2), we get,
x + 3y + 2z = 6
x + 3(1) + 2(2) = 6
x + 3 + 4 = 6
x = -1
Hence, x = -1, y = 1, z = 2 is the required solution.
![]()
Question 3.
The sum of three numbers is 6. If we multiply third number by 3 and add it to the second number we get 11. By adding first and the third numbers we get a number which is double the second number. Use this information and find a system of linear equations. Find the three numbers using matrices.
Solution:
Let the three numbers be x, y and z. According to the given conditions,
x + y + z = 6.
3z + y = 11, i.e., y + 3z = 11 and x + z = 2y,
i.e., x – 2y + z = 0
Hence, the system of the linear equations is
x + y + z = 6
y + 3z = 11
x – 2y + z = 0
These equations can be written in the matrix form as :

By equality of matrices,
x + y + z = 6 …(1)
y + 3z = 11 …(2)
-3y = -6 …(3)
From (3), y = 2
Substituting y = 2 in (2), we get,
2 + 3z = 11
∴ 3z = 9 ∴ z = 3
Put y = 2, z — 3 in (1), we get,
x + 2 + 3 = 6 ∴ x = 1
∴ x = 1, y = 2, z = 3
Hence, the required numbers are 1, 2 and 3.
Question 4.
The cost of 4 pencils, 3 pens and 2 books is ₹ 150. The cost of 1 pencil, 2 pens and 3 books is ₹ 125. The cos of 6 pencils, 2 pens and 3 books is ₹ 175. Fild the cost of each item by using Matrices.
Solution:
Let the cost of 1 pencil, 1 pen and 1 book be ₹x, ₹ y, ₹ z respectively.
According to the given conditions,
4x + 3y + 2z = 150
x + 2y + 3z = 125
6x + 2y + 3z = 175
The equations can be written in matrix form as :
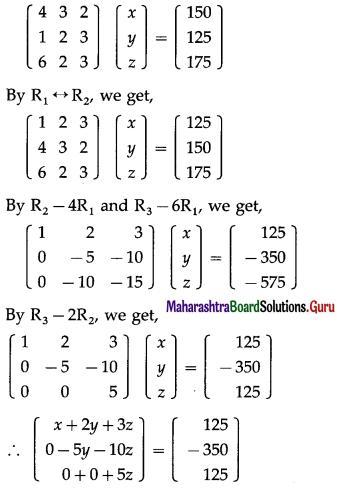
By equality of matrices,
x + 2y + 3z = 125 …(1)
-5y – 10z = -350 …(2)
5z = 125 …(3)
From (3), z = 25
Substituting z = 25 in (2), we get
-5y – 10(25) = -350
∴ -5y = -350 + 250 = -100
∴ y = 20
Substituting y = 20, z = 25 in (1), we get
x + 2(20) + 3(25) = 125
∴ x = 125 – 40 – 75 = 10
∴ x = 10, y = 20, z = 25
Hence, the cost of 1 pencil is ₹ 10, 1 pen is ₹ 20 and 1 book is ₹ 25.
![]()
Question 5.
The sum of three numbers is 6. Thrice the third number when added to the first number, gives 7. On adding three times first number to the sum of second and third number, we get 12. Find the three numbers by using Matrices.
Solution:
Let the numbers be x, y and z.
According to the given conditions,
x + y + z = 6
3z + x = 7, i.e., x + 3z = 7
and 3x + y + z = 12
Hence, the system of linear equations is
x + y + z = 6
x + 3z = 7
3x + y + z = 12
These equations can be written in matrix form as :

By equality of matrices,
x + y + z = 6 …(1)
-y + 2z = 1 …(2)
-3y = -5 …(3)
From (3), y = \(\frac{5}{3}\)
Substituting y = \(\frac{5}{3}\) in (2), we get,
–\(\frac{5}{3}\) + 2z = 1
∴ 2z = 1 + \(\frac{5}{3}\) = \(\frac{8}{3}\)
∴ z = \(\frac{4}{3}\)
Substituting y =\(\frac{5}{3}\), z = \(\frac{5}{3}\) in (1), we get,
x + \(\frac{5}{3}+\frac{4}{3}\) = 6
∴ x = 3
∴ x = 3, y = \(\frac{5}{3}\), z = \(\frac{4}{3}\)
Hence, the required numbers are 3, \(\frac{5}{3}\) and \(\frac{4}{3}\).
Question 6.
The sum of three numbers is 2. If twice the second number is added to the sum of first and third number, we get 1 adding five times the first number to the sum of second and third we get 6. Find the three numbers by using matrices.
Solution:
Let the three numbers be x, y and z.
According to the question,
x + y + 2
x + 2y + z = 1
5x + y + z = 6
The given system of equations can be written in matrix form as follows:
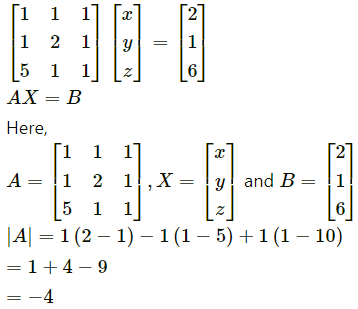

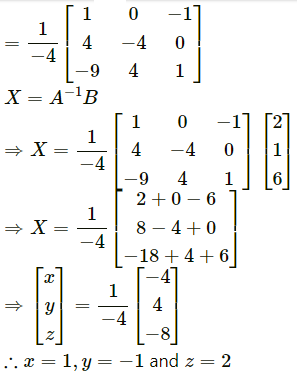
![]()
Question 7.
An amount of ₹ 5000 is invested in three types of investments, at interest rates 6%, 7%, 8% per annum respectively. The total annual income from this investment is ₹ 350. If the total annual income from the first two investments is ₹ 70 more than the income from the third, find the amount of each investment using the matrix method.
Solution:
Let the amounts in three investments by ₹ x, ₹ y, and ₹ z respectively.
Then x + y + z = 5000
Since the rate of interest in these investments are 6%, 7% and 8% respectively, the annual income of the three investments are \(\frac{6 x}{100}\), \(\frac{7 y}{100}\) and \(\frac{8 z}{100}\) respectively.
According to the given conditions,
\(\frac{6 x}{100}+\frac{7 y}{100}+\frac{8 z}{100}\) = 350
i.e. 6x + 7y + 8z = 35000
Also, \(\frac{6 x}{100}+\frac{7 y}{100}\) = \(\frac{8 z}{100}\) + 70
i.e. 6x + 7y – 8z = 7000
Hence, the system of linear equation is
x + y + z = 5000
6x + 7y + 8z = 35000
6x + 7y – 8z = 7000
These equations can be written in matrix form as :

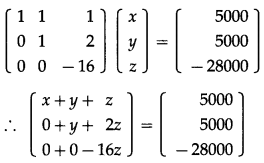
By equality of matrices,
x + y + z = 5000 …(1)
y + 2z = 5000 …(2)
-16z = -28000 ….(3)
From (3), z = 1750
Substituting z = 1750 in (2), we get,
y + 2(1750) = 5000
∴ y = 5000 – 3500 = 1500
Substituting y = 1500, z = 1750 in (1), we get,
x + 1500 + 1750 = 5000
∴ x = 5000 – 3250 = 1750
∴ x = 1750, y = 1500, z = 1750
Hence, the amounts of the three investments are ₹ 1750, ₹ 1500 and ₹ 1750 respectively.
![]()
Question 8.
The sum of the costs of one ook each of Mathematics, Physics and Chemistry is ₹ 210. Total cost of a mathematics book, 2 physics books, and a chemistry book is ₹ 240 Also the total cost of a Mathematics book, 3 physics book and chemistry books is Rs. 300/-. Find the cost of each book, using Matrices.
Class 12 Maharashtra State Board Maths Solution