Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Mathematical Logic Ex 1.2 Questions and Answers.
12th Maths Part 1 Mathematical Logic Exercise 1.2 Questions And Answers Maharashtra Board
Question 1.
Construct the truth table for each of the following statement patterns:
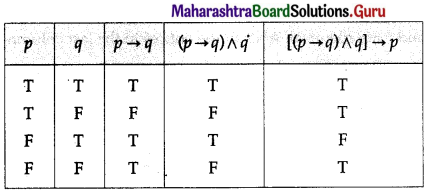
(i) [(p → q) ∧ q] → p
Solution :
Here are two statements and three connectives.
∴ there are 2 × 2 = 4 rows and 2 + 3 = 5 columns in the truth table.
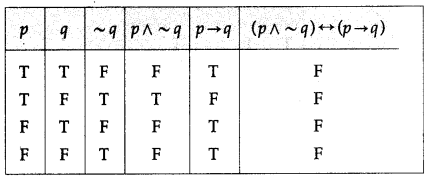
(ii) (p ∧ ~q) ↔ (p → q)
Solution:
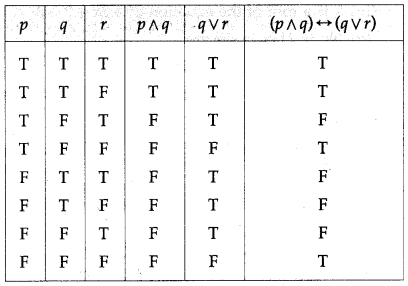
(iii) (p ∧ q) ↔ (q ∨ r)
Solution:
![]()
(iv) p → [~(q ∧ r)]
Solution:
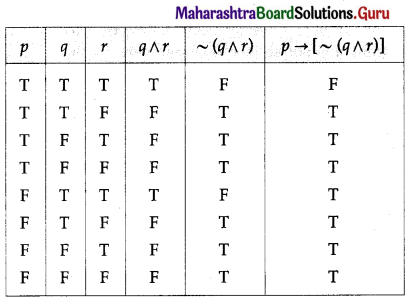
(v) ~p ∧ [(p ∨ ~q ) ∧ q]
Solution:
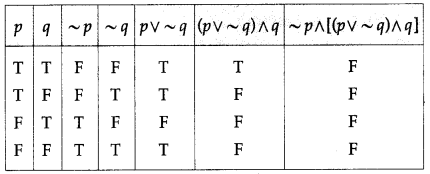
(vi) (~p → ~q) ∧ (~q → ~p)
Solution:
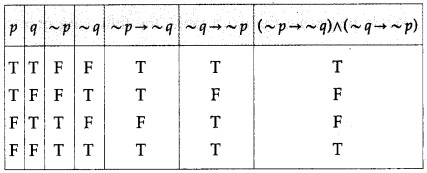
![]()
(vii) (q → p) ∨ (~p ↔ q)
Solution:
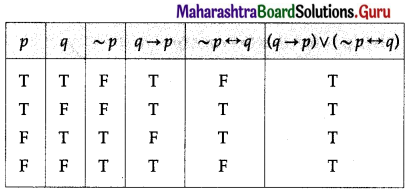
(viii) [p → (q → r)] ↔ [(p ∧ q) → r]
Solution:
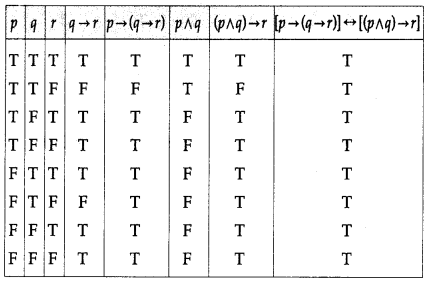
(ix) p → [~(q ∧ r)]
Solution:

(x) (p ∨ ~q) → (r ∧ p)
Solution:
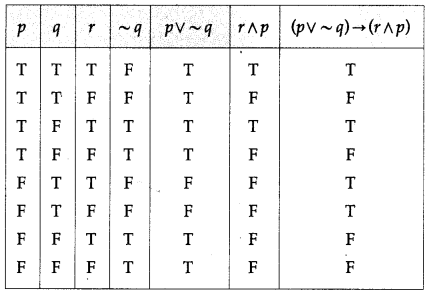
![]()
Question 2.
Using truth tables prove the following logical equivalences.
(i) ~p ∧ q ≡ (p ∨ q) ∧ ~p
Solution:
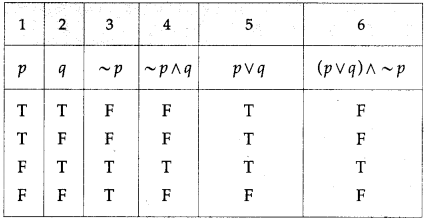
The entries in the columns 4 and 6 are identical.
∴ ~p ∧ q ≡ (p ∨ q) ∧ ~p.
(ii) ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p
Solution:
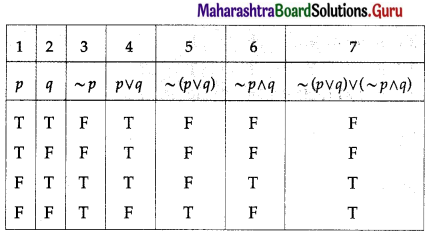
The entries in the columns 3 and 7 are identical.
∴ ~(p ∨ q) ∧ (~p ∧ q) = ~p.
(iii) p ↔ q ≡ ~[(p ∨ q) ∧ ~(p ∧ q)]
Solution:
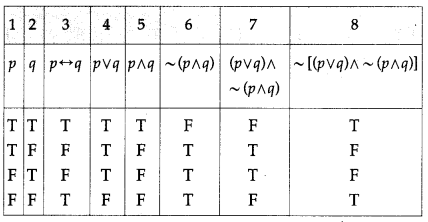
The entries in the columns 3 and 8 are identical.
∴ p ↔ q ≡ ~[(p ∨ q) ∧ ~(p ∧ q)].
![]()
(iv) p → (q → p) ≡ ~p → (p → q)
Solution:
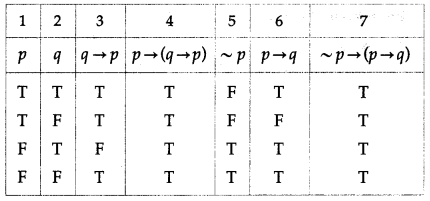
The entries in the columns 4 and 7 are identical.
∴ p → (q → p) ≡ ~p → (p → q).
(v) (p ∨ q ) → r ≡ (p → r) ∧ (q → r)
Solution:
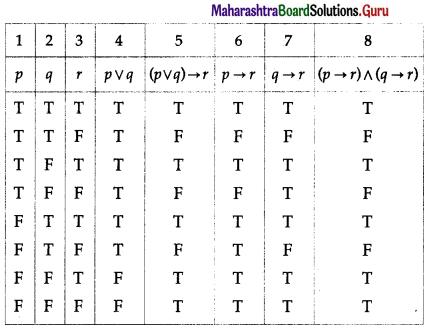
The entries in the columns 5 and 8 are identical.
∴ (p ∨ q ) → r ≡ (p → r) ∧ (q → r).
(vi) p → (q ∧ r) ≡ (p → q) ∧ (p → r)
Solution:
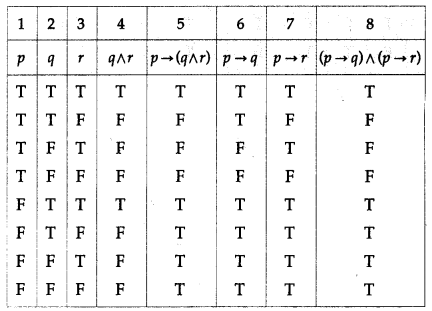
The entries in the columns 5 and 8 are identical.
∴ p → (q ∧ r) ≡ (p → q) ∧ (p → r).
![]()
(vii) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Solution:
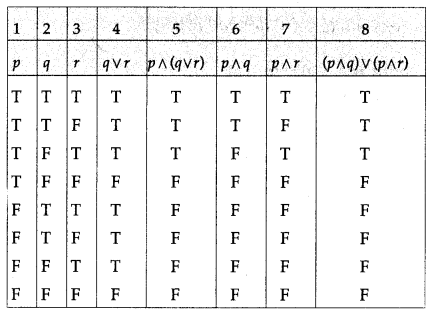
The entries in the columns 5 and 8 are identical.
∴ p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r).
(viii) [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
Solution:
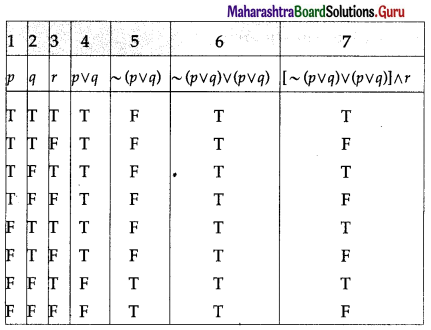
The entries in the columns 3 and 7 are identical.
∴ [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r.
(ix) ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p)
Solution:
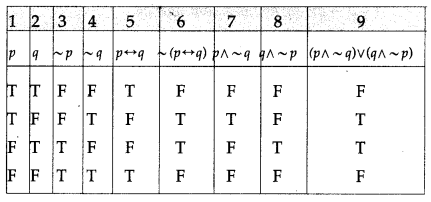
The entries in the columns 6 and 9 are identical.
∴ ~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p).
![]()
Question 3.
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
(i) (p ∧ q) → (q ∨ p)
Solution:
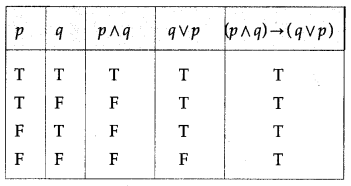
All the entries in the last column of the above truth table are T.
∴ (p ∧ q) → (q ∨ p) is a tautology.
(ii) (p → q) ↔ (~p ∨ q)
Solution:
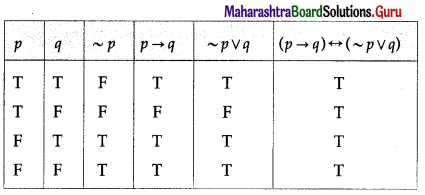
All the entries in the last column of the above truth table are T.
∴ (p → q) ↔ (~p ∨ q) p is a tautology.
(iii) [~(~p ∧ ~q)] ∨ q
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ [~(~p ∧ ~q)] ∨ q is a contingency.
![]()
(iv) [(p → q) ∧ q)] → p
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ [(p → q) ∧ q)] → p is a contingency
(v) [(p → q) ∧ ~q] → ~p
Solution:
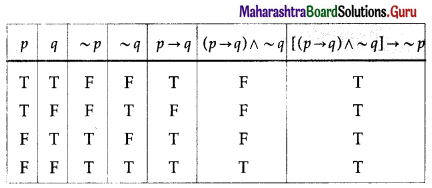
All the entries in the last column of the above truth table are T.
∴ [(p → q) ∧ ~q] → ~p is a tautology.
(vi) (p ↔ q) ∧ (p → ~q)
Solution:
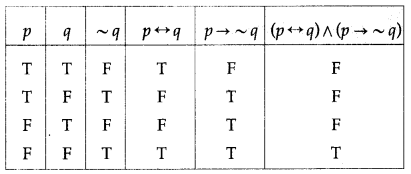
The entries in the last column of the above truth table are neither all T nor all F.
∴ (p ↔ q) ∧ (p → ~q) is a contingency.
![]()
(vii) ~(~q ∧ p) ∧ q
Solution:
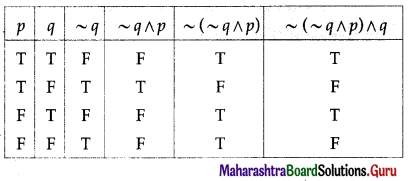
The entries in the last column of the above truth table are neither all T nor all F.
∴ ~(~q ∧ p) ∧ q is a contingency.
(viii) (p ∧ ~q) ↔ (p → q)
Solution:
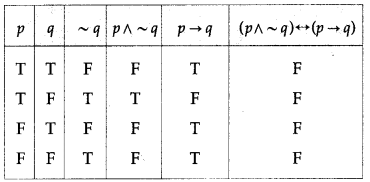
All the entries in the last column of the above truth table are F.
∴ (p ∧ ~q) ↔ (p → q) is a contradiction.
![]()
(ix) (~p → q) ∧ (p ∧ r)
Solution:
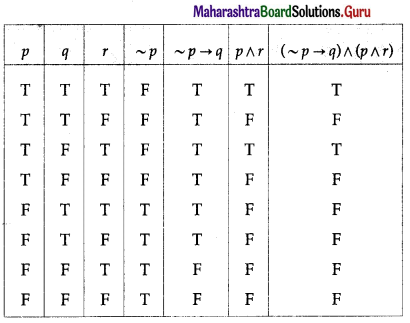
The entries in the last column of the above truth table are neither all T nor all F.
∴ (~p → q) ∧ (p ∧ r) is a contingency.
(x) [p → (~q ∨ r)] ↔ ~[p → (q → r)]
Solution:

All the entries in the last column of the above truth table are F.
∴ [p → (~q ∨ r)] ↔ ~[p → (q → r)] is a contradiction
Class 12 Maharashtra State Board Maths Solution