Class 11

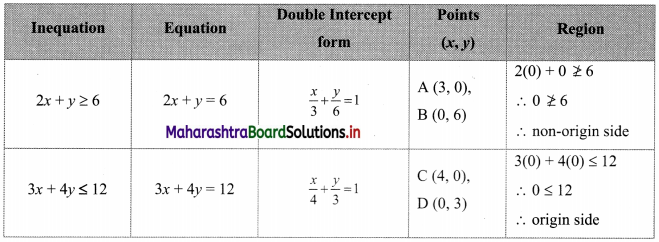
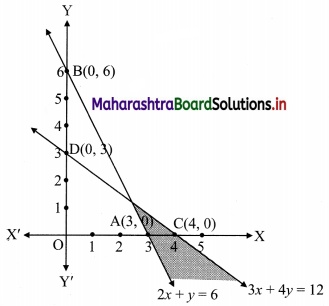
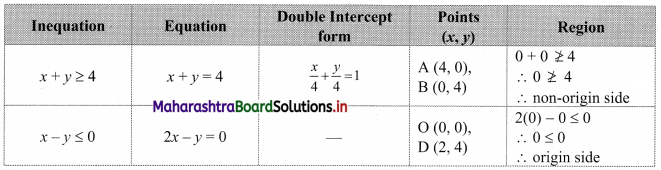
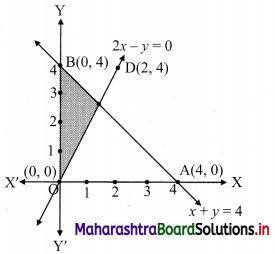
Commercial Mathematics Class 11 Commerce Maths 2 Chapter 9 Exercise 9.6 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Ex 9.6 Questions and Answers.

Std 11 Maths 2 Exercise 9.6 Solutions Commerce Maths

Question 1.
M/s Janaseva sweet mart sold sweets of ₹ 3,86,000. What CGST and SGST he will pay if the rate of GST is 5%?
Solution:
Given that M/s Janaseva sweet mart sold sweets of ₹ 3,86,000
∴ Bill amount = ₹ 3,86,000
GST payable at the rate 5%
∴ CGST and SGST applicable is 2.5% each
∴ CGST on the bill = \(\frac{2.5}{100}\) × 3,86,000 = ₹ 9650
and SGST on the bill = \(\frac{2.5}{100}\) × 3,86,000 = ₹ 9650

Question 2.
Janhavi Gas Agency purchased some gas cylinders for ₹ 5,00,000 and sold them to the customers for ₹ 5,90,000. Find the amount of GST payable and the amount of ITC. 5% GST is applicable.
Solution:
Given that, Janhavi Gas Agency purchased some gas cylinders for ₹ 5,00,000 and GST applicable is 5%.
∴ Input tax (ITC) = 5% of 5,00,000
= \(\frac{5}{100}\) × 5,00,000
= ₹ 25,000
Janhavi Gas Agency sold the gas cylinders for ₹ 5,90,000
∴ Output tax for Janhavi Gas Agency = 5% of 5,90,000
= \(\frac{5}{100}\) × 5,90,000
= ₹ 29,500
GST payable = Output tax – Input tax (ITC)
= 29,500 – 25,000
= ₹ 4500
∴ GST payable for Janhavi Gas Agency is ₹ 4,500 and ITC is ₹ 25,000.

Question 3.
A company dealing in mobile phones purchased mobile phones worth ₹ 5,00,000 and sold the same to customers at ₹ 6,00,000. Find the amount of ITC and amount of GST if the rate of GST is 12%.
Solution:
Given that the rate of GST applicable is 12%.
The company purchased mobile phones worth ₹ 5,00,000.
∴ Input tax (ITC) = 12% of 5,00,000
= \(\frac{12}{100}\) × 5,00,000
= ₹ 60,000
The company dealing in mobile phones sold the same to customers at ₹ 6,00,000.
∴ Output tax of the company = 12% of 6,00,000
= \(\frac{12}{100}\) × 6,00,000
= ₹ 72,000
GST payable for the company = Output tax – Input tax (ITC)
= 72,000 – 60,000
= ₹ 12,000
∴ The ITC for the company is ₹ 60,000 and GST payable is ₹ 12,000.

Question 4.
Prepare business to customers (B2C) tax invoice using given information. Write the name of supplier, address, state, Date, Invoice Number, GSTIN etc. as per your choice
Supplier: ___________
Address: ___________
State: ___________
Date: ___________
Invoice No: ___________
GSTIN: ___________
Particular: Rate of Sarees – ₹ 2750
Rate of GST 5% HSN 5407 – 2 pcs
Rate of Kurta – ₹ 750
Rate of GST 12% HSN 5408
Solution:
Supplier: M/s Swaglife Fashions
Address: 143, Shivaji Rasta, Mumbai 400001
Mobile No. 9263692111
Email: abc@gmail.com
State: Maharashtra
Date: 31/08/19
Invoice No: GST/110
GSTIN: 27ABCDE1234HIZS

∴ Rate of 1 saree = ₹ 2750
∴ Rate of 2 sarees = 2 x 2750 = ₹ 5500
∴ GST on sarees = 12% of 5500
= \(\frac{12}{100}\) × 5500
= ₹ 660
∴ CGST = SGST = ₹ 330
∴ Rate of 1 Kurta = ₹ 750
∴ GST on Kurta = 12% of 750
= \(\frac{12}{100}\) × 750
= ₹ 90
∴ CGST = SGST = ₹ 45

Question 5.
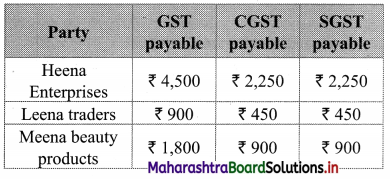
Heena Enterprise sold cosmetics worth ₹ 25,000 to Leena traders, a retailer. Leena Traders sold it further to Meena Beauty Products for ₹ 30,000. Meena Beauty Product sold it further to the customers for ₹ 40,000. The rate of GST is 18%. Find
(i) GST Payable by each party
(ii) CGST and SGST
Solution:
The trading chain,

∴ Output tax for Heena Enterprises = 18% of 25,000
= \(\frac{18}{100}\) × 25,000
= ₹ 4,500
∴ GST payable by Heena Enterprises
Now output tax for Leena traders = 18% of 30,000
= \(\frac{18}{100}\) × 30,000
= ₹ 5,400
∴ GST payable by Leena traders = Output tax – Input tax
= 5,400 – 4,500
= ₹ 900
∴ Output tax for Meena beauty products = 18% of 40,000
= \(\frac{18}{100}\) × 40,000
= ₹ 7,200
∴ GST payable by Meena beauty products = Output tax – Input tax
= 7,200 – 5,400
= ₹ 1,800

(ii) Now, CGST = SGST = \(\frac{\text { GST }}{2}\) = 9%
∴ Statement of GST payable at each stage can be tabulated as:

Question 6.
‘Chitra furnishings’ purchased tapestry (curtain cloth) for ₹ 28,00,000 and sold for ₹ 44,80,000. Rate of GST is 5%. Find
(i) Input Tax
(ii) Output Tax
(iii) ITC
(iv) CGST and SGST
Solution:
Given, that ‘Chitra furnishings’ purchased tapestry (curtain cloth) for ₹ 28,00,000 and rate of GST is 5%
(i) Input tax = 5% of 28,00,000
= \(\frac{5}{100}\) × 28,00,000
= ₹ 1,40,000
The tapestry was sold at ₹ 44,80,000

(ii) Output tax = 5% of 44,80,000
= \(\frac{5}{100}\) × 44,80,000
= ₹ 2,24,000

(iii) Now ITC = Input tax = ₹ 1,40,000
GST payable = Output tax – ITC
= 2,24,000 – 1,40,000
= ₹ 84,000

(iv) CGST = SGST = \(\frac{\text { GST Payable }}{2}\)
= \(\frac{84,000}{2}\)
= ₹ 42,000
∴ CGST = SGST = ₹ 42,000

Question 7.
Two friends ‘Aditi’ and ‘Vaishali’ went to a restaurant. They ordered 2 Masala Dosa costing ₹ 90 each 2 coffee costing ₹ 60 each and 1 sandwich costing ₹ 80. GST is charged at 5%. Find the Total amount of the bill including GST.
Solution:
Aditi and Vaishali ordered for 2 Masala Dosas, 2 Coffees and 1 Sandwich
∴ Total price of their order = 2 × 90 + 2 × 60 + 80 = ₹ 380
GST is charged at 5%
∴ GST on the total order = 5% × 380
= \(\frac{5}{100}\) × 380
= ₹ 19
∴ Total bill amount including GST = 380 + 19 = ₹ 399

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 9.1 Solutions
• 11th Commerce Maths Exercise 9.2 Solutions
• 11th Commerce Maths Exercise 9.3 Solutions
• 11th Commerce Maths Exercise 9.4 Solutions
• 11th Commerce Maths Exercise 9.5 Solutions
• 11th Commerce Maths Exercise 9.6 Solutions
• 11th Commerce Maths Exercise 9.7 Solutions
• 11th Commerce Maths Miscellaneous Exercise 9 Solutions

Probability Class 11 Commerce Maths 2 Chapter 7 Exercise 7.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Probability Ex 7.2 Questions and Answers.

Std 11 Maths 2 Exercise 7.2 Solutions Commerce Maths

Question 1.
A fair die is thrown two times. Find the chance that
(i) product of the numbers on the upper face is 12.
(ii) sum of the numbers on the upper face is 10.
(iii) sum of the numbers on the upper face is at least 10.
(iv) sum of the numbers on the upper face is 4.
(v) the first throw gives an odd number and the second throw gives a multiple of 3.
(vi) both the times die to show the same number (doublet).
Solution:
If a fair die is thrown twice, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
(i) Let A be the event that the product of the numbers on uppermost face is 12.
∴ A = {(2, 6), (3, 4), (4, 3), (6, 2)}
∴ n(A) = 4
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{4}{36}=\frac{1}{9}\)

(ii) Let B be the event that sum of the numbers on uppermost face is 10.
∴ B = {(4, 6), (5, 5), (6, 4)}
∴ n(B) = 3
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{3}{36}=\frac{1}{12}\)

(iii) Let C be the event that sum of the numbers on uppermost face is at least 10 (i.e., 10 or more than 10 which are 10 or 11 or 12)
∴ C = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), ( 6, 6)}
∴ n(C) = 6
∴ P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{6}{36}=\frac{1}{6}\)

(iv) Let D be the event that sum of the numbers on uppermost face is 4.
∴ D = {(1, 3), (2, 2), (3, 1)}
∴ n(D) = 3
∴ P(D) = \(\frac{\mathrm{n}(\mathrm{D})}{\mathrm{n}(\mathrm{S})}=\frac{3}{36}=\frac{1}{12}\)

(v) Let E be the event that 1st throw gives an odd number and 2nd throw gives multiple of 3.
∴ E = {(1, 3), (1, 6), (3, 3), (3, 6), (5, 3), (5, 6)}
∴ n(E) = 6
∴ P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}=\frac{6}{36}=\frac{1}{6}\)

(vi) Let F be the event that both times die shows same number.
∴ F = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
∴ n(F) = 6
∴ P(F) = \(\frac{\mathrm{n}(\mathrm{F})}{\mathrm{n}(\mathrm{S})}=\frac{6}{36}=\frac{1}{6}\)

Question 2.
Two cards are drawn from a pack of 52 cards. Find the probability that
(i) both are black.
(ii) both are diamonds.
(iii) both are ace cards.
(iv) both are face cards.
(v) one is a spade and the other is a non-spade.
(vi) both are from the same suit.
(vii) both are from the same denomination.
Solution:
Two cards can be drawn from a pack of 52 cards in ⁵²C₂ ways.
∴ n(S) = ⁵²C₂
(i) Let A be the event that both the cards drawn are black.
The pack of 52 cards contains 26 black cards.
∴ 2 cards can be drawn from them in ²⁶C₂ ways
∴ n(A) = ²⁶C₂
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{26} \mathrm{C}_{2}}{{ }^{52} \mathrm{C}_{2}}\)

(ii) Let B be the event that both the cards drawn are diamond.
There are 13 diamond cards in a pack of 52 cards.
∴ 2 diamond cards can be drawn from 13 diamond cards in ¹³C₂ ways
∴ n(B) = ¹³C₂
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{13} \mathrm{C}_{2}}{{ }^{52} \mathrm{C}_{2}}\)

(iii) Let C be the event that both the cards drawn are aces.
In a pack of 52 cards, there are 4 ace cards.
∴ 2 ace cards can be drawn from 4 ace cards in ⁴C₂ ways
∴ n(C) = ⁴C₂
∴ P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{4} \mathrm{C}_{2}}{{ }^{52} \mathrm{C}_{2}}\)

(iv) Let D be the event that both the cards drawn are face cards.
There are 12 face cards in a pack of 52 cards.
∴ 2 face cards can be drawn from 12 face cards in ¹²C₂ ways.
∴ n(D) = ¹²C₂
∴ P(D) = \(\frac{\mathrm{n}(\mathrm{D})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{12} \mathrm{C}_{2}}{{ }^{52} \mathrm{C}_{2}}\)

(v) Let E be the event that out of the two cards drawn one is a spade and other is non-spade.
There are 13 spade cards and 39 cards are non-spade cards in a pack of 52 cards.
∴ One spade card can be drawn from 13 spade cards in ¹³C₁ ways and one non-spade card can be drawn from 39 non-spade cards in 39C1 ways.
∴ n(E) = ¹³C₁ . ³⁹C₁
∴ P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{13} \mathrm{C}_{1} \cdot{ }^{39} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{2}}\)

(vi) Let F be the event that both the cards drawn are of the same suit.
A pack of 52 cards consists of 4 suits each containing 13 cards.
2 cards can be drawn from a suit in ¹³C₂ ways.
A suit can be selected in 4 ways.
∴ n(F) = ¹³C₂ × 4
∴ P(F) = \(\frac{\mathrm{n}(\mathrm{F})}{\mathrm{n}(\mathrm{S})}=\frac{4 \times{ }^{13} \mathrm{C}_{2}}{{ }^{52} \mathrm{C}_{2}}\)

(vii) Let G be the event that both the cards drawn are of same denominations.
A pack of cards has 13 denominations and 4 different cards for each denomination
∴ n(G) = 13 × ⁴C₂
∴ P(G) = \(\frac{\mathrm{n}(\mathrm{G})}{\mathrm{n}(\mathrm{S})}=\frac{13 \times{ }^{4} \mathrm{C}_{2}}{{ }^{52} \mathrm{C}_{2}}\)

Question 3.
Four cards are drawn from a pack of 52 cards. Find the probability that
(i) 3 are Kings and 1 is Jack.
(ii) all the cards are from different suits.
(iii) at least one heart.
(iv) all cards are club and one of them is a jack.
Solution:
4 cards can be drawn out of 52 cards in ⁵²C₄ ways.
∴ n(S) = ⁵²C₄
(i) Let A be the event that out of the four cards drawn, 3 are kings and 1 is a jack.
There are 4 kings and 4 jacks in a pack of 52 cards.
∴ 3 kings can be drawn from 4 kings in ⁴C₃ ways.
Similarly, 1 jack can be drawn out of 4 jacks in ⁴C₁ ways.
∴ Total number of ways in which 3 kings and 1 jack can be drawn is ⁴C₃ × ⁴C₁
∴ n(A) = ⁴C₃ × ⁴C₁
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{4} \mathrm{C}_{3} \times{ }^{4} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{4}}\)

(ii) Let B be the event that all the cards drawn are of different suits.
A pack of 52 cards consists of 4 suits each containing 13 cards.
∴ A card can be drawn from each suit in ¹³C₁ ways.
∴ 4 cards can be drawn from 4 different suits in ¹³C₁ × ¹³C₁ × ¹³C₁ × ¹³C₁ ways.
∴ n(B) = ¹³C₁ × ¹³C₁ × ¹³C₁ × ¹³C₁
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{13} \mathrm{C}_{1} \times{ }^{13} \mathrm{C}_{1} \times{ }^{13} \mathrm{C}_{1} \times{ }^{13} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{4}}\)

(iii) Let C be the event that out of the four cards drawn at least one is a heart.
∴ C’ is the event that all 4 cards drawn are non-heart cards.
In a pack of 52 cards, there are 39 non-heart cards.
∴ 4 non-heart cards can be drawn in ³⁹C₄ ways.
∴ n(C’) = ³⁹C₄
∴ P(C’) = \(\frac{\mathrm{n}\left(\mathrm{C}^{\eta}\right)}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{39} \mathrm{C}_{4}}{{ }^{52} \mathrm{C}_{4}}\)
∴ P(C) = 1 – P(C’) = 1 – \(\frac{{ }^{39} \mathrm{C}_{4}}{{ }^{52} \mathrm{C}_{4}}\)

(iv) Let D be the event that all the 4 cards drawn are clubs and one of them is a jack.
In a pack of 52 cards, there are 13 club cards having 1 jack card.
∴ 1 jack can be drawn in ¹C₁ way and the other 3 cards can be drawn from remaining 12 club cards in ¹²C₃ ways.
∴ n(D) = ¹²C₃ × ¹C₁
∴ P(D) = \(\frac{\mathrm{n}(\mathrm{D})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{12} \mathrm{C}_{3} \times{ }^{1} \mathrm{C}_{1}}{{ }^{52} \mathrm{C}_{4}}\)

Question 4.
A bag contains 15 balls of three different colours: Green, Black, and Yellow. A ball is drawn at random from the bag. The probability of a green ball is 1/3. The probability of yellow is 1/5.
(i) What is the probability of blackball?
(ii) How many balls are green, black, and yellow?
Solution:
(i) The bag contains 15 balls of three different colours i.e., green (G), black (B) and yellow (Y)
∴ P(G) = \(\frac{1}{3}\) and P(Y) = \(\frac{1}{5}\)
If a ball is drawn from the bag, then it can be any one of the green, black and yellow.
∴ P(G) + P(B) + P(Y) = 1
∴ \(\frac{1}{3}\) + P(B) + \(\frac{1}{5}\) = 1
∴ P(B) + \(\frac{8}{15}\) = 1
∴ P(B) = 1 – \(\frac{8}{15}\) = \(\frac{7}{15}\)
∴ Probability of black ball is \(\frac{7}{15}\)

(ii) Total number of balls = 15 and
P(G) = \(\frac{1}{3}\), P(B) = \(\frac{7}{15}\), P(Y) = \(\frac{1}{5}\)
∴ number of green balls = \(\frac{1}{3}\) × 15 = 5
number of black balls = \(\frac{7}{15}\) × 15 = 7
and number of yellow balls = \(\frac{1}{5}\) × 15 = 3.

Question 5.
A box contains 75 tickets numbered 1 to 75. A ticket is drawn at random from the box. What is the probability that the
(i) number on the ticket is divisible by 6?
(ii) number on the ticket is a perfect square?
(iii) number on the ticket is prime?
(iv) number on the ticket is divisible by 3 and 5?
Solution:
The box contains 75 tickets numbered 1 to 75.
∴ 1 ticket can be drawn from the box in ⁷⁵C₁ = 75 ways.
∴ n(S) = 75
(i) Let A be the event that number on ticket is divisible by 6.
∴ A = {6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72}
∴ n(A) = 12
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{12}{75}=\frac{4}{25}\)

(ii) Let B be the event that number on ticket is a perfect square.
∴ B = {1, 4, 9, 16, 25, 36, 49, 64}
∴ n(B) = 8
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{8}{75}\)

(iii) Let C be the event that the number on the ticket is a prime number.
∴ C = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73}
∴ n(C) = 21
∴ P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{s})}=\frac{21}{75}=\frac{7}{25}\)

(iv) Let D be the event that number on ticket is divisible by 3 and 5 i.e., divisible by L.C.M. of 3 and 5 i.e., 15
∴ D = {15, 30, 45, 60, 75}
∴ n(D) = 5
∴ P(D) = \(\frac{\mathrm{n}(\mathrm{D})}{\mathrm{n}(\mathrm{S})}=\frac{5}{75}=\frac{1}{15}\)

Question 6.
From a group of 8 boys and 5 girls, a committee of five is to be formed. Find the probability that the committee contains
(i) 3 boys and 2 girls
(ii) at least 3 boys.
Solution:
The group consists of 8 boys and 5 girls i.e., 8 + 5 = 13 persons.
A committee of 5 is to be formed from this group.
∴ 5 persons from 13 persons can be selected in ¹³C₅ ways
∴ n(S) = ¹³C₅
(i) Let A be the event that the committee contains 3 boys and 2 girls.
3 boys from 8 boys can be selected in ⁸C₃ ways and 2 girls from 5 girls can be selected in ⁵C₂ ways
∴ n(A) = ⁸C₃ . ⁵C₂
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{8} \mathrm{C}_{3} \cdot{ }^{5} \mathrm{C}_{2}}{{ }^{13} \mathrm{C}_{5}}\)

(ii) Let B be the event that the committee contains at least 3 boys (i.e., 3 boys and 2 girls or 4 boys and 1 girl or 5 boys and no girl)
∴ n(B) = ⁸C₃ . ⁵C₂ + ⁸C₄ . ⁵C₁ + ⁸C₅ . ⁵C₀
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{8} \mathrm{C}_{3} \cdot{ }^{5} \mathrm{C}_{2}+{ }^{8} \mathrm{C}_{4} \cdot{ }^{5} \mathrm{C}_{1}+{ }^{8} \mathrm{C}_{5} \cdot{ }^{5} \mathrm{C}_{0}}{{ }^{13} \mathrm{C}_{5}}\)

Question 7.
A room has three sockets for lamps. From a collection of 10 light bulbs of which 6 are defective, a person selects 3 bulbs at random and puts them in a socket. What is the probability that the room is lit?
Solution:
Total number of bulbs = 10
Number of defective bulbs = 6
∴ Number of non-defective bulbs = 4
3 bulbs can be selected out of 10 light bulbs in ¹⁰C₃ ways.
∴ n(S) = ¹⁰C₃
Let A be the event that room is lit.
∴ A’ is the event that the room is not lit.
For A’ the bulbs should be selected from the 6 defective bulbs.
This can be done in ⁶C₃ ways.
∴ n(A’) = ⁶C₃
∴ P(A’) = \(\frac{\mathrm{n}\left(\mathrm{A}^{\prime}\right)}{\mathrm{n}(\mathrm{S})}=\frac{{ }^{6} \mathrm{C}_{3}}{{ }^{10} \mathrm{C}_{3}}\)
∴ P(Room is lit) = 1 – P(Room is not lit)

Question 8.
The letters of the word LOGARITHM are arranged at random. Find the probability that
(i) Vowels are always together.
(ii) Vowels are never together.
(iii) Exactly 4 letters between G and H
(iv) begins with O and ends with T
(v) Start with a vowel and ends with a consonant.
Solution:
There are 9 letters in the word LOGARITHM.
These letters can be arranged among themselves in ⁹P₉ = 9! ways.
∴ n(S) = 9!
(i) Let A be the event that vowels are always together.
The word LOGARITHM consists of 3 vowels (O, A, I) and 6 consonants (L, G, R, T, H, M).
3 vowels can be arranged among themselves in = ³P₃ = 3! ways.
Considering 3 vowels as one group, 6 consonants and this group (i.e., altogether 7) can be arranged in ⁷P₇ = 7! ways.
∴ n(A) = 3! × 7!
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{3 ! \times 7 !}{9 !}\)

(ii) Let B be the event that vowels are never together.
Consider the following arrangement
_C_C_C_C_C_C_
6 consonants create 7 gaps.
∴ 3 vowels can be arranged in 7 gaps in ⁷P₃ ways.
Also 6 consonants can be arranged among themselves in ⁶P₆ = 6! ways.
∴ n(B) = 6! × ⁷P₃
∴ P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{6 ! \times{ }^{7} \mathrm{P}_{3}}{9 !}\)

(iii) Let C be the event that exactly 4 letters are arranged between G and H.
Consider the following arrangement
1 2 3 4 5 6 7 8 9
∴ Out of 9 places, G and H can occupy any one of following 4 positions in 4 ways.
1st and 6th, 2nd and 7th, 3rd and 8th, 4th and 9th
Now, G and H can be arranged among themselves in ²P₂ = 2! =2 ways.
Also, the remaining 7 letters can be arranged in remaining 7 places in ⁷P₇ = 7! ways.
∴ n(C) = 4 × 2 × 7! = 8 × 7! = 8!
∴ P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{8 !}{9 !}=\frac{8 !}{9 \times 8 !}=\frac{1}{9}\)

(iv) Let D be the event that word begins with O and ends with T.
Thus first and last letter can be arranged in one way each and the remaining 7 letters can be arranged in remaining 7 places in ⁷P₇ = 7! ways
∴ n(D) = 7! × 1 × 1 = 7!
∴ P(D) = \(\frac{\mathrm{n}(\mathrm{D})}{\mathrm{n}(\mathrm{S})}=\frac{7 !}{9 !}\)

(v) Let E be the event that word starts with vowel and ends with consonant.
There are 3 vowels and 6 consonants in the word LOGARITHM.
∴ The first place can be filled in 3 different ways and the last place can be filled in 6 ways.
Now, remaining 7 letters can be arranged in 7 places in ⁷P₇ = 7! ways
∴ n(E) = 3 × 6 × 7!
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{3 \times 6 \times 7 !}{9 !}\)

Question 9.
The letters of the word SAVITA are arranged at random. Find the probability that vowels are always together.
Solution:
The word SAVITA contains 6 letters. Out of 6 letters, 3 are vowels (A, A, I) and 3 are consonants (S, V, T).
6 letters in which A repeats twice can be arranged among themselves in \(\frac{6 !}{2 !}\) ways.
∴ n(S) = \(\frac{6 !}{2 !}\)
Let A be the event that vowels are always together.
3 vowels (A, A, I) can be arranged among themselves in \(\frac{3 !}{2 !}\) ways.
Considering 3 vowels as one group, 3 consonants and this group (i.e. altogether 4) can be arranged in ⁴P₄ = 4! ways.

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 7.1 Solutions
• 11th Commerce Maths Exercise 7.2 Solutions
• 11th Commerce Maths Exercise 7.3 Solutions
• 11th Commerce Maths Exercise7.4 Solutions
• 11th Commerce Maths Miscellaneous Exercise 7 Solutions

Commercial Mathematics Class 11 Commerce Maths 2 Chapter 9 Miscellaneous Exercise 9 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Miscellaneous Exercise 9 Questions and Answers.

Std 11 Maths 2 Miscellaneous Exercise 9 Solutions Commerce Maths

Question 1.
A man buys a house for ₹ 10 lakh and rents it. He puts 10% of the annual rent aside for repairs, pays ₹ 1,000 as annual taxes, and realizes 8% on his investment thereafter. Find the annual rent of the house.
Solution:
Let ₹ ‘x’ be the annual rent of the house.
The man keeps 10% of the annual rent aside for repairs.
i.e., \(\frac{10}{100}\) × x or ₹ \(\frac{x}{10}\) aside tor repairs.
In addition, he pays ₹ 1000 as annual taxes.
After incurring these expenses he is left with an amount which is 8% of his investment for the house.

∴ The annual rent of the house is ₹ 90,000.

Question 2.
Rose got 30% of the maximum marks in an examination and failed by 10 marks. However, Lily who appeared for the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?
Solution:
Let maximum marks be x
Rose scored 30% of maximum marks
i.e. Rose scored \(\frac{30}{100}\)x
Rose failed by 10 marks
∴ passing marks = \(\frac{30}{100}\)x + 10 …..(i)
Lily scored 40% of maximum marks
i.e. Lily scored \(\frac{40}{100}\)x
Lily scored 15 marks more than passing marks
∴ passing marks = \(\frac{40}{100}\)x – 15 ……(ii)
equating (i) and (ii),
\(\frac{30x}{100}\) + 10 = \(\frac{40x}{100}\) – 15
∴ 10 + 15 = \(\frac{40 x-30 x}{100}\)
∴ 10x = (25)(100)
∴ x = 250
From (i), passing marks = \(\frac{30}{100}\)(250) + 10
= 75 + 10
= 85
∴ Passing marks for the examination were 85.

Question 3.
Ankita’s Salary was reduced by 50%. Again the reduced salary was increased by 50%. Find loss in terms of percentage.
Solution:
Let Ankita’s initial salary be ₹ ‘x’.
Her salary was reduced by 50%.
∴ Ankita’s salary after reduction = x(1 – \(\frac{50}{100}\))
= x(1 – \(\frac{1}{2}\))
= \(\frac{x}{2}\)
Ankita’s reduced salary was then increased by 50%
∴ Ankita’s final salary after the increase

∴ Loss in Ankita’s salary after the decrease and increase = x – \(\frac{3 x}{4}\) = \(\frac{x}{4}\)

∴ Ankita lost 25% of her salary.

Question 4.
By selling 300 lunch boxes, a shopkeeper gains the selling price of 100 lunch boxes. Find his gain percent.
Solution:
Let ₹ x be the selling price (S.P.) of one lunch box.
∴ S.P. of 300 lunch boxes = 300x
and S.P. of 100 lunch boxes = 100x
Gain = 100x ……[given]
C.P. of 300 lunch boxes = S.P. – Gain
= 300x – 100x
= 200x

∴ The shopkeeper’s gain percentage is 50%.

Question 5.
A salesman sold an article at a loss of 10%. If the selling price has been increased by ₹ 80, there would have been a gain of 10%. What was the cost of the article?
Solution:
Let ₹ x be the cost price of the article.
S.P. of the article = x – \(\frac{10}{100}\)x = \(\frac{9x}{100}\) …….(i)
Given that, S.P. increased by ₹ 80 would have given 10% gain

∴ The cost price of the article is ₹ 400

Question 6.
Find the single discount equivalent to a series discount of 10%, 20%, and 15%.
Solution:
Let the marked price be ₹ 100
After 1st discount the price = 100(1 – \(\frac{10}{100}\)) = 90
After 2nd discount the price = 90(1 – \(\frac{20}{100}\)) = 72
After 3rd discount the price = 72(1 – \(\frac{15}{100}\)) = 61.2
∴ The selling price after 3 discounts is ₹ 61.2.
∴ Single equivalent discount = marked price – selling price
= 100 – 61.2
= ₹ 38.8
∴ The single equivalent discount is ₹ 38.8 on ₹ 100.
i.e. The single equivalent discount is 38.8%.

Question 7.
Reshma put an amount at simple interest at a certain rate for 3 years. Had it been put at 2% higher rate, she would have received ₹ 360 more. Find the sum.
Solution:
Let P and R represent the principal amount and rate of interest p.a. respectively.
Given duration = T = 3 years
Simple interest = \(\frac{\mathrm{PRT}}{100}=\frac{3 \mathrm{PR}}{100}\)
Given that, had the amount been kept at 2% more, then the gain would have been ₹ 360 more.

∴ The sum of money is ₹ 6,000.

Question 8.
The compound interest on ₹ 30000 at 7% p.a. is ₹ 4347. What is the period in years?
Solution:
Given that,
Principal (P) = ₹ 30,000
Rate of interest (R) = 7% p.a.
Compound interest = ₹ 4,347
Amount after compound interest

= \(\left(\frac{107}{100}\right)^{2}\)
= (1.07)²
∴ T = 2
∴ Amount is invested for 2 years.

Question 9.
The value of the machine depreciates at the rate of 15% p.a. It was purchased 2 years ago. Its present value is ₹ 7,225. What was the purchase price of the machine?
Solution:
Given,
Rate of depreciation = r = 15%
Number of years = n = 2 years
Present value of machine = P.V. = ₹ 7,225
The purchase price (V) of the machine can be found using

∴ The purchase price of the machine was ₹ 10,000/-.

Question 10.
A tree increases annually by \(\frac{1}{8}\) of its height. By how much will it increase after 2\(\frac{1}{2}\) years. If its length today is 8 m?
Solution:
The height of the tree today is 8m.
The height of the tree increases by \(\frac{1}{8}\)th of its height every year.
At the end of 1st year, height of the tree will be = 8 + \(\frac{1}{8}\) × 8 = 9 m
And, at the end of the 2nd year, height of the tree will be = 9 + \(\frac{1}{8}\) × 9
= 9(1 + \(\frac{1}{8}\))
= 9 × \(\frac{9}{8}\)
= \(\frac{81}{8}\)
After six more months, the height of the tree will be

∴ Increase in the height of the tree after 2\(\frac{1}{2}\) years = 10.75 – 8 = 2.75 m.

Question 11.
A building worth ₹ 1,21,000 is constructed on land worth ₹ 81,000. After how many years will the value of both be the same if land appreciates at 10% p.a and buildings depreciate at 10% p.a.
Solution:
Given,
Value of the building = V.B. = ₹ 1,21,000
Value of land = V.L. = ₹ 81,000/-
Rate of appreciation of land = rate of depreciation of building = r = 10%.
For the value of building and land to be the same.

∴ n = 2 years.
∴ After two years value of the building and land will be the same.

Question 12.
Varun invested 25%, 30%, and 20% of his savings in buying shares of three different companies, ‘A’, ‘B’, and ‘C’ which declared dividends, 10%, 12%, and 15% respectively. If his total income on account of dividends is ₹ 6,370/-, find the amount he invested in buying shares of company ‘B’.
Solution:
Let ‘T’ be Varan’s total savings.
∴ Investment of Varan in:
Company A = 25% of T = \(\frac{25}{100}\) × T = \(\frac{T}{4}\),
Company B = 30% of T = \(\frac{30}{100}\) × T = \(\frac{3T}{10}\),
Company C = 20% of T = \(\frac{20}{100}\) × T = \(\frac{T}{5}\)
Company A, B and C declared dividends 10%, 12% and 15% respectively.
∴ Dividend from company A = 10% of \(\frac{T}{4}\)

∴ Varan invested ₹ 21,000 in company B.

Question 13.
Find the annual dividend received from ₹ 25,000, 8% stock at ₹ 108.
Solution:
Amount invested = ₹ 25,000
Dividend = 8%
Assuming face value F.V. as ₹ 100
Annual income per share = \(\frac{\text { Dividend }}{100} \times \text { Face value }\)
= \(\frac{8}{100}\) × 100
= ₹ 8
Market value of the share M.V. = ₹ 108

Annual dividend on amount invested = Rate of return × amount invested
= \(\frac{7.4}{100}\) × 25,000
= ₹ 1850
∴ Annual dividend of ₹ 1,850 is received from 8% stock at ₹ 108.
Alternate approach
Assuming ₹ 25,000 as the total face value of all the shares.
Since the dividend is 8%,
Annual dividend = \(\frac{8}{100}\) × 25,000 = ₹ 2,000

Question 14.
A, B, and C enter into a partnership. A invests 3 times as much as B invests and B invests two-thirds of what ‘C’ invests. At the end of the year, the profit earned is ₹ 8,800. What is the share of ‘B’?
Solution:
Let ‘a’, ‘b’ and ‘c’ be the amounts invested by A, B and C respectively.
Given that, A invests 3 times as much as B and B invests two third of what ‘C’ invests.
∴ a = 3b and b = \(\frac{2}{3}\)c
∴ \(\frac{a}{b}=\frac{3}{1}\) and \(\frac{b}{c}=\frac{2}{3}\)
or \(\frac{a}{b}=\frac{6}{2}\) and \(\frac{b}{c}=\frac{2}{3}\)
∴ a : b = 6 : 2 and b : c = 2 : 3
∴ a : b : c = 6 : 2 : 3
Given that profit earned = ₹ 8800
∴ Share of ‘B’ in profit = \(\frac{2}{11}\) × 8800 = ₹ 1600
∴ B’share in profit is ₹ 1600.

Question 15.
The ratio of investment of two partners Santa and Banta is 11 : 12 and the ratio of their profits is 2 : 3. If Santa invested the money for 8 months, then for how much time did Banta his money?
Solution:
Let ‘x’ be the time in months for which Banta invested his money
Santa and Banta invested their money in the ratio 11 : 12.
Santa invested his money for 8 months and the ratio of their profits is 2 : 3.
∴ 11 × 8 : 12 × x = 2 : 3
∴ \(\frac{88}{12 x}=\frac{2}{3}\)
∴ x = \(\frac{88 \times 3}{2 \times 12}\)
∴ x = 11
∴ Banta invested his money for 11 months.

Question 16.
Akash, Sameer, and Sid took a house on rent for one year for ₹ 16,236. They stayed together for 4 months and then Sid left the house. After 5 more months, Sameer also left the house. How much rent should each pay?
Solution:
Let ‘R’ be the rent per month to be paid to the landlord.
Given that, Sid left the house after 4 months
∴ Rent paid by Sid = \(\frac{R}{3}\) × 4 = \(\frac{4R}{3}\)
Sameer left the house after another 5 months,
∴ Rent paid by Sameer = \(\frac{R}{2}\) × 5 + \(\frac{R}{3}\) × 4
= R(\(\frac{5}{2}+\frac{4}{3}\))
= \(\frac{23R}{6}\)
Akash stayed in the house for the entire year.
∴ Rent paid by Akash = 3R + \(\frac{R}{2}\) × 5 + \(\frac{R}{3}\) × 4
= R(3 + \(\frac{5}{2}+\frac{4}{3}\))
= \(\frac{41R}{6}\)
∴ The rent paid by the three of them, over that period of one year must be in the proportion.
\(\frac{41 \mathrm{R}}{6}: \frac{23 \mathrm{R}}{6}: \frac{4 \mathrm{R}}{3}\)
i.e. in the proportion
41 : 23 : 8 …..(multiplying throughout by \(\frac{6}{R}\))
Let x be the constant of proportionality.
Rent to be paid by Akash = ₹ 41x
Rent to be paid by Sameer = ₹ 23x
and rent to be paid by Sid = ₹ 8x
The total rent for the house was ₹ 16236.
∴ 41x + 23x + 8x = ₹ 16236
∴ 72x = 16236
∴ x = 225.5
∴ Akash should pay 41x = 41 × 225.5 = ₹ 9245.5
Sameer should pay 23x = 23 × 225.5 = ₹ 5186.5
and Sid should pay 8x = 8 × 225.5 = ₹ 1804

Question 17.
Ashwin Auto Automobiles sold 10 motorcycles. Total sales amount was ₹ 6,80,000. 18% GST is applicable. Calculate how much CGST and SGST the firm has to pay.
Solution:
Given, total sales amount for Ashwin Automobiles was ₹ 6,80,000.
18% GST is applicable.
∴ GST payable = 18% of 6,80,000
= \(\frac{18}{100}\) × 6,80,000
= ₹ 1,22,400
Now CGST = SGST = 9%
= \(\frac{\text { GST payable }}{2}\)
= \(\frac{1,22,400}{2}\)
= ₹ 61,200
∴ CGST = SGST = ₹ 61,200

Question 18.
‘Sweet 16’ A ready made garments shop for Women’s garments, purchased stock for ₹ 4,00,000 and sold that stock for ₹ 5,50,000 (12% GST is applicable) Find,
(i) Input Tax Credit
(ii) CGST and SGST paid by the firm.
Solution:
Given that, stock purchased by ‘Sweet 16’ was worth ₹ 4,00,000
GST applicable is 12%.
∴ Input tax = 12% of 4,00,000
= \(\frac{12}{100}\) × 4,00,000
= ₹ 48,000
∴ Input tax Credit (ITC) = ₹ 48,000
The garment stock was sold for ₹ 5,50,000
Output tax = 12% of 5,50,000
= \(\frac{12}{100}\) × 5,50,000
= ₹ 66,000
∴ GST payable = output tax – ITC
= 66,000 – 48,000
= ₹ 18,000
∴ CGST = SGST = \(\frac{\text { GST payable }}{2}\) = ₹ 9,000

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 9.1 Solutions
• 11th Commerce Maths Exercise 9.2 Solutions
• 11th Commerce Maths Exercise 9.3 Solutions
• 11th Commerce Maths Exercise 9.4 Solutions
• 11th Commerce Maths Exercise 9.5 Solutions
• 11th Commerce Maths Exercise 9.6 Solutions
• 11th Commerce Maths Exercise 9.7 Solutions
• 11th Commerce Maths Miscellaneous Exercise 9 Solutions

Bivariate Frequency Distribution and Chi Square Statistic Class 11 Commerce Maths 2 Chapter 4 Exercise 4.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Bivariate Frequency Distribution and Chi Square Statistic Ex 4.2 Questions and Answers.

Std 11 Maths 2 Exercise 4.2 Solutions Commerce Maths

Question 1.
The following table shows the classification of applications for secretarial and for sales positions according to gender. Calculate the value of ϰ² statistic.

Solution:
Table of observed frequencies.

Expected frequencies are given by
E_ij = \(\frac{R_{i} \times C_{j}}{N}\)
E₁₁ = \(\frac{225 \times 100}{300}\) = 75
E₁₂ = \(\frac{225 \times 200}{300}\) = 150
E₂₁ = \(\frac{75 \times 100}{300}\) = 25
E₂₂ = \(\frac{75 \times 200}{300}\) = 50
Table of expected frequencies.

Question 2.
200 teenagers were asked which takeaway food do they prefer – French fries, burgers, or pizza. The results were-

Compute ϰ² statistic.
Solution:
Table of observed frequencies.

Expected frequencies are given by
E_ij = \(\frac{\mathrm{R}_{\mathrm{i}} \times \mathrm{C}_{\mathrm{j}}}{\mathrm{N}}\)
E₁₁ = \(\frac{50 \times 24}{200}\) = 6
E₁₂ = \(\frac{50 \times 60}{200}\) = 15
E₁₃ = \(\frac{50 \times 116}{200}\) = 29
E₂₁ = \(\frac{150 \times 24}{200}\) = 18
E₂₂ = \(\frac{150 \times 60}{200}\) = 45
E₂₃ = \(\frac{150 \times 116}{200}\) = 87
Table of expected frequencies.

Question 3.
A sample of men and women who had passed their driving test either in 1st attempt or in 2nd attempt
were surveyed. Compute ϰ² statistic.

Solution:
Table of observed frequencies.

Expected frequencies are given by
E_ij = \(\frac{R_{i} \times C_{j}}{N}\)
E₁₁ = \(\frac{60 \times 40}{80}\) = 30
E₁₂ = \(\frac{60 \times 40}{80}\) = 30
E₂₁ = \(\frac{20 \times 40}{80}\) = 10
E₂₂ = \(\frac{20 \times 40}{80}\) = 10
Table of expected frequencies.

Question 4.
800 people were asked whether they wear glasses for reading with the following results.

Compute the ϰ² square statistic.
Solution:
Table of observed frequencies.

Expected frequencies are given by
E_ij = \(\frac{\mathrm{R}_{\mathrm{i}} \times \mathrm{C}_{\mathrm{j}}}{\mathrm{N}}\)
E₁₁ = \(\frac{400 \times 600}{800}\) = 300
E₁₂ = \(\frac{400 \times 200}{800}\) = 100
E₂₁ = \(\frac{400 \times 600}{800}\) = 300
E₂₂ = \(\frac{400 \times 200}{800}\) = 100
Table of expected frequencies.

Question 5.
Out of a sample of 120 persons in a village, 80 were administered a new drug for preventing influenza, and out of the 18 were attacked by influenza. Out of those who are not administered the new drug, 10 persons were not attacked by influenza:
(i) Prepare a two-way table showing frequencies.
(ii) Compute the ϰ² square statistic.
Solution:
(i) The given data can be arranged in the following table.

The observed frequency table can be prepared as follows:

(ii) Expected frequencies are given by
E_ij = \(\frac{R_{i} \times C_{j}}{N}\)
E₁₁ = \(\frac{48 \times 80}{120}\) = 32
E₁₂ = \(\frac{48 \times 40}{120}\) = 16
E₂₁ = \(\frac{72 \times 80}{120}\) = 48
E₂₂ = \(\frac{72 \times 40}{120}\) = 24
Table of expected frequencies.

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 4.1 Solutions
• 11th Commerce Maths Exercise 4.2 Solutions
• 11th Commerce Maths Miscellaneous Exercise 4 Solutions

Linear Inequations Class 11 Commerce Maths 2 Chapter 8 Miscellaneous Exercise 8 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Linear Inequations Miscellaneous Exercise 8 Questions and Answers.

Std 11 Maths 2 Miscellaneous Exercise 8 Solutions Commerce Maths

Solve the following system of inequalities graphically.

Question 1.
x ≥ 3, y ≥ 2
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 2.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 3.
2x + y ≥ 6, 3x + 4y < 12
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 4.
x + y ≥ 4, 2x – y ≤ 0
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 5.
2x – y ≥1, x – 2y ≤ -1
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 6.
x + y ≤ 6, x + y ≥ 4
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 7.
2x + y ≥ 8, x + 2y ≥ 10
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 8.
x + y ≤ 9, y > x, x ≥ 0
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 9.
5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 10.
3x + 4y ≤ 60, x +3y ≤ 30, x ≥ 0, y ≥ 0
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 11.
2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 12.
x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 13.
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 14.
3x + 2y ≤ 150, x + 4y ≥ 80, x ≤ 15, y ≥ 0, x ≥ 0
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 15.
x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 8.1 Solutions
• 11th Commerce Maths Exercise 8.2 Solutions
• 11th Commerce Maths Exercise 8.3 Solutions
• 11th Commerce Maths Miscellaneous Exercise 8 Solutions

Commercial Mathematics Class 11 Commerce Maths 2 Chapter 9 Exercise 9.5 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Ex 9.5 Questions and Answers.

Std 11 Maths 2 Exercise 9.5 Solutions Commerce Maths

Question 1.
Three partners shared the profit in a business in the ratio 5 : 6 : 7. They had partnered for 12 months, 10 months, and 8 months respectively. What was the ratio of their investments?
Solution:
Let the ratio of investments of the three partners be p : q : r.
They partnered for 12 months, 10 months, and 8 months respectively.
∴ The profit shared by the partners will be in proportion to the product of capital invested and their respective time periods.
∴ 12 × p : 10 × q : 8 × r = 5 : 6 : 7

From (i) & (ii), we have
p : q : r = 50 : 72 : 105
∴ The ratio of their investments was 50 : 72 : 105.

Question 2.
Kamala, Vimala and Pramila enter into a partnership. They invest ₹ 40,000, ₹ 80,000 and ₹ 1,20,000 respectively. At the end of the first year, Vimala withdraws ₹ 40,000, while at the end of the second year, Pramila withdraws ₹ 80,000. In what ratio will the profit be shared at the end of 3 years?
Solution:
Given that, Kamala, Vimala, and Pramila invest ₹ 40,000, ₹ 80,000, and ₹ 1,20,000 respectively.
The ratio of profits is to be calculated at the end of 3 years.
Vimala withdraws ₹ 40,000 at the end of the first year.
∴ Vimala invested ₹ 80,000 for one year and 40,000 for 2 years.
Pramila withdraws ₹ 80,000 at the end of the second year.
∴ Pramila invested ₹ 1,20,000 for two years and 40,000 for one year.
Kamala invested ₹ 40,000 for all the 3 years.
∴ The ratio of profits to be shared at the end of 3 years will be
= 40,000 × 3 : 80,000 × 1 + 40,000 × 2 : 1,20,000 × 2 + 40,000 × 1
= 1,20,000 : 1,60,000 : 2,80,000
= 12 : 16 : 28
= 3 : 4 : 7

Alternate Method:
Given that, Kamala, Vimala and Pramila invest ₹ 40,000, ₹ 80,000 & ₹ 1,20,000 respectively.
Given, information can be tabulated as:

∴ The profits to be shared at the end of 3 years will be
= 1,20,000 : 1,60,000 : 2,80,000
= 12 : 16 : 28
= 3 : 4 : 7

Question 3.
Sanjeev started a business investing ₹ 25,000 in 1999. In 2000, he invested an additional amount of ₹ 10,000 and Rajeev joined him with an amount of ₹ 35,000. In 2001, Sanjeev invested another additional amount of ₹ 10,000 and Pawan joined them with an amount of ₹ 35,000. What will be Rajeev’s share in the profit of ₹ 1,50,000 earned at the end of 3rd year from the start of the business in 1999?
Solution:
The given information can be tabulated as:

∴ The ratio of profits to be shared at the end of 3 years will be 1,05,000 : 70,000 : 35,000
i.e. in the proportion 3 : 2 : 1
Given, profit earned ₹ 1,50,000/-
∴ Rajeev’s share in the profit = \(\frac{2}{6}\) × 1,50,000 = ₹ 50,000/-

Question 4.
Teena, Leena, and Meena invest in a partnership in the ratio: 7/2, 4/3, 6/5. After 4 months, Teena increases her share by 50%. If the total profit at the end of one year is ₹ 21,600, then what is Leena’s share in the profit?
Solution:
Investment of Teena, Leena and Meena are in the ratio \(\frac{7}{2}: \frac{4}{3}: \frac{6}{5}\)
After 4 months, Teena’s share increases by 50%.
i.e. \(\frac{7}{2}+\left(\frac{7}{2} \times \frac{50}{100}\right)=\frac{7}{2}+\frac{7}{4}\)
i.e. \(\frac{21}{4}\)
The profit will be shared in the proportion of product of capitals and respective time periods in months.
i.e. \(\frac{7}{2} \times 4+\frac{21}{4} \times 8: \frac{4}{3} \times 12: \frac{6}{5} \times 12\)
i.e. 56 : 16 : \(\frac{72}{5}\)
i.e. 7 : 2 : \(\frac{9}{5}\)
i.e. in the proportion 35 : 10 : 9 …..[Multiplying throughout by 5]
Given that profit at the end of one year = ₹ 21,600/-
∴ Leena’s share in the profit = \(\frac{10}{54}\) × 21,600
= 5 × 800
= 4000
∴ Leena’s share in the profit is ₹ 4000/-.

Question 5.
Dilip and Pradeep invested amounts in the ratio 2 : 1, whereas the ratio between amounts invested by Dilip and Sudip was 3 : 2. If ₹ 1,49,500 was their profit, how much amount did Sudip receive?
Solution:
Let the amounts invested by Dilip, Pradeep and Sudip be ₹ ‘d’, ₹ ‘p’ and ₹ ‘s’ respectively.
Given that, d : p = 2 : 1
∴ d : p = 6 : 3 …..(i)
and d : s = 3 : 2
∴ d : s = 6 : 4 …..(ii)
From (i) and (ii),
d : p : s = 6 : 3 : 4
∴ The ratio of profits to be shared among Dilip, Pradeep and Sudip will be 6 : 3 : 4.
Given, profit earned = ₹ 1,49,500/-
∴ Sudip’s share in the profit = \(\frac{4}{13}\) × 1,49,500
= 4 × 11,500
= ₹ 46,000/-

Question 6.
The ratio of investments of two partners Jatin and Lalit is 11 : 12 and the ratio of their profits is 2 : 3. If Jatin invested the money for 8 months, find for how much time Lalit invested his money.
Solution:
Let ‘x’ be the time in months for which Lalit invested his money
Jatin and Lalit invested their money in the ratio 11 : 12.
Jatin invested his money for 8 months and the ratio of their profits is 2 : 3.
∴ 11 × 8 : 12 × x = 2 : 3
∴ \(\frac{88}{12 x}=\frac{2}{3}\)
∴ x = \(\frac{88 \times 3}{2 \times 12}\)
∴ x = 11
∴ Lalit invested his money for 11 months.

Question 7.
Three friends had dinner at a restaurant. When the bill was received, Alpana paid \(\frac{2}{3}\) as much as Beena paid and Beena paid \(\frac{1}{2}\) as much as Catherin paid. What fraction of the bill did Beena pay?
Solution:
Let ‘T’ be the total bill amount at the restaurant and ‘a’, ‘b’, and ‘c’ be the share of Alpana, Beena, and Catherin respectively.
Given, that Alpana paid \(\frac{2}{3}\) as much as Beena paid
∴ a = \(\frac{2}{3}\) b …..(i)
Also, Beena paid \(\frac{1}{2}\) as much as Catherin paid.
∴ b = \(\frac{1}{2}\) c
∴ c = 2b …….(ii)
∴ Three friends paid the total bill amount.
∴ a + b + c = T …..(iii)
Using (i) and (ii) in (iii), we get

Thus, Beena paid \(\left(\frac{3}{11}\right)^{\text {th }}\) fraction of the total bill amount.

Question 8.
Roy starts a business with ₹ 10,000, Shikha joins him after 2 months with 20% more investment than Roy, after 2 months Tariq joins him with 40% less than Shikha. If the profit earned by them at the end of the year is equal to twice the difference between the investment of Roy and ten times the investment of Tariq. Find the profit of Roy?
Solution:
Given that, Roy starts the business with ₹ 10,000.
Shikha joins him after 2 months with 20% more investment than Roy.
∴ Shikha’s investment = 10,000 + (10,000 × \(\frac{20}{100}\)) = ₹ 12,000
Tariq joins after two more months with an investment 40% less than Shikha.
∴ Tariq’s investment = 12,000 – (12,000 × \(\frac{40}{100}\)) = ₹ 7,200
Now, the profit will be shared in the proportion of product of capitals and respective periods in months.
i.e. 10,000 × 12 : 12,000 × 10 : 7,200 × 8
i.e. in the proportion, 25 : 25 : 12 …..(i) [Dividing throughout by 4,800]
Given that, profit at the end of the year = twice of the difference between investment of Roy and ten times the investment of Tariq.
∴ Profit = 2 [(10 × 7,200) – 10,000]
= 2[72,000 – 10,000]
= 2 × 62,000
= ₹ 1,24,000
∴ Roy’s share of profit = \(\frac{25}{62}\) × 1,24,000 …..[From (i)]
= ₹ 50,000/-

Question 9.
If 4(P’s Capital) = 6(Q’s Capital) = 10 (R’s Capital), then out of the total profit of ₹ 5,580, what is R’s share?
Solution:
Let ‘p’, ‘q’ and ‘r’ be P, Q and R’s Capital for the business respectively.
∴ 4p = 6q = 10r
L.C.M of 4, 6, 10 = 60
∴ We take 4p = 6q = 10r = 60x
∴ p = 15x, q = 10x, r = 6x
∴ p : q : r = 15 : 10 : 6
Given that total profit = ₹ 5580
R’s share in the profit = \(\frac{6}{31}\) × 5580 = ₹ 1080/-

Question 10.
A and B start a business, with A investing the total capital of ₹ 50,000, on the condition that B pays interest at the rate of 10% per annum on his half of the capital. A is a working partner and receives ₹ 1,500 per month from the total profit and any profit remaining is equally shared by both of them. At the end of the year, it was found that the income of A is twice that of B. Find the total profit for the year?
Solution:
Let ‘x’ and ‘y’ be the profits earned by A and B respectively and let ‘z’ be the total profit for the year.
A is the working partner and receives ₹ 1500 per month from the total profit.
i.e. 12 × 1500 = ₹ 18,000 at the end of the year.
The remaining profit is shared between A and B equally.
∴ y = \(\frac{z-18000}{2}\) …..(i)
Thus, profit earned by A at the end of that year is given by
x = 18000 + \(\left(\frac{z-18000}{2}\right)\)
∴ x = \(\frac{z+18000}{2}\) ……(ii)
A invests the entire capital on the condition that B pays A interest at the rate of 10% per annum on his half of the capital.
∴ At the end of the first year,
A will receive \(\frac{10}{100}\) × 25,000 i.e. ₹ 2500/- over and above his share of profit.
∴ A’s income = Profit of A + 2500 = x + 2500
Given that,
income of A = twice the income of B
∴ x + 2500 = 2y …..(iii)
Using (i) and (ii) in (iii), we get
\(\frac{z+18000}{2}\) + 2500 = 2\(\left(\frac{z-18000}{2}\right)\)
z + 18000 + 5000 = 2(z – 18000)
z + 23000 = 2z – 36000
∴ z = 59,000
∴ The total profit for the year = ₹ 59,000/-

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 9.1 Solutions
• 11th Commerce Maths Exercise 9.2 Solutions
• 11th Commerce Maths Exercise 9.3 Solutions
• 11th Commerce Maths Exercise 9.4 Solutions
• 11th Commerce Maths Exercise 9.5 Solutions
• 11th Commerce Maths Exercise 9.6 Solutions
• 11th Commerce Maths Exercise 9.7 Solutions
• 11th Commerce Maths Miscellaneous Exercise 9 Solutions

Linear Inequations Class 11 Commerce Maths 2 Chapter 8 Exercise 8.3 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Linear Inequations Ex 8.3 Questions and Answers.

Std 11 Maths 2 Exercise 8.3 Solutions Commerce Maths

Find the graphical solution for the following system of linear inequations.

Question 1.
x – y ≤ 0, 2x – y ≥ -2
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 2.
2x + 3y ≥ 12, -x + y ≤ 3, x ≤ 4, y ≥ 3
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 3.
3x + 2y ≤ 1800, 2x + 7y ≤ 1400
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 4.
0 ≤ x ≤ 350, 0 ≤ y ≤ 150
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 5.
\(\frac{x}{60}+\frac{y}{90}\) ≤ 1, \(\frac{x}{120}+\frac{y}{75}\) ≤ 1, x ≥ 0, y ≥ 0
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 6.
3x + 2y ≤ 24, 3x + y ≥ 15, x ≥ 4
Solution:
To find a graphical solution, construct the table as follows:


The shaded portion represents the graphical solution.

Question 7.
2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0
Solution:
To find a graphical solution, construct the table as follows:


Shaded portion represents the graphical solution.

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 8.1 Solutions
• 11th Commerce Maths Exercise 8.2 Solutions
• 11th Commerce Maths Exercise 8.3 Solutions
• 11th Commerce Maths Miscellaneous Exercise 8 Solutions

Bivariate Frequency Distribution and Chi Square Statistic Class 11 Commerce Maths 2 Chapter 4 Exercise 4.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Bivariate Frequency Distribution and Chi Square Statistic Ex 4.1 Questions and Answers.

Std 11 Maths 2 Exercise 4.1 Solutions Commerce Maths

Question 1.
The following table gives income (X) and expenditure (Y) of 25 families:

Find
(i) Marginal frequency distributions of income and expenditure.
(ii) Conditional frequency distribution of X when Y is between 300 – 400.
(iii) Conditional frequency distribution of Y when X is between 200 – 300.
(iv) How many families have their income ₹ 300 and more and expenses ₹ 400 and less?
Solution:
The bivariate frequency distribution table for Income (X) and Expenditure (Y) is as follows:

(i) Marginal frequency distribution of income (X):

Marginal frequency distribution of expenditure ( Y):

(ii) Conditional frequency distribution of X when Y is between 300 – 400:

(iii) Conditional frequency distribution of Y when X is between 200 – 300:

(iv) The cells 300 – 400 and 400 – 500 are having income ₹ 300 and more and the cells 200 – 300 and 300 – 400 are having expenditure ₹ 400 and less.
Now, the following table indicates the number of families satisfying the above condition.

∴ There are 17 families with income ₹ 300 and more and expenditure ₹ 400 and less.

Question 2.
Two dice are thrown simultaneously 25 times. The following pairs of observations are obtained.
(2, 3) (2, 5) (5, 5) (4, 5) (6, 4) (3, 2) (5, 2) (4, 1) (2, 5) (6, 1) (3, 1) (3, 3) (4, 3) (4, 5) (2, 5) (3, 4) (2, 5) (3, 4) (2, 5) (4, 3) (5, 2) (4, 5) (4, 3) (2, 3) (4, 1)
Prepare a bivariate frequency distribution table for the above data. Also, obtain the marginal distributions.
Solution:
Let X = Observation on 1st die
Y = Observation on 2nd die
Now, the minimum value of X is 1 and the maximum value is 6.
Also, the minimum value of Y is 1 and the maximum value is 6.
A bivariate frequency distribution can be prepared by taking X as row and Y as a column.
Bivariate frequency distribution is as follows:

Marginal frequency distribution of X:

Marginal frequency distribution of Y:

Question 3.
Following data gives the age of husbands (X) and age of wives (Y) in years. Construct a bivariate frequency distribution table and find the marginal distributions.

Find conditional frequency distribution of age of husbands when the age of wife is 23 years.
Solution:
Given, X = Age of Husbands (in years)
Y = Age of Wives (in years)
Now, the minimum value of X is 25 and the maximum value is 29.
Also, the minimum value of Y is 19 and the maximum value is 23.
Bivariate frequency distribution is as follows:

Marginal frequency distribution of X:

Marginal frequency distribution of Y:

Conditional frequency distribution of X when Y is 23:

Question 4.
Construct a bivariate frequency distribution table of the marks obtained by students in Statistics (X) and English (Y).

Construct a bivariate frequency distribution table for the above data by taking class intervals 20 – 30, 30 – 40, …. etc. for both X and Y. Also find the marginal distributions and conditional frequency distribution of Y when X lies between 30 – 40.
Solution:
Given, X = Marks in Statistics
Y = Marks in English
A bivariate frequency table can be prepared by taking class intervals 20 – 30, 30 – 40,…, etc for both X and Y.
Bivariate frequency distribution is as follows:

Marginal frequency distribution of X:

Marginal frequency distribution of Y:

Conditional frequency distribution of Y when X lies between 30 – 40:

Question 5.
Following data gives height in cms (X) and weight in kgs (Y) of 20 boys. Prepare a bivariate frequency table taking class intervals 150 – 154, 155 – 159,…etc. for X and 35 – 39, 40 – 44,…, etc for Y. Also, find
(i) Marginal frequency distributions.
(ii) Conditional frequency distribution of Y when 155 ≤ X ≤ 159.
(152,40) (160,54) (163,52) (150,35) (154,36) (160,49) (166,54) (157,38)
(159,43) (153,48) (152,41) (158,51) (155,44) (156,47) (156,43) (166,53)
(160,50) (151,39) (153,50) (158,46)
Solution:
Given X = Height in cms.
Y = Weight in kgs.
Bivariate frequency table can be prepared by taking class intervals 150 – 154, 155 – 159, …, etc for X and 35 – 39, 40 – 44,…etc for Y.
The bivariate frequency distribution table is as follows:

Marginal frequency distribution of X:

Marginal frequency distribution of Y:

Conditional frequency distribution of Y when 155 ≤ X ≤ 159:

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 4.1 Solutions
• 11th Commerce Maths Exercise 4.2 Solutions
• 11th Commerce Maths Miscellaneous Exercise 4 Solutions

Permutations and Combinations Class 11 Commerce Maths 2 Chapter 6 Exercise 6.5 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Permutations and Combinations Ex 6.5 Questions and Answers.

Std 11 Maths 2 Exercise 6.5 Solutions Commerce Maths

Question 1.
In how many different ways can 8 friends sit around a table?
Solution:
We know that ‘n’ persons can sit around a table in (n – 1)! ways
∴ 8 friends can sit around a table in 7! ways
= 7 × 6 × 5 × 4 × 3 × 2 × 1
= 5040 ways.
∴ 8 friends can sit around a table in 5040 ways.

Question 2.
A party has 20 participants and a host. Find the number of distinct ways for the host to sit with them around a circular table. How many of these ways have two specified persons on either side of the host?
Solution:
A party has 20 participants.
All of them and the host (i.e., 21 persons) can be seated at a circular table in (21 – 1)! = 20! ways.
When two particular participants be seated on either side of the host.
Host takes chair in 1 way.
These 2 persons can sit on either side of host in 2! ways
Once host occupies his chair, it is not circular permutation any more.
Remaining 18 people occupy their chairs in 18! ways.
∴ Total number of arrangement possible if two particular participants be seated on either side of the host = 2! × 18!

Question 3.
Delegates from 24 countries participate in a round table discussion. Find the number of seating arrangements where two specified delegates are
(i) always together.
(ii) never together.
Solution:
(i) Delegates of 24 countries are to participate in a round table discussion such that two specified delegates are always together.
Let us consider these 2 delegates as one unit.
They can be arranged among themselves in 2! ways.
Also, these two delegates are to be seated with 22 other delegates (i.e. total 23) which can be done in (23 – 1)! = 22! ways.
∴ The total number of arrangements if two specified delegates are always together = 22! × 2!

(ii) When 2 specified delegates are never together then, the other 22 delegates can participate in a round table discussion in (22 – 1)! = 21! ways.
∴ There are 22 places of which any 2 places can be filled by those 2 delegates who are never together.
∴ Two specified delegates can be arranged in ²²P₂ ways.
∴ Total number of arrangements if two specified delegates are never together = ²²P₂ × 21!
= \(\frac{22 !}{(22-2) !}\) × 21!
= \(\frac{22 !}{20 !}\) × 21!
= 22 × 21 × 21!
= 21 × 22 × 21!
= 21 × 22!

Question 4.
Find the number of ways for 15 people to sit around the table so that no two arrangements have the same neighbours.
Solution:
There are 15 people to sit around a table.
∴ They can be arranged in (15 – 1)! = 14! ways.
But, they should not have the same neighbour in any two arrangements.
Around the table, arrangements (i.e. clockwise and anticlockwise) coincide.

∴ Number of arrangements possible for not to have same neighbours = \(\frac{14 !}{2}\)

Question 5.
A committee of 20 members sits around a table. Find the number of arrangements that have the president and the vice president together.
Solution:
A committee of 20 members sits around a table.
But, President and Vice-president sit together.
Let us consider President and Vice-president as one unit.
They can be arranged among themselves in 2! ways.
Now, this unit with the other 18 members of the committee is to be arranged around a table, which can be done in (19 – 1)! = 18! ways.
∴ The total number of arrangements possible if President and Vice-president sit together = 18! × 2!

Question 6.
Five men, two women, and a child sit around a table. Find the number of arrangements where the child is seated
(i) between the two women.
(ii) between two men.
Solution:
(i) 5 men, 2 women, and a child sit around a table
When a child is seated between two women
∴ The two women can be seated on either side of the child in 2! ways.
Let us consider these 3 (two women and a child) as one unit.
Also, these 3 are to be seated with 5 men, (i.e. a total of 6 units) which can be done in (6 – 1)! = 5! ways.
∴ The total number of arrangements if the child is seated between two women = 5! × 2!

(ii) Two men out of 5 men can sit on either side of the child in 5P2 ways.
Let us take two men and a child as one unit.
Now these are to be arranged with the remaining 3 men and 2 women
i.e., a total of 6 events (3 + 2 + 1) is to be arranged around a round table which can be done in (6 – 1)! = 5! ways.
∴ The total number of arrangements, if the child is seated between two men = ⁵P₂ × 5!

Question 7.
Eight men and six women sit around a table. How many sitting arrangements will have no two women together?
Solution:
8 men can be seated around a table in (8 – 1)! = 7! ways.
There are 8 gaps created by 8 men’s seats.
∴ 6 Women can be seated in 8 gaps in ⁸P₆ ways
∴ Total number of arrangements so that no two women are together = 7! × ⁸P₆

Question 8.
Find the number of seating arrangements for 3 men and 3 women to sit around a table so that exactly two women are together.
Solution:

Two women sit together and one woman sits separately.
Women sitting separately can be selected in 3 ways.
The other two women occupy two chairs in one way (as it is a circular arrangement).
They can be seated on those two chairs in 2 ways. Suppose two chairs are chairs 1 and 2 shown in the figure.
Then the third woman has only two options viz chairs 4 or 5.
∴ The third woman can be seated in 2 ways. 3 men are seated in 3! ways
∴ Required number = 3 × 2 × 2 × 3!
= 12 × 6
= 72

Question 9.
Four objects in a set of ten objects are alike. Find the number of ways of arranging them in a circular order.
Solution:
Ten things can be arranged in a circular order of which 4 are alike in \(\frac{9 !}{4 !}\) ways.
∴ Required total number of arrangements = \(\frac{9 !}{4 !}\)

Question 10.
Fifteen persons sit around a table. Find the number of arrangements that have two specified persons not sitting side by side.
Solution:
Since 2 particular persons can’t be sitting side by side.
The other 13 persons can be arranged around the table in (13 – 1)! = 12!
13 people around a table create 13 gaps in which 2 people are to be seated
Number of arrangements of 2 people = ¹³P₂
∴ The total number of arrangements in which two specified persons not sitting side by side = 12! × ¹³P₂
= 12! × 13 × 12
= 13 × 12! × 12
= 12 × 13!

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 6.1 Solutions
• 11th Commerce Maths Exercise 6.2 Solutions
• 11th Commerce Maths Exercise 6.3 Solutions
• 11th Commerce Maths Exercise 6.4 Solutions
• 11th Commerce Maths Exercise 6.5 Solutions
• 11th Commerce Maths Exercise 6.6 Solutions
• 11th Commerce Maths Exercise 6.7 Solutions
• 11th Commerce Maths  Miscellaneous Exercise 6 Solutions

Probability Class 11 Commerce Maths 2 Chapter 7 Exercise 7.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Probability Ex 7.1 Questions and Answers.

Std 11 Maths 2 Exercise 7.1 Solutions Commerce Maths

Question 1.
State the sample space and n(S) for the following random experiments.
(i) A coin is tossed twice. If a second throw results in a tail, a die is thrown.
(ii) A coin is tossed twice. If a second throw results in a head, a die is thrown, otherwise, a coin is tossed.
Solution:
(i) When a coin is tossed twice, the outcomes are HH, HT, TH, TT.
A coin is tossed twice and if the second throw results in a tail, a die is thrown.
Out of the above 4 possibilities, on second throw tail occurs in two cases only i.e., HT, TT.
∴ S = {HH, TH, HT1, HT2, HT3, HT4, HT5, HT6, TT1, TT2, TT3, TT4, TT5, TT6}
∴ n(S) = 14

(ii) When a coin is tossed twice, the outcomes are HH, HT, TH, TT.
Let A be the event that the second throw results in the head when a coin is tossed twice followed by a die is thrown.
∴ A = {HH1, HH2, HH3, HH4, HH5, HH6, TH1, TH2, TH3, TH4, TH5, TH6}
The remaining outcomes i.e., HT, TT are followed by the tossing of a coin.
Let us consider this as event B.
∴ B = {HTT, HTH, TTT, TTH}
The sample space S of the experiment is A ∪ B.
∴ S = {HH1, HH2, HH3, HH4, HH5, HH6, TH1, TH2, TH3, TH4, TH5, TH6, HTT, HTH, TTT, TTH}
∴ n(S) = 16

Question 2.
In a bag, there are three balls; one black, one red, and one green. Two balls are drawn one after another with replacement. State sample space and n(S).
Solution:
The bag contains 3 balls out of which one is black (B), one is red (R) and the other one is green (G).
Two balls are drawn one after the other, with replacement, from the bag.
∴ the sample space S is given by
S = {BB, BR, BG, RB, RR, RG, GB, GR, GG}
∴ n(S) = 9

Question 3.
A coin and die are tossed. State sample space of following events.
(i) A: Getting a head and an even number.
(ii) B: Getting a prime number.
(iii) C: Getting a tail and perfect square.
Solution:
When a coin and a die are tossed the sample space S is given by
S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
(i) A: getting a head and an even number
∴ A = {H2, H4, H6}

(ii) B: getting a prime number
∴ B = {H2, H3, H5, T2, T3, T5}

(iii) C: getting a tail and a perfect square.
∴ C = {T1, T4}

Question 4.
Find the total number of distinct possible outcomes n(S) for each of the following random experiments.
(i) From a box containing 25 lottery tickets and 3 tickets are drawn at random.
(ii) From a group of 4 boys and 3 girls, any two students are selected at random.
(iii) 5 balls are randomly placed into five cells, such that each cell will be occupied.
(iv) 6 students are arranged in a row for photographs.
Solution:
(i) Let S be the event that 3 tickets are drawn at random from 25 tickets
∴ 3 tickets can be selected in ²⁵C₃ ways
∴ n(S) = ²⁵C₃
= \(\frac{25 \times 24 \times 23}{3 \times 2 \times 1}\)
= 2300

(ii) There are 4 boys and 3 girls i.e., 7 students.
2 students can be selected from these 7 students in ⁷C₂ ways.
∴ n(S) = ⁷C₂
= \(\frac{7 \times 6}{2 \times 1}\)
= 21

(iii) 5 balls have to be placed in 5 cells in such a way that each cell is occupied.
∴ The first ball can be placed into one of the 5 cells in 5 ways, the second ball placed into one of the remaining 4 cells in 4 ways.
Similarly, the third, fourth, and fifth balls can be placed in 3 ways, 2 ways, and 1 way, respectively.
∴ a total number of ways of filling 5 cells such that each cell is occupied = 5!
= 5 × 4 × 3 × 2 × 1
= 120
∴ n(S) = 120

(iv) Six students can be arranged in a row for a photograph in ⁶P₆ = 6! ways.
∴ n(S) = 6!
= 6 × 5 × 4 × 3 × 2 × 1
= 720

Question 5.
Two dice are thrown. Write favourable outcomes for the following events.
(i) P: The sum of the numbers on two dice is divisible by 3 or 4.
(ii) Q: sum of the numbers on two dice is 7.
(iii) R: sum of the numbers on two dice is a prime number.
Also, check whether
(a) events P and Q are mutually exclusive and exhaustive.
(b) events Q and R are mutually exclusive and exhaustive.
Solution:
When two dice are thrown, all possible outcomes are
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
(i) P: sum of the numbers on two dice is divisible by 3 or 4.
∴ P = {(1, 2), (1, 3), (1, 5), (2, 1), (2, 2), (2, 4), (2, 6), (3, 1), (3, 3), (3, 5), (3, 6), (4, 2), (4, 4), (4, 5), (5, 1), (5, 3), (5, 4), (6, 2), (6, 3), (6, 6)}

(ii) Q: sum of the numbers on two dice is 7.
∴ Q = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}

(iii) R: sum of the numbers on two dice is a prime number.
∴ R = {(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), (6, 5)}
(a) P and Q are mutually exclusive events as P ∩ Q = φ and
P ∪ Q = {(1, 2), (1, 3), (1, 5), (1, 6), (2, 1), (2, 2), (2, 4), (2, 5), (2, 6), (3, 1), (3, 3), (3, 4), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 6)} ≠ S
∴ P and Q are not exhaustive events as P ∪ Q ≠ S.

(b) Q ∩ R = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
∴ Q ∩ R ≠ φ
Also, Q ∪ R = {(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), (6, 5)} ≠ S
∴ Q and R are neither mutually exclusive nor exhaustive events.

Question 6.
A card is drawn at random from an ordinary pack of 52 playing cards. State the number of elements in the sample space, if
consideration of suits
(i) is not taken into account.
(ii) is taken into account.
Solution:
(i) If consideration of suits is not taken into account, then one card can be drawn from the pack of 52 playing cards in ⁵²C₁ = 52 ways.
∴ n(S) = 52

(ii) If consideration of suits is taken into account, then one card can be drawn from each suit in ¹³C₁ × ⁴C₁
= 13 × 4
= 52 ways.
∴ n(S) = 52

Question 7.
Box-I contains 3 red (R11, R12, R13) and 2 blue (B11, B12) marbles while Box-II contains 2 red (R21, R22) and 4 blue (B21, B22, B23, B24) marbles. A fair coin is tossed. If the coin turns up heads, a marble is chosen from Box-I; if it turns up tails, a marble is chosen from Box-II. Describe the sample space.
Solution:
Box I contains 3 red and 2 blue marbles i.e., (R11, R12, R13, B11, B12)
Box II contains 2 red and 4 blue marbles i.e., (R21, R22, B21, B22, B23, B24)
It is given that a fair coin is tossed and if a head comes then marble is chosen from box I otherwise it is chosen from box II
∴ the sample space is
S = {(H, R11), (H, R12), (H, R13), (H, B11), (H, B12), (T, R21), (T, R22), (T, B21), (T, B22), (T, B23), (T, B24)}

Question 8.
Consider an experiment of drawing two cards at random from a bag containing 4 cards marked 5, 6, 7, and 8. Find the sample space, if cards are drawn
(i) with replacement
(ii) without replacement.
Solution:
The bag contains 4 cards marked 5, 6, 7, and 8.
Two cards are to be drawn from this bag.
(i) If the two cards are drawn with replacement, then the sample space is
S = {(5, 5), (5, 6), (5, 7), (5, 8), (6, 5), (6, 6), (6, 7), (6,8), (7, 5), (7, 6), (7, 7), (7, 8), (8, 5), (8, 6), (8, 7), (8, 8)}

(ii) If the two cards are drawn without replacement, then the sample space is
S = {(5, 6), (5, 7), (5, 8), (6, 5), (6, 7), (6, 8), (7, 5), (7, 6), (7, 8), (8, 5), (8, 6), (8, 7)}

11th Commerce Maths Digest Pdf

• 11th Commerce Maths Exercise 7.1 Solutions
• 11th Commerce Maths Exercise 7.2 Solutions
• 11th Commerce Maths Exercise 7.3 Solutions
• 11th Commerce Maths Exercise7.4 Solutions
• 11th Commerce Maths Miscellaneous Exercise 7 Solutions