Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Ex 9.1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 9 Commercial Mathematics Ex 9.1
Question 1.
Find 77% of 580 + 34% of 390.
Solution:

Question 2.
240 candidates appeared for an examination, of which 204 passed. What is the pass percentage?
Solution:
We find the pass percentage using the unitary method

∴ The pass percentage for the examination is 85%.
Question 3.
What percent of 8.4 kg are 168 grams?
Solution:
Let 168 gms be x% of 8.4 kg
i.e., let 168 gms be \(\frac{x}{100}\) of 8400 gms
∴ 168 = \(\frac{x}{100}\) × 8400
∴ x = \(\frac{168}{84}\) = 2
∴ 168 gms is 2% of 8.4 kg.
![]()
Question 4.
If the length of a rectangle is decreased by 20%, what should be the increase in the breadth of the rectangle so that the area remains the same?
Solution:
Let x and y represent the length and breadth of the rectangle respectively.
∴ The original area of the rectangle = xy
There is a 20% decrease in length.
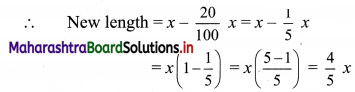
Let k % be the required increase in breadth

Given that the new and old areas should be equal.
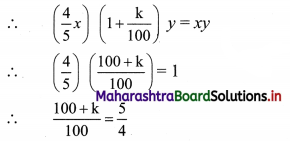
∴ 100 + k = 125
∴ k = 125 – 100 = 25
∴ Breadth should be increased by 25% so that the area remains same.
Question 5.
The price of rice increased by 20%, as a result, a person can have 5kg rice for ₹ 600. What was the initial price of rice per kg?
Solution:
A person can buy 5 kg of rice for ₹ 600 after the increase in price
∴ New price of rice = \(\frac{600}{5}\) = ₹ 120/kg …..(i)
Let ‘x’ be the initial price per kg of rice.
There is a 20% increase in the price of rice.
Thus the new price of the rice will be given as
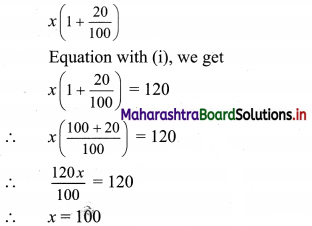
∴ The initial price of rice is ₹ 100 per kg
Question 6.
What percent is 3% of 5%?
Solution:
Let 3% be x % of 5%.
Then \(\frac{3}{100}=\frac{x}{100} \times \frac{5}{100}\)
∴ x = \(\frac{3 \times 100}{5}\) = 60
∴ 3% is 60% of 5%.
![]()
Question 7.
After availing of two successive discounts of 20% each, Madhavi paid ₹ 64 for a book. If she would have got only one discount of 20%, how much additional amount would she have paid?
Solution:
Let the price of the book be ₹ x.
After the first 20% discount, the price of the book becomes
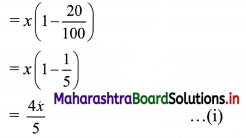
After another 20% discount, the price of the book becomes
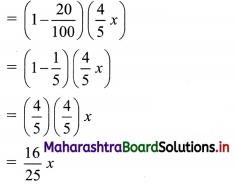
This price = ₹ 64 …..[Given]
∴ \(\frac{16}{25}\)x = 64
∴ x = 4 × 25 = 100
Thus, Amount of the book after one discount = \(\frac{4}{5}\)(100) = 80 …..[from (i)]
∴ The additional amount that Madhavi would have paid = 80 – 64 = ₹ 16
Question 8.
The price of the table is 40% more than the price of a chair. By what percent price of a chair is less than the price of a table?
Solution:
Let ₹ x and ₹ y be the price of a table and chair respectively.
The price of the table is 40% more than the price of a chair
∴ \(\frac{x-y}{y}\) × 100 = 40

We need to find by how much percent is the price of a chair less than that of a table.

∴ The price of a chair is 28.57% less than the price of a table.
![]()
Question 9.
A batsman scored 92 runs which includes 4 boundaries 5 sixes. He scored other runs by running between the wickets. What percent of his total score did he make by running between the wickets?
Solution:
Batsman scores 4 fours (boundaries) and 5 sixes in 92 runs.
Number of runs scored by fours and sixes = 4 × 4 + 5 × 6 = 46
∴ 92 – 46 = 46
Let 46 be x% of 92.
Then 46 = \(\frac{x}{100}\) × 92
∴ x = \(\frac{46 \times 100}{92}=\frac{100}{2}\) = 50
∴ 50% of the total runs were scored by running between the wickets.