Commercial Mathematics Class 11 Commerce Maths 2 Chapter 9 Miscellaneous Exercise 9 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Miscellaneous Exercise 9 Questions and Answers.
Std 11 Maths 2 Miscellaneous Exercise 9 Solutions Commerce Maths
Question 1.
A man buys a house for ₹ 10 lakh and rents it. He puts 10% of the annual rent aside for repairs, pays ₹ 1,000 as annual taxes, and realizes 8% on his investment thereafter. Find the annual rent of the house.
Solution:
Let ₹ ‘x’ be the annual rent of the house.
The man keeps 10% of the annual rent aside for repairs.
i.e., \(\frac{10}{100}\) × x or ₹ \(\frac{x}{10}\) aside tor repairs.
In addition, he pays ₹ 1000 as annual taxes.
After incurring these expenses he is left with an amount which is 8% of his investment for the house.

∴ The annual rent of the house is ₹ 90,000.
Question 2.
Rose got 30% of the maximum marks in an examination and failed by 10 marks. However, Lily who appeared for the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?
Solution:
Let maximum marks be x
Rose scored 30% of maximum marks
i.e. Rose scored \(\frac{30}{100}\)x
Rose failed by 10 marks
∴ passing marks = \(\frac{30}{100}\)x + 10 …..(i)
Lily scored 40% of maximum marks
i.e. Lily scored \(\frac{40}{100}\)x
Lily scored 15 marks more than passing marks
∴ passing marks = \(\frac{40}{100}\)x – 15 ……(ii)
equating (i) and (ii),
\(\frac{30x}{100}\) + 10 = \(\frac{40x}{100}\) – 15
∴ 10 + 15 = \(\frac{40 x-30 x}{100}\)
∴ 10x = (25)(100)
∴ x = 250
From (i), passing marks = \(\frac{30}{100}\)(250) + 10
= 75 + 10
= 85
∴ Passing marks for the examination were 85.
![]()
Question 3.
Ankita’s Salary was reduced by 50%. Again the reduced salary was increased by 50%. Find loss in terms of percentage.
Solution:
Let Ankita’s initial salary be ₹ ‘x’.
Her salary was reduced by 50%.
∴ Ankita’s salary after reduction = x(1 – \(\frac{50}{100}\))
= x(1 – \(\frac{1}{2}\))
= \(\frac{x}{2}\)
Ankita’s reduced salary was then increased by 50%
∴ Ankita’s final salary after the increase
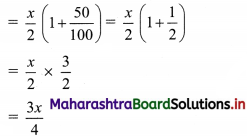
∴ Loss in Ankita’s salary after the decrease and increase = x – \(\frac{3 x}{4}\) = \(\frac{x}{4}\)

∴ Ankita lost 25% of her salary.
Question 4.
By selling 300 lunch boxes, a shopkeeper gains the selling price of 100 lunch boxes. Find his gain percent.
Solution:
Let ₹ x be the selling price (S.P.) of one lunch box.
∴ S.P. of 300 lunch boxes = 300x
and S.P. of 100 lunch boxes = 100x
Gain = 100x ……[given]
C.P. of 300 lunch boxes = S.P. – Gain
= 300x – 100x
= 200x
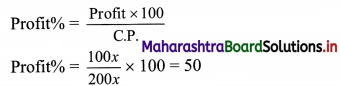
∴ The shopkeeper’s gain percentage is 50%.
Question 5.
A salesman sold an article at a loss of 10%. If the selling price has been increased by ₹ 80, there would have been a gain of 10%. What was the cost of the article?
Solution:
Let ₹ x be the cost price of the article.
S.P. of the article = x – \(\frac{10}{100}\)x = \(\frac{9x}{100}\) …….(i)
Given that, S.P. increased by ₹ 80 would have given 10% gain
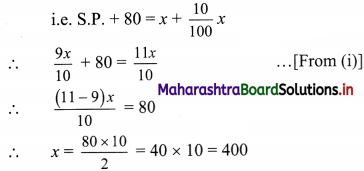
∴ The cost price of the article is ₹ 400
Question 6.
Find the single discount equivalent to a series discount of 10%, 20%, and 15%.
Solution:
Let the marked price be ₹ 100
After 1st discount the price = 100(1 – \(\frac{10}{100}\)) = 90
After 2nd discount the price = 90(1 – \(\frac{20}{100}\)) = 72
After 3rd discount the price = 72(1 – \(\frac{15}{100}\)) = 61.2
∴ The selling price after 3 discounts is ₹ 61.2.
∴ Single equivalent discount = marked price – selling price
= 100 – 61.2
= ₹ 38.8
∴ The single equivalent discount is ₹ 38.8 on ₹ 100.
i.e. The single equivalent discount is 38.8%.
![]()
Question 7.
Reshma put an amount at simple interest at a certain rate for 3 years. Had it been put at 2% higher rate, she would have received ₹ 360 more. Find the sum.
Solution:
Let P and R represent the principal amount and rate of interest p.a. respectively.
Given duration = T = 3 years
Simple interest = \(\frac{\mathrm{PRT}}{100}=\frac{3 \mathrm{PR}}{100}\)
Given that, had the amount been kept at 2% more, then the gain would have been ₹ 360 more.

∴ The sum of money is ₹ 6,000.
Question 8.
The compound interest on ₹ 30000 at 7% p.a. is ₹ 4347. What is the period in years?
Solution:
Given that,
Principal (P) = ₹ 30,000
Rate of interest (R) = 7% p.a.
Compound interest = ₹ 4,347
Amount after compound interest

= \(\left(\frac{107}{100}\right)^{2}\)
= (1.07)2
∴ T = 2
∴ Amount is invested for 2 years.
Question 9.
The value of the machine depreciates at the rate of 15% p.a. It was purchased 2 years ago. Its present value is ₹ 7,225. What was the purchase price of the machine?
Solution:
Given,
Rate of depreciation = r = 15%
Number of years = n = 2 years
Present value of machine = P.V. = ₹ 7,225
The purchase price (V) of the machine can be found using

∴ The purchase price of the machine was ₹ 10,000/-.
Question 10.
A tree increases annually by \(\frac{1}{8}\) of its height. By how much will it increase after 2\(\frac{1}{2}\) years. If its length today is 8 m?
Solution:
The height of the tree today is 8m.
The height of the tree increases by \(\frac{1}{8}\)th of its height every year.
At the end of 1st year, height of the tree will be = 8 + \(\frac{1}{8}\) × 8 = 9 m
And, at the end of the 2nd year, height of the tree will be = 9 + \(\frac{1}{8}\) × 9
= 9(1 + \(\frac{1}{8}\))
= 9 × \(\frac{9}{8}\)
= \(\frac{81}{8}\)
After six more months, the height of the tree will be

∴ Increase in the height of the tree after 2\(\frac{1}{2}\) years = 10.75 – 8 = 2.75 m.
Question 11.
A building worth ₹ 1,21,000 is constructed on land worth ₹ 81,000. After how many years will the value of both be the same if land appreciates at 10% p.a and buildings depreciate at 10% p.a.
Solution:
Given,
Value of the building = V.B. = ₹ 1,21,000
Value of land = V.L. = ₹ 81,000/-
Rate of appreciation of land = rate of depreciation of building = r = 10%.
For the value of building and land to be the same.

∴ n = 2 years.
∴ After two years value of the building and land will be the same.
![]()
Question 12.
Varun invested 25%, 30%, and 20% of his savings in buying shares of three different companies, ‘A’, ‘B’, and ‘C’ which declared dividends, 10%, 12%, and 15% respectively. If his total income on account of dividends is ₹ 6,370/-, find the amount he invested in buying shares of company ‘B’.
Solution:
Let ‘T’ be Varan’s total savings.
∴ Investment of Varan in:
Company A = 25% of T = \(\frac{25}{100}\) × T = \(\frac{T}{4}\),
Company B = 30% of T = \(\frac{30}{100}\) × T = \(\frac{3T}{10}\),
Company C = 20% of T = \(\frac{20}{100}\) × T = \(\frac{T}{5}\)
Company A, B and C declared dividends 10%, 12% and 15% respectively.
∴ Dividend from company A = 10% of \(\frac{T}{4}\)

∴ Varan invested ₹ 21,000 in company B.
Question 13.
Find the annual dividend received from ₹ 25,000, 8% stock at ₹ 108.
Solution:
Amount invested = ₹ 25,000
Dividend = 8%
Assuming face value F.V. as ₹ 100
Annual income per share = \(\frac{\text { Dividend }}{100} \times \text { Face value }\)
= \(\frac{8}{100}\) × 100
= ₹ 8
Market value of the share M.V. = ₹ 108
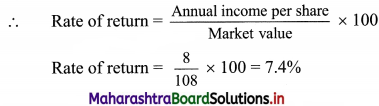
Annual dividend on amount invested = Rate of return × amount invested
= \(\frac{7.4}{100}\) × 25,000
= ₹ 1850
∴ Annual dividend of ₹ 1,850 is received from 8% stock at ₹ 108.
Alternate approach
Assuming ₹ 25,000 as the total face value of all the shares.
Since the dividend is 8%,
Annual dividend = \(\frac{8}{100}\) × 25,000 = ₹ 2,000
Question 14.
A, B, and C enter into a partnership. A invests 3 times as much as B invests and B invests two-thirds of what ‘C’ invests. At the end of the year, the profit earned is ₹ 8,800. What is the share of ‘B’?
Solution:
Let ‘a’, ‘b’ and ‘c’ be the amounts invested by A, B and C respectively.
Given that, A invests 3 times as much as B and B invests two third of what ‘C’ invests.
∴ a = 3b and b = \(\frac{2}{3}\)c
∴ \(\frac{a}{b}=\frac{3}{1}\) and \(\frac{b}{c}=\frac{2}{3}\)
or \(\frac{a}{b}=\frac{6}{2}\) and \(\frac{b}{c}=\frac{2}{3}\)
∴ a : b = 6 : 2 and b : c = 2 : 3
∴ a : b : c = 6 : 2 : 3
Given that profit earned = ₹ 8800
∴ Share of ‘B’ in profit = \(\frac{2}{11}\) × 8800 = ₹ 1600
∴ B’share in profit is ₹ 1600.
![]()
Question 15.
The ratio of investment of two partners Santa and Banta is 11 : 12 and the ratio of their profits is 2 : 3. If Santa invested the money for 8 months, then for how much time did Banta his money?
Solution:
Let ‘x’ be the time in months for which Banta invested his money
Santa and Banta invested their money in the ratio 11 : 12.
Santa invested his money for 8 months and the ratio of their profits is 2 : 3.
∴ 11 × 8 : 12 × x = 2 : 3
∴ \(\frac{88}{12 x}=\frac{2}{3}\)
∴ x = \(\frac{88 \times 3}{2 \times 12}\)
∴ x = 11
∴ Banta invested his money for 11 months.
Question 16.
Akash, Sameer, and Sid took a house on rent for one year for ₹ 16,236. They stayed together for 4 months and then Sid left the house. After 5 more months, Sameer also left the house. How much rent should each pay?
Solution:
Let ‘R’ be the rent per month to be paid to the landlord.
Given that, Sid left the house after 4 months
∴ Rent paid by Sid = \(\frac{R}{3}\) × 4 = \(\frac{4R}{3}\)
Sameer left the house after another 5 months,
∴ Rent paid by Sameer = \(\frac{R}{2}\) × 5 + \(\frac{R}{3}\) × 4
= R(\(\frac{5}{2}+\frac{4}{3}\))
= \(\frac{23R}{6}\)
Akash stayed in the house for the entire year.
∴ Rent paid by Akash = 3R + \(\frac{R}{2}\) × 5 + \(\frac{R}{3}\) × 4
= R(3 + \(\frac{5}{2}+\frac{4}{3}\))
= \(\frac{41R}{6}\)
∴ The rent paid by the three of them, over that period of one year must be in the proportion.
\(\frac{41 \mathrm{R}}{6}: \frac{23 \mathrm{R}}{6}: \frac{4 \mathrm{R}}{3}\)
i.e. in the proportion
41 : 23 : 8 …..(multiplying throughout by \(\frac{6}{R}\))
Let x be the constant of proportionality.
Rent to be paid by Akash = ₹ 41x
Rent to be paid by Sameer = ₹ 23x
and rent to be paid by Sid = ₹ 8x
The total rent for the house was ₹ 16236.
∴ 41x + 23x + 8x = ₹ 16236
∴ 72x = 16236
∴ x = 225.5
∴ Akash should pay 41x = 41 × 225.5 = ₹ 9245.5
Sameer should pay 23x = 23 × 225.5 = ₹ 5186.5
and Sid should pay 8x = 8 × 225.5 = ₹ 1804
![]()
Question 17.
Ashwin Auto Automobiles sold 10 motorcycles. Total sales amount was ₹ 6,80,000. 18% GST is applicable. Calculate how much CGST and SGST the firm has to pay.
Solution:
Given, total sales amount for Ashwin Automobiles was ₹ 6,80,000.
18% GST is applicable.
∴ GST payable = 18% of 6,80,000
= \(\frac{18}{100}\) × 6,80,000
= ₹ 1,22,400
Now CGST = SGST = 9%
= \(\frac{\text { GST payable }}{2}\)
= \(\frac{1,22,400}{2}\)
= ₹ 61,200
∴ CGST = SGST = ₹ 61,200
Question 18.
‘Sweet 16’ A ready made garments shop for Women’s garments, purchased stock for ₹ 4,00,000 and sold that stock for ₹ 5,50,000 (12% GST is applicable) Find,
(i) Input Tax Credit
(ii) CGST and SGST paid by the firm.
Solution:
Given that, stock purchased by ‘Sweet 16’ was worth ₹ 4,00,000
GST applicable is 12%.
∴ Input tax = 12% of 4,00,000
= \(\frac{12}{100}\) × 4,00,000
= ₹ 48,000
∴ Input tax Credit (ITC) = ₹ 48,000
The garment stock was sold for ₹ 5,50,000
Output tax = 12% of 5,50,000
= \(\frac{12}{100}\) × 5,50,000
= ₹ 66,000
∴ GST payable = output tax – ITC
= 66,000 – 48,000
= ₹ 18,000
∴ CGST = SGST = \(\frac{\text { GST payable }}{2}\) = ₹ 9,000
11th Commerce Maths Digest Pdf
- 11th Commerce Maths Exercise 9.1 Solutions
- 11th Commerce Maths Exercise 9.2 Solutions
- 11th Commerce Maths Exercise 9.3 Solutions
- 11th Commerce Maths Exercise 9.4 Solutions
- 11th Commerce Maths Exercise 9.5 Solutions
- 11th Commerce Maths Exercise 9.6 Solutions
- 11th Commerce Maths Exercise 9.7 Solutions
- 11th Commerce Maths Miscellaneous Exercise 9 Solutions