Class 10

Balbharti Maharashtra State Board Class 10 History Solutions Chapter 4 History of Indian Arts Notes, Textbook Exercise Important Questions and Answers.

Std 10 History Chapter 4 Question Answer History of Indian Arts Maharashtra Board

Class 10 History Chapter 4 History of Indian Arts Question Answer Maharashtra Board

History Class 10 Chapter 4 Question Answer Maharashtra Board

Question 1.
(A) Choose the correct option from the given options and complete the statement.
(1) The arts of painting and sculpting are …………….……. .
(a) visual arts
(b) performing arts
(c) folk arts
(d) classical arts
Answer:
(a) visual arts

(2) The …………….……. saw the rise of Mathura school.
(a) Kushana period
(b) Gupta period
(c) Rashtrakuta period
(d) Maurya period
Answer:
(a) Kushana period

(B) Identify and write the wrong pair in the following set.
(1) Qutub Minar – Mehrauli
(2) Gol Gumbaz – Vijapur
(3) Chhatrapati Shivaji Maharaj Railway Terminus – Delhi
(4) Taj Mahal – Agra
Answer:
(3) Wrong Pair: Chhatrapati Shivaji Maharaj Railway Terminus – Delhi

Question 2.
Write short notes.
(1) Art
Answer:

• It is a natural instinct in humans to share their emotions, experience, wisdom acquired with others.
• This act of sharing, results in beautiful creation, called an ‘Art’.
• Art gives us an experience of different elements.
• These elements are expressed through sculpture, singing, painting and dance.
• The crucial factors which are at the root of artistic creation are the imagination power of the artist.
• The sensibility state of his emotions and skills.

(2) Hemadpanti style
Answer:

1. Hemadpanti temples were primarily built in 12th- 13th century.
2. The main feature of this style is its masonry. The walls are built without mortar, by locking stones, using the tenon and mortise joints technique.
3. Hemadpanti temples are built in square¬shaped and star-shaped designs. In the star¬shaped plan, the outer walls of a temple has a zigzag design which gives interesting effect of alternating light and shadow.
4. Tourists are attracted to see these beautiful designs. Hemadpanti temples are found at several places in Maharashtra.

(3) Maratha style of painting
Answer:

• The Maratha style of paintings began to develop in the later half of the 17th century.
• This style consists of coloured paintings which are in form of murals and miniatures used in manuscripts.
• Murals of Maratha style can be seen at the entrance of old wadas, in drawing rooms and on the ceilings of the temples.
• The Maratha style was influenced by the Rajput and European style of paintings.
• The Maratha style of paintings helps us to understand various things about the times in which it was developed such as lifestyle, attires, customs, etc.

Question 3.
Explain the following statements with reasons.
(1) An expert with deep understanding of art history is required in the art market.
Answer:

• There is an independent market for purchase and sale of art objects.
• The authenticity of the object, its standards can only be assessed by an expert.
• Only an artist can know the exact value of an art object or ensure if it is genuine or not.
• So, when art objects are assessed all the above points are considered.
• This requires special expertise. Hence an expert with deep understanding of art history is required for this task.

(2) It is necessary to preserve the tradition like Chitrakathi, which is on the verge of extinction.
Answer:

1. The stories from Ramayana or Mahabharata narrated with the help of wooden puppets and paintings is known as Chitrakathi or Pinguli tradition.
2. It is preserved by the Thakur community.
3. As the Chitrakathi pictures are drawn on papers and painted using col9urs made from natural substances, they deteriorate rapidly if not maintained.
4. Therefore it is necessarý to preserve the tradition like Chitrakathi as it is part of our glorious cultural heritage and is on the verge of extinction.

Question 4.
Complete the following table.

Temple Architecture Naagara	Naagara	Draavida	Hemadpanti
Characteristics
Examples

Answer:

Styles of Temple Architecture	Nagara	Dravid	Hemadpanti
Characteristics	(1) Series of miniature towers are arranged (2) Towers taper towards the top (3) Tower appears to be continuously rising from the base of the temple to the top.	(1) Temple towers resembled pyramid shape. (2) Gopura (main entrance) was large and magnificent than the tower. (3) Mythological stories were carved on walls and ceilings.	(1) The temple structure was star-shaped with outer walls having zigzag design. (2) The walls were built without using any mortar. (3) The stones were locked by using the technique of tenon and mortise joints.
Examples	(1) Konark Sun Temple (2) Lingraj Temple of Bhubaneshwar (3) Kandariya Mahadev temple at Khajuraho	(1) Meenakshi Temple at Madurai (2) Chariot Temple at Mahabalipuram (3) Brihadeeshvara temple at Thanjavur (4) Tirupati Temple	(1) Gondeshwar temple at Sinnar (2) Ambreshwar temple at Ambarnath (3) Aundha Nagnath temple at Hingoli (4) Kopeshwar temple at Khidrapur

Question 5.
Answer the following questions in detail.
(1) Write in detail about folk styles of painting.
Answer:

• The art of rock painting dates back to Stone Age. These rock paintings have preserved the style of folk painting.
• Rock paintings usually depict humans, animals and geometric figures.
• The style of rock paintings seems to be changing according to the cultural changes from Stone age to the beginning of agriculture.
• Man started depicting flora and fauna in a different style and also figures.
• There was difference in colours too. Black and Red were used in rock paintings.
• Colours extracted from natural substances were used.
• The man started using the knowledge he got from the surroundings and nature and depicted it in the pictures.
• In the later stage of development, man started customs such as decorating the walls and courtyards (Rangawali).
• By drawing various figures and symbols or using panels of painting to narrate stories. It helped in the development of folk paintings.

(2) Explain the characteristics of the Islamic architecture in India by giving examples.
Answer:
A blend of Persian, Central Asian, Arabic and pre Islamic native Indian styles created the Islamic architecture of India.
Following are the characteristics of Islamic architecture developed in the medieval period under the patronage of Muslim sultanates:

• Built in Islamic style, the Kutub Minor is the highest minaret in the world. It is 73 metres (240 ft) in height.
• The Taj Mahal built by the Mughal emperor Shah Jah’an is looked’ upon as the paramount* example of Islamic’architecture.
• The Gol Gumbaz at Bijapur in Karnataka built in 17th century is known for its echo which can be heard many times.
• The forts at Agra and Delhi are known for their massive walls of redstone.
• The walls are interrupted by graceful curves and lofty bastions. Red sandstone, domes, arches, minarets, magnificance all combined form characteristics of Islamic architecture.

(3) What kind of professional opportunities are available in the field of arts?
Answer:
Various opportunities are available in different fields of art:

1. Art historian can work in field of journalism. Art students can work in museums, archives, libraries. Information Technology, archaeological research and Indology contribute to recently developed fields like Heritage Management and Cultural Tourism.
2. An expert in art is required to assess the exact value of an art object and also in its sale and purchase. Experts are required in the field of manufacturing of objects for home decoration.
3. Ornaments, artistic creations of metals, earthen pots with colourful designs, objects made from cane and bamboo, beautiful glass objects, attractive textiles and clothing all come are under applied arts.
4. These fields require experts in manufacturing and sales. Hence many opportunities of employment are available in the field of arts.

(4) Observe the illustration of Warli painting on p. 23 and write about:
(a) Depiction of nature
(b) Drawings of human figures
(c) Depiction of occupations
(d) Houses
Answer:

The traditions of Warli painting and Pingul or Chitra Katha in Maharashtra are among the finest examples of folk style of paintings. Divya Somya Mashe, the artist in Thane district has played a great role in making the Warli style of paintings very popular. He has been honored with a number of national and international awards for his paintings. In the year 2011, he was awarded ‘Padmashree’.

Name of the painting tradition:
This picture is from Warli tradition.

Nature’s description:
Artist has sketched trees, leaves and shrubs in the picture. A fish is also drawn.

Sketch of human activities:
Women dancing in a circular pattern is also sketched in the picture.

Designing features:
Pictures of men, women and children are sketched. Warli paintings do not portray the exact objects but only a sketch. Human figures are drawn with the help of a triangle, circle and square which are placed at the tip.

Project
(1) Collect additional information of the World Heritage sites in India.
(2) Observe the sculptors or image-makers at work in your locality and interview them.
Answer:

Memory Map

Question 6.
Complete the sentences by choosing a correct option:
(a) Lalit Kala is also known as …………………… .
(a) Folk art
(b) Aangik Kala
(c) Drik Kala
(d) Nagara art
Answer:
(b) Aangik Kala

(b) Jivya Somya Mashe, an artist in the Thane district played a great role in making the …………………… style of painting very popular.
(a) Chitrakathi
(b) Maratha
(c) Warli
(d) Classical
Answer:
(c) Warli

(c) The Chalukya King, Someshvara, mentioned in …………………… book the tradition of Chitrakathi.
(a) Natyashastra
(b) Kitab-e-Navras
(c) Paintings of Ajanta
(d) Manasollas
Answer:
(d) Manasollas.

(d) The ancient Indian texts mentioned …………………………. styles of Classical Art.
(a) Nine
(b) Thirty-six
(c) Sixty-four
(d) Eighty-four
Answer:
(c) Sixty-four

(e) During the reign, of Mughal Emperor …………………………., the Mughal miniature style showing a blend of Indian and Persian was developed.
(a) Akbar
(b) Aurangzeb
(c) Jahangir
(d) Babur
Answer:
(a) Akbar

(f) Some of the drawings of Gangaram Tambat are preserved in …………………………. university.
(a) Stanford
(b) Cambridge
(c) Oxford
(d) Yale
Answer:
(d) Yale

(g) …………………………. is the characteristic of European style of painting.
(a) Sketching
(b) Exact portrayal of object
(c) Natural colours
(d) Landscape
Answer:
(b) Exact portrayal of object

(h) Replicas of Ajanta paintings was made by
(a) Pestonji Bomanji
(b) Gangaram Tambat
(c) Raja Ravi Verma
(d) James Wales
Answer:
(a) Pestonji Bomanji.

(i) The lion capital of the Ashoka pillar found at …………………………. is the national emblem of India.
(a) Bodhgaya
(b) Patliputra
(c) Sanchi
(d) Sarnath
Answer:
(d) Sarnath

(j) The stupa at …………………………. in Indonesia is the largest stupa in the world.
(a) Ubud
(b) Sigiran
(c) Borobudur
(d) Palembang
Answer:
(c) Borobudur

(k) The …………………………. school of art laid the foundation of Indian iconography.
(a) Gandhar
(b) Nagara
(c) Dravid
(d) Mathura
Answer:
(d) Mathura

(l) The temple architecture developed in India around 4th century C.E. during the …………………………. period.
(a) Kushana
(b) Rashtrakuta
(c) Gupta
(d) Chola
Answer:
(c) Gupta

(m) …………………………. is a blend of Nagara style of architecture of North India and Dravid style of South India.
(a) Gandhar
(b) Mathura
(c) Bhoomija
(d) Vesara
Answer:
(d) Vesara.

(n) The two main branches of the Indian classical music are ………………………… .
(a) Folk music and Vocal
(b) Dadraa and Thumri
(c) Bhajans and Qawwalis
(d) Hindustani music and Carnatic music
Answer:
(d) Hindustani music and Carnatic music

(o) The text of …………………………. written by Bharatmuni is supposed to be the earliest one discussing music and theatre.
(a) Manasollas
(b) Abhilasha Chintamani
(c) Natyashastra
(d) Rasratnakar
Answer:
(c) Natyashastra

(p) Every year the …………………………. festival is held in Pune.
(a) Kala Ghoda
(b) Gunidas
(c) Savai Gandharva
(d) Gharapuri
Answer:
(c) Savai Gandharva

(q) The ruler of Bijapur, Ibrahim Adilshah wrote …………………………. text in Persian language.
(a) Tuzuk-i-Babari
(b) Padmavat
(c) Akbarnama
(d) Kitab-e-Navras
Answer:
(d) Kitab- e-Navras

(r) …………………………. is a prominent name among artists who created a new style of fusion of Indian and Western dance.
(a) Pandit Shivkumar Sharma
(b) Pandit Hariprasad Chaurasia
(c) Pandit Uday Shankar
(d) Ustad Zakir Hussain
Answer:
(a) Pandit Uday Shankar.

Question 7.
Identify the wrong pair in the following and write it:
(1)

Architectural structure	Place
(1) Kutub Minar	(a) Mehrauli
(2) Gol Gumbaz	(b) Bijapur
(3) Chhatrapati Shivaji Maharaj Railway Terminus	(c) Delhi
(4) Taj Mahal	(d) Agra

Answer:
Wrong pair: Chhatrapati Shivaji Maharaj Railway Terminus – Delhi

(2)

Picture	Style
(1) Murals seen in the old wadas at Wai, Menavali	(a) Miniature style
(2) Bhimbetka	(b) Folk painting
(3) Pictures narrating Ramayana and Mahabharata story	(c) Chitrakathi
(4) Painting style in Thane district	(d) Warli painting

Answer:
Wrong pair: Murals seen in the old wadas at Wai, Menavali – Miniature style

(3)

Architectural structure	Style
(1) Chhatrapati Shivaji Maharaj Railway Terminus	(a) Gothic architecture
(2) Gol Gumbaz	(b) Muslim architecture
(3) Temples in South India	(c) Nagara architecture
(4) Gondeshwar Temple	(d) Hemadpanti architecture

Answer:
Wrong pair: Temples in South India – Nagara architecture

(4)

Monument	Emperors
(1) Completed Kutub Minar	(a) Altmash
(2) Construction of Taj Mahal	(b) Emperor Akbar
(3) Gol Gumbaz	(c) Mohammed Adilshah
(4) Built Sanchi Stupa	(d) Emperor Ashoka

Answer:
Wrong pair: Construction of Taj Mahal – Emperor Akbar

Question 3.
Do as directed:
(A) Complete the following concept chart:
(1)

Answer:

(2)

Answer:

(3)

Answer:

(4)

Answer:

(5)

Answer:

(6)

Answer:

(B) Prepare a flow chart on the Development of Indian Iconography.
Answer:

Question 8.
Explain the following concepts:
(a) Style in Art:
Answer:

• Every artist has its own method of working which becomes his style.
• When this style is repeated by several artists over a prolonged period of time it becomes a tradition.
• This tradition is known as an art ‘style’.
• Such traditions are established in every art style. Various art styles are developed over the years in every culture.
• The specific art styles indicate the characteristic of a certain region and period.
• They help us to learn the history of arts of these civilizations.

(b) Classical Style of Paintings:
Answer:

• Art which is expressed within an established frame of consistent rules is known as classical art. The ancient Indian texts mentioned altogether 64 arts.
• The aft of painting is mentioned as alekhyam or alekhya vidya in these texts.
• This alekhya vidya has six main aspects of paintings (Shadange).
• They are shapes and forms (Roopbheda), expressions (Bhava).
• Proportionate depiction of various features of an image (Pramana).
• Aesthetics (Lavanyayojana), resemblance to reality (Sadrushyata) and colour composition (Varnikabhang).
• Agama text of Jainism and in Puranas various arts like painting, sculpting are explained in context of temple architecture.

Question 9.
Write short notes:
(a) Chitrakathi:
Answer:

1. The tradition of narrating stones from Ramayana and Mahabharata with the help of wooden puppets and paintings is known as Chitrakathi. It is also known as Pinguli.
2. This tradition is mentioned in Manasollas, a book written by the Chalukya King Someshvara in the 12th century. People belonging to Thakur community stifi practise this art They are frm village, Pinguli near Kudal in Maharashtra.
3. The Chitrakathi pictures are drawn on paper and painted with natural substances. To complete the narration of a single story it takes around 30 to 50 pictures.
4. These pictures are preserved and are passed on from one generation to another. The artists and government are trying to preserve this tradition which is on the verge of extinction.

(b) Miniature Painting:
Answer:

• Painting in a small size square is called Miniature painting.
• The miniature reached people through manuscripts. The earlier period of miniature painting shows the influence of Persian style.
• The Deccan miniature style was developed under the patronage of the Deccan Sultanate.
• Mughal miniature painting style of painting’ was developed during the reign of Mughal Emperor Akbar. ¡t shows a blend of Indian and Persian style.

(c) Western style of painting:
Answer:

• Indian artists came under the influence of European style of painting during the British period.
• An art school at Shaniwar Wada at Pune was established under the leadership of Scottish artist James Wales.
• J. J. School of art and industry was established in 1857 to offer the courses in European style of painting.
• Pestonji Bomanji made replicas of Ajanta paintings.
• lames Wales had done a portrait of Savai Madhavrao and Nana Phadnavis.
• Exact portrayal of the object of the painting is a characteristic of European style.

(d) Gangaram Tambat:
Answer:

• An art school was established under the leadership of Scottish artist James Wales at Shanivar Wada in Pune.
• Marathi artist Gangaram Tambat worked with James Wales.
• He made drawings of rock-cut caves at Verul and Karle.
• Some of his drawings are preserved in the Yale Centre of British Art of Yale University.

(e) Temple architecture:
Answer:

1. Temple architecture began to develop in India around 4th century C.E. during the Gupta period. In the initial stage of the Gupta period, the temples had only the Sanctum Sanctorum (Garbhagriha) and a Veranda with four columns.
2. Temple architecture reached its peak by the 8th century C. E. and its example is the Kailas temple of Verul. By medieval period various types of temple architecture had developed in India.
3. The styles of tower (Shikar) determined various styles of temple architecture in India. The Nagara style of North India and Dravid style of South India are two prominent styles of Indian temple architecture. A blend of Nagara and Dravid is known as Vesara style.
4. Bhoomija style seen in temples of Maharashtra and Madhya Pradesh has very close resemblance to ‘Nagara’ style.

(f) Indo-Gothic Architecture:
Answer:

1. During the British period, a new architectural style arose in India which was a blend of Indian and Gothic known as Indo-Gothic style of architecture.
2. During the British period, buildings like churches, government offices, residences of top officials, railway stations were built in Indo-Gothic style of architecture.
3. Chhatrapati Shivaji Maharaj Railway Terminus in Mumbai is the finest example of Indo- Gothic style of architecture.

(g) Ttitab-e-Navras:
Answer:

1. Ibrahim Adilshah II, the ruler of Bijapur, wrote a book in Persian language entitled ‘Kitab- e-Navras’. This text is about Indian classical music.
2. It includes the verses suitable for singing. It is a composition of excellent poetry expressed through Dhrupad style giving the experience of ecstasy to the interested audience.
3. The Ncrvras mentioned in Sanskrit literature are explained in this text.

Question 10.
Explain the following sentences with reasons:
(a) Indian performing arts were enriched over time.
Answer:

• A constant stream of rulers like the Greeks, Arabs, Mughals and the British came to India.
• During their rule, Indian people came into contact with their styles of folk art.
• The culture which they brought along lasted and blended with existing streams of Indian performing arts.
• As a result, many styles of classical vocal music, instrumental music and dance came into existence.
• Therefore Indian performing arts enriched over time.

(b) The field of Applied Arts needs professionals.
Answer:

• An artistic creation is combined with utilitarian purpose to make it economically viable in applied arts.
• Many stages of production are reached before the concept of creation becomes a reality.
• Each field in applied arts requires detailed planning and meticulous management at each stage of production.
• Ornaments, earthen pots with colourful designs, objects made from Cane and Bamboo, beautiful glass objects.
• Attractive textiles and clothing all listed under applied arts essentially require trained and skilled individuals at every stage.
• Some of the production processes of artistic objects have a history of certain traditions. It is important to have knowledge of those traditions.

Hence, it is essential to have trained and skilled professionals at every stage.

Question 11.
Answer the following question in 25-30 words:
(a) Write about follk traditions of sculptural art.
Answer:

• The tradition of folk art dates back to the Stone Ages.
• The custom of making clay images for rituals has been prevalent in India since Harappcin times.
• It has continued even today in many regions of Bengal, Bihar, Gujarat and Rajasthan.
• During the festivals, Ganesh idols are made along with the masks of Goddess Gauri.
• Bull figurines are made for the festival of Bailpola.
• Wooden memorials, Veergals (memorial stones), the decorated clay storage bins, etc.
• Are examples of folk tradition of sculptural art.
• The sculptures made for religious and festival reasons became masterpieces of artists’ creation.

(b) Write about Gandhara School of Art.
Answer:

• The regions around Afghanistan showed great influence of Greeks and Persians from 2nd century B.C.E.
• Gandhara style of art was a fusion of Greek- Roman and Indian style.
• Gandhara school was heavily influenced by Greek methodologies.
• The materials used to make sculptures were Grey sandstone. Mud, Lime and Stucco.
• Grey sandstone is more prominently used in Gandhara School of Art.
• The Gandhara school images are known for their anatomical accuracy, spatial depth and foreshortening.
• The sculptures in Gandhara style are found in Taxila, Peshawar and on the North West Frontier.

(c) Write about development of Indian Iconography.
Answer:

• The Kushana period from the 1st – 3rd century C.E. saw the rise of Mathura School of Art.
• The Mathura School of Art laid the foundation of Indian iconography style.
• The Kushana Kings made use of images of various deities on their coins.
• During the Gupta period, the ieonographic rules were formulated and standards for sculptural- art were set.
• The art of making bronze images was developed under the patronage of Chola Kings during 9th-13tji century.
• Bronze idols of gods and goddesses like Siva-Parvati, Natraj, Lakshmi, Vishnu, etc. were made.

(d) Give information about the rock-cut caves in India.
Answer:

• The tradition of rock-cut caves originated in India in the 3rd century B.C.E.
• The entire composition of a rock-cut cave represents a union of architecture and sculptural art.
• The entrances of such rock-cut caves, interiors with its carved columns and images are excellent specimens of sculptural art.
• The paintings on the walls and ceilings have survived till today.
• The rock-cut caves at Ajanta and Verul in Maharashtra were declared as World Heritage Sites in 1983.

(e) Elaborate on the development of temple architecture.
Answer:

• The temple architecture began to develop in India during the Gupta period in 4th century C.E.
• The temples built at the beginning of the Gupta period had only the sanctum sanctorum (Garbhagriha) and a veranda with four columns.
• The magnificent structure of the Kailas temple of Verul gives testimony that temple architecture had reached its peak by the 8th century C.E.
• Different styles of temple architecture were developed by the medieval period. Some of them are Nagara, Dravid, Vesara and Bhoomija.

(f) What efforts were taken in India to make dance and classical music easily accessible to common people?
Answer:
The following efforts were taken to make dance and music easily accessible to people:

• Dance programmes and musical festivals were organised at various places.
• Many people attend these festivals including Indians and foreigners.
• The Savai Gandharva festival of Pune is very famous.

(g) Write about the work of Pandit Uday Shankar.
Answer:

• Pandit Uday .Shankar created a fusion of Indian classical dance and European operti.
• New styles of dancing were developed.
• He also included various folk dances in his style of fusion.

Thus, the scope of Indian performing arts seems to be constantly expanding.

(h) Which fields are related to applied arts ?
Answer:

1. An artistic creation with a utilitarian purpose is called applied arts. Industry and advertisement. Interior Design and production of ornamental objects, Art Design of stage backdrops, Art Direction for films and television are the fields of applied arts.
2. Layout of books, magazines, production of greeting cards, invitation cards, gift objects, calligraphy are also related to applied arts.
3. Still and animated graphics, created with the help of computers are used for various purposes. This field needs experts with technical knowledge.
4. In short, whichever art is known and is applied to create something new becomes applied art.

Question 12.
Read the following passage and answer the questions:
(a) In which states of India are the sites of rock paintings found?
Answer:
The sites of rock paintings are found in the states of Madhya Pradesh, Uttar Pradesh, Bihar, Uttarakhand, Karnataka, Andhra Pradesh and Telangana.

(b) How old is the tradition of rock paintings?
Answer:
The tradition of rock painting dates back to the Stone Age.

(c) What are the features of rock paintings?
Answer:

• Rock paintings depict humans, animals, geometric figures, flora and fauna in various figures and also in colour.
• Natural colours in black and fed are used in them which are extracted from natural substances.
• The style of rock paintings seems to be changing according to the cultural changes from Stone Age to the beginning of agriculture.
• We get to know about ancient people, their natural surroundings and also the way they exploited available natural resources.

Question 13.
Answer the following questions in detail:

(a) Give information on Indian classical sculptural art.
Answer:
The development of folk styles of sculptural art led to the formation of rules for classical sculptural art and it evolved.

1. The folk style of sculpture-making began during the Harappan period. Seals, stones and bronze statues that were made, gives a testimony that the art of sculpture was known to the Indians.
2. It is about 5000 years old or even older tradition.
3. The tradition of the erected stupa started in the times of Ashoka. The stupa at Borobudur in Indonesia is the largest stupa in the world.
4. Gandhara style of sculptural art came to being in the 2nd century B.C.E. and has Greek and Persian influences.
5. During the Kushana reign, Mathura School of art evolved which was a blend of Gandhara School of Art and indigenous art.
6. The rules of Indian iconography was laid during the rule of the Gupta empire. Thus, Indian sculptural tradition has developed into a rich classical sculptural art.

(b) Differentiate between Classical and Folk: art.:
Answer:
Some differences are noted between Classical and Folk art. They are as follows: Classical Art Folk Art

Classical Art	Folk Art
1. Classical art does not have such a long tradition.	1. The tradition of folk art has continued from the prehistoric times.
2. Classical art is not connected to everyday life.	2. Folk art is an integral part of everyday life.
3. It takes a very long time period to master classical art.	3. The creation of folk art has taken place naturally because of people’s involvement.
4. Classical art developed within the established frame of rules.	4. Folk art developed as an integral part of the religious festivals and social life.
5. As classical art follows set rules, different types of styles, methods and schools are developed.	5. Folk art is not bound by any rules.

Brain Teaser

Across:

• Temples built in Maharashtra in 12-13th centuries in this style
• The text written by the ruler of Bijapur, Ibrahim Adilshah II
• Artist who created a fusion of Indian classical dance and European opera
• His drawings are preserved in the Yale Centre of British Art of Yale University

Down:

• The temple of Kailas at Verul
• An art school was established under his leadership in the times of Savai Madhavrao Peshwe
• The art of painting is mentioned as … in ancient Indian text
• Murals of Maratha style of painting can be seen at this place

10th Std History Questions And Answers:

• Historiography Development in the West Class 10 History Questions And Answers
• Historiography Indian Tradition Class 10 History Questions And Answers
• Applied History Class 10 History Questions And Answers
• History of Indian Arts Class 10 History Questions And Answers
• Mass Media and History Class 10 History Questions And Answers
• Entertainment and History Class 10 History Questions And Answers
• Sports and History Class 10 History Questions And Answers
• Tourism and History Class 10 History Questions And Answers
• Heritage Management Class 10 History Questions And Answers

Balbharti Maharashtra State Board Class 10 Geography Solutions Chapter 5 Natural Vegetation and Wildlife Notes, Textbook Exercise Important Questions and Answers.

Std 10 Geography Chapter 5 Question Answer Natural Vegetation and Wildlife Maharashtra Board

Class 10 Geography Chapter 5 Natural Vegetation and Wildlife Question Answer Maharashtra Board

Geography Class 10 Chapter 5 Question Answer Maharashtra Board

Question 1.
On the basis of the information given in the chapter, figures and maps, complete the table below:

S.No	Type of forest	Characteristics	Regions in India	Regions in Brazil
1	Tropical Forests	Broad-leaved evergreen trees.
2	Semi arid thorny vegetation	1. 2.
3	Savannah	Scanty bushes and shrub like trees and rain resistant grass.
4	Tropical semi-deciduous	Mixed type vegetation.
5	Grasslands	Grassland region like the Pampas of Argentina.

Answer:

S. No.	Type of forest	Characteristics	Regions in India	Regions in Brazil
(1)	Tropical Forests	Broad-leaved evergreen trees.	Andaman and Nicobar Islands, the Western Ghats. Some parts of North East India.	Amazon Basin, Guyana Highlands.
(2)	Semi arid thorny vegetation	(a)     Thorny and shrub type vegetation. (b)   Leaves are small in size. Leaves are modified into thorns to minimise evaporation.	Gujarat, Rajasthan, Parts of Madhya Pradesh and Uttar Pradesh.	North-Eastern part of Brazil.
(3)	Savannah	Scanty bushes and shrub like trees and rain resistant grass.		Brazilian Highland.
(4)	Tropical semi-deciduous	Mixed type vegetation.	Central India and South India.	Parana Basin and South Eastern part of Brazil.
(5)	Grasslands	Grassland region like the Pampas of Argentina.	Foothills of Shiwalik hills and Assam.	Southern Brazil.

2. Identify the odd man out:

Question a.
Forest type of Brazil ______.
(a) Thorny bush type vegetation
(b) Evergreen forests
(c) The Himalayan Forests
(d) Deciduous forests
Answer:
(c) The Himalayan Forests

Question b.
With reference to India
(a) Mangrove forests
(b) Mediterranean forests
(c) Thorny bush-type vegetation
(d) Equatorial forests
Answer:
(b) Mediterranean forests

Question c.
With reference to Fauna of Brazil.
(a) Anaconda
(b) Tamairin
(c) Red Panda
(d) Lion
Answer:
(c) Red Panda

Question d.
With reference to flora in India.
(a Deodar
(b) Anjan
(c) Orchid
(d) Banyan
Answer:
(c) Orchid

3. Match the Column:

Column ‘A’	Column ‘B’
Evergreen Forests	(a) Sundari trees
Deciduous forests	(b) Pine
Coastal forests	(c) Pau Brasil
Himalayan forests	(d) Khejari
Thorny and bush type vegetation	(e) Teak
	(f) Orchid

Answer:
1 – c
2 – e
3 – a
4 – b
5 – d

4. Answer in short:

Question a.
Differentiate between the forest types of Brazil and India.
Answer:

Forest type of Brazil	Forest type of India
1. The northern part of Brazil lies in the equatorial region. It receives ample sunshine and heavy rainfall. So dense evergreen forests are seen here.	1. The location of India is far away from the Equator. Heavy rainfall occurs only in the Western Ghats and North Eastern hilly areas. So evergreen forests are seen in these regions.
2. The Highland region of Brazil receives low rainfall. So tropical grasslands are seen in this region.	2. The Peninsula region of India receives rainfall between 1000 mm to 2000 mm, so they are covered by deciduous forests.
3. As there are no tall and long extending mountains in Brazil, Himalayan type forests are not found here.	3. Owing to presence of Himalayas, Himalayan type forests are found in North and North-East of India that are classified on the basis of altitude.
4. Thorny shrubs are found to the North Eastern part of Brazilian Highlands which is also considered to be a Drought Quadrilateral.	4. Thorny shrubs are found in India receiving less than 500 mm of rainfall. It is majorly found in Gujarat, Rajasthan and rain shadow regions of the Western Ghats.

Question b.
Correlate wildlife and natural vegetation in India and Brazil.
Answer:
(i) Depending upon favourable geographical conditions, we find a variety of natural vegetation in India and Brazil. Also depending upon the vegetation we find a variety of wildlife in different regions.

(ii) Grasslands of Brazil like the Savannah and the deciduous forest of India have a large number of herbivores and carnivores.

(iii) The dense evergreen forests of India in the west, north east India and the Amazon Basin of Brazil are a home to a large variety of birds, insects, reptiles along with the herbivores and the carnivores.

(iv) Coastal forests and swampy areas of Pantanal and Sunderbans have mangroves, a variety of birds, fishes and reptiles like crocodiles, alligators and the anacondas in Brazil.

(v) Vegetation provides food and shelter to wildlife but if vegetation is limited like in the Thar desert or the Caatinga it will also limit the variety of animals species.

Question c.
What environmental issues are faced by Brazil and India?
Answer:

• Degradation of environment is happening in Brazil due to illegal smuggling of wild animals, slash and burn agriculture (roca), deforestation, pollution, etc.
• Due to these problems, many endemic species are on the verge of extinction.
• India too faces environmental issues such as poaching, pollution and the fast spreading deforestation.
• Many species of wildlife are on the verge of extinction in India.

Question d.
What are the major causes of degradation of forest in Brazil and India?
Answer:
(i) Forests are being cut down as more area is required to expand the cities. Hence rapid urbanisation is one of the reasons for degradation of forest.

(ii) To ensure continuous food supply to meet the needs of the ever increasing population, more and more area needs to be brought under agriculture. For the expansion of agricultural land, forest areas are being cut down.

(iii) In both India and Brazil, forests are being cut down for firewood and for other domestic needs.

(iv) Slash and Burn agriculture which is also known as Roca in Brazil and Jhum in India is responsible for deforestation.

(v) Apart from all the above reasons, forest fire, pollution, overgrazing, etc. are also responsible for the degradation of forests.

Question e.
Why does the deciduous type vegetation occupy most of India?
Answer:

• Vegetation in a region is affected by the climate and rainfall of the region.
• In dia lies in the tropical zone and it has a monsoon type climate throughout the year.
• Also, a major portion of India receives seasonal rainfall between 1000-2000 mm.
• Deciduous forests thrive well in this condition and these forests shed their leaves during the hot and dry summer so that water is not lost due to evaporation.
• Teak, bamboo, banyan, peepal, etc. are the trees found in deciduous forest of India.

5. Give geographical reasons:

Question a.
The northern part of Brazil is covered with dense forests.
Answer:

• The northern part of Brazil lies in the equatorial region.
• It receives ample sunlight and about 2000 mm of rainfall throughout the year.
• In this region, the growth of vegetation is very rapid.
• So, the northern part of Brazil is covered with dense and evergreen forests.

Question b.
Vegetation is scarce in the high altitude of the Himalayas.
Answer:

• As the altitude increases, the temperature decreases.
• The climate is very cold in the high altitudes. In Jammu and Kashmir and parts of Himalayas temperature drops to -40fiC.
• Also this region is snow-covered for most part of the year.
• Very few species of plants can survive in such extreme conditions. Only seasonally flowering trees are found at higher altitudes.
• Hence, vegetation is scarce in the high altitude of the Himalayas.

Question c.
A wide variety of insect species is found in Brazil.
Answer:

• Insects are mostly found in forests, grasslands and swampy lands.
• Many insects eat leaves, grass and nectar from the plant.
• The evergreen rainforests are seen in the northern parts of Brazil. The grasslands are found in the central parts and Paraguay-Parana river basin. Similarly, swampy lands are found in Pantanal region in Brazil. .
• Therefore, a wide variety of insect’s species is found in Brazil.

Question d.
Wild life in India is decreasing day by day.
Answer:
(i) Wildlife in India is decreasing day by day because of rapidly occurring deforestation, poaching, pollution.

(ii) Expansion of cities to accommodate the growing population is leading to cutting down of the valuable forest which leads to the loss of the habitat of wildlife.

(iii) Also the problem of pollution has become severe due to urbanisation. Various types of pollution have threatened the lives of many of the species.

(iv) Poaching of wildlife species have also led to the loss of wildlife in India.

(v) Agricultural practices like shifting cultivation has also reduced the forest cover leading to loss of wildlife habitat.

Question e.
Like India, there is a need for conservation of forests in Brazil too.
Answer:
(i) Like India, Brazil is facing the problem of degradation of environment due to deforestation, pollution, slash and burn agriculture, illegal smuggling of wild animals, etc.

(ii) Trees are being cut down to obtain wood, leading to large scale deforestation in both countries.

(iii) Also the problem of pollution has become severe due to urbanisation. Various types of pollution have threatened the lives of many of the species.

(iv) Agricultural practices like slash and burn agriculture (roca) has reduced the forest cover in Brazil.

(v) Like India, the problem of illegal smuggling of animals has affected Brazil too.

(vi) Hence there is a need for conservation of forests in both Brazil and India.

Class 10 Geography Chapter 5 Natural Vegetation and Wildlife Intext Questions and Answers

Observe the images given below and discuss on the basis of the following points and answer the following questions:

Question 1.
Can you tell the names of the plants/trees shown in the image?
Answer:
Coffee, cactus, rubber.

Question 2.
Where have you seen these plants before?
Answer:
Brazil.

Question 3.
Name the fauna shown in the image.
Answer:
Rufous bellied thrush, leopard, green anaconda.

Question 4.
Where have you seen them before?
Answer:
On the internet and in movies.

Question 5.
In which country do you find a greater diversity of vegetation? What is the reason behind it?
Answer:
Brazil has a greater diversity of vegetation because of the variation in climatic conditions.

Colours Of Both

Question 1.
In which country do equatorial forests occupy a greater area? What could be the reason behind it?
Answer:
Equatorial forests occupy a greater area in Brazil. This is because the Equator passes through northern part of Brazil. Hence, the climate is generally hot throughout the year. Moreover, this region receives heavy rainfall throughout the year.

Question 2.
Which type of forests found in India are not found in Brazil?
Answer:
Himalayan forests are found in India and not in Brazil.

Question 3.
Which type of forests found in Brazil are found in India too?
Answer:
Evergreen forests, deciduous forests, and thorny shrub type vegetation are found in both Brazil and India.

Question 4.
In which country a greater diversity of vegetation is found? What is the reason behind it?
Answer:
Brazil has a greater diversity of vegetation because of the equatorial climate, ample sunlight, heavy rainfall, and vast forest expanse.

Question 5.
Considering the climate and vegetation types, in which country will forest-based occupations flourish?
Answer:
Forest-based occupations will flourish more in Brazil.

Activity

Question 1.
Correlate geographical conditions and the flora and fauna there? (India)
Answer:
Depending upon favourable geographical conditions, we find a variety of flora and fauna in India.

(i) In the snow-capped regions of Himalayas where precipitation occurs in the form of snow, we find alpine vegetation. Animals like snow leopards and yaks are found who can sustain the extreme cold of the Himalayas.

(ii) The evergreen forest in the Western Ghats have hot and humid conditions with a temperature of 28°C and annual rainfall more than 2000mm. In such are as animals like lions, tigers, elephants, and a variety of birds are seen.

(iii) The coastal forest are home to many turtles, crocodiles, and gavials, etc. One-horned rhinoceroses are found in the swampy, marshy lands of Assam. Mangrove vegetation is found in the saline waters.

(iv) In areas where the climate is hot and dry and the rainfall is low, thorny scrub vegetation is found. Animals like wild ass and camels are common here.

(v) In the regions of medium rainfall. We find deciduous forest, wide variety of animals and birds.

Question 2.
Do you know some other animals too ?
Answer:
Four-horned antelope, black buck, Tibetan yak, giant squirrel (shekaru).

Use your Brain:

Question 1.
Find out in which parts of India agricultural practices like the ‘Roca’ is found? By what names are they called?
Answer:

Slash and Burn Farming in India
Name	Regions
Jhumming	Assam, Meghalaya, Mizoram and Nagaland
Pamlou	Manipur
Dipa	Bastar (Chhattisgarh) and Andaman & Nicobar Islands
Bewar or Dahiya	Madhya Pradesh
Podu or Penda	Andhra Pradesh
Pama Dabi or Koman or Bringa	Odisha
Kumara	Western Ghats
Valre or Waltre	South Eastern Rajasthan
Khi	Himalayan belt
Kuruwa	Jharkhand

Answer the following questions on the basis of map given:

Question 1.
How many mm of rainfall does Tropical forests have?
Answer:
Tropical forests receives rainfall of 1600 mm.

Question 2.
How much rainfall does equatorial forests receive?
Answer:
Equatorial forests receive 2000 mm of rainfall.

Question 3.
Name the types of forests shown in figure.
Answer:
Tropical forests, Equatorial forests, Deciduous forests and Temperate forests are shown in the above figure.

Question 4.
Where are tropical and equatorial forests found in Brazil?
Answer:Tropical and equatorial forests are found in Guyana Highlands and Amazon basin respectively.

Question 5.
Where are deciduous forests and temperate forests found in Brazil?
Answer:
Deciduous forests and Temperate forests are found in Parana Basin and Brazilian Highlands respectively.

Question 6.
What kind of wildlife is seen in Brazilian Highlands?
Answer:
Reptiles and grassland animals are seen in Brazilian Highlands.

Question 1.
Which forests are found in western snow¬capped regions?
Answer:
Himalayan Forests are found in western snow-capped regions.

Question 2.
On which coast do you mainly find the coastal vegetation?
Answer:
The coastal vegetation is mainly found along the Eastern Coast.

Question 3.
Which type of forests occupy maximum area in India ? Why?
Answer:
Deciduous forests are found in the regions receiving rainfall between 1000 mm to 2000 mm Since most of India has rainfall in that range, deciduous forests dominate the Indian subcontinent.

Question 4.
Where do you find thorny and shrub vegetation in India and why?
Answer:
Semi arid areas of Gujarat, Rajasthan, Madhya Pradesh, Chhattisgarh, Uttar Pradesh Maharashtra, Karnataka, Andhra Pradesh, Tamil Nadu and Haryana are the places where thorny and shrub vegetation are found. The thorny forests are found in these regions as the rainfall is less than 500 mm.

Question 1.
Name the species shown on the map.
Answer:
Some of the major species shown on the map are condor, golden lion tamarin, anaconda, crocodile, sword fish, flamingoes, macaw, parrots, rufous bellied thrush.

Question 2.
In which regions are these animals found? Why are their habitats found in these forests?
Answer:

• The dense equatorial forest region is home to golden lion tamarin, condor, anaconda, etc. This is because these forest lie near the Amazon River and receive rainfall throughout the year.
• Swampy lands of Pantanal is home to anacondas and crocodiles because these conditions are favourable for their habitation.
• Sword fish thrives near the South Atlantic Coast due to the extensive continental shelf.

Question 3.
Classify the forest regions in Brazil with reference to their extent.
Answer:

• Equatorial forests are found in the northern part of Brazil and it covers an extensive area.
• Tropical Grasslands (Savanna) is the next major forest type occupying central part of Brazil.
• Hot deciduous forests occupy the southern Brazil whereas swampy lands of Pantanal occupy a small part of Brazil in the south west.
• Thorny shrubs occupy the north western part of Brazil owing to low rainfall whereas Temperate Grasslands (Pampas) occupy south Brazil.

Mark the following on the map of India with the given information:
Question 1.

1. Bengal Tiger
2. Lion
3. Great Indian Bustard
4. Gangetic Dolphin
5. Olive Ridley turtles
6. Swamp deers
7. One-horned rhinos
8. Nilgiri Tahr goat
9. Gharials

Answer:

Class 10 Geography Chapter 5 Natural Vegetation and Wildlife Additional Important Questions and Answers

Choose the correct option and rewrite the statements:

Question 1.
In Brazil, _____ varies due to physiography.
(a) soil
(b) rainfall
(c) agriculture
(d) mineral availability
Answer:
(b) rainfall

Question 2.
In most parts of the _____ region, it rains throughout the year.
(a) temperate
(b) tropical
(c) grasslands
(d) equatorial
Answer:
(d) equatorial

Question 3.
As one moves away from the Equator, _______ decreases.
(a) altitude
(b) forest
(c) rainfall
(d) snowfall
Answer:
(c) rainfall

Question 4.
The _______ forests are found where there is rainfall throughout the year.
(a) tropical
(b) thorny
(c) evergreen
(d) temperate
Answer:
(c) evergreen

Question 5.
Brazil has the/a ______ number of vegetation species in the world.
(a) moderate
(b) largest
(c) low
(d) smallest
Answer:
(b) largest

Question 6.
The rainforests are rightly called the _______.
(a) lungs of the world’
(b) ’limbs of the world’
(c) ’heart of the world’
(d) ’veins of the world’
Answer:
(a) lungs of the world’

Question 7.
Highest biodiversity is found in _____ forests.
(a) thorny
(b) deciduous
(c) evergreen
(d) coastal
Answer:
(c) evergreen

Question 8.
In regions receiving rainfall between 1000 mm to 2000 mm in India, ______ forests are found.
(a) thorny
(b) evergreen
(c) deciduous
(d) tropical
Answer:
(c) deciduous

Question 9.
In regions receiving less than 500 mm of rainfall that experience dry summers for a long time in India, ______ and shrub like vegetation are found.
(a) equatorial
(b) evergreen
(c) grasslands
(d) thorny
Answer:
(d) thorny

Question 10.
In _____ areas, coastal type of vegetation is found.
(a) peninsular
(b) mountainous
(c) rocky
(d) swampy
Answer:
(d) swampy

Question 11.
Coastal type of vegetation is called ____ in India.
(a) Bangar
(b) Sunderbans
(c) Pantanal
(d) Terai
Answer:
(b) Sunderbans

Question 12.
The wood found in Sunderbans is _____ light and durable.
(a) dry
(b) fragile
(c) oily
(d) soft
Answer:
(c) oily

Question 13.
In areas located in the ____ altitude of Himalayas, seasonly flowering trees are found.
(a) highest
(b) lowest
(c) plains
(d) medium
Answer:
(a) highest

Question 14.
In regions with medium altitude of Himalayas, ______ trees are found.
(a) rubber
(b) evergreen
(c) rose wood
(d) coniferous
Answer:
(d) coniferous

Question 15.
At foothills of the Himalayas _____ forests are found.
(a) mixed
(b) teak –
(c) coniferous
(d) pine
Answer:
(a) mixed

Question 16.
The proportion of ________ trees is higher at the foothills of the Himalayas.
(a) sal
(b) deodar
(c) rosewood
(d) pine
Answer:
(a) sal

Question 17.
Teak is mainly found in the _______ type of forest.
(a) Coastal
(b) Thorny and bush
(c) Coniferous
(d) Deciduous
Answer:
(d) Deciduous

Question 18.
A greater diversity of wildlife is found in ________ than any other country in the
world.
(a) India
(b) Russia
(c) Australia
(d) Brazil
Answer:
(d) Brazil

Question 19.
In the swampy areas of Pantanal, _______ are found.
(a) cobras
(b) vipers
(c) huge anacondas
(d) Indian pythons
Answer:
(c) huge anacondas

Question 20.
Among fish varieties, ______ is found in seas of Brazil
(a) mackerel
(b) king fish
(c) sword fish
(d) pink dolphins
Answer:
(c) sword fish

Question 21.
In Brazilian rivers, pink dolphins and ______ are found.
(a) gold fish
(b) piranhas
(c) king fish
(d) mackrels
Answer:
(b) piranhas

Question 22.
One of the major bird species found in Brazil includes _______.
(a) ostrich
(b) flamingoes
(c) kiwi
(d) duck
Answer:
(b) flamingoes

Question 23.
Slash and bum agriculture is also called ______ in Brazil.
(a) kumri
(b) roka (roca)
(c) dry farming
(d) bewar
Answer:
(b) roka (roca)

Question 24.
Hot and humid forests are a home for _______
(a) tiger
(b) elephants
(c) dogs
(d) leopard
Answer:
(b) elephants

Question 25.
One horned rhinoceroses are found in swampy and marshy lands of ______.
(a) Assam
(b) Madhya Pradesh
(c) Telangana
(d) Tamil Nadu
Answer:
(a) Assam

Question 26.
Indian bisons, deers, monkeys are found in the _____ region.
(a) Himalayan
(b) Western Ghats
(c) Peninsular
(d) Deccan
Answer:
(c) Peninsular

Question 27.
The only country where both lions and tigers are found is ______.
(a) Brazil
(b) India
(c) Australia
(d) America
Answer:
(b) India

Question 28.
______ which are huge in size fly high in the Brazilian sky.
(a) Macaws
(b) Kingfishers
(c) Condors
(d) Pheasants
Answer:
(c) Condors

Match the Column:

Question 1.

Column ’A’	Column ‘B’
1. Evergreen Forests	(a) Major portion of Madhya Pradesh
2. Deciduous forests	(b) Arunachal Pradesh
3. Thorny shrubs	(c) Sundarbans
4. Himalayan forests	(d) Western Ghats
5. Coastal forests	(e) Gujarat
	(f) Cold desert in Jammu and Kashmir
	(g) Hot desert in Rajasthan

Answer:
1 – d
2 – a
3 – e
4 – b
5 – c

Question 2.

Column ’A’	Column ‘B’
1. Equatorial forests	(a) Caatinga
2. Grasslands	(b) Pantanal
3. Swampy Lands	(c) Pampas
4. Hot deciduous forests	(d) Amazon river basin
5. Thorny shrubs	(e) Escarpment
	(f) Savanna
	(g) Parana basin

Answer:
1 – d
2 – c
3 – b
4 – e
5 – a

Identify the odd man out:

Question 1.
With reference to Fauna in India.
(a) Anaconda
(b) Elephants
(c) Lion
(d) Tiger
Answer:
(a) Anaconda

Question 2.
With reference to Flora of Brazil.
(a) Pau Brazil
(b) Rubber
(c) Mahogany
(d) Deodar
Answer:
(d) Deodar

Question 3.
With reference to Himalayan Forests.
(a) Seasonal flowering plants
(b) Orchids
(c) Pine
(d) Mixed Forests
Answer:
(b) Orchids

Question 4.
With reference to birds found in Brazil.
(a) Condors
(b) Flamingoes
(c) Macaws
(d) Peacocks
Answer:
(d) Peacocks

Question 5.
With reference to birds found in India.
(a) Peacock
(b) Kingfisher
(c) Duck
(d) Condors.
Answer:
(d) Condors.

Question 6.
With reference to protection of wildlife, Government of India has setup.
(a) Museums
(b) Biosphere reserves
(c) National Parks
(d) Wildlife sanctuaries
Answer:
(a) Museums

Answer the following questions in one sentence:

Question 1.
Where does it rain throughout the year?
Answer:
It rains throughout the year, in most parts of the equatorial region.

Question 2.
As one moves away from the Equator, does the rainfall increase?
Answer:
No, the rainfall decreases as one moves away from the Equator.

Question 3.
Where are evergreen forests found?
Answer:
Evergreen forests are found in the area where it rains throughout the year.

Question 4.
What effect does rainfall have on vegetation?
Answer:
As the rainfall decreases, the density of the vegetation also decreases.

Question 5.
What kind of vegetation is found in places of less rainfall?
Answer:
Various types of grass, short shrubs and thorny vegetation is found in places of less rainfall.

Question 6.
Where are the largest number of vegetation species found in the world?
Answer:
Brazil has the largest number of vegetation species in the world.

Question 7.
What kind of trees are found in Brazil?
Answer:
Trees like Pau Brasil, rubber, mahogany, rosewood and a variety of orchids are found in Brazil.

Question 8.
Why are the evergreen forests called the ‘lungs of the world’?
Answer:
Evergreen forests are called the lungs of the world because they release large amount of oxygen in the environment which helps to reduce the carbon dioxide levels.

Question 9.
Describe the leaves of trees found in evergreen forests.
Answer:
The leaves of trees found in evergreen forests are broad and green.

Question 10.
What quality of wood is found in evergreen forests?
Answer:
The wood found in evergreen forests is hard, heavy and durable.

Question 11.
In which regions are deciduous forests found?
Answer:
Deciduous forests are found in the regions receiving an average amount of rainfall ranging between 1000mm to 2000mm in India.

Question 12.
Which trees are found in deciduous forests?
Answer:
Trees like teak, bamboo, banyan, peepal, etc. are found in deciduous forest.

Question 13.
Which regions experience dry summers for a long time in India?
Answer:
Regions that receive less than 500 mm of rainfall experience dry summers for a long time in India.

Question 14.
Which kind of vegetation is found in regions receiving less than 500 mm of rainfall?
Answer:
Thorny or shrub like vegetation is found in regions receiving less than 500 mm of rainfall.

Question 15.
How are the leaves of trees in the region where there is less than 500 mm of rainfall?
Answer:
The leaves of trees are small in the region where there is less than 500 mm of rainfall.

Question 16.
Where is coastal vegetation found?
Answer:
Coastal vegetation is found in swampy areas, estuaries and lagoons near coastal areas.

Question 17.
What is coastal vegetation called in India?
Answer:
Coastal vegetation is called mangroves or Sunderbans in India.

Question 18.
How is the wood of trees found in coastal vegetation?
Answer:
The wood of trees found in coastal vegetation is oily, light and durable.

Question 19.
How many types of forests are there in the Himalayas?
Answer:
There are three types of forests in the Himalayas based on their altitude.

Question 20.
Which kind of trees are found in regions of high altitude in the Himalayas?
Answer:
Seasonally flowering trees are found in regions of high altitude.

Question 21.
Which type of trees are found in regions with medium altitude in the Himalayas?
Answer:
In regions with medium altitude, coniferous trees like pine, deodar and fir are found.

Question 22.
Where are mixed forests found in India?
Answer:
Mixed forest are found at the foothills of the Himalayas.

Question 23.
Where is greater diversity in wildlife found in the world?
Answer:
A greater diversity in wildlife is found in Brazil than any other country in the world.

Question 24.
Which animal is found in the swampy areas of the Pantanal?
Answer:
Huge anacondas are found in the swampy areas of Pantanal.

Question 25.
Which are the other animals found in Brazil?
Answer:
Animals like guinea pigs, crocodiles, alligators, monkeys, pumas, leopards, etc. are found in Brazil.

Question 26.
Which is the main variety of fish found in the Brazilian sea?
Answer:
Sword fish is mainly found in the Brazilian sea.

Question 27.
Which varieties of fish are found in the rivers of Brazil?
Answer:
Piranhas are found in the rivers of Brazil.

Question 28.
What kind of birds are seen in the Brazilian sky?
Answer:
Condors, parrots, macaws, and flamingoes are found in the Brazilian skies.

Question 29.
Why is degradation of environment happening in Brazil?
Answer:
Degradation of environment is happening in Brazil due to illegal smuggling of wild animals, slash and bum agriculture (roka), deforestation, and pollution.

Question 30.
Where are elephants found in India?
Answer:
Elephants are found in hot and humid forests of India.

Question 31.
Where are one homed rhinoceroses found?
Answer:
One homed rhinoceroses are found in the swampy and marshy lands of Assam.

Question 32.
Which animals are found in the arid lands of India?
Answer:
Wild ass and camels are found in the arid lands of India.

Question 33.
Which animal is found in the snow capped regions of Himalayas?
Answer:
Snow leopards are found in the snow capped regions of the Himalayas.

Question 34.
Which animals are found in the peninsular region of India?
Answer:
Indian Bisons, deer, antelopes, and monkeys are found in the Peninsular region of India.

Question 35.
Which is the only country where both lions and tigers are found?
Answer:
India is the only country where both lions and tigers are found.

Question 36.
Where are turtles, crocodiles and gharials found in India?
Answer:
Turtles, crocodiles and gharials are found in rivers, estuaries, and coastal areas of India.

Question 37.
Which birds are found in the forests and wetlands of India?
Answer:
Birds like peacocks, Indian bustard, kingfishers, peasants, ducks, parakeet, cranes, and pigeons are found in the forests and wetlands of India.

Question 38.
What measures are taken by the Government of India for the protection of wildlife and forests of India?
Answer:
The Government of India has set up a number of national parks, wildlife sanctuaries, bird sanctuaries, and biosphere reserves for the protection of wildlife and forests in India.

Question 39.
Name some plants found in regions having less than 500 mm of rainfall in India.
Answer:
Catechu, acacia, khejri and a variety of cactus like aloevera and agave are found in regions having less than 500 mm of rainfall in India.

Name the following:

Question 1.
The region where it rains throughout the year.
Answer:
Equatorial region.

Question 2.
The forests which are found where it rains throughout the year.
Answer:
Evergreen forests.

Question 3.
Kind of vegetation found in places of less rainfall.
Answer:
Grass, short shrubs, thorny vegetation.

Question 4.
Country where the largest number of vegetation species in the world is located.
Answer:
Brazil.

Question 5.
The types of trees found in Brazil.
Answer:
Pau Brasil, rubber, mahogany, rosewood and variety of orchids.

Question 6.
Other name for rain forests.
Answer:
‘The lungs of the world.’

Question 7.
Trees found in deciduous forests.
Answer:
Teak, bamboo, banyan, peepal.

Question 8.
Type of vegetation found in regions having less than 500 mm of rainfall.
Answer:
Thorny and shrub-like.

Question 9.
Plants found in regions having less than 500 mm of rainfall.
Answer:
Catechu, acacia, khejri and varieties of cactus.

Question 10.
Kind of vegetation found in swampy areas.
Answer:
Coastal type.

Question 11.
Another name of coastal type of vegetation in India.
Answer:
Mangroves or sunderbans.

Question 12.
Kind of trees found in forests located on higher altitudes in the Himalayas.
Answer:
Seasonally flowering trees.

Question 13.
Kind of trees which have grown in forests located on medium altitudes in Himalayas. Coniferous trees like Pine, Deodar and Fir.
Answer:
Region where mixed forests are found in Himalayas.

Question 14.
Foothills of Himalayas.
Answer:
Animal found in the swampy areas of Pantanal.

Question 15.
Huge anacondas.
Answer:
Any two varieties of animals found in Brazil. Guinea pigs and crocodiles.

Question 16.
Kind of fishes found in seas of Brazil.
Answer:
Sword fish.

Question 17.
Fish varieties found in the rivers of Brazil.
Answer:
Pink dolphins and Piranhas.

Question 18.
Any two species of birds found in Brazil.
Answer:
Condors and macaws.

Question 19.
Causes for degradation of environment.
Answer:
Illegal smuggling of wild animals, roka, deforestation and pollution

Question 20.
Region where elephants are found in India.
Answer:
Hot and humid forests.

Question 21.
Animal which is found in the swampy and marshy lands of Assam.
Answer:
One horned rhinoceroses.

Question 22.
Animals which are found in arid lands of India.
Answer:
Wild ass and camels.

Question 23.
Animals which are found in the snowcapped mountain of Himalayas.
Answer:
Yaks and snow leopards.

Question 24.
Animals found in the Peninsular region of India.
Answer:
Indian bisons, deer, antelopes and monkeys.

Question 25.
Country where both lion and tigers are found.
Answer:
India.

Question 26.
Animals found in rivers, estuaries and coastal areas of India.
Answer:
Turtles, crocodiles and garials.

Question 27.
Measures taken by the Government of India to protect wildlife.
Answer:
Setting up of National parks, bird sanctuaries, wildlife sanctuaries and biosphere reserves.

Question 28.
National animal of India.
Answer:
Tiger.

Mark the following on the map of India with the given information:

1. Evergreen forests
2. Deciduous forest
3. Thorny shrubs
4. Himalayan Forests
5. Coastal Forests

Answer:

Mark the following on the map of Brazil with the given information:

1. Equatorial forests
2. Tropical grasslands
3. Swampy lands
4. Hot deciduous forest
5. Caatinga
6. Temperate grasslands

Answer:

Equatorial Forests Tropical Grasslands:Savanna Swampy Lands Hot Deciduous Forest Thorny Shrubs/Caatinga Temperate Grasslands:Pampas

Question 1.
Show the habitats of tigers in India with their names on a map.
Answer:

Question 2.
Why is their habitat found in these regions?
Answer:
Tiger’s habitats are found in these regions because here there are various types of forest areas with different types of herbivorous animals.

Answer the Questions Briefly:

Question 1.
Thorny and shrub-like vegetation is found in regions where there is less or no rainfall.
Answer:

• The regions where there is less or no rainfall have a hot and dry climate.
• The soils in these regions are also rocky and dry.
• Water evaporation in leaves is more since the surface area of exposure is more than that of thorns
• Hence, thorny and shrub-like vegetation is found in regions where there is less or no rainfall to conserve water.

Question 2.
The evergreen rainforests in Brazil are rightly called the ‘Lungs of the world’.
Answer:

• The northern Part of Brazil has dense evergreen forests. .
• These forests release a large amount of oxygen in the environment.
• This helps to reduce carbon dioxide levels.
• Therefore, these rainforests are rightly called the Tungs of the world’.

Question 3.
The largest variety of flora is found in Brazil.
Answer:

• The flora of any region depends upon the amount of rainfall and its physiography.
• Brazil has equatorial forests in high rainfall areas, tropical grasslands and deciduous forests in moderate rainfall areas.
• Western part of Brazil has swampy lands, whereas low rainfall regions have thorny shrubs.
• Temperate grasslands are found in temperate regions.
• Thus, the largest variety of flora is found in Brazil.

Question 4.
Suggest measures for the conservation of wildlife and forest in India?
Answer:
Measures for the conservation of wildlife and forest in India are as follows:

• Restricting wildlife trading and hunting.
• Declaring more national parks and sanctuaries.
• Giving more importance to the protection of endangered animals.
• Controlling felling of trees.
• Implementing afforestation and social forestry programmes.

Write short notes on:

Question 1.
Brazilian Vegetation:
Answer:
(i) In Brazil, rainfall varies due to physiography. In most parts of the Equatorial region, it rains throughout the year.
(ii) As one moves away from the equator, the number of rainy days as well as amount of rainfall reduces.
(iii) This affects the life cycle of the vegetation too.
(iv) Evergreen forests are found in the areas where it rains throughout the year.
(v) In regions which receive rainfall only during certain seasons, the density of the vegetation reduces.
(vi) Instead of forests, various types of grass, short shrubs,,thorny vegetation, etc. are found.
(vii) Brazil has the largest number of vegetation species in the world.
(viii) This includes evergreen vegetation, semi-evergreen, arid, etc.
(ix) One finds trees like Pau Brasil, rubber, mahogany, rosewood and a variety of orchids.

Question 2.
wildlife of Brazil:
Answer:
(i) A greater diversity in wildlife is found in Brazil compared to any other country in the world.
(ii) In the swampy areas of the Pantanal, huge anacondas are found.
Animals, such as guinea pigs, crocodiles,
alligators, monkeys, pumas, leopards, etc. are found.
(iv) Among the fish varieties, mainly swordfish are found in the seas, while pink dolphins and piranhas are found in the rivers .
(v) Condors which are huge in size and fly high in the sky, various types of parrots, macaws, and flamingoes are the major birds found here.
(vi) Millions of insect varieties are also found here.

Question 3.
The wildlife of India:
Answer:
(i) India is also a mega-diverse country in terms of wildlife. There are many species of wildlife in Irdia.
(ii) Elephants are found in hot and humid forests. One-horned rhinoceroses are found in swampy and marshy lands of Assam.
(iii) Wild ass and camels are found in arid lands. Snow leopards and yaks are found in the snow-capped regions of the Himalayas.
(iv) Indian Bisons, deer, antelopes, and monkeys are found in the Peninsular region.
(v) India is the only country in the world where both tigers and lions are found.
(vi) Rivers, estuaries and coastal areas are homes to many turtles, crocodiles, and gavials (gharials).
(vii) The forests and wetlands are the shelters of variety of birds like peacocks, Indian bustard, kingfishers, pheasants, ducks, parakeets, cranes, and pigeons.

10th Std Geography Questions And Answers:

• Field Visit Class 10 Geography Questions And Answers
• Location and Extent Class 10 Geography Questions And Answers
• Physiography and Drainage Class 10 Geography Questions And Answers
• Climate Class 10 Geography Questions And Answers
• Natural Vegetation and Wildlife Class 10 Geography Questions And Answers
• Population Class 10 Geography Questions And Answers
• Human Settlements Class 10 Geography Questions And Answers
• Economy and Occupations Class 10 Geography Questions And Answers
• Tourism, Transport and Communication Class 10 Geography Questions And Answers

Balbharti Maharashtra State Board Class 10 Geography Solutions Chapter 7 Human Settlements Notes, Textbook Exercise Important Questions and Answers.

Std 10 Geography Chapter 7 Question Answer Human Settlements Maharashtra Board

Class 10 Geography Chapter 7 Human Settlements Question Answer Maharashtra Board

Geography Class 10 Chapter 7 Question Answer Maharashtra Board

1. Tick (✓) the correct options:

Question a.
The concentration of settlements is related to following major factors
(a) Proximity to the Sea
(b) Plain region
(c) Availability of water
(d) Climate
Answer:
(c) Availability of water

Question b.
In North-eastern part of Brazil, which types of settlements are found
(a) Nucleated
(b) Linear
(c) Dispersed
(d) Star-shaped
Answer:
(c) Dispersed

Question c.
Where do you find dispersed settlements in India?
(i) Near the rivers
(ii) Near the transport routes
(iii) Hilly areas
(iv) Industrial regions
Answer:
(iii) Hilly areas

Question d.
Concentrated settlements are found in Narmada Valley
(i) Forested land
(ii) Cultivable land
(iii) Undulating topography
(iv) Industries
Answer:
(ii) Cultivable land

Question e.
Which state has the least urbanisation in Brazil?
(i) Para
(ii) Amapa
(iii) Espirito Santo
(iv) Parana
Answer:
(i) Para

2. Give geographical reasons:

Question a.
Availability of water is a major factor affecting settlements.
Answer:
(i) Water is a major factor affecting settlements because water is required for survival of living beings, for purposes like drinking, cooking, agriculture, industries, etc.
(ii) Due to availability of water, agriculture and industries flourish, generating employment opportunities and leading to development of settlements.
(iii) Shortage of water will hamper the growth of agriculture and industries which lead to less development of settlements.

Question b.
In Brazil, majority of population is found in the eastern coastal areas.
Answer:
(i) Although the coastal climate is hot and humid, and flat land is limited due to rugged topography, the eastern coast of Brazil has a good water supply and a large range of natural resources.
(ii) The region has rich fertile soil which is most suitable for coffee cultivation..
(iii) The region is rich in minerals like iron ore and has a steady power supply.
(iv) An excellent transportation facility is also available here.
(v) Due to these factors, agriculture, industries and trade flourish and settlements increase.
So, majority of Brazil’s population is found in the eastern coastal areas.

Question c.
Urbanisation is increasing rapidly in India.
Answer:
(i) In India, there has been growing industrialisation, leading to availability of jobs in urban areas.
(ii) Urban areas have better facilities and amenities like water supply, electricity, health, education, etc.
(iii) There is increasing migration of people from rural areas to urban areas.
(iv) The urban population is increasing due to the expansion of urban centres and emergence of new towns.
So, urbanisation is increasing rapidly in India.

Question d.
Settlements are sparse in north-eastern Brazil.
Answer:
(i) The north east of Brazil is a Highland.
(ii) As this region lies in a rain shadow region it suffers from droughts.
(iii) Due to scanty rainfall and unavailability of resources, agriculture and industries are not well developed.
(iv) Transport facilities are also very poor here. Therefore, settlements are sparse in north – eastern Brazil.

Question e.
Except Delhi and Chandigarh, urbanisation is low in other parts of India.
Answer:
(i) Delhi and Chandigarh are union territories lying in the flat Northern Plains of India.
(ii) Delhi is the capital of India and has an ancient history of urbanisation while Chandigarh is one of the most well-planned cities.
(iii) Both Delhi and Chandigarh have good water supply due to river Yamuna and the Bhakra Canal.
(iv) As compared to the other cities in North India, both the cities have well-developed infrastructure, good transport links and other amenities.
(v) Fast developing industries and commercial centres in these places, offer high employment opportunities leading to urbanisation.
Hence, except Delhi and Chandigarh, urbanisation is low in other parts of India.

3. Answer in short:

Question a.
Write a comparative note on urbanisation in Brazil and India.
Answer:
(i) Rate of urbanisation in higher in Brazil than in India.
(ii) Growth of urbanisation in India has been slow.
E.g. From 18% in 1961 to 31.2% in 2011.
(iii) Growth of urbanisation in Brazil has been rapid.
E.g. From 47.1% in 1960 to 84.6% in 2010.
(iv) Urbanisation has been more in the southern part than in the Northern part of India.
(v) Urbanisation in Brazil has been more in the coastal states of south and southeast than the states in the interior of the west and north.
(vi) India’s rate of urbanisation has increased continously in a fluctuating rate.
(vii) Brazil’s is rate of urbanisation has increased but in a diminishing rate.

Question b.
Differentiate between the human settlements in the Ganga river basin and the Amazon river basin.
Answer:

S.No	Human settlements in the Ganga river basin	Human settlements in the Amazon river basin
(i)	Nucleated settlements are found in Ganga river basin.	(i) Dispersed settlements are found in Amazon river basin.
(ii)	Flat land, availibality of water, fertile soil,favourable climate is suitable for human settlement.	(ii) Unfavourable        climate,      heavy      rainfall, inaccessibility makes the Amazon river basin unsuitable for human settlement.
(iii)	The above conditions along with a good transport network has helped to flourish agriculture and other industries.	(iii) Due to dense evergreen forests and poor transport facility there are restrictions on the use of natural resources, which have affected economic development.

Question c.
Why do human settlements grow in specific locations only?
Answer:
Human settlements depend on various factors like climate, availability of water, slope of the land, level of development.
In India, nucleated human settlements are found in the Ganga River Basin because of flat fertile plains, abundance of water, favourable climate and growth of agriculture and industries. Dispersed settlements are found in Himalayan slopes, eastern and southern Rajasthan because of uneven topography, unfavourable climate and lack of development.

In Brazil, nucleated settlements are found in Sao Paulo and southern coast of Brazil, due to nearness to the ocean, fertile soil, availability of natural minerals like iron ore, steady power supply and good transportation system. Dispersed settlements are found in Northern Brazil due to the inaccessible forests in Amazon river basin, unhealthy climate, limitations on use of natural resources drought region and poor transport connectivity.

Class 10 Geography Chapter 7 Human Settlements Intext Questions and Answers

Geographical Explanation

Study the two types of settlement patterns in India given in figure (a) and (b) Answer the following questions :

Question 1.
Identify the type of settlements?
Answer:
Fig a. Settlement Type is: Nucleated and in Fig. b. Settlement Type is: Linear and Dispersed settlement.

Question 2.
Which one is a nucleated settlement? Why?
Answer:
Fig. a. Shows the image of a Nucleated settlement, because it is a cultivated land and has a centrally located water body.

Question 3.
Which one is a dispersed settlement? What could be the reason behind it?
Answer:
In Fig. b. dispersed settlement is observed due to unsuitable topography.

Question 4.
Can you guess in which regions are these settlements located in India?
Answer:
Settlement in Fig. a. is located in the north Indian plain, it might be the river Ganga Basin and settlement in the Fig. b. is located in hilly terrain covered with forest and also a road passing through leads to a dispersed settlement.

Think About It

Question 1.
Tell whether settlements shown in images (a) and (b) are urban or rural.


Answer:
The image shown in (a) is urban and The image shown in (b) is rural

Lets Recall

Question 1.
Some amenities and facilities are given here. Tick (✓) in the relevant column and complete the table on the basis of their presence in urban and rural areas or both.
Answer:

S.No	Amentity	Available in Villages	Available in Cities
(1)	Petrol Pump	✓	✓
(2)	Theatre		✓
(3)	Weekly Market	✓
(4)	Primary Health Centre	✓
(5)	Police Outpost	✓	✓
(6)	Art Gallery		✓
(7)	Gram Panchayat	✓
(8)	Agricultural Produce Market Committee (APMC)	✓
(9)	Primary School	✓	✓
(10)	Senior School		✓
(11)	College		✓
(12)	Shop	✓	✓
(13)	Multi-speciality Hospital		✓
(14)	Metro station		✓
(15)	Bus station	✓	✓
(16)	University		✓

Try This.

Question 1.
In the figure (a) and (b), you can see images of two settlements in Brazil. One is from the Amazon river basin in Brazil while the other belongs to the coastal area. Observe the settlement patterns carefully and name the types of settlement patterns. Write a comment on their density and types.


Answer:
(1) Fig. (a)
Type settlement pattern: Dispersed settlements as they are lying in the dense forested areas of the Amazon Basin.
Density of Population: Sparse.
(2) Fig. (b)
Type settlement pattern: Nucleated settlements as they are lying in the dense forested areas of the Amazon Basin.
Density of Population: Dense.

Can You Tell

Read the graph below and answer the following questions:

Question 1.
What was the percentage of urbanisation in 1961?
Answer:
The percentage of urbanisation in 1961 was 18%.

Question 2.
In which decade was urbanisation the highest?
Answer:
Highest urbanisation took place in the decade 1971 -1981.

Question 3.
In which decade was the growth of urbanisation lowest?
Answer:
The growth of urbanisation was lowest in the decade 1961-1971.

Question 4.
What was the growth in the percentage of urbanisation between 1961 and 1971?
Answer:
The growth in the percentage of urbanisation between 1961 and 1971 was of 0.20%

Question 5.
What was the growth in the percentage of urbanisation between 1991 and 2011?
Answer:
The growth in the percentage of urbanisation between 1991 and 2011 was of 5.5%.

Question 6.
What inference can you draw regarding India’s urbanisation after reading the graph?
Answer:
After reading the graph, we can say that urbanisation in India is slowly but continuously rising.

Try This

Look at the table. It shows the growth and share of urban population in total population of Brazil. Draw a line graph from this table. Examine the graph carefully and answer the following questions:
Brazil Percentage of urban population (1960 to 2010)

Answer:

Question 1.
What is the interval of the data?
Answer:
The interval of the data is 10 years.

Question 2.
In which period did urbanisation occur rapidly?
Answer:
Urbanisation occured rapidly in the period 1960 – 1970.

Question 3.
Write five sentences analysing the graph.
Answer:
(i) The graph shows the percentage of urbanisation in Brazil from 1960 to 2010.
(ii) The interval of the data is 10 years.
(iii) Clearly there has been a rapid urbanisation in Brazil.
(iv) The highest urbanisation is seen between 1960 to 1970, when urbanisation grew from 47.1% to 56.8%, a growth of 9.7%.
(v) Urbanisation occurred slowly during the decade from 2000 to 2010, at a growth of 3.1%.

Give It a Try

Question 1.
Prepare a choropleth map showing urban population using the data given in the table below.

S.No.	Urban population percentage category	States /UTs falling in the category
(1)	0-20	Himachal Pradesh, Bihar, Assam and Odisha
(2)	21-40	Meghalaya, Uttar Pradesh, Arunachal Pradesh, Chhattisgarh, Jharkhand, Rajasthan, Sikkim, Tripura, Jammu and Kashmir, Nagaland, Manipur, Uttarakhand, West Bengal, Andhra Pradesh, Haryana, A and N Islands, Punjab, Karnataka and M. P.
(3)	41-60	Gujarat, Maharashtra, Dadra and Nagar Haveli, Kerala, Tamil Nadu, Mizoram
(4)	61-80	Goa, Puducherry, Daman and Diu, Lakshadweep
(5)	81 -100	Chandigarh, NCT of Delhi

Answer:

Colours Of Both

Question 1.
Compare the line graph shown in figure and the one drawn by you for Brazil. Write five lines on the changes that have occurred in urbanisation in both the countries, with time.

Answer:
(i) After comparing the graphs of India and Brazil, it is clear that urbanisation in Brazil has been much more rapid as compared to India.

(ii) Urbanisation in Brazil grew from 47.1% in 1960¬70 to 84.6% in 2000-2010. Whereas urbanisation in India grew from 18% in 1961-70 to 31.2% in 2001-2011.

(iii) But Brazil’s rate of urbanisation is showing signs of decline, whereas India’s rate of urbanisation is showing a slow and consistent growth.

(iv) For e.g. the rate of urbanisation in Brazil has decreased from 9.7% in 1960-1970 to 3.1% in 2000¬2010. Whereas the rate of urbanisation in India has increased from 0.2% in 1961-1971 to 3.4% in 2001-2011.

(v) Both Brazil and India are developing countries, but Brazil shows very high urbanisation as compared to India.

Question 2.
Make a short note on the comparison between the settlement patterns in India and Brazil on the basis of the following points:
(i) Location
(ii) Pattern
(iii) Types
(iv) Density
Answer:
India settlement pattern

• Location : Nucleated settlements are found throughout the plateau region of Narmada Valley, paddy lands in Bihar, U.P, Vindhyan Plateau and several other cultivated parts of India.
• Pattern : Nucleated settlements
• Types: Urban
•  Density : High population density

• Location : Dispersed settlements are found in tribal parts covering central part of India, eastern and southern Rajasthan, Himalayan slopes and land with dissected and uneven topography.
• Pattern : Dispersed settlements
• Types: Rural
• Density : Low population density.

Brazilian settlement pattern

• Location: The Southern and South Eastern parts of Brazil – Areas where there is good water supply, a large range of natural resources, rich soil, large supply of natural minerals, steady energy supply, a good transport system, etc.
• Pattern : Nucleated settlement
• Types: Urban
• Density : High population density.

• Location : Brazilian Highlands, Central part, Amazon Basin region : regions with dense forests, unfavourable climate, poor transport limits, limitations on the use and exploitation of natural resources, etc.
• Pattern : Dispersed settlements
• Type : Rural
• Density: Low population density

Give It a Try

Question 1.
“Observe the two satellite images given below. Describe the settlements with respect to physiography, Considering the physiography, where could these settllements be located? Find out their settlement pattern and limitations with respect to their future growth.
Answer:
(i) Location : Both satellite images show human settlements in a mountainous region. One settlement is along mountain slope, while the other is on top of a mountain.
(ii) Pattern : Dispersed settlements.
(iii) Future growth : Further growth for human settlements seems difficult. This is mainly because of the hilly terrain and forested land along the mountain slope.

Study the choropleth map of Brazil showing the Statewise urban population of Brazil and answer the following questions :

Question 1.
Which state (region) in Brazil is the most urbanised?
Answer:
The states of Sao Paulo, Rio de Janeiro, Goias, Espirito Santo in the southeastern part of Brazil and the port Manaus in the north are the most urbanised.

Question 2.
Which state (region) in the least urbanised?
Answer:
The states of Para, Maranhao and Piaui in northern part of Brazil are the least urbanised states.

Use Your Brain Power

Question 1.
Which factors have affected urbanisation in Brazil?
Answer:
(i) In Brazil, rapid urbanisation has taken place in South and South East Coastal regions.
(ii) Being in proximity to the Atlantic Ocean have benefitted these regions immensely in the form of mild climatic conditions.
(iii) Availability of water, fertile soil, natural minerals such as iron ore, good transport system and steady electric supply have positively impacted urbanisation in these parts.
(iv) To the north of the Brazilian Highlands is the rain shadow region of ‘Drought Quadrilateral’ with sparse settlements.

Colours Of Both

Question 1.
Write a paragraph on the settlement pattern, urban and rural settlement and urbanisation in India and Brazil.
Answer:

India settlement pattern

• Location : Nucleated settlements are found throughout the plateau region of Narmada Valley, paddy lands in Bihar, U.P, Vindhyan Plateau and several other cultivated parts of India.
• Pattern : Nucleated settlements
• Types: Urban
•  Density : High population density

• Location : Dispersed settlements are found in tribal parts covering central part of India, eastern and southern Rajasthan, Himalayan slopes and land with dissected and uneven topography.
• Pattern : Dispersed settlements
• Types: Rural
• Density : Low population density.

Brazilian settlement pattern

• Location: The Southern and South Eastern parts of Brazil – Areas where there is good water supply, a large range of natural resources, rich soil, large supply of natural minerals, steady energy supply, a good transport system, etc.
• Pattern : Nucleated settlement
• Types: Urban
• Density : High population density.

• Location : Brazilian Highlands, Central part, Amazon Basin region : regions with dense forests, unfavourable climate, poor transport limits, limitations on the use and exploitation of natural resources, etc.
• Pattern : Dispersed settlements
• Type : Rural
• Density: Low population density

Class 10 Geography Chapter 7 Human Settlements Additional Important Questions and Answers

Choose the correct option and rewrite the statements.

Question 1.
_______ settlements are found in tribal parts covering central part of India.
(a) Nucleated
(b) Linear
(c) Dispersed
(d) Circular
Answer:
(c) Dispersed

Question 2.
The earlier settlements in Brazil were formed by settlers from _______ mainly in coastal areas.
(a) Africa
(b) Asia
(c) Europe
(d) Australia
Answer:
(c) Europe

Question 3.
Sao paulo has _________ settlements.
(a) isolated
(b) nucleated
(c) scattered
(d) dispersed
Answer:
(b) nucleated

Question 4.
Rural areas of Brazil such as the north east highlands suffer from _____ which make it difficult for practising agriculture.
(a) high rainfall
(b) extreme cold
(c) extreme droughts
(d) extreme heat
Answer:
(c) extreme droughts

Question 5.
Settlements become _____ as we go to the central part of Brazil.
(a) sparse
(b) dense
(c) nucleated
(d) triangular
Answer:
(a) sparse

Question 6.
The growth of urbanisation in India has been ________.
(a) quick
(b) moderate
(c) slow
(d) rapid
Answer:
(c) slow

Question 7.
In India, urbanisation has been more in the _______ part.
(a) Western
(b) Eastern
(c) Northern
(d) Southern
Answer:
(d) Southern

Question 8.
Goa is the most urbanised state in India with _______ urban population.
(a) 92%
(b) 52%
(c) 62%
(d) 82%
Answer:
(c) 62%

Question 9.
_____ is more than 80% urban.
(a) Goa
(b) Gujarat
(c) Delhi
(d) Puducherry
Answer:
(c) Delhi

Question 10.
Today, about ______ of Brazil’s population lives in urban area.
(a) 96%
(b) 66%
(c) 86%
(d) 76%
Answer:
(c) 86%

Question 11.
Looking at the growth in a few parts of the country, the government is promoting “Go _______ ” policy which reduces pressure on other densely populated areas.
(a) East
(b) North
(c) South
(d) West
Answer:
(d) West

Question 12.
Urbanisation has occurred more in the _______ states, in Brazil.
(a) inland
(b) coastal
(c) central
(d) north-western
(b) coastal

Question 13.
_________ is a port on the confluence of the Negro and the Amazon rivers, where urbanisation has occurred.
(a) Alagoas
(b) Parana
(c) Manaus
(d) Ceara
(c) Manaus

Find out the correct group :

Question 1.
States of Brazil in having 91% to 100% urban population.
(a) Sao Paulo, Goias, Espirito Santo and Tocantins.
(b) Espirito Santo, Rio De Janeiro, Para and Goias.
(c) Espirito Santo, Goias, Sao Paulo, Rio De Janeiro.
(d) Sao Paulo, Amapa, Santa Catarina, and Rondonia.
Answer:
(c) Espirito Santo, Goias, Sao Paulo and Rio De Janeiro.

Question 2.
States of India having less than 20% of Urbanization.
(a) Meghalaya, Uttar Pradesh, Arunachal Pradesh and Rajasthan. .
(b) Lakshadweep, Daman and Diu, Puducherry and Nagaland.
(c) Tamil Nadu, Mizoram, Gujarat and Maharashtra.
(d) Odisha, Assam, Bihar and Himachal Pradesh.
Answer:
(d) Odisha, Assam, Bihar, Himachal Pradesh.

Question 3.
Nucleated settlements in India.
(a) Vindhyan plateau, Plateau region of Narmada valley, Paddy lands in Bihar and Uttar Pradesh.
(b) Rajasthan, Sikkim, Arunachal Pradesh, and Punjab.
(c) Himalayan slopes, East Rajasthan, Tribal part of Madhya Pradesh and Nagaland.
(d) Vindhyan plateau, Paddy lands in Uttar Pradesh, Land with dissected topography and Bihar.
Answer:
(a) Vindhyan plateau, Plateau region of Narmada valley, Paddy lands in Bihar and Uttar Pradesh.

Question 4.
Dispersed settlements in India.
(a) West coast, West Rajasthan, Paddy lands of Punjab and Mizoram.
(b) Land with dissected topography, South Rajasthan, Vindhya plateau and Uttar Pradesh.
(c) Tribal part of Madhya Pradesh, Himalayan slopes, West and South Rajasthan and Land with the uneven topography.
(d) Himalayan slopes, Narmada Valley, West Rajasthan and South India.
Answer:
(c) Tribal part of Madhya Pradesh, Himalayan slopes, West and South Rajasthan and Land with the uneven topography.

Question 5.
States of India having urbanization between 41% to 60%.
(a) Chandigarh, Daman and Diu, Gujarat and Uttar Pradesh.
(b) Maharashtra, Kerala, Gujarat and Mizoram.
(c) Jharkhand, Karnataka, Maharashtra and Goa.
(d) Andhra Pradesh, West Bengal and Uttarakhand, Assam.
Answer:
(b) Maharashtra, Kerala, Gujarat, Mizoram.

Question 1.
Match the columns:

Column ‘A’		Column ‘B’
(1)	Most urbanised state in India	(a)	Sao Paulo
(2)	Most urbanised state in Brazil	(b)	Goa
(3)	Least urbanised state in India	(c)	Mato Grosso
(4)	Least urbanised	(d)	Himachal Pradesh
	state in Brazil	(e)	Delhi
		(f)	Para

Answer:
1 – b
2 – a
3 – d
4 – f

Are the sentences right or wrong?

Question 1.
India does not have a great tradition of urbanisation.
Answer:
Wrong.

Question 2.
The earlier settlements in Brazil were formed by the settlers from America.
Answer:
Wrong.

Question 3.
North-East Highlands of Brazil suffer from extreme drought.
Answer:
Right.

Question 4.
The growth of urbanisation in India has been very fast, reaching 86% in 2011.
Answer:
Wrong.

Question 5.
In underdeveloped countries, the rate of urbanisation is low.
Answer:
Right.

Give geographical reasons:

Question 1.
Sao Paulo area has nucleated settlements.
Answer:
(i) Sao Paulo is situated in South East coast of Brazil.
(ii) The region has a good water supply.
(iii) It an extensive area under rich fertile soil which is ideal for growing coffee.
(iv) It has a large supply of natural minerals, such as iron ore.
(v) It also has a steady energy supply.
(vi) This region has a good transport system too.
So, Sao Paulo area has nucleated settlements.

Question 2.
The Brazilian government is promoting ‘Go West’ policy.
Answer:
(i) Brazil is one of the few developing countries which is highly urbanised.
(ii) But urbanisation in Brazil is confined to South and South East.
(iii) For e.g. States like Sao Paulo, Goias, Minas Gerais, Rio De Janeiro have very high urban population.
(iv) Western Brazil continues to remain least urbanised, which is creating regional imbalance.
(v) In order to reduce regional imbalance, the Brazil Government is promoting ‘Go-West Policy’.

10th Std Geography Questions And Answers:

• Field Visit Class 10 Geography Questions And Answers
• Location and Extent Class 10 Geography Questions And Answers
• Physiography and Drainage Class 10 Geography Questions And Answers
• Climate Class 10 Geography Questions And Answers
• Natural Vegetation and Wildlife Class 10 Geography Questions And Answers
• Population Class 10 Geography Questions And Answers
• Human Settlements Class 10 Geography Questions And Answers
• Economy and Occupations Class 10 Geography Questions And Answers
• Tourism, Transport and Communication Class 10 Geography Questions And Answers

Balbharti Maharashtra State Board Class 10 Geography Solutions Chapter 9 Tourism, Transport and Communication Notes, Textbook Exercise Important Questions and Answers.

Std 10 Geography Chapter 9 Question Answer Tourism, Transport and Communication Maharashtra Board

Class 10 Geography Chapter 9 Tourism, Transport and Communication Question Answer Maharashtra Board

Geography Class 10 Chapter 9 Question Answer Maharashtra Board

1. State whether right or wrong with reasons.

Question a.
The future of tourism is bright in India due to its natural diversity.
Answer:
Right.

Question b.
Tourism is an invisible trade.
Answer:
Right.

Question c.
The indicator of development in a country is the development of transport in that country.
Answer:
Right

Question d.
Brazil’s time is ahead of India’s time.
Answer:
Wrong

Question 5.
The development of tourism in India has begun recently.
Answer:
Right.

2. Answer in short:

Question a.
Which factors attract more tourists in Brazil?
Answer:
The factors which attract more tourists in Brazil are:

• Clean, white sand beaches
• Attractive seacoasts
• Beautiful islands
• Beautiful orchards
• Deep dense forests of Amazon
• Various birds and animals
• Cities like the new capital city of Brasilia, Rio-de- Janeiro and Sao Paulo.
• Eco-tourism

Question b.
What are the difficulties in the development of the railway system in Brazil’s internal areas?
Answer:

• The densely forested lands of Amazon River Basin and the swampy lands have limited the development of railways in Brazil.
• Large pockets of Brazil are unpopulated. Roadways are the most common mode of transportation in the Eastern part of Brazil and waterways have developed on a commercial basis in the Amazon River.
• The trains are used for long distance transportation of passengers only in a few cities and by tourists. These are the difficulties in the development of the railway system in Brazil’s internal areas.

Question 3.
A plane leaves Brasilia at 11 a.m. on 31st December. The plane crosses 0° Meridian and reaches Vladivostok via New Delhi. Tell the local time, date and day at New Delhi and Vladivostok when the plane leaves Brasilia.

Answer:

Time difference between Brasilia and GMT = 3 hours
Time at GMT = 11 a.m.+3 hours
= 2.00p.m.

Time difference between GMT and New Delhi = 5 hours 30 min.
Time at New Delhi = 2 a.m. + 5 hours 30 min.
= 7 hours 30 min.
= 31st December,
Sunday, 7.30 p.m.

Time difference between
New Delhi and Vladivostok = 4 hours 30 min.
Time at Vladivostok = 7.30 p.m. + 4 hours 30 min.
= 12.00 am

The local time, date and day at Delhi are 7 : 30p.m. , 31st December, Sunday
local time, date and day at Vladivostok are 12 am. , 1st January, Monday.

4. Match the following:

Column A’	Column ’B’
(1)  Trans-Amazonian (2) Road Transport (3)  Rio de Janeiro (4) Manmad	(a)       Tourist  Place Highway (b)      Railway Station in India (c)       Golden Quadrilateral (d)      Major Highway (e)       40° W Meridian

Answer:
1 – d
2 – c
3 – a
4 – b

5. Give geographical reasons:

Question a.
Eco-tourism is being developed more in Brazil.
Answer:

• Eco-tourism means responsible travel to natural areas without causing damage to the environment.
• Brazil has the largest number of vegetation species in the world including Amazon, the largest rainforest of the world and a great diversity of wild life.
• It has clean white sand beaches, attractive seacoasts, beautiful islands and orchards. Looking at the sensitivity of the natural resources in Brazil, ecotourism is being developed here.

Question b.
The internal waterways are not developed in Brazil.
Answer:

• Most of the rivers in Brazil flow with high speed.
• The amount of discharge of many rivers is very huge.
• In Brazil, rigid topography is found at many places near river basins. Many of the areas near rivers are inaccessible.
• Therefore, internal waterways are not developed in Brazil.

Question c.
A dense network of railways has developed in the North Indian Plains.
Answer:

• The North Indian Plains are flat plain lands with a dense population.
• Due to agricultural development, many agro- based industries have developed here.
• Thus there is a high demand for transportation especially railways for movement of freight and passenger transport.

Question d.
Development of transport is important for the country’s progress.
Answer:

• Transport modes help is the movement of humans, animals and goods from one location to another.
• Transport enables social, economic and cultural development of the country.
• Road transport facilitates door-to-door service.
• Rail transport is suitable for long distance and bulky goods.
• Water transport plays an important role in international trade and suitable for bulky goods.
• Air transport provides the fastest means of transportation.

Question e.
We rely on the sea routes for international trade.
Answer:

• Waterways is the cheapest modes of transportation for bulky and perishable goods over long distances.
• International trade includes import and export of goods.
• India is surrounded by Bay of Bengal, Arabian Sea and India Ocean, therefore we have a long coastline.
• So we rely on the sea routes for international trade.

6. Differentiate between:

Question a.
Water transport in the Amazon and the Ganga river.
Answer:

Water transport in the Amazon River	Water Transport in the Ganga River
(i) River Amazon is navigable throughout its course due to its gentle slope. (ii) Boats ply from Equitos in Peru to its mouth i.e., approximately 3700 km. (iii) River Amazon is used for navigation between Brazil and neighbouring countries.	(i) River Ganga is navigable only in its middle and lower course which is gentler as compared to its upper course. (ii) Boats ply from Allahabad to Haldia. i.e. approximately 1620 km. (iii) River Ganga is used for inland transportation.

Question b.
Communication in Brazil and India
Answer:

Communication in Brazil	Communication in India
(i) Telecommunication services in Brazil are well developed and efficient. (ii) Brazil is developing technology to send domestically-made satellites into space with its own rockets.	(i) With the explosion of electronic media, telecommunication industry has become one of the fast growing sectors. (ii) With development of our own satellites, India has come a long way in this field.

Question c.
IST and BRT
Answer:

IST	BRT
(i) 1ST is the Indian Standard Time.	(i) BRT is the Brasilia Time/Brazil Time. (Standard Time)
(ii) India has only one standard time zone.	(ii) Brazil has four time zones.
(iii) The official 1ST is based on 82.5° E longitude	(iii) The official BRT is GMT – 03 which passes
which passes through Allahabad, Uttar Pradesh.	through Brasilia.
(iv) 1ST is 5hrs 30mins ahead of Greenwich Meridian	(iv) BRT is 2,3,4, or 5 hrs behind Greenwich Meridian
(v) Time as India is in the eastern hemisphere.	(v) Time as Brazil is in the western hemisphere.

7. Write short notes on:

Question a.
Modem means of communication:
Answer:
(i) Modern means of communication includes landlines as well as mobile services, television broadcasting and computer/internet access.
(ii) In this era of information and communication technology, digitally enhanced communication devices like mobile phones, smart phones, internet and satellites are being used.

Question b.
Air transport in India:
Answer:
(i) Air transport is more developed in India as compared to Brazil.
(ii) The use of international and internal airways is increasing.
(iii) Important airports from where domestic and foreign travel take place are Mumbai, Delhi, Kolkata, Chennai, Bengaluru, etc.

Question c.
Correlation between physiography and internal waterways:
Answer:
(i) Internal (Inland) waterways comprises of rivers, canals, backwaters, creeks, etc. which are the cheap means of transportation.
(ii) Deep waters, gentle slopes, absence of rapids and waterfalls and the long course of rivers are favourable factors for development of internal waterways.
(iii) The longest waterways in the world is developed in the Amazon river in Brazil which is navigable for around 3700 kms.
(iv) Perennial river like Ganga in India is navigable in its lower course but the peninsular rivers are not used due to shallow waters, shorter course, seasonal nature, etc.

Question d.
Importance of Standard Time:
Answer:
(i) Standard Time is the official time and is commonly accepted all over the country or region.
(ii) The importance of Standard Time is the most, if the country has a vast longitudinal extent, since there will be a great difference between the time of its places located in the eastern and the western parts.
(iii) It helps in making proper schedules of travel, business meeting, co-ordinating the functioning of various organisations, etc.
(iv) Thus Standard Time helps in avoiding confusion regarding day, date and time.

Class 10 Geography Chapter 9 Tourism, Transport and Communication Intext Questions and Answers

Answer the following questions on the basis of the map given.

Observe the map carefully and answer the following questions:


Question 1.
Name the terminal points of the North-South Corridor of Golden quadrilateral Highway.
Answer:
North – Srinagar, South – Kanyakumari.

Question 2.
Name the terminal points of East-West corridor Golden Quadrilateral highway.
Answer:
East – Silchar ; West – Porbandar.

Question 3.
Name the three major ports on the western coast.
Answer:
Porbandar, Mumbai and Cochin are the three major ports on the western coast.

Question 4.
Name the three major ports on the eastern coast.
Answer:

1. Chennai
2. Vishakhapatnam and
3. Haldia

Question 5.
(Kolkata) are the three major ports on the eastern coast. Which parts of India have a spare network of road transport route? Give reason.
Answer:
The northernmost part of India in the state of Jammu and Kashmir does not have any national highway or other roadways, because it is a mountainous region.

Observe the given map carefully and answer the following questions:

Question 1.
What does the map indicate ?
Answer:
The map indicates the important railway routes and airports of India.

Question 2.
Which part of India has many airports compared to the others?
Answer:
The Southern part of India (i.e.) Peninsular India has many airports compared to the other parts of India.

Question 3.
Which part of India has a dense network of rail routes?
Answer:
North Indian plains region has a dense network of rail routes.

Question 4.
Name the northernmost important railway station.
Answer:
Baramulla is the northernmost important railway station.

Question 5.
Name the easternmost important railway station.
Answer:
Tinsukia is the easternmost important railway station.

Question 6.
Name the two westernmost important railway stations.
Answer:
Okha and Naliya are the two westernmost important railway stations.

Try this

Look at the graph and answer the following questions:

Question 1.
Which country attracted more international tourists in the year 1995?
Answer:
India attracted more international tourists in the year 1995.

Question 2.
In which country did more international tourists arrive in the year 2000?
Answer:
More international tourists arrived in Brazil in the year 2000.

Question 3.
In which year can an increase be seen in the number of international tourists in India?
Answer:
An increase in the number of international tourists in India can be seen from the year 2010.

Question 4.
What was the number of international tourists in the year 2015 in both the countries? What was the difference between them?
Answer:
The number of international tourists in India in 2015 was approximately 130 lakhs. The number of international tourists in Brazil in 2015 was 60 lakhs. The difference between India and Brazil in the numbers of international tourists in 2015 was 70 lakh people. (130 lakhs – 60 lakhs).

Question 5.
What could be the reason of increase in tourists in India after the year 2010?
Answer:
There is an increase in tourists coming to India after 2010 because :

• Different types of tourism like eco-tourism, health tourism, business tourism, etc. have been promoted by the Indian Government.
• The quality of travel and stay in India has also improved.

Question 6.
Name the kind of graph shown above.
Answer:
Polyline graph.

Can you tell ?

Look at the graph and answer the following questions:

Question 1.
What type of graph is shown here?
Answer:
The type of graph shown here is a Joint Bar Graph.

Question 2.
What does the graph show?
Answer:
The graph shows:

• The percentage of population engaged in tourism in Brazil and India in 2016.
• The contribution of tourism in GDP by both the countries in 2016.

Question 3.
Which country’s tourism has a larger share in the contribution towards GDP?
Answer:
Brazil’s tourism has a larger share in the contribution towards GDP.

Question 4.
Which country has a larger population engaged in tourism sector but contributes lesser in GDP?
Answer:
India has a larger population engaged in tourism sector but contributes lesser in GDP terms.

Question 5.
How much percentage of India’s population is engaged in tourism?
Answer:
Nearly 9.5 percentage of Indian population is engaged in tourism.

Question 6.
How much is the contribution of tourism in India’s GDP in 2016? .
Answer:
The contribution of tourism in India’s GDP in 2016 is nearly 8.5 per cent.

Make friends with maps

Study the transport map of Brazil and answer the following.

Question 1.
Which means of transport are seen on the map?
Answer:
All the means of transport like roadways, railways, airways, and waterways are seen on the map.

Question 2.
Which means of transport has a denser network?
Answer:
The roadways have a denser network.

Question 3.
Which highway can be seen prominently? Which places does it join?
Answer:
The Trans Amazonian Highway can be seen prominently. It connects Cruzeiro do sul, Porto Velho, Manaus and Brasilia.

Question 4.
What could be the reason for the development of railways in the South-East?
Answer:
(i) South-east Brazil is the richest and the most populated region of the country.
(ii) Agriculture, mining, and tourism are well developed in this part of Brazil.

Question 5.
In which part of Brazil do you see a lesser development of transport network? What could be the reason?
Answer:
(i) Amazon in the north and Pantanal in the west have lesser development of transport network.
(ii) Amazon in the north due to dense forest cover whereas Pantanal is a swampy land.

Think about it.

Question 1.
Considering the development of transport in a place, which factors do you think are responsible for the development of transport in Brazil? Also, think which means of transport could be used in Brazil given its topography and drainage?
Answer:
Considering the development of transport in a place, the factors that are responsible for the development of transport in Brazil are:

• The physiography, accessibility, population, climatic conditions, availability of power/fuel, funds, etc.
• Roads and ports need to be upgraded.
• Railways are few and competitive. They can be increased in the central part.
• With its topography and drainage Brazil should develop more waterways.

Activity

Look at the transport maps of India and the make friends with maps.

Question 1.
Which means of transport are visible on the map?
Answer:
The means of transport used are roadways and waterways.
The means of transport used are railways and airways.

Question 2.
In which part of India is the density of railways more?
Answer:
The density of railways is more in the Northern Plains region.

Question 3.
Name five important ports and airports of India.
Answer:
Ports: Mumbai ,Vishakhapatanam, Haldia, Chennai and Kandla.
Airports: Delhi, Mumbai, Bengaluru, Chennai, and Kolkata.

Question 4.
Which parts of India have a sparse network of transport? What could be the reason?
Answer:
(i) The north and the north-east parts of India have a sparse network of transport.
(ii) Due to mountainous and snow covered areas in the north and the dense inaccesible forest areas of the north-east, the transportation network is sparse here.
(iii) Also these regions have low population and lack of economic opportunities.

Give it a try.

Question 1.
Arun called his mother from Digboi at 7 am. At what local time will his mother pick up his call at Jaisalmer?
Answer:
Arun’s mother will pick his call at 5.00 am. local time at Jaisalmer.

Question 2.
Calculate the difference in time between the two points in minutes.

Westernmost point: Nascente do Rio Moa (07° 32’33″S, 70° 59’W) Easternmost point: Ponta do Seixas, Paraiba (07° 09′ 28″S, 34° 47’W),
Answer:
The difference in time between the Easternmost and the Westernmost part of Brazil is 168 minutes.

Activity

Read the map and answer the following questions:

Question 1.
How many divisions can you see in the map?
Answer:
We can see 4 divisions in the map.

Question 2.
What do these divisions signify?
Answer:
These divisions signify the time zones in Brazil.

Question 3.
What does the term ’behind the GMT’ mean?
Answer:
The Greenwich Meridian Time is a time set with reference to 0° longitude that passes through Greenwich. The countries lying to the west of 0° longitude are ’behind the GMT’.

Question 4.
Which part of Brazil is ahead of other?
Answer:
The easternmost part of Brazil is ahead of the other parts.

Question 5.
By how many minutes is this part ahead of others?
Answer:
60 to 180 minutes.

Question 6.
What does the red line in the map show?
Answer:
The red line in the map is the official BRT which is in the GMT-03 time zone. It is 3 hours behind GMT.

Make friends with maps

Study the map given in figure and answer the following questions:

Question 1.
Calculate the difference between the two longitudinal extremes of mainland India. Is it more than Brazil?
Answer:
The difference between the two longitudinal extremes of east and west mainland India is about 29°.

Question 2.
Which longitude in India is called the Indian Standard Time (IST)?
Answer:
The 82° 30′ E longitude is called Indian Standard Time (IST)

Question 3.
What is the difference between IST and the GMT?
Answer:
The IST time is 5 hours and 30 minutes ahead of the GMT.

Question 4.
How many local times are there in India?
Answer:
There are 29 local times.

Question 5.
How much is the time difference between the western most and the eastern most points of India?
Answer:
Two hours, 120 minutes.

Think about it.

Question 1.
It is 12 noon at Delhi. What would be the local time in Brasilia?
Answer:
If it is 12 noon at Delhi, the local time in Brasilia would be 3.30 a.m. This is because Brasilia is 3 hours behind GMT and Delhi is 5 hours 30 minutes ahead of GMT. Therefore

Time difference between Brasilia and Delhi is of 8 hours 30 mins (3 hours + 5 hours 30 mins) Time at Delhi = 12 noon
Time at Brasilia = 12 noon – 8 hours 30 mins
= 3.30 a.m.

Use your brain power

Question 1.
Saurabh and Ashwini work for a MNC. Two of their regional head offices are located in Brazil in Rio De Janeiro and Manaus, respectively. Both of them have to contact either of the head offices constantly.
As they have to adjust timings according to their head offices, find out their corresponding timings in India, if they work according to office timings in Brazil, i.e 10 a.m. to 5 p.m.
Answer:
(i) Let us assume Saurabh is coordinating with Rio De Janeiro’s head office and Ashwini is coordinating with the head office of Manaus.
(ii) Brazil has four time zones. It is behind the GMT by 2, 3, 4 or 5 hours.
(iii) Rio De Janeiro is in the 2nd time zone which is 3 hours behind GMT (GMT-03) and Manaus is the 3rd time zone which is 4 hours behind GMT (GMT-04).
(iv) Now, the time difference between GMT and 1ST is of 5 hours 30 mins.
They have to make following adjustments :

Saurabh
Rio De Janeiro	GMT	IST
10 a.m.	1 p.m.	6.30 p.m.
5 p.m.	8 p.m.	1.30 a.m.

Ashwini
Manaus	GMT	IST
10 a.m.	2 p.m.	7.30 p.m.
5 p.m.	9 p.m.	2.30 a.m.

Rio De Janeiro is in the 2nd time zone which is 3 hours behind GMT (GMT-03) and Manaus is the 3rd time zone which is 4 hours behind GMT (G
Corresponding timings in India Saurabh: 6.30 p.m. to 1.30 a.m. Ashwini: 7.30 p.m. to 2.30 a.m.

Give it a try

Question 1.
On what basis will you decide how many standard times should be there in a country?
Answer:
The longitudinal extent of a country will help one decide how many standard times should be there in a country.

Class 10 Geography Chapter 9 Tourism, Transport and Communication Additional Important Questions and Answers

Choose the correct option and rewrite the statements:

Question 1.
The new capital city of Brazil is ______.
(a) Rio de Janeiro
(b) Sao Paulo
(c) Manaus
(d) Brasilia
Answer:
(d) Brasilia

Question 2.
A city that attracts a lot of tourists is _______.
(a) Rio de Janeiro
(b) Brasilia
(c) Manaus
(d) Ponta de Seixas
Answer:
(a) Rio de Janeiro

Question 3.
The proportion of the Indian population engaged in tourism is proportionately _____ Brazil.
(a) lower than
(b) higher than
(c) equal to
(d) extremely lesser than
Answer:
(b) higher than

Question 4.
The football stadium at ______ is quite well known
(a) Rio de Janeiro
(b) Manaus
(c) Sao Paulo
(d) Boa Vista
Answer:
(b) Manaus

Question 5.
The most common method of transportation in Brazil is ____.
(a) railways
(b) waterways
(c) roadways
(d) airways
Answer:
(c) roadways

Question 6.
The density of road network in Brazil is concentrated in the ____ part of the country.
(a) southern
(b) northern
(c) western
(d) eastern
Answer:
(d) eastern

Question 7.
The forested lands of the Amazon River basin and the ______ lands have limited the development of roadways in this part of Brazil.
(a) drought-prone
(b) fertile
(c) swampy
(d) semi-arid
Answer:
(c) swampy

Question 8.
Waterways have been developed on a commercial basis in the _____ river.
(a) Amazon
(b) Uruguay
(c) Purus
(d) Aragua
Answer:
(a) Amazon

Question 9.
Boats ply from _____ in Peru to the mouth of the river Amazon.
(a) Lima
(b) Cusco
(c) Equitos
(d) Nazca
Answer:
(c) Equitos

Question 10.
Apart from R. Amazon, another important river for waterways is the ____ Parana river.
(a) south-flowing
(b) north-flowing
(c) east-flowing
(d) west-flowing
Answer:
(a) south-flowing

Question 11.
The contribution of ______ is less in the transportation system of Brazil.
(a) railways
(b) roadways
(c) waterways
(d) airways
Answer:
(d) airways

Question 12.
Railway network is dense in the ______ of India.
(a) hilly states
(b) north-eastern states
(c) central parts of India
(d) north indian plains
Answer:
(b) north-eastern states

Question 13.
Approximately, 95% of foreign trade moves through ______ routes, in India.
(a) road
(b) rail
(c) air
(d) ocean
Answer:
(d) ocean

Question 14.
The westernmost extreme point on mainland Brazil is ______.
(a) Rio Grande
(b) Rio de Janeiro
(c) Nascente do Rio Moa
(d) Ponta do Seixas
Answer:
(c) Nascente do Rio Moa

Question 15.
The easternmost extreme point on mainland Brazil is ______
(a) Rio Grande
(b) Sao Paulo
(c) Ponta do Seixas
(d) Nascente do Rio Moa
Answer:
(c) Ponta do Seixas

Question 16.
Brazil has ______ time zones.
(a) 3
(b) 4
(c) 5
(d) 6
Answer:
(b) 4

Question 17.
(BRT) Brazil time is _____ hours behind GMT.
(a) three
(b) four
(c) five
(d) six
Answer:
(a) three

Question 18.
Today, more than 45% of the Brazilian population has access to the ______.
(a) mobile services
(b) television broadcasting
(c) radio broadcasting
(d) internet
Answer:
(d) internet

Question 19.
The telecommunication infrastructure is fairly modern, particularly in ____ Brazil.
(a) north
(b) north-west
(c) north-east
(d) central-south
Answer:
(d) central-south

Question 20.
______ services in Brazil are well-developed and efficient.
(a) Air
(b) Railway
(c) Helicopter
(d) Telecommunication
Answer:
(d) Telecommunication

Question 21.
With regard to telecommunication infrastructure, the north and ______ are drastically less developed.
(a) south
(b) south-west
(c) north-west
(d) central-south
Answer:
(c) north-west

Question 22.
Over recent years, _______ have led to the rapid expansion of telecommunication services in Brazil.
(a) landline phones
(b) radio broadcasting
(c) television broadcasting
(d) mobile telephones
Answer:
(d) mobile telephones

Question 23.
India has ______ standard time zone/s.
(a) one
(b) two
(c) three
(d) four
Answer:
(a) one

Question 24.
The difference between the two extreme most points in India is about _____.
(a) 120 minutes
(b) 210 minutes
(c) 168 minutes
(d) 186 minutes
Answer:
(a) 120 minutes

Question 25.
The difference between the two extreme most points of Brazil is _______.
(a) 186 minutes
(b) 168 minutes
(c) 120 minutes
(d) 200 minutes
Answer:
(b) 168 minutes

Question 26.
The 82°30’E longitude is the Indian Standard Time longitude which passes though ________.
(a) Allahabad
(b) Ahmedabad
(c) Hyderabad
(d) Muzzaffarabad
Answer:
(a) Allahabad

Question 27.
India is one of the largest users of _______ and internet.
(a) landlines phones
(b) television
(c) radio
(d) smartphones
Answer:
(d) smartphones

Question 28.
About 85% of passenger and 70% of freight traffic are carried by every year in India.
(a) roadways
(b) railways
(c) waterways
(d) airways
Answer:
(a) roadways

Question 29.
______is the official time of Brazil.
(a) GMT-01
(b) GMT-04
(c) GMT-03
(d) GMT-02
Answer:
(c) GMT-03

Question 30.
The prominent highway of Brazil is ________.
(a) Trans Belem Highway
(b) Trans Rio Grande Highway
(c) Trans Amazonian Highway
(d) Trans Brasilia Highway
Answer:
(c) Trans Amazonian Highway

Match the following:

Question 1.

Column ’A’	Column ‘B’
(1) The new capital city	(a) Rio de Janeiro
(2) The city attracting a lot of tourist	(b) Manaus
(3) Football stadium	(c) Peru
(4) Beach	(d) Brasilia
(5) Equitos	(e) Sao Paulo
	(f) Boa Vista

Answer:
1 – d
2 – e
3 – b
4 – a
5 – c

Answer the following questions in one sentence:

Question 1.
State the factors that attract foreign tourists towards India.
Answer:
Foreign tourists visit India to see and understand its rich heritage and culture, for adventure, to avail the health services and for business purposes.

Question 2.
What is the kind of service provided by roadways in India?
Answer:
About 85% of passenger traffic and 70% of freight traffic are carried by roadways every year in India.

Question 3.
How important are the inland waterways in India’s transportation?
Answer:
Inland waterways comprising rivers, canals, backwaters, creeks, etc., which contribute about only 1% to India’s transportation.

Question 4.
In what way are the ocean routes useful for India?
Answer:
Approximately 95% of India’s foreign trade moves through ocean routes.

Question 5.
What kind of advanced space technology is Brazil developing?
Answer:
Brazil is developing technology to send domestically-made satellites into space with its own rockets.

Question 6.
Write a short note about the telecommunication infrastructure in different parts of Brazil.
Answer:
The telecommunication infrastructure is fairly modern, particularly in central-south Brazil, but the north and north-west are drastically less developed.

Question 7.
Why have roadways not developed in the north and north-western part?
Answer:
The forested lands of the Amazon River basin and the swampy lands have limited the development of roadways in the north and north-western region.

Question 8.
Which time zone is considered to be the official Brazilian time?
Answer:
GMT-03 Time Zone is considered to be the official Brazilian time.

Distinguish between:

Question 1.
The use of railways in Brazil and India.
Answer:

The use of railway in Brazil	The use of railway in India
(i) Railways have not developed very well in Brazil.	(i) Compared to Brazil, India has a denser network of railways.
(ii) The use of trains for long distance transportation is restricted to a few urban tourist routes though it is cheaper.	(ii) Freight and passenger transport have been facilitated due to the development of the railways, which are considered very important for the growth of Indian economy.
(iii) Dense network of railways have developed in south and south-east Brazil as compared to other parts of Brazil.	(iii) Dense network of railways have developed in the North-Indian Plains as compared to other parts of India.

Question 2.
The longitudinal extent of India and Brazil
Answer:

The longitudinal extent of Brazil	The longitudinal extent of India
(i) Extreme westernmost point: Nascente do Rio Moa. (70°59’W)	(i) Extreme westernmost point : Ghuar Mota. (70°E)
(ii) Extreme easternmost point: Ponta do Seixas.(34047′ w)	(ii) Extreme easternmost point: Kibithu. (97°E)
(iii) Time difference is 168 minutes approximately 2 hrs 48 minutes.	(iii) Time difference is 120 minutes on mainland i.e., approximately 2 hrs.
(iv) There is a vast time difference between the extreme most points of Brazil due to vast longitudinal extent.	(iv) There is comparatively less time difference between the extreme points of India.

Question 3.
The density of roadways in Brazil and India.
Answer:

The density of roadways in Brazil	The density of roadways in India
(i) Roadways account for more than half of the transportation system in the country.	(i)    As compared to Brazil, India has a denser network of transport. About 85% of passenger and 70% of freight traffic are carried by road every year.
(ii) Density of road network is high in the eastern	(ii) Density of road network is high in the North
part of the country.	Indian Plains in the northern part of India.

Question 1.
Mark the following on an outline map of Brazil. Name the following:

1. The new capital city of Brazil.
2. Two cities that attract a lot of tourist.
3. A south-flowing river important for waterways.
4. The easternmost extreme point of mainland Brazil.
5. The westernmost extreme point part of mainland Brazil.

Answer:

Question 2.
Show the following on a given outline map of Brazil.
Given index:

(A) Ports:

• Vitoria
• Manaus

(B) Airports:

• Brasilia
• Campo Grande

(C) Railway Junctions:

• Sao Paulo
• Rio de Janeiro

Answer:

Question 3.
Show the following on a given outline map of India. Give index:
Given index:
(A) Ports:

• Chennai
• Porbandar
• Kochin
• Kandla
• Kolkata

(B) Airports :

• Bengaluru
• Delhi
• Pune
• Thiruvananthapuram

(C) Railway Junctions :

• Mumbai
• Itarsi
• Kota
• Nagpur

Answer:

Give geographical reasons:

Question 1.
India’s contribution of tourism to its GDP appears lesser than Brazil and population engaged seems higher.
Answer:
(i) The number of international tourists visiting India in 2015 was more than that of Brazil.
(ii) Even though this is true, the share of tourism sector in the GDP is less than that of Brazil.
(iii) Apart from this, the proportion of Indian population engaged in tourism is higher than that of Brazil.
(iv) This is primarily dependent on the size of the population of those countries and the size of the GDP.
(v) According to the data available, the population of India is more than Brazil and so is its GDP.
(vi) As the GDP of India is higher than Brazil’s GDP to GDP appears lesser than Brazil’s and population engaged seems higher.

Question 2.
Railways are important for the growth of the Indian economy.
Answer:
(i) Railways are very important for a vast country like India where the distance between places is long.
(ii) Freight and passenger transport have been facilitated due to the development of the railways.
(iii) The more the facilities available for passenger transport and freight transport, the more growth in the economy.
Thus, the railways are very important for the Indian economy’s growth.

Question 3.
Brazil’s time is not ahead of India’s time.
Answer:
(i) The GMT i.e, Greenwich Mean Time, divides the globe into eastern and western hemisphere.
(ii) India lies to the east of GMT and Brazil lies to the West of GMT.
(iii) Places lying to the east of GMT, are ahead of time and places lying to the west of GMT (like Brazil) are behind time.

Question 4.
The future of tourism is bright in India.
Answer:
(i) India is rich in natural beauty that includes mountains, forests, plateaus, plains, islands, coastal areas, beaches, etc.
(ii) India also has a rich heritage and a huge variety of cultural and historical attractions.
(iii) In recent years new forms of tourism have been developed in India like Eco tourism, Agro tourism, Medical tourism, Film tourism, etc.
(iv) Also infrastructural facilities, branding and marketing initiatives have helped to promote Indian tourism.
So the future of tourism is bright in India.

Question 5.
Tourism is an invisible trade.
Answer:
(i) Tourism belongs to the service sector as various services are provided to the tourists.
(ii) For e.g., hotels, lodges, transport, food, entertainment, etc.
(iii) Tourism increase the GDP of economy without exchange of goods.
Thus, tourism is an invisible trade.

Question 6.
he indicator of development in a country is the development of transport in that country.
Answer:
(i) Transportation facilitates trade and creates employment opportunities.
(ii) With the development of transport there is socio-economic and cultural development of the country.
Hence it is an indicator of development in a country.

10th Std Geography Questions And Answers:

• Field Visit Class 10 Geography Questions And Answers
• Location and Extent Class 10 Geography Questions And Answers
• Physiography and Drainage Class 10 Geography Questions And Answers
• Climate Class 10 Geography Questions And Answers
• Natural Vegetation and Wildlife Class 10 Geography Questions And Answers
• Population Class 10 Geography Questions And Answers
• Human Settlements Class 10 Geography Questions And Answers
• Economy and Occupations Class 10 Geography Questions And Answers
• Tourism, Transport and Communication Class 10 Geography Questions And Answers

Balbharti Maharashtra State Board Class 10 Geography Solutions Chapter 2 Location and Extent Notes, Textbook Exercise Important Questions and Answers.

Std 10 Geography Chapter 2 Question Answer Location and Extent Maharashtra Board

Class 10 Geography Chapter 2 Location and Extent Question Answer Maharashtra Board

Geography Class 10 Chapter 2 Question Answer Maharashtra Board

1. Are the sentences right or wrong. ? Rewrite the wrong ones

Question a.
Brazil is mainly located in the Southern Hemisphere.
Answer:
Right

Question b.
Tropic of Capricorn passes through the middle of India.
Answer:
Wrong. Tropic of Cancer passes through the middle of India.

Question c.
The longitudinal extent of Brazil is less than India.
Answer:
Wrong. The longitudinal extent of Brazil is more than India.

Question d.
Equator passes through the northern part of Brazil.
Answer:
Right

Question e.
Brazil has a coastline along the Pacific Ocean.
Answer:
Wrong. Brazil has a coastline along the Atlantic. Ocean.

Question f.
Pakistan is a neighbouring country to the south east of India.
Answer:
Wrong. Pakistan is neighbouring a country to the north west of India.

Question g.
The southern part of India is called Peninsula.
Answer:
Right.

2. Answer in brief:

Question a.
What problems did Brazil and India face after independence?
Answer:
(i) India was under the British rule for almost one- and-a-half centuries and it got its independence in the year 1947.
(ii) It faced several problems like three wars, famine situations in various parts and similar issues after independence.
(iii) Brazil gained its independence in 1822 after more than three centuries of Portuguese rule.
(iv) From 1930 to 1985, for more than a half century, it was under a populist military government and it faced global financial difficulties in the late 20th century.
Thus, both India and Brazil faced many problems post-independence.

Question b.
How are Brazil and India different from each other in terms of location?
Answer:
(i) India is located in the northern hemisphere of the earth whereas some part of Brazil lies in the northern hemisphere and most of it lies in the southern hemisphere.
(ii) India entirely lies in the eastern hemisphere whereas, Brazil lies in the western hemisphere.
(iii) India lies in the continent of Asia whereas Brazil lies in the continent of South America.
(iv) India lies in the southern part of the continent of Asia whereas Brazil lies in the northern part of South American continent.

Question c.
Describe the latitudinal and longitudinal extent of India and Brazil.
Answer:
(i) The extent of the mainland India is 8°4’N to 37°6’N latitudes and between 68°7’E to 97°25’E longitudes.
(ii) Indira Point is the southernmost tip of India.
(iii) It is located on 6°45’N parallel.
(iv) The extent of the mainland Brazil is 5°15’N to 33°45′ S latitudes and between to 34°47’W to 73°48’W longitude.

Select the correct option

Question a.
India’s southernmost point is known as __________.
(a) Lakshadweep
(b) Kanyakumari
(c) Indira Point
(d) Port Blair
Answer:
(c) Indira Point

Question b.
These two countries in South America do not share their border with Brazil?
(a) Chile – Ecuador
(b) Argentina – Bolivia
(c) Columbia – French Guiana
(d) Surinam – Uruguay
Answer:
(a) Chile – Ecuador

Question c.
Both the countries have _________ type of government.
Military
(b) Republic
Communist
(d) Presidential
Answer:
(b) Republic

Question d.
Which of the following shapes show the coastal part of Brazil correctly?

Answer:

Question e.
Which of the following shapes show the coastal part of India Correctly?

Answer:

Question f.
Considering hemisphere, which shape correctly represents the hemisphere in which India lies?

Answer:

Question g.
Considering the hemisphere, which correctly represents the hemisphere in which Brazil mainly lies?

Answer:

Class 10 Geography Chapter 2 Location and Extent Intext Questions and Answers

Colours of both
Answer the following questions with respect to the countries that you have studied.

Question 1.
Out of the countries that you have coloured, which country is larger in size?
Answer:
Brazil is larger in size.

Question 2.
Which country has a larger latitudinal extent?
Answer:
Brazil has a larger latitudinal extent.

Question 3.
How do the locations of Brazil and India differ in terms of their positions in their respective continents?
Answer:
Brazil lies in the northern part of the continent of South America, whereas India lies in the southern part of the continent of Asia.

Question 4.
How many states does each of the two countries have?
Answer:
Brazil has 26 states and one federal district. India has 28 states and 8 union territories.

Question 5.
Obtain information regarding the emblems of both the countries, i.e. India and Brazil.
Answer:
India:
The national emblem of India is an adaptation of the Lion capital of Ashoka at Sarnath. The emblem has three lions visible, the fourth being hidden from the view. The four lions symbolise power, courage, confidence and pride. At the bottom is a horse and a bull, and its centre is a wheel (Dharma Chakra). Forming an integral part of the emblem is the motto inscribed in Devanagari Script: Satyameva Jayate (Truth Alone Triumphs)

Brazil:
The national emblem of Brazil is coat of arms shows the Southern cross in a blue circle. The ring of 27 stars around it represents Brazil’s 26 states and the Federal District. The whole is placed on a star and surrounded by coffee (at the left) and tobacco (at the right), which are the important crops in Brazil. The blue ribbon contains the official name of Brazil (Republica Federativa Do Brazil – Federative Republic of Brazil) in the first line. In the second, the date of the federative republic’s establishment (November 15, 1889) is written.

Give it a try.

Question 1.
The imperial power which ruled Brazil also ruled a part of India. Find out when that part of India achieved independence?
Answer:
Answer: In India, Goa, Diu and Daman, Dadra and Nagar Haveli were under Portuguese rule. These regions got independence on 19th December 1961.

Match the column:

Question 1.

Column ‘A’	Column ‘B’
(1)      Dance form of Brazil (2)      Capital of India (3)      Capital of Brazil (4)      Coffee pot of world	(a)     Brazil (b)     Samba (c)     New Delhi (d)     Brasilia (e)     Bangladesh (f)     Myanmar

Answer:
1 – b
2 – c
3 – d
4 – a

Question 2.

Column ‘A’	Column ‘B’
(1) Country to the south of Brazil	(a) China
(2) Sea to the west of India	(b) Uruguay
(3) Second largest populated country	(c) Arabian sea
(4) Coffee pot of the world Imperial power ruled Brazil	(d) India
	(e) Portuguese
	(f) Japan

Answer:
1 – b
2 – c
3 – d
4 – e

Answer the following questions in one sentence:

Question 1.
Which is the second largest populated country in the world?
Answer:
India is the second-largest populated country in the world.

Question 2.
Which country is called the ‘coffee pot’ of the world’?
Answer:
Brazil is called the coffee pot of the world.

Question 3.
Which dance form is famous in Brazil?
Answer:
Samba is the famous dance form of Brazil.

Question 4.
Name the capital of India?
Answer:
The capital of India is New Delhi.

Question 5.
When did India gain Independence?
Answer:
India got independence on 15th August 1947.

Question 6.
When did Brazil gain independence?
Answer:
Brazil gained its independence on 7th September 1822.

Question 7.
Which countries are located to the north of Brazil?
Answer:
Venezuela, Guyana, Suriname and French Guiana are situated to the north of Brazil

Question 8.
Which countries are located to the west of Brazil?
Answer:
Colombia, Peru, Bolivia, Paraguay and Argentina are situated to the west of Brazil.

Question 9.
Which country is situated to the south of Brazil?
Answer:
Uruguay is situated to the south of Brazil.

Question 10.
Which ocean lies to the east of Brazil?
Answer:
The North and South Atlantic Ocean lies to the east of Brazil.

Question 11.
Which countries are situated to the east of India?
Answer:
Myanmar and Bangladesh are situated to the east of India.

Question 12.
Which countries are situated to the north of India?
Answer:
China, Bhutan and Nepal are situated to the north of India.

Question 13.
Which sea lies to the west of India?
Answer:
Arabian sea lies to the west of India.

Question 14.
Which countries lie to the south of India?
Answer:
Srilanka, Maldives and Indonesia lie to the south of India.

Question 15.
What is the location of the southernmost tip of India?
Answer:
The location of the southernmost tip of India (Indira Point) is 6°45′ N parallel.

Question 16.
According to the equator, in which hemisphere is Brazil located?
Answer:
Some part of Brazil lies in the northern hemisphere, while most of it lies in the southern hemisphere.

Question 17.
In which hemispheres is India located?
Answer:
India is located in the northern and eastern hemispheres.

Question 18.
What type of government does Brazil have today?
Answer:
Today, Brazil has Federal Presidential Republic type of government.

Question 19.
What type of government does India have today?
Answer:
Today, India has Federal Parliamentary Republic type of government.

Question 20.
Where does the name Brazil come from?
Answer:
The name Brazil comes from ‘Pau Brasil’, a local wooded tree.

Question 21.
Who established the early settlement in Brazil?
Answer:
The Portuguese settlers established the early settlement in Brazil.

Question 22.
Distinguish between: Location of India and Brazil
Answer:

India	Brazil
(i) India is located at 8°4’N to 37°6’N latitude and between 68°7’E to 97°25’E longitudes.	(i) Brazil is located at 5°15’N to 33°45’S latitudes and between 34°47’W to 73°48’W.
(ii) It is located in the northern and eastern hemispheres.	(ii) Some part of Brazil lies in the northern hemisphere, while most of it lies in the southern hemisphere. Brazil also lies in the western hemisphere.
(iii) India is located in the southern part of the Asian continent.	(iii) Brazil is located in the northern part of South American continent.

Question 23.
Find the difference between the post-independence characteristics of India and Brazil.
Answer:

Brazil	India
(i) Brazil gained its independence in 1822. From 1930 to 1985, for more than half a century, it was under a populist military government. Presently, Brazil has Federal Presidential Republic type of government	(i) India got its independence in the year 1947. It has Federal Parliamentary Republic type of government.
(ii) The proportion of older people that is non – working population is high.	(ii) The proportion of youth, i.e. working population is high.
(iii )It has overcome global financial difficulties in the late 20th century	(iii) It has faced several problems like three wars, famine situations in various parts and similar issues after independence.
(iv) Sex ratio and literacy rate is high in Brazil.	(iv) Sex ratio and literacy rate is low in India.

Observe the map and answer the following questions.

Question 1.
Identify the countries and water bodies around India and complete the following table.


To the North
To the East
To the South
To the West
Answer:

No.	Directions	Neighbouring Countries/ Oceans
(1)	North	China, Bhutan, Nepal
(2)	South	Indian Ocean, Sri Lanka, Maldives, Indonesia
(3)	East	Myanmar, Bangladesh, Bay of Bengal
(4)	West	Arabian Sea, Pakistan, Afghanistan

Question 2.
Identify Brazil’s neighbouring countries and oceans. Complete the following table.


(a) To the North
(b) To the South
(c) To the East
(d) To the West
Answer:

No.	Directions	Neighbouring Countries	Oceans
(1)	North	Venezuela, Guyana, Suriname, French Guiana	North Atlantic Ocean
(2)	South	Uruguay	South Atlantic Ocean
(3)	East		South Atlantic Ocean
(4)	West	Peru, Bolivia, Paraguay, Colombia, Argentina

Question 3.
Show the following on an outline of the world map.
(a) Name all the continents and oceans of the world.
(b) Colour Brazil and India using different colours and name them.
(c) Draw equator on the map and write its value in degrees.
(d) Show the symbol for direction.
Answer:

Give geographical reasons:

Question 1.
Brazil is called the ‘coffee pot of the world’.
Answer:
(i) Brazil ranks first in the world in the terms of production of coffee.
(ii) It produces nearly 40% of the total coffee production in the world.
(iii) It is the largest exporter of coffee.
Therefore, Brazil is called the ‘coffee pot of the world’.

Question 2.
Brazil is known as the country having third longest land border.
Answer:
(i) Brazil has the world’s third longest land border, after China and Russia.
(ii) It shares its boundaries with all South American countries, except Chile and Ecuador, totalling 16,885 Kilometers.
(iii) Brazil has borders with 10 different countries, which are Argentina, Bolivia, Colombia, French Guiana, Guyana, Paraguay, Peru, Suriname, Uruguay and Venezuela.
(iv) Hence, Brazil is called the country having third longest land borders.

Question 3.
India is looked upon as a young country.
Answer:
(i) The proportion of youth in India’s population is high.
(ii) This forms a major part of the working population.
(iii) According to 2011 census the percentage of working population is more than 50 %.
(iv) Hence, India is looked upon as a young country.

Question 4.
India’s economic development has paced up. OR India is considered as a major global market.
Answer:
(i) Despite facing several problems after independence, today India is a major developing country of the world.
(ii) It is because of various reforms from time to time, that India’s economic development has paced up.
(iii) So, it is considered to be a global market.

Answer in brief:

Question 1.
What problems did Brazil and India face after independence?
Answer:
(i) India was under the British rule for almost one-and-a-half centuries and it got its independence in the year 1947.
(ii) It faced several problems like three wars, famine situations in various parts and similar issues after independence.
(iii) Brazil gained its independence in 1822 after more than three centuries of Portuguese rule.
(iv) From 1930 to 1985, for more than a half century, it was under a populist military government and it faced global financial difficulties in the late 20th century.
Thus, both India and Brazil faced many problems post-independence.

Question 2.
How are Brazil and India different from each other in terms of location?
Answer:
(i) India is located in the northern hemisphere of the earth whereas some part of Brazil lies in the northern hemisphere and most of it lies in the southern hemisphere.
(ii) India entirely lies in the eastern hemisphere whereas, Brazil lies in the western hemisphere.
(iii) India lies in the continent of Asia whereas Brazil lies in the continent of South America.
(iv) India lies in the southern part of the continent of Asia whereas Brazil lies in the northern part of South American continent.

Question 3.
Describe the latitudinal and longitudinal extent of India and Brazil.
Answer:
(i) The extent of the mainland India is 8°4’N to 37°6’N latitudes and between 68°7’E to 97°25’E longitudes.
(ii) Indira Point is the southernmost tip of India.
(iii) It is located on 6°45’N parallel.
(iv) The extent of the mainland Brazil is 5°15’N to 33°45′ S latitudes and between to 34°47’W to 73°48’W longitude.

Class 10 Geography Chapter 2 Location and Extent Additional Important Questions and Answers

Name the following:
Question 1.
The second-largest populated country in the world.
Answer:
India

Question 2.
The country is famous for its spices in the world.
Answer:
India

Question 3.
The country is known as the ‘coffee pot’ of the world.
Answer:
Brazil

Question 4.
The famous dance form of Brazil.
Answer:
Samba

Question 5.
Hemispheres in which India is located.
Answer:
Northern and eastern hemispheres.

Question 6.
A continent in which India is located.
Answer:
Asia

Question 7.
The latitudinal extent of India.
Answer:
8°4’N to 37°6’N

Question 8.
The longitudinal extent of India.
Answer:
68°7’E to 97°25’E

Question 8.
Foreign power which ruled Brazil for more than three centuries.
Answer:
Portuguese.

Question 9.
Independence day of Brazil.
Answer:
7th September 1822.

Question 10.
Type of Government in Brazil from 1930 to 1985.
Answer:
Populist Military Government.

Question 11.
The latitudinal extent of Brazil.
Answer:
5°15’N to 33°45’S.

Question 12.
The longitudinal extent of Brazil.
Answer:
34°47’W to 73°48’W

Choose the correct option and rewrite the statements:

Question 1.
The second largest populated country in the world is _________.
(a) China
(b) Brazil
(c) India
(d) Russia
Answer:
(c) India

Question 2.
Brazil is famous for ________ type of dance form.
(a) Salsa
(b) Samba
(c) Ballet
(d) Tango
Answer:
(b) Samba

Question 3.
The country known as the ‘coffee pot’ of the world is _______.
(a) Brazil
(b) India
(c) China
(d) Pakistan
Answer:
(a) Brazil

Question 4.
India is located in the ________ part of the Asian continent.
(a) southern
(b) northern
(c) northeastern
(d) western
Answer:
(a) southern

Question 5.
Brazil gained independence in _______.
(a) 1890
(b) 1980
(c) 1822
(d) 1820
Answer:
(c) 1822

Question 6.
Capital of Brazil is _______.
(a) Kabul
(b) Kaula Lumpur
(c) Brasilia
(d) Monaco
Answer:
(c) Brasilia

Question 7.
Capital of India is _____.
(a) Patna
(b) New Delhi
(c) Dispur
(d) Chandigarh
Answer:
(b) New Delhi

Question 8.
India was under ___ rule for almost one and a half-century.
(a) Portuguese
(b) African
(c) Russian
(d) British
Answer:
(d) British

Question 9.
For more than a half-century, Brazil was under a _____ government.
(a) Populist military
(b) Monarchy
(c) Constitutional government
(d) Dictatorial
(a) Populist military

Question 10.
Most part of the of mainland Brazil lies in the ______ hemisphere.
(a) northern
(b) southern
(c) eastern
(d) northwestern
Answer:
(b) southern

Question 11.
Brazil was ruled by ______ imperial power which also ruled a part of India.
(a) Portuguese
(b) British
(c) Indonesia
(d) Pakistan
Answer:
(a) Portuguese

10th Std Geography Questions And Answers:

• Field Visit Class 10 Geography Questions And Answers
• Location and Extent Class 10 Geography Questions And Answers
• Physiography and Drainage Class 10 Geography Questions And Answers
• Climate Class 10 Geography Questions And Answers
• Natural Vegetation and Wildlife Class 10 Geography Questions And Answers
• Population Class 10 Geography Questions And Answers
• Human Settlements Class 10 Geography Questions And Answers
• Economy and Occupations Class 10 Geography Questions And Answers
• Tourism, Transport and Communication Class 10 Geography Questions And Answers

Balbharti Maharashtra State Board Class 10 Political Science Solutions Chapter 5 Challenges faced by Indian Democracy Notes, Textbook Exercise Important Questions and Answers.

Std 10 Political Science Chapter 5 Question Answer Challenges faced by Indian Democracy Maharashtra Board

Class 10 Political Science Chapter 5 Challenges faced by Indian Democracy Question Answer Maharashtra Board

Political Science Class 10 Chapter 5 Question Answer Maharashtra Board

Question 1.
Choose the correct option from the given options and complete the sentences.
(1) In a democracy …………………….. participate in elections and get political power.
(a) political parties
(b) courts
(c) social organisations
(d) none of the above
Answer:
(a) political party

(2) The major challenge faced by all democratic nations in the world is ……………………. .
(a) Religious conflicts
(b) Naxal activities
(c) Deepening the roots of democracy
(d) Importance to muscle power
Answer:
(c) Deepening the roots of democracy

Question 2.
State whether following statements are true or false. Give reasons for your answer.
(1) Alertness is required to sustain democracy.
Answer:
The above statement is True.

1. In order to make democracy successful it should be practised by people in all aspects of their life. It should not remain limited at the government level.
2. Conscious effort should be taken to keep the rights of the people intact.
3. The different challenges faced by democracy like corruption,violence and criminalisation should be tackled timely and strictly. It is necessary that people and the government should remain alert for the sustenance of democracy.

(2) Importance of the problems of farmers and tribals has increased in the left extremist movement.
Answer:
The above statement is False.

• Landlords confiscated lands of farmers and tribals.
• Naxalite movement was started to remove injustice against the landless farmers and tribals.
• But later the problems of farmers and tribals lost its focus and became violent.
• They adopted violent ways like to attack army, police and oppose the government.
• The importance of farmers and tribals decreased in the leftist movement.

(3) People may lose confidence in the democratic process due to corruption during elections.
Answer:
The above statement is True.

• In order to strengthen democracy, it is important to conduct elections in a free and fair atmosphere.
• There are instances of .the election process getting affected by corruption.
• Bogus voting, bribing the voters, abducting voters and ballot boxes, distributing articles to lure voters and other such things take place.
• All these things make people lose faith in the democratic process.

Question 3.
Explain the concept.
(1) Left-extremism
(2) Corruption
Answer:

• It is a form of dishonest or unethical conduct for personal gain by people at influential position.
• It is found at all levels economic, political, social and at government levels. The misuse power is also corruption.
• Bogus voting, giving bribe to voters, are examples of corruption in the election process.
• Hoarding of goods and then selling them at price more than the market yalue is also a way of corruption.
• Corruption in the public and private sector is the biggest problem in India.
• People develop distrust and dissatisfaction about the entire system. They lose trust in democracy because of corruption.

Question 4.
Answer the following questions in brief.
(1) Which factors are required for the success of democracy in India?
Answer:
The following factors are required for the success of democracy in India:

• Though democracy is the government of majority the opinions of minorities, religious, ethnic and lingustic should be included in the decision-making process.
• Stringent laws must be implemented to stop criminalisation of politics.
• Efforts should be made not only at the level of the government but also at social and personal level.
• Decisions about important public policies should be taken after interaction with the people.. Participation of people should increase in all government undertakings.

(2) What are the effects of criminalisation of politics?
Answer:
The following effects are seen due to criminalisation of politics:

• Money and muscle power gets undue importance.
• Violence increases during elections and it becomes difficult to hold elections in free and fair environment.
• Terror seizes the mind of people and their participation becomes less in administration.
• People lose their tolerance and the development of democracy does not take place.

(3) What efforts are undertaken to bring transparency in political process?
Answer:
The following efforts are made to bring transparency in political process:

• An independent Election Commission is appointed to hold free and fair elections.
• Stringent laws are made to stop criminalisation of politics.
• Laws are formed to stop corruption in politics and elections.
• Courts have banned people who are corrupt and those having criminal background or criminal allegations from taking part in political process.

Project
(1) What measures will you suggest to control corruption? Make a list of it.
(2) Organise a group discussion in your class on the problem of terrorism in India.
(3) Present a street play on ‘how to get rid of addiction?
Answer:

Memory Map

Question 5.
Choose the correct option from the given options and complete the sentences:
(a) ………………….. is a continuous and living process.
(a) Military rule
(b) Democracy
(c) Dictatorship
(d) Monarchy
Answer:
(b) Democracy

(b) The main objective of democracy is ………………….. .
(a) to hold elections
(b) public welfare
(c) public campaigns
(d) social work
Answer:
(b) public welfare

(c) Voting, elections, government structure, etc. is only ………………….. form of democracy.
(a) economic
(b) political
(c) social
(d) all-inclusive
Answer:
(b) political

(d) In order to make democracy meaningful the Government of India adopted …………………. .
(a) internal party elections
(b) public welfare schemes
(c) decentralisation of power
(d) protection of democratic values.
Answer:
(c) decentralisation of power

(e) Naxalite movement began to remove injustice done to …………………. .
(a) workers and dalits
(b) middle and lower class
(c) poor and common class
(d) landless farmers and tribals
Answer:
(d) landless farmers and tribals

(f) The …………………. in India is making conscious efforts to make political process transparent,
(a) Parliament
(b) Government
(c) Judiciary
(d) Political parties
Answer:
(c) Judiciary

(g) Due to increase in ………………….., there is increase in religious conflict.
(a) communalism
(b) terrorism
(c) corruption
(d) casteism
Answer:
(a) communalism

(h) In order to make democracy successful in India, participation of …………………. should increase.
(a) government
(b) people
(c) political parties
(d) social organization
Answer:
(b) people

Question 6.
Explain with reasons whether the following statements are true or false:

(a) Communalism does not cause much harm to the nation.
Answer:
The above statement is False.

• Increase in communalism leads to religious conflict in the country.
• Increasing conflicts in turn create frictions in society and destroy social unity.
• It creates division in society resulting in terrorist activities.
• People’s participation also reduces in the democratic process.
• This ultimately creates instability in society and democracy comes in danger.

Hence communalism harms the nation to a great extent.

(b) The opinion of the minorities should not be taken into consideration.
Answer:
The above statement is False.

1. Even though the government of the majority community comes to power, it should adhere to the democratic principle that government should work for the welfare of all communities.
2. In democracy, opinion of all the communities should be valued instead of giving importance only to the majority community.
3. All religious, linguistics, ethnic and caste groups should be part of the decision-making process of the government. Hence, to avoid injustice to minorities their opinion should also be taken into consideration.

(c) Democracy is the best form of governance.
Answer:
The above statement is True.

• The freedom and rights of the people remain intact in democracy.
• In democracy, values like liberty, equality, social justice, secularism and fraternity are nurtured in the real sense.
• Welfare of the people is the main aim of’ democracy.
• People do not enjoy so much freedom in any other form of government. Hence, democracy is the best form of governance.

(d) Majority opinion has a lot of importance in Democracy.
Answer:
The above statement is True.

• In a democracy, the political party getting majority of votes comes to power.
• Parliament takes all the decisions by majority.
• Democracy aims at the welfare of the majority of the people.

Therefore, majority opinion has a lot of importance in Democracy.

Question 7.
Explain the concept:
(a) Decentralisation:
Answer:

• If complete power rests in the hands of government it gives rise to dictatorship.
• Therefore division of power between legislature, executive and judiciary is essential.
• This division of power is known as Decentralisation.
• Decentralisation safeguards the freedom of the people.
• People participate in the functioning of the government.
• With increased participation, people become aware of their responsibilities.
• Decentralisation has great importance in democracy.

(b) Criminalisation of politics:
Answer:

• Participation of criminals in political process is criminalisation of politics. It is a serious problem and a threat to our democratic system.
• Political parties or candidates spread terror among people using money and muscle power.
• Political parties who give candidature to people with criminal background are responsible for violence during elections.
• Such candidates after coming to power continue their criminal activities.

They create financial scams and trouble the opponents. Criminalisation of politics weakens democracy.

Question 8.
Write short notes:
(a) Communalism and Terrorism:
Answer:

• Communalism and Terrorism causes great harm to nation. Communalism emerges out of narrow religious pride.
• Increasing communalism triggers religious conflict in the country. Religious conflict hampers social stability.
• Society gets divided on communal lines. Communalism gives rise to terrorism.
• People’s participation in democratic process in reduced to a great extent due to terrorism.
• It causes great damage to our nation.

Question 9.
Do as directed:
(1)

Answer:

(2)

Answer:

(3)

Asnwer:

(4)

Answer:

Question 10.
Answer the following questions in brief:
(a) What challenges are faced at global level by democracy?
Answer:
The following challenges are faced by democracy at global level:

• Many democratic countries in the world face the threat of military regime.
• It becomes important to propagate democracy which safeguards people’s rights and freedom.
• All-inclusive democracy is real democracy which should be adopted and practised instead of adopting just political form of democracy.

(b) What improvements are required for democracy to be deep rooted?
Answer:
The following improvements are required for democracy to be deep rooted:

• Values like freedom, equality, fraternity, justice, peace and humanitarianism should be practised and nurtured by all sections in the society.
• Autonomy should be given to various social organisation and assimilqje all the sections of the society.
• Empowerment to the citizens, free and fair elections and independent judiciary is necessary.
• Adoption of a form of democracy which gives preference to public welfare.

(c) What measures are adopted by India to strengthen democracy?
Answer:
In order to strengthen democracy following measures are adopted by India:

• Decentralisation of power.
• Reservation for minorities and women so that they get a share in power.
• The values of liberty, equality, secularism and social justice adopted by our Constitution.
• At administrative level various projects like Education for all, Clean Bharat campaign.
• Gram Samruddhi Yojana, Mahatma Gandhi National Rural Employment Guarantee Scheme are undertaken.

Question 11.
Give your opinion:
(a) What is your opinion about participation of people in various undertakings of the government?
Answer:

• There will be change in the public policies of the government.
• There will be interaction between all sections of society and exchange of ideas.
• There will be transparency in government administration and problems like corruption will be tackled.
• More public welfare schemes will get implemented and no one will feel that injustice is done to them or they are left out.

(b) Are internal elections held by political parties?
Answer:

• It is mandatory to hold internal elections in a political party.
• Elections are held for various posts like president, treasurer and secretary.
• Elections are held after every 3 years as per the niles laid down by the Election Commission of Itdia.
• The paity which does not abide by the rule loses recognition.
• Because of such elections, there can never be dominance of any single person on a party.
• Democracy sustains within the party. In Indian democracy the internal elections are held by all the parties regularly.
• Another challenge before democratic nations is to ensure that democracy becomes deep rooted.
• Freedom, equality, fraternity and justice, peace, development and humanitarianism are the values that should be practiced at all levels of the society.
• The mass support for this purpose can be gathered only through democratic means.

(c) In spite of economic reforms China accepted dominance of only one party. Is China a democratic nation?
Answer:

• After the Communist revolution in 1948 China became a republic.
• After the formation of the republic, the Communist party of China became a dominant party.
• All the offices in the party are elected through internal elections.
• But in practice, there is dictatorship of the Communist party. Democracy is for namesake in China.
• In such a situation, the people do not enjoy freedom as in true democracy.
• However, China accepted economic reforms and became part of World Trade Organization.
• Another challenge before democratic nations is to ensure that democracy becomes deep rooted.
• Freedom, equality, fraternity and justice, peace, development and humanitarianism are the values that should be practiced at all levels of the society.
• The mass support for this purpose can be gathered only through democratic means.

(d) Do you think there should be family monopoly in politics?
Answer:

• There is no place for family monopoly in politics.
• The elected representatives serve the people till their term lasts.
• People vote out the inefficient representatives out of power in next election.
• If there is monopoly of one family, the perspective of democracy becomes narrow, common people cannot share power.
• If any inefficient heir comes to power, he or she could be a great loss for the party, people as well as the nation.
• Family monopoly in politics is a major problem before democracy in India.
• Monopoly of just one family in politics reduces democratic space. Common people cannot participate in the public sector.

Hence there should be no family monopoly in politics.

10th Std Political Science Questions And Answers:

• Chapter 1 Working of the Constitution Class 10 Political Science Questions And Answers
• Chapter 2 The Electoral Process Class 10 Political Science Questions And Answers
• Chapter 3 Political Parties Class 10 Political Science Questions And Answers
• Chapter 4 Social and Political Movements Class 10 Political Science Questions And Answers
• Chapter 5 Challenges faced by Indian Democracy Class 10 Political Science Questions And Answers

Balbharti Maharashtra State Board Class 10 History Solutions Chapter 6 Entertainment and History Notes, Textbook Exercise Important Questions and Answers.

Std 10 History Chapter 6 Question Answer Entertainment and History Maharashtra Board

Class 10 History Chapter 6 Entertainment and History Question Answer Maharashtra Board

History Class 10 Chapter 6 Question Answer Maharashtra Board

Question 1.
(A) Choose the correct option from the given options and complete the statement.
(1) ……… are supposed to be the first keertankar in Maharashtra.
(a) Saint Dnyanehshwar
(b) Saint Tukaram
(c) Saint Namdev
(d) Saint Eknath
Answer:
(c) Saint Namdev

(2) Baburao painter made the movie, …………………….. .
(a) Pundalik
(b) Raja Harischandra
(c) Sairandhri
(d) Bajirao-Mastani
Answer:
(c) Sairandhri

(B) Identify and write the wrong pair in the following set.
(1) Raigadala Jevha Jag Yete – Vasant Kanetkar
(2) Tilak Ani Agarkar – Vishram Bedekar
(3) Sashtang Namaskar – Acharya Atre
(4) Ekach Pyala – Annasaheb Kirloskar
Answer:
(4) Wrong Pair: Ekach Pyala – Annasaheb Kirloskar

Question 2.
Complete the following chart.

	Bhajan	Keertan	Lalit	Bharud
Characteristics
Examples

Answer:

Sr.No.	Point	Bhajan	Keertan	Lalit	Bharud
1	Characteristics	Singing songs in praise of God and chanting his name accompanied by Taal (Cymbals), Pakhvaj and Mridangam	(1) Naman and Nirupanacha Abhang and Nirupan comprise the Poorvarang (2) Narration of a story to illustrate main theme is Uttarrang	(1) Deity is invoked during festival to fulfill desire (2) It is performed in a theatrical style. Stories of Krishna, Rama and great devotees are presented during performances	It is a metaphorical song with spiritual and ethical teachings.
2	Examples	Bhajans of Saint Tulsidas, Saint Tukadoji Maharaj and Saint Namdev	Naraadiya Keertan and Mahatma Phule’s Keertan	Popular in Konkan and Goa	Bharuds of Saints Eknath, Namdev and Dnyaneshwar.

Question 3.
Write short notes:
(1) Need of entertainment
Answer:

• Entertainment of excellent quality is essential for healthy growth of a person as it is an integral part of one’s life?
• To break the boredom of routine life and keep the mind lively and fresh we need gome entertainment.
• It makes us feel more energetic and our efficiency at- work improves.
• Hobbies and games are pursued for entertainment which eventually develops personality.
• Entertainment refreshes our mind and helps to distress.
• Lack of entertainment in one’s life will lead to monotonous life and boredom.

(2) Marathi Theatre
Answer:

• Theatre is a place devoted to performances either solo or collective, of performing arts.
• The 19th century saw a great development of the Marathi Theatre.
• Vishnudas Bhave was known as the father of the Marathi Theatre.
• In the initial years historical, mythological plays were performed along with light farcical plays.
• The plays had no written script.
• The tradition of having a complete written script began with the play ‘Thorale Madhavrao Peshwe’ in 1861.
• At the end of 19th century,„ the tradition of musical plays started.
• Historical themes and social problems were presented through these plays.
• The popular plays by Acharya Atre like Udyacha Sansar, Gharabaher helped the Marathi theatre to sustain through a temporary decline. Vasant Kanetkar, Vishram Bedekar, Acharya Atre, enriched the Marathi theatre.

(3) Entertainment and professional opportunities
Answer:

• There are many professions associated with theatre and cinema.
• Professional hairstylists, costume designers, make-up artists, art directors who put up stage backdrops are required in theatre.
• Directors, technicians, actors, lightmen, costume and jewellery designers and assistants are required too. Experts in music and script writers, singers are required.
• Cinema requires all of them along with dance directors, singers, cameramen, dialogue writers and story writers. Scholars of history can work in this field as art directors.

Question 4.
Explain the following statements with reasons.
(1) Expertise in history is important in the film industry.
Answer:
It is essential to have knowledge of history while making films on historical’ events or a person. .

• If the movie has a historical theme then art directors are required to create backdrop designs showcasing the atmosphere of that period.
• To write movie dialogues, the knowledge of the culture and language as spoken in that period is necessary.
• It is important to have knowledge of appropriate hairstyles, costumes, jewellery make¬up of that era.
• Scholars of history are required who can work as art directors or as consultants to the art director.
• Experts in field of history can find many professional opportunities.

(2) Bharuds composed by Saint Eknath are popular in Maharashtra.
Answer:

• Saint Eknath composed Bharuds with the purpose of educating people on various aspects of life.
• Bharuds composed by Saint Eknath had a wide range of subjects, dramatic quality, easy rhythm and humour.
• People liked the way it was performed.
• A message was given in a humorous way.

Question 5.
Answer the following questions in detail.
(1) Why is Maharashtra known as the land that nurtured the Indian film industry?
Answer:

1. The contribution of Madanrao Madhavrao Pitale, the Patwardhan family of Kalyan and Harishchandra Sakharam Bhatvadekar is very important in the development of Indian movies.
2. Dadasaheb Torane, A. E Karandikar, S. N. Patankar, V. E Divekar sought help from foreign technicians and made a movie entitled Pundalik. It was released in Mumbai in 1912.
3. ‘Raja Harischandra’ was the first movie to be processed completely in India. It was released in Mumbai in 1913.
4. The credit of making a full-length movie goes to Maharashtra.
   Therefore Maharashtra is known as the land that nurtured the Indian film industry.

(2) What is Powada?
Answer:

1. Powada is a dramatic narration by altematingly reciting poetry and prosaic extracts. Powada narrates great deeds of heroic men and women in a very forceful and inspiring style.
2. The Powada composed by – Adnyandas, a contemporary poet of Chhatrapati Shivaji Maharaj which narrated the incident of Afzal Khan’s death and battle of Simhgarh composed by Tulsidas are very famous.
3. In the British period, Powadas narrating the stories of Umaji Naik, Chaphekar brothers and Mahatma Gandhi were composed.
4. During the Samyukta Maharashtra Movement the Powadas were used as medium of creating public awareness.

Project
Get the lyrics of any one of Saint Eknath’s Bharud, and enact it in the cultural programme of your school.

Question 6.
Complete the sentences by choosing the correct option:
(a) In the 18th century, ………………………. started a Phad of Dashavatara artists which used to perform all over Maharashtra.
(a) Saint Gadge Maharaj
(b) Adnyandas
(c) Tulsidas
(d) Shyamiji Naik Kale
Answer:
(d) Shyamji Naik Kale

(b) Traditionally, ………………………. is supposed to be the founder of keertan tradition.
(a) Saint Namdev
(b) Saint Eknath
(c) Naradmuni
(d) Saint Gadge Maharaj
Answer:
(c) Naradmuni

(c) The Powada composed by the poet ………………………. on the incident of the killing of Afzal Khan is well-known.
(a) Adnyandas
(b) Tulsidas
(c) Ramdas
(d) Surdas
Answer:
(a) Adnyandas.

(d) Compositions of ………………………. are not part of Bhajans sung in Karnataka.
(a) Purandardas
(b) Surdah
(c) Bodhendraguruswami
(d) Thyagraj
Answer:
(b) Surdas

(e) Varkari sect has developed a glorious tradition of ………………………. by chanting God’s name.
(a) Powada
(b) Dashavatari Natak
(c) Bhajan-Keertan
(d) Bharud
Answer:
(c) Bhajan-Keertan

(f) Powada composed by Tulsidas on the battle of ………………………. is very well known.
(a) Panhala
(b) Raigarh
(c) Pratapgad
(d) Simhgarh
Answer:
(d) Simhgarh

(g) Powadas composed by ………………………. were not the part of Samyukta Maharashtra Movement.
(a) Amarsheikh
(b) Patthe Bapurao
(c) Annabhau Sathe
(d) Gawankar
Answer:
(b) Patthe Bapurao

(h) ………………………. is known as the Father of Marathi theatre.
(a) V. J. Kirtane
(b) Dattopant Patwardhan
(c) Vishnudas Bhave
(d) Annasaheb Kirloskar
Answer:
(c) Vishnudas Bhave.

(i) started the tradition of having a complete written script.
(a) V. J. Kirtane
(b) Vishnudas Bhave
(c) Shripad Krishna Kolhatkar
(d) Govind Ballal Deval
Answer:
(a) V. J. Kirtane

(j) In the latter half of the 19th century, made special efforts to introduce classical khyal music in Maharashtra.
(a) Bhimsen Joshi
(b) Kumar Gandharva
(c) Kishori Amonkar
(d) Balkrishnabuva Ichalkaranjikar
Answer:
(d) Balkrishnabuva Ichalkaranjikar

(k) In India, is the first one to make a cine camera.
(a) Anandrao Painter
(b) Baburao Painter
(c) Dadasaheb Torne
(d) Dadasaheb Phalke
Answer:
(a) Anandrao Painter

(l) In 1925, made a movie Bajirao Mastani, which was later on banned by the British Government under the suspicion of spreading nationalistic sentiments.
(a) Sanjay Leela Bhansali
(b) Dadasaheb Phalke
(c) Baburao Painter
(d) Bhalaji Pendharkar
Answer:
(d) Bhalaji Pendharkar

(m) was the first woman producer of: Marathi movies.
(a) Kamalabai Mangarulkar
(b) Devika Rani
(c) Amirbai Karnataki
(d) Kanandevi
Answer:
(a) Kamalabai Mangalurkar.

Question 7.
Identify the wrong pair in the following and write it:
(1)

Name of the Play	Playwright
(1) Raygadala Jevha Jag Yete	Vasant Kanetkar
(2) Tilak Ani Agarkar	Vishram Bedekar
(3) Sashtang Namaskar	Acharya Atre
(4) Ekach Pyala	Annasaheb Kirloskar

Answer:
Wrong pair: Ekach Pyala – Annasaheb Kirloskar

(2)

First release	Movie
(1) First full length movie released in India	Raja Harishchandra
(2) First historical film in India	Simhgarh
(3) Movie dealing with real social issues	Savkari Pash
(4) Indian movie which got international acclaim	Saint Dnyaneshwar

Answer:
Wrong pair: Indian movie which got international acclaim — Saint Dnyaneshwar

(3)

Film producer	Produced Biographical Movies on
(1) Acharya Atre	Ram Shastri
(2) Vishram Bedekar	Vasudev Balwant Phadke
(3) Dinakar D. Patil	Dhanya te Santaji Dhanaji
(4) Prabhakar Pendharkar	Bal Shivaji

Answer:
Wrong Pair: Acharya Atre – Ram Shashtri

(4)

(1) Keechakvadh	Krishnaji Prabhakar Khadilkar
(2) Ekach Pyala	Ram Ganesh Gadkari
(3) Ithe Oshalala Mrutyu	Vasant Kanetkar
(4) Natasamrat	Vijay Tendulkar

Answer:
Wrong Pair: Natasamrcrt -Vijay Tendulkar

(5)

Work	Saint
(1) Gave momentum to the Bhakti movement in Gujarat	Saint Kabir
(2) First Keertankar of Maharashtra	Saint Namdev
(3) Popularised Khanjiri Bhajan	Saint Tukdoji Maharaj
(4) Tradition of Rashtriya Keertan was started	Dattopant Patwardhan

Answer:
Wrong Pair: Gave momentum to Bhakti movement in Gujarat — Saint Kabir

(6)

(1) The first play in Marathi	Seetaswayamvar
(2) First play having  complete written script	Thorale  Madhavrao
(3) Metaphorical Drama	Udyacha Sanskar
(4) Play based on Shakespeare’s King Lear	Natasamrat

Answer:
Metaphorical Drama-Udyacha Sanskar.

(7)

Name of the Play	Playwright
(1) Thorale Madhavrao Peshwe	V. J. Kirtane
(2) Ekach Pyala	Annasaheb Kirloskar
(3) Sangeet Sharada	Shripad Krishna Kolhatkar
(4) Sangeet Manapaman	Krishnaji Prabhakar Khadilkar

Answer:
Wrong Pair: Sangeet Sharada – Shripad Krishna Kolhatkar

Question 8.
Complete the graphical presentation:
(a) Prepare concept map on:
(1) Types of Puppets:

Answer:

(2) Saints who popularised Bhajans:

Answer:

(3) Plays by famous Playwrights:

Answer:

(4) Saints who popularised Bhajans in North India:

Answer:

(b) Prepare a flow chart on the development of Marathi Theatre:
Answer:
Development of Marathi Theatre:

Question 9.
Explain the concept:
(1) Dashavatara Theatre:
Answer:

• The stories presented in Dashavatara shows are based on the ten incarnations of Vishnu.
• The method of acting, make-up, costumes in Dashavatara show is set by the tradition.
• It is mostly a musical show but there may be a few spontaneous dialogues.
• At the beginning of the show, Sutradhar, the narrator invokes Lord Ganesha, for its successful run.
• Dashavatara is part of the folk theatre in Maharashtra which has its origin in mythological plays.

(2) Bhajan:
Answer:

• Singing songs in praise of God and chanting God’s name accompanied by instruments like taal (cymbals), mridangam, pakhavaj is known as Bhajan.
• Bhajan is an important element of devotional music for those who are on the path of devotion.
• Varkari sect made Bhajans accessible to all.
• There are two types of Bhajans, Chakri and Songi BhajAnswer:
• Devotees keep moving in circular fashion and without break in Chakri Bhajan.
• In Songi Bhajan, singer-actors act as devotees and deliver dialogues in the form of devotional songs.

(3) Bharud:
Answer:

• Bharud can be described as a metaphorical song that has spiritual and ethical lessons. Bharud is similar to road show.
• Bharud is popular because of its wide range of subjects, humorous presentation, dramatic quality and easy rhythm.
• Bharuds are composed with the purpose of educating people on various aspects of life.
• Even though Bharuds of Saint Eknath are famous, bharuds were composed by many saints including Saint Dnyaneshwar.

(4) Keertan.
Answer:

• Keertan involves oratory, singing, acting, dancing and story telling.
• Naradmuni is assumed to be the founder of Keertan tradition.
• It is pure glorification of god. It is also a medium to educate the masses about good values of life and very purpose of human life.
• There are two parts in Naraadiya keertan Poorvarang and Uttarrang. Poorvarang comprises of Naman.
• Nirupanacha Abhang and Nirupan; Uttarrang comprises of narration of a story to illustrate the main theme.
• Keertan has two traditions in Maharashtra – Naraadiya and Varakari.

(5) Documentaries: (You would like to know this: Textbook page 44)
Answer:

• A film which gives information, inspires and educates people and is a short film is a documentary.
• Documentaries were made on freedom struggle, national leaders, social issues and superstitions, forts, animal species, sports, etc.
• They were aimed at creating public awareness about various issues.
• They are shown in the cinema theatres before the start of the main movie.

Question 10.
Write short notes:
(a) Means of Entertainment:
Answer:

• Entertainment is an integral part of man’s life. Man has developed many means of entertainment since ancient times.
• Ancient times saw the rise of festivals, fairs, sports, dance-music, etc.
• The means of entertainment changed with times.
• Television, mobiles, video games and movies and such other modem means of entertainment were introduced.
• Folk music, classical music, plays, books, newspapers, magazines are some mediums of entertainment which are available. Different types of sports, hobbies and travel too are means of entertainment.

(b) Lalit:
Answer:

1. Lalit is an old form of entertainment popular in Konkan, Maharashtra and Goa. It belongs to the tradition of Naaradiya Keertan.
2. It is presumed that the presiding deity is present on the throne. It is invoked by the people as it is widely believed that the deity fulfils all the wishes.
3. Stories of Krishna, Rama and of great devotees are presented during the performance.
4. Lalit forms a part of the backdrop of modem Marathi theatre.

(c) Keechakvadh: (Do You Know? Textbook page 43)
Answer:

• Krishnaji Prabhakar Khadilkar wrote Keechakvadh in the pre-independence era. It was a metaphorical drama.
• It was based on the incident of Keechakvadh described in the epic, Mahabharata.
• Draupadi represented helpless Mother India, while Yudhishthira represented the moderates and Bheem the extremists.
• Keechak represented the insolent Viceroy Lord Curzon.
• The audience used to perceive characters in this fashion and feel* enraged about the imperialistic British rule.

(d) Natashmrat: (Do You .Know? Textbook page 43)
Answer:

• The renowned author-poet Vishnu Waman Shirwadkar, also knpwn as Kusumagraj wrote Natasctmrat.
• It is styled after Shakespeare’s well known play ‘King Lear’.
• Ganpatrao Belvalkar, the tragic protagonist of Natasamrat represents a blend of two well-known personalities of early Marathi stage Ganpatrao Joshi and Nanasaheb.
• The traits of both great actors are found in the main character of Natasamrat.
• Natasamrat is a tragic story of an aging actor who gives his entire wealth to his sons and is humiliated by them.
• This play was very popular and created history on stage performance and in playwriting.

(e) Tamasha (Folk theatre):
Answer:

1. Tamasha is a Persian word which means a pleasing sight. Tamasha emerged as an independent form in the 18th century absorbing the traits of folk theatre and classical arts.
2. Tamasha is classified into ‘Sangeet Bari’ and ‘Dholakicha Phad’. Dance and music are more important than drama in Sangeet Bari. Tamasha with drama as main part was developed later. It included Vag, the dramatic part a little later.
3. The show begins by singing the praise of Lord Ganesha, known as Gana. It is followed with the presentation of Gavalan.
4. The second part of Tamasha presents the Vag. The plays like ‘Vichchha Mazi Puri Kara’ or ‘Gadhavache Lagna’ were very popular.

Question 11.
Explain the following statements with reasons:
(a) Puppetry is an oldest form of entertainment.
Answer:

• Puppet show was an important form of entertainment.
• The remains of clay dolls have been found in the excavations at the archaeological sites of Harappa, Egypt and Greece civilisations.
• Information on puppets is found in the texts like Mahabharata and in Panchatrantra stories.
• The ancient text Mahabharat has a mention that puppetry was one of the 64 arts.

(b) Vishnudas Bhave is known as the Father of Marathi Theatre.
Answer:

• The origins of the Marathi theatre can be traced to Dashavatara tradition. Lalit forms a backdrop of Marathi theatre.
• Seetaswayamvar, the first play, written and presented by Vishnudas Bhave was very successful.
• The movement of stage plays started by Vishnudas Bhave was followed in Maharashtra by historical, mythological and also light farcical stage plays.
• The farcical plays dealt with social issues in a humorous way. Therefore, he is known as the Father of Marathi theatre.

Question 12.
Answer the following questions in 25 – 30 words:
(a) Make a list of various types of entertainment and classify them into different categories. (Try to do it: Textbook Page 39)
Answer:

• Entertainment can be classified into two categories, active and passive.
• Active entertainment means an individual’s mental-physical participation. In passive entertain-ment, a person may not be an actual participant.
• To play cricket is active form of entertainment but to watch a cricket match is passive entertainment.
• To participate in festivals, fairs, celebrations is active entertainment but to watch as audience is passive entertainment.

(b) Write about Dashavatara form of folk theatre.
Answer:

• The stories presented in Dashavatara are based on the 10 incarnations of Lord Vishnu.
• The method of acting, make-up, costumes in Dashavatara shows is set by the tradition.
• The show is mostly musical but sometimes there may be a few spontaneous dialogues.
• The characters representing gods use wooden masks. At the start of the show, the sutradhara invokes Lord Ganesha.
• The show ends by breaking dahihandi, followed by aarati, praising the God.
• This is part of folk theatre in Maharashtra.
• Dashavatara shows are presented in the regions of Konkan and Goa after the harvesting season is over.

(c) What is required to be a Keertankar?
Answer:
The following qualities are required to be a Keertankar:

• A Keertankar also known as Haridas or Kathekaribuva needs to be very well informed.
• He should have wide experience and knowledge of the world.
• He should be well-versed in mythological and social subjects.
• He needs to train himself in qratory, singing, musical instruments, dance and humour. .
• He should dress in a traditional way.

(d) Write about the contributions of Bhosale family to drama.
Answer:

• The Bhosale family of Tanjore were successors of Chhatrapati- Shivaji Maharaj. They were patrons of arts.
• The rulers of the Bhosale family encouraged dramas in Marathi and in southern languages.
• Some of them have written a few plays and also translated Sanskrit plays.

(e) What is the contribution of Vishnudas Bhave and V. J. Kirtane to Marathi theatre?
Answer:

1. Vishnudas Bhave presented the first play, Seetaswyamwar, on stage. Initially no written scripts were used for plays. Only the lyrics were written and dialogues were spontaneous.
2. The movement started by him was followed in Maharashtra by historical, mythological and also light farcical stage plays. He is known as the Father of the Marathi theatre.
3. V. J. Kirtane was the first author who wrote the script of Thorale Madhavrao Peshwe in 1861 and its printed copy was made available.
4. It was the beginning of the tradition of having a complete written script ready before staging the play.

(f) Explain the nature of Rashtriya Keertan.
Answer:

• During the independence movement, a new type of Keertan was developed known as Rashtriya Keertan.
• It is performed in the same way as Naradiya Keertan.
• It placed more importance on creating awareness by narrating the life stories of great leaders of the Indian independence movement, scientists, social reforms, etc.
• Dattopant Patwardhan of Wai started Rashtriya Keertan.

Question 13.
Read the following passage and answer the questions:
(a) Who presented the play ‘Seetaswayamvar’?
Answer:
‘Seetaswayamvar’ was the first play presented by Vishnudas Bhave.

(b) Who wrote the musical play ‘Sharada’?
Answer:
Govind Ballal Deval wrote the musical play Sharada.

(c) How can plays bring about social awakening?
Answer:

• As theatre is an audio-visual medium, it creates a strong impact on the audience.
• They commented on evil customs, traditions, superstitions in our society. This started the reformation process.
• Sharada, a musical play, written by Govind Ballal Deval shed light on the evil custom of marrying young girls to aged men in a humorous style.
• ‘Ekach Pyala’ by Ram Ganesh Gadkari made the society aware about the evil effects of drinking.

Question 14.
Answer the following questions in detail:
(a) Write about the art of Puppetry.
Answer:

• The Kathputali is a traditional art of puppetry which has two styles.
• One that developed in Rajasthan and the other in South India.
• In ancient India, materials like wood, wool, leather, horns and ivory were used to make puppets.
• The role of the narrator known as Sutradhar is very crucial in stage show.
• The stage for this puppetry show is very small but the puppeteers use light and sound effects in an ingenious way.
• Shadow puppets, hand puppets, string puppets and wooden puppets are used in Kathputali shows.
• The artists who perform Kathputali shows are found in Uttar Pradesh, Maharashtra, Rajasthan, Telangana, Karnataka and Kerala.

(b) Write about the development of Indian film industry.
Answer:

1. Cinema is a medium that brings together art and technology. With the advent of the technology of motion pictures the film industry came into being. It gave rise to the era of silent movies.
2. The technology of sound recording paved the way for talkies. Dadasaheb Torane, A. P Karandikar, S. N. Patankar and V. E Divekar made the movie Pundalik with help from foreign techniciAnswer: This was a great step in the development of the art.
3. Dadasaheb Phalke made a full length movie, completely processed in India. He made silent movies and documentaries also.
4. Baburao Painter’s cousin, Anandrao Painter made the first cine-camera. Baburao Painter made many historical movies and a movie on realistic social issues. Bhalaji Pendharkar made movies invoking nationalist sentiments.
5. Kamalabai Mangarulkar was the first woman producer, who made movies in Marathi as well as Hindi.
6. Prabhat Film Company made many religious, historical, mythological and social movies. Production studios like Bombay Talkies, Rajkamal Productions, R. K. Studios, Navketan played significant role in development of the Indian film Industry. Period from 1961 to 1981 is the golden period of Indian film industry.

Question 15.
Identify the given picture and write about his contribution:

Answer:

1. The given picture is of Dadasaheb Phalke who is known as the Father of Indian Film Industry.
2. He released the first movie ‘Raja Harishchandra’ in Mumbai in 1913. He directed the movie which was entirely processed in India for the first time.
3. He made silent movies named as Mohini- Bhasmasur, Savitri-Satyavana.
4. He also made documentaries on the rock cut caves of Verul and pilgrim centres of Nashik and Tryambakeshwar. Later, he made historical and mythological movies.
5. The Government of India has honoured him by instituting Dadasaheb Phalke Award given for lifetime contribution to cinema, which is considered one of the most prestigious awards.

10th Std History Questions And Answers:

• Historiography Development in the West Class 10 History Questions And Answers
• Historiography Indian Tradition Class 10 History Questions And Answers
• Applied History Class 10 History Questions And Answers
• History of Indian Arts Class 10 History Questions And Answers
• Mass Media and History Class 10 History Questions And Answers
• Entertainment and History Class 10 History Questions And Answers
• Sports and History Class 10 History Questions And Answers
• Tourism and History Class 10 History Questions And Answers
• Heritage Management Class 10 History Questions And Answers

Balbharti Maharashtra State Board Class 10 Political Science Solutions Chapter 1 Working of the Constitution Notes, Textbook Exercise Important Questions and Answers.

Std 10 Political Science Chapter 1 Question Answer Working of the Constitution Maharashtra Board

Class 10 Political Science Chapter 1 Working of the Constitution Question Answer Maharashtra Board

Political Science Class 10 Chapter 1 Question Answer Maharashtra Board

Question 1.
Choose the correct option from the given options and complete the sentences.
(1) In Maharashtra …………………… seats are reserved for women in local self-governing institutions.
(a) 25%
(b) 30%
(c) 40%
(d) 50%
Answer:
(d) 50%

(2) Which of the following laws created a favorable environment for women to secure freedom and self-development?
(a) Right to Information Act
(b) Dowry Prohibition Act
(c) Food Security Act
(d) None of the above
Answer:
(b) Dowry Prohibition Act

(3) The essence of democracy is ……………………
(a) universal adult franchise.
(b) decentralisation of power.
(c) policy of reservation of seats.
(d) judicial decisions.
(d) Judicial decisions
Answer:
(b) decentralization of power

Question 2.
State whether the following statements are true or false. Give reasons for your answer.

(1) Indian democracy is considered the largest democracy in the world.
Answer:
The above statement is True.

• Indian Constitution cancelled all the conditions which were put for voting before independence thereby increasing the number of voters.
• The Constitution adopted adult suffrage which has facilitated all adult men and women to cast their vote.
• The age limit to vote was reduced to 18 years from 21 years which gave opportunity of political participation to the young generation. No other democratic country in the world has voters- in such large numbers.

Hence, Indian democracy is the largest democracy in the world.

(2) Secrecy in the working of Government has increased due to the Right to Information.
Answer:
The above statement is False.

• To strengthen democracy and increase mutual trust between the government and the people, it is very important that the people should know about ‘the functioning of the government.
• Transparency and accountability are the hallmarks of good governance.
• With Right to Information given to the citizens, Government became more transparent. Thus, the Right to Information has reduced element of secrecy in administration.

(3) The nature of the Constitution is seen as a living document.
Answer:
The above statement is True.

• Parliament has the powers to make changes in the Constitution according to the changing circumstances and conditions.
• However, it should be done without tampering or changing the basic structure of the Constitution.
• As it has kept itself abreast with the changes, S the Constitution became a live and dynamic document instead of a rigid one

Question 3.
Explain the following concepts.

(1) Right based approach
Answer:

• India adopted democracy after independence. Each government which came to power took efforts to make the democratisation process more profound.
• In the initial stages, these governments considered citizens as ‘beneficiaries’.
• After the year 2000, the approach towards citizens changed. Democratic reforms were considered as ‘rights’ of citizens.
• Hence, the Right to Information, Education and Food Security was granted not as beneficiaries but as rights of the citizens. This approach is known as Rights Based Approach.

(2) Right to information
Answer:

• In order to bring transparency in the administration and make it accountable, Indian citizens are given Right to Information.
• Right to Information helped in promoting harmony between government and people and empowered the citizens.
• It brought transparency in administration, made the government realise that they are answerable to people.
• It has helped to reduce the element of secrecy which surrounded the functioning of the government. It made the government open and transparent.

(3) Women representation in the Loksabha.
Answer:

• The Constitution of India empowers women by granting them equal status with men and equal political rights.
• 22 women were elected in the Lok Sabha elections held in 1951-52. Their number increased to 66 in 2014 elections.
• Reservation has been increased to 50% in local self-governing institutions in Maharashtra and in many other states.
• If the number of women representative increased in Lok Sabha, it will help in reducing incidents of violence against women and increase their involvement in the decision-making process.

Question 4.
Answer in brief.
(1) What are the effects of reducing the voting age from 21 years to 18 years?
Answer:

• Earlier the Indian Constitution had fixed the voting age of 21 years.
• The voting age was lowered to 18 years.
• The young voters secured the right to vote and the increased number of voters was unparalleled. ‘
• They got the right to decide how their representative should be. ,
• Moreover, it provided to the unrepresented youth an opportunity to become part of political process being literate and politically conscious.
• It increased the scope of democracy by including the youth of the country thus making it the largest democracy in the world.

(2) What is meant by establishment of social justice?
Answer:
Establishing social justice means:

• To eliminate the practices and beliefs which are responsible for injustice towards a person or a community and which hampers collective progress of society should be eliminated.
• Government policies should be all inclusive which means it should aim at accommodating different sections of society.
• There should not be any discrimination based on caste, creed, religion, gender, language, property, region or place of birth.
• All should get equal opportunities for development.

(3) Which decision of the Court has resulted in protection of honour and dignity of women?
Answer:

• The apex court has given several judgments which have helped in protection of honour and prestige of women.
• Court gave judgement on Right to alimony as well as Right to equal remuneration.
• Women have an equal share in the property of husband and father. This gave them financial security. Dowry prohibition Act was a measure for women empowerment.
• The Act against sexual harrassment. Domestic Violence Prohibition Act are also very important in the direction of women empowerment.
• All these acts emphasised the need to protect women and protect their self-esteem and dignity rejecting the traditional forms of domination and authoritarianism.

Project
(1) Which information can be secured with the help of the right to information? Find out with the help of your teachers.
(2) Make a list of concessions given by the Government for the students of minority communities?
(3) Visit the official website of the National election commission and collect more information about it.
(4) Take an interview of women representations from local self-governing institutions from your area.

Memory Map

Q. Complete the sentences by choosing the correct option:

1. Right to Information came into force from
(a) 2002
(b) 2004
(c) 2005
(d) 2006
Answer:
(c) 2005

2. The Indian government has been working in accordance with principle of the
(a) Parliament
(b) President
(c) Constitution
(d) Party
Answer:
(c) Constitution

3. Men and women above years of age can vote in India.
(a) 15
(b) 18
(c) 21
(d) 25
Answer:
(b) 18

4. can make amendments to the Constitution.
(a) President
(b) Prime Minister
(c) Council of Ministers
(d) Parliament
Answer:
(d) Parliament

5. got recognition because of 73rd and 74th Amendments to the Constitution.
(a) Parliament
(b) Local self-governing institutions
(c) Legislative council
(d) Cooperative societies
Answer:
(b) Local self- governing institutions

6. ………………….. has made the government more transparent.
(a) Equality
(b) Freedom
(c) Right to Information
(d) Social Justice
Answer:
(c) Right to Information

7. and are two features of good governance.
(a) Popular, populist
(b) Efficient, democratic
(c) Transparent, responsible
(d) Equality, decentralization
Answer:
(c) Transparency, responsible.

Q. State whether the following statements are true or false:

1. Indian democracy is evidently unsuccessful.
Answer:
The above statement is False.

• India has the largest number of voters as compared to any other democratic nation in the world.
• Free and fair elections which are held regularly is the key for successful democracy.
• Recurring elections have helped in understanding the political process. As the voting age was reduced from 21 to 18 years, the political participation has increased.
• Increasing participation of the people in the political process and political contest shows that Indian democracy is successful.

2. There is less friction in all inclusive democracy.
Answer:
The above statement is True.

• To establish social justice and equality is the aim of democracy. .
• If all the sections of society are given equal opportunities without any discrimination then all 8 components come into the main stream.
• In fact, democracy is the process of accommodating different sections of society which ultimately reduces the social conflict.

Q. Explain the following concepts:

1. Decentralisation:
Answer:

• Division of power within, a country is known as Decentralisation.
• Under dictatorship and military rule, the power is centred around one person or a group of individuals.
• But in democracy the power is divided among Centre, State and Local Self-governing institutions. Decentralisation is the core of democracy.
• Decentralisation can stop the misuse of power and facilitate common people to participate in democracy.

2. Provisions regarding Minorities:
Answer:

• Constitution has adopted several measures for the protection of the rights of minorities.
• Several policies have been adopted by the government to provide them the opportunities in education and employment.
• The Constitution has prohibited any form of discrimination on the basis of caste, creed, religion, language and region.
• The Constitution provided rights to the minorities to protect and conserve their language, culture and establish educational institutions

3. Policy of Reservation of Seats:
Answer:

• Some sections of Indian society were denied social justice.
• They were deprived of educational and employment opportunities. It was essential to bring them in the main stream of society.
• The policy was adopted to give reservation to Scheduled Castes and Scheduled Tribes in educational institutions and public employment.
• Seats were also reserved for Other Backward Classes. Reservation policy gave the deprived classes justice and opportunities for development.

Q. Complete the Concept Map:

1. Complete the Concept Map:

Answer:

2. important to understand:

Answer:

3. please understand:

Answer:

Q. Answer the following questions in brief:

1. What are the provisions made in the Directive Principles regarding decentralization?
Answer:
The Directive Principles of the Indian Constitution has made provisions for decentralization of power. It means:

• Indian Constitution has divided the power between the centre, state and local self-governing institutions.
• The guidelines about empowering the local self-governing bodies are given in the Constitution.
• After independence, 73rd and 74th Amendment to the Constitution in 1992 has given constitutional status to the local self-governing bodies.
• Due to this, there is increase in the participation by the people at grass root level. Democracy was put into practice which eventually got strengthened. Decentralisation curbed the misuse of power.

2. What were the measures taken to increase the number of women in politics?
Answer:

• The 73rd and 74th Constitutional Amendment provided reservation of 33% seats for women in local self governing institutions.
• This reservation has been increased to 50% in Maharashtra and many other states.
• One-third seats and the offices (posts) of Sarpanch, Mayor, etc. are reserved for women. Several policies have been adopted to remove illiteracy among women and to make available opportunities for their development.
• A bill is tabled in the house to reserve 50% seats in Legislative Assembly and Parliament.

3. The Judiciary in India has played an important role in strengthening democracy. Explain.
Answer:

• The Judiciary has always taken into consideration the fundamental objectives of the Constitution and also the intention of its framers.
• While interpreting the Constitution, it has taken care that its basic structure is not altered as Constitution is foundation of our democracy.
• The important role played by judiciary is in strengthening and helping democracy to achieve the objectives of social justice and equality.

4. Which particular Laws/Acts created a favourable environment for the protection of freedom of women and secure their development?
Answer:

1. Several policies have been adopted in the post-independence period for empowering women.
2. Provisions were made in the Constitution to provide opportunities for progress.
3. Many laws were passed to empower them. They are:
   • Right to have equal share in the property of father and husband.
   • Dowry Prohibition Act.
   • Act against Sexual Harassment.
   • Domestic Violence Prohibition Act.

Q. Give your opinion:

1. What measures should be adopted to increase the number of women in representative democracy?
Answer:
Several restrictions were imposed in the name of traditions and practices, making’ the workspace of women limited to home.

• To curb injustice the representation of women should increase in all institutions. The 73rd and 74th Amendment reserved 33% of seats for women in local self governing institutions.
• Access to more and more social and political fields should be made available for women. They should be involved in the decision-making process and work for their betterment.
• This would ultimately lead to eliminating injustice done to them and will enhance their self respect and status.

2. Do you agree that Indian democracy has become profound?
Answer:
I entirely agree that Indian democracy has become profound.

• The Indian Constitution has laid down representative structure of democracy.
• The actual practice of the principles of democracy is the essence of representative system.
• People have direct representation in Lok Sabha, Rajya Sabha and Local Self-Government Institutions.
• Free and fair elections are held at regular intervals to elect representatives.
• Citizens cast their votes weighing the public issues and policies related to it. All the above factors show that Indian democracy has become profound.

3. Do you think that citizens in India should 8 have the right to employment? (Discuss – Textbook page 70)
Answer:
I agree that all Indian citizens should get I employment.

• If they are deprived of employment opportunities their families would face hunger and starvation.
• Incident of crime will increase in society.
• Democracy will collapse leading to chaos.
• More and more employment opportunities S should be generated for their progress.

4. According to you, if everyone gets the right to shelter, how will it affect democracy in 8 India?
Answer:

• Food, clothing and shelter are the basic necessities of a man.
• Shelter is not only his necessity but also his right.
• A permanent need is to get settled in life. 8 If a man gets a home, a large part of his struggle 8 in life will come to an end.
• The financial burden will be low and he will x work with honesty and will contribute in nation’s X progress.
• Home for all creates a healthy society. It has an all-round social, economical and psychological effect to strengthen democracy and make it 8 profound.

5. What steps should be taken to stop injustice done to the Backward Classes? OR What efforts should be made to prevent x atrocities?
Answer:
The backward classes have suffered for thousands of years. I feel the following measures x will remove injustice done to the backward classes:

• Atrocities laws should be made stringent.
• Fast courts should be set up to handle such cases.
• Stringent punishment should be given if 8 found guilty.
• Efforts should be made to improve economic 8 status of the backward classes.
• The Government should make efforts to establish social justice and equality. .

6. What efforts should be made to bring in all the features of good governance in democracy?
Answer:
For the successful functioning of democracy, good governance is very essential.

• People should elect good and professional candidates.
• People should keep watch on the work done by them.
• Corrupt candidates should not be elected or re-elected.
• People should respond to various policies which are beneficial for society.
• People should pressurise the government to start various developmental policies for country’s progress.

Q. B Can you tell the reasons for the following changes?

1. Some seats were reserved for women to increase their participation in political process.
Answer:

• Women empowerment movement started after independence.
• All the countries in the world started increasing number of women representatives.
• The 73rd and 74th constitutional amendment reserved 33% seats for women in local self- governing institutions.
• Some seats are kept reserved for women to increase their participation in political process.
• Some seats are kept reserved for weaker sections of the society so that they can get a share in political power.
• The State Election Commission has been established. The 11th and 12th schedule was added to the constitution.

2. Some seats are kept reserved for weaker sections of the society so that they can get a share in political power.
Answer:

• The weaker sections suffered injustice for thousand of years.
• The opportunities of education and employment had been denied to them.
• In order to establish social justice and equality, reservations are now given to the weaker sections.

3. The State Election Commissions were set up.
Answer:

• Elections for the Parliament and State Assemblies are conducted by the National Election Commission.
• It was impossible to put upon the local self government bodies the responsibility of conducting elections. Hence the State Election Commissions were formed.

4. 11th and 12th Schedule was added to the Constitution.
Answer:

• The 11th schedule of Indian Constitution was added in 1992 by the 73rd Constitution Amendment Act. This schedule contains 29 subjects related to panchayat.
• The 74th Amendment to the Constitution added 12th schedule and covered 18 subjects related to the Municipalities.
• ”It gave constitutional status to Municipalities and Panchayats and aimed to strengthen rural and urban governments so that they can function efficiently.

10th Std Political Science Questions And Answers:

• Chapter 1 Working of the Constitution Class 10 Political Science Questions And Answers
• Chapter 2 The Electoral Process Class 10 Political Science Questions And Answers
• Chapter 3 Political Parties Class 10 Political Science Questions And Answers
• Chapter 4 Social and Political Movements Class 10 Political Science Questions And Answers
• Chapter 5 Challenges faced by Indian Democracy Class 10 Political Science Questions And Answers

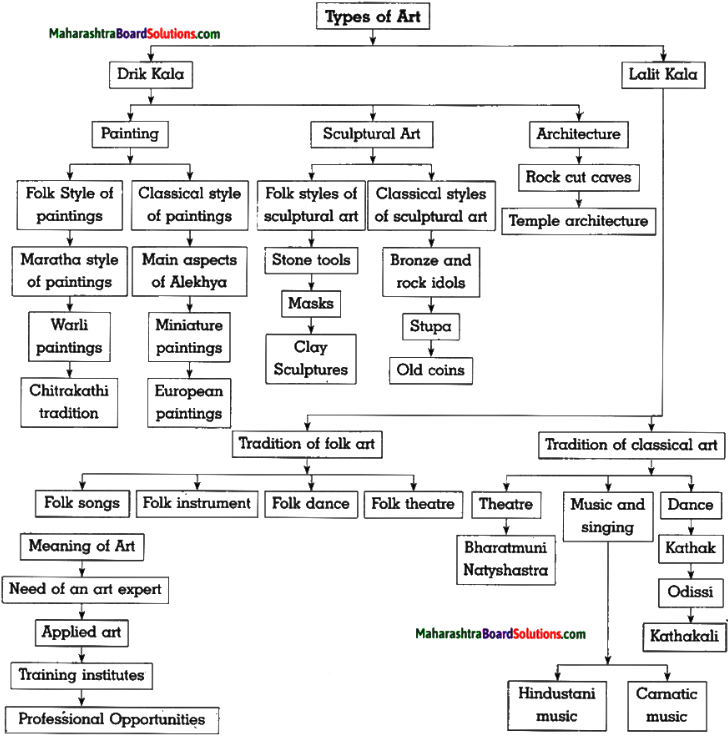
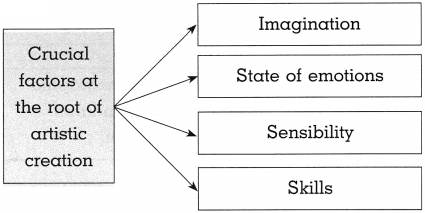
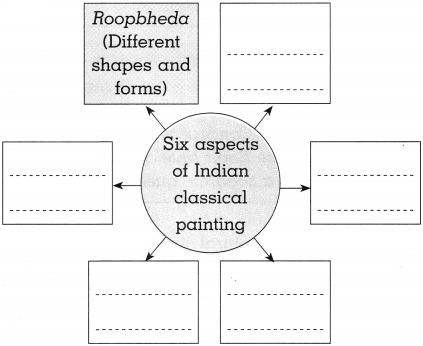
Balbharti Maharashtra State Board Class 10 Geography Solutions Chapter 3 Physiography and Drainage Notes, Textbook Exercise Important Questions and Answers.

Std 10 Geography Chapter 3 Question Answer Physiography and Drainage Maharashtra Board

Class 10 Geography Chapter 3 Physiography and Drainage Question Answer Maharashtra Board

Geography Class 10 Chapter 3 Question Answer Maharashtra Board

1. Complete the sentences by choosing the right option :

Question a.
Brazil is covered mainly by _________.
(a) highlands
(b) mountainous region
(c) plains
(d) dissected hills
Answer:
(a) highlands

Question b.
Like Brazil, India too has __________.
(a) high mountains
(b) west flowing rivers
(c) ancient plateau
(d) snow-capped mountains
Answer:
(c) ancient plateau

Question c.
The Amazon Basin is mainly ________.
(a) characterized by droughts
(b) filled by swamps
(c) covered by dense forests
(d) fertile
Answer:
(c) covered by dense forests

Question d.
Amazon is a large river in the world. Near its mouth ___________.
(a) deltaic regions are found
(b) no deltas are found
(c) deposition of sediment occurs
(d) fishing is done
Answer:
(b) no deltas are found

Question e.
The Lakshadweep Islands of the Arabian Sea are _________.
(a) made from the part separated by mainland
(b) coral islands
(c) volcanic islands
(d) continental islands
Answer:
(b) coral islands

Question f.
To the foothills of the Aravalis _________.
(a) lies the Budelkhand Plateau
(b) lies the Malwa Plateau
(c) lies the Mewad Plateau
(d) lies the Deccan Plateau
Answer:
(c) lies the Mewad Plateau

2. Answer the following Questions:

Question a.
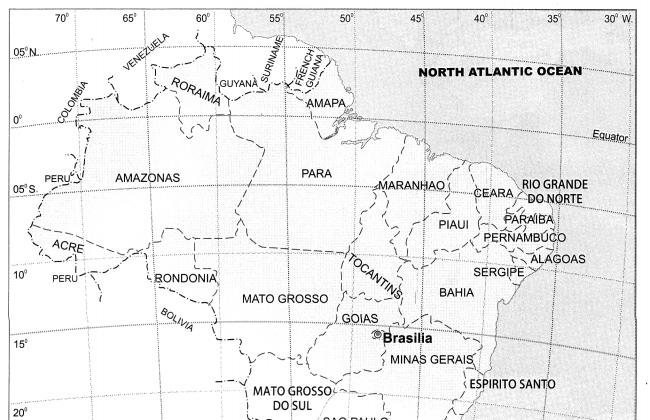
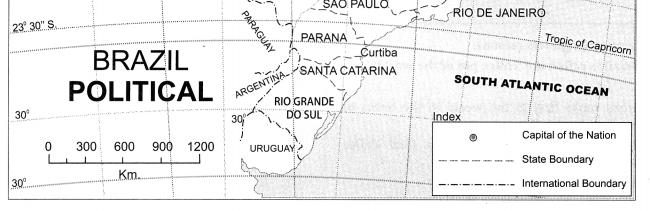
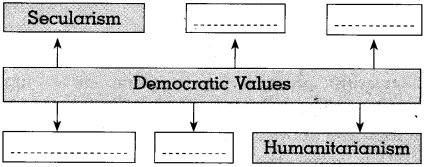
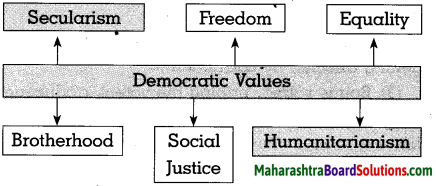
Differentiate between the physiography of Brazil and India
Answer:

The Physiography of India	The Physiography of Brazil
The physiographic divisions of India are the Himalayas, the North Indian Plains and the Peninsula, Coastal Plains, and the Islands.	The physiographic divisions of Brazil are: The Highlands, The Great Escarpment, The Coastal region, The Plains and The Islands.
There are long and high mountain ranges in northern and north eastern part of India in the form of Himalayan ranges. The Western Ghats and the Eastern Ghats lie to the west and east of the Peninsular region. The average altitude of the Greater Himalayas is around 6000m.	In Brazil there are no high and continuous mountain ranges. The eastern side of the Highlands is demarcated because of the Escarpment. The Great Escarpment located in south-eastern part of the Highlands has an altitude of 790m in this region with the height gradually decreasing.
In India the Plains occupy a wide area in the north. The Plains lie between the Himalayas in the North and the Peninsula in the South. It extends from Rajasthan in the West to Assam in the East. The Coastal Plains lie to the west and east of the Peninsula.	In Brazil the Amazon Basin in the North and the Parana-Paraguay Basin to the South West constitutes the Plains. Also a narrow coastal plain is confined to the North and the East.
The Peninsular Plateau region of India lies to the South of the North Indian Plains and is divided into 2 groups, the The Central Highlands and the Deccan Plateau.	In Brazil the Highlands occupy an extensive area in the South and is described as the Brazilian Highlands or the Brazilian Shield. Also to the North lies the Guyana Highland.
The islands in India are either volcanic or coral in origin.	The islands in Brazil are mainly depositional and some of them are coral in nature.

Question b.
What measures are being taken to control pollution in the rivers of India?
Answer:
Rivers in India are getting polluted due to the sewage and effluents being added to it and thus affecting its quality. Following measures are being taken to control pollution in the rivers in India.

(i) Treating of the sewage before draining it into the rivers.
(ii) Reducing the use of pesticides and insecticides as they drain into the water sources and pollute it.
(iii) Discharge of industrial effluents into rivers without proper treatment is now controlled.
(iv) Reusing the water for different purposes which reduces the overuse and pollution of water.
(v) Carrying out the cleaning and purification of the river water under the National River Conservation Plan (NRCP).
(vi) Creating awareness in the people about the importance of rivers and harmful effects of pollution.
(vii) Setting up of Pollution Control Boards (PCB) at the state and national level to curb pollution.

Question c.
Explain the characteristics of the North Indian Plains.
Answer:
(i) This division lies between Himalayan Mountains in the north and the Peninsula in the south.

(ii) Similarly, it extends from Rajasthan and Punjab in the west to Assam in the east.

(iii) It is mostly a flat low lying area.

(iv) The North Indian Plains are divided into two parts. The part lying to the east of the Aravalis is the basin of the river Ganga and is therefore known as the Ganga Plains. It slopes eastward.

(v) Most of the Indian state of West Bengal and Bangladesh together constitute the delta of Ganga-Brahmaputra system. It is known as the Sunderbans. It is considered to be the world’s largest delta.

(vi) The western part of the North Indian Plains is occupied by desert known as the Thar Desert or Marusthali. Most of Rajasthan is occupied by this desert.

(vii) To the north of the desert lie the plains of Punjab.

(viii) This region is spread to the west of Aravalis and Delhi ranges. These plains have formed as a result of the depositonal work by river Satluj and its tributaries. The slope of the plains is towards the west.
Because the soil here is very fertile, agriculture is largely practised in this region.

Question d.
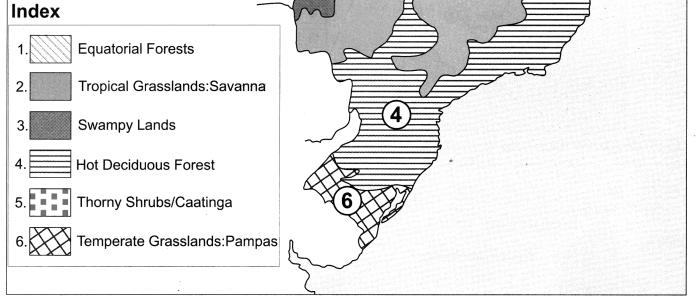
What could be the reasons behind the formation of swamps in the extensive continental location of Pantanal?
Answer:
Pantanal is one of the largest wetlands in the world, lying in the south west part of the highland areas.
It is a region of swamps and marshes in northwestern part of Mato Grosso do Sul in Brazil and it extends into Argentina too.
This region is drained by the river Paraguay and its tributaries.
They collect the water from the highland areas and deposit the sediments in the low lying Pantanal region.
Pantanal is a gently sloped basin which is submerged throughout the year due to the filling of the sediments and water in the depression area of the Pantanal.

Question e.
Which are the major water divides of India give examples.
Answer:
A mountain or an upland which separates two drainage basins is known as a Water Divide. The major Water Divides of India are :

Western Ghats: The Western Ghats acts as a water divide and separates the west flowing rivers like Zuari, Mandvi, Vaitama draining into the Arabian Sea, from the east flowing rivers like the Godavari, Krishna and Kaveri draining into the Bay of Bengal.

Vindhya ranges: It divides the drainage basin of the River Ganga and the River Narmada.

Aravali ranges : The Aravali ranges separate the west flowing river Luni from the east flowing river Banas.

Satpuda ranges: The Satpudas separate the Narmada drainage basin and the Tapi drainage basin.

Question 3.
Write notes on :
Answer:
a. Amazon River Basin:
(i) Amazon collects its headwaters from the eastern slopes of Andes Mountains in Peru.

(ii) Amazon River receives huge discharge. This is about 2 lakh m³/s.

(iii) As a result, Amazon washes off the load supplied to it from the catchment

(iv) Consequently, sediments are not deposited even at the mouth.

(v) A dense network of distributaries, which is a characteristic feature of river mouth areas, is by and large absent in the mouth region of Amazon.

(vi) Instead, we find a series of islands developed along the mouth of Amazon, beyond the coastline into the Atlantic Ocean.

(vii) At the mouth, the width of Amazon channel is 150 km.

(viii) Most of the course of the Amazon river is suitable for navigation.

b. Himalayas:
(i) The Himalayas is one of the young fold mountains in the world.

(ii) The Himalayas extend from Pamir Knot in Tajikistan to the east. It is a major mountain system of the Asian continent.

(iii) In India, it extends from Jammu and Kashmir to Arunachal Pradesh.

(iv) The Himalayas is not a single mountain range. There are many parallel ranges in the system.

(v) The southernmost range of Himalayas is known as the Siwaliks. It is also the youngest range.

(vi) Beyond the Siwaliks are Lesser Himalayas (Himachal), Greater Himalayas (Himadri) and Trans Himalayan ranges from south to north.

(vii) These ranges are young to old respectively.

(viii) These mountain ranges can also be divided into Western Himalayas (or Kashmir Himalayas), Central Himalayas (or Kumaun Himalayas) and Eastern Himalayas (or Assam Himalayas).

c. The coasts of Brazil:

(i) Brazil has a coastline of about 7400 km. They are divided into two parts namely northern coast and the eastern coast.

(ii) The northern coast extends from Amapa province in the north to Rio Grande Do Norte in the east. This coast can be called as North Atlantic Coast. From here, the eastern coast extends towards the south.

(iii) The northern coast is characterized by mouths of many rivers including the Amazon. Therefore, this region is a low-lying region.
(iv) On this coast lie the Marajo island, Marajo and Sao Marcos Bays.

(v) Marajo, a large coastal island located between River Amazon and River Tocantins, lies on the northern coast.

(vi) The eastern coast receives a large number of smaller rivers. The only major river which meets the Atlantic Ocean here is Sao Francisco.
(vii) The Brazilian Coast is characterized by a large number of beaches and sand dune complexes.

(viii) The Brazilian Coast is protected in some areas by coral reefs and atoll islands.

d. The Indian Peninsula:

(i) The area lying to the south of North Indian Plains and tapering towards the Indian Ocean is called Indian Peninsula.
(ii) It consists of many plateaus and hill ranges.
(iii) The Aravalis in the north west are the oldest fold mountains here.
(iv) It includes a series of plateaus bordering the Plains, Vindhyas and Satpuda ranges in the central part and the hilly regions of Western and Eastern Ghats.

e. The Great Escarpment:

(i) An Escarpment is a long, steep slope especially one at the edge of a plateau.

(ii) Though the Great Escarpment occupies a I very small area, the nature of its slope and the effect it has on the climate makes is a separate
physiographic region.

(iii) The eastern side of the Brazilian Highland is demarcated because of the escarpment.

(iv) In this region, the altitude of the escarpment is 790 m.

(v) In some regions, the height decreases gradually.

(vi) The escarpment is very steep particularly from Sao Paulo to Porto Alegre.

(vii) The escarpment acts as a barrier to the Southeast Trade Winds giving rise to the rainshadow area in the northeast part of the highlands. The region to the north of this area is called ‘Drought Quadrilateral’.

4. Write geographical reasons:

Question a.
There are no west flowing rivers in Brazil.
Answer:
(i) Many rivers originating from the terminal portion of the Brazilian highlands flow northwards to meet the Amazon river and finally terminate in the Atlantic Ocean.

(ii) Sao Francisco River flows 1000 kms towards the north and then turns east to join the Atlantic Ocean.

(iii) The rivers Parana, Paraguay and Uruguay originating from the southern part of Brazilian highlands flow southwest and enter Argentina.

(iv) The Amazon river, originating from the Andes mountain in the west flows eastwards to meet the Atlantic Ocean.

(v) Thus, there are no west flowing rivers in Brazil.

Question b.
There are dissimilarities between the eastern and the western coast of India.
Answer:
(i) The western coast borders the Arabian Sea and the eastern coast borders the Bay of Bengal.

(ii) The western coast is by and large a rocky coast. At places, spurs starting from the Western Ghats have extended right up to the coast. The eastern coast has been formed as a result of depositional work of rivers.

(iii) The width of the western coast is narrow, whereas that of the eastern coast is wide.

(iv) Short and swift rivers originating from Western Ghats form estuaries on the western coast, whereas, because of the gentle slope the east flowing rivers flowing at low speed deposit sediments and form deltas on the eastern coast.

(v) Thus there are dissimilarities between the eastern and the western coasts of India.

Question c.
There are fewer natural ports on the eastern coast of India.
Answer:
(i) The eastern coast borders the Bay of Bengal. It has been formed as a result of depositional work of rivers.
(ii) Many east flowing rivers have formed deltas at their mouth due to the gentle slope.
(iii) Sediments deposited by the river makes the coast shallow.
(iv) Therefore there are fewer natural ports on the eastern coast of India.

Question d.
As compared to Amazon, the pollution in river Ganga affects human life greatly.
Answer:
(i) The Amazon Basin is a sparsely populated region of Brazil.. Unfavourable climate, heavy rainfall, inaccessibility and dense forest are the barriers for development of human settlements and industrialisation here.

(ii) On the other hand, the Ganga Plain region is one of the most densely populated regions of India.

(iii) Due to flat fertile plains, availability of water, suitable climate, dense human settlements have been established in this region.

(iv) Mining activities in the Amazon Basin causes pollution in the Amazon River, whereas industrial and domestic sewage adds to the pollution of

River Ganga. Thus as compared to Amazon, the pollution in River Ganga affects human life greatly, as the Ganga Plain is more densely populated as compared to the Amazon Plains.

5. Identify the correct group:

Question a.
The order of the physiographic units in Brazil while going from North West to South East
(i) Parana River basin – Guyana Highlands – Brazilian Highlands
(ii) Guyana Highlands – Amazon river basin – Brazilian Highlands
(iii) Coastal plains – Amazon River basin – Brazilian Highlands
Answer:
Guyana Highlands – Amazon River basin – Brazilian Highlands

Question b.
These Rivers of Brazil are north-flowing
(i) Juruaka – Xingu – Aragua
(ii) Negro – Branco – Paru
(iii) Japura – Jurua – Purus
Answer:
Juruaka – Xingu – Aragua

Question c.
The order of plateaus of India from south to north.
(i) Karnataka – Maharashtra – Bundelkhand
(ii) Chhota Nagpur – Malwa – Marwad
(iii) Telangana – Maharashtra – Marwad
Answer:
Karnataka – Maharashtra – Bundelkhand

Class 10 Geography Chapter 3 Physiography and Drainage Intext Questions and Answers

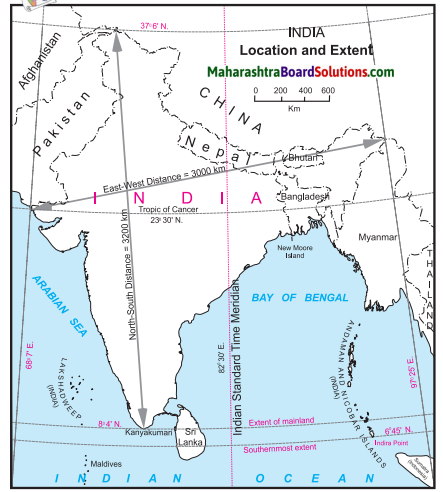
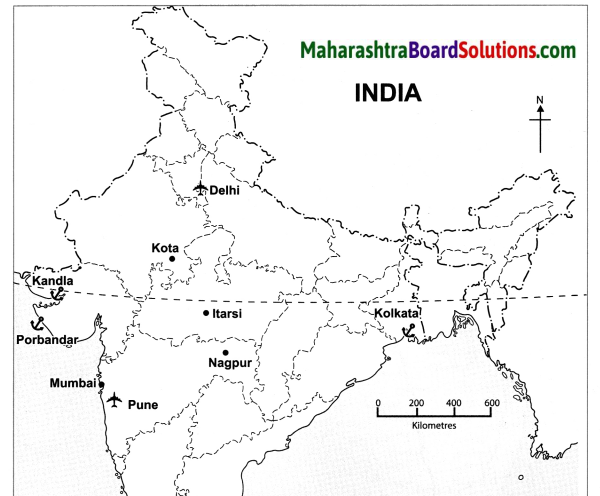
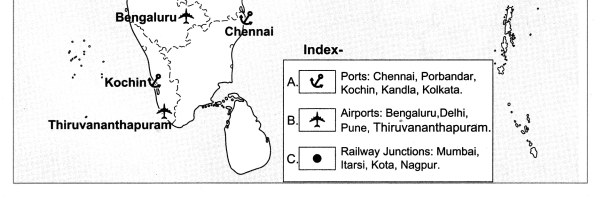
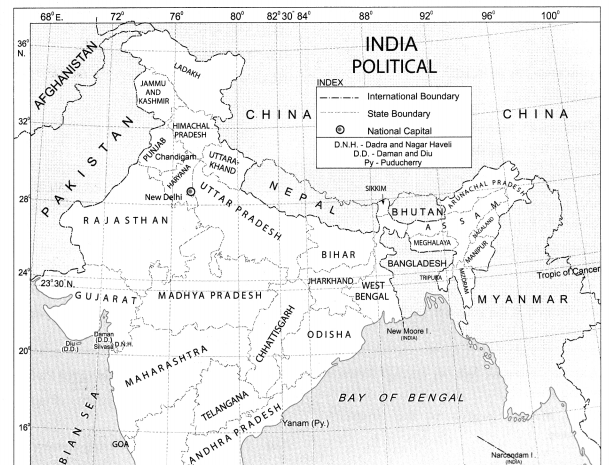
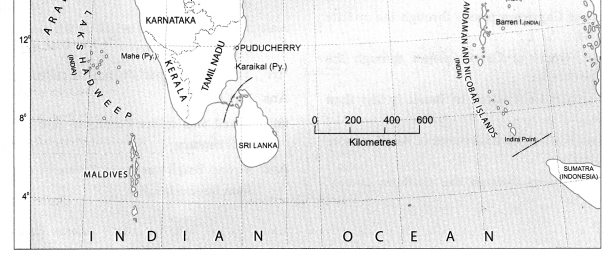
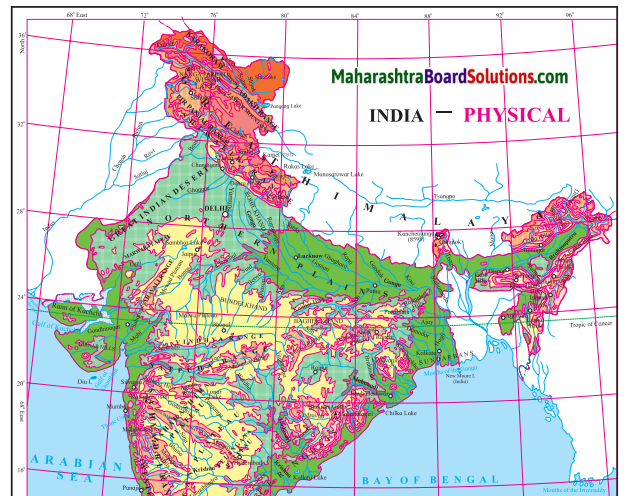
Observe the map and answer the following questions.

Physiography And Drainage Map Questions And Answers Question 1.
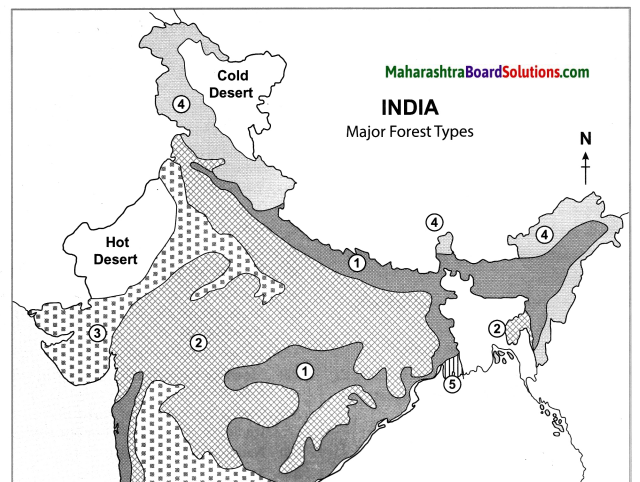
In which direction does the region with an altitude of more than 6000m lie in India ?
Answer:
The region with an altitude of more than 6000m lies part of India towards the north and north eastern.

Physiography And Drainage Questions And Answers  Question 2.
Look for the south-flowing river in the peninsular region. In which river basin does it lie?
Answer:
River Wardha and Vainganga are the south flowing river in the peninsular region. These lie in the Godavari river basin.

Physiography And Drainage Question 3.
In which direction is the slope of the region in the north shown in dark green.
Answer:
The region in the north shown in dark green is the North Indian Plain. It slopes towards the east.

Geography Class 10 Chapter 3 Physiography And Drainage Question 4.
Make a list of plateaus located in between Aravalli ranges and Chhota Nagpur Plateau.
Answer:
Plateaus located in between Aravalli ranges and Chhota Nagpur Plateau are Mewad Plateau, Bundelkhand, Baghelkhand and Malwa Plateau.

Physiography And Drainage Of India And Brazil Notes  Question 5.
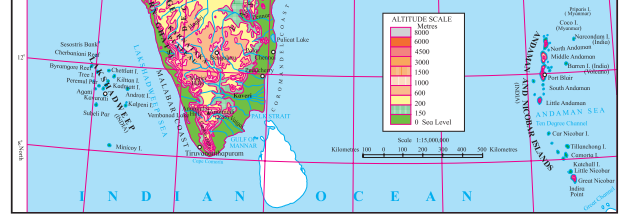
Name the peak shown in the Eastern Ghats.
Answer:
Mahendragiri (1600m) and Malayagiri (1187m) are the peak shown in the Eastern Ghats.

Physiography And Drainage 10th Question 6.
Which mountains demarcate the deep plains of Brahmaputra?
Answer:
Dafla Hills, Naga Hills, Garo, Khasi and Jaintia Hills demarcate the deep plains of Brahmaputra.

Physiography And Drainage Class 10  Question 7.
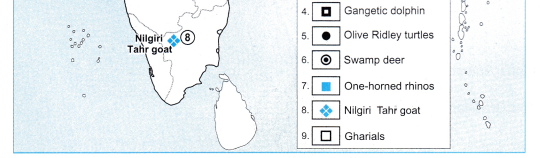
Give the relative location of the Nilgiri Hills.
Answer:
Nilgiri Hills lie at the convergence of Western Ghats and Eastern Ghats in the southern part of the Deccan Pleateau.

10th Physiography Chapter 3 In Marathi Question Answer  Question 8.
In which direction does the height of Sahyadri hills increase?
Answer:
The height of Sahayadri hills increase towards the south.

Question 9.
The Vindhyas act as a water divide between which two river basins?
Answer:
The Vindhyas acts as a water divide between Ganga river system and Narmada river system.

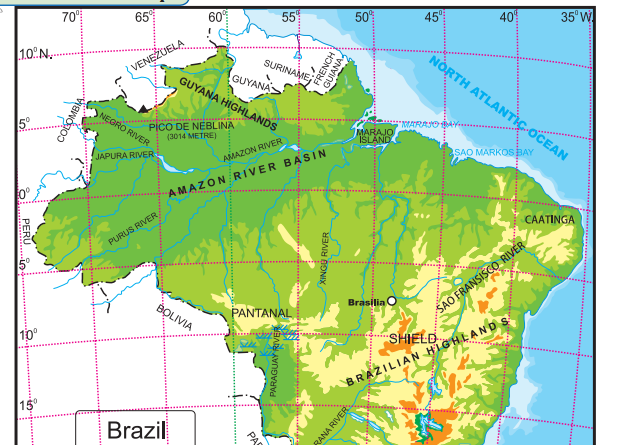
Observe the map and answer the following questions.

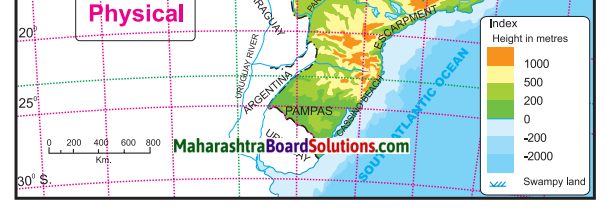
Question 1.
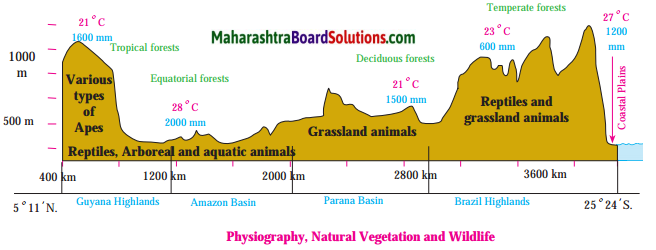
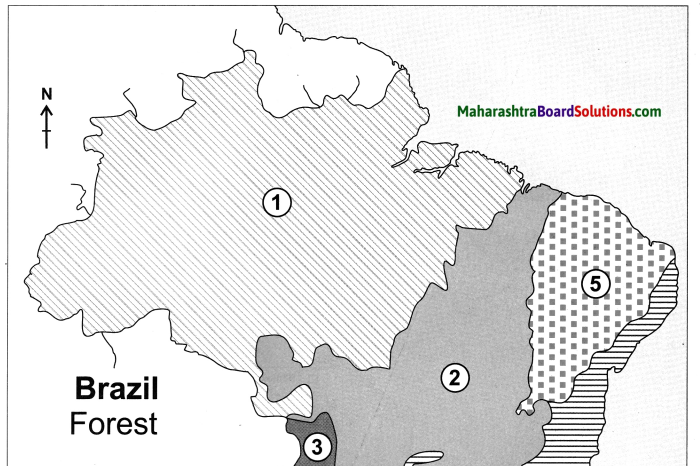
What is the range of altitude of the Amazon river basin?
Answer:
The range of altitude of the Amazon river basin is from 0 metres to 200 metres.

Question 2.
Between which two highlands is the Amazon river basin located?
Answer:
The Amazon river basin is located between the Guyana Highlands and the Brazilian Highlands.

Question 3.
Observe the region with the altitude of 500 to 1000 metres. Describe the locational extent of this region in yellow with reference to the direction.
Answer:
The region in yellow represents the Brazilian Highlands. They cover most of the eastern and southern parts of Brazil.

Question 4.
What do the isolated regions shown in yellow indicate?
Answer:
The isolated region shown in yellow indicate the Brazilian Highlands or the Brazilian Plateau or the Brazilian Shield.

Question 5.
Besides the Amazon river basin, where else do you find regions with an altitude of less than 200m?
Answer:
Besides the Amazon basin the other regions with an altitude of less than 200m are the Pampas, Parana and Paraguay basin, as well as the Eastern and Northen coastal region.

Question 6.
Describe the plateau region with height of 200 to 500m through which tributaries of Amazon flow in your own words.
Answer:
The highlands here gradually slope towards north and slopes are not very steep. The tributaries of Amazon, eg. Xingu river flowing through this region make rapids and waterfalls.

Question 10.
Enumerate the characteristics of the Western Ghats.
Answer:
(i) The Western Ghats are a continuous chain of mountains extending from north to south for about 1600 km. They run parallel to the west cost of India.
(ii) In the north, i.e., in Maharashtra and Karnataka these mountain ranges are referred as Sahyadris and in the south they are referred as Annamalai hills.
(iii) The height of the Western Ghats increases towards the south.
(iv) These hill ranges comprise of many peaks such as Kalsubai Peak (1646 m) located to the north and Anaimudi Peak (2695 m) located to the south of Western Ghats.
(v) The highest peak of Western Ghats is Anaimudi Peak (2695 m) located in Annamalai hills.
(vi) The western slope of the Western Ghats is steep while the eastern slope is gentle
(vii) The Western Ghats acts as a water divide for the rivers flowing towards Arabian Sea and Bay of Bengal.

Question 11.
Compare the Eastern Ghats and Western Ghats
Answer:

S.no	Eastern Ghats		Western Ghats
(i)	The Eastern Ghats run along the eastern coast of India in the north east to south west direction.		(i)	The Western Ghats also known as Sahyadris run in the north-south direction along the western coast of India.
(ii)	It forms the eastern boundary of the Deccan Plateau.                                          .		(ii)	It forms the western boundary of Deccan Plateau.
(hi)	It is not continuous, but is broken at many places by rivers like Godavari and Krishna.		(iii)	The Western Ghats is like a continuous wall like structure, but is broken at same places by passes.
(iv)	Comparatively less number of rivers originate from the Eastern Ghats.		(iv)	It is a source of many westward and eastward flowing rivers.
(v)	The average altitude of the Eastern Ghats is low (600 mts) but they are wider than Western Ghats.		(v)	The average altitude of the Western Ghats is high (900-1600 mts) but it is narrower in width than Eastern Ghats.
(vi)	Highest peak of Eastern Ghats is Jindhagada (1690 m)		(vi)	Highest peak of Western Ghats is Anaimudi Peak (2695 m)

Question 12.
Why are the Western Ghats called a water divide ?
Answer:
The Western Ghats divide the basins of the west flowing rivers like Vaitama, Mandovi, etc. flowing towards the Arabian sea from those of the east flowing rivers like Godavari, Krishna, etc. flowing towards the Bay of Bengal.

Answer the following Questions:

Question 1.
Differentiate between the Physiography of Brazil and India.
Answer:

The Physiography of India	The Physiography of Brazil
(i) The physiographic divisions of India are the Himalayas, the North Indian Plains and the Peninsula, Coastal Plains, and the Islands.	(i) The physiographic divisions of Brazil are: The Highlands, The Great Escarpment, The Coastal region, The Plains and The Islands.
(ii) There are long and high mountain ranges in northern and north eastern part of India in the form of Himalayan ranges. The Western Ghats and the Eastern Ghats lie to the west and east of the Peninsular region. The average altitude of the Greater Himalayas is around 6000m.	(ii) In Brazil there are no high and continuous mountain ranges. The eastern side of the Highlands is demarcated because of the Escarpment. The Great Escarpment located in south-eastern part of the Highlands has an altitude of 790m in this region with the height gradually decreasing.
(iii) In India the Plains occupy a wide area in the north. The Plains lie between the Himalayas in the North and the Peninsula in the South. It extends from Rajasthan in the West to Assam in the East. The Coastal Plains lie to the west and east of the Peninsula.	(iii) In Brazil the Amazon Basin in the North and the Parana-Paraguay Basin to the South West constitutes the Plains. Also a narrow coastal plain is confined to the North and the East.
(iv) The Peninsular Plateau region of India lies to the South of the North Indian Plains and is divided into 2 groups, the The Central Highlands and the Deccan Plateau.	(iv) In Brazil the Highlands occupy an extensive area in the South and is described as the Brazilian Highlands or the Brazilian Shield. Also to the North lies the Guyana Highland.
(v) The islands in India are either volcanic or coral in origin.	(v) The islands in Brazil are mainly depositional and some of them are coral in nature.

Question 2.
What measures are being taken to control pollution in the rivers of India?
Answer:
Rivers in India are getting polluted due to the sewage and effluents being added to it and thus affecting its quality. Following measures are being taken to control pollution in the rivers in India.

• Treating of the sewage before draining it into the rivers.
• Reducing the use of pesticides and insecticides as they drain into the water sources and pollute it.
• Discharge of industrial effluents into rivers without proper treatment is now controlled.
• Reusing the water for different purposes which reduces the overuse and pollution of water.
• Carrying out the cleaning and purification of the river water under the National River Conservation Plan (NRCP).
• Creating awareness in the people about the importance of rivers and harmful effects of pollution.
• Setting up of Pollution Control Boards (PCB) at the state and national level to curb pollution.

Question 3.
Explain the characteristics of the North Indian Plains.
Answer:
(i) This division lies between Himalayan Mountains in the north and the Peninsula in the south.

(ii) Similarly, it extends from Rajasthan and Punjab in the west to Assam in the east.

(iii) It is mostly a flat low lying area.

(iv) The North Indian Plains are divided into two parts. The part lying to the east of the Aravalis is the basin of the river Ganga and is therefore known as the Ganga Plains. It slopes eastward.

(v) Most of the Indian state of West Bengal and Bangladesh together constitute the delta of Ganga-Brahmaputra system. It is known as the Sunderbans. It is considered to be the world’s largest delta.

(vi) The western part of the North Indian Plains is occupied by desert known as the Thar Desert or Marusthali. Most of Rajasthan is occupied by this desert.

(vii) To the north of the desert lie the plains of Punjab.

(viii) This region is spread to the west of Aravalis and Delhi ranges. These plains have formed as a result of the depositonal work by river Satluj and its tributaries. The slope of the plains is towards the west.

(ix) Because the soil here is very fertile, agriculture is largely practised in this region.

Question 4.

What could be the reasons behind the formation of swamps in the extensive continental location of Pantanal?
Answer:
Pantanal is one of the largest wetlands in the world, lying in the south west part of the highland areas.

It is a region of swamps and marshes in northwestern part of Mato Grosso do Sul in Brazil and it extends into Argentina too.
This region is drained by the river Paraguay and its tributaries.

They collect the water from the highland areas and deposit the sediments in the low lying Pantanal region.

Pantanal is a gently sloped basin which is submerged throughout the year due to the filling of the sediments and water in the depression area of the Pantanal.

Question 5.

Which are the major water divides of India give examples.
Answer:
A mountain or an upland which separates two drainage basins is known as a Water Divide. The major Water Divides of India are :

Western Ghats: The Western Ghats acts as a water divide and separates the west flowing rivers like Zuari, Mandvi, Vaitama draining into the Arabian Sea, from the east flowing rivers like the Godavari, Krishna and Kaveri draining into the Bay of Bengal.

Vindhya ranges: It divides the drainage basin of the River Ganga and the River Narmada.

Aravali ranges: The Aravali ranges separate the west flowing river Luni from the east flowing river Banas.

Satpuda ranges: The Satpudas separate the Narmada drainage basin and the Tapi drainage basin.

( Colours of Both )
Use the physical maps of India, Brazil and the indices to answer the following:

Question 1.
In which parts do the areas with highest altitude lie in both the countries, respectively?
Answer:
In India, the Himalayas occupying the northern and the north eastern part name highest altitude. In Brazil, the Escarpment occupying the southern part has highest altitude and the highest peak Pico de Neblina lies to the north in the Guyana Highlands.

Question 2.
In which country is the range of altitude higher?
Answer:
India has higher range of altitude as compared to Brazil.

Question 3.
Compare the highest range of altitudes given in both the countries. What difference do you see?
Answer:
The highest range of altitude in Brazil is more than 1000m, whereas in India, the highest range of altitude is more than 8000 m.

Question 4.
In which direction is the slope of the Amazon river basin region?
Answer:
The slope of Amazon Basin is towards the east.

Question 5.
In which direction is the slope of the Deccan Plateau of India ?
Answer: The slope of Deccan Plateau is towards the east.

Question 6.
Tell the regions of rain shadow in both the countries.
Answer:
The rain shadow regions of India are eastern side of Western Ghats on the Deccan Plateau and western side of Eastern Ghats. The rain shadow region of Brazil lies in the north eastern part of the Great Escarpment.

Question 7.
Write a comparative note on the basins of Ganga and Amazon river. You may consider following points for the comparison.
Answer:

Points for comparison	Ganga River Basin	Amazon River Basin
(1) Size of catchment area	Spreading across the northern and eastern parts of India the Ganga River basin has a total catchment area of 10,16,124 sq. km.	Spreading across the northern parts of Brazil the Amazon River basin has a total catchment area of 70,50,000 sq. km.
(2) Their relative location within respective countries	The Ganga river basin lies to the south of the Himalayas in the North Indian plains and also occupies the northern part of the peninsula, i.e. the Central Highlands.	The Amazon river basin occupies the entire region in the north of Brazil right from the Guyana Highlands to the northern part of the Brazilian Highlands.
(3) Headwater regions of rivers.	Ganga river originates from the Gangotri Glacier in Uttarakhand.	The Amazon river originates from the eastern slopes of Andes Mountains in Peru.
(4) Orientation of the rivers	The Ganga flows eastwards passing through the states of Uttar Pradesh, Bihar and West Bengal and terminates into the Bay of Bengal. One of its branch enters into Bangladesh.	The Amazon river flows from the west to the east entirely through the states of Amazonas and Para in northern Brazil and terminates into the North Atlantic Ocean.
(5) Major tributaries and their orientation	(i)    Yamuna is the major right bank tributary of the river Ganga originating from the Yamunotri Glacier and meeting river Ganga at Allahabad. Other right bank tributaries originating from the Peninsula like river Chambal, Ken, Shon, Damodar, etc. flow northwards and join river Ganga. (ii)  The left bank tributaries like river Gomati, Ghagra, Gandak, and Kosi flow south and meet river Ganga.	(i)    Rivers like Negro, Branka, Paru flow south from the Guyana Highlands and meet the Amazon river as left bank tributaries. (ii)  River Madeira, Juruaka, Xingu and Tocantins flow northwards and join the Amazon river at its right bank.
(6) Any other point(s)	(i)    The Ganga river basin is densely populated due to the deposition of fertile alluvial soil and plenty of water available for agriculture. (ii)  Fertile plains and deltas are formed. (iii)River Ganga is 2525 km long. (iv)Water discharge is 16,648 cu.m, per sec.	(i)    Amazon river basin is sparsely populated due to dense equatorial rain forests, unfavourable climate and lack of transport links. (ii)  No deltas are formed but islands have developed along the mouth of the Amazon River. (iii) River Amazon is 6400 km long. (iv)   Water discharge is 2,09,000 cu.m, per sec.

Question 8.
Distinguish between:
Eastern Ghats and Western Ghats.
Answer:

S.no	Eastern Ghats		Western Ghats
(i)	The Eastern Ghats run along the eastern coast of India in the north east to south west direction.		(i)	The Western Ghats also known as Sahyadris run in the north-south direction along the western coast of India.
(ii)	It forms the eastern boundary of the Deccan Plateau.                                          .		(ii)	It forms the western boundary of Deccan Plateau.
(hi)	It is not continuous, but is broken at many places by rivers like Godavari and Krishna.		(iii)	The Western Ghats is like a continuous wall like structure, but is broken at same places by passes.
(iv)	Comparatively less number of rivers originate from the Eastern Ghats.		(iv)	It is a source of many westward and eastward flowing rivers.
(v)	The average altitude of the Eastern Ghats is low (600 mts) but they are wider than Western Ghats.		(v)	The average altitude of the Western Ghats is high (900-1600 mts) but it is narrower in width than Eastern Ghats.
(vi)	Highest peak of Eastern Ghats is Jindhagada (1690 m)		(vi)	Highest peak of Western Ghats is Anaimudi Peak (2695 m)

Class 10 Geography Chapter 3 Physiography and Drainage Additional Important Questions and Answers

Choose the correct option and rewrite the statements:

Question 1.
The part of North Indian Plains lying to the east of the Aravalis is called ____.
(a) Ganga Plains
(b) Brahmaputra Plains
(c) Kaveri Plains
(d) Krishna Plains
Answer:
(a) Ganga Plains

Question 2.
The delta of Ganga-Brahmaputra system is called ________.
(a) Sunderbans
(b) Parnaiba
(c) Amazon
(d) Marajo
Answer:
(a) Sunderbans

Question 3.
The western part of the North Indian Plains occupied by deserts known as ________.
(a) Thar Desert or Marusthali
(b) Gobi Desert
(c) The Deccan Thorn scrub Desert
(d) Spiti Valley Cold Desert
Answer:
(a) Thar Desert or Marusthali

Question 4.
The area lying to the south of North Indian Plains and tapering towards Indian Ocean is called _____.
(a) Himalayas
(b) Peninsula
(c) Western Ghats
(d) Indira Point
Answer:
(b) Peninsula

Question 4.
The in the north west of Peninsular India are the oldest fold mountains.
(a) Aravalis
(b) Satpudas
(c) Karakoram range
(d) Vindhya range
Answer:
(a) Aravalis

Question 6.
The ______ rivers in India are seasonal in nature.
(a) Northern
(b) Peninsular
(c) Himalayan
(d) Mountainous
Answer:
(b) Peninsular

Question 6.
River _______ is the second largest river system in India in terms of catchment area.
(a) Krishna
(b) Godavari
(c) Brahmaputra
(d) Ganga
Answer:
(b) Godavari

Question 7
The major river of Peninsula flows through the states of Karnataka and Tamil Nadu,
(a) Kaveri
(b) Indus
(c) Ganga
(d) Brahmaputra
Answer:
(a) Kaveri

Question 8.
India is blessed with a long coastline extending for approximately
(a) 8000 km
(b) 5000 km
(c) 7500 km
(d) 7900 km
Answer:
(c) 7500 km

Question 9.
The islands in the Arabian sea are called _______ islands.
(a) Andaman and Nicobar
(b) Barren
(c) Marajo
(d) Lakshadweep
Answer:
(d) Lakshadweep

Question 10
_____ is the southernmost range of the Himalayas.
(a) Himadri
(b) Lesser Himalayas
(c) Siwaliks
(d) Kumaon Himalayas
Answer:
(c) Siwaliks

Question 12.
The Islands in the Bay of Bengal are called _______ islands.
(a) Andaman and Nicobar
(b) Maldives
(c) Corsela
(d) Lakshadweep
Answer:
(a) Andaman and Nicobar

Question 13.
The highest peak of Brazil is called _______.
(a) Pico de Neblina
(b) Mount Everest
(c) Kanchenjunga
(d) Mount Roraima
Answer:
(a) Pico de Neblina

Question 14.
The acts as a barrier to the south-east trade winds giving rise to the rain shadow area in the north – eastern part of the highlands in Brazil.
(a) Coastal Plains
(b) Escarpment
(c) Plateaus
(d) Pantanal wetlands
Answer:
(b) Escarpment

Question 15.
Amazon collects its headwaters from the eastern
slopes of Andes mountains in
(a) Uruguay
(b) Peru
(c) Ecuador
(d) Columbia
Answer:
(b) Peru

Question 16.
The Island is the only active volcano of India.
(a) Majuli
(b) St. Mary’s
(c) Barren
(d) Lakshadweep
Answer:
(c) Barren

Question 17.
______ is a large coastal island located between the mouths of river Amazon and river Tocantins,
(a) Pantanal
(b) Plata
(c) Paraniba
(d) Marajo
Answer:
(d) Marajo

Question 18.
_______ is one of the largest wetlands in the world.
(a) Plata
(b) Marajo
(c) Pantanal
(d) Paraniba
Answer:
(c) Pantanal

Question 19.
The Paraguay and the Parana rivers form the catchment of River in Argentina.
(a) Paraniba
(b) Plata
(c) Pantanal
(d) Marajo
Answer:
(b) Plata

Question 20.
____ River enters the Atlantic Ocean near Salvador town.
(a) Marajo
(b) Puraguaco
(c) Plata
(d) Parana
Answer:
(b) Puraguaco

Question 21.
The river ______ flows through Pakistan and then meets the Arabian Sea.
(a) Ganga
(b) Chambal
(c) Indus
(d) Brahmaputra
Answer:
(c) Indus

Question 22.
Ganga receives as its tributary in its lower reaches in Bangladesh.
(a) Satluj
(b) Indus
(c) Brahmaputra
(d) Ravi
Answer:
(c) Brahmaputra

Identify the correct group:

Question 1.
Parallel ranges of Himalayas from south to north
(i) Siwaliks – Lesser Himalayas – Greater Himalayas
(ii) Trans Himalayas – Kumaun – Shiwaliks
(iii) Kashmir Himalayas – Kumaun Himalayas – Assam Himalayas
Answer:
Siwaliks – Lesser Himalayas – Greater Himalayas

Question 2.
Physiographic division of India from north to south
(i) The Himalayas – The North Indian Plains – The Peninsula
(ii) The Peninsula – The Great Escarpment – The North Indian Plains
(iii) Coastal Plains – Islands – Himalayas
Answer:
The Himalayas – The North Indian Plains – The Peninsula .

Question 3.
Physiographic divisions of Brazil
(i) The Himalayas – The North Indian Plain – The Peninsula
(ii) The Highlands – The Great Escarpment – The Plains
(iii) Islands – Peninsula – Coastal Plains
Answer:
The Highlands – The Great Escarpment – The Plains

Question 4.
Three major River Basins of Brazil
(i) Ganga Basin – Brahmaputra Basin – Narmada Basin.
(ii) Paraguay Parana Basin – Amazon Basin – Sao Francisco
(iii) Godavari Basin – Krishna Basin – Kaveri Basin.
Answer:
Paraguay Parana Basin – Amazon Basin – Sao Francisco

Question 5. The order of subdivisions of North Indian Plains from west to east.
(i) Marusthali – Ganga Plains – Sunderbans
(ii) Pamir; Knot – Punjab Plains – Marusthali
(iii) Sunderbans – Vindhyas – Western Ghats
Answer:
Marusthali – Ganga Plains – Sunderbans

Match the column:

Question 1.

Column ‘A’	Column ‘B’
(1)     Western Himalayas (2)     Central Himalayas (3)     Eastern Himalayas	(a)      Siwaliks (b)     Assam Himalayas (c)      Kashmir Himalayas (d)     Kumaun Himalayas

Answer:
1-c
2-d
3-b

Question 2.

Column ‘A’	Column ‘B’
(1) Himalayas	(a)  the western and eastern part of the Peninsula.
(2)   North Indian Plains	(b) consists of many plateaus and hill ranges
(3)   The Peninsula	(c) one of the young fold mountains in the world.
(4) The Coastal Plains	(d) lies between Himalayan mountains in the north and the Peninsula in the south.
(5) The Island group	(e) are located more than 300 km away from the mainland in the Atlantic ocean.
	(f) small and large islands along the coast of the mainland.

Answer:
1 – c
2 – d
3 – b
4 – a
5 -f

Question 3.

Column ‘A’	Column ‘B’
(1) The southernmost point of India	(a) Gangotri
(2) The highlands in eastern Brazil	(b) Andes mountains
(3) The origin of Ganga	(c) Guyana Highlands
(4) The origin of Amazon	(d) Indira Point
(5) The southern most point of mainland India	(e) Kanyakumari
	(f) The Great Escarpment

Answer:
1 – d
2 -f
3 – a
4 – b
5 – e

Question 4.

S.no	Column ‘A’	Column ‘B’
1.	Longest river of India	(a) Sao Francisco
2.	Second largest river of India	(b) Godavari
3	Longest river of Brazil	(c)    Ganga (d)    Brahmaputra (e)    Amazon

Answer:
1 – c
2 – b
3 – e

Answer the following in one sentence:

Question 1.
Which mountain is considered as one of the young fold mountains in the world?
Answer:
The Himalayas are considered as one of the young fold mountains in the world.

Question 2.
What is the southernmost range of Himalayas called?
Answer:
The southernmost range of Himalayas is called the Siwaliks.

Question 3.
Where are the North Indian Plains located?
Answer:
The North Indian Plains lies between Himalayan Mountains in the north and the Peninsula in the south.

Question 4.
Where are the Ganga Plains located?
Answer:
The Ganga Plains lie to the east of the Aravalli in the North Indian Plain.

Question 5.
What constitutes the delta of Ganga-Brahmaputra system?
Answer:
Most of the West Bengal state of India and Bangladesh together constitute the delta of Ganga Brahmaputra system.

Question 6.
What are Sunderbans?
Answer:
The delta region of Ganga-Brahmaputra system are called the Sunderbans and it extends from Indian state of West Bengal to Bangladesh.

Question 7.
What is the length of the coastline of India?
Answer:
The length of the coastline of India is approximately 7500 km.

Question 8.
Why do the rivers originating from Western Ghats form estuaries?
Answer:
Rivers originating from Western Ghats are short and swift, hence they form estuaries.

Question 9.
What are the islands located in the Arabian Sea called?
Answer:
The Islands located in the Arabian sea are called Lakshadweep Islands.

Question 10.
What are the islands located in the Bay of Bengal called?
Answer:
The islands located in the Bay of Bengal are called Andaman and Nicobar Islands.

Question 11.
Name the only active volcano in India.
Answer:
Barren Island is the only active volcano in India located in Andaman and Nicobar Islands.

Question 12.
Which is the highest peak in Brazil?
Answer:
The highest peak in Brazil is Pico de Neblina.

Question 13.
What acts as a barrier to the South East trade winds giving rise to rainshadow area in the northeastern part of the highlands in Brazil?
Answer:
The Escarpment acts a barrier to the South East Trade winds giving rise to rainshadow area in the northeastern part of the highlands in Brazil.

Question 14.
Name the coastal island located between the mouths of river Amazon and river Tocantins.
Answer:
Marajo is a large coastal island located between the mouths of River Amazon and River Tocantins.

Question 15.
What are most of the Amazon Plains covered with?
Answer:
Most of the Amazon Plains are covered with tropical rainforests.

Question 16.
Where is Pantanal located?
Answer:
Pantanal is located in the northwestern part of Mato Grosso Do Sul in Brazil and it extends into Argentina.

Question 17.
What is a ‘Drought Quadrilateral’?
Answer:
The rain shadow region of Trade Winds lying in the northern part of Brazil is called ’Drought Quadrilateral’.

Question 18.
What is the Brazilian coast characterized by?
Answer:
The Brazilian coast is characterised by a large number of beaches and sand dune complexes.

Question 19.
What protects the Brazilian coast?
Answer:
The Brazilian coast is protected in some areas by coral reefs and atoll islands.

Question 20.
What is Pantanal?
Answer:
Pantanal, which is a region of swamps and marshes is one of the largest wetlands in the world. Located in the northwestern part of Mato Grosso Do Sul in Brazil.

Question 21.
From where does Amazon collect its head waters?
Answer:
Amazon collects its headwaters from the eastern slopes of the Andes Mountains in Peru.

Question 22.
Where does the river Sao Francisco flow?
Answer:
The river flows towards the north for a distance of about 1000 km. over the Brazilian plateau and takes a sharp eastward turn to enter the coastal : strip along the Atlantic Ocean.

Question 23.
Which rivers meet the North Atlantic Ocean?
Answer:
River Paraniba and River Itapecuru meet the North Atlantic Ocean.

Question 24.
Which two river systems are covered under the Himalayan Drainage System?
Answer:
The Himalayan Drainage System cover two major river systems such as the Indus river system and the Ganga river system.

Question 25.
What are ’Kayals’?
Answer:
The coastal rivers in Kerala have long extending backwaters near their mouths, which are locally known as ’Kayals.’

Question 26.
Name the three major river basins of Brazil.
Answer:
The three major river basins of Brazil are Amazon Basin, Paraguay-Parana system in the southwest and Sao Francisco in the eastern part of the highland.

Question 27.
What is the approximate discharge of Amazon river?
Answer:
The approximate discharge of Amazon river is about 2 lakh m3/s.

Question 28.
Where are the rivers Paraguay-Parana located?
Answer:
The rivers Paraguay and Parana are located in the south-western part of Brazil.

Question 29.
Which is the third important river of Brazil?
Answer:
Sao Francisco is the third important river of Brazil.

Question 30.
How are Indian rivers classified?
Answer:
The rivers in India are classified into Himalayan and Peninsular rivers.

Question 31.
Name the major tributary of river Ganga.
Answer:
Yamuna, originating at Yamunotri is a major tributary of Ganga.

Question 32.
From where do Himalayas extend?
Answer:
The Himalayas extend from Pamir Knot in Tajikistan to the east.

Question 33.
Which physical division lies between the Himalayas and the Peninsula?
Answer:
The North Indian Plains lie between the Himalayas in the north and the Peninsula in the south.

Question 34.
Which physical division forms the core of the South American continent?
Answer:
The Brazilian and Guyana Highlands forms the core of the South American continent.

Question 35.
The Guyana highlands cover, which states of Brazil?
Answer: The Guyana highlands cover the states of Roraima, Para and Amapa in Brazil.

Question 36.
Because of which physical division is the eastern side of Brazilian highlands are demarcated?
Answer:
The eastern side of Brazilian highlands are demarcated because of the Great Escarpment.

Question 37.
Which is the largest plain land of Brazil?
Answer:
The Amazon plains lying in the northern part is the largest plain land of Brazil.

Question 38.
On which coast of India are deltas found?
Answer:
Deltas are found on the eastern coast of India.

Name the following:

Question 1.
Five major physiographic divisions of India.
Answer:
The Himalayas, The North Indian Plains, The Peninsula, Coastal Plains and Island groups.

Question 2.
West-East division of Himalayas.
Answer:
Western Himalayas (Kashmir Himalayas),
Central Himalayas (Kumaun Himalayas) and Eastern Himalayas (Assam Himalayas).

Question 3.
Region constituting delta of Ganga-Brahmaputra system or world’s largest delta. .
Answer:
Sunderbans.

Question 4.
Coast bordering Arabian sea.
Answer:
Western Coast.

Question 5.
Coast bordering Bay of Bengal.
Answer:
Eastern Coast.

Question 6.
Islands in the Arabian Sea.
Answer:
Lakshadweep Islands.

Question 7.
Islands in the Bay of Bengal.
Answer:
Andaman and Nicobar Islands.

Question 8.
Other name of Thar Desert.
Answer:
Marusthali.

Question 9.
Ranges in the central part of India.
Answer:
Vindhyas and Satpuda.

Question 10.
Physiographic divisions of Brazil.
Answer:
The Highlands, The Great Escarpment, The Coasts, The Plains, The Island group.

Question 11.
Length of coastline of Brazil.
Answer:
Approximately 7400 km

Question 12.
Major river basins of Brazil.
Answer:
Amazon Basin, Paraguya-Parana system, Sao Francisco.

Question 13.
Two main Himalayan river basins of India.
Answer:
Ganga river basin and Indus river basin.

Question 14.
Origin of Ganga in Himalayas
Answer:
Gangotri Glacier

Question 15.
Major tributary of Ganga
Answer:
Yamuna river.

Question 16.
Tributaries of River Indus.
Answer:
Rivers Jhelum, Chenab, Ravi, Beas, and Satluj.

Question 17.
Origin of River Satluj.
Answer:
Mansarovar.

Question 18.
Rivers flowing into the Gulf of Khambhat.
Answer:
Rivers Tapi, Narmada, Mahi, and Sabarmati.

Question 19.
River basin located to the south of River Godavari.
Answer:
Basin of River Krishna.

Question 20.
Plains formed due to depositional work of river Satluj.
Answer:
Punjab Plains.

Question 21.
Tributaries of Peninsula joining the Ganga basin.
Answer:
Rivers Chambal, Ken, Betawa, Shon, and Damodar.

Question 22.
States having short and swift river systems.
Answer:
Kerala, Karnataka, Goa and Maharashtra.

Question 23.
River originating from the eastern slopes of Western Ghats.
Answer:
Rivers Godavari, Krishna and Kaveri.

Question 24.
Largest wetlands in the world.
Answer:
Pantanal.

Question 25.
Highest peak of Brazil
Answer:
Pico de Neblina.

Question 26.
Western border of Indian Peninsula.
Answer:
Western Ghats.

Question 27.
Eastern border of Indian Peninsula.
Answer:
Eastern Ghats.

Question 28.
Oldest fold mountains of India.
Answer:
Aravallis.

Question 29.
Major mountain system of Asia.
Answer:
Himalayas.

Identify the type on the basis of the statement

Question 1.
A landform formed due to deposition of sediment carried by a river as the flow leaves its mouth and enters slower-moving or standing water.
Answer:
Delta.

Question 2.
The area where land meets the sea or ocean, or a line that forms the boundary between the land and the ocean or a lake.
Answer:
Coast.

Question 3.
Portion of land drained by a river and its tributaries.
Answer:
River Basin.

Question 4.
majority of its border, (Usually three sides) while being connected to a mainland from which it extends.
Answer:
The Peninsula.

Question 5.
A steep slope or long cliff that forms as an effect of faulting or erosion and separates two relatively leveled areas having differing elevations.
Answer:
Escarpment.

Question 6.
Any piece of land that is surrounded by water all the sides.
Answer:
Island.

 Mark the following on the map with the given information:

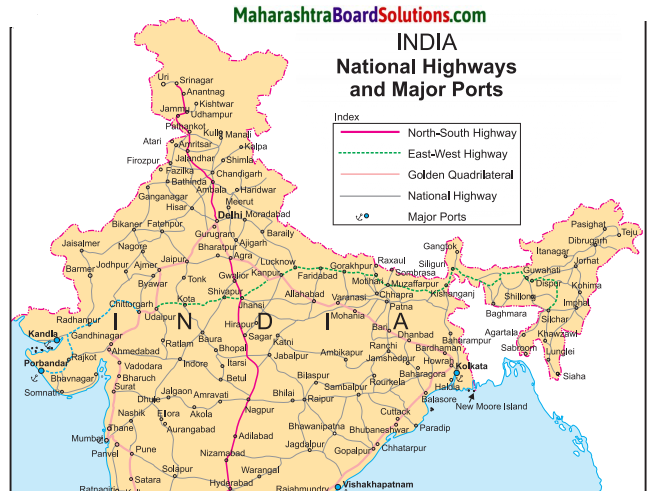
Question 1.
On the outline map of India.
(a) Aravali hills
(b) Himalayas/Greater Himalayas
(c) Vindhya Range and Satpuda Range
(d) Gulf of Mannar
(e) Western Ghats
(f) Eastern Ghats
(g) Gulf of Kutch
(h) Gulf of Khambhat
(i) K2
(j) Sunderbans
(k) Thar Desert/Marusthali
Answer:

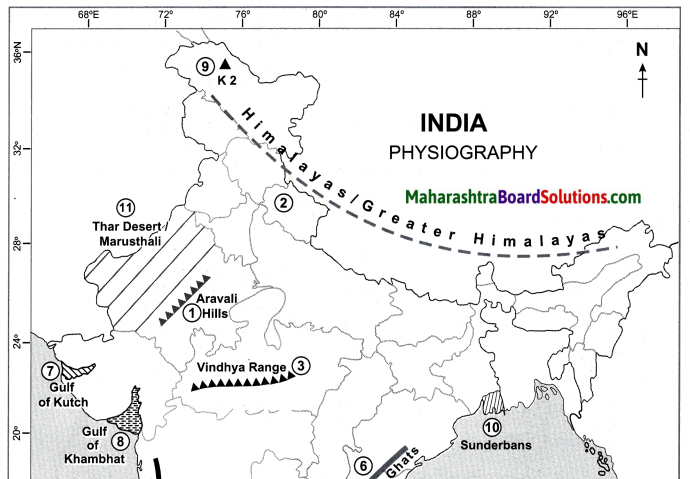
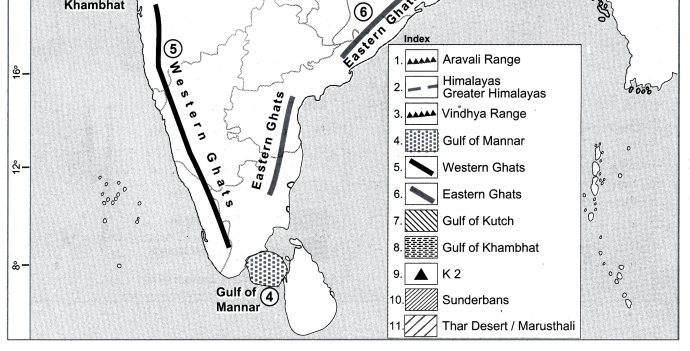
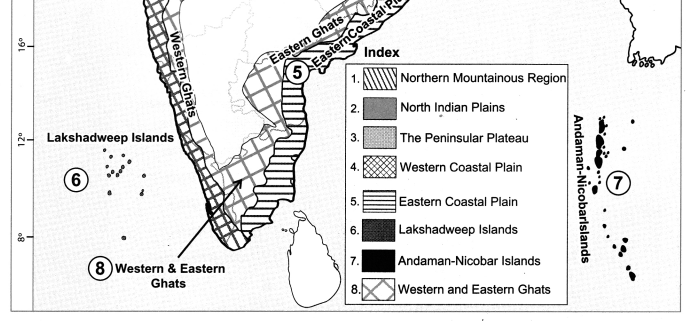
Question 2.
On the outline map of India mark the following.
(a) Northern Mountainous Region
(b) North Indian Plains
(c) The Peninsular Plateau
(d) Western Coastal Plain
(e) Eastern Coastal Plain
(f) Lakshadweep Island
(g) Andman-Nicobar Islands
(h) Western and Eastern Ghats
Answer:

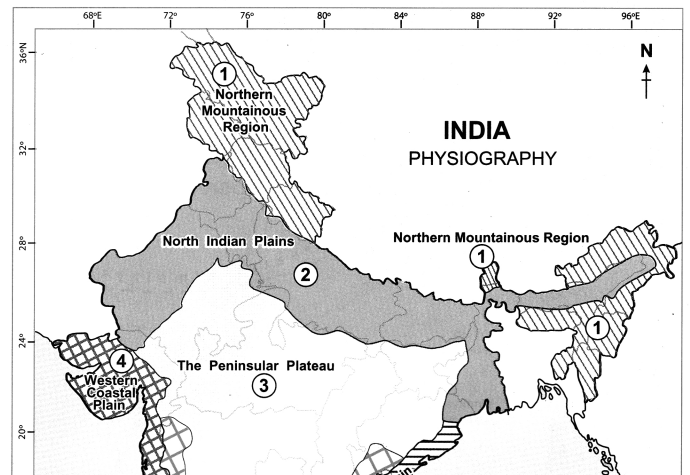
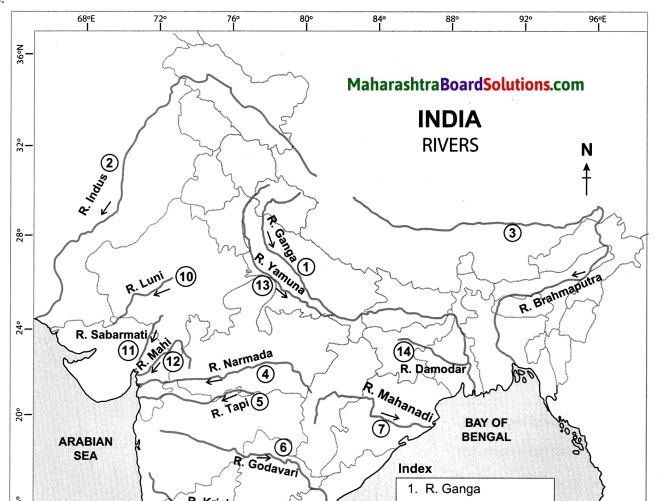
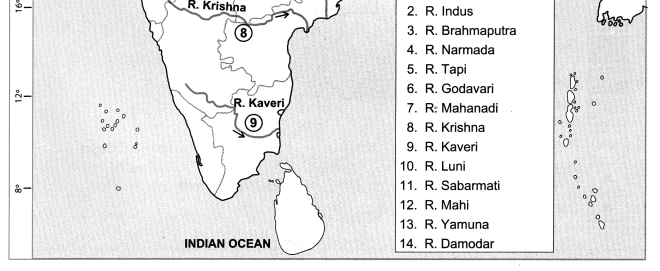
Question 3.
Show the following on the outline map of India.
(a) R. Ganga
(b) R. Indus
(c) R. Brahmaputra
(d) R. Narmada
(e) R. Tapi
(f) R. Godavari
(g) R. Mahanadi
(h) R. Krishna
(i) R. Kaveri
(j) R. Luni
(k) R. Sabarmati
(l) R. Mahi
(m) R. Yamuna
(n) R. Damodar
Answer:

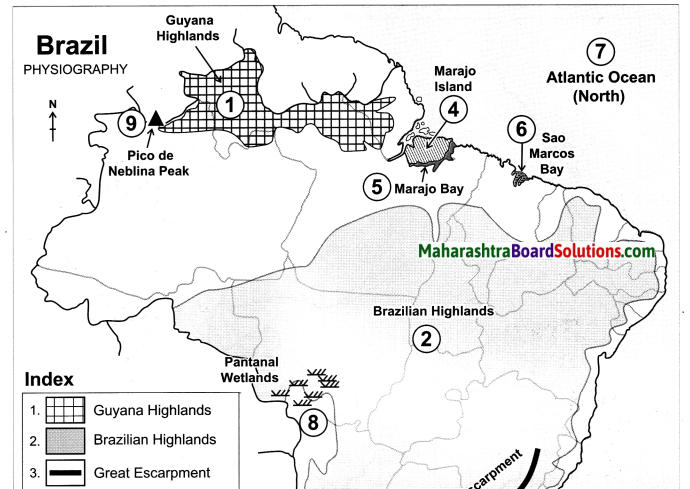
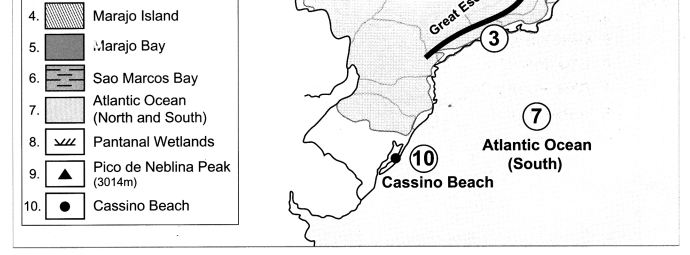
Question 4.
On the outline map of Brazil, mark the following:
(a) Guyana Highlands
(b) Brazilian Highlands
(c) Great Escarpment
(d) Marajo Island
(e) Marajo Bay
(f) Sao Marcos Bay
(g) Atlantic Ocean
(h) Pantanal Wetlands
(i) Pico De Neblina Peak
(j) Cassino Beach
Answer:

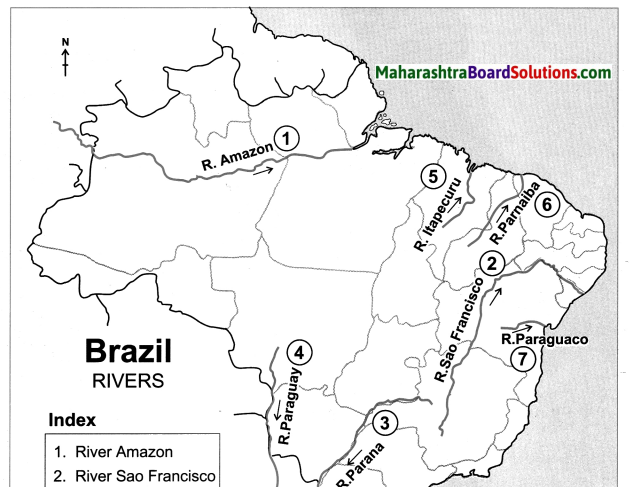
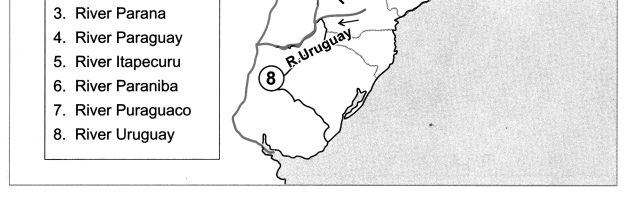
Question 5.
On an outline map of Brazil, show all major rivers of Brazil.
(a) River Amazon
(b) River Sao Francisco
(c) River Parana
(d) River Paraguay
(e) River Itapecuru
(f) River Paraniba
(g) River Puraguaco
(h) River Uruguay
Answer:

Answer the following questions:

Question 1.
There are no deltas on the western coast of India.
Answer:
(i) Deltas are formed in the coastal areas where there is gentle slope, because the rivers slow down forming distributaries and channels.

(ii) The western coast bordering the Western Ghats are by and large rocky coasts having a narrow width.

(iii) Many short and swift seasonal rivers originate from the steep western slopes of the Western Ghats.

(iv) As the rivers flow through steep slopes, their velocity increases. So there is very little deposition
made by them.

(v) Hence, there are no deltas on the western coast of India.

Question 2.
Many deltas are found along the Eastern coast of India.
Answer:
(i) The eastern coast borders the Bay of Bengal. It has been formed as a result of depositional work of rivers.

(ii) Many east flowing rivers rising from the Western and Eastern Ghats after travelling a long distance join the Bay of Bengal at this coast.

(iii) Because of the gentle slope of the land, rivers flow at lower velocities and deposit the sediments brought with them at the coast.
Therefore, this coast is comparatively wider than the west.

(iv) As a result, deltas are found along the eastern coast of India.

Question 3.
The region to the north of the Escarpment is called Drought Quadrilateral.
Answer:
(i) The eastern side of the Highlands is demarcated because of the Escarpment having an altitude of 790 m.

(ii) The Escarpment acts as a barrier to the Southeast trade winds and cause orographic type of rainfall in the coastal region.

(iii) Beyond the highlands the effect of these winds gets reduced leading to minimal rainfall.

(iv) A rain shadow region is formed to the north east of the Escarpment. Thus, the region to the north of this area is called “Drought Quadrilateral”.

Question 4.
The Amazon Plains are covered by inaccessible tropical rainforest.
Answer:
(i) The northern part of Brazil lying between the Equator and the Tropic of Capricorn, i.e. in the Tropical zone is covered largely by the Amazon Plains.

(ii) Amazon plains lying between the Guyana highlands and the Brazilian highlands form the largest plain land of Brazil.

(iii) The Amazon valley receives very heavy rainfall of around 2000 mm and the average temperature here is 25 to 28°C.

(iv) These conditions favor the dense growth of tropical rain forests. Due to frequent flooding and dense undergrowth, these forests are largely inaccessible.

Question 5.
Pantanal is called the largest wetlands in the world.
Answer:
(i) Pantanal lies towards the south western part of the highland area in Brazil.

(ii) Roughly 80% of the Pantanal flood plains are submerged during the rainy season.

(iii) This region is filled with swamps and marshes from the northwestern part of Mato Grosso Do Sul in Brazil till Argentina.

(iv) Hence Pantanal is called the largest wetland in the world.

Question 6.
Agriculture is widely practised in the plains of Punjab region.
Answer:
(i) Plains of Punjab lie to the north of Rajasthan. This region is spreads to the west of Aravalis and Delhi ranges.

Question 1. These plains have formed as a result of the depositional work by river Sutluj and its tributaries.

(iii) Since the soil here is very fertile, agriculture is largely practised in this region.

(iv) Thus, due to.the availability of fertile soil and ample water suppy agriculture is practised here.

Question 7.
Write notes on :
Answer:

The Western Ghats:

(i) Western Ghats also known as Sahyadri (Benevolent Mountains) is a mountain range that runs parallel to the western coast of the Indian peninsula.

(ii) The range runs north to south along the western : edge of the Deccan Plateau, and separates the plateau from a narrow coastal plain, called West coastal plan, along the Arabian Sea.

(iii) The range starts near the border of Gujarat and Maharashtra, south of the Tapi river, and runs approximately 1,600 km through the states of Maharashtra, Goa, Karnataka, Kerala and Tamil Nadu ending near Kanyakumari, at the southern tip of India.

(iv) The altitude of the western Ghats increases towards the south.

Island group of India:

(i) India has many small and large islands along the coast of the mainland. These are included in the coastal island group.

(ii) Besides, India has two large group of islands, one each in the Arabian Sea and in the Bay of Bengal.

(iii) The islands in the Arabian Sea are known as Lakshadweep whereas the islands in the Bay of Bengal are called the Andaman and Nicobar Islands.

(iv) Most of the islands in Lakshadweep are atoll islands.

(v) They are small in extent and not very high.

(vi) Islands in the Andaman group are mainly volcanic islands.

(vii) They are large with hills in their interior parts, which includes an island called Barren Island which has the only active volcano in India. There are atolls in the Nicobar group too.

 Brazilian Highlands:

(i) Southern Brazil is occupied by an extensive plateau. It is known as the Brazilian Highlands or the Brazilian Shield or the Brazilian Plateau.

(ii) Brazilian and Guyana Highlands together form the core of South American continent.

(iii) The main part of the Guyana Highlands is in Venezuela and it extends up to French Guiana. In Brazil, it covers the states of Roraima, Para and Amapa in the north.

(iv) The lower part of these highlands is found in Brazil. But the highest peak of Brazil, Pico de Neblina, 3014 m lies on the border between Brazil and Venezuela.

(v) The regions to the east and south of the Brazilian highlands have an altitude of more than 1000m. But in other parts, the altitude is between 500 to 1000m.

(vi) The highlands gradually slope towards north and the slopes are not very steep.

(vii) The tributaries of Amazon flowing through this region make rapids and waterfalls. Towards the north the slopes are steep but not abrupt. A number of rivers originate from the terminal portion of the highlands and flow northwards to meet Atlantic Ocean.

(viii) Some major rivers like Uruguay, Paraguay and Parana originate from the southern slopes of the highlands and enter Argentina. Its slope towards the east is steep and it appears in the form of an escarpment.

Coastal Plains of India:

(i) India is blessed with a long coastline extending for approximately 7500 km.

(ii) It lies to the western and eastern part of the Peninsula. Its western and eastern coastlines show remarkable dissimilarities.

(iii) The western coast borders the Arabian Sea. It is by and large a rocky coast.

(iv) At places, spurs starting from the Western Ghats have extended right up to the western coast. Its width is also less.

(v) Rivers originating from Western Ghats are short and swift and hence they form estuaries and not deltas.

(vi) The eastern coast borders the Bay of Bengal. It has formed as a result of depositional work of rivers.

(vii) Many east flowing rivers rising from the Western and Eastern Ghats meet the eastern coast.

(viii) Because of the gentle slope of the land, rivers flow at lower velocities and deposit the sediments brought with them at the eastern coast. As a result, deltas are found along this coast.

The Plains of Brazil:

(i) The plains in Brazil are confined to two areas namely the Amazon basin in the north and Paraguay-Parana source region in the southwest.

(ii) Amazon plains lying between the two highlands form the largest plain land of Brazil.

(iii) Amazon plains lying in the northern parts of Brazil generally slope eastwards.

(iv) The Amazon basin is quite wide in the west (about 1300 km) and it narrows eastward. Its width is minimum where the Guyana Highlands and Brazilian Highland come closer. (240 km.)

(v) As the river approaches the Atlantic Ocean, the width of the plains increases.

(vi) These are mostly forested areas and largely inaccessible due to frequent flooding and dense undergrowth. Most of the Amazon plains are covered by tropical rainforests.

(vii) The other plains in Brazil are located to the southwestern part of the highlands. They form the source region of Paraguay and Parana rivers.

(viii) The source region of Paraguay slopes towards the south while the source region of Parana slopes towards the southwest.

(ix) Pantanal is one of the largest wetlands in the world. It lies towards the southwest part of the highland areas. It is a region of swamps and marshes in northwestern part of Mato Grosso Do Sul in Brazil and it extends into Argentina.

Coastal Rivers of Brazil:

(i) Brazil has a number of short coastal rivers.
Question 1. The coastal area being densely populated these rivers attain significance.
(iii) River Pamaiba and River Itapecuru flowing northwards meet the North Atlantic Ocean.
(iv) The rivers that enter South Atlantic Ocean collect their headwaters along the escarpment.
(v) River Puraguaco enters the Atlantic Ocean near Salvador town.

Paraguay – Parana system:

(i) These two rivers are located in the southwestern part of Brazil.
(ii) Both the rivers form the catchment of River Plata in Argentina.
(iii) These two rivers and river Uruguay in extreme south of the highlands collect their headwaters from the southern portion of the highlands.

Indus River System:

(i) Indus and its tributaries (Jhelum, Beas, Chenab, Ravi and Satluj) drain the Western Himalayas i.e., they flow through the state of Jammu and Kashmir.

(ii) They flow almost parallel to each other.

(iii) A major tributary of river Indus, the Satluj, originates near Mansarovar and flows westwards.

(iv) Punjab Plains have formed from the depositional work of this river and its tributaries.

(v) Indus flows through Pakistan and then meets the Arabian Sea.

Ganga River System:

(i) The river Ganga originates from the Gangotri glacier and crosses the Himalayas to become an east-flowing river.

(ii) Many tributaries of the Ganga also flow in a similar manner.

(iii) River Yamuna, originating at Yamunotri, is a major tributary of Ganga.

(iv) Another major tributary of the Ganga flows through the northern part of the Greater Himalayas, crosses the Himalayas to enter India.

(v) When it flows through the Himalayas it is called Tsang Po.

(vi) When it crosses the Himalayas, it is called Dihang and its eastward flow thereafter is called as Brahmaputra.

(vii) From time to time, Ganga meets its tributaries, hence its discharge increases.

(viii) Ganga receives Brahmaputra as its tributary in its lower reaches in Bangladesh. The huge volume of water and huge deposition has led to the formation of a large delta.

(ix) Besides these Himalayan rivers, Ganga receives a number of tributaries from Peninsula like Shon, Damodar, etc.

Rivers Meeting the Arabian Sea:

(i) The west flowing rivers occupying the area between the Western Ghats and the Arabian Sea are short in length but swift.

10th Std Geography Questions And Answers:

• Field Visit Class 10 Geography Questions And Answers
• Location and Extent Class 10 Geography Questions And Answers
• Physiography and Drainage Class 10 Geography Questions And Answers
• Climate Class 10 Geography Questions And Answers
• Natural Vegetation and Wildlife Class 10 Geography Questions And Answers
• Population Class 10 Geography Questions And Answers
• Human Settlements Class 10 Geography Questions And Answers
• Economy and Occupations Class 10 Geography Questions And Answers
• Tourism, Transport and Communication Class 10 Geography Questions And Answers

Balbharti Maharashtra State Board Class 10 History Solutions Chapter 3 Applied History Notes, Textbook Exercise Important Questions and Answers.

Std 10 History Chapter 3 Question Answer Applied History Maharashtra Board

Class 10 History Chapter 3 Applied History Question Answer Maharashtra Board

History Class 10 Chapter 3 Question Answer Maharashtra Board

Question 1.
(a) Choose the correct option from the given options and complete the statement.
(1) The earliest museum in the world was discovered in the excavations at the city of ……………..………. .
(a) Delhi
(b) Harappa
(c) Ur
(d) Kolkata
Answer:
(c) Ur

(2) The National Archives of India is in ……………..………. .
(a) New Delhi
(b) Kolkata
(c) Mumbai
(d) Chennai
Answer:
(a) New Delhi

(b) Identify and write the wrong pair in the following set.
(1) Kootiyattam- Sanskrit theatre, Kerala
(2) Ramman- Dance form in West Bengal
(3) Ramlila- Traditional Performance of the Ramayana in Uttar Pradesh
(4) Kalbelia- Folk songs and dances of Rajasthan.
Answer:
(2) Wrong pair: Ramman – Dance form in West Bengal

Question 2.
Explain the following concepts :
(1) Applied History
Answer:

•  When one subject is applied to different fields and conclusions are derived, it is known as application of that subject.
• When objectives of History are applied to other subjects; new conclusions are obtained.
• This is known as ‘Applied History’. It is also known as Public History.
• We get insights of the events that took place in the past through history.
• Applied History is concerned with application of knowledge of history to provide guidance in finding solutions.
• Contemporary social issues and include them in social planning.
• Thus Applied History’ is a field of study concerned with the application of history for the benefit of people in contemporary and future times.

(2) Archives
Answer:

•  A place where historical documents are preserved is called an ‘Archive’.
• Many old documents, official records, old films, records of treaties are kept at this place.
• We get references of original documents because of Archives.
• A study of historical events of a particular period is possible.
• We come to know about language, script used in a particular period/era.
• The National Archives of India is in Delhi. It is the largest Archive in Asia.
• Every state in India maintains its archives independently.

Question 3.
Complete the following concept chart.

Answer:

Question 4.
Explain the following statements with reasons.
(1) It is essential to study the history of technology.
Answer:

• Man acquired different skills at various stages in his evolution process.
• From mxking stone tools to developing new techniques of agriculture production, he learnt many skills and entered in the age of science.
• Agricultural production, commodity production, architecture, engineering, etc.
• underwent several changes. Production increased manifold bcause of technology.
• Hence, it is necessary to know the history of technology in order to understand the development in mechanisation and mutual dependence between science and technology.

(2) The list of world Heritage Sites is announced by UNESCO.
Answer:

• Cultural heritage is a form of human creation. It is a cultural treasure that has been inherited from our ancestors.
• We feel connected to it and hence preserve and conserve it.
• This heritage is our asset that binds us to our past and hence we should preserve it for the benefit of future generations.
• In order to save this heritage, UNESCO has announced some directives.
• On the basis of those directives, list of sites, and traditions are declared as ‘World Heritage’.
• It has helped us in promoting these sites as tourist places.

Question 5.
Write elaborate answers
(1) How is the method of history useful in the research of
(a) Science
(b) Arts
(c) Management Studies
Answer:
Each field has its own history of building’ knowledge. The direction of development in every field is dependent on the stcrte of available knowledge in that field. The method of history has proved valuable in the research of various fields.

(a) Science: Scientific discoveries /invenfions take place because of humdn efforts to satisfy needs and curiosity. These efforts are based on scientific knowledge that already existed. Knowledge of the history of science helps in understanding the reasons, chronology and factors that facilitated a scientific invention/discovery. Knowledge of history of science helps in every field.

(b) Art: Development of any style of art lies in their expression through intellectual, emotional and cultural traditions. While studying any art form we have to understand the history of its traditions, the key to the expressions in it, and emotional temperament of the artist. Prevalent art style in the given period can be understood with the help of cultural history.

(c) Management Studies: All components like means of production, human resources, processes of production, the chain of market and sales, etc. are interrelated and require management.

Different social and economic institutions are involved in these industrial and commercial processes. Knowledge of similar functional systems of the past is essential to bring about changes, improvements and make the management smooth and efficient. It becomes necessary to know its history.

(2) How can we correlate applied history with our present?
Answer:
History gives us knowledge about the events that happened in past. Applied history helps us in understanding how the knowledge can be put to use for our benefit as well as for the benefit of future generations. Applied history is correlated with our present in the following ways:

(1) Knowledge of our past helps us in deciding our course of action in present. The.heritage of our ancestors exists in tangible and intangible- form. We have the curiosity to know more about our part because they represent the creative thoughts and traditions of that period.

(2) With the help of applied history we can not only come to know about the heritage but also conserve and preserve it.

(3) We can be better equipped to face social challenges in the present because the knowledge of history can provide guidance in finding solutions to contemporary social issues and incorporate them in the ’social planning.

(4) The direction of future development is S decided when we rightly analyse our present with our knowledge of the past acquired through applied history.

(3) Suggest at least 10 solutions for the preservation of the sources of history.
Answer:
There are three types of sources which are used to study history. They are written, oral and material sources. These sources are preserved in different ways. According to me, the following measures should be taken to preserve the sources:

1. A regular repair and maintenance work of forts, memorials and palaces should be carried out. Timely action should be taken to avoid vandalisation of historic and public places.
2. Historical coins, weapons should be handled with precaution and utmost care. They should be kept in a safe place to avoid the possibility of theft.
3. Social awareness regarding the conservation and preservation of our cultural and natural heritage should be created. People will develop affinity towards the heritage and feel connected.
4. Variations in environment and climatic conditions pose a threat to monumental structures. Humidity, dampness, moulds and pollution cause irrevocable damage to manuscripts, rare artefacts, statues, coins, etc.
5. To protect them, special arrangements have to be made like rooms with controlled temperature or sanitising and detoxing the rooms.
6. Oral literature like owis, folk songs should be compiled and written down.
7. Public training programmes should be conducted for understanding the importance of history.
8. Experts from different fields should be involved in preservation and conservation projects. S Stringent laws should be enacted to protect the monuments.
9. Above all, people’s participation in conservation and preservation process is paramount.

(4) What objectives can be fulfilled through the heritage projects.
Answer:
The following objectives can be fulfilled through the heritage projects:

• Preservation, conservation and development of heritage sites can be done without any change in its original state/ structure.
• The local social structure and psychology of the local people, challenges they face in the present situations and their expectations can be surveyed.
• In the process of completing the project of conservation, preservation and development of a heritage site due precaution should be taken to avoid hurting the sentiments of the local people.
• Participation of the local people in the proposed project can be facilitated.
• In order to engage and employ the local skills in a creative way and create better opportunities of livelihood, it becomes easier to design systematic plans.

Project
Show the Indian heritage sites on the map of India.
Answer:

Memory Map

Question 6.
Complete the sentences by choosing the correct option:
(a) ……………………… Institute of Art, Design and Technology at Bengaluru has an independent department named ‘Centre for Public History’.
(a) Pitch
(b) INTACH
(c) Shrushti
(d) AIMS
Answer:
(c) Shrushti

(b) ……………………… is the mother of science and all other branches of knowledge.
(a) Philosophy
(b) History
(c) Technology
(d) Mythology
Answer:
(a) Philosophy

(c) In order to preserve and conserve cultural and natural heritage for the benefit of future generations ……………………… has given directives.
(a) UNICEF
(b) UN
(c) UNESCO
(d) INTACH
Answer:
(c) UNESCO

(d) The ……………………… in the Satara District of the Western Ghats is included in the list of World Natural Heritage.
(a) Balaghat Mountain
(b) Melghat
(c) Masai Plateau
(d) Kas Plateau
Answer:
(d) Kas Plateau

(e) The main office of the National Film Archives of India is situated at ……………………… .
(a) Delhi
(b) Mumbai
(c) Pune
(d) Nagpur
Answer:
(c) Pune

(f) Excavations at the city of ‘Ur’ in Mesopotamia were conducted by ……………………… .
(a) Nathaniel Wallick
(b) Ennigaldi
(c) Leonard Wolley
(d) Sir John Marshall
Answer:
(c) Leonard Wolley.

Question 7.
Identify the wrong pair in the following, and write it:

(1) Kootiyattam	(a) Sanskrit theatre, Kerala
(2) Ramman	(b) Dance form in West Bengal
(3) Ramlila	(c) Traditional performance of Ramayana in Uttar Pradesh
(4) Kalbelia	(d) Folk songs and dances of Rajasthan

Answer:
Wrong pair: Ramman – Dance form in West Bengal

(2)

Cultural Heritage	Place
(1) Red Fort	(a) Udaipur
(2) Jantar Mantar	(b) Jaipur
(3) Brihadeeshvara Temple	(c) Thanjavur
(4) Capital Complex	(d) Chandigarh

Answer:
Wrong pair: Red Fort – Udaipur

Question 8.
Complete the graphical presentation:
(1)

Answer:

(2)

Answer:

(3)

Answer:

Question 9.
Explain the following concept:
(a) Natural Heritage:
Answer:

• In Cultural heritage what we inherit is man-made but Natural heritage is bestowed upon us by Nature.
• The concept of natural heritage gives importance to the thought of biodiversity.
• The following things are included in natural heritage:
  • Fauna
  • Flora
  • Ecology required for sustaining animal and plant life, flora and fauna of a particular region.
  • Geomorphic characteristics, sanctuaries, mountain ranges, river valleys, lakes and dams are all part of natural heritage.

Question 10.
Write short notes:
(a) Importance of Applied History:
Answer:

• Applied History is a field of study which helps us understand our ancient heritage.
• We realise the importance of preserving our heritage.
• The process of preservation and conservation of tangible and intangible heritage sites generate employment opportunities.
• The study of Applied History help us to get a better understanding of the present and can provide guidance for the future.

(b) Preservation of cultural heritage of India:
Answer:
Conservation and preservation of India’s cultural heritage is done at different levels:

1. Archaeological Survey of India (ASI) is an important body of Indian government which mainly does the work of conservation and preservation along with State Departments of Archaeology.
2. INTACH (Indiqn National Trust for Art and Cultural Heritage) is actively working in this field.
3. Local self-government bodies, social institutions all over India, people who have love for history are seen involved in the work of preservation of our heritage.
4. The work of conservation and preservation of cultural and natural heritage requires participation of experts from various fields as well as local people.

(c) Indian Museum:
Answer:

• The Indian Museum at Kolkata is the oldest museum and one of the important heritage sites of India.
• Nathaniel Wallich, a Danish botanist, founded the museum in 1814 C.E. He was also its first curator.
• The museum has three main departments Arts, Archaeology and Anthropology.
• Other affiliated departments are conservation, publication, photography, exhibition- presentation, model-making, training, library and security.

(d) National Film Archives:
Answer:

• The main office of the National Rim Archives of India is located at Pune and was established in 1964.
• It functions as the Media Unit of the Ministry of Information and Broadcasting of the Indian Government.
• It was established with the view of three objectives. They are:
  • To search and obtain the rare Indian films and preserve our heritage for the benefit of future generations.
  • To categorise important aspects of films, create documentation and do research.
  • To establish a centre for dissemination of ‘films culture’.

Question 11.
Explain the following statements giving reasons:
(a) It is essential to study the history of philosophy.
Answer:

• With the passage of time, many schools of thought came into existence with different ideologies.
• These ideologies had their effect on people and society as a whole.
• What led to the origin of various ideologies, the intellectual tradition giving rise to those ideologies and their historical development needs to be researched.
• To know about the progress of those ideologies, their development and expansion or downfall we need to have knowledge of the history of philosophy.

(b) It is important to know the history of Industry and Commerce.
Answer:

• With the growth of industry and trade, the field of mutual social transactions also expand.
• It promoted development of the network of cultural interactions.
• As the nature of market and commerce changed sp did the nature of human relationships and the social organisation.
• This series of changes is influenced by prevalent culture, social structure and economic system.
• All this is an integral part of the industrial and commercial management.

Therefore, it becomes important to know the history of Industry and Commerce.

(c) It is necessary to preserve and conserve our natural and cultural heritage.
Answer:

• The visible and invisible relics of the past exist in the present.
• They represent the thought and traditions of our ancestors.
• We nurture some kind of curiosity and attraction towards them.
• The history of our heritage links us with our origin.

Therefore, it becomes necessary to preserve and conserve for our future benefit as well as for the benefit of future generations.

Question 12.
Answer the following in 25-30 words:
(a) Explain the concept of ‘Public History’.
Answer:

• Public History also known as ‘Applied History’ is a field of study concerned with the application of history for the benefit of people in the contemporary and future life.
• It provides solutions to the contemporary social issues and incorporate them in social planning.
• It helps to overcome misgivings about history and makes history meaningful in everyday life connecting people to history.

(b) What is the role of UNESCO in the context of heritage sites?
Answer:
The role of UNESCO, the global agency of United Nations, is as follows:

• For preservation and conservation of natural and cultural heritage which is in a ruined state because of years of neglect, UNESCO has announced some directive principles.
• The organisation announces list which includes the names of sites and traditions which meet the criteria.
• On the basis of those directives it declares a list of site and traditions of world heritage.

(c) Find out the cultural heritage sites located in Maharashtra and write their names.
Answer:
The following places in Maharashtra are included in the list of cultural heritage sites declared by UNESCO:

• Ajanta Caves
• Verul (Ellora) Caves and Kailas Temple
• Elephanta Caves
• Chhatrapati Shivaji Maharaj Terminus, Mumbai.

Many forts like the Raigad, Devgiri, Janjira and Sindhudurg are part of the cultural heritage Of Maharashtra though they are not included in the list.

(d) What are the misgivings about history among the people?
Answer:
There are many misgivings about history among the people:

• History is a subject only for historians and students who pursue higher studies in history.
• It has no relevance or applicability in our day-to-day life.
• History is nothing but piece of information about the battles fought by kings and politics.
• History cannot be connected to an economically productive field.

(e) Where can we trace the roots of philosophy?
Answer:

• Ancient people all over the world tried to speculate the relationship between the universe and human existence.
• This gave rise to various myths about origin of this world, universal order, human life.
• Imagination about gods and goddesses, rituals to please them and philosophical explanation of rituals.
• Thus, the roots of philosophy can be traced in these speculations and ponderings of mythological stories.

(f) What are the opportunities created by affiliated professional fields of Applied History?
Answer:
Affiliated fields of Applied History which include museums, archives, tourism ‘and hospitality, entertainment, mass media, etc. needs the following professionals:

• Experts like Historians, Archaeologists, Sociologists, legal experts, etc. are assigned new projects.
• Officers like Managers, Secretaries and Directors are taken into service.
• Technicians like engineers, architects, skilled photographers, laboratory assistants, archive management professionals are hired.
• Tourist guides, boarding and lodging, food services, entertainment and related business get a wide scope for flourishing.

(g) What are the main objectives of ‘National Film Archives’?
Answer:
The main objectives of ‘National Rim Archives’ are as follows:

• To research and obtain the rare Indian films.
• To preserve such films for the benefit of future generations.
• To categorise the important aspects of films to create documentation, catalogue them -and carry out research in the field.
• To establish a centre for dissemination of films culture.

(h) How can we increase people’s participation in the field of applied history?
Answer:

• The field of applied history includes museums, archives, collection and maintenance of artefacts.
• Tourism creates interest in history.
• Awareness is created among people to preserve ancient monuments and sites in their vicinity.
• This realisation increases people’s participation in the field of applied history.

(i) Write information on World Heritage sites in Maharashtra.
Answer:
Maharashtra is endowed with many natural and historical sites. Among them the prominent ones are Ajanta caves, Verul caves, Gharapuri/Elephanta caves and Chhatrapati Shivaji Maharaj Terminus Railway Station at Mumbai.

Chhatrapati Shivaji Maharaj Terminus is finest example of Indo-Gothic architecture emerged in India during British rule. It stands witness to the British empire, freedom struggle and transformation of our country into a modern nation. It needs conservation as it a architectural marvel which stood the test of times recently when there was a terror attack on Mumbai city.

(j) What is the role of Applied History?
Answer:
The role of Applied History is as follows:

• In public training programmes for understanding the importance of history.
• Using knowledge of history, to create awareness regarding the conservation and preservation of our cultural and natural heritage.
• To facilitate participation of people in various projects and programmes related to applied history even in their capacity as tourists.
• To enhance professional skills of people and to develop industrial commercial field.
• To carry out preparatory work and plan for effective implementation of heritage projects.

Question 13.
Read the given passage carefully and answer the questions given below:
(a) Who built this museum?
Answer:
This museum was built by Ennigaldi, the princess of Mesopotamia.

(b) Where was the earliest museum in the world discovered? Who discovered it?
Answer:
The earliest museum in the world was discovered in the city of ‘Ur’ in Mesopotamia. It was discovered by Leonard Woolley.

(c) What is a noteworthy feature of this museum?
Answer:
A noteworthy feature of this museum is the clay tablets inscribed with the descriptions of exhibited artefacts.

Question 14.
Write elaborate answers: OR Answer in detail:
(a) Who does the work of conservation and preservation of the cultural heritage of Indian?
Answer:
The preservation and conservation of Indian cultural heritage is done at various stages:

• The work of preservation and conservation primarily falls under jurisdiction of the Archaeological Survey of India.
• In addition, INTACH (Indian National Trust for Art and Cultural Heritage) is also actively working .in this field.
• Experts from various fields and local people too participate in the work of conservation and preservation of natural and cultural heritage.

Question 15.
Observe the picture and write information about it:

Answer:

• This picture is of the largest Indian rock-cut ancient Hindu temple located in the Ellora cave.
• This famous rock-cut Shiva temple was constructed during the reign of Rashtrakuta king Krishna I.
• It is regarded as a marvel of architecture.
• It bears an eloquent testimony to the high level skill attained by India in the arts of sculpture and architecture under the Rashtrakuta patronage.
• A sculpture of an elephant and a pillar can be seen in the picture.
• The famous rock cut temple in Maharashtra was declared as a world heritage site by UNESCO in 1983.

Brain Teaser

Hints:
Across:
(1) Queen’s stepwell at Patan
(2) Dancing, singing, drumming ritual of Manipur
(3) Religious festival and ritual theatre of Garhwal
(4) Archaeological site of Nalanda University
(5) World famous monument at Agra
(6) Famous city built by emperor Akbar marking his victory
(7) Sanskrit Theatre: Kerala

Down:
(1) The traditional performance of Ramayan in Uttar Pradesh
(2) Ellora caves also known as caves
(3) Observatory at Jaipur, Rajasthan
(4) Group of monuments at (place) in Karnataka
(5) Archaeological park at Pavagadh
(6) Folk songs and dances of Rajasthan
(7) A ritual theatre of Kerala

10th Std History Questions And Answers:

• Historiography Development in the West Class 10 History Questions And Answers
• Historiography Indian Tradition Class 10 History Questions And Answers
• Applied History Class 10 History Questions And Answers
• History of Indian Arts Class 10 History Questions And Answers
• Mass Media and History Class 10 History Questions And Answers
• Entertainment and History Class 10 History Questions And Answers
• Sports and History Class 10 History Questions And Answers
• Tourism and History Class 10 History Questions And Answers
• Heritage Management Class 10 History Questions And Answers