Prasanna

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.5 8th Std Maths Answers Solutions Chapter 15 Area.

Area Class 8 Maths Chapter 15 Practice Set 15.5 Solutions Maharashtra Board

Std 8 Maths Practice Set 15.5 Chapter 15 Solutions Answers

Question 1.
Find the areas of given plots. (All measures are in meters.)

Solution:
i. Here, ∆QAP, ∆RCS are right angled triangles and ☐QACR is a trapezium.
In ∆QAP, l(AP) = 30 m, l(QA) = 50 m
A(∆QAP)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(AP) x l(QA)
= \(\frac { 1 }{ 2 }\) x 30 x 50
= 750 sq. m
In ☐QACR, l(QA) = 50 m, l(RC) = 25 m,
l(AC) = l(AB) + l(BC)
= 30 + 30 = 60 m
A(☐QACR)
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
= \(\frac { 1 }{ 2 }\) x [l(QA) + l(RC)] x l(AC)
= \(\frac { 1 }{ 2 }\) x (50 + 25) x 60
= \(\frac { 1 }{ 2 }\) x 75 x 60
= 2250 sq.m
In ∆RCS, l(CS) = 60 m, l(RC) = 25 m A(∆RCS)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(CS) x l(RC)
= \(\frac { 1 }{ 2 }\) x 60 x 25
= 750 sq. m
In ∆PTS, l(TB) = 30 m,
l(PS) = l(PA) + l(AB) + l(BC) + l(CS)
= 30 + 30 + 30 + 60
= 150m
A(∆PTS) = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x l(PS) x l(TB)
= \(\frac { 1 }{ 2 }\) x 150 x 30
= 2250 sq. m
∴ Area of plot QPTSR = A(∆QAP) + A(☐QACR) + A(∆RCS) + A(∆PTS)
= 750 + 2250 + 750 + 2250
= 6000 sq. m
∴ The area of the given plot is 6000 sq.m.

ii. In ∆ABE, m∠BAE = 90°, l(AB) = 24 m, l(BE) = 30 m
∴ [l(BE)]² = [l(AB)]² + [l(AE)]²
…[Pythagoras theorem]
∴ (30)² = (24)² + [l(AE)]²
∴ 900 = 576 + [l(AE)]²
∴ [l(AE)]² = 900 – 576
∴ [l(AE)]² = 324
∴ l(AE) = √324 = 18 m
…[Taking square root of both sides]
A(∆ABE)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(AE) x l(AB)
= \(\frac { 1 }{ 2 }\) x 18 x 24
= 216 sq. m
In ∆BCE, a = 30m, b = 28m, c = 26m

∴ Area of plot ABCDE
= A(∆ABE) + A(∆BCE) + A(∆EDC)
= 216 + 336 + 224
= 776 sq. m
∴ The area of the given plot is 776 sq.m.
[Note: In the given figure, we have taken l(DF) = 16 m]

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.4 8th Std Maths Answers Solutions Chapter 15 Area.

Area Class 8 Maths Chapter 15 Practice Set 15.4 Solutions Maharashtra Board

Std 8 Maths Practice Set 15.4 Chapter 15 Solutions Answers

Question 1.
Sides of a triangle are 45 cm, 39 cm and 42 cm, find its area.
Solution:
Sides of a triangle are 45 cm, 39 cm and 42 cm.
Here, a = 45cm, b = 39cm, c = 42cm
Semi perimeter of triangle = s = \(\frac { 1 }{ 2 }(a+b+c)\)
= \(\frac { 1 }{ 2 }(45+39+42)\)
= \(\frac { 126 }{ 2 }\)
= 63
Area of a triangle

∴ The area of the triangle is 756 sq.cm.

Question 2.
Look at the measures shown in the given figure and find the area of ☐PQRS.

Solution:
A (☐PQRS) = A(∆PSR) + A(∆PQR)
In ∆PSR, l(PS) = 36 m, l(SR) = 15 m
A(∆PSR)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(SR) x l(PS)
= \(\frac { 1 }{ 2 }\) x 15 x 36
= 270 sq.m
In ∆PSR, m∠PSR = 90°
[l(PR)]² = [l(PS)]² + [l(SR)]²
…[Pythagoras theorem]
= (36)² + (15)²
= 1296 + 225
∴ l(PR)² = 1521
∴ l(PR) = 39m
…[Taking square root of both sides]
In ∆PQR, a = 56m, b = 25m, c = 39m

A(☐PQRS) = A(∆PSR) + A(∆PQR)
= 270 + 420
= 690 sq. m
∴ The area of ☐PQRS is 690 sq.m

Question 3.
Some measures are given in the figure, find the area of ☐ABCD.

Solution:
A(☐ABCD) = A(∆BAD) + A(∆BDC)
In ∆BAD, m∠BAD = 90°, l(AB) = 40m, l(AD) = 9m
A(∆BAD) = \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(AB) x l(AD)
= \(\frac { 1 }{ 2 }\) x 40 x 9
= 180 sq. m
In ∆BDC, l(BT) = 13m, l(CD) = 60m
A(∆BDC) = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x l(CD) x l(BT)
= \(\frac { 1 }{ 2 }\) x 60 x 13
= 390 sq. m
A (☐ABCD) = A(∆BAD) + A(∆BDC)
= 180 + 390
= 570 sq. m
∴ The area of ☐ABCD is 570 sq.m.

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.3 8th Std Maths Answers Solutions Chapter 15 Area.

Area Class 8 Maths Chapter 15 Practice Set 15.3 Solutions Maharashtra Board

Std 8 Maths Practice Set 15.3 Chapter 15 Solutions Answers

Question 1.
In the given figure, ☐ABCD is a trapezium, side AB || side DC, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area ☐ABCD.

Solution:
☐ABCD is a trapezium, side AB || side DC,
l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm,
Area of a trapezium = \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A (☐ABCD) = \(\frac { 1 }{ 2 }\) x [l(AB) + l(DC)] x l(AD)
= \(\frac { 1 }{ 2 }\) x (13 + 9) x 8
= \(\frac { 1 }{ 2 }\) x 22 x 8
= 11 x 8
= 88 sq.cm
∴ The area of ☐ABCD is 88 sq. cm.
[Note: The question is modified.]

Question 2.
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
Solution:
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm and its height is 4.2 cm.
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
= \(\frac { 1 }{ 2 }\) x (8.5 + 11.5) x 4.2
= \(\frac { 1 }{ 2 }\) x 20 x 4.2
= 10 x 4.2
= 42 sq. cm
∴ The area of the trapezium is 42 sq. cm.

Question 3.
☐PQRS is an isosceles trapezium. l(PQ) = 7 cm, seg PM ⊥ seg SR, l(SM) = 3 cm. Distance between two parallel sides is 4 cm, find the area of ☐PQRS.

Solution:
☐PQRS is an isosceles trapezium.
l(PQ) = 7 cm, seg PM ⊥ seg SR,
l(SM) = 3 cm, l(PM) = 4cm
Draw seg QN ⊥ seg SR.
In ☐PMNQ,
seg PQ || seg MN
∠PMN = ∠QNM = 90°
∴ ☐PMNQ is a rectangle.

Opposite sides of a rectangle are congruent.
∴ l(PM) = l(QN) = 4 cm and
l(PQ) = l(MN) = 7 cm
In ∆PMS, m∠PMS = 90°
∴ [l(PS)]² = [l(PM)]² + [l(SM)]² … [Pythagoras theorem]
∴ [l(PS)]² = (4)² + (3)²
∴ [l(PS)]² = 16 + 9 = 25
∴ l(PS) = √25 = 5 cm
…[Taking square root of both sides]
☐PQRS is an isosceles trapezium.
∴ l(PS) = l(QR) = 5 cm
In ∆QNR, m ∠QNR = 90°
∴ [l(QR)]² = [l(QN)]² + [l(NR)]²
… [Pythagoras theorem]
∴ (5)² = (4)² + [l(NR)]²
∴ 25 = 16 + [l(NR)]²
∴ [l(NR)]² = 25 – 16 = 9
∴ l(NR) = √9 = 3 cm
…[Taking square root of both sides]
l(SR) = l(SM) + l(MN) + l(NR)
= 3 + 7 + 3
= 13 cm
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A(☐PQRS) = \(\frac { 1 }{ 2 }\) x [l(PQ) + l(SR)] x l(PM)
= \(\frac { 1 }{ 2 }\) x (7+ 13) x 4
= \(\frac { 1 }{ 2 }\) x 20 x 4
= 40 sq.cm
∴ The area of ☐PQRS is 40 sq. cm.

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 7 Co-ordinate Geometry.

9th Standard Maths 2 Practice Set 7.1 Chapter 7 Co-ordinate Geometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 7.1 Chapter 7 Co-ordinate Geometry Questions With Answers Maharashtra Board

Question 1.
State in which quadrant or on which axis do the following points lie.
i. A(-3, 2)
ii. B(-5, -2)
iii. K(3.5, 1.5)
iv. D(2, 10)
V. E(37, 35)
vi. F(15, -18)
vii. G(3, -7)
viii. H(0, -5)
ix. M(12, 0)
x. N(0, 9)
xi. P(0, 2.5)
xii. Q(-7, -3)
Solution:

Question 2.
In which quadrant are the following points?
i. whose both co-ordinates are positive.
ii. whose both co-ordinates are negative.
iii. whose x co-ordinate is positive and the y co-ordinate is negative.
iv. whose x co-ordinate is negative and y co-ordinate is positive.
Solution:
i. Quadrant I
ii. Quadrant III
iii. Quadrant IV
iv. Quadrant II

Question 3.
Draw the co-ordinate system on a plane and plot the following points.
L(-2, 4), M(5, 6), N(-3, -4), P(2, -3), Q(6, -5), S(7, 0), T(0, -5)
Solution:

Maharashtra Board Class 9 Maths Chapter 7 Co-ordinate Geometry Practice Set 7.1 Intext Questions and Activities

Question 1.
Plot the points R(-3,-4), S(3,-l) on the same co-ordinate system. (Textbook pg. no. 93)
Steps for plotting the points:
i. Draw X-axis and Y-axis on the plane. Show the origin.
ii. Draw a line parallel to Y-axis at a distance of 3 units in the -ve direction of X-axis.
iii. Draw another line parallel to X-axis at a distance of 4 units in the -ve direction of Y-axis.
iv. Intersection of these lines is the point R (-3, -4).
v. The point S can be plotted in the same manner.

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 6 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 6 Circle.

9th Standard Maths 2 Problem Set 6 Chapter 6 Circle Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Problem Set 6 Chapter 6 Circle Questions With Answers Maharashtra Board

Question 1.
Choose correct alternative answer and fill in the blanks.

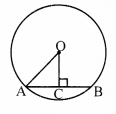
i. Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence, the length of the chord is ____.
(A) 16 cm
(B) 8 cm
(C) 12 cm
(D) 32 cm
Answer:

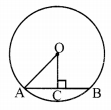
∴ OA² = AC² + OC²
∴ 10² = AC² + 6²
∴ AC² = 64
∴ AC = 8 cm
∴ AB = 2(AC)= 16 cm
(A) 16 cm

ii. The point of concurrence of all angle bisectors of a triangle is called the ____.
(A) centroid
(B) circumcentre
(C) incentre
(D) orthocentre
Answer:
(C) incentre

iii. The circle which passes through all the vertices of a triangle is called ____.
(A) circumcircle
(B) incircle
(C) congruent circle
(D) concentric circle
Answer:
(A) circumcircle

iv. Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ____.
(A) 12 cm
(B) 13 cm
(C) 14 cm
(D) 15 cm
Answer:

OA² = AC² + OC²
∴ OA² = 12² + 5²
∴ OA² = 169
∴ OA = 13 cm
(B) 13 cm

v. The length of the longest chord of the circle with radius 2.9 cm is ____.
(A) 3.5 cm
(B) 7 cm
(C) 10 cm
(D) 5.8 cm
Answer:
Longest chord of the circle = diameter = 2 x radius = 2 x 2.9 = 5.8 cm
(D) 5.8 cm

vi. Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie ____.
(A) on the centre
(B) inside the circle
(C) outside the circle
(D) on the circle
Answer:
l(OP) > radius
∴Point P lies in the exterior of the circle.
(C) outside the circle

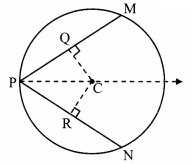
vii. The lengths of parallel chords which are on opposite sides of the centre of a circle are 6 cm and 8 cm. If radius of the circle is 5 cm, then the distance between these chords is _____.
(A) 2 cm
(B) 1 cm
(C) 8 cm
(D) 7 cm
Answer:

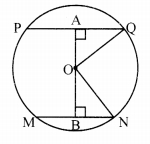
PQ = 8 cm, MN = 6 cm
∴ AQ = 4 cm, BN = 3 cm
∴ OQ² = OA² + AQ²
∴ 5² = OA² + 4²
∴ OA² = 25 – 16 = 9
∴ OA = 3 cm
Also, ON² = OB² + BN²
∴ 5² = OB² + 3²
∴ OB = 4 cm
Now, AB = OA + OB = 3 + 4 = 7 cm

Question 2.
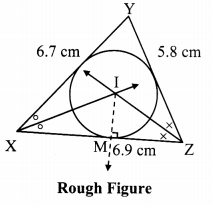
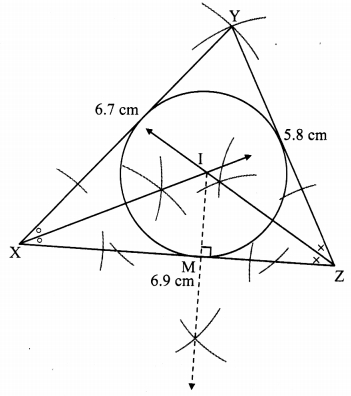
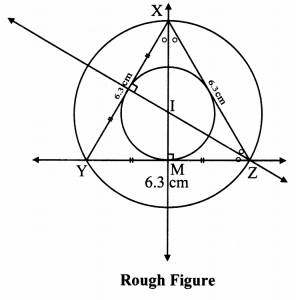
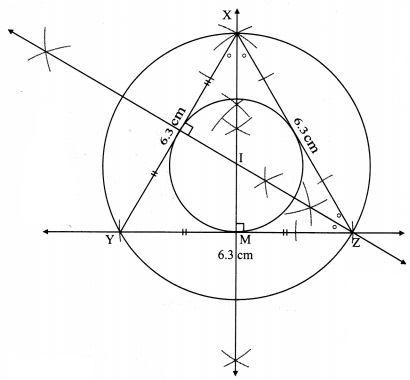
Construct incircle and circumcircle of an equilateral ADSP with side 7.5 cm. Measure the radii of both the circles and find the ratio of radius of circumcircle to the radius of incircle.
Solution:


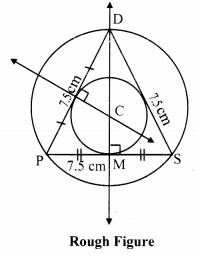
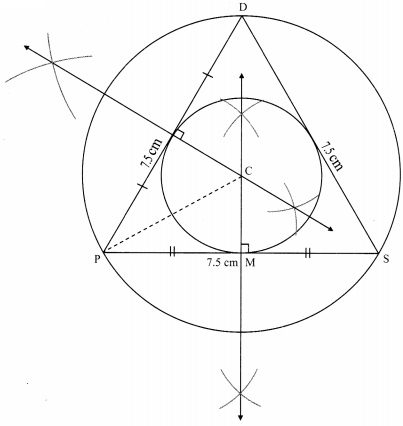
Steps of construction:
i. Construct ∆DPS of the given measurement.
ii. Draw the perpendicular bisectors of side DP and side PS of the triangle.
iii. Name the point of intersection of the perpendicular bisectors as point C.
iv. With C as centre and CM as radius, draw a circle which touches all the three sides of the triangle.
v. With C as centre and CP as radius, draw a circle which passes through the three vertices of the triangle.

Radius of incircle = 2.2 cm and Radius of circumcircle = 4.4 cm

Question 3.
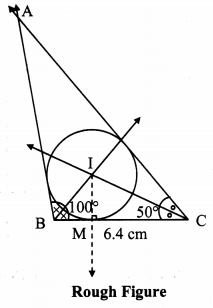
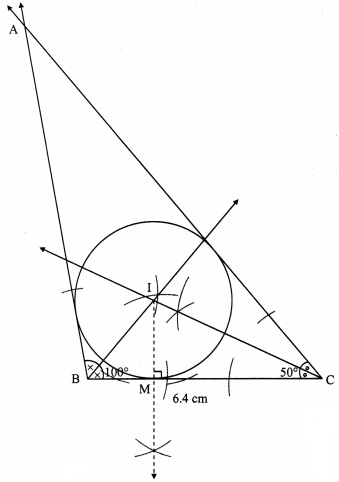
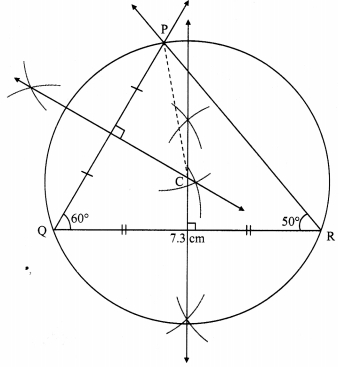
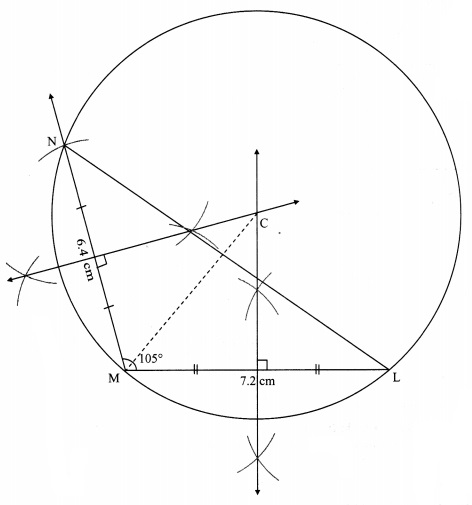
Construct ∆NTS where NT = 5.7 cm. TS = 7.5 cm and ∠NTS = 110° and draw incircle and circumcircle of it.
Solution:


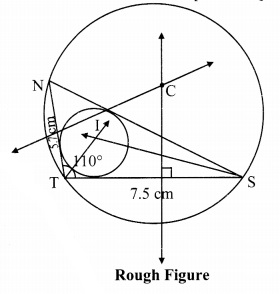
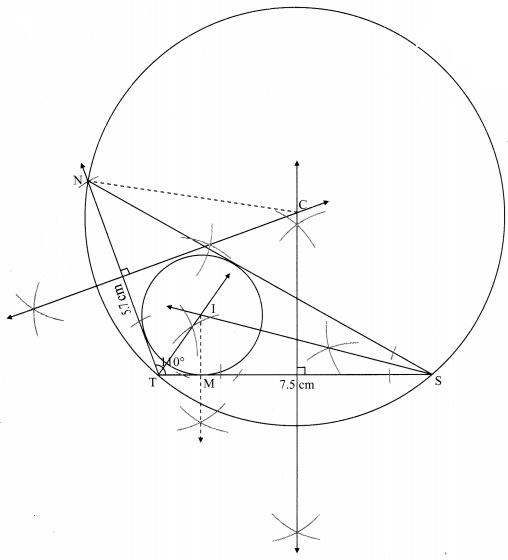
Steps of construction:
For incircle:
i. Construct ∆NTS of the given measurement.
ii. Draw the bisectors of ∠T and ∠S. Let these bisectors intersect at point I.
iii. Draw a perpendicular IM on side TS. Point M is the foot of the perpendicular.
iv. With I as centre and IM as radius, draw a circle which touches all the three sides of the triangle.
For circumcircle:
i. Draw the perpendicular bisectors of side NT and side TS of the triangle.
ii. Name the point of intersection of the perpendicular bisectors as point C.
iii. Join seg CN
iv. With C as centre and CN as radius, draw a circle which passes through the three vertices of the triangle.

Question 4.
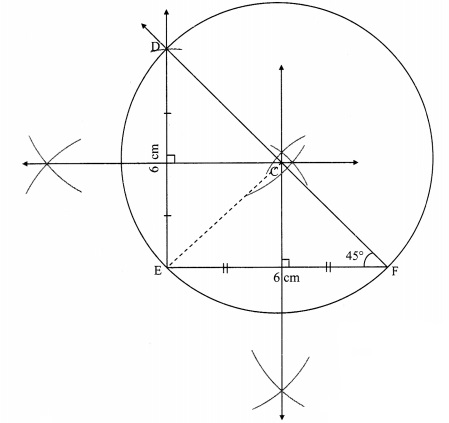
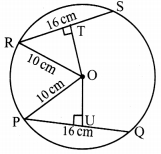
In the adjoining figure, C is the centre of the circle, seg QT is a diameter, CT = 13, CP = 5. Find the length of chord RS.

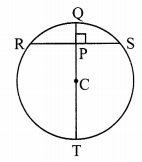
Given: In a circle with centre C, QT is a diameter, CT = 13 units, CP = 5 units
To find: Length of chord RS
Construction: Join points R and C.
Solution:

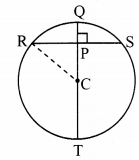
i. CR = CT= 13 units …..(i) [Radii of the same circle]
In ∆CPR, ∠CPR = 90°
∴ CR² = CP² + RP² [Pythagoras theorem]
∴ 13² = 5² + RP² [From (i)]
∴ 169 = 25 + RP² [From (i)]
∴ RP² = 169 – 25 = 144
∴ RP = \(\sqrt { 144 }\) [Taking square root on both sides]
∴ RP = 12 cm ….(ii)

ii. Now, seg CP _L chord RS [Given]
∴ RP = \(\frac { 1 }{ 2 }\) RS [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
∴ 12 = \(\frac { 1 }{ 2 }\) RS [From (ii)]
∴ RS = 2 x 12 = 24
∴ The length of chord RS is 24 units.

Question 5.
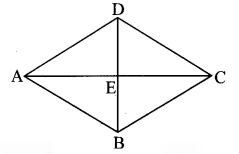
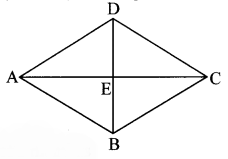
In the adjoining figure, P is the centre of the circle. Chord AB and chord CD intersect on the diameter at the point E. If ∠AEP ≅ ∠DEP, then prove that AB = CD.

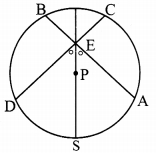
Given: P is the centre of the circle.
Chord AB and chord CD intersect on the diameter at the point E. ∠AEP ≅ ∠DEP
To prove: AB = CD
Construction: Draw seg PM ⊥ chord AB, A-M-B
seg PN ⊥ chord CD, C-N-D
Proof:

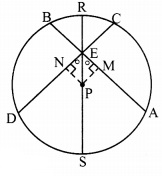
∠AEP ≅ ∠DEP [Given]
∴ Seg ES is the bisector of ∠AED.
PoInt P is on the bisector of ∠AED.
∴ PM = PN [Every point on the bisector of an angle is equidistant from the sides of the angle.]
∴ chord AB ≅ chord CD [Chords which are equidistant from the centre are congruent.]
∴ AB = CD [Length of congruent segments]

Question 6.
In the adjoining figure, CD is a diameter of the circle with centre O. Diameter CD is perpendicular to chord AB at point E. Show that ∆ABC is an isosceles triangle.

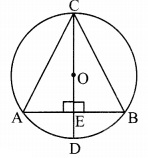
Given: O is the centre of the circle.
diameter CD ⊥ chord AB, A-E-B
To prove: ∆ABC is an isosceles triangle.
Proof:
diameter CD ⊥ chord AB [Given]
∴ seg OE ⊥ chord AB [C-O-E, O-E-D]
∴ seg AE ≅ seg BE ……(i) [Perpendicular drawn from the centre of the circle to the chord bisects the chord]
In ∆CEA and ∆CEB,
∠CEA ≅ ∠CEB [Each is of 90°]
seg AE ≅ seg BE [From (i)]
seg CE ≅ seg CE [Common side]
∴ ∆CEA ≅ ∆CEB [SAS test]
∴ seg AC ≅ seg BC [c. s. c. t.]
∴ ∆ABC is an isosceles triangle.

Maharashtra Board Class 9 Maths Chapter 6 Circle Problem Set 6 Intext Questions and Activities

Question 1.
Every student in the group should do this activity. Draw a circle in your notebook. Draw any chord of that circle. Draw perpendicular to the chord through the centre of the circle. Measure the lengths of the two parts of the chord. Group leader should prepare a table as shown below and ask other students to write their observations in it. Write the property which you have observed. (Textbook pg. no. 77)


Answer:
On completing the above table, you will observe that the perpendicular drawn from the centre of a circle on its chord bisects the chord.

Question 2.
Every student from the group should do this activity. Draw a circle in your notebook. Draw a chord of the circle. Join the midpoint of the chord and centre of the circle. Measure the angles made by the segment with the chord.
Discuss about the measures of the angles with your friends. Which property do the observations suggest ? (Textbook pg. no. 77)

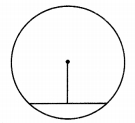
Answer:
The meausure of the angles made by the drawn segment with the chord is 90°. Thus, we can conclude that, the segment joining the centre of a circle and the midpoint of its chord is perpendicular to the chord.

Question 3.
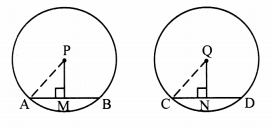
Draw circles of convenient radii. Draw two equal chords in each circle. Draw perpendicular to each chord from the centre. Measure the distance of each chord from the centre. What do you observe? (Textbook pg. no. 79)
Answer:
Congruent chords of a circle are equidistant from the centre.

Question 4.
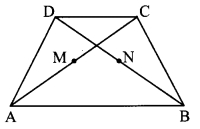
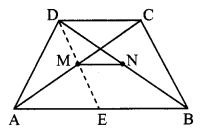
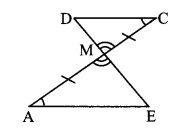
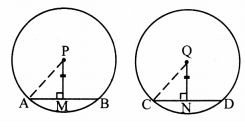
Measure the lengths of the perpendiculars on chords in the following figures.

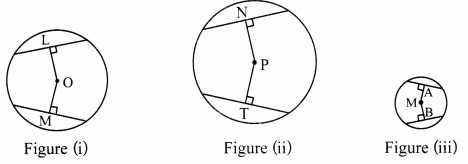
Did you find OL = OM in fig (i), PN = PT in fig (ii) and MA = MB in fig (iii)?
Write the property which you have noticed from this activity. (Textbook pg. no. 80)
Answer:
In each figure, the chords are equidistant from the centre. Also, we can see that the measures of the chords in each circle are equal.
Thus, we can conclude that chords of a circle equidistant from the centre of a circle are congruent.

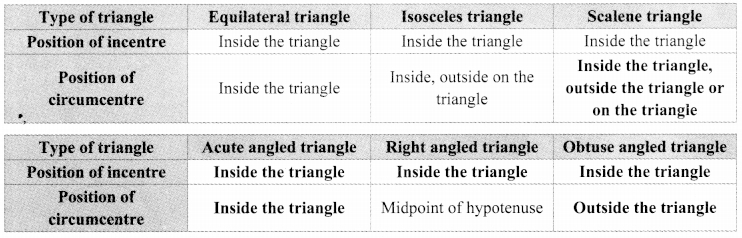
Question 5.
Draw different triangles of different measures and draw in circles and circumcircles of them. Complete the table of observations and discuss. (Textbook pg. no. 85)
Answer:

Class 9 Maths Digest

• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5.3 Class 9 Answers
• Practice Set 5.4 Class 9 Answers
• Practice Set 5.5 Class 9 Answers
• Problem Set 5 Class 9 Answers
• Practice Set 6.1 Class 9 Answers
• Practice Set 6.2 Class 9 Answers
• Practice Set 6.3 Class 9 Answers
• Problem Set 6 Class 9 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.2 8th Std Maths Answers Solutions Chapter 15 Area.

Area Class 8 Maths Chapter 15 Practice Set 15.2 Solutions Maharashtra Board

Std 8 Maths Practice Set 15.2 Chapter 15 Solutions Answers

Question 1.
Lengths of the diagonals of a rhombus are 15 cm and 24 cm, find its area.
Solution:
Lengths of the diagonals of a rhombus are 15 cm and 24 cm.
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × 15 × 24
= 15 × 12
= 180 sq.cm
∴ The area of the rhombus is 180 sq. cm.

Question 2.
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.
Solution:
Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm.
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × 16.5 × 14.2
= 16.5 × 7.1
= 117.15 sq cm
∴ The area of the rhombus is 117.15 sq. cm.

Question 3.
If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?
Solution:
Let ₹ABCD be the rhombus. Diagonals AC and BD intersect at point E.

l(AC) = 48 cm …(i)
l(AE) = \(\frac { 1 }{ 2 }l(AC)\) …[Diagonals of a rhombus bisect each other]
= \(\frac { 1 }{ 2 }\) × 48 …[From (i)]
= 24 cm …(ii)
Perimeter of rhombus = 100 cm …[Given]
Perimeter of rhombus = 4 × side
∴ 100 = 4 × l(AD)
∴ l(AD) = \(\frac { 100 }{ 4 }\) = 25 cm …(iii)
In ∆ADE,
m∠AED = 90° …[Diagonals of a rhombus are perpendicular to each other]
∴ [l(AD)]² = [l(AE)]² + [l(DE)]² … [Pythagoras theorem]
∴ (25)² = (24)² + l(DE)² … [From (ii) and (iii)]
∴ 625 = 576 + l(DE)²
∴ l(DE)² = 625 – 576
∴ l(DE)² = 49
∴ l(DE) = √49
… [Taking square root of both sides]
l(DE) = 7 cm …(iv)
l(DE) = \(\frac { 1 }{ 2 } l(BD)\) ….[Diagonals of a rhombus bisect each other]
∴ 7 = \(\frac { 1 }{ 2 } l(BD)\) …[From (iv)]
∴ l(BD) = 7 × 2
= 14 cm …(v)
Area of a rhombus
= \(\frac { 1 }{ 2 }\) × product of lengths of diagonals
= \(\frac { 1 }{ 2 }\) × l(AC) × l(BD)
= \(\frac { 1 }{ 2 }\) × 48 × 14 … [From (i) and (v)]
= 48 × 7
= 336 sq.cm
∴ The area of the quadrilateral is 336 sq.cm.

Question 4.
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq.cm, find its perimeter.
Solution:
Let ₹ABCD be the rhombus.
Diagonals AC and BD intersect at point E.
l(AC) = 30 cm …(i)
and A(₹ABCD) = 240 sq. cm .. .(ii)

Area of the rhombus = \(\frac { 1 }{ 2 }\) × product of lengths of diagonal
∴ 240 = \(\frac { 1 }{ 2 }\) × l(AC) x l(BD) …[From (ii)]
∴ 240 = \(\frac { 1 }{ 2 }\) × 30 × l(BD) …[From (i)]
∴ l(BD) = \(\frac { 240\times 2 }{ 30 }\)
∴ l(BD) = 8 × 2 = 16 cm …(iii)
Diagonals of a rhombus bisect each other.
∴ l(AE) = \(\frac { 1 }{ 2 }l(AC)\)
= \(\frac { 1 }{ 2 }\) × 30 … [From (i)]
= 15 cm …(iv)
and l(DE) = \(\frac { 1 }{ 2 }l(BD)\)
= \(\frac { 1 }{ 2 }\) × 16
= 8 cm
In ∆ADE,
m∠AED = 90°
…[Diagonals of a rhombus are perpendicular to each other]
∴[l(AD)]² = [l(AE)]² + [l(DE)]²
…[Pythagoras theorem]
∴l(AD)² = (15)² + (8)² … [From (iv) and (v)]
= 225 + 64
∴l(AD)² = 289
∴l(AD) = √289
…[Taking square root of both sides]
∴l(AD) = 17 cm
Perimeter of rhombus = 4 × side
= 4 × l(AD)
= 4 × 17
= 68 cm
∴The perimeter of the rhombus is 68 cm.

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.1 8th Std Maths Answers Solutions Chapter 15 Area.

Area Class 8 Maths Chapter 15 Practice Set 15.1 Solutions Maharashtra Board

Std 8 Maths Practice Set 15.1 Chapter 15 Solutions Answers

Question 1.
If base of a parallelogram is 18 cm and its height is 11 cm, find its area.
Solution:
Given, base = 18 cm, height = 11 cm
Area of a parallelogram = base × height
= 18 × 11
= 198 sq.cm
∴ Area of the parallelogram is 198 sq.cm.

Question 2.
If area of a parallelogram is 29.6 sq. cm and its base is 8 cm, find its height.
Solution:
Given, area of a parallelogram = 29.6 sq.cm,
base = 8 cm
Area of a parallelogram = base × height
∴ 29.6 = 8 × height
∴ height = \(\frac { 29.6 }{ 8 }\) = 3.7 cm
∴ Height of the parallelogram is 3.7 cm.

Question 3.
Area of a parallelogram is 83.2 sq.cm. If its height is 6.4 cm, find the length of its base.
Solution:
Given, area of a parallelogram = 83.2 sq.cm, height = 6.4 cm
Area of a parallelogram = base × height
∴ 83.2 = base × 6.4
∴ base = \(\frac { 83.2 }{ 6.4 }\) = 13 cm
∴ The length of the base of the parallelogram is 13 cm.

Maharashtra Board Class 8 Maths Chapter 15 Area Practice Set 15.1 Intext Questions and Activities

Question 1.
Draw a big enough parallelogram ABCD on a paper as shown in the figure.
Draw perpendicular AE on side BC.
Cut the right angled ∆AEB. Join it with the remaining part of ₹ABCD as shown in the figure.
The new figure formed is a rectangle.
The rectangle is formed from the parallelogram.
So, areas of both the figures are equal.
Base of parallelogram is one side (length) of the rectangle and its height is the other side (breadth) of the rectangle.
∴ Area of a parallelogram = base × height (Textbook pg. no.94)

Solution:
Draw a big enough parallelogram ABCD on a paper as shown in the figure.
Draw perpendicular AE on side BC.
Cut the right angled ∆AEB. Join it with the remaining part of ₹ABCD as shown in the figure.
The new figure formed is a rectangle.
The rectangle is formed from the parallelogram.
So, areas of both the figures are equal.
Base of parallelogram is one side (length) of the rectangle and its height is the other side (breadth) of the rectangle.
∴ Area of a parallelogram = Area of a rectangle = length × breadth = base × height

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 6 Circle.

9th Standard Maths 2 Practice Set 6.3 Chapter 6 Circle Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 6.3 Chapter 6 Circle Questions With Answers Maharashtra Board

Question 1.
Construct ∆ABC such that ∠B =100°, BC = 6.4 cm, ∠C = 50° and construct its incircle.
Solution:


Steps of construction:
i. Construct ∆ABC of the given measurement.
ii. Draw the bisectors of ∠B and ∠C. Let these bisectors intersect at point I.
iii. Draw a perpendicular IM on side BC. Point M is the foot of the perpendicular.
iv. With I as centre and IM as radius, draw a circle which touches all the three sides of the triangle.

Question 2.
Construct ∆PQR such that ∠P = 70°, ∠R = 50°, QR = 7.3 cm and construct its circumcircle.
Solution:
In ∆PQR,
m∠P + m∠Q + m∠R = 180° … [Sum of the measures of the angles of a triangle is 180°]
∴ 70° + m∠Q + 50° = 180°
∴ m∠Q = 180° – 70° + m∠Q + 50° = 180°
∴ m∠Q = 180° – 70° – 50°
∴ m∠Q = 60°


Steps of construction:
i. Construct A PQR of the given measurement.
ii. Draw the perpendicular bisectors of side PQ and side QR of the triangle.
iii. Name the point of intersection of the perpendicular bisectors as point C.
iv. Join seg CP
v. With C as centre and CP as radius, draw a circle which passes through the three vertices of the triangle.

Question 3.
Construct ∆XYZ such that XY = 6.7 cm, YZ = 5.8 cm, XZ = 6.9 cm. Construct its incircle.
Solution:


Steps of construction:
i. Construct ∆XYZ of the given measurement
ii. Draw the bisectors of ∠X and ∠Z. Let these bisectors intersect at point I.
iii. Draw a perpendicular IM on side XZ. Point M is the foot of the perpendicular.
iv. With I as centre and IM as radius, draw a circle which touches all the three sides of the triangle.

Question 4.
In ∆LMN, LM = 7.2 cm, ∠M = 105°, MN = 6.4 cm, then draw ∆LMN and construct its circumcircle.
Solution:


Steps of construction:
i. Construct ∆LMN of the given measurement.
ii. Draw the perpendicular bisectors of side MN and side ML of the triangle.
iii. Name the point of intersection of the perpendicular bisectors as point C.
iv. Join seg CM
v. With C as centre and CM as radius, draw a circle which passes through the three vertices of the triangle.

Question 5.
Construct ∆DEF such that DE = EF = 6 cm. ∠F = 45° and construct its circumcircle.
Solution:


Steps of construction:
i. Construct ∆DEF of the given measurement.
ii. Draw the perpendicular bisectors of side DE and side EF of the triangle.
iii. Name the point of intersection of perpendicular bisectors as point C.
iv. Join seg CE
v. With C as centre and CE as radius, draw a circle which passes through the three vertices of the triangle.

Maharashtra Board Class 9 Maths Chapter 6 Circle Practice Set 6.3 Intext Questions and Activities

Question 1.
Draw any equilateral triangle. Draw incircle and circumcircle of it. What did you observe while doing this activity? (Textbook pg. no. 85)
i. While drawing incircle and circumcircle, do the angle bisectors and perpendicular bisectors coincide with each other?
ii. Do the incentre and circumcenter coincide with each other? If so, what can be the reason of it?
iii. Measure the radii of incircle and circumcircle and write their ratio.
Solution:


Steps of construction:
i. Construct equilateral ∆XYZ of any measurement.
ii. Draw the perpendicular bisectors of side XY and side YZ of the triangle.
iii. Draw the bisectors of ∠X and ∠Z.
iv. Name the point of intersection of the perpendicular bisectors and angle bisectors as point I.
v. With I as centre and IM as radïus, draw a circle which touches all the three sides of the triangle.
vi. With I as centre and IZ as radius, draw a circle which passes through the three vertices of the triangle.
[Note: Here, point of intersection of perpendicular bisector and angle bisector is same.]

i. Yes.
ii. Yes.
The angle bisectors of the angles and the perpendicular bisectors of the sides of an equilateral triangle are coincedent. Hence, its incentre and circumcentre coincide.
iii. Radius of circumcircle = 3.6 cm,
Radius of incircle = 1.8 cm
\(\text { Ratio }=\frac{\text { Radius of circumcircle }}{\text { Radius of incircle }}=\frac{3.6}{1.8}=\frac{2}{1}=2 : 1\)

Class 9 Maths Digest

• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5.3 Class 9 Answers
• Practice Set 5.4 Class 9 Answers
• Practice Set 5.5 Class 9 Answers
• Problem Set 5 Class 9 Answers
• Practice Set 6.1 Class 9 Answers
• Practice Set 6.2 Class 9 Answers
• Practice Set 6.3 Class 9 Answers
• Problem Set 6 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 5 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

9th Standard Maths 2 Problem Set 5 Chapter 5 Quadrilaterals Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Problem Set 5 Chapter 5 Quadrilaterals Questions With Answers Maharashtra Board

Question 1.
Choose the correct alternative answer and fill in the blanks.

i. If all pairs of adjacent sides of a quadrilateral are congruent, then it is called ____.
(A) rectangle
(B) parallelogram
(C) trapezium
(D) rhombus
Answer:
(D) rhombus

ii. If the diagonal of a square is 22√2 cm, then the perimeter of square is ____.
(A) 24 cm
(B) 24√2 cm
(C) 48 cm
(D) 48√2 cm
Answer:
In ∆ABC,
AC² = AB² + BC²

∴ (12² √2 )² = AB² + AB²
∴ \( A B^{2}=\frac{12^{2} \times 2}{2}=12^{2}\)
∴ AB = 12 cm
∴ Perimeter of □ABCD = 4 x 12 = 48 cm
(C) 48 cm

iii. If opposite angles of a rhombus are (2x)° and (3x – 40)°, then the value of x is ____.
(A) 100°
(B) 80°
(C) 160°
(D) 40°
Answer:
2x = 3x – 40 … [Pythagoras theorem]
∴ x = 40°
(D) 40°

Question 2.
Adjacent sides of a rectangle are 7 cm and 24 cm. Find the length of its diagonal.
Solution:

Let □ABCD be the rectangle.
AB = 7 cm, BC = 24 cm
In ∆ABC, ∠B = 90° [Angle of a rectangle]
AC² = AB² + BC² [Pythagoras theorem]
= 7² + 24²
= 49 + 576
= 625
AC = √625 [Taking square root of both sides]
= 25 cm
∴ The length of the diagonal of the rectangle is 25 cm.

Question 3.
If diagonal of a square is 13 cm, then find its side.
Solution:

Let □PQRS be the square of side x cm.
∴ PQ = QR = x cm …..(i) [Sides of a square]
∴ In ∆PQR, ∠Q = 90° [Angle of a square]
∴ PR² = PQ² + QR² [Pythagoras theorem]
∴ 13 = x + x [From (i)]
∴ 169 = 2x²

The length of the side of the square is 6.5√2 cm.

Question 4.
Ratio of two adjacent sides of a parallelogram is 3 : 4, and its perimeter is 112 cm. Find the length of its each side.
Solution:

Let □STUV be the parallelogram.
Ratio of two adjacent sides of a parallelogram is 3 : 4.
Let the common multiple be x.
ST = 3x cm and TU = 4x cm
∴ ST = UV = 3x cm
TU = SV = 4x cm …..(i) [Opposite sides of a parallelogram]
Perimeter of □STUV = 112 [Given]
∴ ST + TU + UV + SV = 112
∴ 3x + 4x + 3x + 4x = 112 [From (i)]
∴ 14x = 112
∴ x = \(\frac { 112 }{ 14 }\)
∴ x = 8
∴ ST = UV = 3x = 3 x 8 = 24 cm
∴ TU = SV = 4x = 4 x 8 = 32 cm [From (i)]
∴ The lengths of the sides of the parallelogram are 24 cm, 32 cm, 24 cm and 32 cm.

Question 5.
Diagonals PR and QS of a rhombus PQRS are 20 cm and 48 cm respectively. Find the length of side PQ.
Solution:

□PQRS is a rhombus. [Given]
PR = 20 cm and QS = 48 cm [Given]
∴ PT = \(\frac { 1 }{ 2 }\) PR [Diagonals of a rhombus bisect each other]
= \(\frac { 1 }{ 2 }\) x 20 = 10 cm
Also, QT = \(\frac { 1 }{ 2 }\) QS [Diagonals of a rhombus bisect each other]
= \(\frac { 1 }{ 2 }\) x 48 = 24 cm

ii. In ∆PQT, ∠PTQ = 90° [Diagonals of a rhombus are perpendicular to each other]
∴ PQ² = PT² + QT² [Pythagoras- theorem]
= 10² + 24²
= 100 + 576
∴ PQ² = 676
∴ PQ = \(\sqrt {676 }\) [Taking square root of both sides]
= 26 cm
∴ The length of side PQ is 26 cm.

Question 6.
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50°, then find the measure of ∠MPS.
Solution:

□PQRS is a rectangle.
∴ PM = \(\frac { 1 }{ 2 }\) PR …(i)
MS = \(\frac { 1 }{ 2 }\) QS …(ii) [Diagonals of a rectangle bisect each other]
Also, PR = QS …..(iii) [Diagonals of a rectangle are congruent]
∴ PM = MS ….(iv) [From (i), (ii) and (iii)]
In ∆PMS,
PM = MS [From (iv)]
∴ ∠MSP = ∠MPS = x° …..(v) [Isosceles triangle theorem]
∠PMS = ∠QMR = 50° ……(vi) [Vertically opposite angles]
In ∆MPS,
∠PMS + ∠MPS + ∠MSP = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ 50° +x + x = 180° [From (v) and (vi)]
∴ 50° + 2x= 180
∴ 2x= 180-50
∴ 2x= 130
∴ x = \(\frac { 130 }{ 2 }\) = 65°
∴ ∠MPS = 65° [From (v)]

Question 7.
In the adjoining figure, if seg AB || seg PQ , seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR, then prove that seg BC || seg QR and seg BC ≅ seg QR.

Solution:
Given: seg AB || seg PQ , seg AB ≅ seg PQ,
seg AC || seg PR, seg AC ≅ seg PR
To prove: seg BC || seg QR, seg BC ≅ seg QR
Proof:
Consider □ABQP,
seg AB || seg PQ [Given]
seg AB ≅ seg PQ [Given]
∴ □ABQP is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]
∴ segAP || segBQ …..(i)
∴ seg AP ≅ seg BQ …..(ii) [Opposite sides of a parallelogram]
Consider □ACRP,
seg AC || seg PR [Given]
seg AC ≅ seg PR [Given]
∴ □ACRP is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]
∴ seg AP || seg CR …(iii)
∴ seg AP ≅ seg CR …….(iv) [Opposite sides of a parallelogram]
Consider □BCRQ,
seg BQ || seg CR
seg BQ ≅ seg CR
∴ □BCRQ is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]
∴ seg BC || seg QR
∴ seg BC ≅ seg QR [Opposite sides of a parallelogram]

Question 8.
In the adjoining figure, □ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that PQ || AB and PQ = \(\frac { 1 }{ 2 }\) ( AB + DC).

Given : □ ABCD is a trapezium.
To prove:
Construction: Join points A and Q. Extend seg AQ and let it meet produced DC at R.
Proof:

seg AB || seg DC [Given]
and seg BC is their transversal.
∴ ∠ABC ≅ ∠RCB [Alternate angles]
∴ ∠ABQ ≅ ∠RCQ ….(i) [B-Q-C]
In ∆ABQ and ∆RCQ,
∠ABQ ≅∠RCQ [From (i)]

seg BQ ≅ seg CQ [Q is the midpoint of seg BC]
∠BQA ≅ ∠CQR [Vertically opposite angles]
∴ ∆ABQ ≅ ∆RCQ [ASA test]
seg AB ≅ seg CR …(ii) [c. s. c. t.]
seg AQ ≅ seg RQ [c. s. c. t.]
∴ Q is the midpoint of seg AR. ….(iii)

In ∆ADR,
Points P and Q are the midpoints of seg AD and seg AR respectively. [Given and from (iii)]

∴ seg PQ || seg DR [Midpoint theorem]
i.e. seg PQ || seg DC ……..(iv) [D-C-R]
But, seg AB || seg DC …….(v) [Given]
∴ seg PQ || seg AB [From (iv) and (v)]
In ∆ADR,

Question 9.
In the adjoining figure, □ABCD is a trapezium. AB || DC. Points M and N are midpoints of diagonals AC and DB respectively, then prove that MN || AB.

Solution:
Given: □ABCD is a trapezium. AB || DC.
Points M and N are midpoints of diagonals AC and DB respectively.
To prove: MN || AB
Construction: Join D and M. Extend seg DM to meet seg AB at point E such that A-E-B.
Proof:
seg AB || seg DC and seg AC is their transversal. [Given]
∴ ∠CAB ≅ ∠ACD [Alternate angles]
∴ ∠MAE ≅ ∠MCD ….(i) [C-M-A, A-E-B]
In ∆AME and ∆CMD,

∠AME ≅ ∠CMD [Vertically opposite angles]
seg AM ≅ seg CM [M is the midpoint of seg AC]
∠MAE ≅∠MCD [From (i)]
∴ ∆AME ≅ ∆CMD [ASA test]
∴ seg ME ≅ seg MD [c.s.c.t]
∴ Point M is the midpoint of seg DE. …(ii)
In ∆DEB,

Points M and N are the midpoints of seg DE and seg DB respectively. [Given and from (ii)]
∴ seg MN || seg EB [Midpoint theorem]
∴ seg MN || seg AB [A-E-B]

Maharashtra Board Class 9 Maths Chapter 5 Quadrilaterals Problem Set 5 Intext Questions and Activities

Question 1.
Draw five parallelograms by taking various measures of lengths and angles. (Textbook page no. 59)

Question 2.
Draw a parallelogram PQRS. Draw diagonals PR and QS. Denote the intersection of diagonals by letter O. Compare the two parts of each diagonal with a divider. What do you find? (Textbook page no. 60)

Answer:
seg OP = seg OR, and seg OQ = seg OS
Thus we can conclude that, point O divides the diagonals PR and QS in two equal parts.

Question 3.
To verify the different properties of quadrilaterals.

Material: A piece of plywood measuring about 15 cm x 10 cm, 15 thin screws, twine, scissor.
Note: On the plywood sheet, fix five screws in a horizontal row keeping a distance of 2 cm between any two adjacent screws. Similarly make two more rows of screws exactly below the first one. Take care that the vertical distance between any two adjacent screws is also 2 cm.
With the help of the screws, make different types of quadrilaterals of twine. Verify the properties of sides and angles of the quadrilaterals. (Textbook page no. 75)

Class 9 Maths Digest

• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5.3 Class 9 Answers
• Practice Set 5.4 Class 9 Answers
• Practice Set 5.5 Class 9 Answers
• Problem Set 5 Class 9 Answers
• Practice Set 6.1 Class 9 Answers
• Practice Set 6.2 Class 9 Answers
• Practice Set 6.3 Class 9 Answers
• Problem Set 6 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 6 Circle.

9th Standard Maths 2 Practice Set 6.2 Chapter 6 Circle Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 6.2 Chapter 6 Circle Questions With Answers Maharashtra Board

Question 1.
Radius of circle is 10 cm. There are two chords of length 16 cm each. What will be the distance of these chords from the centre of the circle ?
Given: In a circle with centre O,
OR and OP are radii and RS and PQ are its congruent chords.
PQ = RS= 16 cm,
OR = OP = 10 cm
seg OU ⊥ chord PQ, P-U-Q
seg OT ⊥ chord RS, R-T-S
To find: Distance of chords from centre of the circle.
Solution:

i. PU = \(\frac { 1 }{ 2 }\)(PQ) [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
∴ PU= \(\frac { 1 }{ 2 }\) x 16 = 8 cm …(i)

ii. In ∆OUP, ∠OUP = 90°
∴ OP² = OU² + PU² [Pythagoras theorem]
∴ 10² = OU² + 8² [From (i)]
∴ 100 = OU² + 64
∴ OU² = 100 – 64 = 36
∴ OU = √36 [Taking square root on both sides]
∴ OU = 6 cm

iii. Now, OT = OU [Congruent chords of a circle are equidistant from the centre.]
∴ OT = OU = 6cm
∴ The distance of the chords from the centre of the circle is 6 cm.

Question 2.
In a circle with radius 13 cm, two equal chords are at a distance of 5 cm from the centre. Find the lengths of chords.
Given: In a circle with cente O,
OA and OC are the radii and AB and CD are its congruent chords,
OA = OC = 13cm
0E = OF = 5 cm
seg 0E ⊥ chord CD, C-E-D
seg OF ⊥ chord AB. A-F-B
To find: length of the chords
Solution:

i. In ∆AFO, ∠AFO = 90°
∴ AO² = AF² + FO² [Pythagoras theorem]
∴ 13² = AF² + 5²
∴ 169 = AF² + 25
∴ AF² = 169-25
∴ AF² = 144
∴ AF = \(\sqrt { 144 }\) [Taking square root on both sides]
∴ AF = 12 cm …..(i)

ii. Now AF = \(\frac { 1 }{ 2 }\)AB [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
∴ 12 = \(\frac { 1 }{ 2 }\) (AB) [From (i)]
∴ AB = 12 x 2 = 24 cm
∴ CD = AB = 24 cm [chord AB ≅ chord CD]
∴ The lengths of the two chords are 24 cm each.

Question 3.
Seg PM and seg PN are congruent chords of a circle with centre C. Show that the ray PC is the bisector of ∠NPM.
Given: Point C is the centre of the circle.
chord PM ≅ chord PN
To prove: Ray PC is the bisector of ∠NPM.
Construction: Draw seg CR ⊥ chord PN, P-R-N
seg CQ ⊥ chord PM, P-Q-M
Proof:

chord PM chord PN [Given]
seg CR ⊥ chord PN
seg CQ ⊥ chord PM [Construction]
∴ segCR ≅ segCQ ….(i) [Congruent chords are equidistant from the centre]
In ∆PRC and ∆PQC,
∠PRC ≅ ∠PQC [Each is of 90°]
segCR ≅ segCQ [From (i)]
seg PC ≅ seg PC [Common side]
∴ ∆PRC ≅ ∆PQC [Hypotenuse side test]
∴ ∠RPC ≅ ∠QPC [c. a. c. t.]
∴ ∠NPC ≅ ∠MPC [N- R-P, M-Q-P]
∴ Ray PC is the bisector of ∠NPM.

Maharashtra Board Class 9 Maths Chapter 6 Circle Practice Set 6.2 Intext Questions and Activities

Question 1.
Prove the following two theorems for two congruent circles. (Textbook pg. no. 81)
i. Congruent chords in congruent circles are equidistant from their respective centres.
ii. Chords of congruent circles which are equidistant from their respective centres are congruent.
Write ‘Given’. ‘To prove’ and the proofs of these theorems.
Solution:
(i) Congruent chords in congruent circles are equidistant from their respective centres.
Given: Point P and point Q are the centres of congruent circles.
chord AB ≅ chord CD
seg PM ⊥ chord AB, A-M-B
seg QN ⊥ chord CD, C-N-D
To prove: PM = QN

Construction: Draw seg PA and seg QC.
Proof:
seg PM ⊥ chord AB, seg QN ⊥ chord CD [Given]
∴ AM = \(\frac { 1 }{ 2 }\)(AB) ………(i) [Perpendicular drawn from the centre of the circle to the
∴ CN = \(\frac { 1 }{ 2 }\)(CD) ……..(ii) chord bisects the chord.]
But, AB = CD ………(iii) [Given]
∴ AM = CN [From (i), (ii) and (iii)]
i.e., segAM ≅ segCN ….(iv) [Segments of equal lengths]
In ∆PMA and ∆QNC,
∠PMA ≅ ∠QNC [Each is of 90°]
hypotenuse PA ≅ hypotenuse QC [Radii of congruent circles]
seg AM ≅ seg CN [From (iv)]
∴ ∆PMA ≅ ∆QNC [Hypotenuse side test]
∴ segPM ≅ segQN [c. s. c. t.]
∴ PM ≅ QN [Length of congruent segments]

(ii) Chords of congruent circles which are equidistant from their respective centres are congruent.

Given: Point P and point Q are the centres of congruent circles.
seg PM ⊥ chord AB, A-M-B
seg QN ⊥ chord CD, C-N-D
PM = QN
To prove: chord AB ≅ chord CD
Construction: Draw seg PA and seg QC.
Proof:
In ∆PMA and ∆QNC,
∴ ∠PMA ≅ ∠QNC [Each is of 90°]
seg PM ≅ seg QN [Given]
hypotenuse PA ≅ hypotenuse QC [Radii of the congruent circles]
∴ ∆PMA ≅ ∆QNC [Hypotenuse side test]
∴ seg AM ≅ seg CN [c. s. c. t.]
∴ AM = CN ….(i) [Length of congruent segments]
Now, seg PM ⊥ chord AB, and seg QN ⊥ chord CD
∴ AM = \(\frac { 1 }{ 2 }\)(AB) …(ii)
∴ CN = \(\frac { 1 }{ 2 }\) (CD) ..(iii) [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
∴ AB = CD [From (i), (ii) and (ii)]
∴ chord AB ≅ chord CD [Segments of equal lengths]

Class 9 Maths Digest

• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5.3 Class 9 Answers
• Practice Set 5.4 Class 9 Answers
• Practice Set 5.5 Class 9 Answers
• Problem Set 5 Class 9 Answers
• Practice Set 6.1 Class 9 Answers
• Practice Set 6.2 Class 9 Answers
• Practice Set 6.3 Class 9 Answers
• Problem Set 6 Class 9 Answers