Bhagya

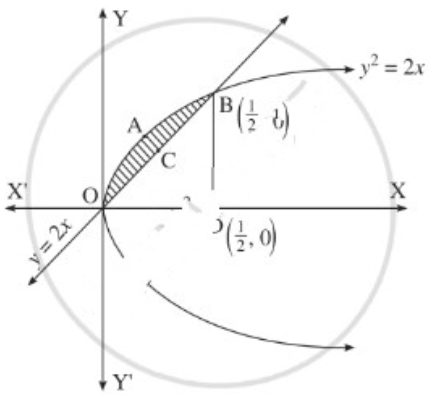
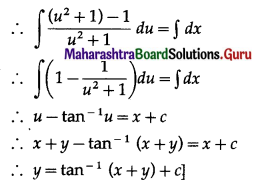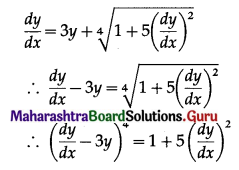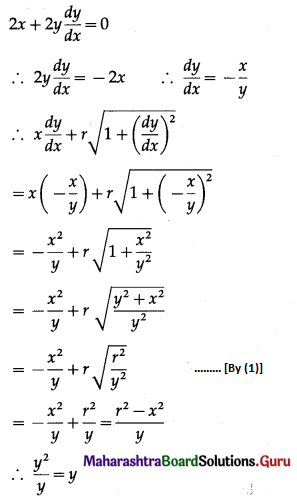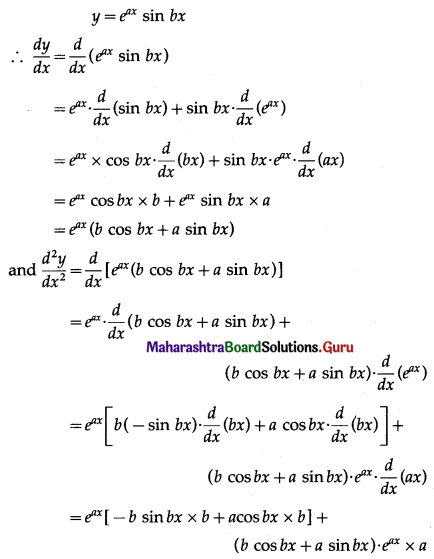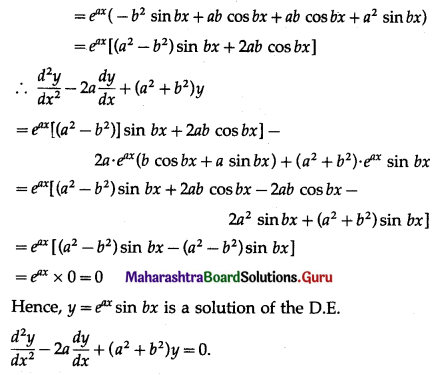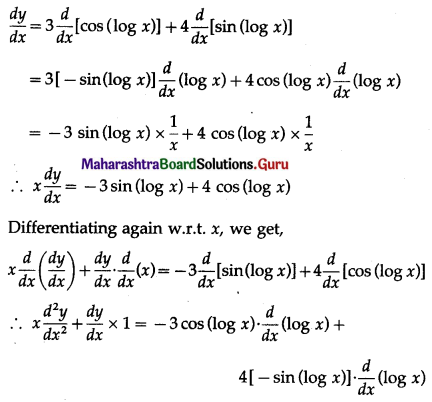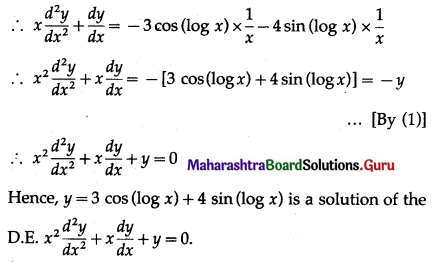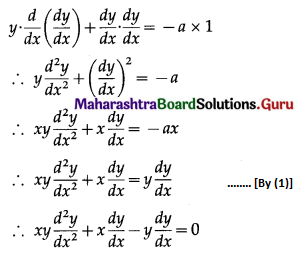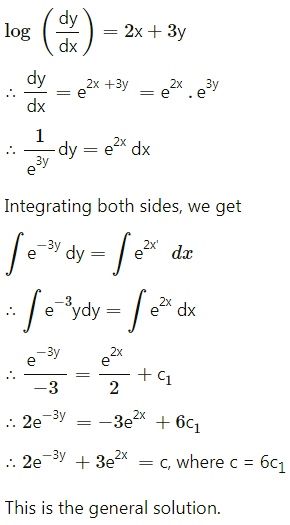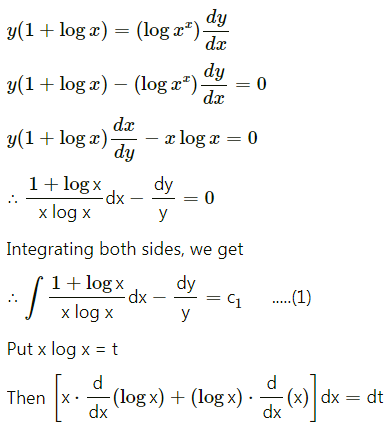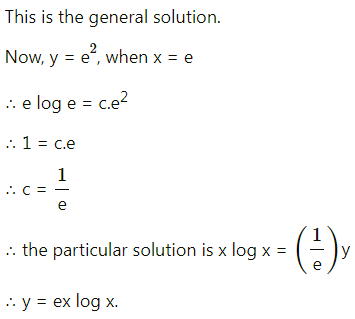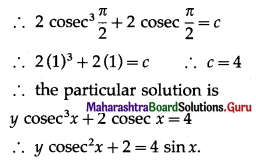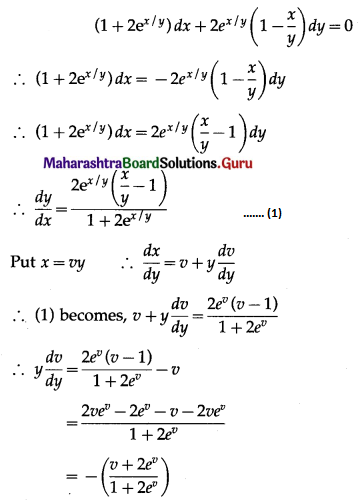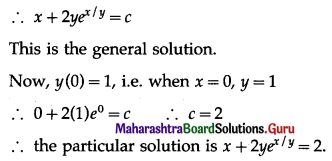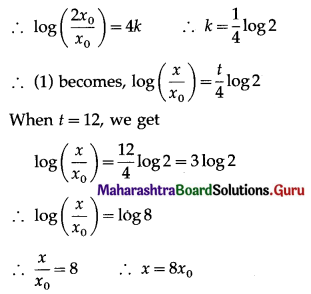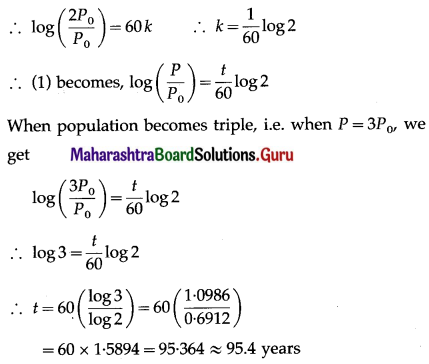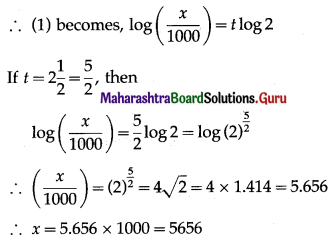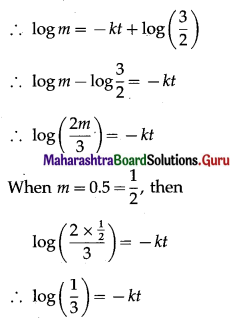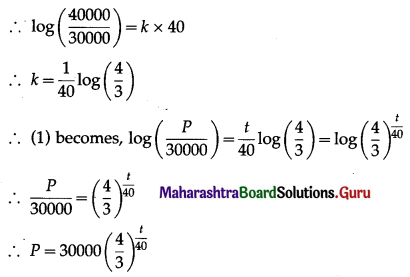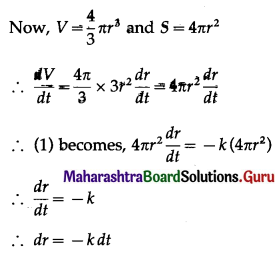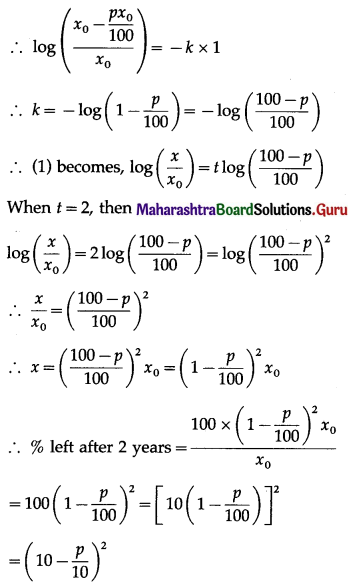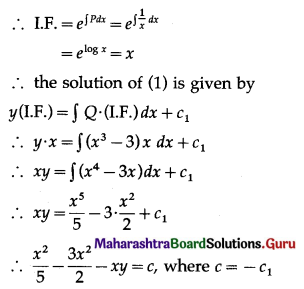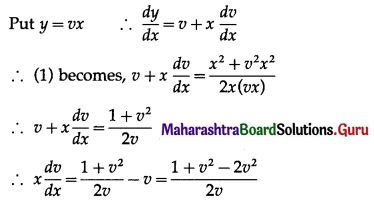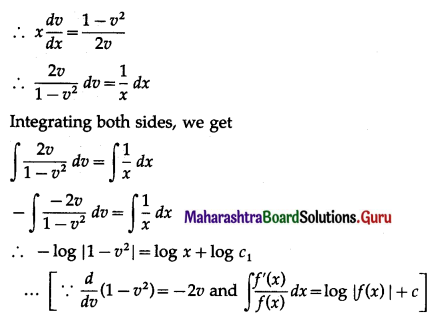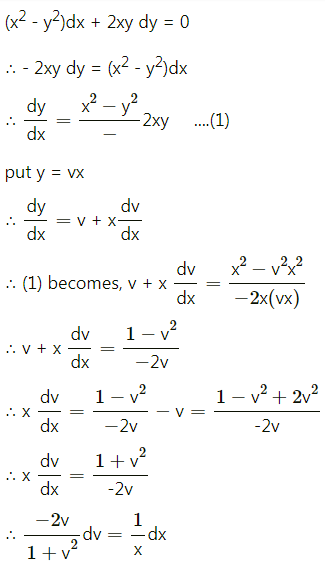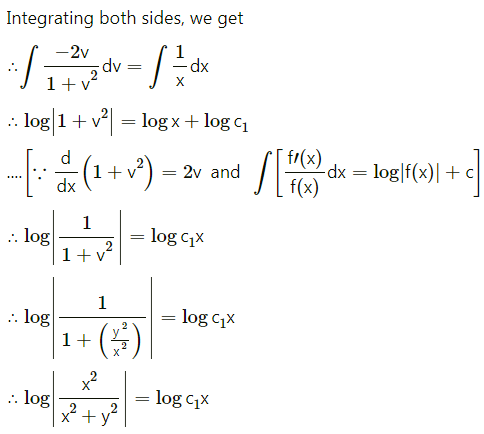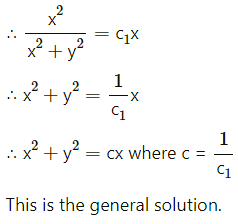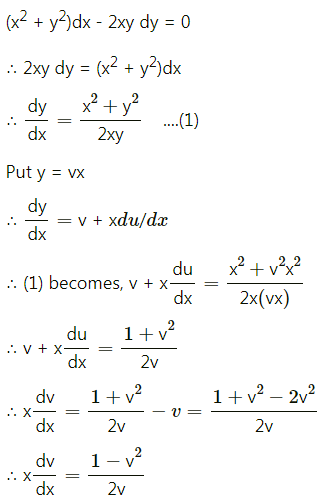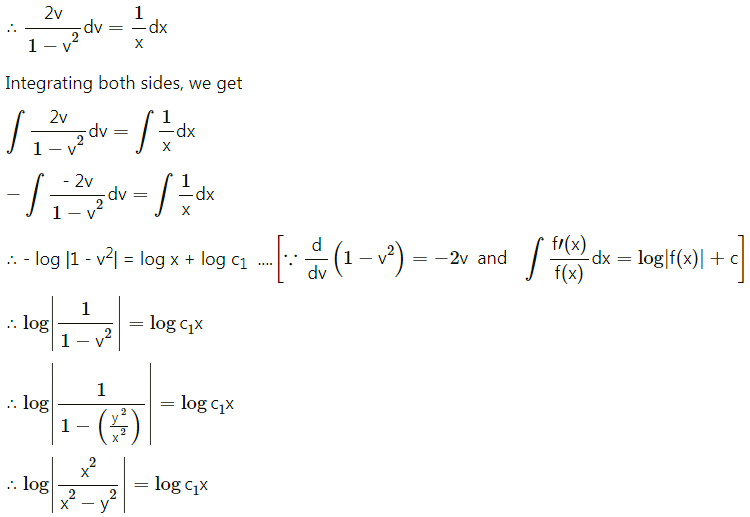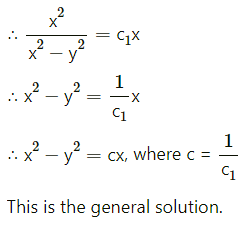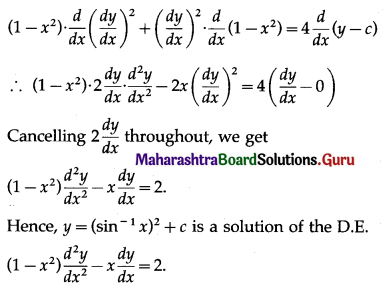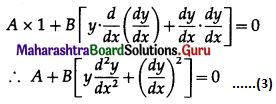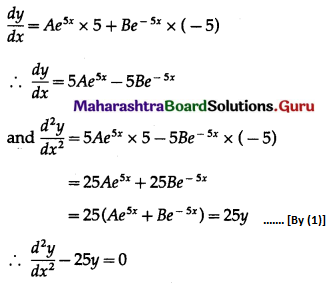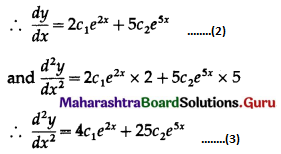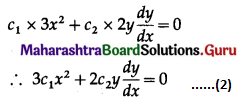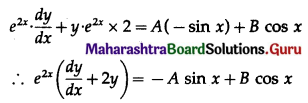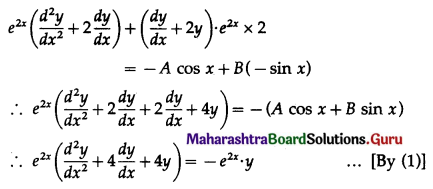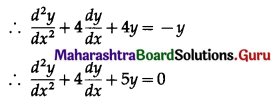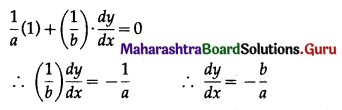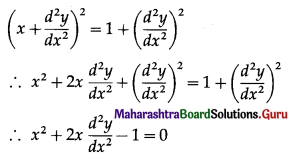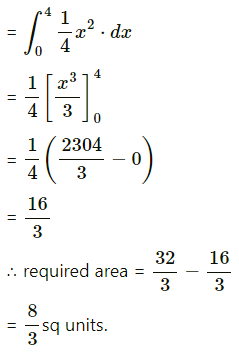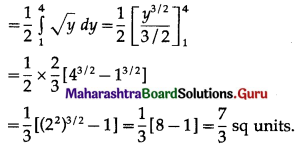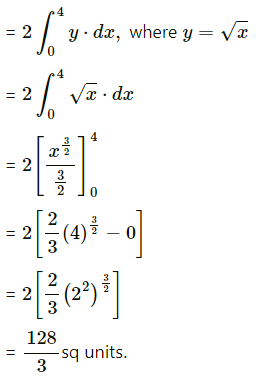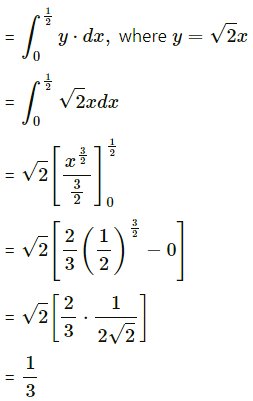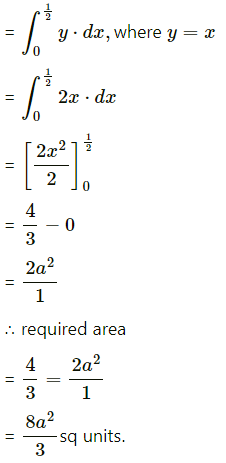Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Probability Distributions Ex 7.1 Questions and Answers.

12th Maths Part 2 Probability Distributions Exercise 7.1 Questions And Answers Maharashtra Board

Question 1.
Let X represent the difference between a number of heads and the number of tails when a coin is tossed 6 times. What are the possible values of X?
Solution:
When a coin is tossed 6 times, the number of heads can be 0, 1, 2, 3, 4, 5, 6.
The corresponding number of tails will be 6, 5, 4, 3, 2, 1, 0.
∴ X can take values 0 – 6, 1 – 5, 2 – 4, 3 – 3, 4 – 2, 5 – 1, 6 – 0
i.e. -6, -4, -2, 0, 2, 4, 6.
∴ X = {-6, -4, -2, 0, 2, 4, 6}.

Question 2.
An urn contains 5 red and 2 black balls. Two balls are drawn at random. X denotes the number of black balls drawn. What are the possible values of X?
Solution:
The urn contains 5 red and 2 black balls.
If two balls are drawn from the urn, it contains either 0 or 1 or 2 black balls.
X can take values 0, 1, 2.
∴ X = {0, 1, 2}.

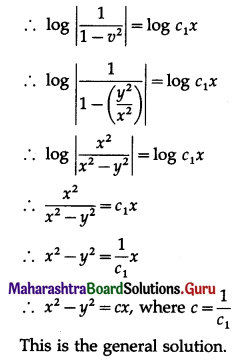
Question 3.
State which of the following are not the probability mass function of a random variable. Give reasons for your answer.

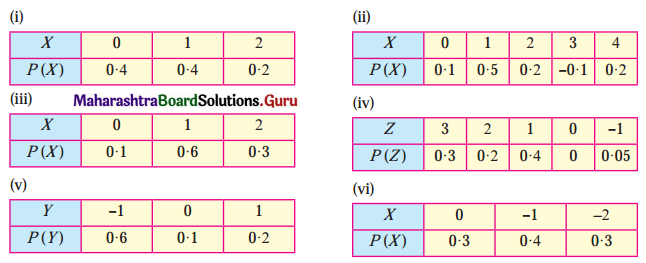
Solution:
P.m.f. of random variable should satisfy the following conditions:
(a) 0 ≤ p_i ≤ 1
(b) Σp_i = 1.

(i)

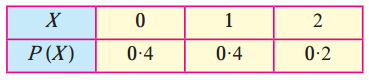
(a) Here 0 ≤ p_i ≤ 1
(b) Σp_i = 0.4 + 0.4 + 0.2 = 1
Hence, P(X) can be regarded as p.m.f. of the random variable X.

(ii)

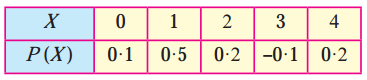
P(X = 3) = -0.1, i.e. P_i < 0 which does not satisfy 0 ≤ P_i ≤ 1
Hence, P(X) cannot be regarded as p.m.f. of the random variable X.

(iii)

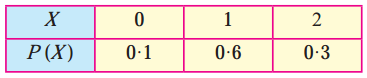
(a) Here 0 ≤ p_i ≤ 1
(b) ∑p_i = 0.1 + 0.6 + 0.3 = 1
Hence, P(X) can be regarded as p.m.f. of the random variable X.

(iv)

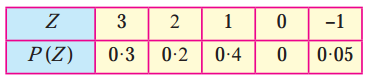
Here ∑p_i = 0.3 + 0.2 + 0.4 + 0 + 0.05 = 0.95 ≠ 1
Hence, P(Z) cannot be regarded as p.m.f. of the random variable Z.

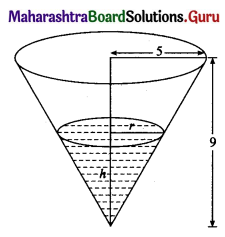
(v)

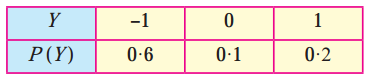
Here ∑p_i = 0.6 + 0.1 + 0.2 = 0.9 ≠ 1
Hence, P(Y) cannot be regarded as p.m.f. of the random variable Y.

(vi)

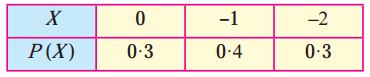
(a) Here 0 ≤ p_i ≤ 1
(b) ∑p_i = 0.3 + 0.4 + 0.3 = 1
Hence, P(X) can be regarded as p.m.f. of the random variable X.

Question 4.
Find the probability distribution of
(i) number of heads in two tosses of a coin.
(ii) number of tails in the simultaneous tosses of three coins.
(iii) number of heads in four tosses of a coin.
Solution:
(i) For two tosses of a coin the sample space is {HH, HT, TH, TT}
Let X denote the number of heads in two tosses of a coin.
Then X can take values 0, 1, 2.
∴ P[X = 0] = P(0) = \(\frac{1}{4}\)
P[X = 1] = P(1) = \(\frac{2}{4}\) = \(\frac{1}{2}\)
P[X = 2] = P(2) = \(\frac{1}{4}\)
∴ the required probability distribution is

(ii) When three coins are tossed simultaneously, then the sample space is
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Let X denotes the number of tails.
Then X can take the value 0, 1, 2, 3.
∴ P[X = 0] = P(0) = \(\frac{1}{8}\)
P[X = 1] = P(1) = \(\frac{3}{8}\)
P[X = 2] = P(2) = \(\frac{3}{8}\)
P[X = 3] = P(3) = \(\frac{1}{8}\)
∴ the required probability distribution is

(iii) When a fair coin is tossed 4 times, then the sample space is
S = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTHT, HTTH, THHT, THTH, TTHH, HTTT, THTT, TTHT, TTTH, TTTT}
∴ n(S) = 16
Let X denotes the number of heads.
Then X can take the value 0, 1, 2, 3, 4
When X = 0, then X = {TTTT}
∴ n(X) = 1
∴ P(X = 0) = \(\frac{n(X)}{n(S)}=\frac{1}{16}\)
When X = 1, then
X = {HTTT, THTT, TTHT, TTTH}
∴ n(X) = 4
∴ P(X = 1) = \(\frac{n(X)}{n(S)}=\frac{4}{16}=\frac{1}{4}\)
When X = 2, then
X = {HHTT, HTHT, HTTH, THHT, THTH, TTHH}
∴ n(X) = 6
∴ P(X = 2) = \(\frac{n(X)}{n(S)}=\frac{6}{16}=\frac{3}{8}\)
When X = 3, then
X = {HHHT, HHTH, HTHH, THHH}
∴ n(X) = 4
∴ P(X = 3) = \(\frac{n(X)}{n(S)}=\frac{4}{16}=\frac{1}{4}\)
When X = 4, then X = {HHHH}
∴ n(X) = 1
∴ P(X = 4) = \(\frac{n(X)}{n(S)}=\frac{1}{16}\)
∴ the probability distribution of X is as follows:

Question 5.
Find the probability distribution of a number of successes in two tosses of a die, where success is defined as a number greater than 4 appearing on at least one die.
Solution:
When a die is tossed twice, the sample space s has 6 × 6 = 36 sample points.
∴ n(S) = 36
The trial will be a success if the number on at least one die is 5 or 6.
Let X denote the number of dice on which 5 or 6 appears.
Then X can take values 0, 1, 2.
When X = 0 i.e., 5 or 6 do not appear on any of the dice, then
X = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}
∴ n(X) = 16.
∴ P(X = 0) = \(\frac{n(X)}{n(S)}=\frac{16}{36}=\frac{4}{9}\)
When X = 1, i.e. 5 or 6 appear on exactly one of the dice, then
X = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4)}
∴ n(X) = 16
∴ P(X = 1) = \(\frac{n(X)}{n(S)}=\frac{16}{36}=\frac{4}{9}\)
When X = 2, i.e. 5 or 6 appear on both of the dice, then
X = {(5, 5), (5, 6), (6, 5), (6, 6)}
∴ n(X) = 4
∴ P(X = 2) = \(\frac{n(X)}{n(S)}=\frac{4}{36}=\frac{1}{9}\)
∴ the required probability distribution is

Question 6.
From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.
Solution:
Here, the number of defective bulbs is the random variable.
Let the number of defective bulbs be denoted by X.
∴ X can take the value 0, 1, 2, 3, 4.
Since the draws are done with replacement, therefore the four draws are independent experiments.
Total number of bulbs is 30 which include 6 defectives.
∴ P(X = 0) = P(0) = P(all 4 non-defective bulbs)
= \(\frac{24}{30} \times \frac{24}{30} \times \frac{24}{30} \times \frac{24}{30}\)
= \(\frac{256}{625}\)
P(X = 1) = P (1) = P (1 defective and 3 non-defective bulbs)

P(X = 2) = P(2) = P(2 defective and 2 non-defective)

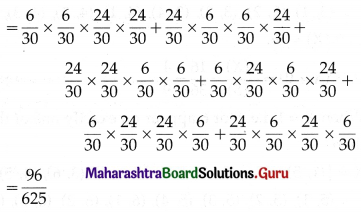
P(X = 3) = P(3) = P(3 defectives and 1 non-defective)

P(X = 4) = P(4) = P(all 4 defectives)
= \(\frac{6}{30} \times \frac{6}{30} \times \frac{6}{30} \times \frac{6}{30}\)
= \(\frac{1}{625}\)
∴ the required probability distribution is

Question 7.
A coin is biased so that the head is 3 times as likely to occur as the tail. If the coin is tossed twice. Find the probability distribution of a number of tails.
Solution:
Given a biased coin such that heads is 3 times as likely as tails.
∴ P(H) = \(\frac{3}{4}\) and P(T) = \(\frac{1}{4}\)
The coin is tossed twice.
Let X can be the random variable for the number of tails.
Then X can take the value 0, 1, 2.
∴ P(X = 0) = P(HH) = \(\frac{3}{4} \times \frac{3}{4}=\frac{9}{16}\)
P(X = 1) = P(HT, TH) = \(\frac{3}{4} \times \frac{1}{4}+\frac{1}{4} \times \frac{3}{4}=\frac{6}{16}=\frac{3}{8}\)
P(X = 2) = P(TT) = \(\frac{1}{4} \times \frac{1}{4}=\frac{1}{16}\)
∴ the required probability distribution is

Question 8.
A random variable X has the following probability distribution:

Determine:
(i) k
(ii) P(X < 3) (iii) P(X > 4)
Solution:
(i) Since P (x) is a probability distribution of x,
\(\sum_{x=0}^{7} P(x)=1\)
⇒ P(0) + P(1) + P(2) + P(3) + P(4) + P(5) + P(6) + P(7) = 1
⇒ 0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k – 1 = 0
⇒ 10k² + 10k – k – 1 = 0
⇒ 10k(k + 1) – 1(k + 1) = 0
⇒ (k + 1)(10k – 1) = 0
⇒ 10k – 1 = 0 ……..[∵ k ≠ -1]
⇒ k = \(\frac{1}{10}\)

(ii) P(X< 3) = P(0) + P(1) + P(2)
= 0 + k + 2k
= 3k
= 3(\(\frac{1}{10}\))
= \(\frac{3}{10}\)

(iii) P(0 < X < 3) = P (1) + P (2)
= k + 2k
= 3k
= 3(\(\frac{1}{10}\))
= \(\frac{3}{10}\)

Question 9.
Find expected value and variance of X for the following p.m.f.:

Solution:
We construct the following table to calculate E(X) and V(X):

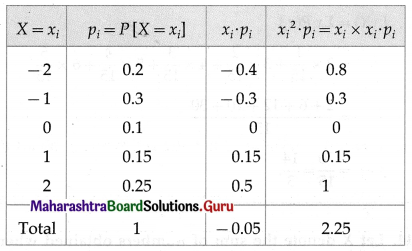
From the table,
Σx_ip_i = -0.05 and \(\Sigma x_{i}^{2} \cdot p_{i}\) = 2.25
∴ E(X) = Σx_ip_i = -0.05
and V(X) = \(\Sigma x_{i}^{2}+p_{i}-\left(\sum x_{i}+p_{i}\right)^{2}\)
= 2.25 – (-0.05)²
= 2.25 – 0.0025
= 2.2475
Hence, E(X) = -0.05 and V(X) = 2.2475.

Question 10.
Find expected value and variance of X, where X is the number obtained on the uppermost face when a fair die is thrown.
Solution:
If a die is tossed, then the sample space for the random variable X is
S = {1, 2, 3, 4, 5, 6}
∴ P(X) = \(\frac{1}{6}\); X = 1, 2, 3, 4, 5, 6.

Hence, E(X) = 3.5 and V(X) = 2.9167.

Question 11.
Find the mean number of heads in three tosses of a fair coin.
Solution:
When three coins are tossed the sample space is {HHH, HHT, THH, HTH, HTT, THT, TTH, TTT}
∴ n(S) = 8
Let X denote the number of heads when three coins are tossed.
Then X can take values 0, 1, 2, 3
P(X = 0) = P(0) = \(\frac{1}{8}\)
P(X = 1) = P(1) = \(\frac{3}{8}\)
P(X = 2) = P(2) = \(\frac{3}{8}\)
P(X = 3) = P(3) = \(\frac{1}{8}\)
∴ mean = E(X) = Σx_iP(x_i)
= \(0 \times \frac{1}{8}+1 \times \frac{3}{8}+2 \times \frac{3}{8}+3 \times \frac{1}{8}\)
= \(0+\frac{3}{8}+\frac{6}{8}+\frac{3}{8}\)
= \(\frac{12}{8}\)
= 1.5

Question 12.
Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
Solution:
When two dice are thrown, the sample space S has 6 × 6 = 36 sample points.
∴ n(S) = 36
Let X denote the number of sixes when two dice are thrown.
Then X can take values 0, 1, 2
When X = 0, then
X = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}
∴ n(X) = 25
∴ P(X = 0) = \(\frac{n(X)}{n(S)}=\frac{25}{36}\)
When X = 1, then
X = {(1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
∴ n(X) = 10
∴ P(X = 1) = \(\frac{n(X)}{n(S)}=\frac{10}{36}\)
When X = 2, then X = {(6, 6)}
∴ n(X) = 1
∴ P(X = 2) = \(\frac{n(X)}{n(S)}=\frac{1}{36}\)
∴ E(X) = ΣxiP(xi)
= \(0 \times \frac{25}{36}+1 \times \frac{10}{36}+2 \times \frac{1}{36}\)
= \(0+\frac{10}{36}+\frac{2}{36}\)
= \(\frac{1}{3}\)

Question 13.
Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers. Find E(X).
Solution:
Two numbers are chosen from the first 6 positive integers.
∴ n(S) = \({ }^{6} C_{2}=\frac{6 \times 5}{1 \times 2}\) = 15
Let X denote the larger of the two numbers.
Then X can take values 2, 3, 4, 5, 6.
When X = 2, the other positive number which is less than 2 is 1.
∴ n(X) = 1
∴ P(X = 2) = P(2) = \(\frac{n(X)}{n(S)}=\frac{1}{15}\)
When X = 3, the other positive number less than 3 can be 1 or 2 and hence can be chosen in 2 ways.
∴ n(X) = 2
P(X = 3) = P(3) = \(\frac{n(X)}{n(S)}=\frac{2}{15}\)
Similarly, P(X = 4) = P(4) = \(\frac{3}{15}\)
P(X = 5) = P(5) = \(\frac{4}{15}\)
P(X = 6) = P(6) = \(\frac{5}{15}\)
∴ E(X) = Σx_iP(x_i)
= \(2 \times \frac{1}{15}+3 \times \frac{2}{15}+4 \times \frac{3}{15}+5 \times \frac{4}{15}+6 \times \frac{5}{15}\)
= \(\frac{2+6+12+20+30}{15}\)
= \(\frac{70}{15}\)
= \(\frac{14}{3}\)

Question 14.
Let X denote the sum of numbers obtained when two fair dice are rolled. Find the standard deviation of X.
Solution:
If two fair dice are rolled then the sample space S of this experiment is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Let X denote the sum of the numbers on uppermost faces.
Then X can take the values 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

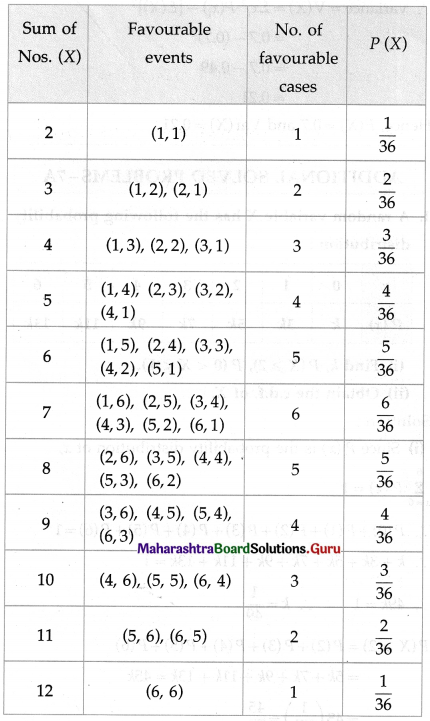
∴ the probability distribution of X is given by

Question 15.
A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. One student is selected in such a manner that each has the same chance of being chosen and the age X of the student is recorded. What is the probability distribution of the random variable X? Find mean, variance, and standard deviation of X.
Solution:
Let X denote the age of the chosen student. Then X can take values 14, 15, 16, 17, 18, 19, 20, 21.
We make a frequency table to find the number of students with age X:

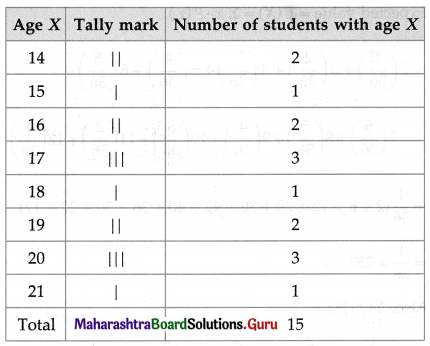
The chances of any student selected are equally likely.
If there are m students with age X, then P(X) = \(\frac{m}{15}\)
Using this, the following is the probability distribution of X:


Variance = V(X) = \(\Sigma x_{i}^{2}\) . P(x_i) – [E(X)]²
= 312.2 – (17.53)²
= 312.2 – 307.3
= 4.9
Standard deviation = √V(X) = √4.9 = 2.21
Hence, mean = 17.53, variance = 4.9 and standard deviation = 2.21.

Question 16.
In a meeting, 70% of the member’s favour and 30% oppose a certain proposal. A member is selected at random and we take X = 0 if he opposed and X = 1 if he is in favour. Find E(X) and Var(X).
Solution:
X takes values 0 and 1.
It is given that
P(X = 0) = P(0) = 30% = \(\frac{30}{100}\) = 0.3
P(X = 1) = P(1) = 70% = \(\frac{70}{100}\) = 0.7
∴ E(X) = Σx_i . P(x_i) = 0 × 0.3 + 1 × 0.7 = 0.7
Also, \(\Sigma x_{i}^{2} \cdot P\left(x_{i}\right)\) = 0 × 0.3 + 1 × 0.7 = 0.7
∴ Variance = V(X) = \(\Sigma x_{i}^{2} \cdot P\left(x_{i}\right)-[E(X)]^{2}\)
= 0.7 – (0.7)²
= 0.7 – 0.49
= 0.21
Hence, E(X) = 0.7 and Var(X) = 0.21.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 7.1 Class 12 Maths 2
• Exercise 7.2 Class 12 Maths 2
• Miscellaneous Exercise 7 Class 12 Maths 2
• Exercise 8.1 Class 12 Maths 2
• Miscellaneous Exercise 8 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Miscellaneous Exercise 6 Questions and Answers.

12th Maths Part 2 Differential Equations Miscellaneous Exercise 6 Questions And Answers Maharashtra Board

(I) Choose the correct option from the given alternatives:

Question 1.
The order and degree of the differential equation \(\sqrt{1+\left(\frac{d y}{d x}\right)^{2}}=\left(\frac{d^{2} y}{d x^{2}}\right)^{\frac{3}{2}}\) are respectively……..
(a) 2, 1
(b) 1, 2
(c) 3, 2
(d) 2, 3
Answer:
(d) 2, 3

Question 2.
The differential equation of y = c² + \(\frac{c}{x}\) is…….
(a) \(x^{4}\left(\frac{d y}{d x}\right)^{2}-x \frac{d y}{d x}=y\)
(b) \(\frac{d y}{d x^{2}}+x \frac{d y}{d x}+y=0\)
(c) \(x^{3}\left(\frac{d y}{d x}\right)^{2}+x \frac{d y}{d x}=y\)
(d) \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}-y=0\)
Answer:
(a) \(x^{4}\left(\frac{d y}{d x}\right)^{2}-x \frac{d y}{d x}=y\)

Question 3.
x² + y² = a² is a solution of ………
(a) \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}-y=0\)
(b) \(y=x \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}+a^{2} y\)
(c) \(y=x \frac{d y}{d x}+a \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}\)
(d) \(\frac{d^{2} y}{d x^{2}}=(x+1) \frac{d y}{d x}\)
Answer:
(c) \(y=x \frac{d y}{d x}+a \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}\)

Question 4.
The differential equation of all circles having their centres on the line y = 5 and touching the X-axis is
(a) \(y^{2}\left(1+\frac{d y}{d x}\right)=25\)
(b) \((y-5)^{2}\left[1+\left(\frac{d y}{d x}\right)^{2}\right]=25\)
(c) \((y-5)^{2}+\left[1+\left(\frac{d y}{d x}\right)^{2}\right]=25\)
(d) \((y-5)^{2}\left[1-\left(\frac{d y}{d x}\right)^{2}\right]=25\)
Answer:
(b) \((y-5)^{2}\left[1+\left(\frac{d y}{d x}\right)^{2}\right]=25\)

Question 5.
The differential equation y \(\frac{d y}{d x}\) + x = 0 represents family of ………
(a) circles
(b) parabolas
(c) ellipses
(d) hyperbolas
Answer:
(a) circles

Hint:
y \(\frac{d y}{d x}\) + x = 0
∴ ∫y dy + ∫x dx = c
∴ \(\frac{y^{2}}{2}+\frac{x^{2}}{2}=c\)
∴ x² + y² = 2c which is a circle.

Question 6.
The solution of \(\frac{1}{x} \cdot \frac{d y}{d x}=\tan ^{-1} x\) is……
(a) \(\frac{x^{2} \tan ^{-1} x}{2}+c=0\)
(b) x tan^-1x + c = 0
(c) x – tan^-1x = c
(d) \(y=\frac{x^{2} \tan ^{-1} x}{2}-\frac{1}{2}\left(x-\tan ^{-1} x\right)+c\)
Answer:
(d) \(y=\frac{x^{2} \tan ^{-1} x}{2}-\frac{1}{2}\left(x-\tan ^{-1} x\right)+c\)

Question 7.
The solution of (x + y)² \(\frac{d y}{d x}\) = 1 is…….
(a) x = tan^-1(x + y) + c
(b) y tan^-1(\(\frac{x}{y}\)) = c
(c) y = tan^-1(x + y) + c
(d) y + tan^-1(x + y) = c
Answer:
(c) y = tan^-1(x + y) + c

Question 8.
The Solution of \(\frac{d y}{d x}=\frac{y+\sqrt{x^{2}-y^{2}}}{2}\) is……
(a) sin^-1(\(\frac{y}{x}\)) = 2 log |x| + c
(b) sin^-1(\(\frac{y}{x}\)) = log |x| + c
(c) sin(\(\frac{x}{y}\)) = log |x| + c
(d) sin(\(\frac{y}{x}\)) = log |y| + c
Answer:
(b) sin^-1(\(\frac{y}{x}\)) = log |x| + c

Question 9.
The solution of \(\frac{d y}{d x}\) + y = cos x – sin x is……
(a) y e^x = cos x + c
(b) y e^x + e^x cos x = c
(c) y e^x = e^x cos x + c
(d) y² e^x = e^x cos x + c
Answer:
(c) y e^x = e^x cos x + c
Hint:
\(\frac{d y}{d x}\) + y = cos x – sin x
I.F. = \(e^{\int 1 d x}=e^{x}\)
∴ the solution is y . e^x = ∫(cos x – sin x) e^x + c
∴ y . e^x = e^x cos x + c

Question 10.
The integrating factor of linear differential equation x \(\frac{d y}{d x}\) + 2y = x² log x is……..
(a) \(\frac{1}{x}\)
(b) k
(c) \(\frac{1}{n^{2}}\)
(d) x²
Answer:
(d) x²
Hint:
I.F. = \(e^{\int \frac{2}{x} d x}\)
= e^{2 log x}
= x²

Question 11.
The solution of the differential equation \(\frac{d y}{d x}\) = sec x – y tan x is…….
(a) y sec x + tan x = c
(b) y sec x = tan x + c
(c) sec x + y tan x = c
(d) sec x = y tan x + c
Answer:
(b) y sec x = tan x + c

Hint:
\(\frac{d y}{d x}\) = sec x – y tan x
∴ \(\frac{d y}{d x}\) + y tan x = sec x
I.F. = \(e^{\int \tan x d x}=e^{\log \sec x}\) = sec x
∴ the solution is
y . sec x = ∫sec x . sec x dx + c
∴ y sec x = tan x + c

Question 12.
The particular solution of \(\frac{d y}{d x}=x e^{y-x}\), when x = y = 0 is……
(a) e^x-y = x + 1
(b) e^x+y = x + 1
(c) e^x + e^y = x + 1
(d) e^y-x = x – 1
Answer:
(a) e^x-y = x + 1

Question 13.
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) is a solution of……..
(a) \(\frac{d^{2} y}{d x^{2}}+y x+\left(\frac{d y}{d x}\right)^{2}=0\)
(b) \(x y \frac{d^{2} y}{d x^{2}}+2\left(\frac{d y}{d x}\right)^{2}-y \frac{d y}{d x}=0\)
(c) \(y \frac{d^{2} y}{d x^{2}}+2\left(\frac{d y}{d x}\right)^{2}+y=0\)
(d) \(x y \frac{d y}{d x}+y \frac{d^{2} y}{d x^{2}}=0\)
Answer:
(b) \(x y \frac{d^{2} y}{d x^{2}}+2\left(\frac{d y}{d x}\right)^{2}-y \frac{d y}{d x}=0\)

Question 14.
The decay rate of certain substances is directly proportional to the amount present at that instant. Initially, there are 27 grams of substance and 3 hours later it is found that 8 grams left. The amount left after one more hour is……
(a) 5\(\frac{2}{3}\) grams
(b) 5\(\frac{1}{3}\) grams
(c) 5.1 grams
(d) 5 grams
Answer:
(b) 5\(\frac{1}{3}\) grams

Question 15.
If the surrounding air is kept at 20°C and the body cools from 80°C to 70°C in 5 minutes, the temperature of the body after 15 minutes will be…..
(a) 51.7°C
(b) 54.7°C
(c) 52.7°C
(d) 50.7°C
Answer:
(b) 54.7°C

(II) Solve the following:

Question 1.
Determine the order and degree of the following differential equations:
(i) \(\frac{d^{2} y}{d x^{2}}+5 \frac{d y}{d x}+y=x^{3}\)
Solution:
The given D.E. is \(\frac{d^{2} y}{d x^{2}}+5 \frac{d y}{d x}+y=x^{3}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. is of order 2 and degree 1.

(ii) \(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}=\sqrt[5]{1+\frac{d y}{d x}}\)
Solution:
The given D.E. is \(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}=\sqrt[5]{1+\frac{d y}{d x}}\)
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{2 \times 5}=1+\frac{d y}{d x}\)
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{10}=1+\frac{d y}{d x}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 10.
∴ the given D.E. is of order 3 and degree 10.

(iii) \(\sqrt[3]{1+\left(\frac{d y}{d x}\right)^{2}}=\frac{d^{2} y}{d x^{2}}\)
Solution:
The given D.E. is \(\sqrt[3]{1+\left(\frac{d y}{d x}\right)^{2}}=\frac{d^{2} y}{d x^{2}}\)
On cubing both sides, we get
\(1+\left(\frac{d y}{d x}\right)^{2}=\left(\frac{d^{2} y}{d x^{2}}\right)^{3}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 3.
∴ the given D.E. is of order 2 and degree 3.

(iv) \(\frac{d y}{d x}=3 y+\sqrt[4]{1+5\left(\frac{d y}{d x}\right)^{2}}\)
Solution:
The given D.E. is

This D.E. has the highest order derivative \(\frac{d y}{d x}\) with power 4.
∴ the given D.E. is of order 1 and degree 4.

(v) \(\frac{d^{4} y}{d x^{4}}+\sin \left(\frac{d y}{d x}\right)=0\)
Solution:
The given D.E. is \(\frac{d^{4} y}{d x^{4}}+\sin \left(\frac{d y}{d x}\right)=0\)
This D.E. has highest order derivative \(\frac{d^{4} y}{d x^{4}}\).
∴ order = 4
Since this D.E. cannot be expressed as a polynomial in differential coefficient, the degree is not defined.

Question 2.
In each of the following examples verify that the given function is a solution of the differential equation.
(i) \(x^{2}+y^{2}=r^{2} ; x \frac{d y}{d x}+r \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}=y\)
Solution:
x² + y² = r² ……. (1)
Differentiating both sides w.r.t. x, we get

Hence, x² + y² = r² is a solution of the D.E.
\(x \frac{d y}{d x}+r \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}=y\)

(ii) y = e^ax sin bx; \(\frac{d^{2} y}{d x^{2}}-2 a \frac{d y}{d x}+\left(a^{2}+b^{2}\right) y=0\)
Solution:

(iii) y = 3 cos(log x) + 4 sin(log x); \(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\)
Solution:
y = 3 cos(log x) + 4 sin (log x) …… (1)
Differentiating both sides w.r.t. x, we get

(iv) xy = ae^x + be^-x + x²; \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+x^{2}=x y+2\)
Solution:

(v) x² = 2y² log y, x² + y² = xy \(\frac{d x}{d y}\)
Solution:
x² = 2y² log y ……(1)
Differentiating both sides w.r.t. y, we get

∴ x² + y² = xy \(\frac{d x}{d y}\)
Hence, x² = 2y² log y is a solution of the D.E.
x² + y² = xy \(\frac{d x}{d y}\)

Question 3.
Obtain the differential equation by eliminating the arbitrary constants from the following equations:
(i) y² = a(b – x)(b + x)
Solution:
y² = a(b – x)(b + x) = a(b² – x²)
Differentiating both sides w.r.t. x, we get
2y \(\frac{d y}{d x}\) = a(0 – 2x) = -2ax
∴ y \(\frac{d y}{d x}\) = -ax …….(1)
Differentiating again w.r.t. x, we get

This is the required D.E.

(ii) y = a sin(x + b)
Solution:
y = a sin(x + b)

This is the required D.E.

(iii) (y – a)² = b(x + 4)
Solution:
(y – a)² = b(x + 4) …….(1)
Differentiating both sides w.r.t. x, we get
\(2(y-a) \cdot \frac{d}{d x}(y-a)=b \frac{d}{d x}(x+4)\)

(iv) y = \(\sqrt{a \cos (\log x)+b \sin (\log x)}\)
Solution:
y = \(\sqrt{a \cos (\log x)+b \sin (\log x)}\)
∴ y² = a cos (log x) + b sin (log x) …….(1)
Differentiating both sides w.r.t. x, we get

(v) y = Ae^3x+1 + Be^-3x+1
Solution:
y = Ae^3x+1 + Be^-3x+1 …… (1)
Differentiating twice w.r.t. x, we get

This is the required D.E.

Question 4.
Form the differential equation of:
(i) all circles which pass through the origin and whose centres lie on X-axis.
Solution:

Let C (h, 0) be the centre of the circle which pass through the origin. Then radius of the circle is h.
∴ equation of the circle is (x – h)² + (y – 0)² = h²
∴ x² – 2hx + h² + y² = h²
∴ x² + y² = 2hx ……..(1)
Differentiating both sides w.r.t. x, we get
2x + 2y \(\frac{d y}{d x}\) = 2h
Substituting the value of 2h in equation (1), we get
x² + y² = (2x + 2y \(\frac{d y}{d x}\)) x
∴ x² + y² = 2x² + 2xy \(\frac{d y}{d x}\)
∴ 2xy \(\frac{d y}{d x}\) + x² – y² = 0
This is the required D.E.

(ii) all parabolas which have 4b as latus rectum and whose axis is parallel to Y-axis.
Solution:
Let A(h, k) be the vertex of the parabola which has 4b as latus rectum and whose axis is parallel to the Y-axis.
Then equation of the parabola is
(x – h)² = 4b(y – k) ……. (1)
where h and k are arbitrary constants.

Differentiating both sides of (1) w.r.t. x, we get
2(x – h). \(\frac{d}{d x}\)(x – h) = 4b . \(\frac{d}{d x}\)(y – k)
∴ 2(x – h) x (1 – 0) = 4b(\(\frac{d y}{d x}\) – 0)
∴ (x – h) = 2b \(\frac{d y}{d x}\)
Differentiating again w.r.t. x, we get
1 – 0 = 2b \(\frac{d^{2} y}{d x^{2}}\)
∴ 2b \(\frac{d^{2} y}{d x^{2}}\) – 1 = 0
This is the required D.E.

(iii) an ellipse whose major axis is twice its minor axis.
Solution:
Let 2a and 2b be lengths of the major axis and minor axis of the ellipse.
Then 2a = 2(2b)
∴ a = 2b
∴ equation of the ellipse is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ \(\frac{x^{2}}{(2 b)^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ \(\frac{x^{2}}{4 b^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ x² + 4y² = 4b²
Differentiating w.r.t. x, we get
2x + 4 × 2y \(\frac{d y}{d x}\) = 0
∴ x + 4y \(\frac{d y}{d x}\) = 0
This is the required D.E.

(iv) all the lines which are normal to the line 3x + 2y + 7 = 0.
Solution:
Slope of the line 3x – 2y + 7 = 0 is \(\frac{-3}{-2}=\frac{3}{2}\).
∴ slope of normal to this line is \(-\frac{2}{3}\)
Then the equation of the normal is
y = \(-\frac{2}{3}\)x + k, where k is an arbitrary constant.
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=-\frac{2}{3} \times 1+0\)
∴ 3\(\frac{d y}{d x}\) + 2 = 0
This is the required D.E.

(v) the hyperbola whose length of transverse and conjugate axes are half of that of the given hyperbola \(\frac{x^{2}}{16}-\frac{y^{2}}{36}=k\).
Solution:
The equation of the hyperbola is \(\frac{x^{2}}{16}-\frac{y^{2}}{36}=k\)
i.e., \(\frac{x^{2}}{16 k}-\frac{y^{2}}{36 k}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a² = 16k, b² = 36k
∴ a = 4√k, b = 6√k
∴ l(transverse axis) = 2a = 8√k
and l(conjugate axis) = 2b = 12√k
Let 2A and 2B be the lengths of the transverse and conjugate axes of the required hyperbola.
Then according to the given condition
2A = a = 4√k and 2B = b = 6√k
∴ A = 2√k and B = 3√k
∴ equation of the required hyperbola is
\(\frac{x^{2}}{A^{2}}-\frac{y^{2}}{B^{2}}=1\)
i.e., \(\frac{x^{2}}{4 k}-\frac{y^{2}}{9 k}=1\)
∴ 9x² – 4y² = 36k, where k is an arbitrary constant.
Differentiating w.r.t. x, we get
9 × 2x – 4 × 2y \(\frac{d y}{d x}\) = 0
∴ 9x – 4y \(\frac{d y}{d x}\) = 0
This is the required D.E.

Question 5.
Solve the following differential equations:
(i) log(\(\frac{d y}{d x}\)) = 2x + 3y
Solution:

(ii) \(\frac{d y}{d x}\) = x²y + y
Solution:

(iii) \(\frac{d y}{d x}=\frac{2 y-x}{2 y+x}\)
Solution:

(iv) x dy = (x + y + 1) dx
Solution:

(v) \(\frac{d y}{d x}\) + y cot x = x² cot x + 2x
Solution:
\(\frac{d y}{d x}\) + y cot x = x cot x + 2x ……..(1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q, where P = cot x and Q = x² cot x + 2x
∴ I.F. = \(e^{\int P d x}\)
= \(e^{\int \cot x d x}\)
= \(e^{\log (\sin x)}\)
= sin x
∴ the solution of (1) is given by
y(I.F.) = ∫Q . (I.F.) dx + c
∴ y sin x = ∫(x² cot x + 2x) sin x dx + c
∴ y sinx = ∫(x² cot x . sin x + 2x sin x) dx + c
∴ y sinx = ∫x² cos x dx + 2∫x sin x dx + c
∴ y sinx = x² ∫cos x dx – ∫[\(\frac{d}{d x}\left(x^{2}\right)\) ∫cos x dx] dx + 2∫x sin x dx + c
∴ y sin x = x² (sin x) – ∫2x(sin x) dx + 2∫x sin x dx + c
∴ y sin x = x² sin x – 2∫x sin x dx + 2∫x sin x dx + c
∴ y sin x = x² sin x + c
∴ y = x² + c cosec x
This is the general solution.

(vi) y log y = (log y² – x) \(\frac{d y}{d x}\)
Solution:

(vii) 4 \(\frac{d x}{d y}\) + 8x = 5e^-3y
Solution:

Question 6.
Find the particular solution of the following differential equations:
(i) y(1 + log x) = (log xx) \(\frac{d y}{d x}\), when y(e) = e²
Solution:

(ii) (x + 2y²) \(\frac{d y}{d x}\) = y, when x = 2, y = 1
Solution:


This is the general solution.
When x = 2, y = 1, we have
2 = 2(1)² + c(1)
∴ c = 0
∴ the particular solution is x = 2y².

(iii) \(\frac{d y}{d x}\) – 3y cot x = sin 2x, when y(\(\frac{\pi}{2}\)) = 2
Solution:
\(\frac{d y}{d x}\) – 3y cot x = sin 2x
\(\frac{d y}{d x}\) = (3 cot x) y = sin 2x ……..(1)
This is the linear differential equation of the form

(iv) (x + y) dy + (x – y) dx = 0; when x = 1 = y
Solution:

(v) \(2 e^{\frac{x}{y}} d x+\left(y-2 x e^{\frac{x}{y}}\right) d y=0\), when y(0) = 1
Solution:

Question 7.
Show that the general solution of defferential equation \(\frac{d y}{d x}+\frac{y^{2}+y+1}{x^{2}+x+1}=0\) is given by (x + y + 1) = c(1 – x – y – 2xy).
Solution:

Question 8.
The normal lines to a given curve at each point (x, y) on the curve pass through (2, 0). The curve passes through (2, 3). Find the equation of the curve.
Solution:
Let P(x, y) be a point on the curve y = f(x).
Then slope of the normal to the curve is \(-\frac{1}{\left(\frac{d y}{d x}\right)}\)
∴ equation of the normal is

This is the general equation of the curve.
Since, the required curve passed through the point (2, 3), we get
2² + 3² = 4(2) + c
∴ c = 5
∴ equation of the required curve is x² + y² = 4x + 5.

Question 9.
The volume of a spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after t seconds.
Solution:
Let r be the radius and V be the volume of the spherical balloon at any time t.
Then the rate of change in volume of the spherical balloon is \(\frac{d V}{d t}\) which is a constant.


Hence, the radius of the spherical balloon after t seconds is \((63 t+27)^{\frac{1}{3}}\) units.

Question 10.
A person’s assets start reducing in such a way that the rate of reduction of assets is proportional to the square root of the assets existing at that moment. If the assets at the beginning are ₹ 10 lakhs and they dwindle down to ₹ 10,000 after 2 years, show that the person will be bankrupt in 2\(\frac{2}{9}\) years from the start.
Solution:
Let x be the assets of the presort at time t years.
Then the rate of reduction is \(\frac{d x}{d t}\) which is proportional to √x.
∴ \(\frac{d x}{d t}\) ∝ √x
∴ \(\frac{d x}{d t}\) = -k√x, where k > 0
∴ \(\frac{d x}{\sqrt{x}}\) = -k dt
Integrating both sides, we get
\(\int x^{-\frac{1}{2}} d x\) = -k∫dt
∴ \(\frac{x^{\frac{1}{2}}}{\left(\frac{1}{2}\right)}\) = -kt + c
∴ 2√x = -kt + c
At the beginning, i.e. at t = 0, x = 10,00,000
2√10,00,000 = -k(0) + c
∴ c = 2000
∴ 2√x = -kt + 2000 ……..(1)
Also, when t = 2, x = 10,000
∴ 2√10000 = -k × 2 + 2000
∴ 2k = 1800
∴ k = 900
∴ (1) becomes,
∴ 2√x = -900t + 2000
When the person will be bankrupt, x = 0
∴ 0 = -900t + 2000
∴ 900t = 2000
∴ t = \(\frac{20}{9}=2 \frac{2}{9}\)
Hence, the person will be bankrupt in \(2 \frac{2}{9}\) years.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 6.1 Class 12 Maths 2
• Exercise 6.2 Class 12 Maths 2
• Exercise 6.3 Class 12 Maths 2
• Exercise 6.4 Class 12 Maths 2
• Exercise 6.5 Class 12 Maths 2
• Exercise 6.6 Class 12 Maths 2
• Miscellaneous Exercise 6 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.6 Questions and Answers.

12th Maths Part 2 Differential Equations Exercise 6.6 Questions And Answers Maharashtra Board

Question 1.
In a certain culture of bacteria, the rate of increase is proportional to the number present. If it is found that the number doubles in 4 hours, find the number of times the bacteria are increased in 12 hours.
Solution:
Let x be the number of bacteria in the culture at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
\(\int \frac{d x}{x}\) = k∫dt + c
∴ log x = kt + c
Initially, i.e. when t = 0, let x = x₀
log x₀ = k × 0 + c
∴ c = log x₀
∴ log x = kt + log x₀
∴ log x – log x₀ = kt
∴ log(\(\frac{x}{x_{0}}\)) = kt ………(1)
Since the number doubles in 4 hours, i.e. when t = 4, x = 2x₀

∴ the number of bacteria will be 8 times the original number in 12 hours.

Question 2.
If the population of a country doubles in 60 years; in how many years will it be triple (treble) under the assumption that the rate of increase is proportional to the number of inhabitants?
[Given log 2 = 0.6912, log 3 = 1.0986]
Solution:
Let P be the population at time t years.
Then \(\frac{d P}{d t}\), the rate of increase of population is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant
∴ \(\frac{d P}{P}\) = k dt
On integrating, we get
\(\int \frac{d P}{P}\) = k∫dt + c
∴ log P = kt + c
Initially i.e. when t = 0, let P = P₀
∴ log P₀ = k x 0 + c
∴ c = log P₀
∴ log P = kt + log P₀
∴ log P – log P₀ = kt
∴ log(\(\frac{P}{P_{0}}\)) = kt ……(1)
Since, the population doubles in 60 years, i.e. when t = 60, P = 2P₀

∴ the population becomes triple in 95.4 years (approximately).

Question 3.
If a body cools from 80°C to 50°C at room temperature of 25°C in 30 minutes, find the temperature of the body after 1 hour.
Solution:
Let θ°C be the temperature of the body at time t minutes.
The room temperature is given to be 25°C.
Then by Newton’s law of cooling, \(\frac{d \theta}{d t}\), the rate of change of temperature, is proportional to (θ – 25).


∴ the temperature of the body will be 36.36°C after 1 hour.

Question 4.
The rate of growth of bacteria is proportional to the number present. If initially, there were 1000 bacteria and the number doubles in 1 hour, find the number of bacteria after 2½ hours. [Take √2 = 1.414]
Solution:
Let x be the number of bacteria at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
\(\int \frac{d x}{x}\) = k∫dt + c
∴ log x = kt + c
Initially, i.e. when t = 0, x = 1000
∴ log 1000 = k × 0 + c
∴ c = log 1000
∴ log x = kt + log 1000
∴ log x – log 1000 = kt
∴ log(\(\frac{x}{1000}\)) = kt ……(1)
Now, when t = 1, x = 2 × 1000 = 2000
∴ log(\(\frac{2000}{1000}\)) = k
∴ k = log 2

∴ the number of bacteria after 2½ hours = 5656.

Question 5.
The rate of disintegration of a radioactive element at any time t is proportional to its mass at that time. Find the time during which the original mass of 1.5 gm will disintegrate into its mass of 0.5 gm.
Solution:
Let m be the mass of the radioactive element at time t.
Then the rate of disintegration is \(\frac{d m}{d t}\) which is proportional to m.


∴ log(3)^-1 = -kt
∴ -log 3 = -kt
∴ t = \(\frac{1}{k}\) log 3
∴ the original mass will disintegrate to 0.5 gm when t = \(\frac{1}{k}\) log 3

Question 6.
The rate of decay of certain substances is directly proportional to the amount present at that instant. Initially, there is 25 gm of certain substance and two hours later it is found that 9 gm are left. Find the amount left after one more hour.
Solution:
Let x gm be the amount of the substance left at time t.
Then the rate of decay is \(\frac{d x}{d t}\), which is proportional to x.


∴ \(\frac{x}{25}=\frac{27}{125}\)
∴ x = \(\frac{27}{5}\)
∴ the amount left after 3 hours \(\frac{27}{5}\) gm.

Question 7.
Find the population of a city at any time t, given that the rate of increase of population is proportional to the population at that instant and that in a period of 40 years, the population increased from 30,000 to 40,000.
Solution:
Let P be the population of the city at time t.
Then \(\frac{d P}{d t}\), the rate of increase of population is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant.
∴ \(\frac{d P}{P}\) = k dt
On integrating, we get
\(\int \frac{1}{P} d P\) = k∫dt + c
∴ log P = kt + c
Initially, i.e. when t = 0, P = 30000
∴ log 30000 = k × 0 + c
∴ c = log 30000
∴ log P = kt + log 30000
∴ log P – log 30000 = kt
∴ log(\(\frac{P}{30000}\)) = kt …….(1)
Now, when t = 40, P = 40000

∴ the population of the city at time t = 30000\(\left(\frac{4}{3}\right)^{\frac{t}{40}}\).

Question 8.
A body cools according to Newton’s law from 100°C to 60°C in 20 minutes. The temperature of the surroundings is 20°C. How long will it take to cool down to 30°C?
Solution:
Let θ°C be the temperature of the body at time t.
The temperature of the surrounding is given to be 20°C.
According to Newton’s law of cooling


∴ the body will cool down to 30°C in 60 minutes, i.e. in 1 hour.

Question 9.
A right circular cone has a height of 9 cm and a radius of the base of 5 cm. It is inverted and water is poured into it. If at any instant the water level rises at the rate of \(\left(\frac{\pi}{A}\right)\) cm/sec, where A is the area of the water surface
at that instant, show that the vessel will be full in 75 seconds.
Solution:

Let r be the radius of the water surface and h be the height of the water at time t.
∴ area of the water surface A = πr² sq cm.
Since height of the right circular cone is 9 cm and radius of the base is 5 cm.
\(\frac{r}{h}=\frac{5}{9}\)
∴ r = \(\frac{5}{9} h\)
∴ area of water surface, i.e. A = \(\pi\left(\frac{5}{9} h\right)^{2}\)
∴ A = \(\frac{25 \pi h^{2}}{81}\) ……..(1)
The water level, i.e. the rate of change of h is \(\frac{d h}{d t}\) rises at the rate of \(\left(\frac{\pi}{A}\right)\) cm/sec.

∴ t = \(\frac{81 \times 9 \times 25}{3 \times 81}\) = 75
Hence, the vessel will be full in 75 seconds.

Question 10.
Assume that a spherical raindrop evaporates at a rate proportional to its surface area. If its radius originally is 3 mm and 1 hour later has been reduced to 2 mm, find an expression for the radius of the raindrop at any time t.
Solution:
Let r be the radius, V be the volume and S be the surface area of the spherical raindrop at time t.
Then V = \(\frac{4}{3}\)πr³ and S = 4πr²
The rate at which the raindrop evaporates is \(\frac{d V}{d t}\) which is proportional to the surface area.
∴ \(\frac{d V}{d t}\) ∝ S
∴ \(\frac{d V}{d t}\) = -kS, where k > 0 ………(1)

On integrating, we get
∫dr = -k∫dt + c
∴ r = -kt + c
Initially, i.e. when t = 0, r = 3
∴ 3 = -k × 0 + c
∴ c = 3
∴ r = -kt + 3
When t = 1, r = 2
∴ 2 = -k × 1 + 3
∴ k = 1
∴ r = -t + 3
∴ r = 3 – t, where 0 ≤ t ≤ 3.
This is the required expression for the radius of the raindrop at any time t.

Question 11.
The rate of growth of the population of a city at any time t is proportional to the size of the population. For a certain city, it is found that the constant of proportionality is 0.04. Find the population of the city after 25 years, if the initial population is 10,000. [Take e = 2.7182]
Solution:
Let P be the population of the city at time t.
Then the rate of growth of population is \(\frac{d P}{d t}\) which is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k = 0.04
∴ \(\frac{d P}{d t}\) = (0.04)P
∴ \(\frac{1}{P}\) dP = (0.04)dt
On integrating, we get
\(\int \frac{1}{P} d P\) = (0.04) ∫dt + c
∴ log P = (0.04)t + c
Initially, i.e., when t = 0, P = 10000
∴ log 10000 = (0.04) × 0 + c
∴ c = log 10000
∴ log P = (0.04)t + log 10000
∴ log P – log 10000 = (0.04)t
∴ log(\(\frac{P}{10000}\)) = (0.04)t
When t = 25, then
∴ log(\(\frac{P}{10000}\)) = 0.04 × 25 = 1
∴ log(\(\frac{P}{10000}\)) = log e ……[∵ log e = 1]
∴ \(\frac{P}{10000}\) = e = 2.7182
∴ P = 2.7182 × 10000 = 27182
∴ the population of the city after 25 years will be 27,182.

Question 12.
Radium decomposes at a rate proportional to the amount present at any time. If p percent of the amount disappears in one year, what percent of the amount of radium will be left after 2 years?
Solution:
Let x be the amount of the radium at time t.
Then the rate of decomposition is \(\frac{d x}{d t}\) which is proportional to x.


Hence, \(\left(10-\frac{p}{10}\right)^{2} \%\) of the amount will be left after 2 years.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 6.1 Class 12 Maths 2
• Exercise 6.2 Class 12 Maths 2
• Exercise 6.3 Class 12 Maths 2
• Exercise 6.4 Class 12 Maths 2
• Exercise 6.5 Class 12 Maths 2
• Exercise 6.6 Class 12 Maths 2
• Miscellaneous Exercise 6 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.5 Questions and Answers.

12th Maths Part 2 Differential Equations Exercise 6.5 Questions And Answers Maharashtra Board

Question 1.
Solve the following differential equations:
(i) \(\frac{d y}{d x}+\frac{y}{x}=x^{3}-3\)
Solution:
\(\frac{d y}{d x}+\frac{y}{x}=x^{3}-3\) …….(1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + P . y = Q, where P = \(\frac{1}{x}\) and Q = x³ – 3

This is the general solution.

(ii) cos²x . \(\frac{d y}{d x}\) + y = tan x
Solution:

(iii) (x + 2y³) \(\frac{d y}{d x}\) = y
Solution:

(iv) \(\frac{d y}{d x}\) + y . sec x = tan x
Solution:
\(\frac{d y}{d x}\) + y sec x = tan x
∴ \(\frac{d y}{d x}\) + (sec x) . y = tan x ……..(1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + P . y = Q, where P = sec x and Q = tan x
∴ I.F. = \(e^{\int P d x}\)
= \(e^{\int \sec x d x}\)
= \(e^{\log (\sec x+\tan x)}\)
= sec x + tan x
∴ the solution of (1) is given by
y (I.F.) = ∫Q . (I.F.) dx + c
∴ y(sec x + tan x) = ∫tan x (sec x + tan x) dx + c
∴ (sec x + tan x) . y = ∫(sec x tan x + tan²x) dx + c
∴ (sec x + tan x) . y = ∫(sec x tan x + sec²x – 1) dx + c
∴ (sec x + tan x) . y = sec x + tan x – x + c
∴ y(sec x + tan x) = sec x + tan x – x + c
This is the general solution.

(v) x \(\frac{d y}{d x}\) + 2y = x² . log x
Solution:

(vi) (x + y) \(\frac{d y}{d x}\) = 1
Solution:
(x + y) \(\frac{d y}{d x}\) = 1
∴ \(\frac{d x}{d y}\) = x + y
∴ \(\frac{d x}{d y}\) – x = y
∴ \(\frac{d x}{d y}\) + (-1) x = y ……….(1)
This is the linear differential equation of the form

This is the general solution.

(vii) (x + a) \(\frac{d y}{d x}\) – 3y = (x + a)⁵
Solution:

(viii) dr + (2r cot θ + sin 2θ) dθ = 0
Solution:
dr + (2r cot θ + sin 2θ) dθ = 0
∴ \(\frac{d r}{d \theta}\) + (2r cot θ + sin 2θ) = 0
∴ \(\frac{d r}{d \theta}\) + (2 cot θ)r = -sin 2θ ………(1)
This is the linear differential equation of the form dr
\(\frac{d r}{d \theta}\) + P . r = Q, where P = 2 cot θ and Q = -sin 2θ

This is the general solution.

(ix) y dx + (x – y²) dy = 0
Solution:
y dx + (x – y²) dy = 0
∴ y dx = -(x – y²) dy
∴ \(\frac{d x}{d y}=-\frac{\left(x-y^{2}\right)}{y}=-\frac{x}{y}+y\)
∴ \(\frac{d x}{d y}+\left(\frac{1}{y}\right) \cdot x=y\) ………(1)
This is the linear differential equation of the form

This is the general solution.

(x) \(\left(1-x^{2}\right) \frac{d y}{d x}+2 x y=x\left(1-x^{2}\right)^{\frac{1}{2}}\)
Solution:

(xi) \(\left(1+x^{2}\right) \frac{d y}{d x}+y=e^{\tan ^{-1} x}\)
Solution:

Question 2.
Find the equation of the curve which passes through the origin and has the slope x + 3y – 1 at any point (x, y) on it.
Solution:
Let A(x, y) be the point on the curve y = f(x).
Then slope of the tangent to the curve at the point A is \(\frac{d y}{d x}\).
According to the given condition,
\(\frac{d y}{d x}\) = x + 3y – 1
∴ \(\frac{d y}{d x}\) – 3y = x – 1 ………(1)
This is the linear differential equation of the form

This is the general equation of the curve.
But the required curve is passing through the origin (0, 0).
∴ by putting x = 0 and y = 0 in (2), we get
0 = 2 + c
∴ c = -2
∴ from (2), the equation of the required curve is 3(x + 3y) = 2 – 2e^3x i.e. 3(x + 3y) = 2 (1 – e^3x).

Question 3.
Find the equation of the curve passing through the point \(\left(\frac{3}{\sqrt{2}}, \sqrt{2}\right)\) having slope of the tangent to the curve at any point (x, y) is \(-\frac{4 x}{9 y}\).
Solution:
Let A(x, y) be the point on the curve y = f(x).
Then the slope of the tangent to the curve at point A is \(\frac{d y}{d x}\).
According to the given condition
\(\frac{d y}{d x}=-\frac{4 x}{9 y}\)
∴ y dy = \(-\frac{4}{9}\) x dx
Integrating both sides, we get
∫y dy= \(-\frac{4}{9}\) ∫x dx
∴ \(\frac{y^{2}}{2}=-\frac{4}{9} \cdot \frac{x^{2}}{2}+c_{1}\)
∴ 9y² = -4x² + 18c₁
∴ 4x² + 9y² = c where c = 18c₁
This is the general equation of the curve.
But the required curve is passing through the point \(\left(\frac{3}{\sqrt{2}}, \sqrt{2}\right)\).
∴ by putting x = \(\frac{3}{\sqrt{2}}\) and y = √2 in (1), we get
\(4\left(\frac{3}{\sqrt{2}}\right)^{2}+9(\sqrt{2})^{2}=c\)
∴ 18 + 18 = c
∴ c = 36
∴ from (1), the equation of the required curve is 4x² + 9y² = 36.

Question 4.
The curve passes through the point (0, 2). The sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at any point by 5. Find the equation of the curve.
Solution:
Let A(x, y) be any point on the curve.
Then slope of the tangent to the curve at the point A is \(\frac{d y}{d x}\).
According to the given condition
x + y = \(\frac{d y}{d x}\) + 5
∴ \(\frac{d y}{d x}\) – y = x – 5 ………(1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + P . y = Q, where P = -1 and Q = x – 5
∴ I.F. = \(e^{\int P d x}=e^{\int-1 d x}=e^{-x}\)
∴ the solution of (1) is given by

This is the general equation of the curve.
But the required curve is passing through the point (0, 2).
∴ by putting x = 0, y = 2 in (2), we get
2 = 4 – 0 + c
∴ c = -2
∴ from (2), the equation of the required curve is y = 4 – x – 2e^x.

Question 5.
If the slope of the tangent to the curve at each of its point is equal to the sum of abscissa and the product of the abscissa and ordinate of the point. Also, the curve passes through the point (0, 1). Find the equation of the curve.
Solution:
Let A(x, y) be the point on the curve y = f(x).
Then slope of the tangent to the curve at the point A is \(\frac{d y}{d x}\).
According to the given condition
\(\frac{d y}{d x}\) = x + xy
∴ \(\frac{d y}{d x}\) – xy = x ……….. (1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q, where P = -x and Q = x
∴ I.F. = \(e^{\int P d x}=e^{\int-x d x}=e^{-\frac{x^{2}}{2}}\)
∴ the solution of (1) is given by
y . (I.F.) = ∫Q . (I.F.) dx + c

This is the general equation of the curve.
But the required curve is passing through the point (0, 1).
∴ by putting x = 0 and y = 1 in (2), we get
1 + 1 = c
∴ c = 2
∴ from (2), the equation of the required curve is 1 + y = \(2 e^{\frac{x^{2}}{2}}\).

Class 12 Maharashtra State Board Maths Solution 

• Exercise 6.1 Class 12 Maths 2
• Exercise 6.2 Class 12 Maths 2
• Exercise 6.3 Class 12 Maths 2
• Exercise 6.4 Class 12 Maths 2
• Exercise 6.5 Class 12 Maths 2
• Exercise 6.6 Class 12 Maths 2
• Miscellaneous Exercise 6 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.4 Questions and Answers.

12th Maths Part 2 Differential Equations Exercise 6.4 Questions And Answers Maharashtra Board

I. Solve the following differential equations:

Question 1.
\(x \sin \left(\frac{y}{x}\right) d y=\left[y \sin \left(\frac{y}{x}\right)-x\right] d x\)
Solution:

Question 2.
(x² + y²) dx – 2xy . dy = 0
Solution:
(x² + y²) dx – 2xy dy = 0
∴ 2xy dy = (x² + y²) dx
∴ \(\frac{d y}{d x}=\frac{x^{2}+y^{2}}{2 x y}\) ………(1)

Question 3.
\(\left(1+2 e^{\frac{x}{y}}\right)+2 e^{\frac{x}{y}}\left(1-\frac{x}{y}\right) \frac{d y}{d x}=0\)
Solution:

Question 4.
y² dx + (xy + x²) dy = 0
Solution:
y² dx + (xy + x²) dy = 0
∴ (xy + x²) dy = -y² dx
∴ \(\frac{d y}{d x}=\frac{-y^{2}}{x y+x^{2}}\) ……..(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
Substituting these values in (1), we get

Question 5.
(x² – y²) dx + 2xy dy = 0
Solution:

Question 6.
\(\frac{d y}{d x}+\frac{x-2 y}{2 x-y}=0\)
Solution:

Question 7.
\(x \frac{d y}{d x}-y+x \sin \left(\frac{y}{x}\right)=0\)
Solution:

Question 8.
\(\left(1+e^{\frac{x}{y}}\right) d x+e^{\frac{x}{y}}\left(1-\frac{X}{y}\right) d y=0\)
Solution:

Question 9.
\(y^{2}-x^{2} \frac{d y}{d x}=x y \frac{d y}{d x}\)
Solution:

Question 10.
xy \(\frac{d y}{d x}\) = x² + 2y², y(1) = 0
Solution:

Question 11.
x dy + 2y · dx = 0, when x = 2, y = 1
Solution:
∴ x dy + 2y · dx = 0
∴ x dy = -2y dx
∴ \(\frac{1}{y} d y=\frac{-2}{x} d x\)
Integrating, we get

This is the general solution.
When x = 2, y = 1, we get
4(1) = c
∴ c = 4
∴ the particular solution is x²y = 4.

Question 12.
x² \(\frac{d y}{d x}\) = x² + xy + y²
Solution:
x² \(\frac{d y}{d x}\) = x² + xy + y²
∴ \(\frac{d y}{d x}=\frac{x^{2}+x y+y^{2}}{x^{2}}\) ………(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)

Question 13.
(9x + 5y) dy + (15x + 11y) dx = 0
Solution:
(9x + 5y) dy + (15x + 11y) dx = 0
∴ (9x + 5y) dy = -(15x + 11y) dx
∴ \(\frac{d y}{d x}=\frac{-(15 x+11 y)}{9 x+5 y}\) ………(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)

Question 14.
(x² + 3xy + y²) dx – x² dy = 0
Solution:
(x² + 3xy + y²) dx – x² dy = 0
∴ x² dy = (x² + 3xy + y²) dx
∴ \(\frac{d y}{d x}=\frac{x^{2}+3 x y+y^{2}}{x^{2}}\) ………(1)

Question 15.
(x² + y²) dx – 2xy dy = 0.
Solution:

Class 12 Maharashtra State Board Maths Solution 

• Exercise 6.1 Class 12 Maths 2
• Exercise 6.2 Class 12 Maths 2
• Exercise 6.3 Class 12 Maths 2
• Exercise 6.4 Class 12 Maths 2
• Exercise 6.5 Class 12 Maths 2
• Exercise 6.6 Class 12 Maths 2
• Miscellaneous Exercise 6 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.3 Questions and Answers.

12th Maths Part 2 Differential Equations Exercise 6.3 Questions And Answers Maharashtra Board

Question 1.
In each of the following examples verify that the given expression is a solution of the corresponding differential equation.
(i) xy = log y + c; \(\frac{d y}{d x}=\frac{y^{2}}{1-x y}\)
Solution:
xy = log y + c
Differentiating w.r.t. x, we get

Hence, xy = log y + c is a solution of the D.E.
\(\frac{d y}{d x}=\frac{y^{2}}{1-x y^{\prime}}, x y \neq 1\)

(ii) y = (sin^-1x)² + c; (1 – x²) \(\frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}=2\)
Solution:
y = (sin^-1 x)² + c …….(1)
Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get

(iii) y = e^-x + Ax + B; \(e^{x} \frac{d^{2} y}{d x^{2}}=1\)
Solution:
y = e^-x + Ax + B
Differentiating w.r.t. x, we get

∴ \(e^{x} \frac{d^{2} y}{d x^{2}}=1\)
Hence, y = e^-x + Ax + B is a solution of the D.E.
\(e^{x} \frac{d^{2} y}{d x^{2}}=1\)

(iv) y = x^m; \(x^{2} \frac{d^{2} y}{d x^{2}}-m x \frac{d y}{d x}+m y=0\)
Solution:
y = x^m
Differentiating twice w.r.t. x, we get

This shows that y = x^m is a solution of the D.E.
\(x^{2} \frac{d^{2} y}{d x^{2}}-m x \frac{d y}{d x}+m y=0\)

(v) y = a + \(\frac{b}{x}\); \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
Solution:
y = a + \(\frac{b}{x}\)
Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get

Hence, y = a + \(\frac{b}{x}\) is a solution of the D.E.
\(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)

(vi) y = e^ax; x \(\frac{d y}{d x}\) = y log y
Solution:
y = e^ax
log y = log e^ax = ax log e
log y = ax …….(1) ……..[∵ log e = 1]
Differentiating w.r.t. x, we get
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = a × 1
∴ \(\frac{d y}{d x}\) = ay
∴ x \(\frac{d y}{d x}\) = (ax)y
∴ x \(\frac{d y}{d x}\) = y log y ………[By (1)]
Hence, y = e^ax is a solution of the D.E.
x \(\frac{d y}{d x}\) = y log y.

Question 2.
Solve the following differential equations.
(i) \(\frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}}\)
Solution:

(ii) log(\(\frac{d y}{d x}\)) = 2x + 3y
Solution:

(iii) y – x \(\frac{d y}{d x}\) = 0
Solution:
y – x \(\frac{d y}{d x}\) = 0
∴ x \(\frac{d y}{d x}\) = y
∴ \(\frac{1}{x} d x=\frac{1}{y} d y\)
Integrating both sides, we get
\(\int \frac{1}{x} d x=\int \frac{1}{y} d y\)
∴ log |x| = log |y| + log c
∴ log |x| = log |cy|
∴ x = cy
This is the general solution.

(iv) sec²x . tan y dx + sec²y . tan x dy = 0
Solution:
sec²x . tan y dx + sec²y . tan x dy = 0
∴ \(\frac{\sec ^{2} x}{\tan x} d x+\frac{\sec ^{2} y}{\tan y} d y=0\)
Integrating both sides, we get
\(\int \frac{\sec ^{2} x}{\tan x} d x+\int \frac{\sec ^{2} y}{\tan y} d y=c_{1}\)
Each of these integrals is of the type
\(\int \frac{f^{\prime}(x)}{f(x)} d x\) = log |f(x)| + c
∴ the general solution is
∴ log|tan x| + log|tan y | = log c, where c₁ = log c
∴ log |tan x . tan y| = log c
∴ tan x . tan y = c
This is the general solution.

(v) cos x . cos y dy – sin x . sin y dx = 0
Solution:
cos x . cos y dy – sin x . sin y dx = 0
\(\frac{\cos y}{\sin y} d y-\frac{\sin x}{\cos x} d x=0\)
Integrating both sides, we get
∫cot y dy – ∫tan x dx = c₁
∴ log|sin y| – [-log|cos x|] = log c, where c₁ = log c
∴ log |sin y| + log|cos x| = log c
∴ log|sin y . cos x| = log c
∴ sin y . cos x = c
This is the general solution.

(vi) \(\frac{d y}{d x}\) = -k, where k is a constant.
Solution:
\(\frac{d y}{d x}\) = -k
∴ dy = -k dx
Integrating both sides, we get
∫dy = -k∫dx
∴ y = -kx + c
This is the general solution.

(vii) \(\frac{\cos ^{2} y}{x} d y+\frac{\cos ^{2} x}{y} d x=0\)
Solution:
\(\frac{\cos ^{2} y}{x} d y+\frac{\cos ^{2} x}{y} d x=0\)
∴ y cos²y dy + x cos²x dx = 0
∴ \(x\left(\frac{1+\cos 2 x}{2}\right) d x+y\left(1+\frac{\cos 2 y}{2}\right) d y=0\)
∴ x(1 + cos 2x) dx + y(1 + cos 2y) dy = 0
∴ x dx + x cos 2x dx + y dy+ y cos 2y dy = 0
Integrating both sides, we get
∫x dx + ∫y dy + ∫x cos 2x dx + ∫y cos 2y dy = c₁ ……..(1)
Using integration by parts

Multiplying throughout by 4, this becomes
2x² + 2y² + 2x sin 2x + cos 2x + 2y sin 2y + cos 2y = 4c₁
∴ 2(x² + y²) + 2(x sin 2x + y sin 2y) + cos 2y + cos 2x + c = 0, where c = -4c₁
This is the general solution.

(viii) \(y^{3}-\frac{d y}{d x}=x^{2} \frac{d y}{d x}\)
Solution:

(ix) 2e^x+2y dx – 3 dy = 0
Solution:

(x) \(\frac{d y}{d x}\) = e^x+y + x² e^y
Solution:

∴ 3e^x + 3e^-y + x³ = -3c₁
∴ 3e^x + 3e^-y + x³ = c, where c = -3c₁
This is the general solution.

Question 3.
For each of the following differential equations, find the particular solution satisfying the given condition:
(i) 3e^x tan y dx + (1 + e^x) sec²y dy = 0, when x = 0, y = π
Solution:
3e^x tan y dx + (1 + e^x) sec²y dy = 0

(ii) (x – y²x) dx – (y + x²y) dy = 0, when x = 2, y = 0
Solution:
(x – y²x) dx – (y + x²y) dy = 0
∴ x(1 – y²) dx – y(1 + x²) dy = 0

When x = 2, y = 0, we have
(1 + 4)(1 – 0) = c
∴ c = 5
∴ the particular solution is (1 + x²)(1 – y²) = 5.

(iii) y(1 + log x) \(\frac{d x}{d y}\) – x log x = 0, y = e², when x = e
Solution:
y(1 + log x) \(\frac{d x}{d y}\) – x log x = 0

(iv) (e^y + 1) cos x + e^y sin x \(\frac{d y}{d x}\) = 0, when x = \(\frac{\pi}{6}\), y = 0
Solution:
(e^y + 1) cos x + e^y sin x \(\frac{d y}{d x}\) = 0

\(\int \frac{f^{\prime}(x)}{f(x)} d x\) = log|f(x)| + c
∴ from (1), the general solution is
log|sin x| + log|e^y + 1| = log c, where c₁ = log c
∴ log|sin x . (e^y + 1)| = log c
∴ sin x . (e^y + 1) = c
When x = \(\frac{\pi}{4}\), y = 0, we get
\(\left(\sin \frac{\pi}{4}\right)\left(e^{0}+1\right)=c\)
∴ c = \(\frac{1}{\sqrt{2}}\)(1 + 1) = √2
∴ the particular solution is sin x . (e^y + 1) = √2

(v) (x + 1) \(\frac{d y}{d x}\) – 1 = 2e^-y, y = 0, when x = 1
Solution:

This is the general solution.
Now, y = 0, when x = 1
∴ 2 + e⁰ = c(1 + 1)
∴ 3 = 2c
∴ c = \(\frac{3}{2}\)
∴ the particular solution is 2 + e^y = \(\frac{3}{2}\) (x + 1)
∴ 2(2 + e^y) = 3(x + 1).

(vi) cos(\(\frac{d y}{d x}\)) = a, a ∈ R, y (0) = 2
Solution:
cos(\(\frac{d y}{d x}\)) = a
∴ \(\frac{d y}{d x}\) = cos^-1 a
∴ dy = (cos^-1 a) dx
Integrating both sides, we get
∫dy = (cos^-1 a) ∫dx
∴ y = (cos^-1 a) x + c
∴ y = x cos^-1 a + c
This is the general solution.
Now, y(0) = 2, i.e. y = 2,
when x = 0, 2 = 0 + c
∴ c = 2
∴ the particular solution is
∴ y = x cos^-1 a + 2
∴ y – 2 = x cos^-1 a
∴ \(\frac{y-2}{x}\) = cos^-1a
∴ cos(\(\frac{y-2}{x}\)) = a

Question 4.
Reduce each of the following differential equations to the variable separable form and hence solve:
(i) \(\frac{d y}{d x}\) = cos(x + y)
Solution:

(ii) (x – y)² \(\frac{d y}{d x}\) = a²
Solution:

(iii) x + y \(\frac{d y}{d x}\) = sec(x² + y²)
Solution:

Integrating both sides, we get
∫cos u du = 2 ∫dx
∴ sin u = 2x + c
∴ sin(x² + y²) = 2x + c
This is the general solution.

(iv) cos²(x – 2y) = 1 – 2 \(\frac{d y}{d x}\)
Solution:

Integrating both sides, we get
∫dx = ∫sec²u du
∴ x = tan u + c
∴ x = tan(x – 2y) + c
This is the general solution.

(v) (2x – 2y + 3) dx – (x – y + 1) dy = 0, when x = 0, y = 1
Solution:
(2x – 2y + 3) dx – (x – y + 1) dy = 0
∴ (x – y + 1) dy = (2x – 2y + 3) dx
∴ \(\frac{d y}{d x}=\frac{2(x-y)+3}{(x-y)+1}\) ………(1)
Put x – y = u, Then \(1-\frac{d y}{d x}=\frac{d u}{d x}\)

∴ u – log|u + 2| = -x + c
∴ x – y – log|x – y + 2| = -x + c
∴ (2x – y) – log|x – y + 2| = c
This is the general solution.
Now, y = 1, when x = 0.
∴ (0 – 1) – log|0 – 1 + 2| = c
∴ -1 – o = c
∴ c = -1
∴ the particular solution is
(2x – y) – log|x – y + 2| = -1
∴ (2x – y) – log|x – y + 2| + 1 = 0

Class 12 Maharashtra State Board Maths Solution 

• Exercise 6.1 Class 12 Maths 2
• Exercise 6.2 Class 12 Maths 2
• Exercise 6.3 Class 12 Maths 2
• Exercise 6.4 Class 12 Maths 2
• Exercise 6.5 Class 12 Maths 2
• Exercise 6.6 Class 12 Maths 2
• Miscellaneous Exercise 6 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.2 Questions and Answers.

12th Maths Part 2 Differential Equations Exercise 6.2 Questions And Answers Maharashtra Board

Question 1.
Obtain the differential equation by eliminating the arbitrary constants from the following equations:
(i) x³ + y³ = 4ax
Solution:
x³ + y³ = 4ax ……..(1)
Differentiating both sides w.r.t. x, we get
3x² + 3y² \(\frac{d y}{d x}\) = 4a × 1
∴ 3x² + 3y² \(\frac{d y}{d x}\) = 4a
Substituting the value of 4a in (1), we get
x³ + y³ = (3x² + 3y² \(\frac{d y}{d x}\)) x
∴ x³ + y³ = 3x³ + 3xy² \(\frac{d y}{d x}\)
∴ 2x³ + 3xy² \(\frac{d y}{d x}\) – y³ = 0
This is the required D.E.

(ii) Ax² + By² = 1
Solution:
Ax² + By² = 1
Differentiating both sides w.r.t. x, we get
A × 2x + B × 2y \(\frac{d y}{d x}\) = 0
∴ Ax + By \(\frac{d y}{d x}\) = 0 ……..(1)
Differentiating again w.r.t. x, we get

Substituting the value of A in (1), we get

This is the required D.E.

Alternative Method:
Ax² + By² = 1 ……..(1)
Differentiating both sides w.r.t. x, we get
A × 2x + B × 2y \(\frac{d y}{d x}\) = 0
∴ Ax + By \(\frac{d y}{d x}\) = 0 ……….(2)
Differentiating again w.r.t. x, we get,

The equations (1), (2) and (3) are consistent in A and B.
∴ determinant of their consistency is zero.

This is the required D.E.

(iii) y = A cos(log x) + B sin(log x)
Solution:
y = A cos(log x) + B sin (log x) ……. (1)
Differentiating w.r.t. x, we get

(iv) y² = (x + c)³
Solution:
y² = (x + c)³
Differentiating w.r.t. x, we get

This is the required D.E.

(v) y = Ae^5x + Be^-5x
Solution:
y = Ae^5x + Be^-5x ……….(1)
Differentiating twice w.r.t. x, we get

This is the required D.E.

(vi) (y – a)² = 4(x – b)
Solution:
(y – a)² = 4(x – b)
Differentiating both sides w.r.t. x, we get
2(y – a) . \(\frac{d}{d x}\)(y – a) = 4 \(\frac{d}{d x}\)(x – b)
∴ 2(y – a) . (\(\frac{d y}{d x}\) – 0) = 4(1 – 0)
∴ 2(y – a) \(\frac{d y}{d x}\) = 4
∴ (y – a) \(\frac{d y}{d x}\) = 2 ……..(1)
Differentiating w.r.t. x, we get

This is the required D.E.

(vii) y = a + \(\frac{a}{x}\)
Solution:
y = a + \(\frac{a}{x}\)
Differentiating w.r.t. x, we get

Substituting the value of a in (1), we get

This is the required D.E.

(viii) y = c₁e^2x + c₂e^5x
Solution:
y = c₁e^2x + c₂e^5x ………(1)
Differentiating twice w.r.t. x, we get
\(\frac{d y}{d x}\) = c₁e^2x × 2 + c₂e^5x × 5

The equations (1), (2) and (3) are consistent in c₁e^2x and c₂e^5x
∴ determinant of their consistency is zero.

This is the required D.E.

Alternative Method:
y = c₁e^2x + c₂e^5x
Dividing both sides by e^5x, we get

This is the required D.E.

(ix) c₁x³ + c₂y² = 5.
Solution:
c₁x³ + c₂y² = 5 ……….(1)
Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get

The equations (1), (2) and (3) in c₁, c₂ are consistent.
∴ determinant of their consistency is zero.

This is the required D.E.

(x) y = e^-2x(A cos x + B sin x)
Solution:
y = e^-2x(A cos x + B sin x)
∴ e^2x . y = A cos x + B sin x ………(1)
Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get


This is the required D.E.

Question 2.
Form the differential equation of family of lines having intercepts a and b on the coordinate axes respectively.
Solution:
The equation of the line having intercepts a and b on the coordinate axes respectively, is
\(\frac{x}{a}+\frac{y}{b}=1\) ……….(1)
where a and b are arbitrary constants.
[For different values of a and b, we get, different lines. Hence (1) is the equation of family of lines.]
Differentiating (1) w.r.t. x, we get

Differentiating again w.r.t. x, we get \(\frac{d^{2} y}{d x^{2}}=0\)
This is the required D.E.

Question 3.
Find the differential equation all parabolas having length of latus rectum 4a and axis is parallel to the X-axis.
Solution:

Let A(h, k) be the vertex of the parabola whose length of latus rectum is 4a.
Then the equation of the parabola is (y – k)² = 4a (x – h), where h and k are arbitrary constants.
Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get

This is the required D.E.

Question 4.
Find the differential equation of the ellipse whose major axis is twice its minor axis.
Solution:
Let 2a and 2b be lengths of major axis and minor axis of the ellipse.
Then 2a = 2(2b)
∴ a = 2b
∴ equation of the ellipse is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
i.e., \(\frac{x^{2}}{(2 b)^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ \(\frac{x^{2}}{4 b^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ x² + 4y² = 4b²
Differentiating w.r.t. x, we get
2x + 4 × 2y \(\frac{d y}{d x}\) = 0
∴ x + 4y \(\frac{d y}{d x}\) = 0
This is the required D.E.

Question 5.
Form the differential equation of family of lines parallel to the line 2x + 3y + 4 = 0.
Solution:
The equation of the line parallel to the line 2x + 3y + 4 = 0 is 2x + 3y + c = 0, where c is an arbitrary constant.
Differentiating w.r.t. x, we get
2 × 1 + 3 \(\frac{d y}{d x}\) + 0 = 0
∴ 3 \(\frac{d y}{d x}\) + 2 = 0
This is the required D.E.

Question 6.
Find the differential equation of all circles having radius 9 and centre at point (h, k).
Solution:
Equation of the circle having radius 9 and centre at point (h, k) is
(x – h)² + (y – k)² = 81 …… (1)
where h and k are arbitrary constant.
Differentiating (1) w.r.t. x, we get

Differentiating again w.r.t. x, we get

From (2), x – h = -(y – k) \(\frac{d y}{d x}\)
Substituting the value of (x – h) in (1), we get


This is the required D.E.

Question 7.
Form the differential equation of all parabolas whose axis is the X-axis.
Solution:

The equation of the parbola whose axis is the X-axis is
y² = 4a(x – h) …… (1)
where a and h are arbitrary constants.
Differentiating (1) w.r.t. x, we get
2y \(\frac{d y}{d x}\) = 4a(1 – 0)
∴ y \(\frac{d y}{d x}\) = 2a
Differentiating again w.r.t. x, we get

This is the required D.E.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 6.1 Class 12 Maths 2
• Exercise 6.2 Class 12 Maths 2
• Exercise 6.3 Class 12 Maths 2
• Exercise 6.4 Class 12 Maths 2
• Exercise 6.5 Class 12 Maths 2
• Exercise 6.6 Class 12 Maths 2
• Miscellaneous Exercise 6 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.1 Questions and Answers.

12th Maths Part 2 Differential Equations Exercise 6.1 Questions And Answers Maharashtra Board

1. Determine the order and degree of each of the following differential equations:

Question (i).
\(\frac{d y}{d x^{2}}+X\left(\frac{d y}{d x}\right)+y=2 \sin x\)
Solution:
The given D.E. is \(\frac{d y}{d x^{2}}+X\left(\frac{d y}{d x}\right)+y=2 \sin x\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. is of order 2 and degree 1.

Question (ii).
\(\sqrt[3]{1+\left(\frac{d y}{d x}\right)^{2}}=\frac{d^{2} y}{d x^{2}}\)
Solution:
The given D.E. is \(\sqrt[3]{1+\left(\frac{d y}{d x}\right)^{2}}=\frac{d^{2} y}{d x^{2}}\)
On cubing both sides, we get
\(1+\left(\frac{d y}{d x}\right)^{2}=\left(\frac{d^{2} y}{d x^{2}}\right)^{3}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 3.
∴ the given D.E. is of order 2 and degree 3.

Question (iii).
\(\frac{d y}{d x}=\frac{2 \sin x+3}{\frac{d y}{d x}}\)
Solution:
The given D.E. is \(\frac{d y}{d x}=\frac{2 \sin x+3}{\frac{d y}{d x}}\)
∴ \(\left(\frac{d y}{d x}\right)^{2}\) = 2 sin x + 3
This D.E. has highest order derivative \(\frac{d y}{d x}\) with power 2.
∴ the given D.E. is of order 1 and degree 2.

Question (iv).
\(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}+x=\sqrt{1+\frac{d^{3} y}{d x^{3}}}\)
Solution:
The given D.E. is \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}+x=\sqrt{1+\frac{d^{3} y}{d x^{3}}}\)
On squaring both sides, we get
\(\left(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}+x\right)^{2}=1+\frac{d^{3} y}{d x^{3}}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 1.
∴ the given D.E. has order 3 and degree 1.

Question (v).
\(\frac{d^{2} y}{d t^{2}}+\left(\frac{d y}{d t}\right)^{2}+7 x+5=0\)
Solution:
The given D.E. is \(\frac{d^{2} y}{d t^{2}}+\left(\frac{d y}{d t}\right)^{2}+7 x+5=0\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. has order 2 and degree 1.

Question (vi).
(y”‘)2 + 3y” + 3xy’ + 5y = 0
Solution:
The given D.E. is (y”‘)2 + 3y” + 3xy’ + 5y = 0
This can be written as:
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}+3 \frac{d^{2} y}{d x^{2}}+3 x \frac{d y}{d x}+5 y=0\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 2.
∴ The given D.E. has order 3 and degree 2.

Question (vii).
\(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\cos \left(\frac{d y}{d x}\right)=0\)
Solution:
The given D.E. is \(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\cos \left(\frac{d y}{d x}\right)=0\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\)
∴ order = 2
Since this D.E. cannot be expressed as a polynomial in differential coefficients, the degree is not defined.

Question (viii).
\(\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{\frac{3}{2}}=8 \frac{d^{2} y}{d x^{2}}\)
Solution:
The given D.E. is \(\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{\frac{3}{2}}=8 \frac{d^{2} y}{d x^{2}}\)
On squaring both sides, we get
\(\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{3}=8^{2} \cdot\left(\frac{d^{2} y}{d x^{2}}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 2.
∴ the given D.E. has order 2 and degree 2.

Question (ix).
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{\frac{1}{2}} \cdot\left(\frac{d y}{d x}\right)^{\frac{1}{3}}=20\)
Solution:
The given D.E. is \(\left(\frac{d^{3} y}{d x^{3}}\right)^{\frac{1}{2}} \cdot\left(\frac{d y}{d x}\right)^{\frac{1}{3}}=20\)
∴ \(\left(\frac{d^{3} y}{d x^{3}}\right)^{3} \cdot\left(\frac{d y}{d x}\right)^{2}=20^{6}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 3.
∴ the given D.E. has order 3 and degree 3.

Question (x).
\(x+\frac{d^{2} y}{d x^{2}}=\sqrt{1+\left(\frac{d^{2} y}{d x^{2}}\right)^{2}}\)
Solution:
The given D.E. is \(x+\frac{d^{2} y}{d x^{2}}=\sqrt{1+\left(\frac{d^{2} y}{d x^{2}}\right)^{2}}\)
On squaring both sides, we get

This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. has order 2 and degree 1.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 6.1 Class 12 Maths 2
• Exercise 6.2 Class 12 Maths 2
• Exercise 6.3 Class 12 Maths 2
• Exercise 6.4 Class 12 Maths 2
• Exercise 6.5 Class 12 Maths 2
• Exercise 6.6 Class 12 Maths 2
• Miscellaneous Exercise 6 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Application of Definite Integration Miscellaneous Exercise 5 Questions and Answers.

12th Maths Part 2 Application of Definite Integration Miscellaneous Exercise 5 Questions And Answers Maharashtra Board

I. Choose the correct option from the given alternatives:

Question 1.
The area bounded by the region 1 ≤ x ≤ 5 and 2 ≤ y ≤ 5 is given by
(a) 12 sq units
(b) 8 sq units
(c) 25 sq units
(d) 32 sq units
Answer:
(a) 12 sq units

Question 2.
The area of the region enclosed by the curve y = \(\frac{1}{x}\), and the lines x = e, x = e² is given by
(a) 1 sq unit
(b) \(\frac{1}{2}\) sq units
(c) \(\frac{3}{2}\) sq units
(d) \(\frac{5}{2}\) sq units
Answer:
(a) 1 sq unit

Question 3.
The area bounded by the curve y = x³, the X-axis and the lines x = -2 and x = 1 is
(a) -9 sq units
(b) \(-\frac{15}{4}\) sq units
(c) \(\frac{15}{4}\) sq units
(d) \(\frac{17}{4}\) sq units
Answer:
(c) \(\frac{15}{4}\) sq units

Question 4.
The area enclosed between the parabola y² = 4x and line y = 2x is
(a) \(\frac{2}{3}\) sq units
(b) \(\frac{1}{3}\) sq units
(c) \(\frac{1}{4}\) sq units
(d) \(\frac{3}{4}\) sq units
Answer:
(b) \(\frac{1}{3}\) sq units

Question 5.
The area of the region bounded between the line x = 4 and the parabola y² = 16x is
(a) \(\frac{128}{3}\) sq units
(b) \(\frac{108}{3}\) sq units
(c) \(\frac{118}{3}\) sq units
(d) \(\frac{218}{3}\) sq units
Answer:
(a) \(\frac{128}{3}\) sq units

Question 6.
The area of the region bounded by y = cos x, Y-axis and the lines x = 0, x = 2π is
(a) 1 sq unit
(b) 2 sq units
(c) 3 sq units
(d) 4 sq units
Answer:
(d) 4 sq units

Question 7.
The area bounded by the parabola y² = 8x, the X-axis and the latus rectum is
(a) \(\frac{31}{3}\) sq units
(b) \(\frac{32}{3}\) sq units
(c) \(\frac{32 \sqrt{2}}{3}\) sq units
(d) \(\frac{16}{3}\) sq units
Answer:
(b) \(\frac{32}{3}\) sq units

Question 8.
The area under the curve y = 2√x, enclosed between the lines x = 0 and x = 1 is
(a) 4 sq units
(b) \(\frac{3}{4}\) sq units
(c) \(\frac{2}{3}\) sq units
(d) \(\frac{4}{3}\) sq units
Answer:
(d) \(\frac{4}{3}\) sq units

Question 9.
The area of the circle x² + y² = 25 in first quadrant is
(a) \(\frac{25 \pi}{3}\) sq units
(b) 5π sq units
(c) 5 sq units
(d) 3 sq units
Answer:
(a) \(\frac{25 \pi}{3}\) sq units

Question 10.
The area of the region bounded by the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) is
(a) ab sq units
(b) πab sq units
(c) \(\frac{\pi}{a b}\) sq units ab
(d) πa² sq units
Answer:
(b) πab sq units

Question 11.
The area bounded by the parabola y² = x and the line 2y = x is
(a) \(\frac{4}{3}\) sq units
(b) 1 sq unit
(c) \(\frac{2}{3}\) sq unit
(d) \(\frac{1}{3}\) sq unit
Answer:
(a) \(\frac{4}{3}\) sq units

Question 12.
The area enclosed between the curve y = cos 3x, 0 ≤ x ≤ \(\frac{\pi}{6}\) and the X-axis is
(a) \(\frac{1}{2}\) sq unit
(b) 1 sq unit
(c) \(\frac{2}{3}\) sq unit
(d) \(\frac{1}{3}\) sq unit
Answer:
(d) \(\frac{1}{3}\) sq unit

Question 13.
The area bounded by y = √x and line x = 2y + 3, X-axis in first quadrant is
(a) 2√3 sq units
(b) 9 sq units
(c) \(\frac{34}{3}\) sq units
(d) 18 sq units
Answer:
(b) 9 sq units

Question 14.
The area bounded by the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) and the line \(\frac{x}{a}+\frac{y}{b}=1\) is
(a) (πab – 2ab) sq units
(b) \(\frac{\pi a b}{4}-\frac{a b}{2}\) sq units
(c) (πab – ab) sq units
(d) πab sq units
Answer:
(b) \(\frac{\pi a b}{4}-\frac{a b}{2}\) sq units

Question 15.
The area bounded by the parabola y = x² and the line y = x is
(a) \(\frac{1}{2}\) sq unit
(b) \(\frac{1}{3}\) sq unit
(c) \(\frac{1}{6}\) sq unit
(d) \(\frac{1}{12}\) sq unit
Answer:
(c) \(\frac{1}{6}\) sq unit

Question 16.
The area enclosed between the two parabolas y² = 4x and y = x is
(a) \(\frac{8}{3}\) sq units
(b) \(\frac{32}{3}\) sq units
(c) \(\frac{16}{3}\) sq units
(d) \(\frac{4}{3}\) sq units
Answer:
(c) \(\frac{16}{3}\) sq units

Question 17.
The area bounded by the curve y = tan x, X-axis and the line x = \(\frac{\pi}{4}\) is
(a) \(\frac{1}{3}\) log 2 sq units
(b) log 2 sq units
(c) 2 log 2 sq units
(d) 3 log 2 sq units
Answer:
(a) \(\frac{1}{3}\) log 2 sq units

Question 18.
The area of the region bounded by x² = 16y, y = 1, y = 4 and x = 0 in the first quadrant, is
(a) \(\frac{7}{3}\) sq units
(b) \(\frac{8}{3}\) sq units
(c) \(\frac{64}{3}\) sq units
(d) \(\frac{56}{3}\) sq units
Answer:
(d) \(\frac{56}{3}\) sq units

Question 19.
The area of the region included between the parabolas y² = 4ax and x² = 4ay, (a > 0) is given by
(a) \(\frac{16 a^{2}}{3}\) sq units
(b) \(\frac{8 a^{2}}{3}\) sq units
(c) \(\frac{4 a^{2}}{3}\) sq units
(d) \(\frac{32 a^{2}}{3}\) sq units
Answer:
(a) \(\frac{16 a^{2}}{3}\) sq units

Question 20.
The area of the region included between the line x + y = 1 and the circle x² + y² = 1 is
(a) \(\frac{\pi}{2}-1\) sq units
(b) π – 2 sq units
(c) \(\frac{\pi}{4}-\frac{1}{2}\) sq units
(d) π – \(\frac{1}{2}\) sq units
Answer:
(c) \(\frac{\pi}{4}-\frac{1}{2}\) sq units

(II) Solve the following:

Question 1.
Find the area of the region bounded by the following curve, the X-axis and the given lines:
(i) 0 ≤ x ≤ 5, 0 ≤ y ≤ 2
(ii) y = sin x, x = 0, x = π
(iii) y = sin x, x = 0, x = \(\frac{\pi}{3}\)
Solution:
(i) Required area = \(\int_{0}^{5} y d x\), where y = 2
= \(\int_{0}^{5} 2 d x\)
= \([2 x]_{0}^{5}\)
= 2 × 5 – 0
= 10 sq units.

(ii) The curve y = sin x intersects the X-axis at x = 0 and x = π between x = 0 and x = π.

Two bounded regions A₁ and A₂ are obtained. Both the regions have equal areas.
∴ required area = A₁ + A₂ = 2A₁

(iii) Required area = \(\int_{0}^{\pi / 3} y d x\), where y = sin x

Question 2.
Find the area of the circle x² + y² = 9, using integration.
Solution:
By the symmetry of the circle, its area is equal to 4 times the area of the region OABO.
Clearly, for this region, the limits of integration are 0 and 3.

From the equation of the circle, y² = 9 – x².
In the first quadrant, y > 0
∴ y = \(\sqrt{9-x^{2}}\)
∴ area of the circle = 4 (area of the region OABO)

Question 3.
Find the area of the ellipse \(\frac{x^{2}}{25}+\frac{y^{2}}{16}=1\) using integration.
Solution:

By the symmetry of the ellipse, its area is equal to 4 times the area of the region OABO.
Clearly, for this region, the limits of integration are 0 and 5.
From the equation of the ellipse
\(\frac{y^{2}}{16}=1-\frac{x^{2}}{25}=\frac{25-x^{2}}{25}\)
∴ y² = \(\frac{16}{25}\) (25 – x²)
In the first quadrant y > 0
∴ y = \(\frac{4}{5} \sqrt{25-x^{2}}\)
∴ area of the ellipse = 4(area of the region OABO)

Question 4.
Find the area of the region lying between the parabolas:
(i) y² = 4x and x² = 4y
(ii) 4y² = 9x and 3x² = 16y
(iii) y² = x and x² = y.
Solution:
(i)

For finding the points of intersection of the two parabolas, we equate the values of y² from their equations.
From the equation x² = 4y, y = \(\frac{x^{2}}{4}\)
y = \(\frac{x^{4}}{16}\)
\(\frac{x^{4}}{16}\) = 4x
∴ x⁴ – 64x = 0
∴ x(x³ – 64) = 0
∴ x = 0 or x³ = 64 i.e. x = 0 or x = 4
When x = 0, y = 0
When x = 4, y = \(\frac{4^{2}}{4}\) = 4
∴ the points of intersection are 0(0, 0) and A(4, 4).
Required area = area of the region OBACO = [area of the region ODACO] – [area of the region ODABO]
Now, area of the region ODACO = area under the parabola y² = 4x, i.e. y = 2√x between x = 0 and x = 4

(ii)

For finding the points of intersection of the two parabolas, we equate the values of 4y² from their equations.
From the equation 3x² = 16y, y = \(\frac{3 x^{2}}{16}\)
∴ y = \(\frac{3 x^{4}}{256}\)
∴ \(\frac{3 x^{4}}{256}\) = 9x
∴ 3x⁴ – 2304x = 0
∴ x(x³ – 2304) = 0
∴ x = 0 or x³ = 2304 i.e. x = 0 or x = 4
When x = 0, y = 0
When x = 4, y = \(\frac{4^{2}}{4}\)
∴ the points of intersection are O(0, 0) and A(4, 4).
Required area = area of the region OBACO = [area of the region ODACO] – [area of the region ODABO]
Now, area of the region ODACO = area under the parabola y² = 4x,
i.e. y = 2√x between x = 0 and x = 4

Area of the region ODABO = area under the rabola x² = 4y,
i.e. y = \(\frac{x^{2}}{4}\) between x = 0 and x = 4

(iii)

For finding the points of intersection of the two parabolas, we equate the values of y² from their equations.
From the equation x² = y, y = \(\frac{x^{2}}{y}\)
∴ y = \(\frac{x^{2}}{y}\)
∴ \(\frac{x^{2}}{y}\) = x
∴ x² – y = 0
∴ x(x³ – y) = 0
∴ x = 0 or x³ = y
i.e. x = 0 or x = 4
When x = 0, y = 0
When x = 4, y = \(\frac{4^{2}}{4}\) = 4
∴ the points of intersection are O(0, 0) and A(4, 4).
Required area = area of the region OBACO = [area of the region ODACO] – [area of the region ODABO]
Now, area of the region ODACO = area under the parabola y² = 4x,
i.e. y = 2√x between x = 0 and x = 4

Area ofthe region ODABO = area under the rabola x² = 4y,
i.e. y = \(\frac{x^{2}}{3}\) between x = 0 and x = 4

Question 5.
Find the area of the region in the first quadrant bounded by the circle x² + y² = 4 and the X-axis and the line x = y√3.
Solution:

For finding the points of intersection of the circle and the line, we solve
x² + y² = 4 ………(1)
and x = y√3 ……..(2)
From (2), x² = 3y²
From (1), x² = 4 – y²
3y² = 4 – y²
4y² = 4
y² = 1
y = 1 in the first quadrant.
When y = 1, r = 1 × √3 = √3
∴ the circle and the line intersect at A(√3, 1) in the first quadrant
Required area = area of the region OCAEDO = area of the region OCADO + area of the region DAED
Now, area of the region OCADO = area under the line x = y√3, i.e. y = \(\frac{x}{\sqrt{3}}\) between x = 0
and x = √3

Question 6.
Find the area of the region bounded by the parabola y² = x and the line y = x in the first quadrant.
Solution:
To obtain the points of intersection of the line and the parabola, we equate the values of x from both equations.

∴ y² = y
∴ y² – y = 0
∴ y(y – 1) = 0
∴ y = 0 or y = 1
When y = 0, x = 0
When y = 1, x = 1
∴ the points of intersection are O(0, 0) and A(1, 1).
Required area = area of the region OCABO = area of the region OCADO – area of the region OBADO
Now, area of the region OCADO = area under the parabola y² = x i.e. y = +√x (in the first quadrant) between x = 0 and x = 1

Area of the region OBADO = area under the line y = x between x = 0 and x = 1

Question 7.
Find the area enclosed between the circle x² + y² = 1 and the line x + y = 1, lying in the first quadrant.
Solution:

Required area = area of the region ACBPA = (area of the region OACBO) – (area of the region OADBO)
Now, area of the region OACBO = area under the circle x² + y² = 1 between x = 0 and x = 1

Area of the region OADBO = area under the line x + y = 1 between x = 0 and x = 1

∴ required area = \(\left(\frac{\pi}{4}-\frac{1}{2}\right)\) sq units.

Question 8.
Find the area of the region bounded by the curve (y – 1)² = 4(x + 1) and the line y = (x – 1).
Solution:
The equation of the curve is (y – 1)² = 4(x + 1)
This is a parabola with vertex at A (-1, 1).
To find the points of intersection of the line y = x – 1 and the parabola.
Put y = x – 1 in the equation of the parabola, we get
(x – 1 – 1)² = 4(x + 1)
∴ x² – 4x + 4 = 4x + 4
∴ x² – 8x = 0
∴ x(x – 8) = 0
∴ x = 0, x = 8
When x = 0, y = 0 – 1 = -1
When x = 8, y = 8 – 1 = 7
∴ the points of intersection are B (0, -1) and C (8, 7).

To find the points where the parabola (y – 1)² = 4(x + 1) cuts the Y-axis.
Put x = 0 in the equation of the parabola, we get
(y – 1)² = 4(0 + 1) = 4
∴ y – 1 = ±2
∴ y – 1 = 2 or y – 1 = -2
∴ y = 3 or y = -1
∴ the parabola cuts the Y-axis at the points B(0, -1) and F(0, 3).
To find the point where the line y = x – 1 cuts the X-axis.
Put y = 0 in the equation of the line, we get
x – 1 = 0
∴ x = 1
∴ the line cuts the X-axis at the point G (1, 0).
Required area = area of the region BFAB + area of the region OGDCEFO + area of the region OBGO
Now, area of the region BFAB = area under the parabola (y – 1)² = 4(x + 1), Y-axis from y = -1 to y = 3

Since, the area cannot be negative,
Area of the region BFAB = \(\left|-\frac{8}{3}\right|=\frac{8}{3}\) sq units.
Area of the region OGDCEFO = area of the region OPCEFO – area of the region GPCDG

Since, area cannot be negative,
area of the region = \(\left|-\frac{1}{2}\right|=\frac{1}{2}\) sq units.
∴ required area = \(\frac{8}{3}+\frac{109}{6}+\frac{1}{2}\)
= \(\frac{16+109+3}{6}\)
= \(\frac{128}{6}\)
= \(\frac{64}{3}\) sq units.

Question 9.
Find the area of the region bounded by the straight line 2y = 5x + 7, X-axis and x = 2, x = 5.
Solution:
The equation of the line is
2y = 5x + 7, i.e., y = \(\frac{5}{2} x+\frac{7}{2}\)
Required area = area of the region ABCDA = area under the line y = \(\frac{5}{2} x+\frac{7}{2}\) between x = 2 and x = 5

Question 10.
Find the area of the region bounded by the curve y = 4x², Y-axis and the lines y = 1, y = 4.
Solution:

By symmetry of the parabola, the required area is 2 times the area of the region ABCD.
From the equation of the parabola, x² = \(\frac{y}{4}\)
In the first quadrant, x > 0
∴ x = \(\frac{1}{2} \sqrt{y}\)
∴ required area = \(\int_{1}^{4} x d y\)

Class 12 Maharashtra State Board Maths Solution 

• Exercise 4.1 Class 12 Maths 2
• Exercise 4.2 Class 12 Maths 2
• Miscellaneous Exercise 4 Class 12 Maths 2
• Exercise 5.1 Class 12 Maths 2
• Miscellaneous Exercise 5 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Application of Definite Integration Ex 5.1 Questions and Answers.

12th Maths Part 2 Application of Definite Integration Exercise 5.1 Questions And Answers Maharashtra Board

1. Find the area of the region bounded by the following curves, X-axis, and the given lines:

(i) y = 2x, x = 0, x = 5.
Solution:
Required area = \(\int_{0}^{5} y d x\), where y = 2x
= \(\int_{0}^{5} 2x d x\)
= \(\left[\frac{2 x^{2}}{2}\right]_{0}^{5}\)
= 25 – 0
= 25 sq units.

(ii) x = 2y, y = 0, y = 4.
Solution:
Required area = \(\int_{0}^{4} x d y\), where x = 2y
= \(\int_{0}^{4} 2 y d y\)
= \(\left[\frac{2 y^{2}}{2}\right]_{0}^{4}\)
= 16 – 0
= 16 sq units.

(iii) x = 0, x = 5, y = 0, y = 4.
Solution:
Required area = \(\int_{0}^{5} y d x\), where y = 4
= \(\int_{0}^{5} 4 d x\)
= \([4 x]_{0}^{5}\)
= 20 – 0
= 20 sq units.

(iv) y = sin x, x = 0, x = \(\frac{\pi}{2}\)
Solution:
Required area = \(\int_{0}^{\pi / 2} y d x\), where y = sin x
= \(\int_{0}^{\pi / 2} \sin x d x\)
= \([-\cos x]_{0}^{\pi / 2}\)
= -cos \(\frac{\pi}{2}\) + cos 0
= 0 + 1
= 1 sq unit.

(v) xy = 2, x = 1, x = 4.
Solution:
For xy = 2, y = \(\frac{2}{x}\)
Required area = \(\int_{1}^{4} y d x\), where y = \(\frac{2}{x}\)
= \(\int_{1}^{4} \frac{2}{x} d x\)
= \([2 \log |x|]_{1}^{4}\)
= 2 log 4 – 2 log 1
= 2 log 4 – 0
= 2 log 4 sq units.

(vi) y² = x, x = 0, x = 4.
Solution:

The required area consists of two bounded regions A1 and A2 which are equal in areas.
For y² = x, y = √x
Required area = A₁ + A₂ = 2A₁

(vii) y² = 16x, x = 0, x = 4.
Solution:

The required area consists of two bounded regions A1 and A2 which are equal in areas.
For y² = x, y = √x
Required area = A₁ + A₂ = 2A₁

2. Find the area of the region bounded by the parabola:

(i) y² = 16x and its latus rectum.
Solution:
Comparing y² = 16x with y² = 4ax, we get
4a = 16
∴ a = 4
∴ focus is S(a, 0) = (4, 0)

For y² = 16x, y = 4√x
Required area = area of the region OBSAO
= 2 [area of the region OSAO]

(ii) y = 4 – x² and the X-axis.
Solution:
The equation of the parabola is y = 4 – x²
∴ x² = 4 – y
i.e. (x – 0)² = -(y – 4)
It has vertex at P(0, 4)
For points of intersection of the parabola with X-axis,
we put y = 0 in its equation.
∴ 0 = 4 – x²
∴ x² = 4
∴ x = ± 2
∴ the parabola intersect the X-axis at A(-2, 0) and B(2, 0)

Required area = area of the region APBOA
= 2[area of the region OPBO]

3. Find the area of the region included between:

(i) y² = 2x and y = 2x.
Solution:
The vertex of the parabola y² = 2x is at the origin O = (0, 0).

To find the points of intersection of the line and the parabola, equaling the values of 2x from both the equations we get,
y² = y
∴ y² – y = 0
∴ y = 0 or y = 1
When y = 0, x = \(\frac{0}{2}\) = 0
When y = 1, x = \(\frac{1}{2}\)
∴ the points of intersection are 0(0, 0) and B(\(\frac{1}{2}\), 1)
Required area = area of the region OABCO = area of the region OABDO – area of the region OCBDO
Now, area of the region OABDO = area under the parabola y² = 2x between x = 0 and x = \(\frac{1}{2}\)

Area of the region OCBDO = area under the line y = 2x between x = 0 and x = \(\frac{1}{2}\)

(ii) y² = 4x and y = x.
Solution:
The vertex of the parabola y² = 4x is at the origin O = (0, 0).

To find the points of intersection of the line and the parabola, equaling the values of 4x from both the equations we get,
∴ y² = y
∴ y² – y = 0
∴ y(y – 1) = 0
∴ y = 0 or y = 1
When y = 0, x = \(\frac{0}{2}\) = 0
When y = 1, x = \(\frac{1}{2}\)
∴ the points of intersection are O(0, 0) and B(\(\frac{1}{2}\), 1)
Required area = area of the region OABCO = area of the region OABDO – area of the region OCBDO
Now, area of the region OABDO = area under the parabola y² = 4x between x = 0 and x = \(\frac{1}{2}\)

Area of the region OCBDO = area under the line y = 2x between x = 0 and x = \(\frac{1}{2}\)

(iii) y = x² and the line y = 4x.
Solution:
The vertex of the parabola y = x² is at the origin 0(0, 0)
To find the points of the intersection of a line and the parabola.

Equating the values of y from the two equations, we get
x² = 4x
∴ x² – 4x = 0
∴ x(x – 4) = 0
∴ x = 0, x = 4
When x = 0, y = 4(0) = 0
When x = 4, y = 4(4) = 16
∴ the points of intersection are 0(0, 0) and B(4, 16)
Required area = area of the region OABCO = (area of the region ODBCO) – (area of the region ODBAO)
Now, area of the region ODBCO = area under the line y = 4x between x = 0 and x = 4
= \(\int_{0}^{4} y d x\), where y = 4x
= \(\int_{0}^{4} 4 x d x\)
= 4\(\int_{0}^{4} x d x\)
= 4\([latex]\int_{0}^{4} x d x\)[/latex]
= 2(16 – 0)
= 32
Area of the region ODBAO = area under the parabola y = x² between x = 0 and x = 4
= \(\int_{0}^{4} y d x\), where y = x2
= \(\int_{0}^{4} x^{2} d x\)
= \(\left[\frac{x^{3}}{3}\right]_{0}^{4}\)
= \(\frac{1}{3}\) (64 – 0)
= \(\frac{64}{3}\)
∴ required area = 32 – \(\frac{64}{3}\) = \(\frac{32}{3}\) sq units.

(iv) y² = 4ax and y = x.
Solution:
The vertex of the parabola y² = 4ax is at the origin O = (0, 0).

To find the points of intersection of the line and the parabola, equaling the values of 4ax from both the equations we get,
∴ y² = y
∴ y² – y = 0
∴ y(y – 1) = 0
∴ y = 0 or y = 1
When y = 0, x = \(\frac{0}{2}\) = 0
When y = 1, x = \(\frac{1}{2}\)
∴ the points of intersection are O(0, 0) and B(\(\frac{1}{2}\), 1)
Required area = area of the region OABCO = area of the region OABDO – area of the region OCBDO
Now, area of the region OABDO
= area under the parabola y² = 4ax between x = 0 and x = \(\frac{1}{2}\)

Area of the region OCBDO
= area under the line y
= 4ax between x = 0 and x = \(\frac{1}{4 a x}\)

(v) y = x² + 3 and y = x + 3.
Solution:
The given parabola is y = x² + 3, i.e. (x – 0)² = y – 3
∴ its vertex is P(0, 3).

To find the points of intersection of the line and the parabola.
Equating the values of y from both the equations, we get
x² + 3 = x + 3
∴ x² – x = 0
∴ x(x – 1) = 0
∴ x = 0 or x = 1
When x = 0, y = 0 + 3 = 3
When x = 1, y = 1 + 3 = 4
∴ the points of intersection are P(0, 3) and B(1, 4)
Required area = area of the region PABCP = area of the region OPABDO – area of the region OPCBDO
Now, area of the region OPABDO
= area under the line y = x + 3 between x = 0 and x = 1

Area of the region OPCBDO = area under the parabola y = x² + 3 between x = 0 and x = 1

Class 12 Maharashtra State Board Maths Solution 

• Exercise 4.1 Class 12 Maths 2
• Exercise 4.2 Class 12 Maths 2
• Miscellaneous Exercise 4 Class 12 Maths 2
• Exercise 5.1 Class 12 Maths 2
• Miscellaneous Exercise 5 Class 12 Maths 2