Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Definite Integration Ex 4.2 Questions and Answers.
12th Maths Part 2 Definite Integration Exercise 4.2 Questions And Answers Maharashtra Board
I. Evaluate:
Question 1.
\(\int_{1}^{9} \frac{x+1}{\sqrt{x}} \cdot d x\)
Solution:

Question 2.
\(\int_{2}^{3} \frac{1}{x^{2}+5 x+6} \cdot d x\)
Solution:

Question 3.
\(\int_{0}^{\pi / 4} \cot ^{2} \cdot d x\)
Solution:

The integral does not exist since cot 0 is not defined.
![]()
Question 4.
\(\int_{-\pi / 4}^{\pi / 4} \frac{1}{1-\sin x} \cdot d x\)
Solution:


Question 5.
\(\int_{3}^{5} \frac{1}{\sqrt{2 x+3}-\sqrt{2 x-3}} \cdot d x\)
Solution:

Question 6.
\(\int_{0}^{1} \frac{x^{2}-2}{x^{2}+1} \cdot d x\)
Solution:


Question 7.
\(\int_{0}^{\pi / 4} \sin 4 x \sin 3 x \cdot d x\)
Solution:

![]()
Question 8.
\(\int_{0}^{\pi / 4} \sqrt{1+\sin 2 x} \cdot d x\)
Solution:
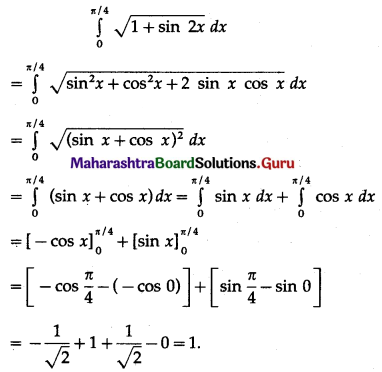
Question 9.
\(\int_{0}^{\pi / 4} \sin ^{4} x \cdot d x\)
Solution:

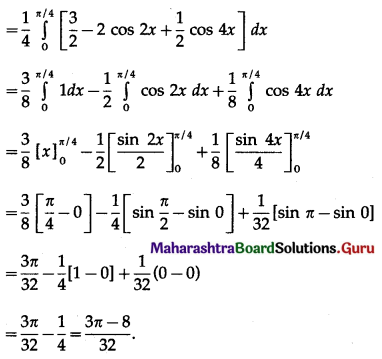
Question 10.
\(\int_{-4}^{2} \frac{1}{x^{2}+4 x+13} \cdot d x\)
Solution:

Question 11.
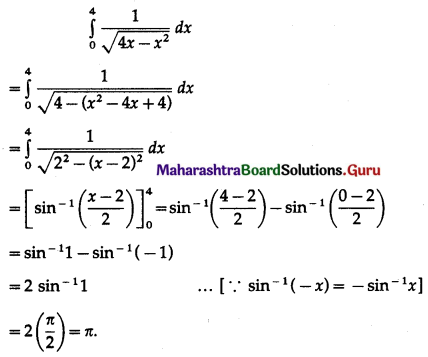
\(\int_{0}^{4} \frac{1}{\sqrt{4 x-x^{2}}} \cdot d x\)
Solution:
Question 12.
\(\int_{0}^{1} \frac{1}{\sqrt{3+2 x-x^{2}}} \cdot d x\)
Solution:

Question 13.
\(\int_{0}^{\pi / 2} x \cdot \sin x \cdot d x\)
Solution:
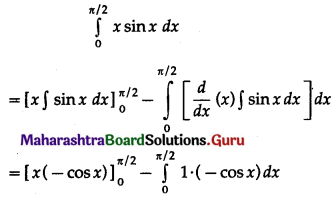
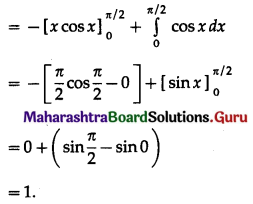
![]()
Question 14.
\(\int_{0}^{1} x \cdot \tan ^{-1} x \cdot d x\)
Solution:
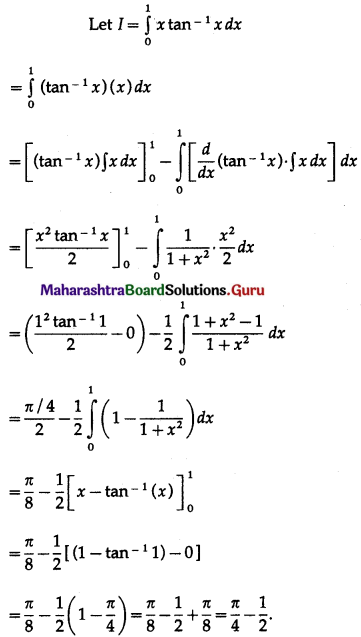
Question 15.
\(\int_{0}^{\infty} x \cdot e^{-x} \cdot d x\)
Solution:
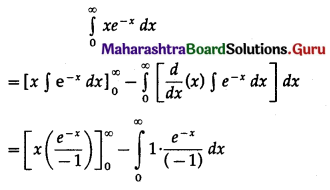
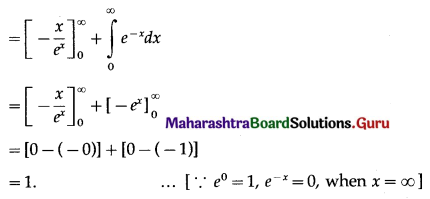
II. Evaluate:
Question 1.
\(\int_{0}^{\frac{1}{\sqrt{2}}} \frac{\sin ^{-1} x}{\left(1-x^{2}\right)^{\frac{3}{2}}} \cdot d x\)
Solution:


Question 2.
\(\int_{0}^{\pi / 4} \frac{\sec ^{2} x}{3 \tan ^{2} x+4 \tan x+1} \cdot d x\)
Solution:

![]()
Question 3.
\(\int_{0}^{4 \pi} \frac{\sin 2 x}{\sin ^{4} x+\cos ^{4} x} \cdot d x\)
Solution:

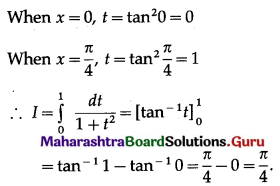
Question 4.
\(\int_{0}^{2 \pi} \sqrt{\cos x} \cdot \sin ^{3} x \cdot d x\)
Solution:

Question 5.
\(\int_{0}^{\pi / 2} \frac{1}{5+4 \cos x} \cdot d x\)
Solution:

Question 6.
\(\int_{0}^{\pi / 4} \frac{\cos x}{4-\sin ^{2} x} \cdot d x\)
Solution:

Question 7.
\(\int_{0}^{\pi / 2} \frac{\cos X}{(1+\sin x)(2+\sin x)} \cdot d x\)
Solution:

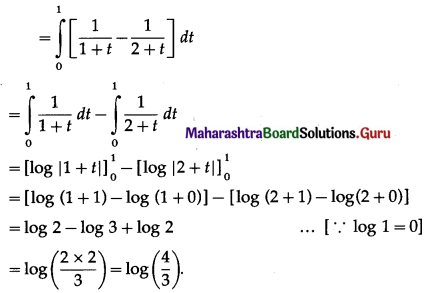
Question 8.
\(\int_{-1}^{1} \frac{1}{a^{2} e^{x}+b^{2} e^{-x}} \cdot d x\)
Solution:

![]()
Question 9.
\(\int_{0}^{\pi} \frac{1}{3+2 \sin x+\cos x} \cdot d x\)
Solution:
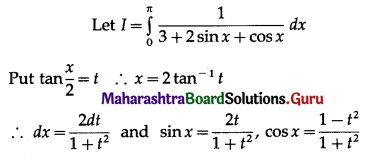

Question 10.
\(\int_{0}^{\pi / 4} \sec ^{4} x \cdot d x\)
Solution:

Question 11.
\(\int_{0}^{1} \sqrt{\frac{1-x}{1+x}} \cdot d x\)
Solution:


Question 12.
\(\int_{0}^{\pi} \sin ^{3} x(1+2 \cos x)(1+\cos x)^{2} \cdot d x\)
Solution:



Question 13.
\(\int_{0}^{\pi / 2} \sin 2 x \cdot \tan ^{-1}(\sin x) \cdot d x\)
Solution:


![]()
Question 14.
\(\int_{\frac{1}{\sqrt{2}}}^{1} \frac{\left(e^{\cos ^{-1} x}\right)\left(\sin ^{-1} x\right)}{\sqrt{1-x^{2}}} \cdot d x\)
Solution:



Question 15.
\(\int_{2}^{3} \frac{\cos (\log x)}{x} \cdot d x\)
Solution:

III. Evaluate:
Question 1.
\(\int_{0}^{a} \frac{1}{x+\sqrt{a^{2}-x^{2}}} \cdot d x\)
Solution:


![]()
Question 2.
\(\int_{0}^{\pi / 2} \log \tan x \cdot d x\)
Solution:
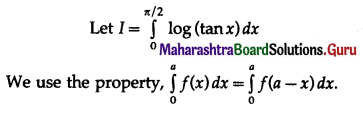

Question 3.
\(\int_{0}^{1} \log \left(\frac{1}{x}-1\right) \cdot d x\)
Solution:

Question 4.
\(\int_{0}^{\pi / 2} \frac{\sin x-\cos x}{1+\sin x \cdot \cos x} \cdot d x\)
Solution:

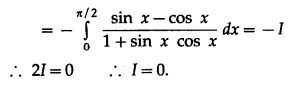
Question 5.
\(\int_{0}^{3} x^{2}(3-x)^{\frac{5}{2}} \cdot d x\)
Solution:

Question 6.
\(\int_{-3}^{3} \frac{x^{3}}{9-x^{2}} \cdot d x\)
Solution:
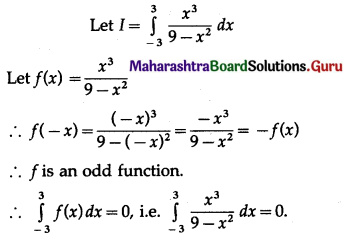
![]()
Question 7.
\(\int_{-\pi / 2}^{\pi / 2} \log \left(\frac{2+\sin x}{2-\sin x}\right) \cdot d x\)
Solution:
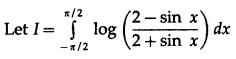

Question 8.
\(\int_{-\pi / 4}^{\pi / 4} \frac{x+\frac{\pi}{4}}{2-\cos 2 x} \cdot d x\)
Solution:



Question 9.
\(\int_{-\pi / 4}^{\pi / 4} x^{3} \cdot \sin ^{4} x \cdot d x\)
Solution:
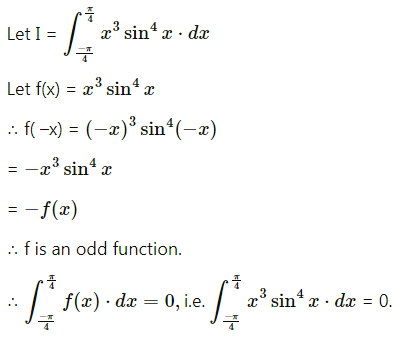
Question 10.
\(\int_{0}^{1} \frac{\log (x+1)}{x^{2}+1} \cdot d x\)
Solution:


![]()
Question 11.
\(\int_{-1}^{1} \frac{x^{3}+2}{\sqrt{x^{2}+4}} \cdot d x\)
Solution:

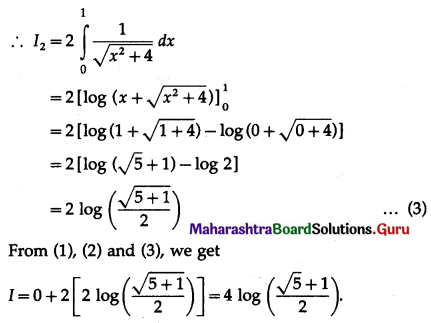
Question 12.
\(\int_{-a}^{a} \frac{x+x^{3}}{16-x^{2}} \cdot d x\)
Solution:
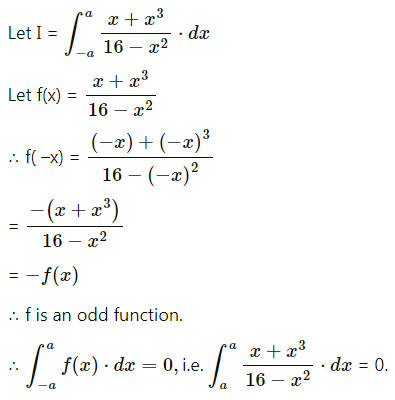
Question 13.
\(\int_{0}^{1} t^{2} \sqrt{1-t} \cdot d t\)
Solution:

Question 14.
\(\int_{0}^{\pi} x \cdot \sin x \cdot \cos ^{2} x \cdot d x\)
Solution:
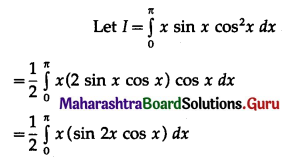


![]()
Question 15.
\(\int_{0}^{1} \frac{\log x}{\sqrt{1-x^{2}}} \cdot d x\)
Solution:




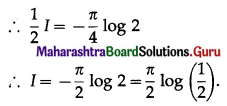
Class 12 Maharashtra State Board Maths Solution